Решение алгебраических и трансцендентных уравнений
Вы можете изучить и скачать доклад-презентацию на тему Решение алгебраических и трансцендентных уравнений. Презентация на заданную тему содержит 22 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!
Презентации» Математика» Решение алгебраических и трансцендентных уравнений
Слайды и текст этой презентации
Слайд 1
Описание слайда:
Решение алгебраических и трансцендентных уравнений
Слайд 2
Описание слайда:
Слайд 3
Описание слайда:
Слайд 4
Описание слайда:
Слайд 5
Описание слайда:
Слайд 6
Описание слайда:
Слайд 7
Описание слайда:
Слайд 8
Описание слайда:
Слайд 9
Описание слайда:
Слайд 10
Описание слайда:
Слайд 11
Описание слайда:
Слайд 12
Описание слайда:
Слайд 13
Описание слайда:
Слайд 14
Описание слайда:
Алгоритм данного метода:
Алгоритм данного метода:
1. Определить начальные данные (a, b, ).
2.Если нужная точность достигнута (| b — a | < ) то п.6
3.Найти середину очередного отрезка (c=(a+b)/2).
4.Если значения функции в точках а и c одного знака (f(a)*f(c)>0), то в качестве следующего отрезка взять правую половину (а=c), иначе левую (b=c).
5.Иди к п.2.
6.Напечатать ответ (( a + b ) / 2 )
Определить начальные данные (a, b, ).
2.Если нужная точность достигнута (| b — a | < ) то п.6
3.Найти середину очередного отрезка (c=(a+b)/2).
4.Если значения функции в точках а и c одного знака (f(a)*f(c)>0), то в качестве следующего отрезка взять правую половину (а=c), иначе левую (b=c).
5.Иди к п.2.
6.Напечатать ответ (( a + b ) / 2 )
Слайд 15
Описание слайда:
Методом половинного деления уточнить корень уравнения Методом половинного деления уточнить корень уравнения x4 + 2 x3 – x – 1 = 0 лежащий на отрезке 0, 1.
Слайд 16
Описание слайда:
Метод хорд Применяется в том случае, когда f'(X) и f»(X) не изменяют знака на отрезке [a,b], т.е. функция f(X) на отрезке [a,b] монотонна и не имеет точек перегиба
Слайд 17
Описание слайда:
Метод хорд
Слайд 18
Описание слайда:
Метод хорд
Слайд 19
Описание слайда:
Найти положительный корень уравнения (методом хорд)
x3 – 0,2 x2 – 0,2 х – 1,2 = 0
с точностью = 0,01.
Слайд 20
Описание слайда:
Метод Ньютона (касательной) В качестве исходной точки х0 выбирается тот конец интервала [а, b], которому отвечает ордината того же знака, что и знак f (х).
Слайд 21
Описание слайда:
Метод простой итерации f(х) = 0 x = ϕ(x).
Слайд 22
Описание слайда:
Решить уравнение x3 – x – 1 = 0, на интервале 1<x<2
Tags Решение алгебраических и трансцендентных уравнений
Похожие презентации
Ошибка! Введите корректный Email!
Рассеяние при низких и при высоких энергиях
Лекция 4.
 Рассеяние при низких и при высоких энергиях
Рассеяние при низких и при высоких энергиях§ 4.1. Рассеяние при низких энергиях. Длина рассеяния, обобщенная длина рассеяния, эффективный радиус взаимодействия
Разложение по парциальным волнам является и удобным способом
приближенного решения задачи рассеяния на сферически-симметричном
потенциале, и способом параметризации экспериментальных данных о
процессе рассеяния. Согласно соотношению (3.33), при малых энергиях
частиц вклад высших парциальных волн в амплитуду рассеяния быстро падает
с ростом ℓ. Если kd << 1, то достаточно знать лишь несколько первых фаз δℓ, а в пределе
k → 0 вообще лишь фазу s-волны δ0, чтобы хорошо
описать процесс рассеяния. На этом основан так называемый фазовый анализ
рассеяния, который, будучи модельно независимым способом параметризации
амплитуды рассеяния, широко применяется в разных областях физики. Как
видно из (3.25), (3.26), характерным признаком процесса рассеяния в условиях kd
<< 1 («длинноволновое
приближение») является малая (а в пределе k → 0 вообще исчезающая)
угловая анизотропия рассеяния.
Перейдем к описанию процесса рассеяния при предельно малых энергиях, когда достаточно ограничиться взаимодействием частицы с силовым центром в s-состоянии.
Из (3.33) следует, что при Е → 0 фаза s-волны δ0(k) пропорциональна импульсу частицы к. Соответствующий коэффициент пропорциональности является единственным параметром, через которые выражаются все характеристики процесса рассеяния при малых энергиях частицы. Определим длину рассеяния предельным соотношением
| (4.1) |
Подставляя (4.1) в (3.25), а также учитывая, что при k → 0 все фазы δℓ с ℓ ≠ 0 стремятся к нулю быстрее, чем δ0, получаем
| ƒ|E→0 = -a, | (4.2) |
т.е. длина рассеяния есть амплитуда рассеяния (с обратным знаком) в пределе нулевой энергии частицы. При этом
При этом
| σ|E→0 = 4πа2. | (4.3) |
Что говорят величина и знак длины рассеяния о характере взаимодействия частицы с силовым центром? Для ответа на этот вопрос рассмотрим, каков с точки зрения профиля волновой функции «геометрический» смысл длины рассеяния. Во внешней области (r > d) волновая функция, описывающая s-рассеяние частиц, имеет, согласно (3.41), вид
| u0(r) = rR0(r) = const · sin(kr + δ0), r > d ; | (4.4) |
при этом мы выразили сферическую функцию Бесселя и сферическую функцию Неймана через тригонометрические функции:
J0 = sinx/x,
n0 = cosx/x . | (4.5) |
Распространим вьфажение (4.4) и на внутреннюю область:
| v0(r) = const · sin(kr + δ0), г − любое. | (4.6) |
При k → 0 и малых r функция v0(r) − прямая линия:
| v0(r)|k→0 ≈ const · k(r − a). | (4.7) |
| Рис. 4.1. Профиль волновой функции и длина рассеяния частицы. |
Таким образом, значение длины рассеяния а − это координата точки, в которой пересекается с
осью абсцисс касательная к функции v0(r), если построить эту функцию при
к → 0 (точнее при выполнении двух условий: кг << 1 и |ка| << 1). Геометрический смысл длины рассеяния виден из рис. 4.1. Здесь показаны
три ситуации, возможные при сшивании внутренней и внешней волновых
функций по «границе» области взаимодействия. Случай А относится к
потенциалу отталкивания, случаи Б и В − к потенциалу притяжения; во всех
случаях d − средний радиус взаимодействия.
Геометрический смысл длины рассеяния виден из рис. 4.1. Здесь показаны
три ситуации, возможные при сшивании внутренней и внешней волновых
функций по «границе» области взаимодействия. Случай А относится к
потенциалу отталкивания, случаи Б и В − к потенциалу притяжения; во всех
случаях d − средний радиус взаимодействия.
В случае А и В длина рассеяния а положительна. Однако в случае
В случае Б длина рассеяния а отрицательна (фаза положительна). Из рисунка видно, что в этом случае волновая функция также «втягивается» в область взаимодействия, но значительно слабее, чем в случае В: поведение функций u0(r) и функции v0(r) во внутренней области не так сильно различается между собой в случае Б, как в случае В.
 Переход от одной
ситуации к другой легко понять, предположив, что, отправляясь от случая Б
мы постепенно увеличиваем амплитуду взаимодействия частицы с силовым
центром. При этом будет возрастать скорость осцилляции волновой функции
u
Переход от одной
ситуации к другой легко понять, предположив, что, отправляясь от случая Б
мы постепенно увеличиваем амплитуду взаимодействия частицы с силовым
центром. При этом будет возрастать скорость осцилляции волновой функции
uv0(r) изменится на противоположный (длина рассеяния а изменит знак): мы перешли к случаю В. Нетрудно предположить, что такой переход должен быть сопряжен с качественным изменением и каких-то других свойств системы.
Действительно, при переходе от ситуации Б к ситуации В в яме возникает связанное состояние частицы. Рассмотрим случай, когда энергия связи εb такого только что возникшего связанного состояния еще очень мала:
| εb << |V|, | (4. 8) 8) |
здесь V − средняя глубина взаимодействия. Пусть ub(r) = rRb(r) − волновая функция этого состояния. Её поведение во внешней области не зависит от характера потенциала:
| ub(r) ~ e-κr, r > d, | (4.9) |
где κ = (2μεb)1/2/ћ. Сравним волновую функцию ub(r) с волновой функцией u0(r), описывающей процесс рассеяния на том же потенциале при очень малых энергиях. Очевидно, что форма этих двух функций во внутренней области (r < d) при εb → 0 и k → 0 одна и та же. А это значит, что и логарифмические производные этих двух функций на границе внутренней и внешней областей также совпадают:
(u0‘/u0)|r=d = (ub‘/ub)|r=d . | (4.10) |
Подставляя сюда u0(r) из (4.4), a ub(r) из (4.9), получаем при к → 0
| k · ctg(δ0)|k→0 = -κ, | (4.11) |
или в соответствии с (4.1)
| (4.12) |
Итак, если в потенциальной яме имеется слабо связанное s-состояние,
длина рассеяния частицы такой ямы положительна, а её величина а
полностью определяется энергией связи частицы.
Приведенные выше рассуждения относительно перехода от ситуации Б к
ситуации В, изображенных на рис. 4.1, полезно продолжить. Проследим за
изменением профиля волновой функции u0(r) при дальнейшем увеличении
амплитуды взаимодействия (глубина ямы). Переход от случая В к случаю Г
сопровождается непрерывным уменьшением длины рассеяния. Далее (случай Д) длина рассеяния
попадает в интервал 0 < а < d. Это происходит одновременно с тем,
как нуль функции u0(r), который в случае Б −Г находится где-то справа от
d, перемещается во внутреннюю область. При дальнейшем увеличении
глубины ямы длина рассеяния проходит через нуль, и возникает ситуация,
сходная со случаем Б.
Далее (случай Д) длина рассеяния
попадает в интервал 0 < а < d. Это происходит одновременно с тем,
как нуль функции u0(r), который в случае Б −Г находится где-то справа от
d, перемещается во внутреннюю область. При дальнейшем увеличении
глубины ямы длина рассеяния проходит через нуль, и возникает ситуация,
сходная со случаем Б.
Таким образом, по мере непрерывного увеличения глубины ямы происходит
циклическое изменение параметра сшивания внутренней и внешней волновых
функций задачи рассеяния, а вместе с ними − и величины и знака длины
рассеяния. Завершению каждого «цикла» сопутствует появлению в яме нового
связанного состояния.
Рассмотренные выше случаи Б, В, Г, Д относились к потенциалу
притяжения, а случай А − к потенциалу отталкивания. Заметим, однако, что
поведение функции v0(r) во внешней области в случае Д сходно с тем, что
происходит в случае А (изменение знака всей функции, конечно,
несущественно). Другими словами, если в яме притяжения существует
связанное состояние, то может случиться, что при к → 0 s-волна
искажается (во внешней области) этой ямой так же, как потенциалом
отталкивания.
Пример: s-рассеяние на прямоугольной яме.
Задача s-рассеяния на прямоугольной яме − одна из немногих, когда
без численных расчетов удается получить точные результаты для фазы и
всех других характеристик рассеяния. Мы воспользуемся этим случаем,
чтобы проиллюстрировать общие выводы, сделанные выше.
Пусть V0 − глубина, a d − радиус прямоугольной ямы. Число связанных s-состояний Ns в такой яме определяется неравенством [1, с. 121]
| k0d/π − 1/2 < Ns < k0d/π + 1/2 , | (4.13) |
где
| k0 = (2μV0)1/2/ћ . | (4.14) |
Таким образом, первое связанное состояние появляется при k0d > π/2,
n-е − при k0d > (n − 1/2)π.
Фазу s-волны при рассеянной частице такой ямы легко получить из (3. 49):
49):
| (4.15) |
где, согласно (3.47), K = (2μ(V0 + E)/ћ2)1/2. Отсюда получаем для длины рассеяния
| (4.16) |
| Рис. 4.2. Длина рассеяния частицы прямоугольной ямой в зависимости от параметров ямы. |
На рис. 4.2 видны диапазоны изменения длины рассеяния а в разных интервалах величины Kd. Решая трансцендентное
уравнение
х − tgх = 0, получаем, что длина рассеяния обращается в нуль в
точках Kd = 0, 4.49, 7.76 и т.д. Слева от каждой из них на рисунке
обозначены интервалы величины Kd, где а заключено в пределах 0 < а
< d; здесь внешняя волновая функция такая же, как при рассеянии на
бесконечном отталкивающем потенциале. В точках Kr = π/2, 3π/2, 5π/2 и т.д. длина рассеяния меняется скачком от а =
−∞
до а = +∞. Из (4.13) видно, что как раз при переходе величины Kr, через
эти точки в яме возникают новые связанные состояния.
В точках Kr = π/2, 3π/2, 5π/2 и т.д. длина рассеяния меняется скачком от а =
−∞
до а = +∞. Из (4.13) видно, что как раз при переходе величины Kr, через
эти точки в яме возникают новые связанные состояния.
До сих пор мы интересовались лишь рассеянием в пределе k → 0, а формулой (4.15), справедливой при любом
k, воспользовались лишь как
вспомогательной. Теперь обратимся к описанию s-рассеяния при ненулевых,
хотя и малых, энергиях.
Введём понятие обобщённой длины рассеяния:
| 1/a(k) ≡ -k·ctgδ0(k). | (4.17) |
Очевидно, в пределе k → 0 обобщённая длина рассеяния a(k) превращается в длину рассеяния а. Представим правую часть выражения (4.17) в виде разложения по степеням k. Из соотношений (3.10) и (3.29) видно, что 1/a(k) − это четная функция k, поэтому ее разложение содержит только четные степени k. При малых k проходит следующая параметризация обобщённой длины рассеяния:
(4. 18) 18) |
где 0(k4) − член разложения высшего порядка, который мы отбросим.
Параметр r0 носит название эффективного радиуса потенциала
взаимодействия.
Таким образом, длина рассеяния а и эффективный радиус r0 являются
двумя независимыми параметрами, через которые можно выразить фазу s-волны во всей области малых энергий частицы. Это утверждение
справедливо для потенциала конечного радиуса, имеющего произвольную
форму. Отсюда следует, в частности, что если изучать экспериментально
рассеяние частицы потенциалом лишь при малых энергиях − в области
применимости разложения (4.18), то нельзя получить более детальную информацию о форме потенциала, чем ее может дать простейшая модель прямоугольной ямы.
ОПИСАНИЕ ДИНАМИКИ КОЛЕБАНИЯМИ МОСТОВОЙ КОНСТРУКЦИИ В СЛАБОЙ МЕРЕ
Каспийский университет, г. Алматы
Номер: 6-1
Год: 2016
Страницы: 149-154
Журнал: Актуальные проблемы гуманитарных и естественных наук
Скачать статью
Ключевые слова
активное демпфирование, управление надежностью, реактивная сила, управление надежностью мостов, active damping, control of reliability, reaction force, bridge reliable management
Просмотр статьи
⛔️ (обновите страницу, если статья не отобразилась)
Аннотация к статье
В работе предложен подход к описанию динамики колебаний пролетной части моста через взвешенные усредненные величины. Данное преобразование, несмотря на частичную потерю детализации информации о динамике конструкции позволяет получить новый класс уравнений для управления надежностью мостовой конструкции.
Данное преобразование, несмотря на частичную потерю детализации информации о динамике конструкции позволяет получить новый класс уравнений для управления надежностью мостовой конструкции.
Текст научной статьи
Введение В теоретических исследованиях динамики колебаний мостовых конструкций часто используются решения уравнения колебаний пролетной части, которое можно записать в виде: , (1) где:однородный оператор, профиль пролетной части в момент времени t, распределенная сила, приложенная к пролету. В распространенных случаях решения (1) отвечает общему для различных способов нахождения решения (1) критерию меры: (2) Здесь представляет определенное приближение решения, полученное на n-ом шаге построения решения. Мера, устанавливаемая (2) имеет смысл для любого способа построения решения (1). Соответственно число n может, например, выражать число сделанных итераций в численном расчете или выражать n-ю частную сумму ряда периодических функций в аналитическом подходе. Если в частном случае задача допускает аналитическое решение в виде явной функции, то тогда можно положить: n = 0 и (x,t). Критерием пригодности этих решений, вне зависимости от того, как они были получены, является условие (2), которое можно назвать сильной мерой для решения (1), поскольку данное выражение формально совпадает с метрикой равномерной (сильной) сходимости, когда функции находится в виде разложения по функциям базиса оператора . Решения в сильной мере для некоторых практических задач имеют избыточную информативность. Существуют инженерные приложения, в которых поточечная детализация функций не столь существенна, а избыточность данных усложняет картину процесса. Рассматриваемая задача относится к случаю, когда интегральные характеристики оказываются полезнее локальных величин, несмотря на утрату детальной информации. Постановка задачи Данная задача возникает в связи с предложением объединить устройство активного демпфирования моста [1], и систему мониторинга мостовой конструкции [2;3] в согласованно действующую цепочку безопасности сооружения. Система мониторинга, по результатам измерений в конечном числе точек, восстанавливает функциональный профиль пролетной части , совершающей колебания под действием нагрузки (рисунок 1).
Критерием пригодности этих решений, вне зависимости от того, как они были получены, является условие (2), которое можно назвать сильной мерой для решения (1), поскольку данное выражение формально совпадает с метрикой равномерной (сильной) сходимости, когда функции находится в виде разложения по функциям базиса оператора . Решения в сильной мере для некоторых практических задач имеют избыточную информативность. Существуют инженерные приложения, в которых поточечная детализация функций не столь существенна, а избыточность данных усложняет картину процесса. Рассматриваемая задача относится к случаю, когда интегральные характеристики оказываются полезнее локальных величин, несмотря на утрату детальной информации. Постановка задачи Данная задача возникает в связи с предложением объединить устройство активного демпфирования моста [1], и систему мониторинга мостовой конструкции [2;3] в согласованно действующую цепочку безопасности сооружения. Система мониторинга, по результатам измерений в конечном числе точек, восстанавливает функциональный профиль пролетной части , совершающей колебания под действием нагрузки (рисунок 1). Устройство гашения колебаний воздействует на пролетную часть через реактивную силу, которая в общем случае зависит от отклонения точки контакта пролета с подвижным штоком устройства. В отличие от традиционной работы демпферов, реактивная сила в данном случае определяется не локальным поведением пролетной части в точке крепления демпфера, а вырабатывается алгоритмом, учитывающим полный профиль колебания пролетной части и механическое состояние критических узлов конструкции. Информация о профиле поставляется системой мониторинга и играет в данной случае роль сигнала обратной связи. Данные мониторинга используются для формирования функции реактивной силы — закона сопротивления демпфера его отклонению от положения равновесия и, возможно, от скорости движения штока. Таким образом, создается открытая колебательная система с контурами, образованными пролетной частью моста с вынуждающей силой и активным демпфером с реактивной силой под управлением обратной связи. Рис. 1. Балочная модель моста под внешней нагрузкой.
Устройство гашения колебаний воздействует на пролетную часть через реактивную силу, которая в общем случае зависит от отклонения точки контакта пролета с подвижным штоком устройства. В отличие от традиционной работы демпферов, реактивная сила в данном случае определяется не локальным поведением пролетной части в точке крепления демпфера, а вырабатывается алгоритмом, учитывающим полный профиль колебания пролетной части и механическое состояние критических узлов конструкции. Информация о профиле поставляется системой мониторинга и играет в данной случае роль сигнала обратной связи. Данные мониторинга используются для формирования функции реактивной силы — закона сопротивления демпфера его отклонению от положения равновесия и, возможно, от скорости движения штока. Таким образом, создается открытая колебательная система с контурами, образованными пролетной частью моста с вынуждающей силой и активным демпфером с реактивной силой под управлением обратной связи. Рис. 1. Балочная модель моста под внешней нагрузкой.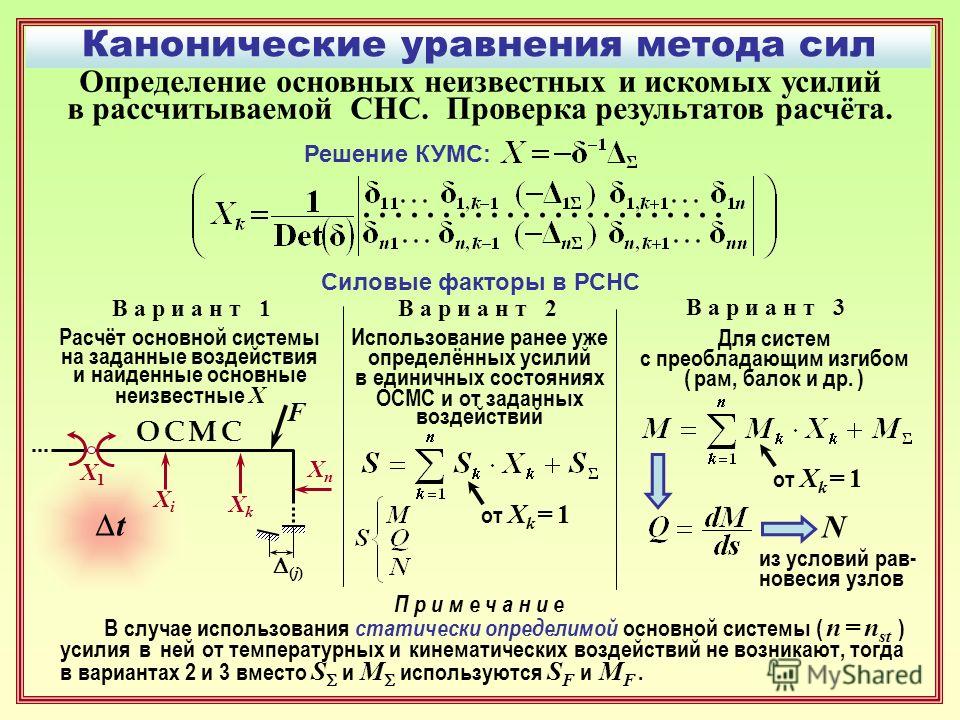 Шток демпфера соединяется с пролетной частью моста в точке подвеса (рисунок 2). Движения штока задает отклонение точки подвеса от положения равновесия — . Масса зоны подвеса — m. Рис.2. Соединение активного демпфера с пролетной частью Динамика балочного моста будет описываться в модели колебаний упругой неразрезной балки [4]. Пролетная часть моста длины , поддерживаемая опорами, описывается системой из N уравнений движения отдельных пролетов, имеющих длины () и одинаковые для всех пролетов значения постоянных параметров . (3) Граничные условия на торцевых устоях соответствуют свободно вращающемуся шарнирному соединению: Полный профиль пролетной части — получается путем сращивания на стыке пролетов при условии непрерывности . Можно выделить часть пролета, непосредственно контактирующую с оголовком опоры, например, отложив малые отрезки балки длиной отложенные в обе стороны от оголовка опоры. Если вместо опоры установлен шток демпфирующего устройства, то сегмент длиной и массой в расчетах можно принять за часть механизма подвеса штока демпфирующего устройства (см.
Шток демпфера соединяется с пролетной частью моста в точке подвеса (рисунок 2). Движения штока задает отклонение точки подвеса от положения равновесия — . Масса зоны подвеса — m. Рис.2. Соединение активного демпфера с пролетной частью Динамика балочного моста будет описываться в модели колебаний упругой неразрезной балки [4]. Пролетная часть моста длины , поддерживаемая опорами, описывается системой из N уравнений движения отдельных пролетов, имеющих длины () и одинаковые для всех пролетов значения постоянных параметров . (3) Граничные условия на торцевых устоях соответствуют свободно вращающемуся шарнирному соединению: Полный профиль пролетной части — получается путем сращивания на стыке пролетов при условии непрерывности . Можно выделить часть пролета, непосредственно контактирующую с оголовком опоры, например, отложив малые отрезки балки длиной отложенные в обе стороны от оголовка опоры. Если вместо опоры установлен шток демпфирующего устройства, то сегмент длиной и массой в расчетах можно принять за часть механизма подвеса штока демпфирующего устройства (см. рисунок 2). Граничные условия на опорах дополняютcя условиями сопряжения смежных пролетов: (4) Для дальнейшего можно ограничиться случаем двух опорного моста с демпфером на опоре, поскольку количество рассматриваемых опор не принципиально для данного рассмотрения. Целесообразно ввести координаты для каждого пролета: (5) которые удобны тем, что: в данных координатах область любого пролета изменяется в пределах ; координата концов балки равны нулю для обоих торцов пролетной части; координата точки повеса демпфера в каждом пролете равна единице. Тогда условие сопряжения пролетов будет: (6) где , масса штока вместе с зоной подвеса демпфера. В пределе малого масса стремиться к конечному пределу, а третья производная — терпит разрыв, создавая наряду с весом зоны подвеса нагружающее усилие на оголовок опоры. Запишем отклонение точек пролета в виде суммы относительного и переносного движений (см. рисунок 3): (7) Подставим (7) в (6) и (3), тогда с учетом наличия реактивной силы демпфера, уравнения колебаний при составят систему: (8а) (8b) Рис.
рисунок 2). Граничные условия на опорах дополняютcя условиями сопряжения смежных пролетов: (4) Для дальнейшего можно ограничиться случаем двух опорного моста с демпфером на опоре, поскольку количество рассматриваемых опор не принципиально для данного рассмотрения. Целесообразно ввести координаты для каждого пролета: (5) которые удобны тем, что: в данных координатах область любого пролета изменяется в пределах ; координата концов балки равны нулю для обоих торцов пролетной части; координата точки повеса демпфера в каждом пролете равна единице. Тогда условие сопряжения пролетов будет: (6) где , масса штока вместе с зоной подвеса демпфера. В пределе малого масса стремиться к конечному пределу, а третья производная — терпит разрыв, создавая наряду с весом зоны подвеса нагружающее усилие на оголовок опоры. Запишем отклонение точек пролета в виде суммы относительного и переносного движений (см. рисунок 3): (7) Подставим (7) в (6) и (3), тогда с учетом наличия реактивной силы демпфера, уравнения колебаний при составят систему: (8а) (8b) Рис.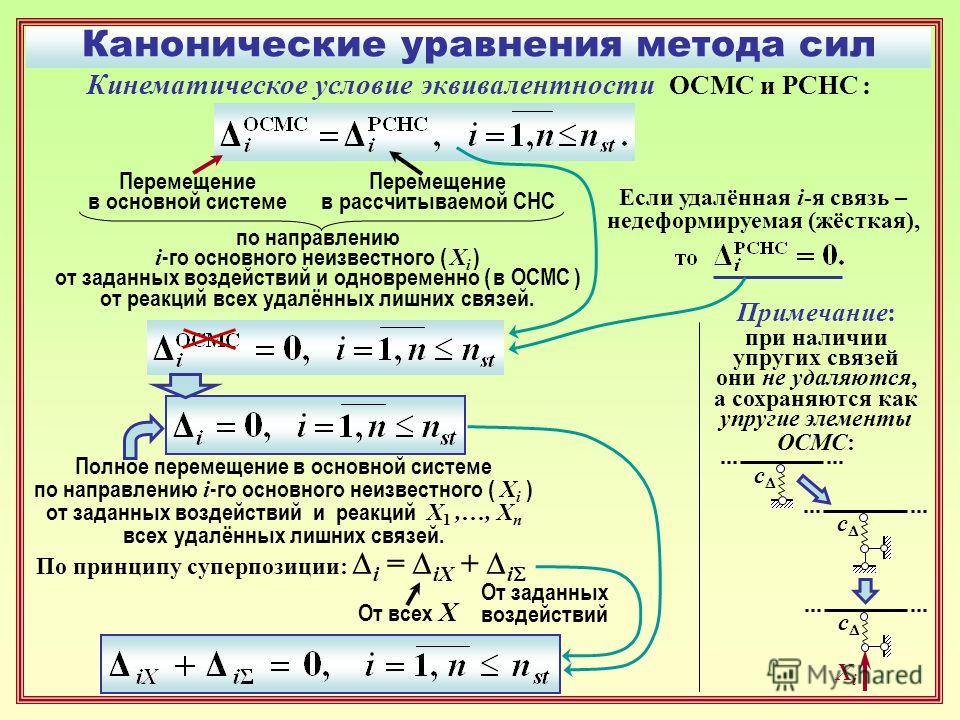 3. Иллюстрация к задаче Система мониторинга мостовой конструкции [2] восстанавливает профиль по данным измерений. Эта информация используется активным демпфером, который может воздействовать на вид или параметры функции реактивной силы под управлением сигнала обратной связи. Данная постановка относится к обратным задачам динамики мостовой конструкции и рассматривается в системе взаимодействующих открытых колебательных контуров, охваченных обратной связью. Основная задача в таком подходе состоит в определении алгоритма управления видом и параметрами реактивной силы, нивелирующей вредные для конструкции колебания пролетной части. Описание в слабой мере Система мониторинга восстанавливает приближенный профиль пролетной части, проводя измерения через определенные промежутки времени. Движение пролетной части обладает бесконечным набором восстановленных профилей, многие из которых мало отличаются друг от друга, но считаются разными в сильной мере (2). В этом случае, каждому возбужденному колебанию, которое может почти не отличаться от нормальной моды должен ставиться в соответствие определенный закон управления демпфером — функции реактивной силы .
3. Иллюстрация к задаче Система мониторинга мостовой конструкции [2] восстанавливает профиль по данным измерений. Эта информация используется активным демпфером, который может воздействовать на вид или параметры функции реактивной силы под управлением сигнала обратной связи. Данная постановка относится к обратным задачам динамики мостовой конструкции и рассматривается в системе взаимодействующих открытых колебательных контуров, охваченных обратной связью. Основная задача в таком подходе состоит в определении алгоритма управления видом и параметрами реактивной силы, нивелирующей вредные для конструкции колебания пролетной части. Описание в слабой мере Система мониторинга восстанавливает приближенный профиль пролетной части, проводя измерения через определенные промежутки времени. Движение пролетной части обладает бесконечным набором восстановленных профилей, многие из которых мало отличаются друг от друга, но считаются разными в сильной мере (2). В этом случае, каждому возбужденному колебанию, которое может почти не отличаться от нормальной моды должен ставиться в соответствие определенный закон управления демпфером — функции реактивной силы . Указанный путь мало приемлем для практики, поскольку предполагает непрерывное видоизменение функции реактивной силы вслед за любым малым изменение возмущения. Реальное устройство управления демпфированием не способно реализовать такое количество видов и параметров воздействия. Кроме того, форма индивидуального алгоритма управления демпфированием, может существенно отличаться даже для двух близких колебаний. Желательно, чтобы управление колебаниями свелось к конечному числу модификаций функции , что необходимо инженерным реализациям и, при этом система управления включалась бы только при опасных проявлениях. Другими словами, система управления должна оперировать не с отдельными функциями профиля колебаний пролетной части, а в целом выделять подмножество функций, несущих потенциальную угрозу. С этой целью можно ввести дополнительную стадию обработки сигнала обратной связи, на которой ценой потери локальной информации первичные профили колебаний преобразуются в некоторое обобщенное представление, сохраняющее признаки опасной ситуации.
Указанный путь мало приемлем для практики, поскольку предполагает непрерывное видоизменение функции реактивной силы вслед за любым малым изменение возмущения. Реальное устройство управления демпфированием не способно реализовать такое количество видов и параметров воздействия. Кроме того, форма индивидуального алгоритма управления демпфированием, может существенно отличаться даже для двух близких колебаний. Желательно, чтобы управление колебаниями свелось к конечному числу модификаций функции , что необходимо инженерным реализациям и, при этом система управления включалась бы только при опасных проявлениях. Другими словами, система управления должна оперировать не с отдельными функциями профиля колебаний пролетной части, а в целом выделять подмножество функций, несущих потенциальную угрозу. С этой целью можно ввести дополнительную стадию обработки сигнала обратной связи, на которой ценой потери локальной информации первичные профили колебаний преобразуются в некоторое обобщенное представление, сохраняющее признаки опасной ситуации. Пусть некоторая, пока неопределенная произвольная функция. Выполним с (8a) следующее преобразование (9) Первый интеграл в (9) после последовательного интегрирования по частям приводится к виду: (10) С учетом граничных условий: (11) и дополнительных условий, которыми можно ограничить выбор подходящей функции : (12) интеграл (9) приводится к виду: (13) Потребуем теперь, чтобы функция p(x) в () удовлетворяла дифференциальному уравнению: (14) при условиях (12). Такая функция существует и равна: (15) где корень трансцендентного уравнения: (16) Решение (14) в силу (15) является единственной собственной функцией (1) при условиях данной задачи (11). Исходя из полученного соотношения: (17) образуем функцию слабой меры : Введем обозначения для новых параметров и образов исходных функций: (18) (19) Тогда образом системы (8) , будет служить: (20a) (20b) (20c) Исключая третьи производные из системы (20) и вводя обозначения: , (21) , (22) (23) получаем уравнение управления демпфированием колебаний пролетной части в виде: (24) где: — постоянный параметр, определяемый конструкцией пролетной части и механизмом демпфера.
Пусть некоторая, пока неопределенная произвольная функция. Выполним с (8a) следующее преобразование (9) Первый интеграл в (9) после последовательного интегрирования по частям приводится к виду: (10) С учетом граничных условий: (11) и дополнительных условий, которыми можно ограничить выбор подходящей функции : (12) интеграл (9) приводится к виду: (13) Потребуем теперь, чтобы функция p(x) в () удовлетворяла дифференциальному уравнению: (14) при условиях (12). Такая функция существует и равна: (15) где корень трансцендентного уравнения: (16) Решение (14) в силу (15) является единственной собственной функцией (1) при условиях данной задачи (11). Исходя из полученного соотношения: (17) образуем функцию слабой меры : Введем обозначения для новых параметров и образов исходных функций: (18) (19) Тогда образом системы (8) , будет служить: (20a) (20b) (20c) Исключая третьи производные из системы (20) и вводя обозначения: , (21) , (22) (23) получаем уравнение управления демпфированием колебаний пролетной части в виде: (24) где: — постоянный параметр, определяемый конструкцией пролетной части и механизмом демпфера. Система обыкновенных дифференциальных уравнений (21-23) описывает динамику обратной задачи в интегральных величинах, вместо системы уравнений в частных производных (8) для локальных функций прямой задачи. Величины и определяются информацией измеренной системой мониторинга и образованы из функций времени — образами профиля пролетной части в слабой мере под действием преобразования (9). Сам профиль восстанавливается по совокупности данных в конечном множестве точек измерения. Данная операция сглаживает локальные отличия, как ошибок восстановления, так и в амплитудах различающихся мод и представляет собой унифицированное описание колебаний, когда частью характеристик процесса можно пренебречь. Таким образом, величины являются входящими условиями обратной задачи. В общем случае данная обратная задача не имеет единственного решения в силу не замкнутости используемой системы уравнений. По этой причине можно искать ее решение, обычным в инженерной практике путем моделирования реакции демпфера на заданные возмущения.
Система обыкновенных дифференциальных уравнений (21-23) описывает динамику обратной задачи в интегральных величинах, вместо системы уравнений в частных производных (8) для локальных функций прямой задачи. Величины и определяются информацией измеренной системой мониторинга и образованы из функций времени — образами профиля пролетной части в слабой мере под действием преобразования (9). Сам профиль восстанавливается по совокупности данных в конечном множестве точек измерения. Данная операция сглаживает локальные отличия, как ошибок восстановления, так и в амплитудах различающихся мод и представляет собой унифицированное описание колебаний, когда частью характеристик процесса можно пренебречь. Таким образом, величины являются входящими условиями обратной задачи. В общем случае данная обратная задача не имеет единственного решения в силу не замкнутости используемой системы уравнений. По этой причине можно искать ее решение, обычным в инженерной практике путем моделирования реакции демпфера на заданные возмущения. Это означает, что в численных экспериментах будет варьируемой функцией, а вид и параметры реактивной силы будут искомыми величинами в модели, описываемой уравнением: (25) Наиболее технически доступный случай реализации управляемой реактивной силы выражается функцией вида: (26) Диапазон изменения параметров определяется конструкцией устройства демпфирования, алгоритм управления параметрами рассчитывается по модели (24), тогда: (27) Задача моделирования заключается в подборе параметров устройства, которые с одной стороны лежат в технически и экономически доступном диапазоне, с другой стороны, обеспечивают гашение вредных воздействий, задаваемых функцией . Результаты и анализ моделирования будут приведены в последующей работе.
Это означает, что в численных экспериментах будет варьируемой функцией, а вид и параметры реактивной силы будут искомыми величинами в модели, описываемой уравнением: (25) Наиболее технически доступный случай реализации управляемой реактивной силы выражается функцией вида: (26) Диапазон изменения параметров определяется конструкцией устройства демпфирования, алгоритм управления параметрами рассчитывается по модели (24), тогда: (27) Задача моделирования заключается в подборе параметров устройства, которые с одной стороны лежат в технически и экономически доступном диапазоне, с другой стороны, обеспечивают гашение вредных воздействий, задаваемых функцией . Результаты и анализ моделирования будут приведены в последующей работе.
Энциклопедия элементарной математики. Книга 3 (функции и пределы, основы анализа)
Павел Сергеевич Александров, Алексей Иванович Маркушевич, Александр Яковлевич Хинчин
М.-Л., ГТТИ, 1952. 559 с.
Тираж 50000 экз.
| |||||||||||
Книга посвящена вопросам анализа, а именно, функциям и пределам. Наряду с учением об элементарных функциях и обстоятельно изложенной теорией пределов, сюда вошли также наиболее элементарные сведения из дифференциального и интегрального исчисления, теории рядов и сведения о функциях комплексного переменного.
Содержание
Предисловие.
Элементарные функции действительного переменного. Пределы последовательностей и функций. Общее понятие функции.
(В.Л.Гончаров)
Глава I. Общие сведения об элементарных функциях и графиках уравнений.
§ 1. Элементарные функции.
§ 2. Графические представления. Приёмы точечных построений.
§ 3. Простейшие преобразования графиков.
§ 4. Прямая и обратная функции.
§ 5. Элементарное исследование функций (постановка вопроса и некоторые общие приёмы).
Глава II. Обзор элементарных функций и их графиков.
§ 6. Классификация рациональных функций.
§ 7. Целые положительные степени.
§ 8. Многочлены первой степени (линейные функции).
§ 9. Многочлены (трёхчлены) второй степени.
§ 10. Многочлены третьей степени.
§ 11. Биквадратные многочлены.
§ 12. Многочлены высших степеней.
§ 13. Целые отрицательные степени.
§ 14. Дробные линейные функции.
§ 15. Дробные функции второй степени.
§ 16. Дробные рациональные функции (общий случай).
§ 17. Алгебраические иррациональные функции.
Алгебраические иррациональные функции.
§ 18. Примеры исследования алгебраических функций.
§ 19. Элементарные трансцендентные функции.
§ 20. Показательная функция.
§ 21. Функции, связанные с показательной.
§ 22. Логарифмическая функция.
§ 23. Функции, связанные с логарифмической.
§ 24. Произвольная степенная функция.
§ 25. Основные (целые) тригонометрические функции: синус и косинус.
§ 26. Простые гармонические колебания.
§ 27. Тригонометрические многочлены.
§ 28. Многочлены Чебышева.
§ 29. Тангенс и другие дробные тригонометрические функции.
§ 30. Представление функций, рационально зависящих от тригонометрических, через одну или две из них.
§ 31. Примеры исследования функций, рационально зависящих от тригонометрических. Тригонометрические уравнения.
§ 32. Обратные тригонометрические функции.
Обратные тригонометрические функции.
§ 33. Исследование многочленов Чебышева. Их минимальное свойство.
Глава III. Пределы числовых последовательностей и пределы функций.
§ 34. Конечные и бесконечные числовые последовательности.
§ 35. Общее определение бесконечной числовой последовательности.
§ 36. Теорема Больцано-Вейерштрасса о существовании предельной точки.
§ 37. Примеры. Предел как единственная предельная точка.
§ 38. Предел последовательности; классическое определение и основные свойства.
§ 39. Обобщение понятия предела (пределы в «несобственном смысле»).
§ 40. Предел функции на бесконечности.
§ 41. Односторонний предел функции в конечной точке.
§ 42. Двусторонний предел. Понятие непрерывности.
§ 43. Примеры непрерывных функций.
§ 44. Пределы при монотонном изменении. Число e.
Глава IV. Пределы последовательностей функций. Свойства непрерывных функций.
§ 45. Простая сходимость.
§ 46. Общее понятие функции одной действительной переменной.
§ 47. Свойства непрерывных функций.
§ 48. Равномерная сходимость последовательности непрерывных функций.
§ 49. Теорема Вейерштрасса-Бернштейна о приближении непрерывной функции с помощью рациональных многочленов.
§ 50. Доказательство теоремы.
§ 51. Определение показательной функции. Продолжение непрерывной функции за пределы всюду плотного множества.
§ 52. Теорема Больцано и проблема существования однозначной обратной функции.
§ 53. Функциональные уравнения и элементарные функции.
Глава V. Общее понятие функции.
§ 54. Соответствие между множествами.
§ 55. Геометрические образы в многомерных пространствах.
§ 56. Пространственные отображения.
Пространственные отображения.
§ 57. Метрические пространства.
§ 58. Понятие предела в метрическом пространстве.
§ 59. Топологические пространства.
§ 60. Алгебра множеств. Производное множество. Замкнутость и связность.
§ 61. Непрерывные отображения и их свойства.
§ 62. Гомеоморфные отображения.
§ 63. Верхняя и нижняя границы числовых множеств или последовательностей. Верхний и нижний пределы числовых множеств или последовательностей.
Производные, интегралы и ряды.
(И.П.Натансон)
Введение.
Глава I. Производные.
§ 1. Производная и дифференциал.
1. Задачи, приводящие к понятию производной.
2. Определение производной.
3. Дифференцируемость и непрерывность. Односторонние производные.
4. Производные простейших элементарных функций.
5. Дифференцирование обратных функций.
6. Правила комбинирования формул дифференцирования.
7. Дифференциал.
8. Производные и дифференциалы высшего порядка.
9. Частные производные и полный дифференциал.
§ 2. Важнейшие теоремы о производных.
10. Теоремы Ферма и Ролля.
11. Формулы Лагранжа и Коши. Правило Лопиталя.
12. Формула Тейлора.
13. Исследования П.Л.Чебышева и С.Н.Бернштейна.
§ 3. Применение дифференциального исчисления к исследованию функций.
14. Признаки постоянства и монотонности функции.
15. Экстремум функции.
16. Нахождение наибольшего и наименьшего значений функции на замкнутом промежутке.
Глава II. Интегралы.
§ 4. Неопределенные интегралы.
17. Основные понятия.
Основные понятия.
18. Интегрирование с помощью подстановки.
19. Интегрирование по частям.
20. Общие замечания по поводу интегрирования элементарных функций.
§ 5. Определённые интегралы.
21. Задачи, приводящие к понятию определённого интеграла.
22. Определённый интеграл.
23. Основные свойства интеграла.
24. Интеграл, как функция верхнего предела.
25. Вычисление определённого интеграла с помощью неопределённого.
26. Формула Валлиса.
27. Приближённое вычисление определённых интегралов.
§ 6. Приложения интегрального исчисления.
28. Вычисление площадей.
29. Вычисление объёмов.
30. Длина дуги кривой.
31. Площадь поверхности вращения.
32. Общие указания по поводу приложений интегрального исчисления и его связей с дифференциальным исчислением.
Глава III. Ряды.
§ 7. Ряды с постоянными членами.
33. Основные понятия.
34. Простейшие свойства рядов.
35. Положительные ряды.
36. Знакочередующиеся ряды.
37. Абсолютная сходимость.
38. Вопрос о перестановке членов ряда. Умножение рядов.
§ 8. Степенные ряды.
39. Промежуток сходимости.
40. Свойства суммы степенного ряда.
41. Разложение логарифма и составление таблиц логарифмов.
42. Разложение арктангенса и вычисление π.
43. Общие замечания по поводу разложения функций в степенные ряды.
44. Биномиальный ряд.
45. Очерк аналитической теории тригонометрических функций.
Элементарные функции комплексного переменного.
(В.Л.Гончаров)
§ 1. Рациональные функции.
Рациональные функции.
§ 2. Пределы. Ряды.
§ 3. Показательная функция. Синус и косинус.
§ 4. Выражение тригонометрических функций через показательную.
§ 5. Гиперболические и тригонометрические функции.
§ 6. Логарифм.
§ 7. Произвольная степень.
§ 8. Обратные тригонометрические и гиперболические функции.
§ 9. Производная.
§ 10. Интеграл.
§ 11. Приближение функций многочленами.
§ 12. Первообразная функция.
§ 13. Интеграл Коши.
§ 14. Понятие аналитической функции.
§ 15. Свойства аналитических функций.
§ 16. Геометрический смысл аналитических функций.
§ 17. Примеры конформных отображений.
Алфавитный указатель.
Список литературы
- Книга 1. Арифметика. (1951, 448 с.)
- Книга 2.
 Алгебра. (1951, 424 с.)
Алгебра. (1951, 424 с.)
- Книга 3. Функции и пределы, основы анализа. (1952, 559 с.)
- Книга 4. Геометрия. (1963, 568 с.)
- Книга 5. Геометрия. (1966, 624 с.)
| |||||||||||
Постоянный адрес этой страницы: http://math.ru/lib/59
80я Международная научная конференция ЕНО
80я Международная научная конференция Евразийского Научного Объединения (октябрь 2021)
Развитие науки и образования в условиях мировой нестабильности // Сборник научных работ 80й Международной научной конференции Евразийского Научного Объединения (г. Москва, октябрь 2021). — Москва : ЕНО, 2021. — 382 с.
Москва, октябрь 2021). — Москва : ЕНО, 2021. — 382 с.
80 International Scientific Conference of Eurasian Scientific Association (October 2021)
Development of science and education in the context of global instability // Scientific articles collection of the 80 International Scientific Conference of Eurasian Scientific Association (Moscow, October 2021). — Moscow : ESA, 2021. — 382 pp.
Часть 1 (стр. 1 — 88)
Часть 2 (стр. 89 — 166)
Часть 3 (стр. 167 — 246)
Часть 4 (стр. 247 — 312)
Часть 5 (стр. 313 — 382)
Статьи на elibrary.ru (+РИНЦ):
Часть 1
Часть 2
Часть 3
Часть 4
Часть 5
Физико-математические науки
Приближение индикатора ADX классическими и модифицированными sinc-аппроксимациями и исследование погрешностей, Агапов К.А.
Асимптотическое поведение решений сингулярно возмущенных уравнений с точками перевала, Алыбаев К. С., Матанов Ш.М.
С., Матанов Ш.М.
Экспериментальные доказательства неверности изучаемой в учебниках физики версии специальной теории относительности и истинности альтернативной её версии, Антонов А.А.
Простейшая математическая модель образования фибрина в аневризмах кровеносных капилляров, Волосова Н.К., Басараб М.А., Волосов К.А., Волосова А.К., Пастухов Д.Ф., Пастухов Ю.Ф.
О разрешимости второй начально-краевой задачи для нелинейного обобщенного уравнения Буссинеска, Дурмонбаева З.А.
Граничная обратная задача с интегральным переопределением для псевдопараболического уравнения, Муканбетова А.Т.
Разрешимость трансцендентного уравнения с квазиполиномиальной правой частью, Нуятов А.А., Бельмесова С.С.
Поиск наилучшего приближения в метрике квадратичного отклонения ступенчатыми функциями для обратной функции плотности распределения Коши. (Определение уровней восстановления для плотности распределения Коши), Пастухов Ю.Ф., Волосова Н.К., Волосов К.А., Волосова А.К., Пастухов Д. Ф., Пастухов А.Ю., Карлов М.И.
Ф., Пастухов А.Ю., Карлов М.И.
Зависимость показателя преломления от оптической среды и диаметра фотонов, Раимкулов М.Н.
Физический Барьер и тупик мышления, Федоров Ю.А.
Анизотропия толщин поверхностного слоя и энергии связи поверхности щелочноземельных элементов, Юров В.М., Портнов В.С.
Технические науки
Construction of a mathematical model of a basic electrical circuit, taking into account its configuration, Amirov M.M., Tastanbekova B.U., Kolboev B.R., Nazarova A.S., Nyshanbaeva K.U.
Инновациялық мультимедия технологияны пайдалану тиімділігі, Амиров М.М., Бекназарова Р.К., Жайлаубаев Н.М.
Ақпараттық жүйелерді құру принциптері, Амиров М.М., Тастанбекова Б.О., Сейтханова А.Б.
Исследование динамики изменения скорости течения жидкого масла по продольному сечению круглой трубы, Бабаев Д.Д., Белый В.С.
Современные проблемы в области менеджмента землеустроительных и кадастровых работ, Бурнашов А.С., Борисов Е.А.
К вопросу эффективности технологии гидроизоляции «белая ванна», Гонтарь М. А.
А.
Разработка устройства для сушки зерна и анализ результатов лабораторного исследования, Данилов Д.Ю.
Выбор солнечной панели для жилого дома, Каплина Т.Ю.
Автоматизация обработки строительных смет, Пальмов С.В., Кравчина А.В.
Описание алгоритма проведения экспериментальных исследований по идентификации параметров математической модели импульсной системы преобразования энергии, Слегтина В.А.
Реализация алгоритма удержания позиции квадрокоптером в воздухе на основе фильтра Маджвика, Тукмачева Ю.А.
Исследование теплообмена при изготовлении ролика с упрочненным внешним слоем в процессе плазменной наплавки, Шестаков Н.И., Журавлева Ю.М., Никонова Е.Л., Петрова Г.М., Шестакова Е.А., Антонова Ю.В.
Применение спутниковой навигационной аппаратуры для обеспечения радиорелейной связи в движении, Якушенко С.А., Снежко В.К., Веркин С.С., Егрушев В.Е., Антонов В.В., Чеканова Е.В.
Медицинские науки
Epidemiology of dengue in Rajasthan, Mamatkulova N. M., Abdimomunova B.T., Gora R., Moldoev M.I.
M., Abdimomunova B.T., Gora R., Moldoev M.I.
Оценка эффективности нескольких типов формул для расчета мощности интраокулярной линзы в российской офтальмологической практике, Альноелати Альмасри M.A., Стебнев B.C.
Анализ причин осложнений при брюшном тифе в настоящее время, Закирова Ж.С., Жолдошев С.Т., Абдимомунова Б.Т.
Альтернатива в лечении молочных зубов с диагнозом необратимый пульпит, Кругом С.В.
Осложнения сахарного диабета у жителей мегаполиса, Максумова Н.В., Фаттахов В.В.
Вклад В.Эйнтховена в развитие электрокардиографии, Маммаева Ж.Б., Маммаева Н.Б., Вязовцева В.В.
Опасность злокачественной опухоли желудка, Маммаева Ж.Б., Маммаева Н.Б., Вязовцева В.В.
Болезнь века — атеросклероз, Маммаева Ж.Б., Маммаева Н.Б., Вязовцева В.В.
Слюна как биологический маркер заболеваний, Милехина С.А., Румянцева М.П., Поендаева А.А.
COVID-19: четыре возможных сценария развития пандемии, Реутов В.П.
Ветеринарные науки
Подбор и синтез праймеров для наработки генов, кодирующих протективные белки M. bovis, Абитаев Р.Т., Шораева К.А., Нурпейсова А.С., Сырым Н.С., Абай Ж.С., Джекебеков К.К., Сармыкова М.К., Еспембетов Б.А., Касенов М.М.
bovis, Абитаев Р.Т., Шораева К.А., Нурпейсова А.С., Сырым Н.С., Абай Ж.С., Джекебеков К.К., Сармыкова М.К., Еспембетов Б.А., Касенов М.М.
Определение антибиотикочувствительности штаммов Streptococcus equi, Сармыкова М.К., Зинина Н.Н., Еспембетов Б.А., Сырым Н.С., Серикбай Е.Б., Самбетбаев А.А.
Экономические науки
Анализ налоговых доходов бюджетной системы в Кыргызской Республике ., Абдраимова Б.К., Асанов Р.К., Мусуралиева М.М., Байзакова А.
Кыргыз Республикасынын экономикасында туризм тармагынын мааниси, Айбашев М.Ж., Капарова Г.С.
Современные этапы развития внешнеторгового сотрудничества между Кыргызской Республикой и Россией, Алымбеков И.К.
Региональные туристские кластеры Кыргызской Республики: предпосылки создания и развития, Атышов К.А., Коч Х., Кадыралиев М.Т., Токторов А.А.
Внешнеэкономическая деятельность как фактор эффективного развития субъектов малого и среднего предпринимательства в Российской Федерации, Габитов И.М., Гарипова Л. В.
В.
Проблемы развития рынка информационных технологий в условиях пандемии, Жолобова А.И., Макаров В.В., Павлова Е.В.
Роль транспортных маршрутов в повышении эффективности туристической отрасли, Капарова Г.С.
Методические аспекты трансформационного анализа периферийного высшего экономического образования, Миляева Л.Г.
Оценка лесных экосистем Каратал-Жапырыкского государственного природного заповедника, Омуралиева Д.К., Ибраева Н.М., Асан уулу К., Чороев Б.
Российская нефтегазовая индустрия в условиях декарбонизации мировой экономики, Чочиев В.Ю.
Юридические науки
Features of conducting a forensic medical examination of a suspect in the investigation of violent sexual crimes ., Smirnov R.Y., Chavgun A.A., Krat S.A.
Торги в электронной форме: положительные стороны и недостатки, Водницкая П.А.
О процессуальных аспектах реабилитации в рамках уголовного судопроизводства умершего лица, Глебова Д.Р.
Правовое регулирование предупреждения насилия в отношении женщин, Джоробекова А. М., Жумабай уулу М.
М., Жумабай уулу М.
К вопросу о современном состоянии насилия в отношении женщин, Жумабай уулу М.
Особенности национальной стратегии кибербезопасности США, Зудаева В.В.
Признаки рецидива преступлений по уголовному законодательству, Илиджев А.А.
Особенности правового регулирования проведения государственных закупок в зарубежных странах ., Иругова А.Р.
Интегративный подход к пониманию права, Караташ О.М.
Контракт в сфере закупок как общеправовая ценность, Маркина А.В.
Налоговые проверки как форма налогового контроля, Маркина А.В.
Способы совершенствования управления жилищно-коммунальным хозяйством муниципального образования, Петриченко Д.Г.
К вопросу о понятии личного обыска как следственного действия, Прохорова Т.Л., Сытников В.О.
Правовое регулирование правоотношений субъектами государственной охраны: историко-правовой анализ, Пухнаревич М.С.
Некоторые аспекты изучения взаимодействия пешеходов и водителей транспортных средств, Тарасов А. Ю., Тарасова И.А.
Ю., Тарасова И.А.
Филологические науки
Discourse as a communicative model of communication, Bezzemelnaya O.A.
Особенности переводов кыргызской поэзии в первой половине ХХ века, Бейшеналиева Б.А.
Английские составные технические термины с субстантивными ономасиологическими базисами: относятся ли они к синтаксическим или морфологическим структурам?, Генералов В.А.
Қазақ мифтік кейіпкерлерінің карнавалы, Курманаева А.Ж., Бейілхан Е.Б.
Символика крыльев в лирическом портрете О.Э. Мандельштама: на материале поэтических посвящений М.И. Цветаевой, Леонтьева А.Ю., Ускова В.С.
ДВИЖЕНИЕ, НАПРАВЛЕНИЕ, ДОРОГА, УЛИЦА, их вероятная этимология, Сомсиков А.И.
КОН, КОНЬ, КОНЕЦ, КОНТАКТ, ЗАКОН, КОНФУЗ, Сомсиков А.И.
БРА, БРАТ, БРАТЬ, БРОСАТЬ, БРЕМЯ, БРЕННЫЙ, Сомсиков А.И.
ЛЮСТРА, ЛЮСТРАЦИЯ, ИЛЛЮСТРАЦИЯ, их вероятная этимология, Сомсиков А.И.
ВЛАСТЬ, ИНСТАНЦИЯ, СТОЯТЬ и СТАН, Сомсиков А.И.
ОПАСНОСТЬ и ПАСКА, Сомсиков А.И.
ЛИЦО и ПОЛИС, их вероятная этимология, Сомсиков А. И.
И.
ВЕРА, ВЕРСИЯ, ИНВЕРСИЯ, ВЕРТЕТЬ, ВЕТЕР, их вероятная этимология, Сомсиков А.И.
Педагогические науки
Оценка использования интерактивных технологий обучения в рамках курса патологической физиологии в ДВГМУ, Амиров Т.Б., Сысоева О.В., Яковенко И.Г., Самарина Е.Ю., Пинаева О.Г., Вдовенко С.В.
Подготовка инженерных кадров в сфере кадастровых работ, Архипов И.В.
Внеучебная работа студентов по формированию инклюзивного взаимодействия, Борисов Е.А.
Языковая среда как важнейший фактор обучения иностранным языкам, Гитайло Е.Н.
Особенности и риски взаимодействия поколений в условиях мировой нестабильности, Грохольская О.Г
Индивидуальный подход к выбору вида спорта в современном настольном теннисе, Демчук Е.Е.
Технология спортивной тренировки. Теория и методика атлетизма, Карлышева К.О., Калинкина Е.В.
Методическое сопровождение педагога дошкольного образовательного учреждения в процессе формирования его экологической культуры, Кутькина Т. Л.
Л.
Методы и средства создания компьютерной анимации и мультипликации, Микаелян А.К., Ишмаева А.И., Абдрахманов И.Н., Марченко В.И.
Особенности преодоления дислексических расстройств у младших школьников в условиях инклюзии, Михайлова А.А.
Нейрографика как арт-терапевтический метод в работе со студентами, Мутовина Н.В., Казакова М.А.
Применение ребусов на уроке информатики, Нефедова В.Ю., Карнаух К.П.
Особенности гражданско-патриотического воспитания в условиях воспитательной среды физико-инженерного факультета, Соболева Т.Г., Синицкая В.В.
Влияние темперамента личности на отношение к элективным курсам по физической культуре и спорту в вузе, Струкова Л.Г., Пантюхова Е.А.
Сравнительная характеристика уровня соматического здоровья студентов НовГУ, занимающихся настольным теннисом и баскетболом в рамках секционных занятий по физической культуре, Цветков М.С.
К проблеме адаптации и использования новых стратегий обучения в контексте смешанного обучения, Шаповалова Т. Р., Медведева Г.Г.
Р., Медведева Г.Г.
Роль педагога в формировании у школьников устойчивого интереса к культурному наследию родного края, Шишов В.В., Бортникова С.А., Хатунцева Е.А.
Политические науки
Институт Курултая в Кыргызстане и Лойя-Джирга в Афганистане: сравнительный политологический анализ, Мохаммад И.Ш.
Влияние современных информационных технологий на функционирование власти, Салгириев А.Р., Газиев В.З., Менциев А.У., Матыева А.Р.
Информационные ресурсы и конфликтогены функционирования политических элит на Северном Кавказе, Салгириев А.Р., Солтамурадов М.Д., Галбацов С.С.
Географические науки
Проблема пожаров в Якутии, Андреев Д.В., Данилова С.С.
Изменение состояния основных пахотных почв Иссык-Кульской котловины при длительном использовании их в земледелии, Тенирбердиев Н.К., Мамытканов С.А., Дуйшонакунов М.Т., Мамырбаева Н.К.
Геолого-минералогические науки
Глобальное потепление — реальность или миф: факты, гипотезы, обсуждение, Подымов И. С., Подымова Т.М.
С., Подымова Т.М.
Эмпирические методы измерения концентрации взвешенных наносов на примере Ганноверского эксперимента, Подымов И.С., Подымова Т.М., Грюне Й.
Науки о Земле
«Тихий Дон» как предвестник экологической катастрофы, Литвинов Н.Д., Гостева С.Р., Шахов С.В.
Антропогенное воздействие вблизи особо охраняемой природной территории «Ландшафтно-рекреационный парк «Тихая бухта», Рысак Е.С.
Выбор направления утилизации отходов городских очистных сооружений, Смирнов Ю.Д., Сучков Д.В., Быстров Е.М.
«Трансцендентные величины» — BHARATI.RU
Play
Stop
Next»
«Prev
«Трансцендентные величины» | Лекция Б.Ч. Бхарати Свами от 6 мая 2007 года, Москва, Кисельный (присутствует фоновый шум)- Кто имеет право быть аморальным? (00:00)
- В бесконечности любая последовательность повторяется (05:35)
- То, что за гранью опыта (06:36)
- Цель материалистической цивилизации (11:08)
- Внутренняя гармония (13:05)
- Душа не стремится к состоянию покоя (15:50)
- Движение есть отражение Божественной воли (19:04)
- У кого ещё искать защиты, как ни у Кришны?! (21:10)
- На каком этапе человек отказывается от знаний? (23:34)
- Признаки отказа души от религиозности и знания (30:34)
- Он религиозен и всеведущ (32:52)
- Милость и прощение (39:11)
- Независимость даётся только с ответственностью (47:55)
- Господь один, но взаимоотношения у Него разные (51:51)
- Стресс со знаком «плюс» (57:30)
- Молитесь о том, что бы вспомнить о Кришне (61:02)
- Вечное сознание (64:13)
- Только по милости (66:48)
https://www. youtube.com/watch?v=vLSWKjVmzas
youtube.com/watch?v=vLSWKjVmzas
Трансцендентные величины
# 00:00
Кто имеет право быть аморальным?
Слушатель: В праве ли мы говорить о Боге, который испражняется в домах, ворует? Ну что это ещё и так далее и так далее. Вот именно испражняется, мочится, ворует и… (неразборчиво)
Б.Ч. Бхарати Свами: Не думаю, что проповедь должна быть акцентирована на том, что кто-то испражняется, то есть он попирает нормы людской морали. Сама по себе мораль – это вещь искусственная, поэтому, если существует закон, в том числе и моральный закон, это значит, что он регулирует какую-то деятельность. Если есть нормы морали, это автоматически означает отделение морали от не морали. То есть если есть мораль, значит, есть и аморальность. То есть нужно признать факт, что существует аморальность. Теперь вопрос: кто имеет право или кому на роду написано быть аморальным? Аморальность, признаём, существует. Если есть нормы поведения, это означает, что есть отклонения от нормы. Норма не может существовать вне, закон не может существовать вне беззакония. Закон вводится для того, чтобы уменьшить беззаконие. Правильно? Если есть мораль, значит, есть и аморальность. Теперь вопрос возникает: кто в праве поступать аморально? Поскольку от аморальности мы не способны избавиться как от понятия, кто может вести себя аморально? Ответ только один: только Господь Бог.
Норма не может существовать вне, закон не может существовать вне беззакония. Закон вводится для того, чтобы уменьшить беззаконие. Правильно? Если есть мораль, значит, есть и аморальность. Теперь вопрос возникает: кто в праве поступать аморально? Поскольку от аморальности мы не способны избавиться как от понятия, кто может вести себя аморально? Ответ только один: только Господь Бог.
Только Господь Бог имеет право быть аморальным. Другие не могут. Почему? Потому что нормы морали по определению вводятся Им. Если есть мораль, значит, законы этой морали вводятся кем-то высшим. Кем бы они ни вводились, тот, кто вводит их, имеет право от них отклоняться. Поэтому то, что Господь ведет себя аморально, это подтверждает то, что Он Господь, потому что только Он имеет на это право, остальные должны подчиняться. Почему так? Это философская истина – там, где существует множество, там обязательно есть закон или закономерность, математическое правило. Там, где есть множество в математике, обязательно есть закономерность. Не существует в математическом множестве при увеличении в бесконечность, не может быть случайности. Когда-то обязательно происходит повтор. То есть в бесконечности происходит повтор этой последовательности. Даже если на таком участке, на маленьком, нам кажется, что цифры совершенно хаотично поставлены, то, когда мы увеличиваем множественный ряд до бесконечности, мы обязательно найдем последовательность. То есть там, где существует множество, там обязательно есть закономерность.
Не существует в математическом множестве при увеличении в бесконечность, не может быть случайности. Когда-то обязательно происходит повтор. То есть в бесконечности происходит повтор этой последовательности. Даже если на таком участке, на маленьком, нам кажется, что цифры совершенно хаотично поставлены, то, когда мы увеличиваем множественный ряд до бесконечности, мы обязательно найдем последовательность. То есть там, где существует множество, там обязательно есть закономерность.
Господь, Его ещё называют Эката, то есть Он единый и неповторимый, Его продублировать невозможно, Его ещё называют Васудева. Васудева означает Единый. То есть там, где один, там нет закономерности, то есть Он может делать всё что угодно. Если ты один и никого рядом нет, то ты не связан никакими нормами морали. Правильно? Вот Господь, Он один. Он не связан никакими нормами морали. Поэтому тогда возникает вопрос: почему Он аморален? Да потому, что Он не обязан соблюдать эти нормы, потому что Он един, Он один и, кроме Него, ничего не существует. Всё, что мы видим, любое разнообразие и любое множество, – это лишь часть Его. Любой фрагмент есть часть бесконечности. Поэтому Он не соблюдает нормы морали. Я уж не знаю, где они взяли, что Он мочится и испражняется в домах? Я просто не дошел до этого места ещё. Но даже если нормой поведения является не мочиться и не испражняться в чужих домах, то Он может себе позволить не соблюдать эти нормы. «Когда был Ленин маленький, с кудрявой головой, он тоже бегал в валенках по горке ледяной.» Ленин же всегда мудр, тем не менее когда-то он бегал в валенках по горке ледяной. Так же и Кришна, Он всегда мудр, но когда-то Он давал Себе волю. Какие-то, может, сомнения есть?
Всё, что мы видим, любое разнообразие и любое множество, – это лишь часть Его. Любой фрагмент есть часть бесконечности. Поэтому Он не соблюдает нормы морали. Я уж не знаю, где они взяли, что Он мочится и испражняется в домах? Я просто не дошел до этого места ещё. Но даже если нормой поведения является не мочиться и не испражняться в чужих домах, то Он может себе позволить не соблюдать эти нормы. «Когда был Ленин маленький, с кудрявой головой, он тоже бегал в валенках по горке ледяной.» Ленин же всегда мудр, тем не менее когда-то он бегал в валенках по горке ледяной. Так же и Кришна, Он всегда мудр, но когда-то Он давал Себе волю. Какие-то, может, сомнения есть?
# 05:35
В бесконечности любая последовательность повторяется
Что касается числа Пи, то мы говорим не об очень больших величинах, а о бесконечно больших величинах. В бесконечности любая последовательность повторяется, потому что число «пи» задано закономерностью. Окружность, деленная на диаметр, – это уже закон. Закон означает счисление. Там, где есть счисление, там обязательно появится закономерность, просто мы не способны ее видеть.
Закон означает счисление. Там, где есть счисление, там обязательно появится закономерность, просто мы не способны ее видеть.
Слушатель: (неразборчиво)
Б. Ч. Бхарати Свами: В видимом горизонте количество. Мы же число Пи выражаем в десятеричном счислении. Мы же можем в одиннадцатиричном или двенадцатеричном, как хотим, можем в двоичном.
# 06:36
То, что за гранью опыта
Слушатель: Я просто беседовал со своим знакомым, и задали вопрос, что такое трансцендентное… (неразборчиво) Не то что (неразборчиво), а математически. Трансцендентное нельзя выразить материально.
Б.Ч. Бхарати Свами: В математике трансцендентное там другое.
Слушатель: Другое в том смысле, что…
Б. Ч. Бхарати Свами: Нет, в математике трансцендентное означает неподдающееся счислению и всё. Что такое майа? Что такое трансцендентное? Трансцендентное – это то, что за границами майи. Майа с санскрита переводится как измерение или счисление, то, что можно выразить, то, что можно исчислить, – это иллюзия, то есть майа. То, что нельзя исчислить, – это трансцендентное. В математике то же самое: что нельзя посчитать, называется трансцендентным.
Майа с санскрита переводится как измерение или счисление, то, что можно выразить, то, что можно исчислить, – это иллюзия, то есть майа. То, что нельзя исчислить, – это трансцендентное. В математике то же самое: что нельзя посчитать, называется трансцендентным.
Слушатель: Трансцендентное – ушедшее из пределов материализма.
Б.Ч. Бхарати Свами: Но мы под словом «трансцендентное» понимаем то, что находится за гранью чувственного опыта. Это и есть трансцендентное. В математике трансцендентное –- это то, что нельзя исчислить. В общем, это где-то перекликается, но мы под трансцендентным понимаем то, что невозможно уразуметь, не пощупать материальными чувствами, нельзя испытать. То, что за гранью опыта, то, что за гранью понимания, – это трансцендентное. Соответственно, граница трансцендентного очень зыбкая. Для одного граница понимания находится на этом уровне, для кого-то – на другом уровне. Трансцендентное, как горизонт, всегда отдаляется. Для мудреца трансцендентное – это где-то очень высоко, для нас трансцендентное – это то, что за гранью там Луны. Трансцендентно то, что очень большое, то есть что бесконечно большое, что бесконечно малое. Джива, или сознание, – это трансцендентное, неисчислимое, нас нельзя вычислить. Или нас нельзя, душу, или сознание, невозможно испытать, сознание не подчиняется закономерностям. Сознание не является результатом сложения чего-то. То есть сознание, или джива, есть предельно малая величина. Предельно малая величина по определению не является результатом сложения чего-то, то есть не является множеством. Мы с вами не множество, поэтому мы не подчиняемся законам. Понимаете? Нас нельзя анализировать, то есть разложить, разобрать. Поэтому мы трансцендентны. Сознание трансцендентно, но оно бесконечно малое. Его нельзя подсчитать, сознание нельзя предсказать, как душа поведет себя в следующее мгновение, потому что душа не подчиняется законам счисления, нельзя определить. Но есть трансцендентная величина, которая бесконечно великая.
Для мудреца трансцендентное – это где-то очень высоко, для нас трансцендентное – это то, что за гранью там Луны. Трансцендентно то, что очень большое, то есть что бесконечно большое, что бесконечно малое. Джива, или сознание, – это трансцендентное, неисчислимое, нас нельзя вычислить. Или нас нельзя, душу, или сознание, невозможно испытать, сознание не подчиняется закономерностям. Сознание не является результатом сложения чего-то. То есть сознание, или джива, есть предельно малая величина. Предельно малая величина по определению не является результатом сложения чего-то, то есть не является множеством. Мы с вами не множество, поэтому мы не подчиняемся законам. Понимаете? Нас нельзя анализировать, то есть разложить, разобрать. Поэтому мы трансцендентны. Сознание трансцендентно, но оно бесконечно малое. Его нельзя подсчитать, сознание нельзя предсказать, как душа поведет себя в следующее мгновение, потому что душа не подчиняется законам счисления, нельзя определить. Но есть трансцендентная величина, которая бесконечно великая. Мы называем это «Господь Бог». То есть бесконечность нельзя исчислить и нельзя исчислить элементарную частицу бесконечности. И то, и другое трансцендентно.
Мы называем это «Господь Бог». То есть бесконечность нельзя исчислить и нельзя исчислить элементарную частицу бесконечности. И то, и другое трансцендентно.
# 11:08
Цель материалистической цивилизации
Материалисты считают, что сознание, или душа, есть результат сочетания материи. Материя движется и на определенном этапе начинает себя осознавать. Поскольку сознание ищет какую-то гармонию, какую-то радость, то материалисты говорят: «Раз мы произошли из материи, то и радость мы можем получить, передвигая материальные обстоятельства. Создавая материальные обстоятельства, мы можем найти то, что ищем, – счастье, гармонию». Духовные люди говорят, что, поскольку душа или сознание не является результатом соединения материи, а является результатом вычленения из чего-то Божественного, то и гармонию душа, предельно маленькая частица сознания, может найти в йоге, то есть в соединении с бесконечностью, там нужно искать свою судьбу – в служении, в отношениях со Всевышним. Материалисты обратное говорят: «Нет, раз мы произошли из материи, то и счастье мы можем найти в материи». И весь путь материалистической цивилизации заключается в том, чтобы найти такие условия в материи, в которых тебе будет всегда хорошо. Они это называют прогрессом науки. Цель науки – это найти такие материальные условия, в которых тебе будет хорошо.
Материалисты обратное говорят: «Нет, раз мы произошли из материи, то и счастье мы можем найти в материи». И весь путь материалистической цивилизации заключается в том, чтобы найти такие условия в материи, в которых тебе будет всегда хорошо. Они это называют прогрессом науки. Цель науки – это найти такие материальные условия, в которых тебе будет хорошо.
# 13:05
Внутренняя гармония
Но поскольку в этом уравнении в самом начале заложена ошибка – мы не являемся результатом соединения материи, то как бы мы ни меняли величины во второй половине уравнения, мы никогда не обретем гармонии и счастья. Ни с помощью власти, денег, телесных удовольствий мы не сможем найти гармонии. Просто невозможно по определению. Так верующие полагают. То есть внутренняя гармония, или состояние, его еще называют состоянием йоги, гармонией с Абсолютной Величиной, не зависит от внешних обстоятельств, и даже не нужно быть мудрецом, чтобы понять, что радость не зависит от внешних условий. Иногда человеку радостно, когда плохая погода, когда, казалось бы, все рушится, все, на что он надеялся, все рушится, а внутри ему хорошо. А иногда все хорошо как бы, другие ему завидуют, а внутри ему омерзительно, нет внутренней гармонии. То есть внутренняя гармония совершено не связана с внешними обстоятельствами. Такова природа частицы сознания. Когда она ощущает свою связь с Сверхсубъектом, с Господом Богом, тогда наступает действительно гармония. Когда эта связь рушится и душа пытается найти гармонию во внешних обстоятельствах, тогда, как бы она ни меняла условия своего существования, она всегда будет несчастна. Таков непреложный закон. Только потому что мы больше, так сказать, связаны родовой пуповиной, мы связаны с Господом, Он нас создал, а не материя. Мы ближе к Нему, чем к тому, что мы наблюдаем. Он ближе к нам, чем что бы то ни было. Он присутствует везде, как в бесконечной плоскости любая точка находится в центре. Господь – центр всего, а мы точки. Мы можем быть с Ним очень близко всегда, где бы мы ни находились.
Иногда человеку радостно, когда плохая погода, когда, казалось бы, все рушится, все, на что он надеялся, все рушится, а внутри ему хорошо. А иногда все хорошо как бы, другие ему завидуют, а внутри ему омерзительно, нет внутренней гармонии. То есть внутренняя гармония совершено не связана с внешними обстоятельствами. Такова природа частицы сознания. Когда она ощущает свою связь с Сверхсубъектом, с Господом Богом, тогда наступает действительно гармония. Когда эта связь рушится и душа пытается найти гармонию во внешних обстоятельствах, тогда, как бы она ни меняла условия своего существования, она всегда будет несчастна. Таков непреложный закон. Только потому что мы больше, так сказать, связаны родовой пуповиной, мы связаны с Господом, Он нас создал, а не материя. Мы ближе к Нему, чем к тому, что мы наблюдаем. Он ближе к нам, чем что бы то ни было. Он присутствует везде, как в бесконечной плоскости любая точка находится в центре. Господь – центр всего, а мы точки. Мы можем быть с Ним очень близко всегда, где бы мы ни находились.
# 15:50
Душа не стремится к состоянию покоя
Буддисты и майавади излагают иную точку зрения. Они говорят, что дисгармония появляется там, где существует движение. Почему? Потому что они наблюдают, что всякое движение подчиняется закону энтропии. Всё в этом мире подвержено энтропии. Энтропия – это постепенное угасание. То есть мироздание, которое наполнено движением, стремится к состоянию покоя. Это в физике называется энтропией – постепенное угасание, состояние полного баланса, равновесия. Из-за этого они заключают, что, поскольку все стремится к покою, точнее, все видимое нами стремится к покою, то состояние покоя естественно. Это очень соблазнительный вывод. Представьте себе: все, что мы наблюдаем, стремится к покою. Следовательно, покой, раз всё к нему стремится, самое естественное для нас. То есть это изначальное состояние и то состояние, к которому мы должны прийти. Это состояние они называют самадхи, мукти, просветление, нирвана и т. д. В разных религиях по-разному, в разных философских школах по-разному. Эта нирвана – состояние полного покоя, или состояние безразличия, полное уединение. Но этот вывод тоже с самого начала в уравнении ошибка. Действительно всё, что мы наблюдаем с вами, стремится к состоянию покоя. Но когда-то это мироздание было выведено из состояния покоя. Понятно, что оно всё стремится к состоянию покоя, но, находясь когда-то в состоянии покоя, вдруг оно вышло из равновесия, следовательно, то, что вывело из состояния равновесия бытие, было более предвечно, то есть было изначально. Следовательно, более естественное состояние – это состояние движения. Несмотря на то, что наблюдаемый нами мир угасает, тем не менее изначальное состояние – это, наоборот, движение, потому что импульс движения вывел из состояния покоя мироздание. То есть сознание наблюдает, что всё стремится к состоянию покоя, но само по себе сознание не есть это всё. Мы видим, что внешний мир угасает, идет к состоянию замирания, но я-то не есть часть внешнего мира.
д. В разных религиях по-разному, в разных философских школах по-разному. Эта нирвана – состояние полного покоя, или состояние безразличия, полное уединение. Но этот вывод тоже с самого начала в уравнении ошибка. Действительно всё, что мы наблюдаем с вами, стремится к состоянию покоя. Но когда-то это мироздание было выведено из состояния покоя. Понятно, что оно всё стремится к состоянию покоя, но, находясь когда-то в состоянии покоя, вдруг оно вышло из равновесия, следовательно, то, что вывело из состояния равновесия бытие, было более предвечно, то есть было изначально. Следовательно, более естественное состояние – это состояние движения. Несмотря на то, что наблюдаемый нами мир угасает, тем не менее изначальное состояние – это, наоборот, движение, потому что импульс движения вывел из состояния покоя мироздание. То есть сознание наблюдает, что всё стремится к состоянию покоя, но само по себе сознание не есть это всё. Мы видим, что внешний мир угасает, идет к состоянию замирания, но я-то не есть часть внешнего мира.
Слушатель: Материя стремится?
Б. Ч. Бхарати Свами: Материя стремится. Материя когда-то была выведена из состояния покоя, и она возвращается в состояние покоя. Это называется энтропия. То есть если ничего не трогать, то всё замрет, всё придет в состояние полного баланса.
# 19:04
Движение есть отражение Божественной воли
Но я-то не есть материя. И то, что вывело материю из состояния покоя, более предвечно. Это и есть та самая Божественная сила, которая никогда не останавливается, она всегда играет. Это и есть Кришна. И каждое движение, каждое действие в этом, наблюдаемом нами мире, – это и есть отголосок того первого движения Божественного. Каждое движение – это и есть небольшое отражение божественной воли. Понимаете? Это как если мы возьмем бильярдный стол, и шары туда положим, и одним шаром ударим очень сильно, то вот это движение первого шара расколется на все остальные движения. И, сколько бы лет ни прошло, любое движение любого из этих шариков будет отголоском самого первого движения. Понимаете? Потому что само по себе созвездие шаров на бильярдном столе не могло расколоться. Должен быть какой-то шар, который привел их в состояние движения. Точно так же, какое бы движение мы ни совершали и ни видели в мироздании, это и есть отголосок самого первого, Божественного, Божественной воли. Так, по крайней мере, мудрецы видят Бога везде. Они говорят, что Господь везде. Это не значит, что они видят Его с бородой или с дудочкой. Прямо везде видят. Нет, это значит все. Там, где есть разнообразие, это отголосок изначального Божественного, Божественной воли, Демиурга, импульса, первого импульса. Следовательно, первоимпульс, Божественная воля, предвечна. Она существует до того, как возник мир. А что более естественно? То, что более предвечно.
Понимаете? Потому что само по себе созвездие шаров на бильярдном столе не могло расколоться. Должен быть какой-то шар, который привел их в состояние движения. Точно так же, какое бы движение мы ни совершали и ни видели в мироздании, это и есть отголосок самого первого, Божественного, Божественной воли. Так, по крайней мере, мудрецы видят Бога везде. Они говорят, что Господь везде. Это не значит, что они видят Его с бородой или с дудочкой. Прямо везде видят. Нет, это значит все. Там, где есть разнообразие, это отголосок изначального Божественного, Божественной воли, Демиурга, импульса, первого импульса. Следовательно, первоимпульс, Божественная воля, предвечна. Она существует до того, как возник мир. А что более естественно? То, что более предвечно.
# 21:10
У кого ещё искать защиты, как не у Кришны?
И, потом, кому ещё предаваться, как не тому, кто не подчиняется законам морали и вообще никаким законам? Кому еще можно предаться? Даже в этом мире, если нас кто-то обидел, мы у кого ищем защиты? У того, кто не подчиняется законам. Мы ищем такого милицейского начальника, которому закон не писан, который обладает такой властью, что для него законы не писаны. Например, кто-то с вами поступил несправедливо, вы обращаетесь в милицию, а милиция говорит: «Ну, знаете, по закону его нельзя привлечь к ответственности, потому что по закону он поступил с вами правильно». Что вам остается делать? Идти к тому, кто не подчиняется закону, такому высокому должностному лицу, который поднимет руку и скажет: «Так! Вот у этого отобрать, этому отдать». Всё. У кого еще искать защиты, как не у Кришны? Если бы Кришна подчинялся законам, то какой же Он Бог тогда? Даже законам морали? Это значит, в трудную минуту на Него нельзя было бы положиться. Потому что, когда вдруг бы понадобилась помощь и Он сказал бы: «Знаешь, все-таки по законам морали это все не очень хорошо. Хоть ты и мой преданный, помочь Я тебе не могу, потому что закон морали я не могу нарушить», какой же Он тогда Бог? Даже в этом мире мы ищем покровительства или убежища у того, кто не подчиняется законам.
Мы ищем такого милицейского начальника, которому закон не писан, который обладает такой властью, что для него законы не писаны. Например, кто-то с вами поступил несправедливо, вы обращаетесь в милицию, а милиция говорит: «Ну, знаете, по закону его нельзя привлечь к ответственности, потому что по закону он поступил с вами правильно». Что вам остается делать? Идти к тому, кто не подчиняется закону, такому высокому должностному лицу, который поднимет руку и скажет: «Так! Вот у этого отобрать, этому отдать». Всё. У кого еще искать защиты, как не у Кришны? Если бы Кришна подчинялся законам, то какой же Он Бог тогда? Даже законам морали? Это значит, в трудную минуту на Него нельзя было бы положиться. Потому что, когда вдруг бы понадобилась помощь и Он сказал бы: «Знаешь, все-таки по законам морали это все не очень хорошо. Хоть ты и мой преданный, помочь Я тебе не могу, потому что закон морали я не могу нарушить», какой же Он тогда Бог? Даже в этом мире мы ищем покровительства или убежища у того, кто не подчиняется законам. Что же говорить вообще о мироздании?
Что же говорить вообще о мироздании?
Слушатель: Ну оно же не всегда так.
Б. Ч. Бхарати Свами: Что не всегда так?
Слушатель: Ну такой закон, по которому Он не поможет.
Б.Ч. Бхарати Свами: Кто не поможет?
Слушатель: Ну Он же и закон одновременно?
Б.Ч. Бхарати Свами: Это всегда так. Вы неправильно понимаете. Тот, кто издает законы, не обязан им подчиняться.
Слушатель: Это не факт, что преданный нарушил закон морали, найдет прибежище и защиту у Кришны. Это же все зависит от стадии преданности, правильно?
Б. Ч. Бхарати Свами: Ну, может, вы и правы. Действительно, Он не может защитить, не во всех ситуациях. Погорячился я, наверное, сегодня. Он не Всемогущий.
Слушатель: Нет, Всемогущий , почему. У Него свой промысел непостижимый.
# 23:34
На каком этапе человек отказывается от знаний?
Слушатель: А на каком этапе человек отказывается от знаний? (неразборчиво)
Б. Ч. Бхарати Свами: На определенном этапе нашего движения к Абсолютной реальности знания начинают мешать. Когда душа чувствует, что знания мешают, потому что знания – это всегда расчет. Знание – это всегда исчисление, это просчет плодов, просчет какой-то пользы. И, когда душа понимает, что в отношениях с Господом Богом нет никакой пользы, тогда она отказывается от знаний. То есть отношения со Всевышним совершенно бесполезны. Когда-то на пути к Абсолютной Реальности, к Абсолютной Красоте, знание становится нашим врагом, а потом и набожность становится врагом, то есть вот эта религиозность. Да, потому что религиозность – это какие-то рамки. Эти рамки позволяют нам вырваться из темницы на свободу. Религия позволяет обрести спасение, вырваться из когтей иллюзии. Но на свободе религиозность или рамки, только сковывают, они загоняют нас в новую темницу.
Ч. Бхарати Свами: На определенном этапе нашего движения к Абсолютной реальности знания начинают мешать. Когда душа чувствует, что знания мешают, потому что знания – это всегда расчет. Знание – это всегда исчисление, это просчет плодов, просчет какой-то пользы. И, когда душа понимает, что в отношениях с Господом Богом нет никакой пользы, тогда она отказывается от знаний. То есть отношения со Всевышним совершенно бесполезны. Когда-то на пути к Абсолютной Реальности, к Абсолютной Красоте, знание становится нашим врагом, а потом и набожность становится врагом, то есть вот эта религиозность. Да, потому что религиозность – это какие-то рамки. Эти рамки позволяют нам вырваться из темницы на свободу. Религия позволяет обрести спасение, вырваться из когтей иллюзии. Но на свободе религиозность или рамки, только сковывают, они загоняют нас в новую темницу.
Слушатель: (неразборчиво)
Б. Ч. Бхарати Свами: Да. Но распространенная ошибка, когда преданный или религиозный человек на первых этапах, сделав несколько первых шагов, думает: «Теперь мне не нужны ни знания, ни религиозность», и отказывается от этого, и снова низвергает себя в иллюзию, в материализм. В нашей теологии есть известная беседа между Раманандой Раем и Господом Чайтаньей. Наши учителя объясняют, что эта беседа является продолжением беседы Кришны и Арджуны перед битвой на Курукшетре и заключительными словами Кришны, после того как Он сказал, какие существуют нормы поведения, в какие рамки следует себя поставить, чтобы вступить во взаимоотношения с Абсолютным Самодуром, с бесконечностью. То есть в «Бхагавад-гите» Кришна устанавливает определенные рамки для души, стремящейся к отношениям с Абсолютом. Но в конце-концов Кришна говорит: «А теперь ты должен все эти рамки выбросить. Как только ты предался Мне, тебе эти рамки не нужны». И, спустя какое-то время, когда тот же самый Арджуна беседовал с Кришной, но уже в облике Рамананды Рая и Господа Чайтаньи, Господь Чяайтанья ему объясняет, что, когда ты полностью предался и, когда ты совершенно свободен в отношениях с Абсолютом, что происходит дальше? То есть лекарство или религия нам нужны. Лекарство нам нужно для того, чтобы вылечиться, а чем же должен питаться тот, кто вылечился? Вот вопрос.
В нашей теологии есть известная беседа между Раманандой Раем и Господом Чайтаньей. Наши учителя объясняют, что эта беседа является продолжением беседы Кришны и Арджуны перед битвой на Курукшетре и заключительными словами Кришны, после того как Он сказал, какие существуют нормы поведения, в какие рамки следует себя поставить, чтобы вступить во взаимоотношения с Абсолютным Самодуром, с бесконечностью. То есть в «Бхагавад-гите» Кришна устанавливает определенные рамки для души, стремящейся к отношениям с Абсолютом. Но в конце-концов Кришна говорит: «А теперь ты должен все эти рамки выбросить. Как только ты предался Мне, тебе эти рамки не нужны». И, спустя какое-то время, когда тот же самый Арджуна беседовал с Кришной, но уже в облике Рамананды Рая и Господа Чайтаньи, Господь Чяайтанья ему объясняет, что, когда ты полностью предался и, когда ты совершенно свободен в отношениях с Абсолютом, что происходит дальше? То есть лекарство или религия нам нужны. Лекарство нам нужно для того, чтобы вылечиться, а чем же должен питаться тот, кто вылечился? Вот вопрос.
То есть «Бхагавад-гита» заканчивается на том этапе, когда врач говорит, что ты должен делать, чтобы вылечиться и каковы являются признаки здорового сознания, когда ты перестаешь быть пациентом. Это – «отказаться от всех правил и предписаний и просто предаться Мне», – Кришна говорит. Отказаться от всяких норм морали, которым ты когда-то следовал, отказаться от норм поведения, которым ты следовал, и просто жить со Мной, влиться в эту лилу, в эту игру. И дальше, это понятно, то есть все способы религии есть лекарство. Но, когда ты вылечился, чем ты должен заниматься, что ты должен есть? Какую диету соблюдать? Какие упражнения делать? Вот в беседе с Раманандой Раем Господь рассказывает, чем занимается душа, которая отвергла всякие нормы морали, нормы нравственности, всякую религию, долг, обязательства и просто стала свободной в отношениях с Богом. Что она дальше делает? Потому что «Гита» это не объясняет. «Гита» говорит: «Стань свободным в отношениях со Мной». А что это значит? Вот тут и возникает этот вопрос: на каком этапе душа должна отказаться от знаний? На этом этапе, когда душа излечилась, когда душе уже не нужны костыли для того, чтобы вступить в отношения с Абсолютной Красотой.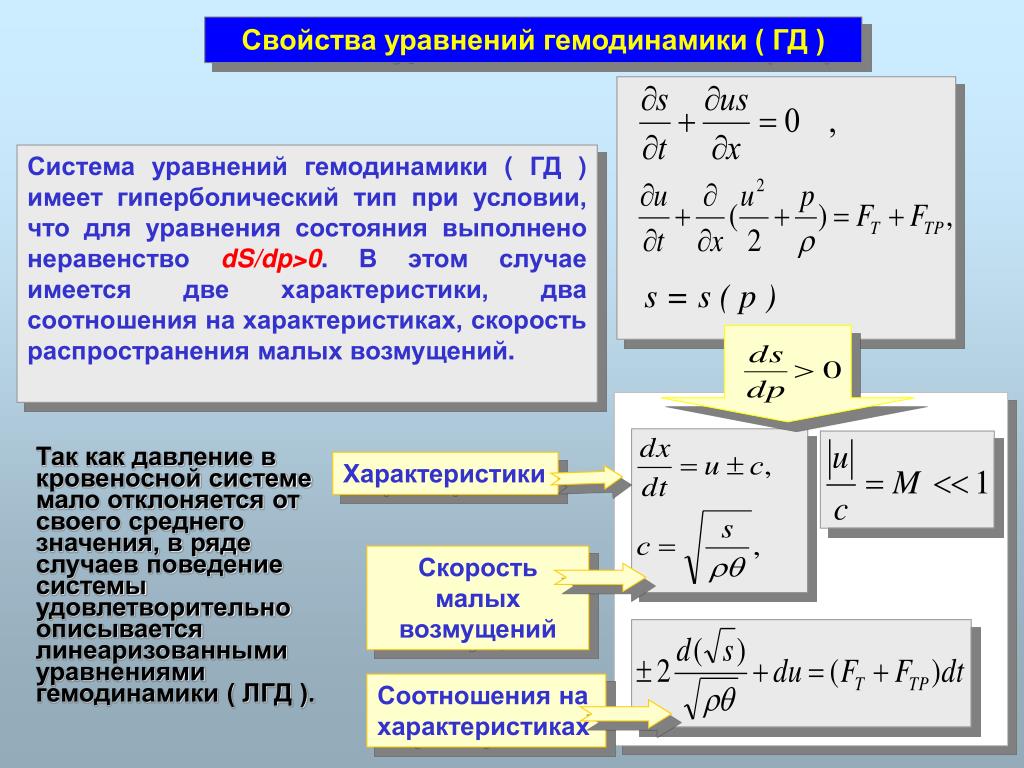 Вот тогда ей не нужны знания, тогда ей не нужна религия. До этого нужна религия, причем, чем больше душа находится в иллюзии, чем больше она обременена страхами и иллюзией, тем строже она должна соблюдать нормы религии, той или иной религии. Чем буйнее больной, тем сильнее смирительная рубашка. Если хотите, то религия является той самой смирительной рубашкой. Но, когда ты излечился, тебе не нужна смирительная рубашка, религия не нужна. Правда, многие больные думают, что и сейчас она уже не нужна. (смеётся) Это ошибка сахаджий: они сами решают, когда они излечились.
Вот тогда ей не нужны знания, тогда ей не нужна религия. До этого нужна религия, причем, чем больше душа находится в иллюзии, чем больше она обременена страхами и иллюзией, тем строже она должна соблюдать нормы религии, той или иной религии. Чем буйнее больной, тем сильнее смирительная рубашка. Если хотите, то религия является той самой смирительной рубашкой. Но, когда ты излечился, тебе не нужна смирительная рубашка, религия не нужна. Правда, многие больные думают, что и сейчас она уже не нужна. (смеётся) Это ошибка сахаджий: они сами решают, когда они излечились.
# 30:34
Признаки отказа души от религиозности и знания
То есть каковы признаки, когда душа должна отказаться от знаний и от религии? Когда религиозность или набожность становится источником гордыни, источником высокого самомнения, тогда нужно отказаться от религиозности и знания. Это лакмусовая бумажка, которой можно определить, религиозность нужна тебе или не нужна. Когда человек думает, что он соблюдает те или иные правила и предписания и это ему гарантирует отношения со Всевышним, что он поймал за хвост фортуну, что исключительно соблюдение религиозных правил гарантирует ему, что Господь низойдет и заберет его, тогда набожность и религиозность становится его врагом. Покуда набожность и религиозность есть источник смирения для нас, если мы видим, ощущаем своё ничтожество, свою низменность и в этом нам помогает соблюдение религиозных норм, тогда это нам полезно. Как только эти религиозные нормы превращаются для нас в источник гордыни, тогда они становятся для нас вредны. Или знания. Когда вы думаете, что, сдав экзамен на знание Священных Писаний, получив диплом бхакти-шастры, вы получаете гарантированный билет в царство Божие, вот тогда это будет злом. Покуда вы думаете, что знание лишь поможет вам лучше служить Абсолютной Реальности, тогда знание идет вам на пользу. Для этого нужно быть искренним с собой. Какие-то сомнения, может быть? Может, кто-то обеспокоен чем-то?
Покуда набожность и религиозность есть источник смирения для нас, если мы видим, ощущаем своё ничтожество, свою низменность и в этом нам помогает соблюдение религиозных норм, тогда это нам полезно. Как только эти религиозные нормы превращаются для нас в источник гордыни, тогда они становятся для нас вредны. Или знания. Когда вы думаете, что, сдав экзамен на знание Священных Писаний, получив диплом бхакти-шастры, вы получаете гарантированный билет в царство Божие, вот тогда это будет злом. Покуда вы думаете, что знание лишь поможет вам лучше служить Абсолютной Реальности, тогда знание идет вам на пользу. Для этого нужно быть искренним с собой. Какие-то сомнения, может быть? Может, кто-то обеспокоен чем-то?
#32:52
Он религиозен и всеведущ
Пожалуйста.
Слушатель: Вот из 64-х качеств Кришны одно качество – это всеведущность и другое качество – религиозность. Получается, что душа должна обладать хотя бы одним из тех качеств, и Кришна, обладая один этими качествами, Ему не интересно общаться с теми, у кого нет ни одного качества, то есть отказываются… (неразборчиво). То есть и от остальных качеств тоже приходится отказываться, и Кришне не интересно общаться с такими душами, которые от всего отказались, отказались от этих качеств, когда Сам Он и всеведущ и религиозен.
То есть и от остальных качеств тоже приходится отказываться, и Кришне не интересно общаться с такими душами, которые от всего отказались, отказались от этих качеств, когда Сам Он и всеведущ и религиозен.
Б. Ч. Бхарати Свами: Религиозен – это, значит, из Него исходит религия. Закон не может существовать без законодателя. То есть кто-то должен артикулировать закон, он должен сказать: «Вот так надо поступать, а вот так не надо поступать». Это половина, одна сторона медали. Другая сторона медали – Он еще должен сделать так, чтобы закон соблюдался. То есть Он должен наказывать отступников от закона и поощрять тех, кто следует закону. В этом смысле Он религиозен. От Него исходит всякий закон, будь то моральный закон, религиозный закон или физический закон. В этом смысле Он религиозен. То есть Он источник закона. Но источник не обязан подчиняться законам. Царь создает закон для своих подданных, но сам он не подчиняется законам. Это означает, что он может изменить нормы религии прямо противоположно. Во власти Всевышнего изменить нормы религии. Сейчас какие существуют общепризнанные нормы? Не убий, не укради. Он может в одночасье изменить их. Это в Его силе. Он может сказать: «Убить и украсть – это праведно, а не убивать и не красть – это не праведно». Ему ничто не помешает это сделать. Какой бы дикостью нам это ни казалось, Он вполне может это сделать. То есть религия – это то, что Он хочет. Вот что значит – «Он религиозен». Религиозен – это не значит, что Он подчиняется законам. Это значит, что Он эти законы религии создает. А Всеведущий – это, значит, что Он сознает все, то есть Он присутствует везде. Нам предлагается быть прямой противоположностью Бога.
Во власти Всевышнего изменить нормы религии. Сейчас какие существуют общепризнанные нормы? Не убий, не укради. Он может в одночасье изменить их. Это в Его силе. Он может сказать: «Убить и украсть – это праведно, а не убивать и не красть – это не праведно». Ему ничто не помешает это сделать. Какой бы дикостью нам это ни казалось, Он вполне может это сделать. То есть религия – это то, что Он хочет. Вот что значит – «Он религиозен». Религиозен – это не значит, что Он подчиняется законам. Это значит, что Он эти законы религии создает. А Всеведущий – это, значит, что Он сознает все, то есть Он присутствует везде. Нам предлагается быть прямой противоположностью Бога.
Слушатель: А какой смысл отказываться от всего? И будет ли интересно общаться с нами, когда мы от всего откажемся?
Б. Ч. Бхарати Свами: Если Он Всемогущий, то для того, чтобы общаться со Всемогущим, чтобы со Всемогущим были гармоничные отношения, нужно быть бессильным. Если Он Всеведущий, чтоб гармонично общаться с Ним, чтобы наши отношения были гармоничными, мы должны быть неведающими. Когда родитель общаются со своим сыном малолетним, ему не интересно, знает ли он таблицу умножения или нет. Его привлекают в сыне не знания, а беззащитность и бескорыстность отношений. Господа ничем нельзя привлечь, ничем нельзя удивить, ни знаниями, ни силой, потому что Он обладает всем этим в полной мере. Единственное, что пленит Его, – это наша добровольная зависимость от Него, наша полная преданность. Когда мы сдаемся Ему на милость и не ждем ничего в ответ, не ждем от Него никаких благ, тогда это и пленит Его сердце. Когда ребенок зависит от тебя, тогда ты покровительствуешь ему; как только ребенок начинает проявлять признаки независимости от тебя, тогда ты ему предоставляешь свободу. Пик отношений, пик любовных отношений – это тогда, когда беззащитный показывает свою полную зависимость от Всемогущего. Бесконечно малое может быть в гармонии с бесконечно большим. Как только бесконечно малое начинает расти, тогда оно перестает представлять интерес для бесконечно большого, потому что оно начинает показывать ему свою значимость.
Когда родитель общаются со своим сыном малолетним, ему не интересно, знает ли он таблицу умножения или нет. Его привлекают в сыне не знания, а беззащитность и бескорыстность отношений. Господа ничем нельзя привлечь, ничем нельзя удивить, ни знаниями, ни силой, потому что Он обладает всем этим в полной мере. Единственное, что пленит Его, – это наша добровольная зависимость от Него, наша полная преданность. Когда мы сдаемся Ему на милость и не ждем ничего в ответ, не ждем от Него никаких благ, тогда это и пленит Его сердце. Когда ребенок зависит от тебя, тогда ты покровительствуешь ему; как только ребенок начинает проявлять признаки независимости от тебя, тогда ты ему предоставляешь свободу. Пик отношений, пик любовных отношений – это тогда, когда беззащитный показывает свою полную зависимость от Всемогущего. Бесконечно малое может быть в гармонии с бесконечно большим. Как только бесконечно малое начинает расти, тогда оно перестает представлять интерес для бесконечно большого, потому что оно начинает показывать ему свою значимость. Непонятно? Не согласны?
Непонятно? Не согласны?
Слушатель: Бесконечно малое всегда останется бесконечно малым, если оно… (неразборчиво)
Б. Ч. Бхарати Свами: Это правильно. Но иногда бесконечно малому начинает казаться, что оно что-то из себя представляет. Мы всегда будем ничтожны по сравнению с Бесконечной Реальностью, но иногда нам будет казаться, что мы что-то из себя представляем. Как Лев Толстой говорил, что душа человеческая как дробь. Числитель – это то, что она есть, а знаменатель – это то, что она о себе мыслит, то, что ей кажется. Чем больше мы себя мыслим, тем меньше мы становимся. Мы бесконечно малое, но нам вдруг начинает казаться, что мы что-то из себя представляем, что мы познали мир, мы обладаем какими-то знаниями, какой-то силой, что-то подчиняется нам. Доходит это до высшей своей стадии, когда мы считаем, что мы цари природы. Материалисты говорят, что мы венец эволюции, соответственно, мы стоим над мирозданием. Потому что мы самое высшее творение природы, следовательно, мы цари. А так называемые религиозные люди говорят, что Бог нас сотворил по образу и подобию, значит, мы как боги. В результате одно и то же: что ты материалист, что ты из утверждения, что Он создал нас по образу и подобию делаешь вывод, что мы – это Он.
А так называемые религиозные люди говорят, что Бог нас сотворил по образу и подобию, значит, мы как боги. В результате одно и то же: что ты материалист, что ты из утверждения, что Он создал нас по образу и подобию делаешь вывод, что мы – это Он.
# 39:11
Милость и прощение
Слушатель: (неразборчиво)
Б. Ч. Бхарати Свами: Не важно, что он подразумевает под Христом. Мы же тоже примерно в нашей теологии говорим, что Кришна выше, чем бог. Кришна не бог, Он выше него. Если бог и Кришна вступят в противоречие, то мы изберем Кришну. Почему? Потому что бог – это олицетворение справедливости, олицетворение судьи, который наказывает неправедников и поощряет праведников. То есть он есть олицетворение справедливости. Но Кришна выше справедливости. Кришна стоит над истиной и над ложью. Поэтому я не знаю, что Достоевский под Христом понимал. Если он подразумевал всепрощение, тогда перед ним можно шляпу снять, конечно. Потому что под богом понимается справедливый бог. Иудейский бог – антипод Христа. Иудейский бог говорил: «Око за око, зуб за зуб». Как с тобой поступили, так и ты имеешь право поступить со своим обидчиком. Христос пришел и принес совершенно противоположную идею. Тебя ударили по щеке, а ты подставь другую, то есть будь милосерден, не отвечай по заслугам, потому что Господь к тебе милостив и ты не имеешь право судить других, ты должен тоже быть милостив. То есть в христианской молитве верующий обращается к Богу: «Прости мне мои грехи, как я прощаю должникам своим», то есть своим обидчикам. Это, конечно, идея милосердия. Она выше, чем справедливость. То есть Иисус Христос дал более высокую идею. Естественно, можно сказать, что со временем эту идею снова превратили в идею справедливости. Снова появилось понятие ада и рая. Если ты уверовал во Христа, то ты попадешь в рай; не уверовал, то попадешь в ад навсегда. И снова здоровая идея милости вернулась, превратилась в идею справедливости. Но изначально это, конечно, высокая идея. В Христианстве, в данном контексте, милость отождествляется с прощением.
Иудейский бог – антипод Христа. Иудейский бог говорил: «Око за око, зуб за зуб». Как с тобой поступили, так и ты имеешь право поступить со своим обидчиком. Христос пришел и принес совершенно противоположную идею. Тебя ударили по щеке, а ты подставь другую, то есть будь милосерден, не отвечай по заслугам, потому что Господь к тебе милостив и ты не имеешь право судить других, ты должен тоже быть милостив. То есть в христианской молитве верующий обращается к Богу: «Прости мне мои грехи, как я прощаю должникам своим», то есть своим обидчикам. Это, конечно, идея милосердия. Она выше, чем справедливость. То есть Иисус Христос дал более высокую идею. Естественно, можно сказать, что со временем эту идею снова превратили в идею справедливости. Снова появилось понятие ада и рая. Если ты уверовал во Христа, то ты попадешь в рай; не уверовал, то попадешь в ад навсегда. И снова здоровая идея милости вернулась, превратилась в идею справедливости. Но изначально это, конечно, высокая идея. В Христианстве, в данном контексте, милость отождествляется с прощением. Когда мы просим у Бога милости, мы подразумеваем прощение. И это как раз выражено в молитве «Отче наш, прости мне так же, как я прощаю должникам своим».
Когда мы просим у Бога милости, мы подразумеваем прощение. И это как раз выражено в молитве «Отче наш, прости мне так же, как я прощаю должникам своим».
А в вайшнавизме идея милости и идея прощения – это совершенно разные вещи, они антиподы. Когда преданный просит у Господа, молит о милости, он не подразумевает прощение, не просит, чтоб меня простили так же, как я другим прощаю. Он под милостью понимает: «Позволь мне служить твоим рабам. Не надо меня прощать». Но, поскольку жизнь, в общем, вещь совершенно бессмысленная, то преданный просит наполнить эту жизнь смыслом. Каким? Служить слугам Всевышнего. Вот этим смыслом преданный наполняет свою жизнь. Вообще, жизнь как таковая – совершенно бессмысленная вещь. Жизнь – это просто ощущение. Мы живем, только покуда ощущаем. Жизнь и ощущение – это синонимы. Потому что, когда ты в отключке, что называется, то ты не живешь. У тебя может сердце работать, у тебя может слюновыделение происходить, дефекация и т. д. Да? Но это не жизнь. Жизнь – это ощущение. Вот настолько бессмысленная вещь жизнь. Жизнь – это просто последовательность ощущений. И когда кто-то хочет жить долго, это, значит, он просто хочет долго ощущать. Если мы начнем разбирать какие это ощущения, эти ощущения всего навсего: прикосновения, запах, отделения одного цвета от другого, вкус и слух. Вот это мы называем жизнью. То есть, когда кто-то говорит: «Я хочу пожить подольше», это, значит, он хочет побольше отличать один цвет от другого, побольше запахов ощутить, побольше вкусов, поприкасаться, конечно, к мягкому и теплому. (смеются). Мы перечислили вкус. То есть тот, кто хочет продлить свою жизнь, просто хочет продлить пять этих ощущений. Если мы начнем разбирать, что такое жизнь, мы придем к выводу, что она совершенно бессмысленна, это просто набор каких-то ощущений, и всё. Вот ради этого мы и живем – просто ощущать что-то.
Вот настолько бессмысленная вещь жизнь. Жизнь – это просто последовательность ощущений. И когда кто-то хочет жить долго, это, значит, он просто хочет долго ощущать. Если мы начнем разбирать какие это ощущения, эти ощущения всего навсего: прикосновения, запах, отделения одного цвета от другого, вкус и слух. Вот это мы называем жизнью. То есть, когда кто-то говорит: «Я хочу пожить подольше», это, значит, он хочет побольше отличать один цвет от другого, побольше запахов ощутить, побольше вкусов, поприкасаться, конечно, к мягкому и теплому. (смеются). Мы перечислили вкус. То есть тот, кто хочет продлить свою жизнь, просто хочет продлить пять этих ощущений. Если мы начнем разбирать, что такое жизнь, мы придем к выводу, что она совершенно бессмысленна, это просто набор каких-то ощущений, и всё. Вот ради этого мы и живем – просто ощущать что-то.
Нет, можно прикрываться какими-то высокими лозунгами, что мы хотим счастья будущим поколениям, мы хотим мира во всем мире и так далее. Но, чтобы не лукавить, это просто мы хотим продлить ощущения. И вайшнав понимает бессмысленность жизни как череды ощущений и обращается к Господу, «что моя жизнь совершенно бессмысленная штука. Можно, я наполню ее смыслом другим, не ощущениями, а можно я буду служить тем, кто служит Тебе? И если Ты разрешишь мне это, разрешишь мне служить Твоим рабам, тогда я это назову милостью». То есть в вайшнавизме прощение и милость не то что разные вещи, а диаметрально противоположные. А в христианстве, наверное, не во всем, но в том пласте, о котором мы с вами говорим, милость, когда раб Божий обращается за милостью к Богу, он подразумевает «Прости меня», и это как раз сформулировано в молитве: «Прости мне так же, как я прощаю должникам». Это он называет милостью.
Но, чтобы не лукавить, это просто мы хотим продлить ощущения. И вайшнав понимает бессмысленность жизни как череды ощущений и обращается к Господу, «что моя жизнь совершенно бессмысленная штука. Можно, я наполню ее смыслом другим, не ощущениями, а можно я буду служить тем, кто служит Тебе? И если Ты разрешишь мне это, разрешишь мне служить Твоим рабам, тогда я это назову милостью». То есть в вайшнавизме прощение и милость не то что разные вещи, а диаметрально противоположные. А в христианстве, наверное, не во всем, но в том пласте, о котором мы с вами говорим, милость, когда раб Божий обращается за милостью к Богу, он подразумевает «Прости меня», и это как раз сформулировано в молитве: «Прости мне так же, как я прощаю должникам». Это он называет милостью.
Для вайшнава милость – другое. Но прощение христианского толка, конечно, выше, чем справедливость иудейского толка. Бог, как носитель справедливости, несомненно ниже, чем Бог, как дарующий прощение. Но Бог, дарующий прощение, несомненно ниже, чем Бог дарующий милость в форме служения Его слугам. Хотя эти вещи можно спутать легко. Когда какой-нибудь верующий трудится ради блага живущих на Земле, говорит: «Я служу людям». Но что значит «он служит людям»? Это, значит, он продлевает им жизнь, продлевает им возможность больше ощущать вкусы, различать цвета. Это он называет служить людям. Вайшнав, когда говорит: «Я служу людям», это он говорит о том, что я хочу дать им шанс послужить рабам Бога. Принести благо людям в нашем понимании – это позволить им больше чувствовать, больше видеть цветов, больше слышать звуков. Для вайшнава послужить людям или принести благо людям – это значит дать им идею красоты. В чем она заключается? В служении Его рабам. Так, может, скомкано, но я попытался, как мог, объяснить.
Хотя эти вещи можно спутать легко. Когда какой-нибудь верующий трудится ради блага живущих на Земле, говорит: «Я служу людям». Но что значит «он служит людям»? Это, значит, он продлевает им жизнь, продлевает им возможность больше ощущать вкусы, различать цвета. Это он называет служить людям. Вайшнав, когда говорит: «Я служу людям», это он говорит о том, что я хочу дать им шанс послужить рабам Бога. Принести благо людям в нашем понимании – это позволить им больше чувствовать, больше видеть цветов, больше слышать звуков. Для вайшнава послужить людям или принести благо людям – это значит дать им идею красоты. В чем она заключается? В служении Его рабам. Так, может, скомкано, но я попытался, как мог, объяснить.
# 47:55
Независимость дается только с ответственностью
Слушатель: Махарадж, а можно вопрос в связи с основанием… (неразборчиво) Когда ребенок появляется на свет, он является… (неразборчиво) …дитя любви, но не корысти… (неразборчиво) …возникает нежелание вплоть до нежелания рожать детей…
Б. Ч. Бхарати Свами: А все равно вам этого не избежать. Так что в чем вопрос-то?
Ч. Бхарати Свами: А все равно вам этого не избежать. Так что в чем вопрос-то?
Слушатель: Даже не спрашивают… (неразборчиво)
Б. Ч. Бхарати Свами: Когда душа заявляет о своей независимости, то Господь Бог разрешает ей быть независимой. Но при этом в довесок Господь Бог дает еще и ответственность. Нельзя быть свободным и безответственным. То есть, когда ребенок растет и он полностью зависит от тебя, то ты заботишься о нем, ты чувствуешь свое моральное предназначение служить ему, потому что без тебя он погибнет. Но, когда ребенку исполняется 15 или 16 лет, он говорит: «Мама, я уже самостоятельный, я имею право принимать собственные решения». И тогда ты, как мать, даешь ему эту свободу. И это тоже является частью отцовства или частью родительства. Когда ребенок заявляет о своей самостоятельности, предоставить ему эту самостоятельность является частью ответственности родителей. Точно так же Господь Бог: когда мы зависим от Него, когда мы сдались Ему на милость, то Он заботится о нас, когда мы не думаем. Маленький ребенок не думает: «А что я получу от отношений с мамой, спасет она меня или не спасет?» Она его спасет, потому что он не думает об этом. Когда ребенок начинает подрастать и начинает вычислять: «Что будет, если вот здесь я послушаюсь маму, а здесь не послушаюсь?» Тогда вот это вот самое грехопадение, первородный грех, то есть мы вкушаем плод знаний. Что будет, если я пойду своим путем? Мы как бы с этим «меседжем» обращаемся ко Всевышнему: «Что будет, если я сам вкушу плод знаний? Почему я должен полностью зависеть от Тебя в этом Эдемском саду? Может быть, мне все-таки пора повзрослеть?» И Господь, будучи милосердным, разрешает нам выйти из этого Эдемского сада. Это, конечно, всё аллегорически, да, чтоб мы не подумали. Вот точно так же мы приходим в этот свет, попадаем в этот мир, и у нас есть идея самостоятельности.
Маленький ребенок не думает: «А что я получу от отношений с мамой, спасет она меня или не спасет?» Она его спасет, потому что он не думает об этом. Когда ребенок начинает подрастать и начинает вычислять: «Что будет, если вот здесь я послушаюсь маму, а здесь не послушаюсь?» Тогда вот это вот самое грехопадение, первородный грех, то есть мы вкушаем плод знаний. Что будет, если я пойду своим путем? Мы как бы с этим «меседжем» обращаемся ко Всевышнему: «Что будет, если я сам вкушу плод знаний? Почему я должен полностью зависеть от Тебя в этом Эдемском саду? Может быть, мне все-таки пора повзрослеть?» И Господь, будучи милосердным, разрешает нам выйти из этого Эдемского сада. Это, конечно, всё аллегорически, да, чтоб мы не подумали. Вот точно так же мы приходим в этот свет, попадаем в этот мир, и у нас есть идея самостоятельности.
Что касается материнства, то помимо того, что вы даете жизнь ребенку, вы его еще обрекаете на смерть, если вы ему не дадите идею вечности – то, что он не ребенок, а он душа, заключенная в это тело. Тело меняется: сегодня оно детское, завтра оно отроческое, потом взрослое, потом стариковское. Но, как бы ни менялись тела, сознание, или душа, остается неизменным. Если вы не дадите это знание ребенку, то вы будете повинны в его смерти. Это смертный грех – родить кого-то. Потому что вы обрекаете его на смерть. Если вы ему не объясните, что он никогда не умрет, то он умрет.
Тело меняется: сегодня оно детское, завтра оно отроческое, потом взрослое, потом стариковское. Но, как бы ни менялись тела, сознание, или душа, остается неизменным. Если вы не дадите это знание ребенку, то вы будете повинны в его смерти. Это смертный грех – родить кого-то. Потому что вы обрекаете его на смерть. Если вы ему не объясните, что он никогда не умрет, то он умрет.
# 51:51
Господь один, но взаимоотношения у Него разные
Слушатель: (неразборчиво)
Б. Ч. Бхарати Свами: Я просто разобрал идею. Я просто разобрал две концепции. Я понимаю…
Слушатель: (неразборчиво)
Б. Ч. Бхарати Свами: Есть концепция справедливости, а есть концепция милосердия.
Слушатель: Ну милосердие…
Б. Ч. Бхарати Свами: Если есть справедливость, то есть носитель справедливости. А если есть милосердие, то есть носитель милосердия. Поэтому как бы мы ни называли их, конечно, всё исходит из единого источника. Единый источник порождает и милосердие, и милость, и справедливость, и ревностность. Например, в Библии говорится, что Господь ревностный. То есть Он ревнив или мстителен, другими словами.
Единый источник порождает и милосердие, и милость, и справедливость, и ревностность. Например, в Библии говорится, что Господь ревностный. То есть Он ревнив или мстителен, другими словами.
Слушатель: Но это та самая смирительная рубашка, о которой вы говорили. (неразборчиво) А то, что идет от смирения, освобождает от смирения.
Б. Ч. Бхарати Свами: Тем не менее мы разделяем эти смирительные рубашки. Мы разделяем носителей. Бог, который покарал иудеев за неправедность, за то, что они ослушались Его, – это один лик Бога, а Бог, который смилостивился над ними, несмотря на то, что они Его ослушались, – это другой лик Бога. Несмотря на то, что это одно и то же, одна и та же личность, но Он проявляет себя по-разному. Поэтому мы и говорим, что есть милосердие, а есть справедливость.
Слушатель: (неразборчиво) …такую благодать, такую свободу. (неразборчиво) …не учитывают простые вещи… (неразборчиво)
Б. Ч. Бхарати Свами: Пример с главой государства, аналогия с главой государства. С разными гражданами он может проявлять разные свои лики. С одними он злобен, он мстителен, к другим он справедлив, а к другим он милостив. Если его близкий друг или сын его близкого друга на своем джипе раздавил двух таджиков, то его за это не посадят, а ему скажут: «Напиши заявление, что твой джип вчера украли, и не ты раздавил, а так…» Понимаете? Ему ничего не будет. С одними он справедлив, с другими он милосерден. Но при этом он один и тот же. Как судья с преступниками, он справедлив, а когда он приходит домой, то его собственный ребенок катается у него на спине и он играет роль лошадки. Ни один преступник в зале суда не может себе этого позволить. При этом это одна и та же личность.
Ч. Бхарати Свами: Пример с главой государства, аналогия с главой государства. С разными гражданами он может проявлять разные свои лики. С одними он злобен, он мстителен, к другим он справедлив, а к другим он милостив. Если его близкий друг или сын его близкого друга на своем джипе раздавил двух таджиков, то его за это не посадят, а ему скажут: «Напиши заявление, что твой джип вчера украли, и не ты раздавил, а так…» Понимаете? Ему ничего не будет. С одними он справедлив, с другими он милосерден. Но при этом он один и тот же. Как судья с преступниками, он справедлив, а когда он приходит домой, то его собственный ребенок катается у него на спине и он играет роль лошадки. Ни один преступник в зале суда не может себе этого позволить. При этом это одна и та же личность.
Слушатель: (неразборчиво)
Б. Ч. Бхарати Свами: С чем вы спорите? Я не понимаю в чем моя ошибка? Что я не…
Слушатель: В отношении… (неразборчиво) …и отношении к амнистии.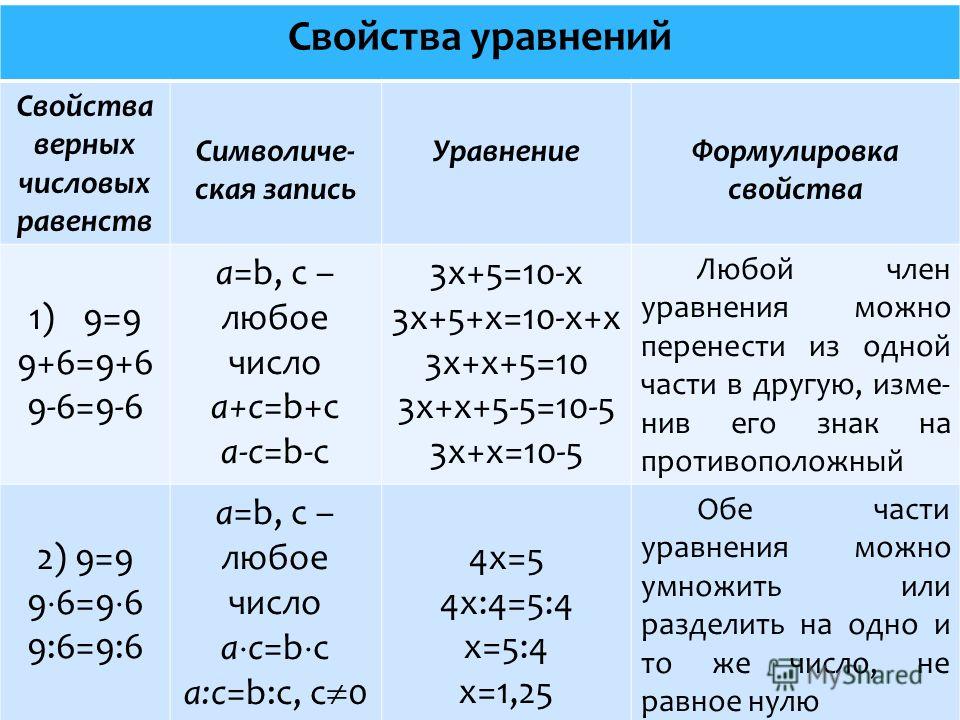
Б. Ч. Бхарати Свами: Тот, кто сдался Ему на милость имеет с Ним одни отношения. Тот, кто просит у Него справедливости, имеет с Ним другие отношения. Если мы просим у Него справедливости, то мы будем судимы по справедливости. А если мы не просим у Него справедливости, а милости, то Он может нам простить грехи. Но это Он один и тот же. Поэтому мы и говорим, что Библейский завет – один, Новый завет – другой.
Слушатель: Ну, как бы в общей концепции… (неразборчиво)
Б. Ч. Бхарати Свами: Разные концепции, но принадлежат одному источнику.
Слушатель: (неразборчиво)
Б. Ч. Бхарати Свами: Ладно, я просто не христианин и не очень люблю…
Слушатель: (неразборчиво)
Б. Ч. Бхарати Свами: Угу. Какие-то…
Слушатель: Сомнения терзают мою душу. Можно ли считать разговор о Боге как обо всем, а с этого аспекта как разговор ни о чем?
Б. Ч. Бхарати Свами: Можно.
Ч. Бхарати Свами: Можно.
Слушатель: То есть в принципе…
Б. Ч. Бхарати Свами: Ответил на ваш вопрос? Можно считать.
Слушатель: Ну, а правильно это будет? Или это опять-таки это…
Б. Ч. Бхарати Свами: Вопрос: можно считать? Конечно, можно.
Слушатель: А правильно это будет?
Б. Ч. Бхарати Свами: А что значит правильно?
Слушатель: Так считать, вот для меня, допустим, необразованного?
Б. Ч. Бхарати Свами: Есть вопросы по существу? Может, сейчас..
Слушатель: (неразборчиво) …ответственность матери перед ребенком… (неразборчиво)
Б. Ч. Бхарати Свами: То же самое. Я имел в виду родитель с большой буквы. Мы говорим о понятии родитель. Если дитя обнаруживает свою полную зависимость от него, от родителя, какого бы пола он ни был, то родитель заботится о нем.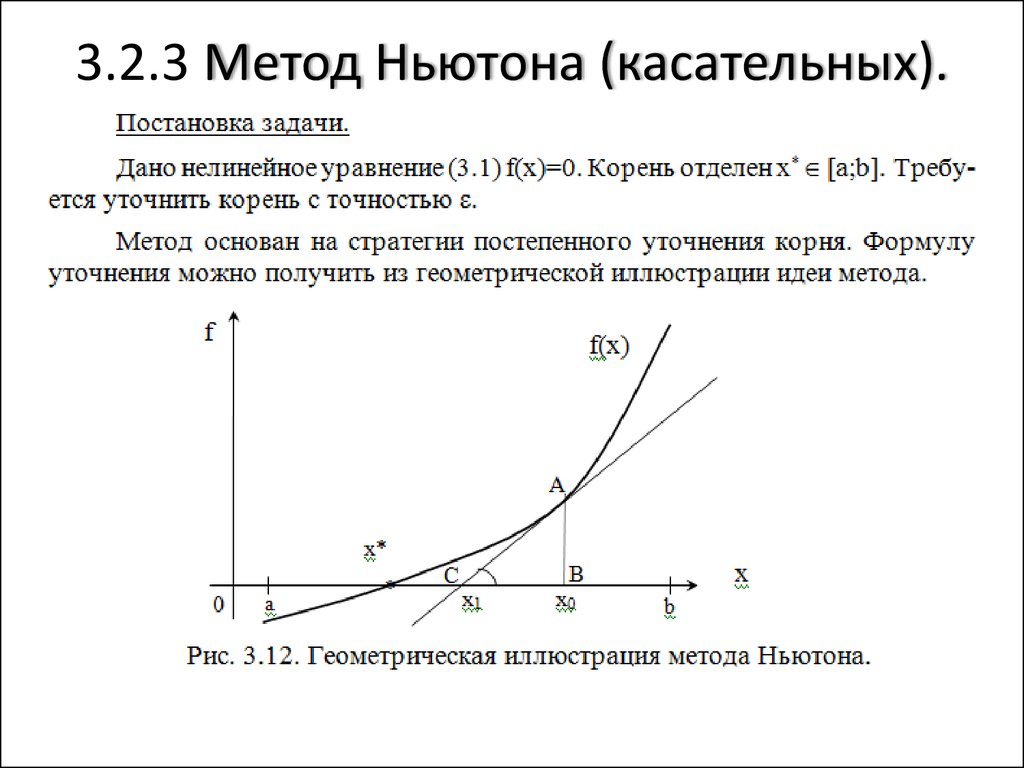 Если дитя заявляет о своей самостоятельности, то родитель дает ему самостоятельность.
Если дитя заявляет о своей самостоятельности, то родитель дает ему самостоятельность.
Слушатель: В мире люди рождаются, а в духовном мире есть рождение?
# 57:30
Стресс со знаком «плюс»
Б. Ч. Бхарати Свами: В духовном мире нет рождения.
Слушатель: А как туда попадают тогда?
Б. Ч. Бхарати Свами: Просыпаются.
Слушатель: (неразборчиво)
Б. Ч. Бхарати Свами: В духовном мире нет ни рождения, ни смерти. Есть игра, или, как еще говорят, стресс со знаком «плюс». То есть там существуют эмоции, существуют страсти, существуют отношения, но они со знаком «плюс», стресс со знаком «плюс». Когда жители Вриндавана видят, как Кришна танцует на головах ядовитого змея, они в обморок падают от шока, потому что им кажется, что сейчас змей… Змей был такой ядовитый, что птицы, которые пролетали над рекой, падали замертво, всё было отравлено, а Кришна у него на головах танцевал. А тот не просто подставлял головы, а пытался укусить за ноги, тысячеглавый змей Калия. Когда соплеменники Кришны видели это, они в обморок попадали. То есть это было расстройство, но со знаком «плюс», эмоции, но со знаком «плюс». Страх, но другой – страх потерять своего Господина, Господина своего сердца. Здесь тоже присутствует страх, но страх потерять нажитое. Страх потерять нажитое тело, мы же столько накапливали вес. И как? Потерять это всё в двадцать лет? Или всю жизнь копил счет, цифры копил, и потерять это всё? Страх, страшно. Что ж я делать буду? Или столько людей тебя почитали, столько тебя считали хорошим человеком. И что теперь стать плохим человеком? Главное, чтобы они не узнали об этом. Вот страх. Там страх потерять хозяина, а здесь страх потерять подчиненных. Потому что, если ты за долгие годы своей жизни приобрел репутацию добропорядочного человека, соответственно, ты боишься потерять свое доброе имя. Другими словами, что значит доброе имя? Это мнение других о тебе, хорошее мнение о тебе у других.
А тот не просто подставлял головы, а пытался укусить за ноги, тысячеглавый змей Калия. Когда соплеменники Кришны видели это, они в обморок попадали. То есть это было расстройство, но со знаком «плюс», эмоции, но со знаком «плюс». Страх, но другой – страх потерять своего Господина, Господина своего сердца. Здесь тоже присутствует страх, но страх потерять нажитое. Страх потерять нажитое тело, мы же столько накапливали вес. И как? Потерять это всё в двадцать лет? Или всю жизнь копил счет, цифры копил, и потерять это всё? Страх, страшно. Что ж я делать буду? Или столько людей тебя почитали, столько тебя считали хорошим человеком. И что теперь стать плохим человеком? Главное, чтобы они не узнали об этом. Вот страх. Там страх потерять хозяина, а здесь страх потерять подчиненных. Потому что, если ты за долгие годы своей жизни приобрел репутацию добропорядочного человека, соответственно, ты боишься потерять свое доброе имя. Другими словами, что значит доброе имя? Это мнение других о тебе, хорошее мнение о тебе у других. Страх потерять честь, беречь свою честь, чтобы о тебе думали как о порядочном человеке, страх потерять почитателей. А там страх другой – потерять Хозяина. Здесь потерять подчиненных, а там Хозяина. Один и тот же страх, но один со знаком «плюс», а другой со знаком «минус».
Страх потерять честь, беречь свою честь, чтобы о тебе думали как о порядочном человеке, страх потерять почитателей. А там страх другой – потерять Хозяина. Здесь потерять подчиненных, а там Хозяина. Один и тот же страх, но один со знаком «плюс», а другой со знаком «минус».
Слушатель: Я слышал, один преданный сказал, что с преданностью не рождаются, она там есть. Так ли это?
Б. Ч. Бхарати Свами: Не знаю. Есть вопросы? (смеются)
Слушатель: Не, но правильно ли считать, что каждый преданный? Согласны со мной?
Б. Ч. Бхарати Свами: Правильно. Вопросы есть?
# 61:02
Молитесь о том, чтобы вспомнить о Кришне
Слушатель: А как из-за страха не терять память о Кришне? Страха не забыть и несколько тысяч лет, где невозможно даже подумать о Кришне?
Б. Ч. Бхарати Свами: Пока вам нужно молиться не о том, чтобы не забыть Кришну, а о том, чтобы вспомнить. Потому что тот мультик, что вы прокручиваете в мозгу, – это не Кришна, скорее всего. Я же не знаю, что там у вас. Вспомнить можно, вернее, не забыть можно то, с чем ты соприкоснулся. Если ты ни с чем не соприкасался, как ты можешь об этом забыть? Но нам святые говорят, что, если вы соприкоснулись с Кришной, вы уже не сможете забыть о Нем. В «Бхагавад-гите» Кришна говорит: «Кто вернулся в мою обитель, кто соприкоснулся с Ним по сути, тот никогда не возвращается в мир иллюзии». Что значит «не возвращается в мир иллюзии»? Это не значит, что через тридцать тысяч лет он не родится. Это значит, что его ничего не будет из иллюзии привлекать. Попасть в материальный мир – это значит привлечься ложными ценностями. Это власть, деньги, уважение, набожность, знания, сила. Вот эти ложные ценности, то, чем мы живем, то, ради чего мы живем. Ради денег, уважения, чтобы о нас хорошего мнения другие были, чтобы оставить после себя след, чтобы навсегда остаться в памяти следующих поколений. Вот то, ради чего мы живем, – это и есть материальный мир.
Потому что тот мультик, что вы прокручиваете в мозгу, – это не Кришна, скорее всего. Я же не знаю, что там у вас. Вспомнить можно, вернее, не забыть можно то, с чем ты соприкоснулся. Если ты ни с чем не соприкасался, как ты можешь об этом забыть? Но нам святые говорят, что, если вы соприкоснулись с Кришной, вы уже не сможете забыть о Нем. В «Бхагавад-гите» Кришна говорит: «Кто вернулся в мою обитель, кто соприкоснулся с Ним по сути, тот никогда не возвращается в мир иллюзии». Что значит «не возвращается в мир иллюзии»? Это не значит, что через тридцать тысяч лет он не родится. Это значит, что его ничего не будет из иллюзии привлекать. Попасть в материальный мир – это значит привлечься ложными ценностями. Это власть, деньги, уважение, набожность, знания, сила. Вот эти ложные ценности, то, чем мы живем, то, ради чего мы живем. Ради денег, уважения, чтобы о нас хорошего мнения другие были, чтобы оставить после себя след, чтобы навсегда остаться в памяти следующих поколений. Вот то, ради чего мы живем, – это и есть материальный мир. Но тот, кто соприкоснулся с подлинной ценностью, ценность, которую нельзя купить, как мы всегда говорим, что ценно только то, что нельзя купить. Если у чего-то есть цена, это уже не ценно, потому что это можно приобрести, значит, это продается. Самое ценное то, что не продается. Если ты соприкоснулся с нечто, что не продается, – Красота и Любовь, тогда ты уже никогда не вернешься в мир покупных ценностей: власть, деньги, богатство. Ты уже никогда сюда не вернешься, даже если ты получишь какое-то тело здесь, это не значит, что ты будешь в материальном мире. Материальный мир – это не круглый шарик, вселенная. Материальный мир – это мир отношений. Материальный мир – это не физический мир, это мир корыстных отношений. Если тебе повстречалось то, что не продается, ты никогда не будешь искать то, что продается. Как только ты соприкоснулся с Прекрасной Реальностью, тогда у тебя не будет страха родиться в этом мире. Еще какие-то сомнения, может быть?
Но тот, кто соприкоснулся с подлинной ценностью, ценность, которую нельзя купить, как мы всегда говорим, что ценно только то, что нельзя купить. Если у чего-то есть цена, это уже не ценно, потому что это можно приобрести, значит, это продается. Самое ценное то, что не продается. Если ты соприкоснулся с нечто, что не продается, – Красота и Любовь, тогда ты уже никогда не вернешься в мир покупных ценностей: власть, деньги, богатство. Ты уже никогда сюда не вернешься, даже если ты получишь какое-то тело здесь, это не значит, что ты будешь в материальном мире. Материальный мир – это не круглый шарик, вселенная. Материальный мир – это мир отношений. Материальный мир – это не физический мир, это мир корыстных отношений. Если тебе повстречалось то, что не продается, ты никогда не будешь искать то, что продается. Как только ты соприкоснулся с Прекрасной Реальностью, тогда у тебя не будет страха родиться в этом мире. Еще какие-то сомнения, может быть?
# 64:13
Вечное сознание
Слушатель: (неразборчиво)
Б. Ч. Бхарати Свами: Да, только не нужно сроки ставить. Он, кстати, там и добавил, говорит: «Я не знаю, когда, но все, кто соприкоснулся с идеей вайшнавизма, обречены на спасение» и он говорит: «Только не ставьте сроки».
Ч. Бхарати Свами: Да, только не нужно сроки ставить. Он, кстати, там и добавил, говорит: «Я не знаю, когда, но все, кто соприкоснулся с идеей вайшнавизма, обречены на спасение» и он говорит: «Только не ставьте сроки».
Слушатель: (неразборчиво)
Б. Ч. Бхарати Свами: Ну, конечно. Вы понимаете, просто искать Красоту или искать Абсолютную Реальность – это сам по себе великий результат. Не нужно искать ничего по ходу. Жить ради этого – это уже величайшее достижение.
Слушатель: (неразборчиво) Любой материальный срок… (неразборчиво)
Б. Ч. Бхарати Свами: А что значит «материальный срок»? Как вот мы говорим: «Тебе 30 лет, тебе 40 лет, тебе 50 лет». Это что значит? Это, значит, Земля проделала какое-то расстояние в полёте. Мы это говорим: «30 лет». А если, допустим, ты родился на корабле космическом, который просто прямо летит, вот сколько тебе лет? Как там года считать? По часам? Но, а если они собьются, батарейка кончится? Вот мы – это и есть тот самый круг самсары, мы попали в него и говорим: «Сколько тебе лет?» Можно же говорить: «Мне 5 миллионов километров». А в бесконечности как посчитать километры? То есть, когда ты летишь и вокруг звезды или объекты мелькают, ты можешь свою скорость засечь, сказать, сколько километров ты пролетел, соответственно, сколько тебе лет. А когда ты летишь и нет звезд, ты даже не сможешь скорость свою определить. Вот ты летишь, и бесконечное пространство, и ты один. Сколько тебе лет? Нисколько. Ты просто есть, и всё. Ты сознаешь своё бытие. Вот это и есть чистое сознание, душа. Она просто сознаёт своё бытие. Неважно, сколько вот эта кожа пролетела вокруг Солнца. Считай, что ты просто бесконечное пространство. Причём тут 30 тысяч лет? Душа вечна, сознание вечно. Сомнения какие-то, может быть, возражения?
А в бесконечности как посчитать километры? То есть, когда ты летишь и вокруг звезды или объекты мелькают, ты можешь свою скорость засечь, сказать, сколько километров ты пролетел, соответственно, сколько тебе лет. А когда ты летишь и нет звезд, ты даже не сможешь скорость свою определить. Вот ты летишь, и бесконечное пространство, и ты один. Сколько тебе лет? Нисколько. Ты просто есть, и всё. Ты сознаешь своё бытие. Вот это и есть чистое сознание, душа. Она просто сознаёт своё бытие. Неважно, сколько вот эта кожа пролетела вокруг Солнца. Считай, что ты просто бесконечное пространство. Причём тут 30 тысяч лет? Душа вечна, сознание вечно. Сомнения какие-то, может быть, возражения?
# 66:48
Только по милости
Слушатель: (неразборчиво) …богатство, которое нельзя купить… (неразборчиво) …задешево.
Б. Ч. Бхарати Свами: Что значит «дешево»?
Слушатель: (неразборчиво)
Б. Ч. Бхарати Свами: Какое богатство?
Ч. Бхарати Свами: Какое богатство?
Слушатель: Ну, которое приобретают.
Б. Ч. Бхарати Свами: Нет, приобрести Его никак нельзя. Только милостью.
Слушатель: Ну я про это и говорю. (неразборчиво)
Б. Ч. Бхарати Свами: Ни за что не купить.
Слушатель: Ни за что?
Б. Ч. Бхарати Свами: Нет, конечно. То есть «ни за что» – это не значит деньги, это, значит, усилия. Никакими усилиями ты не можешь приобрести Господа как своего…
Слушатель: (неразборчиво)
Б. Ч. Бхарати Свами: Да, вы понимаете. Такого хозяина, как Бог, нельзя купить никакими усилиями.
Слушатель: (неразборчиво)
Б. Ч. Бхарати Свами: Но ты можешь Им обладать, но как хозяином. Как два раба встречаются и говорят: «У тебя кто хозяин?» – «У меня этот хозяин. Мой хозяин вот этот». Хотя он и употребляет слово «мой», при этом он, по сути, говорит: «Я принадлежу Ему». Но семантически он говорит: «Это мой хозяин», а по сути: «Я Ему принадлежу». Вот такого хозяина, как Абсолютная Красота, что на санскрите звучит как «Кришна», нельзя купить никакими усилиями. То есть тот, кто говорит: «Мой хозяин – Кришна», не может сказать, за что он Его купил. Посчастливилось! Повезло! Всех остальных хозяев можно купить, даже бога можно купить, бога справедливого. Если ты соблюдаешь заповеди, то Он становится к тебе милосердным.
Но семантически он говорит: «Это мой хозяин», а по сути: «Я Ему принадлежу». Вот такого хозяина, как Абсолютная Красота, что на санскрите звучит как «Кришна», нельзя купить никакими усилиями. То есть тот, кто говорит: «Мой хозяин – Кришна», не может сказать, за что он Его купил. Посчастливилось! Повезло! Всех остальных хозяев можно купить, даже бога можно купить, бога справедливого. Если ты соблюдаешь заповеди, то Он становится к тебе милосердным.
Слушатель: (неразборчиво)
Б. Ч. Бхарати Свами: Но если ты соблюдаешь заповеди, то тебе гарантировано, что ты попадешь в Царство Божие.
Слушатель: А если заповедями не гарантировано, (неразборчиво) через веру нужно идти, но никто не говорил, что гарантировано.
Б. Ч. Бхарати Свами: Тогда сдаюсь, да, вы правы. Если так сказано, то – да.
Слушатель: (неразборчиво)
Б. Ч. Бхарати Свами: Ну, я, видите ли, дилетант в писании христианском. То, что я слышал. Вот приходит какой-нибудь грешник и говорит: «Батюшка, я согрешил». Батюшка ему говорит: «Прочитай молитву три раза, и все грехи тебе отпущу» .
То, что я слышал. Вот приходит какой-нибудь грешник и говорит: «Батюшка, я согрешил». Батюшка ему говорит: «Прочитай молитву три раза, и все грехи тебе отпущу» .
Слушатель: (неразборчиво)
Б. Ч. Бхарати Свами: Ну тут вы…
Слушатель: (неразборчиво)
Б. Ч. Бхарати Свами: Вот, или пожертвуй индульгенцию, пожертвуй столько и получишь отпущение грехов.
Слушатель: (неразборчиво)
Б. Ч. Бхарати Свами: Вот. Поэтому я сужу о теологии по этим фрагментам. Приходит грешник, покаялся – ему простили. Через неделю он снова пришел, опять покаялся – ему вот эти недельные грехи простили. И так каждую неделю.
Слушатель: (неразборчиво)
Б. Ч. Бхарати Свами: Таким образом, он покупает, он просит прощения и покупает отпущение грехов.
Слушатель: (неразборчиво)
Б. Ч. Бхарати Свами: Ну, уж, вы, прямо, совсем!
Ч. Бхарати Свами: Ну, уж, вы, прямо, совсем!
Слушатель: (неразборчиво)
Б. Ч. Бхарати Свами: Всё, наверное, на сегодня.
Транскрипция: Читралекха Д. Д.
Корректор: Вишнуприя Д. Д.
Трансцендентальные уравнения Последние исследовательские работы
Общее количество документов
183
(пять лет 51)
H-индекс
17
(пять лет 4)
Решатель трансцендентных уравнений: новая нейронная сеть для решения трансцендентных уравнений
Гоцзюнь Ван ◽
Вэйцзюнь Ли ◽
Цзинъи Лю ◽
Линьцзюнь Сун ◽
Липин Чжан ◽
…
Нейронная сеть ◽
Трансцендентное уравнение
Дальнейшие результаты по экспоненциально устойчивой устойчивости неопределенных весов соединений рекуррентных нейронных сетей нейтрального типа
Вэньсяо Си ◽
Тао Се ◽
Бивен Ли
Экспоненциальная стабильность ◽
Глобальная экспоненциальная стабильность ◽
Нейтральный тип ◽
Верхние границы ◽
Трансцендентное уравнение ◽
Кусочно-постоянные аргументы ◽
Кусочная постоянная ◽
Измерительный механизм ◽
Двойное соединение ◽
Тот самый
В этой статье представлены дальнейшие результаты по устойчивости глобальной экспоненциальной устойчивости рекуррентной нейронной сети с кусочно-постоянными аргументами и нейтральными членами (NPRNN) при неопределенных весах связи.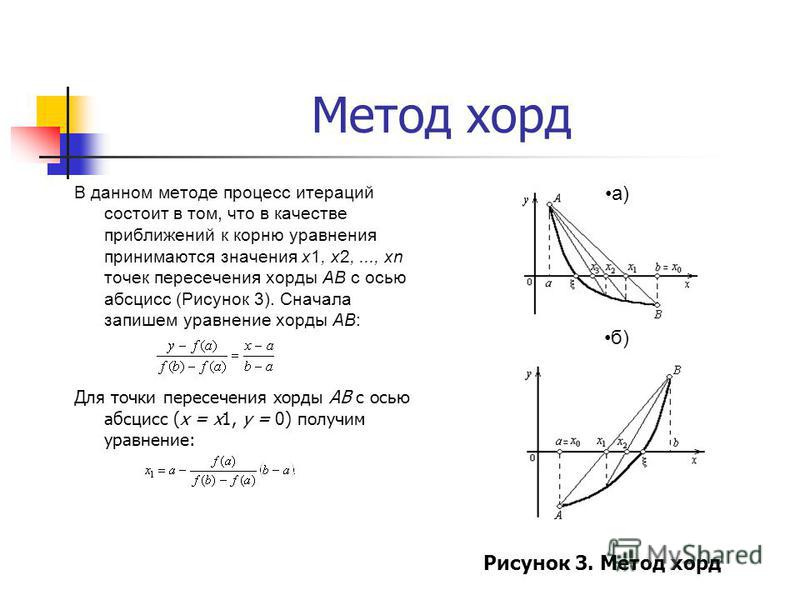 Оценка верхних границ двух категорий факторов помех и создание механизма измерения неопределенных весов двойного соединения являются основными задачами и проблемами. Таким образом, с одной стороны, предоставляются новые достаточные критерии верхних оценок нейтральных членов и кусочных аргументов, гарантирующие глобальную экспоненциальную устойчивость НПНС. С другой стороны, разрешенная замкнутая область весов двойной связи характеризуется трансцендентным уравнением с четырьмя переменными, основанным на предыдущем устойчивом NPRNN. Таким образом, два интерференционных фактора и двойные неопределенные веса связи взаимно ограничиваются в модели параметра-неопределенности NPRNN, что приводит к динамической эволюционной взаимосвязи. Наконец, для проверки эффективности полученных результатов приводятся сравнения численного моделирования со стабильными и нестабильными случаями.
Оценка верхних границ двух категорий факторов помех и создание механизма измерения неопределенных весов двойного соединения являются основными задачами и проблемами. Таким образом, с одной стороны, предоставляются новые достаточные критерии верхних оценок нейтральных членов и кусочных аргументов, гарантирующие глобальную экспоненциальную устойчивость НПНС. С другой стороны, разрешенная замкнутая область весов двойной связи характеризуется трансцендентным уравнением с четырьмя переменными, основанным на предыдущем устойчивом NPRNN. Таким образом, два интерференционных фактора и двойные неопределенные веса связи взаимно ограничиваются в модели параметра-неопределенности NPRNN, что приводит к динамической эволюционной взаимосвязи. Наконец, для проверки эффективности полученных результатов приводятся сравнения численного моделирования со стабильными и нестабильными случаями.
Решение проблемы пасущихся коз: конфликт между красотой и прагматизмом
Роберт Дж. Маркс II
Закрытая форма ◽
Численная оценка ◽
Решение закрытой формы ◽
Трансцендентное уравнение ◽
Форма решения ◽
Решения закрытой формы ◽
Контурные интегралы ◽
Прикладной математик ◽
Чистый математик ◽
Идеал
Каково идеальное решение задачи по математике? Это зависит от вашей ботанической идеологии. Чистые математики преклоняются перед красотой математического результата. Особенно красивы решения закрытой формы. Инженеры и прикладные математики, напротив, ориентируются на результат независимо от его красоты. Если решение существует и может быть вычислено, этого достаточно. Работа сделана. Примером может служить решение задачи о пасущихся козлах. Недавно было найдено решение в замкнутой форме в виде отношения двух контурных интегралов для задачи о пасущихся козлах, и его красота вызвала восхищение чистых математиков. Для инженера и математика-прикладника численное решение задачи о пасущемся козле приходит из легко выводимого трансцендентного уравнения. Трансцендентное уравнение, известное какое-то время, не считалось достаточно красивым решением для чистых математиков, поэтому они продолжали поиски, пока не нашли решение в замкнутой форме. Численная оценка трансцендентного уравнения не так красива. Он не в закрытом виде. Но точность решения может быть непосредственно оценена с точностью до любой желаемой точности.
Чистые математики преклоняются перед красотой математического результата. Особенно красивы решения закрытой формы. Инженеры и прикладные математики, напротив, ориентируются на результат независимо от его красоты. Если решение существует и может быть вычислено, этого достаточно. Работа сделана. Примером может служить решение задачи о пасущихся козлах. Недавно было найдено решение в замкнутой форме в виде отношения двух контурных интегралов для задачи о пасущихся козлах, и его красота вызвала восхищение чистых математиков. Для инженера и математика-прикладника численное решение задачи о пасущемся козле приходит из легко выводимого трансцендентного уравнения. Трансцендентное уравнение, известное какое-то время, не считалось достаточно красивым решением для чистых математиков, поэтому они продолжали поиски, пока не нашли решение в замкнутой форме. Численная оценка трансцендентного уравнения не так красива. Он не в закрытом виде. Но точность решения может быть непосредственно оценена с точностью до любой желаемой точности. Чтобы проиллюстрировать это, мы выводим и решаем трансцендентное уравнение для обобщения задачи о пасущихся козлах.
Чтобы проиллюстрировать это, мы выводим и решаем трансцендентное уравнение для обобщения задачи о пасущихся козлах.
ЭФФЕКТИВНОЕ ПРИГОТОВЛЕНИЕ БИЭКСИТОНОВ В СИСТЕМЕ «КВАНТОВАЯ ТОЧКА-МЕТАЛЛИЧЕСКИЕ НАНОЧАСТИЦЫ» С ПОМОЩЬЮ ВКЛ-ВЫКЛ-ИМПУЛЬСОВ
Афанасий Смпоний ◽
Дионисис Стефанатос ◽
Эммануэль Паспалакис
Квантовая точка ◽
Последовательность импульсов ◽
Связанная система ◽
Лазерные импульсы ◽
Трансцендентное уравнение ◽
Металлическая наночастица ◽
Матричные уравнения ◽
Металлическая наночастица ◽
Линейно поляризованный ◽
Система наночастиц
Мы рассматриваем гибридную наноструктуру, состоящую из полупроводниковой квантовой точки, связанной с металлической наночастицей, и исследуем эффективное создание биэкситонного состояния в квантовой точке при запуске из основного состояния и использовании линейно поляризованных лазерных импульсов с двухпозиционной модуляцией. С помощью численного моделирования уравнений матрицы плотности связанной системы мы показываем, что простая последовательность импульсов включения-выключения-включения, ранее полученная для случая изолированной квантовой точки, может эффективно подготовить биэкситонное состояние даже в присутствии наночастицы. для различных межчастичных расстояний и сдвигов энергии биэкситона. Длительности импульсов в последовательности получаются из решения трансцендентного уравнения.
С помощью численного моделирования уравнений матрицы плотности связанной системы мы показываем, что простая последовательность импульсов включения-выключения-включения, ранее полученная для случая изолированной квантовой точки, может эффективно подготовить биэкситонное состояние даже в присутствии наночастицы. для различных межчастичных расстояний и сдвигов энергии биэкситона. Длительности импульсов в последовательности получаются из решения трансцендентного уравнения.
Топография дна и устойчивость морского ледяного покрова
Ольга Васильевна Сергиенко ◽
Дункан Дж. Уингхэм
Скорость накопления ◽
Градиент напряжения ◽
Ледяной щит ◽
Трансцендентное уравнение ◽
Позиция линии ◽
Линейный поток ◽
Ледяные потоки ◽
Топография кровати ◽
Линия заземления ◽
Стабильность
Абстрактный
В данной статье исследуется влияние топографии и прочности основания на положение линии заземления, поток и устойчивость быстро скользящих ледяных потоков. Это достигается за счет предположения, что плавучесть ледяного потока мала и того же порядка, что и продольный градиент напряжения. Сделав это предположение о масштабировании, роль базального градиента и скорости аккумуляции становится явной в выражении низшего порядка для потока льда на линии заземления, а также дает трансцендентное уравнение для положения линии наземной линии. Он также вводит в условия устойчивости члены по базисной кривизне и градиенту скорости накопления. Эти выражения возвращаются к общепринятым выражениям в обстоятельствах, когда градиент толщины на линии заземления велик, что, как показано, является следствием нелинейности потока. Поведение потока в линии заземления проиллюстрировано для различных топографий пластов и мощностей. Мы показываем, что при наличии топографии дна в горизонтальном масштабе в несколько десятков толщин льда поток и стабильность линии заземления имеют более сложные зависимости от уклона дна, чем те, которые связаны с «гипотезой нестабильности морского ледникового щита», и что нестабильные положения линии заземления могут возникать на проградных пластах, а также стабильные положения на ретроградных пластах.
Это достигается за счет предположения, что плавучесть ледяного потока мала и того же порядка, что и продольный градиент напряжения. Сделав это предположение о масштабировании, роль базального градиента и скорости аккумуляции становится явной в выражении низшего порядка для потока льда на линии заземления, а также дает трансцендентное уравнение для положения линии наземной линии. Он также вводит в условия устойчивости члены по базисной кривизне и градиенту скорости накопления. Эти выражения возвращаются к общепринятым выражениям в обстоятельствах, когда градиент толщины на линии заземления велик, что, как показано, является следствием нелинейности потока. Поведение потока в линии заземления проиллюстрировано для различных топографий пластов и мощностей. Мы показываем, что при наличии топографии дна в горизонтальном масштабе в несколько десятков толщин льда поток и стабильность линии заземления имеют более сложные зависимости от уклона дна, чем те, которые связаны с «гипотезой нестабильности морского ледникового щита», и что нестабильные положения линии заземления могут возникать на проградных пластах, а также стабильные положения на ретроградных пластах.
Решение трансцендентного уравнения источника тока Видлара с использованием обычных научных калькуляторов
Ахмед Обаид Мохамед
Источник тока ◽
Трансцендентное уравнение
ОЦЕНКА ПЕРЕМЕЩЕНИЯ КУЛАЧКОВОГО ПОСЛЕДОВАТЕЛЯ МЕТОДОМ REGULA FALSI
КОЛАВОЛЕ АДЕСОЛА ОЛАДЕХО ◽
ДАРЕ АДЕРИБИГБЕ АДЕТАН ◽
АДЕКОЛА ОЛАЙНКА ОКЕ ◽
РАХАМАН АБУ ◽
ГАНИУ АЙУЛА ЛАМИД
Высокоскоростной ◽
Угловое смещение ◽
Трансцендентное уравнение ◽
Начальная догадка ◽
Наборы данных ◽
кулачковый последователь ◽
Высокоскоростное вращение ◽
скорость вращения ◽
Открытие и закрытие ◽
Метод Регулы Фальси
Кулачок — это механический компонент, который преобразует круговое движение в возвратно-поступательное с помощью сопряженного компонента, называемого толкателем. Основная цель этой работы состояла в том, чтобы изучить и проанализировать смещение кулачкового толкателя с помощью метода Regula Falsi и проверить его ввод с помощью моделирования MATLAB и FORTRAN. Было проведено исследование угла поворота и перемещения толкателя, равного радиусу кулачка, заданного трансцендентным уравнением для нахождения точного решения. Такие параметры, как начальное предположение, окончательное предположение, счетчик итераций и желаемое смещение, участвуют в определении углового смещения кулачковой системы при вращении с высокой скоростью. Анализ был выполнен с использованием компьютерного программирования, которое позволяет проверить полученные результаты и установить, являются ли входные данные правильными или нет для перемещения в системе толкателя кулачка. Вывод компьютера показал результаты двух наборов данных, которые дали решения, и двух, которые не дали. Результаты показали, что программу можно использовать для нахождения углового смещения, соответствующего заданному смещению толкателя для любого кулачка; если функция CAMF изменена, чтобы включить соответствующую функцию радиуса, r(x). Результаты также показали, что при половинном цикле вращения кулачка, что эквивалентно (x = 3,142 рад), есть решение, которое обеспечило бы желаемое перемещение толкателя (открытие и закрытие клапанов).
Было проведено исследование угла поворота и перемещения толкателя, равного радиусу кулачка, заданного трансцендентным уравнением для нахождения точного решения. Такие параметры, как начальное предположение, окончательное предположение, счетчик итераций и желаемое смещение, участвуют в определении углового смещения кулачковой системы при вращении с высокой скоростью. Анализ был выполнен с использованием компьютерного программирования, которое позволяет проверить полученные результаты и установить, являются ли входные данные правильными или нет для перемещения в системе толкателя кулачка. Вывод компьютера показал результаты двух наборов данных, которые дали решения, и двух, которые не дали. Результаты показали, что программу можно использовать для нахождения углового смещения, соответствующего заданному смещению толкателя для любого кулачка; если функция CAMF изменена, чтобы включить соответствующую функцию радиуса, r(x). Результаты также показали, что при половинном цикле вращения кулачка, что эквивалентно (x = 3,142 рад), есть решение, которое обеспечило бы желаемое перемещение толкателя (открытие и закрытие клапанов).
Асимптотика главного собственного значения лапласиана в двумерных периодических областях с малыми ловушками
Ф. ПАКИН-ЛЕФЕВР ◽
С. ИЯНИВУРА ◽
М.Дж. УОРД
Функция Грина ◽
Функция Грина ◽
Основное собственное значение ◽
Представление серии ◽
Трансцендентное уравнение ◽
Схема итерации ◽
Точки решетки ◽
Обычная часть ◽ 92}\]
. Разложение этого главного собственного значения происходит по степеням
\[\nu \equiv — 1/\log (\varepsilon {d_c})\]
, где D
с
— логарифмическая емкость набора ловушек. Явное трехчленное приближение для этого главного собственного значения получено с использованием сильной теории локализованных возмущений, при этом коэффициенты в этом ряду оцениваются численно с использованием явной формулы для нейтральной к источнику периодической функции Грина и ее регулярной части. Кроме того, в терминах регулярной части периодической функции Гельмгольца Грина выводится трансцендентное уравнение для улучшенного приближения к главному собственному значению, которое эффективно суммирует все логарифмические члены по степеням v. Используя метод суммирования Эвальда, чтобы сначала получить быстро сходящееся представление бесконечного ряда для этой регулярной части, простая схема итераций Ньютона для трансцендентного уравнения реализуется для численной оценки улучшенного «логарифмического» приближения к основному собственному значению. Из численного расчета задачи на собственные значения УЧП, заданной на фундаментальной ячейке Вигнера–Зейтца (WS) для решетки, показано, что трехчленная асимптотика для главного собственного значения хорошо согласуется с численным результатом только для довольно малой ловушки радиус. Напротив, асимптотический результат с логарифмической суммой обеспечивает очень близкое приближение к главному собственному значению, даже когда радиус ловушки лишь умеренно мал. Для круглой ловушки выводятся первые несколько трансцендентных поправочных членов, которые дополнительно улучшают логарифмическую аппроксимацию для главного собственного значения. Наконец, численно показано, что среди всех решеток Браве с фиксированной площадью примитивной ячейки главное собственное значение максимизируется при правильном гексагональном расположении ловушек.
Используя метод суммирования Эвальда, чтобы сначала получить быстро сходящееся представление бесконечного ряда для этой регулярной части, простая схема итераций Ньютона для трансцендентного уравнения реализуется для численной оценки улучшенного «логарифмического» приближения к основному собственному значению. Из численного расчета задачи на собственные значения УЧП, заданной на фундаментальной ячейке Вигнера–Зейтца (WS) для решетки, показано, что трехчленная асимптотика для главного собственного значения хорошо согласуется с численным результатом только для довольно малой ловушки радиус. Напротив, асимптотический результат с логарифмической суммой обеспечивает очень близкое приближение к главному собственному значению, даже когда радиус ловушки лишь умеренно мал. Для круглой ловушки выводятся первые несколько трансцендентных поправочных членов, которые дополнительно улучшают логарифмическую аппроксимацию для главного собственного значения. Наконец, численно показано, что среди всех решеток Браве с фиксированной площадью примитивной ячейки главное собственное значение максимизируется при правильном гексагональном расположении ловушек.
Аналитические решения дробной математической модели концентрации опухолевых клеток при постоянной скорости гибели
Наджма Ахмед ◽
Нехад Али Шах ◽
Фарман Али ◽
Дмитрий Виеру ◽
Ф.Д. Заман
Математические модели ◽
Раковые клетки ◽
Опухолевые клетки ◽
Аналитические решения ◽
Интегральное преобразование ◽
Преобразование Ганкеля ◽
Трансцендентное уравнение ◽
Эволюция опухоли ◽
Радиальная координата ◽
Положительные корни
Аналитически исследованы две обобщенные математические модели с памятью на концентрацию опухолевых клеток с использованием методов цилиндрической координаты и интегрального преобразования. Обобщение состоит в формулировке двух математических моделей с дробной производной Капуто-времени, моделей, которые подходят для того, чтобы подчеркнуть влияние истории эволюции опухоли на нынешнее поведение концентрации раковых клеток. На границе области рассматривалась колеблющаяся во времени концентрация раковых клеток. Найдены аналитические решения дробно-дифференциальных уравнений математических моделей с использованием преобразования Лапласа по переменной времени и конечного преобразования Ганкеля по радиальной координате. Необходимые в нашем исследовании положительные корни трансцендентного уравнения с функцией Бесселя J0(r)=0 определялись с помощью подпрограммы rn=root(J0(r),r,(2n−1)π/4, (2n+3)π/4),n=1,2,… программы Mathcad 15. Установлено, что эффекты памяти сильнее проявляются при малых значениях времени t. Этот аспект выделен на графических иллюстрациях, анализирующих поведение концентрации опухолевых клеток. Кроме того, концентрация раковых клеток симметрична относительно радиального угла, и ее значения стремятся к нулю при больших значениях времени t.
На границе области рассматривалась колеблющаяся во времени концентрация раковых клеток. Найдены аналитические решения дробно-дифференциальных уравнений математических моделей с использованием преобразования Лапласа по переменной времени и конечного преобразования Ганкеля по радиальной координате. Необходимые в нашем исследовании положительные корни трансцендентного уравнения с функцией Бесселя J0(r)=0 определялись с помощью подпрограммы rn=root(J0(r),r,(2n−1)π/4, (2n+3)π/4),n=1,2,… программы Mathcad 15. Установлено, что эффекты памяти сильнее проявляются при малых значениях времени t. Этот аспект выделен на графических иллюстрациях, анализирующих поведение концентрации опухолевых клеток. Кроме того, концентрация раковых клеток симметрична относительно радиального угла, и ее значения стремятся к нулю при больших значениях времени t.
Ферромагнитный гистерезис по статистической сумме Гейзенберга и методы его обработки в моделировании намагниченности наночастиц
Нана Чычкало ◽
Сергей Лебле
Раздел Функция ◽
Петли гистерезиса ◽
Система уравнений ◽
Трансцендентное уравнение ◽
Сферические частицы ◽
Функции раздела ◽
Биржевой интеграл ◽
Поверхностные слои ◽
Уравнение материала ◽
Различия
Теория намагничивания Гейзенберга {\it ab initio} разработана для применения к многослойным наночастицам. Теория основана на модификации функций распределения и статистической суммы с учетом разницы между обменным интегралом и числами ближайших соседей, которые изменяют систему результирующего трансцендентного уравнения для намагниченности и ее обращения, формируя либо кривую парамагнитного типа, либо картины петель гистерезиса. Уравнения получены в рамках построения статистической суммы Гейзенберга путем гейтлеровской диагонализации матрицы энергии через неприводимые представления перестановочной группы симметрии. Комбинация с распределением Гаусса дает явное выражение статистической суммы в асимптотическом пределе] при большом диапазоне спинов через трансцендентную функцию. Обменный интеграл, как параметр уравнения состояния (материального уравнения), вычисляется по значению температуры Кюри с помощью формулы, полученной в рамках представленной теории. Предложены методы обработки данных совместного решения системы уравнений материала. Многозначная функция петли гистерезиса найдена путем сочетания графического подхода и специальной процедуры исключения ошибочных пиков и провалов паттернов.
Теория основана на модификации функций распределения и статистической суммы с учетом разницы между обменным интегралом и числами ближайших соседей, которые изменяют систему результирующего трансцендентного уравнения для намагниченности и ее обращения, формируя либо кривую парамагнитного типа, либо картины петель гистерезиса. Уравнения получены в рамках построения статистической суммы Гейзенберга путем гейтлеровской диагонализации матрицы энергии через неприводимые представления перестановочной группы симметрии. Комбинация с распределением Гаусса дает явное выражение статистической суммы в асимптотическом пределе] при большом диапазоне спинов через трансцендентную функцию. Обменный интеграл, как параметр уравнения состояния (материального уравнения), вычисляется по значению температуры Кюри с помощью формулы, полученной в рамках представленной теории. Предложены методы обработки данных совместного решения системы уравнений материала. Многозначная функция петли гистерезиса найдена путем сочетания графического подхода и специальной процедуры исключения ошибочных пиков и провалов паттернов. Теория и методы расчета применяются к сферическим частицам с учетом отдельных поверхностных слоев. Вклад поверхностных слоев, заданных числом ближайших соседей и обменных интегралов, в общую намагниченность исследуется для двухслойной и трехслойной моделей, обсуждаются и сравниваются графически.
Теория и методы расчета применяются к сферическим частицам с учетом отдельных поверхностных слоев. Вклад поверхностных слоев, заданных числом ближайших соседей и обменных интегралов, в общую намагниченность исследуется для двухслойной и трехслойной моделей, обсуждаются и сравниваются графически.
Загрузи больше …
Mathematica 7, Иоганн Кеплер и трансцендентальные корни — блог Вольфрама
Каждый, кто изучал математику в средней школе, знает о полиномиальных уравнениях. Но как быть с уравнениями, включающими другие функции? Произнесите уравнения типа x == 1 — Sin[x].
Это трансцендентные уравнения, и они проявляются в миллионах различных областей математических приложений. Но о них редко говорят — возможно, потому, что они в каком-то смысле смущают: математики мало что могут сказать о них.
Полиномиальные уравнения и алгебраические числа, представляющие их решения, стали одним из величайших достижений чистой математики. За последние полтысячелетия на полиномиальных уравнениях была построена огромная математическая конструкция.
А вот с трансцендентными уравнениями почти ничего не сделано.
Дело не в том, что они не важны. Фактически, то, что многие люди считают самым первым компьютером, сделанным из дерева Вильгельмом Шикардом в 1623 году, было построено специально для того, чтобы помогать находить решения уравнений вида x == 1 — e Sin[x].
Иоганн Кеплер находился в процессе построения своих астрономических таблиц Рудольфина, и его убийственная технология определения долготы планеты в заданное время требовала решения того, что сейчас называется уравнением Кеплера: по сути, трансцендентного уравнения x == 1 — e Грех [х].
Приложив значительные усилия и, возможно, с помощью компьютера, Кеплер составил таблицу решений этого уравнения:
Трансцендентные уравнения возникали много раз по мере развития математической физики — особенно в краевых задачах и задачах на собственные значения.
Но, в отличие от алгебраических чисел, очень мало было известно о решениях даже очень ограниченных классов трансцендентных уравнений.
Одним из нововведений Mathematica 3 было введение объектов Root[], которые могли символически представлять любой корень любого полиномиального уравнения, и с ними можно было символически манипулировать, как с любым другим точным числом.
Около десяти лет назад мы начали думать о том, можно ли расширить концепцию объектов Root[] на трансцендентные уравнения.
Сначала это казалось пугающим. Везде были теоремы о неразрешимости (из комбинаций тригонометрических функций легко составить произвольное диофантово уравнение). И конструктивных общих теорем почти не было.
Однако были признаки надежды. Такие вещи, как теорема Вейерштрасса о факторизации, которая является трансцендентным обобщением основной теоремы алгебры, создавали впечатление, что должен существовать систематический способ подсчета и обозначения корней для многих трансцендентных уравнений.
Несколько лет назад у нас появились конкретные идеи о том, как это могло бы работать. Поначалу они казались совершенно непрактичными. Но постепенно мы увидели, как использовать всевозможные расширенные функции символьных и числовых вычислений в системе Mathematica , чтобы сделать ее практичной.
Но постепенно мы увидели, как использовать всевозможные расширенные функции символьных и числовых вычислений в системе Mathematica , чтобы сделать ее практичной.
А в Mathematica 7 мы собрали все вместе, чтобы впервые создать систематизированную обработку большого класса трансцендентных корней.
До Mathematica 7 мы могли получать точные решения только для уравнений, которые можно было свести к полиномам (и обратным функциям). Но в Mathematica 7 с трансцендентными корнями уравнения, которые мы могли решить за последние 20 лет, представляют собой набор нулевой меры по сравнению с тем, что мы можем решить сегодня!
Так как же нам решать трансцендентные уравнения?
Мы начнем с рассмотрения класса голоморфных функций — по существу многочленов бесконечной степени. Голоморфная функция часто имеет бесконечно много корней. Но ключевым фактом является то, что корни всегда счетны, и, что более важно, в данной замкнутой и ограниченной области может быть только конечное число корней.
Теперь мы можем использовать сложный анализ. Учитывая область, мы можем сказать, сколько корней находится внутри нее, либо непосредственно вычислив число оборотов вокруг ее границы, либо используя численное интегрирование и теорему Коши.
Как только мы подсчитали количество корней в регионе, у нас есть множество методов для определения их приблизительного местоположения. (Некоторые методы основаны на вычислительной геометрии и пересечениях кривых, некоторые — на арифметике комплексных интервалов, а некоторые — на обобщенных собственных значениях, полученных из теоремы Коши.) Имея приблизительные положения корней, мы затем используем ньютоновские итерационные методы, чтобы сосредоточиться на корнеплоды. И, наконец, мы используем интервальную арифметику Mathematica, чтобы доказать, что внутри каждой небольшой области, которую мы идентифицировали, может быть только один корень.
(Здесь есть некоторая тонкость. Доказательство нулевой эквивалентности, вообще говоря, неразрешимо, и это проявляется в том, что в патологических случаях в принципе может потребоваться неограниченно большая точность, чтобы отличить несколько корней от близко расположенных одиночных корней. )
)
In В некотором смысле фундаментальная проблема обращения с трансцендентными корнями заключается в том, чтобы найти способ их обозначить. И если мы можем получить область, которая, как известно, содержит только один корень, то мы можем пометить этот корень в Mathematica , задав число произвольной точности, значение которого является центром области, а точность дает граничный радиус для области. .
Еще до Mathematica 7 у нас были символические объекты Root для представления корней уравнения: Root[f,…] представлял корень уравнения f[x]==0. Но до Mathematica 7 f[x] должен был быть полиномом.
Тем не менее, мы планировали заранее. Так что в Mathematica 7 все, что нам нужно было сделать, это сказать, что в Root[f,…] f[x] может быть трансцендентной функцией, а затем изобрести способ маркировки различных объектов Root.
Но, сделав это, мы получим объект Root[…], который обеспечивает точное символьное описание любого трансцендентного корня — так же, как Sqrt[2] или Pi^2 обеспечивают точное символическое описание чисел.
А поскольку система Mathematica последовательно символична, мы можем сразу же использовать любое из этих символических описаний чисел везде, где в системе нам нужно число — будь то в уравнениях или неравенствах, или в линейной алгебре, или в аргументе функции, или где угодно .
В некотором смысле то, что мы делаем с трансцендентными корнями, заключается в том, чтобы обобщить Mathematica так же, как была обобщена сама математика.
Первый содержит целые числа. Затем вводятся рациональные числа для решения линейных уравнений. Затем алгебраические числа для решения полиномиальных уравнений.
Теперь система Mathematica 7 вводит еще один класс «конструктивных чисел» — трансцендентные корни, решающие трансцендентные уравнения. И тогда это дает нам возможность работать с этими трансцендентными корнями.
Вот пример. Во-первых, мы используем Reduce, чтобы перейти от уравнения к символическому трансцендентному корню.
Мы можем вычислить корень с любой точностью.
Или мы можем просто использовать его символически и получить точные результаты.
Mathematica 7 предлагает всевозможные способы работы с трансцендентными уравнениями.
Он имеет целый набор подстановок и преобразований для преобразования уравнений, представленных трансцендентным образом, в композиции полиномиальных уравнений и функций с определенными обратными.
Обычно лучше всего, когда в трансцендентном уравнении есть конечный диапазон значений переменных. Но он может обрабатывать бесконечные диапазоны, когда задействованные функции имеют периодичность.
Существуют и другие классы трансцендентных уравнений, которые Mathematica 7 обрабатывает совершенно другими методами. Например, он разрешает вложенные логарифмические уравнения над вещественными числами, создавая поля Харди и выполняя символьный анализ структур выражений.
Нам удалось продвинуться на удивление далеко с трансцендентными уравнениями в Mathematica 7. Но, конечно, это еще не конец истории.
Но, конечно, это еще не конец истории.
В Mathematica 7 мы имеем дело с голоморфными функциями. Мы не придумали, как бороться с обрезкой веток или точками накопления. Или многомерные функции. Или как сделать RootReduce[] для комбинаций трансцендентных корней.
Но очень приятно видеть, что некоторая чистая математика, которую мы сделали, немедленно ввела целый новый класс уравнений, которые можно обрабатывать символически, и открыла всевозможные новые области применения.
Также приятно осознавать, что — спустя 385 лет — убийственная технология Кеплера для построения астрономических таблиц может быть сведена всего к одной строке ввода Mathematica 7.
Справочник по численным методам решения алгебраических и трансцендентных уравнений
Select country/regionUnited States of AmericaUnited KingdomAfghanistanÅland IslandsAlbaniaAlgeriaAmerican SamoaAndorraAngolaAnguillaAntigua and BarbudaArgentinaArmeniaArubaAustraliaAustriaAzerbaijanBahamasBahrainBangladeshBarbadosBelgiumBelizeBeninBermudaBhutanBoliviaBonaire, Sint Eustatius and SabaBosnia and HerzegovinaBotswanaBrazilBritish Indian Ocean TerritoryBritish Virgin IslandsBruneiBulgariaBurkina FasoBurundiCambodiaCameroonCanadaCanary IslandsCape VerdeCayman IslandsCentral African RepublicChadChileChinaChristmas IslandCocos (Keeling) IslandsColombiaComorosCongoCook IslandsCosta RicaCroatiaCubaCuraçaoCyprusCzech RepublicDemocratic Republic of the CongoDenmarkDjiboutiDominicaDominican RepublicEcuadorEgyptEl SalvadorEquatorial GuineaEritreaEstoniaEthiopiaFalkland Islands (Malvinas )Фарерские островаФедеративные Штаты МикронезииФиджиФинляндияФранцияФранцузская ГвианаФранцузская ПолинезияГабонГамбияГрузияГерманияГанаГибралтарГрецияГренландияГренадаГваделупаГуамГватемалаГернсиГвинеяG uinea-BissauGuyanaHaitiHondurasHong KongHungaryIcelandIndiaIndonesiaIranIraqIrelandIsle of ManIsraelItalyJamaicaJapanJerseyJordanKazakhstanKenyaKiribatiKuwaitKyrgyzstanLaoLatviaLesothoLiberiaLibyaLiechtensteinLuxembourgMacaoMacedoniaMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall IslandsMartiniqueMauritaniaMauritiusMayotteMexicoMoldovaMonacoMongoliaMontenegroMontserratMoroccoMozambiqueMyanmarNamibiaNepalNetherlandsNew CaledoniaNew ZealandNicaraguaNigerNiueNorfolk IslandNorth KoreaNorthern Mariana IslandsNorwayOmanPakistanPalauPanamaPapua New GuineaParaguayPeruPhilippinesPitcairnPolandPortugalPuerto RicoQatarRéunionRomaniaRwandaSaint BarthélemySaint HelenaSaint Kitts and NevisSaint LuciaSaint Martin (French part)Saint Pierre and MiquelonSaint Vincent and the GrenadinesSamoaSan MarinoSao Tome and PrincipeSaudi ArabiaSenegalSerbiaSeychellesSierra LeoneSingaporeSint Maarten (Dutch part)SlovakiaSloveniaSolomon IslandsSomaliaSouth AfricaSouth Georgia и Южные Сандвичевы острова Южная Кор eaSouth SudanSpainSri LankaSudanSurinameSvalbard and Jan MayenSwazilandSwedenSwitzerlandSyriaTaiwanTajikistanTanzaniaThailandTimor LesteTogoTokelauTongaTrinidad and TobagoTunisiaTurkeyTurkmenistanTurks and Caicos IslandsTuvaluUgandaUkraineUnited Arab EmiratesUruguayUS Virgin IslandsUzbekistanVanuatuVatican CityVenezuelaVietnamWallis and FutunaWestern SaharaYemenZambiaZimbabwe
Варианты покупкиЭлектронная книга $72,95
Налог с продаж рассчитывается при оформлении заказа
Бесплатная доставка по всему миру
Нет минимального заказа
Описание алгебраические и трансцендентные уравнения.
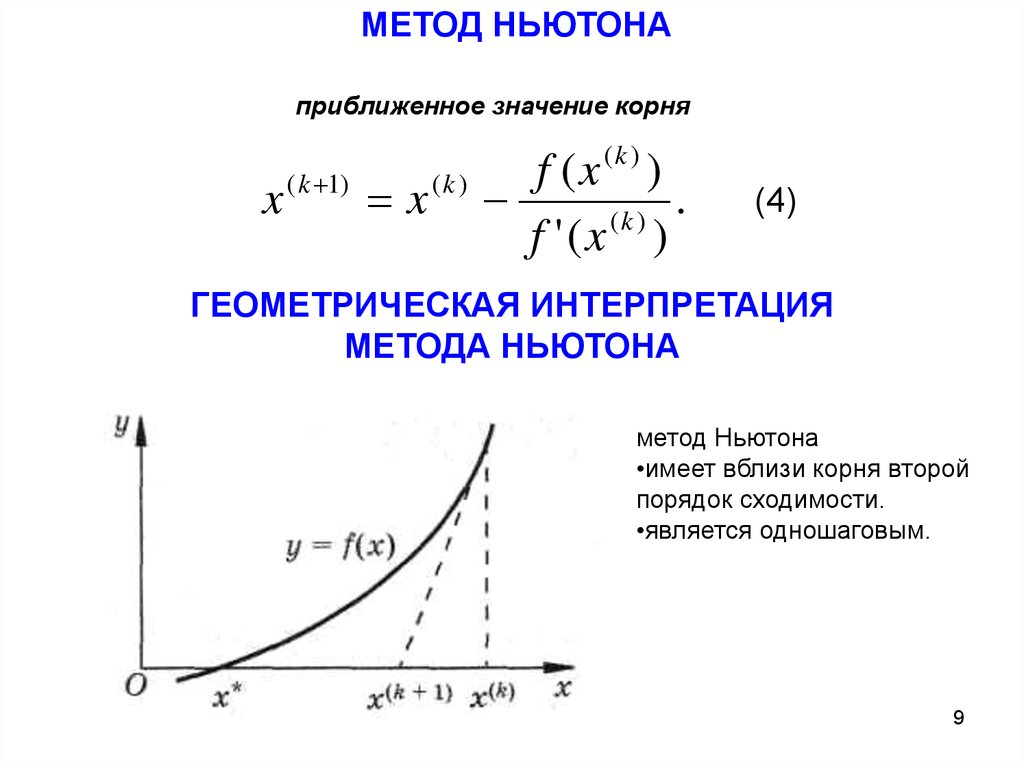 Эта книга указывает хорошо обоснованный план решения приближенного уравнения. Эта книга, состоящая из шести глав, начинается с обзора решения различных уравнений. Затем в этом тексте излагается нетрадиционная теория решения приближенных уравнений. В других главах рассматриваются приближенные методы вычисления корней алгебраических уравнений. В этой книге обсуждаются также методы уточнения корней, необходимые для практического применения метода Берстоя. В последней главе рассматриваются методы решения одновременных линейных уравнений, которые подразделяются на прямые методы и методы последовательных приближений. Эта книга является ценным пособием для студентов, инженеров и научных работников институтов и промышленных предприятий, применяющих математические методы при решении технических задач.
Эта книга указывает хорошо обоснованный план решения приближенного уравнения. Эта книга, состоящая из шести глав, начинается с обзора решения различных уравнений. Затем в этом тексте излагается нетрадиционная теория решения приближенных уравнений. В других главах рассматриваются приближенные методы вычисления корней алгебраических уравнений. В этой книге обсуждаются также методы уточнения корней, необходимые для практического применения метода Берстоя. В последней главе рассматриваются методы решения одновременных линейных уравнений, которые подразделяются на прямые методы и методы последовательных приближений. Эта книга является ценным пособием для студентов, инженеров и научных работников институтов и промышленных предприятий, применяющих математические методы при решении технических задач.Содержание
-
Предисловие
Предисловие автора
Введение
Глава I. Исходные сведения о многочленах и трансцендентных функциях
Точное деление
3. 2. Теорема Безу
2. Теорема Безу
3.3. Редукция порядка алгебраического уравнения 90–422 3.4. Алгоритм Евклида. Извлечение кратных корней
4. Изменение аргумента многочлена
4.1. Процесс последовательного деления
4.2. Вычисление значений производных
5. Многочлены с вещественными и комплексными коэффициентами
5.1. Комплексно-сопряженные числа
5.2. Замена уравнения с комплексными коэффициентами уравнением с вещественными коэффициентами
5.3. Замена уравнения с комплексными коэффициентами одновременными уравнениями 904-22 5.4. Метод А.П.Доморьяда
5.5. Сопряженное свойство комплексных корней 90–422 5.6. Понижение порядка уравнения в случае комплексного корня
6. Расчетные схемы для умножения и деления многочленов
6.1. Расчетная схема для умножения многочленов
6.2. Стрип-метод
6.3. Схема деления одного многочлена на другой
6.4. Полосовой метод (для деления)
7. Схема Горнера и ее применение. Вычисление значения многочлена
7. 1. Расчетная схема преобразования вида у = х — а аргумента
1. Расчетная схема преобразования вида у = х — а аргумента
7.2. Вычисление значения полинома с действительными коэффициентами для комплексного значения аргумента x = a + iβ
7.3. Вычисление производной комплексного значения аргумента
8. Число корней и пределы корней многочлена
8.1. Количество корней
8.2. Определение пределов корней по теореме Маклорена
8.3. Пределы для комплексных корней
Глава II. Операции с приближенными числами
1. Приближенное число. Абсолютные и относительные погрешности
1.1. Написание приблизительных чисел
1.2. Сокращенное написание приблизительных чисел
2. Округление
3. Операции с приближенными числами
3.1. Ошибка суммы
3.2. Ошибка продукта
3.3. Суммирование ошибок
4. Погрешность вычисления значения многочлена
5. Решение приближенных уравнений
5.1. Безусловные, условные и полные ошибки
5.2. Вычисление безусловной ошибки
6. План решения приближенного уравнения
6. 1. Расчет условной ошибки
1. Расчет условной ошибки
6.2. Пример
7. Снижение точности при понижении порядка алгебраического выражения
Глава III. Методы приближенного определения корней
1. Графический метод
1.1. Решение уравнений
1.2. Некоторые особенности алгебраических уравнений
2. Приближенное определение корней многочлена с помощью формул Виета
2.1. Формула Вьетнама
2.2. Вычисление больших корней
2.3. Вычисление меньших корней
3. Метод Н.И.Лобачевского
3.1. Основная идея метода
3.2. Преобразование многочлена
3.3. Расчетная схема преобразования многочлена
3.4. Вычисление модулей корней 90–422 3.5. Вычисление корней с известными модулями
3.6. Пара неизвестных корней
3.7. Две пары комплексных корней с разными модулями
3.8. Метод Бродецкого-Смиля. Основная идея
3.9. Метод Бродецкого-Смиля. Расчетная схема
3.10. Формулы Беста
3.11. Потеря точности в методе Лобачевского
3.12. Пример
3. 13. Решение трансцендентных уравнений
13. Решение трансцендентных уравнений
4. Метод И. Бернулли
4.1. Расчетная схема для случая алгебраического уравнения
4.2. Свойство последовательности {µk}
4.3. Вычисление корней
4.4. Вычисление вторых по величине корней
4.5. Потеря точности при вычислении первого корня
4.6. Скорость сходимости
4.7. Общее замечание
4.8. Пример
4.9. Решение трансцендентных уравнений
5. Метод итераций
5.1. Суть метода
5.2. Условия сходимости
5.3. Скорость сходимости
5.4. Потеря точности
5.5. Пример
6. Метод Лина
6.1. Суть метода
6.2. Расчетная схема
6.3. Условия и быстрота сходимости 7. Метод Н.В.Палувера
7.1. Основная идея метода
7.2. Расчетная схема
8. Сравнение методов
Глава IV. Методы получения более точных корней, уже найденных
1. Метод линейной интерполяции
1.1. Расчеты методом линейной интерполяции
1.2. Сходимость процесса
1.3. Пример
2. Метод Ньютона
Метод Ньютона
2.1. Расчеты
2.2. О точности вычислений
2.2. Примеры
2.4. Обобщенный метод Ньютона
3. Метод Берстой
3.1. Суть метода
3.2. Расчетная схема
3.3. Пример
3.4. Применение метода вычисления комплексных корней с известными модулями
4. Метод А.Ю.Белостоцкого
4.1. Суть метода
4.2. Расчетная схема
4.3. Пример
5. Итерация с квадратичной сходимостью
5.1. Основная идея метода
5.2. Первый метод вычисления К(х)
5.3. Второй метод вычисления К(х) 904-22 5.4. Повышение точности вещественных корней
5.5. Повышение точности квадратных делителей
6. Методы улучшения сходимости
6.1. Сходимость, как у геометрической прогрессии
6.2. Осцилляторная сходимость
6.3. Квадратичная сходимость
6.4. Применение методов улучшения сходимости
6.5. Примеры
6.6. Улучшение сходимости в методе Лина
7. Сравнение методов
Глава V. Решение уравнений низких порядков и извлечение корней
1. Квадратные уравнения
Квадратные уравнения
1.1. Общие формулы
1.2. Вычисление корней с помощью логарифмической линейки
2. Уравнения третьего порядка
2.1. Решение с помощью таблиц
2.2. Формула Кардано
2.3. Вычисление корней с помощью логарифмической линейки
3. Уравнения четвертого порядка
4. Уравнения пятого порядка
5. Извлечение корней
5.1. Метод Ньютона
5.2. Обобщение метода Ньютона 90–422 5.3. Метод итерации
5.4. Итерация с квадратичной сходимостью
Глава VI. Решение одновременных уравнений
1. Метод исключения
2. Графический метод
3. Метод итерации
3.1. Расчетная схема
3.2. Условия сходимости
3.3. Метод Зейделя
3.4. Скорость сходимости
3.5. Пример
4. Метод Ньютона
4.1. Суть метода
4.2. Пример
4.3. Обобщенные методы
4.4. Наблюдение
5· Метод наискорейшего спуска
6. Сравнение методов решения одновременных нелинейных уравнений
7. Методы решения одновременных линейных уравнений
Приложение — Таблица для решения кубических уравнений
Литература
Index
Product details
- No.
 of pages: 216
of pages: 216 - Language: English
- Copyright: © Pergamon 1961
- Published: January 1, 1961
- Imprint: Pergamon
- eBook ISBN: 9781483225678
Об авторе
Загускин В.Л.
Рейтинги и обзоры
Написать рецензию
К настоящему времени нет отзывов к «Справочник по численным методам решения алгебраических и трансцендентных уравнений»
Решение трансцендентных уравнений MCQ [Бесплатный PDF] — Целевой вопрос Ответ на решение викторины по трансцендентным уравнениям ставим метод Bisection?
- Решения для брекетинга
- Графическое решение
- Эмпирические решения
- Пробные решения
Ответ (Подробное решение ниже)
Вариант 1: Решения в скобках
Объяснение:
Методы кронштейнов:
- Все методы Брекирования всегда сочетаются.
- Мы должны начать с начального интервала [a,b], где f(a) и f(b) имеют противоположные знаки.

- Поскольку график y = f(x) непрерывной функции непрерывен, он пересечет абсциссу в точке с нулем x = ‘a’, лежащим где-то в интервале [a,b].
- Одним из способов проверки численного метода решения уравнения f(x) = 0 является проверка его работоспособности на многочлене, корни которого известны.
Метод деления пополам:
Используется для поиска корня функции. Корень функции f(x) = a такой, что f(a)= 0
Свойство: если функция f(x) непрерывна на отрезке [a…b] и знак f(a) ≠ знак f (б). Существует значение c, принадлежащее [a…b], такое, что f(c) = 0, означает, что c является корнем между [a….b]
Примечание:
Метод деления пополам разрезает интервал на 2 половины и проверяет, какая половина содержит корень уравнения.
1) Допустим интервал [a, b] .
2) Разрезать интервал посередине, чтобы найти m : m = (a + b)/2
3) Знак f(m) не совпадает с f(a), продолжить поиск в новом интервале.
Решение трансцендентных уравнений MCQ Вопрос 2:
Первое приближение к вещественному корню уравнения x 3 — 2×2 — 2 = 0 по методу regula falsi между 2 и 3 равно
- 2,95
- 2,22
- 2,56
- 2,09
Ответ (подробное решение ниже)
Вариант 2:
В заданном интервале [a,b], если f(a) и f(b) имеют разные знаки, то аппроксимация корня с помощью метода ложных правил определяется выражением
\({x_1} = \frac{ {a\;f\left( b \right) — b\;f\left( a \right)}}{{f\left( b \right) — f\left( a \right)}} \)
здесь а = 2, b = 3
f(a) = 8 — 8 — 2 = — 2, f(b) = 7,
Первое приближение будет
\(x_1= \frac{{\left( 2 \right)\left( {7 } \right) — \left( 3 \right)\left( { — 2} \right)}}{{7- \left( { -2} \right)}}\)
⇒ x1 = 2,22
Решение трансцендентных уравнений MCQ Вопрос 3:
Корень уравнения x 3 – 4x – 9 = 0 с использованием метода деления пополам в четыре этапа:0587
Ответ (подробное решение ниже)
Вариант 2 : 2,6875
Пусть f(x) = x 3 – 4x – 9
Поскольку f(2) отрицательно, а f(3) положительно, корень лежит между 2 и 3
Первое приближение к корню равно
\({x_1} = \frac{1}{2}\left( {2 + 3} \right) = 2,5\)
Тогда f(x 1 ) = 2,5 3 – 4(2,5) – 9 = -3,375
т. е. отрицательно. Корень лежит между x 1 и 3. Таким образом, второе приближение к корню равно
е. отрицательно. Корень лежит между x 1 и 3. Таким образом, второе приближение к корню равно
\({x_2} = \frac{1}{2}\left( {{x_1} + 3} \right) = 2,75\)
Тогда f(x 2 ) = (2,75) 3 – 4(2,75) – 9 = 0,7969, т.е. положительный.
Корень лежит между x 1 и x 2 . Таким образом, третье приближение к корню равно
\({x_3} = \frac{1}{2}\left( {{x_1} + {x_2}} \right) = 2,625\)
Тогда f(x 3 ) = (2,625) 3 – 4(2,625) – 9 = -1,4121 т.е. отрицательное
Корень лежит между x 2 и х 3 . Таким образом, четвертое приближение к корню равно
\({x_4} = \frac{1}{2}\left( {{x_2} + {x_3}} \right) = 2,6875\)
Следовательно, корень 2,6875 примерно.
Следовательно, вариант 2 является правильным вариантом.
Решение трансцендентных уравнений MCQ Вопрос 4:
Вычислить корень функции f(x) = x2 – 3 после двух итераций методом деления пополам на интервале [0, 2]
- 1,5
- 2,5
- 3,5
- 4,5
Ответ (подробное решение ниже)
Опция 1: 1,5
Объяснение:
Дайте X 0 = 0,0643
. = -3 = -ve, f(x1) = 1 = +ve
= -3 = -ve, f(x1) = 1 = +ve
Итак, корень лежит между 0 и 2
1-я итерация:
\({x_2} = \frac{{0 + 2}}{2 } = 1\)
f(x 2 ) = 1 – 3 = -2 (-ve)
Итак, корень лежит между 1 и 2
2-я итерация:
\({x_3} = \frac{{1 + 3}}{2}\)
∴ x 3 = 1,5
Решение трансцендентных уравнений MCQ Вопрос 5:
Принимая x0 = 0, x1 = 1 (первоначальные предположения) значение x после первого шага для уравнения x = e – x с использованием метода Regula-falsi:
- 0,613
- 1,456
- 0,143
- 0,956
- Метод ложного положения гарантированно сходится.
- Сходимость медленная, так как она сходится первого порядка.

- Это не обязательно монотонная сходимость к корню, но чаще всего она превосходит метод деления пополам.
- точка пересечения оси y и кривой AB
- точка пересечения оси y и хорды AB
- точка пересечения оси x и аккорд AB
- Точка пересечения оси x и оси y
- Решения для брекетинга
- Графическое решение
- Эмпирические решения
- Пробные решения
- All Brackting Методы.
- Мы должны начать с начального интервала [a,b], где f(a) и f(b) имеют противоположные знаки.
- Поскольку график y = f(x) непрерывной функции непрерывен, он пересечет абсциссу в точке с нулем x = ‘a’, лежащим где-то в интервале [a,b].
- Одним из способов проверки численного метода решения уравнения f(x) = 0 является проверка его работоспособности на многочлене, корни которого известны.

- 3,375
- 3,5
- Очень медленное
- Экспоненциальный
- квадратичный
- Очень быстрый
2,3737
2,3736
2,3838
2,3625
- Нажмите Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа в систему.
- Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
- Просмотр институциональных учетных записей, предоставляющих доступ.
4 Ответ 2 ниже (подробное решение 2)
Вариант 1 : 0,613
Концепция:
Неправильный метод:
Учитывая, что f(x) = 0
Если f(a)×f(b)
\({x_i} = \frac{{af\left( b \right) — bf\left( a \right)}}{{f\left( b \right) — f\left( a \right) }}\)
Важные моменты:
Расчет:
f(x) = x – e – x
f (0) = – 1
f(1) = 0,632
x2 = \(\frac{{{x_0}f\left( {{x_1}} \right)\;- \;{x_1}f\left( {{x_0}} \right)}}{{f\left( {{x_1}} \right)\;- \;f \left( {{x_0}} \right)}}\)
= 0,613
Верхнее решение трансцендентных уравнений Целевые вопросы MCQ
Метод деления пополам применяется для вычисления нуля функции f(x) = x 4 – х 3 – х 2 – 4 в промежутке [1, 9]. Метод сходится к решению после _______ итераций.
Ответ (подробное решение ниже)
Вариант 2 : 3
Концепция:
Метод деления пополам:
Используется для поиска корня функции. Корень функции f(x) = a такой, что f(a)= 0
Свойство: если функция f(x) непрерывна на отрезке [a…b] и знак f(a) ≠ знак f (б). Существует значение c, принадлежащее [a…b], такое, что f(c) = 0, означает, что c является корнем между [a…. b]
b]
Примечание :
Метод деления пополам разрезает интервал на 2 половины и проверяет, какая половина содержит корень уравнения.
1) Допустим интервал [a…b] .
2) Разрежьте интервал посередине, чтобы найти m : \(m =\frac{{a+b}}{{2}}\)
3) знак f(m) не совпадает с f(a) продолжить поиск в новом интервале.
Расчет:
Метод деления пополам применяется к заданной задаче с [1, 9]
После 1 итерации
\({x_1} = \frac{{1\; + \;9}}{2} = 5\)
Теперь, поскольку f(x 1 ) > 0, x 2 заменяет x 1
Теперь x 0 = 1 и x 1 = 5
И после 2 й итерации
\({x_2} = \frac{{1\; + \;5}}{2 } = 3\)
Теперь, поскольку f(x 1 ) f(x 2 ) > 0, x 2 заменяет x 1 и x 0 = 1 и x
7 3 90 и после 3 рд итерация\({x_2} = \frac{{1\; + \;3}}{2} = 2\)
Теперь f(x 2 ) = f(2) = 2 4 – 2 3 – 2 2 – 4 = 0
Таким образом, метод сходится точно к корню за 3 итерации.
Поделиться в WhatsApp
Один действительный корень многочлена P(x) = x 3 — x — 1 лежит в интервале [1,2] и для нахождения его значения используется метод деления пополам, минимальное количество итераций, необходимое для достижения точности до два десятичных знака 9n}}}\)
⇒ 2n ≥ 100
Теперь 2 6 = 64, 2 7 = 128
Скачать решение PDF
Поделиться в WhatsApp
В методе regula falsi точка пересечения кривой AB и оси x заменяется на:
Ответ (подробное решение ниже)
Вариант 3: Точка пересечения оси x и хорды AB
Пояснение:
Метод
Метод начинается с двух предполагаемых значений x 0 и x 1 для корня, таких что f(x 0 ) f(x 1 )
Формула итерации имеет вид –
\({x_2} = \frac{{{x_0}f\left( {{x_1}} \right) — {x_1}f\left( {{x_0}} \ right)}}{{f\left( {{x_1}} \right) — f\left( {{x_0}} \right)}}\)
\( \Rightarrow {x_{n + 1}} = \frac{{{x_{n — 1}}f\left( {{x_n}} \right) — {x_n}f\left( {{x_ {n — 1}}} \right)}}{{f\left( {{x_n}} \right) — f\left( {{x_{n — 1}}} \right)}}\)
Графически это можно показать, проведя хорду между (x o ,f Xo ) и (x 1 ,f X1 ) и увидев, что точка взаимодействия с осью x равна x 2
В следующей итерации корень находится между x 0 и x 2 или между х 1 и х 2 .
Итак, x 2 заменяет либо x o , либо x 1 в зависимости от того, является ли f(x o ) f(x 2 ) 1) f(x 2 )
Скачать решение PDFПоделиться в WhatsApp
К какой из следующих категорий мы можем отнести метод деления пополам?
Ответ (Подробное решение ниже)
Вариант 1: Решения в скобке
Объяснение:
Методы брекета:
Метод деления пополам:
Используется для поиска корня функции. Корень функции f(x) = a такой, что f(a)= 0
Свойство: если функция f(x) непрерывна на отрезке [a…b] и знак f(a) ≠ знак f (б). Существует значение c, принадлежащее [a…b], такое, что f(c) = 0, означает, что c является корнем между [a….b]
Примечание:
Метод деления пополам разрезает интервал на 2 половины и проверяет, какая половина содержит корень уравнения.
1) Допустим интервал [a, b] .
2) Разрезать интервал посередине, чтобы найти m : m = (a + b)/2
3) Знак f(m) не совпадает с f(a), продолжить поиск в новом интервале.
Скачать решение PDFПоделиться в WhatsApp
Только один из действительных корней f(x) = x 6 – x – 1 лежит в интервале 1 ≤ x ≤ 2, и для нахождения его значения используется метод деления пополам. Для достижения точности 0,001 необходимое минимальное количество итераций составляет __________. 9n}}}\)
9n}}}\)
⇒ 2 n ≥ 1000
Минимальное число n, удовлетворяющее вышеуказанному условию, равно n = 10.
Скачать решение PDFПоделиться в WhatsApp
Решение трансцендентных уравнений MCQ Вопрос 11:
Первое приближение к вещественному корню уравнения x 3 — 3x 2 — 2 = 0 методом ложных правил между 3 и 4 равно
3- 904 21 2,825 3,125
Ответ (подробное решение ниже)
Опция 1: 3.125
Концепция;
В данном интервале [a,b], если f(a) и f(b) имеют противоположные знаки, то аппроксимация корня с использованием метода ложных правил дается выражением
\({x_1} = \frac {{a\;f\left( b \right) — b\;f\left( a \right)}}{{f\left( b \right) — f\left( a \right)}} \)
здесь a = 3, b = 4
f(a) = 27 — 27 — 2 = -2, f(b) = 14,
Первое приближение будет
\(x_1= \frac{{\ влево( 3 \вправо)\влево( {14} \вправо) — \влево( 4 \вправо)\влево( { — 2} \вправо)}}{{14 — \влево( { -2} \вправо)} }\)
⇒ x 1 = 3,125
Решение трансцендентных уравнений MCQ Вопрос 12:
Метод деления пополам применяется для вычисления нуля функции f(x) = x 4 – x 0 6 x 8 – 0 2 – 4 на интервале [1, 9]. Метод сходится к решению после _______ итераций.
Метод сходится к решению после _______ итераций.
Ответ (подробное решение ниже)
Вариант 2 : 3
Концепция:
Метод деления пополам:
Используется для поиска корня функции. Корень функции f(x) = a такой, что f(a)= 0
Свойство: если функция f(x) непрерывна на отрезке [a…b] и знак f(a) ≠ знак f(b). Существует значение c, принадлежащее [a…b], такое, что f(c) = 0, означает, что c является корнем между [a….b]
Примечание :
Метод деления пополам разрезает интервал на 2 половины и проверьте, какая половина содержит корень уравнения.
1) Допустим интервал [a…b] .
2) Разрежьте интервал посередине, чтобы найти m : \(m =\frac{{a+b}}{{2}}\)
3) знак f(m) не совпадает с f(a) продолжить поиск в новом интервале.
Расчет:
Метод деления пополам применяется к заданной задаче с [1, 9]
После 1 итерации
\({x_1} = \frac{{1\; + \;9}}{ 2} = 5\)
Теперь, поскольку f(x 1 ) > 0, x 2 заменяет x 1
Теперь x 0 = 1 и x 1
0 = 5 2 nd итерация\({x_2} = \frac{{1\; + \;5}}{2} = 3\)
Теперь, поскольку f(x 1 ) f(x 2 ) > 0, x 2 заменяет x 1 и x 0 = 1 и x 1 = 3 и после 3 rd итерация = \frac
\({x_{2} \; + \;3}}{2} = 2\)
Теперь f(x 2 ) = f(2) = 2 4 – 2 3 – 2 2 – 4 = 0
Таким образом, метод сходится точно к корню за 3 итерации.
Решение трансцендентных уравнений MCQ Вопрос 13:
Сходимость метода деления пополам равна
Ответ (подробное решение ниже)
Опция 1: очень медленное
4. Actenge. . Хотя ошибка не убывает монотонно, средняя скорость сходимости равна ½. Итак, немного изменив определение порядка сходимости, можно сказать, что метод сходится линейно со скоростью 1/2.
Важные моменты:
Итерационный метод | Конвергенция |
Метод деления пополам | Очень медленно |
Метод Регулы-Фалси | Заказ – 1 |
Метод Ньютона-Рафсона | Заказ – 2 |
Метод секущих | Заказ – 1. |
Метод последовательного приближения | Заказ – 1 |
Решение трансцендентных уравнений MCQ Вопрос 14:
Один вещественный корень многочлена P(x) = x 3 — x — 1 лежит в интервале [1,2], и для его нахождения используется метод деления пополам. значение, минимальное количество итераций, необходимое для достижения точности до двух знаков после запятой, составляет 9n}}}\)
⇒ 2n ≥ 100
Теперь 2 6 = 64, 2 7 = 128
Уравнения MCQ Вопрос 15:
Корень уравнения x 3 — x — 11 = 0, правильный до четырех знаков после запятой с использованием метода деления пополам (после 3 итераций), предположим, что начальный корень лежит между 2,3 и 2,4
Ответ (подробное решение ниже)
Вариант 4 :
2,3625
Из данных вариантов корень лежит между 2,3 и 2,4.
f(2,3) = -1,133
f(2.4) = 0,424 > 0
поэтому \(x_1=\frac {2,3+2,4}{2}=2,35\)
Теперь f(2,35) = — 0,372
\(x_2=\frac {2,4+2,35}{2}=2,375\)
снова f(2,375) = 0,02148 > 0
\(x_3=\frac {2.35+2.375}{2}=2.3625\)
Доказательство существования трансцендентных чисел | по математике и размышлениям
… и как сравнить бесконечное?
Вот милый способ доказать существование трансцендентных чисел. Это требует *всего* интереса к математике и сочетается с кратким руководством по бесконечности и канторовскому аргументу диагонализации! Мы также увидим, что трансцендентных чисел «больше», чем нетрансцендентных.
Внизу: аргумент Кантора о диагонализации в основании 2. Подробнее об этом позже!
Канторовский аргумент диагонализации в двоичном виде. Но с основанием 10, как мы увидим, удобнее 🙂 Трансцендентное число — это число, которое нельзя записать в виде корня многочлена с целыми коэффициентами. Числа, являющиеся корнями многочлена с целыми коэффициентами, называются алгебраическими.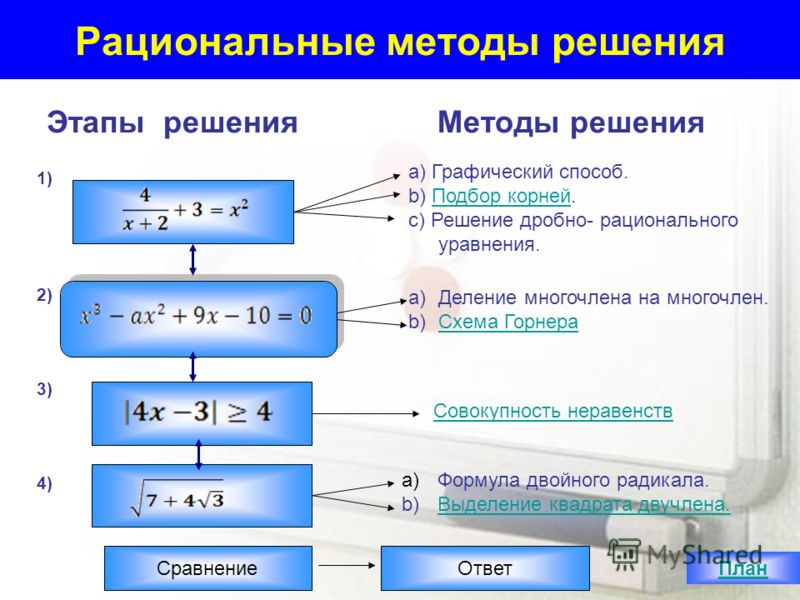
Как ни странно, не так уж трудно* доказать их существование, но очень-очень трудно доказать трансцендентность числа. * Сравнительно говоря.
Например, квадратный корень из 1,5 НЕ трансцендентен, потому что он решает уравнение 2x² -3 = 0,
В то время как пи, известное число пи, ЯВЛЯЕТСЯ трансцендентным, потому что не существует многочлена с целыми коэффициентами, для которого оно является корнем (хотя доказать это сложно и использовать теорему Линдеманна-Вейерштрасса). Итак, мы займемся немного странным вопросом. Мы хотим доказать, что трансцендентные числа существуют, не обязательно имея возможность привести пример одного из них!
[Несколько слов об обозначениях. (1) Иногда я буду называть многочлены с целыми коэффициентами алгебраическими уравнениями. (2) Счетно бесконечный список — это список с бесконечным числом элементов, но мы можем перечислить их все. Немного более формально, мы можем спаривать элементы в списке с положительными целыми числами, так что для каждого элемента списка имеет смысл спросить, какой это элемент списка. Простейшим примером являются сами положительные целые числа: 5-й элемент положительных целых чисел равен 5, 6-й элемент равен 6, и, вообще говоря, N-й элемент равен N. Другой способ взглянуть на счетно бесконечный список состоит в том, что это список, в котором вы никогда не дойдете до конца, но при счете «вверх» от начального элемента требуется лишь конечное количество времени, чтобы достичь любого конкретного элемента списка. список. Вы не можете считать «до бесконечности», но если у вас достаточно времени, вы можете сосчитать до 1 миллиона.)
Простейшим примером являются сами положительные целые числа: 5-й элемент положительных целых чисел равен 5, 6-й элемент равен 6, и, вообще говоря, N-й элемент равен N. Другой способ взглянуть на счетно бесконечный список состоит в том, что это список, в котором вы никогда не дойдете до конца, но при счете «вверх» от начального элемента требуется лишь конечное количество времени, чтобы достичь любого конкретного элемента списка. список. Вы не можете считать «до бесконечности», но если у вас достаточно времени, вы можете сосчитать до 1 миллиона.)
(Примечание. Мы используем аргумент диагонализации Кантора на шаге 3).
Счетно бесконечное означает, что теоретически мы создаем список, и для любого алгебраического числа, которое вы хотите назвать, мы можем указать на его позицию в списке. Этот раздел может показаться немного сложным при первом прочтении, поэтому не беспокойтесь, если поначалу он будет немного запутанным. Если вы чувствуете, что слишком застряли на каком-либо этапе, вы можете поверить мне на слово, что это правда, и перейти к шагу 2.
Полезный пример: целые числа счетно бесконечны
Например, целые числа счетны. Рассмотрим список (0, -1, 1, 2, -2, 3, -3, …)
Да, список можно продолжать бесконечно, но если я дам вам число, может быть, 50 или, может быть, -10¹⁰⁰⁰⁰⁰, вы в конце концов найдете это конечное число элементов в этом списке.
Пары целых чисел счетно бесконечны
Прежде чем читать нижеследующее, давайте представим, что у вас есть большой квадрат людей. Вы можете посчитать группу людей несколькими способами. Вы можете считать людей несколькими способами. Вы можете подсчитать каждый столбец, а затем подсчитать количество строк. Вы можете посчитать каждую диагональ и просуммировать их.
Проблема с бесконечной сеткой заключается в том, что если вы начнете обратный отсчет одного из столбцов, вы никогда не дойдете до конца. Да, вы бы доказали, что людей так много, что подмножество их содержится в исчисляемом списке, , но , и вы не смогли бы доказать, что также — список, включающий их всех.
Вместо этого считаем по диагоналям. К счастью, на каждой диагонали есть конечное число людей. (См. схему ниже). Мы можем поместить все диагонали в счетный список, а затем найти, на какой диагонали находится элемент.0005 спасибо Tex stackexchange:)
Это доказывает, что существует счетное количество пар целых чисел. Если вы дадите мне пару целых чисел, это будет точка в сетке, и поэтому она находится на некоторой диагонали, скажем, на К-й диагонали. Но в первых K диагоналях всего 1+2+3+…+K элементов, поэтому этот элемент будет найден в первых K(K+1)/2 элементах нашего списка. т.е. каждая возможная пара целых чисел находится где-то в нашем списке.
Например, если вы дали мне пару (3,2), которая находится на 4-й диагонали, так как 4-я диагональ содержит все пары, сумма которых равна 5 (посмотрите на диаграмму, если вы мне не верите) . Мы знаем, что он содержится в первых 1+2+3+4 элементах, то есть 10, или 4*5/2 = 20/2 = 10, как я и обещал.
Триплеты целых чисел счетно бесконечны
Теперь давайте проделаем еще один трюк.
Теперь мы доказали, что все пары целых чисел счетно бесконечны. Но тройка целых чисел — это пара… целого числа и пары целых чисел! (В любом случае они хранят одну и ту же информацию)
(a,b,c) = (a, (b,c))
Так как нам удалось найти счетный список, содержащий все пары целых чисел, это то же самое проблема, как и раньше, так как мы можем просмотреть наш список всех возможностей для (b,). Если мы разделим каждую отдельную пару (b,c) меткой A, то мы хотим найти все списки вида (a, A), где A — элемент из другого счетно бесконечного списка. (Не нужно заглядывать под капот A, все, что нам нужно помнить, это то, что это счетный список).
Мы можем сделать то же самое СНОВА! Если мы хотим рассмотреть все списки вида (a, b, c, d), где a, b, c, d — целые числа, мы теперь рассматриваем это как (a, A), где A — одно из счетно бесконечных списков. список троек (b,c,d)! Мы доказываем, что все списки из 5 целых чисел счетны аналогично. Затем списки из 6 целых чисел. И так далее, и так далее. Это приводит к…
Это приводит к…
Все комбинации K целых чисел счетно бесконечны
Докажем это с помощью домино. Ну, по индукции, что в принципе одно и то же.
Если все (K-1) длинных списков целых чисел счетно бесконечны, мы используем тот же трюк, что и раньше. Мы абстрагируемся от деталей найденного нами списка, а просто воспользуемся тем, что он счетный, и он исчерпывающий, т.е. перебирает все возможные комбинации. Тогда все комбинации (a, A) исчерпывают списки целых чисел с K элементами, поскольку K элемент может быть разложен на первый элемент, a, и оставшийся список, содержащий K-1 элементов.
Это в основном аргумент домино. Каждый случай доказывает следующий случай, поэтому мы можем быть уверены, что каждая костяшка костяшки выпадет при условии, что выпадет первая костяшка костяшки.
Количество («мощность») многочленов с целыми корнями счетно бесконечно. Число корней многочленов с целыми корнями счетно бесконечно.
Мы представляем каждое алгебраическое уравнение в виде списка.
Например, уравнение 5x²-4x+2=0 можно представить как (5,-4,2).
Каждое алгебраическое уравнение имеет «максимальный член». Максимальный член приведенного выше уравнения равен x² с коэффициентом 5. Максимальный член x⁷+7x-9=0 равен x⁷ с коэффициентом 1. Обычно этот член представляет собой наибольшую степень x с коэффициентом ненулевой коэффициент.
У нас есть все алгебраические уравнения, максимальный член которых равен 1. Это уравнения вида ax+b=0. Мы можем найти счетный список, содержащий все эти уравнения. Поскольку каждое из этих уравнений имеет не более одного решения, мы можем содержать все решения такого уравнения в счетно бесконечном списке .
Уравнения, максимальный член которых равен 2, являются квадратными уравнениями вида ax²+bx+c=0. Все такие уравнения с целыми коэффициентами также можно найти в счетном списке. Но все эти уравнения имеют не более двух корней (как, напомним, мы можем разложить многочлены на произведение x минус их корни). Поэтому мы получаем наш список раньше, но вместо этого записываем два решения (или, может быть, одно, или ни одного для некоторых уравнений), тогда как раньше мы бы написали в уравнении. Таким образом, нам потребуется не более в два раза длиннее для достижения корня уравнения, чем в нашем предыдущем списке, чтобы достичь уравнения , но мы все же добираемся туда.
Поэтому мы получаем наш список раньше, но вместо этого записываем два решения (или, может быть, одно, или ни одного для некоторых уравнений), тогда как раньше мы бы написали в уравнении. Таким образом, нам потребуется не более в два раза длиннее для достижения корня уравнения, чем в нашем предыдущем списке, чтобы достичь уравнения , но мы все же добираемся туда.
Это продолжается. Для уравнений с максимальным членом размера k у нас есть не более k корней, и мы можем провернуть тот же трюк: мы получаем счетный список всех таких уравнений, а затем вставляем k корней. Для достижения корня уравнения может потребоваться в k раз больше шагов, чем для достижения уравнения в нашем исходном списке, но мы все равно доберемся до него за конечное число шагов.
Теперь мы выстраиваем ОГРОМНУЮ сетку точек. Эта сетка точек содержит КАЖДОЕ решение алгебраического уравнения. Первая строка — наш счетно бесконечный список или все корни алгебраических уравнений размера 1. Вторая строка — наш счетно бесконечный список всех корней алгебраических уравнений размера 2 и так далее.
Вторая строка — наш счетно бесконечный список всех корней алгебраических уравнений размера 2 и так далее.
Используя наш предыдущий прием, идем по диагоналям. Это дает нам счетный список, содержащий всех решений многочленов с целыми коэффициентами .
Предположим, ваш злой заклятый враг (дьявол, сталин, ваш надоедливый младший брат…) вручает вам список, содержащий все реальные числа. Можете ли вы доказать, что они лгут, когда утверждают, что список содержит все настоящие числа ?
Конечно, можно.
В их списке можно составить число , а не . На самом деле, мы можем сделать это, ограничившись числом меньше единицы.
Чтобы построить свой номер, посмотрите на первый номер в списке вашего злого противника. Теперь выберите свою первую цифру, цифру для столбца «10-е», чтобы она отличалась от цифры для столбца «10-е». Это довольно просто, так как есть 10 цифр на выбор, а они могут использовать только одну.
Теперь, для второй цифры, выберите цифру вашего сотого столбца, чтобы она отличалась от их.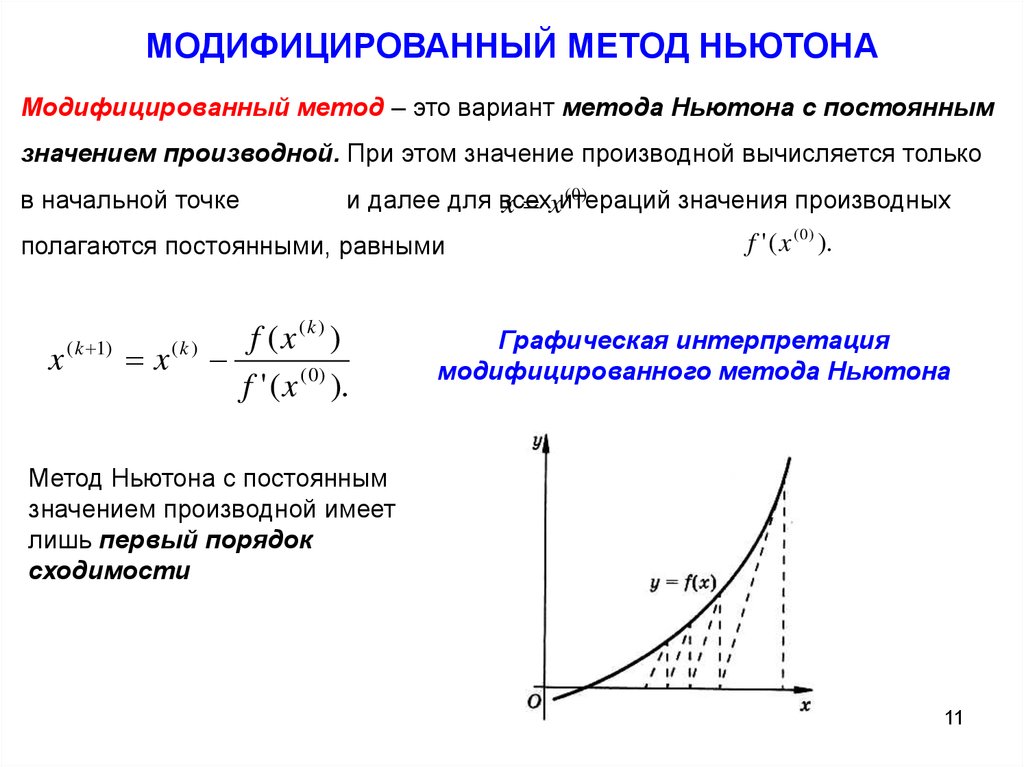 И так далее .
И так далее .
С несколькими пустяковыми деталями (которые не меняют сути доказательства и, вероятно, отвлекают от него при первом чтении), если ваш злой враг скажет: ага! моя 7-я, 102-я, 12048121-я или N-я цифра — это число, которое вы составили, тогда вы можете доказать их неправоту — в конце концов, вы выбрали свою 7-ю цифру, чтобы она отличалась от 7-го числа в их списке, и вы выбрали свою 102-ю цифру, чтобы сделать его отличным от их 102-го номера, и, когда вы туда доберетесь, вы выбрали свою 12048121-ю цифру, чтобы она отличалась от их 12048121-го номера.
Итак, не существует списков, содержащих все действительные числа .
Объединяя наши предыдущие шаги, мы приходим к выводу!
Нам удалось показать, что существует только счетно бесконечное число алгебраических чисел. Говоря математическим языком, нам удалось показать, что их мощность «счетна». т.е. мы могли бы составить список, содержащий их все.
Затем мы показали, что не существует счетно бесконечного списка, содержащего все действительные числа.
Итак, в нашем списке, включающем все алгебраические числа, должно отсутствовать множество действительных чисел (пропущено неисчислимое множество!).
Поздравляем, вы только что поняли аргумент Кантора о диагонализации, одно из главных достижений математики XIX века, наряду с аргументами мощности, а затем применили его к забавной задаче о трансцендентальных числах 🙂
Корни трансцендентального уравнения, связанного с Некоторое разностно-дифференциальное уравнение | Журнал Лондонского математического общества
Фильтр поиска панели навигации Журнал Лондонского математического обществаЭтот выпускLMS JournalsMathematicsBooksJournalsOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Журнал Лондонского математического обществаЭтот выпускLMS JournalsMathematicsBooksJournalsOxford Academic Термин поиска на микросайте
Расширенный поиск
Журнальная статья
Получить доступ
Н. Д. Хейс
Д. Хейс
Н. Д. Хейс
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
Журнал Лондонского математического общества , том s1-25, выпуск 3, июль 1950 г., страницы 226–232, https://doi.org/10.1112/jlms/s1-25.3.226
Опубликовано:
01 июля 1950 г.
История статьи
Получено:
14 октября 1949 г.
Опубликовано:
01 июля 1950 г.
Фильтр поиска панели навигации Журнал Лондонского математического обществаЭтот выпускLMS JournalsMathematicsBooksJournalsOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Журнал Лондонского математического обществаЭтот выпускLMS JournalsMathematicsBooksJournalsOxford Academic Термин поиска на микросайте
Расширенный поиск
Предварительный просмотр первой страницы статьи PDF
Закрыть
Этот контент доступен только в формате PDF.
© Oxford University Press
© Oxford University Press
Раздел выпуска:
ПРИМЕЧАНИЯ И ДОКУМЕНТЫ
В настоящее время у вас нет доступа к этой статье.
Скачать все слайды
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Вход через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.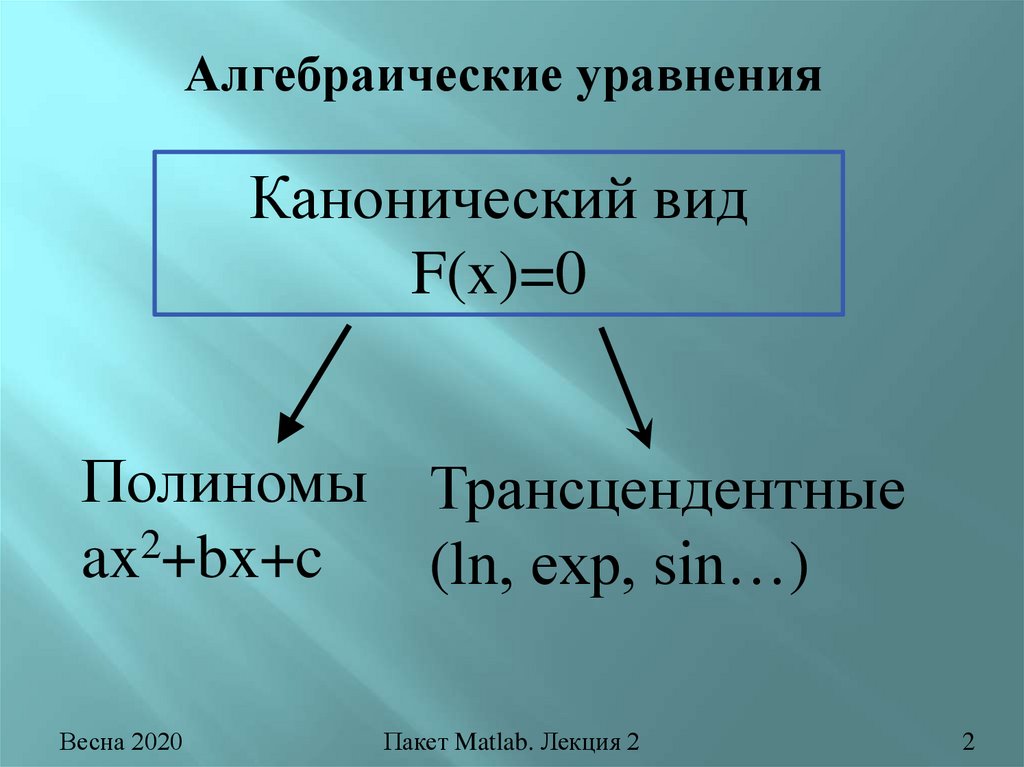 Смотри ниже.
Смотри ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.

 Алгебра. (1951, 424 с.)
Алгебра. (1951, 424 с.)
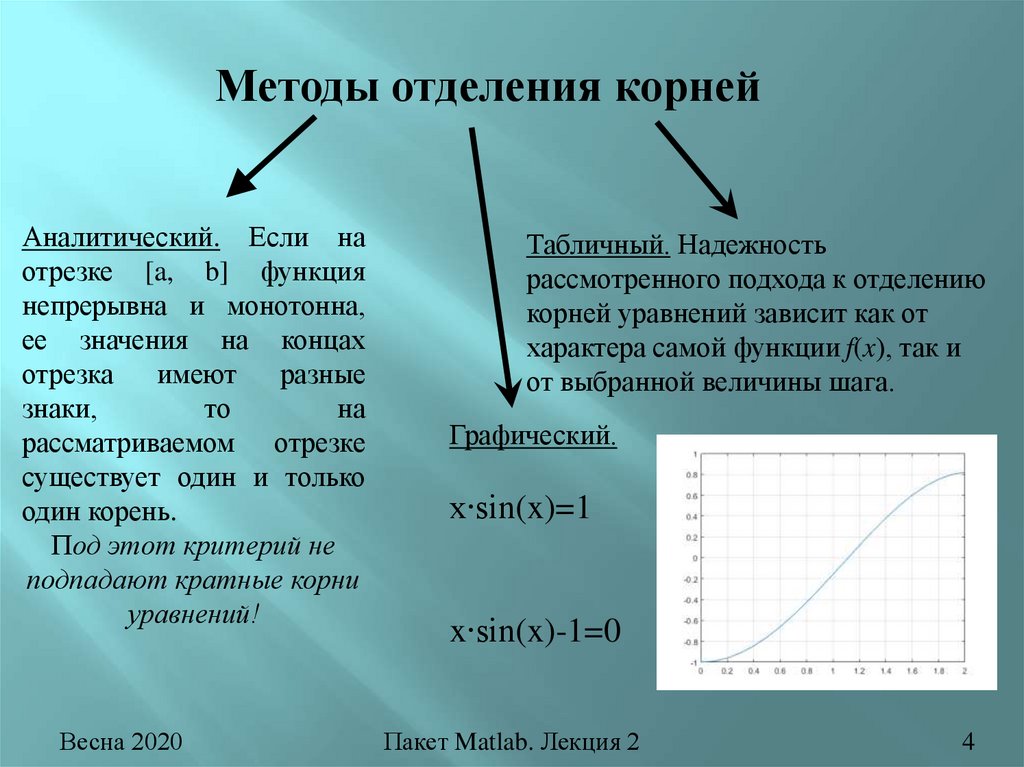 2. Теорема Безу
2. Теорема Безу  1. Расчетная схема преобразования вида у = х — а аргумента
1. Расчетная схема преобразования вида у = х — а аргумента  1. Расчет условной ошибки
1. Расчет условной ошибки 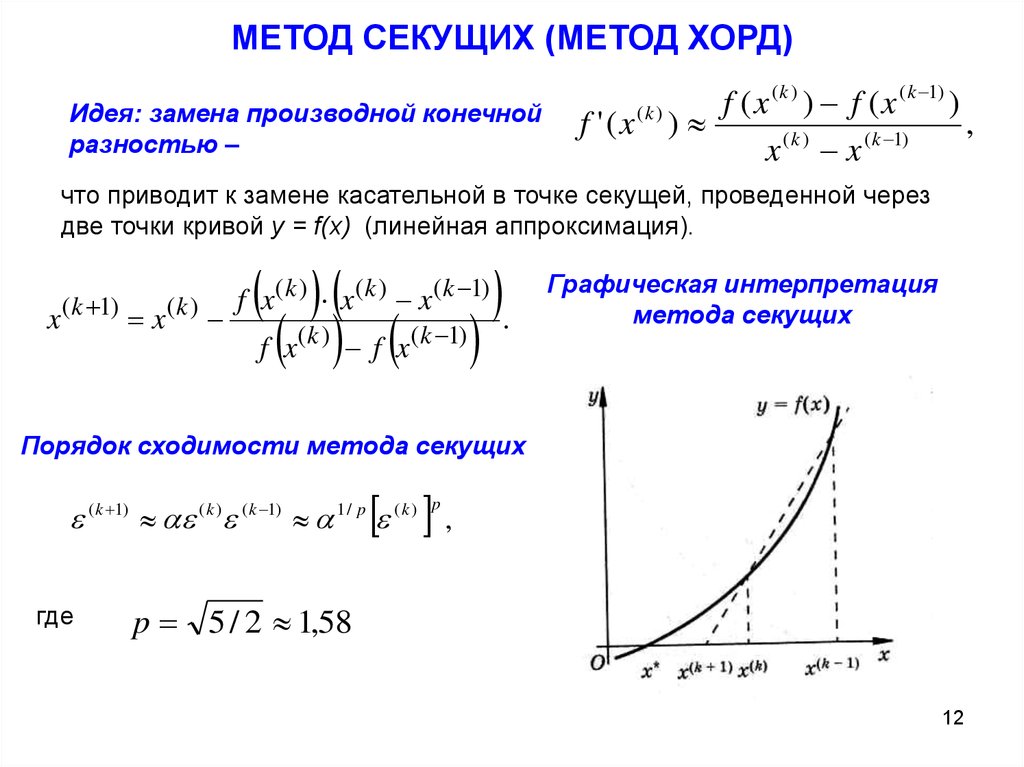 13. Решение трансцендентных уравнений
13. Решение трансцендентных уравнений  Метод Ньютона
Метод Ньютона  Квадратные уравнения
Квадратные уравнения  of pages: 216
of pages: 216


 62
62 Д. Хейс, Корни трансцендентного уравнения, связанного с некоторым дифференциально-разностным уравнением, Журнал Лондонского математического общества , том s1-25, выпуск 3, июль 1950 г., страницы 226–232, https:/ /doi.org/10.1112/jlms/s1-25.3.226
Д. Хейс, Корни трансцендентного уравнения, связанного с некоторым дифференциально-разностным уравнением, Журнал Лондонского математического общества , том s1-25, выпуск 3, июль 1950 г., страницы 226–232, https:/ /doi.org/10.1112/jlms/s1-25.3.226