Упрощение скнф онлайн: Построение таблицы истинности онлайн | СКНФ | СДНФ | Полином Жегалкина | Таблица истинности булевой функции онлайн

Содержание

Упрощение и оптимизация логических схем. (Лекция 3)

Похожие презентации:

3D печать и 3D принтер

Видеокарта. Виды видеокарт

Анализ компании Apple

Трансформаторы тока и напряжения

Транзисторы

Устройство стиральной машины LG. Электрика

Конструкции распределительных устройств. (Лекция 15)

Электробезопасность. Правила технической эксплуатации электроустановок

Магнитные пускатели и контакторы

Работа на радиостанциях КВ и УКВ диапазонов. Антенны военных радиостанций. (Тема 5.1)

1. Упрощение логических схем

1. Группировка
Применение закона ассоциативности
Применение тождеств – законы отрицания
Пример:
Возможно использование тождества не относящееся к базовым
Пример:
Теорема о непротиворечивости
Пример:
Пусть В·С = Х, а D·E = Y, тогда
Применяя теорему непротиворечивости получаем:
Приведение выражения к каноническому виду с последующем
упрощением
1.

Выражение записанное в дизъюнктивной форме можно привести к СДНФ
путём умножения импликат на множитель типа
2.После
раскрытия
скобок,
члены
выражения
могут
быть
перегруппированы, что в результате получится упрощенное выражение.
так
Порядок
выполнения
операций:
сначала
выполняются
операции
конъюнкций, а затем дизъюнкций. В сложных логических выражениях
для задания порядка выполнения используют скобки.
При необходимости для формирования групп можно ввести повторяющиеся
члены.
Пример:
Использование теоремы де Моргана
После инвертирования правых частей
Пример:
Минимизация с помощью карт Карно
Правила разметки:
Вертикальная ось размечается независимо от горизонтальной.
Начинать разметку можно с любого сочетания переменных.
Все сочетания переменных должны быть перечислены.
Для соседних клеток сочетания переменных должны отличаться не более
чем одним знаком.
Соседними являются крайние клетки строки или столбца.

Диаграмма Вейча
Правила составления контуров
Контуры должны быть прямоугольными и содержать количество единиц,
равное 2n, где n – целое число, т.е. в контуре может быть 1, 2, 4, 8. и т. д.
единиц.
Количество единиц в контуре должно быть максимальным, при этом
контуры могут пересекаться между собой.
Количество контуров должно быть минимальным, но все единицы
должны быть охвачены контурами.
Пример 1:
СДНФ → ДНФ
Пример 2:
СДНФ → ДНФ
Пример 3:
СДНФ → ДНФ
Пример 4:
СКНФ → КНФ

13. Построение логических схем

При построении логических схем следует придерживаться следующей
последовательности:
Этап I. Составление таблицы истинности производится на основе
задания содержащего неформальные признаки (определения,
«хотелки») допускающие неоднозначную трактовку.
Основная цель – формализация задания.
Результат этапа – составление задания, неоднозначное
толкование которого невозможно, то есть составление полностью и
однозначно определённой таблицы истинности.

Этап II. Если функция определена не на всех наборах аргументов, то
доопределить функцию нулями или единицами, но так, чтобы
уменьшить число членов СДНФ прямой функции или её инверсии.
Этап III. По полностью определённой таблице истинности составить
СДНФ или несколько СДНФ в зависимости от количества вариантов
доопределения.
Этап IV. Минимизировать СДНФ любым доступным методом.
Этап V. Реализовать получившиеся дизъюнктивные формы на логическом
базисе заданного семейства элементов.
Этап VI. Оценить двойственный вариант логической схемы с учётом
изменения числа входных и выходных инверторов.
Этап VII. Попытаться найти такую декомпозицию функции, чтобы каждый
фрагмент полученного разложения зависел от возможно меньшего числа
аргументов, чем исходная функция. Попытаться выполнить это

различными способами.
Этап VIII. Выбрать из полученных на этапах V, VI, VII вариантов наиболее
подходящих с точки зрения поставленной задачи
Оценка качества функциональных схем
Основные критерии качества функциональной схемы:
1.

Время задержки распространения сигнала – Т
2. Аппаратурные затраты – W
Пример.
На логических элементах серии К155 построить оптимальную схему
реализующую ДНФ вида:
Вариант А
К155ЛН1
T = 3t
W = ЛН1 + ЛР3 = 5·1/6 +1 =22/12
Рассмотрим другие варианты реализации заданной переключательной функции
Применив правило де Моргана получим:
К155ЛА3
К155ЛА4
Т = 3·t
Вариант Б
W = 1ЛН1 + 1ЛА3 + 1ЛА4 =
= 3·1/6 + 2·1/4 + 1·1/3 = 16/12
Преобразуем выражение так, чтобы уменьшить количество инверторов на
входе:
К155ЛР1
Вариант В
T = 2·t
W = 1ЛР1 + 1ЛН1 + 1ЛЛ1 =
= 1·1/2 + 1·1/6 + 1·1/4 = 11/12
К155ЛЛ1
T = 3·t
W = 1ЛИ1 + 1ЛЛ1 + 1ЛА3 =
= 1·1/4 + 1·1/4 + 1·1/4 = 9/12
Вариант Д
T = 1·t
W = 12/12 = 1
Вариант Г
Решением задачи оптимизации, с несколькими критериями, является
множество Парето.
х доминирует над х* “по Парето”, если х не хуже х* по всем
критериям и хотя бы по одному критерию превосходит х*.

В таком случае в
выборе х* нет смысла, так как х по всем параметрам не уступает, а по какимто и превосходит х.
Говорят, что
Если рассматривать всего два критерия, то на рисунке 1 показана область
пространства, доминируемая решением А. Эта область «замкнута»: элементы
на ее границе также доминируемы А.
Элемент х* {X} – называется
“оптимальным по Парето”, если не
существует такого х {X} , который
будет “лучше”
Рисунок 1 – Доминируемые решения
х*.
Множество оптимальных “по Парето” решений, то есть недоминируемых

решений также называют Парето фронтом.
Рисунок 2 – Парето фронт
Соотношение величин задержек Т и аппаратурных затрат W
W дано в 1/12 долях
• – реальные схемы
х – гипотетические схемы
Множество объектов
оптимальных по Парето.

English Русский Правила

7. Синтез логических выражений. Синтез логических выражений.

Используя таблицу истинности любой логической формулы, можно определить ее в СДНФ или СКНФ.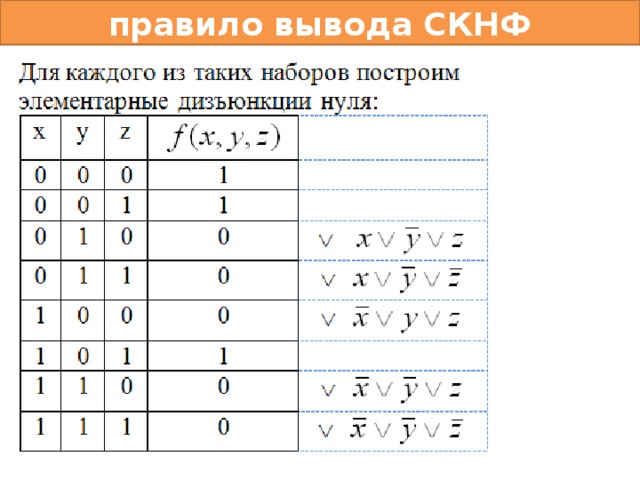 Для построения СДНФ в таблице истинности необходимо выбрать строки, в которых функция принимает значение 1 и сформировать конституанту 0. Переменная будет находиться в этой конституанте без знака отрицания, если она принимает значение 1 в этой строке и с отрицанием в противном случае. Соединить полученные конституанты знаком дизъюнкции.

Для получения СКНФ ищутся строки, в которых функция принимает значение 0. Строятся конституанты 1. Переменная берется со знаком отрицания, если она равна 1 и наоборот. Конституанты соединяются знаком конъюнкции.

Пример: Дана таблица истинности. Построить СДНФ и СКНФ.

x	y	z	f
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	1
1	1	1	0

СДНФ:

СКНФ:

Метод Петрика.

Алгоритм Квайна. Диаграммы Вейча.

Минимизация булевых функции

Под минимизацией булевых функций понимается нахождение наиболее простого представления этой функции в виде суперпозиции функций, составляющих какую-нибудь фиксированную функционально полую систему Sбулевых функций. Наиболее простым обычно считается представление, содержащее наименьшее возможное число суперпозиций. При решении задачи минимизации важную роль играет понятие импликанты.

Булева функция называется импликантой функции, если на любом значении переменных, на котором значениеgравно 1, значениеfтакже равно 1.

Простой импликантой функции fназывается элементарное произведение, являющееся импликантойfи такое, что никакая его собственная часть (то есть произведение, получаемое изgотбрасыванием одного или нескольких компонент) уже не является импликантой функцииf.

Дизъюнкция любого множества импликант одной и той же функции является импликантой этой функции.

Дизъюнкция всех простых импликант булевой функции совпадает с этой функцией и называется сокращенной дизъюнктивной нормальной формой.

Сокращенная нормальная форма является более экономной, чем СДНФ. Однако часто допускает дальнейшее упрощение за счет того, что некоторые из простых импликант могут поглощаться дизъюнкцией других простых импликант. Например, в сокращенной ДНФ простая импликантаyzпоглощается дизъюнкцией остальных элементов формы:.

Однако справедливо следующее утверждение для сокращенной дизъюнктивной формы. Если сокращенная ДНФ не содержит никакой переменной, входящей в нее одновременно с отрицанием и без него, то эта форма является минимальной дизъюнктивной формой.

Приведение к минимальной нормальной форме от сокращенной ДНФ можно осуществит с помощью импликантной таблицы. Импликантная таблица представляет собой прямоугольную таблицу, строки которой обозначаются различными простыми импликантами, а столбцы конституантами единицы, на которых функция обращается в единицу.

На пересечении p-й строкиk-го столбца импликантной таблицы ставится * тогда и только тогда, когда импликанта составляет некоторую часть конституантыk. Для примера:


*	*
		*	*
			*	*
	*			*

Система Sпростых импликант булевых функцийfназывается приведенной, если эта система полна и никакая ее часть не является полной системой импликант функцииf. Дизъюнкция всех простых импликант, составляющихS, называется приведенной или тупиковой дизъюнктивной нормальной формой. Всякая минимальная ДНФ является тупиковой ДНФ.

Выделение приведенной системы простых импликант может быть проведено на основе импликантной таблицы. Для этой цели надо выбрать минимальные системы строк таблицы так, чтобы для каждого столбца среди выбранных строк нашлась хотя бы одна строка содержащая звездочку. Этот метод является методом перебора и практически применим для простых импликантных таблиц. В случае сложных таблиц можно применять алгебраический метод Петрика.

Суть этого метода заключается в том, что по импликантной таблице строится некоторое выражение, называемое конъюнктивным представлением этой таблицы. Для этого производится обозначение всех простых импликант различными буквами (например, A,B,C, …). После этого для каждого столбцаимпликантной таблицы строится дизъюнкция

всех букв, обозначающих строки, на пересечении которых со столбцом стоит *. Беря произведение полученныхq_для всех столбцов, конъюнктивное представление таблицы. Обозначим для нашего примера :. Тогда получим следующее представление таблицы:

Если в конъюнктивном представлении раскрыть все скобки в соответствии с законом дистрибутивности, получим дизъюнктивное представление.

Простые импликанты, символы которых в любой фиксированный терм дизъюнктивного представления составляют полную систему простых импликант функции.

Выполняя в дизъюнктивном представлении импликантной таблицы все элементарные поглощения и устраняя повторения в соответствии с тождествами АА=А и АА = А, приходим к приведенному дизъюнктивному представлению импликантной таблицы.

Термам этого представления соответствуют все приведенные системы простых импликант функции.

В примере получим:

То есть получим 2 приведенные системы простых импликант (A,B,C) и (A,B,D). Им соответствуют две тупиковые ДНФ исходной функции:

Забронируйте билеты на региональные поезда на SNCF Connect

Откройте для себя лучшие регионы Франции с TER

Велосипед бесплатно
Доступ для инвалидов

Путешествуйте по своему региону по лучшим тарифам с TER

Поиск

Стоит знать

Вы опоздали на поезд или расписание изменилось? Вы можете сесть на другой поезд в тот же день или, в некоторых случаях, на автобус TER, до или после первоначально выбранной поездки, соблюдая дату, маршрут и ценовые условия купленного билета.

ДВИЖЕНИЕ ПОЕЗДА: Чтобы узнать, ходит ли ваш поезд, помощник SNCF и информация о дорожном движении SNCF обновляются в 17:00. и предоставлять достоверную информацию о поездах TER, курсирующих на следующий день. Узнать больше.

Нормандия
Париж и его окрестности
Эльзас и Восточная Франция
Бретань
Юго-западная Франция
Лион и Рона-Альпы
Бордо
Лазурный Берег
Прованс

Наслаждайтесь региональными тарифами

Ваши региональные тарифы
Теперь вы можете купить билеты TER онлайн в SNCF Connect 9.0003
Ваш билет на мобильном телефоне
Билет не нужно подтверждать на вокзале. Перейдите в мобильное приложение SNCF Connect
.
Последняя минута
Нужно сэкономить время? Войдите в свою учетную запись клиента, чтобы купить билеты в 2 клика

Все ответы на ваши вопросы

Билет TER можно распечатать прямо дома. Ваш билет можно загрузить в приложении SNCF Connect со страницы подтверждения заказа, из вашего электронного письма с подтверждением или через «Мои заказы» с вашим ссылочным номером вашего бронирования.

Вот регионы, для которых вы можете забронировать TER: Бретань / Центр-Валь-де-Луара / Новая Аквитания / Верхняя Франция / / Бургундия Франш-Конте / Окситания / Нормандия / Овернь-Рона-Альпы / Прованс-Альпы Французская Ривьера/Великий Восток/Пэи-де-ла-Луара.

Для поездки TER посетите веб-сайт sncf.com, чтобы подать заявку.

По каким причинам я не могу найти свой поезд?
— Возможно, ваш поезд еще не выставлен на продажу
— Работы могут быть запланированы в вашем путешествии
— Цена может быть недоступна
— Ваш поезд не может быть продан на сайте

Подтверждение проезда для билетов TER недоступно. Ваш билет служит доказательством.

SNCF Connect: наш гид

Фото предоставлено (баннер): Шаттерсток

С SNCF Connect легко организовать транспорт в любую точку Франции. Используйте наше приложение и веб-сайт, чтобы:

спланировать свое путешествие, купить билеты на поезд и произвести обмен
найти лучший маршрут от двери до двери
получать информацию о ситуации на дорогах и оповещения в режиме реального времени
покупать и продлевать региональные карты и проездные

SNCF Connect: типы транспорт

С SNCF Connect у вас есть доступ ко всем нашим предложениям для путешествий:

TGV INOUI
OUIGO
INTERCITÉS
TER
Transilien и общественный транспорт в районе Парижа
Thalys
Eurostar
TGV Lyria
автобусные маршруты
предложения совместного использования

Вскоре этот список будет включать в себя активную и совместную мобильность во всех регионах Франции.

Совершенно новые функции

Упрощенное сопоставление маршрутов

В SNCF Connect есть одно окно поиска для всего, что вам нужно. И сайт, и приложение интуитивно понятны, поэтому легко найти свой маршрут, набрав или сказав несколько ключевых слов. Просто введите адрес, станцию, достопримечательность, местоположение или номер поезда, и результаты появятся независимо от того, путешествуете ли вы через границу или по городу.

Упрощенная покупка

Покупка билета, карты или абонемента теперь проще и прозрачнее:

Когда вы покупаете или бронируете билет, SNCF Connect показывает вам лучшую цену и количество доступных мест по самым низким тарифам. .
Мы поможем вам найти лучшее предложение для ваших нужд. Пример: если дисконтная карта даст вам более выгодную сделку, SNCF Connect предложит правильную карту и покажет, сколько вы сэкономите на самой первой поездке.
Если у вас более одной дисконтной карты, вы увидите тарифы и условия для каждой из них.
Вы можете добавить несколько поездок в корзину, оплатить их сразу и получить к ним доступ после покупки в одном месте.

Интегрированный пригородный транспорт

SNCF Connect позволяет вам получить доступ к предложениям TER, включая региональные дисконтные карты и билеты, а также к картам Navigo и билетам T+ для парижского региона. И вы можете сохранить свои любимые маршруты одним щелчком мыши прямо на главной странице.

Связь между TGV INOUI и TER? SNCF Connect позволяет экономить со скидками по региональным картам, картам Avantage и картам вознаграждения за междугородние поездки.

Более быстрое и бесперебойное послепродажное обслуживание

Обменяйте или отмените поездку на INTERCITÉS, TER, TGV INOUI и/или международные поезда всего за несколько кликов. Отменить все бронирование или только исходящую или входящую часть — новый вариант. Взаимодействие со службой поддержки также легче отслеживать, поскольку SNCF Connect отображает всю вашу историю.