1. | 10 + х = 29 19 | 2. | х — 14 = 21 35 |
3. | 34 – у = 18 16 | 3. | 28 · у = 84 3 |
1. | 5х + 8х = 13 1 | 2. | 6х + 7х = 26 2 |
3. | 3у + 9у = 24 2 | 4. | 4у + 8у = 36 3 |
5. | 4а + 7а = 22 2 | 6. | 2а + 9a = 33 3 |
7. | 14c – 6c = 16 2 | 8. | 16k – 8k = 24 3 |
9. | 17m – 8m = 36 4 | 10. | 15m – 6m = 45 5 |
11. | 24d – 17d = 21 3 | 12. | 23d – 16d = 28 4 |
13. | 4x + 10x – 13 = 1 1 | 14. | 5x + 9x – 12 = 2 1 |
15. | 11y – 8y + 7 = 13 2 | 16. | 12y – 9y + 8 = 17 3 |
17. | 3a + 16 + a — 8 = 20 3 | 18. | 4a + 11 + a – 3 = 28 4 |
19. | 5b +12 — b — 4 = 32 6 | 20. | 6b + 14 – b – 6 = 43 7 |
Учебно-методический материал по алгебре (5 класс) по теме: «Упрощение выражений», урок в 5 классе
Статья участвует в конкурсе Образование 3.0
АННОТАЦИЯ:
Тема урока – «Упрощение выражений», 5 класс
Необходимое оборудование и материалы для занятия – персональный компьютер, мультимедиа проектор.
Описание мультимедийного продукта (медиапродукта) — конспект урока + презентационное сопровождение.
Цель использования медиапродукта (презентации) на занятии:
— организовать деятельность учащихся по получению новых знаний учащихся по теме, позволяет увеличить темп обучения;
— использование презентации позволит изучаемый материал выстроить в чёткой логической последовательности;
— обеспечивает применение знаний к решению прикладных задач, отработку вычислительного навыка;
— позволяет учитывать различные каналы восприятия, активизирует лево-правополушарные способы восприятия информации учащимися.
СЦЕНАРИЙ УРОКА:
Цель урока:
Учить применять распределительное свойство умножения при упрощении выражений.
Решение примеров и задач по теме с использованием ИКТ; формирование и развитие познавательной мотивации учащихся к получению новых знаний.
Совершенствовать вычислительные навыки учащихся.
Структура урока:
I. Организационный момент.
II. Устный счет. Сообщение темы урока.
III. Актуализация опорных знаний.
IV. Изучение нового материала.
V. Закрепление изученного материала.
VI. Физкультминутка.
VII. Работа по теме урока.
VIII. Подведение итогов учебной деятельности, домашнее задание.
Приложение:
Презентация к уроку «Упрощение выражений», для создания которой использована программа PowerPoint из пакета программ Microsoft Office 2007г., копия в программе Microsoft Office 2003г.
Ход урока:
I. Организационный момент.
II. Устный счет. Сообщение темы урока.
Учитель: Математический язык — это язык чисел, букв, символов, рисунков и чертежей. На этом языке пишут при помощи своего особого алфавита. Для математических записей используют буквы латинского алфавита, цифры, знаки действий и много других символов, с которыми вы пока не знакомы. Изучать математический алфавит и учиться писать cлова и предложения на математическом языке вы будете в течение всего времени учебы в школе и после школы, какую бы специальность вы не выбрали. Очень важно уметь «переводить» математические записи на обычный язык и наоборот (слайд 2).
1. Восстановите цепочку вычислений (слайд 3 — 4):
30 ∙ 3 → ? — 45 → ? : 15 → ? ∙ 17 → ? + 49 → ?(ответы появляются в ячейках по щелчку)
19 ∙ 4 → ? + 8 → ? : 3 → ? + 22 → ? : 2 → ? (ответы появляются в ячейках по щелчку)
63 : 9 → ? + 23 → ? : 6 → ? ∙ 7 → ? + 15 → ? (ответы появляются в строке по щелчку)
41 — ? = 20 ∙ ? = 140 + ? = 200 : ? = 40 : ? = 2(ответы появляются в строке по щелчку)
2. Решите задачи (слайд 5 — 6):
А) На 5 грузовиках 75 ящиков. Сколько ящиков на шести таких машинах? [90 ящиков]
Б) Токарь за 1 час делает 15 деталей, а его ученик 11 деталей. Сколько деталей сделают они за 8 часов работы. Решите задачу двумя способами.
3. Используя цифры 0, 1, 2, 3, запишите наибольшее и наименьшее четырехзначные числа (слайд 7).
Учитель: Сегодня на уроке мы повторим правила, которые вы изучали в начальной школе, дадим им новое название и будем учиться применять их при упрощении выражений.
III. Актуализация опорных знаний.
Распределительное свойство умножения относительно сложения (вычитания) (слайд 8 — 9).
Выражения ( 5+4) ∙ 3 и 5 ∙ 3+ 4∙ 3 имеют одно и тоже значение. По рисунку видно, почему эти выражения равны.
ВЫВОД: Для того чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить полученные произведения.
Это правило выражает распределительное свойство умножения относительно сложения.
С помощью букв его записывают так: (a + b) c = ac + bc
Одинаковые значения имеют и выражения (9- 5) ∙ 3 и 9 ∙ 3 – 5 ∙ 3.
ВЫВОД: Для того чтобы умножить разность на число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе.
Это правило называют распределительным свойством умножения относительно вычитания.
С помощью букв его записывают так: (a — b) c = ac – bc
Вычислите, используя распределительное свойство умножения (слайд 10):
(100+2) ∙ 22
(200-2) ∙ 15
90 ∙ 25 + 10 ∙ 25
123 ∙ 27 — 23 ∙ 27
23 ∙ 16 + 16 ∙ 27
40 ∙ 87 — 39 ∙ 87 ( проверка с помощью анимации по щелчку)
IV. Изучение нового материала.
Выполните задания по данному условию (слайд 11):
На столе стоят три вазы с розами. В первой вазе х роз, во второй – в 2 раза больше, а в третьей в 3 раза больше, чем в первой.
Запишите выражения для следующих величин:
число роз во второй вазе;
число роз в третьей вазе;
число роз во второй и третьей вазах вместе.
(Ответы возникают на слайде по щелчку: 2х, 3х, 2х + 3х)
Используя распределительный закон, преобразуйте выражение 2х + 3х (слайд 12).
Проверь себя: 2х + 3х = 2 ∙ х + 3 ∙ х = ( 2+3) ∙ х = 5 ∙ х = 5х
Выражение мы записали в более простом виде или, как говорят математики, упростили.
Такие преобразования, в результате которых получается более простое выражение, называют упрощением выражений.
Рассмотрим выражение 5х. Это произведение числа 5 и буквы х. Говорят, что число 5 – это числовой множитель или коэффициент, а буква х – буквенный множитель.
Упрощая выражение 2х + 3х, мы сложили коэффициенты 2 и 3 , а буквенный множитель оставили без изменения.
Подумайте, как, используя распределительный закон, упростить выражение 8у – 5у (слайд13).
УПРОСТИТЕ:
7х + 2х 11у – 3у
9а + 6а 13с – 3с
(для проверки ответы возникают по щелчку)
Для упрощения выражений также применяют сочетательное свойство умножения.
3х ∙ 5 ∙ 10 = (3 ∙ 5 ∙ 10)х = 150х
4 ∙ 2у ∙ 15 = (4 ∙ 2 ∙ 15)у = 120у
V. Закрепление изученного материала.
- Упростите, если возможно, выражение (слайд 14):
17m + 5m; 24b + 7a — 5a; 6a – a; y – 8; 9c + 4c — 6c; 5 + 12n – 2n.
- Упростите выражение:
15a ∙ 4; 3b ∙ 12; 17a ∙5b; 11a ∙ 7b; c∙ 18 ∙ d ∙ 3; x ∙ 9 ∙ 4 ∙ y.
- Запишите на математическом языке (слайд 15):
Цена хризантемы а р. за один цветок, а цена одной розы – на 30 р. больше.
А) цену розы;
Б) стоимость пяти хризантем;
В) стоимость трех роз;
Г) стоимость букета из пяти хризантем и трёх роз.
- Запишите на математическом языке:
Цена слив х р. за 1 кг, а алыча стоит на 7 р. дешевле.
А) цену алычи;
Б) стоимость двух килограмм слив;
В) стоимость шести килограмм алычи;
Г) стоимость двух килограмм слив и шести килограммов алычи вместе.
- Упростите выражение и найдите его значение (слайд 16, проверка на слайде 17):
5х + 8х при х = 13
12у – 6у при у = 6
9а + 7а при а = 16
39х – 5х -4х + 28 при х = 3
28 – 18у + 6у при у = 2
VI. Физкультминутка (гимнастика для глаз, слайды 18 — 22).
VII. Работа по теме урока.
- Решите уравнение (слайд 23):
15а – 8а = 21;
3х – х = 12;
4у + 2у – у = 20;
2а + 8а + 37 = 107.
- Найдите при каком значении буквы (слайд 24):
А) выражение 7х больше 4х на 51;
Б) сумма 8а и 3а равна 4466.
VIII. Итог урока. Задание на дом (слайд 25-26)
1) Сформулируйте распределительное свойство умножения относительно сложения и относительно вычитания.
2) Поясните как с помощью этих свойств упрощаются выражения вида 7а + 3а, 20у -7у.
3) Для выражения левого столбика найдите пару из правого столбика. Соедините их стрелочками.
5х + 3х – 4 8а
4а ∙ 3 12а
2а –а + 7а 45х
12х – 7х + 2 8х + 4
4х ∙ 6 ∙ 2 2 + 5х
9 ∙ х ∙ 5 48х
3х
Задание на дом: № 563, №566, 586(а-г).
Используемая литература: (слайд 27)
- Виленкин Н.Я. Математика 5.- М.: Мнемозина, 2007.
- Жохов В.И. Преподавание математики в 5-6 классах – М: Вербум-М,2000;
- Зубарева И.И., Мордкович А.Г. Математика, 5.- М.: Мнемозина, 2004.
- Кузнецова Г.М., Миндюк Н.Г. Программы для общеобразовательных школ, гимназий, лицеев математика 5-11 классы – М: Дрофа, 2004.
- Чесноков А.С., Нешков К.И. Дидактические материалы по математике для 5 класса.- М.: Классикс Стиль, 2007.
- Шмырева Г.Г. Сборник задач с экономическим содержанием.- Владимир,1994.
- http://www.intergu.ru/infoteka . Коллекция картинок для уроков математики в Сетевом сообществе педагогов «Интернет – государство учителей», автор Савченко Елена Михайловна.
Вывод: Оценивая эффективность этого урока, я хочу отметить следующие моменты:
- Все ученики класса были включены в активную деятельность на уроке;
- Деятельность учителя инициировала у учащихся такие логические операции как анализ, синтез, сравнение;
- Использование презентации «Упрощение выражений» позволило изучаемый материал выстроить в чёткой логической последовательности, рассмотреть множество задач для закрепления изученного материала;
- Применение данных технологий на уроках отражает дух современности, в связи с чем все происходящее на уроке воспринимается учащимися по-другому: с большим интересом, что в конечном итоге положительно отражается на уровне их успеваемости;
- Поставленные на уроке учебные задачи выполнены на оптимальном уровне.
Можно отметить бесспорный факт, что внедрение новых информационных технологий, использование мультимедиа значительно повышает качество образовательного процесса, а главное, эффективно влияет на познавательную мотивацию детей. Компьютер позволяет делать уроки, не похожими друг на друга, способствует интересу к ученью.
Использование информационных технологий в процессе обучения способствует интенсификации процесса обучения, осуществлению индивидуального и дифференцированного подходов к учащимся, повышению педагогической квалификации и профессионального мастерства учителя, повышению эффективности учебного процесса в области овладения умениями самостоятельного извлечения знаний, развитию личности обучаемого, подготовке ученика к комфортной жизни в условиях информационного общества.
АРХИВ К УРОКУ СОДЕРЖИТ:
- Пояснительная записка к медиаресурсу;
- Конспект урока;
- Презентация к уроку (медиаресурс).
Идет прием заявок на участие в фестивале методических идей «Пеликан» от АНО «ЦПИ «Ариадна»
Методическая разработка по алгебре (5 класс) по теме: «Упрощение выражений» 5 класс
Тема урока: «Упрощение выражений»
Цели:
- Организовать контроль оценку и коррекцию знаний учащихся по теме «Упрощение выражений»;
- Способствовать развитию математического слуха, речи и мышления;
- Побуждать учащихся к само- и взаимоконтролю, воспитывать познавательную активность, самостоятельность, упорство в достижении цели.
Задачи:
Закрепить: умения упрощать выражения
Воспитывать: самостоятельность
Развивать: устный счет
Оборудование: учебник, дид .материал, карточки
Тип урока: закрепление материала
Средства зад. на доске, по карточкам
Формы: коллективная, индивидуальная, самостоятельная.
Методы и приемы: практические, словесные, наглядные
Технология: здоровьесбережения
Планируемый результат: должны самостоятельно уметь упрощать выражения ; уметь решать уравнения и задачи на части.
Ход урока.
I. Организационный момент . Рефлексия.
— Здравствуйте, ребята! Присаживайтесь! Откройте свои тетради и запишите число и тему нашего урока. А тема нашего урока — «Упрощение выражений».
II. Актуализация опорных знаний .
Цель: повторить определения и применение их на практике.
а) Запишите на доске:
Как с помощью букв записывается распределительное свойство умножения относительно сложения?
Как с помощью букв записывается распределительное свойство умножения
относительно вычитания?
б) Устный счет:
упростите выражения
5х + 3х – 4 8а
(5 + у) ∙ 4 4х
4а ∙ 3 45х
2а – а + 7а 48х
12у – 7у – 2 8х – 4
4х ∙ 6 ∙ 2 20 + 4у
9 ∙ х ∙ 5 12а
5у – 2
3у
Какие выражения остались без пары?
Какие свойства применялись при упрощении выражений?
Для чего нужно хорошо уметь упрощать выражения, где это пригодится?
Сегодня на уроке мы будем решать задачи и уравнения, и эти умения нам пригодятся.
III. Формирование практических умений и навыков.
Цель: проверить умение работать с тестом, проверить усвоенность материала
а) Работа у доски.
1. Упростить выражение:
24а + 16а = 40а
13k + k = 14k
12х – х = 11х
3n – 2n + n = 2n
2. Найти значение выражения:
77п – 37п, если п = 18
3. 37m + 63m, если m = 8
4. Решить уравнение:
48у – 25у = 437 23у = 437 у = 19 | 15а – а – 16 = 82 14а -16 = 82 14а = 82 + 16 14а = 98 а = 7 |
б) Выполнение тестовой самостоятельной работы. Ответы на слайд. Взаимопроверка.
Тестовая самостоятельная работа
1 – В 1.Упростите: 13х + 5х а)18; б)18х; в)8х m + 12m а)13m; б)10m; в)10 10у – 2у а)10у; б)8у; в)8 8b + 3b – b а)13b; б)10b; в)12 2.Решите уравнения: 2х + 9х = 902 а) 9922; б) 80; в) 82 3. Найдите значение выражения: 45х + 55х, если х = 48 а) 48; б) 4800; в) 480 | 2 – В 12х + 7х а)19х; б)19; в)5х 5х + х а)5х; б)6х; в)6 26а – 23а а)3а; б)13; в)49а 20с – 6с – с а)13с; б)13; в)14с 30у – 2у = 532 а) 14896; б)10; в)19 86у – 66у, если у = 70 а)14; б)1400; в)140 |
Взаимопроверка.
Поднимите руки, кто выполнил на «5», «4», «3».Поставьте свои оценки на лист «оценки знаний».
в) Физкультминутка (через 20 мин)
Цель: поддерживать интерес к сохранению и укреплению своего здоровья
Начинаем бег на месте
Финиш метров через 200
Раз-два, Раз-два, Раз-два,
Хватит, хватит прибежали
Потянулись, отдышались
Вот мы руки развели
Словно удивились
И вдруг другу до земли
В пояс поклонились
Наклонились, выпрямились
Ниже, ниже, не ленитесь,
Поклонитесь, улыбнитесь.
г) Выполнить у доски задачу:
Латунь состоит из 2 частей цинка и 3 частей меди. Сколько граммов меди в куске латуни массой 450 г?
Цинк – 2 ч
Медь – 3 ч
Пусть х гр – приходится на 1 грамм, тогда 2х + 3х = 450
х = 90гр – приходится на 1 г
2)3 ∙ 90 = 270 г – масса меди
д) У доски выполнить с подробным разбором №588
Пусть х домов на одной стороне, тогда на второй стороне – 2х. После постройки 12 домов стало
х + 2х + 12 = 99
3х = 99 – 12
х = 87:3
х = 29 домов – на 1 стороне
29 ∙ 2 = 58 домов на другой стороне
Ответ: 20 домов и 58 домов.
е) Комментированное выполнение на местах № 57
Цель: проверить умение комментировать задания с места, и умение записывать под диктовку.
3а + 17 + 3а + 14 = 6а + 31
k + 35 + 4k + 26 = 5k + 61
ж) выполнить задания на внимательность: найди ошибку!
3а + 7а = 10а
26х – 12х = 14х
15у – 6у + 2 = 9у + 2
8 ∙ у ∙ 20 = 160у
(6 + х) ∙ 2 = 12 + 2х
100х ∙ 3 = 300х
2с ∙ 7 ∙ 2 = 28с
4х + 3х – х = 6х
з) Выполнить у доски №574 (а)
Цель: проверить умения решать уравнения.
3х + 7х + 18 = 178
10х = 178 – 18
х = 160 : 10
х = 16
Ответ: х = 16.
и) Выполнение самостоятельной работы на «3», «4», «5» по карточкам.
Самостоятельная работа на «3» , на «4» , на «5».
В – I
«3». Упростите выражения:
18а + 22а 6х + 4 + 2х + 7
с + 14с 7 + 6у + у + 4
4х + х 12х + 12х – 6х
12 у – 7у 13у – у – у
25а – 13а 3а – 3а + 8а
«4». Решите уравнение:
а) 25х + 9х = 1394
б) 9а – а + 14 = 94
в) 37у = 444
«5». Для оклеивания комнаты и коридора купили 25 рулонов обоев. Сколько рулонов обоев пойдет на оклеивание стен в комнате, если для нее нужно в 4 раза больше, чем для коридора.
В – II
«3». Упростите выражения
25х + 15х 7у + 8 + 3у + 9
8а + а 5 + 7х + х + 11
с + 19с 9k + 9k – 4k
12у – 3у 4у – 3у + у
21а – 20а 8с + с – 9с
«4». Решите уравнения:
а) 30у – 2у = 532
б) а + 6а – 5 = 72
в) х : 17 = 34
«5». В книге напечатаны рассказ и повесть, которые вместе занимают 70 страниц. Повесть занимает в 4 раза больше страниц, чем рассказ. Сколько страниц занимает рассказ и сколько повесть?
к) А сейчас к вам в гости придет фокусник и задаст вам устное задание .
Задумайте число. Прибавьте к нему 12, затем вычтите 7. К результату прибавьте 8. Скажите, сколько получилось? А фокусник отгадает вами загаданное число.
х – 13 = …
Подумайте до следующего урока: как можно узнать это число.
Вот закончился урок,
Подведём сейчас итог,
Мы много вспомнили, друзья,
Без этого никак нельзя.
Правила мы повторили,
На практике их применили
Задачи, находя решенье,
Развивают мышленье,
Память и внимание,
Закрепляли знания.
А теперь, внимание,
Домашнее задание:
Повторить п.14, № 623, № 625(а),
Не вызовет оно проблем,
Решенье ход известен всем.
Урок закончен, друзья,
До скорого свиданья.
IV . Домашнее задание: п. 14, №623, №625(а), подробно разобрать решение.
V. Итог урока
Цель: поддерживать интерес к изучению предмета:
— выставление оценок за урок
— рефлексия.
— продолжите фразу на экране.
-Чем мы сегодня занимались?
-Кто считает, что он достоин другой оценки?
-Что вам больше всего запомнилось?
Спасибо за работу!
Онлайн урок: Упрощение выражений по предмету Математика 5 класс
Упростить выражение- значит найти эквивалентное ему выражение, которое будет короче (содержащее минимум знаков, символов, математических операций) и проще для вычислений и дальнейших преобразований.
После упрощения выражения значение этого выражения остается прежним.
Упрощение выражений выполняется на основе свойств математических операций над числами, не зависимо от того арифметическое это выражение или алгебраическое.
Изученные нами раннее свойства сложения, вычитания, умножения, деления позволяют преобразовывать и упрощать математические выражения.
Рассмотрим основные методы упрощения математических выражений.

1. Метод группировки
Сочетательное и переместительное свойства сложения и умножения часто используют для преобразования выражений.
Удобно использовать переместительное и сочетательное свойства, группируя числа, объединяя их по определенному признаку, чтобы в результате они давали круглые числа или легко считались.
Группировка слагаемых подразумевает объединение в группы нескольких слагаемых.
Группировка множителей- это объединение нескольких множителей в группы.
 Упростим числовое выражение 242 + 183 +58 + 17.
Упростим числовое выражение 242 + 183 +58 + 17.Для упрощения данного выражения воспользуемся переместительным и сочетательным свойством сложения.
Сгруппируем числа 242 и 58 и числа 183 и 17.
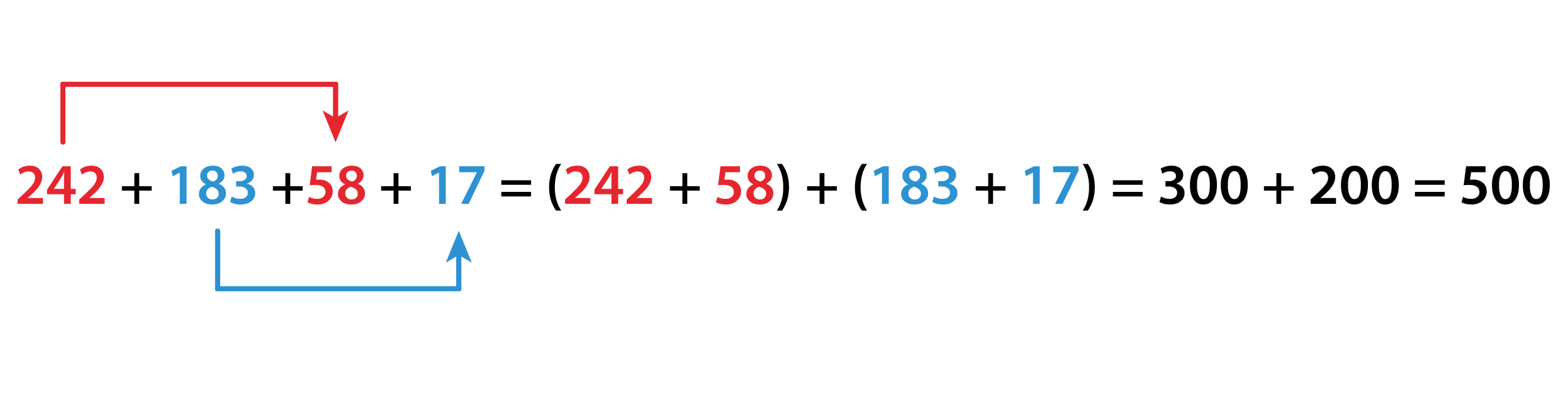

Упростим числовое выражение 12 ∙
Воспользуемся переместительным свойством умножения.
Сгруппируем числа 12 и 5 и числа 9 и 1.
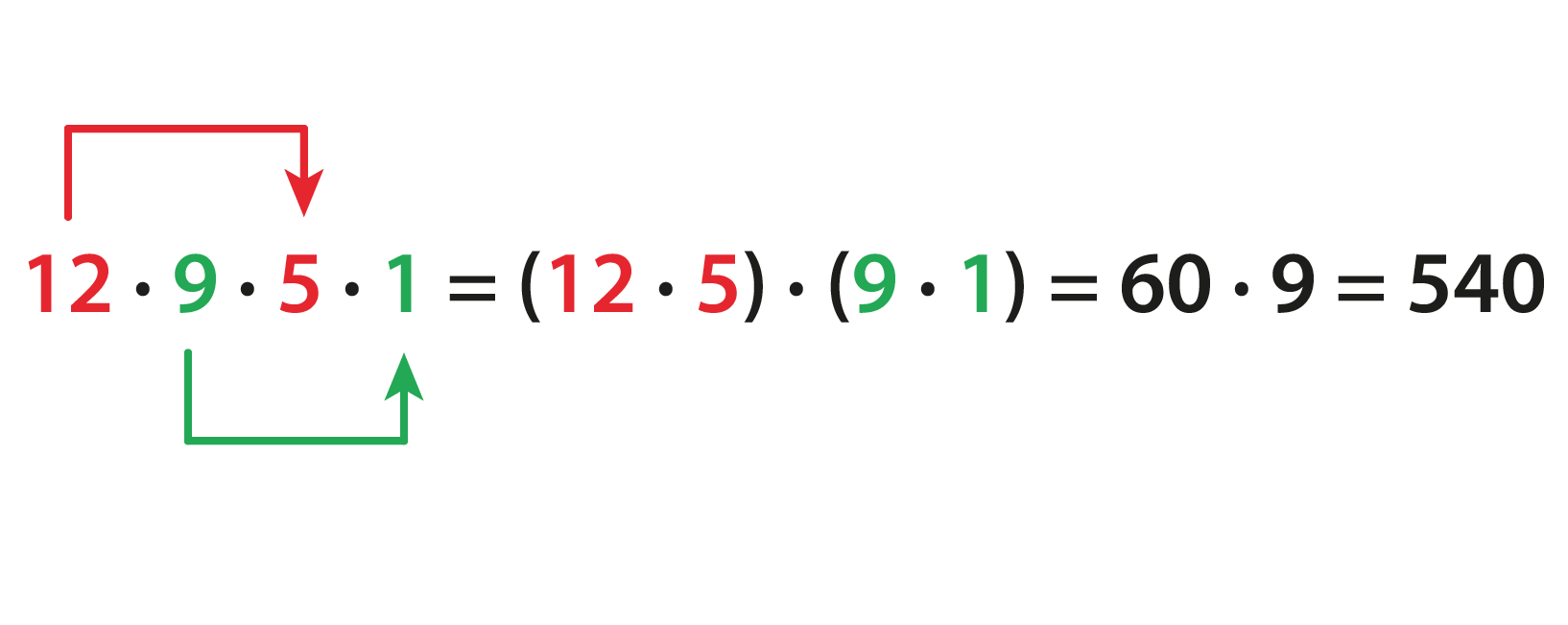
Рассмотрим пример упрощения буквенного выражения.
У меня есть дополнительная информация к этой части урока!
 Закрыть
Закрыть Важно помнить, что буквенное выражение (алгебраическое выражение) всегда содержит хотя бы одну букву.
(Например, алгебраическими выражениями можно считать а + 12; b ÷ 3; х — 15 + 6 и т.д.)
Буквенные выражения так же могут содержать несколько одинаковых букв или состоять из разных букв.
(Например, а + 4а — 3; b÷ 3; х — 15у + 26 и т.д.).
Число, стоящее перед переменными, называют числовым коэффициентом выражения.
Коэффициент обычно пишут перед буквенным множителем.
Если нет коэффициента перед буквой или произведением букв, то считается, что он равен единице.
Так как любое число, умноженное на единицу (или единицы на любое число), равняется самому себе.
Например, а ∙ b ∙ c = 1 ∙ а ∙
Выражение может состоять только из букв.
(Например, (а + b) — c; х + у — z; a ∙ b и т.д.)
Разные буквы имеют различное значение.
А если в выражении встречается одна и та же буква несколько раз, то во всех случаях она имеет одно и тоже значение.
Чтобы не путаться, можно для каждой буквы образно представить свой предмет.
Например, рассмотрим выражение 7x— 4y + y.
Представим, что x— это мороженное, y-это конфеты.


В результате получим: 7 мороженных минус 4 конфеты и плюс еще 1 конфета.
Невозможно из мороженного вычесть конфеты, однако конфеты с конфетами сложить можно.
4 конфеты + 1 конфета = 5 конфет.
Чтобы сложить слагаемые, которые имеют одинаковую буквенную часть, необходимо сложить коэффициенты и результат умножить на буквенную часть.
В итоге для нашего выражения получим следующее.
4y и y имеют одинаковую буквенную часть- это переменная y, следовательно,
4y + y = (4 + 1)y = 5y.

Запишем тождественное равенство.
7x— 4y + y
Числа, которые имеют одинаковую буквенную часть, можно складывать и вычитать.

Упростим выражение 2а ∙ 4b ∙ 3c.
Сначала выполним перестановку множителей в исходном выражении, объединяя множители в одну группу
Сгруппируем отдельно числовые и буквенные множители.
2а ∙ 4b ∙ 3c = (2 ∙ 4 ∙ 3) ∙ (а ∙ b ∙ c) = 24 ∙ а ∙ b ∙ c
В полученном выражении число 24, стоящее перед буквенной частью a, b, c— это числовой коэффициент выражения.
Часто математические выражения содержат скобки.
Скобки имеют особое значение в выражении, например, указывают очередность арифметических операций.
Порой удобно избавиться от скобок и перейти к тождественно равному выражению без скобок, нежели производить в них вычисления.
2. Упрощение выражений со скобками (раскрытие скобок).
Перейти от выражения со скобками к выражению без скобок- это значит раскрыть (опустить) скобки.
Правило раскрытия скобок основано на распределительном свойстве умножения относительно сложения и вычитания.
Чтобы умножить сумму нескольких чисел на число, можно каждое слагаемое умножить на это число, а полученные произведения сложить.
(a + b) c = ac + bc
Неважно с какой стороны располагается число с.
Таким образом, умножая число на сумму чисел, необходимо это число умножить на каждое слагаемое, а полученные произведения сложить.
c (a + b) = ac + bc
Распределительное свойство умножения относительно вычитания выполняется аналогичным образом, соблюдая некоторые нюансы.
Чтобы умножить разность на число, можно умножить на это число сначала уменьшаемое, затем вычитаемое, и из первого произведения вычесть второе.
(a — b) c = c (a — b) = ac — bc
Рассмотрим поясняющие примеры.

Раскроем скобки в выражении 4 ∙ (2а + 3b).
Умножим каждое слагаемое на число 4.
Число 4— это общий множитель для каждого слагаемого, находящегося в скобке.
В нашем выражении- это общий множитель для слагаемых 2а и 3b.
Обычно, раскрывая скобки, промежуточные вычисления записывают в виде цепочки равенств.
4 ∙ (2а + 3b) = 4 ∙ 2а + 4 ∙ 3b
Умножим первое слагаемое 2а на общий множитель 4, для этого необходимо коэффициент 2 умножить на 4, а полученный результат умножить на буквенную часть, получим 8а.
Таким же образом поступим и со вторым слагаемым 3b, для этого необходимо коэффициент 3 умножить на общий множитель 4, а полученный результат умножить на буквенную часть, получим 12b.
Сложим полученные произведения 8а и 12b.
В результате получаем следующее тождественное преобразование.
4 ∙ (2а + 3b) = 4 ∙ 2а + 4 ∙ 3b = 8а + 12b
У меня есть дополнительная информация к этой части урока!
 Закрыть
ЗакрытьВ скобках может быть любое количество слагаемых.
Например, 10 ∙ (2a + 4b + b).
Упростим выражение 10 ∙ (2a + 4b + b).
Можно сначала сгруппировать слагаемые, которые имеют одинаковую буквенную часть (в нашем выражении это 4b и b), затем раскрыть скобки, применив распределительное свойство умножения относительно сложения.
Умножим каждое слагаемое, находящееся в скобке,на их общий множитель, равный 10.
Затем сложим полученные произведения.
10 ∙ (2a + 4b + b) = 10 ∙ (2a + 5b) = 10 ∙ 2а + 10 ∙ 5b = 20а + 50b.
Второй вариант упрощения выражения 10 ∙ (2a + 4b + b) заключается в следующем:
Первым делом, раскроем скобки, применив распределительное свойство умножения относительно сложения, умножим все три слагаемых 2a, 4b, b на их общий множитель, число 10.
Для этого коэффициенты каждого слагаемого умножить на общий множитель 10
10 ∙ 2а + 10 ∙ 4b + 10 ∙ b = 20a + 40b + 10b
Затем сгруппируем слагаемые с одинаковой буквенной частью (в нашем случае это 40b и 10b) и найдем их сумму.
В результате получаем следующее равенство:
10 ∙ 2а + 10 ∙ 4b + 10 ∙ b = 20a + 40b + 10b = 20a + 50b
В первом и во втором варианте тождественные преобразования привели к одному результату 20a + 50b, в полученном выражение отсутствуют скобки, количество арифметических операций уменьшилось

Раскроем скобки в выражении 4 ∙ (2а — 3b).
Воспользуемся распределительным свойством умножения относительно вычитания.
Умножим уменьшаемое 2а на общий множитель 4, для этого необходимо коэффициент 2 умножить на 4, а полученный результат умножить на буквенную часть, получим 8а.
Таким же образом поступим и с вычитаемым 3b, для этого необходимо коэффициент 3 умножить на общий множитель 4, а полученный результат умножить на буквенную часть, получим 12b.
Затем из первого полученного произведения вычтем второе.
В результате получим следующее равенство:
4 ∙ (2а — 3b) = 4 ∙ 2а — 4 ∙ 3b = 8а — 12b.
Рассмотрим правила раскрытия скобок при делении.
Распределительное свойство деления справедливо только в том случае, если скобки стоят в делимом
(a + b) ÷ c = a ÷ c + b ÷ c
(a — b) ÷ c = a ÷ c — b ÷ c
Например, раскроем скобки в выражении (20а + 30b) ÷ 5.
Разделим каждое слагаемое на число 5.
(20а + 30b) ÷ 5 = 20а ÷ 5 + 30b ÷ 5
Разделим первое слагаемое 20а на 5, для этого необходимо коэффициент 20 разделить на 5, а полученный результат умножить на буквенную часть, получим 4а.
Таким же образом поступим и со вторым слагаемым 3b, для этого необходимо коэффициент 30 разделить на 5, а полученный результат умножить на буквенную часть, получим 6b.
Сложим полученные частные 4а и 6b.
В результате получаем следующее тождественное преобразование.
(20а + 30b) ÷ 5 = 20а ÷ 5 + 30b ÷ 5 = 4а + 6b
Однако, если скобки расположены в делителе, т.е. число делят на сумму чисел, то необходимо выполнить действия в скобках (если это возможно), и только потом делимое число разделить на результат, полученный в скобках.
3. Вынесение общего множителя за скобки.
Выражения (a + b) c и ac + bc согласно распределительному свойству умножения имеют одно и то же значение, т.е. распределительный закон умножения можно применять в обратную сторону- выносить общий множитель за скобки.
ac + bc = (a + b) c = c (a + b)
Неважно с какой стороны расположен общий множитель.
Необходимо иметь ввиду, что общим множителем может быть не только число, но и буква или несколько букв, а порой, даже целое выражение.
Рассмотрим несколько примеров.

Упростим выражение 7а + 7b.
Произведения 7а и 7b имеют общий множитель число 7.
Вынесем общий множитель за скобки, исходное выражение примет вид 7 (а + b).
Мы по сути получили произведение общего множителя и выражения в скобках, записанного без общего множителя.
Общий вид решения будет выглядеть так:
7а + 7b = 7 (а + b).

Упростим выражение 3х — 2х + 1.
В данном выражении 3х и 2х имеют в своей записи множитель х— это их общий множитель.
Вынесем общий множитель (переменную х) за скобку.
3х — 2х + 1 = х ∙ (3 — 2) + 1
Выражение в скобках можно вычислить (3 — 2 = 1).
Решением в общем виде будет выглядеть так:
3х — 2х + 1 = х ∙ (3 — 2) + 1 = х ∙ 1 + 1 = х + 1.

Упростим выражение 8х + 2у.
Слагаемые 8х и 2у имеют общий множитель 2, так как 8 представляет собой произведение двух чисел 4 ∙ 2, т.е. исходное выражение можно записать следующим образом:
4 ∙ 2 ∙ х + 2у.
Вынесем общий множитель (число 2) за скобку, получим
4 ∙ 2 ∙ х + 2у = 2 (4х + у).
Решение в общем виде будет записываться так:
8х + 2у = 4 ∙ 2 ∙ х + 2у = 2 (4х + у).
За скобки можно выносить даже целое выражение.
Упростим выражение 4аb + 2b.
Так как 4 = 2 ∙ 2, то 4аb и 2b имеют общий множитель 2.
Кроме того, данные слагаемые имеют одинаковую букву- это буква b, следовательно, 4аb и 2b имеют общий множитель в виде произведения 2b.
Исходное выражение запишем так:
2 ∙ 2аb + 2b
Вынесем общий множитель 2b за скобку.
4аb + 2b = 2 ∙ 2аb + 2b = 2b (2а + 1).
Проверим верно ли мы упростили выражение.
Выполним обратное действие, раскроем скобки.
Известно, при умножении любого числа на единицу (или единицы на число) получится само это число.
В результате получится равенство
2b ∙ (2а + 1) = 2b ∙ 2а + 2b ∙ 1 = 2 ∙ 2 ∙ a ∙ b + 2b = 4аb + 2b.
В итоге получили выражение 4аb + 2b, которое требовалось упростить.
Упрощение математических выражений часто используют при решении уравнений и текстовых задач, решаемых с помощью уравнений.
Решим уравнение 12у + 3у — 2 = 28.
Найдем значение у, при котором данное уравнение превратится в верное равенство.
Первым делом упростим левую часть равенства.
12у и 3у имеют одинаковую буквенную часть, их можно сложить (сложим коэффициенты 12 и 3 и результат умножим на их буквенную часть).
12у + 3у = 15у
Исходное равенство тогда примет следующий вид:
15у — 2 = 28
В этом уравнении уменьшаемое представлено не просто числом, а буквенным выражением 15у.
Нам известно, как связаны между собой компоненты вычитания.
Чтобы найти неизвестное уменьшаемое (15у), необходимо к разности (28) прибавить вычитаемое (2).
15у = 28 + 2
15у = 30
Неизвестное у в данном уравнении является множителем.
Чтобы найти неизвестный множитель (у), нужно произведение (30) разделить на известный множитель (15).
у = 30 ÷ 15
у = 2
Выполним проверку найденного корня.
В исходное уравнение 12у + 3у — 2 = 28 вместо неизвестного числа (у) подставим найденный корень у = 2.
12 ∙ 2 + 3 ∙ 2 — 2 = 28
24 + 6 — 2 = 28
28 = 28
Значение левой и правой части равенства одинаково, значит корень уравнения найден верно.
Запишем ответ.
Ответ: у = 2.
Опуская все наши пояснения и рассуждения, решение уравнения запишем так:
12у + 3у — 2 = 28
15у — 2 = 28
15у = 28 + 2
15у = 30
у = 30 ÷ 15
у = 2
Проверка:
12 ∙ 2 + 3 ∙ 2 — 2 = 28
24 + 6 — 2 = 28
28 = 28
Значит корень уравнения найден верно.
Ответ: у = 2.
Рассмотрим пример текстовой задач, которую можно решить с помощью уравнения.
В двух корзинах было 9 килограммов ягод.
В первой корзине в 2 раза больше ягод, чем во второй.
Сколько килограммов ягод было в каждой корзине?

Пусть х (кг) ягод было в первой корзине.
По условию во второй корзине было ягод в 2 раза больше, тогда
2х (кг) ягод было во второй корзине.
Зная, что в двух корзинах было 9 (кг) ягод, составим уравнение.
х + 2х = 9
Упростим левую часть равенства.
х и 2х имеют одинаковую буквенную часть, их можно сложить (сложим коэффициенты 1 и 2 и результат умножим на их буквенную часть.)
1х + 2х = 3х
Исходное равенство тогда примет следующий вид:
3х = 9
Получили простое уравнение, в котором неизвестен множитель (х).
Чтобы найти неизвестный множитель (х), нужно произведение (9) разделить на известный множитель (3).
х = 9 ÷ 3
х = 3 (кг) ягод было в первой корзинке.
2х = 2 ∙ 3 = 6 (кг) ягод во второй корзинке.
Проверим найденные значения.
Сложим полученное количество ягод в первой и во второй корзинке.
3 кг + 6 кг = 9 (кг) было в двух корзинах.
Решение задачи найдено верно.
Ответ: 3 (кг), 6 (кг).
Урок математики в 5-м классе «Упрощение выражений»
Тип урока: изучение нового материала.
Цель урока: формировать у учащихся умение упрощать буквенные выражения на основе распределительного свойства умножения, ввести понятия подобных членов, числового множителя; способствовать формированию детского коллектива, воспитывать самостоятельность, развивать у учащихся интерес к предмету, знакомить учащихся с историей развития математики.
Задачи урока
Образовательные: обеспечить в ходе урока умение применять распределительное свойство умножения для упрощения буквенных выражений, ввести понятие подобных членов, числового множителя – коэффициента; формировать умение применять распределительное свойство умножения при решении уравнений; продолжить формирование общих учебных умений и навыков: навыки планирования ответа, навыки самоконтроля.
Воспитательные: воспитывать у учащихся интерес к предмету, умение работать в парах, умение слушать товарища, отстаивать свою точку зрения, самостоятельность, навыки самоконтроля.
Развивающие: развивать восприятие, логическое и математическое мышление, умение связывать изученный материал с новым, анализировать, выделять главное; знакомить учащихся с историей развития математики.
Метод обучения: беседа, самостоятельная работа
Оборудование: иллюстрация, плакат с готовым решением 1 и 2 задания IV этапа, плакат с заданием 2 VI этапа, портрет Франсуа Виета, тесты.
Ход урока
I этап. Организация начала урока.
Цель этапа: подготовка к работе на уроке.
Содержание деятельности: приветствие, определение отсутствующих; проверка готовности учащихся к уроку; готовность наглядных пособий, доски, мела и т.д.
Раскрытие общей цели урока.
II этап. Актуализация знаний учащихся
Цель этапа: подготовить учащихся к изучению нового материала
Содержание деятельности
1) Вычислите:
а) 30 + 20 |
б) 60 + 30 |
в) 100 – 90 |
2) Вычислите, применяя законы арифметических действий:
а) 372 + 2444 + 1628;
б) 156 + 1037 + 2063 + 844;
в) 125 . 53 . 8;
г) 52 . 138 + 48 . 138;
д) 67 . 149 + 149 . 33;
е) 150 . 97 – 57 . 150.
3) Решите уравнение: а) х – 2041 = 3059; б) 289 + у = 301; в) z . 93 = 186; г) 100 : a = 25.
4) Сформулируйте распределительное свойство умножения относительно сложения и относительно вычитания.
III этап. Изучение нового материала
Цель этапа: объяснить понятие «упрощение выражения», ввести понятие подобных членов, числового множителя.
Содержание деятельности
1) Задача.
На столе стоят три вазы с гвоздиками. В первой вазе х гвоздик, во второй – в 2 раза больше, а в третьей – в 3 раза больше, чем в первой. Сколько гвоздик во второй и третьей вазах?
1 ваза – х;
2 ваза – 2 . х
3 ваза – 3 . х
Всего во второй и третьей вазах — 2 . х + 3 . х
Преобразуем выражение, применяя распределительное свойство умножения
2 . х + 3 . х = х . ( 2 + 3) = х . 5 = 5х
Итак, распределительное свойство умножения позволяет упрощать буквенные выражения
3а + 7а = а(3 + 7) = 10а
27у – 12у = у(27 – 12) = 15у
49х + х = х(49 + 1) = 50х
63b – b = b(63 – 1) = 62b
Таким образом, данные выражения мы записали в более простом виде, или, как говорят математики, упростили. Такие преобразования, в результате которых получаются более простые выражения называют упрощением выражений.
2) Рассмотрим выражение 3у. Это произведение числа 3 и буквы у. Говорят, что число 3 – числовой множитель, а буква у – буквенный множитель. Числовой множитель обычно в таких выражениях называют коэффициентом.
Упрощая выражения, мы складывали коэффициенты, а буквенный множитель мы оставляли без изменения. Обычно промежуточные записи не делают, а просто пишут 8у – 3у = 5у; 17х + х = 18х.
3) Мы рассмотрели буквенные выражения, у которых одинаковая буквенная часть. Такие выражения называют подобными.
А выражение 27х + 7у упростить нельзя, потому что у них буквенная часть разная.
4) Отметим, что распределительный закон умножения верен не только для двух, а для любого числа слагаемых.
Далее учащимся предлагается Рисунок,
на которой множитель за скобкой сравнивается с предупредительным официантом, который обслуживает всех клиентов в ограниченном скобками зале.
5) Примеры.
Упростить выражение:
а) 2(а + 6) + 3(а + 2) = 2а + 12 + 3а + 6 = 5а + 18
б) 3(а + 2b + 4) + 7(2a + 4b +1) = 3a + 6b + 12 + 14a + 28b + 7 = 17a + 34b + 19
IV этап. Первичная проверка понимания новых знаний и способов деятельности.
Цель этапа: установление обратной связи между учителем и учениками по вопросам содержания нового учебного материала.
Содержание деятельности
1. Упростите следующие выражения. Назовите в полученных выражениях числовой и буквенный множитель. Как называются эти слагаемые?
27х + 29х
12у + 78у
103а – 87а
12b – b
13z + 2z + z – 5z
2. Упростите выражения
2а + 1 + а + 11
7b – 5b + 13 + 2b + 10
13у – у + х + 2х
3. Какое свойство мы использовали при упрощении данных выражений? Почему нельзя упростить выражение 17у – 13а? 2у + 1?
V этап. Закрепление полученных знаний и способов деятельности.
Цель этапа: сформировать у учащихся на основе знаний умение упрощать выражения по «образцу»
Содержание деятельности
1. Упростить выражение:
а) 23а + 37а; д) 27р – 27р; и) 3а + 17 + 3а + 14;
б) 4у + 26у; е) 84b – 80b; к) к + 35 + 4к + 26.
в) 48х + х; ж) 32q – q;
г) у + 56у; з) 1000к – к;
Учащимся дается время для самостоятельного решения для самостоятельного решения этого задания, а затем по готовым ответам проверяют свое решение.
VI этап. Применение знаний и способов деятельности.
Цель этапа: освоение способов деятельности в изменённых условиях
Содержание деятельности
1. Решите уравнение:
а) 4х + 4х = 424;
б) 10к – к = 702;
в) 3х + 7х + 18 = 178;
г) 6у – 2у + 25 = 65.
2. Далее учащимся предлагается самостоятельно решить уравнения и расшифровать слово:
- 15у – 8у = 714;
- 9z + z = 900;
- 4к + 5к + к = 1260;
- 7z + 6z – 13 = 130.
9 |
102 |
100 |
90 |
140 |
12 |
126 |
11 |
с |
в |
а |
и |
у |
г |
е |
т |
Учащимся показывают портрет Ф. Виета.
Франсуа Виет – французский математик. Одним из первых стал числа обозначать буквами.
3. Составьте выражение по условию задачи и упростите получившееся выражение:
1) На книжной полке стояли книги. Из них а книг – сказки, а приключенческих повестей в 5 раз больше. Сколько всего книг на книжной полке?
2) В ящике было у кг яблок, а в мешке в 4 раза больше. На сколько яблок в ящике меньше, чем в мешке?
3) Ниф – Ниф, Нуф – Нуф и Наф — Наф собирали желуди. Ниф – Ниф собрал х желудей, Нуф – Нуф в 3 раза больше,а Наф — Наф в 5 раз больше, чем Ниф – Ниф. Сколько всего желудей собрали три поросенка?
4. Чему равны стороны треугольника АВС, если сторона АС в 3 раза больше стороны АВ, а сторона ВС на 4 см меньше АС, а его периметр равен 24 см?
VII этап. Контроль и самоконтроль знаний и способов деятельности.
Цель этапа: получение информации для сравнения достигнутых результатов учебного занятия с первоначально запланированными задачами.
Содержание деятельности: учащимся предлагается тест на 5минут
1. Упростите выражение: 34х – х + 5х
а) 39х; б) 38х; в) 37х
2. В одном мешке было х кг картофеля, а во втором в 2 раза больше. Сколько
килограммов картофеля было в двух мешках?
а) х; б) 2х; в) 3х; г) 4х.
3. Вася решил у задач, а Миша – на 4 задачи больше. Сколько задач решили Миша и
Вася всего?
а) 4у; б) 6у; в) 2у + 4; г) у + 4.
4. Упростите выражение:
4b + 15 + 3b -10 + b
a) 8b + 5; б) 7b + 5; в) 13b; г) 13
5. Даны два выражения:
9(856 + 342) и 9 .856 + 8 . 856. Какое из выражений больше?
а) равны; б) первое; в) второе.
Далее учащимся предлагается обменяться тетрадями и проверить тесты по готовым ответам на доске. Учащиеся выставляют друг другу оценки.
Ответы.
№ задания |
1 |
2 |
3 |
4 |
5 |
Ответ |
б |
в |
в |
а |
б |
VII этап. Подведение итогов урока.
VIII этап. Домашнее задание: учащимся раздаются карточки с домашним заданием
«Упрощение выражений», математика (5 класс)
Упрощение выражений
Тип урока: закрепление новых знаний и способов действий при решении задач и уравнений.
универсальные учебные действия(УУД)
1
2
3
4
5
6
I. Мотивация к учебной деятельности.
Цели:
-актуализировать требования к обучающемуся с позиций учебной деятельности;
— создать условия для формирования у обучающихся внутренней потребности во включении в учебную деятельность
Создает условия для формирования внутренней потребности обучающихся во включении в учебную деятельность
Чтобы спорилось нужное дело,
Чтобы в жизни не знать неудач,
Вы в поход отправляетесь смело
В мир загадок и сложных задач.
Не беда, что идти далеко,
Вы не бойтесь, что путь будет труден.
Достижения крупные людям
Никогда не давались легко.
С. Я. Маршак
Сегодня на уроке мы продолжим работу над упрощением выражений, решением уравнений
Слушают учителя
Коммуникативные: уметь совместно договариваться о правилах поведения, следовать им;
оформлять свои мысли в устной форме.
Познавательные: уметь использовать модели для решения задач
II.Актуализация и фиксирование индивидуального затруднения в пробном действии; выявление места и причины затруднения.
Цели:
— организовать фиксирование обучающимися индивидуального затруднения;
— выявить место (шаг, операцию) затруднения;
— зафиксировать во внешней речи причину затруднения
Организует фиксирование индивидуального затруднения, выявление места и причины затруднения во внешней речи, обобщение актуализированных знаний
Устный счет (см. приложение, составить словосочетание)
Давайте вспомним и запишем в буквенной форме распределительное свойство умножения относительно сложения и распределительное свойство умножения относительно вычитания:
(a + b) c = ac + bc
(a – b) c = ac – bc
Выполняют задание с проговариванием во внешней речи
Знать распределительное свойство умножения относительно сложения и вычитания, сочетательное свойство умножения. Уметь упрощать выражения
Познавательные: уметь ориентироваться в своей системе знаний (отличать новое от уже известного с помощью учителя, преобразовывать информацию из одной формы в другую).
Коммуникативные: уметь слушать и понимать речь других, оформлять мысли в устной и письменной форме.
Регулятивные: уметь проговаривать последовательность действий на уроке, высказывать свое предположение
III.Обобщение, систематизация знаний и способов действий.
Цели:
— уточнить индивидуальные цели будущих действий;
-организовать составление плана совместных действий
Работа в группах (см. приложение).
Работа с учебником.
№ 556 (а), № 568 (а, б).
Физминутка.
Решите с помощью уравнения задачу:
Маша и Ира нарвали букеты ромашек. Маша нарвала в 2 раза больше цветов, чем Ира. Сколько ромашек нарвала Ира, если всего у них в букетах было 132 ромашки?
Обучающимся предлагается тест на 8 мин. (см. приложение). Затем они обмениваются тетрадями и проверяют тесты по готовым ответам.
Выполняют задание с проговариванием во внешней речи
Выполняют тест, взаимопроверку.
Знать распределительное свойство умножения относительно сложения и вычитания, сочетательное свойство умножения. Уметь упрощать выражения, решать задачи с помощью уравнения
Познавательные: уметь использовать знаково-символические средства, строить логическую цепочку рассуждений.
Коммуникативные: уметь выражать свои мысли с достаточной полнотой и точностью; аргументировать свое мнение и позицию в коммуникации.
Регулятивные: уметь сдерживать себя в ситуации затруднения, осуществлять итоговый и пошаговый контроль по результату.
Личностные: осознавать ответственность за общее дело
IV. Рефлексия учебной деятельности на уроке.
Цели:
— организовать рефлексию и самооценку обучающимися собственной учебной деятельности.
Организует рефлексию, самооценку учебной деятельности
Подведем итог работы на уроке.
Расскажите, чему вы научились.
Оцените свою деятельность на уроке.
Домашнее задание: стр. 91, №614 (в, г),
стр. 92, №618
Отвечают на вопросы. Рассказывают, что узнали. Осуществляют самооценку.
Регулятивные: уметь проговаривать последовательность действий на уроке, оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки.
Личностные: уметь осуществлять самооценку на основе критерия успешности учебной деятельности.
Приложение

Групповая работа
Найдите значение выражения, применяя распределительный закон умножения (вынесите общий множитель за скобки):38 · 37 + 63 · 38 =
4.Найдите значение выражения, применяя распределительный закон умножения:
81 · 8 =
Найдите значение выражения, применяя распределительный закон умножения (вынесите общий множитель за скобки):
25 · 78 — 68 · 25 =
5.Найдите значение выражения, применяя распределительный закон умножения:
6 · 49 =
Найдите значение выражения, применяя распределительный закон умножения (вынесите общий множитель за скобки):
77 · 52 + 23 · 52 =
6.Найдите значение выражения, применяя распределительный закон умножения:
5 · 72 =
Решение:
38 · 37 + 63 · 38 = (37 + 63) · 38 = 100 · 38 = 3800;
25 · 78 — 68 · 25 = (78 – 68) · 25 = 10 · 25 = 250;
77 · 52 + 23 · 52 =(77 + 23) · 52 = 100 · 52 = 5200;
81 · 8 = (80 + 1) · 8 = 80 · 8 + 1 · 8 = 640 + 8 = 648;
6 · 49 = 6 · (50 – 1) = 6 · 50 – 6 · 1 = 300 – 6 = 294;
5 · 72 = 5 · (70 + 2) = 5 · 70 + 5 · 2 = 350 + 10 = 360;
ФИ
Задания
Устный счет
Правила (формулы)
Групповая работа
№ 556 (а)
№ 568 (а, б)
Задача
Тест
Самооценка
(отметка)
Отметка учителя
Общая отметка
Цветные карточки
Таблица (устный счет)
- 1000
77
60
40
814
253
125
1
6100
5
35
0
52
101
14
100
27
0
6100
Тест
задания1
2
3
4
5
Ответ
УПРОЩЕНИЕ ВЫРАЖЕНИЙ 5 класс
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
Предмет
Математика
Класс
5
Учитель
Красникова Наталья Николаевна
Тема урока:
Упрощение выражений
Цель урока:
продолжить работу по формированию умений решать уравнения с использованием распределительного свойства умножения относительно сложения и вычитания; продолжить работу над текстовыми задачами, решаемыми с помощью уравнения
Тип урока:
урок комбинированный.
Деятелъностная цель: формирование у учащихся умений упрощать выражения.
Содержательная цель: расширение понятийной базы за счет включения в нее новых элементов.
Образовательные (формирование познавательных УУД):
Отработать навыки чтения и записи числовых и буквенных выражений;
Формировать умение решать задачи способом составления уравнения;
Проверить уровень усвоения изученной темы;
Развивающие (формирование регулятивных УУД)
Развитие навыков самостоятельной деятельности обучавшихся;
Формирование математически грамотной речи. Уметь правильно понимать термины. Развитие математической зоркости.
Воспитательные (формирование коммуникативных и личностных УУД)
Воспитывать интерес к изучаемому предмету;
Воспитывать коллективные взаимоотношения, взаимопонимания;
Развивать самостоятельность, самоконтроль, наблюдательность.
Методы: проблемно-поисковый, словесный, наглядный, практический.
Оборудование: ПК, мультимедийный проектор, листы урока, мел, доска.
Планируемый результат
Личностные:
Формирование познавательного интереса обучающихся к изучению нового материала, к способам обобщения и систематизации знаний.
Воспитание культуры личности.
Развивать навыки сотрудничества.
Познавательные:
Закреплять навыки и умения применять правила упрощений выражений при решении задач и применение свойств умножения,
Систематизировать знания, уметь обобщать и углублять знания , выбирать и формулировать познавательную цель, выражать смысл ситуации с помощью различных примеров.
Предметные:
Уметь в процессе реальной ситуации применять понятие упрощение выражений.
Уметь планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями её реализации.
Способствовать приобретению учащимися навыков общения при совместной работе;
Делать выводы на основе обобщения знаний.
Регулятивные:
Самостоятельно формулируют познавательную цель и строят свои действия в соответствии с ней;
Планируют собственную деятельность, определяют средства для её осуществления.
Коммуникативные:
Регулировать собственную деятельность посредством речевых действий;
Уметь слушать и вступать в диалог, воспитывать чувство взаимопомощи;
Уважительное отношение к чужому мнению, культуре учебного труда, требовательное отношение к себе и к своей работе.
Технологии
Технология проблемного обучения, игровые технологии, ИКТ
Форма работы
индивидуальная, фронтальная работа, самостоятельная работа.
Технология проведения
Деятельность учителя
Задания для учащихся, выполнение которых приведет к достижению запланированных результатов
Деятельность учеников
Планируемые результаты
предметные
универсальные учебные действия(УУД)
1
2
3
4
5
6
1. Организационный этап
Создать благоприятный психологический настрой на работу
Приветствие, проверка подготовленности к учебному занятию, организация внимания детей.
Сегодня вы работаете с листом рефлексии и самооценки. Оцените свою готовность к уроку. – А вот хорошо ли вы считаете в уме, и на сколько вы внимательны, это мы сейчас и проверим! Внимание на экран! Обсуждение и проверка ответов.
Включаются в деловой ритм урока.
Уметь выполнять основные математические действия.
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.
Регулятивные: организация своей учебной деятельности
Личностные: мотивация учения
Постановка целей и задач урока. Мотивация учебной деятельности учащихся
Цели:
— актуализировать требования
к ученику с позиций учебной
деятельности;
— создать условия для формирования у учеников внутренней потребности во включении в учебную деятельность
Систематизировать изученный материал.
Стимулировать активность ученика на восприятие нового учебного материала.
Подвести к формулированию цели урока и самостоятельному поиску нужной информации.
Но сначала решим несколько упражнений и попробуем назвать тему урока.
1.УСТНО пример А
2.Вычислите устно Б и запишите ответ
15a ∙ 4 =
3b ∙ 12 =
18 ∙ 5b =
11a ∙ 7 =
16 ∙ d ∙ 3 =
x ∙ 5 ∙ 4 ∙ 6 =
3. Упростите В , если возможно:
17m + 5m =
6a – a =
9c + 4c – 6c =
5 + 12n – 2n =
24b + 7a – 5a =
y – 8
Г Верно или не верно
Слушают
Учителя.
Вычисляют устно. Делают записи в листе
Самопроверка.
Самооценивание.
Знать правила упрощения буквенных выражений.
Уметь применять свойства умножения в решении упражнений.
Коммуникативные: уметь совместно договариваться о правилах поведения и общения, следовать им; оформлять свои мысли в устной форме.
Познавательные: уметь использовать модели для решения задач
Найдите пару для выражения, стоящего в левом столбце.
1)5х+13х-4 2)(5+у)*4 3)4а*3
4)15а-а 5)12у-7у-2
6)4х*6*2 7)9*х*5
А)8а Б)4х
В)45х
Г)48х
Д)18х-4
Е)20+4у
Ж)12а
З)5у-2
И)3у
Вычисляют. Сопоставляют величины. Делают записи в листе
Выполняется контроль знаний
Коммуникативные :
Слушать, понимать речь других
Познавательные УУД:
-уметь проводить сравнение по заданным критериям.
.
II. Актуализация и фиксирование индивидуального за-
Затруднения в пробном действии; выявление места и причины затруднения.
Цели:
— организовать фиксирование
учащимися индивидуального
затруднения;
— выявить место (шаг, операцию) затруднения;
— зафиксировать во внешней
речи причину затруднения
Организует
фиксирование
индивидуального затруднения, выявление места и причины
затруднения в речи,
обобщение актуализированных знаний
Какие свойства умножения применяют при решении этих выражений?
Запишите свойства при помощи букв.
Давайте вспомним и запишем
в буквенной форме распределительное свойство умножения относительно сложения и распределительное свойство умножения относительно вычитания:
{а +b ) с = ас + bс
b) с = ac- bc
Назовите тему урока?
Для чего надо уметь упрощать
выражения? Где это пригодится?
Найдите значение выражения:
14у + 380 +у – 380, если у = 20
1 способ (14+1)у+(38-38)=15у
15*20 =300
2 способ 14*20+38+20-38=300
Какой способ более удобный?
Выполните следующие задание удобным способом.
Д)Упростите выражения 1вариант) 3х + 2 + х + 5 =? Х=3
2вариант) 4х – х + 3 + 2 =?х=4
Е) Найдите ошибки при выполнении упрощения буквенного выражения (если они есть)
12в + 4 +13а + в +15 + 12а
1вариант)
12в + 4 +13а + в +15 + 12а = 12в + 25а + 19
2 вариант)
12в + 4 +13а + в +15 + 12а = 38ав + 19
Выполняют
задание
с проговариванием
решения.
Знать распределительное свойство умножения
относительно
сложения и вычитания, сочетательное свойство
свойство умножения.
Уметь упрощать
Выражения.
Познавательные: уметь ориентироваться в своей системе знаний
( уметь отличать новое от уже известного с помощью учителя, преобразовывать информацию из одной формы
в другую).
Коммуникативные: уметь слушать
и понимать речь других, оформлять
мысли в устной и письменной форме.
Регулятивные: уметь проговаривать последовательность действий на уроке, высказывать свое предположение
Организует тематику теста
Молодцы! Ошибки находить вы умеете, но не допускаете ли вы сами ошибок?! Это мы сейчас и проверим. Вам предстоит выполнить тест. Если вы его правильно решите, то узнаете фамилию великого математика. Решая тест, вы должны будете выписать буквы, соответствующие ответам. Приступайте к выполнению задания. ВИЕТ. Эти буквы составили фамилию известного французского математика Франсуа Виета. Он первым начал активно использовать буквы вместо чисел не только в уравнениях, но и в математических выражениях. Имя этого ученого мы еще не раз вспомним в старших класса на уроках алгебры.
Тест. Взаимопроверка, Определяют ответы к заданиям:
1 – В
2 – И
3 – Е
4 — Т
Записывают решение. Самооценка деятельности
Физкультминутка
Организует показ слайдов
— Организация физкультминутки.
Осуществляют пошаговый контроль своих действий, ориентируясь на показ движений
Решите уравнение
13х + 7х = 160
Что нужно сделать перед началом решения?
Упростите левую часть.
Где неизвестное число?
Как найти неизвестный множитель?
Записывают уравнение в листок и находят корень уравнения. Осуществляют пошаговый контроль своих решений.
Выполняют данное задание. Осуществляют самопроверку.
Создание проблемной ситуации.
Задачи: создать проблемную ситуацию; актуализировать опорные знания и умения.
Формулировка задачи через презентацию побуждение к рассуждению и высказыванию своего мнения
Задача №580 стр.88
Прочитайте задачу.
О чем говорится в задаче?
Что сказано про количество стульев?
Что говорится про количество столов? Сколько всего? Обозначай за x то, что требуется найти. Если в вопросе несколько неизвестных, за x обозначай то, которое меньше
Пусть для школы купили x столов. Тогда стульев купили 9x. Всего столов и стульев купили x+9x.
В условии сказано, что всего купили 220 столов и стульев.
Значит, можем составить уравнение:
x+9x=220
10х=220
Х=220:10
Х=22
Что мы нашли?
22 стола купили для школы.
Как найти количество стульев?
Обратите внимание. Что 9*х – количество стульев.
22*9=198 (стульев) купили для школы.
Ответ
Какую тему мы сегодня изучили?
Какие свойства мы применяли при упрощении выражений?
Зачем нужно уметь упрощать выражения?
Сможете вы сами находить и применять эти свойства при решении примеров и уравнений?
Предлагаю самостоятельно решить следующие упражнения.
Учащиеся извлекают необходимую информацию из условия задачи.
Моделируют задачу
Составлять уравнение по условию задачи Уметь решать уравнение.
Учебно-познавательная (переработка, использование информации для решения учебной задачи), коммуникативная (устная, письменная)
Самостоятельное применение полученных знаний.
Задача: закрепление знаний и умений
Подготовила материал
Самостоятельная работа — Каждой группе предлагается задания
1 вариант 2 вариант
Упростите выражение
56х — 34х 64a + 22a
97у + 43у 98b – 75b
7z – 2z + 4 8c + 5c — 5
составьте и решите уравнение
Сумма 2х и 5х равна 156 сумма 18а и 13а равна 31
разность 20у и 3у равна 51 разность 25с и 5с равна 3000
Найдите значение выражения
44х + 25у + 12х — 12у 24а + 36в + 11а — 11в
при х = 1, у = 0 при а = 0, в = 1
По рисунку составьте и решите уравнение
А————В——————-С—————————D
2х 3х 5х
АD= 40 см
Найти АВ Найти ВС
Учащиеся распределяют задания. Выполняют их на листах.
Рефлексия учебной деятельности на уроке.
Цел и:
— организовать рефлексию
и самооценку учениками собственной учебной деятельности
Организует
рефлексию,
самооценку
учебной деятельности
— Подведем итог работы на уроке.
— Какую цель мы ставили? Достигли цели? Назовите тему урока.
— Расскажите, чему вы научились.
— Оцените свою деятельность
на уроке.
Домашнее задание: п. 14, с. 85-88, № 574(а, б,), №618 и № 576(а, б)
Отвечают на вопросы.
Рассказывают, что
узнали. Осуществляют само-
оценку
Формулируют собственную позицию и мнение
Самооценка деятельности на уроке
Осознают мотивацию учебной деятельности и накопление опыта в решении задач
Регулятивные: уметь проговаривать последовательность действий на уроке, оценивать правильность
выполнения действия на уровне адекватной ретроспективной оценки.
Личностные: уметь осуществлять
самооценку на основе критерия успешности учебной деятельности
Решенных примеров упрощения | Примеры вопросов BODMAS
Пожалуйста, ответьте на следующие упрощающие вопросы
Пример 1: Решить: 10 + 10 × 10 ÷ 10.
Sol: Применение правила BODMAS: 10 + 10 × 10 × (1/10) ⇒ 10 +10 = 20
Пример 2: 8 + 8 из 8 ÷ 8 — 34/5
Сол: 8 + 64 ÷ 8 — (34/5) (Примечание: «of» должно быть решено перед «÷»)
= 8 + 8 — (34/5) ⇒ 16 — (34/5) = 46/5
Пример 3: Упростите выражение: 18 — [6 — {4 — (8 — 6 + 3)}]
Sol: Это пример квадратных скобок.Скобки решаются после Bar. Порядок решения скобок: (), {} и [] соответственно. Итак, решение приведенных выше примеров выглядит следующим образом.
= 18 — [6 — {4 — (8 — 9)}] ⇒ 18 — [6 — {4 — (- 1)}]
= 18 — [6 — {4 + 1}] ⇒ 18 — [6 — 5] 18 — [1] = 18 — 1 = 17
Пример 4: Решить
20 + 20 × 20 ÷ 20/20 × 20 ÷ + 20 Sol: 20 + 20 × 20 ÷ 20/20 × 20 ÷ + 20 = 20 + 20 × 20 × (1/2) / 20 × 20 × (1/20) +20
= 20 + 20/20 + 20 = 40/40 = 1
Обязательно прочтите статьи о BODMAS
Пример 5: Упростить: 8 ÷ 8 из 8 + 8/8 ÷ 8 × 8 + 8
Sol: 8 ÷ 8 из 8 + 8/8 ÷ 8 × 8 + 8 ⇒ 8 ÷ 64 + 8/8 × (1/8) × 8 + 8
8 × (1/64) +8/8 +8 = (1/8) +8/16 ⇒ 65/8 × 1/16 = 65/128




Пример 8: 3√125-√? = 3
> Sol: 5-√x = 35 — 3 = √x
√x = 2 ⇒ x = 4.
Пример 9: Решить; 30% от 300 + x% от 50 = 60% от 400.
Sol: 30% от 300 + x% от 50 = 60% от 400.
90 + (x / 2) = 240
x / 2 = 240 — 90
x / 2 = 150 ⇒ x = 150 2 = 300
Пример 10: Решить; 6162 +? + 3330 = 2545.
Sol: 6162 + x + 3330 = 2545
x = 2545 — 6162 — 3330 = 2545 — 9492 = — 6947.
Упрощение выражений с отрицательными показателями
Purplemath
Напомним, что отрицательная степень указывает на то, что нам нужно переместить основание на другую сторону дробной линии. Например:
(«1» в приведенных выше упрощениях приведены для ясности, на тот случай, если вы давно не работали с отрицательными степенями.Обычно их не включают в свою работу.)
В контексте упрощения с помощью экспонент отрицательные показатели могут создавать дополнительные шаги в процессе упрощения. Например:
MathHelp.com
Упростите следующее выражение:
Отрицательные показатели говорят мне переместить базы, поэтому:
Потом отменяю как обычно и получаю:
При работе с показателями вы имеете дело с умножением.Поскольку порядок не имеет значения для умножения, вы часто обнаруживаете, что вы и ваш друг (или вы и учитель) решили одну и ту же задачу, используя совершенно разные шаги, но в итоге получили один и тот же ответ.
Этого следовало ожидать. Если вы делаете каждый шаг правильно, вы должны получать правильные ответы. Не волнуйтесь, если ваше решение не похоже на решение вашего друга; пока вы оба получили правильный ответ, вы, вероятно, оба сделали это «правильно».
Упростите следующее выражение: (–3 x –1 y 2 ) 2
Я могу действовать двумя способами. Я могу либо позаботиться о квадрате снаружи, либо упростить внутри; иначе я могу упростить изнутри, а затем провести квадрат.В любом случае я получу тот же ответ. Чтобы доказать это, я покажу оба пути.
сначала упрощая:
сначала возведение в квадрат:
В любом случае мой ответ тот же:
Упростите следующее выражение: (–5 x –2 y ) (- 2 x –3 y 2 )
Опять же, я могу работать двумя способами: сначала умножить, а затем обработать отрицательные показатели степени, либо обработать экспоненты, а затем умножить полученные дроби.Я покажу оба пути.
В любом случае мой ответ тот же:
Ни один из вышеперечисленных методов решения не является «лучше» или «хуже» другого. То, как вы решите проблему, будет зависеть от вкуса или случайности, поэтому просто делайте то, что лучше для вас.
Упростите следующее выражение:
Отрицательная экспонента есть только на x , а не на 2, поэтому я перемещаю только переменную:
Упростите следующее выражение:
«Минус» на цифре 2 говорит о перемещении переменной; «минус» на 6 означает, что 6 отрицательно.Эти два знака «минус» означают совершенно разные вещи, и не следует путать , а не .
Мне нужно переместить переменную; Я не должен перемещать 6.
Упростите следующее выражение:
Я перемещу одну переменную с отрицательной экспонентой, отменю y и упрощу:
URL: https: // www.purplemath.com/modules/simpexpo2.htm
,Упрощение выражений с показателями: сложные примеры
Purplemath
В этом разделе учебника и в следующем тесте вам предстоит выполнить как минимум несколько очень сложных упражнений по упрощению. Возможно, вы больше никогда не увидите ничего более сложного, но это не так уж и сложно, если вы будете осторожны.
Это , а не попыток сделать три шага одновременно в своей голове! Но если вы методичны и аккуратны, вы сможете получить все баллы.
MathHelp.com
Упростите следующее выражение:
Прежде чем я смогу что-нибудь отменить, мне нужно упростить верхние круглые скобки, потому что в них есть отрицательная экспонента.Я не могу отменить, скажем, a , потому что a 4 на самом деле не лучший. Я могу либо сдвинуть скобки вниз, либо квадрат, а затем упростить; иначе я могу сначала провести отрицательный квадрат, а затем сдвинуть его вверх или вниз. Я покажу оба пути:
перемещая скобки вперед:
сначала возведение в квадрат:
Есть и другие способы упростить вышеизложенное.Пока каждый шаг логически обоснован и вы получаете правильный ответ, ваша конкретная последовательность шагов будет правильной.
Упростите следующее выражение:
Это особый случай. Отрицательная экспонента означает, что все, что находится наверху, должно идти снизу, а все, что находится внизу, должно идти сверху.Поэтому я просто переверну дробь (не забывая менять степень с отрицательной на положительную) и упросту оттуда:
Примечание. Этот метод «переворота дроби» работает только в том случае, если отрицательный показатель степени равен целой дроби .
Упростите следующее выражение:
Есть , так что много способов сделать это.Я покажу четыре:
Метод A: перевернуть внутрь, упростить,
сделать отрицательный куб, перевернуть,
и упростить:
Метод B: перевернуть внутрь, упростить,
перевернуть дробь и куб:
Метод C: перевернуть дробь,
упростить внутри, куб, перевернуть
отрицательные показатели,
и упростить:
Метод D: перевернуть дробь,
перевернуть отрицательные показатели,
упростить и куб:
Вы должны ожидать, что увидите в своем тесте хотя бы одно упражнение, которое будет таким же сложным, как этот последний пример.Хотя вы можете редко, если вообще когда-либо, снова увидеть подобное упражнение, развитие навыков заботы и организации, необходимых для их надежного выполнения, сослужит вам хорошую службу на всю оставшуюся карьеру.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в упрощении с показателями степени. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/simpexpo3.htm
,Упрощение экспоненциальных выражений | Purplemath
Purplemath
Чтобы упростить работу с экспонентами, не думайте, что вам нужно работать только с правилами для экспонентов или прямо из них. Часто проще работать непосредственно с определением и значением показателя степени. Например:
Правила говорят мне добавить экспоненты.Но когда я начал заниматься алгеброй, у меня были проблемы с соблюдением правил, поэтому я просто подумал о том, что означают показатели. « a 6 » означает «шесть копий a , умноженных вместе», а « a 5 » означает «пять копий a , умноженных вместе». Итак, если я умножу эти два выражения вместе, я получу одиннадцать копий на , умноженных вместе. То есть:
MathHelp.com

a 6 × a 5 = ( a 6 ) ( a 5 )
= ( аааааа ) ( ааааа )
= аааааааааа
= а 11
Таким образом:
Упростите следующее выражение:
Правила экспоненты говорят мне вычесть экспоненты.Но допустим, я снова забыл правила. «6 8 » означает, что у меня восемь копий из шести сверху; «6 5 » означает, что у меня есть пять копий из 6 внизу.
Сколько у меня лишних шестерок и где они? У меня есть три лишних шестерки, и они на высоте. Тогда:
Если в инструкциях вам также не сказано «оценивать», вы, вероятно, должны оставить такие проблемы с числовым показателем, как эта, в форме показателя.Если вы не уверены, можете добавить «= 216» на всякий случай.
Упростите следующее выражение:
Сколько у меня дополнительных копий t и где они? У меня есть две лишние копии, сверху:
Как только вы освоитесь с вопросом «сколько у меня статистов и где они?» рассуждая, вы обнаружите, что вам не нужно все записывать и устранять повторяющиеся факторы.Ответы станут для вас очевидными.
Упростите следующее выражение:
Этот вопрос немного отличается, потому что больший показатель степени находится у члена в знаменателе. Но основная аргументация остается прежней.
Сколько у меня дополнительных копий из 5 и где они? У меня есть шесть дополнительных копий, и они внизу:
Примечание. Если вы примените правило вычитания, вы получите 5 3–9 = 5 –6 , что математически верно, но почти наверняка не является тем ответом, который они ищут.
Независимо от того, учили ли вы отрицательные показатели степени, когда они говорят «упрощать», они имеют в виду «упростить выражение, чтобы оно не имело отрицательных или нулевых степеней».Некоторые студенты будут пытаться обойти эту проблему со знаком минус, произвольно переключая знак, чтобы волшебным образом получить «5 6 » сверху (а не ниже «1»), но это неверно.
Давайте перейдем к более сложным выражениям.
Упростите следующее выражение:
Я не должен забывать, что «5» и «3» — это просто числа.Поскольку 3 не делится на 5, я не могу отменить числа.
И я не должен пытаться вычитать числа, потому что 5 и 3 в дроби « 5 / 3 » совсем не то же самое, что 5 и 3 в рациональном выражении « x 5 / x 3 «. Числовая часть 5 / 3 остается как есть.
Для переменных у меня есть две дополнительные копии x сверху, поэтому ответ:
Любой из ответов, выделенных фиолетовым цветом, должен быть приемлемым: единственная разница заключается в форматировании; они означают одно и то же.
Это достаточно просто: все с нулевой степенью равно 1.
(–46 x 2 y 3 z ) 0 = 1
Часть в скобках по-прежнему упрощается до 1, но на этот раз «минус» стоит перед скобками; то есть он не находится под властью, поэтому экспонента не касается.Итак, в данном случае ответ:
.— (46 x 2 y 3 z ) 0 = –1
Упростите следующее выражение:
Я могу исключить общий множитель 5 в числовой части дроби:
Теперь мне нужно посмотреть на каждую из переменных.Сколько у меня лишних штук и где они? У меня есть два лишних и сверху. У меня есть один лишний b внизу. И у меня одинаковые номера c сверху и снизу, поэтому они полностью отменяются. Это дает мне:
URL: https: // www.purplemath.com/modules/simpexpo.htm
,