Дробно-рациональные выражения 8 класс онлайн-подготовка на Ростелеком Лицей
Эквивалентные преобразования для упрощения выражений
Многие задачи в современном мире решаются с использованием большого количества компьютерных вычислений. Скорость вычислений напрямую зависит от эффективности алгоритма, который использует компьютер. Чем меньше операций нужно выполнить для решения конкретной задачи, тем эффективнее алгоритм. Чтобы вычислить значение следующего выражения, нужно сделать 29 операций:
А значение выражения можно найти, выполнив всего лишь одну. Но, оказывается, исходное выражение эквивалентно выражению (при условии, что ):
Это значит, что с помощью эквивалентных преобразований его можно упростить и привести к виду . В этом мы сейчас убедимся, изучив технику преобразования дробно-рациональных выражений.
Работа любого механизма – будь то часы, смартфон или крупная корпорация – всегда зависит от работоспособности составляющих его частей.
Точность механических часов обеспечивается слаженной работой всех шестерёнок, и если хотя бы одна из них будет с дефектом, то весь механизм окажется бракованным. При этом по отдельности любая из шестерёнок кажется бесполезной – по ней время не определишь.
Похожая ситуация может возникнуть и при изучении математики: многие уроки и даже целые темы могут по отдельности казаться ненужными и бесполезными. Но не стоит забывать, что всё это – составляющие единого механизма, который позволяет нам решать множество прикладных задач: от бытовых до экономических и технологических.
Математической моделью для решения многих задач являются уравнения или их системы. Для того чтобы решать уравнения (причём решать быстро и эффективно – о чём мы только что говорили), нужно уметь упрощать различные математические конструкции. Мы уже умеем работать с многочленами: приводить подобные слагаемые, раскладывать на множители, работать с формулами сокращённого умножения. Всё это мы научились применять для упрощения целых алгебраических выражений, т.
е. выражений, которые могут содержать операции сложения, вычитания и умножения чисел и переменных, а также операцию деления на число. Например:
Действия с дробями
Сегодня мы поговорим о том, как упрощать дробно-рациональные выражения. Они отличаются от целых выражений тем, что содержат операции деления на переменные. Например:
Как упрощать такие выражения? Для выполнения любой задачи нужна чёткая последовательность действий – алгоритм. Конечно, можно действовать наугад, как при поиске выхода из лабиринта. Но, чтобы выйти наверняка, лучше подыскать верный алгоритм – например, идти так, чтобы правая рука не отрывалась от стенки.
Для работы с выражениями, содержащими дроби, вы уже знаете все необходимые алгоритмы:
1. Сокращение дробей – дробь можно упростить, разложив на множители её числитель и знаменатель и сократив одинаковые множители:
2. Для сложения и вычитания дробей нужно привести их к общему знаменателю:
3.
Для умножения двух дробей нужно перемножить их числители и знаменатели:
Соответственно, при возведении дроби в степень необходимо возвести в степень и числитель, и знаменатель:
4. Деление дробей – чтобы разделить выражение на дробь, нужно умножить его на обратную дробь:
Эти алгоритмы можно применить и для дробей, содержащих переменные. При этом нам понадобятся уже полученные навыки действий с многочленами (в частности, разложения многочленов на множители).
ОДЗ
Вспомнив, как работать с обычными дробями и многочленами, вы без труда справитесь с упрощением дробно-рациональных выражений. Естественно, мы ещё потренируемся делать это на конкретных примерах. Но прежде обратим внимание на важный момент.
Работая с любым объектом, нужно знать границы его применимости. Для этого и существуют инструкции. В инструкциях к лекарственным препаратам, например, указывают, в каких ситуациях их следует применять, а в каких, наоборот, категорически запрещено.
Можно привести и более близкий к математике пример: нельзя сложить принципиально разные величины – 2 кг и 3 см. Точнее, сложить можно, только вот результат вряд ли будет нести для нас какой-то смысл.
Если говорить о числах, то сложить, вычесть или умножить можно любые два действительных числа – в результате снова получится действительное число. Поэтому при работе с целыми алгебраическими выражениями у нас не возникало никаких ограничений, переменные могли принимать любые значения. При этом даже если в выражении встречалось деление (например, ), то, по определению целого выражения, в знаменателе стояло конкретное число (не переменная) и мы точно знали, что оно не будет равняться 0.
Действительно, деление – операция с ограничением: деление на 0 не определено. В дробно-рациональных выражениях в знаменателе может встречаться переменная. Поэтому при каких-то значениях переменной знаменатель выражения может обратиться в 0, т.е. выражение при таком значении переменной будет не определено, его значение нельзя будет вычислить.
Например, в выражении переменная может принимать любые значения, кроме 2, поскольку при знаменатель обращается в 0 и значение выражения найти нельзя.
Все значения переменной, при которых выражение будет определено (можно вычислить его значение), называются областью допустимых значений (сокращённо – ОДЗ).
В нашем примере ОДЗ: .
Пока единственным источником недопустимых значений переменных (которые не войдут в ОДЗ) для нас будут только знаменатели дробей, которые входят в выражение – они не должны равняться 0. В дальнейшем мы встретим и другие ограничения на значения переменных, которые встречаются в различных алгебраических выражениях.
Чтобы после упрощения получилось выражение, эквивалентное исходному, необходимо, чтобы ОДЗ переменных в обоих выражениях была одинаковой. Рассмотрим подробнее на примере.
Пример 1. Упростить выражение:
Решение
Знаменатель не должен быть равен нулю, т.е. ОДЗ: .
Упростим выражение (вспомним ФСУ: ):
После упрощения мы получили, на первый взгляд, эквивалентное выражение.
Кажется, что переменная может принимать любые значения. Но давайте подставим в оба выражения . Поскольку они эквивалентны, мы должны получить один и тот же результат:
В чём же дело, почему результаты разные? А дело в том, что ОДЗ должна остаться неизменной. Т.е., получив выражение, нужно ещё указать, что . Поэтому не забывайте об ОДЗ при упрощении дробно-рациональных выражений и решении соответствующих уравнений.
Ответ: .
Сокращение дробно-рациональных выражений
Как мы уже упоминали, для упрощения выражения с дробями можно использовать 4 основные действия:
- сокращение дроби,
- сложение/вычитание дробей,
- умножение и возведение дробей в степень,
- деление дробей.
Давайте вспомним, как нужно поступать с обыкновенными дробями в каждом из этих случаев, и применим эти же алгоритмы для дробно-рациональных выражений.
Алгоритм действий при сокращении числовой дроби:
a.
разложить числитель и знаменатель на простые множители,
b. сократить одинаковые множители.
Пример:
Другой способ сокращения дроби
Возможно, вы задались вопросом: зачем раскладывать на простые множители? Можно ведь увидеть, что оба числа чётные, и сократить дробь на 2: .
Дальше заметим, что оба числа делятся на 6, это уже видно и из таблицы умножения. Сократив на 6, получим: .
Снова числа чётные, сократив на 2, получим всё тот же ответ: .
Да, такой способ решения возможен. Но это подбор: по некоторым признакам угадывать, на что можно сократить дробь. Во-первых, для такого подхода нет алгоритма (вспомните пример с выходом из лабиринта наугад и по определённой схеме), а во-вторых, нет гарантии, что таким образом мы сможем максимально сократить дробь. Чтобы прийти к конечной цели, нужен чёткий алгоритм. Разложение на простые множители и дальнейшее сокращение как раз являются шагами такого алгоритма.
При работе с дробно-рациональными выражениями необходимо разложить числитель и знаменатель на простые множители.
Но не в том смысле, что это будут простые числа, а в том, что полученные множители должны быть как можно проще, т.е. многочленами как можно меньшей степени.
Мы много тренировались раскладывать многочлены на множители и вот теперь сможем применить эти навыки для упрощения дробно-рациональных выражений. Если забыли, как выносить общий множитель, группировать слагаемые или применять ФСУ, то рекомендуем посмотреть урок (Разложение многочленов на множители).
Пример 2. Сократить дробь .
Решение
Разложим на множители числитель и знаменатель дроби.
В числителе можно увидеть разность квадратов и использовать ФСУ:
Мы уже разложили числитель на множители. Получились многочлены второй степени. Можно ли их упростить и получить произведение многочленов первой степени? Первый множитель разложить не удаётся, а вот во втором снова можно увидеть формулу сокращённого умножения (ФСУ). Тогда .
Перейдём к знаменателю. В нём можно увидеть другую ФСУ – полный квадрат суммы :
Получаем:
Видим одинаковые множители в числителе и знаменателе, на них можно сократить:
Задание почти выполнено.
Нам осталось проверить, что ОДЗ исходного и полученного выражений совпадает. Действительно, в знаменателе исходного выражения:
И в знаменателе полученного выражения: . То есть полученное выражение действительно эквивалентно исходному.
Ответ: .
Чаще всего в задачах на упрощение дробно-рациональных выражений делается оговорка: «упростить выражение при всех допустимых значениях переменных». Это означает, что можно заниматься только эквивалентными преобразованиями, не обращая внимания на ОДЗ, подразумевается, что переменные ограничены общим ОДЗ как для исходного, так и для упрощённого выражения. В дальнейшем, если не оговорено иное, в этом уроке мы будем упрощать выражения при всех допустимых значениях переменных.
При поиске одинаковых множителей нужно быть внимательным, ведь слагаемые в них могут быть переставлены местами. Попробуйте найти одинаковые множители в числителе и знаменателе дроби: .
Нашли? Действительно, , так что эти два множителя одинаковые и их можно сократить:
Кроме того, множители могутотличаться знаком.
Так говорят о выражениях, в одном из которых можно заменить знаки на противоположные и получить второе выражение. Например, и . Переставив слагаемые во втором множителе местами, получим:. Если заменить все знаки на противоположные, то мы получим :
Итак, если вы нашли множители, которые отличаются знаком, нужно в одном из них вынести знак минус за скобки, а затем уже сократить. Например:
Сложение и вычитание дробно-рациональных выражений
Для сложения и вычитания дробей необходимо привести их к общему знаменателю. Для этого мы будем пользоваться уже известным нам алгоритмом:
- разложить на простые множители знаменатели дробей,
- найти общие множители в знаменателях дроби,
- умножить числитель и знаменатель каждой дроби на недостающие множители, чтобы знаменатели стали одинаковыми,
- сложить (вычесть) числители дробей, знаменатель оставить прежним.
Пример 3.
Выполнить вычитание:
Решение
Общие множители В первой дроби не хватает множителя , во второй – множителей :
Ответ: .
При работе с дробно-рациональными выражениями алгоритм абсолютно такой же. При этом не стоит забывать, что общие множители знаменателей могут отличаться знаком и порядком слагаемых.
Пример 4. Выполнить вычитание:
Решение
Раскладываем знаменатели на множители:
Во второй дроби разложим знаменатель методом группировки:
Получаем:
Отметим общие множители и – они отличаются лишь порядком слагаемых.
Тогда умножаем числители и знаменатели дробей на недостающие множители и :
Знаменатели одинаковы, вычитаем числители:
Ответ: .
Мы выполнили вычитание. Полученное выражение можно ещё упростить, проверив, сократится ли дробь. Подробнее об упрощении этой дроби ниже.
Упрощение дроби
Пример 1.
Упростить выражение:
Решение
Знаменатель уже разложен на множители, осталось разложить на множители числитель.
Сейчас в числителе слагаемых, они не содержат общих множителей. Поэтому сначала раскрываем скобки:
Раскладываем на множители: .
В итоге получили дробь:
Видим, что общих множителей нет, значит, дробь нельзя сократить.
Ответ: .
Обратите внимание: если нас просят упростить выражение, то дают подсказку – это точно можно сделать. Поэтому в числителях и/или знаменателях дробей подобраны такие многочлены, которые обязательно должны раскладываться на множители (за очень редким исключением). А значит, нужно только перебрать известные нам методы: вынесение за скобки, группировка и ФСУ – какой-то обязательно должен подойти. Вопрос только во времени. Чем больше заданий вы решите, тем меньше времени у вас будет уходить на то, чтобы понять, какие именно многочлены надо раскладывать на множители и каким именно способом.
Умножение и возведение дробно-рациональных выражений в степень
Умножение и возведение алгебраических дробей в степень происходит так же, как и в случае числовых дробей. Тут нет никаких «подводных камней»: при умножении отдельно умножаем числители, отдельно – знаменатели. При возведении в степень также отдельно возводится в степень числитель и знаменатель дроби.
Пример 5. Выполнить умножение:
Решение
Можно было бы так и оставить, но явно видны ФСУ, которые можно применить:
Тогда .
Ответ: .
Деление дробно-рациональных выражений
Для деления выражения на дробь нужно умножить это выражение на обратную дробь. Здесь также всё происходит аналогично действиям с числовыми дробями.
Пример 6. Выполнить деление, указать ОДЗ выражения: .
Решение
Найдём ОДЗ. Во-первых, каждая из двух дробей должна быть определена, т.
е. их знаменатели не должны быть равны 0:
Кроме того, вторая дробь не должна равняться нулю, чтобы не было деления на ноль. Это значит, что и числитель этой дроби не должен быть равен нулю (дробь равна 0 тогда и только тогда, когда её числитель равен 0): .
Получили три условия: .
Из первого условия следует, что . Во втором и третьем разложим правые части на множители:
Чтобы произведение множителей не было равно нулю нужно, чтобы каждый из множителей не был равен нулю:
Условия и эквиваленты, поэтому получаем следующую ОДЗ исходного выражения: .
Выполним деление, как умножение на перевёрнутую дробь:
Ответ: .
Мы выполнили деление. Полученную дробь можно упростить, сократив её. Попробуйте сделать это самостоятельно, а с решением можно ознакомиться ниже.
Упрощение дроби
Пример 1. Упростить:
Решение
Числитель и знаменатель дроби уже разложены на множители, но пока что не видно общих.
Поэтому продолжим разложение на множители:
Получим дробь: .
Множители и отличаются лишь знаком. Аналогично и . Вынесем за скобки:
Сократим одинаковые множители. Также учтём, что . Получим:
Обратите внимание: ОДЗ полученного выражения: . Чтобы выражения были эквивалентными, нужно потребовать дополнительно следующее:
Ответ: .
Заключение
На следующем уроке мы потренируемся упрощать дробно-рациональные выражения и выполнять с ними различные действия.
Список рекомендованной литературы:
- Никольский С.М., Решетников Н.Н., Потапов М.К., Шевкин А.В. Алгебра. 8 класс. Учебник. ФГОС. М., «Просвещение», 2018.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. Алгебра. 8 класс. Учебник. М., «Просвещение», 2018.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б./Под ред. Теляковского С.А. Алгебра. 8 класс. Учебник.
М., «Просвещение», 2018.
М., «Просвещение», 2018.
Рекомендованные ссылки на ресурсы сети Интернет:
- Интернет-портал «yaklass.ru» (Источник)
- Интернет-портал «school-assistant.ru»(Источник)
- Интернет-портал «cleverstudents.ru» (Источник)
Домашнее задание:
1. Доказать, что дробь не имеет смысла ни при каких значениях переменной :
2. Упростить выражение:
3. Упростить выражение и найти его значение при :
Репетиторство 8 класс
Определение и примеры алгебраических дробей
Рациональные выражения делятся на целые и дробные выражения.
Определение. Рациональная дробь – дробное выражение вида , где – многочлены. – числитель, – знаменатель.
Примеры рациональных выражений: – дробные выражения; – целые выражения. В первом выражении, к примеру, в роли числителя выступает , а знаменателя – .
Значение алгебраической дроби, как и любого алгебраического выражения, зависит от численного значения тех переменных, которые в него входят. В частности, в первом примере значение дроби зависит от значений переменных и , а во втором только от значения переменной .
Вычисление значения алгебраической дроби и две основные задачи на дроби
Рассмотрим первую типовую задачу: вычисление значения рациональной дроби при различных значениях входящих в нее переменных.
Пример 1. Вычислить значение дроби при а) , б) , в)
Решение. Подставим значения переменных в указанную дробь: а) , б) , в) – не существует (т. к. на ноль делить нельзя).
Ответ: а) 3; б) 1; в) не существует.
Как видим, возникает две типовые задачи для любой дроби: 1) вычисление дроби, 2) нахождение допустимых и недопустимых значений буквенных переменных.
Определение. Допустимые значения переменных – значения переменных, при которых выражение имеет смысл.
Множество всех допустимых значений переменных называется ОДЗ или область определения.
Допустимые (ОДЗ) и недопустимые значения переменных в дробях с одной переменной
Значение буквенных переменных может оказаться недопустимым, если знаменатель дроби при этих значениях равен нулю. Во всех остальных случаях значение переменных являются допустимыми, т. к. дробь можно вычислить.
Пример 2. Установить, при каких значениях переменной не имеет смысла дробь .
Решение. Чтобы данное выражение имело смысл, необходимо и достаточно, чтобы знаменатель дроби не равнялся нулю. Таким образом, недопустимыми будут только те значения переменной, при которых знаменатель будет равняться нулю. Знаменатель дроби , поэтому решим линейное уравнение:
.
Следовательно, при значении переменной дробь не имеет смысла.
Ответ: -5.
Из решения примера вытекает правило нахождения недопустимых значений переменных – знаменатель дроби приравнивается к нулю и находятся корни соответствующего уравнения.
Рассмотрим несколько аналогичных примеров.
Пример 3. Установить, при каких значениях переменной не имеет смысла дробь.
Решение. .
Ответ. .
Пример 4. Установить, при каких значениях переменной не имеет смысла дробь .
Решение..
Встречаются и другие формулировки данной задачи – найти область определения или область допустимых значений выражения (ОДЗ). Это означает – найти все допустимые значения переменных. В нашем примере – это все значения, кроме . Область определения удобно изображать на числовой оси.
Для этого на ней выколем точку , как это указано на рисунке:
Рис. 1
Таким образом, областью определения дроби будут все числа, кроме 3.
Ответ..
Пример 5. Установить, при каких значениях переменной не имеет смысла дробь .
Решение..
Изобразим полученное решение на числовой оси:
Рис. 2
Ответ.
.
Графическое представление области допустимых (ОДЗ) и недопустимых значений переменных в дробях
Пример 6. Установить, при каких значениях переменных не имеет смысла дробь .
Решение.. Мы получили равенство двух переменных, приведем числовые примеры: или и т. д.
Изобразим это решение на графике в декартовой системе координат:
Рис. 3. График функции
Координаты любой точки, лежащей на данном графике, не входят в область допустимых значений дроби.
Ответ. .
Случай типа «деление на ноль»
В рассмотренных примерах мы сталкивались с ситуацией, когда возникало деление на ноль. Теперь рассмотрим случай, когда возникает более интересная ситуация с делением типа .
Пример 7. Установить, при каких значениях переменных не имеет смысла дробь .
Решение..
Получается, что дробь не имеет смысла при . Но можно возразить, что это не так, потому что: .
Может показаться, что если конечное выражение равно 8 при , то и исходное тоже возможно вычислить, а, следовательно, имеет смысл при . Однако, если подставить в исходное выражение, то получим – не имеет смысла.
Ответ..
Чтобы подробнее разобраться с этим примером, решим следующую задачу: при каких значениях указанная дробь равна нулю?
(дробь равна нулю, когда ее числитель равен нулю) . Но необходимо решить исходное уравнение с дробью, а она не имеет смысла при , т. к. при этом значении переменной знаменатель равен нулю. Значит, данное уравнение имеет только один корень .
Правило нахождения ОДЗ
Таким образом, можем сформулировать точное правило нахождения области допустимых значений дроби: для нахождения ОДЗ дроби необходимо и достаточно приравнять ее знаменатель к нулю и найти корни полученного уравнения.
Мы рассмотрели две основные задачи: вычисление значения дроби при указанных значениях переменных и нахождение области допустимых значений дроби.
Рассмотрим теперь еще несколько задач, которые могут возникнуть при работе с дробями.
Разные задачи и выводы
Пример 8. Докажите, что при любых значениях переменной дробь .
Доказательство. Числитель – число положительное. . В итоге, и числитель, и знаменатель – положительные числа, следовательно, и дробь является положительным числом.
Доказано.
Пример 9. Известно, что , найти .
Решение. Поделим дробь почленно . Сокращать на мы имеем право, с учетом того, что является недопустимым значением переменной для данной дроби.
Ответ..
Основное свойство обыкновенной дроби
Вспомним основное свойство обыкновенной дроби: значение дроби не изменится, если ее числитель и знаменатель одновременно умножить или разделить на одно и то же отличное от нуля число. Напомним, что деление числителя и знаменателя дроби на одно и то же отличное от нуля число называется сокращением.
Например: , при этом значение дробей не изменяется. Однако зачастую при применении данного свойства многие допускают стандартные ошибки:
1) — в приведенном примере допущена ошибка деления только одного слагаемого из числителя на 2, а не всего числителя. Правильная последовательность действий выглядит таким образом: или .
2) — здесь мы видим похожую ошибку, однако, кроме этого еще в результате деления получен 0, а не 1, что является еще более частой и грубой ошибкой.
Теперь необходимо перейти к рассмотрению алгебраической дроби. Вспомним это понятие из предыдущего урока.
Определение. Рациональная (алгебраическая) дробь – дробное выражение вида , где – многочлены. – числитель, – знаменатель.
Алгебраические дроби являются, в некотором смысле, обобщением обыкновенных дробей и над ними можно проводить те же операции, что и над обыкновенными дробями.
Основное свойство алгебраической дроби
Основное свойство алгебраической дроби – и числитель, и знаменатель дроби можно умножать и делить на один и тот же многочлен (одночлен) или число, отличное от нуля.
Это будет тождественное преобразование алгебраической дроби. Вспомним, что как и ранее, деление числителя и знаменателя дроби на одно и то же отличное от нуля выражение называется сокращением.
Основное свойство алгебраической дроби позволяет сокращать дроби и приводить их к наименьшему общему знаменателю.
Примеры сокращения обыкновенных дробей
Для сокращения обыкновенных дробей мы прибегали к основной теореме арифметики, разлагали и числитель, и знаменатель на простые множители.
Определение.Простое число – натуральное число, которое делится только на единицу и само себя. Все остальные натуральные числа называются составными. 1 не является ни простым, ни составным числом.
Пример 1. а) , где множители, на которые разложены числители и знаменатели указанных дробей, являются простыми числами.
Ответ.; .
Примеры сокращения алгебраических дробей
Следовательно, для сокращения дробей необходимо предварительно разложить на множители числитель и знаменатель дроби, а затем разделить их на общие множители.
Т.е. следует владеть методами разложения многочленов на множители.
Пример 2. Сократить дробь а), б) , в) .
Решение. а) . Необходимо заметить, что в числителе находится полный квадрат, а в знаменателе разность квадратов. После сокращения необходимо указать, что , во избежание деления на ноль.
б) . В знаменателе выносится общий числовой множитель, что полезно делать практически в любом случае, когда это возможно. Аналогично с предыдущим примером указываем, что .
в) . В знаменателе выносим за скобки минус (или, формально, ). Не забываем, что при сокращении .
Ответ. ; ; .
Теперь приведём пример на приведение к общему знаменателю, делается это аналогично с обыкновенными дробями.
Приведение обыкновенных дробей к общему знаменателю
Пример 3. Привести к общему знаменателю дроби и .
Решение. Для нахождения наименьшего общего знаменателя необходимо найти наименьшее общее кратное (НОК) двух знаменателей, т.
е. НОК(3;5). Иными словами, найти наименьшее число, которое делится на 3 и на 5 одновременно. Очевидно, что это число 15, записать это можно таким образом: НОК(3;5)=15 – это и будет общий знаменатель указанных дробей.
Чтобы преобразовать знаменатель 3 в 15, его необходимо умножить на 5, а для преобразования 5 в 15, его необходимо умножить на 3. По основному свойству алгебраической дроби следует умножить на те же числа и соответствующие числители указанных дробей.
и .
Ответ.; .
Пример 4. Привести к общему знаменателю дроби и .
Решение. Проведем аналогичные предыдущему примеру действия. Наименьшее общее кратное знаменателей НОК(12;18)=36. Приведем к этому знаменателю обе дроби:
и .
Ответ.; .
Сокращение сложных обыкновенных дробей
Теперь рассмотрим примеры, демонстрирующие применение техники сокращения дробей для их упрощения в более сложных случаях.
Пример 5.
Вычислить значение дроби: а) , б) , в) .
а) . При сокращении пользуемся правилом деления степеней .
б) .
в) .
Сокращение сложных алгебраических дробей
После того, как мы повторили использование основного свойства обыкновенной дроби, можно перейти к рассмотрению алгебраических дробей.
Пример 6. Упростить дробь и вычислить при заданных значениях переменных: а) ; , б) ;
Решение. При подходе к решению возможен следующий вариант – сразу же подставить значения переменных и начать расчет дроби, но в таком случае решение сильно усложняется и необходимое на его решение время увеличивается, не говоря уже об опасности ошибиться в сложных вычислениях. Поэтому удобно сначала упростить выражение в буквенном виде, а затем уже подставить значения переменных.
а) . При сокращении на множитель необходимо проверить, не обращается ли он в ноль в указанных значениях переменных.
При подстановке получаем , что дает возможность сокращения на данный множитель.
б) . В знаменателе выносим минус, как мы это уже делали в примере 2. При сокращении на снова проверяем не делим ли мы на ноль: .
Ответ.; .
Приведение алгебраических дробей к общему знаменателю
Пример 7. Привести к общему знаменателю дроби а) и , б) и , в) и .
Решение. а) В данном случае подойдем к решению следующим образом: не будем пользоваться понятием НОК, как во втором примере, а просто умножим знаменатель первой дроби на знаменатель второй и наоборот – это позволит привести дроби к одинаковому знаменателю. Конечно же, не забываем при этом умножать и числители дробей на такие же выражения.
. В числителе раскрыли скобки, а в знаменателе воспользовались формулой разности квадратов.
. Аналогичные действия.
Видно, что такой способ позволяет умножить знаменатель и числитель одной дроби на тот элемент из знаменателя второй дроби, которого не хватает.
С другой дробью проводятся аналогичные действия, и знаменатели приводятся к общему.
б) Проделаем аналогичные с предыдущим пунктом действия:
. Умножим числитель и знаменатель на тот элемент знаменателя второй дроби, которого не хватало (в данном случае на весь знаменатель).
. Аналогично.
в) . В данном случае мы умножили на 3 (множитель который присутствует в знаменателе второй дроби и отсутствует в первой).
.
Ответ. а) ; , б) ; , в) ; .
На данном уроке мы изучили основное свойство алгебраической дроби и рассмотрели основные задачи с его использованием. На следующем уроке мы более подробно разберем приведение дробей к общему знаменателю с использованием формул сокращенного умножения и метода группировки при разложении на множители.
Упрощение алгебраических дробей — GCSE Maths
Введение
Что такое упрощение алгебраических дробей?
Упрощение алгебраических произведений и частных
Как упростить алгебраические дроби
Рабочий лист «Упрощение алгебраических дробей»
Распространенные заблуждения
Практика упрощения вопросов с алгебраическими дробями
Упрощение алгебраических дробей GCSE вопросы
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Что такое упрощение алгебраических дробей?
Упрощение алгебраических произведений и частных
Как упростить алгебраические дроби
Рабочий лист «Упрощение алгебраических дробей»
Распространенные заблуждения
Практика упрощения вопросов с алгебраическими дробями
Упрощение алгебраических дробей Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем об упрощении алгебраических дробей, в том числе о различных степенях x, квадратичных вычислениях и разности двух квадратов.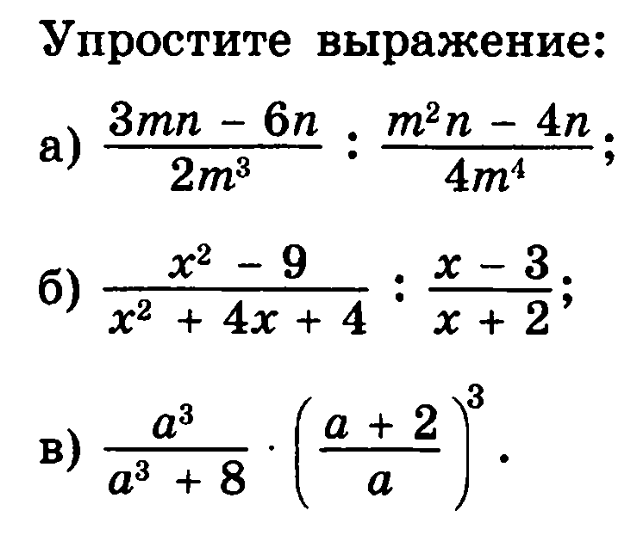
Существуют также упрощенные рабочие листы с алгебраическими дробями, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое упрощение алгебраических дробей?
Упрощение алгебраических дробей — это упрощение дроби, содержащей алгебру, таким образом, что числитель и знаменатель не содержат общих множителей.
Для этого нам нужно найти общие множители между числителем и знаменателем, которые можно сократить.
Чтобы упростить алгебраические дроби, вы должны уметь считать с дробями.
Если мы хотим выразить \frac{a}{b}+\frac{c}{d} или \frac{a}{b} — \frac{c}{d} в виде одной дроби, нам нужно найти общий знаменатель, а затем сложите или вычтите полученные дроби.
Общая форма при добавлении дробей:
\frac{a}{b}+\frac{c}{d}=\frac{a\times{d}}{b\times{d}}+\frac {b\times{c}}{b\times{d}}=\frac{ad+bc}{bd}
Общая форма для вычитания дробей:
\frac{a}{b}-\frac{c}{d}=\frac{a\times{d}}{b\times{d}}-\frac{b\times{c}}{b \times{d}}=\frac{ad-bc}{bd}
Вычислить \frac{2}{5}+\frac{1}{4}
Таким образом, если a = 2, b = 5, c = 1 и d = 4 , мы можем сказать, что
\frac{2}{5}+\frac{1}{4}=\frac{8}{20}+\frac{5}{20}=\frac{8+5}{20}=\frac{ 13}{20}
Ниже приведено визуальное представление этой задачи.
Преобразуя дроби так, чтобы они имели общий знаменатель (в данном случае 20 ), мы делим дроби на более мелкие части, затем суммируем эти части, используя знание эквивалентных дроби.
Мы можем использовать это для упрощения алгебраических выражений :
Например.
Давайте посмотрим на \frac{5x}{15}
Здесь члены 5x и 15 имеют общий делитель 5 .
Если бы мы записали это как два произведения, мы бы получили \frac{5\times{x}}{5\times{3}} .
Мы можем упростить это с помощью , отменив общий множитель числа 5 из числителя и знаменателя
Итак, найдя наибольший общий делитель числителя и знаменателя, мы можем показать, что дробь \frac{5x}{15} может быть выражена как более простая алгебраическая дробь \frac{x}{3} .
Мы можем использовать знания об упрощении алгебраических дробей для решения уравнений, включающих алгебраические дроби.
Подробнее об этом читайте в уроке об алгебраических дробях.
Пошаговое руководство: Алгебраические дроби
Что такое упрощение алгебраических дробей? 94
Как упростить алгебраические дроби
Чтобы упростить алгебраические дроби:
- Выполните необходимые вычисления в вопросе (+ — \times\div) .
- Разложите на множители числитель и знаменатель .
- Отменить общий множитель и при необходимости упростить еще больше .
Объясните, как упростить алгебраические дроби
Рабочий лист «Упрощение алгебраических дробей»
Получите бесплатный рабочий лист по упрощающим алгебраическим дробям, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
ИксРабочий лист по упрощению алгебраических дробей
Получите бесплатный рабочий лист по упрощению алгебраических дробей, содержащий более 20 вопросов и ответов.
СКАЧАТЬ БЕСПЛАТНО
Примеры упрощения алгебраических дробей
Пример 1: Умножение алгебраических дробей
Упростите алгебраическое выражение
\ гидроразрыва {5} {х + 2} \ раз \ гидроразрыва {х + 2} {10}
- Выполните все вычисления, необходимые в вопросе (+−\times\div) .
\frac{5}{x+2}\times\frac{x+2}{10}=\frac{5x+10}{10x+20}
2 Разложить на множители числитель и знаменатель .
\frac{5x+10}{10x+20}=\frac{5(x+2)}{10(x+2)}
3 Отменить общий множитель и при необходимости упростить еще больше .
\frac{5(x+2)}{10(x+2)}=\frac{5}{10}=\frac{1}{2}
Пример 2. Сложение алгебраических дробей
Упростить алгебраическое выражение\ гидроразрыва {10} {6 + 2x} + \ гидроразрыва {3} {x + 3}
Выполните все необходимые расчеты в вопросе (+-\times\div) .
\begin{выровнено} &\frac{10}{6+2x}+\frac{3}{x+3}=\frac{10(x+3)}{(6+2x)(x+3)}+\frac{3 (6+2x)}{(x+3)(6+2x)}\\\\ &=\frac{10(x+3)+3(6+2x)}{(6+2x)(x+3)} \\\\ &=\frac{10x+30+18+6x}{(6+2x)(x+3)} \\\\ &=\frac{16x+48}{(6+2x)(x+3)} \end{выровнено}
Полезный совет: не раскрывайте сразу двойные скобки в знаменателе. Одна из скобок может быть общим множителем с числителем и в конечном итоге аннулируется.
Разложить на множители числитель и знаменатель .
\frac{16x+48}{(6+2x)(x+3)}=\frac{16(x+3)}{2(3+x)(x+3)}
Отменить общий множитель и при необходимости упростить
\frac{16(x+3)}{2(3+x)(x+3)}=\frac{16}{2(3+x)}=\frac{8}{3+x}
Пример 3: Линейный ÷ линейный
Упростите алгебраическую дробь
\фракция{6x+12}{10x+20}
Выполните все необходимые расчеты в вопросе (+-\times\div) .
Здесь нет необходимости выполнять вычисления, так как у нас есть одна дробь.
Разложить на множители числитель и знаменатель .
\frac{6x+12}{10x+20}=\frac{6(x+2)}{10(x+2)}
Отмените общий множитель и при необходимости упростите дальше .
\frac{6(x+2)}{10(x+2)}=\frac{6}{10}=\frac{3}{5} 9{2}-64}=\frac{(x+7)(x+8)}{(x+8)(x-8)}
Отменить общий множитель и при необходимости упростить еще раз .
\frac{(x+7)(x+8)}{(x+8)(x-8)}=\frac{x+7}{x-8}
Распространенные заблуждения
- Игнорирование знаменателей
При задании уравнения, включающего алгебраическую дробь, знаменатели игнорируются, поэтому на вопрос дается неверный ответ.
- Добавление знаменателей
При сложении двух дробей знаменатель должен совпадать. Распространенным заблуждением для сложения двух дробей является сложение числителей и знаменателей вместе, потому что этот метод подчеркивается при рассмотрении умножения дробей.
- Неправильное аннулирование членов
Увидев один и тот же член в числителе и знаменателе, может возникнуть неправильное представление о том, что они оба могут быть аннулированы.
- Неправильное раскрытие двойных скобок
При раскрытии двойных скобок каждое слагаемое в скобке необходимо умножить на каждое слагаемое в другой скобке. Из-за того, что числитель не рассматривается как отдельное выражение, при умножении скобок делаются ошибки.
- Сбор непохожих терминов
Простые алгебраические выражения, такие как 5x + 4, могут быть неправильно упрощены для получения 9x, поскольку x игнорируется; предполагается, что 5x + 4 совпадает с (5 + 4)x, что неверно.
- Неправильное разложение в одну скобку
При разложении в одну скобку неправильный метод возникает, когда скобка просто ставится между числом и x первого члена, а затем вокруг последнего члена в выражении .
{2}-4}{х+2} 9{2}-16}{3x-4} можно упростить до 3x+4 .
(5 баллов)
Показать ответ
(a)
Джастин имеет правильный ответ, но он не показал правильное понимание
(1)
. факторизовал числитель, чтобы получить (x+2)(x-2)
(1)
Затем он может сократить общий множитель (x+2) , оставив решение x-2
92-16=(3х+4)(3х-4)(1)
\ гидроразрыв {(3x+4)(3x-4)}{(3x-4)}=3x+4
(1)
3. Полностью упростить
\ гидроразрыва {2x + 1} {2x + 10} \ div {\ гидроразрыва {3 + 6x} {x + 5}}
(4 балла)
Показать ответ
\frac{2x+1}{2x+10}\div{\frac{3+6x}{x+5}}=\frac{2x+ 1}{2x+10}\times{\frac{x+5}{3+6x}}
(1)
= \ frac {2x + 1} {2 (x + 5)} \ times {\ frac {x + 5} {3 (1 + 2x)}}
(1)
=\ гидроразрыва {(2x+1)(x+5)}{6(x+5)(2x+1)}
(1)
=\фракция{1}{6}
(1)
Контрольный список для изучения
Теперь вы научились:
- Упрощать алгебраические выражения и управлять ими (включая те, которые содержат сурды {и алгебраические дроби}) с помощью:
Все еще застряли?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning.
Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Узнайте больше о нашей программе повторения GCSE по математике.
Упрощение выражения с помощью дробной черты
Результаты обучения
- Определите отрицательные дроби, которые эквивалентны, если их отрицательный знак находится в другом месте
- Упростите выражения, содержащие дроби, используя порядок операций
Куда ставится знак минус в дроби? Обычно перед дробью ставится знак «минус», но иногда встречаются дроби с отрицательным числителем или знаменателем. Помните, что дроби обозначают деление. Дробь [latex]\Large-\frac{1}{3}[/latex] может быть результатом деления [latex]\Large\frac{-1}{3}[/latex], отрицательного числа на положительное , или деления [латекс]\большой\фрак{1}{-3}[/латекс], положительного числа на отрицательное. Когда числитель и знаменатель имеют разные знаки, частное отрицательно.
Если и числитель и знаменатель отрицательны, то сама дробь положительна, потому что мы делим отрицательное число на отрицательное.
[латекс]\Large\frac{-1}{-3}\normalsize=\Large\frac{1}{3}\quad\quad\normalsize\Large\frac{\text{negative}}{\text {negative}}=\text{positive}[/latex]
Размещение отрицательного знака в дроби
Для любых положительных чисел [latex]a\text{ и }b[/latex],
[latex]\ Large\frac{-a}{b}\normalsize=\Large\frac{a}{-b}\normalsize=\Large-\frac{a}{b}[/latex]
Пример
Какие из следующих дробей эквивалентны [латекс]\большой\фрак{7}{-8}[/латекс]?
[латекс]\Large\frac{-7}{-8},\frac{-7}{8},\frac{7}{8},-\frac{7}{8}[/latex]
Решение:
Частное положительного и отрицательного отрицательно, поэтому [латекс]\большой\фрак{7}{-8}[/латекс] отрицательно. Из перечисленных дробей [латекс]\большой\фрак{-7}{8},-\фрак{7}{8}[/латекс] также отрицательны.
попробуй
Полосы дробей действуют как символы группировки. Выражения над и под разделительной чертой следует рассматривать так, как если бы они были заключены в круглые скобки. Например, [латекс]\большой\фрак{4+8}{5 — 3}[/латекс] означает [латекс]\влево(4+8\вправо)\дел\влево(5 — 3\вправо)[/ латекс].