Упростите логическое выражение: Упрощение логических выражений — Логика

Методическое пособие Электронный вариант Преподавателю и

Упростите логическое выражение или укажите его результат (при его одно… — Учеба и наука

Калькулятор булевой алгебры — онлайн-упрощение булевых логических выражений

Калькулятор логической алгебры — онлайн-упроститель логических выражений

Елена Васильевна

Альфия

Вениамин Шемякин

Упрощение логических выражений

Ответы на вопросы (FAQ)

Исходный код

Cite dCode

Что такое логическое выражение? (Определение)

Как упростить/минимизировать логическое выражение?

Что такое методы упрощения булевой алгебры?

Как показать/продемонстрировать, что 2 логических выражения равны?

Что такое закон де Моргана?

Что такое дизъюнктивная или конъюнктивная нормальная форма?

Как показать пошаговые расчеты?

Содержание

Главная

Другое
Экономика
Финансы
Маркетинг
Астрономия
География
Туризм
Биология
История
Информатика
Культура
Математика
Физика
Философия
Химия
Банк
Право
Военное дело
Бухгалтерия
Журналистика
Спорт
Психология
Литература
Музыка
Медицина

страница 1страница 2страница 3страница 4

Пример 1

Упростите логическое выражение F= ¬((A v B)→ ¬(B v C)).

Это логическое выражение необходимо привести к нормальной форме, т.к. в нем присутствует импликация и отрицание логической операции.

Избавимся от импликации и отрицания. Воспользуемся (9). Получится:

(AvB)→(BvC)= (AvB)&(BvC).

Применим закон двойного отрицания (4).Получим:

(A v В) & (В v С) = (A v В) & (B v С).

Применим правило дистрибутивности (16). Получим:

(A v В) & (B v С)= (AvB)&Bv(AvB)&C

Применим закон коммутативности (18) и дистрибутивности (16). Получим:

( AvB)&Bv(AvB)&C = A&BvB&BvA&CvB&C.

Применим (7) и получим:

A&BvB&BvA&CvB&C= A&BvBvA&CvB&C

Применим (16), т.е. вынесем за скобки В.
Получим:

A&BvBvA&CvB&C= B& (Av1)vA&CvB&C.

Применим (6). Получим:

B& (Av1) vA&CvB&C= BvA&CvB&C.

Переставим местами слагаемые , сгруппируем и вынсем В за скобки. Получим:

BvA&CvB&C = B& (1vC)vA&C.

Применим (6) и получим ответ:

B&(1vC)vA&C=BvA&C.

Ответ: F= ¬((AvB)→ ¬(BvC))= BvA&C.

121

(AvB)&Bv(AvB)&C

15 15

A8lBvB&BvA&CvB&€

A&BvBvA&CvB&C

выносим за скобки В

B&{Avl)vA&CvB&C

BvA&CvB&C.

группируем и выносим В за скобки

B&(lvC)vA&C 6
I V. Закрепление изученного

№1

Упростите выражение:

F = ¬ (A&B) v ¬ (BvC).
F = (A→B) v (B→A).
F = A&CvĀ&C.
F =AvBvCvAvBvC
Ответы :

F = ¬ (A&B) v ¬ (BvC) =AvB.
F= (A→B) v (B→A) = 1.
F = A&CvĀ&C=C.
F =AvBvCvAvBvC=1.

№2

Упростите выражение:

1) F = ¬(X&Yv ¬(X&Y)).

F = X&¬ (YvX).
F = (XvZ) & (XvZ) & (YvZ).
Ответы:

F = ¬(X&Yv ¬(X&Y)) = 0.

F = X&¬ (YvX) = X&Y.

F = (XvZ) & (XvZ) & (YvZ) =X& (YvZ).

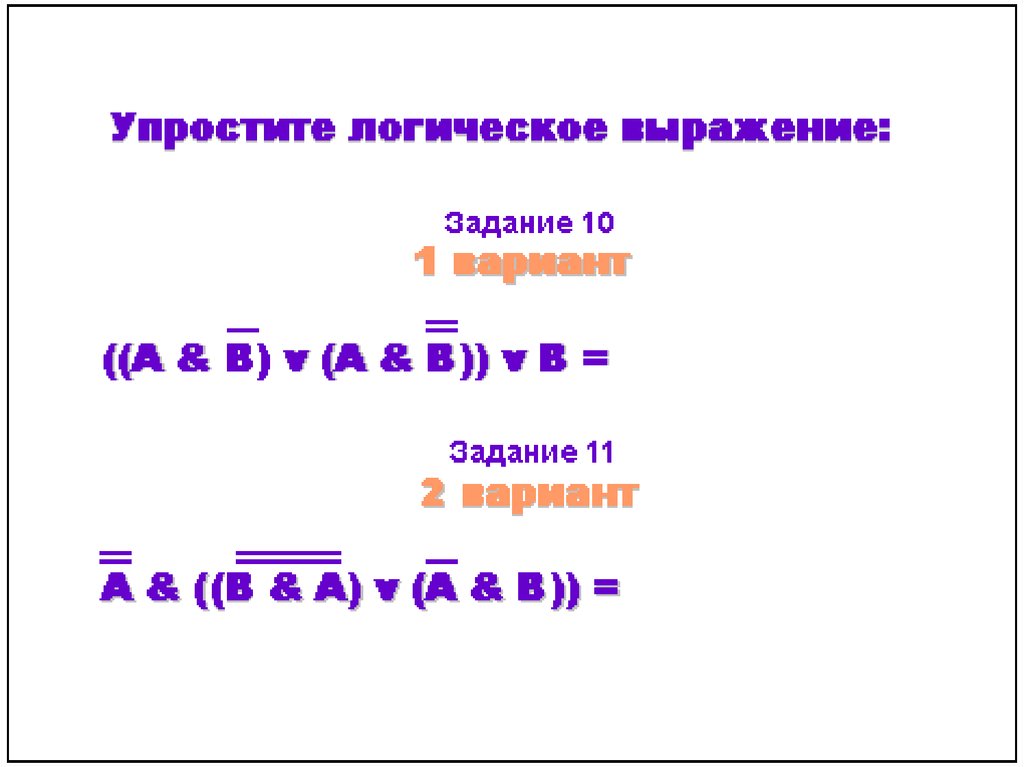
V. Итоги урока

Оценить работу класса и назвать учащихся, отличившихся на уроке.

Домашняя работа

Уровень знания: знать формулы законов и правил логики.

Уровень понимания: упростите логические выражения:

F = Av (A&B).
F = A& (AvB).
F = (AvB) & (BvA) & (CvB).
F = (1V (AvB)) V ((AvC) &1).

Уровень применения: как составить расписание.

При составлении расписания учителя высказали следующие пожелания: учитель физики хочет иметь первый и второй урок; учитель химии — первый или третий; учитель информатики — второй или третий. Предложите возможные варианты расписания.

Творческий уровень: дана следующая логическая схема. Упростите ее, используя минимальное количество вентилей.

Подсказка: постройте к схеме логическое выражение, упростите его и нарисуйте новую схему.

Соберите электрическую схему упрощенного логического выражения.

назад к оглавлению

Уроки 4-5. Решение задач

Презентация

Цели: закрепить полученные знания, умения, навыки; научить учащихся решать логические задачи. Требования к знаниям и умениям.

Учащиеся должны знать:

-основные понятия и определения.

Учащиеся должны уметь:

-строить логические схемы по логическому выражению и наоборот;

-решать логические задачи, используя законы логики.
Программно — дидактическое обеспечение: ПК, элементы для сбора электрических цепей, таблицы, плакаты, кроссворд, инструкции к работе.

Ход урока

I. Постановка целей урока

Как создать свою модель логической схемы.
Помогаем найти правду и установить истину.

II.Проверка домашнего задания
Проверяется у доски.

Задание по карточкам для индивидуального опроса.

Упростите логические выражения:

l) A&B v A

2)A&B v A.

Упростите логические выражения:

¬(X vY)
¬(X &Y)

Запишите следующие высказывания в виде логических выражений:

«Я поеду в деревню к бабушке и, если встречу там друзей, то интересно проведу время».
«Неверно, что если солнце светит, то ветер дует только тогда, когда идет дождь».

Запишите следующие высказывания в виде логических выражений:

«Если будет светить солнце, то ребята пойдут гулять, а если пойдет дождь, то ребята останутся дома».
«Если учитель на уроке рассказывает интересно, то ни Маша, ни Саша, ни Аня не будут смотреть в окно».

III. Решение задач

Работа в группах

Пояснение: приготовьте заранее и распечатайте следующую инструкцию к работе в группах. Группы сформируйте дифференцированно, чтобы каждый ученик поработал в соответствии со своим уровнем обучености. Выдайте каждой группе инструкцию к работе.

Инструкция к работе

Тема: Повторение.

Цель работы:

построить логическую схему;
продемонстрировать и объяснить ее работу.

Оборудование: вентили, провода, переключатели.

Ход работы

Упростите логическое выражение.
Постройте таблицу истинности полученного логического выражения.

Постройте логическую схему данного упрощенного логического выражения.
Продемонстрируйте и объясните работу схемы. Покажите, что схема
работает в соответствии с таблицей истинности.

Задания для работы:

Группа 1

Выражение: F = ¬ (А&В) v ¬ (В&С).

Ответ: F = ¬ (A&B) v ¬ (В&С) =AvBvBvC =AvBvC.

Логическая схема:

Группа 2.

Выражение: F = ¬ (X&YvY&Z)vZ&X.

Ответ: F = ¬ (X&YvY&Z)vZ&X= ¬ (Y&(YvZ))vZ&X= ¬Yv(XvY)vZ&X=

= YvX&ZvZ &X= YvX& (ZvZ) =Yv X.

Логическая схема:

Группа 3.

Выражение: F = A&Bv Dv ¬ (A vВ).

Ответ: F = A&Bv Dv ¬ (A vВ) = A&Bv DvA v В= B& (Av A) v D=BvD.

Логическая схема:

2. Решение логических задач

Как правило, логические задачи формулируются на естественном языке. В этом случае в ходе решения необходимо соблюдать следующие этапы:

Внимательно изучить условие.
Выделить простые высказывания и обозначить их латинскими буквами.
Записать условие задачи на языке алгебры логики.
Составить конечную формулу, для этого объединить логическим умножением формулы каждого утверждения, приравнять произведение к единице.
Упростить формулу.
Проанализировать полученный результат или составить таблицу истинности, найти по таблице значения переменных, для которых значение функции равно 1.
Записать ответ.
№1

Синоптик объявляет прогноз погоды на завтра и утверждает следующее:

Если не будет ветра, то будет пасмурная погода без дождя.
Если будет дождь, то будет пасмурно и без ветра.
Если будет пасмурная погода, то будет дождь и не будет ветра.
Так какая же погода будет завтра?

Решение:

Выделим простые высказывания и запишем их через переменные:

А — «Ветра нет». В — «Пасмурно». С — «Дождь».

Запишем логические функции (сложные высказывания).

а) «Если не_будет ветра, то будет пасмурная погода без дождя» — А→В&С.

б) «Если будет дождь, то будет пасмурно и без ветра» — С → В&А.

в) «Если будет пасмурная погода, то будет дождь и не будет ветра»-

В→С&А.

Запишем произведение указанных функций: (А →B&С) & (С → В& А) & (В→С&А)
Упростим формулу (А →B&С) & (С → В& А) & (В→С&А)=

= (А& B vС & A& A v В& C & В v B& С&C&A) & ( C v B&A) =

= A& В& (C v B &A) = A& В& C v A&  В& B&A = A&В&C

Приравняем результат к единице: А & В & С = 1.
Проанализируем результат: логическое произведение равно 1, если
каждый множитель равен 1. Поэтому: А = 1, В = 1, С = 1. Значит: А=0,
В=0, С=0.

7. Ответ: погода будет ясная, без дождя, но ветреная.
№2

Андрей, Аня и Маша решили пойти в кино. Каждый из них высказал свои пожелания по поводу выбора фильма.

Андрей сказал: «Я хочу посмотреть французский боевик».

Маша сказала: «Я не хочу смотреть французскую комедию».

Аня сказала: «Я хочу посмотреть американскую мелодраму».

Каждый из них слукавил в одном из двух пожеланий. На какой фильм пошли ребята?

Решение:

1. Выделим простые высказывания и запишем их через переменные:

А — «Французский фильм»

В — «Боевик»

С — «Комедия»

2. Запишем логические функции (сложные высказывания). Учтем условие о том, что каждый из ребят оказался прав_в одном предположении:

а) «Французский боевик» — A&В v A &В

б) «Американскую мелодраму» — ̿̿A&BvA&̿B

в) «Не французская комедия» — ًA& C vA&C

3. Запишем _произедение указанных функций:

(A& В v A &В)& (̿̿A&BvA&̿B)&(ًA& C vA&C).

4. Упростим формулу: =(A & В v A &В)&( ̿̿A&BvA&̿B)&( ًA& C vA&C)=

(A&B&A&B vA&B&A&BvA&B&A&B)&(A&CvA&C) = =(A&BvA&B)&(A&CvA&C)=A&B&CvA&B&C.

Приравняем результат к единице: A&B&CvA&B&C=l
Составим таблицу истинности:

А	В	С	A&B&CvA&B&С
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	0
1	1	1	0

Найдем по таблице значения переменных, для которых F = 1

А)

Б)

Проанализируем результат: результат Б) не является решением, т. к. в ответе Маши оба утверждения оказываются неверными, что противоречит условию задачи. Результат А) полностью удовлетворяет условию задачи и поэтому является верным решением.
Ответ: ребята выбрали американский боевик.

V. Итоги уроков

Оцените работу класса и назовите учащихся, отличившихся на уроке.

Домашнее задание

I. Уровень знания и понимания: подготовиться к контрольной работе.

Уровень применения:

Задача 1

Кто из ребят играет в шахматы, если известно, что:

если играет Андрей или Виктор, то Сергей не играет;
если Виктор не играет, то играют Сергей и Дмитрий;
Сергей играет.
Задача 2

Маша, Саша и Миша во время летней практики нашли старинную амфору и показали учителю истории. Он попросил высказать каждого их них предположения о том, что это за амфора. Ребята сказали:

Маша: «Эта амфора греческая и изготовлена в V веке».

Саша: «Эта амфора финикийская и изготовлена в III веке».

Миша: «Эта амфора не греческая и изготовлена в IV веке».

Каждый из ребят оказался прав только в одном предположении. Где и в каком веке была изготовлена амфора?

назад к оглавлению

Урок 6. Контрольная работа

(Раздать ученикам карточки с заданиями)

Вариант 1

Запишите следующие логические высказывания в виде логического выражения. определив простые высказывания и используя логические операции:

На уроке информатики старшеклассники отвечали на вопросы учителя и выполняли практическую работу.
Если сумма цифр числа делится на 3, то число делится на 3.

Составьте таблицу истинности логического выражения:

F= Av ¬B&¬ (AvB).

Нарисуйте логическую схему для следующего логического выражения и определите значения сигналов на входах и выходе: F=A&B v B & C.
Упростите логическое выражение: F=Xv ¬ (Y v ¬ (X&Y)).
Решите задачу:

Компьютер вышел из строя. Известно, что:

Если монитор неисправен, то исправна видеокарта, но не исправна оперативная память.
Если видеокарта исправна, то исправна оперативная память, но неисправен монитор.
Если исправна оперативная память, то исправна видеокарта, но неисправен монитор.

Исправен ли монитор?

Вариант 2

Запишите следующие логические высказывания в виде логического выражения. определив простые высказывания и используя логические операции:

Число 2005 нечетное и четырехзначное.
Если Солнце всходит на востоке, то заходит оно на западе.

Составьте таблицу истинности логического выражения:

F= A& B v ¬ (A &B).

Нарисуйте логическую схему для следующего логического выражения и определите значения сигналов на входах и выходе: F=A&B v C v A.
Упростите логическое выражение: F= (Xv Y) & (Y v Z) &Y.
Решите задачу:

Кто из учеников идет на олимпиаду по физике, если известно следующее:

Если Миша идет, то идет Аня, но не идет Маша.
Если Маша не идет на олимпиаду, то идет Аня, но не идет Миша.
Если Аня идет, то идет Миша, но не идет Маша.

Ответы и решения.

Вариант 1

А) А — «Старшеклассники отвечали на вопросы учителя».

В — «Выполняли практическую работу».

F = А&В.

Б) А — «Сумма цифр числа делится на 3».

В — «Число делится на три». F = А→B

Схема.

F=Xv ¬ (Y v ¬ (X&Y))=X
Решение:

А — монитор исправен.

В — видеокарта исправна.

С — ОЗУ исправно.

F= (A→B&C) & (B→C&A) & (C→B&A) =A&B&C.

A&B&C = 1 A=1, B=0, C=0.

Ответ: монитор исправен.

Вариант 2

1. А) А — «Число 2005 нечетное».

В — «Число 2005 четырехзначное».

F = А&В.

В) А — «Солнце восходит на востоке»

В — «Солнце заходит на западе».

F = А→В.
2.

F= (X v Z) &(X v Z) &Y = X &Y.
Маша идет на олимпиаду, а Аня и Миша не идут.

назад к оглавлению

Урок 7. Использование логических устройств в вычислительной технике

следующая страница >>
Смотрите также:

Методическое пособие Электронный вариант Преподавателю и

737.68kb.

4 стр.

Методическое пособие по дисциплине «Статистика» для специальности «Экономика и бухгалтерский учет (по отраслям): Методическое пособие /Под редакцией В. Ю. Ершовой

1269.9kb.

12 стр.

Практикум по курсу «Электронный маркетинг» Технологии создания Web-сайтов Москва 2003 Составители: Н. Б. Завьялова

643.92kb.

1 стр.

Учебно-методическое пособие Ижевск 2012 резьбовые соединения учебно-методическое пособие Ижевск 2012 (075)

420. 54kb.

3 стр.

Методическое пособие для студентов высших и средних сельскохозяйственных заведений

1135.14kb.

6 стр.

Методическое пособие по выполнению курсовых работ по курсу

153.17kb.

1 стр.

Методическое пособие по курсам «Электрическая часть электростанций и подстанций»

344.65kb.

1 стр.

Учебно-методическое пособие для курсового проектирования Барнаул 2009 (072) Скребковые конвейеры: Учебно-методическое пособие для курсовогоо проектирования / Сост.: И. Л. Новожилов, В. Н. Самородова, Барнаул, 2009. 25 с

403.45kb.

2 стр.

Методическое пособие и описание лабораторной работы (препринт) Составители: д т. н. Кирьянов К. Г. аспирант Семенчуков И. В

326.55kb.

3 стр.

Методическое пособие «От простого к сложному»

151. 3kb.

1 стр.

Учебно-методическое пособие москва военное издательство 1987

961.99kb.

6 стр.

Учебно-методическое пособие Краснодар: Кубанский гос ун-т, 2004, 104 с

61.49kb.

1 стр.






Лучший ответ по мнению автора

01.

12.15

Лучший ответ по мнению автора

Читать ответы

Читать ответы

Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Информатика

Похожие вопросы

Решено

Имеется пять карточек, на которых написаны цифры от 1 до 5. Наудачу выбирают 3 карточки и составляют из них трехзначное число. Найдите вероятность того, что полученное число меньше 200.

Решено

Дана последовательность “12”. К ней применяют следующий алгоритм: в конец строки дописывают ее зеркальную копию, а затем к цифрам, стоящим на четных…

Решено

Чем отличается chat-конференция от телеконференции?

Решено

Для чего используются ярлыки объектов?

Решено

Помогите, пожалуйста. 8 класс.

Пользуйтесь нашим приложением

Поиск инструмента

Найдите инструмент в dCode по ключевым словам:

Просмотрите полный список инструментов dCode

Калькулятор логических выражений

Инструмент/калькулятор для упрощения или минимизации логических выражений (булева алгебра), содержащих логические выражения с И, ИЛИ, НЕ, XOR.

Результаты

Калькулятор логических выражений — dCode

Метки: Символьные вычисления, Электроника

dCode и многое другое

dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Калькулятор логических выражений/упрощение/минификатор
Формат результата
Любой формат
Дизъюнктивная нормальная форма DNF (сумма произведений/SOP/Minterms)
Конъюнктивная нормальная форма CNF (произведение сумм/POS/Maxterms)
Только вентили НЕ-И (НЕ-И ⊼)
Только вентили ИЛИ-НЕ (НЕ-ИЛИ ⊽)

Нотация

Алгебраические (*, +, !)
Логические (∧, ∨, ¬)
Программирование (& ||, ~)
Буквенное (И, ИЛИ, НЕ)

См. также: Таблица истинности — Решатель уравнений — Двоичный код

A Логическое выражение (или Логическое выражение) — это математическое выражение, использующее Булева алгебра , которая использует логические значения (0 или 1, истина или ложь) в качестве переменных и имеет логические значения в качестве результата/упрощения. Выражение может содержать такие операторы, как конъюнкция (И), дизъюнкция (ИЛИ) и отрицание (НЕ).

Для упрощения булевых уравнений можно использовать различные методы: помимо классического развития через ассоциативность, коммутативность, дистрибутивность и т. д., таблицы истинности или диаграммы Венна обеспечивают хороший обзор выражений.

Пример: Исходное выражение (LaTeX) $$ \overline{a \land b \land (c \lor \bar{d})} \lor \bar{b} $$

dCode допускает несколько синтаксисов:

Алгебраическая запись

Пример: !(ab(c+!d))+!b с неявным умножением ab = a AND b и ! (восклицательный знак) для строки : логический НЕ .

Логические/компьютерные обозначения

Пример: !(a&&b&&(c||!d))||!b с двойным символом и (амперсанд) для И и двойным символом | (прямая, вертикальная черта) для логического ИЛИ .

Буквенное обозначение

Пример: НЕ (a И b И (c ИЛИ НЕ d)) ИЛИ НЕ b

Для одного и того же выражения может быть несколько минимальных представлений, dCode предоставляет решение и выводит алгебраическое обозначение.

Некоторые обозначения неоднозначны, избегайте функционального обозначения ‘XOR(a,b)’ для записи a XOR b , также избегайте суффикса штрих/апостроф перед `a’ и предпочтите !a .

Булева алгебра обладает многими свойствами (булевыми законами):

1 — Элемент идентичности: $0$ нейтрален для логического ИЛИ, тогда как $1$ нейтрален для логического И

$$a + 0 = a \\a . 1 = a $$

2 — Поглощение: $1$ поглощает для логического ИЛИ, а $0$ поглощает для логического И

$$ a + 1 = 1 \\ a.0 = 0 $$

3 — Идемпотентность: многократное применение одной и той же операции не меняет значение

$$ a + a = a + a + \cdots + а = а \ а . а = а . а . \cdots . a = a $$

4 — Инволюция или двойное дополнение: противоположность противоположности $ a $ est $ a $

$$ a = \overline{\overline{a}} = !(!a) $$

5 — Дополнительность по противоречию: $ a $ AND $ \text{not}(a) $ невозможно, поэтому ложно и равно $ 0 $

$$ а . \overline{a} = 0 $$

6 — Дополнительность по исключенному третьему: $ a $ OR $ \text{not}(a) $ всегда истинно, поэтому $ 1 $

$$ a + \overline{ a} = 1 $$

7 — Закон ассоциативности: скобки между одинаковыми операторами бесполезны

$$ a.(b.c) = (a.b).c = a.b.c \\ a+(b+c) = (a+b) +c = a+b+c $$

8 — Закон коммуникативности: порядок не имеет значения

$$ a.b = b. a \\ a+b = b+a $$

9 — Закон распределения: И распределено над ИЛИ, но также ИЛИ распределяется по И

$$ a.(b+c) = a.b + a.c \\ a+(b.c) = (a+b).(a+c) $$

10 — Законы Де Моргана (подробнее см. ниже)

$$ \overline{a+b} = \overline{a}.\overline{b} \\ \overline{a.b} = \overline{a}+\overline{b} $$

11 — Другие упрощения комбинации указанных выше

$$ a.(a+b) = a \\ a+(a.b) = a \\ (a.b) + (a.!b) = a \\ (a+b).(a+ !b) = a \\ a + (!a.b) = a + b \\ a.(!a + b) = a.b \\ a.b + \overline{a}.c = a.b + \overline{a}.c + b.c $$

Метод 1: упростите их , пока не получите то же самое написание в булевой алгебре .

Метод 2: путем вычисления их таблицы истинности , которая должна быть идентичной.

Законы Де Моргана часто используются для перезаписи логических выражений. Обычно они формулируются так: не (а и б) = (не а) или (не б) и не (а или б) = (не а) и (не б) . Вот эквивалентные логические записи:

$$ \overline{(a \land b)} \leftrightarrow (\overline{a}) \lor (\overline{b}) \iff \overline{AB} = \overline{a} + \overline{b } $$

$$ \overline{(a \lor b)} \leftrightarrow (\overline{a}) \land (\overline{b}) \iff \overline{a+b} = \overline{a} . \overline{b} $$

В логике можно использовать разные форматы для обеспечения лучшей читабельности или удобства использования.

Нормальная дизъюнктивная форма (DNF) использует сумму произведений (SOP):

Пример: (a&&c)||b

Нормальная конъюнктивная форма (CNF) или клаузальная форма использует произведение сумм (POS):

Пример: (a+b).(b). +c)

Шаги расчета, какими их может себе представить человек, для решателя не существуют. Выполняемые операции являются бинарными побитовыми и не соответствуют выполняемым при разрешении с помощью карандаша и бумаги.

dCode сохраняет право собственности на исходный код «Калькулятора логических выражений». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Калькулятор логических выражений», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Булевых выражений». Функции калькулятора (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, script или доступ к API для «Калькулятора логических выражений» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
Напоминание: dCode можно использовать бесплатно.

Копирование и вставка страницы «Калькулятор логических выражений» или любых его результатов разрешено, если вы цитируете dCode!
Ссылка на источник (библиография):
Калькулятор логических выражений на dCode.fr [онлайн-сайт], получено 18 ноября 2022 г., https://www.dcode.fr/boolean-expressions-calculator

Сводка

Упрощение логических выражений
Что такое логическое выражение? (Определение)
Как упростить/уменьшить логическое выражение?
Что такое методы упрощения булевой алгебры?
Как показать/продемонстрировать, что 2 логических выражения равны?
Что такое закон де Моргана?
Что такое дизъюнктивная или конъюнктивная нормальная форма?
Как показать пошаговые расчеты?

Похожие страницы

Таблица истинности
Решатель уравнений
Двойной логический
Булевы Minterms и Maxterms
Binary Code
Math Expression Simplifier
Remove Parentheses
DCODE’S TOOLS LIST

Support

Paypal
Patreon
More

Forum/Help

Keywords

bool,boole,boolean ,выражение,алгебра,логика,логическое,упростить,упрощение,и,или,не,исключающее ИЛИ,амперсанд,труба,восклицательный знак,морган

Ссылки

▲

Av ¬B&¬(AvB)

Поиск инструмента

Найдите инструмент в dCode по ключевым словам:

Просмотрите полный список инструментов dCode

Калькулятор логических выражений

Результаты

Калькулятор логических выражений — dCode

Теги: Символьные вычисления, Электроника

dCode и многое другое задачи решать каждый день!
Предложение ? обратная связь? Жук ? идея ? Запись в dCode !