Пользуясь правилами сложения векторов упростите выражение мс
Прежде чем приступить к тематике статьи, напомним основные понятия.
Вектор – отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху. При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.
Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху.
Длина вектора – величина, равная или большая нуля, определяющая длину отрезка, составляющего вектор.
Коллинеарные векторы – лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.
Сложение двух векторов
Исходные данные: векторы a → и b → . Для выполнения над ними операции сложения необходимо из произвольной точки undefined отложить вектор A B → , равный вектору а → ; из полученной точки undefined – вектор В С → , равный вектору b → . Соединив точки undefined и C , получаем отрезок (вектор) А С → , который и будет являться суммой исходных данных. Иначе описанную схему сложения векторов называют правилом треугольника.
Соединив точки undefined и C , получаем отрезок (вектор) А С → , который и будет являться суммой исходных данных. Иначе описанную схему сложения векторов называют правилом треугольника.
Геометрически сложение векторов выглядит так:
– для неколлинеарных векторов:
– для коллинеарных (сонаправленных или противоположнонаправленных) векторов:
Сложение нескольких векторов
Взяв за основу описанную выше схему, мы получаем возможность произвести операцию сложения векторов в количестве более 2: поочередно прибавляя каждый последующий вектор.
Исходные данные: векторы a → , b → , c → , d → . Из произвольной точки А на плоскости необходимо отложить отрезок (вектор), равный вектору a → ; затем от конца полученного вектора откладывается вектор, равный вектору b → ; далее – по тому же принципу откладываются последующие векторы. Конечной точкой последнего отложенного вектора будет точка B , а полученный отрезок (вектор) A B → – суммой всех исходных данных.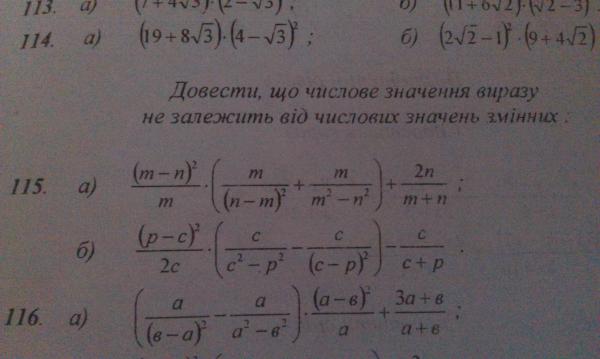 Описанную схему сложения нескольких векторов называют также правилом многоугольника .
Описанную схему сложения нескольких векторов называют также правилом многоугольника .
Геометрически оно выглядит следующим образом:
Отдельной схемы действия по вычитанию векторов нет, т.к. по сути разность векторов a → и b → есть сумма векторов a → и – b → .
Умножение вектора на число
Чтобы произвести действие умножения вектора на некое число k , необходимо учитывать следующие правила:
– если k > 1 , то это число приведет к растяжению вектора в k раз;
– если 0 k 1 , то это число приведет к сжатию вектора в 1 k раз;
– если k 0 , то это число приведет к смене направления вектора при одновременном выполнении одного из первых двух правил;
– если k = 1 , то вектор остается прежним;
– если одно из множителей – нулевой вектор или число, равное нулю, результатом умножения будет нулевой вектор.
Исходные данные:
1) вектор a → и число k = 2 ;
2) вектор b → и число k = – 1 3 .
Геометрически результат умножения в соответствии с указанными выше правилами будет выглядеть следующим образом:
Свойства операций над векторамиОписанным выше операциям над векторами присущи свойства, некоторые из которых очевидны, а прочие можно обосновать геометрически.
Исходные данные: векторы a → , b → , c → и произвольные действительные числа λ и μ .
- Свойство коммутативности: a ⇀ + b → = b → + a → .
- Свойство ассоциативности: ( a → + b → ) + c → = a → + ( b → + c → ) .
- Свойство использования нейтрального элемента по сложению (нулевой вектор 0 → ⃗). Это очевидное свойство: a → + 0 → = a →
- Свойство использования нейтрального элемента по умножению (число, равное единице): 1 · a → = a → . Это очевидное свойство, не предполагающее никаких геометрических преобразований.
- Любой ненулевой вектор a → имеет противоположный вектор – a → и верным является равенство: a → + ( – a → ) = 0 → .
 Указанное свойство – очевидное.
Указанное свойство – очевидное. - Сочетательное свойство операции умножения: ( λ · µ ) · a → = λ · ( µ · a → ) . Например, растяжение вектора при умножении на число 10 можно произвести, сначала растянув вектор в 2 раза, а затем полученный результат еще в 5 раз. Также возможен вариант умножения на число 10 при сжатии вектора в 5 раз и последующего растяжения полученного результата в 50 раз.
- Первое распределительное свойство (очевидно): ( λ + µ ) · a → = λ · a → + µ · a → .
- Второе распределительное свойство: λ · ( a → + b → ) = λ · a → + λ · b → .
Геометрически это свойство определяется подобием треугольников:
Свойства коммутативности и ассоциативности дают возможность складывать векторы в произвольном порядке.
Перечисленные свойства операций позволяют осуществлять необходимые преобразования векторно-числовых выражений аналогично привычным числовым. Рассмотрим это на примере.
Задача: упростить выражение a → – 2 · ( b → + 3 · a → )
Решение
– используя второе распределительное свойство, получим: a → – 2 · ( b → + 3 · a → ) = a → – 2 · b → – 2 · ( 3 · a → )
– используя свойство коммутативности, меняем местами слагаемые: a → – 2 · b → – 6 · a → = a → – 6 · a → – 2 · b →
– затем по первому распределительному свойству получаем: a → – 6 · a → – 2 · b → = ( 1 – 6 ) · a → – 2 · b → = – 5 · a → – 2 · b → Краткая запись решения будет выглядеть так: a → – 2 · ( b → + 3 · a → ) = a → – 2 · b → – 2 · 3 · a → = 5 · a → – 2 · b →
Ответ: a → – 2 · ( b → + 3 · a → ) = – 5 · a → – 2 · b →
Reshak. ru – сборник решебников для учеников старших классов. Здесь можно найти решебники, ГДЗ, переводы текстов по школьной программе. Практически весь материал, собранный на сайте – сделанный для людей. Все решебники выполнены качественно, с приятной навигацией. Вы сможете скачать гдз, решебник английского, улучшить ваши школьные оценки, повысить знания, получить намного больше свободного времени.
ru – сборник решебников для учеников старших классов. Здесь можно найти решебники, ГДЗ, переводы текстов по школьной программе. Практически весь материал, собранный на сайте – сделанный для людей. Все решебники выполнены качественно, с приятной навигацией. Вы сможете скачать гдз, решебник английского, улучшить ваши школьные оценки, повысить знания, получить намного больше свободного времени.
Главная задача сайта: помогать школьникам в решении домашнего задания. Кроме того, весь материал гдз совершенствуется, добавляются новые сборники решений.
Информация
© adminreshak.ru
Ответ оставил Гость
Если твой вопрос не раскрыт полностью, то попробуй воспользоваться поиском на сайте и найти другие ответы по предмету Геометрия.
Презентация по геометрии Умножение вектора на число(9 класс). доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация на тему Презентация по геометрии Умножение вектора на число(9 класс). , предмет презентации: Алгебра. Этот материал в формате pptx (PowerPoint) содержит 20 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
, предмет презентации: Алгебра. Этот материал в формате pptx (PowerPoint) содержит 20 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Умножение вектора на число.
9 класс.
Учитель математики
ГЬОУ Гимназия № 1592
Кушнаренко Л.В.
г. Москва.
ПОВТОРЕНИЕ:
1) Постройте сумму а + b,
используя правило треугольника.
а
b
c
Построение:
d
Дано:
а
b
1)
a + b
2) Постройте сумму с + d,
используя правило параллелограмма .
а
b
c
Построение:
d
Дано:
с
d
2)
c + d
3) Постройте разность с — b, используя
теорему о разности векторов.
а
b
c
Построение:
d
Дано:
с
-b
3)
с — b
4) Постройте разность d — а,
используя правило вычитания векторов .
а
b
c
Построение:
d
Дано:
а
d
4)
х = d – a, значит d = а + х
d — a
5) Упростите выражение:
1 вариант.
CA – OB – CD + AB =
2 вариант.
BA + CD – OD – CA =
= CA + BO + DC + AB =
= DC + CA + AB + BO =
= DO.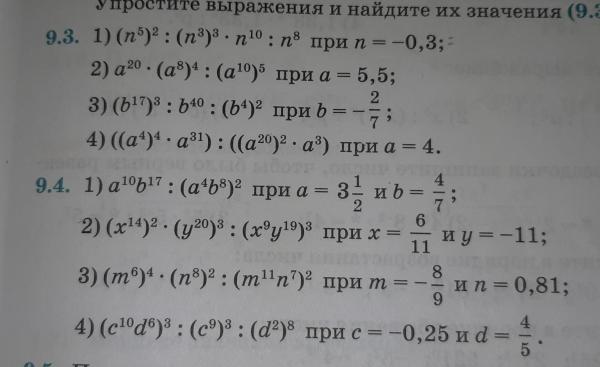
= BA + CD + DO + AC =
= BA + AC + CD + DO =
= BO.
Умножение вектора на число.
Умножение вектора на число
Произведением вектора на число t называется вектор, длина которого равна , а направление остается прежним, если t>0, и меняется на противоположное, если t
Произведение вектора на число -1 называется вектором, противоположным и обозначается По определению, вектор имеет направление, противоположное вектору и
Произведение вектора на число t обозначается . По определению,
Свойства
Для умножения вектора на число справедливы свойства, аналогичные свойствам умножения чисел, а именно:
Свойство 1. (сочетательный закон).
Свойство 2. (первый распределительный закон).
Свойство 3. (второй распределительный закон).
Что получается при умножении
вектора на число?
а
b
c
d
2а
3b
0,5с
— 0,5d
РЕШЕНИЕИ ЗАДАЧ:
№ 775, 776(в,г), 778, 782.
Упражнение 1
В треугольнике АВС укажите векторы:
а)
б)
в)
г)
Упражнение 2
В параллелограмме АВСD укажите векторы:
а)
б)
в)
г)
д)
Упражнение 3
Точки M и N — середины сторон соответственно АВ и АС треугольника АВС. Выразите векторы: а) ; б) ; в) ; г) ; д) через векторы ,
Упражнение 4
Отрезки АА1, ВВ1, СС1 — медианы треугольника АВС. Выразите векторы: а) ; б) ; в) через векторы и
Выразите векторы: а) ; б) ; в) через векторы и
Упражнение 5
Упростите выражение:
а)
б)
Упражнение 6
Сторона равностороннего треугольника АВС равна а. Найдите: а) ; б) .
Ответ: а) a;
б) a.
Упражнение 7
Ответ: а) -2;
В треугольнике АВС АВ = 6, ВС = 8, B = 90°. Найдите: а) ; б) ; в) ; г) .
б) 10;
в) -2;
г) 10.
Домашняя работа.
Повторить материал пунктов 82- 86,
выполнить №№ 776(а,б), 777, 779.
Скачать презентацию
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
Докажите что векторы м а б с н 2а б с и п 8а б с компланарны
Доказать, что векторы m, n, p — компланарные, если вектор m = a + b — с, n = 2a — b + с , p = 8a — b + c?
Доказать, что векторы m, n, p — компланарные, если вектор m = a + b — с, n = 2a — b + с , p = 8a — b + c.
Доказать, что векторы m, n, p — компланарные, если вектор m = a + b — с, n = 2a — b + с , p = 8a — b + c.
Вектор АВ + вектор ВС + вектор DD1 + вектор СD = вектор АВ — вектор СС1 =?
Вектор АВ + вектор ВС + вектор DD1 + вектор СD = вектор АВ — вектор СС1 =.
Известно что вектор а( — 2 ; 5), вектор b(1 ; — 2) ?
Известно что вектор а( — 2 ; 5), вектор b(1 ; — 2) .
Найдите координаты векторов вектор с = вектор а + вектор б.
Вектор н = вектор б — вектор а.
Вектор м = 2 вектор а + 3 вектор б?
Доказать, что любой вектор в пространстве раскладывается на три компланарных вектора?
Доказать, что любой вектор в пространстве раскладывается на три компланарных вектора.
Упростить выражение : вектор РВ — вектор ОД + вектор МС — вектор РА + вектор ВМ + вектор ОА?
Упростить выражение : вектор РВ — вектор ОД + вектор МС — вектор РА + вектор ВМ + вектор ОА.
Решите , пожалуйста?
Тема — компланарные векторы.
Вектор а = вектор m + 2 вектора, вектор b = 2 вектора n — вектор m, вектор m равен 3, вектор n равен 2?
Вектор а = вектор m + 2 вектора, вектор b = 2 вектора n — вектор m, вектор m равен 3, вектор n равен 2.
А вектор, bвектор , с вектор Найти х, если векотры компланарны?
А вектор, bвектор , с вектор Найти х, если векотры компланарны.
Упростите выражение : а) 2(вектор m + вектор n) — 3(вектор 4m — вектор n) + вектор m ; b) вектор m — 3( вектор n — вектор 2m + p) + 5 ( вектор p — вектор 4m )?
Упростите выражение : а) 2(вектор m + вектор n) — 3(вектор 4m — вектор n) + вектор m ; b) вектор m — 3( вектор n — вектор 2m + p) + 5 ( вектор p — вектор 4m ).
Дан куб АВСDA1B1C1D1 определите являются ли вектора компланарными : а) АВ1, АD и В1D б) АВ, АD, АА1 №2 АВСDA1B1C1D1 найдите вектор начало и конец которого являются вершинами куба, равный сумме векторо?
Дан куб АВСDA1B1C1D1 определите являются ли вектора компланарными : а) АВ1, АD и В1D б) АВ, АD, АА1 №2 АВСDA1B1C1D1 найдите вектор начало и конец которого являются вершинами куба, равный сумме векторов.
А) С1В1 + С1D1 + CC1 б) АВ + А1D1 + AA1 №3 Разложите в параллелепипеде векторы : а)вектор АС1 по векторам АВ, АD и АА1 б) вектор АА1 по векторам D1A1, D1C1 и А1С.
Проверить условие компланарности трёх векторов : а) (1, 1, 1) ; в) (2, — 3, 5) ; с) (4, 0, 2)?
Проверить условие компланарности трёх векторов : а) (1, 1, 1) ; в) (2, — 3, 5) ; с) (4, 0, 2).
На странице вопроса Доказать, что векторы m, n, p — компланарные, если вектор m = a + b — с, n = 2a — b + с , p = 8a — b + c? из категории Геометрия вы найдете ответ для уровня учащихся 10 — 11 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.
Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.
1) боковые ребра равны(р — б треугольник), а основание меньше бок. Ребра на 3 м, P = 15, 6. Значит бок ребра в сумме дают 12. 4( одно ребро = 6. 2), а основание = 3. 2 2) когда основание больше на 3 метра, то бок ребро = 4. 2, а основание = 7. ..
SinA = tgA / корень (1 + tg в квадрате А) = (1 / 2 х корень6) / корень ( 1 + 1 / 24) = = (1 / 2 х корень6) / (5 / 2 х корень6) = 1 / 5ВС = sinA х АВ = 1 / 5 х 10 = 2.
Б — да, ответствующие углы раны, В — да, сумма соседних углов = 180 градусов а — нет . Накрест лежащие углы не равны г — нет, сумма соседних углов не равна 180 градусов.
Помойму 30 но это не точно.
Нет, не всегда теоремы равенства треугольников знаешь .
Получ. Они образуют перпендикуляр.
Давайте я попробую помочь. : ).
1. нехай АВС — рівнобедрений трикутник ; АС = 4 см, АВ = 11см ; ВС = АВ = 11 см(АВС рівнобедрений), тоді Р = АВ + ВС + АС = 11 + 11 + 4 = 26(см) 2. Нехай АВС — рівнобедрений трикутник ; АС = 8см, Р = 26см ; у рівнобедреному трикутнику бічні сторони ..
Короче, вот тебе решение с чертежом. Я сама пыталась решить, но ничо не поняла) ответ скорее всего удалят.
Рисунка не будет, ибо там рисовать нечего. Обычный треугольник АВС только с продолженной стороной АС, там и будет угол в 150° Дано : ΔАВС — равносторонний. ∠С(внешний) = 150° Найти : ∠В Решение : 1)∠С = 180° — 150° = 30° (смежные углы) 2)∠А = ∠С = ..
Докажите, что векторы m=a+2b+3c, n=2a-b-c, p=3a-4b-5c компланарны. Непременно с доскональным
Обоснуйте, что векторы m=a+2b+3c, n=2a-b-c, p=3a-4b-5c компланарны. Непременно с подробным объяснением. Если решите использовать определитель, то
Если решите использовать определитель, то
растолкуйте как им пользоваться. Но желанно использовать более простой способ. Помогите.
- Anastasija Nemscveridze
- Геометрия
- 2019-03-13 01:38:02
- 0
- 1
Видно, что p=2n-m, т.к. 2(2a-b-c)-(a+2b+3c)=3a-4b-5c. Т.е. вектор p есть линейная композиция векторов m и n, а это и значит, что они компланарны.
Даны некомпланарные векторы а, b и с . Докажите, что векторы I, m и п компланарны, и разложите один из них
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
ЕНТ-2014, вариант 0002
По вашим просьбам!
1. Требуется упростить выражение. Запишем каждый множитель данного выражения в виде степени с основанием 3.
2. Решить уравнение: 2у5+8у3=0.
Выносим общий множитель за скобки: 2у3(у2+4)=0. Это произведение будет равно нулю, если множитель у3=0, т.е. если у=0, так как выражение в скобках у2+4>0 при любом значении у.
3. Решить систему показательных уравнений:
5. Решить неравенство:
7. В арифметической прогрессии d=2, n=50, Sn=2650. Найдите первый и n-й члены.
Сумма nпервых членов арифметической прогрессии определяется по формуле:
2650 = (а1 + 49) ∙ 50, отсюда а1 + 49 = 2650 : 50 или а1 + 49 = 53 ⇒ а1 = 4.Формула n-го члена арифметической прогрессии:
an = a1 + (n — 1)d. Тогда а50 = 4 +(50 – 1)∙2 = 4 + 49∙2 = 4 + 98 = 102.
Тогда а50 = 4 +(50 – 1)∙2 = 4 + 49∙2 = 4 + 98 = 102.
8. Найдите функцию, обратную данной:
1) Выразим х через у. Для этого возведем обе части данного равенства в квадрат. Получаем у2=х-3, отсюда х=у2+3. 2) Вместо х напишем у, а вместо у напишем х. Получаем функцию, обратную данной: у=х2+3.
9. Радиус основания цилиндра равен 6 см, высота 5 см. Найдите диагональ осевого сечения.
Пусть нам дан цилиндр с осевым сечением AA1B1B. Это сечение представляет собой прямоугольник, диагональ которого AB1 требуется найти. AB1 — гипотенуза прямоугольного треугольника ABB1, в котором известны катеты АВ = 2·6=12 см и BB1=5 см. По теореме Пифагора получаем:
AB12 =AB2+BB12 ⇒ AB12 =122+52=144+25=169 ⇒ AB1=13cм.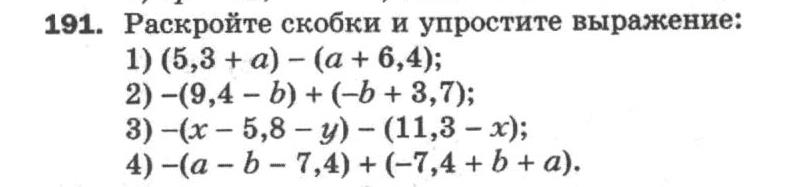
10. Решить систему уравнений:
Необходимо избавиться от знака модуля. Модуль неотрицательного числа равен самому этому числу. Модуль отрицательного числа равен противоположному ему числу. Так как х=0 не является корнем первого уравнения, то возможны значения х:
1) х > 0 и 2) x < 0. Раскрываем модульные скобки в каждом из этих случаев.
11. Одно из трех чисел равно 32 и оно составляет 0,4 их суммы, а второе число составляет 0,2 суммы. Найдите второе и третье число.
Итак, пусть первое число равно 32, второе — х, а третье — у.
Зная, что число 32 составляет 0,4 от суммы всех чисел, составим первое уравнение системы: 0,4·(32+х+у)=32. (Чтобы найти дробь от числа, нужно умножить эту дробь на данное число). Упростим, разделив обе части равенства на 0,4. Тогда первое уравнение примет вид: 32+х+у=80 (*). Зная, что второе число х составляет 0,2 от суммы всех чисел, составим второе уравнение системы: 0,2·(32+х+у)=х. Разделим обе части этого равенства на 0,2, получаем уравнение: 32+х+у=5х (**). Вычтем из (*) равенство (**). Получаем: 0=80-5х. Отсюда х=16. Подставим это значение в любое из уравнений, например в (*). Тогда 32+16+у=80. Отсюда у=32. Ответ: 16 и 32.
Разделим обе части этого равенства на 0,2, получаем уравнение: 32+х+у=5х (**). Вычтем из (*) равенство (**). Получаем: 0=80-5х. Отсюда х=16. Подставим это значение в любое из уравнений, например в (*). Тогда 32+16+у=80. Отсюда у=32. Ответ: 16 и 32.
13. Решить систему уравнений:
14. Решить тригонометрическое уравнение:
15. На графике функции у=х2+х-5 взята точка А. Касательная к графику, проведенная через точку А, наклонена к оси Ох под углом, тангенс которого равен 5. Найдите абсциссу точки А.
Используем геометрический смысл производной: f’(xo)=tgα, где xo — абсцисса точки касания (точки А). Производная данной функции y’=2x+1. По условию tgα=5. Получаем равенство: 2хо+1=5, отсюда хо=2.
16. Найдите скорость точки, движущейся прямолинейно по закону: x(t) = 3t2 + t – 1 (см) в момент времени t = 3 с.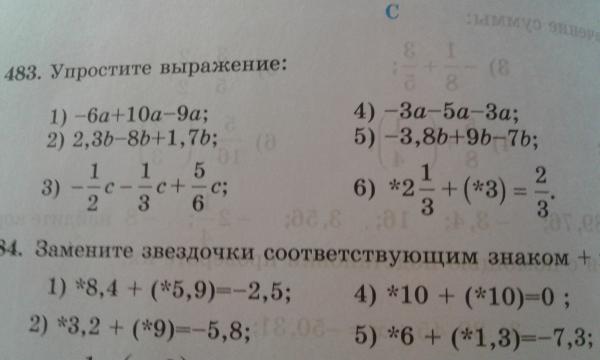
Скорость – это производная пути по времени: v(t) = x’(t).
Находим скорость v(t) = x’(t) = (3t2 + t – 1)’ = 6t + 1. Подставим t = 3. Получаем:
v(3) = 6 ∙ 3 + 1 = 18 + 1 = 19 (cм/с).
17. Каким должен быть радиус окружности, чтобы длина ее была в два раза больше суммы длин окружностей с радиусами 11 см и 47 см.
Длины данных окружностей с радиусами 11 см и 47 см соответственно равны 22π см и 94π см (нашли по формуле длины окружности: С=2πR). Складываем эти длины и получаем С=116π см. Длина новой окружности в два раза больше, значит равна 2·116π см. Если записать это выражение так: 2π·116 см, то становится понятным, что искомый радиус должен быть равен 116 см.
18. Треугольник вписан в окружность так, что одна из его сторон проходит через центр окружности, а две другие удалены от него на 6 см и четыре корня из трех см. Найдите площадь треугольника.
19. Площадь ромба, лежащего в основании пирамиды, равна 600 см2, а площадь круга, вписанного в ромб, равна 100 см2. Определите объем пирамиды, если высоты ее боковых граней равны 26 см.
Определите объем пирамиды, если высоты ее боковых граней равны 26 см.
Так как высоты боковых граней равны, то вершина пирамиды проектируется в центр вписанного в ромб круга, так как стороны ромба должны быть равноудалены от и от центра круга. Точка О — центр круга является точкой пересечения диагоналей ромба.
20. Сократите дробь:
Можно догадаться, что в числителе дроби формула разности квадратов двух выражений: a2-b2=(a-b)(a+b). Применив эту формулу мы представим числитель в виде произведения двух множителей, причем, один из них будет таким же, как знаменатель, что позволит нам сократить дробь.
21. Разложите на множители: a2b2-4a3b4+ab+abc-4a2b3c+c.
Эти 6 слагаемых нужно сгруппировать так, чтобы из каждой группы можно было вынести за скобки общий множитель и при этом, в скобках должны получаться одинаковые выражения; затем это одинаковое выражение в скобках еще раз выносят за скобки. Попробуем сгруппировать по три слагаемых:
Попробуем сгруппировать по три слагаемых:
a2b2-4a3b4+ab+abc-4a2b3c+c = (a2b2-4a3b4+ab)+(abc-4a2b3c+c). Из каждой скобки выносим общий множитель:
ab(ab-4a2b3+1)+c(ab-4a2b3+1). Вот у нас получились одинаковые выражения в скобках, т.е. одинаковые множитель, который выносим за скобки и окончательно получаем:
(ab-4a2b3+1)(ab+c).
22. Решить неравенство: 2sin2x+5cosx<4.
Так как sin2x+cos2x=1, то заменим sin2x =1 – cos2x, тогда неравенство примет вид:
2∙(1 – cos2x) + 5cosx<4. Раскроем скобки и перенесем 4 в левую часть неравенства:
2-2cos2x+5cosx-4<0. Приведем подобные слагаемые: -2cos2x+5cosx-2<0. Умножим обе части неравенства на (-1), при этом знак неравенства поменяется на противоположный:
2cos2x — 5cosx +2 > 0. Сделаем замену переменной: пусть cosx=y, тогда получаем:
Сделаем замену переменной: пусть cosx=y, тогда получаем:
2y2-5y+2>0. Найдем корни квадратного уравнения 2y2-5y+2=0.
Дискриминант D=b2-4ac=52-4∙2∙2=25-16=9=32. Тогда y1=0,5; y2=2. Решениями неравенства 2y2-5y+2>0 будут значения у, удовлетворяющие условиям: y<0,5 или y>2.
Но так как y=cosx, а известно, что |cosx|≤1, то остается y<0,5, т.е. нам остается решить простейшее неравенство cosx<0,5. Изобразим графики функций у=cosx и y=0,5 и определим те значения х, при которых точки кривой у=cosx лежат ниже прямой у=0,5.
24. Преобразуйте выражение:
Определите его значение, если углы между парами данных единичных векторов равны 60°.
Прежде всего раскроем скобки, выполнив умножение. Приведем подобные слагаемые. Используем свойства: 1) квадрат вектора равен квадрату модуля (длины) этого вектора; 2) скалярное произведение двух векторов равно произведению модулей (длин) этих векторов на косинус угла между ними.
Решайте, готовьтесь. Желаю успехов!
Запись имеет метки: преобразования с квадратными корнями, скалярное произведение векторов в ЕНТ-2014, сокращение алгебраической дроби, текстовая задача в ент
Навигация
Урок 17. вектор в пространстве — Геометрия — 10 класс
Сумма векторов
В кубе назовите вектор, равный сумме $\overrightarrow{AB}+\overrightarrow{B_{1} C_{1}}+\overrightarrow{DD_{1}} $
$\overrightarrow{AC_1}$
$\overrightarrow{A_1C}$
$\overrightarrow{BD_1}$
$\overrightarrow{CA_1}$
Оранжевый
Вектор в пространстве
Установите соответствие между выражением и вектором $Х$
Длина вектора
Дано: АВ = 3 ВС = 4 СС1 = 12
Длина вектора АС1 =
Длина вектора
Задача:
Диагонали параллелепипеда пересекаются в точке О.
Варианты ответа (введите порядковый номер):
1) 1,5
2) 0,5
3) -3
4) -2
Вектор в пространстве
Задача:
Упростите выражение и выберите правильный результат преобразования:
$3\overrightarrow{a}+2(\overrightarrow{b}+\frac{1}{2}\overrightarrow{c})-3(\frac{2}{3}\overrightarrow{b}+\overrightarrow{a})+\overrightarrow{c}$
Варианты ответа:
1) $\overrightarrow{2c}$
2) $\overrightarrow{0}$
3) $\overrightarrow{4a}$
4) $\overrightarrow{3b}$
Обратитесь к материалам урока
3 2 4 1
Вектор в пространстве
В тетраэдре ABCD точка Е — середина АD.
Докажите, что $\overrightarrow{FE}=\frac{1}{2}(\overrightarrow{FA}+\overrightarrow{FD})$
Обратитесь к материалам урока
Сложим полученные равенства $\overrightarrow{FA}+\overrightarrow{AE}+\overrightarrow{FD}+\overrightarrow{DE}=2\overrightarrow{FE}$
$\overrightarrow{FA}+\overrightarrow{AE}=\overrightarrow{FE}$
$\overrightarrow{FD}+\overrightarrow{DE}=\overrightarrow{FE}$
Так как $\overrightarrow{AE}+\overrightarrow{DE}=0$, то $\overrightarrow{FA}+\overrightarrow{FD}=2\overrightarrow{FE}$, значит $\overrightarrow{FE}=\frac{1}{2}(\overrightarrow{FA}+\overrightarrow{FD})$
Вектор в пространстве
Задача:
Дано: Ребро куба $ABCDA_{1} B_{1} C_{1} D_{1}$ равно 2.
Найдите $\mid\overrightarrow{BC_{1}}-\overrightarrow{BA_{1}}\mid$
Варианты ответа:
$2\sqrt{2}$ | |
$\frac{\sqrt{2}}{2}$ | |
2 | |
$\sqrt{2}$ |
Свойства векторов
Даны точки А, В, С.
Известно, что $\overrightarrow{AB}=k\overrightarrow{BC}$
Отметьте верные утверждения знаком «+» неверное утверждение знаком «-«.
| Все точки лежат в одной плоскости | Векторы АВ и ВС коллинеарны | Точки А, В и С не лежат на одной прямой |
|---|---|---|
Сумма векторов
Укажите вектор равный …
Варианты ответа:
1) $\overrightarrow{0}$
2) $\overrightarrow{AC}$
3) $2\overrightarrow{BD}$
Вспомните правила действий над векторами
Длина вектора
АВ = 5 AC = 4 BC = 3 BD = 6 AD = 4
M, N, K середины ребер AC, BC, CD.
Укажите длину векторов:
Обратитесь к материалам урока
Свойства векторов
Даны векторы $\overrightarrow{MK}-\overrightarrow{AK} -\overrightarrow{MN}$ и $\overrightarrow{DC}-\overrightarrow{DA}-\overrightarrow{NC}$.
Являются ли векторы
1) противоположными__
2) равными__
3) сонаправленными__
Ответьте на вопросы вариантами 1, если да и 2, если нет
Обратитесь к материалам урока
Вектор в пространстве
АВСА1В1С1 — правильная призма. F и K середины ребер A1B1 и B1C1
Какое утверждение неверное?
Обратитесь к материалам урока
$\overrightarrow{KF}=\frac{1}{2}\overrightarrow{AC}$
$\mid\overrightarrow{AF}\mid=\mid\overrightarrow{BK}\mid$
$\overrightarrow{AF}=\overrightarrow{BK}$
Векторы в кубе
Ответьте на вопросы
По рисунку
Векторы в кубе
Укажите векторы.
Варианты ответа:
1) B1D1
2) D1A
3) DC1
4) B1C
Сбросить ответы Сохранить и перейти к следующему
а) двух; б) I рёх; в) четырех векторов, заданных вершинами этого многоугольника.
О ЛГЛГ к ВС + ВС ВС(к + \) д nr r>f~l
Значит, MN = = ~—-. Отсюда следует, что М/v и В С
2
сонаправлены, а значит, и коллинеарны.
этап (перевод полученного ответа с векторного языка на геометрический).
Если MN и ВС коллинеарны, то MN \\ВС, а так kzlkAD || #С, то
MN || ADvl
MN= AD+ ПС .
2
При решении данной задачи были задействованы следующие умения:
переводить геометрические термины на векторный язык и наоборот;
выполнять операции над векторами;
представлять вектор в виде произведения вектора на число;
выполнять преобразования векторных равенств.
Эти умения и их совокупности должны формироваться с помощью специальных упражнений. Группы таких упражнений на формирование каждого действия приведены в учебном пособии Г. И. Саранцева «Методика преподана и ия геометрии в девятилетней школе» (Саранск, 1992).
Приведем примеры упражнений из каждой группы.
I.
Упражнения, в которых осуществляется
перевод геометрических терминов на
язык векторов и наоборот.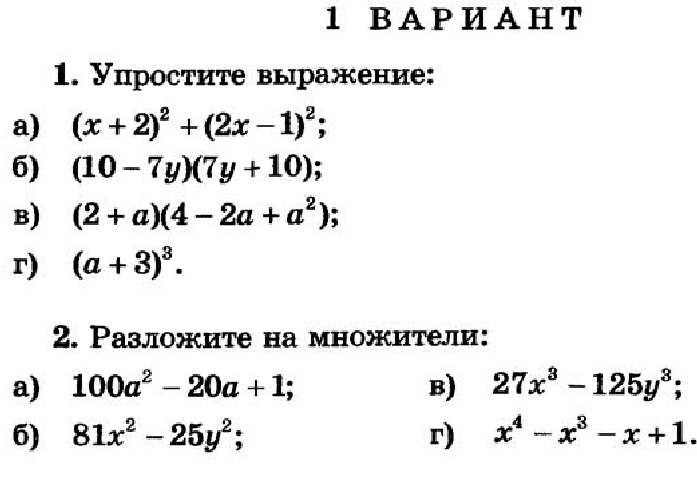
Отрезки АВ и CD параллельны. Напишите это соотношение в векторной форме.
Точка С принадлежит отрезку АВ, причем АС : СВ — т:п. Что означает по на векторном языке?
Известно, что CD = а АВ. Каково геометрическое толкование этого равенства.
Известно, что АВ + ВС = О. Как расположены точки А, В, С?
IL Упражнения на операции с векторами.
Дан вектор АВ . Постройте векторы 2 АВ; АВ .
ABCD — параллелограмм, О-AC nBD. Изобразите векторы: а) АО + СВ; б) АО — DC; в) OD + АВ; г) AD — ВС.

Упражнение 6 выполняется мысленно, не осуществляя при этом непосредственных построений. Такие упражнения важны, так как применение векторов в конкретных ситуациях чаще требует именно этого.
///. Упражнения на представление вектора в виде суммы (разности шчшоров, произведения вектора на число).
Представьте вектор ав в виде суммы векторов ас, dc , bd .
_ _ \CL\_
Вектор cDколлинеарен вектору ав и Выразите один век-
231
тор через другой.
IV. Упражнения на переход от соотношения между векторами к соотношению между их длинами и наоборот.
В каком случае | ОА — OB | = | ОА | -1ОВ | ?
Может ли | АВ + ВС | = | АВ — ВС | ?
Векторы ВС, AD, MN коллинеарны.
 (ВС
+ AD).
(ВС
+ AD).V Упражнения на преобразование векторных равенств,
Упростите выражения: а) АВ + MN + ВС + СА + PQ + NM; б) ОР- ЁР+ KD- КА.
Упростите выражение (а + Ъ — с) (а- b + с), если вектор Ь перпендикулярен вектору с .
Четырехугольник abcd — квадрат. Упростите выражение { ав — 3 вс)2,
VI. Упражнения на нахождение длины вектора и величины угла между векторами.
Известно, что с = а + b ,(а9Ь) = 30°, | а | = 5 см, | Ь | = 3 см. Найдите | с |.
Известно, что векторы а + 2Ъ и 5а -4Ъ взаимно перпендикулярны.
 Какой угол
образуют векторы а
я Ъ , если | а | = | Ъ | = 1?
Какой угол
образуют векторы а
я Ъ , если | а | = | Ъ | = 1?
В процессе выполнения этих упражнений вырабатываются критерии использования векторов для доказательства различных зависимостей. Векторы эффективны при доказательстве: а) параллельности прямых и отрезков; б) принадлежности трёх точек одной прямой; в) перпендикулярности прямых и отрезков и т. д.
Для того чтобы учащиеся научились решать задачи векторным методом, необходимо, прежде всего, научить их решать опорные задачи, при решении которых непосредственно используются эвристики, представленные в таблице 15.
Историческая справка
Считается, что вектор как самостоятельный объект появился в 40-е гг. XIX в., хотя действия с отрезками выполнялись и ранее. Так, представление величин отрезками имело место уже в древнегреческой математике. В «Началах» Евклида изложены основы древнегреческого геометрического исчисления.
 Сложение величин сводилось
к сложению отрезков, умножение величин
— к построению прямоугольника на
соответствующих отрезках, деление — к
операции «приложения» геометрических
фигур. Также ненаправленными отрезками
оперировал Декарт. Но уже немецким
ученым Г. Лейбницем была выдвинута идея
построения векторного исчисления,
близкого к современному. В XVI — XVII вв.
Леонардо да Винчи, Галилео Галилей,
Иоганн Кеплер пользовались направленными
отрезками для наглядного представления
сил в физике и астрономии. Так поступал
и Симон Стевин, который, изучая равновесие
тел на наклонной плоскости, дошел до
разложения силы на составляющие
Сложение величин сводилось
к сложению отрезков, умножение величин
— к построению прямоугольника на
соответствующих отрезках, деление — к
операции «приложения» геометрических
фигур. Также ненаправленными отрезками
оперировал Декарт. Но уже немецким
ученым Г. Лейбницем была выдвинута идея
построения векторного исчисления,
близкого к современному. В XVI — XVII вв.
Леонардо да Винчи, Галилео Галилей,
Иоганн Кеплер пользовались направленными
отрезками для наглядного представления
сил в физике и астрономии. Так поступал
и Симон Стевин, который, изучая равновесие
тел на наклонной плоскости, дошел до
разложения силы на составляющие232
и открыл закон параллелограмма сил. Однако в рассматриваемую эпоху в естествознании еще не оформилось четко понятие векторной величины, а идея алгебраических действий с направленными отрезками лишь зарождалась. Развитие настоящего векторного исчисления относится к XIX в.
Г.
 И. Глейзер в работе [5] выделил три
направления развития векторного
исчисления: геометрическое (исчисление
отрезков), физическое (исследование
векторных величин, встречающихся в
естествознании), алгебраическое (расширение
понятия операции при создании современной
алгебры). Развитие первого направления
связано с именем Каспара Весселя
(Норма’ия). Векторная алгебра на
плоскости (двумерное векторное
пространство) построена им почти так
же, как она излагается в современных
учебниках. Отрезки, имеющие любое
направив же, были введены JI. Карно
(Франция, 1803), он же занимался и действиями
с направленными отрезками, позже
его идеи были систематизированы немецким
математиком А. Мебиусом. У Карно
отсутствует систематическое исчисление
направленных отрезков, содержащееся
у Вссселя. Однако главный труд последнего
«Опыт об аналитическом представлении
направит ия и его применениях» не
оказал никакого влияния на развитие
векторного исчисления, так кик на
протяжении целого столетия ученые не
обращали на него внимания, в то время
как пони гис геометрического
количества Карно, под которым он понимал в основном
направленный о I резок, стали употреблять
передовые математики уже в самом начале
XIX в.
И. Глейзер в работе [5] выделил три
направления развития векторного
исчисления: геометрическое (исчисление
отрезков), физическое (исследование
векторных величин, встречающихся в
естествознании), алгебраическое (расширение
понятия операции при создании современной
алгебры). Развитие первого направления
связано с именем Каспара Весселя
(Норма’ия). Векторная алгебра на
плоскости (двумерное векторное
пространство) построена им почти так
же, как она излагается в современных
учебниках. Отрезки, имеющие любое
направив же, были введены JI. Карно
(Франция, 1803), он же занимался и действиями
с направленными отрезками, позже
его идеи были систематизированы немецким
математиком А. Мебиусом. У Карно
отсутствует систематическое исчисление
направленных отрезков, содержащееся
у Вссселя. Однако главный труд последнего
«Опыт об аналитическом представлении
направит ия и его применениях» не
оказал никакого влияния на развитие
векторного исчисления, так кик на
протяжении целого столетия ученые не
обращали на него внимания, в то время
как пони гис геометрического
количества Карно, под которым он понимал в основном
направленный о I резок, стали употреблять
передовые математики уже в самом начале
XIX в. Некоторые вве- асчшыс Карно
термины и символы, в частности обозначение
вектора с помощью черты наверчу ( А
В, С),
сохранились и в наши дни.
Некоторые вве- асчшыс Карно
термины и символы, в частности обозначение
вектора с помощью черты наверчу ( А
В, С),
сохранились и в наши дни.Наиболее значительный вклад в развитие векторного исчисления внес ирландский математик У. Гамильтон в связи с изложением теории комплексных чисел и учения о ква- к-рн ионах (1853). Именно Гамильтон стал применять понятия «вектор», «скаляр» (от латинского skala — лестница; подобно ступенькам лестницы можно упорядочить действительные числа, вводя понятия «больше» и «меньше», но не комплексные числа, не векторы), «скалярное произведение», «векторное произведение». Независимо от Гамильтона к аналогичным результатам пришел и немецкий ученый Г. Грассман. В 1844 г. в работе «Учение о про- 1ИЖСШгости» он впервые излагает учение об «-мерном евклидовом пространстве. Вместо к*рминов «скалярное произведение», «векторное произведение» он использует соответствию «внутреннее» и «внешнее».
 Векторы
Грассман обозначал жирными буквами
латинско- ю алфавита. Принятое сейчас
обозначение вектора г ввел в 1853 г. О. Коши, а единичные иск горы i,j, к в
том же году Гамильтон.
Векторы
Грассман обозначал жирными буквами
латинско- ю алфавита. Принятое сейчас
обозначение вектора г ввел в 1853 г. О. Коши, а единичные иск горы i,j, к в
том же году Гамильтон.Систематически применял векторное исчисление для потребностей естествознания Л ж Максвелл, а современный вид векторному исчислению придали в конце XIX в. американский физик Дж. Гиббс и английский физик О. Хевисайд.
Систематическое изучение векторов и координат в курсе геометрии основной школы началось в последней трети XX в. в учебниках А. Н. Колмогорова. Изложение учебного ма- юриала осуществлялось в них на основе идеи геометрических преобразований, поэтому век- юр «водился как параллельный перенос, координатный метод в основной школе не изучался (миодились только координаты вектора), этот вопрос подробно рассматривался в старшей школе (в учебниках 3. А. Скопеца).

Вопросы и задания
Как трактуется вектор в математике?
Как определяют понятие «равные векторы» авторы школьных учеб- ми кон геометрии? Опишите методику введения понятия равных векторов.
11|ж недите примеры на усвоение этого понятия.
Как познакомить учащихся с понятием координат вектора?
Сформулируйте признак равенства векторов (в разных формах:
233
[РЕШЕНО] Как упростить векторное выражение? ~ Mathematica ~ AnswerBun.com
Mathematica Вопрос задан 22 февраля 2021 г.
Я занимаюсь векторным анализом. Я понял, что следующее выражение не будет упрощено в Mathematica :
Simplify[Dot[x, y] - Dot[y, x]]
Я думаю, причина в том, что x и y могут быть матрицами, поэтому обычно операция не коммутирует.
 Но для вектора должно выполняться коммутационное соотношение. Чего я не знаю, так это как сказать Mathematica считать x и y векторами.
Но для вектора должно выполняться коммутационное соотношение. Чего я не знаю, так это как сказать Mathematica считать x и y векторами.Кроме того, как я могу расширить
Cross[x + y, z]доCross[x, y] + Cross[y, z]? Я пытался использоватьExpandиExpandAll, но ни один из них не работал.Кстати, в Mathematica можно ли определить абстрактный вектор строки/столбца без явного указания количества записей?
упрощение expressionsvector
4 ответа
Вот способ сделать все, о чем вы просили, автоматически, независимо от Версия Mathematica . Подход основан на специальном символе для идентификации, когда мы имеем дело с вектором: вместо использования таких вещей, как
x,yи т. д. для векторов, теперь принято соглашение, что векторы записываются какvec[x],vec[y]и т. д.Для этой цели можно также определить оболочку
OverVector[x], поскольку она отображается как $vec{x}$. Но для этого поста я хочу, чтобы он был простым, и стрелки не будут легко отображаться в исходном коде ниже.
Но для этого поста я хочу, чтобы он был простым, и стрелки не будут легко отображаться в исходном коде ниже.ClearAll[scalarProduct, vec]; SetAttributes[scalarProduct, {Беспорядковый}] vec /: Dot[vec[x_], vec[y_]] := scalarProduct[vec[x], vec[y]] vec /: Cross[vec[x_], HoldPattern[Plus[y__]]] := Map[Cross[vec[x], #] &, Plus[y]] vec /: Cross[HoldPattern[Plus[y__]], vec[x_]] := Map[Cross[#, vec[x]] &, Plus[y]] scalarProduct /: MakeBoxes[scalarProduct[x_, y_], _] := RowBox[{ToBoxes[x], ".", ToBoxes[y]}] век[х].век[у] (* ==> vec[x].vec[y] *) vec[x].vec[y] == vec[y].vec[x] (* ==> Верно *) Крест[vec[x], vec[a] + vec[b]] (* ==> vec[x][Cross]vec[a] + vec[x][Cross]vec[b] *) Крест[vec[a] + vec[b], vec[x]] (* ==> vec[a][Cross]vec[x] + vec[b][Cross]vec[x] *)Для произведения
Dotя определил поведениеvecтаким образом, что оно оценивается как новая функцияscalarProduct, единственным алгебраическим свойством которой является то, что этоБеспорядок, как вы и ожидали для скалярного произведения векторов. Конечно, это верно только для евклидовых скалярных произведений, поэтому здесь это предположение неявно. Для получения дополнительной информации о том, как работает это определение, см.
Конечно, это верно только для евклидовых скалярных произведений, поэтому здесь это предположение неявно. Для получения дополнительной информации о том, как работает это определение, см. TagSetDelayed.Кроме того,
скалярное произведениеполучает настраиваемый формат отображения, определяя, что он должен снова отображаться, как если бы он был точечным произведением, когда он появляется в функции низкоуровневого форматированияMakeBoxes.Для распределительного свойства перекрестного произведения я придаю
vecдополнительное свойство, заключающееся в том, что когда оно появляется вCrossвместе с выражением headPlus, сумма расширяется. Здесь определенияTagSetDelayedвыполняются для обоих заказов и содержатHoldPattern, чтобы предотвратить слишком раннюю оценкуPlusв определении.Теперь вы можете вернуться с еще многими пожеланиями: например, как насчет мультипликативных скаляров в скалярном или перекрестном произведении, и как насчет матриц.
 Тем не менее, это широкое поле, которое открывает банку червей, поэтому я бы сказал, просто реализуйте минимум функций, которые вы можете использовать символически, а затем приступайте к конкретной рабочей основе, чтобы вместо этого вы могли писать векторы как списки.
Тем не менее, это широкое поле, которое открывает банку червей, поэтому я бы сказал, просто реализуйте минимум функций, которые вы можете использовать символически, а затем приступайте к конкретной рабочей основе, чтобы вместо этого вы могли писать векторы как списки.Другим подходом может быть определение нового символа для пользовательского скалярного произведения. Это сделано в этом вопросе.
Использование
OverVectorКак упоминалось выше, вы можете заменить
vecнаOvervectorвезде в приведенном выше исходном коде, чтобы получить результат с лучшим форматированием. Предполагая, что вы сделали это (я не буду повторять определения с этим изменением), вот несколько примеров:Чтобы ввести эти векторные выражения, обратитесь к вспомогательной палитре Basic Math. Перекрестное произведение может быть введено как Esc
крестEsc .Еще одна вещь, которую вы просили, это использовать антисимметрию векторного произведения в упрощениях.
 Это на самом деле уже сделано, если вы вызовыте
Это на самом деле уже сделано, если вы вызовыте FullSimplify:Правильный ответ от Jens 22 февраля 2021
Если у вас Mathematica , вы можете использовать
векторовиTensorreduce:00099999999999999999 и
. (x | y) [Элемент] Vectors[n], TensorReduce[Dot[x, y] - Dot[y, x]]] (* 0 *) TensorReduce[Dot[x, y] - Dot[y, x], предположения -> (x | y) [элемент] Vectors[n]] (* 0 *) TensorReduce [Cross [x + y, z], предположения -> (x | y | z) [элемент] векторы [n]] (* x[Крест]z + y[Крест]z *) Distribute[Cross[x + y, z]] (* это должно работать во всех предыдущих версиях *) (* x[Крест]z + y[Крест]z *)Ответил kglr 22 февраля 2021 г.
Еще один способ добиться этого, хотя, возможно, и не самый лучший (поскольку это может иметь непредвиденные последствия), — использовать
SetAttributes[Dot, Orderless];
Это заставит коммутировать все точечные произведения (даже матрицы).
 Однако, если вы работаете только с векторами, то это, безусловно, самый чистый способ.
Однако, если вы работаете только с векторами, то это, безусловно, самый чистый способ.Ответ Akoben 22 февраля 2021 г.
$Предположения = (x | y) ∈ Vectors[d, Complexes] Dot[x, y] - Dot[y, x] // TensorExpand
Ответил cvgmt 22 февраля 2021 г.
Добавьте свои ответы!
ИмяЭлектронная почтаДобавьте свой ответПохожие вопросы
Бакуловирусные векторы экспрессии для клеток насекомых и млекопитающих
Сохранить цитату в файл
Формат: Резюме (текст)PubMedPMIDAbstract (текст)CSV
Добавить в коллекции
- Создать новую коллекцию
- Добавить в существующую коллекцию
Назовите свою коллекцию:
Имя должно содержать менее 100 символов
Выберите коллекцию:
Невозможно загрузить вашу коллекцию из-за ошибки
Повторите попыткуДобавить в мою библиографию
- Моя библиография
Невозможно загрузить делегатов из-за ошибки
Пожалуйста, попробуйте еще разВаш сохраненный поиск
Название сохраненного поиска:
Условия поиска:
Тестовые условия поиска
Эл.
 адрес:
(изменить)
адрес:
(изменить)Который день? Первое воскресеньеПервый понедельникПервый вторникПервая средаПервый четвергПервая пятницаПервая субботаПервый деньПервый будний день
Который день? воскресеньепонедельниквторниксредачетвергпятницасуббота
Формат отчета: SummarySummary (text)AbstractAbstract (text)PubMed
Отправить не более: 1 шт. 5 шт. 10 шт. 20 шт. 50 шт. 100 шт. 200 шт.
Отправить, даже если нет новых результатов
Необязательный текст в электронном письме:
Создайте файл для внешнего программного обеспечения для управления цитированием
Обзор
. 2007 г.; 8 (10): 1126-31.
дои: 10.2174/138945007782151351.

Дж. Патрик Кондри 1 , Томас А. Кост
принадлежность
- 1 Отдел биологических реагентов и разработки тестов, GlaxoSmithKline Molecular Discovery Research, 5 Moore Drive, P. O. Box 13398, Research Triangle Park, Северная Каролина 27709, США. [email protected]
- PMID: 17979672
- DOI: 10.2174/138945007782151351
Обзор
Дж. Патрик Кондри и др. Curr Цели наркотиков. 2007 9 октября0004
. 2007 г.; 8 (10): 1126-31.

дои: 10.2174/138945007782151351.
Авторы
Дж. Патрик Кондри 1 , Томас А. Кост
принадлежность
- 1 Отдел биологических реагентов и разработки тестов, GlaxoSmithKline Molecular Discovery Research, 5 Moore Drive, P. O. Box 13398, Research Triangle Park, Северная Каролина 27709, США. [email protected]
- PMID: 17979672
- DOI: 10.2174/138945007782151351
Абстрактный
Функциональная экспрессия рекомбинантных белков стала рутинным, но важным инструментом в современной молекулярной биологии.
 С момента их появления использование бакуловирусных векторов для получения белков для очистки стало одной из наиболее широко используемых систем доставки вирусных генов, поскольку полученные уровни экспрессии трудно сопоставить с любой другой эукариотической системой экспрессии. Обширная инженерия для упрощения и ускорения процесса создания рекомбинантного вируса сделала эту систему доступной практически для любой современной биологической лаборатории. Полезность бакуловирусов расширилась с открытием того, что соответствующим образом модифицированный вирус может опосредовать экспрессию генов в самых разных клеточных линиях млекопитающих и, таким образом, может функционировать в качестве гибкого инструмента разработки клеточных анализов. Широкий спектр применений и потенциал для коммерциализации продуктов требуют рассмотрения ряда аспектов системы.
С момента их появления использование бакуловирусных векторов для получения белков для очистки стало одной из наиболее широко используемых систем доставки вирусных генов, поскольку полученные уровни экспрессии трудно сопоставить с любой другой эукариотической системой экспрессии. Обширная инженерия для упрощения и ускорения процесса создания рекомбинантного вируса сделала эту систему доступной практически для любой современной биологической лаборатории. Полезность бакуловирусов расширилась с открытием того, что соответствующим образом модифицированный вирус может опосредовать экспрессию генов в самых разных клеточных линиях млекопитающих и, таким образом, может функционировать в качестве гибкого инструмента разработки клеточных анализов. Широкий спектр применений и потенциал для коммерциализации продуктов требуют рассмотрения ряда аспектов системы.Похожие статьи
Бакуловирусы как универсальные векторы для экспрессии белков в клетках насекомых и млекопитающих.

Кост Т.А., Кондри Дж.П., Джарвис Д.Л. Кост Т.А. и соавт. Нац биотехнолог. 2005 май; 23(5):567-75. дои: 10.1038/nbt1095. Нац биотехнолог. 2005. PMID: 15877075 Бесплатная статья ЧВК. Обзор.
Бакуловирусные системы экспрессии для производства рекомбинантных белков в клетках насекомых.
Хитчмен Р.Б., Посси Р.Д., Кинг Л.А. Хитчман Р.Б. и др. Недавний Пэт Биотехнолог. 2009;3(1):46-54. дои: 10.2174/187220809787172669. Недавний Пэт Биотехнолог. 2009. PMID: 1
22 Обзор.
Основы экспрессии и применения бакуловирусов.
Кость Т.А., Кемп К.В. Кост Т.А. и соавт. Adv Exp Med Biol. 2016;896:187-97. дои: 10.1007/978-3-319-27216-0_12. Adv Exp Med Biol. 2016. PMID: 27165326 Обзор.

Рекомбинантные бакуловирусы как векторы экспрессии для клеток насекомых и млекопитающих.
Кост Т.А., Кондри Дж.П. Кост Т.А. и соавт. Курр Опин Биотехнолог. 1999 окт; 10 (5): 428-33. doi: 10.1016/s0958-1669(99)00005-1. Курр Опин Биотехнолог. 1999. PMID: 10508635 Обзор.
Эффективная доставка генов в клетки млекопитающих, опосредованная рекомбинантным бакуловирусом, содержащим промотор висповируса ie1, новый челночный промотор между клетками насекомых и клетками млекопитающих.
Гао Х, Ван Ю, Ли Н, Пэн ВП, Сунь Ю, Тонг ГЗ, Цю ХДж. Гао Х и др. Дж Биотехнолог. 2007 г., 31 августа; 131 (2): 138–43. doi: 10.1016/j.jbiotec.2007.06.002. Epub 2007 19 июня. Дж Биотехнолог. 2007. PMID: 17640755
Посмотреть все похожие статьи
Цитируется
Структурная основа воротного механизма натрий-калиевой помпы человека.

Нгуен П.Т., Дейсл С., Файн М., Типпеттс Т.С., Утикава Э., Бай Х.С., Левин Б. Нгуен П.Т. и др. Нац коммун. 2022 8 сентября; 13 (1): 5293. doi: 10.1038/s41467-022-32990-x. Нац коммун. 2022. PMID: 36075933 Бесплатная статья ЧВК.
Применение системы векторов экспрессии бакуловирусов (BEV) для диагностики и лечения COVID-19: обзор.
Азали М.А., Мохамед С., Харун А., Хуссейн Ф.А., Шамсуддин С., Йохан М.Ф. Азали М.А. и соавт. J Genet Eng Biotechnol. 2022 6 июля; 20 (1): 98. doi: 10.1186/s43141-022-00368-7. J Genet Eng Biotechnol. 2022. PMID: 357
Бесплатная статья ЧВК. Обзор.Система векторов экспрессии бакуловирусов/клеток насекомых MultiBac для производства сложных белковых биологических препаратов.

Сари Д., Гупта К., Тимири Говинда Радж Д.Б., Обер А., Дрнцова П., Гарцони Ф., Фицджеральд Д., Бергер И. Сари Д. и др. Adv Exp Med Biol. 2016;896:199-215. дои: 10.1007/978-3-319-27216-0_13. Adv Exp Med Biol. 2016. PMID: 27165327 Бесплатная статья ЧВК. Обзор.
Гены ac53, ac78, ac101 и ac103 являются недавно открытыми основными генами семейства Baculoviridae.
Garavaglia MJ, Miele SA, Iserte JA, Belaich MN, Ghiringhelli PD. Гаравалья М.Дж. и соавт. Дж Вирол. 2012 ноябрь;86(22):12069-79. doi: 10.1128/ОВИ.01873-12. Epub 2012 29 августа. Дж Вирол. 2012. PMID: 22933288 Бесплатная статья ЧВК.
Гетерологическая экспрессия мембранных белков: выбор подходящего хозяина.
Бернода Ф.
 , Фреле-Барран А., Пошон Н., Дементин С., Хивин П., Бутиньи С., Риу Ж.Б., Сальви Д., Сеньерин-Берни Д., Ришо П., Джоярд Дж., Пиньоль Д., Сабати М., Деснос Т., Пебай- Пейрула Э., Даррузе Э., Верне Т., Роллан Н.
Бернода Ф. и соавт.
ПЛОС Один. 2011;6(12):e29191. doi: 10.1371/journal.pone.0029191. Epub 2011 21 декабря.
ПЛОС Один. 2011.
PMID: 22216205
Бесплатная статья ЧВК.
, Фреле-Барран А., Пошон Н., Дементин С., Хивин П., Бутиньи С., Риу Ж.Б., Сальви Д., Сеньерин-Берни Д., Ришо П., Джоярд Дж., Пиньоль Д., Сабати М., Деснос Т., Пебай- Пейрула Э., Даррузе Э., Верне Т., Роллан Н.
Бернода Ф. и соавт.
ПЛОС Один. 2011;6(12):e29191. doi: 10.1371/journal.pone.0029191. Epub 2011 21 декабря.
ПЛОС Один. 2011.
PMID: 22216205
Бесплатная статья ЧВК.
Просмотреть все статьи "Цитируется по"
Типы публикаций
термины MeSH
вещества
Процитируйте
Формат: ААД АПА МДА НЛМ
Отправить по номеру
Упрощенная система для эффективной экспрессии и доставки функциональных зрелых микроРНК в клетки млекопитающих
Abstract
МикроРНК (миРНК) представляют собой некодирующие РНК длиной ~22 нуклеотида, которые участвуют практически во всех аспектах клеточных процессов, поскольку нарушение их регуляции связано со многими патологическими состояниями.
 Зрелые miRNAs (mMIR) генерируются посредством серии жестко регулируемых событий ядерного и цитоплазматического процессинга транскрибируемых первичных, предшественников и mMIR. Эффективные манипуляции с экспрессией микроРНК позволяют нам получить представление о функциях микроРНК и изучить потенциальные терапевтические применения. В настоящее время сверхэкспрессия микроРНК достигается с помощью химически синтезированных миметиков микроРНК или векторов типа «стебель-петля» для экспрессии первичных или исходных микроРНК, которые ограничены низкой эффективностью трансфекции или ограничивающим скорость процессингом микроРНК. Чтобы преодолеть процессинг miRNA, ограничивающий скорость, мы разработали новую стратегию для экспрессии mMIR, которая управляется сходящимися двойными промоторами U6/h2. В качестве проверки концепции мы сконструировали векторы экспрессии mMIR для hsa-miR-223 и hsa-Let-7a-1 и продемонстрировали, что экспрессированные mMIR эффективно подавляют экспрессию гена-мишени, специфически подавляют репортерную активность микроРНК и значительно влияют на клеточная пролиферация, сходная с соответствующими первичными и предшественниками микроРНК.
Зрелые miRNAs (mMIR) генерируются посредством серии жестко регулируемых событий ядерного и цитоплазматического процессинга транскрибируемых первичных, предшественников и mMIR. Эффективные манипуляции с экспрессией микроРНК позволяют нам получить представление о функциях микроРНК и изучить потенциальные терапевтические применения. В настоящее время сверхэкспрессия микроРНК достигается с помощью химически синтезированных миметиков микроРНК или векторов типа «стебель-петля» для экспрессии первичных или исходных микроРНК, которые ограничены низкой эффективностью трансфекции или ограничивающим скорость процессингом микроРНК. Чтобы преодолеть процессинг miRNA, ограничивающий скорость, мы разработали новую стратегию для экспрессии mMIR, которая управляется сходящимися двойными промоторами U6/h2. В качестве проверки концепции мы сконструировали векторы экспрессии mMIR для hsa-miR-223 и hsa-Let-7a-1 и продемонстрировали, что экспрессированные mMIR эффективно подавляют экспрессию гена-мишени, специфически подавляют репортерную активность микроРНК и значительно влияют на клеточная пролиферация, сходная с соответствующими первичными и предшественниками микроРНК. Кроме того, эти векторы экспрессии mMIR можно легко преобразовать в ретровирусные и аденовирусные векторы. В совокупности наша упрощенная система экспрессии mMIR должна стать ценным инструментом для изучения функций микроРНК и/или доставки терапевтических средств на основе микроРНК.
Кроме того, эти векторы экспрессии mMIR можно легко преобразовать в ретровирусные и аденовирусные векторы. В совокупности наша упрощенная система экспрессии mMIR должна стать ценным инструментом для изучения функций микроРНК и/или доставки терапевтических средств на основе микроРНК.Введение
Завершение проекта «Геном человека» и появление высокопроизводительных технологий глубокого секвенирования показали, что, хотя геномы эукариот транскрибируются повсеместно, <2% генома человека транскрибируется в мРНК, кодирующую белок, что оставляет большую часть транскрибируемых некодирующих РНК (нкРНК) генома человека [1,2,3,4,5,6]. По размеру нкРНК делят на две группы: малые нкРНК (<200 нт) и длинные нкРНК или днРНК (>200 нт) [7, 8]. Хотя биологические функции нкРНК еще предстоит полностью понять, все больше данных свидетельствует о том, что нкРНК играют важную регулирующую роль во многих клеточных процессах [5, 7, 8, 9].,10,11]. Тем не менее, малые нкРНК, такие как микроРНК и малые интерферирующие РНК (миРНК), привлекли большое внимание с момента их открытия.

МикроРНК (миРНК или миР) представляют собой малые некодирующие РНК длиной ~22 нуклеотида (нт), которые индуцируют молчание генов, направляя белки Argonaut (AGO) к полностью или частично комплементарным сайтам связывания в 3'-нетранслируемой области (UTR) мРНК-мишени [12,13,14,15,16,17,18]. Первая миРНК была обнаружена в 1993 г. у Caenorhabditis elegans 9.0369 в виде короткой РНК, продуцируемой геном lin-4 , который посттранскрипционно репрессирует мРНК lin-14 [19,20,21]. Позднее было обнаружено, что такие малые регуляторные РНК в изобилии представлены в различных типах животных и впоследствии были названы микроРНК [13]. В настоящее время репозиторий miRNA miRBase перечисляет 1917 предшественников miRNAs (pMIR) и 2654 зрелых miRNAs (mMIR) для человека [22], и было подсчитано, что >60% генов, кодирующих белки человека, содержат предсказанные сайты-мишени miRNA [23].
Короткие одноцепочечные miRNAs первоначально транскрибируются как более длинные первичные транскрипты (или называемые pri-miRNAs), содержащие шпильку РНК из 60–120 нуклеотидов, в которой одна из двух цепей включает mMIR [13].
 Содержащие шпильки pri-miRNA последовательно расщепляются двумя ферментами RNase III, Drosha в ядре и Dicer в цитоплазме, с образованием ~70 нт pMIR и 22 нт mMIR соответственно [13]. pMIR транспортируются в цитоплазму с помощью Exportin-5 и далее обрабатываются Dicer с образованием короткой частично двухцепочечной РНК, в которой одна цепь представляет собой mMIR. mMIR модулируют экспрессию генов посттранскрипционно путем несовершенного связывания мРНК-мишеней в ассоциации с AGO-содержащим многобелковым РНК-индуцированным комплексом молчания [13]. AGOs представляют собой большое семейство белков, которые используют одноцепочечные небольшие нуклеиновые кислоты в качестве направляющих для комплементарных последовательностей в РНК или ДНК, предназначенных для сайленсинга [13, 24]. AGO, нагруженный miRNA, формирует нацеливающий модуль miRNA-индуцированного комплекса молчания, что приводит к репрессии трансляции и/или деградации мРНК-мишеней [13, 25]. Тем не менее, недавние данные показали, что этапы процессинга miRNA могут следовать каноническим путям процессинга и/или многим неканоническим путям биогенеза miRNA, которые взаимодействуют с др.
Содержащие шпильки pri-miRNA последовательно расщепляются двумя ферментами RNase III, Drosha в ядре и Dicer в цитоплазме, с образованием ~70 нт pMIR и 22 нт mMIR соответственно [13]. pMIR транспортируются в цитоплазму с помощью Exportin-5 и далее обрабатываются Dicer с образованием короткой частично двухцепочечной РНК, в которой одна цепь представляет собой mMIR. mMIR модулируют экспрессию генов посттранскрипционно путем несовершенного связывания мРНК-мишеней в ассоциации с AGO-содержащим многобелковым РНК-индуцированным комплексом молчания [13]. AGOs представляют собой большое семейство белков, которые используют одноцепочечные небольшие нуклеиновые кислоты в качестве направляющих для комплементарных последовательностей в РНК или ДНК, предназначенных для сайленсинга [13, 24]. AGO, нагруженный miRNA, формирует нацеливающий модуль miRNA-индуцированного комплекса молчания, что приводит к репрессии трансляции и/или деградации мРНК-мишеней [13, 25]. Тем не менее, недавние данные показали, что этапы процессинга miRNA могут следовать каноническим путям процессинга и/или многим неканоническим путям биогенеза miRNA, которые взаимодействуют с др. клеточными путями [17].
клеточными путями [17].Хорошо известно, что микроРНК участвуют практически во всех клеточных процессах и необходимы для развития, дифференцировки клеток и гомеостаза [13]. На самом деле нарушение регуляции функции миРНК связано с заболеваниями человека [12, 26], особенно при раке [13, 27, 28], поскольку миРНК могут функционировать как онкогены (или онкомиР) [29], так и как супрессоры опухолей [30]. , хотя экспрессия miRNA обычно снижена при большинстве видов рака [13, 27, 28, 31]. Таким образом, очень желательно эффективно манипулировать экзогенной экспрессией микроРНК, чтобы получить представление об их биологических функциях и, в некоторых случаях, изучить их потенциальное терапевтическое применение. Подавление или ингибирование функций миРНК обычно может быть достигнуто с помощью анти-миР, антагомиР, АМО (антисмысловых олигонуклеотидов против миРНК), губок миРНК, ловушек миРНК или кольцевых анти-миР, большинство из которых обычно основано на антисмысловых молекулах. для связывания и отделения микроРНК от их естественных мишеней [18, 32, 33, 34].
 С другой стороны, активация или сверхэкспрессия микроРНК обычно может быть достигнута с использованием химически синтезированных миметиков микроРНК, или shRNA-подобных или интронных векторов экспрессии микроРНК для экспрессии первичных микроРНК (priMIR) или pMIR [35,36,37]. Однако эффективность миметиков микроРНК носит временный характер и ограничивается эффективностью трансфекции. Обычно используемая стратегия экспрессии интронной микроРНК будет зависеть от эффективности процессинга эндогенной микроРНК и может вызывать цитотоксичность из-за перенасыщения аппарата РНКи [37, 38]. Таким образом, существует неудовлетворенная потребность в разработке полностью оптимизированных экспрессирующих микроРНК векторов для эффективной экспрессии микроРНК в культивируемых клетках и животных.
С другой стороны, активация или сверхэкспрессия микроРНК обычно может быть достигнута с использованием химически синтезированных миметиков микроРНК, или shRNA-подобных или интронных векторов экспрессии микроРНК для экспрессии первичных микроРНК (priMIR) или pMIR [35,36,37]. Однако эффективность миметиков микроРНК носит временный характер и ограничивается эффективностью трансфекции. Обычно используемая стратегия экспрессии интронной микроРНК будет зависеть от эффективности процессинга эндогенной микроРНК и может вызывать цитотоксичность из-за перенасыщения аппарата РНКи [37, 38]. Таким образом, существует неудовлетворенная потребность в разработке полностью оптимизированных экспрессирующих микроРНК векторов для эффективной экспрессии микроРНК в культивируемых клетках и животных.Чтобы преодолеть механизм процессинга миРНК/миРНК, ограничивающий скорость, мы разработали новую и упрощенную стратегию для экспрессии mMIR, используя конвергентную экспрессию микроРНК, управляемую двойным промотором U6/h2.
 Мы успешно использовали конвергентную систему, управляемую двойным промотором U6/h2, для экспрессии siРНК [39, 40]. Однако асимметричная природа или несовершенная комплементарность последовательностей 5p-miR и 3p-miR данной miRNA требует другого дизайна. Мы преодолели эту проблему, вставив сигналы остановки транскрипции (последовательность TTTTTAAAAA) между последовательностями 5p-миР (в смысловом направлении) и 3p-миР (в антисмысловом направлении), чтобы остановить транскрипцию 5p-миР и 3p-миР соответственно. . В качестве положительных контролей мы также сконструировали управляемую U6 экспрессию pMIR и обычные системы экспрессии priMIR.
Мы успешно использовали конвергентную систему, управляемую двойным промотором U6/h2, для экспрессии siРНК [39, 40]. Однако асимметричная природа или несовершенная комплементарность последовательностей 5p-miR и 3p-miR данной miRNA требует другого дизайна. Мы преодолели эту проблему, вставив сигналы остановки транскрипции (последовательность TTTTTAAAAA) между последовательностями 5p-миР (в смысловом направлении) и 3p-миР (в антисмысловом направлении), чтобы остановить транскрипцию 5p-миР и 3p-миР соответственно. . В качестве положительных контролей мы также сконструировали управляемую U6 экспрессию pMIR и обычные системы экспрессии priMIR.В качестве проверки концепции мы сконструировали векторы экспрессии pMIR и mMIR для широко изучаемых hsa-miR-223 и hsa-let-7a-1. Мы продемонстрировали, что mMIR эффективно ингибируют экспрессию гена-мишени, специфически подавляют активность репортера, полученного из 3'-UTR целевого гена, и эффективно влияют на пролиферацию клеток способом, сходным с таковым соответствующих систем экспрессии priMIR и pMIR в клеточных линиях человека.
 Кроме того, наш вектор экспрессии mMIR был сконструирован на основе ретровирусного переноса и аденовирусных челночных векторов. Таким образом, конечные конструкции экспрессии mMIR можно легко преобразовать в рекомбинантный ретровирус для стабильной экспрессии или рекомбинантный аденовирус для эффективной кратковременной экспрессии in vitro и in vivo. В совокупности наши результаты демонстрируют, что упрощенная система экспрессии mMIR удобна для пользователя и воспроизводимо эффективна, что должно быть ценным ресурсом для изучения функций микроРНК и / или изучения потенциальных применений терапии на основе микроРНК.
Кроме того, наш вектор экспрессии mMIR был сконструирован на основе ретровирусного переноса и аденовирусных челночных векторов. Таким образом, конечные конструкции экспрессии mMIR можно легко преобразовать в рекомбинантный ретровирус для стабильной экспрессии или рекомбинантный аденовирус для эффективной кратковременной экспрессии in vitro и in vivo. В совокупности наши результаты демонстрируют, что упрощенная система экспрессии mMIR удобна для пользователя и воспроизводимо эффективна, что должно быть ценным ресурсом для изучения функций микроРНК и / или изучения потенциальных применений терапии на основе микроРНК.Материалы и методы
Культура клеток и химические вещества
HEK-293 и линия клеток рака толстой кишки человека HCT116 были получены из Американской коллекции типовых культур (Манассас, Вирджиния, США). Клетки поддерживали в среде DMEM, содержащей 10% фетальной бычьей сыворотки, 100 мкг стрептомицина и 100 единиц пенициллина при 37°C в 5% CO 2 , как сообщалось ранее [41,42,43,44].
 Если не указано иное, все химикаты были приобретены у Sigma-Aldrich (Сент-Луис, Миссури, США) или у Thermo Fisher Scientific (Уолтем, Массачусетс, США).
Если не указано иное, все химикаты были приобретены у Sigma-Aldrich (Сент-Луис, Миссури, США) или у Thermo Fisher Scientific (Уолтем, Массачусетс, США).Конструирование трех типов векторов экспрессии для hsa-miR-223 (MIR223) и hsa-let-7a-1 (MIRLET7A1)
Как показано на рис. изготовили аденовирусный челночный вектор pAdTrace-TOX [45,46,47], который содержит кассету экспрессии, управляемую промотором CMV, и SV40 Pa. Фрагменты геномной ДНК, содержащие первичные hsa-miR-223 (MIR223) и hsa-let-7a-1 ( MIRLET7A1) амплифицировали с помощью ПЦР из геномной ДНК HEK-293 и затем клонировали в вектор pAdTrace-OK, в результате чего были получены векторы экспрессии priMIR223 и priMIRLET7A1 соответственно.
Рис. 1Схематическое изображение трех систем экспрессии микроРНК, сравниваемых в этом исследовании. a Схематическое изображение трех систем экспрессии и возможных режимов их обработки и действия. Обычная первичная система экспрессии miR (priMIR) состоит из клонирования геномного фрагмента длиной 200–500 п.
 н., окружающего единицу транскрипта miR под промотором CMV ( a ). Система экспрессии предшественника miR (pMIR) состоит из управляемой U6 экспрессии последовательности pre-miR, за которой следует строка UUUUU (или TTTTT на диаграмме) в качестве сигнала терминации транскрипции (9).0368 б ). Система экспрессии зрелой miR (mMIR) состоит из конвергентных промоторов U6 и h2, управляемых экспрессией зрелых miR-5p и miR-3p в противоположных направлениях, соответственно, с соответствующим сигналом терминации транскрипции (TTTTT или UUUUU), разделяющим U6. и единиц экспрессии h2. b Два репрезентативных миР, выбранных для исследования проверки принципа действия. Схематические геномные фрагменты и подробные последовательности miR показаны для трех протестированных конструкций экспрессии hsa-miR-223 (MIR223) (9).0368 a ) и hsa-miR-let-7a-1 (MIRLET7A1) ( b ). миР, миРНК или микроРНК; CMV, промотор цитомегаловируса; U6, промотор U6 человека; h2, человеческий промотор h2; PA, сигнал полиаденилирования для терминации транскрипции
н., окружающего единицу транскрипта miR под промотором CMV ( a ). Система экспрессии предшественника miR (pMIR) состоит из управляемой U6 экспрессии последовательности pre-miR, за которой следует строка UUUUU (или TTTTT на диаграмме) в качестве сигнала терминации транскрипции (9).0368 б ). Система экспрессии зрелой miR (mMIR) состоит из конвергентных промоторов U6 и h2, управляемых экспрессией зрелых miR-5p и miR-3p в противоположных направлениях, соответственно, с соответствующим сигналом терминации транскрипции (TTTTT или UUUUU), разделяющим U6. и единиц экспрессии h2. b Два репрезентативных миР, выбранных для исследования проверки принципа действия. Схематические геномные фрагменты и подробные последовательности miR показаны для трех протестированных конструкций экспрессии hsa-miR-223 (MIR223) (9).0368 a ) и hsa-miR-let-7a-1 (MIRLET7A1) ( b ). миР, миРНК или микроРНК; CMV, промотор цитомегаловируса; U6, промотор U6 человека; h2, человеческий промотор h2; PA, сигнал полиаденилирования для терминации транскрипцииИзображение в натуральную величину
Для экспрессии миР-предшественников hsa-miR-223 (pMIR223) и hsa-let-7a-1 (pMIRLET7A1) мы сначала сконструировали ретровирусную pSEB-pmiR и аденовирусный челнок Векторы pAdTrace-pmiR на основе нашей ранее охарактеризованной системы pSOS [39] через систему сборки Gibson (New England Biolabs или NEB, Ипсвич, Массачусетс), как сообщалось [40] (дополнительная рис.
 1a, b). Эти векторы содержат промотор U6, за которым следует Mlu 9.0368 I и Hind III сайтов клонирования. Впоследствии мы клонировали олигокассеты, содержащие последовательности pmiR для hsa-miR-223 и hsa-let-7a-1, с последующим сигналом терминации транскрипции TTTTT, в сайты клонирования Mlu I и Hind III , в результате чего была получена pMIR223. и pMIRLET7A1.
1a, b). Эти векторы содержат промотор U6, за которым следует Mlu 9.0368 I и Hind III сайтов клонирования. Впоследствии мы клонировали олигокассеты, содержащие последовательности pmiR для hsa-miR-223 и hsa-let-7a-1, с последующим сигналом терминации транскрипции TTTTT, в сайты клонирования Mlu I и Hind III , в результате чего была получена pMIR223. и pMIRLET7A1.Для одновременной экспрессии miR-5p и miR-3p mMIR в одном векторе мы сконструировали ретровирусный вектор pSEB-miR и аденовирусный шаттл pAdTrace-miR на основе системы pSOS [39] через систему сборки Gibson (NEB) [40] (дополнительный рис. 2a, b). В этих векторах экспрессия зрелых miR-5p и miR-3p управляется конвергентными промоторами U6 и h2 в противоположных направлениях, соответственно, с соответствующими сигналами терминации транскрипции (TTTTT или UUUUU), встроенными между зрелыми miR. Соответственно, олигокассеты, содержащие зрелые последовательности miR-5p и miR-3p hsa-miR-223 (mMIR223) и hsa-let-7a-1 (mMIRLET7A1), были клонированы в Sal I и Hind 9.
 0368 III сайтов векторов pAdTrace-miR и pSEB-miR, в результате чего получаются конструкции mMIR223 и mMIRLET7A1 соответственно. Все клонирующие соединения и векторы, полученные в результате клонирования олигонуклеотидов, были подтверждены секвенированием ДНК. Подробная информация о сообщенных конструкциях и/или сообщенных векторах доступна по запросу.
0368 III сайтов векторов pAdTrace-miR и pSEB-miR, в результате чего получаются конструкции mMIR223 и mMIRLET7A1 соответственно. Все клонирующие соединения и векторы, полученные в результате клонирования олигонуклеотидов, были подтверждены секвенированием ДНК. Подробная информация о сообщенных конструкциях и/или сообщенных векторах доступна по запросу.Трансфекция клеток
В отчетных исследованиях свежепосеянные субконфлюэнтные клетки трансфицировали с использованием реагента для трансфекции Transporter 5™ на основе линейного полиэтиленимина (PEI) (Polysciences, Inc., Уоррингтон, Пенсильвания) в соответствии с инструкциями производителя. В указанные моменты времени трансфицированные клетки собирали для различных анализов, описанных ниже.
Выделение общей РНК и количественная ПЦР в режиме реального времени (TqPCR)
В конечном итоге трансфицированные клетки подвергали выделению общей РНК с использованием реагента NucleoZOL (Takara Bio USA, Mountain View, CA) в соответствии с инструкцией производителя.
 Для количественного ПЦР-анализа транскриптов мРНК тотальную РНК использовали для обратной транскрипции с гексамером и M-MuLV (NEB). Продукты кДНК разводили в качестве матриц для количественной ПЦР. Праймеры для кПЦР были разработаны по программе Primer3 Plus [48]. Для оценки уровней экспрессии miR, опосредованных тремя системами экспрессии, реакции обратной транскрипции проводили с использованием специфичных для miR обратных праймеров, комплементарных шести 3'-концевым нуклеотидам зрелой miR-5p и/или miR-3p, предшествовала искусственная последовательность ствол-петля из 44 нуклеотидов. Количественный анализ ПЦР в реальном времени на основе SYBR green был выполнен в соответствии с нашим ранее оптимизированным протоколом TqPCR [49].]. Реакции КПЦР проводили в трех повторностях. Все значения экспрессии были нормализованы к экспрессии эталонного гена GAPDH с использованием метода 2 –ΔΔCt [50, 51, 52, 53]. Последовательности праймеров для кПЦР перечислены в дополнительной таблице 1.
Для количественного ПЦР-анализа транскриптов мРНК тотальную РНК использовали для обратной транскрипции с гексамером и M-MuLV (NEB). Продукты кДНК разводили в качестве матриц для количественной ПЦР. Праймеры для кПЦР были разработаны по программе Primer3 Plus [48]. Для оценки уровней экспрессии miR, опосредованных тремя системами экспрессии, реакции обратной транскрипции проводили с использованием специфичных для miR обратных праймеров, комплементарных шести 3'-концевым нуклеотидам зрелой miR-5p и/или miR-3p, предшествовала искусственная последовательность ствол-петля из 44 нуклеотидов. Количественный анализ ПЦР в реальном времени на основе SYBR green был выполнен в соответствии с нашим ранее оптимизированным протоколом TqPCR [49].]. Реакции КПЦР проводили в трех повторностях. Все значения экспрессии были нормализованы к экспрессии эталонного гена GAPDH с использованием метода 2 –ΔΔCt [50, 51, 52, 53]. Последовательности праймеров для кПЦР перечислены в дополнительной таблице 1.
Конструирование репортеров miR-223 и let-7a-1 Gaussia luciferase (GLuc) основе нашего недавно охарактеризованного репортерного вектора pNRGLuc, которые экспрессируют люциферазу Gaussia (GLuc) с множественным клонирующим линкером на 3'-конце кодирующей области GLuc [54, 55]. Как человек
ARRB1 и LIN28B являются хорошо известными мишенями для miR-223 и let-7a-1, которые содержат сайты связывания miR-223 и let-7a-1 в своих 3'-UTR, соответственно, мы ПЦР амплифицировали 3 '-нетранслированные последовательности человеческих ARRB1 (или BUTR) и LIN28B и субколонировали их в вектор pNRGLuc, в результате чего были получены pNRGLuc-BUTR (или GLuc-BUTR) и pNRGLuc-LIN28B (или GLuc-LIN28B) соответственно. Для контрольных репортеров мутации вводили в сайты связывания miR и получали мутацию pNRGLuc-BUTR (или мутацию GLuc-BUTR) и мутацию pNRGLuc-LIN28B (или мутацию GLuc-LIN28B). Все последовательности, амплифицированные с помощью ПЦР, были подтверждены секвенированием ДНК.
Репортерный анализ люциферазы Gaussia (GLuc)
Репортерный анализ GLuc проводили, как описано [56,57,58]. Вкратце, экспоненциально растущие клетки HEK-293 и HCT116 высевали в 12-луночные планшеты для культивирования клеток и коинфицировали различными комбинациями векторов экспрессии miR и/или репортерных плазмид GLuc. Через 72 часа после трансфекции среду для культивирования клеток подвергали анализу активности GLuc с использованием набора для анализа GLuc BioLux (NEB). Каждое условие анализа было выполнено в трех повторностях.
Анализ пролиферации клеток WST-1
Анализ пролиферации клеток WST-1 проводили, как описано [59,60,61,62]. Экспериментально экспоненциально растущие клетки высевали в чашки для культивирования клеток диаметром 60 мм и трансфицировали экспрессионными плазмидами miR или контрольным вектором. Через 16 ч после трансфекции трансфицированные клетки повторно высевали в 96-луночные планшеты для культивирования клеток при 30% слиянии. В незасеянные лунки добавляли культуральную среду и использовали в качестве фонового контроля.
 В указанные моменты времени в каждую лунку добавляли предварительно смешанный WST-1 (Takara Bio USA) и инкубировали при 37 °С в течение 2 часов. Планшеты подвергали считыванию микротитрационных планшетов для получения показаний поглощения при 450 нм. Каждое условие анализа было выполнено в трех повторностях.
В указанные моменты времени в каждую лунку добавляли предварительно смешанный WST-1 (Takara Bio USA) и инкубировали при 37 °С в течение 2 часов. Планшеты подвергали считыванию микротитрационных планшетов для получения показаний поглощения при 450 нм. Каждое условие анализа было выполнено в трех повторностях.Анализ окрашивания кристаллическим фиолетовым
Анализ жизнеспособности клеток кристаллическим фиолетовым проводили, как описано [41, 63, 64, 65]. Вкратце, субконфлюэнтные клетки высевали в чашки для культивирования клеток диаметром 35 мм и трансфицировали плазмидами экспрессии miR или векторным контролем. Через 3 дня после трансфекции клетки окрашивали кристаллическим фиолетовым. Были записаны макрографические изображения окрашенных чашек. Каждое условие выполнялось трижды.
Анализ клеточного цикла
Анализ клеточного цикла проводили, как описано ранее [57, 66, 67]. Экспоненциально растущий HEK-293 и клетки HCT116 высевали в чашки диаметром 60 мм и трансфицировали экспрессионными плазмидами let-7a-1 или векторным контролем.
 Через 48 часов после трансфекции клетки собирали и окрашивали Magic Solution (содержащим 0,05% NP-40, 4% формальдегида, 0,01 мкг/мл Hoechst 33258 в PBS) в течение 30 минут [68]. Окрашенные клетки подвергали анализу методом проточной цитометрии с использованием BD FACSCalibur-HTS. Данные проточной цитометрии количественно анализировали с помощью программного обеспечения FlowJo. Каждое условие анализа выполняли в трех экземплярах.
Через 48 часов после трансфекции клетки собирали и окрашивали Magic Solution (содержащим 0,05% NP-40, 4% формальдегида, 0,01 мкг/мл Hoechst 33258 в PBS) в течение 30 минут [68]. Окрашенные клетки подвергали анализу методом проточной цитометрии с использованием BD FACSCalibur-HTS. Данные проточной цитометрии количественно анализировали с помощью программного обеспечения FlowJo. Каждое условие анализа выполняли в трех экземплярах.Статистический анализ
Количественные анализы проводились в трех экземплярах и/или повторялись в трех независимых партиях. Данные выражали как среднее ± стандартное отклонение. Для анализа статистической значимости использовали однофакторный дисперсионный анализ. Значение p < 0,05 считалось статистически значимым.
Результаты
Дизайн новой системы экспрессии зрелых микроРНК
Для упрощения экзогенной экспрессии микроРНК мы разработали две системы для экспрессии pMIR и mMIR, а затем сравнили их функциональность с обычной системой экспрессии микроРНК, в которой priMIR экспрессия осуществляется с использованием промотора Pol II (например, CMV) для управления фрагментом геномной ДНК размером 200–500 п.
 н., содержащим единицу транскрипта миРНК (рис. 1а, 9).0368 и ). Для экспрессии pMIR мы сконструировали систему экспрессии pMIR, в которой промотор U6 человека используется для управления экспрессией последовательности pre-miR, за которой следует строка из пяти UUUUU (или TTTTT на диаграмме) в качестве сигнала терминации транскрипции (рис. 1а). , б ). Для экспрессии mMIR мы исследовали возможность использования конвергентной системы, управляемой двойным промотором U6/h2, которая успешно использовалась для экспрессии siRNAs [39, 40]. Однако нам пришлось преодолеть асимметричную природу или несовершенную комплементарность последовательностей 5p-миР и 3p-миР данной микроРНК, вставив сигналы остановки транскрипции (цепочка TTTTTAAAAA) между 5p-миР (в смысловом направлении) и 3p. -miR (в антисмысловом направлении) для терминации транскрипции 5p-miR и 3p-miR соответственно. Таким образом, в этой конвергентной системе с двумя промоторами экспрессия mMIR достигается за счет использования конвергентных промоторов U6 и h2 для управления экспрессией зрелых miR-5p и miR-3p в противоположных направлениях, соответственно, с соответствующим сигналом терминации транскрипции (TTTTT).
н., содержащим единицу транскрипта миРНК (рис. 1а, 9).0368 и ). Для экспрессии pMIR мы сконструировали систему экспрессии pMIR, в которой промотор U6 человека используется для управления экспрессией последовательности pre-miR, за которой следует строка из пяти UUUUU (или TTTTT на диаграмме) в качестве сигнала терминации транскрипции (рис. 1а). , б ). Для экспрессии mMIR мы исследовали возможность использования конвергентной системы, управляемой двойным промотором U6/h2, которая успешно использовалась для экспрессии siRNAs [39, 40]. Однако нам пришлось преодолеть асимметричную природу или несовершенную комплементарность последовательностей 5p-миР и 3p-миР данной микроРНК, вставив сигналы остановки транскрипции (цепочка TTTTTAAAAA) между 5p-миР (в смысловом направлении) и 3p. -miR (в антисмысловом направлении) для терминации транскрипции 5p-miR и 3p-miR соответственно. Таким образом, в этой конвергентной системе с двумя промоторами экспрессия mMIR достигается за счет использования конвергентных промоторов U6 и h2 для управления экспрессией зрелых miR-5p и miR-3p в противоположных направлениях, соответственно, с соответствующим сигналом терминации транскрипции (TTTTT). или UUUUU), разделяющих экспрессионные единицы U6 и h2 (рис. 1а, 9).0368 с ). Системы экспрессии pMIR и mMIR были сконструированы в аденовирусном челночном векторе и ретровирусном векторе переноса, поэтому их можно легко использовать для создания рекомбинантных аденовирусов или ретровирусов (дополнительные рисунки 1 и 2).
или UUUUU), разделяющих экспрессионные единицы U6 и h2 (рис. 1а, 9).0368 с ). Системы экспрессии pMIR и mMIR были сконструированы в аденовирусном челночном векторе и ретровирусном векторе переноса, поэтому их можно легко использовать для создания рекомбинантных аденовирусов или ретровирусов (дополнительные рисунки 1 и 2).Чтобы оценить функциональность системы экспрессии mMIR по сравнению с обычными системами экспрессии pri-miR и pMIR, мы провели экспериментальное исследование и сосредоточились на двух хорошо изученных микроРНК, hsa-miR-223 и hsa- лет7а-1. Вкратце, мы сконструировали вектор экспрессии pri-miR-223 путем клонирования ПЦР-амплифицированного фрагмента геномной ДНК человека длиной 200 пар оснований, содержащего miR-223, под контролем промотора CMV, что привело к получению priMIR223. Точно так же pMIR223 и mMIR223 были сконструированы для экспрессии pMIR и зрелой миР-223 соответственно (рис. 1b, 9).0368 и ). Используя тот же набор векторов, мы сконструировали векторы экспрессии для первичного let-7a-1 (priMIRLET7A1), предшественника let-7a-1 (pMIRLET7A1) и зрелого let-7a-1 (mMIRLET7A1) соответственно (рис.
 1b, ). б ).
1b, ). б ).Экзогенная экспрессия зрелой миР-223 может эффективно ингибировать экспрессию гена-мишени в клетках человека
Хорошо известно, что миР-223 функционирует как онкомиР и регулирует многочисленные гены-мишени в пролиферации клеток и других клеточных функциях [34, 69,70,71]. Чтобы проверить, будет ли вектор экспрессии mMIR223 продуцировать функциональную зрелую миР-223 и регулировать экспрессию некоторых генов-мишеней аналогично обычной системе экспрессии pMIR223, мы трансфицировали эти три вектора в две линии клеток человека, HEK-293 и HCT116. Используя анализ qPCR, мы обнаружили, что все три вектора экспрессировали высокие уровни miR-223 в клетках HEK-293 по сравнению с контрольной группой вектора, хотя уровень экспрессии в группе priMIR223, по-видимому, был выше, чем в группах pMIR223 и mMIR223 ( Рис. 2а). Мы выбрали семь хорошо охарактеризованных генов-мишеней miR-223, в том числе ARRB1, CHUK, FBXW7, NFIA, PRDM, RHOB и STMN [34, 70] и проанализировали уровни их экспрессии в трансфицированных клетках HEK-293.
Рис. 2 Наши результаты показывают, что по сравнению с контрольной группой вектора группы pMIR223 и mMIR223 демонстрируют значительно сниженные уровни экспрессии семи протестированных генов-мишеней (рис. 2а). Более того, ингибирование семи протестированных генов-мишеней, опосредованное векторами pMIR223 и mMIR223, было таким же эффективным, как и ингибирование обычного первичного вектора экспрессии miR-223 priMIR223 (рис. 2а).
Наши результаты показывают, что по сравнению с контрольной группой вектора группы pMIR223 и mMIR223 демонстрируют значительно сниженные уровни экспрессии семи протестированных генов-мишеней (рис. 2а). Более того, ингибирование семи протестированных генов-мишеней, опосредованное векторами pMIR223 и mMIR223, было таким же эффективным, как и ингибирование обычного первичного вектора экспрессии miR-223 priMIR223 (рис. 2а).Сравнение ингибирования экспрессии целевого гена, опосредованного тремя системами экспрессии miR-223. Конфлюэнтные клетки HEK-293 ( a ) и HCT116 ( b ) трансфицировали пустым вектором (контроль), mMIR223, pMIR223 или priMIR223. Через 72 часа после трансфекции выделяли тотальную РНК и подвергали анализу TqPCR. Также оценивали экспрессию миР-223, опосредованную тремя системами экспрессии. * p < 0,05 и ** p < 0,01 по сравнению с контрольной группой переносчика
Полноразмерное изображение
Мы провели те же анализы в клетках HCT116.
 Наши результаты показали, что высокие уровни экзогенной экспрессии miR-223 были легко обнаружены в клетках HCT116, хотя вектор priMIR223, по-видимому, снова опосредовал самый высокий уровень экспрессии miR-223 (рис. 2b). Хотя точную причину (причины) различий в уровнях экспрессии еще предстоит понять, это может отражать тот факт, что промотор CMV может быть намного сильнее, чем промоторы U6 и/или h2. Изучив уровни экспрессии выбранных семи генов-мишеней, мы обнаружили, что все три группы, трансфицированные вектором, эффективно ингибировали экспрессию этих генов-мишеней (рис. 2b). Аналогично результатам, полученным в HEK-293, pMIR223- и mMIR223-опосредованное ингибирование экспрессии целевого гена было статистически незначимым по сравнению с priMIR223. В совокупности эти результаты свидетельствуют о том, что наши системы экспрессии pMIR223 и mMIR223 могут продуцировать функциональную miR-223 так же эффективно, как обычно используемая первичная система miR223.
Наши результаты показали, что высокие уровни экзогенной экспрессии miR-223 были легко обнаружены в клетках HCT116, хотя вектор priMIR223, по-видимому, снова опосредовал самый высокий уровень экспрессии miR-223 (рис. 2b). Хотя точную причину (причины) различий в уровнях экспрессии еще предстоит понять, это может отражать тот факт, что промотор CMV может быть намного сильнее, чем промоторы U6 и/или h2. Изучив уровни экспрессии выбранных семи генов-мишеней, мы обнаружили, что все три группы, трансфицированные вектором, эффективно ингибировали экспрессию этих генов-мишеней (рис. 2b). Аналогично результатам, полученным в HEK-293, pMIR223- и mMIR223-опосредованное ингибирование экспрессии целевого гена было статистически незначимым по сравнению с priMIR223. В совокупности эти результаты свидетельствуют о том, что наши системы экспрессии pMIR223 и mMIR223 могут продуцировать функциональную miR-223 так же эффективно, как обычно используемая первичная система miR223.Экзогенная экспрессия зрелой миР-223 специфически ингибирует активность репортера миР-223 в клетках человека п.
 н. миР-223-содержащий сайт связывания фрагмент 3'-UTR человека ARRB1 (BUTR) в линкерные сайты нашего ранее описанного репортерного вектора микроРНК pNRGLuc [34]. Мы также сконструировали контрольный репортер, мутировав сайт связывания миР-223 BUTR (т.е. GLuc-BUTR-Mut) (рис. 3а). Когда репортер GLuc-BUTR или мутантный контрольный репортер GLuc-BUTR Mut котрансфицировали векторами экспрессии miR-223 в клетки HEK-293, мы обнаружили, что все три группы векторов экспрессии miR-223 проявляли значительное ингибирующее действие на активность GLuc по сравнению с с контрольной группой с имитацией переносчика (рис. 3б, 9).0368 и ). Кроме того, ингибирующий эффект был довольно специфичным, поскольку эти векторы не ингибировали значительно активность GLuc контрольного репортера, который имеет мутированный сайт связывания miR-223 (Fig. 3b, a ). Аналогичные результаты были получены в клетках HCT116. Мы обнаружили, что все три группы векторов экспрессии miR-223 проявляли значительное ингибирующее действие на активность GLuc в группе GLuc-BUTR, но не в группе GLuc-BUTR-Mut, по сравнению с контрольной группой ложного вектора (рис.
н. миР-223-содержащий сайт связывания фрагмент 3'-UTR человека ARRB1 (BUTR) в линкерные сайты нашего ранее описанного репортерного вектора микроРНК pNRGLuc [34]. Мы также сконструировали контрольный репортер, мутировав сайт связывания миР-223 BUTR (т.е. GLuc-BUTR-Mut) (рис. 3а). Когда репортер GLuc-BUTR или мутантный контрольный репортер GLuc-BUTR Mut котрансфицировали векторами экспрессии miR-223 в клетки HEK-293, мы обнаружили, что все три группы векторов экспрессии miR-223 проявляли значительное ингибирующее действие на активность GLuc по сравнению с с контрольной группой с имитацией переносчика (рис. 3б, 9).0368 и ). Кроме того, ингибирующий эффект был довольно специфичным, поскольку эти векторы не ингибировали значительно активность GLuc контрольного репортера, который имеет мутированный сайт связывания miR-223 (Fig. 3b, a ). Аналогичные результаты были получены в клетках HCT116. Мы обнаружили, что все три группы векторов экспрессии miR-223 проявляли значительное ингибирующее действие на активность GLuc в группе GLuc-BUTR, но не в группе GLuc-BUTR-Mut, по сравнению с контрольной группой ложного вектора (рис. 3b, 9).0368 б ). Эти результаты также предполагают, что система экспрессии mMIR223 может продуцировать miR-223 столь же эффективно, как и обычные первичные системы экспрессии miR223 и pMIR223. Рис. 3
3b, 9).0368 б ). Эти результаты также предполагают, что система экспрессии mMIR223 может продуцировать miR-223 столь же эффективно, как и обычные первичные системы экспрессии miR223 и pMIR223. Рис. 3 Сравнение ингибирования активности репортера миР-223, опосредованного тремя системами экспрессии миР-223. a Конструирование репортера miR-223 Gaussia luciferase (GLuc) с использованием человеческого β-аррестина 3'-UTR (3'BUTR), который содержит сайт связывания miR-223. Репортер сайта связывания мутанта (3'BUTR-Mut) также был сконструирован в качестве контроля. b Субконфлюэнтные клетки HEK-293 ( a ) и HCT116 ( b ) котрансфицировали различными комбинациями репортерных векторов и экспрессионных плазмид miR-223. Активность GLuc оценивали через 72 часа после трансфекции. Анализы были сделаны в трехкратной повторности. ** p < 0,01 по сравнению с контрольной группой GLuc-BUTR + вектора (имитация)
Изображение в натуральную величину далее мы проанализировали биологические эффекты экзогенно экспрессируемой миР-223 на жизнеспособность и пролиферацию клеток.
Рис. 4 При трансфекции векторов pMIR223 и mMIR223 HEK-293 и клетки HCT116, мы обнаружили, что, основываясь на анализе окрашивания кристаллическим фиолетовым, плотность клеток значительно увеличилась по сравнению с плотностью клеток контрольной группы вектора в обеих клеточных линиях (фиг. 4a, a , b ). В соответствии с результатами, полученными в результате количественного ПЦР-анализа экспрессии гена-мишени и анализа репортера miR-223, увеличение плотности клеток в группах трансфекции pMIR223 и mMIR223 было аналогично наблюдаемому в priMIR223 (рис. 4a).
При трансфекции векторов pMIR223 и mMIR223 HEK-293 и клетки HCT116, мы обнаружили, что, основываясь на анализе окрашивания кристаллическим фиолетовым, плотность клеток значительно увеличилась по сравнению с плотностью клеток контрольной группы вектора в обеих клеточных линиях (фиг. 4a, a , b ). В соответствии с результатами, полученными в результате количественного ПЦР-анализа экспрессии гена-мишени и анализа репортера miR-223, увеличение плотности клеток в группах трансфекции pMIR223 и mMIR223 было аналогично наблюдаемому в priMIR223 (рис. 4a).Сравнение повышенной клеточной пролиферативной активности, опосредованной тремя системами экспрессии миР-223. a Анализ кристаллического фиолетового. Субконфлюэнтные клетки HEK-293 ( a ) и HCT116 ( b ) трансфицировали указанными экспрессионными плазмидами miR-223 или векторным контролем. Клетки фиксировали для окрашивания кристаллическим фиолетовым через 3 дня после трансфекции.
 Анализы были выполнены в трех повторностях, и показаны репрезентативные результаты. b Анализ пролиферации клеток WST-1. Субконфлюэнт HEK-293 ( a ) и HCT116 ( b ) клетки трансфицировали указанными экспрессионными плазмидами miR-223 или векторным контролем. В указанные моменты времени в каждую лунку добавляли субстрат WST-1 и инкубировали в течение 2 часов с последующим измерением поглощения при 450 нм. Анализы были сделаны в трехкратной повторности. * p < 0,05 и ** p < 0,01 по сравнению с контрольной группой переносчиков
Анализы были выполнены в трех повторностях, и показаны репрезентативные результаты. b Анализ пролиферации клеток WST-1. Субконфлюэнт HEK-293 ( a ) и HCT116 ( b ) клетки трансфицировали указанными экспрессионными плазмидами miR-223 или векторным контролем. В указанные моменты времени в каждую лунку добавляли субстрат WST-1 и инкубировали в течение 2 часов с последующим измерением поглощения при 450 нм. Анализы были сделаны в трехкратной повторности. * p < 0,05 и ** p < 0,01 по сравнению с контрольной группой переносчиковИзображение в натуральную величину
Мы также провели более количественный анализ пролиферации клеток WST-1. Когда три вектора экспрессии miR-223, pMIR223, mMIR223 и priMIR223, трансфицировали в HEK-293 и HCT116, мы обнаружили, что скорость пролиферации клеток была значительно увеличена через 72 и 96 часов после трансфекции по сравнению с контрольной группой вектора в обеих клеточных линиях (рис. 4b, a , b ).
 Таким образом, эти результаты в совокупности демонстрируют, что экзогенная экспрессия miR-223, опосредованная mMIR223, может достигать биологических функций, сходных с обычно используемой системой экспрессии priMIR priMIR223 или pMIR223.
Таким образом, эти результаты в совокупности демонстрируют, что экзогенная экспрессия miR-223, опосредованная mMIR223, может достигать биологических функций, сходных с обычно используемой системой экспрессии priMIR priMIR223 или pMIR223.Экзогенная экспрессия зрелого let-7a-1 (mMIRLET7A1) эффективно ингибирует экспрессию целевого гена в клетках человека
Чтобы убедиться в общей применимости описанных векторов экспрессии pMIR и mMIR, мы выбрали для тестирования другую хорошо изученную микроРНК let-7a-1 и сконструированную зрелую (mMIRLET7A1), а также обычный priMIR (priMIRLET7A1) и предшественник ( pMIRLET7A1) экспрессионные векторы (рис. 1b, b ). Мы протестировали три вектора на двух линиях клеток человека, HEK-293 и HCT116 соответственно. Используя анализ qPCR, мы обнаружили, что все три вектора экспрессировали высокие уровни let-7a-1 в клетках HEK-293 по сравнению с контрольной группой вектора (рис. 5a). Экспрессия трех генов-мишеней let-7a-1, LIN28, HMGA2 и C-MYC [72, 73, 74] эффективно ингибировались mMIRLET7A1 на уровне, сравнимом с уровнем priMIRLET7A1 или pMIRLET7A1, по сравнению с контрольной группой вектора (рис.
Рис. 5 5a).
5a).Сравнение ингибирования экспрессии целевого гена, опосредованного тремя системами экспрессии let-7a-1. Конфлюэнтные клетки HEK-293 ( a ) и HCT116 ( b ) трансфицировали пустым вектором (контроль), mMIRLET7A1, pMIR LET7A1 или priMIR LET7A1. Через 72 часа после трансфекции выделяли тотальную РНК и подвергали анализу TqPCR. Также оценивали экспрессию let-7a-1, опосредованную тремя системами экспрессии. * p < 0,05 и ** p < 0,01 по сравнению с контрольной группой вектора
Изображение в натуральную величину
Такие же анализы были проведены в клетках HCT116. Мы обнаружили, что высокие уровни экзогенной экспрессии let-7a-1 были легко обнаружены в клетках HCT116 (рис. 5b). Изучив уровни экспрессии трех тестовых генов-мишеней, мы обнаружили, что все три группы, трансфицированные вектором, эффективно ингибировали экспрессию этих генов-мишеней (рис. 5b). Кроме того, подавление экспрессии генов-мишеней, опосредованное mMIRLET7A1, было статистически незначимым по сравнению с экспрессией priMIRLET7A1 или pMIRLET7A1.
 Таким образом, эти результаты дополнительно предполагают, что система экспрессии mMIRLET7A1 может продуцировать функциональный let-7a-1 так же эффективно, как обычная первичная система экспрессии let-7a-1 или pMIRLET7A1.
Таким образом, эти результаты дополнительно предполагают, что система экспрессии mMIRLET7A1 может продуцировать функциональный let-7a-1 так же эффективно, как обычная первичная система экспрессии let-7a-1 или pMIRLET7A1.Экзогенная экспрессия зрелого let-7a-1 (mMIRLET7A1) специфически ингибирует активность репортера let-7a-1 в клетках человека. 525 bp let-7a-1-сайт связывания, содержащий фрагмент 3'-UTR транскрипта LIN28B
человека в линкерные сайты pNRGLuc [34]. Контрольный репортер также был сконструирован путем мутации сайта связывания let-7a-1 (т.е. GLuc-LIN28B-Mut) (фиг. 3а). Когда репортер GLuc-LIN28B или мутантный контроль GLuc-LIN28B-Mut котрансфицировали векторами экспрессии let-7a-1 в HEK-293, мы обнаружили, что все три вектора экспрессии let-7a-1 проявляли значительное ингибирующее действие на активность GLuc по сравнению с контрольной группой с ложным вектором (фиг. 6b, и ). Кроме того, ингибирующий эффект был специфическим, поскольку эти векторы не ингибировали значительно активность GLuc мутантного контрольного репортера (фиг. 6b, и ). Точно так же в клетках HCT116 мы обнаружили, что три вектора экспрессии let-7a-1 проявляли значительное ингибирующее действие на активность GLuc репортера GLuc-LIN28B, но не в отношении контрольного репортера GLuc-LIN28B-Mut, по сравнению с контрольной группой с ложным вектором. (рис. 6б, б ). Эти данные дополнительно указывают на то, что система экспрессии mMIRLET7A1 может продуцировать функциональный let-7a-1 так же эффективно, как обычная первичная система экспрессии let-7a-1 или pMIRLET7A1. Рис. 6
6b, и ). Точно так же в клетках HCT116 мы обнаружили, что три вектора экспрессии let-7a-1 проявляли значительное ингибирующее действие на активность GLuc репортера GLuc-LIN28B, но не в отношении контрольного репортера GLuc-LIN28B-Mut, по сравнению с контрольной группой с ложным вектором. (рис. 6б, б ). Эти данные дополнительно указывают на то, что система экспрессии mMIRLET7A1 может продуцировать функциональный let-7a-1 так же эффективно, как обычная первичная система экспрессии let-7a-1 или pMIRLET7A1. Рис. 6 Сравнение ингибирования активности репортера let-7a-1, опосредованного тремя системами экспрессии let-7a-1. a Конструирование репортера let-7a-1 GLuc с использованием 3'-UTR LIN28B человека, который содержит сайт связывания let-7a-1. Репортер сайта связывания мутанта (Mut 3'-UTR) также был сконструирован в качестве контроля. b Субконфлюэнтные клетки HEK-293 ( a ) и HCT116 ( b ) котрансфицировали различными комбинациями репортерных векторов и экспрессионных плазмид let-7a-1.
 Активность GLuc оценивали через 72 часа после трансфекции. Анализы были сделаны в трехкратной повторности. ** p < 0,01 по сравнению с контрольной группой GLuc-LIN28B + вектора (имитация)
Активность GLuc оценивали через 72 часа после трансфекции. Анализы были сделаны в трехкратной повторности. ** p < 0,01 по сравнению с контрольной группой GLuc-LIN28B + вектора (имитация)Изображение в полный размер
Экзогенная экспрессия зрелого let-7a-1 (mMIRLET7A1) эффективно ингибирует пролиферацию клеток и развитие клеточного цикла
МикроРНК let-7a-1 функционирует как микроРНК-супрессор опухолей [72,73,74,75]. Здесь мы также проанализировали биологические эффекты экзогенно экспрессированного let-7a-1 на жизнеспособность клеток, пролиферацию клеток и ход клеточного цикла. Когда векторы mMIRLET7A1 трансфицировали в клетки HEK-293 и HCT116, анализ окрашивания кристаллическим фиолетовым показал, что плотность клеток значительно снизилась, аналогично группе трансфекции priMIRLET7A1 или pMIRLET7A1, по сравнению с группой контроля вектора в обеих клеточных линиях (рис. 7а, а , б ).
Рис. 7Сравнение пролиферативной активности клеток, ингибируемых let-7a-1, опосредованной тремя системами экспрессии let-7a-1.
 a Анализ кристаллического фиолетового. Субконфлюэнтные клетки HEK-293 ( a ) и HCT116 ( b ) трансфицировали указанными экспрессионными плазмидами let-7a-1 или векторным контролем. Клетки фиксировали для окрашивания кристаллическим фиолетовым через 3 дня после трансфекции. Анализы были выполнены в трех повторностях, и показаны репрезентативные результаты. b Анализ пролиферации клеток WST-1. Субконфлюэнтные клетки HEK-293 ( a ) и HCT116 ( b ) трансфицировали указанными экспрессионными плазмидами let-7a-1 или векторным контролем. В указанные моменты времени в каждую лунку добавляли субстрат WST-1 и инкубировали в течение 2 часов с последующим измерением поглощения при 450 нм. Анализы были сделаны в трехкратной повторности. * p < 0,05, ** p < 0,01 по сравнению с контрольной группой переносчиков. c Анализ клеточного цикла. Субконфлюэнт HEK-293 ( a , b ) и HCT116 ( c , d ) трансфицировали указанными экспрессионными плазмидами let-7a-1 или векторным контролем.
a Анализ кристаллического фиолетового. Субконфлюэнтные клетки HEK-293 ( a ) и HCT116 ( b ) трансфицировали указанными экспрессионными плазмидами let-7a-1 или векторным контролем. Клетки фиксировали для окрашивания кристаллическим фиолетовым через 3 дня после трансфекции. Анализы были выполнены в трех повторностях, и показаны репрезентативные результаты. b Анализ пролиферации клеток WST-1. Субконфлюэнтные клетки HEK-293 ( a ) и HCT116 ( b ) трансфицировали указанными экспрессионными плазмидами let-7a-1 или векторным контролем. В указанные моменты времени в каждую лунку добавляли субстрат WST-1 и инкубировали в течение 2 часов с последующим измерением поглощения при 450 нм. Анализы были сделаны в трехкратной повторности. * p < 0,05, ** p < 0,01 по сравнению с контрольной группой переносчиков. c Анализ клеточного цикла. Субконфлюэнт HEK-293 ( a , b ) и HCT116 ( c , d ) трансфицировали указанными экспрессионными плазмидами let-7a-1 или векторным контролем. Через 48 часов после трансфекции клетки собирали и подвергали анализу клеточного цикла. Анализы были выполнены в трех повторностях, и показаны репрезентативные результаты ( и , и ). Количественные анализы проводили для определения % количества клеток в различных фазах ( b , d ). * р < 0,05 и ** p < 0,01 по сравнению с контрольной группой вектора
Через 48 часов после трансфекции клетки собирали и подвергали анализу клеточного цикла. Анализы были выполнены в трех повторностях, и показаны репрезентативные результаты ( и , и ). Количественные анализы проводили для определения % количества клеток в различных фазах ( b , d ). * р < 0,05 и ** p < 0,01 по сравнению с контрольной группой вектораИзображение в полный размер
Количественный анализ пролиферации клеток WST-1 также показал, что три вектора экспрессии let-7a-1, pMIRLET7A1, mMIRLET7A1 и priMIRLET7A1, были трансфицированы в клетки HEK-293 и HCT116, мы обнаружили, что скорость пролиферации клеток была значительно снижена через 72 и 96 часов после трансфекции по сравнению с контрольной группой вектора в обеих клеточных линиях (рис. 7b, a 9).0369, б ). В совокупности эти результаты демонстрируют, что экзогенная экспрессия let-7a-1, опосредованная mMIRLET7A1, может достигать биологических функций, сходных с обычно используемой системой экспрессии priMIRLET7A1 или pMIRLET7A1.

Наконец, мы исследовали влияние экзогенно экспрессируемого let-7a-1 на ход клеточного цикла. Было показано, что при трансфекции клеток HEK-293 вектор mMIRLET7A1, аналогичный вектору priMIRLET7A1 или pMIRLET7A1, увеличивает % клеток, представленных в фазе G1, при снижении % клеток в фазе S по сравнению с контрольным вектором (фиг. 7с, а , б ). Было показано, что при трансфекции в клетки HCT116 вектор mMIRLET7A1 вместе с вектором priMIRLET7A1 или pMIRLET7A1 увеличивает % клеток, представленных в фазе G1 (фиг. 7c, c , d ). Интересно, что в отличие от клеток НЕК-293, экспрессия экзогенного let-7a-1 приводила к снижению % клеток в фазах G2/M, в то время как в фазе S существенных изменений не наблюдалось (рис. 7в, ab vs cd). ). В совокупности эти результаты демонстрируют, что вектор mMIRLET7A1 может экспрессировать биологически активную форму миРНК let-7a-1, которая функционально неотличима от формы, экспрессируемой обычной первичной миРНК let-7a-1 или системой экспрессии pMIRLET7A1.

Обсуждение
Чтобы разработать удобный для пользователя подход к эффективной экспрессии функциональных микроРНК, мы разработали упрощенную стратегию экспрессии микроРНК путем использования конвергентных двойных промоторов U6/h2 для управления экспрессией mMIR. Несмотря на то, что конвергентная система U6/h2, управляемая двойным промотором, была успешно использована для экспрессии siRNAs [39, 40], асимметричная природа или несовершенная комплементарность последовательностей 5p-miR и 3p-miR данной miRNA представляет собой техническую проблему. Мы преодолели эту проблему, вставив сигналы остановки транскрипции TTTTTAAAAA между последовательностями 5p-miR (в смысловом направлении) и 3p-miR (в антисмысловом направлении), чтобы прекратить транскрипцию 5p-miR и 3p-miR соответственно.
Сравнивая с обычно используемыми системами экспрессии priMIR и pMIR, мы продемонстрировали, что oncomiR hsa-miR-223, экспрессируемый в зрелой (mMIR223) форме, эффективно ингибирует экспрессию гена-мишени, специфически подавляет репортерную активность miR-223 и стимулирует клетки.
 пролиферацию клеток HEK-293 и HCT116, аналогичным образом, сравнимую с пролиферацией первичной системы экспрессии миР-223 или предшественника миР-223 (pMIR223). Точно так же онкосупрессор hsa-let-7a-1, экспрессируемый в зрелых формах let-7a-1, эффективно ингибировал экспрессию генов-мишеней, репортерную активность, полученную из 3'-UTR LIN28B, а также пролиферацию клеток и развитие клеточного цикла. которые были неотличимы от традиционно выраженного первичного let-7a-1 или предшественника let-7a-1. Примечательно, что наши экспрессионные векторы mMIR были сконструированы на основе ретровирусного переноса и аденовирусных челночных векторов. Таким образом, конечные конструкции экспрессии микроРНК могут быть легко преобразованы в рекомбинантный ретровирус для стабильной экспрессии или рекомбинантный аденовирус для эффективной временной экспрессии in vitro и in vivo. В совокупности наши результаты демонстрируют, что упрощенная система экспрессии mMIR удобна для пользователя и воспроизводимо эффективна, что должно быть ценным ресурсом для изучения функций микроРНК и / или изучения потенциальных применений терапии на основе микроРНК.
пролиферацию клеток HEK-293 и HCT116, аналогичным образом, сравнимую с пролиферацией первичной системы экспрессии миР-223 или предшественника миР-223 (pMIR223). Точно так же онкосупрессор hsa-let-7a-1, экспрессируемый в зрелых формах let-7a-1, эффективно ингибировал экспрессию генов-мишеней, репортерную активность, полученную из 3'-UTR LIN28B, а также пролиферацию клеток и развитие клеточного цикла. которые были неотличимы от традиционно выраженного первичного let-7a-1 или предшественника let-7a-1. Примечательно, что наши экспрессионные векторы mMIR были сконструированы на основе ретровирусного переноса и аденовирусных челночных векторов. Таким образом, конечные конструкции экспрессии микроРНК могут быть легко преобразованы в рекомбинантный ретровирус для стабильной экспрессии или рекомбинантный аденовирус для эффективной временной экспрессии in vitro и in vivo. В совокупности наши результаты демонстрируют, что упрощенная система экспрессии mMIR удобна для пользователя и воспроизводимо эффективна, что должно быть ценным ресурсом для изучения функций микроРНК и / или изучения потенциальных применений терапии на основе микроРНК.
Сверхэкспрессия функциональных микроРНК в течение длительного времени является сложной задачей эффективным и надежным способом. В большинстве случаев сверхэкспрессия микроРНК достигается за счет использования химически синтезированных миметиков микроРНК, которые в основном производятся из коммерческих источников. Хотя этот подход эффективен и широко используется, эффективность миметиков микроРНК носит временный характер и зависит от эффективности трансфекции, которая может сильно различаться в разных клеточных линиях. Кроме того, использование синтезированных миметиков miRNA для исследований на животных in vivo может быть технически сложным и/или профилактически дорогим.
Для экспрессии микроРНК в клетках и, возможно, у животных было использовано несколько стратегий. Одной из обычно используемых систем экспрессии микроРНК является использование промотора Pol II, такого как CMV, SV40 или энхансер CMV/промотор β-актина (CA), или промоторов Pol III для управления экспрессией priMIR, который содержится в 200 Фрагмент геномной ДНК –500 пн [76, 77].
 Были предприняты попытки экспрессировать несколько микроРНК или шРНК-подобных структур «стебель-петля» в одном транскрипте или полицистронном транскрипте [78,79].,80,81]. Преимуществами этой системы являются сильная транскрипционная активность промотора Pol II и легкое включение индуцируемости экспрессии микроРНК. В ходе тщательного изучения экспрессии кшРНК-подобных стволовых-петлевых pri-миРНК, управляемой Pol II и Pol III, Furukawa et al. [77] обнаружили, что при экспрессии конструкции, содержащей геномные последовательности размером 100 п.н. или менее, фланкирующие область, кодирующую микроРНК, промоторы CMV, CMVi и CA были более эффективными, чем промоторы PGK. Однако не гарантируется автоматическая эффективная обработка priMIR. На самом деле было показано, что предшественники miRNA могут не эффективно обрабатываться для образования зрелых форм miRNAs в некоторых типах клеток или при определенных условиях [77]. Тем не менее, управляемая U6 структура «стебель-петля» миРНК приводит к большей разнице между 5'- и 3'-цепями дуплекса миРНК в опосредованных миРНК супрессивных эффектах на экспрессию репортерного гена, чем pri-миРНК, полученная из промотора pol II.
Были предприняты попытки экспрессировать несколько микроРНК или шРНК-подобных структур «стебель-петля» в одном транскрипте или полицистронном транскрипте [78,79].,80,81]. Преимуществами этой системы являются сильная транскрипционная активность промотора Pol II и легкое включение индуцируемости экспрессии микроРНК. В ходе тщательного изучения экспрессии кшРНК-подобных стволовых-петлевых pri-миРНК, управляемой Pol II и Pol III, Furukawa et al. [77] обнаружили, что при экспрессии конструкции, содержащей геномные последовательности размером 100 п.н. или менее, фланкирующие область, кодирующую микроРНК, промоторы CMV, CMVi и CA были более эффективными, чем промоторы PGK. Однако не гарантируется автоматическая эффективная обработка priMIR. На самом деле было показано, что предшественники miRNA могут не эффективно обрабатываться для образования зрелых форм miRNAs в некоторых типах клеток или при определенных условиях [77]. Тем не менее, управляемая U6 структура «стебель-петля» миРНК приводит к большей разнице между 5'- и 3'-цепями дуплекса миРНК в опосредованных миРНК супрессивных эффектах на экспрессию репортерного гена, чем pri-миРНК, полученная из промотора pol II. [77], предполагая, что промотор U6 может быть более подходящим для управления экспрессией priMIR. Наши результаты показали, что экспрессия pri-miRNA, управляемая pMIR U6, является высокоэффективной и функциональной.
[77], предполагая, что промотор U6 может быть более подходящим для управления экспрессией priMIR. Наши результаты показали, что экспрессия pri-miRNA, управляемая pMIR U6, является высокоэффективной и функциональной.В другом широко используемом методе используются системы экспрессии интронных микроРНК [35,36,37]. Эта стратегия возникла в результате открытия интронных миРНК (также называемых «миртрон»), которые образуются в результате процессинга интронов и отличаются от межгенных миРНК потребностью в РНК-полимеразе II и компонентах механизма сплайсинга для их биогенеза [82,83]. ,84]. Такие короткие интронные шпильки miRNAs могут миновать стадию расщепления Drosha и вместо этого процессируются аппаратом сплайсинга и ферментом, расщепляющим лариат, с получением pMIR-подобных шпилек [82,83,84,85]. За прошедшие годы было разработано несколько вариаций такой системы экспрессии интронной микроРНК. Ву и др. [35, 36] сконструировали векторы экспрессии микроРНК и кшРНК, такие как pSM155 и pSM30, путем размещения кассет искусственной экспрессии микроРНК на основе микроРНК внутри синтетических интронов, чтобы воспользоваться преимуществами процессинга микроРНК и механизмов сплайсинга РНК.
 Совсем недавно сообщалось, что мультиплексная платформа экспрессии микроРНК и трансгенов, использующая нативные локусы интронных микроРНК, обеспечивает одновременную репрессию и экспрессию последовательностей, кодирующих белок, что может облегчить применение одновременного молчания генов и корректирующей экспрессии трансгена в некоторых случаях, таких как полигенные терапевтические мишени. гены лекарственной устойчивости, гены вируса и хозяина, участвующие в жизненном цикле вируса, или онкогены и гены-супрессоры опухолей [37]. Однако идентификация естественных последовательностей микроРНК интронов человека может быть сложной, если не непрактичной.
Совсем недавно сообщалось, что мультиплексная платформа экспрессии микроРНК и трансгенов, использующая нативные локусы интронных микроРНК, обеспечивает одновременную репрессию и экспрессию последовательностей, кодирующих белок, что может облегчить применение одновременного молчания генов и корректирующей экспрессии трансгена в некоторых случаях, таких как полигенные терапевтические мишени. гены лекарственной устойчивости, гены вируса и хозяина, участвующие в жизненном цикле вируса, или онкогены и гены-супрессоры опухолей [37]. Однако идентификация естественных последовательностей микроРНК интронов человека может быть сложной, если не непрактичной.Основной проблемой экзогенной сверхэкспрессии priMIR, shRNA-подобных или pMIR является то, что эффективность продукции mMIR зависит от эндогенного процессинга miRNA и может вызывать цитотоксичность из-за перенасыщения аппарата процессинга RNAi [37, 38, 86]. Фактически, Ago2 был идентифицирован как основная детерминанта, ограничивающая скорость как in vitro, так и in vivo эффективности, токсичности и персистенции RNAi [86].
 Было показано, что в исследовании на мышах коэкспрессия Ago-2/Xpo-5 на основе вектора усиливала U6-управляемое молчание кшРНК экзогенных и эндогенных печеночных мишеней, снижала гепатотоксичность и продлевала стабильность РНК-интерференции более чем на 3 месяца [86]. . Было показано, что избыточная экспрессия Ago2 значительно повышает эффективность подавления мРНК в клеточной культуре до десяти раз, что сопровождается уменьшением побочных эффектов [87].
Было показано, что в исследовании на мышах коэкспрессия Ago-2/Xpo-5 на основе вектора усиливала U6-управляемое молчание кшРНК экзогенных и эндогенных печеночных мишеней, снижала гепатотоксичность и продлевала стабильность РНК-интерференции более чем на 3 месяца [86]. . Было показано, что избыточная экспрессия Ago2 значительно повышает эффективность подавления мРНК в клеточной культуре до десяти раз, что сопровождается уменьшением побочных эффектов [87].Вместе мы разработали новую и упрощенную стратегию для эффективной экспрессии mMIR. Эта система теоретически должна обходить большую часть механизмов процессинга siRNA/miRNA, включая участие Drosha, Expotin-5 и Dicer1, хотя она все еще требует, чтобы белки Ago выполняли функцию молчания генов. Таким образом, наша система экспрессии mMIR легко настраивается и должна в целом улучшить применение экспериментов с микроРНК in vitro и in vivo.
Каталожные номера
- ">
Маттик Дж.С., Макунин И.В. Некодирующая РНК. Хум Мол Жене. 2006;1:R17–29.15 Спец. №
Артикул КАС Google ученый
Гуттман М., Амит И., Гарбер М., Френч К., Лин М.Ф., Фельдсер Д. и др. Сигнатура хроматина обнаруживает более тысячи высококонсервативных больших некодирующих РНК у млекопитающих. Природа. 2009; 458: 223–7.
КАС пабмед ПабМед Центральный Статья Google ученый
Карнинчи П., Касукава Т., Катаяма С., Гоф Дж., Фрит М.С., Маэда Н. и др. Транскрипционный ландшафт генома млекопитающих. Наука. 2005; 309:1559–63.
КАС пабмед Статья Google ученый
Джебали С., Дэвис К.А., Меркель А., Добин А., Лассманн Т., Мортазави А. и др. Ландшафт транскрипции в клетках человека. Природа. 2012; 489:101–8.
КАС пабмед ПабМед Центральный Статья Google ученый
">St Laurent G, Wahlestedt C, Kapranov P. Ландшафт классификации длинных некодирующих РНК. Тенденции Жене. 2015; 31: 239–51.
Артикул КАС Google ученый
Чех Т.Р., Стейтц Ю.А. Революция некодирующих РНК отбрасывает старые правила для создания новых. Клетка. 2014; 157:77–94.
КАС пабмед Статья Google ученый
Сабин Л.Р., Делас М.Дж., Хэннон Г.Дж. Догма рухнула: множество влияний РНК на геном. Мол Ячейка. 2013;49:783–94.
КАС пабмед Статья Google ученый
Brosnan CA, Voinnet O.
 Длинные и короткие некодирующие РНК. Curr Opin Cell Biol. 2009 г.;21:416–25.
Длинные и короткие некодирующие РНК. Curr Opin Cell Biol. 2009 г.;21:416–25.КАС пабмед Статья Google ученый
Жакье А. Сложный эукариотический транскриптом: неожиданная всеобъемлющая транскрипция и новые малые РНК. Нат Рев Жене. 2009; 10: 833–44.
КАС пабмед Статья Google ученый
Капранов П., Уиллингем А.Т., Джингерас Т.Р. Полногеномная транскрипция и значение для геномной организации. Нат Рев Жене. 2007; 8: 413–23.
КАС пабмед Статья Google ученый
Soifer HS, Rossi JJ, Saetrom P. МикроРНК при заболеваниях и потенциальное терапевтическое применение. Мол Тер. 2007;15:2070–9.
КАС пабмед Статья Google ученый
Геберт ЛФР, Макрей И.
 Дж. Регуляция функции микроРНК у животных. Nat Rev Mol Cell Biol. 2019;20:21–37.
Дж. Регуляция функции микроРНК у животных. Nat Rev Mol Cell Biol. 2019;20:21–37.КАС пабмед ПабМед Центральный Статья Google ученый
Murchison EP, Hannon GJ. микроРНК в движении: биогенез микроРНК и механизм РНКи. Curr Opin Cell Biol. 2004; 16: 223–9.
КАС пабмед Статья Google ученый
Чен К., Раевски Н. Эволюция регуляции генов транскрипционными факторами и микроРНК. Нат Рев Жене. 2007; 8: 93–103.
КАС пабмед Статья Google ученый
Ха М, Ким В.Н. Регуляция биогенеза микроРНК. Nat Rev Mol Cell Biol. 2014;15:509–24.
КАС пабмед Статья Google ученый
Трейбер Т., Трейбер Н., Мейстер Г. Регуляция биогенеза микроРНК и ее взаимодействие с другими клеточными путями.
 Nat Rev Mol Cell Biol. 2019;20:5–20.
Nat Rev Mol Cell Biol. 2019;20:5–20.КАС пабмед Статья Google ученый
Рупаймул Р., Слэк Ф.Дж. Терапия микроРНК: к новой эре лечения рака и других заболеваний. Nat Rev Drug Discov. 2017;16:203–22.
КАС пабмед Статья Google ученый
Lee RC, Feinbaum RL, Ambros V. C. elegans гетерохронный ген lin-4 кодирует малые РНК с антисмысловой комплементарностью по отношению к lin-14. Клетка. 1993; 75: 843–54.
КАС пабмед Статья Google ученый
Wightman B, Ha I, Ruvkun G. Посттранскрипционная регуляция гетерохронного гена lin-14 с помощью lin-4 опосредует формирование временного паттерна у C. elegans . Клетка. 1993; 75: 855–62.
КАС пабмед Статья Google ученый
">Козомара А., Гриффитс-Джонс С. miRBase: аннотирование микроРНК с высокой достоверностью с использованием данных глубокого секвенирования. Нуклеиновые Кислоты Res. 2014;42:D68–73. Проблема с базой данных
CAS Статья пабмед Google ученый
Friedman RC, Farh KK, Burge CB, Bartel DP. Большинство мРНК млекопитающих являются консервативными мишенями для микроРНК. Геном Res. 2009; 19:92–105.
КАС пабмед ПабМед Центральный Статья Google ученый
Swarts DC, Jore MM, Westra ER, Zhu Y, Janssen JH, Snijders AP, et al. ДНК-управляемая интерференция ДНК прокариотическим аргонавтом.
 Природа. 2014; 507: 258–61.
Природа. 2014; 507: 258–61.КАС пабмед ПабМед Центральный Статья Google ученый
Йонас С., Изаурральде Э. К молекулярному пониманию подавления генов, опосредованного микроРНК. Нат Рев Жене. 2015;16:421–33.
КАС пабмед Статья Google ученый
Эстеллер М. Некодирующие РНК при заболеваниях человека. Нат Рев Жене. 2011; 12:861–74.
КАС пабмед Статья Google ученый
Лин С., Грегори Р.И. Пути биогенеза микроРНК при раке. Нат Рев Рак. 2015;15:321–33.
КАС пабмед ПабМед Центральный Статья Google ученый
Бракен С.П., Скотт Х.С., Гудолл Г.Дж. Перспектива сетевой биологии функции и дисфункции микроРНК при раке. Нат Рев Жене.
 2016;17:719–32.
2016;17:719–32.КАС пабмед Статья Google ученый
Вентура А., Янг А.Г., Уинслоу М.М., Линто Л., Мейснер А., Эркеланд С.Дж. и др. Направленная делеция выявляет существенные и перекрывающиеся функции кластеров miR-17-92 семейства miRNA. Клетка. 2008; 132: 875–86.
КАС пабмед ПабМед Центральный Статья Google ученый
Такамизава Дж., Кониси Х., Янагисава К., Томида С., Осада Х., Эндох Х. и др. Снижение экспрессии микроРНК let-7 при раке легкого человека связано с сокращением послеоперационной выживаемости. Рак Рез. 2004;64:3753–6.
КАС пабмед Статья Google ученый
Lu J, Getz G, Miska EA, Alvarez-Saavedra E, Lamb J, Peck D, et al. Профили экспрессии микроРНК классифицируют рак человека. Природа. 2005; 435:834–8.

КАС пабмед Статья Google ученый
Бак Р.О., Холленсен А.К., Миккельсен Дж.Г. Управление микроРНК с помощью ингибиторов типа приманки, кодируемых вектором. Мол Тер. 2013;21:1478–85.
КАС пабмед ПабМед Центральный Статья Google ученый
Бак Р.О., Миккельсен Дж.Г. Губки микроРНК: поглощают микроРНК для регуляции экспрессии генов. Wiley Inter Rev Rna. 2014;5:317–33.
КАС Статья Google ученый
Шу Ю., Ву К., Цзэн З., Хуан С., Цзи С., Юань С. и др. Упрощенная система для экспрессии циклических ингибиторов миРНК для стабильного и мощного подавления функций миРНК. Молекулярные нуклеиновые кислоты. 2018;13:556–67.
КАС пабмед ПабМед Центральный Статья Google ученый
">Wu P, Wilmarth MA, Zhang F, Du G. Векторы экспрессии микроРНК и кшРНК на основе процессинга мРНК и микроРНК. Методы Мол Биол. 2013;936:195–207.
КАС пабмед Статья Google ученый
Сейхан А.А. Платформа мультиплексной экспрессии микроРНК и трансгенов для одновременной репрессии и экспрессии кодирующих белок последовательностей. Мол Биосист. 2016;12:295–312.
КАС пабмед Статья Google ученый
Grimm D, Streetz KL, Jopling CL, Storm TA, Pandey K, Davis CR, et al. Летальный исход у мышей из-за перенасыщения клеточных путей микроРНК/коротких шпилечных РНК. Природа. 2006; 441: 537–41.

КАС пабмед Статья Google ученый
Luo Q, Kang Q, Song WX, Luu HH, Luo X, An N и др. Отбор и проверка оптимальных сайтов-мишеней siRNA для РНК-интерференционного молчания генов. Ген. 2007; 395:160–9.
КАС пабмед Статья Google ученый
Дэн Ф., Чен С., Ляо З., Ян З., Ван З., Дэн И. и др. Упрощенная и универсальная система для одновременной экспрессии нескольких siРНК в клетках млекопитающих с использованием сборки ДНК Gibson. ПЛОС Один. 2014;9:e113064.
ПабМед ПабМед Центральный Статья КАС Google ученый
Шу И, Ян С, Цзи С, Чжан Л, Би И, Ян К. и др. Обратимо иммортализованные мезенхимальные стволовые клетки, полученные из пуповины человека (UC-MSC), реагируют на BMP9-индуцированную остеогенную и адипогенную дифференцировку.
 Джей Селл Биохим. 2018;119:8872–86.
Джей Селл Биохим. 2018;119:8872–86.КАС пабмед ПабМед Центральный Статья Google ученый
Yan S, Zhang R, Wu K, Cui J, Huang S, Ji X и др. Характеристика важной роли костного морфогенетического белка 9 (BMP9) в остеогенной дифференцировке мезенхимальных стволовых клеток (МСК) посредством РНК-интерференции. Гены Дис. 2018;5:172–84.
КАС пабмед ПабМед Центральный Статья Google ученый
Yu X, Chen L, Wu K, Yan S, Zhang R, Zhao C, et al. Создание и функциональная характеристика обратимо иммортализованных клубочковых подоцитов мыши (imPOD). Гены Дис. 2018; 5: 137–49.
КАС пабмед ПабМед Центральный Статья Google ученый
Zeng Z, Huang B, Huang S, Zhang R, Yan S, Yu X и др. Разработка чувствительного репортера транскриптов на основе флуоресцентного белка для высокопроизводительного скрининга негативных модуляторов днРНК.
 Гены Дис. 2018;5:62–74.
Гены Дис. 2018;5:62–74.КАС пабмед ПабМед Центральный Статья Google ученый
Луо Дж., Дэн З.Л., Луо С., Тан Н., Сонг В.С., Чен Дж. и др. Протокол для быстрого создания рекомбинантных аденовирусов с использованием системы AdEasy. Нат Проток. 2007;2:1236–47.
КАС пабмед Статья Google ученый
Ван Н., Чжан Х., Чжан Б.К., Лю В., Чжан З., Цяо М. и др. Опосредованный аденовирусом эффективный перенос генов в культивируемые трехмерные органоиды. ПЛОС Один. 2014;9:e93608.
ПабМед ПабМед Центральный Статья КАС Google ученый
Zhang H, Wang J, Deng F, Huang E, Yan Z, Wang Z и др. Каноническая передача сигналов Wnt действует синергетически на индуцированную BMP9 остео/одонтобластическую дифференцировку стволовых клеток апикального сосочка зуба (SCAP).
 Биоматериалы. 2015;39:145–54.
Биоматериалы. 2015;39:145–54.КАС пабмед Статья Google ученый
Untergasser A, Cutcutache I, Koressaar T, Ye J, Faircloth BC, Remm M, et al. Primer3 – новые возможности и интерфейсы. Нуклеиновые Кислоты Res. 2012;40:e115.
КАС пабмед ПабМед Центральный Статья Google ученый
Zhang Q, Wang J, Deng F, Yan Z, Xia Y, Wang Z и др. TqPCR: анализ qPCR с приземлением со значительно улучшенной чувствительностью обнаружения и эффективностью амплификации SYBR green qPCR. ПЛОС ОДИН. 2015;10:e0132666.
ПабМед ПабМед Центральный Статья КАС Google ученый
Zhao C, Zeng Z, Qazvini NT, Yu X, Zhang R, Yan S. et al. Термочувствительный каркас из оксида графена на основе цитрата усиливает регенерацию кости из стимулированных BMP9 мезенхимальных стволовых клеток жировой ткани.
 ACS Biomater Sci Eng. 2018;4:2943–55.
ACS Biomater Sci Eng. 2018;4:2943–55.КАС пабмед ПабМед Центральный Статья Google ученый
Fan J, Wei Q, Liao J, Zou Y, Song D, Xiong D и др. Неканоническая передача сигналов Wnt играет важную роль в модуляции канонической Wnt-регулируемой стволовости, пролиферации и терминальной дифференцировки печеночных предшественников. Онкотаргет. 2017;8:27105–19.
ПабМед ПабМед Центральный Статья Google ученый
Hu X, Li L, Yu X, Zhang R, Yan S, Zeng Z и др. CRISPR/Cas9-опосредованные обратимо иммортализованные стромальные стволовые клетки костного мозга мыши (СКМСК) сохраняют мультипотентные свойства мезенхимальных стволовых клеток (МСК). Онкотаргет. 2017;8:111847–65.
ПабМед ПабМед Центральный Статья Google ученый
">Ляо Дж., Вэй К., Цзоу Й., Фань Дж., Сонг Д., Цуй Дж. и др. Передача сигналов Notch усиливает индуцированное BMP9 образование кости, способствуя процессу сопряжения остеогенеза и ангиогенеза в мезенхимальных стволовых клетках (MSCs). Cell Physiol Biochem. 2017;41:1905–23.
КАС пабмед Статья Google ученый
Ляо Дж., Юй С., Ху С., Фан Дж., Ван Дж., Чжан З. и др. lncRNA h29 опосредует индуцированную BMP9 остеогенную дифференцировку мезенхимальных стволовых клеток (MSC) посредством передачи сигналов Notch. Онкотаргет. 2017; 8: 53581–601.

ПабМед ПабМед Центральный Статья Google ученый
Ю С, Лю Ф, Цзэн Л, Хе Ф, Чжан Р, Ян С и др. Никлозамид проявляет мощную противораковую активность и синергизирует с сорафенибом в клетках рака почки человека. Cell Physiol Biochem. 2018;47:957–71.
КАС пабмед Статья Google ученый
Дэн Ю., Чжан Дж., Ван З., Ян З., Цяо М., Йе Дж. и др. Антибиотик монензин взаимодействует с ингибиторами EGFR и оксалиплатином, подавляя пролиферацию клеток рака яичников человека. Научный доклад 2015; 5:17523.
КАС пабмед ПабМед Центральный Статья Google ученый
Zhang F, Li Y, Zhang H, Huang E, Gao L, Luo W и др. Антигельминтное средство мебендазол усиливает действие цисплатина на подавление клеточной пролиферации и способствует дифференцировке плоскоклеточного рака головы и шеи (ПГШШ).
 Онкотаргет. 2017;8:12968–82.
Онкотаргет. 2017;8:12968–82.ПабМед ПабМед Центральный Статья Google ученый
Дэн И, Ван З, Чжан Ф, Цяо М, Ян З, Вэй Ц и др. Блокада передачи сигналов ИФР повышает чувствительность клеток рака яичников человека к антигельминтным никлозамид-индуцированным антипролиферативным и противораковым действиям. Cell Physiol Biochem. 2016; 39: 871–88.
КАС пабмед Статья Google ученый
Gao JL, Lv GY, He BC, Zhang BQ, Zhang H, Wang N и др. Метаболит сапонина женьшеня 20(S)-протопанаксадиол ингибирует рост опухоли, воздействуя на несколько сигнальных путей рака. Oncol Rep. 2013; 30:292–8.
КАС пабмед ПабМед Центральный Статья Google ученый
He BC, Gao JL, Luo X, Luo J, Shen J, Wang L, et al. Гинзенозид Rg3 ингибирует рост колоректальной опухоли за счет подавления передачи сигналов Wnt/ss-катенина.
 Int J Oncol. 2011; 38: 437–45.
Int J Oncol. 2011; 38: 437–45.КАС пабмед Статья Google ученый
He BC, Gao JL, Zhang BQ, Luo Q, Shi Q, Kim SH, et al. Тетрандин ингибирует передачу сигналов Wnt/бета-катенин и подавляет рост опухоли при колоректальном раке человека. Мол Фарм. 2011;79:211–9.
КАС Статья Google ученый
Lu S, Wang J, Ye J, Zou Y, Zhu Y, Wei Q, et al. Костный морфогенетический белок 9(BMP9) индуцирует эффективное костеобразование из обратимо иммортализованных мультипотентных мезенхимальных стволовых клеток жирового происхождения (iMAD). Am J Transl Res. 2016;8:3710–30.
КАС пабмед ПабМед Центральный Google ученый
Сун Д., Чжан Ф., Рейд Р.Р., Йе Дж., Вэй К., Ляо Дж. и др. BMP9 индуцирует остеогенез и адипогенез в иммортализованных предшественниках черепных швов человека из открытых швов пациентов с краниосиностозом.
 J Cell Mol Med. 2017; 21: 2782–95.
J Cell Mol Med. 2017; 21: 2782–95.КАС пабмед ПабМед Центральный Статья Google ученый
Liao Z, Nan G, Yan Z, Zeng L, Deng Y, Ye J и др. Антигельминтный препарат никлозамид ингибирует пролиферативную активность клеток остеосаркомы человека, воздействуя на несколько сигнальных путей. Цели лекарств против рака Curr. 2015;15:726–738.
КАС пабмед Статья Google ученый
Ли Р., Чжан В., Цуй Дж., Шуй В., Инь Л., Ван И и др. Нацеливание на рост остеосаркомы человека, стимулируемый BMP9, путем инактивации передачи сигналов Notch. Цели лекарств против рака Curr. 2014; 14: 274–85.
КАС пабмед Статья Google ученый
Li Y, Wagner ER, Yan Z, Wang Z, Luther G, Jiang W, et al. Кальций-связывающий белок S100A6 ускоряет рост остеосаркомы человека, стимулируя пролиферацию клеток и ингибируя остеогенную дифференцировку.
 Cell Physiol Biochem. 2015; 37: 2375–92.
Cell Physiol Biochem. 2015; 37: 2375–92.КАС пабмед Статья Google ученый
Zhou L, An N, Haydon RC, Zhou Q, Cheng H, Peng Y и др. Ингибитор тирозинкиназы STI-571/Gleevec подавляет сигнальную активность бета-катенина. Рак Летт. 2003; 193:161–70.
КАС пабмед ПабМед Центральный Статья Google ученый
Эскела-Кершер А, Слэк Ф.Дж. Онкомиры - микроРНК, играющие роль в развитии рака. Нат Рев Рак. 2006;6:259–69.
КАС пабмед Статья Google ученый
Ханеклаус М., Герлик М., О'Нил Л.А., Мастерс С.Л. миР-223: инфекция, воспаление и рак. J Интерн Мед. 2013; 274: 215–26.
КАС пабмед ПабМед Центральный Статья Google ученый
Gao Y, Lin L, Li T, Yang J, Wei Y.
 Роль микроРНК-223 в развитии рака: функция, диагностика и терапия. Ген. 2017; 616:1–7.
Роль микроРНК-223 в развитии рака: функция, диагностика и терапия. Ген. 2017; 616:1–7.КАС пабмед Статья Google ученый
Торнтон Дж. Э., Грегори Р. И. Как Lin28 let-7 контролирует развитие и заболевание? Тенденции клеточной биологии. 2012; 22: 474–82.
КАС пабмед ПабМед Центральный Статья Google ученый
Lee H, Han S, Kwon CS, Lee D. Биогенез и регуляция микроРНК let-7 и их функциональные последствия. Белковая клетка. 2016;7:100–13.
КАС пабмед Статья Google ученый
Бальзо Дж., Менезес М.Р., Цао С., Хаган Дж.П. Путь LIN28/let-7 при раке. Фронт Жене. 2017;8:31.
ПабМед ПабМед Центральный Статья КАС Google ученый
">Qiu X, Friedman JM, Liang G. Создание гибкого вектора экспрессии множественных микроРНК путем связывания микроРНК-предшественников. Biochem Biophys Res Commun. 2011; 411: 276–80.
КАС пабмед ПабМед Центральный Статья Google ученый
Furukawa N, Sakurai F, Katayama K, Seki N, Kawabata K, Mizuguchi H. Оптимизация вектора экспрессии микроРНК для функционального анализа микроРНК. J Управление выпуском. 2011;150:94–101.
КАС пабмед Статья Google ученый
Zhu X, Santat LA, Chang MS, Liu J, Zavzavadjian JR, Wall EA, et al. Универсальный подход к интерференции множественных генов РНК с использованием коротких шпилечных РНК на основе микроРНК.
 BMC Мол Биол. 2007; 8:98.
BMC Мол Биол. 2007; 8:98.ПабМед ПабМед Центральный Статья КАС Google ученый
Ely A, Naidoo T, Arbuthnot P. Эффективное подавление экспрессии генов с помощью модульных тримерных кассет экспрессии Pol II, содержащих челноки микроРНК. Нуклеиновые Кислоты Res. 2009 г.;37:e91.
ПабМед ПабМед Центральный Статья КАС Google ученый
Снайдер Л.Л., Ахмед И., Стил Л.Ф. РНК-полимераза III может управлять полицистронной экспрессией функциональных интерферирующих РНК, напоминающих микроРНК. Нуклеиновые Кислоты Res. 2009;37:e127.
ПабМед ПабМед Центральный Статья КАС Google ученый
Осорио Л., Гийсберс Р., Оливерас-Сальва М., Михилс А., Дебисер З., Ван ден Оте С. и др. Вирусные векторы, экспрессирующие одну РНК с короткой шпилькой на основе микроРНК, приводят к сильному подавлению генов in vitro и in vivo.
 Дж Биотехнолог. 2014;169: 71–81.
Дж Биотехнолог. 2014;169: 71–81.КАС пабмед Статья Google ученый
Линь С.Л., Ин С.И. Замалчивание генов in vitro и in vivo с использованием интронных микроРНК. Методы Мол Биол. 2006; 342: 295–312.
КАС пабмед Google ученый
Руби Дж. Г., Ян Ч., Бартел Д.П. Интронные предшественники микроРНК, которые обходят процессинг Drosha. Природа. 2007; 448:83–6.
КАС пабмед ПабМед Центральный Статья Google ученый
Окамура К., Хаген Дж.В., Дуан Х., Тайлер Д.М., Лай Э.К. Путь миртрона генерирует регуляторные РНК класса микроРНК у дрозофилы. Клетка. 2007; 130:89–100.
КАС пабмед ПабМед Центральный Статья Google ученый
Westholm JO, Lai EC.
 Миртроны: биогенез микроРНК посредством сплайсинга. Биохимия. 2011; 93:1897–904.
Миртроны: биогенез микроРНК посредством сплайсинга. Биохимия. 2011; 93:1897–904.КАС пабмед ПабМед Центральный Статья Google ученый
Гримм Д., Ван Л., Ли Дж.С., Шурманн Н., Гу С., Борнер К. и др. Белки Argonaute являются ключевыми детерминантами эффективности, токсичности и персистенции РНК-интерференции в печени взрослых мышей. Дж. Клин Инвестиг. 2010;120:3106–19.
КАС пабмед Статья ПабМед Центральный Google ученый
Борнер К., Ниопек Д., Котуньо Г., Калденбах М., Панкерт Т., Виллемсен Дж. и др. Надежное усиление РНК-интерференции за счет сверхэкспрессии человеческого Argonaute-2 из плазмид, вирусных векторов и клеточных линий. Нуклеиновые Кислоты Res. 2013;41:e199.
ПабМед ПабМед Центральный Статья КАС Google ученый
Куинн Дж.Дж., Чанг Х.И. Уникальные особенности биогенеза и функции длинных некодирующих РНК. Нат Рев Жене. 2016;17:47–62.
КАС пабмед Статья Google ученый
Ли Р., Файнбаум Р., Амброс В. Краткая история короткой РНК. Клетка. 2004; 116:S89–92. 1 шт. после S6
CAS пабмед Статья Google ученый
Wu J, Bonsra AN, Du G. Векторы pSM155 и pSM30 для экспрессии миРНК и кшРНК. Методы Мол Биол. 2009; 487: 205–19.
КАС пабмед Google ученый
Чжао С., Цзян В., Чжоу Н., Ляо Дж., Ян М., Ху Н. и др. Sox9 усиливает индуцированную BMP2 хондрогенную дифференцировку путем подавления Smad7 в мезенхимальных стволовых клетках (МСК). Гены Дис. 2017;4:229–39.
КАС пабмед ПабМед Центральный Статья Google ученый
Роуш С., Слэк Ф.Дж. Семейство микроРНК let-7. Тенденции клеточной биологии. 2008; 18: 505–16.
КАС пабмед Статья Google ученый
Загрузить ссылки
Благодарности
Представленная работа была частично поддержана исследовательскими грантами от Фонда постдокторских исследований Китая (JF), Чунцинской программы поддержки инновационных талантов постдокторантов (JF), Национальной ключевой программы исследований и разработок Китая (2016YFC1000803 и 2011CB707906), Национальных институтов здравоохранения (CA226303 до ТКП), Министерства обороны США (OR130096 в JMW) и Общество исследования сколиоза (TCH и MJL). YF, RZ, ZZ, BH и BZ получили аспирантскую стипендию Китайского стипендиального совета. Этот проект также был частично поддержан Грантом поддержки онкологического центра Чикагского университета (P30CA014599) и Национальным центром развития трансляционных наук Национальных институтов здравоохранения посредством гранта номер UL1 TR000430. ТКП также поддержали Фонд поддержки исследований Мэйбл Грин Майерс и Фонд выпускников ортопедической хирургии Чикагского университета. Источники финансирования не участвовали в разработке исследования; при сборе, анализе и интерпретации данных; при написании отчета; и в решении представить статью для публикации.
YF, RZ, ZZ, BH и BZ получили аспирантскую стипендию Китайского стипендиального совета. Этот проект также был частично поддержан Грантом поддержки онкологического центра Чикагского университета (P30CA014599) и Национальным центром развития трансляционных наук Национальных институтов здравоохранения посредством гранта номер UL1 TR000430. ТКП также поддержали Фонд поддержки исследований Мэйбл Грин Майерс и Фонд выпускников ортопедической хирургии Чикагского университета. Источники финансирования не участвовали в разработке исследования; при сборе, анализе и интерпретации данных; при написании отчета; и в решении представить статью для публикации.
Информация об авторе
Авторы и организации
Ключевая лаборатория диагностической медицины Министерства образования и Школа лабораторной медицины Чунцинского медицинского университета, 400016, Чунцин, Китай Wang & Ailong Huang
Лаборатория молекулярной онкологии, отделение ортопедической хирургии и реабилитационной медицины, Медицинский центр Чикагского университета, Чикаго, Иллинойс, 60637, США
Цзямин Фань, Исяо Фэн, Руи Чжан, Вэньвэнь Чжан, Йи Шу, Цзунъюэ Цзэн, Шифэн Хуан, Линхуань Чжан, Бо Хуан, Ди Ву, Бо Чжан, Си Ван, Ян Лэй, Чжэньюй Е, Лин Чжао, Дайгуй Цао, Лицзюань Ян, Сянь Чен, Бин Лю, Уильям Вагстафф, Фанг Хэ, Сяосин Ву, Цзин Чжан, Дженнифер Мориатис Вульф, Майкл Дж.
 Ли, Рекс С. Хейдон, Хью Х. Луу, Тонг-Чуан Хэ и Шуцзюань Ян
Ли, Рекс С. Хейдон, Хью Х. Луу, Тонг-Чуан Хэ и Шуцзюань ЯнАффилированные больницы Медицинского университета Чунцина, 400016, Чунцин, Китай
Исяо Фэн, Вэньвэнь Чжан, И Шу, Шифэн Хуан, Линхуань Чжан, Ян Лэй, Лин Чжао, Дайгуй Цао, Фан Хэ, Сяосин Ву и Цзин Чжан
Отделение клинической лабораторной медицины, Первая дочерняя больница Гуйянского колледжа традиционной китайской медицины, 550001, Гуйян, Китай
Руи Чжан
Отделение клинической лабораторной медицины, Вторая дочерняя больница Университета Наньчан, 330006 , Наньчан, Китай
Бо Хуан
Ключевая лаборатория ортопедической хирургии провинции Ганьсу и отделения ортопедической хирургии, акушерства и гинекологии, Первая и Вторая больницы Университета Ланьчжоу, 730030, Ланьчжоу, Китай
Bo Zhang & Lijuan Yang
Department of General Surgery, The Second Affiliated Hospital of Soochow University, 215004, Suzhou, China
Zhenyu Ye
Department of Orthopaedic Surgery, Chongqing General Hospital, 400021, Chongqing, Китай
Дайгуй Цао
Отделение клинической лабораторной медицины, Больница-филиал Университета Циндао, 266061, Циндао, Китай
Сиань Чен
Школа наук о жизни, Юго -западный университет, 400715, Чунцин, Китай
Bin Liu
Кафедра клинической лабораторной медицины, больница провинции Гичжоу
Shujuju -yan yan yan
Shujuju J
Авторы
- Jiaming Fan
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Yixiao Feng
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Ruyi Zhang
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Wenwen Zhang
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Yi Shu
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Zongyue Zeng
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Shifeng Huang
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Linghuan Zhang
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Академия
- Bo Huang
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Di Wu
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Бо Чжан
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Xi Wang
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Yan Lei
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Zhenyu Ye
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Лин Чжао
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Академия
- Daigui Cao
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Lijuan Yang
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Xian Chen
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Бин Лю
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- William Wagstaff
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Fang He
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Xiaoxing Wu
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Jing Zhang
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Jennifer Moriatis Wolf
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Майкл Дж.
 Ли
ЛиПосмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Rex C. Haydon
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Hue H. Luu
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Ailong Huang
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Академия
- Тонг-Чуан Хэ
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Shujuan Yan
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Авторы, переписывающиеся
Переписка с Тонг-Чуан Хэ или Шуцзюань Ян.

Декларации этики
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Дополнительная информация
Примечание издателя: Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.
Дополнительная информация
Доп. Таблица 1
Доп. Рисунок 1
Доп. Рисунок 2
Права и разрешения
Открытый доступ Эта статья находится под лицензией Creative Commons Attribution 4.0 International License, которая разрешает использование, совместное использование, адаптацию, распространение и воспроизведение на любом носителе или в любом формате при условии, что вы укажете первоначальных авторов и источник, предоставите ссылку на лицензию Creative Commons и указать, были ли внесены изменения. Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons для статьи, если иное не указано в кредитной строке материала.
 Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или превышает разрешенное использование, вам необходимо получить разрешение непосредственно от правообладателя. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/4.0/.
Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или превышает разрешенное использование, вам необходимо получить разрешение непосредственно от правообладателя. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/4.0/.Перепечатка и разрешения
Об этой статье
Дополнительная литература
Оптимизация кассеты экспрессии миР-22 для доставки rAAV при диабете
- Ли Ян
- Веня Ду
- Бяо Донг
Молекулярная биомедицина (2022)
Взаимодействие микроРНК-хозяина и иммунных клеток: актуальность нанотерапии для здоровья человека
- Йогеш Шарма
- Адеш К.
 Шайни
Шайни - Рина В. Сайни
Иммунологические исследования (2022)
Лицево-лопаточно-плечевая мышечная дистрофия: генетика, активация генов и передача сигналов ниже по течению в отношении последних терапевтических подходов: обновление
- Тереза Шетцль
- Ларс Кайзер
- Ханс-Петер Дайнер
Orphanet Journal of Rare Diseases (2021)
Доклинические экспериментальные применения внеклеточных везикул СККМ, нагруженных микроРНК
- Зафер Четин
- Эюп И.
 Сайгили
Сайгили - Эмель Сокуллу
Обзоры и отчеты по стволовым клеткам (2021)
Роль микроРНК-3085 в функции хондроцитов
- Линь Ле
- Линцзы Ню
- Трейси Э. Свинглер
Научные отчеты (2020)
Упрощение выражений | nool
Перейти к основному содержанию
Домашняя страница Технологического института Онтарио
nool
Алгебраические выражения иногда могут выглядеть беспорядочно, поскольку они содержат не только числа, но и буквы алфавита.
 Давайте подробнее рассмотрим, как мы можем упростить эти выражения.
Давайте подробнее рассмотрим, как мы можем упростить эти выражения.Чтобы упростить алгебраическое выражение, мы должны собрать одинаковые термины. При упрощении алгебраического выражения находится эквивалентное выражение, которое проще исходного. Обычно это означает, что упрощенное выражение меньше исходного выражения. Существует множество различных видов алгебраических выражений, поэтому стандартной процедуры для их упрощения не существует. Вот список шагов, которым нужно следовать.
- Подготовьте алгебраическое выражение для упрощения (например, путем расширения).
- Определите и сгруппируйте похожие термины.
- Объедините похожие термины.
Пример: Упростите выражение 5x + 3y -9z -8x + 6y.
Решение:
Выражение не нужно готовить, поэтому сначала определите и сгруппируйте одинаковые члены:
(5x - 8x) + (3y + 6y) - 9z
Затем объедините одинаковые члены:
-3x + 9y - 9z
Пример: Упростите выражение 4(5a - 4b) -7(6a + 2b).

Решение:
Сначала подготовьте выражение для упрощения (расширьте): 20a - 16b - 42a- 14b
Затем определите и сгруппируйте одинаковые термины: (20a - 42a) + (-16b - 14b)
Наконец, объедините одинаковые термины: -22a - 20b
Важно понимать, что не все алгебраические выражения можно упростить. Например, выражение 56a - 8b + 7c -5 не может быть упрощено дальше, так как в выражении нет одинаковых членов.
Закончим еще одним примером выражения, в котором есть произведения и частные простых множителей, включающих степени с одним и тем же основанием. Их можно легко упростить, добавляя и вычитая индексы степеней (используя экспоненциальные законы).
Пример: Упростить выражение 24W 4 x 5 Z ÷ 2wyz 2
Решение:
5 /yz
Пример - Объединение рациональных выражений:
com/embed/QUvaUXUsy24">Как избежать распространенных математических ошибок при упрощении:
2 9 Упрощение с объяснением20004Векторная алгебра в анализе данных полногеномной экспрессии | Геномная биология
- Исследования
- Открытый доступ
- Опубликовано:
- Финни Г. Курувилла 1 ,
- Питер Дж. Парк 2 и
- Стюарт Л. Шрайбер 1
Биология генома , том 3 , номер статьи: research0011.1 (2002 г.) Процитировать эту статью
19 тыс. обращений
36 цитирований
Сведения о показателях
Abstract
Background
Данные тысяч экспериментов по профилированию транскрипции в различных организмах, от дрожжей до человека, теперь общедоступны.
 Как лучше всего анализировать эти данные, остается важной проблемой. Для этой цели использовались различные инструменты, включая иерархическую кластеризацию, самоорганизующиеся карты и анализ основных компонентов. В частности, концепции векторной алгебры оказались полезными при изучении данных экспрессии всего генома.
Как лучше всего анализировать эти данные, остается важной проблемой. Для этой цели использовались различные инструменты, включая иерархическую кластеризацию, самоорганизующиеся карты и анализ основных компонентов. В частности, концепции векторной алгебры оказались полезными при изучении данных экспрессии всего генома.Результаты
Здесь мы представляем основу, основанную на векторной алгебре для анализа профилей транскрипции, которая геометрически интуитивно понятна и эффективна в вычислительном отношении. Понятия векторной алгебры, такие как углы, величины, подпространства, разложение по сингулярным числам, базисы и проекции, имеют естественные и мощные интерпретации при анализе данных микрочипов. Углы, в частности, предлагают строгий метод определения «сходства» и полезны при оценке утверждений исследования на основе микрочипов. Мы представляем анализ образцов клеток, обработанных рапамицином, иммунодепрессантом, действие которого было тщательно изучено с помощью микрочипов.
 Кроме того, алгебраическая концепция основы для пространства дает возможность упростить анализ данных и раскрыть ограниченное количество векторов экспрессии, чтобы охватить транскрипционный диапазон клеточного поведения.
Кроме того, алгебраическая концепция основы для пространства дает возможность упростить анализ данных и раскрыть ограниченное количество векторов экспрессии, чтобы охватить транскрипционный диапазон клеточного поведения.Выводы
Эта структура представляет собой компактную, мощную и масштабируемую конструкцию для анализа и вычислений. Поскольку объем данных микрочипов в открытом доступе растет, эти векторные методы актуальны для определения статистической значимости. Эти подходы также хорошо подходят для извлечения биологически значимой информации при анализе сигнальных сетей.
Исходная информация
Тремя целями большинства экспериментов с микрочипами являются описание, классификация или характеристика. Например, микроматрицы использовались для всестороннего описания диоксиального сдвига, прохождения клеточного цикла, спорообразования и эффектов обработки малой молекулой [1,2,3,4]. Они использовались для классификации типа рака данного образца или классификации групп совместно регулируемых генов [5,6,7,8].
 Наконец, микрочипы использовались для характеристики биологических систем путем сравнения клеток дикого типа и мутантных клеток с целью получения механистического понимания [9].,10,11].
Наконец, микрочипы использовались для характеристики биологических систем путем сравнения клеток дикого типа и мутантных клеток с целью получения механистического понимания [9].,10,11].Поиск согласованных резких изменений в экспрессии генов или поиск дифференциальной экспрессии данного гена был успешным методом анализа данных профилирования транскрипции, особенно при описании или характеристике [4,12]. Часто следователи используют ручной подход к выполнению этих задач. Однако ручные подходы к анализу данных иногда непрактичны или громоздки, что вдохновляет на разработку инструментов для достижения трех целей, описанных выше. Различные методы, такие как иерархическая кластеризация, k - означает, что кластеризация и самоорганизация карт были успешно реализованы, особенно в классификации [13].
Поскольку количество общедоступных профилей только для Saccharomyces cerevisiae в настоящее время превышает 500, существует большая потребность в правильном использовании этой информации для понимания функции клетки.
 По крайней мере три независимых международных проекта были созданы для использования в качестве управляемых базами данных репозиториев данных полногеномной экспрессии [14]. Прилагаются большие усилия для систематизации хранения данных, особенно с использованием XML (расширяемый язык разметки), для обеспечения функциональной совместимости этих баз данных и связанных с ними инструментов анализа.
По крайней мере три независимых международных проекта были созданы для использования в качестве управляемых базами данных репозиториев данных полногеномной экспрессии [14]. Прилагаются большие усилия для систематизации хранения данных, особенно с использованием XML (расширяемый язык разметки), для обеспечения функциональной совместимости этих баз данных и связанных с ними инструментов анализа.Связанная с этим потребность, которая в меньшей степени удовлетворялась, — это систематизация анализа данных экспрессии. Это требование распространяется не только на анализ, но и на педагогику, и на практические аспекты реализации алгоритмов. Различные исследования в литературе успешно применяли инструменты векторной алгебры для анализа данных экспрессии всего генома [11,15,16]. Однако основа для анализа профилей транскрипции с использованием векторной алгебры еще не кодифицирована. Здесь мы представляем такую структуру. Обычные статистические меры имеют естественные аналоги в векторной алгебре, которые имеют визуальную интерпретацию и легко реализуются на компьютере.
 В этих рамках анализ данных экспрессии всего генома преобразуется в изучение многомерных векторных пространств. Многие мощные теоремы, разработанные в векторной алгебре, могут быть применены к этим пространствам, и эти теоремы предлагают биологически важные идеи. Элементы векторного пространства также можно анализировать статистически. Эта конструкция имеет аналитическую и педагогическую привлекательность.
В этих рамках анализ данных экспрессии всего генома преобразуется в изучение многомерных векторных пространств. Многие мощные теоремы, разработанные в векторной алгебре, могут быть применены к этим пространствам, и эти теоремы предлагают биологически важные идеи. Элементы векторного пространства также можно анализировать статистически. Эта конструкция имеет аналитическую и педагогическую привлекательность.Результаты и обсуждение
Конструирование векторов экспрессии
Эксперименты по профилированию транскрипции предлагают различные виды измерений в зависимости от используемой технологии. Один тип технологии (с использованием неконкурентной гибридизации) измеряет абсолютную экспрессию генов, а второй тип (с использованием конкурентной гибридизации) измеряет относительную экспрессию генов. Микрочип, который использует конкурентную гибридизацию, дает список кратных изменений для каждого гена между измеряемыми условиями или типами клеток. Данные с микрочипа, в котором используется неконкурентная гибридизация, могут быть «разделены» (после надлежащей нормализации) на другой микрочип того же типа для получения кратности изменения каждого гена из одного состояния в другое.
 На практике даже те исследователи, которые используют неконкурентные технологические платформы, обычно интерпретируют и публикуют кратные изменения между условиями или штаммами, а не абсолютные уровни экспрессии генов. Поэтому это исследование будет сосредоточено на анализе значений кратности изменения, которые в дальнейшем называются профилем транскрипции или экспрессии.
На практике даже те исследователи, которые используют неконкурентные технологические платформы, обычно интерпретируют и публикуют кратные изменения между условиями или штаммами, а не абсолютные уровни экспрессии генов. Поэтому это исследование будет сосредоточено на анализе значений кратности изменения, которые в дальнейшем называются профилем транскрипции или экспрессии.Существует три распространенных типа значений, которые могут быть связаны с кратностью изменения гена. Во-первых, знаковое кратное изменение (например, +1,6 или -2,3-кратное изменение, соответствующее индукции или вытеснению соответственно) имеет наиболее интуитивную привлекательность, но имеет прерывность, охватывающую от -1,0 до +1,0, что может быть проблематично. Второй тип, беззнаковое кратное изменение (например, 1,6-кратное или 0,43-кратное изменение, что опять-таки соответствует индукции или вытеснению соответственно), не имеет такого разрыва, но ограничено слева нулем и неограничено справа. Эта асимметрия относительно единства препятствует анализу.
 Третий тип, логарифм (по основанию 2, по основанию 10 или натуральный) беззнакового кратного изменения, несомненно, является наиболее податливым. Отсутствие кратного изменения экспрессии представлено нулем, индукция положительна, а репрессия отрицательна. Самое главное, нет разрывов или асимметрии.
Третий тип, логарифм (по основанию 2, по основанию 10 или натуральный) беззнакового кратного изменения, несомненно, является наиболее податливым. Отсутствие кратного изменения экспрессии представлено нулем, индукция положительна, а репрессия отрицательна. Самое главное, нет разрывов или асимметрии.После получения набора профилей транскрипции (где каждый профиль представляет собой набор кратных изменений для набора генов) можно создать матрицу данных с генами в виде строк и экспериментами в виде столбцов (рис. 1а). Имея в виду эту картину, генерация векторов из матрицы данных (логарифмы беззнаковых кратных изменений) является естественной операцией, для которой существует очевидная конструкция.
Рисунок 1Два взаимодополняющих метода понимания профиля транскрипции. (a) Показаны два профиля транскрипции трех генов. Строки образуют генные векторы, а столбцы — экспериментальные векторы. (b) При типичном сравнении профилей векторы генов наносятся в двух измерениях, где оси представляют эксперименты, а точки — гены.
 Данные из (а) нанесены на график. Дополнительные гены добавляют точки на график, но он остается двухмерным. (c) В векторном подходе оси — это гены, а точки — эксперименты. Данные из (а) также нанесены здесь. Дополнительные гены не добавляли бы к графу никаких точек (то есть всегда было бы только два вектора), но пространство, в котором находятся векторы, увеличивалось бы в размерах.
Данные из (а) нанесены на график. Дополнительные гены добавляют точки на график, но он остается двухмерным. (c) В векторном подходе оси — это гены, а точки — эксперименты. Данные из (а) также нанесены здесь. Дополнительные гены не добавляли бы к графу никаких точек (то есть всегда было бы только два вектора), но пространство, в котором находятся векторы, увеличивалось бы в размерах.Полноразмерное изображение
Определение. Для p профилей транскрипции, измеряющих экспрессию n генов, пусть s ij представляют собой логарифм экспрессии гена и в эксперименте и . Вектор
[s i 1 s i 2 ...s ip ] Т
определяется как «генный вектор». Точно так же
определяется как «экспериментальный вектор». По построению вектор гена имеет размерность 90 368 p 90 369, а вектор эксперимента имеет размерность 90 368 n 90 369.
 «Вектор экспрессии» представляет собой вектор гена или экспериментальный вектор. Верхний индекс T обозначает транспонирование.
«Вектор экспрессии» представляет собой вектор гена или экспериментальный вектор. Верхний индекс T обозначает транспонирование.Легко видеть, что относительно матрицы данных вектор генов состоит из элементов строки, а вектор эксперимента состоит из элементов столбца (рис. 1а). По соглашению векторы рассматриваются как столбцы, а не как строки. Экспериментальные векторы уже являются столбцами, поэтому генные векторы переносятся из строк в столбцы.
В наиболее распространенной схеме сравнения двух профилей «облако» генов наносится на диаграмму рассеяния. Это представление представляет собой просто отображение n двумерных генных векторов (рис. 1b). Он хорошо подходит для обнаружения определенных генов, экспрессия которых варьируется между экспериментами. По мере добавления в матрицу новых экспериментов размерность пространства увеличивается, но количество точек остается фиксированным. Учитывая большое количество экспериментов, гены, имеющие сходную биологическую регуляцию, остаются в близлежащих областях многомерных пространств.
 В сочетании с анализом последовательностей промоторов и рассмотрением структуры хроматина изучение генных векторов полезно в исследованиях регуляции транскрипции.
В сочетании с анализом последовательностей промоторов и рассмотрением структуры хроматина изучение генных векторов полезно в исследованиях регуляции транскрипции.Существует еще один, дополнительный подход к профилям экспрессии или, в более общем смысле, к многомерным статистическим данным [17]. Хотя анализ генных векторов является мощным инструментом, он менее эффективен для демонстрации взаимосвязей между профилями. Это связано с тем, что наложение облаков тысяч генных векторов может не дать проницательной картины из-за множества точек зрения. В альтернативном методе анализа профиль экспрессии рассматривается как всего лишь одна точка в многомерном пространстве. Поскольку эта точка фиксирует ту же информацию, что и диаграмма рассеяния генных векторов, она должна находиться в гораздо более многомерном пространстве. В этом пространстве отношения между профилями становятся более очевидными. Вместо того, чтобы строить графики генов, теперь можно строить эксперименты (рис. 1с). Когда в матрицу данных добавляются новые профили, размер пространства остается фиксированным, но количество точек увеличивается, что является обратным случаем генных векторов.
 Хотя многомерное пространство экспериментальных векторов не может быть визуализировано, отношения векторов в пространстве часто можно понять, используя интуицию в двух- или трехмерном случае. Сила векторной алгебры заключается в ее способности масштабироваться — понятия, уравнения и теоремы плавно (обычно одинаково) перемещаются в более высокие измерения.
Хотя многомерное пространство экспериментальных векторов не может быть визуализировано, отношения векторов в пространстве часто можно понять, используя интуицию в двух- или трехмерном случае. Сила векторной алгебры заключается в ее способности масштабироваться — понятия, уравнения и теоремы плавно (обычно одинаково) перемещаются в более высокие измерения.Если предположить, что на микрочипе представлено n генов, теоретически возможно, что каждый профиль даст n -мерный экспериментальный вектор. Однако из-за плохого обнаружения редких транскриптов, дефектов на микроматрице или экспериментальной ошибки профиль экспрессии на практике дает менее n значений. Таким образом, остается три основных варианта проведения анализа. Во-первых, отсутствие данных может быть заявлено как отсутствие изменений в экспрессии и вставка нуля в позицию этого гена. Этот подход, как правило, слишком упрощен для использования в дальнейшем анализе.
Второй вариант - оценить недостающее значение на основе других профилей и вставить его в вектор.
 Например, мы можем найти ген, наиболее похожий на отсутствующий ген, судя по всем другим экспериментам, а затем заменить отсутствующее значение значением аналогичного гена для этого эксперимента. Для надежности мы также можем найти наиболее похожие тыс. генов и использовать среднее значение этих генов для этого эксперимента в качестве замены. Сравнительное исследование показало, что это k - метод ближайших соседей работает лучше, чем заполнение пропущенных значений нулями или средними значениями этого гена в других экспериментах [18]. В литературе по статистике есть более сложные методы вменения, но их полезность, учитывая сложные расчеты, еще не ясна.
Например, мы можем найти ген, наиболее похожий на отсутствующий ген, судя по всем другим экспериментам, а затем заменить отсутствующее значение значением аналогичного гена для этого эксперимента. Для надежности мы также можем найти наиболее похожие тыс. генов и использовать среднее значение этих генов для этого эксперимента в качестве замены. Сравнительное исследование показало, что это k - метод ближайших соседей работает лучше, чем заполнение пропущенных значений нулями или средними значениями этого гена в других экспериментах [18]. В литературе по статистике есть более сложные методы вменения, но их полезность, учитывая сложные расчеты, еще не ясна.Наконец, размер векторного пространства может быть меньше, чем n , где интересующие профили экспрессии содержат данные для всех генов в этом пространстве. Поскольку отсутствующие данные не оцениваются, это наиболее консервативный метод анализа, хотя и ценой отбрасывания некоторых данных.
Угол вектора соответствует коэффициенту корреляции Пирсона
Одним из наиболее фундаментальных показателей в статистике является коэффициент корреляции Пирсона (обозначаемый как r ).
 Это представляет собой широко используемую меру сходства между n -кортежами. С векторами экспрессии геометрическая картина сходства состоит в том, что векторы указывают в одном и том же направлении пространства экспрессии. Эта картинка эквивалентна двум векторам с небольшим углом между ними. Когда векторы экспрессии не коррелированы, они ортогональны. Это приводит к следующему замечанию.
Это представляет собой широко используемую меру сходства между n -кортежами. С векторами экспрессии геометрическая картина сходства состоит в том, что векторы указывают в одном и том же направлении пространства экспрессии. Эта картинка эквивалентна двум векторам с небольшим углом между ними. Когда векторы экспрессии не коррелированы, они ортогональны. Это приводит к следующему замечанию.Примечание 1. Корреляция векторов экспрессии соответствует углу θ между этими векторами. Малый угол ( r около 1) подразумевает корреляцию, Угол около 90° ( r около нуля) подразумевает отсутствие корреляции, а угол около 180° ( r около -1) подразумевает антикорреляцию.
Это замечание мотивировано рассмотрением взаимосвязи между коэффициентом корреляции Пирсона ( r ) и векторным углом (θ). (Мы используем обозначение, где <, > представляет скалярное произведение, также называемое скалярным произведением, и где cov(,) — это ковариация между упорядоченными n -кортежи.
 ) Для двух векторов x и y формулы для r и θ:
) Для двух векторов x и y формулы для r и θ:и внутренний продукт меняются местами. На практике аргумент обратного косинуса и r почти идентичны, потому что ковариация по существу представляет собой скалярное произведение с поправкой на среднее, а средние значения векторов выражения близки к нулю. (На самом деле ковариация и скалярный продукт идентичны для векторов с нулевым средним значением.) Таким образом, ни одна из мер не имеет преимущества из-за почти одинаковой производительности на реальных данных выражения (рис. 2а).
Рисунок 2Связь между коэффициентом корреляции Пирсона и углом, а также статистическое распределение углов. (a) Были рассчитаны коэффициенты корреляции Пирсона и углы между 180 парами реальных профилей транскрипции. Сопоставление одного показателя с другим показывает их тесную взаимосвязь. (b) Статистическое распределение углов в большом и разнообразном наборе данных (300 профилей) [19] вычислялось путем вычисления углов между всеми возможными парами (всего 44 850 углов) векторов экспрессии.
 Данные были взяты с веб-сайта Rosetta Inpharmatics [34], а программное обеспечение, используемое для расчета углов, общедоступно для загрузки с нашего веб-сайта [20].
Данные были взяты с веб-сайта Rosetta Inpharmatics [34], а программное обеспечение, используемое для расчета углов, общедоступно для загрузки с нашего веб-сайта [20].Изображение в полный размер
Для генных векторов углы являются мерой того, насколько похожи два гена экспрессируются в экспериментах. Для векторов экспериментов углы являются мерой того, насколько похожи два эксперимента по генам. Для экспериментальных векторов количественный смысл распределения θ может быть получен путем изучения набора разнообразных профилей транскрипции. Был получен и опубликован набор из 300 профилей транскрипции в S. cerevisiae из широкого спектра генных делеций и обработок [19].]. Мы преобразовали эти профили в экспериментальные векторы и вычислили все возможные углы между векторами (всего 44 850 углов). (Компьютерный исходный код, написанный в Matlab™, общедоступен на нашем веб-сайте [20]). Эти углы дали распределение со средним значением 88,4° (близко к ортогональному, как и ожидалось) и стандартным отклонением 7,4° (рис.
 2b). На практике мы обнаружили, что 60° и 120° являются полезными пороговыми значениями значимости корреляции или антикорреляции соответственно.
2b). На практике мы обнаружили, что 60° и 120° являются полезными пороговыми значениями значимости корреляции или антикорреляции соответственно.Метод векторной алгебры проиллюстрирован с использованием общедоступного набора данных. Профиль транскрипции небольшой молекулы рапамицина был профилирован тремя исследовательскими группами в четырех отдельных исследованиях [4,11,21,22]. Он имеет очень драматический профиль экспрессии, в котором сотни генов быстро (в течение нескольких минут) активируются или подавляются. Известно, что белковые мишени рапамицина (белки Tor) воспринимают питательные вещества. При обработке в качестве экспериментального вектора искали другие экспериментальные векторы, которые имели малый угол с вектором рапамицина. Против того же набора из 300 различных профилей экспрессии, описанных ранее [19] не удалось найти ни одного вектора, который имел бы угол менее 60° с экспериментальным вектором рапамицина (данные не показаны). Однако в другом исследовании были идентифицированы два вектора с меньшими углами к вектору экспрессии рапамицина (углы 44° и 47°) [11].
 Эти подобные векторы соответствовали удалению высококачественного углерода или азота из среды. Таким образом, можно сделать вывод, что белки Tor регулируют реакцию на качество среды по углероду и азоту. Это пример использования углов для определения функций неохарактеризованных белков.
Эти подобные векторы соответствовали удалению высококачественного углерода или азота из среды. Таким образом, можно сделать вывод, что белки Tor регулируют реакцию на качество среды по углероду и азоту. Это пример использования углов для определения функций неохарактеризованных белков.Очевидно, что углы обеспечивают количественную меру для утверждения полногеномного сходства. Эта мера важна при заявлениях о мишени небольшой молекулы, эффектах делеции гена или специфичности лекарства. Ортогональные углы (подразумевающие некорреляцию), когда ожидается или заявлено сходство, вызывают вопросы о достоверности рассматриваемой гипотезы.
Отношение величин является естественной второй метрикой для сравнения двух векторов экспрессии
Преимуществом векторной алгебры является расширение от углов до отношений величин, для которых другие формулировки неудобны или не имеют аналогов. Два четырехмерных вектора x = [1 0 2 -1] T и y = [2 0 4 -2] T имеют θ = 0 (подразумевая, что r = 1).
 Однако существует важное различие между векторами, не идентифицированными этими мерами, поскольку мы можем заметить, что y = 2 x . Эта информация фиксируется путем вычисления отношения величин векторов.
Однако существует важное различие между векторами, не идентифицированными этими мерами, поскольку мы можем заметить, что y = 2 x . Эта информация фиксируется путем вычисления отношения величин векторов.Замечание 2. Помимо угла, отношение величин векторов (α) является второй мерой подобия двух векторов экспрессии. Для двух векторов x и y это вычисляется как: r и θ, заманчиво думать, что величина β = (cov( y , y )/cov( x , x )) 1/2 может вести себя аналогично α . С теми же векторами, что и выше, β = α = 2. При рассмотрении двух векторов x = [2 2 2 2] T и y = [1 2 1 2] T , можно рассчитать, что α = 0,79, ожидаемое значение y является «меньшим» вектором. Однако β = 0,5/0 = ∞. Действительно, компонент среднего вычитания ковариации фундаментально изменяет поведение β по сравнению с α, что делает его непригодной мерой величины вектора экспрессии.
 Элегантная особенность рассмотрения данных микрочипов в качестве векторов экспрессии заключается в том, что и углы, и величины являются естественными измерениями, имеющими важное биологическое значение, как будет обсуждаться в следующих разделах.
Элегантная особенность рассмотрения данных микрочипов в качестве векторов экспрессии заключается в том, что и углы, и величины являются естественными измерениями, имеющими важное биологическое значение, как будет обсуждаться в следующих разделах.Поиск подпространств является важным шагом в анализе векторов экспрессии
Другим преимуществом обработки данных экспрессии как векторов в пространстве, а не как n -кортежей является связанное понятие подпространств. С экспериментальными векторами эта концепция особенно ценна. Векторное пространство эксперимента может быть разделено на подпространства, наиболее естественно, когда подпространства соответствуют совместно регулируемым или функционально связанным генам. Это проще всего сделать с помощью аннотированных списков, в которых гены классифицированы по функциям. Мюнхенский информационный центр белковых последовательностей (MIPS) предоставляет широко используемую функциональную группировку генов [23].
Рассмотрение подпространств почти всегда является неотъемлемой частью анализа.
 С точки зрения определенных подпространств множество различных векторов эксперимента могут «схлопываться» в одинаковые векторы. Это позволяет разложить векторы на суммы общих и различных компонентов. Например, стрессовые реакции дрожжей (такие как повреждение ДНК или тепловой шок) состоят из общего ответа, характерного для стресса, и специфического ответа на конкретный стресс. Идентификация этих подпространств остается целью биологии. Другим примером являются белки Tor, которые имеют множество эффекторов, один из которых называется Ure2p. Сравнение экспрессионных векторов обработки рапамицином с Делеция URE2 показывает, что широкогеномный угол между этими двумя векторами составляет 76°, и поэтому векторы демонстрируют лишь слабую корреляцию. Однако вычисление угла этих же векторов внутри подпространства генов, контролируемых Ure2p, дает угол 13° [11]. В отношении этого подпространства генов обработка рапамицином и делеция URE2 почти идентичны. Эксперименты показывают, что обработка рапамицином приводит к дефосфорилированию Ure2p, что подтверждает этот низкий угол [4,21].
С точки зрения определенных подпространств множество различных векторов эксперимента могут «схлопываться» в одинаковые векторы. Это позволяет разложить векторы на суммы общих и различных компонентов. Например, стрессовые реакции дрожжей (такие как повреждение ДНК или тепловой шок) состоят из общего ответа, характерного для стресса, и специфического ответа на конкретный стресс. Идентификация этих подпространств остается целью биологии. Другим примером являются белки Tor, которые имеют множество эффекторов, один из которых называется Ure2p. Сравнение экспрессионных векторов обработки рапамицином с Делеция URE2 показывает, что широкогеномный угол между этими двумя векторами составляет 76°, и поэтому векторы демонстрируют лишь слабую корреляцию. Однако вычисление угла этих же векторов внутри подпространства генов, контролируемых Ure2p, дает угол 13° [11]. В отношении этого подпространства генов обработка рапамицином и делеция URE2 почти идентичны. Эксперименты показывают, что обработка рапамицином приводит к дефосфорилированию Ure2p, что подтверждает этот низкий угол [4,21]. Таким образом, важно учитывать углы не только для всего генома, но и для важных подпространств.
Таким образом, важно учитывать углы не только для всего генома, но и для важных подпространств.Влияние мутаций на векторные углы и величины
При изучении конкретного процесса с помощью профилирования транскрипции обычно также проводят профилирование транскрипции того же процесса после удаления одного или нескольких генов, о которых известно, что они вовлечены. Например, это было проведено с мутантами с делецией МАР-киназы после обработки феромонами [10], делециями эффекторов белков Tor после обработки рапамицином [11] и делециями lexA после УФ-облучения [24].
Когда эффектор какого-либо процесса удаляется, результирующий вектор часто не является некоррелированным в подпространстве, включающем этот эффектор, но уменьшается по величине. Например, при наличии двух транскрипционных факторов с перекрывающейся специфичностью к некоторым генам делеция одного может быть компенсирована наличием второго с аналогичной (хотя и более слабой) индукцией тех же генов.
 Если эффектор действительно является эксклюзивным регулятором некоторого набора генов, то при его удалении можно ожидать, что результирующий вектор эксперимента в этом подпространстве будет ортогонален (не коррелирован) с исходным вектором. Однако биологические сети, как правило, проявляют избыточность в своем контроле над генами - более обычно ожидается уменьшение величины вектора, чем вращение в сторону перпендикулярности (некорреляция). Таким образом, важно полагаться на координатное использование углов и величин в анализе профиля выражения, что не всегда выполняется в литературе.
Если эффектор действительно является эксклюзивным регулятором некоторого набора генов, то при его удалении можно ожидать, что результирующий вектор эксперимента в этом подпространстве будет ортогонален (не коррелирован) с исходным вектором. Однако биологические сети, как правило, проявляют избыточность в своем контроле над генами - более обычно ожидается уменьшение величины вектора, чем вращение в сторону перпендикулярности (некорреляция). Таким образом, важно полагаться на координатное использование углов и величин в анализе профиля выражения, что не всегда выполняется в литературе.Совместное использование углов и соотношений векторных величин является инструментом для биологических открытий
Когда кто-то характеризует профиль транскрипции нехарактерной делеции гена или обработки малой молекулой, первая операция, которую обычно следует выполнять, — это сравнение этот профиль как экспериментальный вектор со всеми другими доступными экспериментальными векторами из того же организма.
Рисунок 3 Выполняя такое сравнение, можно частично охарактеризовать ген или идентифицировать мишень небольшой молекулы [19].]. Окрашивая результаты сравнения, имитируя схемы ложной окраски, обычно встречающиеся на микроматрицах, можно быстро просмотреть большой набор профилей на наличие коррелированных, некоррелированных или антикоррелированных с эталонным профилем, который тестируется [11]. Красная цветовая схема соответствует корреляции, желтая — некорреляции, а зеленая — антикорреляции (рис. 3). Это общее изображение называется массивом колориметрического сравнения (CCA). Это также может быть выполнено с отношениями векторных величин, где красный цвет представляет большую величину, желтый - неизменную величину, а зеленый - уменьшенную величину.
Выполняя такое сравнение, можно частично охарактеризовать ген или идентифицировать мишень небольшой молекулы [19].]. Окрашивая результаты сравнения, имитируя схемы ложной окраски, обычно встречающиеся на микроматрицах, можно быстро просмотреть большой набор профилей на наличие коррелированных, некоррелированных или антикоррелированных с эталонным профилем, который тестируется [11]. Красная цветовая схема соответствует корреляции, желтая — некорреляции, а зеленая — антикорреляции (рис. 3). Это общее изображение называется массивом колориметрического сравнения (CCA). Это также может быть выполнено с отношениями векторных величин, где красный цвет представляет большую величину, желтый - неизменную величину, а зеленый - уменьшенную величину.Иллюстрация использования массива колориметрических сравнений (CCA) для получения информации о сотовой сети передачи сигналов. (a) Используя данные конкурентной гибридизации при исследовании белков-мишеней рапамицина (Tor) [11], углы между эталонным вектором экспрессии штамма дикого типа, обработанным рапамицином, и четырьмя другими векторами экспрессии представлены на ОСО.
 Профиль клеток, переведенных с глутамина на пролин, показывает, что на уровне всего генома и в пределах показанных подпространств наблюдается сильное сходство (44° на уровне всего генома) с профилем клеток, обработанных рапамицином. Однако клетки, подвергшиеся тепловому шоку, имеют ортогональный (некоррелированный) вектор экспрессии. Удаление гена URE2 ( ure2Δ ) не создает корреляции всего генома, но создает корреляцию в подпространстве генов пути дискриминации азота (NDP). Наконец, клетки, содержащие аллель tap42-11 аллеля TAP42 , обработанные рапамицином, показывают, что Tap42p находится ниже белков Tor в контроле экспрессии генов рибосомных белков. (b) Анализ, аналогичный анализу в (a), может быть выполнен с использованием отношений векторных величин (α). Общий зеленый цвет CCA отражает тот факт, что эти четыре вектора экспрессии имеют меньшую величину, чем эталонный профиль обработки рапамицином. Величина полногеномного вектора экспрессии теплового шока значительно меньше.
Профиль клеток, переведенных с глутамина на пролин, показывает, что на уровне всего генома и в пределах показанных подпространств наблюдается сильное сходство (44° на уровне всего генома) с профилем клеток, обработанных рапамицином. Однако клетки, подвергшиеся тепловому шоку, имеют ортогональный (некоррелированный) вектор экспрессии. Удаление гена URE2 ( ure2Δ ) не создает корреляции всего генома, но создает корреляцию в подпространстве генов пути дискриминации азота (NDP). Наконец, клетки, содержащие аллель tap42-11 аллеля TAP42 , обработанные рапамицином, показывают, что Tap42p находится ниже белков Tor в контроле экспрессии генов рибосомных белков. (b) Анализ, аналогичный анализу в (a), может быть выполнен с использованием отношений векторных величин (α). Общий зеленый цвет CCA отражает тот факт, что эти четыре вектора экспрессии имеют меньшую величину, чем эталонный профиль обработки рапамицином. Величина полногеномного вектора экспрессии теплового шока значительно меньше. Удаление URE2 , однако, увеличивает величину экспрессии подпространства генов NDP до уровней, сравнимых с таковыми в клетках, обработанных рапамицином. Когда TAP42 мутирует в аллель tap42-11 , индукция гена NDP серьезно нарушается, что указывает на то, что Tap42p является важным регулятором экспрессии гена NDP ниже белков Tor. Повторение этого анализа по многим эффекторам и многим подпространствам генов раскрывает массу информации о транскрипционной сети ниже по течению от белков Tor [11].
Удаление URE2 , однако, увеличивает величину экспрессии подпространства генов NDP до уровней, сравнимых с таковыми в клетках, обработанных рапамицином. Когда TAP42 мутирует в аллель tap42-11 , индукция гена NDP серьезно нарушается, что указывает на то, что Tap42p является важным регулятором экспрессии гена NDP ниже белков Tor. Повторение этого анализа по многим эффекторам и многим подпространствам генов раскрывает массу информации о транскрипционной сети ниже по течению от белков Tor [11].Изображение в натуральную величину
Чтобы понять наиболее общие отношения, полезно в первой строке CCA сравнить векторы всего эксперимента. Это дает важную полногеномную характеристику изучаемых профилей — в этих значениях должны быть обоснованы утверждения о глобальном поведении. Как обсуждалось ранее, углы и величины внутри подпространств важны для анализа - поэтому в последующих строках сравниваются одни и те же экспериментальные векторы в различных подпространствах генома.
 Изучая ряд подпространств, этот анализ можно использовать для разделения профиля транскрипции и определения того, какие эффекторы ответственны за определенные паттерны экспрессии. Рассматривая углы всего генома, а также углы внутри интересующих подпространств, CCA раскрывает множество информации об изучаемых векторах экспрессии (рис. 3). CCA также можно использовать для идентификации структуры сигнальных сетей.
Изучая ряд подпространств, этот анализ можно использовать для разделения профиля транскрипции и определения того, какие эффекторы ответственны за определенные паттерны экспрессии. Рассматривая углы всего генома, а также углы внутри интересующих подпространств, CCA раскрывает множество информации об изучаемых векторах экспрессии (рис. 3). CCA также можно использовать для идентификации структуры сигнальных сетей.Разложение по сингулярным числам в анализе профиля выражений
Далее мы исследуем идеи, связанные с уменьшением размерности векторов выражений. Уменьшение размерности является общей проблемой во многих дисциплинах науки и техники. Вопросы включают в себя: каковы основные части информации в профиле транскрипции и что такое шум? Если полный набор генов (около 6000 в 90 368 S. cerevisiae 90 369) несет избыточную информацию, насколько малое подмножество мы можем выбрать? Являются ли большинство профилей транскрипции просто комбинацией меньшего числа профилей транскрипции? Первый инструмент, который мы обсуждаем, — это разложение по сингулярным числам (SVD).

SVD — это матричная факторизация, раскрывающая многие важные свойства матрицы. Это стандартный инструмент во многих областях физических наук, и многие алгоритмы матричной алгебры используют SVD. Учитывая n × p прямоугольную матрицу данных A n × p профилей экспрессии (опять же, где n — количество генов, p 9036), мы можно получить следующую факторизацию:
, где U и V ортонормированы, а D диагональны. (Математические детали SVD можно найти в материалах и методах.) Интуиция, стоящая за SVD, проста. Пусть и я будет i -м столбцом U . Обратите внимание, что этот вектор-столбец имеет размерность n . Лучший вектор (в смысле, который можно сделать математически точным, см. Материалы и методы), который фиксирует (охватывает) экспериментальные векторы A это u 1 . Точно так же лучшие два вектора-столбца, которые охватывают векторы эксперимента A , это u 1 и u 2 .
 В пределе все n векторов u i точно охватывают все экспериментальные векторы A . Точно так же столбцы V в порядке убывания представляют собой p -мерные векторы, которые лучше всего охватывают генные векторы А . Эти идеи лучше всего проиллюстрировать примером.
В пределе все n векторов u i точно охватывают все экспериментальные векторы A . Точно так же столбцы V в порядке убывания представляют собой p -мерные векторы, которые лучше всего охватывают генные векторы А . Эти идеи лучше всего проиллюстрировать примером.Первый столбец U , u 1 лучше всего охватывает (то есть при умножении на константу) столбцы A . Вместе со вторым столбцом A точно захвачено путем взятия линейных комбинаций u 1 и u 2 . В этом случае u 3 и u 4 не нужны для захвата А . Точно так же первый столбец V , v 1 лучше всего охватывает векторы генов (ряды) A . Первое значение по диагонали D измеряет вклад u 1 и v 1 в захват A , а следующее значение измеряет вклад u и 8 6 .
 v 2 изготовитель. В этом случае большой размер первого сингулярного значения указывает на то, что u 1 и v 1 фиксируют большую часть информации в A . Эти значения по диагонали D называются сингулярными значениями A . Матрицы, которые содержат в основном избыточные столбцы (матрицы низкого ранга), имеют сингулярные значения, которые быстро затухают, потому что матрица эффективно натянута на небольшое количество векторов. Однако матрицы, содержащие очень независимые столбцы (матрицы высокого ранга), имеют сингулярные значения, которые медленно затухают. В пределе единичная матрица, имеющая максимально возможный ранг n , имеет сингулярные значения, которые вообще не затухают — все они едины.
v 2 изготовитель. В этом случае большой размер первого сингулярного значения указывает на то, что u 1 и v 1 фиксируют большую часть информации в A . Эти значения по диагонали D называются сингулярными значениями A . Матрицы, которые содержат в основном избыточные столбцы (матрицы низкого ранга), имеют сингулярные значения, которые быстро затухают, потому что матрица эффективно натянута на небольшое количество векторов. Однако матрицы, содержащие очень независимые столбцы (матрицы высокого ранга), имеют сингулярные значения, которые медленно затухают. В пределе единичная матрица, имеющая максимально возможный ранг n , имеет сингулярные значения, которые вообще не затухают — все они едины.Для данных микрочипов SVD можно использовать для выявления доминирующих базовых моделей поведения. Например, изучение данных клеточного цикла [25] с помощью SVD показало, что среди первых векторов U ( u 1 u 2 ,.
 ..) первый соответствует стационарному а последующие соответствуют колебательному поведению, которое можно было бы ожидать от таких данных [15,16]. SVD также можно использовать для «подавления шума» профилей путем пересчета матрицы данных с использованием только значащих и я векторов (значительность определяется чтением i -го единственного числа вдоль диагональной матрицы D .) SVD также можно использовать для оценки пропущенных значений.
..) первый соответствует стационарному а последующие соответствуют колебательному поведению, которое можно было бы ожидать от таких данных [15,16]. SVD также можно использовать для «подавления шума» профилей путем пересчета матрицы данных с использованием только значащих и я векторов (значительность определяется чтением i -го единственного числа вдоль диагональной матрицы D .) SVD также можно использовать для оценки пропущенных значений.Метод, называемый анализом основных компонентов (PCA) [26], тесно связан с SVD. В PCA факторизация применяется к ковариационной матрице данных, а не к исходной матрице данных. Если данные скорректированы по среднему значению, и SVD, и PCA дают одинаковую информацию. Если данные взяты из временного ряда, то главные компоненты могут соответствовать производным данных [27].
К базису векторов выражений
Одной из самых мощных идей линейной алгебры является понятие базисных векторов.
 Помимо построения пространства, базисные векторы могут быть выбраны для выделения важных характеристик данных или просто для эффективного хранения данных. Например, функция sin x может быть выражена как в полиномиальном, так и в экспоненциальном базисе,
Помимо построения пространства, базисные векторы могут быть выбраны для выделения важных характеристик данных или просто для эффективного хранения данных. Например, функция sin x может быть выражена как в полиномиальном, так и в экспоненциальном базисе,Первый базис явно неудобен - он бесконечномерен и мало что дает для понимания. Однако второй базис захватывает синусоиду более компактно и обеспечивает более глубокое понимание. Многие успехи векторной алгебры в сжатии изображений, сглаживании и обнаружении сигналов связаны с идентификацией соответствующих базисных функций.
Эта концепция имеет важное значение при анализе данных профилирования транскрипции. Рассматривая данные как векторы выражения, как правильно выразить данные? Данные изначально лежат в основе генов. Но разве это лучшая основа? Одну смену базиса мы уже рассмотрели - СВД. В этом случае u i и против и векторов являются базисными векторами для пространств векторов эксперимента и векторов генов соответственно.
 Хотя базисные векторы очень эффективны, сами векторы полностью искусственны и не соответствуют реальным профилям.
Хотя базисные векторы очень эффективны, сами векторы полностью искусственны и не соответствуют реальным профилям.Важный вопрос биологии заключается в том, сколько существует различных фундаментальных клеточных состояний или переходов. Может случиться так, что их относительно мало, и что клеточные состояния или переходы по существу являются суперпозициями конечного числа основных состояний или переходов. Этот вопрос легко ставится в пространстве выражений, потому что, если гипотеза верна, полный набор профилей выражений можно исследовать для наименьшего числа базисных векторов, которые могут построить почти идентичный весь набор. Если профиль добавляется в матрицу данных и не может быть адекватно построен другими существующими профилями, то он становится базисным вектором. Набор базисных векторов, сформированный этой процедурой, можно рассматривать как содержащий строительные блоки клеточного состояния или переходного пространства. Таким образом, было бы интересно попытаться найти базисные векторы для всех экспериментальных векторов, используя фактические экспериментальные векторы, а не искусственные базисы, которые мало что дают.

Во-первых, как можно оценить, сколько базисных векторов требуется? Эта задача соответствует оценке ранга матрицы данных. Эта проблема нахождения приблизительного ранга матрицы, k , является общей. СВД, как описано выше, часто используется. Используя SVD, обычно ищут резкое падение сингулярных значений для оценки ранга. Предположим, что сингулярные значения падают ниже определенного порога при некотором значении. Это значение служит логичным выбором для к . На самом деле первые k векторов u i из A служат наилучшей основой для соединения A . Однако в нашем случае мы хотим, чтобы базисные векторы были подмножеством исходных векторов A . Это более сложная проблема.
Мы исследовали эти концепции, используя два больших набора данных профилей транскрипции, созданных в S. cerevisiae : набор из 300 ранее проанализированных профилей экспрессии и второй набор из более чем 170 профилей экспрессии различных реакций дрожжей на окружающую среду [19].
Рисунок 4 ,28]. Мы преобразовали эти наборы в матрицы данных экспериментальных векторов и вычислили сингулярные значения каждой матрицы. Для каждой матрицы сингулярные значения быстро затухали (рис. 4). Этот распад показывает, что столбцы матрицы далеки от ортогональности, а базис содержит небольшое количество u i векторов могут эффективно захватывать исходную матрицу. Интересно, что затухание сингулярных значений откликов окружающей среды было намного быстрее, чем более разнообразный набор из 300 профилей (сравните рис. 4b с 4a). Это связано с ограниченным количеством реакций, которыми обладают дрожжевые клетки при стрессе. Это также предполагает, что существует небольшое количество переходов строительных блоков, которым могут подвергаться дрожжи, и что другое поведение является, по крайней мере частично, суперпозицией этих переходов.
,28]. Мы преобразовали эти наборы в матрицы данных экспериментальных векторов и вычислили сингулярные значения каждой матрицы. Для каждой матрицы сингулярные значения быстро затухали (рис. 4). Этот распад показывает, что столбцы матрицы далеки от ортогональности, а базис содержит небольшое количество u i векторов могут эффективно захватывать исходную матрицу. Интересно, что затухание сингулярных значений откликов окружающей среды было намного быстрее, чем более разнообразный набор из 300 профилей (сравните рис. 4b с 4a). Это связано с ограниченным количеством реакций, которыми обладают дрожжевые клетки при стрессе. Это также предполагает, что существует небольшое количество переходов строительных блоков, которым могут подвергаться дрожжи, и что другое поведение является, по крайней мере частично, суперпозицией этих переходов.Использование SVD для оценки количества основных векторов экспрессии, необходимых для эффективного покрытия набора профилей.
 (a) Набор из 300 различных профилей экспрессии [19] был преобразован в матрицу векторов экспрессии и вычислены сингулярные значения, нормализованные таким образом, чтобы первое сингулярное значение было равно 1. (b) Набор 173 профиля различных реакций дрожжей на окружающую среду [28] были преобразованы в матрицу векторов экспрессии и обработаны, как в (а).
(a) Набор из 300 различных профилей экспрессии [19] был преобразован в матрицу векторов экспрессии и вычислены сингулярные значения, нормализованные таким образом, чтобы первое сингулярное значение было равно 1. (b) Набор 173 профиля различных реакций дрожжей на окружающую среду [28] были преобразованы в матрицу векторов экспрессии и обработаны, как в (а).Изображение в натуральную величину
Но как найти эти строительные блоки, фундаментальные векторы экспрессии в наборе профилей? Вместо использования u i векторов из SVD (которые представляют собой линейные комбинации векторов эксперимента) было бы полезно определить, какие фактические векторы эксперимента наиболее полезны для формирования основы для матрицы. То есть было бы полезно выражать профили через другие профили (базовые векторы), а не просто как списки генов (рис. 5). Существует ряд возможных алгоритмов для идентификации этих векторов базисного эксперимента.
Рисунок 5 Мы протестировали различные алгоритмы, особенно те, которые используют проекции 9.0398 и я векторов на A , чтобы идентифицировать оптимальные базисные векторы-кандидаты. (Исходный код одного из таких алгоритмов общедоступен в Интернете по адресу [20].) Хотя небольшие подмножества экспериментальных векторов могут охватывать весь набор экспериментальных векторов, было обнаружено, что существует много таких подмножеств экспериментальных векторов, которые имеют сравнимый охват. способность к A (данные не показаны). Это говорит о том, что клетка, вероятно, имеет небольшое количество фундаментальных переходов, хотя многие разные группы переходов (представленные экспериментальными векторами), по-видимому, почти одинаково способны охватывать транскрипционный диапазон клеточного поведения.
Мы протестировали различные алгоритмы, особенно те, которые используют проекции 9.0398 и я векторов на A , чтобы идентифицировать оптимальные базисные векторы-кандидаты. (Исходный код одного из таких алгоритмов общедоступен в Интернете по адресу [20].) Хотя небольшие подмножества экспериментальных векторов могут охватывать весь набор экспериментальных векторов, было обнаружено, что существует много таких подмножеств экспериментальных векторов, которые имеют сравнимый охват. способность к A (данные не показаны). Это говорит о том, что клетка, вероятно, имеет небольшое количество фундаментальных переходов, хотя многие разные группы переходов (представленные экспериментальными векторами), по-видимому, почти одинаково способны охватывать транскрипционный диапазон клеточного поведения.Профиль транскрипции рапамицина, выраженный двумя чередующимися основаниями. Слева показана часть традиционной основы для профиля транскрипции (показаны только пять генов из примерно 6000).
 Экспериментальный вектор обработки рапамицином был спроецирован на пять экспериментальных векторов, показанных справа. Коэффициенты для вектора экспрессии рапамицина в этой пятимерной основе показаны в крайнем правом углу.
Экспериментальный вектор обработки рапамицином был спроецирован на пять экспериментальных векторов, показанных справа. Коэффициенты для вектора экспрессии рапамицина в этой пятимерной основе показаны в крайнем правом углу.Полноразмерное изображение
При таком поведении, возможно, идеальными базисными векторами для переходного пространства будут базисные вектора для экспериментов, в которых выборочно модулируется только один сигнальный путь. Этого можно достичь с помощью небольших молекул, таких как рапамицин, которые избирательно модулируют один сигнальный путь с полной специфичностью. Если бы у вас была коллекция небольших молекул, которые могли бы избирательно модулировать каждый сигнальный путь в клетке, тогда можно было бы просто спроецировать экспериментальный вектор на экспериментальные векторы этих небольших молекул и определить, какие пути активированы и в какой степени. Это сразу же охарактеризовало бы профиль экспрессии на очень мощной основе, которая обеспечивает глубокое понимание биологии.

Выводы
Мы описали различные методы, основанные на векторной алгебре, для анализа данных экспрессии всего генома. Некоторые из этих методов использовались ранее, но мы обнаружили, что, рассматривая профили экспрессии как векторы, либо в смысле генов, либо в смысле экспериментов, мы получаем более глубокое понимание существующих методов и можем использовать эти идеи в новых направлениях.
Угол между двумя векторами по существу эквивалентен коэффициенту корреляции Пирсона, и изучение изменений величин, а также углов дает важную биологическую информацию. В частности, мы обнаружили, что разложение векторного пространства эксперимента на набор меньших подпространств с использованием, например, функциональных категорий приводит к краткому, но полезному описанию биологической системы (рис. 3). Эти типы полногеномных описаний необходимы для понимания больших объемов сложных данных экспрессии. Мышление в терминах векторных пространств естественным образом привело к идее оптимальных базисных векторов, но с ограничением, что эти базисные векторы принадлежат исходному набору векторов выражений.
 Это может быть полезным способом характеристики профилей экспрессии. Мы описали полезность разложения по сингулярным числам как инструмента для уменьшения размерности проблемы и того понимания, которое оно дает для решения проблемы нахождения базисных векторов.
Это может быть полезным способом характеристики профилей экспрессии. Мы описали полезность разложения по сингулярным числам как инструмента для уменьшения размерности проблемы и того понимания, которое оно дает для решения проблемы нахождения базисных векторов.Полный анализ данных экспрессии всего генома включает множество вопросов, которые здесь не обсуждаются. Недавно была отмечена важность предварительной обработки и нормализации для исправления различных артефактов [29,30]. Искусственно большие кратные изменения, вызванные малыми значениями соотношений (красный/зеленый или наоборот), должны быть численно ограничены в экспериментах по конкурентной гибридизации. Присвоение уровня значимости наблюдаемым изменениям уровней экспрессии также является важным вопросом, и к нему обращались с помощью ряда различных подходов, чаще всего с получением статистической модели шума для получения оценок кратных изменений [31,32]. . Для массивов олигонуклеотидов существуют аналогичные, а иногда и более сложные проблемы для тех же шагов.
 Наконец, существует множество методов кластеризации и интеллектуального анализа данных для понимания структуры данных другими способами. Соответствующие методы следует выбирать тщательно, в зависимости от типа данных и вопросов, на которые необходимо ответить. Поскольку количество данных экспрессии быстро увеличивается, больше инструментов, таких как разработанные здесь, будут играть важную роль в понимании биологических состояний и переходов.
Наконец, существует множество методов кластеризации и интеллектуального анализа данных для понимания структуры данных другими способами. Соответствующие методы следует выбирать тщательно, в зависимости от типа данных и вопросов, на которые необходимо ответить. Поскольку количество данных экспрессии быстро увеличивается, больше инструментов, таких как разработанные здесь, будут играть важную роль в понимании биологических состояний и переходов.Материалы и методы
Программное обеспечение
Компьютерное программное обеспечение было написано на языке программирования Matlab™ и общедоступно для загрузки с нашего веб-сайта [20].
Разложение сингулярного значения (SVD)
SVD - это матричный фактор:
, где D - диагональ и U и V - ортонормические ( UU
- 2
- 9.
- 9.
- 2
- 2
- 6
- 2
- 6
- 2 T. = I N × N и VV T = V T v = I P = I P = I PA 6 = I 68 P68686868.
 9696 = I 68 P68.6. Диагональные записи D являются сингулярными значениями σ 1 ≥ σ 2 ≥ ... ≥ σ p и столбцы { и я } i = 1,..., n из U и { в и } i = 1,..., p из V называются левым и правым сингулярными векторами соответственно. Для данных микрочипов мы предполагаем, что n > p , поскольку мы обычно представляем матрицу данных как имеющую n строк для генов и p строк для экспериментов, и мы предполагаем, что столбцы линейно независимы.
9696 = I 68 P68.6. Диагональные записи D являются сингулярными значениями σ 1 ≥ σ 2 ≥ ... ≥ σ p и столбцы { и я } i = 1,..., n из U и { в и } i = 1,..., p из V называются левым и правым сингулярными векторами соответственно. Для данных микрочипов мы предполагаем, что n > p , поскольку мы обычно представляем матрицу данных как имеющую n строк для генов и p строк для экспериментов, и мы предполагаем, что столбцы линейно независимы.Геометрическая визуализация СВД следующая. Когда A n × p применяется к p -мерной сфере, в результате получается n -мерный эллипс, главные оси которого вытянуты с коэффициентами σ 1 .
 ., о р по направлениям у и ,...,у р соответственно. (Правые сингулярные векторы v и — оси сферы, которые сопоставляются с u i от до Av i = σ i и и .) Полезность СВД часто основывается на том факте, что она отвечает на следующий важный вопрос: каково наилучшее приближение к А с использованием матрицы более низкого ранга? (Термин «лучший» можно определить математически.) Это важно, потому что сопоставимая матрица с меньшим рангом может сделать основную структуру матрицы более очевидной. Другой способ написания A = UDV T равно:
., о р по направлениям у и ,...,у р соответственно. (Правые сингулярные векторы v и — оси сферы, которые сопоставляются с u i от до Av i = σ i и и .) Полезность СВД часто основывается на том факте, что она отвечает на следующий важный вопрос: каково наилучшее приближение к А с использованием матрицы более низкого ранга? (Термин «лучший» можно определить математически.) Это важно, потому что сопоставимая матрица с меньшим рангом может сделать основную структуру матрицы более очевидной. Другой способ написания A = UDV T равно:Тогда математически можно показать, что наилучшее приближение размерности k получается частичной суммой первых k слагаемых [33].
 Иногда термины σ i и и v i T называются «характеристическими модами». Это представление аналогично представлению сигнала суммой его мод Фурье. SVD можно использовать для удаления шума из данных путем пересчета суммы с малыми сингулярными значениями, установленными на ноль.
Иногда термины σ i и и v i T называются «характеристическими модами». Это представление аналогично представлению сигнала суммой его мод Фурье. SVD можно использовать для удаления шума из данных путем пересчета суммы с малыми сингулярными значениями, установленными на ноль.Измерение базисного качества
Пусть A будет матрицей n × p , где столбцы A представляют набор из p профилей транскрипции по n генов. k векторов экспрессии выбраны из A в качестве основы для полного набора. Пусть B будет матрицей, столбцы которой состоят из k векторов экспрессии ( B , следовательно, равно n × k ). Способность B формировать основу для остальных p - k векторов A (обозначенных x i ) проверяется применением теоремы о проекции.
 Пусть P будет матрицей проекции для B , то есть P = B ( B T B ) -1 T 9 . Мера перекрывающей способности основания B по направлению к x i равно:
Пусть P будет матрицей проекции для B , то есть P = B ( B T B ) -1 T 9 . Мера перекрывающей способности основания B по направлению к x i равно:Пока γ не станет ниже определенного порога для исходной матрицы A , можно протестировать другую коллекцию из k векторов экспрессии или k можно увеличить до включать больше базисных векторов.
В выражении для γ числитель представляет собой «вектор остатков», часть x i , который не мог быть захвачен B . Нормализованная величина остаточного вектора измеряет, насколько хорошо x я может быть построен из k столбцов B .
Ссылки
DeRisi JL, Iyer VR, Brown PO: Изучение метаболического и генетического контроля экспрессии генов в геномном масштабе.
 Наука. 1997, 278: 680-686. 10.1126/наука.278.5338.680.
Наука. 1997, 278: 680-686. 10.1126/наука.278.5338.680.ПабМед КАС Статья Google ученый
Чо Р.Дж., Кэмпбелл М.Дж., Винцелер Э.А., Стейнмец Л., Конвей А., Водика Л., Вольфсберг Т.Г., Габриэлян А.Е., Ландсман Д., Локхарт Д.Дж., Дэвис Р.В.: Полногеномный транскрипционный анализ митотического клеточного цикла. Мол Ячейка. 1998, 2: 65-73.
ПабМед КАС Статья Google ученый
Чу С., ДеРизи Дж., Эйзен М., Малхолланд Дж., Ботштейн Д., Браун П.О., Херсковиц И.: Транскрипционная программа спорообразования у почкующихся дрожжей. Наука. 1998, 282: 699-705. 10.1006/jmbi.1998.2134.
ПабМед КАС Статья Google ученый
Hardwick JS, Kuruvilla FG, Tong JK, Shamji AF, Schreiber SL: Модулируемая рапамицином транскрипция определяет подмножество сигнальных путей, чувствительных к питательным веществам, которые непосредственно контролируются белками Tor.
 Proc Natl Acad Sci USA. 1999, 96: 14866-14870. 10.1073/пнас.96.26.14866.
Proc Natl Acad Sci USA. 1999, 96: 14866-14870. 10.1073/пнас.96.26.14866.ПабМед КАС ПабМед Центральный Статья Google ученый
Голуб Т.Р., Слоним Д.К., Тамайо П., Хуард С., Гаасенбек М., Месиров Дж.П., Коллер Х., Лох М.Л., Даунинг Дж.Р., Калиджиури М.А. и др.: Молекулярная классификация рака: открытие класса и предсказание класса по экспрессии генов мониторинг. Наука. 1999, 286: 531-537. 10.1016/S0378-4371(00)00404-0.
ПабМед КАС Статья Google ученый
Росс Д.Т., Шерф У., Эйзен М.Б., Перу С.М., Рис С., Спеллман П., Айер В., Джеффри С.С., Ван де Рейн М., Уолтем М. и др.: Систематические вариации в паттернах экспрессии генов в линиях раковых клеток человека . Нат Жене. 2000, 24: 227-235. 10.1038/73432.
ПабМед КАС Статья Google ученый
">
Perou CM, Sorlie T, Eisen MB, van de Rijn M, Jeffrey SS, Rees CA, Pollack JR, Ross DT, Johnsen H, Akslen LA и др.: Молекулярные портреты опухолей молочной железы человека. Природа. 2000, 406: 747-752. 10.1038/35021093.
ПабМед КАС Статья Google ученый
Brazma A, Jonassen I, Vilo J, Ukkonen E: Предсказание регуляторных элементов гена in silico в геномном масштабе. Геном Res. 1998, 8: 1202-1215.
ПабМед КАС ПабМед Центральный Google ученый
Holstege FC, Jennings EG, Wyrick JJ, Lee TI, Hengartner CJ, Green MR, Golub TR, Lander ES, Young RA: Анализ регуляторной схемы эукариотического генома. Клетка. 1998, 95: 717-728.
ПабМед КАС Статья Google ученый
Робертс С.Дж., Нельсон Б., Мартон М.Дж., Стоутон Р.
 , Мейер М.Р., Беннет Х.А., Хе Ю.Д., Дай Х., Уокер В.Л., Хьюз Т.Р. профили экспрессии генов. Наука. 2000, 287: 873-880. 10.1126/наука.287.5454.873.
, Мейер М.Р., Беннет Х.А., Хе Ю.Д., Дай Х., Уокер В.Л., Хьюз Т.Р. профили экспрессии генов. Наука. 2000, 287: 873-880. 10.1126/наука.287.5454.873.ПабМед КАС Статья Google ученый
Шамджи А.Ф., Курувилла Ф.Г., Шрайбер С.Л.: Разделение программы транскрипции, индуцированной рапамицином, среди эффекторов белков Tor. Карр Биол. 2000, 10: 1574-1581. 10.1016/С0960-9822(00)00866-6.
ПабМед КАС Статья Google ученый
Clark EA, Golub TR, Lander ES, Hynes RO: Геномный анализ метастазов показывает важную роль RhoC. Природа. 2000, 406: 532-535. 10.1038/35020106.
ПабМед КАС Статья Google ученый
Бразма А., Вило Дж.: Анализ данных экспрессии генов. ФЭБС лат. 2000, 480: 17-24. 10.1016/С0014-5793(00)01772-5.
ПабМед КАС Статья Google ученый
Бразма А., Робинсон А., Кэмерон Г., Эшбернер М.: Универсальный магазин данных микрочипов. Природа. 2000, 403: 699-700. 10.1038/35001676.
ПабМед КАС Статья Google ученый
Холтер Н.С., Митра М., Маритан А., Чеплак М., Банавар Дж.Р., Федоров Н.В.: Фундаментальные паттерны, лежащие в основе профилей экспрессии генов: простота из сложности. Proc Natl Acad Sci USA. 2000, 97: 8409-8414. 10.1073/пнас.150242097.
ПабМед КАС ПабМед Центральный Статья Google ученый
Альтер О., Браун П.О., Ботштейн Д.: Разложение по сингулярным числам для обработки и моделирования данных экспрессии всего генома. Proc Natl Acad Sci USA. 2000, 97: 10101-10106. 10.1073/пнас.97.18.10101.
ПабМед КАС ПабМед Центральный Статья Google ученый
Wickens TD: Геометрия многомерной статистики. Под редакцией: Хиллсдейл, Нью-Джерси. 1995, Лоуренс Эрлбаум Ассошиэйтс
Google ученый
- Jiaming Fan
Троянская О., Кантор М., Шерлок Г., Браун П., Хасти Т., Тибширани Р., Ботштейн Д., Альтман Р.Б.: Методы оценки недостающих значений для ДНК-микрочипов. Биоинформатика. 2001, 17: 520-525. 10.1093/биоинформатика/17.6.520.
ПабМед КАС Статья Google ученый
Hughes TR, Marton MJ, Jones AR, Roberts CJ, Stoughton R, Armor CD, Bennett HA, Coffey E, Dai H, He YD и др.: Функциональное открытие с помощью сборника профилей экспрессии. Клетка. 2000, 102: 109-126.
ПабМед КАС Статья Google ученый
Лаборатория Стюарта Шрайбера. [http://www.schreiber.chem.harvard.edu]
">Bertram PG, Choi JH, Carvalho J, Ai W, Zeng C, Chan TF, Zheng XF: Трехсторонняя регуляция Gln3p с помощью TOR, Ure2p и фосфатаз. Дж. Биол. Хим. 2000, 275: 35727-35733. 10.1074/jbc.M004235200.
ПабМед КАС Статья Google ученый
Mewes HW, Heumann K, Kaps A, Mayer K, Pfeiffer F, Stocker S, Frishman D: MIPS: база данных геномов и белковых последовательностей. Нуклеиновые Кислоты Res. 1999, 27: 44-48. 10.1093/нар/27.1.44. [http://www.mips.biochem.mpg.de/]
PubMed КАС ПабМед Центральный Статья Google ученый
">Spellman PT, Sherlock G, Zhang MQ, Iyer VR, Anders K, Eisen MB, Brown PO, Botstein D, Futcher B: Комплексная идентификация генов, регулирующих клеточный цикл дрожжей Saccharomyces cerevisiae , с помощью гибридизации на микрочипах. Мол Биол Селл. 1998, 9: 3273-3297.
ПабМед КАС ПабМед Центральный Статья Google ученый
Джонсон Р.А., Вичерн Д.В.: Прикладной многомерный статистический анализ. Верхнее седло. Под редакцией: Ривер, Нью-Джерси. 1998, Прентис Холл
Google ученый
">Gasch AP, Spellman PT, Kao CM, Carmel-Harel O, Eisen MB, Storz G, Botstein D, Brown PO: Программы геномной экспрессии в ответ дрожжевых клеток на изменения окружающей среды. Мол Биол Селл. 2000, 11: 4241-4257.
ПабМед КАС ПабМед Центральный Статья Google ученый
Tseng GC, Oh MK, Rohlin L, Liao JC, Wong WH: Вопросы анализа микрочипов кДНК: фильтрация качества, нормализация каналов, модели вариаций и оценка эффектов генов. Нуклеиновые Кислоты Res. 2001, 29: 2549-2557. 10.1093/нар/29.12.2549.
ПабМед КАС ПабМед Центральный Статья Google ученый
">Chen Y, Dougherty ER, Bittner ML: Решения на основе соотношений и количественный анализ изображений микрочипов кДНК. J Биомед Оптика. 1997, 2: 364-374. 10.1117/1.429838.
КАС Статья Google ученый
Ньютон М.А., Кендзиорски К.М., Ричмонд К.С., Блаттнер Ф.Р., Цуй К.В.: О дифференциальной изменчивости коэффициентов экспрессии: улучшение статистических выводов об изменениях экспрессии генов на основе данных микрочипов. J Компьютерная биология. 2001, 8: 37-52. 10.1089/106652701300099074.
ПабМед КАС Статья Google ученый
">Розетта Инфарматикс. [http://www.rii.com]
Cardenas ME, Cutler NS, Lorenz MC, Di Como CJ, Heitman J: Сигнальный каскад TOR регулирует экспрессию генов в ответ на питательные вещества. Гены Дев. 1999, 13: 3271-3279. 10.1101/гад.13.24.3271.
ПабМед КАС ПабМед Центральный Статья Google ученый
Курсель Дж., Ходурский А., Питер Б., Браун П.О., Ханавальт П.С.: Сравнительные профили экспрессии генов после воздействия УФ-излучения у дикого типа и SOS-дефицитных Кишечная палочка . Генетика. 2001, 158: 41-64.
ПабМед КАС ПабМед Центральный Google ученый
Raychaudhuri S, Stuart JM, Altman RB: Анализ основных компонентов для обобщения экспериментов с микрочипами: применение к временным рядам спорообразования. Pac Symp Biocomput. 2000, 455-466.
Google ученый
Yang YH, Dudoit S, Luu P, Speed TP: Нормализация данных микрочипа кДНК. В микрочипах: оптические технологии и информатика. Под редакцией: Биттнер М.Л., Чен Ю., Дорсел А.Н., Догерти Э.Р. 2001, Беллингем: Международное общество оптической инженерии, 141-152.
Глава Google ученый
Голуб Г.Х., ван Кредит С.Ф.: Матричное вычисление. Балтимор, Мэриленд: Издательство Университета Джона Хопкинса:. 1996
Google ученый
Ссылки для скачивания
Информация об авторе
Авторы и филиалы
Медицинский институт Говарда Хьюза, Центр геномных исследований Бауэра, кафедра химии и химической биологии, Гарвардский университет, Кембридж, Массачусетс, 02138, США
Финни Г. Курувилла и Стюарт Л. Шрайбер
Факультет биостатистики, Гарвардская школа Общественного здравоохранения, Программа информатики, Детская больница, Гарвардская медицинская школа, Бостон, Массачусетс, 02115, США
Peter J Park
Авторы
- Finny G Kuruvilla
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Peter J Park
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Stuart L Schreiber
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
Автор, ответственный за переписку
Связь с
Стюарт Л Шрайбер.
Права и разрешения
Перепечатка и разрешения
Об этой статье
[PDF] Упрощенная система вектора экспрессии бакуловирус-AAV в сочетании с одноэтапной аффинной очисткой позволяет получить запасы rAAV с высоким титром из клеток насекомых.
- DOI: 10.1038/mt.2009.128
- Идентификатор корпуса: 24547972
@article{Smith3009ASB,
title={Упрощенная система экспрессионного вектора бакуловирус-AAV в сочетании с одностадийной аффинной очисткой дает запасы rAAV с высоким титром из клеток насекомых.},
автор = {Ричард Дж. Х. Смит, Джастин Р. Леви и Роберт Котин},
journal={Молекулярная терапия: журнал Американского общества генной терапии},
год = {2009},
объем={17 11},
страницы={
1888-96 гг.
}
} - Richard J. H. Smith, J. Levy, R. Kotin
- Опубликовано 1 ноября 2009 г.

- Биология
- Молекулярная терапия: журнал Американского общества генной терапии Производство rAAV) в последнее время приобрело большой интерес, поскольку область генной терапии, опосредованной rAAV, приближается к клинической практике. В частности, производство векторов rAAV в клетках насекомых с использованием технологии рекомбинантных бакуловирусов оказалось эффективным и масштабируемым способом производства rAAV. Здесь мы описываем метод получения rAAV серотипов 1 и 2 в клетках насекомых с использованием упрощенного вектора экспрессии бакуловирус-AAV…
Посмотреть в PubMed
doi.orgРекомбинантный бакуловирус эффективно генерирует рекомбинантные аденоассоциированные вирусные векторы в культивируемых клетках и личинках насекомых Приложения для переноса генов
- M. Mietzsch
Биология
- 2014
В этой работе разработан OneBac, состоящий из стабильного насекомого Sf9клеточные линии, несущие молчащие копии генов rep и cap AAV1–12, индуцированные при заражении одним бакуловирусом, который также несет геном rAAV, который сочетает в себе полные варианты серотипа AAV со способностью к стабильному наращиванию производства, что в настоящее время является узким местом для перехода AV от испытаний генной терапии до рутинного клинического лечения.

Химически определенная экспрессионная система высокой плотности на основе клеток насекомых для масштабируемого производства векторов AAV
Популяризация системы OneBac, полученной из рекомбинантных бакуловирусов, для увеличения масштабов производства всех рекомбинантных аденоассоциированных вирусных векторов серотипов
- Yang Wu, Zengpeng Han, Fuqiang Xu
Biology
Biorxiv
- 2020
Одиночная программа Systevived Onebac System Wress Word Propure Laboring Laboring Laboring Laboring Laboring Laboring Laboring Laboring Laboring Labory Uping Laborypure Laborypure Labory Properiou , rAAV серотипов 1-13 демонстрируют различную активность в отношении трансдукции in vitro и тропизмов клеточного типа.
OneBac: платформа для масштабируемого и высокотитрового производства векторов аденоассоциированного вируса серотипов 1-12 для генной терапии.
- M. Mietzsch, Sabrina Grasse, R.
 Heilbronn
Heilbronn Biology
Гена терапии человека
- 2014
Для масштабируемого высокопроизводительного выработки. Производство с высокой высокой точки состоящий из стабильных клеточных линий Sf9 насекомых, несущих молчащие копии генов rep и cap AAV1-12, индуцированных при инфицировании одним бакуловирусом, который также несет геном rAAv.
OneBac 2.0: клеточные линии Sf9 для получения векторов AAV1, AAV2 и AAV8 с минимальной инкапсуляцией чужеродной ДНК.
- M. Mietzsch, Henrik Hering, E. Hammer, M. Agbandje-McKenna, S. Золотухин, R. Heilbronn
Биология
Методы генной терапии человека
- 2017 90 представляет собой прогресс в масштабируемом производстве с высоким титром различных серотипов AAV, что приводит к частицам AAV с минимальной упаковкой чужеродной ДНК.
OneBac 2.0: клеточные линии Sf9 для получения векторов AAV5 с повышенной инфекционностью и минимальным инкапсулированием чужеродной ДНК.

- M. Mietzsch, V. Casteleyn, S. Weger, S. Zolotukhin, R. Heilbronn
Биология
Генная терапия человека
- 2015
Надежная система для производства суперобильных рекомбинантных векторов AAV VP1
Two-Step Small Scale Purification of Recombinant Adeno-Associated Viruses
- Shih-Heng Chen, Amy B. Papaneri, Mitzie Walker, Erica Scappini, R. D. Keys, N. Martin
Biology
bioRxiv
- 2019
Простой и эффективный метод очистки рекомбинантных AAV от небольших количеств исходного материала с помощью двухэтапного метода очистки, который устраняет необходимость сбора фракций и трудоемкой оценки отдельных фракционированных аликвот на титр и чистоту.

Получение и очистка рекомбинантных аденоассоциированных векторов.
- Lijun Wang, V. Blouin, Nicole Brument, Mahajoub Bello-Roufai, Achille François
Биология
Методы молекулярной биологии
- 2011
- M. Urabe, Chuantian Ding, R. Kotin
Биология
Генная терапия человека
- 2002
- G. Gao, G. Qu, J. Wilson
Биология
Генная терапия человека
- 2000
- K. Clark, X. Liu, J. Mcgrath, P. Johnson
Биология
Генная терапия человека
- 1999
- J. Rabinowitz, F. Rolling, R. Samulski
Biology
Journal of Virology
- 2002
- Дж. Мегроус, М. Аукойн, Д. Джейкоб, П. Чахал, Н. Аркан, А. Камен
Биология, инженерия
Прогресс биотехнологии
- 2005
- A. Auricchio, M. Hildinger, E. O'Connor, G. Gao, J. Wilson
Biology
Генная терапия человека
- 2001
0 Обзор существующих систем производства и очистки векторов аденоассоциированного вируса (AAV), а также описаны преимущества и недостатки каждой системы.
ПОКАЗАНЫ 1-10 ИЗ 31 ССЫЛОК
СОРТИРОВАТЬ ПОСоответствиеНаиболее влиятельные документыНедавность
Успешное получение псевдотипированных векторов rAAV с использованием модифицированной бакуловирусной системы экспрессии.
Клетки насекомых как фабрика по производству векторов аденоассоциированного вируса типа 2.
от 293 rAAV, продуцируемый клетками, как определено на основе физических свойств и биологической активности.

Очистка векторов рекомбинантных аденоассоциированных вирусов с помощью колоночной хроматографии и ее эффективность in vivo.
Было бы осуществимо подготовить коммерческие векторы AAV в масштабе и чистоте, необходимых для клинических и потенциальных применений путем объединения нового, полностью масштабируемого процесса очистки, описанного здесь, с методом производства B50/гибрид.
Высокоочищенные рекомбинантные аденоассоциированные вирусные векторы являются биологически активными и не содержат обнаруживаемых хелперных вирусов и вирусов дикого типа.
Разработана одностадийная схема очистки, совмещенная с гепариновой аффинностью использование стабильных клеточных линий-продуцентов для производства rAAV, чтобы сделать коммерческое производство векторов AAV для использования человеком действительно жизнеспособным и практичным.

Бессывороточное производство и очистка на колонке аденоассоциированного вируса типа 5.
Перекрестная упаковка генома вектора одного аденоассоциированного вируса (AAV) типа 2 в несколько серотипов AAV обеспечивает трансдукцию с широкой специфичностью
3, 2 и 4, которые установили иерархию для эффективной трансдукции серотип-специфического вектора в зависимости от ткани-мишени.
Стратегии производства векторов рекомбинантных аденоассоциированных вирусов для применения в генной терапии с использованием бакуловирусной технологии.
В этом обзоре рассматриваются стратегии производства rAAV с использованием бакуловирусной технологии в различных масштабах с использованием различных конфигураций биореакторов, а также вопросы обработки и характеристики продукта.

Производство рекомбинантных аденоассоциированных вирусных векторов с использованием системы культивирования суспензий бакуловирусов/клеток насекомых: от встряхиваемых колб до 20-литрового биореактора
-2 производства BEVS в различных масштабах в биореакторах и указывает на то, что требуется дальнейшая оптимизация для производства при высокой плотности клеток.
Выделение высокоинфекционных и чистых векторов аденоассоциированного вируса типа 2 с помощью одноступенчатой гравитационной колонки.
колоночная очистка AAV2 с помощью гравитационного потока на основе его сродства к гепарину без ультрацентрифугирования и различных векторных препаратов, полученных с помощью этого метода, воспроизводимо показала высокие титры, инфекционность и чистоту.


 Указанное свойство – очевидное.
Указанное свойство – очевидное.
 (ВС
+ AD).
(ВС
+ AD). Какой угол
образуют векторы а
я Ъ , если | а | = | Ъ | = 1?
Какой угол
образуют векторы а
я Ъ , если | а | = | Ъ | = 1? Сложение величин сводилось
к сложению отрезков, умножение величин
— к построению прямоугольника на
соответствующих отрезках, деление — к
операции «приложения» геометрических
фигур. Также ненаправленными отрезками
оперировал Декарт. Но уже немецким
ученым Г. Лейбницем была выдвинута идея
построения векторного исчисления,
близкого к современному. В XVI — XVII вв.
Леонардо да Винчи, Галилео Галилей,
Иоганн Кеплер пользовались направленными
отрезками для наглядного представления
сил в физике и астрономии. Так поступал
и Симон Стевин, который, изучая равновесие
тел на наклонной плоскости, дошел до
разложения силы на составляющие
Сложение величин сводилось
к сложению отрезков, умножение величин
— к построению прямоугольника на
соответствующих отрезках, деление — к
операции «приложения» геометрических
фигур. Также ненаправленными отрезками
оперировал Декарт. Но уже немецким
ученым Г. Лейбницем была выдвинута идея
построения векторного исчисления,
близкого к современному. В XVI — XVII вв.
Леонардо да Винчи, Галилео Галилей,
Иоганн Кеплер пользовались направленными
отрезками для наглядного представления
сил в физике и астрономии. Так поступал
и Симон Стевин, который, изучая равновесие
тел на наклонной плоскости, дошел до
разложения силы на составляющие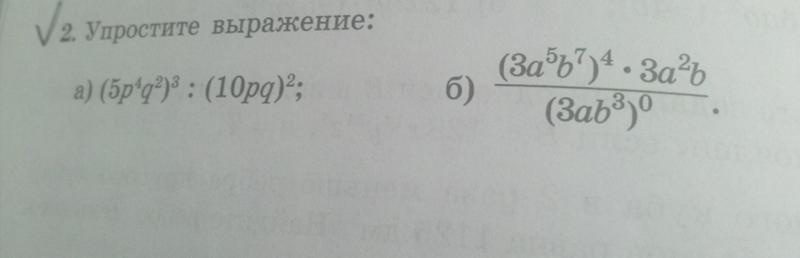 И. Глейзер в работе [5] выделил три
направления развития векторного
исчисления: геометрическое (исчисление
отрезков), физическое (исследование
векторных величин, встречающихся в
естествознании), алгебраическое (расширение
понятия операции при создании современной
алгебры). Развитие первого направления
связано с именем Каспара Весселя
(Норма’ия). Векторная алгебра на
плоскости (двумерное векторное
пространство) построена им почти так
же, как она излагается в современных
учебниках. Отрезки, имеющие любое
направив же, были введены JI. Карно
(Франция, 1803), он же занимался и действиями
с направленными отрезками, позже
его идеи были систематизированы немецким
математиком А. Мебиусом. У Карно
отсутствует систематическое исчисление
направленных отрезков, содержащееся
у Вссселя. Однако главный труд последнего
«Опыт об аналитическом представлении
направит ия и его применениях» не
оказал никакого влияния на развитие
векторного исчисления, так кик на
протяжении целого столетия ученые не
обращали на него внимания, в то время
как пони гис геометрического
количества Карно, под которым он понимал в основном
направленный о I резок, стали употреблять
передовые математики уже в самом начале
XIX в.
И. Глейзер в работе [5] выделил три
направления развития векторного
исчисления: геометрическое (исчисление
отрезков), физическое (исследование
векторных величин, встречающихся в
естествознании), алгебраическое (расширение
понятия операции при создании современной
алгебры). Развитие первого направления
связано с именем Каспара Весселя
(Норма’ия). Векторная алгебра на
плоскости (двумерное векторное
пространство) построена им почти так
же, как она излагается в современных
учебниках. Отрезки, имеющие любое
направив же, были введены JI. Карно
(Франция, 1803), он же занимался и действиями
с направленными отрезками, позже
его идеи были систематизированы немецким
математиком А. Мебиусом. У Карно
отсутствует систематическое исчисление
направленных отрезков, содержащееся
у Вссселя. Однако главный труд последнего
«Опыт об аналитическом представлении
направит ия и его применениях» не
оказал никакого влияния на развитие
векторного исчисления, так кик на
протяжении целого столетия ученые не
обращали на него внимания, в то время
как пони гис геометрического
количества Карно, под которым он понимал в основном
направленный о I резок, стали употреблять
передовые математики уже в самом начале
XIX в. Некоторые вве- асчшыс Карно
термины и символы, в частности обозначение
вектора с помощью черты наверчу ( А
В, С),
сохранились и в наши дни.
Некоторые вве- асчшыс Карно
термины и символы, в частности обозначение
вектора с помощью черты наверчу ( А
В, С),
сохранились и в наши дни. Векторы
Грассман обозначал жирными буквами
латинско- ю алфавита. Принятое сейчас
обозначение вектора г ввел в 1853 г. О. Коши, а единичные иск горы i,j, к в
том же году Гамильтон.
Векторы
Грассман обозначал жирными буквами
латинско- ю алфавита. Принятое сейчас
обозначение вектора г ввел в 1853 г. О. Коши, а единичные иск горы i,j, к в
том же году Гамильтон.
 Но для вектора должно выполняться коммутационное соотношение. Чего я не знаю, так это как сказать Mathematica считать x и y векторами.
Но для вектора должно выполняться коммутационное соотношение. Чего я не знаю, так это как сказать Mathematica считать x и y векторами. Но для этого поста я хочу, чтобы он был простым, и стрелки не будут легко отображаться в исходном коде ниже.
Но для этого поста я хочу, чтобы он был простым, и стрелки не будут легко отображаться в исходном коде ниже. Конечно, это верно только для евклидовых скалярных произведений, поэтому здесь это предположение неявно. Для получения дополнительной информации о том, как работает это определение, см.
Конечно, это верно только для евклидовых скалярных произведений, поэтому здесь это предположение неявно. Для получения дополнительной информации о том, как работает это определение, см. 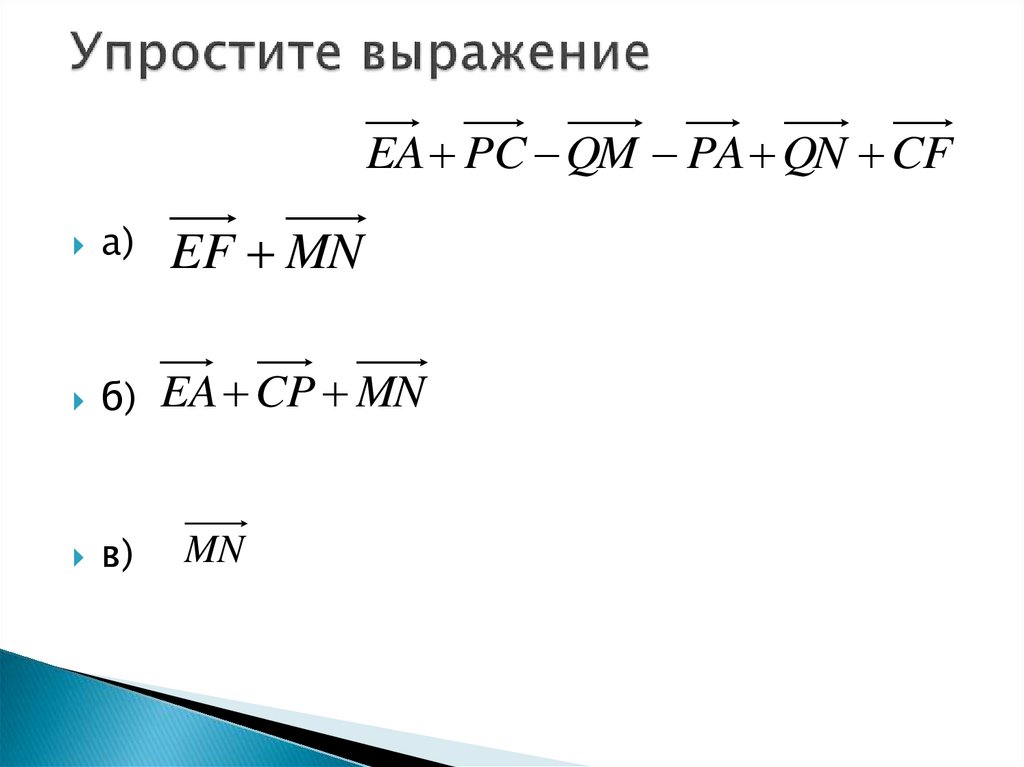 Тем не менее, это широкое поле, которое открывает банку червей, поэтому я бы сказал, просто реализуйте минимум функций, которые вы можете использовать символически, а затем приступайте к конкретной рабочей основе, чтобы вместо этого вы могли писать векторы как списки.
Тем не менее, это широкое поле, которое открывает банку червей, поэтому я бы сказал, просто реализуйте минимум функций, которые вы можете использовать символически, а затем приступайте к конкретной рабочей основе, чтобы вместо этого вы могли писать векторы как списки. Это на самом деле уже сделано, если вы вызовыте
Это на самом деле уже сделано, если вы вызовыте  Однако, если вы работаете только с векторами, то это, безусловно, самый чистый способ.
Однако, если вы работаете только с векторами, то это, безусловно, самый чистый способ. адрес:
(изменить)
адрес:
(изменить)

 С момента их появления использование бакуловирусных векторов для получения белков для очистки стало одной из наиболее широко используемых систем доставки вирусных генов, поскольку полученные уровни экспрессии трудно сопоставить с любой другой эукариотической системой экспрессии. Обширная инженерия для упрощения и ускорения процесса создания рекомбинантного вируса сделала эту систему доступной практически для любой современной биологической лаборатории. Полезность бакуловирусов расширилась с открытием того, что соответствующим образом модифицированный вирус может опосредовать экспрессию генов в самых разных клеточных линиях млекопитающих и, таким образом, может функционировать в качестве гибкого инструмента разработки клеточных анализов. Широкий спектр применений и потенциал для коммерциализации продуктов требуют рассмотрения ряда аспектов системы.
С момента их появления использование бакуловирусных векторов для получения белков для очистки стало одной из наиболее широко используемых систем доставки вирусных генов, поскольку полученные уровни экспрессии трудно сопоставить с любой другой эукариотической системой экспрессии. Обширная инженерия для упрощения и ускорения процесса создания рекомбинантного вируса сделала эту систему доступной практически для любой современной биологической лаборатории. Полезность бакуловирусов расширилась с открытием того, что соответствующим образом модифицированный вирус может опосредовать экспрессию генов в самых разных клеточных линиях млекопитающих и, таким образом, может функционировать в качестве гибкого инструмента разработки клеточных анализов. Широкий спектр применений и потенциал для коммерциализации продуктов требуют рассмотрения ряда аспектов системы.
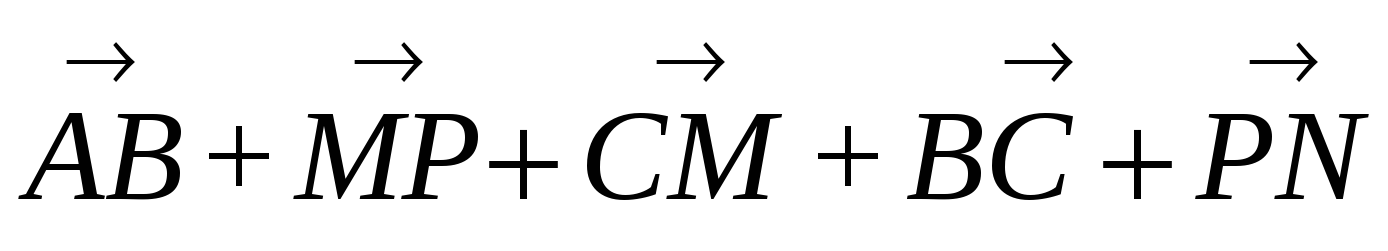


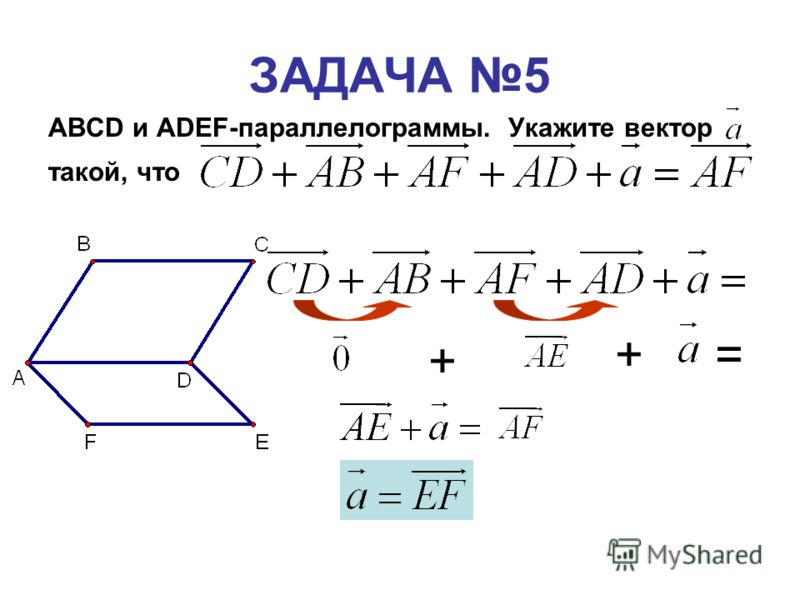 , Фреле-Барран А., Пошон Н., Дементин С., Хивин П., Бутиньи С., Риу Ж.Б., Сальви Д., Сеньерин-Берни Д., Ришо П., Джоярд Дж., Пиньоль Д., Сабати М., Деснос Т., Пебай- Пейрула Э., Даррузе Э., Верне Т., Роллан Н.
Бернода Ф. и соавт.
ПЛОС Один. 2011;6(12):e29191. doi: 10.1371/journal.pone.0029191. Epub 2011 21 декабря.
ПЛОС Один. 2011.
PMID: 22216205
Бесплатная статья ЧВК.
, Фреле-Барран А., Пошон Н., Дементин С., Хивин П., Бутиньи С., Риу Ж.Б., Сальви Д., Сеньерин-Берни Д., Ришо П., Джоярд Дж., Пиньоль Д., Сабати М., Деснос Т., Пебай- Пейрула Э., Даррузе Э., Верне Т., Роллан Н.
Бернода Ф. и соавт.
ПЛОС Один. 2011;6(12):e29191. doi: 10.1371/journal.pone.0029191. Epub 2011 21 декабря.
ПЛОС Один. 2011.
PMID: 22216205
Бесплатная статья ЧВК.