2+n-72)=1/(n+9)заказ решений на аукционе за минимальную цену с максимальным качеством
Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:
- решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
- написание лабораторных, рефератов и курсовых
- выполнение заданий по литературе, русскому или иностранному языку.
Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.
Объединение сервисов в одну систему
Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:
- Форум, где посетители обмениваются идеями и помогают друг другу
- Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
- Аукцион, где цена за товар или услугу определяется в результате торгов
- Система рейтингов, где участники могут оценивать ответы друг друга.
Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Причем, чем больше рейтинг пользователя, тем более значимым становится его голосПринцип работы
Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.
Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.
Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.
Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте).
Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.
За счет чего будет развиваться сервис
Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.
Второе – удобный сервис для заказчиков и для желающих заработать на решениях.
Преимущества для заказчиков
Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.
Преимущества для решающих задания
Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.
Преимущества для владельца сервиса
Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике.
В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.
Что необходимо для создания сервиса
- Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.
- Выбрать платежную систему.
- Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
- Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.
ГДЗ. Математика 5 класс Тарасенкова. Уравнения.
Категория: —>> Математика 5 класс Тарасенкова.
Задание: —>> 553 — 569 570 — 586
наверх
|
|
Задание 553.
Какое из чисел 4. 5, 8 и 10 является корнем уравнения:
Решение:
| 1) 5; | 2) 10; | 3) 4. |
Задание 554.
Решите уравнение устно:
Решение:
| 1) 15 + x: = 55, x = 40; | 3) 60 — y = 45, y = 15; | 5) 88 : x = 8, x = 11; |
| 2) х — 22 = 42, x = 64; | 4) у * 12 = 12, y = 1; | 6) у : 10 = 40, y = 400. |
Задание 555.
Можно ли решить уравнение:
| 1) 8x = 0; | 2) 0 : y = 25; | 3) 5х = 5 | 4) 12 : y = 0? |
Решение:
1) x = 0; 2) Не имеет решений; 3) x = 1; 4) Не имеет решений;
Задание 556.
Решите уравнение:
Решение:
1)28 + (45 + х) = 100;
| 11) 121 : (х — 45) = 11;
|
Задание 557.
Решите уравнение:
Решение:
1) 65 + (х + 23) = 105;
| 6) 9х + 50 = 86;
|
Задание 558.
Составьте уравнение, корнем которого является число:
| а) 8; | б) 14. |
Решение:
| а) 2y = 16; | б) x + 7 = 21. |
Задание 559.
Составьте уравнение, корнем которого является число.
| а) 5; | б) 9. |
Решение:
| а) 25 : x = 5; | б) 5x = 45. |
Задание 560.
Некоторое число увеличили на 67 и получили число 109. Найдите это число.
Решение:
- Некоторое число — x.
- x + 67 = 109;
- x = 109 — 67;
- x = 42.
- Ответ: число 42.
Задание 561.
К некоторому числу прибавили 38 и получили число 245. Найдите это число.
Решение:
- x + 38 = 245;
- x = 245 — 38;
- x = 207.
- Ответ: 207.
Задание 562.
Некоторое число увеличили в 24 раза и получили число 1968. Найдите это число.
Решение:
- 24x = 1968;
- x = 1968 : 24;
- x = 82.
- Ответ: 82.
Задание 563.
Некоторое число уменьшили в 18 раз и получили число 378. Найдите это число.
Решение:
- x : 18 = 378;
- x = 378 * 18;
- x = 6804.
- Ответ: 6408.
Задание 564.
Некоторое число уменьшили на 22 и получили число 105. Найдите это число.
Решение:
- x — 22 = 105;
- x = 105 + 22;
- x = 127.
- Ответ: 127.
Задание 565.
Из числа 128 вычли некоторое число и получили 79. Найдите это число.
Решение:
- 128 — x = 79;
- x = 128 — 79;
- x = 49.
- Ответ: 49.
Задание 566.
Составьте и решите уравнение:
- 1) сумма удвоенного числа х и числа 39 равна 81;
- 2) разность чисел 32 и y в 2 раза меньше числа 64;
- 3) частное суммы чисел х и 12 и числа 2 равно 40;
- 4) сумма чисел х и 12 в 3 раза больше числа 15;
- 5) частное разности чисел у и 12 и числа 6 равно 18;
- 6) утроенная разность чисел у и 17 равна 63.
Решение:
- 1) 2x + 39 = 81
- 2x = 81 — 39;
- 2x = 42;
- x = 42 : 2;
- x = 21;
- 2) (32 — y) * 2 = 64
- 32 — y = 64 : 2;
- 32 — y = 32;
- y = 32 — 32;
- y = 0;
- 3) (x + 12) : 2 = 40
- x + 12 = 40 * 2;
- x + 12 = 80;
- x = 80 — 12;
- x = 68;
- 4) (x + 12) : 3 = 15
- x + 12 = 15 * 3;
- x + 12 = 45;
- x = 45 — 12;
- x = 33;
- 5) (y — 12) : 6 = 18
- y — 12 = 18 * 6;
- y — 12 = 108;
- y = 108 + 12;
- y = 120;
- 6) (y — 17) * 3 = 63
- y — 17 = 63 : 3;
- y — 17 = 21;
- y = 21 + 17;
- y = 38;
Задание 567.
Составьте и решите уравнение:
- 1) разность утроенного числа у и числа 41 равна 64;
- 2) сумма чисел 9 и х в 5 раз меньше числа 80;
- 3) частное суммы чисел у и 10 и числа 4 равно 16;
- 4) разность утроенного числа х и числа 17 равна 10.
Решение:
- 1) 3y — 41 = 64
- 3y = 64 + 41;
- 3y = 105;
- y = 105 : 3;
- y = 15;
- 2) (9 + x) * 5 = 80
- 9 + x = 80 : 5;
- 9 + x = 16;
- x = 16 — 9;
- x = 7;
- 3) (y + 10) : 4 = 16
- y + 10 = 16 * 4;
- y + 10 = 64;
- y = 64 — 10;
- y = 54;
- 4) 3x — 17 = 10
- 3x = 10 + 17;
- 3x = 27;
- x = 27 : 3;
- x = 9;
Задание 568.
Некоторое число увеличили на 5 и полученное число удвоили.
В результате получили число 22. Найдите неизвестное число.
Решение:
- (x + 5) * 2 = 22;
- x + 5 = 22 : 2;
- x + 5 = 11;
- x = 11 — 5;
- x = 6;
Задание 569.
Некоторое число увеличили в 7 раз и полученное число уменьшили на 54. В результате получили число 100. Найдите неизвестное число.
Решение:
- 7x — 54 = 100;
- 7x = 100 + 54;
- 7x = 154;
- x = 154 : 7;
- x = 22;
Задание: —>> 553 — 569 570 — 586
3 класс — уравнения. Задачи на решение уравнеий по математике примеры
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Скачать:Уравнения.
Решение уравнений (PDF)
Интерактивные тренажеры для 3 класса
Т.Е.Демидовой
Б.П.Гейдмана
Математика за 10 минут
Уравнения на сложение и вычитание
1. Реши уравнения.
| 56 — х = 23 | х + 17 = 78 | у — 25 = 34 |
| 49 + y = 67 | 38 — y = 22 | y + 40 = 79 |
2. Заданы выражения: d + 45 и d — 25. Определи значения заданных выражений при:
2.1. d = 36;2.2. d = 52;
2.3. d = 48;
2.4. d = 44.
3. Составь уравнения, содержащие операцию сложения или вычитания, и реши их.
3.1. Используй числа: 56, 78 и переменную X.3.2. Используй числа: 6, 43 и переменную A.
3.3. Используй числа: 12, 54 и переменную В.
3.4. Используй числа: 34, 91 и переменную X.
3.5. Используй числа: 56, 32 и переменную A.
3.6. Используй числа 11, 17 и переменную В.
4. Выбери пример, решением которого является число 32.
| 67 — х = 24 | х + 56 = 98 | у — 5 = 27 |
10.
Вставьте вместо … число так, чтобы получилось верное равенство.
| 12 + … = 67 | 56 — … = 48 | … + 23 = 92 | … — 45 = 32 |
| 45 — … = 11 | 59 — … = 29 | … + 32 = 94 | … + 53 = 88 |
11. Реши задачи.
11.1. До ремонта в школьной столовой находилось 34 стола. После ремонта привезли еще 46 столов. Сколько столов находится в столовой?11.2. На складе находилось 12 мешков с мукой, затем привезли еще 58 мешков и ещё 14 мешков. Сколько мешков с мукой находится на складе?
11.3. Полина собрала с грядки 18 ягод клубники, затем ещё 32 ягоды. Сколько всего ягод клубники собрала Полина?
Уравнения на умножение и деление
1. Реши уравнения.
| 56 : х = 8 | х * 17 = 68 | у : 25 = 2 |
| 28 : y = 4 | 12 * y = 60 | y * 4 = 100 |
2. Реши задачи.
2.1. В кафе стояло 16 стульев. После ремонта кафе количество стульев увеличилось в 3 раза.
Сколько стульев находится в кафе после ремонта?2.2. В механическом цеху завода находилось 56 станков. Одну четвертую часть станков отправили на ремонт. Сколько станков отправили на ремонт и сколько осталось в цеху?
2.3. На рынке продавец продавал ягоды смородины, всего у него было 68 кг ягод. В течении дня он продал половину имеющихся у него ягод. Сколько кг ягод он продал?
3. Составь уравнения, содержащие операцию умножения или деления, и реши их.
3.1. Используй числа: 8, 56 и переменную X.3.2. Используй числа: 6, 42 и переменную A.
3.3. Используй числа: 3, 69 и переменную В.
3.4. Используй числа: 4, 92 и переменную X.
3.5. Используй числа: 39, 3 и переменную A.
3.6. Используй числа: 18, 2 и переменную В.
Уравнения на сложение и вычитание. Упражнения для закрепления навыков. Вариант № 1.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 50.
Реши уравнения на сложение и вычитание.
1) x + 0 = 4 y + 0 = 4 22 — x = 4 38 — y = 25
2) x + 2 = 3 y + 18 = 21 7 — x = 4 3 — y = 1
3) x + 3 = 4 y + 1 = 20 8 — x = 7 8 — y = 5
4) x + 2 = 17 y + 1 = 18 15 — x = 6 44 — y = 14
5) x + 6 = 7 y + 23 = 42 32 — x = 25 24 — y = 2
6) x + 16 = 34 y + 6 = 11 24 — x = 3 31 — y = 15
7) x + 22 = 26 y + 27 = 44 32 — x = 12 39 — y = 18
8) x + 1 = 29 y + 13 = 19 9 — x = 2 35 — y = 19
9) x + 28 = 34 y + 3 = 4 21 — x = 11 16 — y = 2
10) x + 11 = 31 y + 17 = 45 36 — x = 31 12 — y = 0
Уравнения на сложение и вычитание. Вариант № 2.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 50.
Реши уравнения на сложение и вычитание.
1) x + 16 = 20 y + 5 = 10 29 — x = 14 32 — y = 24
2) x + 6 = 14 y + 4 = 6 40 — x = 22 11 — y = 2
3) x + 8 = 30 y + 21 = 38 46 — x = 32 23 — y = 2
4) x + 13 = 32 y + 1 = 2 11 — x = 5 31 — y = 10
5) x + 27 = 38 y + 43 = 48 39 — x = 15 37 — y = 31
6) x + 11 = 47 y + 0 = 3 27 — x = 0 2 — y = 1
7) x + 2 = 7 y + 16 = 41 22 — x = 4 16 — y = 9
8) x + 3 = 10 y + 22 = 24 44 — x = 4 5 — y = 0
9) x + 5 = 20 y + 13 = 32 7 — x = 3 44 — y = 9
10) x + 14 = 25 y + 4 = 18 31 — x = 16 25 — y = 11
Уравнения на сложение и вычитание.
Вариант № 3. Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 50.
Реши уравнения на сложение и вычитание.
1) x + 4 = 13 y + 40 = 47 48 — x = 32 30 — y = 8
2) x + 12 = 25 y + 9 = 10 16 — x = 10 41 — y = 37
3) x + 4 = 20 y + 7 = 20 23 — x = 0 45 — y = 13
4) x + 9 = 25 y + 16 = 41 22 — x = 11 48 — y = 39
5) x + 8 = 22 y + 3 = 28 4 — x = 3 46 — y = 0
6) x + 11 = 38 y + 9 = 16 17 — x = 15 14 — y = 8
7) x + 2 = 5 y + 12 = 15 20 — x = 18 12 — y = 9
8) x + 8 = 21 y + 0 = 2 5 — x = 4 23 — y = 6
9) x + 4 = 27 y + 2 = 10 4 — x = 2 12 — y = 11
10) x + 19 = 33 y + 12 = 28 27 — x = 18 50 — y = 7
Уравнения на сложение и вычитание. Вариант № 4.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 50.
Реши уравнения на сложение и вычитание.
1) x + 35 = 48 y + 3 = 33 34 — x = 3 36 — y = 35
2) x + 17 = 19 y + 6 = 45 8 — x = 4 25 — y = 13
3) x + 1 = 3 y + 3 = 45 12 — x = 1 3 — y = 0
4) x + 2 = 9 y + 25 = 33 12 — x = 0 28 — y = 2
5) x + 0 = 3 y + 20 = 36 30 — x = 28 35 — y = 7
6) x + 25 = 47 y + 3 = 14 39 — x = 27 16 — y = 1
7) x + 6 = 27 y + 2 = 3 29 — x = 28 17 — y = 15
8) x + 11 = 28 y + 2 = 17 35 — x = 31 42 — y = 6
9) x + 3 = 32 y + 13 = 25 39 — x = 27 10 — y = 0
10) x + 6 = 18 y + 29 = 50 45 — x = 26 2 — y = 0
Уравнения на сложение и вычитание. Вариант № 5.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 50.
Реши уравнения на сложение и вычитание.
1) x + 6 = 16 y + 19 = 21 26 — x = 4 5 — y = 3
2) x + 11 = 30 y + 13 = 18 24 — x = 3 23 — y = 14
3) x + 28 = 43 y + 1 = 3 4 — x = 3 32 — y = 9
4) x + 5 = 42 y + 0 = 3 43 — x = 24 25 — y = 11
5) x + 13 = 21 y + 5 = 17 10 — x = 8 3 — y = 2
6) x + 2 = 8 y + 36 = 39 6 — x = 2 30 — y = 11
7) x + 9 = 46 y + 20 = 35 45 — x = 42 24 — y = 3
8) x + 1 = 15 y + 1 = 2 7 — x = 2 47 — y = 25
9) x + 31 = 41 y + 0 = 18 32 — x = 3 26 — y = 3
10) x + 1 = 44 y + 18 = 34 4 — x = 3 46 — y = 30
Уравнения на сложение и вычитание.
Вариант № 6. Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 50.
Реши уравнения на сложение и вычитание.
1) x + 15 = 19 y + 15 = 41 31 — x = 5 20 — y = 2
2) x + 5 = 9 y + 1 = 44 25 — x = 13 11 — y = 6
3) x + 34 = 40 y + 23 = 44 25 — x = 13 28 — y = 19
4) x + 6 = 13 y + 6 = 41 47 — x = 26 40 — y = 30
5) x + 4 = 37 y + 26 = 33 18 — x = 17 27 — y = 25
6) x + 13 = 30 y + 0 = 38 8 — x = 1 10 — y = 5
7) x + 4 = 39 y + 10 = 13 43 — x = 41 25 — y = 0
8) x + 30 = 45 y + 2 = 44 36 — x = 0 46 — y = 7
9) x + 11 = 14 y + 8 = 24 45 — x = 8 1 — y = 0
10) x + 31 = 36 y + 15 = 21 19 — x = 18 12 — y = 0
Уравнения на сложение и вычитание. Вариант № 7.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 50.
Реши уравнения на сложение и вычитание.
1) x + 4 = 8 y + 1 = 4 15 — x = 6 25 — y = 5
2) x + 23 = 50 y + 25 = 35 32 — x = 1 43 — y = 36
3) x + 3 = 4 y + 1 = 2 1 — x = 0 41 — y = 36
4) x + 11 = 24 y + 17 = 22 15 — x = 6 8 — y = 1
5) x + 17 = 28 y + 19 = 30 18 — x = 12 30 — y = 7
6) x + 4 = 6 y + 18 = 44 1 — x = 0 11 — y = 9
7) x + 1 = 21 y + 5 = 6 44 — x = 5 39 — y = 7
8) x + 14 = 17 y + 7 = 8 46 — x = 20 19 — y = 8
9) x + 11 = 13 y + 22 = 32 2 — x = 1 39 — y = 30
10) x + 2 = 11 y + 7 = 33 19 — x = 11 37 — y = 0
Уравнения на сложение и вычитание. Вариант № 8.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 50.
Реши уравнения на сложение и вычитание.
1) x + 10 = 14 y + 9 = 25 39 — x = 17 46 — y = 2
2) x + 22 = 27 y + 5 = 24 24 — x = 20 7 — y = 6
3) x + 11 = 47 y + 8 = 24 35 — x = 2 23 — y = 1
4) x + 26 = 44 y + 0 = 46 49 — x = 32 46 — y = 10
5) x + 3 = 11 y + 0 = 4 9 — x = 0 49 — y = 26
6) x + 14 = 20 y + 2 = 6 44 — x = 29 15 — y = 1
7) x + 19 = 28 y + 10 = 12 10 — x = 9 9 — y = 2
8) x + 5 = 42 y + 2 = 30 19 — x = 7 32 — y = 18
9) x + 5 = 22 y + 7 = 13 45 — x = 18 11 — y = 3
10) x + 1 = 2 y + 0 = 5 28 — x = 4 3 — y = 1
Уравнения на сложение и вычитание.
Вариант № 9. Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 50.
Реши уравнения на сложение и вычитание.
1) x + 12 = 32 y + 0 = 14 8 — x = 4 23 — y = 21
2) x + 12 = 40 y + 6 = 10 21 — x = 14 10 — y = 9
3) x + 4 = 5 y + 20 = 32 29 — x = 15 25 — y = 9
4) x + 6 = 10 y + 19 = 20 29 — x = 11 7 — y = 3
5) x + 3 = 30 y + 2 = 5 34 — x = 32 1 — y = 0
6) x + 13 = 16 y + 27 = 36 19 — x = 4 29 — y = 28
7) x + 6 = 44 y + 2 = 42 23 — x = 21 28 — y = 19
8) x + 5 = 20 y + 35 = 48 39 — x = 2 7 — y = 5
9) x + 30 = 31 y + 5 = 13 7 — x = 1 13 — y = 12
10) x + 9 = 12 y + 20 = 30 19 — x = 12 45 — y = 38
Уравнения на сложение и вычитание. Вариант № 10.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 50.
Реши уравнения на сложение и вычитание.
1) x + 32 = 43 y + 4 = 35 17 — x = 16 28 — y = 18
2) x + 10 = 17 y + 6 = 45 23 — x = 8 6 — y = 1
3) x + 3 = 21 y + 12 = 37 16 — x = 11 41 — y = 21
4) x + 0 = 2 y + 7 = 8 3 — x = 0 7 — y = 6
5) x + 17 = 27 y + 30 = 32 39 — x = 30 45 — y = 9
6) x + 7 = 26 y + 37 = 46 4 — x = 1 26 — y = 21
7) x + 8 = 29 y + 0 = 16 34 — x = 18 31 — y = 27
8) x + 12 = 36 y + 3 = 10 25 — x = 23 11 — y = 0
9) x + 3 = 7 y + 3 = 18 31 — x = 1 13 — y = 8
10) x + 4 = 7 y + 0 = 1 20 — x = 2 11 — y = 5
Уравнения на сложение и вычитание. Вариант № 11.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 50.
Реши уравнения на сложение и вычитание.
1) x + 28 = 47 y + 7 = 28 7 — x = 5 46 — y = 43
2) x + 26 = 36 y + 19 = 36 19 — x = 2 4 — y = 2
3) x + 7 = 14 y + 4 = 33 36 — x = 7 46 — y = 13
4) x + 2 = 13 y + 23 = 27 32 — x = 6 47 — y = 7
5) x + 13 = 16 y + 1 = 29 36 — x = 23 46 — y = 17
6) x + 0 = 12 y + 2 = 5 20 — x = 4 19 — y = 2
7) x + 22 = 37 y + 22 = 32 45 — x = 41 15 — y = 13
8) x + 2 = 5 y + 6 = 12 7 — x = 6 42 — y = 33
9) x + 0 = 21 y + 20 = 26 43 — x = 9 10 — y = 7
10) x + 21 = 38 y + 0 = 21 50 — x = 20 50 — y = 24
Уравнения на сложение и вычитание.
Вариант № 12. Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 50.
Реши уравнения на сложение и вычитание.
1) x + 23 = 24 y + 0 = 5 11 — x = 8 37 — y = 29
2) x + 31 = 40 y + 32 = 42 7 — x = 0 20 — y = 19
3) x + 3 = 6 y + 49 = 50 31 — x = 26 45 — y = 4
4) x + 11 = 38 y + 31 = 50 10 — x = 2 12 — y = 5
5) x + 0 = 4 y + 4 = 7 21 — x = 1 31 — y = 19
6) x + 2 = 10 y + 28 = 38 37 — x = 33 25 — y = 12
7) x + 23 = 41 y + 1 = 43 16 — x = 0 34 — y = 21
8) x + 11 = 38 y + 5 = 12 39 — x = 2 48 — y = 13
9) x + 8 = 12 y + 1 = 4 32 — x = 8 29 — y = 7
10) x + 2 = 3 y + 39 = 48 14 — x = 8 40 — y = 11
Уравнения на сложение и вычитание. Вариант № 13.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 50.
Реши уравнения на сложение и вычитание.
1) x + 0 = 11 y + 3 = 9 24 — x = 16 15 — y = 12
2) x + 21 = 29 y + 32 = 40 38 — x = 37 2 — y = 0
3) x + 17 = 32 y + 26 = 32 25 — x = 4 6 — y = 4
4) x + 19 = 20 y + 12 = 14 43 — x = 23 20 — y = 14
5) x + 10 = 11 y + 24 = 30 39 — x = 28 10 — y = 5
6) x + 17 = 43 y + 28 = 38 2 — x = 0 10 — y = 1
7) x + 25 = 48 y + 9 = 13 8 — x = 5 18 — y = 17
8) x + 3 = 6 y + 35 = 39 7 — x = 0 30 — y = 27
9) x + 1 = 8 y + 5 = 42 29 — x = 25 24 — y = 18
10) x + 13 = 38 y + 13 = 17 13 — x = 5 46 — y = 14
Уравнения на сложение и вычитание. Вариант № 14.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 50.
Реши уравнения на сложение и вычитание.
1) x + 5 = 13 y + 15 = 40 1 — x = 0 8 — y = 7
2) x + 44 = 50 y + 16 = 26 17 — x = 14 8 — y = 4
3) x + 5 = 12 y + 17 = 19 21 — x = 15 3 — y = 2
4) x + 5 = 6 y + 26 = 37 4 — x = 0 37 — y = 22
5) x + 14 = 30 y + 12 = 22 11 — x = 2 19 — y = 2
6) x + 11 = 32 y + 17 = 26 30 — x = 12 25 — y = 22
7) x + 9 = 11 y + 22 = 31 43 — x = 6 5 — y = 2
8) x + 5 = 26 y + 2 = 3 24 — x = 7 35 — y = 3
9) x + 11 = 35 y + 17 = 40 41 — x = 14 20 — y = 1
10) x + 2 = 3 y + 41 = 48 23 — x = 8 23 — y = 12
Уравнения на сложение и вычитание. Вариант № 15.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 50.
Реши уравнения на сложение и вычитание.
1) x + 9 = 20 y + 13 = 50 34 — x = 20 35 — y = 23
2) x + 41 = 49 y + 14 = 44 27 — x = 10 5 — y = 0
3) x + 7 = 10 y + 3 = 17 44 — x = 32 50 — y = 8
4) x + 2 = 9 y + 19 = 29 36 — x = 20 2 — y = 0
5) x + 23 = 41 y + 7 = 32 9 — x = 2 40 — y = 10
6) x + 13 = 30 y + 27 = 30 12 — x = 4 24 — y = 0
7) x + 12 = 43 y + 0 = 1 3 — x = 2 17 — y = 0
8) x + 22 = 40 y + 0 = 23 20 — x = 13 32 — y = 5
9) x + 26 = 31 y + 3 = 4 39 — x = 27 19 — y = 6
10) x + 6 = 33 y + 17 = 22 39 — x = 1 44 — y = 31
Уравнения на сложение и вычитание.
Вариант № 16. Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 50.
Реши уравнения на сложение и вычитание.
1) x + 4 = 11 y + 3 = 9 13 — x = 2 15 — y = 9
2) x + 22 = 35 y + 19 = 48 8 — x = 7 16 — y = 2
3) x + 23 = 44 y + 7 = 12 43 — x = 28 42 — y = 7
4) x + 5 = 38 y + 17 = 23 42 — x = 39 16 — y = 0
5) x + 13 = 18 y + 4 = 33 34 — x = 15 50 — y = 5
6) x + 0 = 2 y + 4 = 46 34 — x = 27 23 — y = 14
7) x + 13 = 25 y + 22 = 39 47 — x = 9 37 — y = 20
8) x + 18 = 26 y + 30 = 44 19 — x = 8 24 — y = 19
9) x + 29 = 50 y + 5 = 15 48 — x = 17 34 — y = 16
10) x + 10 = 48 y + 3 = 5 30 — x = 26 31 — y = 6
Уравнения на сложение и вычитание. Вариант № 17.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 50.
Реши уравнения на сложение и вычитание.
1) x + 10 = 17 y + 23 = 27 49 — x = 37 35 — y = 7
2) x + 1 = 6 y + 5 = 35 22 — x = 1 42 — y = 25
3) x + 22 = 42 y + 7 = 22 38 — x = 3 31 — y = 1
4) x + 16 = 27 y + 45 = 47 24 — x = 17 32 — y = 20
5) x + 25 = 41 y + 3 = 19 50 — x = 3 28 — y = 21
6) x + 9 = 26 y + 7 = 26 21 — x = 6 36 — y = 18
7) x + 4 = 5 y + 19 = 47 21 — x = 12 28 — y = 10
8) x + 19 = 42 y + 17 = 23 7 — x = 0 3 — y = 1
9) x + 6 = 23 y + 8 = 9 44 — x = 24 41 — y = 21
10) x + 16 = 28 y + 1 = 30 21 — x = 5 48 — y = 5
Уравнения на сложение и вычитание. Вариант № 18.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 50.
Реши уравнения на сложение и вычитание.
1) x + 14 = 20 y + 3 = 10 49 — x = 42 11 — y = 3
2) x + 7 = 22 y + 10 = 25 8 — x = 4 31 — y = 24
3) x + 4 = 47 y + 1 = 2 31 — x = 25 18 — y = 13
4) x + 9 = 30 y + 5 = 10 49 — x = 47 25 — y = 21
5) x + 6 = 38 y + 28 = 36 18 — x = 15 2 — y = 1
6) x + 6 = 43 y + 2 = 9 35 — x = 34 12 — y = 10
7) x + 4 = 12 y + 5 = 46 26 — x = 15 13 — y = 5
8) x + 3 = 9 y + 7 = 11 46 — x = 25 24 — y = 16
9) x + 26 = 50 y + 21 = 30 48 — x = 11 18 — y = 1
10) x + 27 = 35 y + 8 = 29 28 — x = 2 6 — y = 3
Уравнения на сложение и вычитание. Вариант № 19.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 50.
Реши уравнения на сложение и вычитание.
1) x + 6 = 8 y + 5 = 16 44 — x = 24 4 — y = 2
2) x + 4 = 5 y + 8 = 48 28 — x = 1 23 — y = 17
3) x + 4 = 13 y + 20 = 25 10 — x = 6 28 — y = 6
4) x + 11 = 26 y + 17 = 37 21 — x = 20 49 — y = 47
5) x + 4 = 45 y + 5 = 17 43 — x = 39 12 — y = 9
6) x + 22 = 32 y + 7 = 10 5 — x = 1 42 — y = 24
7) x + 9 = 43 y + 18 = 39 36 — x = 8 37 — y = 21
8) x + 19 = 22 y + 30 = 42 23 — x = 5 44 — y = 26
9) x + 4 = 7 y + 14 = 48 26 — x = 20 35 — y = 30
10) x + 3 = 6 y + 5 = 31 17 — x = 9 33 — y = 10
Уравнения на сложение и вычитание.
Вариант № 1. Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 9 = 18 y + 4 = 26 96 — x = 22 71 — y = 25
2) x + 14 = 50 y + 36 = 37 35 — x = 32 56 — y = 26
3) x + 10 = 25 y + 56 = 71 80 — x = 0 86 — y = 18
4) x + 58 = 83 y + 1 = 82 72 — x = 21 85 — y = 40
5) x + 12 = 99 y + 48 = 65 13 — x = 9 69 — y = 36
6) x + 67 = 72 y + 9 = 75 79 — x = 16 62 — y = 5
7) x + 5 = 9 y + 21 = 35 81 — x = 12 4 — y = 0
8) x + 6 = 77 y + 6 = 28 82 — x = 78 22 — y = 14
9) x + 1 = 12 y + 49 = 50 64 — x = 47 2 — y = 0
10) x + 20 = 21 y + 28 = 75 98 — x = 47 79 — y = 73
Реши уравнения на сложение, вычитание, умножение и деление. Вариант № 2.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 31 = 100 y + 11 = 43 34 — x = 16 2 — y = 1
2) x + 13 = 56 y + 61 = 95 58 — x = 32 87 — y = 55
3) x + 0 = 30 y + 25 = 91 51 — x = 44 38 — y = 32
4) x + 10 = 28 y + 8 = 9 52 — x = 39 90 — y = 29
5) x + 1 = 10 y + 89 = 97 24 — x = 14 35 — y = 32
6) x + 21 = 25 y + 2 = 19 56 — x = 44 10 — y = 5
7) x + 32 = 59 y + 19 = 38 68 — x = 12 65 — y = 23
8) x + 33 = 36 y + 2 = 16 88 — x = 63 40 — y = 10
9) x + 13 = 19 y + 1 = 12 20 — x = 5 25 — y = 17
10) x + 61 = 67 y + 15 = 30 38 — x = 16 72 — y = 11
Реши уравнения на сложение, вычитание, умножение и деление. Вариант № 3.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 57 = 58 y + 31 = 40 49 — x = 3 87 — y = 59
2) x + 76 = 87 y + 20 = 57 31 — x = 2 26 — y = 23
3) x + 1 = 4 y + 43 = 84 31 — x = 10 64 — y = 28
4) x + 21 = 30 y + 8 = 20 70 — x = 56 19 — y = 0
5) x + 40 = 84 y + 3 = 13 18 — x = 7 45 — y = 21
6) x + 14 = 15 y + 2 = 5 1 — x = 0 28 — y = 12
7) x + 91 = 94 y + 56 = 79 71 — x = 0 49 — y = 40
8) x + 28 = 39 y + 16 = 39 60 — x = 34 99 — y = 95
9) x + 45 = 64 y + 4 = 51 81 — x = 65 54 — y = 0
10) x + 41 = 76 y + 29 = 43 53 — x = 8 52 — y = 12
Реши уравнения на сложение, вычитание, умножение и деление. Вариант № 4.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 26 = 61 y + 31 = 49 63 — x = 8 33 — y = 7
2) x + 5 = 44 y + 16 = 17 5 — x = 3 23 — y = 21
3) x + 69 = 88 y + 2 = 46 35 — x = 4 74 — y = 23
4) x + 19 = 96 y + 0 = 8 47 — x = 18 8 — y = 7
5) x + 4 = 19 y + 63 = 66 63 — x = 5 7 — y = 6
6) x + 20 = 70 y + 3 = 9 75 — x = 63 49 — y = 26
7) x + 13 = 29 y + 43 = 46 3 — x = 1 4 — y = 3
8) x + 19 = 54 y + 6 = 42 39 — x = 23 9 — y = 4
9) x + 52 = 60 y + 76 = 95 1 — x = 0 3 — y = 0
10) x + 12 = 20 y + 21 = 67 14 — x = 6 97 — y = 78
Реши уравнения на сложение, вычитание, умножение и деление.
Вариант № 5. Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 37 = 87 y + 11 = 26 93 — x = 66 94 — y = 76
2) x + 16 = 75 y + 6 = 79 95 — x = 3 90 — y = 9
3) x + 6 = 13 y + 55 = 76 61 — x = 39 28 — y = 11
4) x + 59 = 77 y + 28 = 32 73 — x = 7 85 — y = 4
5) x + 5 = 65 y + 25 = 96 89 — x = 67 95 — y = 93
6) x + 4 = 62 y + 10 = 50 37 — x = 19 64 — y = 23
7) x + 9 = 24 y + 40 = 42 77 — x = 50 18 — y = 16
8) x + 36 = 49 y + 58 = 61 61 — x = 56 87 — y = 5
9) x + 17 = 54 y + 12 = 23 56 — x = 9 21 — y = 2
10) x + 32 = 46 y + 8 = 22 8 — x = 4 90 — y = 71
Реши уравнения на сложение, вычитание, умножение и деление. Вариант № 6.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 24 = 63 y + 49 = 58 56 — x = 22 14 — y = 1
2) x + 25 = 33 y + 49 = 67 26 — x = 5 22 — y = 12
3) x + 50 = 62 y + 22 = 87 79 — x = 37 44 — y = 42
4) x + 6 = 59 y + 27 = 48 63 — x = 32 76 — y = 54
5) x + 50 = 60 y + 55 = 87 25 — x = 7 73 — y = 63
6) x + 0 = 1 y + 46 = 94 62 — x = 52 67 — y = 66
7) x + 16 = 55 y + 19 = 54 21 — x = 1 13 — y = 10
8) x + 21 = 42 y + 49 = 60 89 — x = 56 100 — y = 4
9) x + 17 = 60 y + 25 = 77 6 — x = 3 94 — y = 81
10) x + 3 = 15 y + 4 = 8 33 — x = 30 89 — y = 18
Реши уравнения на сложение, вычитание, умножение и деление. Вариант № 7.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 7 = 27 y + 49 = 83 14 — x = 8 92 — y = 42
2) x + 30 = 63 y + 29 = 68 41 — x = 21 61 — y = 18
3) x + 1 = 6 y + 5 = 78 15 — x = 10 77 — y = 26
4) x + 18 = 65 y + 20 = 25 29 — x = 24 12 — y = 11
5) x + 92 = 97 y + 0 = 49 61 — x = 22 33 — y = 24
6) x + 39 = 75 y + 28 = 99 17 — x = 7 52 — y = 0
7) x + 0 = 45 y + 36 = 77 80 — x = 68 98 — y = 62
8) x + 14 = 35 y + 43 = 49 51 — x = 34 98 — y = 19
9) x + 7 = 25 y + 49 = 96 79 — x = 36 67 — y = 49
10) x + 62 = 91 y + 34 = 56 44 — x = 29 58 — y = 9
Реши уравнения на сложение, вычитание, умножение и деление. Вариант № 8.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 24 = 64 y + 30 = 70 96 — x = 28 21 — y = 16
2) x + 77 = 89 y + 10 = 48 6 — x = 2 62 — y = 43
3) x + 37 = 62 y + 11 = 16 58 — x = 24 20 — y = 13
4) x + 45 = 80 y + 79 = 96 94 — x = 16 82 — y = 10
5) x + 34 = 45 y + 2 = 44 93 — x = 13 20 — y = 9
6) x + 61 = 89 y + 0 = 48 44 — x = 29 6 — y = 0
7) x + 15 = 17 y + 1 = 47 44 — x = 37 55 — y = 46
8) x + 1 = 2 y + 30 = 43 32 — x = 11 93 — y = 63
9) x + 9 = 48 y + 90 = 98 38 — x = 0 41 — y = 0
10) x + 5 = 25 y + 28 = 55 10 — x = 2 84 — y = 20
Реши уравнения на сложение, вычитание, умножение и деление.
Вариант № 9. Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 8 = 53 y + 0 = 7 53 — x = 41 46 — y = 45
2) x + 15 = 51 y + 17 = 20 77 — x = 19 100 — y = 30
3) x + 3 = 17 y + 39 = 78 52 — x = 33 81 — y = 66
4) x + 46 = 91 y + 55 = 97 21 — x = 14 85 — y = 13
5) x + 0 = 5 y + 4 = 36 4 — x = 2 62 — y = 42
6) x + 12 = 36 y + 1 = 5 97 — x = 91 48 — y = 37
7) x + 3 = 16 y + 40 = 43 68 — x = 57 88 — y = 9
8) x + 23 = 64 y + 34 = 100 75 — x = 11 44 — y = 10
9) x + 1 = 29 y + 11 = 83 80 — x = 15 91 — y = 13
10) x + 12 = 82 y + 7 = 21 25 — x = 1 49 — y = 1
Реши уравнения на сложение, вычитание, умножение и деление. Вариант № 10.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 6 = 85 y + 0 = 53 93 — x = 62 99 — y = 61
2) x + 6 = 21 y + 34 = 81 76 — x = 1 82 — y = 79
3) x + 3 = 69 y + 2 = 3 17 — x = 15 79 — y = 17
4) x + 19 = 55 y + 33 = 34 2 — x = 1 22 — y = 2
5) x + 15 = 21 y + 26 = 89 15 — x = 13 88 — y = 75
6) x + 69 = 79 y + 8 = 69 91 — x = 90 65 — y = 6
7) x + 7 = 51 y + 55 = 83 9 — x = 4 1 — y = 0
8) x + 2 = 12 y + 88 = 95 40 — x = 37 76 — y = 45
9) x + 35 = 86 y + 60 = 85 23 — x = 13 52 — y = 23
10) x + 21 = 57 y + 47 = 51 28 — x = 8 91 — y = 13
Реши уравнения на сложение, вычитание, умножение и деление. Вариант № 11.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 3 = 8 y + 20 = 97 49 — x = 30 51 — y = 32
2) x + 10 = 82 y + 60 = 96 19 — x = 4 2 — y = 0
3) x + 27 = 41 y + 23 = 99 52 — x = 11 12 — y = 9
4) x + 37 = 66 y + 15 = 42 42 — x = 5 100 — y = 6
5) x + 11 = 19 y + 16 = 83 86 — x = 25 60 — y = 25
6) x + 1 = 62 y + 51 = 52 1 — x = 0 99 — y = 18
7) x + 0 = 3 y + 83 = 98 60 — x = 41 45 — y = 33
8) x + 19 = 23 y + 1 = 83 63 — x = 30 13 — y = 2
9) x + 13 = 84 y + 3 = 43 12 — x = 9 39 — y = 17
10) x + 7 = 46 y + 4 = 7 73 — x = 15 24 — y = 6
Реши уравнения на сложение, вычитание, умножение и деление. Вариант № 12.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 10 = 27 y + 57 = 75 28 — x = 23 39 — y = 6
2) x + 47 = 86 y + 46 = 60 51 — x = 6 92 — y = 40
3) x + 11 = 14 y + 16 = 69 74 — x = 27 49 — y = 30
4) x + 60 = 76 y + 74 = 75 14 — x = 3 65 — y = 4
5) x + 6 = 15 y + 79 = 87 77 — x = 11 73 — y = 65
6) x + 12 = 24 y + 21 = 49 76 — x = 60 26 — y = 19
7) x + 24 = 58 y + 0 = 1 7 — x = 1 88 — y = 60
8) x + 14 = 17 y + 57 = 90 83 — x = 41 40 — y = 7
9) x + 27 = 43 y + 15 = 23 20 — x = 11 23 — y = 12
10) x + 5 = 100 y + 36 = 90 19 — x = 14 43 — y = 31
Реши уравнения на сложение, вычитание, умножение и деление. Вариант № 13.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 13 = 40 y + 38 = 97 95 — x = 9 17 — y = 2
2) x + 60 = 62 y + 46 = 93 43 — x = 2 22 — y = 17
3) x + 26 = 28 y + 70 = 88 35 — x = 29 91 — y = 38
4) x + 75 = 91 y + 65 = 79 7 — x = 3 46 — y = 32
5) x + 7 = 34 y + 20 = 39 60 — x = 17 93 — y = 4
6) x + 27 = 51 y + 16 = 42 97 — x = 39 86 — y = 69
7) x + 1 = 2 y + 16 = 23 64 — x = 54 59 — y = 31
8) x + 7 = 18 y + 73 = 92 62 — x = 53 78 — y = 62
9) x + 46 = 60 y + 35 = 60 69 — x = 40 44 — y = 23
10) x + 10 = 32 y + 15 = 42 59 — x = 37 84 — y = 18
Реши уравнения на сложение, вычитание, умножение и деление.
Вариант № 14. Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 8 = 24 y + 38 = 40 33 — x = 11 74 — y = 9
2) x + 13 = 20 y + 26 = 28 86 — x = 1 100 — y = 42
3) x + 1 = 99 y + 64 = 95 69 — x = 22 61 — y = 4
4) x + 4 = 29 y + 1 = 6 41 — x = 31 45 — y = 25
5) x + 6 = 11 y + 79 = 90 3 — x = 2 47 — y = 6
6) x + 26 = 33 y + 14 = 83 59 — x = 14 11 — y = 10
7) x + 26 = 42 y + 8 = 58 52 — x = 26 9 — y = 3
8) x + 38 = 46 y + 31 = 34 75 — x = 35 95 — y = 78
9) x + 91 = 96 y + 31 = 51 42 — x = 33 88 — y = 23
10) x + 3 = 11 y + 31 = 42 73 — x = 39 81 — y = 67
Реши уравнения на сложение, вычитание, умножение и деление. Вариант № 15.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 38 = 60 y + 33 = 43 38 — x = 36 80 — y = 20
2) x + 35 = 96 y + 22 = 27 52 — x = 42 12 — y = 5
3) x + 0 = 10 y + 15 = 42 23 — x = 3 59 — y = 53
4) x + 26 = 63 y + 1 = 3 84 — x = 51 12 — y = 4
5) x + 30 = 98 y + 0 = 56 83 — x = 5 52 — y = 7
6) x + 24 = 48 y + 0 = 17 90 — x = 44 95 — y = 72
7) x + 55 = 90 y + 52 = 65 47 — x = 39 53 — y = 36
8) x + 6 = 12 y + 13 = 21 95 — x = 17 24 — y = 13
9) x + 25 = 92 y + 41 = 59 22 — x = 8 86 — y = 23
10) x + 1 = 5 y + 16 = 26 24 — x = 2 63 — y = 22
Реши уравнения на сложение, вычитание, умножение и деление. Вариант № 16.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 6 = 12 y + 58 = 67 93 — x = 80 3 — y = 0
2) x + 14 = 93 y + 0 = 81 56 — x = 24 69 — y = 50
3) x + 20 = 21 y + 45 = 55 20 — x = 17 43 — y = 28
4) x + 2 = 7 y + 23 = 48 26 — x = 22 84 — y = 4
5) x + 34 = 48 y + 18 = 29 89 — x = 39 9 — y = 0
6) x + 5 = 57 y + 53 = 90 93 — x = 75 66 — y = 17
7) x + 21 = 71 y + 60 = 86 67 — x = 4 24 — y = 1
8) x + 41 = 56 y + 42 = 60 44 — x = 18 18 — y = 17
9) x + 23 = 47 y + 56 = 83 11 — x = 4 93 — y = 49
10) x + 9 = 16 y + 1 = 2 69 — x = 64 59 — y = 56
Реши уравнения на сложение, вычитание, умножение и деление. Вариант № 17.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 15 = 33 y + 11 = 58 81 — x = 64 44 — y = 4
2) x + 30 = 63 y + 44 = 53 72 — x = 68 93 — y = 68
3) x + 45 = 46 y + 21 = 52 6 — x = 5 81 — y = 58
4) x + 0 = 6 y + 11 = 60 56 — x = 51 11 — y = 5
5) x + 4 = 20 y + 46 = 99 50 — x = 41 16 — y = 15
6) x + 18 = 34 y + 53 = 91 39 — x = 24 5 — y = 0
7) x + 18 = 98 y + 10 = 12 39 — x = 14 8 — y = 3
8) x + 64 = 73 y + 60 = 69 44 — x = 38 9 — y = 8
9) x + 2 = 17 y + 22 = 31 86 — x = 0 78 — y = 7
10) x + 32 = 61 y + 72 = 95 25 — x = 3 42 — y = 0
Реши уравнения на сложение, вычитание, умножение и деление. Вариант № 18.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 17 = 34 y + 61 = 81 70 — x = 49 46 — y = 20
2) x + 43 = 89 y + 90 = 93 67 — x = 38 1 — y = 0
3) x + 23 = 45 y + 27 = 75 18 — x = 10 28 — y = 2
4) x + 1 = 55 y + 20 = 50 9 — x = 6 32 — y = 1
5) x + 29 = 43 y + 17 = 37 47 — x = 28 62 — y = 2
6) x + 64 = 91 y + 46 = 73 60 — x = 33 61 — y = 5
7) x + 59 = 63 y + 20 = 74 97 — x = 72 95 — y = 4
8) x + 1 = 95 y + 8 = 39 27 — x = 24 14 — y = 6
9) x + 46 = 80 y + 45 = 56 32 — x = 13 97 — y = 93
10) x + 15 = 43 y + 35 = 73 37 — x = 11 74 — y = 24
Реши уравнения на сложение, вычитание, умножение и деление.
Вариант № 19. Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 57 = 82 y + 26 = 52 34 — x = 13 33 — y = 3
2) x + 1 = 3 y + 0 = 2 73 — x = 33 44 — y = 6
3) x + 66 = 98 y + 40 = 75 51 — x = 47 69 — y = 48
4) x + 3 = 27 y + 19 = 53 99 — x = 73 45 — y = 43
5) x + 0 = 10 y + 4 = 83 59 — x = 17 35 — y = 4
6) x + 3 = 48 y + 9 = 19 9 — x = 4 12 — y = 0
7) x + 3 = 7 y + 33 = 84 62 — x = 39 9 — y = 4
8) x + 29 = 55 y + 27 = 65 56 — x = 55 37 — y = 32
9) x + 1 = 29 y + 99 = 100 9 — x = 2 79 — y = 58
10) x + 62 = 71 y + 12 = 16 9 — x = 6 96 — y = 51
ГДЗ по математике 4 класс учебник Моро, Бантова 1 часть
- Тип: ГДЗ, Решебник.
- Автор: Моро М. И., Волкова С. И., Бантова М. А.
- Год: 2020.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
❤️️Ответ к странице 13. Математика 4 класс учебник 1 часть. Авторы: М.И. Моро, М.А. Бантова.
Решебник — страница 13Готовое домашнее задание
Объясни решение по плану:
Ответ:
Делю сотни: сотен 8.
Разделю 8 на 3. В частном будет 2 сотни.
Умножу: 2 ∙ 3 = 6. Разделили 6 сотен.
Вычту: 8 − 6 = 2.
Сравню остаток с делителем: число оставшихся сотен меньше, чем 3; можно продолжать деление.
Делю десятки: 2 сотни и 2 десятка – это 22 десятка.
Разделю 22 на 3. В частном будет 7 дес.
Умножаю 7 ∙ 3 = 21 дес.
Вычитаю 22 − 21 = 1. Сравниваю остаток с делителем: число оставшихся десятков меньше, чем 3; можно продолжать деление.
Делю единицы: 1 дес. и 5 ед.
– это 15 единиц.
Делю 15 на 3. В частном будет 5 единиц.
Умножаю 5 ∙ 3 = 15.
Вычитаю 15 − 15 = 0. Единицы разделили все. Деление закончено.
Ответ: 275.
Номер 60.
Выполни деление с объяснением.
Ответ:
564 : 4
Делю сотни: сотен 5.
Разделю 5 на 4. В частном будет 1 сотня.
Умножу: 1 ∙ 4 = 4. Разделили 4 сотни.
Вычту: 5 − 4 = 1.
Сравню остаток с делителем: число оставшихся сотен меньше, чем 4; можно продолжать деление.
Делю десятки: 1 сотня и 6 десятков – это 16 десятков.
Разделю 16 на 4. В частном будет 4 дес.
Умножаю 4 ∙ 4 = 16 дес.
Вычитаю 16 − 16 = 0.
Делю единицы:
Делю 4 на 4. В частном будет 1 единица.
Умножаю 1 ∙ 4 = 4.
Вычитаю 4 − 4 = 0. Единицы разделили все. Деление закончено.
Ответ: 141.
471 : 3
Делю сотни: сотен 4.
Разделю 4 на 3.
В частном будет 1 сотня.
Умножу: 1 ∙ 3 = 3. Разделили 3 сотен.
Вычту: 4 − 3 = 1.
Сравню остаток с делителем: число оставшихся сотен меньше, чем 3; можно продолжать деление.
Делю десятки: 1 сотня и 7 десятков – это 17 десятков.
Разделю 17 на 3. В частном будет 5 дес.
Умножаю 5 ∙ 3 = 15 дес.
Вычитаю 17 − 15 = 2. Сравниваю остаток с делителем: число оставшихся десятков меньше, чем 3; можно продолжать деление.
Делю единицы: 2 дес. и 1 ед. – это 21 единица.
Делю 21 на 3. В частном будет 7 единиц.
Умножаю 7 ∙ 3 = 21.
Вычитаю 21 − 21 = 0. Единицы разделили все. Деление закончено.
Ответ: 157.
296 : 2
Делю сотни: сотен 2.
Разделю 2 на 2. В частном будет 1 сотня.
Умножу: 1 ∙ 2 = 2.
Вычту: 2 − 2 = 0.
Делю десятки:
Разделю 9 на 2. В частном будет 4 дес.
Умножаю 4 ∙ 2 = 8 дес.
Вычитаю 9 − 8 = 1. Сравниваю остаток с делителем: число оставшихся десятков меньше, чем 2; можно продолжать деление.
Делю единицы: 1 дес. и 6 ед. – это 16 единиц.
Делю 16 на 2. В частном будет 8 единиц.
Умножаю 8 ∙ 2 = 16.
Вычитаю 16 − 16 = 0. Единицы разделили все. Деление закончено.
Ответ: 148.
792 : 4
Делю сотни: сотен 7.
Разделю 7 на 4. В частном будет 1 сотня.
Умножу: 1 ∙ 4 = 4. Разделили 4 сотни.
Вычту: 7 − 4 = 3.
Сравню остаток с делителем: число оставшихся сотен меньше, чем 4; можно продолжать деление.
Делю десятки: 3 сотни и 9 десятков – это 39 десятков.
Разделю 39 на 4. В частном будет 9 дес.
Умножаю 9 ∙ 4 = 36 дес.
Вычитаю 39 − 36 = 3. Сравниваю остаток с делителем: число оставшихся десятков меньше, чем 4; можно продолжать деление.
Делю единицы: 3 дес. и 2 ед. – это 32 единицы.
Делю 32 на 4. В частном будет 8 единиц.
Умножаю 8 ∙ 4 = 32.
Вычитаю 32 − 32 = 0. Единицы разделили все. Деление закончено.
Ответ: 198.
Номер 61.
1) На одной полке 25 книг, а на другой – на b книг меньше. Объясни, что обозначают выражения: 25 − b, 25 + (25 − b).
2) Измени условие задачи, чтобы она решалась так:
Ответ:
1) 25 − b – число книг на другой полке.
25 + (25 − b) – число книг на обеих полках.
2) На одной полке 25 книг, а на другой – в b раз меньше.
25 : b – число книг на другой полке.
25 + 25 : b – число книг на двух полках.
Номер 62.
В школу привезли 10 пачек учебников, по 20 штук в каждой пачке, и ещё 18 учебников. Сколько всего учебников привезли?
Ответ:
1) 20 ∙ 10 = 200 (шт.) – в 10 пачках.
2) 200 + 18 = 218 (шт.)
Ответ: 218 учебников привезли.
Номер 63.
Ответ:
Номер 64.
Вспомни таблицу умножения и скажи, чему равен х в каждом уравнении.
Ответ:
8 ∙ х = 56 х : 7 = 9 72 : х = 9 х = 7 х = 63 х = 8
Номер 65.
1) Начерти 2 отрезка: длина первого 10 см, а длина второго составляет пятую часть длины первого отрезка.
2) Начерти отрезок, третья часть которого равна 3 см.
Ответ:
1) 10 : 5 = 2 (см)
2) 3 ∙ 3 = 9 (см)
Номер 66.
Ответ:
Номер 67.
Убери 2 палочки, чтобы осталось 4 одинаковых квадрата.
Ответ:
Задание внизу страницы
Вычисли.
Ответ:
Задание на полях страницы
Ребус.
Ответ:
Рейтинг
Выберите другую страницу
1 часть
| Учебник Моро | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
|---|
2 часть
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 |
|---|
Ваше сообщение отправлено!
+
ГДЗ по Математике 6 класс Дорофеев, Шарыгин.
РешебникНомера
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 | 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 | 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 | 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 | 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 | 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 | 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 | 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 | 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 | 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 | 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 | 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 | 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 | 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 | 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 | 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 | 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 | 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 | 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 | 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 | 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 | 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 | 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 | 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 | 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 | 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 | 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 | 801 | 802 | 803 | 804 | 805 | 806 | 807 | 808 | 809 | 810 | 811 | 812 | 813 | 814 | 815 | 816 | 817 | 818 | 819 | 820 | 821 | 822 | 823 | 824 | 825 | 826 | 827 | 828 | 829 | 830 | 831 | 832 | 833 | 834 | 835 | 836 | 837 | 838 | 839 | 840 | 841 | 842 | 843 | 844 | 845 | 846 | 847 | 848 | 849 | 850 | 851 | 852 | 853 | 854 | 855 | 856 | 857 | 858 | 859 | 860 | 861 | 862 | 863 | 864 | 865 | 866 | 867 | 868 | 869 | 870 | 871 | 872 | 873 | 874 | 875 | 876 | 877 | 878 | 879 | 880 | 881 | 882 | 883 | 884 | 885 | 886 | 887 | 888 | 889 | 890 | 891 | 892 | 893 | 894 | 895 | 896 | 897 | 898 | 899 | 900 | 901 | 902 | 903 | 904 | 905 | 906 | 907 | 908 | 909 | 910 | 911 | 912 | 913 | 914 | 915 | 916 | 917 | 918 | 919 | 920 | 921 | 922 | 923 | 924 | 925 | 926 | 927 | 928 | 929 | 930 | 931 | 932 | 933 | 934 | 935 | 936 | 937 | 938 | 939 | 940 | 941 | 942 | 943 | 944 | 945 | 946 | 947 | 948 | 949 | 950 | 951 | 952 | 953 | 954 | 955 | 956 | 957 | 958 | 959 | 960 | 961 | 962 | 963 | 964 | 965 | 966 | 967 | 968 | 969 | 970 | 971 | 972 | 973 | 974 | 975 | 976 | 977 | 978 | 979 | 980 | 981 | 982 | 983 | 984 | 985 | 986 | 987 | 988 | 989 | 990 | 991 | 992 | 993 | 994 | 995 | 996 | 997 | 998 | 999 | 1000 | 1001 | 1002 | 1003 | 1004 | 1005 | 1006 | 1007 | 1008 | 1009 | 1010 | 1011 | 1012 | 1013 | 1014 | 1015 | 1016 | 1017 | 1018 | 1019 | 1020 | 1021 | 1022 | 1023 | 1024 | 1025 | 1026 | 1027 | 1028 | 1029 | 1030 | 1031 | 1032 | 1033 | 1034 | 1035 | 1036 | 1037 | 1038 | 1039 | 1040 | 1041 | 1042 | 1043 | 1044 | 1045 | 1046 | 1047 | 1048 | 1049 | 1050 | 1051 | 1052 | 1053 | 1054 | 1055 | 1056 | 1057 | 1058 |
Чему вы научились.
Обязательные уменияГлава 1. ДРОБИ И ПРОЦЕНТЫ
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Глава 2.
ПРЯМЫЕ НА ПЛОСКОСТИ В ПРОСТРАНСТВЕ| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Глава 3. ДЕСЯТИЧНЫЕ ДРОБИ
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Глава 4.
ДЕЙСТВИЯ С ДЕСЯТИЧНЫМИ ДРОБЯМИ| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
Глава 5.
ОКРУЖНОСТЬ| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Глава 6. ОТНОШЕНИЯ И ПРОЦЕНТЫ
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Глава 7.
СИММЕТРИЯ| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Глава 8.
ВЫРАЖЕНИЯ, ФОРМУЛЫ, УРАВНЕНИЯ| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Глава 9.
ЦЕЛЫЕ ЧИСЛА| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Глава 10.
МНОЖЕСТВА, КОМБИНАТОРИКА| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Глава 11.
РАЦИОНАЛЬНЫЕ ЧИСЛА| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
Глава 12.
МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
ГДЗ по математике для 6 класса Дорофеева – это сборник готовых домашних заданий по задачам и примерам из учебника по арифметике, составленного известными российскими авторами – Г.
В. Дорофеевым, И.Ф. Шарыгиным, С.Б. Суворовым и др. Он используется в большинстве общеобразовательных школ России.
Структура ГДЗ по учебнику математики шестого класса от Дорофеева
Во шестом классе школьники углубленно изучают арифметику. Эти знания помогут им постигнуть алгебру и геометрию в старших классах, а также физику, геометрию, химию. Шестиклассники изучают многоугольники и многогранники, обыкновенные и десятичные дроби, проценты и отношения, уравнения с одной переменной, а также множества и комбинаторика.
ГДЗ по математике 6 класса Дорофеева, составленные на основе учебника 2016-2019 гг. в его 4-м издании, включают в себя примеры и задачи на такие темы:
- дроби и проценты;
- прямые на плоскости и в пространстве;
- десятичные дроби;
- действия с десятичными дробями;
- окружность и прямая;
- отношения и проценты;
- центральная и осевая симметрия;
- выражения, формулы, уравнения;
- целые числа
- множества и комбинаторика;
- рациональные числа;
- многоугольники и многогранники.
Изучение перечисленных тем помогает в постижении алгебры и геометрии в старшей школе. Однако для этого важно не просто зазубрить правила и списать в тетрадь готовые домашние задания. Стоит понять теоремы на научиться применять их в решении примеров, задач и уравнений.
Готовые домашние задания для 6 класса на сайте ГДЗ Путина помогают не только ученикам средних школ, но и их родителям. Они могут проверить домашнюю работу своих детей и отказаться от услуг репетитора.
Онлайн-решения от ГДЗ Путина по математике 6 класса к Дорофееву
В интернете немало сайтов с готовыми домашними заданиями по арифметике. При этом ресурс ГДЗ от Путина имеет немало преимуществ для шестиклассников и родителей:
- наличие нескольких вариантов решения примеров и задач;
- ответы по самым свежим изданиям учебников российских школ;
- оформление готовых домашних заданий по требованиям Минобразования РФ;
- круглосуточный доступ со смартфона, планшета, компьютера.
Приведенные факторы делают ГДЗ по математике 6 класса к учебнику Дорофеева удобными и практичными в использовании. Ответы на задачки, примеры и уравнения в нескольких вариантах упростят постижение арифметики шестиклассниками.
Готовые домашние задания включают в себя детальные алгоритмы выполнения примеров и уравнений, что помогает легко разобраться со сложными темами дома без посещения дополнительных занятий.
Популярные решебники
ГДЗ по Математике 6 класс: Виленкин Н.Я.
Издатель: Виленкин Н.Я. Жохов В.И. Чесноков А.С. Шварцбурд С.И. 2013/2019г.
ГДЗ по Математике 6 класс: Мерзляк А.Г.
Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г. / 2019г.
ГДЗ по Математике 6 класс: Никольский С.М.
Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников, А.В. Шевкин. 2015-2018
ГДЗ по Математике 6 класс: Зубарева, Мордкович
Издатель: И.
И. Зубарева, А.Г. Мордкович. 2014-2019г.
ГДЗ по Математике 6 класс: Дорофеев Г.В.
Издатель: Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. 2016-2019г.
3-8
Чтобы найти a и b, составим решаемую систему.-1,576 -2,288 -3,192 -4,144 -6,96 -8,72 -9,64 -12,48 -16,36 -18,32 -24,24
Поскольку ab отрицательно, a и b имеют противоположные знаки. Поскольку a+b положителен, положительное число имеет большее абсолютное значение, чем отрицательное. Перечислите все такие пары целых чисел, которые дают произведение -576.
-1+576=575 -2+288=286 -3+192=189 -4+144=140 -6+96=90 -8+72=64 -9+64=55 -12+48=36 -16+36=20 -18+32=14 -24+24=0
Подсчитайте сумму для каждой пары. 9{2}-4ac}}{2a}.
x=\frac{-64±\sqrt{4096-4\times 9\left(-64\right)}}{2\times 9}
Square 64.
x=\frac{-64± \sqrt{4096-36\left(-64\right)}}{2\times 9}
Умножить -4 на 9.
x=\frac{-64±\sqrt{4096+2304}}{2 \times 9}
Умножить -36 на -64.
x=\frac{-64±\sqrt{6400}}{2\times 9}
Прибавьте 4096 к 2304.
x=\frac{-64±80}{2\times 9}
Возьмите квадратный корень из 6400.
x=\frac{-64±80}{18}
Умножьте 2 раза на 9.
x=\frac{16}{18}
Теперь решите уравнение x=\frac{-64±80}{18}, когда ± равно плюсу. Прибавьте -64 к 80.
x=\frac{8}{9}
Сократите дробь \frac{16}{18} до наименьшего члена, извлекая и сокращая 2.
x=\frac{-144 }{18}
Теперь решите уравнение x=\frac{-64±80}{18}, когда ± минус. Вычтите 80 из -64.
x=-8
Разделите -144 на 18.
x=\frac{8}{9} x=-8
Теперь уравнение решено. 9{ 2 } — 4 x — 5 = 0
Тригонометрия
4 \sin \theta \cos \theta = 2 \sin \theta
Линейное уравнение
y = 3x + 4
Арифметика 939 181811 91
Матрица
\left[ \begin{array} { l l } { 2 } & { 3 } \\ { 5 } & { 4 } \end{array} \right] \left[ \begin{array} { l l l } { 2 } & { 0 } & { 3 } \\ { -1 } & { 1 } & { 5 } \end{массив} \right]
Одновременное уравнение
\left. \begin{cases} { 8x+2y = 46 } \\ { 7x+3y = 47 } \end{cases} \right. 9{2}+2 x-3}
занимательная математика — Решите следующее уравнение: $\sqrt {x + \sqrt {4x + \sqrt {16x + \sqrt {64x + 5}}}} — \sqrt x= 1$
спросил
Изменено 6 лет, 9 месяцев назад
Просмотрено 5к раз
$\begingroup$
В прошлой экзаменационной работе был следующий вопрос, который показался мне интересным.
Я пытался попробовать, но не нашел никаких решений. Как бы с этим справиться?
$$\sqrt {x + \sqrt {4x + \sqrt {16x + \sqrt {64x + 5}}}} — \sqrt x = 1$$
Я вижу связь между $4x$, $16x$ и $64x$, так что, может быть, большее можно упростить до меньшего?
Я призываю вас работать в экзаменационной среде (таким образом, не используя ничего, кроме ручки, бумаги и, возможно, калькулятора).
РЕДАКТИРОВАТЬ: В моем вопросе отсутствовал $-\sqrt x$ в конце, извините!
развлекательно-математические радикалы
$\endgroup$
7
$\begingroup$
$$\sqrt {x + \sqrt {4x + \sqrt {16x + \sqrt {64x + 5}}}} = 1+ \sqrt x$$
Возведение в квадрат $$ \sqrt {4x + \sqrt {16x + \sqrt {64x + 5}}} = 1+ 2\sqrt x$$
Возведение в квадрат $$ \sqrt {16x + \sqrt {64x + 5}} = 1+ 4\sqrt x$$
Квадрат $$ \sqrt {64x + 5} = 1+ 8\sqrt x$$
Возведение в квадрат $$ 5 = 1+ 16\sqrt x$$
$\endgroup$
4
$\begingroup$
Это очень интуитивный подход, основанный на том факте, что я нахожусь в экзаменационной комнате без компьютера и даже без калькулятора.
6-92-120x-4.$$
Используя полиномиальный решатель, есть шесть действительных корней и комплексно-сопряженная пара без очевидного простого значения.
Это ставит под сомнение корректность постановки задачи.
$\endgroup$
5
$\begingroup$
\begin{выравнивание*} \sqrt {x + \sqrt {4x + \sqrt {16x + \sqrt {64x + 5}}}} — \sqrt x & = 1\\ \sqrt {x + \sqrt {4x + \sqrt {16x + \sqrt {64x + 5}}}} & = 1+\sqrt{x}\\ х + \sqrt {4x + \sqrt {16x + \sqrt {64x + 5}}} & = 1+x+2\sqrt{x}\\ \sqrt {4x + \sqrt {16x + \sqrt {64x + 5}}} & = 1+2\sqrt{x}\\ 4x + \sqrt {16x + \sqrt {64x + 5}} & = 1+4x+4\sqrt{x}\\ \sqrt {16x + \sqrt {64x + 5}} & = 1+4\sqrt{x}\\ 16x + \sqrt {64x + 5} & = 1+16x+8\sqrt{x}\\ \sqrt {64x + 5} & = 1+8\sqrt{x}\\ 64x + 5 & = 1+64x+16\sqrt{x}\\ 16\sqrt{x} & = 4\\ х & =\фракция{1}{16}. \end{выравнивание*}
$\endgroup$
$\begingroup$
Лучшее решение, которое я могу себе представить, — это многократно возводить в квадрат, а затем использовать численные методы для нахождения корней полученного многочлена, а затем проверять наличие посторонних ответов в нашем возведении в квадрат.
$\endgroup$
14
$\begingroup$
С дополнительным $\sqrt x$ вы просто возводите в квадрат обе стороны и продолжаете делать это, чудесным образом некоторые термины сокращаются 🙂
$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
г.
Оценка пространственной корреляции и конвергенции распределения ресурсов здравоохранения Китая: данные из региона дельты реки Янцзы | Архивы общественного здравоохранения
- Исследования
- Открытый доступ
- Опубликовано:
- Юйцин Шен 1 и
- Цзешэн Сун ORCID: orcid.org/0000-0001-5705-8308 1
Архивы общественного здравоохранения том 80 , Номер статьи: 207 (2022) Процитировать эту статью
Сведения о показателях
Абстрактный
Фон
Несбалансированное распределение ресурсов здравоохранения в Китае в основном возникает из-за различий между городом и деревней и между городами, решение которых было целью реформ в течение последних десятилетий.
Оценка пространственной корреляции и конвергенции может помочь понять влияние быстроразвивающегося медицинского рынка Китая и последних реформ здравоохранения.
Методы
Метод энтропийного веса был использован для построения индекса обеспеченности ресурсами здравоохранения (HRS) с использованием данных 41 города в кластере в дельте реки Янцзы (YRD) с 2007 по 2019 год.. Коэффициент Дагума Джини, оценка ядерной плотности, карта Морана I и кластерная карта LISA использовались для характеристики пространственно-временной эволюции и агломерации ресурсов здравоохранения, а затем использовалась пространственная панельная модель для оценки конвергенции β путем включения пространственной эффект, неоднородность города и реформы здравоохранения.
Результаты
Предложение медицинских ресурсов в регионе YRD значительно увеличивается и быстро конвергентно. Существует значительная пространственная корреляция и агломерация между провинциями и городами, а значительный эффект пространственного перелива также обнаружен в 9 странах.
2196 β сходимость. Не обнаружено доказательств того, что последние реформы здравоохранения повлияли на сбалансированное распределение и конвергенцию ресурсов здравоохранения.
Заключение
Долгосрочные инвестиции Китая в последние десятилетия привели к более сбалансированному распределению и конвергенции ресурсов здравоохранения между городами. Однако последние реформы здравоохранения не способствуют сбалансированному распределению ресурсов здравоохранения со стороны предложения, и в будущих исследованиях необходим анализ спроса.
Основные моменты
⦁ В этом документе представлено более полное измерение ресурсов здравоохранения с использованием метода энтропийного веса и трех измерений финансовых, человеческих и материальных ресурсов.
⦁ Это исследование предполагает, что при обсуждении распределения ресурсов здравоохранения следует уделять больше внимания пространственному взаимодействию между различными регионами.
⦁ Методология пространственно-временного распределения и конвергентной регрессии используется для проведения исследования справедливости в здравоохранении, чтобы отобразить характерные факты, эволюцию и влияющие факторы межрегионального распределения ресурсов здравоохранения.
⦁ Реформы здравоохранения могут быть добавлены к оценкам пространственной панельной модели конвергенции, которая предоставляет данные о возможных политических последствиях соответствующих реформ.
Отчеты экспертной оценки
История вопроса
Неравное распределение медицинских ресурсов является важной глобальной проблемой [1]. В условиях экзогенного воздействия пандемии коронавирусной болезни 2019 (COVID-19) это означает серьезное неравенство в праве на выживание и здоровье. Инвестиции в здравоохранение становятся одним из приоритетов общественного здравоохранения во всем мире. Наибольший рост как реального ВВП, так и расходов на здравоохранение во всем мире происходит в странах Евразии с формирующимся рынком, в основном представленных семеркой развивающихся рынков (EM7), Бразилией, Россией, Индией, Китаем и Южной Африкой (БРИКС), а также другими развивающимися рынками [2].
. Реформы здравоохранения на этих развивающихся рынках влияют на структуру глобальных расходов на здравоохранение, что в основном связано с реформами, проведенными в Китае [3]. Тем не менее, еще предстоит выяснить, способствует ли увеличение расходов на здравоохранение, происходящее в странах с формирующимся рынком, внутреннему балансу распределения ресурсов между различными регионами в этих странах, и все еще необходимо лучшее понимание пространственной корреляции, которую такой рост расходов оказывает на распределение ресурсов между странами. различные внутренние области.
После того, как в 2003 году разразился кризис тяжелого острого респираторного синдрома (ТОРС), китайское правительство начало выделять больше средств местным (окружным/поселковым) больницам, чтобы восстановить местную систему общественного здравоохранения, которая была сильно ослаблена из-за долгосрочная рыночная реформа [4]. В марте 2009 года Китай начал новый раунд реформ здравоохранения, четко предложив, чтобы увеличение расходов на здравоохранение было сосредоточено на стороне спроса, общественном здравоохранении и на низовом уровне.
Но эти реформы, как правило, уделяли больше внимания оборудованию медицинской инфраструктуры и меньше внимания медицинскому персоналу и его человеческому капиталу. Таким образом, пациенты по-прежнему охотнее выбирают лечение в (городских) больницах высокого уровня, создавая структурную проблему перегрузки, при которой сосуществуют перегруженность больниц высокого уровня и простаивающие ресурсы больниц низкого уровня [5].
После 2010 г. некоторые из пилотных провинций Китая в области медицинской реформы начали проводить реформу нисходящих ресурсов здравоохранения, представленную сочетанием нисходящих врачей, перетеканием человеческого капитала из больниц высокого уровня и размещением бренда в больницах низкого уровня, чтобы для расширения возможностей диагностики и лечения последнего, привлечения притока человеческого капитала и изменения ожиданий пациентов. В 2015 и 2017 годах эта реформа привлекла внимание китайского правительства и получила распространение по всей стране [6, 7].
Между тем, начиная с 2015 года, некоторые пилотные провинции и города, в том числе Шанхай и Чжэцзян, приступили к реализации комплексной медицинской реформы с упором на медицинские цены, медицинское страхование и закупку фармацевтических препаратов для снижения медицинских расходов и создания более эффективной иерархической системы диагностики и лечения. Однако вопрос о том, привели ли прошлые реформы к более сбалансированному распределению ресурсов здравоохранения и эффекту конвергенции, остается открытым.
Предыдущие публикации использовали неоклассическую теорию конвергенции для оценки конвергенции динамики расходов на здравоохранение. Основная перспектива исследования — оценка и сравнение конвергенции нескольких стран. Исследования Европейского союза (ЕС), Организации экономического сотрудничества и развития (ОЭСР) и других стран показали, что расходы на здравоохранение в странах ЕС имеют статистически значимые характеристики σ-конвергенции и β-конвергенции [8], а расходы на здравоохранение на душу населения расходы стран ОЭСР имеют клубную конвергенцию [9].
Однако единого равновесия в расходах на здравоохранение для стран Африки к югу от Сахары не существует, хотя были выявлены три клуба конвергенции [10]. В других исследованиях изучались разные регионы в отдельных странах, но в качестве показателя также в основном использовались расходы на здравоохранение. Исследования подтвердили наличие конвергенции расходов на здравоохранение в штатах США [11], а также обнаружили, что индийские штаты можно разделить на два клуба конвергенции расходов на здравоохранение [12]. Кроме того, расходы на здравоохранение во всех округах Китая имеют тенденцию к сближению [13]. Однако распределение ресурсов здравоохранения не ограничивается показателями расходов на здравоохранение, но должно также включать другие показатели обеспечения ресурсами здравоохранения, такие как количество медицинских работников и коек. Хотя в нескольких исследованиях обсуждалась конвергенция отдельных показателей, таких как количество коек и количество врачей [14], в нашем обзоре литературы не было обнаружено исследований, в которых использовался бы всеобъемлющий индекс обеспеченности ресурсами здравоохранения, включая параметры человеческих, материальных и финансовых ресурсов, и выполненных работ.
соответствующие оценки сходимости.
Существующие исследования признали, что несбалансированное распределение медицинских услуг в Китае является наиболее серьезной и неотложной проблемой государственной службы [15, 16]. В рамках административной иерархии больницы высокого уровня получают больше государственных финансовых ресурсов и, таким образом, могут привлекать более качественный человеческий капитал [17]. Возникающее в результате отсутствие потенциала обслуживания, а также неодобрение и недоверие пациентов еще больше ослабляют способность больниц низкого уровня привлекать пациентов [18]. Считалось, что реформа здравоохранения 2009 г. ускорила конвергенцию ресурсов провинциального здравоохранения в Китае, но она все еще медленнее, чем валовой внутренний продукт (ВВП) на душу населения [19].]. Кроме того, некоторые исследования показали, что дисбаланс продолжает оставаться серьезным. Одно из объяснений связано с существенным дисбалансом материальных и финансовых ресурсов между регионами [20].
Другое объяснение связано с реформой здравоохранения 2009 г., предполагающей, что расширение охвата медицинским страхованием ослабило финансовые ограничения пациентов, что побудило их выбирать больницы высокого уровня [21]. Однако в существующих исследованиях не обсуждались дисбаланс и конвергенция в контексте последних реформ здравоохранения и их последствия.
В некоторых исследованиях пространственное распределение ресурсов здравоохранения оценивалось с использованием различных показателей, в том числе коэффициента Джини [22, 23], для анализа динамики предложения ресурсов здравоохранения и эффектов реформ как во времени, так и в пространстве, в основном с данными на уровне провинций. Проблема заключается в том, что региональные различия в обеспечении ресурсами здравоохранения часто возникают в пределах одной провинции, особенно между столицами провинций, центральными городами и периферийными городами, в которых преобладают сельские районы. Таким образом, оценка на уровне провинции не может точно отразить различия между городскими и сельскими районами в распределении ресурсов здравоохранения.
При этом меньше внимания уделяется пространственному соотношению, неоднородности городов разного размера/уровня и влиянию последних реформ. Хотя в нескольких исследованиях использовались данные на уровне больниц и пациентов для оценки последствий политики реформ, таких как реформа нисходящих ресурсов и комбинация лечения, и были представлены доказательства их влияния на стимулирование пациентов выбирать больницы низкого уровня и улучшение эффективности распределения ресурсов [24, 25], неясно, вызвали ли эти реформы эффекты конвергенции на макроуровне между городами и регионами.
Поскольку пространственная корреляция распределения ресурсов здравоохранения в основном происходит между соседними городами, городские кластеры могут быть подходящим объектом исследования для обсуждения пространственной корреляции и конвергенции предложения ресурсов здравоохранения. В данной статье основное внимание уделяется городскому кластеру в дельте реки Янцзы (YRD), который включает Шанхай, Цзянсу, Чжэцзян и Аньхой.
В «Концепции комплексного регионального развития дельты реки Янцзы» , предложенной китайским правительством [26], более сбалансированное распределение ресурсов здравоохранения было указано в качестве цели региональной интеграции. Более того, доступность данных по этому региону лучше, чем по другим регионам Китая. Мы собрали данные по 41 городу YRD на уровне префектуры и выше с 2007 по 2019 год.провести эмпирическое исследование. Выборка включает Шанхай с населением около 25 миллионов человек, а также Ханчжоу, Сучжоу, Нанкин, Хэфэй и Нинбо с населением около 10 миллионов человек в каждом, а также города уровня префектуры с обширными сельскими районами. Масштабы и конкретные города дельты реки Янцзы показаны на рис. 4 в Приложении.
По сравнению с существующей литературой, эта статья вносит следующие новые вклады: (1) Эта статья включает пространственную корреляцию в кластере городов YRD в анализ распределения ресурсов здравоохранения и впервые предоставляет данные о распределении ресурсов здравоохранения в Китае.
с репрезентативным кластером из 41 города на уровне префектуры и выше. (2) В данной статье измерение пространственно-временного распределения сочетается с оценкой конвергенции, что позволяет нам понять характерные факты распределения ресурсов здравоохранения в регионе YRD, а также включает в анализ городскую неоднородность. (3) Это первая попытка оценить эффекты конвергенции последних реформ, в которых нисходящая реформа ресурсов здравоохранения и комплексная медицинская реформа включены в эмпирическую оценку.
Структура этой статьи следующая: обзор литературы, представлены методы и данные, использованные в этой статье, отчеты о характерных фактах и результатах оценки сходимости, и последний раздел завершается.
Обзор литературы
Сбалансированное распределение ресурсов здравоохранения направлено на согласование спроса и предложения, тем самым способствуя выравниванию медицинских услуг в регионах [5]. Это также будет иметь жизненно важное значение для снижения перегруженности больниц высокого уровня и расходов на диагностику и лечение пациентов.
Для измерения распределения ресурсов здравоохранения можно использовать два подхода. Первый подход заключается в наблюдении поперечного пространственного распределения с помощью ряда показателей измерения. Если в дальнейшем будет введено временное измерение, можно будет также обсудить эволюционный тренд [27]. Если различные области поперечного сечения включены в географическую информационную систему (ГИС), мы могли бы интуитивно понять тенденцию пространственно-временной эволюции [28]. Однако из-за существования поперечной неоднородности показатели измерений не могут контролировать влияние гетерогенных факторов, поэтому мы не можем фиксировать характеристики пространственно-временной эволюции сопоставимым образом для разных регионов [29].]. Поэтому другой подход использует методы регрессии для контроля влияния разнородных предметов. Методика оценки конвергенции, разработанная для исследований экономического роста, может быть использована для оценки конвергенции распределения ресурсов здравоохранения [30].
Три отрасли литературы имеют отношение к этому исследованию.
Первая ветвь литературы обычно использует для анализа один или несколько показателей измерения, включая индекс агломерации, коэффициент вариации, коэффициент Джини и индекс Тейла [31, 32]. Среди них индекс агломерации используется для измерения отношения населения или географической площади в конкретном регионе к объему существующих ресурсов здравоохранения. Хотя это может отражать сбалансированную степень распределения ресурсов здравоохранения между различными группами в одном и том же регионе [33], это не может выявить сбалансированную степень распределения ресурсов внутри группы. Напротив, коэффициент вариации, т. е. отношение стандартного отклонения уровня обеспеченности ресурсами здравоохранения в пределах конкретной территории к его среднему арифметическому, может лучше измерять степень сбалансированности распределения ресурсов внутри группы [34].
Из-за отсутствия объективных оценочных ориентиров для вышеупомянутых двух показателей ученые также используют коэффициент Джини и индекс Тейла с определенным диапазоном значений (∈ [0,1]) и объективный оценочный ориентир для оценки.
Ранний коэффициент Джини использовался для отражения неравенства доходов жителей [35], но он не мог отражать общий внутренний баланс. Поэтому Дагум [36] предложил разложимый коэффициент Джини, который может разлагать общие региональные различия по подгруппам и эффективно решать проблемы перекрытия среди наблюдаемых выборок. Индекс Тейла получен методом энтропии (или групповой энтропии) [37, 38], но не учитывается влияние географической доступности [39].]. Из-за многовходных и многовыходных характеристик ресурсов здравоохранения одним из методов является использование анализа оболочки данных (DEA) для измерения относительной эффективности группы подразделений, принимающих решения, с несколькими входами и несколькими выходами [40, 41]. Альтернативным методом является использование метода энтропийных весов для построения индекса спроса/предложения ресурсов здравоохранения на основе данных с несколькими входами и выходами [42].
Основываясь на приведенных выше показателях измерения, существующая эмпирическая литература по распределению ресурсов здравоохранения в Китае в основном сосредоточена на всей стране или отдельном административном регионе в качестве объекта исследования.
Оценки на основе индекса агломерации показали, что степень агломерации ресурсов здравоохранения в экономически развитых провинциях/городах относительно высока, тогда как географическая доступность ресурсов здравоохранения в экономически слаборазвитых провинциях/городах слаба [43]. Существуют очевидные различия в распределении ресурсов здоровья в разных провинциях, таких как Сычуань [44], Чжэцзян [45] и Хэнань [46], которые имеют разные характеристики агломерации в зависимости от численности населения и географического района. Йи и др. (2020) измерили коэффициент вариации и не нашли σ конвергенция в восточном, центральном и западном Китае; то есть различия в эффективности здравоохранения внутри Китая могут постепенно увеличиваться [47]. Однако другая оценка, основанная на коэффициенте Дагум Джини, показывает, что общие, внутрирегиональные и межрегиональные различия в предложении основных медицинских и медицинских услуг уменьшились в течение 2007–2018 гг. [22]. Кроме того, индекс Тейла использовался для демонстрации того, что различия в распределении ресурсов в разных провинциях связаны с разными источниками.
Например, различия в распределении ресурсов здравоохранения в провинции Аньхой в основном вызваны внутрирегиональными различиями [48], а в провинции Хайнань — межрегиональными различиями [49].].
Второе направление исследований изучает пространственную корреляцию распределения ресурсов здравоохранения с использованием ГИС или других инструментов пространственного анализа. Преимущество в том, что он позволяет наглядно представить различия в пространственном распределении ресурсов здравоохранения. Существует три широко используемых метода пространственного анализа. Исследовательский метод анализа пространственных данных (ESDA) в основном использует модель Морана I для анализа пространственной корреляции экономических и социальных атрибутов пространственной единицы [50], а также может использовать кластерную карту LISA для представления агломерационных характеристик единицы. конкретной области. Оценка плотности ядра (KDE) аппроксимирует плотность вероятности выборки для визуализации пространственных точек характеризующей области [51].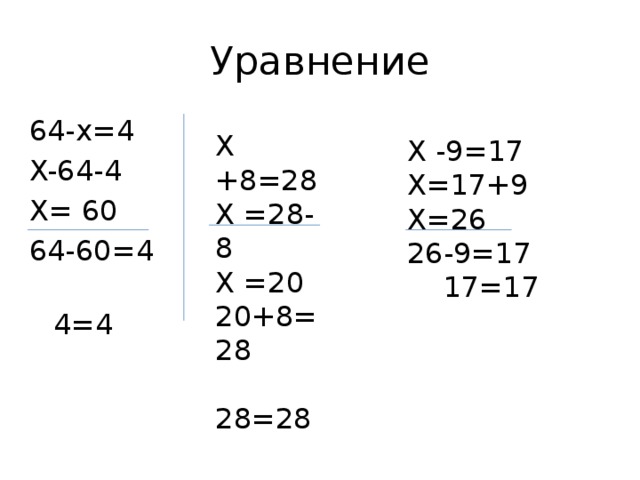
Метод KDE может представить пространственное распределение всей территории, что дополняет результаты анализа ESDA. Метод эллипса стандартного отклонения (SDE) строит эллипс стандартного отклонения, чтобы отразить преобладающее направление распределения пространственных элементов и дисперсию каждого направления, что, подобно кластерной карте LISA, может компенсировать тот факт, что карта KDE не может отображать особенности распространения по конкретным регионам [52].
Пространственный статистический анализ может проводиться на разных уровнях, таких как вся страна, городские кластеры и отдельные города. Что касается национального измерения, анализ KDE показал, что снабжение ресурсами здравоохранения между провинциями Китая имеет тенденцию к росту; однако поляризацию можно обнаружить как в национальном, так и в восточном регионах, в то время как в центральном и западном регионах эффект градиента отсутствует [22]. Очень немногие исследования были сосредоточены на измерениях городов уровня префектур, и результаты исследования Морана I и кластерная карта LISA показали, что картина пространственной корреляции предложения ресурсов здравоохранения сильно изменилась; а центральный, западный и северо-восточный регионы показали высокие-высокие агломерационные характеристики [53].
Однако в других исследованиях сообщается, что пространственное распределение ресурсов здравоохранения между городами, как правило, сбалансировано, а в переходной зоне от восточного побережья к центральному региону существуют регионы низкой агломерации с концентрированным распределением [28]. Вышеупомянутое эмпирическое исследование с использованием городских данных на уровне префектур использовало аналогичный метод, но дало противоречивые результаты из-за различий в периоде исследования и методах обработки, используемых для показателей. Наконец, в большинстве пространственных статистических исследований в качестве объектов исследования берутся конкретные города и используется метод SDE для изучения пространственного распределения ресурсов здравоохранения в городах [23, 54, 55].
Третье направление исследований включает очень мало исследований, в которых используется панельная эконометрическая модель для изучения тенденций агломерации или конвергенции ресурсов здравоохранения и влияющих факторов пространственных различий.
Согласно нашему опросу, в большинстве предыдущих исследований для оценки конвергенции использовались панельные данные провинциального уровня. Например, Zhou (2018) обнаружил условную конвергенцию β , но не абсолютную конвергенцию β между провинциями с помощью отдельных показателей [29].]. А рост медицинских расходов и региональная финансовая автономия подтолкнут региональные ресурсы здравоохранения на путь конвергенции. Пан и др. (2017) подтвердили долгосрочную тенденцию абсолютной и условной β конвергенции государственных расходов на здравоохранение в Китае [56]. Учитывая многовходные и многовыходные характеристики ресурсов здравоохранения, в некоторых исследованиях DEA использовался для измерения общей факторной производительности (TFP) разных провинций и оценки ее сходимости [57]. Установлено, что общий уровень СФП провинциальных ресурсов здравоохранения в Китае невысок, но рост СФП имеет абсолютную и условную β конвергенция и представляет региональные различия.
Хотя эффект пространственного перелива наблюдается в конвергенции распределения ресурсов здравоохранения β [30], согласно нашему поиску, ни одно исследование не включало пространственный эффект в анализ на уровне города в контексте последних реформ здравоохранения в Китае.
Подводя итог, можно сказать, что пространственные различия в распределении ресурсов здравоохранения в Китае привлекли большое внимание. Как известно, дисбаланс в распределении ресурсов здравоохранения в Китае в основном возникает между городскими и сельскими районами, а также между центральными и периферийными районами, и недавно проведенные реформы здравоохранения могут иметь незначительные последствия. Таким образом, последние исследования должны быть сосредоточены на городских кластерах в провинциях и соседних провинциях, а также учитывать неоднородность городов и возможное влияние реформ здравоохранения. Соответственно, один репрезентативный регион может быть использован для получения новых данных о распределении ресурсов здравоохранения и оценке результатов реформ в Китае.
В этой статье YRD используется в качестве объекта исследования и исследуется пространственная корреляция между городами, чтобы интуитивно изобразить пространственное динамическое распределение ресурсов здравоохранения с помощью многомерного индекса. Затем модель пространственной панели использовалась для анализа конвергенции ресурсов здравоохранения в регионе YRD.
Методы и данные
Методы
Сначала мы строим индекс обеспеченности ресурсами здравоохранения (HRS) с использованием метода энтропийных весов, анализируем региональные различия, а затем исследуем источники различий с помощью метода декомпозиции коэффициента Джини, предложенного Dagum [36]. ]. Пусть G — коэффициент Джини, j и h — количество регионов, i и r — количество городов в регионе, k представляют собой общее количество регионов, n представляют общее количество городов, а n j ( n h в числе 9 городов из 9 регионов) ( ч) .
Далее, Y IJ ( Y RH) представляет HRS of City I ( R) в регионе J ( R) в регионе J ( R) в регионе J ( R) . y}\) представляет собой среднее арифметическое HRS. Можно получить следующее уравнение: 9{2} \overline{y}} } } }$$
(1)
После расчета общего коэффициента Джини тыс. регионов сортируются в соответствии со средним HRS в YRD, а именно y 1 ≤… ≤ y J ≤ … Y K , а затем коэффициент GINI G -это дезитчено на три части: 1). w ), (2) вклад межрегиональной разницы ( G nb ), and (3) transvariation density contribution ( G t ), which meet the requirements of G = G w + G nb + G т .
Далее мы используем метод KDE для изучения динамики пространственного распределения HRS в YRD. В частности, мы используем I Морана для изучения пространственной корреляции HRS YRD. Если Морана I является значимым, карта кластеров LISA будет использоваться для определения того, являются ли локальные типы корреляции и кластеры в разных регионах статистически значимыми. Когда значение Морана I равно [− 1, 0), 0 и (0, 1], это означает соответственно отрицательную корреляцию, нерелевантность и положительную корреляцию. Согласно карте кластеров LISA, можно выделить четыре типа отношений пространственной агломерации. идентифицировать: (1) область высокой-высокой агломерации (тип HH), (2) область высокой-низкой агломерации (тип HL), (3) область низкой-низкой агломерации (тип LL) и (4) область низкой-высокой агломерации площадь (тип LH)
Как оценка сходимости σ , так и оценка сходимости β обычно используются в анализе сходимости [58].
Первая оценка не опирается на эконометрическую модель и использует коэффициент вариации для измерения, что может подтвердить предыдущие результаты коэффициента Джини. β сходимости можно разделить на абсолютную β сходимость и условную β сходимость. Первый используется для оценки того, сойдется ли предложение ресурсов здравоохранения в различных регионах к одной и той же стационарной точке равновесия без учета факторов неоднородности города. Что еще более важно, мы включаем пространственные факторы, неоднородность и политику в области здравоохранения в качестве контрольных переменных в условное β сходимость для более полной оценки.
Модель абсолютной сходимости β задается следующим образом:
$$\ln (\frac{{y_{i,t+1} }}{{y_{i,t} }}) = \alpha + \beta \ln (y_{i,t} ) + \mu_{i} + \eta_{t} + \varepsilon_{it}$$
(2)
, где i представляет город; t представляет время; y i,t +1 и y i,t представляют HRS города i в t + 1 период и t период соответственно; ln( y i,t +1 /y i,t ) represents the annual growth rate of HRS in city i during the period from t to t + 1 ; и β — оцениваемый параметр сходимости, где β < 0 означает абсолютный тренд сходимости β , а в противном случае указывает на наличие тренда расхождения.
α — постоянный член; μ i и η t представляют региональный и временной эффекты соответственно; и ε it представляет член случайных помех. Формула скорости сходимости: \(v = — \frac{1}{TS}\ln (1 + \beta)\), где TS представляет промежуток времени.
Если в модель включены разнородные факторы, такие как состояние экономического развития, размер города и финансовые возможности правительства, модель условного β сходимость устанавливается следующим образом:
$$\ln (\frac{{y_{i,t+1} }}{{y_{i,t} }}) = \alpha + \beta \ln ( y_{i,t} ) + \gamma \ln (X_{i,t} ) + \mu_{i} + \eta_{t} + \varepsilon_{it}$$
(3)
, где X i,t – управляющая переменная; γ – оцениваемый параметр управляющей переменной; а смысл остальных переменных тот же, что и в формуле (2).
Учитывая возможное влияние политики и внешних шоков на условное β сходимость, имеем:
$$\ln (\frac{{y_{i,t+1} }}{{y_{i,t} }}) = \alpha + \beta \ln (y_ {i,t} ) + \gamma \ln (X_{i,t} ) + \delta P_{i,t} + \tau [\ln (y_{i,t} ) \times P_{i,t} ] + \mu_{i} + \eta_{t} + \varepsilon_{it}$$
(4)
где P i,t — фиктивная переменная политики, где if region i начинает реализовывать политику в период t , затем P i,t присваивается значение 1 в течение периода t и позже, а P i,t присваивается значение 0 до периода t ; а δ представляет влияние политики на скорость роста HRS; τ представляет влияние политики на конвергенцию HRS.
С учетом пространственной корреляции построим пространственную эконометрическую модель конвергенции β . Чтобы определить точную форму пространственных эффектов, входящих в панельную модель, мы сначала оценим следующие три пространственные модели в абсолютном 9{N} {W_{ij} \ln (y_{i,t} )} + \mu_{i} + \eta_{t} + \varepsilon_{it}$$
(7)
Уравнение (5) пространственная авторегрессионная модель конвергенции β (SAR), а уравнения. (6) и (7) — пространственная ошибка β модели сходимости (SEM) и пространственная модель сходимости Дубина β (SDM) соответственно. В этих уравнениях ρ представляет собой коэффициент пространственного эффекта объясняемой переменной, отражающий влияние объясняемой переменной в соседних городах; λ представляет собой коэффициент пространственного эффекта члена ошибки, отражающий случайный толчок; θ представляет собой коэффициент пространственного эффекта объясняющей переменной, отражающий влияние объясняющей переменной соседних городов; и W ij представляет матрицу пространственных весов.
В этой статье мы используем обратную весовую матрицу расстояния.
После оценки трех вышеупомянутых моделей пространственных панелей, следуя Alhorst [59] и Han [60], мы тестируем и выбираем соответствующие пространственные эконометрические модели. Во-первых, тест множителя Лагранжа (LM) выполняется на основе традиционной панельной модели. Если тест LM значим, будет использоваться модель SDM. Затем тест отношения правдоподобия (LR) и тест Хаусмана используются для определения индивидуальных/временных эффектов и фиксированных/случайных эффектов. Затем используются тесты Вальда и LR, чтобы определить, можно ли преобразовать модель SDM в модель SEM или SAR. Если ухудшенный результат не соответствует результату теста LM, будет выбрана модель SDM. В условном β сходимости, мы также используем ту же стратегию для определения конкретной формы пространственной эконометрической модели.
Данные и переменные
По данным Государственного совета (2019 г.) [26], регион дельты реки Янцзы (YRD) включает Шанхай (SH), Цзянсу (JS), Чжэцзян (ZJ) и Аньхой (AH), состоящий из из 41 города уровня префектуры и выше. Основные переменные и данные, использованные в этом исследовании, представлены ниже.
Поскольку ресурсы здравоохранения включают человеческие, материальные и финансовые ресурсы [11], для каждого из трех вышеуказанных аспектов в зависимости от наличия данных выбираются два показателя, а для построения индекса HRS используется метод энтропийных весов [22, 61]. Источник данных и вес указаны в таблице 1. Результаты HRS для 41 города YRD с 2007 по 2019 год.представлены в Таблице 11 в Приложении. Можно видеть, что HRS YRD и субпровинциальных регионов демонстрирует непрерывную тенденцию к росту с некоторыми различиями между провинциями.
Таблица 1 Оценка индексной системы HRSПолная таблица
Для оценки условной конвергенции β необходимо контролировать факторы неоднородности по городам. В соответствии с доступностью данных мы включаем в модель следующие контрольные переменные: размер города (SIZE), уровень экономического развития (ВВП), уровень урбанизации (UR), финансовые возможности правительства (GFC) и уровень финансовой самодостаточности государства. (ГФС) [62,63,64]. Определения и источники данных этих переменных представлены в таблице 2. Логарифмическая обработка используется для устранения размерной разницы.
Полноразмерная таблица
Поскольку наличие медицинских университетов/колледжей может повлиять на HRS конкретного города, мы разделяем городские подвыборки в соответствии с наличием медицинских университетов/школ и медицинские программы магистратуры в начальном году выборки. Данные о медицинском образовании разных городов представлены в Таблице 12 Приложения.
Мы также включили основные реформы здравоохранения в эмпирическую модель. Переменные политики включают нисходящую реформу ресурсов здравоохранения (DHR) и комплексную медицинскую реформу (CMR). Реформа ресурсов здравоохранения по нисходящей направлена на поощрение сбалансированного распределения за счет создания комбинаций лечения и увеличения государственных инвестиций [65]. В разных городах обычно были разные сроки проведения реформ. За момент реформы принимаем время первого документа, выданного местными управлениями (органами) здравоохранения, или время организации первой лечебной комбинации (см. Таблицу 12 в Приложении). Затем мы определяем один политический фиктивный DHR, установив послереформенный период равным 1, а дореформенный период равным 0,9.1811
Комплексная медицинская реформа направлена на снижение затрат на диагностику и лечение и достижение цели иерархической диагностики и лечения. В феврале 2015 года провинции Цзянсу и Аньхой были определены в качестве пилотных провинций для комплексной медицинской реформы, за ними последовали Чжэцзян и Шанхай в мае 2016 года. Дата публикации местными органами здравоохранения или официальная дата начала реформы используется в качестве временной точки реформы. , так что у нас есть фиктивный CMR. Следует отметить, что в случае запуска указанной реформы до 1 июля текущего года значение 1 присваивается текущему году, а в случае запуска реформы после 1 июля текущего года значение 1 будет назначаться со следующего года.
Динамика пространственного распределения ресурсов здравоохранения
Коэффициент Дагума Джини и результаты конвергенции σ
Поскольку мы берем Шанхай в качестве одной городской выборки на поперечном сечении, расчет коэффициента Дагума Джини дает результаты для трех провинций YRD, кроме Шанхая, но Шанхай включен в анализ межрегиональных различий и разложение различий. Для сравнения с измерениями коэффициента Джини мы также сообщаем об измерениях конвергенции σ , полученных с коэффициентом вариации.
Как показано на рис. 1(a), средний коэффициент Джини в провинции Чжэцзян является самым низким, со значением ниже 0,15 в 2007 г., что указывает на очень сбалансированное распределение ресурсов здравоохранения. На начальном этапе наибольший средний коэффициент Джини (> 0,25) был в провинции Аньхой. Хотя коэффициенты Джини всех трех провинций демонстрировали тенденцию к снижению в период выборки, провинция Аньхой имела самую сильную тенденцию к снижению, при этом коэффициент Джини достиг самого низкого уровня в 2019 году (< 0,05). Аналогичная тенденция обнаруживается при использовании коэффициента вариации, как показано на рис. 1 (b), что указывает на значительную σ тенденция конвергенции.
Оценка коэффициента Дагум Джини и коэффициента вариации в дельте реки Янцзы, Китай, 2007–2019 гг. Источник: рассчитано авторами с использованием программного обеспечения MATLAB
Полноразмерное изображение
На рисунке 1(c) дополнительно представлены результаты коэффициента Дагум Джини для попарного сравнения четырех провинций/городов. Можно видеть, что в ранний период выборки региональная разница между Шанхаем и Аньхой была самой большой, а региональная разница между Цзянсу и Чжэцзян была наименьшей. Различия между провинциями Чжэцзян и Аньхой, Цзянсу и Аньхой, а также Чжэцзян и Цзянсу были относительно небольшими в течение периода выборки. Более того, различия между регионами имеют тенденцию к снижению до 2012 г., а затем возрастают при колебаниях. В целом, различия в распределении ресурсов здравоохранения в регионе YRD уменьшились за период выборки.
Чтобы лучше понять источник этих наблюдаемых различий, мы, следуя Dagum (2007), разложили коэффициент Джини на три компонента [36]. Среднегодовые показатели взносов G W , G NB и G T и 23.7%, 54,6%. Из рис. 1(d) видно, что доля вклада межрегиональных различий быстро увеличивалась после 2012 г. и к 2019 г. превысила 70%.. Доля вклада внутрирегиональных различий уменьшалась медленно, но доля вклада интенсивности трансвариации, которая измеряет взаимодействие между межрегиональными различиями и внутрирегиональными различиями, уменьшалась быстро и достигла почти 10% в 2019 г. Это говорит о том, что мы должны платить больше внимания пространственно-временному распределению между провинциями и городскими группами.
Оценки кривой плотности ядра
Чтобы дополнительно зафиксировать пространственную динамику распределения ресурсов здравоохранения в провинциях YRD, мы использовали метод KDE для представления кривых плотности ядра HRS в выбранные годы (рис. 2). Центр кривой плотности ядра постепенно смещался вправо, указывая на то, что HRS в YRD и родственных провинциях значительно увеличился. Согласно морфологии распределения на рис. 2 (а), высота кривой плотности ядра YRD сначала увеличивалась, а затем уменьшалась, сначала сужалась, а затем расширялась. Эти изменения свидетельствуют о том, что степень дисперсности ЖРД сначала уменьшилась, а затем увеличилась. Та же тенденция наблюдается в Аньхой и Цзянсу, в то время как степень дисперсии в Чжэцзяне практически не изменилась. С точки зрения пластичности распределения правый хвост кривой плотности ядра указывает на то, что города с более высоким предложением ресурсов здравоохранения будут расти быстрее, как показано на рис. 2 (a) и (c). В частности, Цзянсу демонстрирует феномен левостороннего движения, что указывает на то, что его внутреннее замедление и ускорение могут сосуществовать. Бимодальные и мультимодальные кривые плотности ядра соответствуют тенденциям внутренней полярности и мультиполярной дифференциации соответственно. К 2019 году в YRD и трех провинциях в период выборки явных различий больше не наблюдалось.. Подводя итог, можно сказать, что во всех провинциях, включая YRD, произошла эволюция распределения ресурсов здравоохранения от децентрализации к агломерации, а затем к децентрализации. Среди них Аньхой демонстрирует наиболее очевидную особенность агломерации, которая аналогична результатам в разделе «Коэффициент Джини Дагум» и раздел «Результаты конвергенции σ».
Распределение плотности ядер в дельте реки Янцзы, Китай, 2007–2019 гг. Источник: создано авторами с использованием программного обеспечения MATLAB
9.1810 Изображение в натуральную величинуПространственная динамика агломераций
Для исследования пространственной корреляции HRS в YRD сначала была оценена I Морана, а затем была использована кластерная карта LISA для визуального отображения динамики агломераций между городами. Как показано в таблице 3, все значения Морана I больше 0 при уровне значимости 5%. Значительно положительное значение Морана I указывает на то, что в течение периода выборки существует значительная положительная пространственная корреляция, что свидетельствует о включении пространственных факторов в это исследование.
Полная таблица
Кластер LISA отображает и визуализирует характеристики агломерации и диффузии городов YRD. Результаты кластера LISA представлены в Таблице 13 в Приложении. На рисунке 3 показано, что распределение ресурсов здравоохранения в YRD демонстрирует эффект агломерации. Район высокой-высокой агломерации сместился из средне-восточного региона YRD на юг. Сучжоу сохранил свои позиции как центральный город высокой агломерации, но положение Шанхая постепенно снизилось. К 2019 году, три других крупных крупных города агломерации, за исключением Сучжоу, расположены в провинции Чжэцзян. Между тем, регионы агломерации с низким уровнем агломерации постепенно перемещаются из Цзянсу в Аньхой. К 2019 году все основные города агломерации с низким уровнем агломерации были расположены в Аньхое, в то время как основной город района агломерации с низким уровнем агломерации изменился с Сюаньчэн, Аньхой, на Цзясин, провинция Чжэцзян. Между тем, регионы высокой-низкой агломерации сместились из Хуайбэй и Хуайнань, а Нанкин и Сюйчжоу имеют особенно заметные характеристики высокой-низкой агломерации. Таким образом, в течение периода выборки регионы агломерации с низкой и низкой агломерацией постепенно перемещались из Цзянсу в Аньхой, Чжэцзян получает больше регионов с высокой агломерацией, а Цзянсу имеет стабильное состояние агломерации с высокой и высокой агломерацией.
Кластерные карты LISA обеспеченности ресурсами здравоохранения в дельте реки Янцзы, Китай, 2007–2019 гг. Источник: Создано авторами с использованием программного обеспечения GeoDa
Изображение в натуральную величину
Результаты оценки панельной модели
Результаты оценки эталонной модели
Перед оценкой панельной модели нам сначала необходимо определить точную форму, в которой пространственные эффекты входят панельная модель. Результаты в таблице 4 показывают, что тесты LM и Robust LM отклоняют нулевую гипотезу на уровне значимости 5% в обоих абсолютных β сходимости и условные β оценки сходимости, указывающие на существование пространственных эффектов. Тесты LR показали, что существуют как индивидуальные, так и временные эффекты, а результаты пространственного теста Хаусмана предполагают, что мы должны использовать модель пространственной панели с фиксированным эффектом. Тест LR и тест Вальда абсолютной сходимости β показали, что SDM может выродиться в SAR или SEM, и указали на SEM в тестах LM и Robust LM, поэтому модель SEM с двусторонними фиксированными эффектами была выбрана для абсолютного β оценка сходимости. Тесты LR и Вальда при условной сходимости β показали, что SDM не может выродиться в SAR или SEM, а условия запаздывания и члены ошибок были значительными в тестах LM и Robust LM. Поэтому для условной оценки сходимости β была выбрана двусторонняя модель SDM с фиксированными эффектами.
Полноразмерная таблица
Используя уравнения. (2) и (3) для регрессии, в таблице 5 мы сначала сообщаем о β результатов сходимости без учета пространственных эффектов. Видно, что коэффициенты регрессии β HRS в модели (1) и модели (3) как ниже нуля, так и статистически значимы, указывая на то, что скорость роста HRS отрицательно коррелирует с начальным уровнем выравнивания; то есть существует абсолютная сходимость β и условная сходимость β со скоростью сходимости 5,31% и 8,22% соответственно. Затем мы включаем пространственный эффект в оценку, как показано в таблице 5. Согласно результатам оценки модели (2) и модели (4), обеспеченность ресурсами здравоохранения в регионе YRD все еще значительно сходится, со скоростью 5,27. % и 8,61% соответственно. Этот результат обеспечивает поддержку результатов оценки модели (1) и модели (3). В то же время результаты оценки ρ / λ , который является параметром, описывающим пространственные эффекты, показывают, что пространственные эффекты значительно положительны, указывая на то, что эффект пространственного перелива ускорит снабжение ресурсами здравоохранения в соседних городах. Этот вывод согласуется с результатами, представленными в разд. 4.
Полная таблица
Среди пяти городских неоднородных контрольных переменных в условном β оценка конвергенции, уровень экономического развития (ВВП) и финансовые возможности правительства (GFC) являются значительно положительными независимо от того, включен ли пространственный фактор. Это указывает на то, что GDP и GFC способствуют улучшению HRS в конкретном городе. Объясняется это тем, что более быстрое экономическое развитие стимулирует спрос жителей на общественные блага, включая ресурсы здравоохранения; Между тем, это также позволяет отдельным городам выделять больше средств для увеличения своего предложения [66]. Эти результаты согласуются с выводами Cheng et al. [67]. Однако коэффициенты пространственного эффекта двух вышеуказанных факторов незначительны, что свидетельствует о том, что уровень экономического развития и финансовые возможности государства не оказывают побочного эффекта на соседние города в HRS.
Кроме того, переменная уровня урбанизации (УР) была значимой только в пространственной панельной модели, что указывает на то, что агломерация населения в городские районы в пределах определенного города может помочь улучшить уровень распределения ресурсов здравоохранения. Однако оценочный коэффициент был положительным, но незначительным в модели без пространственных эффектов, что напоминает нам о необходимости относиться к этому результату с осторожностью. Наконец, оценочные коэффициенты размера города (SIZE) и уровня финансовой самодостаточности государства (GFS) несущественны. Тем не менее, в некоторых исследованиях сообщается, что влияние показателя фискальной самодостаточности значительно положительно для общенациональных и провинциальных выборок [30]. Причина может заключаться в том, что уровень фискальной самодостаточности (в среднем 44%) сильно различается по провинциям Китая, тогда как уровень фискальной самодостаточности на уровне городов (в среднем 68%) в YRD в целом высок, что ослабляет его влияние на распределение ресурсов здравоохранения. Однако его пространственный коэффициент (W × ln_GFS) значительно отрицательный, что позволяет предположить, что требуются дополнительные эмпирические данные.
Для дальнейшего изучения влияния вышеупомянутых переменных городской неоднородности на скорость конвергенции β мы добавили их интерактивные условия с HRS в эмпирические модели. Ради идентифицируемости модели для оценки используется панельная модель без пространственных эффектов. Результаты в таблице 6 еще раз подтверждают положительное влияние уровня экономического развития (ВВП) и финансовых возможностей государства (ГФП) на HRS. ВВП не влияет на скорость конвергенции; тогда как GFC значительно увеличивает скорость сходимости. Кроме того, влияние государственной финансовой самодостаточности (GFS) и размера города (SIZE) по-прежнему незначительно, но этот результат следует интерпретировать в свете того факта, что размер города значительно снижает скорость конвергенции в YRD, учитывая значительно положительный результаты ln_SIZE × β. В нем подчеркивается негативное влияние увеличения размера города на сбалансированное распределение ресурсов здравоохранения, что требует дополнительных эмпирических доказательств.
Полноразмерная таблица
Тест на устойчивость
город также имеет значение для снабжения ресурсами здравоохранения, нам необходимо проверить надежность приведенных выше эмпирических результатов. Мы проводим два разных теста: (1) преобразование матрицы пространственных весов и (2) определение того, существуют ли медицинские школы или программы для выпускников. Поскольку на пространственную обратную весовую матрицу расстояния, использованную в предыдущей статье, может влиять географический район конкретного города, расстояние между двумя соседними городами может быть больше, чем расстояние между несмежными городами; поэтому мы сначала используем весовую матрицу пространственной смежности для проверки надежности (таблица 7). Можно видеть, что коэффициенты сходимости по-прежнему значительно отрицательны, а коэффициенты пространственного эффекта значительно положительны. Между тем, оценочные коэффициенты аналогичны тем, которые представлены в таблице 5. Эти результаты показывают, что оценки, полученные с использованием пространственной обратной матрицы расстояний, являются надежными.
Полноразмерная таблица
Теперь мы разделяем подвыборки для городов, чтобы выполнить тест на устойчивость. Таблица 8 показывает, что в разных подвыборках коэффициенты оценки абсолютной сходимости β и условной сходимости β являются значительно отрицательными, что указывает на робастную сходимость в области YRD. Более того, в разных моделях снова обнаруживаются значительные пространственные эффекты. Кроме того, пространственный эффект подвыборок медицинских учебных заведений значительно отрицательный, что указывает на то, что города с медицинскими учебными заведениями имеют эффект агломерации ресурсов, который ослабляет HRS в соседних городах. При сужении размера выборки до городов с высшим медицинским образованием получаются аналогичные результаты. Поскольку агломерация может быть связана с численностью городского населения, по мнению Госсовета [69], для дальнейшей оценки используются подвыборки типа I (≤ 5 миллионов) и типа II (> 5 миллионов) (таблица 14 в приложении). Надежные результаты снова получены для конвергенции и пространственных эффектов.
Полная таблица
Влияние политики реформы здравоохранения
Теперь мы исследуем влияние последних реформ здравоохранения. Поскольку воздействие может иметь скачкообразный эффект в начале реформы, а также может повлиять на скорость сходимости после начала реформы, в эмпирическую модель вводится фиктивная переменная и ее взаимодействие. Таблица 9свидетельствует о том, что нисходящая реформа ресурсов здравоохранения не дает мощного скачкообразного эффекта с отрицательным, но иногда незначительным знаком. Это также не оказывает существенного влияния на скорость конвергенции HRS. Этот результат устойчив как для абсолютной, так и для условной оценки сходимости β . Однако этот результат не следует интерпретировать как неэффективность нисходящей реформы ресурсов здравоохранения. Напротив, некоторые исследования показали, что эта реформа эффективна для стимулирования пациентов к выбору больниц низкого уровня [65].
Полная таблица
Нам также необходимо оценить влияние комплексной медицинской реформы, начатой в 2015 г. (табл. 10). Можно видеть, что, хотя есть некоторые доказательства того, что фиктивная реформа оказывает негативное влияние на улучшение HRS, этот эффект становится незначительным, когда добавляется член взаимодействия с β . Член взаимодействия незначителен как в абсолютном β сходимость и условная β оценка сходимости. Эти результаты не дают убедительных доказательств влияния этой реформы на распределение ресурсов здравоохранения, что согласуется с выводом Wang [70].
Полная таблица
Обсуждение
Несбалансированное распределение ресурсов здравоохранения является общей проблемой во всем мире. Однако такой дисбаланс в Китае в основном возникает между центральными (обычно столичными) городами с высокоуровневыми больницами и периферийными городами с обширными сельскими районами и низкоуровневыми больницами, что характеризуется сосуществованием перегруженности высокоуровневых больниц и неиспользуемых ресурсов. низкоуровневых [5]. За последние два десятилетия китайское правительство начало увеличивать инвестиции в больницы низкого уровня и способствовать притоку медицинского человеческого капитала в больницы низкого уровня, чтобы способствовать выравниванию распределения ресурсов здравоохранения. Однако в предыдущих исследованиях в основном использовались данные провинциального уровня и игнорировалась пространственная корреляция [29]., 56, 57]. Впервые мы используем данные городов уровня префектуры в репрезентативном регионе YRD для оценки пространственного распределения и конвергенции HRS в Китае, предоставляя эмпирические данные об изменении распределения ресурсов здравоохранения в Китае за последние десятилетия.
Наши эмпирические результаты показывают, что HRS в 41 городе на уровне префектуры и выше в YRD значительно увеличивается, а результаты коэффициента Джини и коэффициента вариации (конвергенция σ ) показывают, что дисбаланс значительно уменьшился, что аналогично результаты Чена и Хана [22]. Несмотря на то, что в разных городах одной провинции наблюдается уменьшение разницы в HRS, различия между провинциями все еще остаются очевидными. Поскольку HRS в Китае в основном финансируется местными органами власти ниже провинциального уровня, трудно сузить различия между провинциями только за счет усилий местных органов власти, и это по-прежнему важная проблема, которую необходимо решить в будущей реформе здравоохранения Китая.
Оценка конвергенции HRS также подтверждает вышеупомянутый вывод о том, что распределение ресурсов здравоохранения в регионе YRD улучшилось. Абсолютная оценка конвергенции β указывает на более устойчивый равновесный тренд в пределах YRD, однако условная оценка конвергенции β показывает, что межгородская неоднородность оказывает существенное влияние на скорость конвергенции. Эти выводы по-прежнему верны при изменении матрицы пространственных весов и дифференциации подвыборок регрессии. Мы также обнаружили, что города с более сильными государственными финансовыми возможностями и медицинским образованием имеют более высокий уровень конвергенции. Причина в том, что улучшение финансовых возможностей правительства означает, что у местных органов власти есть больше финансовых средств для инвестирования в общественные блага, такие как ресурсы здравоохранения, что способствует сближению городов [63]. Кроме того, у городов с медицинским образованием есть многолетние накопленные преимущества агломерации ресурсов медицинского образования, которые могут способствовать развитию HRS города, обеспечивая предложение человеческого капитала для медицинского рынка конкретного города.
Результаты кластерных карт Moran I и LISA сообщают о значительной пространственной положительной корреляции HRS в регионе YRD, а также об эффекте агломерации и диффузии различных городов в географическом пространстве, что предполагает, что игнорирование пространственного эффекта приведет к смещенной оценке. полученные результаты. Кроме того, наша оценка пространственной панельной модели также выявила значительные пространственные побочные эффекты распределения ресурсов здравоохранения в регионе YRD, что было подтверждено общенациональным исследованием Xin [30]. Тем не менее, следует отметить, что если в конкретном городе есть медицинские школы или есть программы для выпускников медицинских вузов, это окажет негативное пространственное влияние на соседние города, что еще раз указывает на эффект агломерации ресурсов медицинского образования.
В последние годы Китай ввел нисходящую реформу ресурсов здравоохранения и комплексную медицинскую реформу. В существующей литературе считалось, что эти реформы способствуют более сбалансированному распределению ресурсов здравоохранения с использованием данных на уровне провинций или микроданных больниц на уровне сообщества [24, 71], в других литературах считалось, что эти реформы мало на это влияют [21]. . В этой статье мы используем фиктивную реформу в модели, чтобы оценить ее эффект конвергенции. Мы обнаружили, что недавние реформы не оказали существенного влияния на конвергенцию HRS. Объяснение заключается в том, что нисходящая реформа ресурсов здравоохранения в основном способствовала перетоку и перетеканию человеческого капитала из (городских) больниц высокого уровня в больницы низкого уровня посредством государственных заказов и субсидирования затрат, а ее политический эффект был сосредоточен на стороне спроса путем привлечения пациентов в больницы низкого уровня. Таким образом, влияние реформы нисходящих ресурсов здравоохранения сильно отличается от реформы, начатой в 2003 г., направленной на улучшение инфраструктуры больниц низкого уровня. В то время как комплексная медицинская реформа сосредоточена на реформах, таких как цены на медицинские услуги, заработная плата медицинских работников и медицинское страхование, ее влияние на предложение ресурсов здравоохранения относительно слабое.
С точки зрения международных исследований это исследование может дать некоторые полезные выводы. Во-первых, мы признаем, что распределение ресурсов здравоохранения требует финансового роста с точки зрения расходов на здравоохранение, а также увеличения человеческих и материальных ресурсов, измеряемых такими показателями, как количество врачей и коек. По сравнению с предыдущими исследованиями в этой статье использовался метод энтропийного веса для построения индекса обеспеченности ресурсами здравоохранения на основе трех измерений человеческих, материальных и финансовых ресурсов, что позволяет более полно измерить распределение ресурсов здравоохранения в конкретном регионе. Во-вторых, наши эмпирические результаты демонстрируют наличие значительных пространственных эффектов между соседними регионами, что свидетельствует о необходимости полного учета пространственной корреляции при изучении межрегиональных рынков здравоохранения внутри страны. Наконец, мы добавили переменные политики в области здравоохранения в традиционную регрессионную модель конвергенции, что могло бы предоставить альтернативную методологию оценки последствий реформы здравоохранения для политики и, таким образом, улучшить наше понимание межрегиональной конвергенции, вызванной реформами здравоохранения.
Нам необходимо сообщить об ограничениях этого исследования. Во-первых, хотя мы строим индекс HRS из нескольких измерений на основе имеющихся данных, в индекс не включен фактор человеческого капитала. Поэтому индекс предложения может не в полной мере отражать качественное изменение предложения ресурсов. Во-вторых, тесная пространственная связь и конвергенция в YRD могут отражать эффект реформы ресурсов здравоохранения в Китае за последние десятилетия. Однако, если данные будут доступны в будущем, это исследование следует распространить на все провинции и различные городские кластеры в Китае, чтобы отразить огромные различия между городами по всей стране. Наконец, как нисходящая реформа ресурсов здравоохранения, так и комплексная медицинская реформа в основном сосредоточены на стороне спроса, и поэтому они не оказывают существенного влияния на конвергенцию HRS. Будущие исследования должны собрать данные о спросе для построения индекса спроса и оценки пространственного распределения и конвергенции спроса в Китае. Такие усилия углубят наше понимание последствий последних реформ здравоохранения в Китае.
Выводы и последствия для политики
Этот документ посвящен одному репрезентативному региону, YRD, и включает факторы пространственной корреляции для изучения пространственной модели и конвергенции распределения ресурсов здравоохранения Китая в контексте последних реформ здравоохранения. Мы используем мультииндексные измерения и технологию пространственной панельной регрессии для оценки пространственно-временной эволюции и динамики пространственной корреляции распределения ресурсов здравоохранения в YRD. Это исследование также включает факторы городской неоднородности и реформы здравоохранения и оценивает их предельные эффекты.
Установлено, что за период выборки с 2007 по 2019 год HRS в YRD значительно увеличился и быстро сходился. Между тем между провинциями и городами существовала значительная пространственная корреляция и агломерация, и все результаты оценки указывали на накопление преимуществ конкретных городов и их агломерационный эффект ресурсов в региональной интеграции. Кроме того, в отличие от заявленной правительством Китая цели реформы по содействию сбалансированному распределению ресурсов, наше эмпирическое исследование не обнаружило убедительных доказательств того, что последние реформы, в том числе реформа нисходящих ресурсов здравоохранения и комплексная медицинская реформа, могут помочь улучшить уровень конвергенции здравоохранения. ресурсы в YRD.
Это исследование показывает, что в условиях устойчивого и быстрого экономического роста увеличение долгосрочных инвестиций в инфраструктуру и человеческие ресурсы в учреждениях здравоохранения на местах, начатое в 2003 году, способствовало продвижению HRS и конвергенции между центральными и периферийными городами. В этом процессе конвергенции для будущих реформ важно выявить регионы с низким уровнем предложения ресурсов и более медленными темпами конвергенции, а затем предоставить целевую поддержку. Неоднородность города, характеризующаяся численностью населения и различиями в медицинском образовании, по-разному влияет на скорость конвергенции и порождает различные пространственные эффекты, что также подчеркивает необходимость обратить внимание городских властей на выдающуюся роль высокоуровневых больниц и медицинского образования в скопление ресурсов здравоохранения.
Доступность данных и материалов
Набор данных, использованный в этой статье, предоставляется по запросу.
Ссылки
Гваткин Д.Р. Тенденции неравенства в отношении здоровья в развивающихся странах. Ланцет Глоб Здоровье. 2017;5(4):371–2.
Артикул Google ученый
Яковлевич М., Тимофеев Ю., Эккерт Н. и др. Влияние расходов на здравоохранение на общественное здравоохранение в странах БРИКС. J Sport Health Sci. 2019;8:516–9.
ПабМед ПабМед Центральный Статья Google ученый
Яковлевич М. Сравнение исторических структур медицинских расходов в странах БРИКС и G7. J Med Econ. 2016;19(1):70–6.
ПабМед Статья Google ученый
Чи, Флорида.
Реформа системы управления общественным здравоохранением, основанная на идее приоритета здоровья людей. Административная реформа. 2020; 4:4–12.Google ученый
Сунь З.С., Ван С.Х., Барнс С.Р. Понимание перегруженности медицинского рынка Китая: перспектива структуры стимулов. План политики здравоохранения. 2016;31(3):391–401.
Артикул Google ученый
Госсовет. Руководящие заключения Главного управления Государственного совета по содействию построению иерархической системы диагностики и лечения. 2015 г. Доступно по адресу: http://www.gov.cn/zhengce/content/2015-09./11/content_10158.htm.
Google ученый
Госсовет. Руководящие заключения Главного управления Государственного совета по содействию созданию и развитию комбинированного лечения. 2017 г.
Доступно по адресу: http://www.gov.cn/zhengce/content/2017-04/26/content_5189071.htm.Google ученый
Nixon J. Дискуссионный документ 183 Конвергенция расходов на здравоохранение и результатов в отношении здоровья в Европейском союзе 1960–1995. Нурс Менеджмент. 2001;8(2):39.
Google ученый
Panopoulou E, Pantelidis T. Конвергенция расходов на здравоохранение на душу населения и результатов в отношении здоровья в странах ОЭСР. Экон. 2011;44(30):3909–20.
Артикул Google ученый
Traoré O. Конвергенция государственных расходов на здравоохранение в странах Африки к югу от Сахары: имеет ли значение клубная конвергенция? Health Econ Rev. 2021;11(1):21.
ПабМед ПабМед Центральный Статья Google ученый
Юкта К., Параманик Р. Анализ конвергенции расходов на здравоохранение в индийских штатах: имеют ли значение политические факторы? ГеоЖурнал. 2020;87(4):1469–78.
Google ученый
Чжан Г., Чжан Л., Ву С. и др. Конвергенция государственных расходов на здравоохранение уездов Китая: подушная доля и вклад. BMC Health Serv Res. 2016;16(1):1–11.
Google ученый
Liang D, Zhang DL, Huang JY, Schweitzer S. Приводит ли быстрый и устойчивый экономический рост к конвергенции ресурсов здравоохранения. Расследование. 2016;53:0046958016631699.
ПабМед ПабМед Центральный Google ученый
Ху Р. Анализ стратегии распределения государственных медицинских ресурсов с точки зрения предложения. Новый Запад. 2016;21:16–7.
Google ученый
Du C, Zhu HP. Логика развития городской системы медицины и здравоохранения Китая. Общественная наука Китая. 2016; 8: 66–89.
Google ученый
Ван Дж, Ван XY. Исследование интеграции медицинских услуг в Китае: эволюция политики и теоретический механизм. J Общественный человек. 2021;18(3):152–67.
Google ученый
Джин С.Т., Ли Б., Ян Ю.
К. Сокращает ли экономическое развитие разрыв в поставках основных медицинских и медицинских ресурсов между регионами? – метрологическая проверка по 287 городским панельным данным. Мировой регистрационный стад. 2021;30(1):192–203.Google ученый
Чжэн Дж.С. Исследование равновесия распределения ресурсов здравоохранения в Китае. Ресурс исцеления подбородка. 2019;22(5):362–6.
Google ученый
Chen JQ, Xu S, Gao J. Смешанное влияние новой реформы здравоохранения в Китае на охват медицинским страхованием и эффективность использования медицинских услуг. Int J Env Res Pub He. 2020;17(5):1–13.
Google ученый
Чен З.И., Хан Ю.Г. Динамическое развитие и пространственные различия в предложении основных медицинских и медицинских услуг. J Zhongnan Univ Econ Law.
2021;2:53–64.Google ученый
Ченг Д.Ю., Фу Д., Ли С. Изучение характеристик пространственного распределения основных медицинских и медицинских учреждений в Вурумуци. мед соц. 2019;32(4):42–6.
Google ученый
Ян Ю.Ю., Фу М.Ю. Оценка системного эффекта дифференцированной диагностики и лечения. Ста Децис. 2019;35(23):105–8.
Google ученый
Чжан ХХ, Чен С.Р. Количественная оценка эффекта реализации политики иерархической медицинской реформы в Китае: на примере города Сямэнь. Фуцзянь Трибьюн. 2019;2:192–204.
Google ученый
ЦК КПК, Госсовет. Набросок Плана развития региональной интеграции дельты реки Янцзы. 2019 г. Доступно по адресу: http://www.gov.cn/zhengce/2019-12/01/content_5457442.
html.Google ученый
Лян В.Дж., Тан Ю.М. Исследование пространственного неравновесного распределения ресурсов здравоохранения в Китае. Здоровье Эконом Res. 2018;9: 66–71.
Google ученый
млн лет ZF, Yin SG, Qiao WY, et al. Состояние пространственного равновесия и его эволюция во времени уровня обеспеченности медицинскими ресурсами здравоохранения в Китае. Sci Geogr Sin. 2018;38(6):869–76.
Google ученый
Чжоу Ю, Ю Ю С. Анализ состояния распределения и пути конвергенции ресурсов здравоохранения в Китае: на основе панельных данных провинций. Лечение подбородка эконом. 2018;37(3):46–9.
Google ученый
Xin CC, Li J, Yang CF. Исследование региональных различий и пространственной конвергенции медицинских услуг в Китае.
Чин Дж. Популярные науки. 2020; 1: 65–77.Google ученый
Sun CZ, Liu YY, Chen LX и др. Пространственно-временные различия интенсивности водного следа на основе коэффициента Джини и индекса Тейла в Китае. Акта Эколь Син. 2010;30(5):1312–21.
Google ученый
Хао Ю.Б., Пей К.Ю., Лу Ф. и др. Исследование справедливости конфигурации и эффективности ресурсов здравоохранения в Китае в конце «двенадцатой пятилетки». Исцеление подбородка Res. 2017;20(6):511–5.
Google ученый
Ван Ю.Ю., Ли Ю.Ю., Цинь С.С. и др. Исследование справедливости распределения ресурсов медицинских и медицинских услуг первичного уровня в Китае в зависимости от степени агломерации. Состояние здоровья Чин Дж. 2019;36(6):874-7.
Google ученый
Каквани Северная Каролина. Неравенство доходов и бедность: методы оценки и применения в политике. Оксфорд: Издательство Оксфордского университета; 1980.
Дагум С. Новый подход к разложению коэффициента неравенства доходов Джини. Империя Экон. 1997;22(4):515–31.
Артикул Google ученый
Yang Y, Yao CQ, Zhang JS и др. Пространственный агломерационный анализ исследовательских талантов в городской группе среднего течения реки Янцзы. Геосп Инф. 2018;16(9):5–10.
Google ученый
Чжан И, Чжан С, Ван ZQ. Исследование справедливости и влияющих факторов на распределение ресурсов здравоохранения в Синьцзяне с 2004 по 2016 год: комплексная перспектива, основанная на «справедливости населения» и «географической справедливости».
Chin Health Serv Управление. 2019;36(7):499–509.Google ученый
Су Б.Б., Лю С.Дж., Лу Ю.Дж. и др. Оценка распределения человеческих ресурсов первичной медико-санитарной помощи в Китае: на основе степени агломерации. Политика здравоохранения Чин Дж. 2021;14(4):49–54.
Google ученый
Цзян С., Мин Р., Фан П.К. Влияние реформы здравоохранения на эффективность государственных окружных больниц в Китае. BMC Health Serv Res. 2017;17(1):838.
ПабМед ПабМед Центральный Статья Google ученый
Чжан Ю.К., Ван Г.Л. Оценка эффективности обслуживания низовых медицинских и медицинских учреждений Китая на основе методов DEA и RSR. Chin Health Serv Управление. 2019;36(4):261–5.
КАС Google ученый
Чжан Т., Сунь Л.К., Ли С.Т. и др. Анализ справедливости и эффективности распределения ресурсов общественного здравоохранения в Китае: на основе HRAD и DEA. Политика здравоохранения Чин Дж. 2017;10(9):57–62.
Google ученый
Zhang C, Zhao XH, Ni J и др. Анализ справедливости распределения ресурсов здравоохранения в провинции Сычуань в зависимости от степени агломерации. Mod Prev Med. 2020;47(19): 3530–5.
Google ученый
Ху Х.М., Чен Д.В., Гао К.С. и др. Оценка распределения ресурсов здравоохранения в Чжэцзяне в зависимости от степени агломерации. Экономика здоровья подбородка.
2016;35(7):56–9.Google ученый
He JJ, Fu WS, Li Z и др. Оценка степени агломерации распределения человеческих ресурсов здравоохранения в провинции Хэнань. мед соц. 2019;32(9):14–9.
Google ученый
Yi M, Peng JC, Zhang L, et al. Эффективно ли распределение медицинских и медицинских ресурсов? характерные факты региональной неоднородности Китая. Int J Equity Health. 2020;19(1):89.
ПабМед ПабМед Центральный Статья Google ученый
Guo YX, Song GQ, Zhou RR, et al. Исследование текущей ситуации и справедливости распределения ресурсов здравоохранения в провинции Аньхой. Исцеление подбородка Res. 2018;21(4):318–22.
Google ученый
Хуан З.К., Фэн З.М., Чжан Ц.
И. Справедливость распределения ресурсов здравоохранения в провинции Хайнань: оценка с помощью индекса Тейла. Chin J Public Health. 2016;32(4):527–30.Google ученый
Су Б.Л., Ши Т. Измерение выравнивания распределения ресурсов общественного здравоохранения на основе пространственно-временного масштаба. Состояние здоровья Чин Дж. 2014;31(2):307–11.
г. Google ученый
Ли ГЗ, Ли СХ. Анализ регионального неравенства и динамики расходов на здравоохранение в Китае. Стат Децис. 2018;34(15):94–7.
Google ученый
Xie YY, Nian X, Ma HH и др. Характеристики пространственного распределения и влияющие факторы служб здравоохранения в Китае. J Huazhong Norm Univ. 2018;52(5):713–22.
Google ученый
Huo QL, Tang XM, Wang HY и др. Пространственное распределение и доступность медицинских учреждений в районе Люпаньшань. Научная карта Surv. 2021;46(7):189–95.
Google ученый
г. Лю Б., Дин ПК, Цинь Дж. Дж. Исследование пространственной структуры медицинских услуг в Пекине на основе данных POI. J Baoji Univ Arts Sci. 2020;40(3):72–6.
Google ученый
Пан Дж., Ван П., Цинь XZ и др. Несоответствие и конвергенция: расходы правительства провинции Китая на здравоохранение. ПЛОС ОДИН. 2017;8(8):e71474.
Артикул КАС Google ученый
Ислам Н. Что мы узнали из дебатов о конвергенции? Дж. Экон Сурв. 2003; 17: 309–62.
Артикул Google ученый
Элхорст JP. Программное обеспечение Matlab для пространственных панелей. Int Regional Sci Rev. 2015;37(3):389–405.
Артикул Google ученый
Хан Ф, Ян Л.Г. Как агломерация производителей услуг способствует модернизации производственной структуры. Управлять миром. 2020;36(2):72–94.
Google ученый
Мао Ю.Н., Ван С.В., Фэн Р.Х. и др. Исследование скринингового индекса оценки эффективности больниц на основе DEA.
Здоровье Эконом Res. 2015;8:15–9.Google ученый
Ву Ю.Ю. Влияние фискальной децентрализации на предложение местных услуг здравоохранения. Здоровье Эконом Res. 2021;38(4):16–20.
Google ученый
Ян Ю.Н., Тан Дж.Л. Эмпирические измерения и факторы, влияющие на равенство общественного здоровья: анализ эмпирических данных провинций с 2004 по 2013 год. Fujian Tribune. 2016;12:32–40.
Google ученый
Ye J. О влиянии урбанизации на выравнивание базового медицинского обслуживания в провинциях: на основе данных по шести центральным провинциям. J Zhongnan Univ Econ Law. 2016;1:45–53.
Google ученый
Сунь З.С., Ван С.Х., Чжао Х.Дж. и др. Повышает ли реформа нисходящих ресурсов удовлетворенность пациентов и меняет ли выбор поставщиков медицинских услуг? Расследование.
2020;54(1):59–61.Google ученый
Li JG, Li ZY, Zhu YF и др. Уравнивание базовых услуг общественного здравоохранения между округами: ограничительные факторы и государственная политика. Опубликовано Fin Res. 2013;11:29–32.
КАС Google ученый
Ченг Л.Х., Ян Д.Г. Несоответствие характеристик пространственно-временной эволюции ресурсов здравоохранения в регионе Урумчи-Чанцзи. J Univ Chin Acad Sci. 2018;35(3):382–90.
Google ученый
Su CW, Deng ZB, Li LP и др. Эволюция пространственной картины и конвергенция индекса развития водной экоцивилизации в Китае. J Univ Chin Acad Sci. 2021;36(5):1282–301.
Google ученый
Госсовет. Уведомление Государственного совета о корректировке стандартов классификации городов по размерам.
2014 г. http://www.gov.cn/zhengce/content/2014-11/20/content_9225.htm.Google ученый
Ван XY. Оценка эффекта комплексной политики медицинской реформы. Мод Эконом Рез. 2019;7:24–34.
КАС Google ученый
Duan H, Zhang YN, Hou YC и др. Исследование влияния политики медицинского альянса на работоспособность первичных медицинских учреждений по месту жительства. J Gansu Admin Inst. 2020; 4:4–16.
Google ученый
Апергис Н. и др. Конвергенция расходов на здравоохранение в штатах США. Soc Indic Res. 2017; 133:303–16.
Артикул Google ученый
Hu HS, Wu SQ. Исследование по структурной оптимизации основных государственных услуг на основе улучшения чувства выгоды. Финансы и торговая экономика. 2019;40(12):35–49.
Google ученый
Ли Б., Чжан Д.С. Исследование распределения ресурсов здравоохранения в провинции Хэнань с 2006 по 2014 год. Chin Heal Res. 2017;20(1):49–55.
Google ученый
Ю Дж.Л., Ян С.Г. Региональные различия и факторы, влияющие на уровень снабжения Китая медицинскими и медицинскими ресурсами. Стат Децис. 2021;37(6):69–72.
Google ученый
Чжэн В.С., Цзян Х.С., Ай Х.Р. и др. Анализ регионального неравенства обеспеченности основными медицинскими ресурсами в Китае. геогр рез. 2015;34(11):2049–60.
Google ученый
Ю Ю.Н. Анализ роста и конвергенции общей факторной производительности ресурсов здоровья в Китае. Стат Децис. 2018;34(18):111–5.
Google ученый
Скачать ссылки
Благодарности
Мы выражаем благодарность соответствующим провинциальным и муниципальным комиссиям здравоохранения за предоставление ценных данных.
Финансирование
Авторы благодарят Шанхайский исследовательский центр развития за финансовую поддержку (2020-YJ-C05).
Информация об авторе
Авторы и организации
Школа финансов и бизнеса, Шанхайский педагогический университет — Шанхай, Шанхай, Китай
Yuqing Shen & Zesheng Sun
Авторы
- Yuqing Shen
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Zesheng Sun
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Вклады
ZS предоставил концепцию, дизайн работы и отредактировал рукопись. YS участвовал в сборе данных, анализе и составлении рукописи. Автор(ы) прочитал(и) и утвердил окончательный вариант рукописи.
Автор, ответственный за переписку
Зешэн Сун.
Декларация этики
Одобрение этики и согласие на участие
Неприменимо.
Согласие на участие
Не применимо.
Конкурирующие интересы
Отсутствие конкурирующих интересов для объявления.
Дополнительная информация
Примечание издателя
Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.
Приложение
Приложение
Рисунок 4, таблицы 11, 12, 13 и 14.
Рис. 4Область дельты реки Янцзы в Китае. Источник: Авторы
Полный размер изображения
Таблица 11 Результаты измерений MRS с 2007 по 2019 годПолная таблица
Таблица 12 Реформы здравоохранения и медицинского образования в дельте реки Янцзы, КитайПолная таблица
Таблица 13 Результаты Кластер LISA в дельте реки Янцзы, КитайПолная таблица
Таблица 14 β результаты регрессии конвергенции для подвыборок городов разного размераПолная таблица
Права и разрешения
Открытый доступ Эта статья находится под лицензией Creative Commons Attribution 4. 0 International License, которая разрешает использование, совместное использование, адаптацию, распространение и воспроизведение на любом носителе или в любом формате при условии, что вы укажете оригинал. автор(ы) и источник, предоставьте ссылку на лицензию Creative Commons и укажите, были ли внесены изменения. Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons на статью, если иное не указано в кредитной строке материала. Если материал не включен в лицензию Creative Commons статьи, а ваше предполагаемое использование не разрешено законом или выходит за рамки разрешенного использования, вам необходимо получить разрешение непосредственно от правообладателя. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/4.0/. Отказ Creative Commons от права на общественное достояние (http://creativecommons.org/publicdomain/zero/1.0/) применяется к данным, представленным в этой статье, если иное не указано в кредитной линии данных.
Перепечатки и разрешения
Об этой статье
Топ 36 Сколько столовых ложек в 64 унциях 142 Новый ответ
от Join Nguyen
Вы ищете информацию, статьи, знания по теме маникюрные салоны открытые в воскресенье рядом со мной сколько столовых ложек в 64 унциях в гугле, вы не находите нужной информации! Вот лучший контент, собранный и составленный командой https://toplist.avitour.vn, а также другие связанные темы, такие как: сколько столовых ложек в 64 унциях 64 унции до столовых ложек
Содержание
Соответствуют ли 2 столовые ложки 1 унции?
В унции 2 столовые ложки . Итак, для 2 унций вам понадобится 4 столовые ложки, для 4 унций 8 столовых ложек, для 6 унций 12 столовых ложек, для 8 унций 16 столовых ложек, для 10 унций 20 столовых ложек.
Сколько стаканов воды составляет 64 унции?
Доказательства употребления алкоголя 8 стаканов воды каждый день
Для человека, потребляющего 2000 калорий в день, это в сумме составляет 2000 мл (примерно 64 унции) или восемь стаканов по 8 унций.
Сколько унций составляет столовую ложку?
Столовая ложка — это единица измерения объема, равная трем чайным ложкам или ½ жидкой унции .
Как измерить сухие унции?
В США принято следующее: если сухой ингредиент указан в унциях, это единица веса, которую следует измерять по шкале . Если влажный ингредиент указан в унциях, это жидкие унции, и его следует измерять во влажном мерном стакане.
Сколько столовых ложек в сухой унции кофе?
В любом случае, из 1-фунтового мешка кофейных зерен получится 16 чашек кофе по 16 унций при тех же размерах 4 столовых ложки или 1 унция кофе для приготовления чашки кофе на 16 унций.
Что происходит, когда вы выпиваете 64 унции воды в день?
Выпивая 64 унции воды каждый день, вы поможете системам вашего организма нормально функционировать . Вы также поможете компенсировать потерю воды во время энергичных тренировок или занятий спортом.
Не много ли 64 унции воды в день?
Возможно, вы слышали, что вам следует выпивать восемь стаканов воды по 8 унций (237 миллилитров) в день (всего 64 унции или около 1,9 литра). Это неправильный ответ. Согласно обзору исследований 2002 года, несмотря на распространенность этого легко запоминающегося правила, нет никаких научных доказательств, подтверждающих его .
Сколько воды нужно выпивать в день, чтобы похудеть?
Согласно исследованиям, употребление 1-2 литров воды в день должно быть достаточным для снижения веса.
Является ли унция сливочного сыра такой же, как столовая ложка?
Переводы измерения для сливочного сыра
1/16 чашки: 0,5 унции | 1 столовая ложка | 15 грамм | 1/2 порции. 1/8 чашки: 1 унция | 2 столовые ложки | 30 грамм | 1 порция.
Сколько стоит унция в чашках?
Чтобы получить количество чашек из жидких унций, нужно разделить количество унций на 8. Таким образом, 1 унция, деленная на 8, равняется 1/8 чашки .
2 унции равны 2 столовым ложкам?
Сколько столовых ложек в унции жидкости? В унции жидкости 2 столовые ложки, поэтому мы используем это значение в приведенной выше формуле. Жидкие унции и столовые ложки — это единицы, используемые для измерения объема.
Как измерить 1 унцию?
Для измерения унций выберите мерный стакан для жидкости или сухого вещества . Если вы измеряете жидкость, поставьте мерный стакан на плоскую поверхность и налейте жидкость в стакан. Не забудьте наклониться, чтобы посмотреть размеры сбоку чашки. Убедитесь, что жидкость достигает нужного размера.
2 унции равны 2 столовым ложкам?
Сколько столовых ложек в унции жидкости? В унции жидкости 2 столовые ложки, поэтому мы используем это значение в приведенной выше формуле. Жидкие унции и столовые ложки — это единицы, используемые для измерения объема.
Как измерить 2 унции?
Вы можете видеть линии на мерном стакане для 1/2 стакана или 1/4 стакана, но не для унций. Чтобы преобразовать 2 унции в чашки, вы можете просто использовать вместо 1/4 чашки . Чтобы получить количество чашек из жидких унций, нужно разделить количество унций на 8.
Чему равна 1 унция в чашках?
Таблица перевода жидких унций в стаканы
| Жидкие унции | Чашки |
|---|---|
| 1 жидкая унция | 0,125 |
| 2 жидких унции | 0,25 |
| 3 жидких унции | 0,375 |
| 4 жидких унции | 0,5 |
19 тг 2, 2022
Сколько унций в столовой ложке
Сколько унций в столовой ложке
Перевести 64 унции в столовые ложки
- Автор статьи: www.calculateme.com
- Отзывов от пользователей: 20419 Оценок
- Лучшие рейтинги: 4,2
- Самый низкий рейтинг: 1
- Краткое содержание статьи: Статьи о преобразовании 64 унций в столовые ложки Преобразование 64 унций в столовые ложки ; 64,17, 128,34; 64,18, 128,36; 64,19, 128,38; 64. 20, 128.4. …
- Самые популярные ключевые слова: Если вы ищете Конвертировать 64 унции в столовые ложки Конвертировать 64 унции в столовые ложки ; 64,17, 128,34; 64,18, 128,36; 64,19, 128,38; 64.20, 128.4. Насколько велика 64 унции? Что такое 64 унции в столовых ложках? Этот простой калькулятор позволит вам легко преобразовать 64 жидких унции в столовые ложки.
- Содержание:
Подробнее
Сколько столовых ложек в унции – более здоровые шаги
- Автор статьи: healthiersteps.com
- Отзывов от пользователей: 5649 Оценок
- Лучшие рейтинги: 4,2
- Самый низкий рейтинг: 1
- Краткое изложение содержания статьи: Статьи о том, сколько столовых ложек в унции – более здоровые шаги Обновление …
- Самые популярные ключевые слова: Ищете ли вы, сколько столовых ложек в унции – более здоровые шаги Обновление Столовые ложки и унции являются наиболее часто используемыми показателями для ингредиентов Итак, давайте рассмотрим, сколько столовых ложек в унции.
- Содержание:
Что такое унция
Что такое столовая ложка
Сколько столовых ложек в унции
Общие сведения о жидких и сухих ингредиентах
Как измерять жидкие ингредиенты
Как отмерять сухие ингредиенты
Как отмерять сухие ингредиенты в унциях
В чем разница между жидкими и сухими унциями
Можно ли использовать один и тот же мерный стакан для сухих и жидких ингредиентов
Заключение о том, сколько столовых ложек в унции
Другие статьи по теме
Присоединяйтесь к нашему списку рассылки
Ямайская каша из кукурузной муки
Веганский санкочо
Можно ли заморозить болгарский перец
Сколько столовых ложек в унции – более полезные шагиПодробнее
Выпивать 8 стаканов воды в день: правда или вымысел?
- Автор статьи: www.healthline.com
- Отзывов от пользователей: 19996 Оценок
- Лучшие оценки: 3,7
- Самый низкий рейтинг: 1
- Краткое содержание статьи: Статьи о выпивке 8 стаканов воды в день: правда или вымысел? Обновление …
- Самые популярные ключевые слова: Ищете ли вы Выпивать 8 стаканов воды в день: правда или вымысел? Обновление Многие эксперты рекомендуют выпивать восемь стаканов воды по 8 унций в день. В этой статье исследуется наука, стоящая за этим утверждением.
- Содержание:
Доказательства употребления 8 стаканов воды в день
Продукты и напитки, кроме воды, могут способствовать обезвоживанию организма
Достаточное количество воды полезно для здоровья
Сколько воды вы должны выпивать каждый день
Практический результат
Напиток 8 Стаканы воды в день: правда или вымысел?Подробнее
64 Унции жидкости в Столовые ложки | 64 жидких унции в столовые – Convertilo
- Автор статьи: convertilo.com
- Отзывов от пользователей: 14967 Оценок
- Лучшие оценки: 3,9
- Самый низкий рейтинг: 1
- Краткое содержание статьи: Статьи о 64 жидких унциях в столовых ложках | 64 жидких унции в столовые ложки – Convertilo 64 Flu Ounces равно 128 Столовых ложек. Поэтому, если вы хотите рассчитать, сколько столовых ложек содержится в 64 унциях гриппа, вы можете сделать это с помощью … …
- Самые популярные ключевые слова: Ищете ли вы 64 жидких унций в Столовые ложки | 64 жидких унции в столовые ложки – Convertilo 64 Flu Ounces равно 128 Столовых ложек. Поэтому, если вы хотите рассчитать, сколько столовых ложек содержится в 64 жидких унциях, вы можете сделать это с помощью … Преобразуйте 64 жидких унции в столовые ложки (64 жидких унции в столовые) с помощью нашего конвертера объема. Сколько столовых ложек в 64 жидких унциях. 64 жидких унции равно количеству столовых ложек. Что такое 64 жидких унции в столовых ложках.
- Содержание:
Конвертер единиц измерения
Как преобразовать 64 жидких унции в столовые ложки
жидкие унции в столовые ложки таблица перевода
Недавние преобразования Унции жидкости в Столовые ложки
Последние преобразования
64 Унции жидкости в Столовые ложки | 64 жидких унции в столовые – ConvertiloПодробнее
Сколько столовых ложек [США] в 64 унциях [США, жидкости]?
- Автор статьи: www.howmany.wiki
- Отзывов от пользователей: 47052 Оценок
- Лучшие оценки: 4,8
- Самый низкий рейтинг: 1
- Краткое содержание статьи: Статьи о том, сколько столовых ложек [США] в 64 унциях [США, жидкости]? 64 унции [US, liqu] = 128 (128) столовых ложек [US]; 65 унций [US, liqu] = 130 (130) столовых ложек [US]. …
- Ключевые слова, которые чаще всего ищут: Ищете ли вы Сколько столовых ложек [США] в 64 унциях [США, жидкости]? 64 унции [US, liqu] = 128 (128) столовых ложек [US]; 65 унций [US, liqu] = 130 (130) столовых ложек [US]. 👍 Здесь вы можете узнать, сколько столовых ложек [США] содержится в 64 унциях [США, жидкости], а также в любом количестве унций [США, жидкости]. Наши конвертеры единиц измерения включают преобразование для: объема, веса, длины, температуры и т. д.
- Содержание:
HowManywiki
Свяжитесь с нами! ✘
Как преобразовать
64 унции [жидкость США] в
столовых ложек [США]
унций [США, жидкость] в Столовые ложки [США].
Преобразование проб
Сколько столовых ложек [США] в 64 унциях [США, жидкости]?Подробнее
Перевести 64 унции в столовые ложки
- Автор статьи: www.dollartimes.com
- Отзывов от пользователей: 26866 Оценок
- Лучшие оценки: 4,1
- Самый низкий рейтинг: 1
- Краткое изложение содержания статьи: Статьи о Преобразовании 64 унций в столовые ложки Преобразование 64 унций в столовые ложки · 64,00 жидких унций = 128,0 столовых ложек · 64,01 жидких унций = 128,0 столовых ложек · 64,02 жидких унций = 128,0 столовых ложек · 64,03 жидких унций = 128,1 столовых ложек4 · 64,03 жидких унции = 128,1 ст. = 128,1 … …
- Ключевые слова, которые чаще всего ищут: Преобразовать 64 унции в столовые ложки Преобразовать 64 унции в столовые ложки жидкая унция = 128,1 …
- Содержание:
Подробнее
Преобразование унций (oz) в столовые ложки
- Автор статьи: www.asknumbers.com
- Отзывов от пользователей: 12619 Оценок
- Лучшие оценки: 3,1
- Самый низкий рейтинг: 1
- Резюме содержания статьи: Статьи о конвертации унций (oz) в столовые ложки Конвертер унций в столовые ложки (oz to tbsp), формула и таблица преобразования, чтобы узнать, сколько столовых ложек в унциях. …
- Самые популярные ключевые слова: Если вы ищете конвертер унций (oz) в столовые ложки Преобразователь унций в столовые ложки (oz to tbsp), формула и таблица преобразования, чтобы узнать, сколько столовых ложек в унциях. Конвертер унций в столовые ложки (oz to tbsp), формула и таблица преобразования, чтобы узнать, сколько столовых ложек в унциях.
- Содержание:
Сколько столовых ложек в унции
Как преобразовать столовые ложки в унции (столовые ложки в унции) 9Преобразование 1811 унций (oz) в столовые ложки
Подробнее
64 грамма в столовые ложки – Easy Conversion Plus Calculator
- Автор статьи: www.fiscalflamingo.com
- Отзывов от пользователей: 15791 Оценок
- Лучшие оценки: 4,1
- Самый низкий рейтинг: 1
- Краткое содержание статьи: Статьи о 64 граммах в столовых ложках – Easy Conversion Plus Calculator 64 грамма (г) равно 4,267 столовых ложек (столовых ложек) · 64 г = 4,267 столовых ложек … …
- Самые популярные ключевые слова: Если вы ищете 64 грамма в столовые ложки — Easy Conversion Plus Calculator 64 грамма (г) равно 4,267 столовых ложек (столовых ложек) · 64 г = 4,267 столовых ложек … Легко конвертируйте 64 грамма в столовые ложки прямо сейчас! Кроме того, попробуйте наш простой в использовании калькулятор граммов в столовые ложки. 64 грамма равно…
- Содержание:
64 грамма в столовые ложки (от 64 г в TBSP) Общая преобразование
64 грамма в калькулятор преобразования столовых ложек
Как преобразовать 64 г в TBSP
Общие граммы в плену
.Преобразование 64 граммов в другие единицы измерения
Что такое грамм
Что такое столовая ложка
64 грамма в столовые ложки – Easy Conversion Plus CalculatorПодробнее
64 Столовые ложки в унции
- Автор статьи: coolconversion.com
- Отзывов от пользователей: 4562 Оценок
- Лучшие оценки: 3,1
- Самый низкий рейтинг: 1
- Краткое содержание статьи: Статьи о 64 столовых ложках в унциях Чтобы преобразовать любое значение в столовых ложках в унции, просто умножьте значение в столовых ложках на коэффициент преобразования 0,5. Итак, 64 столовые ложки умножить на 0,5 равно … … .
- Самые популярные ключевые слова: Если вы ищете 64 Столовые ложки в унции Чтобы преобразовать любое значение в столовых ложках в унции, просто умножьте значение в столовых ложках на коэффициент преобразования 0,5. Таким образом, 64 столовые ложки, умноженные на 0,5, равно … Узнайте, как преобразовать столовые ложки в унции и каков коэффициент преобразования, а также формулу преобразования. 64 унции равны 32 столовым ложкам.
- Содержание:
Карта сайта
Таблица преобразования столовых ложек в унции около 64 столовых ложек
Преобразование объема образца
64 столовых ложек в унцииПодробнее
Сколько столовых ложек в 64 унциях? – Ответы
- Автор статьи: qa.answers.com
- Отзывов от пользователей: 42781 Оценок
- Лучшие рейтинги: 4,6
- Самый низкий рейтинг: 1
- Краткое содержание статьи: Статьи о том, сколько столовых ложек в 64 унциях? – Ответы В: Сколько столовых ложек в 64 унциях? Напишите свой ответ… Отправить. Остались вопросы? увеличить … …
- Самые популярные ключевые слова: Ищете ли вы Сколько столовых ложек в 64 унции? – Ответы В: Сколько столовых ложек в 64 унциях? Напишите свой ответ… Отправить. Остались вопросы? увеличить … 64 унции воды — это 128 столовых ложек.
- Содержание:
Математика и арифметика
Сколько пинт в галлоне
Сколько квартов в галлоне
Сколько чашек в кварте
Сколько фунтов в тонне песка
Добавьте свой ответ
Предметы
Лучшие категории
Компания
Продукт
Юридическая информация
Сколько столовых ложек в 64 унциях? – ОтветыПодробнее
Смотрите больше статей в той же категории здесь: https://toplist.avitour.vn/blog/.
Сколько столовых ложек в унции
В детстве почти все мы были сбиты с толку различными показателями измерения, или, скажем так, многие из нас до сих пор сбиты с толку. Фунты, граммы, унции, столовые ложки и чашки — все они используются для измерения ингредиентов рецепта. Столовые ложки и унции являются наиболее часто используемыми единицами измерения ингредиентов, и преобразование унций в столовые ложки и наоборот может привести к путанице.
г.В этой статье мы рассмотрим детали и проясним ваши двусмысленности относительно столовых ложек и унций. Итак, давайте копать!
Также см. Сколько унций в чашке? Сколько столовых ложек в чашке? и сколько граммов в унции?
Что такое унция?
Унция — единица массы, наиболее часто используемая в Великобритании и США. Один фунт состоит из 16 унций и является наименьшей мерой веса. Его обычно обозначают как «oz», что происходит от итальянского и испанского слова «Onza». Известная как жидкая унция США, это единица объема, используемая для измерения жидких веществ.
г.Что такое столовая ложка?
Столовая ложка — это ненаучная, но очень широко используемая единица объема, которая очень хорошо работает в кулинарии, фитотерапии и т. д. Это название посуды, используемой для измерения в рецептах. 1 столовая ложка равна 1/16 чашки. Буквальное значение столовой ложки — сервировочная ложка; однако во многих местах большая ложка, используемая для еды, называется столовой ложкой.
Сколько столовых ложек в унции?
Если вам нужно узнать, сколько столовых ложек в унции, вы можете использовать таблицу преобразования или калькулятор, чтобы узнать. В унции 2 столовые ложки. Итак, для 2 унций вам понадобится 4 столовые ложки, для 4 унций 8 столовых ложек, для 6 унций 12 столовых ложек, для 8 унций 16 столовых ложек, для 10 унций 20 столовых ложек.
г.Общие сведения о жидких и сухих ингредиентах:
На кухне сухие ингредиенты — это те, которые можно измерить по объему, а жидкие ингредиенты — это те, которые необходимо измерить по весу. При отмеривании сухих ингредиентов лучше всего использовать набор мерных чашек или ложек. При отмеривании жидких ингредиентов следует использовать набор весов.
Как измерять жидкие ингредиенты?
Самый распространенный способ измерения жидкостей — по объему, но это может быть не лучшим способом для некоторых ингредиентов. Например, если вы измеряете мед в миллилитрах, будет сложно определить, сколько меда у вас осталось в банке, если вы не знаете, сколько миллилитров в столовой ложке или сколько столовых ложек в чашке.
г.Чтобы точно отмерять жидкости и избежать путаницы при использовании жидких ингредиентов, таких как мед или масло, используйте специальные мерные чашки, на которых есть размеры.
Стаканчики Унции 1 стакан 8 жидких унций 2 стакана 16 жидких унций 4 стакана 32 жидких унции
Как отмерять сухие ингредиенты?
Сухие ингредиенты — это невлажные ингредиенты, такие как мука, сахар и соль. Их можно измерить по весу или по объему. Не существует универсального стандарта для измерения сухих ингредиентов. Наиболее распространенным методом является использование чашек и столовых ложек, но есть и другие методы, такие как измерение с помощью чайных ложек или весов.
г.Лучший способ отмерять количество сухих ингредиентов — это использовать весы или мерные чашки, поскольку они имеют легко читаемые показания и могут измерять в различных единицах измерения.
Столовые ложки Унции 2 Столовые ложки 1 Унция 4 Столовые ложки 2 Унция 8 Столовые ложки 4 Унция 12 Столовые ложки 6 Унция
Как вы измеряете сухие унции?
Если сухой ингредиент указан в унциях, это единица веса, которую следует взвешивать на весах.
г.В чем разница между жидкими и сухими унциями?
Если в рецепте указано количество сухого ингредиента в одну унцию, лучше всего взвесить этот ингредиент на весах. Если рецепт требует количества жидкости в унции, вы можете отмерить его в мерном стаканчике для жидкости.
Можно ли использовать один и тот же мерный стакан для сухих и жидких ингредиентов?
Нас часто спрашивают, нужны ли им отдельные мерные стаканы для влажных и сухих ингредиентов. Если вы серьезно относитесь к выпечке, ответ — да! Хотя мерные стаканы для жидкостей и сухих веществ имеют одинаковый объем, разница в том, что каждый из них специально разработан для лучшего измерения соответствующих ингредиентов.
г.Заключение о том, сколько столовых ложек в унции:
Итак, для тех, кто запутался и постоянно путается во время выпечки и готовки, у вас есть шанс сделать правильный рецепт.
Воспользуйтесь таблицей преобразования и правильными измерениями, которые у нас есть для вас, и приступайте к работе. Имейте в виду, что шкала и правильное измерение играют неотъемлемую роль, при этом приступайте к работе и используйте измерения, которые мы упомянули для вас выше.
Другие статьи по теме
г.Если вам понравился этот пост о том, сколько столовых ложек в унции, и вы хотели бы увидеть больше, присоединяйтесь ко мне на Youtube, Instagram, Facebook и Twitter!
Выпивать 8 стаканов воды в день: правда или вымысел?
Вы, наверное, слышали, что вам нужно выпивать восемь стаканов воды по 8 унций (240 мл) каждый день. Это полгаллона воды (около 2 литров). Это утверждение стало общепризнанным фактом, и его очень легко запомнить. Но есть ли правда в этом совете, или это всего лишь миф? В этой статье рассматриваются доказательства, лежащие в основе правила «восемь стаканов в день», и то, сколько воды нам нужно каждый день.
г.Доказательства употребления 8 стаканов воды каждый день Трудно точно определить, где и когда возникло правило «восемь стаканов в день». Есть теории, что это может быть основано на потреблении жидкости 1 мл на калорию потребляемой пищи. Для человека, придерживающегося диеты из 2000 калорий в день, это составляет 2000 мл (примерно 64 унции) или восемь стаканов по 8 унций. Тем не менее, все больше исследований показывают, что эта широкая рекомендация может оказаться слишком большой для одних людей и недостаточной для других. Хотя, безусловно, существуют обстоятельства, при которых потребность в воде увеличивается, здоровым людям, как правило, не нужно потреблять воду в таких больших количествах. С другой стороны, недостаточное употребление воды может вызвать легкое обезвоживание, определяемое как потеря 1-2% массы тела из-за потери жидкости. В этом состоянии вы можете испытывать усталость, головную боль и ухудшение настроения (1).
г.Продукты и напитки, кроме воды, могут способствовать гидратации Не только обычная вода снабжает ваш организм водой. Другие напитки, такие как молоко и фруктовый сок, также учитываются. Вопреки распространенному мнению, напитки с кофеином и легкие алкогольные напитки, такие как пиво, также могут способствовать потреблению жидкости, по крайней мере, когда они употребляются в умеренных количествах (2, 3, 4). Многие продукты, которые вы едите, также содержат значительное количество воды. Количество воды, которую вы получаете с пищей, зависит от количества богатых водой продуктов, которые вы едите. Фрукты и овощи особенно богаты водой, а такие продукты, как мясо, рыба и яйца, также имеют относительно высокое содержание воды.
Употребление достаточного количества воды полезно для здоровья Вам необходимо пить достаточное количество воды, чтобы избежать обезвоживания организма. Вообще говоря, это означает возмещение воды, которую вы теряете с дыханием, потом, мочой и фекалиями. Употребление достаточного количества воды может принести пользу для здоровья, в том числе: Потеря веса. Употребление достаточного количества воды может помочь вам сжечь больше калорий, снизить аппетит, если употреблять ее перед едой, и снизить риск долгосрочного увеличения веса (8).
Употребление достаточного количества воды может помочь вам сжечь больше калорий, снизить аппетит, если пить ее перед едой, и снизить риск долгосрочного увеличения веса ( ). Лучшая физическая работоспособность. Умеренное обезвоживание может ухудшить физическую работоспособность. Потеря всего 2% воды, содержащейся в организме, во время тренировки может повысить утомляемость и снизить мотивацию (9).).
Умеренное обезвоживание может ухудшить физическую работоспособность. Потеря всего 2% воды, содержащейся в вашем организме, во время тренировки может повысить утомляемость и снизить мотивацию (9). Уменьшение выраженности головных болей. Для тех, кто склонен к головным болям, употребление дополнительного количества воды может уменьшить интенсивность и продолжительность приступов. У обезвоженных людей вода может помочь облегчить симптомы головной боли (10, 11).
Для тех, кто склонен к головным болям, употребление дополнительного количества воды может снизить интенсивность и продолжительность приступов.
г.Людям с обезвоживанием употребление достаточного количества воды может помочь предотвратить и облегчить запоры. Однако необходимы дополнительные исследования этого возможного эффекта. Снижение риска образования камней в почках. Хотя необходимы дополнительные исследования, есть некоторые доказательства того, что увеличение потребления воды может помочь предотвратить рецидив камней в почках у людей со склонностью к их образованию (13, 14). Резюме: Поддержание водного баланса может способствовать снижению веса, повышению физической работоспособности, избавлению от запоров и многому другому.
г.Сколько воды нужно выпивать каждый день? На этот вопрос нет однозначного ответа.
64 Унции жидкости в Столовые ложки – 64 жидкие унции в столовые ложки
Определение единиц
Давайте посмотрим, как определяются обе единицы измерения в этом преобразовании, в данном случае жидкие унции и столовые ложки:
жидкая унция (жидкая унция)
Жидкая унция (сокращенно жидкая унция, жидкая унция или унция жидкая) представляет собой единицу объема.