Уравнение через дискриминант: § Дискриминант. Решение квадратных уравнений через дискриминант

§ Дискриминант. Решение квадратных уравнений через дискриминант

Как решать квадратные уравнения Дискриминант Неполные квадратные уравнения

Мы уже разобрали, как решать квадратные уравнения. Теперь давайте более подробно рассмотрим, что называют дискриминантом квадратного уравнения.

Вернемся к нашей формуле для нахожденя корней квадратного уравнения.

x_1;2 =

−b ± √b2 − 4ac

2a

Запомните!

Выражение «b² − 4ac», которое находится под корнем, принято называть дискриминантом и обозначать буквой «D».

По-другому, через дискриминант формулу нахождения корней квадратного уравнения можно записать так:

x_1;2 =

−b ± √D

2a

, где «D = b² − 4ac»

По одной из версий термин «Дискриминант» произошел от латинского discriminantis, что означает «отличающий» или «различающий».

В зависимости от знака «D» (дискриминанта) квадратное уравнение может иметь два, один или ни одного корня. Рассмотрим все три случая.

I случай

D > 0
(дискриминант больше нуля)

2x² + 5x −7 = 0

D = b² − 4ac
D = 5² − 4 · 2 · (−7)
D = 25 + 56
D = 81
D > 0

x_1;2 =

−b ± √D

2a

x_1;2 =

−5 ± √81

2 · 2

x_1;2 =

−5 ± 9

4

x1 = −5 + 9 4	x2 = −5 − 9 4
x1 =	x2 =
x1 = 1	x2 = −3
x1 = 1	x2 = −3

Ответ: x₁ = 1; x₂ = −3

Вывод: когда «D > 0» в квадратном уравнении два корня.

---

II случай

D = 0
(дискриминант равен нулю)

16x² − 8x + 1 = 0

D = b² − 4ac
D = (−8)² − 4 · 16 · 1
D = 64 − 64
D = 0

x_1;2 =

−b ± √D

2a

x_1;2 =

− (−8) ± √0

32

x_1;2 =

8 ± 0

32

x =

x =

Ответ: x =

Вывод: когда «D = 0» в квадратном уравнении один корень.

---

III случай

D (дискриминант меньше нуля)

9x² − 6x + 2 = 0

D = b² − 4ac

D = (−6)² − 4 · 9 · 2
D = 36 − 72
D = −36
D

x_1;2 =

−b ± √D

2a

x_1;2 =

− (−6) ± √−36

32

Ответ: нет действительных корней

Вывод: когда «D

Как решать квадратные уравнения Дискриминант Неполные квадратные уравнения

---

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».

Оставить комментарий:

Отправить

---

Квадратное уравнение. Дискриминант. Теорема Виета. • СПАДИЛО

Определение

Уравнение вида ax²+bx+c=0, где a,b,c – любые числа, причем a≠0, называют квадратным уравнением. Числа a,b,c принято называть коэффициентами, при этом a – первый коэффициент, b – второй коэффициент, c – свободный член.

Квадратное уравнение может иметь не более двух корней. Решить такое уравнение – это значит найти все его корни или доказать, что их нет.

Дискриминант

Количество корней квадратного уравнения зависит от такого элемента, как дискриминант (обозначают его буквой D).

Нахождение корней квадратного уравнения

Дискриминант – это такой математический инструмент, который позволяет нам определять количество корней. Он выражается определенной формулой:

D=b²–4ac

• Если D>0, то уравнение имеет два различных корня. Их находят по формуле:

• Если D<0, то уравнение не имеет корней.
• Если D=0, то уравнение имеет два равных корня, их записывают и находят как один:

Рассмотрим решение квадратных уравнений на примерах.

Пример №1. Решить уравнение х²–2х–3=0. Определяем коэффициенты: а=1, b=–2, c=–3. Находим дискриминант: D=b²–4ac=(–2)²–41(–3)=4+12=16. Видим, что дискриминант положительный, значит, уравнение имеет два различных корня, находим их:

Пример №2. Решить уравнение 5х²+2х+1=0. Определяем коэффициенты: а=5, b=2, c=1. D=b²–4ac=2²–4=4–20=–16, D<0, уравнение не имеет корней.

Пример №3. Решить уравнение х²–6х+9=0. Определяем коэффициенты: а=1, b=–6, c=9.

D=b²–4ac=(–6)²–4=36–36=0, D=0, 1 корень

Теорема Виета

Приведенные квадратные уравнения

Среди квадратных уравнений встречаются такие, у которых первый коэффициент равен 1 (обратим внимание на пример 1 и 3), такие уравнения называются приведенными.

Приведенные квадратные уравнения можно решать не только с помощью дискриминанта, но и с помощью теоремы Виета.

Теорема Виета

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком; произведение корней равно третьему коэффициенту.

х₁+х₂= –b

х₁•х₂= с

Корни с помощью данной теоремы находятся устно способом подбора. Рассмотрим это на примерах.

Пример №4. Решить уравнение х²–10х+21=0. Выпишем коэффициенты: а=1, b=–10, c=21. Применим теорему Виета:

х₁+х₂=–(–10)=10

х₁х₂=21

Начинаем с произведения корней, которое является положительным числом, значит оба корня либо отрицательные, либо положительные. Предполагаем, что это могут быть либо 3 и 7, либо противоположные им числа. Теперь смотрим на сумму, она является положительным числом, поэтому нам подходит пара чисел 3 и 7. Проверяем: 3+7=10, 37=21. Значит, корнями данного уравнения являются числа 3 и 7.

Пример №5. Решить уравнение: х²+5х+4=0. Выпишем коэффициенты: а=1, b=5, c=4. По теореме Виета:

х₁+х₂=–5

х₁х₂=4

Видим, что произведение корней равно 4, значит оба корня либо отрицательные, либо положительные. Видим, что сумма отрицательная, значит, будем брать два отрицательных числа, нам подходят –1 и –4. Проверим:

–1+(–4)=–5

(–1)(–4)=4

Ответ: –1 и –4

Задание OM2002 Решить уравнение: х2−2х+√5−х=√5−х+24

---

Данное уравнение является квадратным. Но в его условии присутствует квадратный корень, что усложняет нам задачу для нахождения его корней, в том плане, что необходимо увидеть, какие же ограничения на переменную х здесь будут.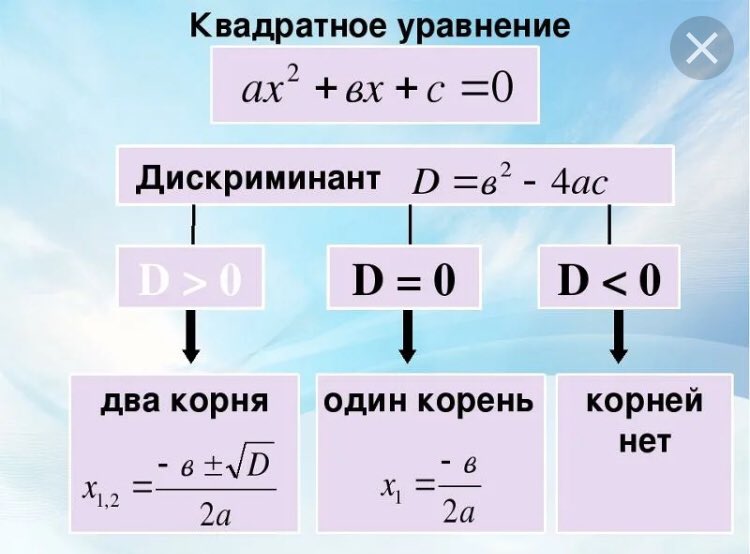

Записываем обязательно в начале решения, что подкоренное выражение может быть только равным нулю или положительным числом (правило извлечения квадратного корня): ограничение на х: 5−х≥0

Решаем полученное неравенство: −х≥−5, отсюда х≤5. Следовательно, для ответа мы будем выбирать значения, которые меньше или равны 5.

Решаем наше квадратное уравнение, перенося все слагаемые из правой части в левую, изменяя при этом знаки на противоположные и приводя подобные слагаемые (выражения с квадратным корнем взаимоуничтожаются):

  х2−2х+√5−х − √5−х− 24=0

Получим приведенное квадратное уравнение, корни которого можно найти подбором по теореме Виета:

 х2−2х− 24=0

Итак, корнями уравнения х2−2х− 24=0 будут числа -4 и 6.

Теперь выбираем корень, обращая внимание на наше ограничение на х, т.е. корень должен быть меньше или равен 5. Таким образом, запишем, что 6 – это посторонний корень, так как 6 не≤5, а число минус 4 записываем в ответ нашего уравнения, так как −4≤5 .

Ответ: -4

pазбирался: Даниил Романович | обсудить разбор

Алла Василевская | Просмотров: 12.6k

Дискриминант — Квадратичные функции

Задачи  

• Учащиеся смогут найти дискриминант, используя формулу дискриминанта.
• Учащиеся смогут определить, сколько решений имеет уравнение.

Все о дискриминанте

Что такое дискриминант?

Дискриминант — это число, которое можно вычислить из любого квадратного уравнения. Когда квадратное уравнение находится в стандартной форме, где a ≠ 0: 92 срок. Формула для дискриминанта :

Что говорит нам дискриминант?

Помните ли вы, что решение (решения) квадратного уравнения находятся там, где график пересекает ось x. Эти точки также известны как нулей , корней , решений и x-пересечений . Дискриминант предоставляет важную информацию о количестве решений любого квадратного уравнения до решения, чтобы найти решения.

Количество решений квадратного уравнения: b² − 4ac > 0, дискриминант больше нуля, положительный дискриминант: два действительных решения b² − 4ac = 0, дискриминант равен нулю. Одно действительное решение b² − 4ac < 0, дискриминант меньше нуля, отрицательный дискриминант: нет действительных решений Обратите внимание, как дискриминант и количество решений влияют на график квадратичной функции справа. Причина, по которой количество решений зависит от дискриминанта, будет более ясна в следующем уроке, Квадратичная формула. Короче говоря, дискриминант является частью квадратичной формулы. Математически использование квадратного корня как части формулы приводит к различному количеству решений в зависимости от знака подкоренного числа (числа под квадратным корнем). Квадратный корень из положительного числа дает два решения (+/-), что дает два решения. (т.е. sqrt(25) = +5 и -5) Квадратный корень из нуля равен нулю, что дает только одно решение. Квадратный корень из отрицательного числа не определен как действительное число, что приводит к отсутствию реальных решений. (т.е. sqrt(-25) не определено)

Применение формулы дискриминанта

Даже не вычисляя, что такое корни, мы можем узнать количество действительных решений, просто изучив дискриминант квадратичной функции. Найдем количество действительных решений следующей функции с помощью дискриминанта: 92-4 (3) (-5) Наконец, упростите, используя правильный порядок операций, PEMDAS. 16+60=76  Дискриминант равен 76, что положительно. Это означает, что существует два реальных решения. Посмотрите скринкаст справа для того же примера.

Дополнительные примеры

Пример 1: 92 — 4(9)(1) Наконец, упрощаем.              36- 36=0 Дискриминант равен нулю, что означает, что существует одно действительное решение этой квадратичной функции. Мы можем проверить ответ, построив график с помощью калькулятора или GeoGebra (см. график справа). Как видите, есть только один х-перехват или одно реальное решение.

92 — 4(1)(1) Наконец, упростите.               1 — 4 = -3 Дискриминант отрицательный, то есть действительных решений нет. Мы можем проверить ответ, построив график с помощью калькулятора или GeoGebra (см. график справа). Получили ли вы ту же функцию, что и ниже? Касается ли функция оси X? Существует ли какое-либо решение этого уравнения?

Независимая практика

Попробуйте пройти следующую викторину, чтобы попрактиковаться в своих навыках.

Quizlet Практика

Теперь, когда вы попрактиковались, попробуйте пройти тест Quizlet, чтобы проверить свое мастерство.

Тест-викторина

Двигаясь вперед

После того, как вы наберете 80 % в тесте Quizlet, указанном выше, перейдите к следующему уроку, Квадратичная формула.

Дополнительные ресурсы

Хотите еще немного попрактиковаться в поиске дискриминанта? Ознакомьтесь со следующими ресурсами:

• Учебные программы SAS: Войдите в систему и найдите QL #891: Понимание дискриминанта квадратного уравнения
  
• Академия Хана: Дискриминант и типы решений квадратного уравнения
  

Вопросы?

Если у вас есть какие-либо вопросы относительно этой онлайн-инструкции или о том, как ее использовать, вернитесь на главную страницу или обратитесь к своему инструктору. Если у вас есть какие-либо вопросы относительно содержания курса, свяжитесь с вашим преподавателем, используя ссылку «Контакты» справа.

Контакт

Фотография заголовка, использованная в рамках Creative Commons от: Pallavpareek
Khanacademy. «Дискриминант квадратных уравнений». Видеоклип онлайн. Ютуб. Youtube, 12 марта 2010 г. Интернет. 17 июня 2013 г.
Махалодотком. «Квадратичная формула: как использовать дискриминант для определения корней». Видеоклип онлайн. Ютуб. Youtube, 3 февраля 2011 г. Интернет. 17 июня 2013 г.

Квадратичная формула и дискриминант: примеры

До сих пор мы использовали такие методы, как построение графиков, разложение на множители и применение свойства квадратного корня для нахождения точных решений некоторых квадратных уравнений. Мы также научились решать квадратные уравнения, дополняя квадрат.

Хотя некоторые из этих методов кажутся лучшим вариантом для решения любого типа квадратного уравнения, он может оказаться довольно сложным, если в данном квадратном уравнении участвуют дроби или десятичные дроби. Однако не бойтесь! Оказывается, есть решение для решения любая форма квадратного уравнения, выраженная в соответствии с приведенным выше определением. Это известно как квадратичная формула.

Квадратная формула — важный инструмент, используемый для определения решений любого заданного квадратного уравнения. Мы можем применить эту концепцию при решении квадратных уравнений, которые нельзя разложить на множители с помощью стандартных методов факторизации.

Обратите внимание, что мы действительно можем использовать квадратную формулу для нахождения решений любой формы квадратных уравнений, даже тех, которые можно разложить на множители.

Квадратная формула

Прежде чем мы углубимся в эту тему, давайте сначала вспомним стандартную форму квадратного уравнения.

Стандартная форма квадратного уравнения : ax2+bx+c=0, где a≠0.

Имея это в виду, давайте теперь представим квадратную формулу.

Для квадратного уравнения вида, где решения даются квадратичной формулой ,

x=-b±b2-4ac2a.

Обратите внимание, что квадратичная формула имеет ‘ ±’ знак. Это означает, что формула дает два решения, а именно

x=-b-b2-4ac2a и x=-b+b2-4ac2a.

Учитывая, что квадратичная формула сообщает нам корни данного квадратного уравнения, мы можем легко найти эти точки и построить график более точно.

Вывод квадратичной формулы

Квадратичная формула получается путем завершения квадрата. В этом разделе шаг за шагом объясняется его вывод, как показано ниже.

Учитывая общую форму квадратного уравнения ax2+bx+c=0:

Шаг 1: Разделите выражение на a

x2+bax+ca=0

Шаг 2: Вычтите ca с каждой стороны

x2 +bax=-ca

Шаг 3 : Заполните квадрат

x2+bax+b2a2=-ca+b2a2⇒x2+bax+b2a2=-ca+b24a2

Шаг 4: Факторизация левой части и упрощение правой части

x+b2a2=b2-4ac4a2

Шаг 5: Квадратный корень с каждой стороны

Не забудьте знак «±»!

x+b2a=±b2-4ac4a2⇒x+b2a=±b2-4ac2a

Шаг 6: Вычесть b2a с каждой стороны

x=±b2-4ac2a-b 2a

Шаг 7 : Упростите выражение

x=-b±b2-4ac2a

Примечание: этот метод заполнения квадрата подробно объясняется в теме Заполнение квадратов 900 31 . Это обсуждение содержит четко проработанные примеры, которые показывают, как этот вывод применяется к данному квадратному уравнению. Проверьте это, если вы хотите изучить это более подробно!

Дискриминант

В следующих разделах мы рассмотрим свойства корней заданных квадратных уравнений. Мы познакомимся с новым понятием, называемым дискриминантом. Дискриминант играет решающую роль в понимании природы корней квадратного уравнения.

Прежде чем мы рассмотрим идею дискриминанта, нам нужно ознакомиться с несколькими важными терминами, которые помогут нам понять это обсуждение. Начнем с определения рационального и иррационального корня.

Рациональный корень — это решение, которое можно выразить как частное двух целых чисел.

Они представлены в виде pq, где p и q — целые числа, где p — константа многочлена, а q — старший коэффициент.

Иррациональный корень — это решение, которое нельзя выразить как частное двух целых чисел. Они часто представлены бесконечно неповторяющимися десятичными знаками или сурдами.

Далее мы определим, что значит быть полным квадратом. Эта концепция имеет решающее значение, когда мы начинаем использовать квадратную формулу, поскольку она определяет, являются ли корни нашего данного квадратного уравнения рациональными или иррациональными, как мы скоро увидим!

Полный квадрат — это целое число, являющееся квадратом целого числа, то есть произведение некоторого целого числа на себя. Это принимает вид p×p=p2, где p — целое число. По существу, p2=p.

Примеры включают 9 (3 ² ), 16 (4 ² ), 25 (5 ² ) и т. д.

Теперь, когда мы рассортировали ключевые определения, давайте перейдем к концепции дискриминант и его связь со свойствами корней.

Дискриминант и свойства корней

Чтобы найти количество корней в данном квадратном уравнении, мы будем использовать дискриминант . Мы также можем определить тип корней выражения.

Дискриминант квадратного многочлена используется для определения количества и типа решений квадратного уравнения. Описывается формулой

D=b2-4ac.

Обратите внимание, что это компонент внутри квадратного корня в квадратичной формуле.

Условие дискриминанта имеет три случая.

Случай 1: D > 0

Когда определитель больше нуля, или, другими словами, b ² – 4ac > 0 , мы получаем два действительных различных корня. Это может быть дополнительно классифицировано следующим образом.

1. Если b ² – 4ac — полный квадрат, то у нас есть два действительных рациональных корня;

2. Если b ² – 4ac не является полным квадратом, то у нас есть два действительных иррациональных корня.

График для этого случая показан ниже.

Дискриминантный случай, когда D > 0, StudySmarter Originals

Случай 2: D = 0

Когда определитель равен нулю, или, другими словами, b ^{2 –} 4ac = 0 9024 9 , получаем один настоящий корень. Это также известно как повторяющийся корень. График для этого случая показан ниже.

Дискриминантный случай, когда D = 0, StudySmarter Originals

Случай 3: D

< 0

Когда определитель меньше нуля, или, другими словами, b ² – 4ac < 0 , мы получаем два комплексно-сопряженных корня. Это означает, что наше решение имеет вид a + bi , где a — действительная часть, а b — мнимая часть. График для этого случая показан ниже.

Дискриминантный случай, когда D < 0, StudySmarter Originals

Напомним, что мнимой единицей является i=-1ori2=-1

Использование квадратичной формулы и дискриминанта для поиска корней

В этом разделе мы рассмотрим некоторые рабочие примеры, демонстрирующие применение квадратичной формулы и дискриминанта для поиска решений заданного квадратного уравнения.

Два действительных рациональных корня

Решите следующее квадратное уравнение.

x2-12x-28=0

Вычислите дискриминант и определите количество и тип корней, которые содержит это выражение. Затем используйте квадратную формулу для оценки ее решений.

Решение

Шаг 1 : Определить a, b и c

a=1,b=-12andc=-28

Шаг 2 : Вычислить дискриминант

D=b2-4ac =(-12)2 -4(1)(-28)⇒D=144+112⇒D=256

Поскольку D > 0, существуют два действительных различных корня.

Шаг 3 : Найдите решения

Используя квадратичную формулу, получаем D, или другими словами b2-4ac=D

⇒x=12±162

Здесь b2-4ac=D=256 — полный квадрат, поэтому мы получаем пару рациональных корней

x=12-162=-42=-2andx=12+162=282 =14

Таким образом, решения равны x=-2 и x=14.

Ниже приведен график для этого квадратного уравнения. Зеленые точки представляют решения выражения.

Пример 1, StudySmarter Originals

Два действительных иррациональных корня

Решите следующее квадратное уравнение.

2×2+4x-5=0

Вычислите дискриминант и определите количество и тип корней, которые содержит это выражение. Затем используйте квадратную формулу, чтобы оценить их решения.

Решение

Шаг 1 : Определить a, b и c

a=2,b=4andc=-5

Шаг 2 : Вычислить дискриминант 9 0021

Д=(4)2-4 (2)(-5)⇒D=16+40⇒D=56

Поскольку D > 0, имеются два действительных различных корня.

Шаг 3 : Найдите решения

Используя квадратную формулу, мы получаем

x=-(4)±562(2)⇒x=-4±2144

Здесь b2-4ac=D=56 не является полным квадратом, поэтому мы получаем пару иррациональных корней

x=-4-2144=-1-142=-2,87(исправить до двух знаков после запятой) и x=-4+2144=-1+142=0,87(исправить до двух знаков после запятой)

Таким образом, решения равны x =-2,87 и х=0,87.

Ниже приведен график для этого квадратного уравнения. Зеленые точки представляют решения выражения.

Пример 2, StudySmarter Originals

Обратите внимание, что вы можете сохранить корни в точной форме и что десятичные разряды являются приблизительным ответом.

Один вещественный повторяющийся корень

Решите следующее квадратное уравнение.

x2+22x+121=0

Вычислите дискриминант и определите количество и тип корней, которые содержит это выражение. Затем используйте квадратную формулу, чтобы оценить их решения.

Решение

Шаг 1 : Определите a, b и c

a=1,b=22andc=121

Шаг 2: Вычислите дискриминант 9 0021

Д=(22)2-4( 1)(121)⇒D=484-484⇒D=0

Поскольку D = 0, существует один действительный отдельный корень.

Шаг 3 : Найдите решения

Используя квадратичную формулу, мы получаем

x=-(22)±02(1)

Заметим, что 0=0

⇒x=-222⇒x =-11

Таким образом, решение x=-11.

Ниже приведен график для этого квадратного уравнения. Зеленые точки представляют решения выражения.

Пример 3, StudySmarter Originals

Два комплексных корня

Решите следующее квадратное уравнение.

x2-4x+13=0

Вычислите дискриминант и определите количество и тип корней, которые содержит это выражение. Затем используйте квадратную формулу, чтобы оценить их решения.

Раствор

Шаг 1 : Определить a, b и c

a=1,b=-4andc=13

Шаг 2 : Вычислить дискриминант

D=(-4)2-4(1)(13 )⇒D=16-52⇒D=-36

Поскольку D < 0, имеются два комплексно-сопряженных корня.

Шаг 3 : Найдите решения

Используя квадратичную формулу, мы получаем

x=-(-4)±-362(1)

Заметим, что -1=i

⇒x=4±i362 ⇒ x=4±6i2

Упрощая, получаем

⇒x=2±3i

Таким образом, решения равны x=2-3i и x=2+3i.

Ниже приведен график для этого квадратного уравнения. Зеленые точки представляют решения выражения.

Пример 4, StudySmarter Originals

Обратите внимание, что на этом графике нет помеченных решений. Это связано с тем, что решения являются мнимыми и не могут быть отображены на стандартной декартовой плоскости. Декартова плоскость представлена ​​действительными числами, а не мнимыми числами! В этом случае мы можем по существу «предполагать» форму графика на основе коэффициента x ² член и что точка пересечения с осью y задана исходным квадратным уравнением.

Дискриминант кубического уравнения

В этом разделе мы рассмотрим дискриминант кубического уравнения и определим типы корней выражения, учитывая значение его дискриминанта.

Для кубического уравнения (общая) форма 2 описывается формулой

D=18abcd+b2c2-4b3d-4ac3-27a2d2.

Формула для вычисления дискриминанта кубических уравнений может быть довольно длинной. Вопросы, где может быть применена эта формула, часто редко встречаются в этой программе. Тем не менее, может быть полезно знать, как это делается для ясности.

Как и в квадратичном случае, дискриминант для кубических уравнений имеет три условия.

Случай 1: D > 0

Когда дискриминант больше нуля, мы получаем три (различных) действительных корня.

Допустим, у нас есть кубическое уравнение x3-6×2+11x-6=0.

Здесь дискриминант равен D=4>0.

Следовательно, у нас есть три различных действительных корня. Факторизация этого выражения дает

(x-1)(x-2)(x-3)=0

Таким образом, корни x=1,x=2 и x=3.

График показан ниже.

Пример 5, StudySmarter Originals

Случай 2: D = 0

Случай 2(a): Если дискриминант равен нулю и b ² = 3ac, получаем три повторяющихся действительных корня (отличающийся тройной корень).

Допустим, у нас есть кубическое уравнение x3-3×2+3x-1=0.

Здесь дискриминант равен D=0.

Далее, (-3)2=9=3(1)(3)=9.

Следовательно, у нас есть три повторяющихся действительных корня. Факторизация этого выражения дает

(x-1)3=0

Таким образом, корни равны x=1.

График показан ниже.

Пример 6, StudySmarter Originals

Случай 2(b): Если дискриминант равен нулю и b ² ≠ 3ac, мы получаем два повторяющихся действительных корня (отличный двойной корень) и один действительный (отличный) корень.

Допустим, у нас есть кубическое уравнение x3-4×2+5x-2=0.

Здесь дискриминант равен D=0.

Далее, (-4)2=16≠3(1)(5)=15.

Следовательно, у нас есть два повторяющихся действительных корня и один действительный корень. Факторизация этого выражения дает

(x-1)2(x-2)=0

Таким образом, корни равны x=1 и x=2.

График показан ниже.

Пример 7, StudySmarter Originals

Случай 3: D

< 0

Когда дискриминант меньше нуля, мы получаем один (различный) действительный корень и пару комплексно-сопряженных корней.

No related posts.