3.7. Цилиндры второго порядка
Определение 1. Цилиндрической поверхностью называется поверхность, образованная параллельными между собой прямыми, называемыми ее образующими.
Если какая-нибудь плоскость, пересекающая все образующие цилиндрические поверхности, пересекает ее по линии Р, то эта линия называется направляющей этой цилиндрической поверхности.
Теорема. Если в пространстве введена декартова система координат и уравнение в плоскостихОу является уравнением некоторой линии Р, то это уравнение в пространстве есть уравнение цилиндрической поверхности L с направляющей линией Р, а образующие параллельны оси Oz (рис.3.19, а).
Доказательство. Точка лежит на цилиндрической поверхностиL тогда и только тогда, когда проекция точкиМ на плоскость хОу параллельно оси Oz лежит на линии
Рис. 3.19
Аналогичные заключения имеют место для уравнений вида (рис. 3.19, б) и(рис.3.19, в).
Определение 2. Цилиндрические поверхности, направляющими которых есть линии второго порядка, называются цилиндрическими поверхностями второго порядка.
Существуют три типа цилиндров второго порядка: эллиптический (рис.3.20)
, (5.42)
гиперболический (рис.3.21)
, (5.43)
параболический (рис.3.22)
. (5.44)
Рис. 3.20 Рис. 3.21 Рис. 3.22
Для цилиндров, заданных уравнениями (5.42), (5.43) и (5.44), направляющими линиями являются соответственно эллипс
,
гипербола
,
парабола
,
а
образующие параллельны оси Oz.
Замечание. Как мы видели, конические и цилиндрические поверхности второго порядка имеют прямолинейные образующие, причем каждая из этих поверхностей может быть образована движением прямой в пространстве.
Оказывается, что среди всех поверхностей второго порядка, кроме цилиндра и конуса, прямолинейными образующими обладают еще однополостный гиперболоид и гиперболический параболоид, причем, так же, как и в случае цилиндра и конуса, обе эти поверхности могут быть образованы движением прямой в пространстве (см. специальную литературу).
В общем уравнении поверхности второго порядка
(5.45)
содержатся следующие группы членов:
а) квадратичная форма
, (5.46)
где ;
б) линейная форма
, (5.47)
где ;
в)
свободный член
.
Чтобы привести уравнение (5.45) к каноническому виду, необходимо, в первую очередь, осуществить такое преобразование координат , а, следовательно, и связанный с ней ортонормированный базис, которое преобразует квадратичную форму (5.46) к каноническому виду (см. кн.2, гл.8, §3, п.3.1).
Матрица этой квадратичной формы имеет вид
,
где , т.е. матрицаА – симметрическая. Обозначим через собственные числа, а черезортонормированный базис, составленный из собственных векторов матрицы А. Пусть
–
матрица перехода от базиса к базису, а– связанная с этим базисом новая система координат.
Тогда при преобразовании координат
(5.48)
квадратичная форма (5.46) примет канонический вид
,
где .
Теперь, применяя
преобразование координат (5.
48) к линейной
форме (5.47), получим
,
где ,– новые коэффициенты формы (5.47).
Таким образом, уравнением (5.45) принимает вид
+.
Это уравнение может быть приведено к канонической форме с помощью параллельного переноса системы координат по формулам
После осуществления преобразования системы координат путем параллельного переноса (5.49), общее уравнение поверхности второго порядка (5.45) относительно декартовой системы координат будет выражать одну из следующих семнадцати поверхностей:
1) эллипсоид
2) мнимый эллипсоид
3) однополостный гиперболоид
4) двуполостной гиперболоид
5) конус
6) мнимый конус
7) эллиптический параболоид
8) гиперболический параболоид
9) эллиптический цилиндр
10) мнимый эллиптический цилиндр
11) две мнимые пересекающиеся плоскости
12) гиперболический цилиндр
13) две пересекающиеся плоскости
14) параболический цилиндр
15) две параллельные плоскости
16) две мнимые параллельные плоскости
17) две совпадающие плоскости
Пример.
Определить вид и расположение поверхности,
заданной относительно декартовой
прямоугольной системы координат
и связанным с ней ортонормированным
базисомуравнением
(5.50)
Приведем квадратичную форму
(5.51)
к каноническому виду. Матрица этой формы имеет вид
.
Определим собственные числа этой матрицы из характеристического уравнения
.
Отсюда 1 = 2, 2 = 0, 3 = 3.
Теперь находим собственные векторы матрицы А: 1) пусть , тогда из уравненияили в координатной форме
находим , где– любое число, и, следовательно,, а. Из всего множества коллинеарных вектороввыбираем вектор, модуль которого, т.е. нормируем вектор.
2) для имеем
.
Отсюда , где– любое число. Тогда, а. Нормируя вектор, находим единичный вектордля направления, задаваемого вектором:
,
где .
3) , тогда для компонентвектораимеем систему
Откуда , где– любое число, и, следовательно,, а. Нормируя вектор, находим единичный вектордля направления, задаваемого вектором:
,
где .
Перейдем теперь от ортонормированного базиса к ортонормированному базису, составленного из собственных векторов матрицыА и свяжем с последним базисом новую декартову прямоугольную систему координат. Матрица перехода для такого преобразования имеет вид
,
а координаты преобразуются по формулам
(5.52)
Применяя данное преобразование координат к квадратичной форме (5.51), приведем ее к каноническому виду
,
где
.
Определим теперь, какой вид имеет линейная формула
, где ,
.
Таким образом, если систему координат преобразовать по формулам (5.52), то относительно новой системы координатрассматриваемая поверхность второго порядка задается уравнением
(5.53)
Уравнение (5.53) приводим к канонической форме с помощью параллельного переноса системы координат по формулам
после чего, уравнение поверхности относительно системы координат принимает вид
или
Это уравнение выражает эллиптический цилиндр, направляющий эллипс которого расположен в координатной плоскости , а образующие прямые параллельны оси
Замечание.
Схема приведения общего уравнения
поверхности второго порядка к каноническому
виду, изложенная в этом параграфе, может
быть примененена и к приведению общего
уравнения кривой второго порядка к
каноническому виду.
Гиперповерхности второго порядка — Теория по линейной алгебре (Математика)
Гиперповерхности второго порядка
Мы будем использовать обозначение для арифметического пространства со стандартно введенным скалярным произведением (п. 1.6). В силу теоремы 1.3 и особенностей вычисления скалярного произведения в ортонормированном базисе мы можем отождествить с любое конечномерное евклидово пространство. Векторы этого пространства будем называть также его точками. «Базис» в этом разделе, если не оговорено противное, означает ортонормированный базис.
Определение 1.31 Гиперповерхность второго порядка в (-мерная гиперповерхность) есть множество точек , удовлетворяющее уравнению:
, (1)
где — некоторый фиксированный самосопряженный линейный оператор, — некоторый постоянный вектор, — некоторая вещественная константа.
Фиксируя какой-то базис , перепишем (1) в виде:
, (2)
где
,
.
Вместо (2) можно записать также
(3)
Таким образом, в уравнении гиперповерхности второго порядка (в каком бы виде мы его ни записали — (1), (2) или (3)) можно выделить три части: квадратичную форму, определенную некоторым самосопряженным оператором, линейную форму и числовую константу. Для размерностей 2 и 3 говорят о кривых и поверхностях второго порядка соответственно. Иногда и в общем случае мы будем говорить просто «поверхность» вместо «гиперповерхности». Гиперповерхности второго порядка называют еще и гиперквадриками.
Наша ближайшая цель состоит в построении классификации гиперповерхностей второго порядка на основе общего анализа уравнений (1)-(3). Тем самым будет строго обоснована (выведена) та чисто описательная классификация, которую мы рассматривали в первом семестре.
Приведем квадратичную форму, фигурирующую в уравнении поверхности к каноническому виду методом ортогональных преобразований (п. 1.15).
Получим следующее представление уравнения (3):
, (4)
где
,
— собственные числа оператора , а — матрица соответствующего ортогонального преобразования, диагонализирующего указанный оператор.
Теперь рассмотрим следующие случаи.
Случай 1. Все собственные числа положительны, ранг квадратичной формы равен размерности пространства:
Тогда квадратичная форма положительно определена — гиперповерхности соответствующие этому случаю называются эллипсоидами.
Уравнение эллипсоида можно преобразовать, выделяя по каждой переменной полный квадрат:
,
или
, (5)
где
,
Положим в (5)
,
получим
(6)
Возможны следующие случаи ( и отвечающие им классы эллипсоидов):
1)
В этом случае, положив , получим уравнение
(7)
Числа называются полуосями эллипсоида.
При равенстве всех полуосей ( ) получаем гиперсферу радиуса .
В трехмерном случае (переобозначая переменные и полуоси) придем к известному из курса аналитической геометрии уравнению эллипсоида:
Если в последнем уравнении две из трех полуосей равны между собой, получаем поверхность, называемую эллипсоидом вращения.
В двумерном случае получаем обычный эллипс:
2)
В этом случае аналогично уравнению (7) получим
(8)
Ясно, что (8) не может удовлетвориться в вещественной области. Определяемая этим уравнением поверхность носит название мнимого эллипсоида. Очевидно, мнимый эллипсоид не имеет ни одной точки в пространстве .
3)
Здесь имеем
(9)
Уравнению (9) удовлетворяет только нулевой вектор. Эта поверхность, выродившаяся в точку, называется вырожденным эллипсоидом.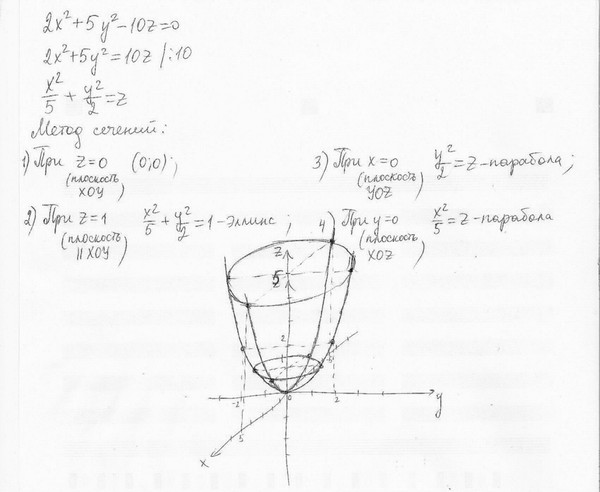
Итак, чтобы от исходного уравнения гиперквадрики (3), определяющий некоторый эллипсоид, перейти к уравнению (6), мы совершили два преобразования: первое, линейное, приводит задающую поверхность квадратичную форму к каноническому виду, выявляя ее ранг и сигнатуру; второе, нелинейное, а именно сдвиг на вектор , переносит начало координат в соответствующем аффинном пространстве начало координат в точку, координаты которой в каноническом базисе квадратичной формы совпадают с одноименными координатами указанного вектора переноса и которая называется центром данной поверхности. Подчеркнем, что этот перенос начала координат имеет место в такой форме только при совпадении ранга квадратичной формы с размерностью пространства. Гиперповрехности, имеющие центр, называются центральными. Как видим, эллипсоиды суть центральные поверхности.
Случай 2. Все собственные числа отличны от нуля, но среди них есть и положительные, и отрицательные; ранг квадратичной формы равен размерности пространства:
В этом случае получаем поверхности, именуемые гиперболоидами.
Гиперболоиды также являются центральными поверхностями, и общее уравнение гиперболоида легко, как и уравнение эллипсоида преобразовать к виду ( при !):
(10)
Величины называются полуосями гиперболоида. В трехмерном случае имеем два типа гиперболоидов:
1) однополостные — сигнатура квадратичной формы в (10) равна 1:
(однополостный гиперболоид с осью симметрии, совпадающей с осью ).
2) двуполостные — сигнатура квадратичной формы в (10) равна -1:
(двуполостный гиперболоид с осью симметрии, совпадающей с осью ).
В плоском случае получаем два вида гиперболы:
(с фокусами на оси абсцисс) и
(с фокусами на оси ординат).
В классе гиперболоидов можно выделить подкласс вырожденных поверхностей, называемых конусами. Этот случай (выделяемый иногда в особый, вне случая гиперболоидов) получается при (в уравнении вида (6)). Тогда вместо уравнения (10) будем иметь:
(11)
Трехмерный конус, ось симметрии которого совпадает с осью аппликат, задается уравнением:
При получаем круговой конус.
В двумерном случае конус вырождается в пару прямых:
Случай 3. Ранг квадратичной формы строго меньше размерности пространства:
В рамках этого соотношения ранга квадратичной формы и размерности пространства рассмотрим несколько подслучаев:
3.1. , т.е., .
Выделение полных квадратов в уравнении (4) теперь даст:
,
или
,
если обозначить
Положив в последнем уравнении
,
получим
(12)
Если в (12) , мы получим класс гиперповерхностей второго порядка, называемых параболоидами.
Если стоящая в (12) квадратичная форма имеет сигнатуру , то параболоид называется эллиптическим; в противном случае получаем гиперболический параболоид («седловую» поверхность).
В уравнении (12) можно сделать преобразование, заменив
и переписав (12) в виде:
(13)
Таким образом, исследуя уравнение параболоида, мы, как и в случае центральных поверхностей (эллипсоидов и гиперболоидов), совершили сначала линейное преобразование (ортогональное), перейдя базису, каноническому для квадратичной формы ранга , фигурирующей в исходном уравнении.
После этого мы совершили нелинейное преобразование сдвига, перенеся начало координат в точку , которая называется вершиной параболоида. Заметим, что первые координат вершины суть координаты центра той центральной поверхности, которая определяется квадратичной формой ранга . Размерность этой поверхности будет также на единицу меньше размерности параболоида и составит . Для эллиптического параболоида эта поверхность является — мерным эллипсоидом, а для гиперболического — — мерным гиперболоидом.
Если размерность пространства равна двум, то параболоид превращается в обычную «школьную» параболу:
.
В трехмерном случае уравнение эллиптического параболоида, ось симметрии которого совпадает с осью аппликат, есть
В любом сечении плоскостью, перпендикулярной оси аппликат, мы получим эллипс — обычный, вырожденный (сечение плоскостью ) или мнимый (если , это будет сечение при отрицательном ). При возникает параболоид вращения (с осью вращения ).
Гиперболический параболоид («седло») имеет уравнение:
.
В любом сечении плоскостью, перпендикулярной оси аппликат, на сей раз получим гиперболу, вырождающуюся в плоскости в пару прямых. Сечения выше и ниже указанной координатной плоскости дадут пару сопряженных гипербол (т.е., гипербол, фокусы которых находятся на двух взаимно перпендикулярных осях).
Когда же в уравнении (12) , из уравнения исчезнет переменная , и мы получаем поверхность, именуемую центральным -мерным цилиндром.
В трехмерном пространстве (при условии, что образующая цилиндра перпендикулярна плоскости ) имеем:
— эллиптический цилиндр;
— гиперболический цилиндр.
Центр цилиндра — точка с координатами (в каноническом базисе квадратичной формы):
Эта точка есть не что иное как центр соответствующей центральной гиперповерхности (эллипсоида или гиперболоида), имеющей на единицу меньшую, чем сам цилиндр, размерность. Эта поверхность называется направляющей цилиндра. Так, для трехмерного эллиптического цилиндра направляющей будет эллипс (в частности, окружность — тогда получаем круговой цилиндр), для гиперболического — гипербола.
Заметим, что на плоскости цилиндр вырождается в пару параллельных прямых:
3.2. .
Вместо уравнения (12) получим тогда уравнение вида:
, (14)
причем, сумма, стоящая в скобках, содержит не менее двух слагаемых.
Полагая в (14)
,
получим (при условии, что хотя бы один коэффициент в сумме линейных слагаемых отличен от нуля) уравнение поверхности, которая называется параболическим цилиндром:
(15)
Последнее преобразование, приводящее к уравнению (15), не является, вообще говоря, ортогональным, но по теореме об ортогонализации полученный базис всегда можно преобразовать к ортонорму.
Бесплатная лекция: «Культура России» также доступна.
Если же в (14) линейная форма вырождается в нуль, получаем поверхность, которая будет центральным цилиндром размерности .
Так при и при невырожденной линейной форме получим параболический цилиндр с уравнением вида:
Образующая этого цилиндра совпадает с осью аппликат, тогда как направляющей будет парабола, определяемая (но уже в плоскости !) тем же уравнением.
В случае же нулевой линейной формы получим центральный цилиндр, выродившийся в пару параллельных плоскостей.
Мы полностью описали классификацию гиперповерхностей второго порядка.
2$ с осью в точке $z$. Я не вижу, где в уравнении находится «$z$». В книге (calc 3), которую я использую, упоминается, что уравнение работает для любого $z$, но я не вижу, где в уравнении находится выход $z$Вот выдержка из книги, единственная часть, в которой есть ссылка к основному уравнению цилиндра, так как я прочитал 1-2 главы после этой точки (это текст векторного расчета из 4 глав)
- геометрия
$\endgroup$
4 92$$
Ссылка: Формула для цилиндра
Я искал ее некоторое время, поэтому оставляю ее здесь, чтобы помочь любому, кто ее ищет!
$\endgroup$
1
$\begingroup$
Уравнение объекта — это способ определить, является ли точка частью объекта.
2=0$, потому что в действительных числах единственным решением этого уравнения является $x=0$ и $y=0$. 92$ все, что вы делаете, это увеличиваете радиус/площадь поперечного сечения. Однако у вас все еще есть уравнение, удовлетворяющее любому значению z, как и сама ось z.
$\endgroup$
$\begingroup$
Это неявное уравнение цилиндра: точка $(x,y,z)$ лежит на цилиндре, если она удовлетворяет уравнению. Здесь важно то, что в уравнении $z$ встречается , а не . Это означает, что если некоторая точка $(x,y,z)$ лежит на цилиндре, то другая точка $(x,y,z’)$, отличающаяся от первой только изменением своей координаты $z$, будет удовлетворять одно и то же уравнение и, следовательно, лежат на одном и том же цилиндре. Вот где в игру вступает ось $z$.
Альтернативой этим неявным уравнениям могут быть параметрические уравнения, которые описывают, как вы вычисляете координаты точек, используя три параметра, например.
$(r\sin\varphi+a,r\cos\varphi+b,z)$ для $\varphi\in[0,2\pi),z\in\mathbb R$.
$\endgroup$
$\begingroup$
Люди склонны чрезмерно усложнять, когда уже есть интуиция для этой концепции. Возьмем, к примеру, двумерный график, и вы хотите построить $x = 2$. Вы начертите вертикальную линию, проходящую через $x = 2$, так как в школе вы узнали, что это 92$ описывает окружность на плоскости x/y; радиуса $r$ с центром $(a, b)$. Его решения включают в себя все комбинации $x$ и $y$, составляющие двумерный круг, и никакие другие точки.
Теперь для трехмерного пространства у нас также есть ось Z. Для каких значений $z$ справедливо уравнение?
Поскольку $z$ не упоминается в уравнении, оно верно для всех $z$, положительных, нулевых или отрицательных.
Таким образом, уравнение описывает бесконечный цилиндр.
$\endgroup$ 9{2n} = 1 $$
с $n\in\mathbb{N}$, $n\neq0$.
Чем больше $n$, тем более гладкими будут верхняя и нижняя кромки, полученные в результате «среза» бесконечного цилиндра.
См., например, https://www.wolframalpha.com/input/?i=plot+x%5E2%2By%5E2%2Bz%5E20+%3D+1
Гладкий цилиндр
$\endgroup$
Поверхности, часть 3
Поверхности, часть 3|
|
Поверхности и контурные графики
Часть 3: Цилиндры
Цилиндр представляет собой поверхность, очерченную перемещением плоской кривой вдоль
прямая линия в пространстве. Например, правый круговой цилиндр показан
ниже перевод окружности в xy -плоскость по прямой
линия, параллельная оси z .
(«Правильно» в названии означает
что перенос осуществляется по линии, перпендикулярной плоскости «образующей
круг.»)
Мы можем использовать это описание, чтобы написать уравнение поверхности: «производящая окружность» на плоскости x 2 + г 2 =16. Если мы интерпретируем это уравнение имеет три переменных (с коэффициентом 0 для z ), уравнение описывает каждую точку на поверхности.
Эта идея работает для всех цилиндров которые параллельны одной из осей координат. Например, если мы переведем парабола y 2 = z в плоскости yz вдоль х -ось, получаем параболический цилиндр определяемый одно и то же уравнение. (Как и в предыдущем примере, это «правильный» цилиндр, но, конечно, это не круговой цилиндр.) Следующий рисунок представляет собой график этого параболического цилиндра.
Уравнения для обоих
круговой и параболический цилиндры квадратичны, поэтому технически они
квадратичные поверхности.