|
Ответы |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Решено
Помогите пожалуйста решить задачу 4-го класса.
Сколькими нулями оканчивается произведение всех натуральных чисел от 41 до 64 включительно
Решено
Такие проценты Положительные числа A и B таковы, что число AA составляет 5 % от числа 3A+5B. Сколько процентов от этого числа составляет число B?
Медиана равностороннего треугольника равна 13√3.Найдите его сторону. Решение плиз
Решено
К вертикальной стене прижали деревянный…
тригонометрия — Доказательство cos(AB) и геометрическая интуиция
$\begingroup$
На приведенном выше рисунке $a,b$ — единичные векторы. Угол между ними равен $A-B$.
Легко заметить, что выделенная зеленым цветом часть: $$\cos A \cos B$$
Это означает, что пурпурная часть должна быть $$\sin A \sin B$$
Есть ли способ элегантно доказать это? Моя работа:
Я попробовал разные соотношения треугольников, потом много триггерных упрощений и пришел к ответу.
Я даже не хочу пытаться снова. Это большой беспорядок.
Я надеялся получить более геометрическое представление о пурпурном сегменте. Любая помощь?
Почему я ищу геометрическую интуицию:
Произведение $\cos A \cos B$ изменяется при вращении плоскости
Произведение $\sin A \sin B$ изменяется при вращении плоскости
Но их сумма $\ cos A \cos B + \sin A \sin B $ не меняется!
Я полностью понимаю алгебру — матрица вращения ортонормирована и сохраняет скалярное произведение: $$(Ra)’ Rb = a’R’Rb = a’Ib = a\cdot b$$
Ищу геометрическую интуицию, если возможно…
- тригонометрия
$\endgroup$
$\begingroup$
Разделите вертикальную линию от $a$ на две части по пурпурной линии, скажем, $x$ и $y$, так что $x+y=\sin \alpha$.
Углы, образованные на концах вертикали из $a$, являются соответственными углами и равны $\beta$.
Вертикаль из $a$ также разбивает пурпурную линию на $x\sin\beta$ и $y\sin\beta$, и $(x+y)\sin\beta = \sin\alpha\sin\beta $. 92 \тета = 1$, мы получаем $$ 2 — 2 \cos(A — B) = 2 — 2 \cos A \cos B — 2 \sin A \sin B \tag{3} $$
Упрощая (4), получаем тригонометрическое тождество $$ \cos(A — B) = \cos A \cos B + \sin A \sin B $$
$\endgroup$
1
$\begingroup$
Вы должны добавить что-нибудь к своей картине.
Пусть $\угол AOC=x$, $\угол BOC=y$, $OA=1$. Тогда $OB=\cos(x-y)$. $\угол FAD=\угол BOC=y$. Также $OB=OE+EB=OE+DF=OD\cos y+AD\sin y=\cos x\cos y+\sin x \sin y$. Тогда $\cos(x-y)=\cos x\cos y+\sin x \sin y$
$\endgroup$
1
Если A и B — острые углы, такие что cosA = cosB, то докажите, что A = B
Тригонометрия — это, по сути, изучение взаимосвязи между углами и сторонами треугольника.
Это одна из широко используемых тем математики, которая используется в повседневной жизни. Он включает в себя операции над прямоугольным треугольником, то есть треугольником, один из углов которого равен 90°. Есть некоторые термины, которые мы должны знать, прежде чем идти дальше. Эти термины,
- Гипотенуза – это сторона, противоположная прямому углу в прямоугольном треугольнике. Это самая длинная сторона прямоугольного треугольника. На рисунке 1 сторона AC является гипотенузой.
- Перпендикуляр – Перпендикуляр треугольника, соответствующий особо острому углу θ, является стороной, противоположной углу θ. На рисунке 1 сторона AB — это перпендикуляр, соответствующий углу θ.
- Основание – это сторона, примыкающая к особенно острому углу θ. На рис. 1 сторона ВС является основанием, соответствующим углу θ.
Рисунок 1
Как было сказано ранее, тригонометрия изображает отношения между углами и сторонами прямоугольного треугольника. Это отношение представлено стандартными отношениями и дается следующим образом треугольника.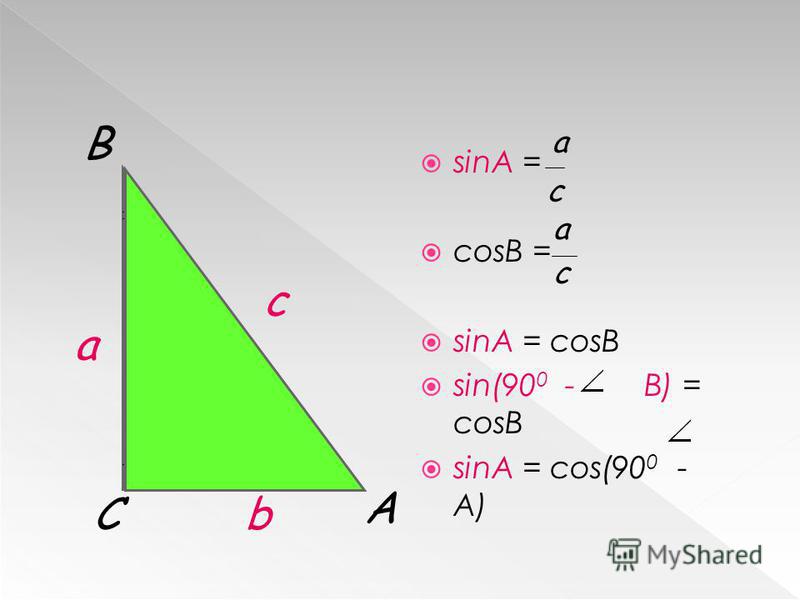
sinθ = перпендикуляр/гипотенуза = p/h
- Косинус (cos) – Косинусом угла θ называется отношение длины основания, соответствующего углу θ, к длине гипотенузы треугольника.
cosθ = основание/гипотенуза = b/h
- Тангенс (тангенс) основание для определенного угла треугольника.
cosθ = основание/гипотенуза = b/h
- Котангенс (котангенс) – обратная величина тангенса.
cotθ = 1/tanθ = основание/перпендикуляр = b/p
- Секанс (сек) – обратная величина косинуса.
secθ = 1/cosθ = гипотенуза/основание = h/b
- Косеканс (косеканс) – это величина, обратная синусу.
cosecθ = 1/sinθ = гипотенуза/перпендикуляр = h/p
Если A и B — острые углы такие, что cosA = cosB, то докажите, что A = B
Решение:
Дано,
cos A = cos B
Предположим, что треугольник выглядит примерно так, как показано на рисунке.
2, с острыми углами A и B.
Рис. 2 ,
AC/AB = BC/AB
Чтобы уравнение было правильным, AC должно быть равно BC
=> угол A = угол B (поскольку углы, противоположные равным сторонам, равны)
Аналогичные вопросы
Вопрос 1. Если A и B — острые углы, такие что sin A = sin B, то проверьте, является ли A = B.
Решение:
Дано,
sin A = sin B
Предположим, что треугольник выглядит как на рисунке 2 с острыми углами A и B.
Тогда sin A = BC/AB ⇢ (i)
sin B = AC/AB ⇢ (ii)
Так как sin A = sin B
Следовательно,
BC/AB = AC/AB
Чтобы уравнение было правильным, AC должно быть равно BC
=> угол A = угол B противоположные равным сторонам равны)
Вопрос 2: Если A и B — острые углы, такие что tan A = tan B, то проверьте, является ли A = B.
tan A = tan B
Предположим, что треугольник выглядит как цифра 2 с острыми углами A и B.
Тогда tan A = BC/AC ⇢ (i)
tan B = AC/BC ⇢ (ii)
Поскольку tan A = tan B
Следовательно,
BC/AC = AC/BC
Для Чтобы уравнение было правильным, AC должно быть равно BC
=> угол A = угол B (поскольку углы, противоположные равным сторонам, равны)
Вопрос 3: Если A и B — острые углы такие, что cot A = кроватка B, затем проверьте, является ли A = B.
Решение:
Дано,
кроватка A = кроватка B
Предположим, что треугольник выглядит как цифра 2 с острыми углами A и B.
Тогда кроватка A = AC/BC ⇢ (i)
кроватка B = BC/ AC ⇢ (ii)
Поскольку кроватка A = кроватка B
Следовательно,
AC/BC = BC/AC
Чтобы уравнение было правильным, AC должен быть равен BC
=> угол A = угол B (поскольку углы, противоположные равным сторонам, равны)
Вопрос 4.