Геометрические приложения алгебры логики
Геометрические приложения алгебры логики
ОглавлениеПРЕДИСЛОВИЕГЛАВА ПЕРВАЯ. ЭЛЕМЕНТЫ ЛОГИКИ 1. Машинный способ задания функции и построение функций 2. Полные системы функций 3. Булевы функции 4. Булевы функции двух переменных 5. Основные свойства булевых функций 6. Дизъюнктивная и конъюнктивная нормальные формы 7. Полные системы булевых функций 8. Минимизация булевых функций 9. Двузначные предикаты ГЛАВА ВТОРАЯ. R-ФУНКЦИИ 2. Ветви класса R-функций 3. Свойства R-функций 4. Построение булевой функции, соответствующей заданной R-функции 5. Построение R-функций по заданной булевой функции 6. R-функции, соответствующие булевым функциям двух переменных 7. О минимизации R-функций 8. Свойства R-конъюнкции, R-дизъюнкции и R-отрицания 9.  R-функции и бесконечнозначная логика R-функции и бесконечнозначная логика10. Некоторые дифференциальные свойства R-конъюкции и R-дизъюнкции ГЛАВА ТРЕТЬЯ. МЕТОДЫ АЛГЕБРЫ ЛОГИКИ В АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ 2. Геометрическая интерпретация формул булевой алгебры 3. Постановка задачи о построении уравнения границы области (D) по заданной логике ее построения с помощью областей … 4. Пересечение областей 5. Объединение областей 6. Уравнение границы произвольной области 7. Задача о построении уравнений границ и частичные булевы функции 8. Уравнение границы области в трехмерном пространстве 9. Уравнения разомкнутых линий и поверхностей 10. Уравнение области 11. Уравнение произвольного чертежа 12. Об алгоритмической полноте средств аналитической геометрии ГЛАВА ЧЕТВЕРТАЯ. НОРМАЛЬНОЕ УРАВНЕНИЕ ЧЕРТЕЖА 3. Свойства нормальных функций 4. Теорема о нормальном уравнении объединения чертежей 5. Некоторые вспомогательные соотношения 6. 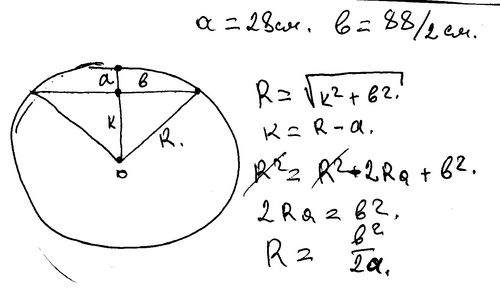 Нормальное уравнение отрезка Нормальное уравнение отрезка7. Нормальное уравнение дуги окружности 8. Нормальное уравнение произвольного чертежа, составленного из дуг окружностей и отрезков прямых 9. Нормальная функция чертежа, содержащего элементы размерности, равной двум 10. Векторная нормальная функция чертежа 11. Верхняя нормальная функция 12. Выпуклая оболочка чертежа 13. Верхняя нормальная функция чертежа, составленного из дуг окружностей и отрезков ГЛАВА ПЯТАЯ. МЕТОДЫ ОПТИМАЛЬНОГО ПЛАНИРОВАНИЯ 2. Оптимальное планирование 3. Методы решения задач оптимального планирования 4. Семейства гиперповерхностей, определяемые уравнениями вида … 5. Учет ограничений в задаче оптимального планирования ГЛАВА ШЕСТАЯ. ЗАДАЧИ ОПТИМАЛЬНОГО РАСКРОЯ 2. Уравнение произвольно расположенной выкройки 3. Условия взаимного непересечения выкроек 4. Склеенные выкройки 5. Использование нормального уравнения 6. Условия непересечения многоугольников 7. Размещение выкроек на материале 8. 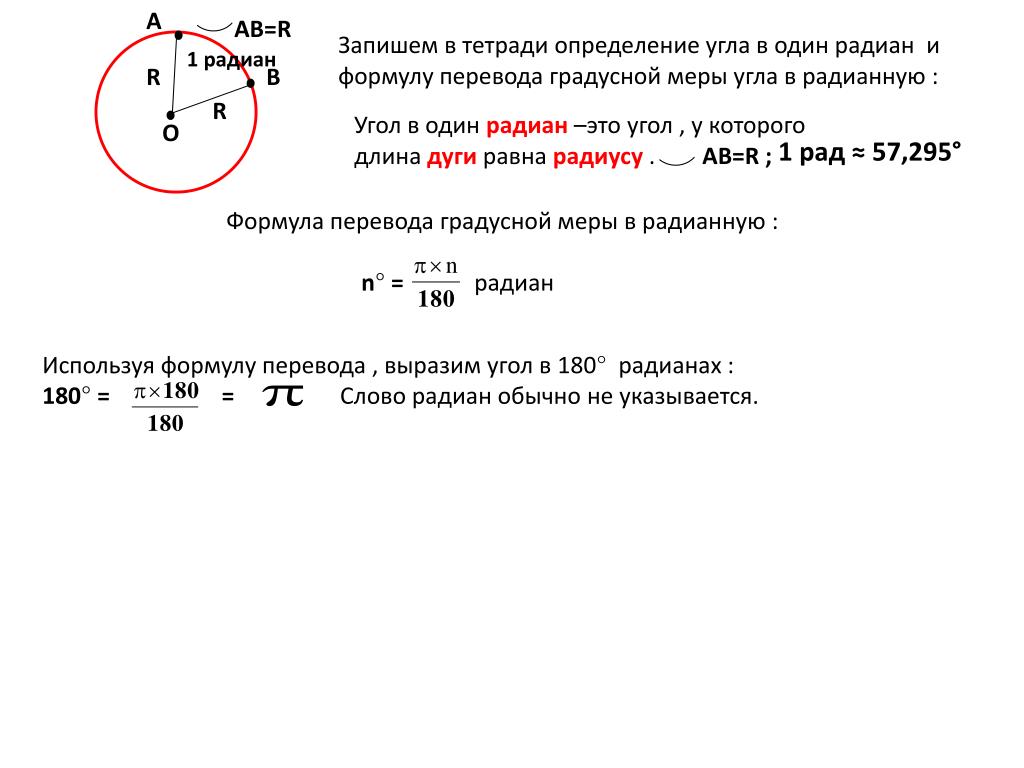 Оптимальный раскрой Оптимальный раскрой9. Постановка некоторых задач оптимального раскроя 10. Задача оптимального раскроя с круговыми выкройками при наличии ограничений на расстояния между ними 11. Некоторые примеры с выкройками некруговой формы 12. Об уменьшении количества локальных экстремумов 13. Задачи оптимального раскроя с неподвижными границами ГЛАВА СЕДЬМАЯ. КРАЕВЫЕ ЗАДАЧИ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 1. Задачи о минимуме функционала. Метод Ритца 2. Краевые задачи. Метод Бубнова — Галеркина 3. О построении функции w(x, y) 4. Расчет жесткости кручения стержней с профилем сложной формы 6. Пространственная контактная задача теории упругости ЛИТЕРАТУРА |
Параметрическое уравнение дуги (сфера + плоскость) : Чулан (М)
| Limit79 |
| ||
29/08/11 |
| ||
| |||
| Nemiroff |
| |||
20/07/09 |
| |||
| ||||
| Otta |
| |||
09/05/13 |
| |||
| ||||
| Limit79 |
| ||
29/08/11 |
| ||
| |||
| Joker_vD |
| |||
09/09/10 |
| |||
| ||||
| Limit79 |
| ||
29/08/11 |
| ||
| |||
| Joker_vD |
| |||
09/09/10 |
| |||
| ||||
| Limit79 |
| ||
29/08/11 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 8 ] |
Модераторы: Модераторы Математики, Супермодераторы
окружностей — Параметрическое уравнение дуги с заданным радиусом и двумя точками
$\begingroup$
поэтому мне нужно параметрическое уравнение дуги.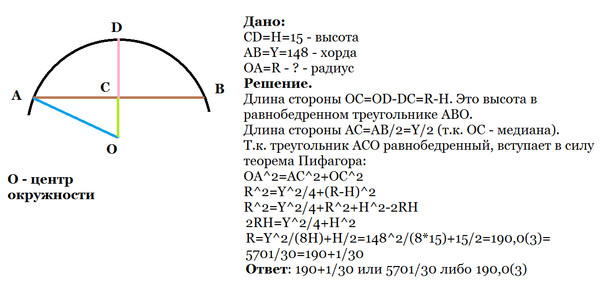 Итак, дуга – это сектор окружности.
Итак, дуга – это сектор окружности.
Параметрическое уравнение окружности: $$ c \equiv f(t) = (\cos(t), \sin(t)),\quad 0\le t < 2\pi $$ Итак, нам просто нужно найти правильный домен функции, на самом деле $t_1$ и $t_2$, начало и конец сектора.
Даны две точки $P_1$ и $P_2$, лежащие на окружности, ее центр и радиус, как найти $t_1$ и $t_2$ по заданным точкам? Мне нужно полное параметрическое уравнение этого.
Заранее спасибо!
- круги
$\endgroup$
4
$\begingroup$
Имея две конечные точки $P$ и $Q$, центр $C$ и радиус $r$, тогда $$ s=2\arctan\left(\frac{P_y-C_y}{P_x-C_x+r}\right) $$ $$ t=2\arctan\left(\frac{Q_y-C_y}{Q_x-C_x+r}\right) $$ Уравнение будет $$ C+r(\cos(\тета),\sin(\тета)) $$ для $\theta$ между $s$ и $t$.
Имейте в виду, что есть две дуги окружности с центром $C$, соединяющие точки $P$ и $Q$.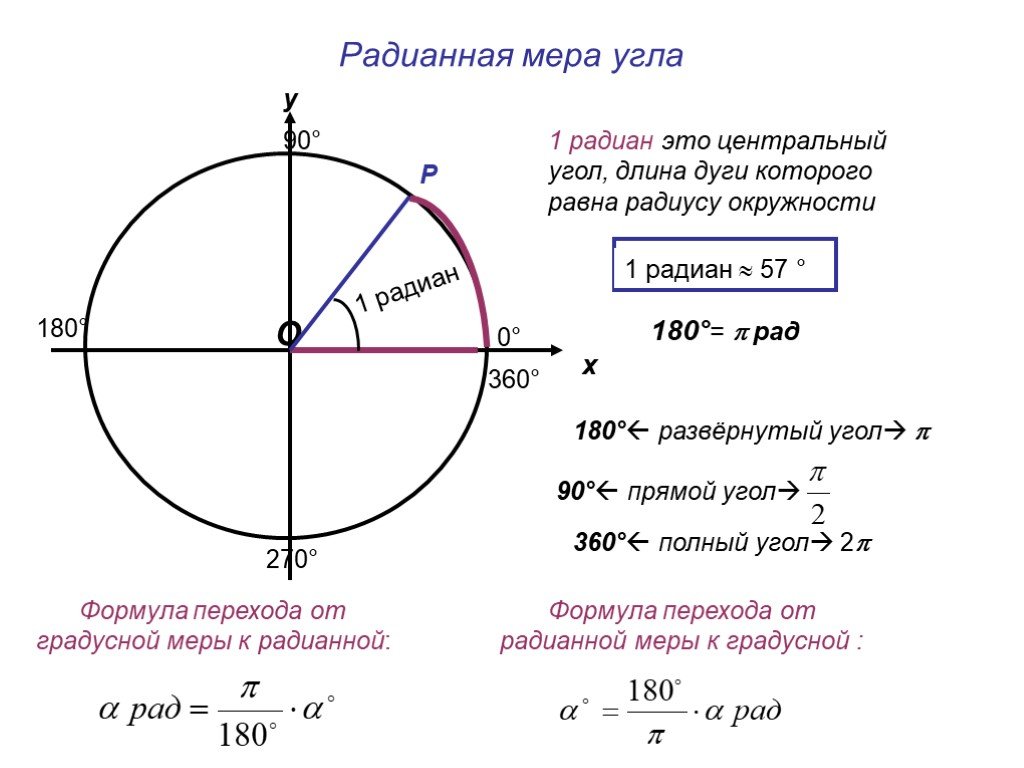 2- \ frac14}
$$
2- \ frac14}
$$
$\endgroup$
4
$\begingroup$
Уравнение в ОП представляет собой параметрическое уравнение окружности с центром в начале координат и радиусом $r=1$.
Параметрическое уравнение окружности радиуса $r$ с центром $C\equiv (a,b)$: $$ f(t)=(a+r\cos t, b+r \sin t) , \quad 0\le t <2\pi $$ Если вы знаете $P_1\equiv (a+r\cos \theta_1, b+r \sin \theta_1) $ и $P_2\equiv (a+r\cos \theta_2, b+r \sin \theta_2) $, то уравнение дуги просто $$ f(t)=(a+r\cos t, b+r \sin t) , \quad \theta_1\le t \le\theta_2 $$ 92}} $$
$\endgroup$
1
$\begingroup$
Поздний ответ, но я думаю, что могу добавить что-то полезное к обсуждению. Когда дан радиус, вы должны выбрать между 2 возможными центрами, а затем между 2 возможными дугами. Вместо этого, учитывая ориентированный угол $\theta$ (против часовой стрелки, если он положительный, или по часовой стрелке, если отрицательный), существует только одна возможная дуга , идущая из точки $P_1=[x_1,y_1]$ в точку $P_2=[x_2,y_2]. $. В таком случае вам не нужно выберите что угодно, и вы можете получить центр $C$ и радиус $r$ из следующего выражения (я использовал Maxima для их получения):
Вместо этого, учитывая ориентированный угол $\theta$ (против часовой стрелки, если он положительный, или по часовой стрелке, если отрицательный), существует только одна возможная дуга , идущая из точки $P_1=[x_1,y_1]$ в точку $P_2=[x_2,y_2]. $. В таком случае вам не нужно выберите что угодно, и вы можете получить центр $C$ и радиус $r$ из следующего выражения (я использовал Maxima для их получения):
$$\mathit{c_x}=\frac{\left(1+ \ cos{(\theta)}\right) \, \left( \mathit{y_1}-\mathit{y_2}\right) +\sin{(\theta)} \left( \mathit{x_1}+\mathit{ x_2}\right) }{2 \sin{(\theta)}}$$
$${c_y}=\frac{\sin{\left(\theta \right) \left({y_1}+{y_2 }\right)}+\left( 1+\cos{\left(\theta \right) }\right)\left( {x_2}-{x_1}\right)}}{2 \sin{\left(\theta \справа) }}$$ 9{2}}}{2 \left( 1-\cos{(\theta)}\right) }$$
$\endgroup$
Нахождение меры дуги окружности по центральному углу — Криста Кинг Математика
Определение длины дуги вокруг окружности
В этом уроке мы рассмотрим дуги окружностей и способы их измерения.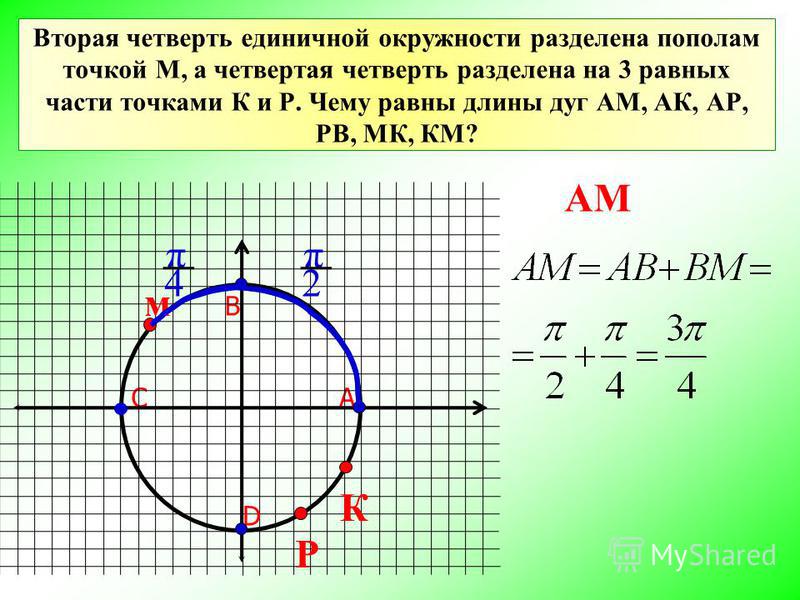 \circ???.
\circ???.
Как найти длину дуги части окружности, исходя из меры центрального угла
Пройти курс
Хотите узнать больше о геометрии? У меня есть пошаговый курс для этого. 🙂
Узнать больше
Нахождение разницы между длинами дуг
Пример
Если ???\overline{AD}??? диаметр круга (с центром в ???C???) на рисунке, в чем разница между мерами ???\overset\frown{DB}??? и дуга ???\overset\frown{AE}????
Примечание. Диаметр — это любой отрезок, проходящий через центр окружности и имеющий обе конечные точки на окружности. Обратите внимание, что диаметр равен удвоенному радиусу и что диаметр делит круг на два полукруга. В этой задаче ???\overline{AD}??? это диаметр, который разбивает круг на полукруги ???AD??? и ???ДА???.
???\overline{AD}??? диаметр окружности, что означает, что сумма мер дуги ???DB??? и дуга ???BA??? ???180^\circ???.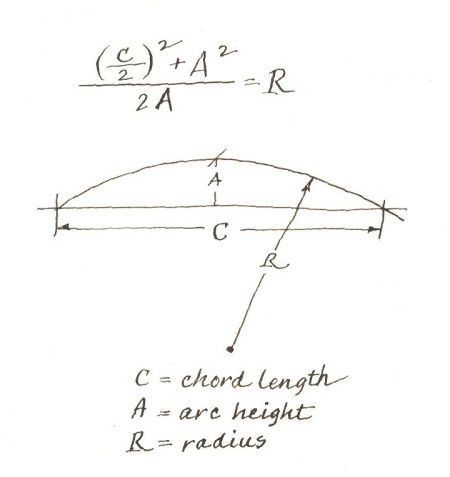


 11.2014, 02:38
11.2014, 02:38  11.2014, 02:44
11.2014, 02:44  11.2014, 02:45
11.2014, 02:45 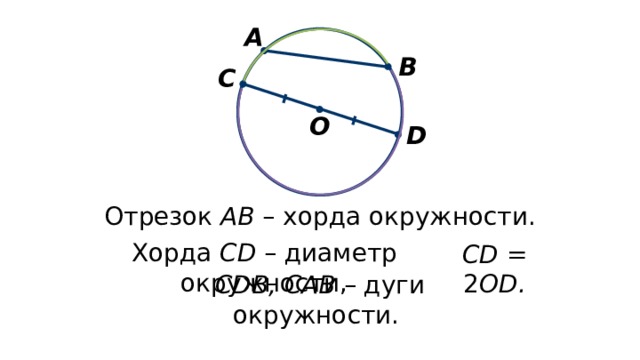


 11.2014, 03:00
11.2014, 03:00 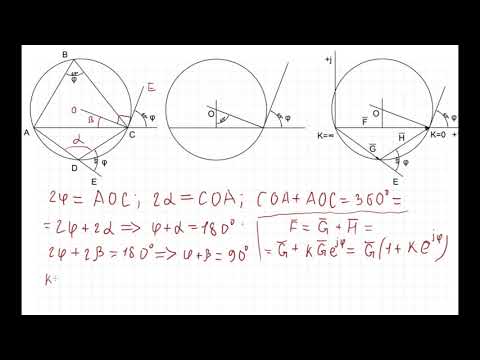 11.2014, 03:08
11.2014, 03:08  11.2014, 03:32
11.2014, 03:32