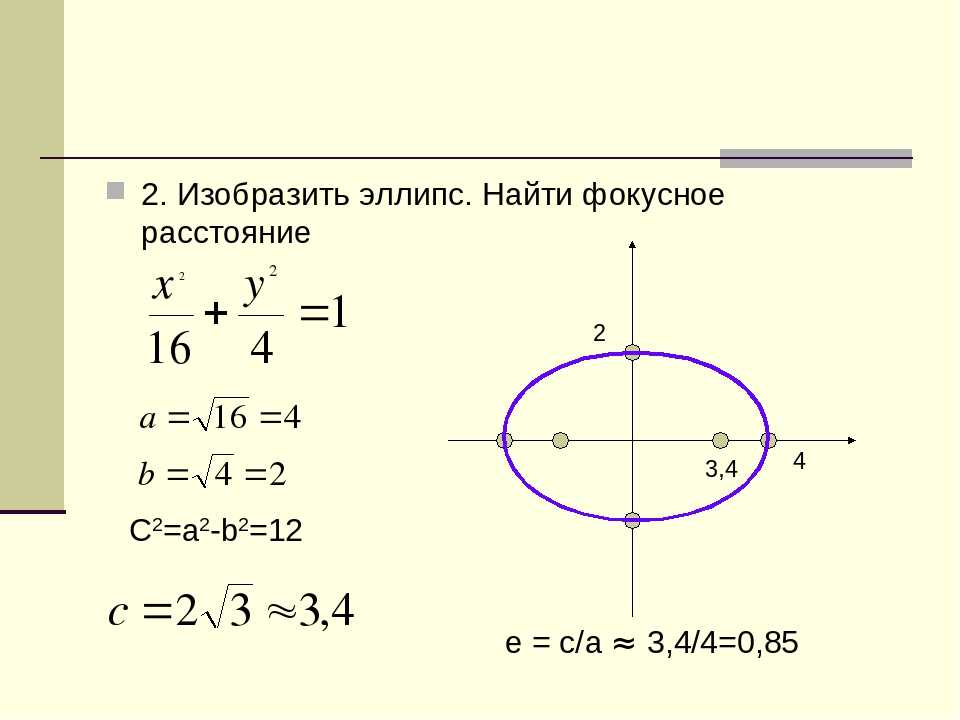
II.3. Канонические уравнения эллипса и гиперболы
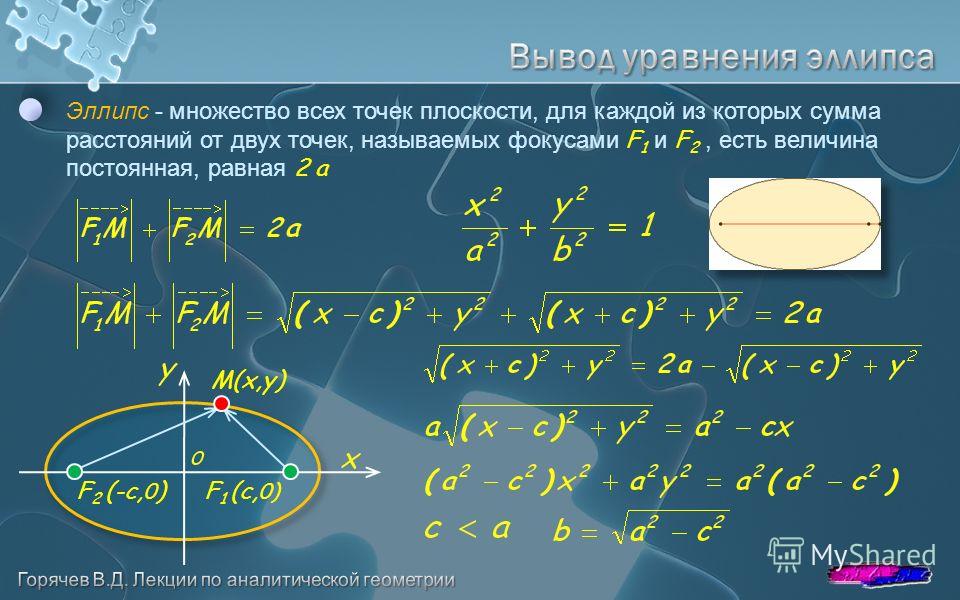
(схема 21) Эллипсом называется геометрическое место точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, равная 2a. Обозначим фокусы через F1 и F2, расстояние между ними через 2c, а сумму расстояний от произвольной точки эллипса до фокусов – через 2a. По определению 2a>2c, то есть a>c . Выберем систему координат так, чтобы фокусы F1 и F2 лежали на оси 0x, а начало координат совпадало с серединой отрезка F1F2. Тогда фокусы имют координаты: F1(–c;0) и F2  Пусть M(x;y) –
произвольная точка эллипса (текущая точка). Тогда по определению эллипса можно записатьПо сути, мы получили уравнение эллипса. Упростим его с помощью ряда несложных математических преобразований:
Так как, a>c, то a2–c2>0, то можно обозначить a2–c2=b2. Тогда последнее уравнение имеет вид: (2.17) Это уравнение равносильно первоначальному. Оно называется каноническим уравнением эллипса – кривой второго порядка. Установим форму эллипса, пользуясь его каноническим
уравнением. 1. Уравнение (2.17) содержит x и y только в четных степенях, поэтому если точка (x;y) принадлежит эллипсу, то ему также принадлежат точки (–x;y), (x;–y), (–x;–y). Отсюда: эллипс симметричен относительно осей 0x и 0y, а также относительно точки O(0;0), которую называют центром эллипса. 2. Найдем точки пересечения эллипса с осями координат. Положив y=0, найдем точки A1(a;0) и A2(–a;0), в которых ось 0x пересекает эллипс. Положив в уравнении (2.17) x=0, находим точки пересечения эллипса с осью 0  Отрезки А1А2, В1В2, а также
их длины 2a и 2b – соответственно большая и малая оси эллипса (рис. 2.4).3. Из уравнения (2.17) следует, что каждое слагаемое в левой части не превосходит единицы, т.е.: . Следовательно, все точки эллипса лежат внутри прямоугольника, ограниченного прямыми x= ± a и y= ± b. 4. В уравнении (2.17) левая часть – сумма неотрицательных слагаемых, т.е. при возрастании одного слагаемого другое будет уменьшаться, если | x| возрастает, |y| уменьшается и наоборот. Из сказанного следует, что эллипс имеет форму
овальной замкнутой кривой. Форма эллипса зависит от отношения. При a=b эллипс превращается в окружность, уравнение эллипса
(2.17) принимает вид: x2+y2=a2.
Отсюда видно, что чем меньше эксцентриситет эллипса, тем будет менее эллипс сплющенным; при ε=0 эллипс превращается в окружность. Пусть M(x;y) – произвольная точка эллипса с фокусами Прямые – директрисы
эллипса. Если r – расстояние от произвольной точки до какого–нибудь фокуса, d – расстояние от этой же точки до соответствующей этому фокусу директрисы (рис. 2.5), то отношениеесть величина постоянная, равная эксцентриситету эллипса: . Из равенства a 2–c2=b2 следует, что a>b. Если же наоборот, то уравнение (2.17) определяет эллипс, большая ось которого 2b лежит на оси 0y, а малая ось 2a – на оси 0x. Фокусы такого эллипса находятся в точках F1(0;c) и F2(0;–c), где . Данный эллипс будет растянут вдоль оси 0y.Пример 2.5. Составить уравнение линии, для каждой точки
которой отношение расстояний от нее до
точки A(3;0) и до прямой x=12, равно числу ε=0,5. Полученное
уравнение привести к простейшему виду. Решение. Пусть M(x;y) – текущая (произвольная) точка искомого
геометрического множества точек. Опустим перпендикуляр По формуле расстояния между двумя точками получаем: Отсюда Полученное уравнение представляет собой эллипс вида где, согласно формуле (2.17). Определим фокусы эллипса F1(–c;0) и F2(c;0). Для эллипса справедливо равенство b2=a2–c2,
откуда c2=a2–b2 =9 и c=3. То есть, F1(–3;0) и F1(3;0)–
фокусы эллипса (точки F2 и A совпадают). Эксцентриситет эллипса Примечание. Если эллипс (окружность) вращать вокруг одной из его осей, то описываемая им поверхность будет эллипсоидом вращения (сферой) Пример 2.6. В геодезии используется система географических координат, основанная на понятии геоида. Геоид – поверхность Земли, ограниченная уровенной поверхностью, продолженной под континенты. Поверхность геоида отличается от физической поверхности Земли, на которой резко выражены горы и океанические впадины. Тело, поверхность которого более всего соответствует поверхности геоида, имеет определенные размеры и ориентирована соответственно в теле Земли, называется референц–эллипсоидом. В нашей стране с 1946 года для всех геодезических работ принят референц–эллипсоид Красовского с параметрами a=6 378 245 м, b= Линия, проходящая вертикально через центр эллипсоида
является полярной осью. Гипербола – геометрическое место точек плоскости, модуль разности расстояний от
каждой из которых до двух данных точек этой плоскости – фокусов, есть величина
постоянная, равная 2a. Обозначим фокусы через F1 и F2, расстояние между ними через 2c, а модуль разности расстояний от каждой точки гиперболы до фокусов через 2a. По определению 2a<2c, то есть a<c. Выберем систему координат , (2. где b2=a2–c2. Гипербола – линия 2–го порядка. Установим форму гиперболы, исходя из ее канонического уравнения. 1. Уравнение (2.18) содержит x и y только в четных степенях. Следовательно, гипербола симметрична относительно осей координат 0x и 0y, и относительно точки O(0;0) – центра гиперболы. 2. Найдем точки пересечения гиперболы с осями координат. Положив в уравнении (2.18) y=0, находим две точки пересечения гиперболы с осью 0x: A1(a;0) и A2(–a;0). Положив в (2.18) x=0, получаем y2= – b2, чего быть не может. Т.е. гипербола ось 0y не пересекает. Точки A1(a;0) и A2(–a;0) – вершины гиперболы, а отрезок |A1A2|=2a – действительная ось. 3. Из уравнения (2.18) следует, что уменьшаемое . Это означает, что точки гиперболы расположены справа от прямой x=a (правая ветвь гиперболы) и слева от прямой x=–a (левая ветвь) (рис. 2.6).
4. Из уравнения (2.18) гиперболы видно, что когда |x| возрастает, то |y| также возрастает. Это следует из того, что разность – сохраняет значение, равноe единице. Следовательно, гипербола имеет форму, состоящую из двух неограниченных ветвей. Прямая L называется асимптотой некоторой неограниченной кривой, если расстояние d от точки M этой кривой до прямой L стремится к нулю при неограниченном
удалении точки M вдоль кривой
от начала координат. Покажем, что гипербола имеет две асимптоты: . Так как данные прямые и гипербола (2.18) симметричны относительно координатных осей, то достаточно рассмотреть только точки, расположенные в первой четверти. Возьмем на прямой точку N, имеющую ту же абсциссу, что и точка M(x;y) на гиперболе . Найдем разность |MN|: Очевидно: так как числитель есть величина постоянная, а знаменатель дроби увеличивается с возравстанием переменной х, то длина отрезка |MN| стремится к нулю. Так как |MN| больше расстояния d от точки M до прямой L, то d стремится к нулю тем более (и подавно). Следовательно, прямые – есть асимптоты гиперболы (рис. 2.7). Эксцентриситет гиперболы – отношение расстояния между фокусами к величине её действительной оси, обозначается ε: . Так как у гиперболы c>a, то эксцентриситет ее больше единицы. Эксцентриситет характеризует форму гиперболы. Так как . Видно, что чем меньше эксцентриситет гиперболы, тем меньше отношение ее полуосей, а значит, тем более вытянут ее основной прямоугольник. Эксцентриситет равносторонней гиперболы равен . Действительно, . Фокальные радиусы , для точек правой ветви гиперболы имеют вид: r1=εx+a, r2=εx–a; для точек левой ветви: r1=–(εx+a), r2=–(εx–a). Прямые называются директрисами гиперболы. Уравнение определяет гиперболу с действительной осью 2b, расположенной на оси 0y, и мнимой осью 2a, расположенной на оси абсцисс (подобная гипербола изображена на рисунке 2.7 пунктиром). Значит, гиперболы и имеют общие асимптоты. Такие гиперболы называются сопряженными. Примечание. Если у кривой 2–го порядка смещен центр в некоторую точку O’(x0;y0), то она называется нецентральной кривой. Уравнение такой кривой имеет вид: Примечание. При вращении гиперболы вокруг ее действительной оси образуется двуполостный гиперболоид, вокруг ее мнимой оси – однополостный гиперболоид Подробно данные уравнения рассмотрены в теме:
«Исследование общего уравнения 2–ой степени» (смотри схему 10), частными
случаями которого являются данные формулы.   Рис 5: Эллипс и его директрисы.   Опишем сначала элементарные свойства эллипса, следующие непосредственно из канонического уравнения (19). 1. Из этого уравнения следует, что если точка $(x,y)$ принадлежит эллипсу, то выполняются неравенства $|x| \leq a $, $|y| \leq b$. Таким образом, все точки эллипса лежат в этом прямоугольнике (конечном!). 2. Так как переменные $x,y$ входят в уравнение эллипса только в квадратах, то из того, что $(x,y)$ лежат на эллипсе следует, что точки $(\pm x, \, \pm y)$ также лежат на эллипсе при любом выборе знаков. Это означает, что эллипс симметричен при отражении относительной осей координат и имеет центр симметрии, точку $O$.   3.4 Прямая на плоскости 3.6 Гипербола   Формула эллипса — GeeksforGeeksЭллипс — это геометрическое место всех точек на плоскости с постоянным расстоянием от двух фиксированных точек на плоскости. Фиксированные места, окруженные кривой, известны как фокусы (сингулярный фокус). Постоянное отношение — это эксцентриситет эллипса, а неподвижная линия — это директриса. Эксцентриситет — это коэффициент эллипса, который показывает удлинение и обозначается буквой «e».
Эллипс имеет овальную форму, а площадь эллипса определяется его большой и малой осями. Площадь эллипса = πab, где a и b — длины большой и малой полуосей эллипса. Эллипс аналогичен другим частям конического сечения, открытым и неограниченным по форме, таким как парабола и гипербола. Что такое эллипс?
Свойства эллипса:
Компоненты эллипса:
Поскольку c a эксцентриситет эллипса всегда больше 1. Кроме того, c 2 = a 2 – b 2. As a result, eccentricity becomes: Формула эллипса Стандартные уравнения для Ellipse
Примеры вопросовВопрос 1: Если длина большой полуоси равна 10 см, а малой полуоси 7 см эллипса. Найдите его площадь. Ответ:
Вопрос 2: Определите основной и незначительный опор oLlips?? Ответ:
Вопрос 3. Каковы уравнения для эллипса? Ответ:
Question 4: Find the lengths for the major axis and minor axis of equation 7x 2 +3y 2 = 21 Ответ:
Вопрос 5: Какова будет площадь эллипса? Ответ:
Определение, параметрическая форма с примерами Эллипс является составным элементом конического сечения и по свойствам связан с окружностью. Вы должны быть знакомы с круговыми паттернами, такими как парабола, эллипс и гипербола. Все точки окружности расположены на определенном расстоянии от центра. Круг не имеет ни ребер, ни вершин, а эллипс в математике имеет овальную форму. Распространенным примером эллипса под коническим сечением в нашей повседневной жизни является форма яйца, беговая дорожка на спортивном стадионе, орбиты планет и т. Определение эллипса: Эллипс — это геометрическое место всех точек на плоскости, сумма длин которых в двух фиксированных точках на плоскости постоянна. Неподвижные точки идентифицируются как фокусы эллипса, которые заключены в кривую. Эллипс также может быть определен как геометрическое место точки, которая движется по плоскости так, что отношение ее расстояния от установленной точки (фокуса) до фиксированного прямого положения (директрисы) является постоянным и меньше единицы, т. е. эксцентриситет e < 1. Эксцентриситет является фактором эллипса, который демонстрирует его удлинение и обозначается буквой «е».
Части эллипса
|
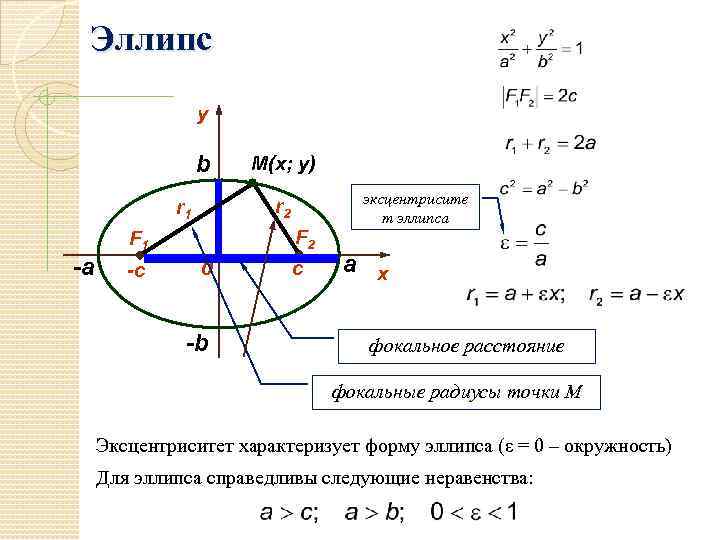Отношение половины расстояния между фокусами к большой полуоси эллипса – эксцентриситет эллипса . Причем
0<ε<1, так как 0<c<a.
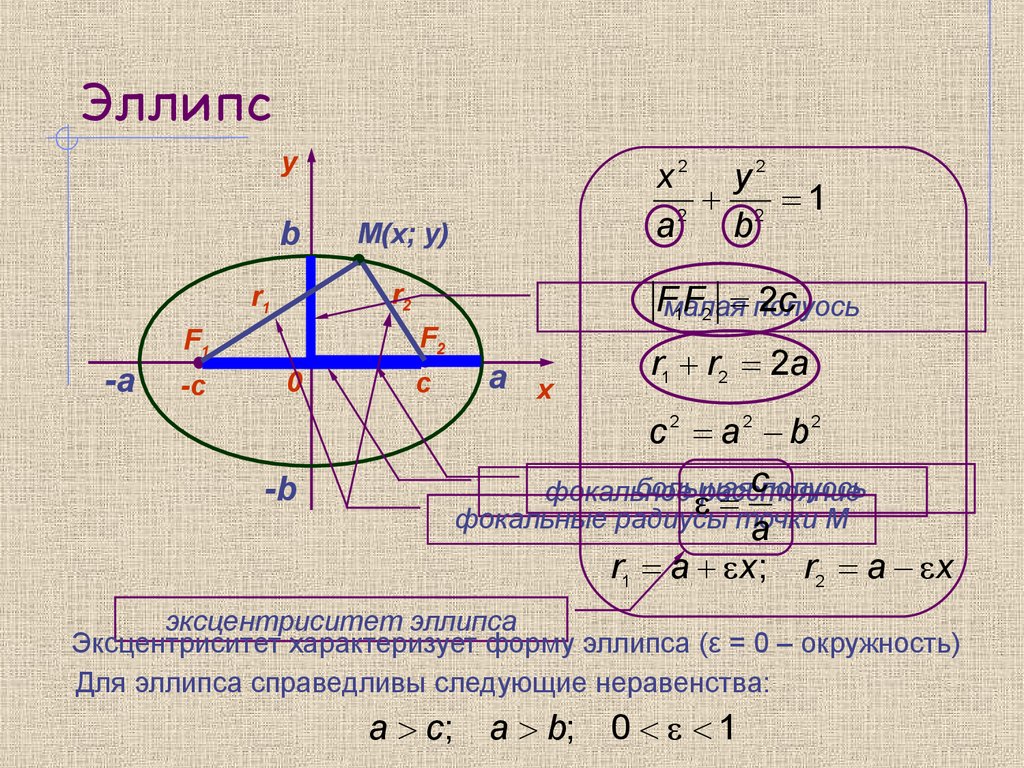
Линия, проходящая через центр эллипсоида,
перпендикулярно к полярной оси, – экваториальной осью. При пересечении
поверхности эллипсоида плоскостью, проходящей через его центр, перпендикулярно
к полярной оси, образуется окружность, называемая экватором. Окружность,
полученная от пересечения поверхности эллипсоида плоскостью, параллельной
плоскости экватора, называется параллелью. Линия пересечения
поверхности эллипсоида с плоскостью, проходящей через заданную точку и полярную
ось, называется меридианом данной точки. Положение точки на земной поверхности
определяется пересечением параллели и меридиана, проходящих через нее. Угол φ между плоскостью экватора и отвесной
линией называется географической широтой. Для определения долгот
точек один из меридианов (Гринвичский) принимают за начальный или нулевой. Угол λ, составленный плоскостью меридиана,
проходящего через данную точку, и плоскостью начального меридиана, называется
географической долготой 
18)
Отрезок |B1B2|=2b,
соединяющий точки B1(0;b) и B2(0;–b) – мнимая ось (рис. 2.6). Прямоугольник
со сторонами 2a и 2b – основной
прямоугольник гиперболы.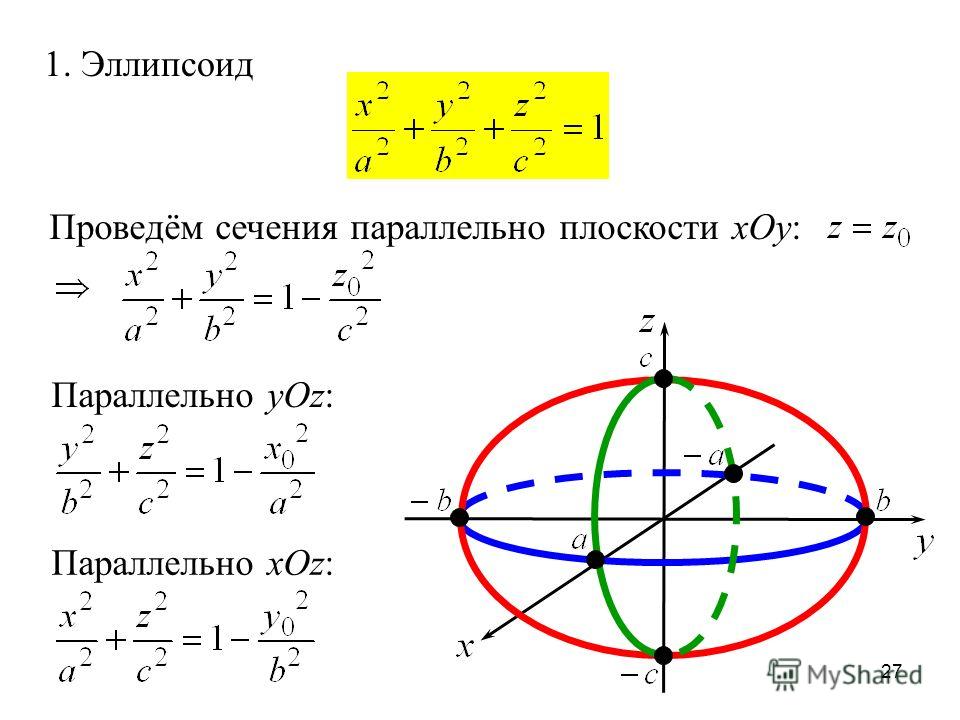
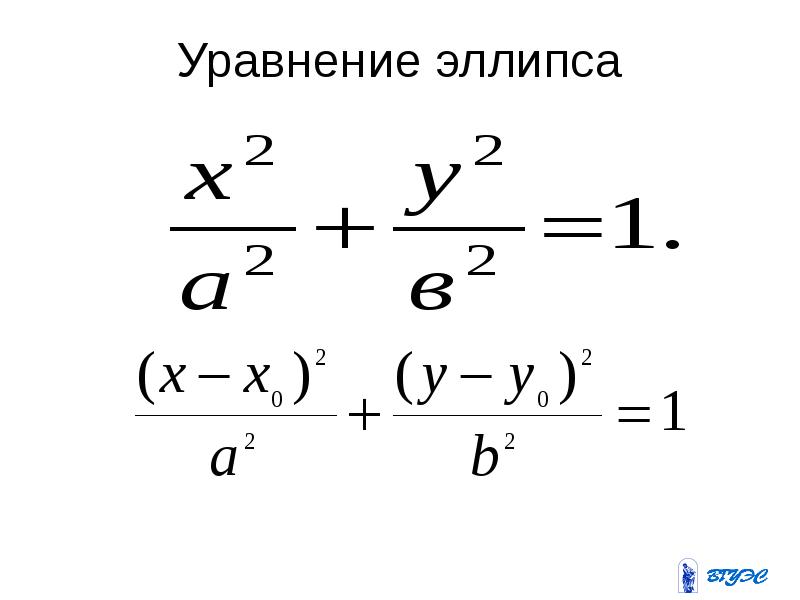
Тот факт, что для гиперболы ε>1, то означает: правая директриса расположена между центром и правой вершиной гиперболы,
левая – между центром и левой вершиной. Директрисы
гиперболы имеют тоже свойство , что и директрисы эллипса.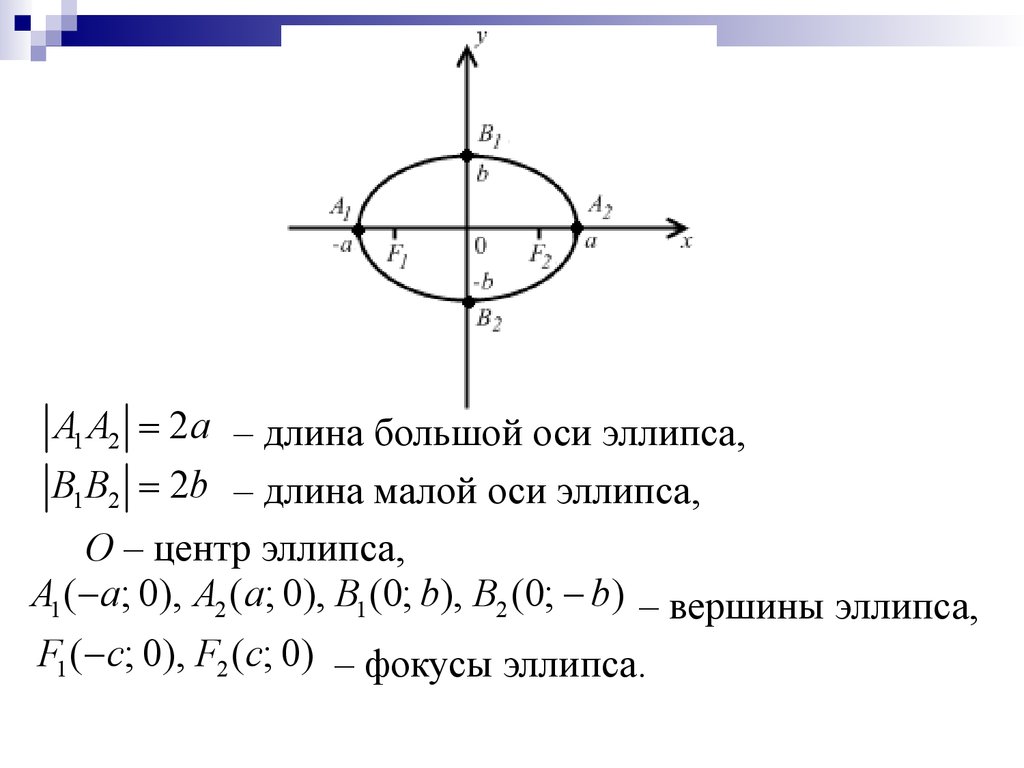 
2}$, точки $(c,0), \, (-c,0)$ называют фокусами эллипса. Величину $\varepsilon = c/a$ называют эксцентриситетом эллипса. Она характеризует вытянутость эллипса. Из определений следует, что для эллипса $0 \leq \varepsilon \leq 1$.
2}{4}=1.
\]
Через точку $(1,1)$ провести хорду, делящуюся в этой точке пополам.
С точки зрения геометрического места эллипс — это набор всех точек на плоскости XY, расстояние которых от двух фиксированных точек (называемых фокусами) в сумме составляет постоянное значение. Эллипс — это тип конического сечения, образованного плоскостью, которая пересекает конус под углом к его основанию. Окружность образуется, когда плоскость пересекает конус параллельно его основанию.
или c 2 = a 2 – b 2 
д.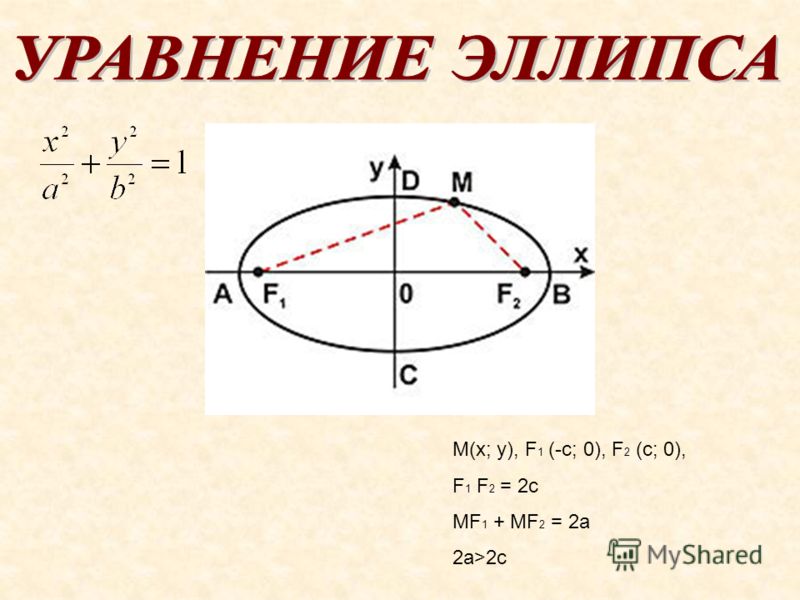
2}=1\) 92}{a}=\frac{2\times4}{4}=\frac{8}{4}=2\)
е. 0≤e<1.