Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
01.15Другие ответы
| ||||||||||||
01.15
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
В буфете тарелок было в.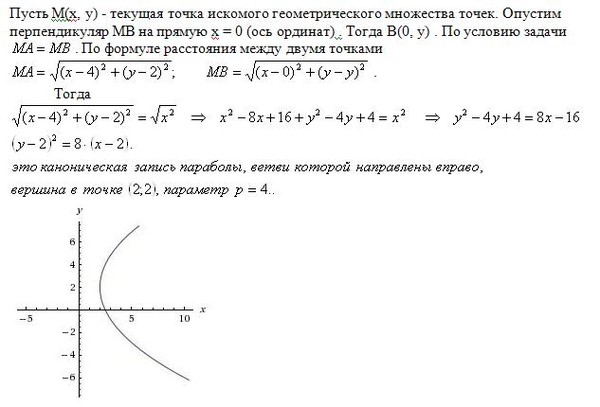
..
Лестница соединяет точки A и B и состоит из 25 ступеней. Высота каждой ступени равна 14 см, а длина – 48 см. Найдите расстояние между точками A и B (в метрах).
Решено
пол комнаты имеющий форму прямоугольника со сторнами 5 м и 6 м требуется покрыть пакретом из прямоугольных дощечек со сторонами 10см и 40см .сколько потребуется таких дощечек
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=17 и MB=19. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Решено
Из пункта А в пункт В,расположенный ниже по течению реки,отправился плот. Одновременно с ним из пункта А вышел катер.Дойдя до В,катер сразу же…
Пользуйтесь нашим приложением
Составьте уравнение геометрического места точек прост- ранства, равноудаленных от точки А.
ГДЗ. Геометрия. 10 класс. Погорелов. § 4 п.24 Задача 8 Составьте уравнение геометрического места точек прост- ранства, равноудаленных от точки А. ГДЗ. Геометрия. 10 класс. Погорелов. § 4 п.24 Задача 8 – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Помогите выполнить задачу.
Составьте уравнение геометрического места точек пространства, равноудаленных от точки А (1; 2; 3) и начала
координат.
ответы
Помогу.
Пусть М(х, у, z) — точка с данным свойством. Тогда
ОМ2 = AM2, то есть
x2 + y2 + z2 = (х-l)2 + (y-2)2 + (z-3)2;
x2 + y2 + z2 = х2-2х+ 1 + у2 — 4у + 4 + z2 — 6z + 9;
2х + 4у + 6z — 14 = 0;
х + 2у + 3z — 7 = 0 — это уравнение плоскости.
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Экскурсии
Мякишев Г.Я.
Досуг
Химия
похожие вопросы 5
Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос
Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
ГДЗЭкзаменыГеометрия9 классЗив Б. Г.
Почему сейчас школьники такие агрессивные ?
Читали новость про 10 классника который растрелял ? как вы к этому относитесь
Новости10 классБезопасность
ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.
Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
Не могу справиться с заданием, §8№26. Какой высоты должна быть….Геометрия 11 класс ГДЗ Погорелов
Не могу справиться с заданием, §8№26.
Сосуд имеет форму полушара радиуса R, дополненного ци-
линдром. Какой высоты должна (Подробнее…)
ГДЗ11 классГеометрияПогорелов А.В.
Это правда, что будут сокращать иностранные языки в школах?
Хочется узнать, когда собираются сократить иностранные языки в школе? Какой в итоге оставят? (Подробнее.
..)
ШколаНовостиИностранные языки
Видео с вопросом: Геометрическое место точек, равноудаленных от двух точек
Стенограмма видео
Существует несколько способов
описание геометрического места комплексного числа 𝑧 с использованием модуля. И в самом деле, мы можем процитировать один из
эти здесь. Для двух заданных постоянных комплексов
чисел, 𝑧 один и 𝑧 два, геометрическое место точки 𝑧, которая удовлетворяет модулю
𝑧 минус 𝑧 один равно модулю 𝑧 минус 𝑧 два — серединный перпендикуляр
отрезка, соединяющего 𝑧 один с 𝑧 двумя. Мы собираемся переписать наше уравнение
так что это выглядит немного больше, как это.
Модуль 𝑧 минус два плюс
четыре 𝑖 можно записать как модуль 𝑧 минус два минус четыре 𝑖. И мы можем переписать 𝑧 плюс два плюс
два 𝑖 как 𝑧 минус минус два минус два 𝑖.
Итак, наше уравнение такое, как показано на рисунке. Итак, мы сравниваем наше уравнение с уравнение в нашем правиле. И мы видим, что 𝑧 единица равна два минус четыре 𝑖 и 𝑧 два, наше второе постоянное комплексное число, равно отрицательному числу два минус два 𝑖. Таким образом, мы можем сказать, что локус 𝑧 — серединный перпендикуляр к отрезку, соединяющему два минус четыре 𝑖 и минус два минус два 𝑖. Вторая часть первой части этого вопроса просит нас найти декартово уравнение этого. Итак, давайте расчистим место.
И что мы собираемся сделать, это
на самом деле нанесите 𝑧 один и 𝑧 два на диаграмму Аргана. 𝑧 один имеет действительную часть от двух и
мнимая часть минус четыре.
Таким образом, он имеет координату два,
минус четыре. 𝑧 два имеет действительную часть отрицательного числа
двойка и мнимая часть отрицательной двойки. Значит его координаты отрицательные
два, минус два. Мы пытаемся найти декартово
уравнение серединного перпендикуляра к отрезку между этими двумя
точки. Поэтому мы будем использовать уравнение
прямая линия. Это 𝑦 минус 𝑦 один равно 𝑚
умножить на 𝑥 минус 𝑥 один. Здесь 𝑥 один 𝑦 один — это точка, которая
линия проходит через нее, а 𝑚 — ее наклон.
Уравнение для 𝑚 равно 𝑦 два минус
𝑦 один на 𝑥 два минус 𝑥 один, изменение 𝑦 разделить на изменение 𝑥. Итак, начнем с поиска
наклон нашего отрезка, отрезка, соединяющего два, минус четыре в
минус два, минус два. Это минус четыре минус минус
два на два минус минус два. Это минус два больше четырех,
что является отрицательной половиной.
Теперь, если мы вызовем 𝑚 sub one, наклон этого отрезка прямой и 𝑚 меньше двух наклон его серединного перпендикуляра, мы знаем, что произведение этих двух, 𝑚 sub one и 𝑚 sub two, отрицательно. один. Альтернативно это можно записать поскольку 𝑚 sub two равно отрицательной единице над 𝑚 sub one. Другими словами, наклон нашего Биссектриса — это отрицательная обратная величина наклона исходной линия. И так наклон нашей Серединный перпендикуляр равен двум.
Но нам нужно найти точку,
проходит через. Так как это перпендикуляр
биссектриса этого отрезка, мы знаем, что она должна проходить через середину. И находим середину по
по сути, нахождение среднего значения двух наших координат. Так что минус два плюс два
больше двух, минус два плюс минус четыре больше двух. Это дает нам середину нуля,
минус три.
И так заменяем то, что есть
в нашу формулу уравнения прямой. Получаем 𝑦 минус минус три
равно удвоенному 𝑥 минус ноль, то есть 𝑦 плюс три равно двум 𝑥, и тогда мы
переставить, вычитая три с обеих сторон. И мы находим, что картезианский
уравнение для геометрического места 𝑧 равно 𝑦 два 𝑥 минус три.
Итак, мы ответили на первый часть этого вопроса. Локус 𝑧 — это серединный перпендикуляр к отрезку между двумя минус четырьмя 𝑖 и минусом два минус два 𝑖. И его декартово уравнение 𝑦 равно двум 𝑥 минус три.
И так возвращаемся ко второму
часть этого вопроса. Это говорит о том, каков минимум
значение модуля 𝑧? Ну, помните, модуль 𝑧
это расстояние между точкой 𝑧 и началом координат. Итак, чтобы найти минимальное значение 𝑧,
нам нужно найти точку на геометрическом месте 𝑧, ближайшую к началу координат.
Теперь мы знаем, что линия
отрезок, соединяющий эту точку с началом координат, будет перпендикулярен нашей линии,
представляет собой геометрическое место 𝑧. Таким образом, наклон этой линии будет
быть таким же, как наклон отрезка, соединяющего наши исходные две точки,
соединение отрицательных двух, отрицательных двух и двух, отрицательных четырех. И, конечно, это был негатив
одна половина.
Назовем эту точку 𝑐. И тогда декартово уравнение для
линия, которая проходит через начало координат и 𝑐 равна 𝑦, равна отрицательной половине
𝑥. 𝑐 лежит в точке
пересечение нашей линии с линией, представляющей геометрическое место 𝑧. Итак, нам нужно решить уравнения
𝑦 равно отрицательной половине 𝑥, а 𝑦 равно двум 𝑥 минус три одновременно. Мы можем добиться этого, приравняв
𝑦. И получаем минус половину 𝑥
равно двум 𝑥 минус три.
Прибавляем половину 𝑥 и три к
обе стороны. И мы находим, что три равно
пять больше двух 𝑥. Затем делим на пять
два, помня, что для деления на дробь надо умножить на
обратную этой дроби. И мы получаем 𝑥 равно
шесть пятых.
Мы ищем
координаты 𝑐. Поэтому мы подставили это значение в
наше предыдущее уравнение 𝑦 равно минус половине 𝑥. И мы получаем 𝑦 равно отрицательному a
половина умножить на шесть пятых, что дает нам 𝑦 равно отрицательным трем пятым. Поэтому мы можем сказать, что точка 𝑐
имеет декартовы координаты шесть пятых, отрицательные три пятых. Минимальное значение модуля
𝑧 находится путем нахождения расстояния между этой точкой и началом координат. Поэтому мы используем пифагорейскую
теорема. Это квадратный корень из суммы
квадраты шести пятых и отрицательные три пятых. Это квадратный корень из 36
25 плюс девять к 25, что является квадратным корнем из 45 из 25.
Теперь мы знаем, что квадратный корень из 25 равно пяти, поэтому мы получаем пятый корень из 45. Но квадратный корень из 45 можно упрощено как три корня из пяти, так как это квадратный корень из девяти, умноженный на квадратный. корень из пяти, а квадратный корень из девяти равен трем. И поэтому мы можем сказать, что минимальное значение модуля 𝑧 равно трем корням из пяти из пяти.
Основы координатной геометрии — Локус: уравнение (часть 1)
Этот урок будет посвящен уравнению с геометрическим местом. Я снова разделю его на две части из-за его длины.
Уравнение геометрического места
Формальное определение: «Уравнение кривой — это отношение, которое существует между координатами всех точек на кривой и которое не выполняется ни для одной точки, не принадлежащей кривой».
Попробуем понять, что это значит.
Если я напишу уравнение, скажем, x + y = 4 и скажу вам, что это представляет собой линию, которая выглядит так…
… это означает, что если вы возьмете любую случайную точку, лежащую на этой прямой, возьмете ее x -координату и прибавите ее к y -координате, вы всегда получите 4 как сумму (потому что уравнение говорит x + y = 4 ).
А если взять любую другую точку, не лежащую на прямой, и сложить ее координаты, то никогда не получится сумма 4 . (Пока не беспокойтесь о том, почему x + y = 4 должно выглядеть как линия, а не что-то другое, например круг. Мы увидим это позже.)
Таким образом, нахождение уравнения для геометрического места означает нахождение отношения, которое выполняется между координатами x и y всех точек на геометрическом месте.
Давайте найдем уравнения для всех локусов, которые мы рассмотрели ранее.
Пример 1 Найти геометрическое место точки, движущейся по плоскости, которая находится на фиксированном расстоянии 5 единиц от оси X .
Пусть P(x, y) будет движущейся точкой. Теперь расстояние этой точки от X ось — это его y -координата.
Поскольку это расстояние равно 5 , мы можем записать это соотношение в виде уравнения
y = 5
Вот и все! Мы получили уравнение, представляющее геометрическое место.
В обратном порядке уравнение y = 5 есть уравнение геометрического места (или кривой), каждая точка, на которой y -координата 5 , или каждые 9Точка 0066 находится на расстоянии 5 единиц от оси X .
Существует также другая возможность y = -5 , также линия, параллельная оси X , на расстоянии 5 единиц, но лежащая на ниже оси .
Пример 2 Найти геометрическое место точки, которая находится на фиксированном расстоянии 4 от начала координат.
Это место (или путь) было кругом. Чтобы найти его уравнение, мы начнем с преобразования данного условия в математическую форму, используя известные нам формулы. 92}\) = 4
⇒ x 2 + y 2 = 16
Следовательно, уравнение на геометрическое место при данных условиях равно + 10 5 9 y 90901 2 2 90 159 = 16 .