II.9. Поверхности второго порядка — МАТЕМАТИКА для обучающихся в агротехнологических вузах
С помощью векторов мы ввели понятие пространства и его размерности, в частности трехмерного. Рассмотрим в нем поверхности, которые «похожи» на поверхности, образованные вращением кривой второго порядка вокруг ее оси симметрии. Например, сфера может быть получена вращением окружности вокруг диаметра. Поверхность, описываемая некоторой линией, вращающейся вокруг неподвижной прямой d, называется поверхностью вращения с осью вращения d. Наряду с такими поверхностями мы встретимся и с более сложными случаями. Пусть в пространстве задана прямоугольная декартова система координат. Поверхность второго порядка – геометрическое место точек, декартовы прямоугольные координаты которых, удовлетворяют уравнению вида , (2. в котором хотя бы один из коэффициентов отличен от нуля. Уравнение (2.48) называется общим уравнением поверхности второго порядка. Уравнение (2.48) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую поверхность второго порядка. В зависимости от значений коэффициентов общего уравнения (2.48) оно может быть преобразовано с помощью параллельного переноса и поворота системы координат к одному из канонических видов, каждому из которых соответствует определённый класс поверхностей второго порядка. Среди них выделяют пять основных классов поверхностей: эллипсоиды, гиперболоиды, параболоиды, конусы и цилиндры. Для каждой из этих поверхностей существует декартова прямоугольная система координат, в которой поверхность задается простым уравнением, называемым каноническим уравнением. Перечисленные поверхности второго
порядка относятся к так называемым нераспадающимся поверхностям второго
порядка. Наша цель – указать канонические уравнения для поверхностей второго порядка и показать, как выглядят эти поверхности. Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением (a > 0, b > 0, c > 0), (2.49) называется эллипсоидом (рис. 2.22). Свойства эллипсоида. 1.
Эллипсоид –
ограниченная поверхность, поскольку из его уравнения следует, что 2. Эллипсоид обладает · центральной симметрией относительно начала координат, · осевой симметрией относительно координатных осей, ·
плоскостной
симметрией относительно начала координат. 3. В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается эллипс (см. рис. 2.22). Так же, как для эллипса, точки пересечения эллипсоида с координатными осями называются вершинами эллипсоида, центр симметрии – центром эллипсоида. Числа а, b, с называются полуосями. Если полуоси попарно различны, то эллипсоид называется трехосным. Если две полуоси равны друг другу, то эллипсоид называется эллипсоидом вращения. Эллипсоид вращения может быть получен вращением эллипса вокруг одной из осей. Примечание. Сфера является частным случаем эллипсоида при а=b=с. Тогда все равные полуоси обозначают R и уравнение (2.49) после умножения на R2 принимает вид . Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением (a > 0, b > 0), (2. называется эллиптическим параболоидом (рис. 2.23). Свойства эллиптического параболоида. 1. Эллиптический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z ≥ 0 и принимает сколь угодно большие значения. 2. Эллиптический параболоид обладает · осевой симметрией относительно оси 0z, · плоскостной симметрией относительно координатных осей 0xz и 0yz. 3. В сечении эллиптического параболоида плоскостью, ортогональной оси 0z, получается эллипс, а плоскостями, ортогональными осям 0x и 0y –парабола. (см. рис. 2.23). Можно
получить эллиптический параболоид симметричный относительно оси 0х или 0у, для чего нужно в уравнении (2.50) поменять между собой переменные х и z или у и z соответственно. Если полуоси равны a=b, то параболоид называется параболоидом вращения и может быть получен вращением параболы вокруг ее оси симметрии. При этом в сечении параболоида вращения плоскостью, перпендикулярной оси 0 z, получается окружность. Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением , (2.51) называется гиперболическим параболоидом (рис. 2.24). Свойства гиперболического параболоида. 1. Гиперболический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число. 2. Гиперболический параболоид обладает · осевой симметрией относительно оси 0z, ·
плоскостной
симметрией относительно координатных плоскостей 0xz и 0yz. 3. В сечении гиперболического параболоида плоскостью, ортогональной оси координат 0z, получается гипербола, а плоскостями, ортогональными осям 0x и 0y, – парабола (см. рис. 2.24). 4. Гиперболический параболоид может быть получен поступательным перемещением в пространстве параболы так, что ее вершина перемещается вдоль другой параболы, ось которой параллельна оси первой параболы, а ветви направлены противоположно, причем их плоскости взаимно перпендикулярны. 5. Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением (a > 0, b > 0, c > 0), (2.52) называется однополостным гиперболоидом (рис. 2.25). Свойства однополостного гиперболоида. 1.
Однополостный
гиперболоид – неограниченная поверхность,
поскольку из его уравнения следует, что z – любое число. 2. Однополостный гиперболоид обладает · центральной симметрией относительно начала координат, · осевой симметрией относительно всех координатных осей, · плоскостной симметрией относительно всех координатных плоскостей. 3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат 0z, получается эллипс, а плоскостями, ортогональными осям 0x и 0y, – гипербола (см. рис. 2.25). Если в уравнении (2.52) a=b, то сечения однополостного гиперболоида плоскостями, параллельными плоскости х0у, являются окружностями. В этом случае поверхность называется однополостным гиперболоидом вращения. Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением (a > 0, b > 0, c > 0), (2. называется двуполостным гиперболоидом (рис. 2.26). Свойства двуполостного гиперболоида. 1. Двуполостный гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что |z|≥c и неограничен сверху. 2. Двуполостный гиперболоид обладает · центральной симметрией относительно начала координат, · осевой симметрией относительно всех координатных осей, · плоскостной симметрией относительно всех координатных плоскостей. 3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат 0z, при |z|>c получается эллипс, при |z|=c – точка, а в сечении плоскостями, перпендикулярными осям 0x и 0y, – гипербола (см. рис. 2.26). Если в уравнении (2.53) a=b , то
сечения двуполостного гиперболоида плоскостями, параллельными плоскости х0у,
являются окружностями. Примечание. Если уравнение поверхности в прямоугольной системе координат имеет вид: F(x2+y2;z)=0, то эта поверхность – поверхность вращения с осью вращения 0z. Аналогично: F(x2 С учетом данного примечания могут быть записаны уравнения для рассмотренных выше поверхностей вращения, если осью вращения являются оси 0х или 0у. Цилиндрическая поверхность образуется движением прямой
линии, скользящей по некоторой неподвижной замкнутой или незамкнутой кривой и
остающейся параллельной своему исходному положению. Множество прямолинейных
образующих представляет собой непрерывный каркас цилиндрической поверхности. Если уравнение поверхности не содержит в явном виде какой–либо переменной, то это уравнение определяет в пространстве цилиндрическую поверхность с образующими, параллельными оси отсутствующего переменного и направляющей, которая в плоскости двух других переменных имеет то же самое уравнение. Достаточно нарисовать на плоскости х0у направляющую, уравнение которой на этой плоскости совпадает с уравнением самой
поверхности, и затем через точки направляющей провести образующие параллельно
оси 0z. Для наглядности следует
построить также одно–два сечения плоскостями, параллельными плоскости х0у.
В каждом таком сечении получим такую же кривую, как и исходная направляющая. Аналогично
поступают, рассматривая направляющую в плоскости х0z или у0z. Цилиндрическая поверхность является бесконечной в направлении своих образующих. Часть замкнутой цилиндрической поверхности, заключенная между двумя плоскими параллельными сечениями, называется цилиндром, а фигуры сечения – его основаниями. Сечение цилиндрической поверхности плоскостью, перпендикулярной ее образующим, называется нормальным. В зависимости от формы нормального сечения цилиндры бывают: 1) эллиптические – нормальное сечение представляет собой эллипс (рис. 2.27а), каноническое уравнение ; (2.54) 2) круговые – нормальное сечение круг, при a=b=r уравнение ; (2. 3) гиперболические – нормальное сечение гипербола (рис. 2.27б), каноническое уравнение ; (2.56) 4) параболические – нормальное сечение парабола (рис. 2.27в), каноническое уравнение x2=2py; (2.57) 5) общего вида – нормальное сечение кривая случайного вида. Если за основание цилиндра принимается его нормальное
сечение, цилиндр называют прямым (рис. 2.27). Если за основание цилиндра
принимается одно из косых сечений, цилиндр называют наклонным. Например,
наклонные сечения прямого кругового цилиндра являются эллипсами. Конической поверхностью называется поверхность, производимая движением прямой, перемещающейся в пространстве так, что она при этом постоянно проходит через неподвижную точку и пересекает данную линию. Данная прямая называется образующей, линия – направляющей, а точка – вершиной конической поверхности (рис. 2.28). Конусом называется тело, ограниченное частью конической поверхности, расположенной по одну сторону от вершины, и плоскостью, пересекающей все образующие по ту же сторону от вершины. Часть конической поверхности, ограниченная этой плоскостью, называется боковой поверхностью, а часть плоскости, отсекаемая боковой поверхностью, – основанием конуса. Перпендикуляр, опущенный из вершины на плоскость основания, называется высотой конуса. Конус называется прямым круговым,
если его
основание есть круг, а высота проходит через центр основания. В курсе геометрии общеобразовательной школы рассматривается только прямой круговой конус, который для краткости называется просто конусом. Если вершина конуса расположена в начале координат, направляющая кривая — эллипс с полуосями а и b, плоскость которого находится на расстоянии с от начала координат, то уравнение эллиптического конуса имеет вид: (a >0, b >0, c >0). (2.58) При а = b конус становится круговым.
Примечание. По аналогии с коническими сечениями (аналогично теореме 2.1) существуют
и вырожденные
поверхности второго порядка. Вопросы для самопроверки |
ГЛАВА 4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Поверхностью второго порядка называется множество точек пространства, удовлетворяющих какому-либо уравнению 2-ой степени.
Теорема. Для любой поверхности второго порядка в пространстве существует ортонормированная система координат, в которой эта поверхность задается каноническим уравнением.
Эта теорема у нас также остаётся пока что без доказательства, но она позволяет классифицировать все поверхности второго порядка.
Классификация поверхностей 2-го порядка
— эллипсоид;
— мнимый эллипсоид;
— точка ;
— однополостный гиперболоид;
— двуполостный гиперболоид;
— конус 2-го порядка;
— эллиптический параболоид;
— эллиптический цилиндр;
— мнимый эллиптический цилиндр;
— ось Oz;
— гиперболический параболоид;
— гиперболический цилиндр;
или — пара пересекающихся плоскостей;
— параболический цилиндр;
или — пара параллельных плоскостей;
— сдвоенная плоскость;
— пара мнимых параллельных плоскостей
§1. Эллиптический, гиперболический и параболический
Эллиптический, гиперболический и параболический
Цилиндры
Пусть в пространстве заданы кривая
и прямая A, пересекающая L. Поверхность, образованная при перемещении прямой А параллельно самой себе так, что, она все время пересекает кривую L, называется Цилиндрической. Прямые, которые получаются при перемещении прямой А называются Образующими этой цилиндрической поверхности, а кривая L – её Направляющей.
Теорема. Уравнение
(1)
В пространстве задает цилиндрическую поверхность, образующие которой параллельны оси
, а уравнение направляющей, лежащей в плоскости , совпадает с уравнением (1).
►Обозначим L — множество точек плоскости, удовлетворяющих (1), а S – множество точек пространства, удовлетворяющих этому же уравнению.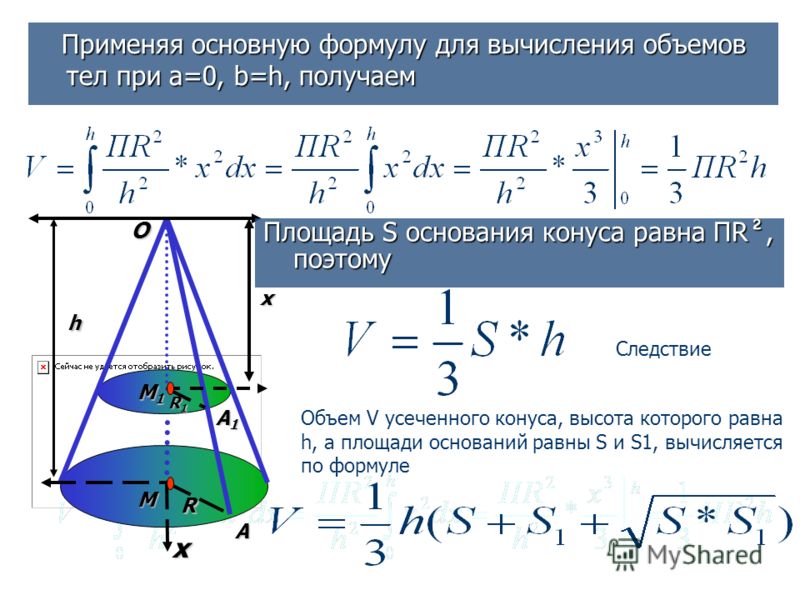 Тогда:
Тогда:
.
Итак, если
, то поверхности S принадлежит вся прямая, проходящая через эту
Рис. 1 точку параллельно оси
(рис. 1), что и доказывает, что S – цилиндрическая поверхность. ◄
Таким образом, уравнения
, , задают цилиндрические поверхности, или цилиндры, с образующими, параллельными оси , а названия «гиперболический», «эллиптический», «параболический» они получили по названию своей направляющей. Гиперболический, эллиптический и параболический цилиндры изображены соответственно на рисунках 2, 3 и 4.
Рис. 2
Рис. 3. Рис. 4.
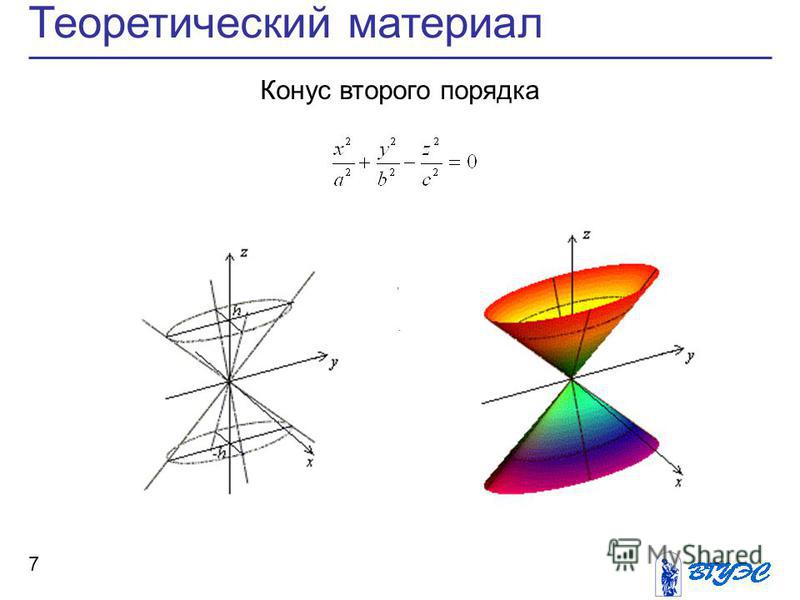
§2. Конус второго порядка
Конусом второго порядка мы назвали поверхность, которая задаётся каноническим уравнением
. (1)
Из этого уравнения видно, что конус проходит через начало координат; симметричен относительно всех координатных осей, координатных плоскостей и относительно начала координат.
Теорема. Если точка
, не совпадающая с началом координат, принадлежит конусу (1), то и вся прямая , проходящая через эту точку и начало координат, принадлежит этому конусу.
►В качестве направляющего вектора прямой
возьмём вектор , тогда её уравнение будет выглядеть так:
.
Таким образом,
.
Итак, конус второго порядка состоит из прямых, проходящих через начало координат.◄
Дальнейшее исследование всех поверхностей будем проводить методом параллельных сечений, который состоит в следующем: пересекаем поверхность плоскостями, параллельными координатным плоскостям, и по виду линий, получающихся в сечениях, делаем вывод о форме поверхности.
Пусть задана поверхность уравнением
. Пересечем эту поверхность плоскостью . Линия пересечения задаются системой:
,
Которая равносильна следующей:
. (2)
(2)
Так как в системе (2) первое уравнение – уравнение цилиндрической поверхности с образующими, параллельными оси , то мы просто линию пересечения заданной поверхности плоскостью заменили линией пересечения той же плоскостью цилиндрической поверхности. Если эту Цилиндрическую поверхность пересечь плоскостями, параллельными плоскости , то в сечениях будут получаться линии, одинаковые по форме. В частности, такую же форму, как и все линии пересечения, будет иметь кривая, лежащая в плоскости , которая является их Проекцией на плоскость (рис. 1). Уравнение же последней кривой, т. е. направляющей цилиндрической поверхности, совпадает с уравнением . ТаКим образом, чтобы получить уравнение проекции на плоскость линии пересечения некоторой поверхности плоскостью следует из системы, задающей эту линию пересечения, исключить (это же справедливо и для проекции линии пересечения двух произвольных поверхностей).
Возвращаясь к исследованию формы конуса (1), пересечем его плоскостью
. В сечении получаем кривую, заданную уравнением:
В сечении получаем кривую, заданную уравнением:
. (3)
При
уравнение (3) задаёт точку — начало координат, т. е. плоскость Пересекает конус в одной только точке – в его вершине. Если , то, разделив (3) на правую часть, получаем уравнение
,
Которое задаёт эллипс с полуосями
. (4)
Рис. 2. Если
растет, то полуоси увеличиваются, т. е. конус состоит из расширяющихся эллипсов. Внешний вид конуса изображен на рис. 2. При конус называется конусом вращения или прямым круговым конусом.
При пересечении конуса плоскостью в сечении можно получить не только эллипс, но также гиперболу и даже параболу, поэтому эти кривые называются коническими сечениями.
§3. Однополостный гиперболоид
Однополостным гиперболоидом называется поверхность, которая задаётся каноническим уравнением:
. (1)
(1)
Так же, как и конус второго порядка, эта поверхность симметрична относительно всех координатных плоскостей, всех координатных осей и относительно начала координат, но, в отличие от конуса, через начало координат не проходит. Пересекая её плоскостью
, получаем кривую с уравнением
,
Которое после преобразований принимает вид
И задаёт эллипс с полуосями:
. (2)
Таким образом, как и конус второго порядка, однополостный гиперболоид состоит из расширяющихся эллипсов. Самый малый эллипс получаем при
. Он называется горловым эллипсом.
Сравнивая (2) и (4) §2, видим, что
и . Таким образом, если однополостный гиперболоид (1) и конус второго порядка
(3)
Пересечь одной и той же плоскостью
, то эллипс для конуса находится внутри эллипса для гиперболоида, значит конус (3) лежит внутри гиперболоида (1). Кроме того,
Кроме того,
. Аналогично получаем, что , т. е. при неограниченном удалении от плоскости однополостный гиперболоид (1) бесконечно близко приближается к конусу (3), который поэтому называется его асимптотическим конусом.
Пересекая однополостный гиперболоид (1) плоскостью
в сечении получаем гиперболу
Рис. 1
с действительной осью — осью . При пересечении же его плоскостью , получаем гиперболу с действительной осью – осью . Однополостный гиперболоид изображен на рис. 1. При он называется однополостным гиперболоидом вращения.
§4. Двуполостный гиперболоид
Двуполостным гиперболоидом называется поверхность, заданная каноническим уравнением
. (1)
Так же, как и конус второго порядка и однополостный гиперболоид, эта поверхность симметрична относительно всех координатных плоскостей, всех координатных осей и относительно начала координат, но опять же, в отличие от конуса, через начало координат не проходит.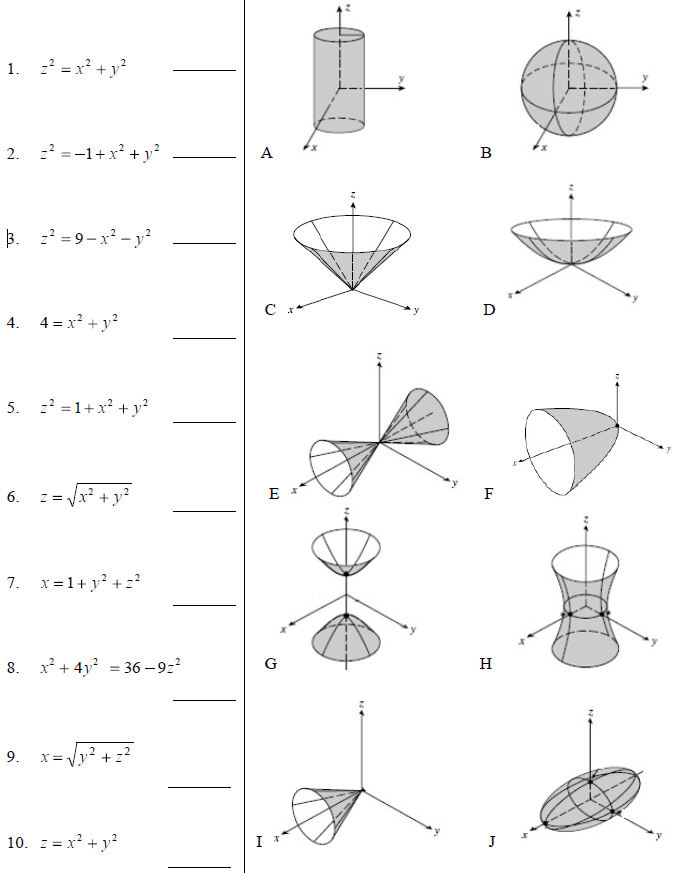 Пересекая двуполостный гипребролоид плоскостью
Пересекая двуполостный гипребролоид плоскостью
получаем кривую с уравнением
. (2)
Из (2) видно, что при
плоскость не пересекается с двуполостным гиперболоидом (1), каждая из плоскостей и пересекает двуполостный гиперболоид в одной точке. Эти точки и называются вершинами двуполостного гиперболоида. Если же , то линией пересечения является эллипс
С полуосями
Рис. 1
. (3)
Наряду с гиперболоидом (1) опять же рассмотрим конус
. (4)
Пересекая гиперболоид (1) и конус (4) одной и той же плоскостью
и сравнивая (3) и (4) §2, делаем вывод: и , т. е. двуполостный гиперболоид (1) лежит внутри конуса (4). Так же, как и в §3, получаем:
и ,
Откуда видно, что при неограниченном удалении от плоскости
двуполостный гиперболоид (1), так же как и однополостный, бесконечно близко приближается к конусу (4) (только уже изнутри), который также называется его асимптотическим конусом.
Пересекая гиперболоид (1) плоскостью
, в сечении получаем гиперболу , а пересекая его плоскостью — гиперболу . Для обеих этих гипербол действительной является ось .
Двуполостный гиперболоид изображён на рис. 1.
§ 5. Эллиптический параболоид
Эллиптический параболоид – это поверхность, заданная каноническим уравнением
. (1)
Эллиптический параболоид симметричен относительно координатных плоскостей
и , а относительно плоскости симметрии не имеет. Если его пересечь плоскостью , то увидим, что при плоскость не пересекается с эллиптическим параболоидом, при в сечении получается единственная точка – начало координат, которая называется вершиной эллиптического параболоида (1), а при линией пересечения является эллипс с полуосями . Таким образом, и эллиптический параболоид состоит из расширяющихся эллипсов.
Пересечём теперь эту поверхность плоскостью
. В сечении получаем кривую, заданную уравнением
В сечении получаем кривую, заданную уравнением
,
Которое после преобразований принимает вид:
. (2) Из (2) видно, что плоскости, параллельные плоскости , пересекают поверхность эллиптического параболоида по параболам, имеющим
Одинаковые фокальные параметры (т. е., по конгруэнтным параболам), ветви которых направлены в сторону положительного направления оси
, причём с ростом вершина параболы смещается вверх. На рис. 1 изображены проекции этих парабол на плоскость . То же самое имеем и при пересечении плоскостями . Уравнения линий пересечения:
,
При проектировании их на плоскость получаем картинку, изображённую на рис. 2. Сам же эллиптический параболоид изображён на рис. 3. При эллиптический параболоид называется параболоидом вращения.
§ 6. Гиперболический параболоид
Гиперболическим параболоидом мы назвали поверхность, каноническое уравнение которой выглядит так:
.
Гиперболический параболоид, так же, как и эллиптический, симметричен относительно координатных плоскостей
и , а относительно плоскости не имеет симметрии.
Пересечём эту поверхность плоскостью
. В сечении получаем кривую, заданную уравнением:
.
Из него мы видим, что плоскости, параллельные плоскости
, пересекают поверхность гиперболического параболоида по параболам, имеющим одинаковые фокальные параметры (т. е., по конгруэнтным параболам), их ветви направлены в сторону отрицательного направления оси , причём с ростом вершина параболы смещается вверх. На рис. 1 изображены проекции этих парабол на плоскость . Если же пересечь гиперболический параболоид плоскостями , то в сечениях получаем кривые
,
Т. е. опять конгруэнтные параболы, но их ветви направлены в сторону положительного направления оси
е. опять конгруэнтные параболы, но их ветви направлены в сторону положительного направления оси
, а с ростом вершина параболы смещается вниз. При проектировании их на плоскость получаем
картинку, изображённую на рис. 2.
Теперь пересечём гиперболический параболоид плоскостью . В сечении получается кривая, заданная уравнением
. (1)
При
это уравнение задаёт пару пересекающихся прямых
Рис. 3
. (2)
Если
, то плоскость пересекает гиперболический параболоид по гиперболам
,
Асимптотами которых являются прямые (2), действительной осью – ось , причём с ростом вершины этих гипербол удаляются от центра (от оси ).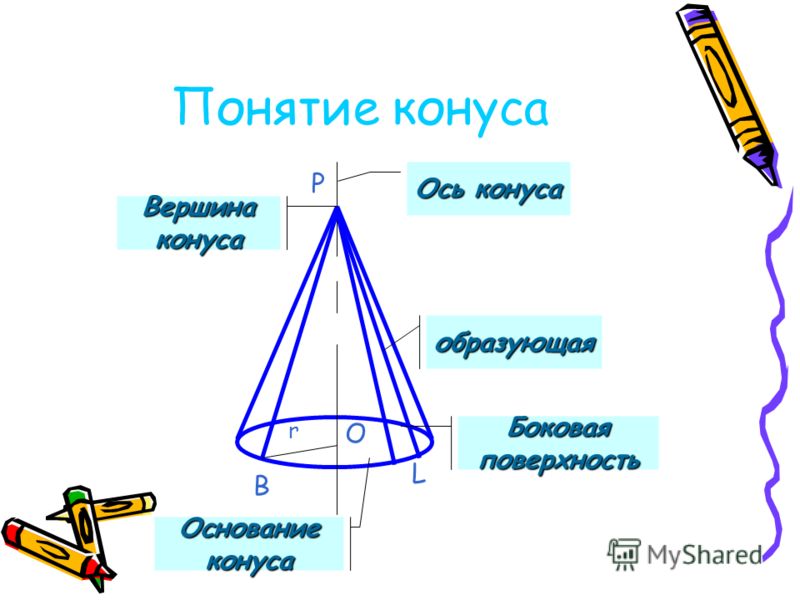 Если же ,
Если же ,
То уравнение (1) задаёт гиперболы
С теми же самыми асимптотами, но с осью
в качестве действительной. Проекции линий пересечения гиперболического параболоида плоскостями на плоскость изображены на рис. 3, а сам гиперболический параболоид — на рис. 4. Эта поверхность напоминает седло, часто её так и называют.
§ 7. Эллипсоид
Эллипсоидом называется поверхность, заданная каноническим уравнением . Пересекая его координатными плоскостями, каждый раз в сечении получаем эллипсы с различными полуосями. Эллипсоид изображён на рис. 1, по внешнему виду он напоминает яйцо. При эллипсоид называется эллипсоидом вращения, а при — это просто сфера.
1
Первый слайд презентации: Аналитическая геометрия в пространстве
Изображение слайда
2
Слайд 2
«Аналитическая геометрия в пространстве» курса «Высшая математика» включает четыре основные темы:
1. Плоскость
2. Прямая в пространстве
3. Взаимное расположение прямой и плоскости в пространстве
4. Поверхности 2-го порядка
Плоскость
2. Прямая в пространстве
3. Взаимное расположение прямой и плоскости в пространстве
4. Поверхности 2-го порядка
Изображение слайда
3
Слайд 3: 1. Плоскость
Основные уравнения плоскости 1. Уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору 2. Общее уравнение плоскости — вектор нормали 3. Уравнение плоскости « в отрезках»
Изображение слайда
4
Слайд 4: Уравнения плоскости
4. Уравнение плоскости, проходящей через три точки Условие компланарности векторов
Изображение слайда
5
Слайд 5: Построение плоскостей
1. Построить плоскость
Находим координаты точек пересечения плоскости с осями координат.
x
0
0
4
y
0
3
0
z
2
0
0
Z
Y
X
2
3
4
Можно привести уравнение плоскости к уравнению «в отрезках»
1) Переносим вправо свободный член уравнения
2) Делим на 12, чтобы получить единицу в правой части
3) Выбираем коэффициенты из числителей
Числа, стоящие в знаменателях, являются длинами отрезков, которые
плоскость отсекает на осях координат
Построить плоскость
Находим координаты точек пересечения плоскости с осями координат.
x
0
0
4
y
0
3
0
z
2
0
0
Z
Y
X
2
3
4
Можно привести уравнение плоскости к уравнению «в отрезках»
1) Переносим вправо свободный член уравнения
2) Делим на 12, чтобы получить единицу в правой части
3) Выбираем коэффициенты из числителей
Числа, стоящие в знаменателях, являются длинами отрезков, которые
плоскость отсекает на осях координат
Изображение слайда
6
Слайд 6: Построение плоскостей
2. Построить плоскость В уравнении отсутствует переменная z. Находим точки пересечения плоскости с осями OX и OY. X 0 10/3 y -2 0 Соединяем точки прямой линией и получаем след плоскости на плоскости XOY. Из точек пересечения проводим прямые, параллельные оси OZ. Z Y X 10/3 -2 Аналогично строятся все плоскости, в уравнении которых отсутствует одна переменная X Y Z 7 2 X Y Z 2 3
Изображение слайда
7
Слайд 7: Построение плоскостей
3. Построить плоскость
В уравнении отсутствуют две переменные x и y. Такая плоскость
проходит параллельно и оси OX, и оси OY, т.е. она проходит
параллельно координатной плоскости XOY через точку z= 8/3 на оси OZ.
Z
Y
X
8/3
0
Аналогично строятся плоскости,
в уравнениях которых отсутствуют
две переменные
Z
X
Y
0
Z
X
Y
9/4
3/5
0
Построить плоскость
В уравнении отсутствуют две переменные x и y. Такая плоскость
проходит параллельно и оси OX, и оси OY, т.е. она проходит
параллельно координатной плоскости XOY через точку z= 8/3 на оси OZ.
Z
Y
X
8/3
0
Аналогично строятся плоскости,
в уравнениях которых отсутствуют
две переменные
Z
X
Y
0
Z
X
Y
9/4
3/5
0
Изображение слайда
8
Слайд 8
Таким образом, 1. если в уравнении плоскости отсутствует одна переменная, то плоскость проходит параллельно той оси координат, переменной которой нет в уравнении. 2. если в уравнении плоскости отсутствует свободный член, то плоскость проходит через начало координат. 3. Если в уравнении плоскости отсутствуют две переменные, то плоскость проходит параллельно координатной плоскости, переменных которой нет в уравнении. Уравнения координатных плоскостей — уравнение плоскости YOZ — уравнение плоскости XOZ — уравнение плоскости XOY
Изображение слайда
9
Слайд 9: Взаимное расположение плоскостей
1. Условие параллельности плоскостей
2. Условие перпендикулярности плоскостей
3. Косинус угла между плоскостями
Угол между плоскостями – это угол между векторами
нормалей этих плоскостей
Условие параллельности плоскостей
2. Условие перпендикулярности плоскостей
3. Косинус угла между плоскостями
Угол между плоскостями – это угол между векторами
нормалей этих плоскостей
Изображение слайда
10
Слайд 10: Расстояние от точки до плоскости
Расстояние от точки до плоскости находится по формуле Правило : для нахождения расстояния от точки до плоскости нужно координаты точки подставить в левую часть уравнения плоскости, разделить на длину вектора нормали плоскости и полученное значение взять по абсолютной величине. Расстояние – величина всегда положительная ! Расстояние – это длина перпендикуляра, опущенного из точки на плоскость
Изображение слайда
11
Слайд 11: 2. Прямая в пространстве.
 Основные уравнения
Основные уравнения
1. Уравнение прямой, проходящей через заданную точку параллельно заданному вектору — канонические уравнения — направляющий вектор 2. Параметрические уравнения 3. Уравнение прямой, проходящей через две заданные точки и
Изображение слайда
12
Слайд 12: Прямая в пространстве. Основные уравнения
4. Общее уравнение прямой в пространстве а) Направляющий вектор б) Нахождение точки на прямой — канонические уравнения прямой
Изображение слайда
13
Слайд 13: Взаимное расположение прямых в пространстве
1. Нахождение угла между прямыми.
Прямые в пространстве заданы каноническими уравнениями, поэтому
угол между прямыми – это угол между направляющими векторами
2. Условия параллельности и перпендикулярности прямых
Условие параллельности прямых
Условие перпендикулярности прямых
Условия параллельности и перпендикулярности прямых
Условие параллельности прямых
Условие перпендикулярности прямых
Изображение слайда
14
Слайд 14: 3. Взаимное расположение прямой и плоскости в пространстве
1. Условие параллельности прямой и плоскости 2. Условие перпендикулярности прямой и плоскости
Изображение слайда
15
Слайд 15: Взаимное расположение прямой и плоскости в пространстве
3. Нахождение угла между прямой и плоскостью
Углом между прямой и плоскостью
считается угол между этой прямой
и ее ортогональной проекцией на
эту плоскость. На рисунке это угол.
Из уравнений прямой и плоскости
известны направляющий вектор
прямой и вектор нормали плоскости.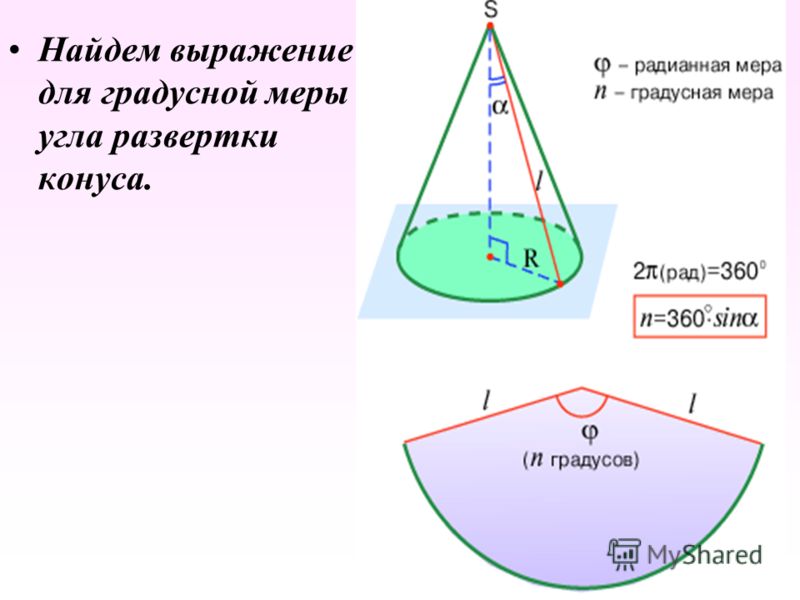 Косинус угла между этими векторами легко можно найти.
Легко заметить, что углы и в сумме дают 90 градусов, а значит
Поэтому при нахождении угла между прямой и плоскостью находят
не косинус, а синус угла. Кроме того, в формуле стоит модуль, так как
синус угла в данной ситуации может быть только положительным
Косинус угла между этими векторами легко можно найти.
Легко заметить, что углы и в сумме дают 90 градусов, а значит
Поэтому при нахождении угла между прямой и плоскостью находят
не косинус, а синус угла. Кроме того, в формуле стоит модуль, так как
синус угла в данной ситуации может быть только положительным
Изображение слайда
16
Слайд 16
Нахождение точки пересечения прямой и плоскости Для нахождения точки пересечения прямой и плоскости нужно составить систему из уравнений прямой и плоскости Для того, чтобы решить систему, переводим уравнение прямой в параметрический вид Подставляем эти уравнения в уравнение плоскости Из этого уравнения находим параметр и подставляем его значение в параметрические уравнения, получим координаты точки пересечения
Изображение слайда
17
Слайд 17: 4.
 Поверхности 2-го порядка
Поверхности 2-го порядка
Общее уравнение плоскости или прямой в пространстве – есть уравнения линейные относительно переменных и Уравнение поверхности 2-го порядка квадратичная часть линейная часть . К поверхностям 2-го порядка относятся : сфера, эллипсоид, гиперболоиды, конусы, параболоиды и цилиндры. Основная задача состоит в умении по уравнению определить тип поверхности, привести само уравнение к каноническому виду и построить поверхность в системе координат. ,
Изображение слайда
18
Слайд 18: Классификация поверхностей второго порядка
Название поверхности Каноническое уравнение Сфера Эллипсоид Однополостной гиперболоид Двуполостной гиперболоид Эллиптический параболоид Гиперболический параболоид Конус Эллиптический цилиндр Гиперболический цилиндр Параболический цилиндр или
Изображение слайда
19
Слайд 19
Поверхности второго порядка СФЕРА ПАРАБОЛОИДЫ ЭЛЛИПСОИДЫ КОНУСЫ ГИПЕРБОЛОИДЫ ЦИЛИНДРЫ ГИПЕРБОЛОИДЫ
Изображение слайда
20
Слайд 20: 1.
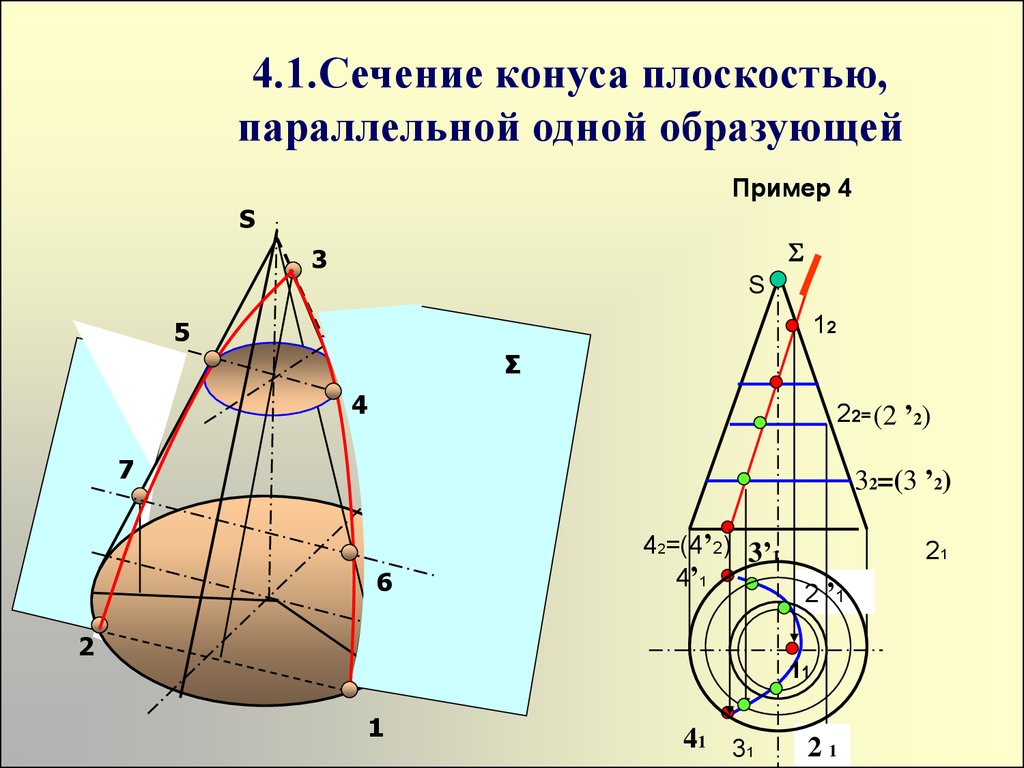 Сфера
Сфера
Определение. Сферой называется множество точек пространства, равноудаленных от одной точки, называемой центром Уравнение сферы со смещенным центром Уравнение сферы с центром в начале координат В уравнение сферы входят квадраты трех переменных, причем коэффициенты при квадратах и знаки при них одинаковые. !
Изображение слайда
21
Слайд 21: Эллипсоид
Каноническое уравнение трехосного эллипсоида имеет вид a b c полуоси эллипсоида. Центр этого эллипсоида находится в начале координат. Уравнение эллипсоида с центром в точке имеет вид Признаки уравнения эллипсоида: Наличие квадратов всех трех переменных Одинаковые знаки при квадратах переменных Разные коэффициенты при квадратах переменных
Изображение слайда
22
Слайд 22: Гиперболоиды
Канонические уравнения гиперболоидов
Каноническое уравнение однополостного
гиперболоида
Признаки уравнения однополостного гиперболоида:
Наличие квадратов всех трех переменных
Разные знаки при квадратах переменных
Один знак минус при квадрате переменной в левой части уравнения,
в правой части плюс 1. полуоси
В зависимости от знака перед единицей в правой части гиперболоиды делятся на одно и двуполостные.
полуоси
В зависимости от знака перед единицей в правой части гиперболоиды делятся на одно и двуполостные.
Изображение слайда
23
Слайд 23: Разные ориентации однополостных гиперболоидов
Ориентация гиперболоида зависит от того, перед какой переменной в каноническом уравнении стоит знак минус. Однополостный гиперболоид с осью симметрии OY Однополостный гиперболоид с осью симметрии OX
Изображение слайда
24
Слайд 24: Гиперболоиды
Каноническое уравнение двуполостного гиперболоида
Признаки уравнения двуполостного гиперболоида:
Наличие квадратов всех трех переменных
Разные знаки при квадратах переменных
Два знака минус в уравнении: один при квадрате переменной
в левой части уравнения, другой в правой части при 1. полуоси
Если из уравнения выразить z, то получим
Т.к.
, то получается, что
Двуполостный гиперболоид на проходит через начало координат.
полуоси
Если из уравнения выразить z, то получим
Т.к.
, то получается, что
Двуполостный гиперболоид на проходит через начало координат.
Изображение слайда
25
Слайд 25: Разные ориентации двуполостного гиперболоида
Каноническое уравнение двуполостного гиперболоида содержит два знака минус в уравнении. Один знак минус оставляем в левой части уравнения, а второй поставим перед единицей в правой части. В таком случае легко определить ось симметрии гиперболоида: перед квадратом какой переменной в левой части уравнения знак минус, та ось системы координат и будет являться осью симметрии.
Изображение слайда
26
Слайд 26: Конусы 2-го порядка
Каноническое уравнение конуса
Признаки уравнения конуса:
Наличие квадратов всех трех переменных
Разные знаки при квадратах переменных
Свободный член в правой части уравнения равен нулю.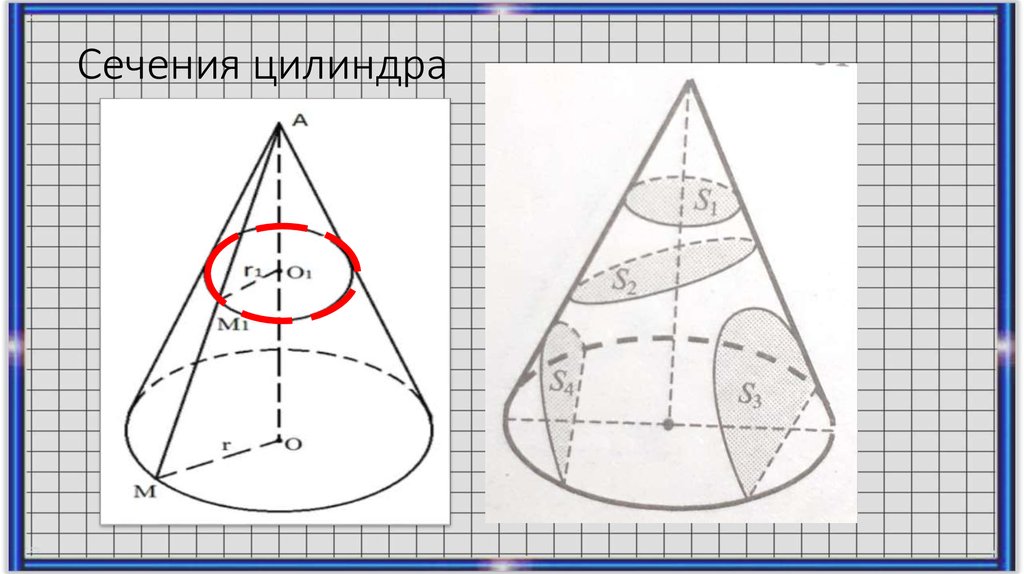 Каноническое уравнение конуса от уравнений гиперболоидов отличает то, что в правой части уравнения стоит не единица, а ноль. Если один знак минус оставляем в левой части уравнения,
то ось симметрии конуса определится также, как и для гиперболоидов: перед квадратом какой переменной в левой части уравнения знак минус, та ось системы координат и будет являться осью симметрии. Для данного уравнения – это ось OZ.
Каноническое уравнение конуса от уравнений гиперболоидов отличает то, что в правой части уравнения стоит не единица, а ноль. Если один знак минус оставляем в левой части уравнения,
то ось симметрии конуса определится также, как и для гиперболоидов: перед квадратом какой переменной в левой части уравнения знак минус, та ось системы координат и будет являться осью симметрии. Для данного уравнения – это ось OZ.
Изображение слайда
27
Слайд 27: Конусы с разными осями симметрии
Ось симметрии конуса определяется по уравнению Конус с осью симметрии OY Конус с осью симметрии OX
Изображение слайда
28
Слайд 28: Параболоиды
Канонические уравнения параболоидов можно записать
в общем виде
Таким образом, в уравнении отсутствует квадрат одной переменной. В зависимости от знака между квадратами двух других переменных различают эллиптические и гиперболические параболоиды
Признаки уравнения эллиптического или кругового параболоида :
Отсутствие квадрата одной из переменных
Одинаковые знаки при квадратах переменных в левой части уравнения
Эллиптический
параболоид
Круговой
параболоид
Если
то
В зависимости от знака между квадратами двух других переменных различают эллиптические и гиперболические параболоиды
Признаки уравнения эллиптического или кругового параболоида :
Отсутствие квадрата одной из переменных
Одинаковые знаки при квадратах переменных в левой части уравнения
Эллиптический
параболоид
Круговой
параболоид
Если
то
Изображение слайда
29
Слайд 29: Различные ориентации эллиптических параболоидов
Характерным признаком уравнения эллиптического параболоида является присутствие всех трех переменных, но одно из них входит в уравнение только в первой степени, т.е. в уравнении параболоида отсутствует квадрат одной переменной. Ось симметрии параболоида параллельна той оси, координата которой в уравнении только в первой степени.
параболоид с осью симметрии OY
параболоид с осью симметрии OX
Можно записать один из видов параболоидов со смещенной вершиной
— вершина параболоида
Возможна также смена направления чаши параболоида. Если в каноническом уравнении в правой части стоит знак минус,
то параболоид направлен в отрицательном направлении оси симметрии.
где
Если в каноническом уравнении в правой части стоит знак минус,
то параболоид направлен в отрицательном направлении оси симметрии.
где
Изображение слайда
30
Слайд 30: Гиперболический параболоид
Каноническое уравнение гиперболического параболоида имеет вид Признаки уравнения гиперболического параболоида: Отсутствие квадрата одной из переменных Разные знаки при квадратах переменных в левой части уравнения Отличительным признаком уравнения гиперболического параболоида является то что в левой части уравнения между квадратами переменных знак минус. Эта поверхность имеет форму седла. Возможны различные варианты ориентации гиперболического параболоида в зависимости от оси симметрии, знаков при квадратах.
Изображение слайда
31
Слайд 31: Цилиндрические поверхности
Цилиндрическая поверхность-это поверхность, которую описывает прямая линия (образующая), которая оставаясь параллельно самой себе движется вдоль некоторой кривой, называемой направляющей. По названию направляющей получают свое название и цилиндры.
Если образующая параллельна какой-либо оси координат, то каноническое уравнение цилиндра не содержит в уравнении соответствующую переменную. В этом случае уравнение цилиндра повторяет уравнение своей направляющей. Вариантов различных уравнений цилиндров достаточно много.
Для построения цилиндра нужно построить направляющую в той плоскости, в которой она задана, а затем «тянуть» эту линию вдоль той оси, координата которой отсутствует в уравнении.
Признаки уравнения цилиндрической поверхности:
В уравнении цилиндрической поверхности отсутствует
одна переменная.
По названию направляющей получают свое название и цилиндры.
Если образующая параллельна какой-либо оси координат, то каноническое уравнение цилиндра не содержит в уравнении соответствующую переменную. В этом случае уравнение цилиндра повторяет уравнение своей направляющей. Вариантов различных уравнений цилиндров достаточно много.
Для построения цилиндра нужно построить направляющую в той плоскости, в которой она задана, а затем «тянуть» эту линию вдоль той оси, координата которой отсутствует в уравнении.
Признаки уравнения цилиндрической поверхности:
В уравнении цилиндрической поверхности отсутствует
одна переменная.
Изображение слайда
32
Слайд 32: Виды цилиндров
Круговые цилиндры:
ось симметрии OZ
ось симметрии OX
ось симметрии OY
На рисунке изображен цилиндр с осью симметрии OZ.
Для построения цилиндра строим окружность радиуса R в плоскости XOY,
а затем «превращаем» эту окружность в цилиндр, вытягивая
вдоль оси симметрии. Можно построить цилиндр и таким способом: нарисовать две или несколько
одинаковых окружностей параллельных друг другу на разной высоте,
а затем соединить их образующими параллельными оси симметрии.
Направляющей линией является окружность.
Можно построить цилиндр и таким способом: нарисовать две или несколько
одинаковых окружностей параллельных друг другу на разной высоте,
а затем соединить их образующими параллельными оси симметрии.
Направляющей линией является окружность.
Изображение слайда
33
Слайд 33
Эллиптические цилиндры ось симметрии OZ ось симметрии OX ось симметрии OY Для построения цилиндра строим эллипс с полуосями a и b в плоскости XOY, а затем «превращаем» этот эллипс в цилиндр, вытягивая вдоль оси симметрии. По внешнему виду при схематическом построении эллиптический и круговой цилиндры выглядят одинаково. Направляющей кривой являются эллипсы
Изображение слайда
34
Слайд 34
Гиперболические цилиндры
ось симметрии OZ
ось симметрии OX
ось симметрии OY
При построении гиперболических цилиндров обязательно нужно
правильно определить мнимую и действительную оси гиперболы и ось
симметрии самого цилиндра. В качестве направляющей этих цилиндров служит гипербола.
В качестве направляющей этих цилиндров служит гипербола.
Изображение слайда
35
Слайд 35
Параболические цилиндры ось симметрии OZ ось симметрии OZ ось симметрии OX ось симметрии OX ось симметрии OY ось симметрии OY При построении цилиндра нужно определить основные параметры параболы: координаты вершины, ось симметрии и направление ветвей, построить параболу, а затем уже строить цилиндр с соответствующей осью симметрии. Направляющей этих цилиндров является парабола.
Изображение слайда
36
Последний слайд презентации: Аналитическая геометрия в пространстве
Изображение слайда
⇐ ПредыдущаяСтр 4 из 4 Определение. Называется гиперболическим параболоидом. Исследуем уравнение (12.7). Рассмотрим сечение плоскостью , т.е. . — парабола симметрична относительно оси с вершнами в начале координат. Теперь рассмотрим сечения (12.7) плоскости, параллельной . — парабола, ветви которой направлены вниз и симметрично относительно . Все эти параболы будут находится, вершинами на восходящей параболе , и как бы перемещаться вершиной по линии предыдущей параболы. Сечение гиперболического параболоида плоскостями, параллельными . — гипербола, симметричная относительно плоскостей . Вывод: Гиперболический параболоид имеет форму седла, обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат называется вершинойгиперболического параболоида. Числа называются его параметрами. Конус Определение. Поверхность, которая определяется уравнением: (12.8) состоит из прямых, проходящих через одну точку, именно, через начало координат и называется конусом. Заметим, что (12.8) однородно, все его члены имеют одну и ту же степень 2. Точка . Теорема:Если некоторая точка лежит на поверхности (12.8), то все точки прямой, которые проходят через начало координат и точку М, также лежат на этой поверхности. Прямые, из которых составлен конус, называются его образующими — вершина. Проведем сечение . — эллипс с полуосями . Если , то в сечении окружность и называется круглым конусом. Рассмотрим уравнение: (12.9) Это уравнение определяет единственную действительную точку . Однако, ввиду аналогии с уравнением (12.8) его часто называют мнимого конуса.
Обобщённая таблица по теме: «Плоскость.
⇐ Предыдущая1234 ©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов. |
Конус | это… Что такое Конус?
Прямой круговой конус.
Прямой и косой круговой конусы с равным основанием и высотой.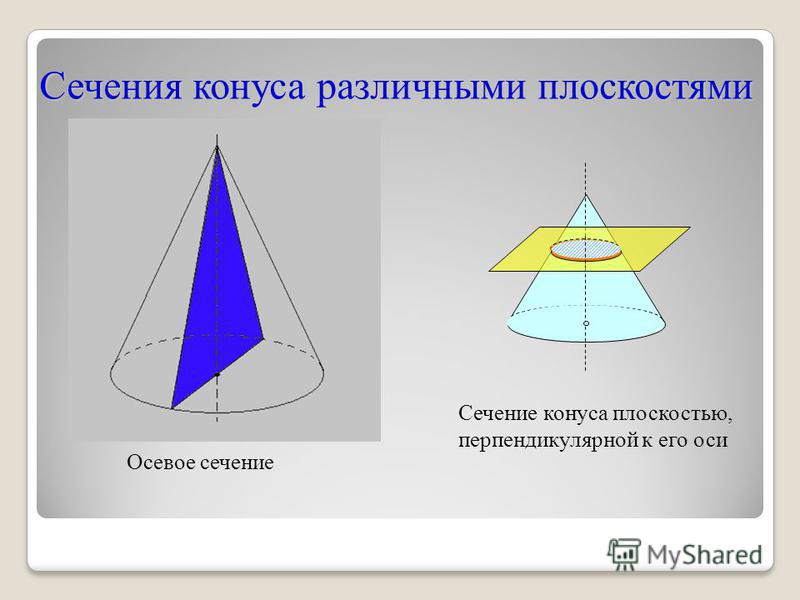 Эти тела обладают одинаковым объёмом.
Эти тела обладают одинаковым объёмом.
Усечённый прямой круговой конус.
У этого термина существуют и другие значения, см. Конус (значения).
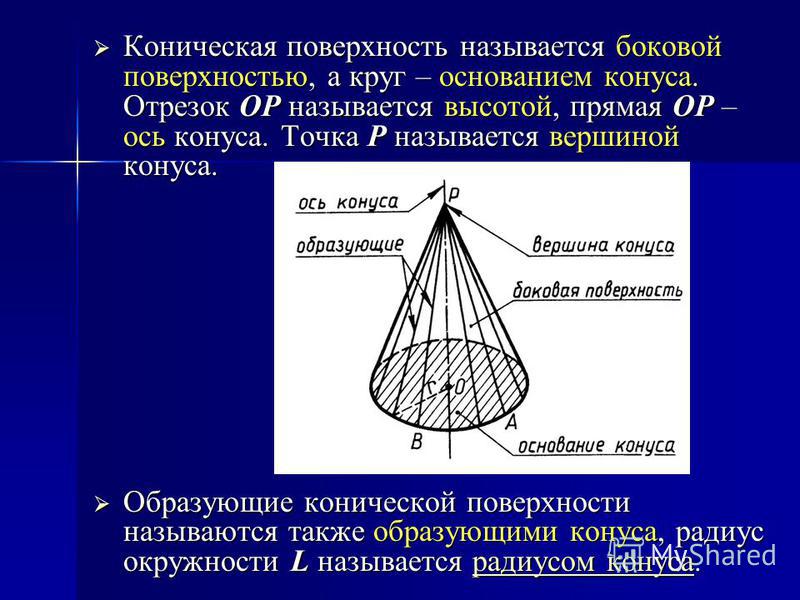
Ко́нус (от др.-греч. κώνος «шишка») — тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. Иногда конусом называют часть такого тела, имеющую ограниченный объём и полученную объединением всех отрезков, соединяющих вершину и точки плоской поверхности (последнюю в таком случае называют основанием конуса, а конус называют опирающимся на данное основание). Если основание конуса представляет собой многоугольник, такой конус является пирамидой.
Содержание
|
Связанные определения
- Отрезок, соединяющий вершину и границу основания, называется образующей конуса.

- Объединение образующих конуса называется образующей (или боковой) поверхностью конуса. Образующая поверхность конуса является конической поверхностью.
- Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса.
- Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).
- Если основание конуса имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром, то конус называется прямым. При этом прямая, соединяющая вершину и центр основания, называется осью конуса.
- Косой (наклонный) конус — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
- Круговой конус — конус, основание которого является кругом.
- Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса).

- Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом (последние два имеют бесконечный объём).
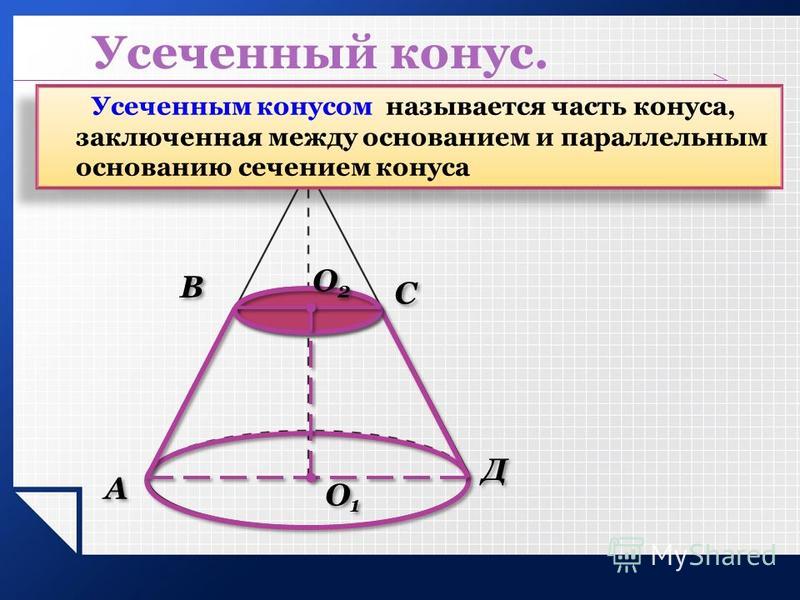
- Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом, или коническим слоем.
Свойства
- Если площадь основания конечна, то объём конуса также конечен и равен трети произведения высоты на площадь основания.
где S — площадь основания, H — высота. Таким образом, все конусы, опирающиеся на данное основание (конечной площади) и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.
- Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от основания.
- Телесный угол при вершине прямого кругового конуса равен
- где — угол раствора конуса.

- Площадь боковой поверхности такого конуса равна
- Площадь поверхности такого конуса равна
- где — радиус основания, — длина образующей.
- Объём кругового конуса равен
- Для усечённого конуса (не обязательно прямого и кругового) объём равен:
где S1 и S2 — площади соответственно верхнего (ближнего к вершине) и нижнего оснований, h и H — расстояния от плоскости соответственно верхнего и нижнего основания до вершины.
- Пересечение плоскости с прямым круговым конусом является одним из конических сечений (в невырожденных случаях — эллипсом, параболой или гиперболой, в зависимости от положения секущей плоскости).
Уравнение конуса
Уравнения, задающие боковую поверхность прямого кругового конуса с углом раствора 2Θ, вершиной в начале координат и осью, совпадающей с осью Oz:
- В сферической системе координат с координатами (r, φ, θ):
- В цилиндрической системе координат с координатами (r, φ, z):
- или
- В декартовой системе координат с координатами (x, y, z):
- Это уравнение в каноническом виде записывается как
где константы a, с определяются пропорцией Отсюда видно, что боковая поверхность прямого кругового конуса представляет собой поверхность второго порядка (она носит название коническая поверхность). В общем виде коническая поверхность второго порядка опирается на эллипс; в подходящей декартовой координатной системе (оси Ох и Оу параллельны осям эллипса, вершина конуса совпадает с началом координат, центр эллипса лежит на оси Oz) её уравнение имеет вид
В общем виде коническая поверхность второго порядка опирается на эллипс; в подходящей декартовой координатной системе (оси Ох и Оу параллельны осям эллипса, вершина конуса совпадает с началом координат, центр эллипса лежит на оси Oz) её уравнение имеет вид
причём a/c и b/c равны полуосям эллипса. В наиболее общем случае, когда конус опирается на произвольную плоскую поверхность, можно показать, что уравнение боковой поверхности конуса (с вершиной в начале координат) задаётся уравнением где функция является однородной, то есть удовлетворяющей условию для любого действительного числа α.
Развёртка
Развёртка прямого кругового конуса
Прямой круговой конус как тело вращения образован прямоугольным треугольником, вращающимся вокруг одного из катетов, где h — высота конуса от центра основания до вершины — является катетом прямоугольного треугольника, вокруг которого происходит вращение.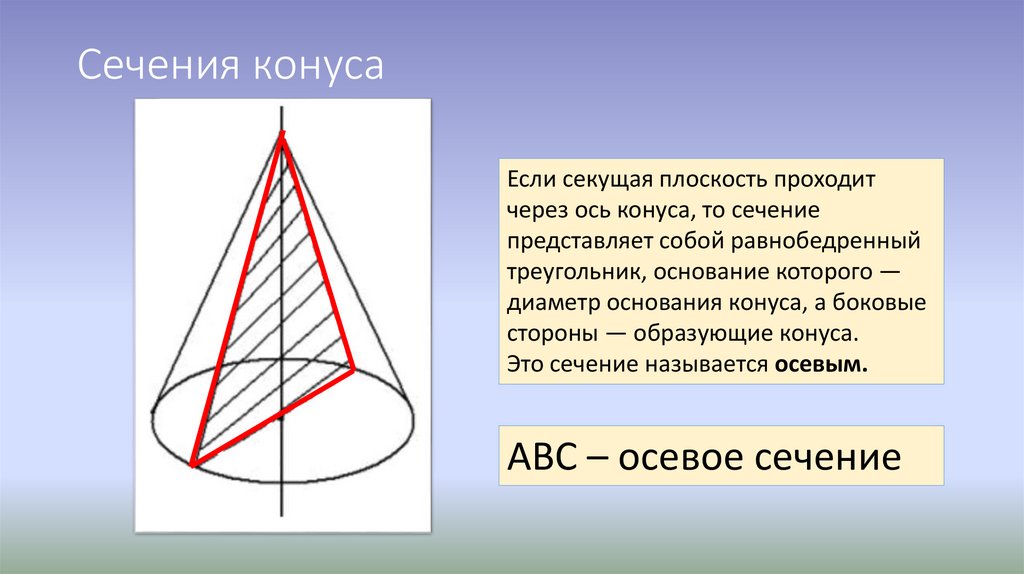 Второй катет прямоугольного треугольника r — радиус в основании конуса. Гипотенузой прямоугольного треугольника является l — образующая конуса.
Второй катет прямоугольного треугольника r — радиус в основании конуса. Гипотенузой прямоугольного треугольника является l — образующая конуса.
В создании развёртки конуса могут использоваться всего две величины r и l. Радиус основания r определяет в развертке круг основания конуса, а сектор боковой поверхности конуса определяет образующая боковой поверхности l, являющаяся радиусом сектора боковой поверхности. Угол сектора в развёртке боковой поверхности конуса определяется по формуле:
- φ = 360°·(r/l).
С имеющимися и полученными значениями можно нарисовать развёртку конуса на бумаге или другом материале, чтобы из развёртки получить конус как наглядное пособие или промышленное изделие.
Вариации и обобщения
- В алгебраической геометрии конус — это произвольное подподмножество векторного пространства над полем , для которого для любого
- В топологии, конус над топологическим пространством есть фактор-пространство по отношению эквивалентности (
См.
 также
также- Коническая поверхность
- Коническое сечение
- Конус (топология)
- Световой конус
- Конус отображения
- Биконус
Литература
- Статья «Конус» в Математической энциклопедии.
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1973.
Конус
У этого термина существуют и другие значения, см. Конус (значения).
Ко́нус (от др.-греч.κώνος «сосновая шишка»),— поверхность, образованная в пространстве множеством лучей (образующих конуса), соединяющих все точки некоторой плоской кривой (направляющей конуса) с данной точкой пространства (вершиной конуса).
Если направляющая конуса — замкнутая кривая, то коническая поверхность служит границей пространственного тела, которое также называют конусом (см. рисунок), а внутренность этой кривой называют основанием конуса, Если основание конуса представляет собой многоугольник, такой конус является пирамидой.
Двойной конус
Иногда вместо лучей рассматривают прямые, тогда получается двойной конус, состоящий из двух симметричных относительно вершины частей.
Конус и связанные с ним конические сечения играют большую роль в математике, астрономии и других науках.
- 1Связанные определения
- 2Типы конусов
- 3Свойства
- 4Уравнение прямого кругового конуса
- 5Развёртка
- 6Вариации и обобщения
- 7См. также
- 8Примечания
- 9Литература
- Боковая поверхность конуса — объединение образующих конуса; образующая поверхность конуса является конической поверхностью.
- Высота конуса — отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка).
- Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).
- Конусность — соотношение высоты и диаметра основания конуса.

- Прямой конус — конус, основание которого имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром; при этом прямая, соединяющая вершину и центр основания, называется осью конуса.
- Косой (или наклонный) конус — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
- Круговой конус — конус, основание которого является кругом.
- Конус вращения, или прямой круговой конус (часто под конусом подразумевают именно его) — конус, который можно получить вращением (то есть тело вращения) прямоугольного треугольника вокруг прямой, содержащей катет треугольника (эта прямая является осью конуса).
- Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом: последние два имеют бесконечный объём.

- Усечённый конус или конический слой — часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием.
- Равносторонний конус — конус вращения, образующая которого равна диаметру основания .
- Если площадь основания конечна, то объём конуса также конечен и равен трети произведения высоты на площадь основания.
- V=13SH,{\displaystyle V={1 \over 3}SH,}
- гдеS — площадь основания, H — высота. Таким образом, все конусы, опирающиеся на данное основание (конечной площади) и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.
- Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от основания.
- Телесный угол при вершине прямого кругового конуса равен
- 2π(1−cosα2),{\displaystyle 2\pi \left(1-\cos {\alpha \over 2}\right),}
- где α — угол раствора конуса.
 {2}),}
{2}),}
- Для произвольного усечённого конуса (не обязательно прямого и кругового) объём равен:
- V=13(h3S2−h2S1),{\displaystyle V={1 \over 3}(H_{2}S_{2}-H_{1}S_{1}),}
- гдеS1{\displaystyle S_{1}} иS2{\displaystyle S_{2}} — площади соответственно верхнего (ближнего к вершине) и нижнего оснований,h2{\displaystyle H_{1}} иh3{\displaystyle H_{2}} — расстояния от плоскости соответственно верхнего и нижнего основания до вершины.
- Пересечение плоскости с прямым круговым конусом является одним из конических сечений (в невырожденных случаях — эллипсом, параболой или гиперболой, в зависимости от положения секущей плоскости).
Уравнения, задающие боковую поверхность прямого кругового конуса с углом раствора 2Θ, вершиной в начале координат и осью, совпадающей с осью Oz:
- В сферической системе координат с координатами (r, φ, θ):
- θ=Θ.
 {n}f(x,y,z)} для любого действительного числа α.
{n}f(x,y,z)} для любого действительного числа α.
Развёртка прямого кругового конуса
Прямой круговой конус как тело вращения образован прямоугольным треугольником, вращающимся вокруг одного из катетов, где h — высота конуса от центра основания до вершины — является катетом прямоугольного треугольника, вокруг которого происходит вращение. Второй катет прямоугольного треугольника r — радиус в основании конуса. Гипотенузой прямоугольного треугольника является l — образующая конуса.
В создании развёртки конуса могут использоваться всего две величины r и l. Радиус основания r определяет в развертке круг основания конуса, а сектор боковой поверхности конуса определяет образующая боковой поверхности l, являющаяся радиусом сектора боковой поверхности. Угол сектораφ{\displaystyle \varphi } в развёртке боковой поверхности конуса определяется по формуле:
- φ = 360°·(r/l).

- В алгебраической геометрии конус — это произвольное подмножествоK{\displaystyle K} векторного пространстваV{\displaystyle V} над полемF{\displaystyle F}, для которого для любогоλ∈F{\displaystyle \lambda \in F}
- λK=K.{\displaystyle \lambda K=K.}
- В топологии конус над топологическим пространством X есть факторпространствоX×[0,∞){\displaystyle X\times [0,\infty )} по отношению эквивалентности(x,0)∼(y,0).{\displaystyle (x,0)\sim (y,0).}
- В линейной алгебре есть понятие выпуклого конуса.
В родственных проектах
- Значения в Викисловаре
- Медиафайлы на Викискладе
- Коническая поверхность
- Коническое сечение
- Конус (топология)
- Световой конус
- Математический энциклопедический словарь, 1988, с. 288.
- Корн Г., Корн Т. . — 2-е изд. — М.: Наука, 1970. — 720 с.
- Конус // . — М.
 : Советская энциклопедия, 1988. — С. . — 847 с.
: Советская энциклопедия, 1988. — С. . — 847 с.
конус в nLab
Пропустить навигационные ссылки | Домашняя страница | Все страницы | Последние версии | Обсудить эту страницу |
СодержимоеЭта статья в основном посвящена конусам в теории гомотопий и теории категорий. Дополнительные сведения о геометрических конусах см. в разделе конус (риманова геометрия) .
Контекст
Теория категорий
Теория категорий
Концепции
категория
функтор
естественная трансформация
Кот
Универсальные конструкции
универсальная конструкция
представимый функтор
сопряженный функтор
лимит/колимит
взвешенный предел
конец/конец
Расширение Кан
Теоремы
Лемма Йонеды
Двойственность Исбелла
Конструкция Гротендика
Теорема о сопряженном функторе
теорема монадичности
теорема о присоединенном подъеме
Двойственность таннака
Двойственность Габриэля-Ульмера
аргумент маленького объекта
Теорема вложения Фрейда-Митчелла
связь между теорией типов и теорией категорий
Удлинители
сноп и теория топоса
теория обогащенных категорий
теория высшей категории
Приложения
- приложения теории (высших) категорий
Изменить эту боковую панель
Пределы и копределы
Пределы и копределы
1-категориальный
- лимит
и колимит
пределы и копределы по примеру
коммутативность пределов и копределов
малый лимит
отфильтрованный колимит
направленный колимит
- последовательный копредел
просеянный колимит
связанный лимит, широкий откат
сохраненный лимит, отраженный лимит, созданный лимит
- Продукт
, Волокнистый продукт, Изменение базы, Побочный продукт, Откат, Выталкивание, Изменение собазы, Уравнитель, Уравнитель, присоединиться, встретиться, Терминальный объект, Исходный объект, Прямой продукт, Прямая сумма
конечный предел
- точный функтор
Расширение Кан
- Удлинитель Йонеда
взвешенный лимит
конец и муфта
2-категорийный
2-предельный
вкладыш
Изоинсертер
Эквайр
инвертор
PIE-лимит
2-откат, объект-запятая
(∞,1)-категориальный
(∞,1)-предел
(∞,1)-откат
- последовательность волокон
Модель-категория
гомотопическое расширение Кана
гомотопический предел
гомотопический продукт
гомотопический эквалайзер
гомотопическое волокно
картографический конус
гомотопический обратный образ
гомотопическая тотализация
гомотопический конец
гомотопический копредел
гомотопический побочный продукт
гомотопический соэквалайзер
гомотопическое коволокно
картографический кокон
гомотопический выталкиватель
гомотопическая реализация
гомотопический коэнд
Изменить эту боковую панель
- Идея
- Определение
- В гомотопической теории
- Как монада
- В теории категорий
- Конусы над диаграммой
- Над диаграммой в (∞,1)(\infty,1)-категории
- См.
 1, а II — стандартный интервал [0,1][0,1]. Тогда декартово произведение X×IX \times I действительно является цилиндром, и конус XX также является конусом.
1, а II — стандартный интервал [0,1][0,1]. Тогда декартово произведение X×IX \times I действительно является цилиндром, и конус XX также является конусом.Это понятие также имеет смысл, когда XX является категорией, если II считается интервальной категорией {0→1}\{ 0 \to 1 \}, то есть порядковым номером 2\mathbf{2}. Обратите внимание, что поскольку категория интервалов направлена, это дает два разных типа конусов, в зависимости от того, какой конец мы сжимаем в точку.
Другим, возможно, более распространенным значением термина «конус» в теории категорий является конус над (или под) диаграммой . Это всего лишь диаграмма категории конусов, как указано выше. В явном виде конус над F:J→CF\colon J \to C — это объект cc в CC, снабженный морфизмом из cc в каждую вершину FF, такой, что каждое 9Возникающий таким образом новый треугольник 0006 коммутирует. Универсальный конус есть предел.
В теории категорий слово кокон иногда используется для случая, когда мы сжимаем другой конец интервала; таким образом, cc оснащен морфизмом в cc из каждой вершины FF (но сам cc все еще принадлежит CC).
 Коконус в этом смысле, который является универсальным, является копределом. Однако следует помнить, что в гомотопической теории слово кокон используется для обозначения другой дуализации.
Коконус в этом смысле, который является универсальным, является копределом. Однако следует помнить, что в гомотопической теории слово кокон используется для обозначения другой дуализации.Это определение обобщается на высшую теорию категорий. В частности, в теории (∞, 1)-категорий конус над ∞-группоидом по существу является конусом в смысле гомотопической теории.
Определение
В гомотопической теории
Если XX — пространство, то конус XX — это гомотопическое выталкивание тождества на XX по единственному отображению в точку:
X→X↓↓*→cone(X ). \множество{ Х&\к&Х\ \вниз & & \вниз \\ * & \к & конус(Х) }\,.
Это гомотопическое выталкивание можно вычислить как обычный выталкивающий конус(X):=X×I⨿X*cone(X) := X\times I \amalg_X *
X→d1X×I↓↓*→cone( ИКС). \множество{ X &\stackrel{d_1}{\to} & X \times I \\ \вниз && \вниз \\ * &\к& конус(X) } \,.
Если XX — симплициальное множество, то конус XX — это соединение XX с точкой.

Конус отображения (см.) морфизма f:X→Yf \двоеточие X\to Y является тогда выталкиванием вдоль ff включения X→cone(X)X \to cone(X).
Как монада
В контексте, где интервалы II могут рассматриваться как моноидные объекты, конструкция конуса как частного цилиндра с одним концом, отождествляемым с точкой,
C(X)=I×X/(0×X )∼p,C(X) = I \times X/(0 \times X) \sim p,
несет структуру монады CC. В таких случаях моноид имеет мультипликативное тождество 11 и поглощающий элемент 00, где умножение на 00 является постоянным отображением в 00. В этом случае CC-алгебра состоит из объекта XX вместе с
Действие моноида a:I×X→Xa: I \times X \to X.
Константа или базовая точка x0:1→Xx_0 \ двоеточие 1 \ до X
такое, что a(0,x)=x0a(0,x) = x_0 для всех xx. Это уравнение может быть выражено в любой категории C\mathbf{C} с конечными произведениями и подходящим интервальным объектом II в виде моноида (например, TopTop, где I=[0,1]I = [0, 1] — моноид при действительное умножение, или под минмин как умножение).
 I & \stackrel{eval_0}{\to} & X.
}
I & \stackrel{eval_0}{\to} & X.
}По общим абстрактным причинам правосопряженный PP имеет структуру комонады, согласно которой CC-алгебры эквивалентны PP-коалгебрам. Рассматривая категорию симплициальных множеств, это тесно связано с декаляцией.
В теории категорий
Если CC является категорией, то конус CC является категорией козапятой? тождества на CC и уникальной карты в терминальную категорию:
C→C↓⇒↓*→cone(C). \множество{ С&\к&С\ \стрелка вниз и \стрелка вправо и \стрелка вниз \\ * & \к & конус(С) }\,.
Опять же, это можно вычислить как выталкивание:
C→d1C×2↓↓*→cone(C). \множество{ C &\stackrel{d_1}{\to} & C \times \mathbf{2} \\ \вниз && \вниз \\ * &\к& конус(С) } \,.
Конус СС можно также представить или определить как результат присоединения нового начального объекта к СС.
Конусы над диаграммой
Конус в категории CC задается категорией JJ вместе с функтором cone(J)→Ccone(J) \to C.
 По универсальному свойству категории козапятой, чтобы дать такой функтор должен дать объект cc из CC, функтор F:J→CF \colon J \to C и естественное преобразование
По универсальному свойству категории козапятой, чтобы дать такой функтор должен дать объект cc из CC, функтор F:J→CF \colon J \to C и естественное преобразованиеT: Δ(c)→FT: \Delta(c) \to F
где Δ(c):J→C\Delta(c):J\to C обозначает постоянный функтор в объекте cc. Такое преобразование называется конусом над диаграммой FF.
Другими словами, конус состоит из морфизмов (называемых компонентами конуса)
Tj:c→F(j),T_j: c \to F(j),
по одному для каждого объекта jj из JJ, совместимые со всеми морфизмами F(f):F(j)→F(k)F(f): F(j) \to F(k) диаграммы в том смысле, что каждая диаграмма 9{оп}.
Над диаграммой в (∞,1)(\infty,1)-категории
Для F:D→CF : D \to C диаграмма (∞,1)-категорий, т.е. )-функтор, (∞,1)(\infty,1)-категория (∞,1)(\infty,1)-конусов над FF есть надквазикатегория, обозначаемая C/FC_{/F}. Его объекты — конусы над FF. Его k-морфизмы являются kk-гомотопиями между конусами. (∞,1)-категориальный предел над FF — это, если он существует, терминальный объект в C/FC_{/F}.

См. также
Они имеют форму теоретико-гомотопического конуса, поэтому, возможно, существует более глубокая связь:
- положительный конус (в упорядоченной группе, такой как операторная алгебра),
- будущий конус (события в лоренцевом многообразии, таком как пространство-время),
- выпуклый конус (в векторном пространстве).
Последняя редакция: 5 ноября 2021 г., 15:25:23. См. историю этой страницы для получения списка всех вкладов в нее.
Сферы, конусы и цилиндры – Окружности и Пи – Матигон
В предыдущих разделах мы изучали свойства окружностей на плоской поверхности. Но наш мир на самом деле трехмерен, поэтому давайте посмотрим на некоторые трехмерные тела, основанные на кругах:
Цилиндр состоит из двух конгруэнтных параллельных окружностей, соединенных изогнутой поверхностью.
Конус имеет круглое основание, соединенное с одной точкой (называемой вершиной).

Каждая точка на поверхности сферы находится на одинаковом расстоянии от ее центра.
Обратите внимание, что определение сферы почти такое же, как определение а, за исключением трех измерений!
Цилиндры
Здесь вы видите цилиндр Газометр в Оберхаузене, Германия. Он использовался для хранения природного газа, который использовался в качестве топлива на близлежащих заводах и электростанциях. Газометр имеет высоту 120 м, а его основание и потолок представляют собой два больших круга радиусом 35 м. Есть два важных вопроса, на которые инженеры, возможно, захотят ответить:
- Сколько природного газа можно хранить? Это цилиндр.
- Сколько стали нужно для изготовления Газометра? Это (приблизительно) размер цилиндра.
Попробуем найти формулы для обоих результатов!
Газометр Оберхаузен
Объем цилиндра
Верх и низ цилиндра представляют собой две конгруэнтные окружности, называемые основаниями .
 высота h цилиндра — это перпендикулярное расстояние между этими основаниями, а радиус r цилиндра — это просто радиус круглых оснований.
высота h цилиндра — это перпендикулярное расстояние между этими основаниями, а радиус r цилиндра — это просто радиус круглых оснований.Мы можем аппроксимировать цилиндр, используя ${n}-сторонний призма . По мере увеличения количества сторон призма все больше и больше становится похожей на цилиндр:
Хотя цилиндр технически не является призмой, у них много общих свойств. В обоих случаях мы можем найти объем, умножив площадь их основания на их высоту . Это означает, что цилиндр с радиусом r и высотой х имеет объем
V=
Помните, что радиус и высота должны использовать одни и те же единицы измерения. Например, если r и h оба в см, тогда объем будет в .
В приведенных выше примерах два основания цилиндра всегда находились непосредственно друг над другом : это называется правым цилиндром .
 Если основания не находятся прямо друг над другом, у нас есть косой цилиндр . Основания по-прежнему параллельны, но стороны как бы «наклоняются» под углом, отличным от 90°.
Если основания не находятся прямо друг над другом, у нас есть косой цилиндр . Основания по-прежнему параллельны, но стороны как бы «наклоняются» под углом, отличным от 90°.Пизанская башня в Италии — это не совсем косой цилиндр.
Объем наклонного цилиндра оказывается точно таким же, как у прямого цилиндра с тем же радиусом и высотой. Это связано с принципом Кавальери , названным в честь итальянского математика Бонавентуры Кавальери: если два твердых тела имеют одинаковую площадь поперечного сечения на каждой высоте, то они будут иметь одинаковый объем.
Представьте, что вы разрезаете цилиндр на множество тонких дисков. Затем мы можем сдвинуть эти диски горизонтально, чтобы получить наклонный цилиндр. Объем отдельных дисков не меняется, когда вы делаете его наклонным, поэтому общий объем также остается постоянным:
Площадь поверхности цилиндра
Чтобы найти площадь поверхности цилиндра, мы должны «развернуть» его в плоскую сетку.
 Вы можете попробовать это сами, например, сняв этикетку с банки с едой.
Вы можете попробовать это сами, например, сняв этикетку с банки с едой.Их два, один вверху и один внизу цилиндра. Изогнутая сторона на самом деле большая.
- Каждый из двух кругов имеет площадь .
- Высота прямоугольника и ширина прямоугольника такие же, как у кругов: .
Это означает, что общая площадь поверхности цилиндра с радиусом r и высотой h равна
A=.
Цилиндры можно найти повсюду в нашем мире — от банок с газировкой до туалетной бумаги или водопроводных труб. Можете ли вы вспомнить какие-либо другие примеры?
Газометр выше имел радиус 35 м и высоту 120 м. Теперь мы можем подсчитать, что его объем примерно равен м3, а площадь поверхности примерно м2.
Конусы
Конус представляет собой трехмерное тело с круглым основанием . Его сторона «сужается вверх», как показано на диаграмме, и заканчивается в одной точке, называемой вершиной .

Радиус конуса — это радиус кругового основания, а высота конуса — это расстояние по перпендикуляру от основания до вершины.
Как и другие формы, которые мы встречали ранее, конусы повсюду вокруг нас: рожки для мороженого, дорожные конусы, некоторые крыши и даже рождественские елки. Что еще вы можете придумать?
Объем конуса
Ранее мы нашли объем цилиндра, аппроксимируя его с помощью призмы. Точно так же мы можем найти объем конуса, аппроксимируя его с помощью пирамиды .
Здесь вы видите ${n}-стороннюю пирамиду. По мере увеличения количества сторон пирамида все больше и больше становится похожей на конус. На самом деле мы могли бы думать о конусе как о пирамиде с бесконечно многими сторонами!
Это также означает, что мы также можем использовать уравнение для объема: V=13база×высота. Основанием конуса является круг, поэтому объем конуса радиусом r и высота h равна
V=
Обратите внимание на сходство с уравнением для объема цилиндра.
 Представьте себе, что нарисован цилиндр вокруг конуса с тем же основанием и высотой — это называется описанным цилиндром . Теперь конус будет занимать в точности объем цилиндра:
Представьте себе, что нарисован цилиндр вокруг конуса с тем же основанием и высотой — это называется описанным цилиндром . Теперь конус будет занимать в точности объем цилиндра:Примечание: Вы можете подумать, что бесконечное множество крошечных сторон в качестве приближения немного «неточно». Математики долго пытались найти более простой способ вычисления объема конуса. В 1900, великий математик Давид Гильберт даже назвал ее одной из 23 самых важных нерешенных проблем математики! Сегодня мы знаем, что это на самом деле невозможно.
Как и цилиндр, конус не обязательно должен быть «прямым». Если вершина находится прямо над центром основания, у нас есть правый конус . В противном случае мы называем его косым конусом .
И снова мы можем использовать принцип Кавальери, чтобы показать, что все наклонные конусы имеют одинаковый объем, если они имеют одинаковое основание и высоту.
Площадь поверхности конуса
Найти площадь поверхности конуса немного сложнее.
 Как и прежде, мы можем распутать конус в свою сеть. Переместите ползунок, чтобы увидеть, что произойдет: в этом случае мы получим один кружок и один .
Как и прежде, мы можем распутать конус в свою сеть. Переместите ползунок, чтобы увидеть, что произойдет: в этом случае мы получим один кружок и один .Теперь нам просто нужно сложить площади обоих этих компонентов. Основание — это круг с радиусом r , поэтому его площадь равна
ABase=.
Радиус сектора равен расстоянию от края конуса до его вершины. Это называется наклонной высотой s конуса, а не такой же, как обычная высота h . Мы можем найти наклонную высоту с помощью Пифагора:
Длина дуги сектора такая же, как у основания: 2πr. Now we can find the area of the sector using the formula we derived in a previous section:
ASector = ACircle×arccircumference = Finally, we just нужно сложить площадь основание и площадь сектора , чтобы получить общую поверхность конуса:
A=
Сферы
Сфера представляет собой трехмерное тело, состоящее из всех точек, находящихся на одинаковом расстоянии из заданного центра C .
 Это расстояние называется радиусом r сферы.
Это расстояние называется радиусом r сферы.Сферу можно представить как «трехмерный круг». Так же, как круг, сфера также имеет диаметр d , длина радиуса, а также хорды и секущие.
В предыдущем разделе вы узнали, как греческий математик Эратосфен вычислил радиус Земли по тени от полюса — он составил 6 371 км. Теперь попробуем найти общий объем и площадь поверхности Земли.
Объем сферы
Чтобы найти объем сферы, мы снова должны использовать принцип Кавальери. Начнем с полушария — сферы, разрезанной пополам по экватору. Также нам понадобится цилиндр такого же радиуса и высоты, как у полусферы, но с «вырезанным» посередине перевернутым конусом.
При перемещении ползунка ниже вы можете увидеть поперечное сечение обеих этих фигур на определенной высоте над основанием:
Попробуем найти площадь поперечного сечения обоих этих тел на высоте h над основанием.

Сечение полушария всегда равно .
Радиус поперечного сечения x является частью прямоугольного треугольника, поэтому мы можем использовать Пифагор:
r2=h3+x2.
Теперь площадь поперечного сечения равна
Поперечное сечение вырезанного цилиндра всегда равно .
Радиус отверстия ч . We can find the area of the ring by subtracting the area of the hole from the area of the larger circle:
A = πr2−πh3 = πr2−h3 Похоже, что оба тела имеют одинаковую площадь поперечного сечения на каждом уровне. По принципу Кавальери оба тела должны иметь одинаковые ! Мы можем найти объем полушария, вычитая объем цилиндра и объем конуса:
VHemisphere = VCylinder−VCone = A sphere consists of hemispheres, which means that its volume must be
V=43πr3.

Земля (приблизительно) представляет собой сферу с радиусом 6 371 км. Следовательно, его объем равен
V = = 1 км3 Средняя плотность Земли составляет 5510 кг/м3. Это означает, что его общая масса равна
Масса=Объем×Плотность≈6×1024 кг
Это 6 с 24 нулями!
Если вы сравните уравнения для объема цилиндра, конуса и сферы, вы можете заметить одно из самых удовлетворительных соотношений в геометрии. Представьте, что у нас есть цилиндр, высота которого равна диаметру его основания. Теперь мы можем идеально разместить конус и сферу внутри него:
+
Этот конус имеет радиус r и высоту 2r. Его объем
=
Радиус этой сферы равен r. Его объем
Этот цилиндр имеет радиус r и высоту 2r. Его объем равен
. Обратите внимание, что если мы возьмем объем конуса и сферы, мы получим в точности объем цилиндра!
Площадь поверхности сферы
Найти формулу площади поверхности сферы очень сложно.
 Одна из причин заключается в том, что мы не можем открыть и «сгладить» поверхность сферы, как мы делали раньше для конусов и цилиндров.
Одна из причин заключается в том, что мы не можем открыть и «сгладить» поверхность сферы, как мы делали раньше для конусов и цилиндров.Это особая проблема при попытке создать карты. Земля имеет изогнутую трехмерную поверхность, но каждая печатная карта должна быть плоской и двухмерной. Это означает, что географам приходится хитрить: растягивать или сжимать определенные области.
Здесь вы можете увидеть несколько разных типов карт, называемых проекциями . Попробуйте переместить красный квадрат и посмотрите, как эта область на самом деле выглядит на глобусе:
Меркатор
Цилиндрический
Robinson
Mollweide
Когда вы перемещаете квадрат по карте, обратите внимание, как размер и форма реальной области меняются на трехмерном глобусе.
Чтобы найти площадь поверхности сферы, мы можем еще раз аппроксимировать ее, используя другую форму — например, многогранник с множеством граней. По мере увеличения количества граней многогранник начинает все больше и больше походить на сферу.

СКОРО: Доказательство площади поверхности сферы
Пространство-время
Пространство-времяHPS 0410 Эйнштейн для всех Назад на страницу основного курса
Джон Д. Нортон
Кафедра истории и философии науки
Университет Питтсбурга- Почему пространство-время?
- Создание пространства-времени
- Световые конусы
- Световые конусы повсюду
- Правильная терминология
- Что с чем связано
- Геометрия пространства-времени Минковского
- Что вы должны знать
Почему пространство-время?
До сих пор все наши рассуждения о специальной теории относительности связано с движением тел в пространстве во времени.
 Если вы еще не
заметил, эти движения могут стать довольно сложными
визуализировать. Возьмем простой случай жезла со световым сигналом.
прыгает взад и вперед между его концами.
Если вы еще не
заметил, эти движения могут стать довольно сложными
визуализировать. Возьмем простой случай жезла со световым сигналом.
прыгает взад и вперед между его концами.Теперь опишем ту же систему в другом кадре. ссылка.
Вспомните, как сложно отслеживать события на концах стержня. В одном случае события отражения сигнала равномерно распределены во времени. В другом они расположены в шахматном порядке. Различия имеет большое значение, так как является проявлением ключевого эффекта относительность одновременности. Но нельзя просто смотреть на рисунок и видеть Эффект. Вы должны разыграть небольшой фильм в своей голове.
В 1907 году математик Германн Минковский исследовал способ визуализации этих процессов. который оказался особенно подходящим для распутывания релятивистские эффекты.  Это было их представление в пространстве-времени.
Довольно загадочные релятивистские эффекты можно понять с помощью
легкость в представлении пространства-времени и работа в теории
теория относительности стала превращаться в работу по геометрии
пространство-время.
Это было их представление в пространстве-времени.
Довольно загадочные релятивистские эффекты можно понять с помощью
легкость в представлении пространства-времени и работа в теории
теория относительности стала превращаться в работу по геометрии
пространство-время.Создание пространства-времени
Мы строим пространство-время делая мгновенные снимки пространства в последовательные моменты время и складывая их. это легче всего представить это, если мы начнем с двухмерного пространства. Снимки, сделанные в разное время, затем складываются, чтобы дать нам трехмерное пространство-время. В этом пространстве-времени маленькое тело в остальные будут представлены вертикальной линией. Чтобы понять, почему это вертикальной, напомним, что она должна пересекать каждое мгновенное пространство на том же месте.  Вертикальная линия сделает это. Если он движется, то
будет пересекать каждое мгновенное пространство в другом месте; а
движущееся тело изображают линией, наклоненной к вертикали.
Вертикальная линия сделает это. Если он движется, то
будет пересекать каждое мгновенное пространство в другом месте; а
движущееся тело изображают линией, наклоненной к вертикали.
Стандартное соглашение (которое я обычно использую) состоит в том, чтобы представить траектории световых сигналов по линиям 45 o к вертикали.На рисунке движущийся стержень представлен траекториями в пространство-время своих концов. Зигзагообразная линия – это световой сигнал, отражающийся туда и обратно между этими двумя концами.
Точка, которая движется по инерции, то есть точка который движется равномерно и прямолинейно в пространстве, изображается прямая линия в пространстве-времени. Ибо такое движение охватывает одинаковое расстояние за то же время. Вот еще один пример.
 Делайте снимки земли
вращается вокруг Солнца в трехмерном пространстве вокруг Солнца в
течение года, которое будет иметь вид:
Делайте снимки земли
вращается вокруг Солнца в трехмерном пространстве вокруг Солнца в
течение года, которое будет иметь вид:Теперь складываем их в третий измерение. Когда мы убираем вещи немного вверх, у нас есть пространство-время. До сих пор мы описывали, как двумерное пространство в сочетании с одним дополнительным измерением времени, чтобы создать три размерное пространство-время, такое как показано выше на рисунках. Наше пространство трехмерный. Поэтому, когда мы добавляем дополнительное измерение времени, мы генерируем четырехмерное пространство-время.
Нет простого способа нарисовать картина четырехмерного пространства-времени.  Визуализация
это может быть очень тяжело. Но это не делает его загадочным.
Это просто другой вид пространства, которое выходит за рамки простого
визуализация. В физике четыре измерения на самом деле довольно
скромный. В статистической механике мы обычно имеем дело с фазой
места в 6 раз больше числа молекул в пробе газа. Даже для небольших
пробы газа, которые могут достигать 10 25 —место с
10000000000000000000000000 размеров. Так что мы не должны слишком бояться
математическим пространством всего с четырьмя измерениями!
Визуализация
это может быть очень тяжело. Но это не делает его загадочным.
Это просто другой вид пространства, которое выходит за рамки простого
визуализация. В физике четыре измерения на самом деле довольно
скромный. В статистической механике мы обычно имеем дело с фазой
места в 6 раз больше числа молекул в пробе газа. Даже для небольших
пробы газа, которые могут достигать 10 25 —место с
10000000000000000000000000 размеров. Так что мы не должны слишком бояться
математическим пространством всего с четырьмя измерениями!Световые конусы
Что скорость света есть постоянная — один из самых важных фактов о пространстве и времени в специальной теории относительности. Этот факт выражается геометрически в пространстве-времени. геометрия через существование световых конусов, или, как это иногда сказал, «структура светового конуса» пространства-времени.

Чтобы увидеть эту структуру, мы представляем событие, на котором это взрыв. Свет будет распространяться от него в расширяющемся сферическая оболочка. В двухмерном пространстве это будет выглядеть как расширяющийся круг, как показано ниже.
Чтобы увидеть эту структуру, мы представляем событие, при котором происходит взрыв. Свет будет распространяться из в расширяющейся сферической оболочке. В двумерном пространстве это будет выглядеть как расширяющийся круг. Анимация делает движение более заметным. Теперь сложите эти пространственные снимки, чтобы сделать пространство-время. Диаграмма пространства-времени, соответствующая похоже на конус. Двигаясь вверх по конусу, мы смотрим в каждую мгновенное пространство, чтобы увидеть, как далеко распространился свет.
 Каждый
пересечение конуса с пространством будет окружностью.
Каждый
пересечение конуса с пространством будет окружностью.На рисунке расширяющийся круг света представлена верхней половиной конуса. Внизу принято рисовать половину конуса, хотя он и не является частью расширения легкий. На самом деле он представляет обратное. Он изображает круг света схлопывается к исходному событию на вершине конуса. Вот этот крах, представленный также в виде анимации.
Финальная анимация теперь показывает связь между различные стадии схлопывания и расширения световой оболочки и сечения светового конуса.
Чтобы был световой конус, нам не нужно свет должен присутствовать. Конусы отображают траектории света взял бы, если бы свет должен был присутствовать. Так как это просто возможности которые нанесены на карту, не обязательно траектории реального света. Пространство-время по-прежнему имеет структуру светового конуса в темноте!
Световые конусы повсюду
Для описания светового конуса мы выбрали событие в пространство-время и вообразил все возможные траектории, по которым может двигаться свет.
 в распространении через это событие. Мы могли бы выбрать
любое событие в пространстве-времени. Мы бы нашли световые конусы в
каждый из них. Это означает, что пространство-время полностью заполнено
легкие конусы. Он есть на каждом мероприятии.
в распространении через это событие. Мы могли бы выбрать
любое событие в пространстве-времени. Мы бы нашли световые конусы в
каждый из них. Это означает, что пространство-время полностью заполнено
легкие конусы. Он есть на каждом мероприятии.Правильная терминология
Если говорить о пространство-время. В результате сформировался достаточно точный словарный запас. важно использовать его правильно. Платить обратите внимание на следующие термины:
Пространство-время Когда мы добавляем к пространству дополнительное измерение времени, мы создаем пространство-время. пространство-время Минковского Нет ничего особенного в пространство-время. Они могут возникнуть в классической физике. Итак, если мы имеем в виду пространство-время, которое также ведет себя так, как требует специальная теория относительности, то у нас есть пространство-время Минковского.
 (Примечание
на потом: когда мы посмотрим на общую теорию относительности, мы встретимся
пространства-времени, которые являются релятивистскими, но не пространства-времени Минковского.)
(Примечание
на потом: когда мы посмотрим на общую теорию относительности, мы встретимся
пространства-времени, которые являются релятивистскими, но не пространства-времени Минковского.)Событие Это отдельные точки пространства-времени. Они представляют точки в пространстве в определенное время.
Timelike Worldline Это траектория движения точки меньше скорости света. Эти кривые содержатся в светлый конус. Они представляют собой траектории обычных частиц, как электрон, протоны и нейтроны, но не фотоны.
Светоподобная кривая Это траектория точки, движущейся со скоростью скорость света — световой сигнал или фотон. Они лежат на поверхность светового конуса.
Пространственноподобная кривая Это кривая, лежащая за пределами света конус. Если объект должен сделать эту кривую своей траекторией, он нужно двигаться быстрее света.

Пространственноподобные гиперповерхности Это мгновенные пространственные снимки пространства-времени. Они трехмерны в случае четырехмерное пространство-время.
Прошлые и будущие световые конусы Все светоподобные кривые через событие формируют световой конус в этом событии. Часть конуса к будущее этого события — будущий световой конус. Часть к прошлое — это световой конус прошлого.
Структура светового конуса Поскольку скорость света обычно считаются самыми быстрыми, когда причины могут распространять свои следствия, как только мы узнаем, как световые конусы распределяются в пространстве, мы можем сказать много о том, что возможно и невозможно причинно в пространство-время. Так что эта раздача представляет для нас большой интерес. это называется структурой светового конуса пространства.
Времяподобная геодезическая Это кривые, которые являются возможными траектории в пространстве-времени инерциально движущихся точек.
 Они есть
прямые линии, лежащие внутри светового конуса. Этот технический термин
«геодезический» будет объяснен позже.
Они есть
прямые линии, лежащие внутри светового конуса. Этот технический термин
«геодезический» будет объяснен позже.Что с чем связано
Знание структуры светового конуса пространства-времени говорит нам что с чем связано. Его важность сопоставима с тем, что изображены на обычных картах стран. Вот карта древнего Греция:
Греция в начале Пелопоннеса война. п. 17 в WS Shepherd, Исторический атлас, Нью-Йорк: Генри Холт и Ко., 1911.Читаем по карте, что если мы в Греции, то можем отправиться на север и в конце концов прибыть во Фракию. Однако мы не можем добраться до Крита; или, по крайней мере, мы не можем добраться до Крита по суше. Мы нужно будет пересечь море.
Каталоги структуры светового конуса аналогичная информация «что с чем связано» для пространства-времени.  Это
раскрывает его самую основную географию.
Это
раскрывает его самую основную географию.Чтобы увидеть, как это работает, выберите любое событие «О» в пространстве-времени. будущий световой конус в О содержит все события в пространство-время, которое может быть достигнуто из O с помощью направленного в будущее времяподобного или легкие изгибы. Если мы делаем обычное предположение, что все причинные процессы распространяются со скоростью света или меньше, делаем вывод что это все события, на которые мы можем причинно воздействовать из O.
Проще говоря, если вы находитесь в точке О, события в переднем световом конусе это только те события, до которых можно достучаться физическим сигналом, например, обычная частица или световая вспышка, которую вы можете излучать.
Для того же события О, прошлое световой конус содержит все события в пространстве-времени, из которых можно достичь события O с помощью направленного в будущее времяподобного или светоподобного кривые. 
Если снова предположить, что все причинные процессы распространяются со скоростью менее или равна скорости света, мы заключаем, что этот прошлый световой конус содержит все события, которые могут причинно повлиять на событие O.
Проще говоря, если вы находитесь в каком-либо событии в прошлом световом конусе O, вы всегда можете послать на О физический сигнал, состоящий из обычного частица или световая вспышка.
Оставшаяся область пространства-времени находится вне как прошлого, так и будущего световых конусов. Это новый вид области, которая не появляется в дорелятивистском пространстве-времени. Это «другой» район. Собирает все события, которые не могут быть связаны с событием O посредством времениподобные или светоподобные кривые. Его события могут быть связаны только с O пространственноподобными кривыми.
 То есть его события «пространственноподобны
отделены» от O.
То есть его события «пространственноподобны
отделены» от O.Если мы предположим, что никакие причинные процессы не распространяются быстрее света, эти события причинно не связаны с О. Если мы находимся в О, мы не может причинно повлиять или быть причинно затронутым событием в событие в этом «другом» регионе. Соответственно, мы не можем обмениваются сигналами между событием в O и любым пространственно-подобным разделенным событие в этом регионе.
В дорелятивистском пространстве-времени нет соответствующей области. В Ньютоновской теории предполагается, что существуют распространения, сколь угодно быстро и даже мгновенно. Пример Мгновенное распространение – это изменения в ньютоновской гравитационной поле. Если бы солнце исчезло, мы бы сразу узнали об этом. Земля, согласно ньютоновской теории, потому что Солнце больше не будет оказывать на нас гравитационное воздействие.

Минковский Геометрия пространства-времени
Пространство-время Минковского имеет геометрию в некотором смысле аналогично геометрии обычного евклидова пространство. Обе они являются «метрическими» геометриями. Это означает, что они геометрии, которые имеют дело с расстояниями.
Евклидова геометрия знакома кейс. Он состоит из двух вещей: набора точек и исчерпывающего инвентаризация расстояний между всеми парами точек. В принципе, нам нужно было бы перечислить все расстояния между каждой точкой и любой другой точкой. На практике задача намного проще. Если мы просто укажем расстояния между каждой точки и ее соседних точек, мы можем тогда определить все оставшиеся дистанции. Я оставлю обсуждение здесь, так как мы вхождение в технические области, которыми нам сейчас не нужно заниматься. 
Одна из самых простых конструкций в Евклидова геометрия — это круг. Круг это просто геометрическое место всех точек, находящихся на одном и том же расстоянии от некоторого назначенный центральный пункт. На рисунке показаны две окружности радиусом 1 и радиуса 2. Они являются локусами всех точек, которые являются единичными. удаленной и на 2 единицы удаленной от центральной точки. Пространство-время Минковского также имеет метрическую геометрию. Вместо евклидовых точек основано на пространственно-временных событиях. Геометрия определяет пространственно-временное расстояние от каждого события до любого другого события в пространство-время. Спецификация немного сложнее, чем у Евклидова геометрия. В евклидовом случае существует только один тип расстояние, измеряемое обычными измерительными рейками.
 В Минковски
пространство-время, есть три типа расстояния, вместе известные как «интервал»
или «пространственно-временной интервал».
В Минковски
пространство-время, есть три типа расстояния, вместе известные как «интервал»
или «пространственно-временной интервал».Самое простое — расстояние от события до другого, которое пространственно как бы отделяется от него. То есть второе событие лежит вне световой конус первого события. Расстояние — это просто расстояние, измеренное в знакомым способом мерными рейками. Его часто называют «правильным расстояние.» (Чтобы получить более четкое представление того, как эта измерительная операция может быть применена ко всем пространственно-подобным событиям отдельно от начального события, нам нужно будет увидеть пространство-время Представление об относительности одновременности. Это тема следующую главу.)
В следующем случае второе событие отделяется во времени с первого события. То есть он находится в свете первого события. конус. Это расстояние в пространстве-времени измеряется часами, которые движутся по инерции от первого события ко второму.
 Время читается на часах
дает нам пространственно-временной интервал между двумя событиями. Его также называют
«подходящее время.»
Время читается на часах
дает нам пространственно-временной интервал между двумя событиями. Его также называют
«подходящее время.»Наконец, второе событие может быть светоподобно отделено от первое событие. То есть он лежит на световом конусе события. Тогда интервал до события равен нулю; и это ноль нет независимо от того, где находится это второе событие на световом конусе.
Строительство в Минковском геометрия пространства-времени, аналогичная евклидову окружности геометрия. Еще раз находим все точки которые представляют собой одну единицу, две единицы и т. д., разделенные в пространстве-времени интервал от нашего начального события. Какие результаты показаны на рисунке. Пунктирные линии представляют световой конус начального события. кривые внутри светового конуса — это геометрическое место точек один единица и два единицы собственного времени, удаленные от него.
 Это гиперболы,
приближаться к световому конусу сколь угодно близко.
Это гиперболы,
приближаться к световому конусу сколь угодно близко.Кривые вне светового конуса также являются гиперболами. Они сейчас места всех точек на одну единицу и две единицы правильного расстояния от исходного события.
Гипеболы являются аналогами Минковского геометрия окружностей в евклидовой геометрии.
Почему фигуры гиперболы? Причину проще всего увидеть в случай, когда место событий отделено постоянным собственным временем от начальное событие. Ситуация физически соответствует многим часам, как показано на фигура. Первый находится в состоянии покоя; второй движется вправо; в третий быстрее движется вправо; и так далее. Первый из них часы работают быстрее всех; второй медленнее; третий еще медленнее; и так далее.

Следовательно, по мере того, как мы будем переходить от часов к часам, часы должны будут путешествовать последовательно дольше (измеряемое во времени инерциальная система отсчета) для того, чтобы часы отсчитывали единицу подходящее время.
Когда мы рисуем диаграмму пространства-времени, мы восстанавливаем показанную фигуру. движение покоящихся в кадре часов кратчайшее, вертикальное линия. Движение самых быстрых часов — это самая длинная линия в право. Все они представляют собой единицу собственного времени длины.
Их конечные точки повторяют показанную гиперболу.
Случай гипербол постоянных правильное расстояние труднее анализировать. Увидев, как относительность одновременность представлена в пространстве-времени в следующей главе. отправная точка. Это оставлено в качестве упражнения для читателя.
Эти цифры имеют почтенную историю в теории относительности.
 теория. Вот как они появились у Минковского.
оригинальные публикации.
теория. Вот как они появились у Минковского.
оригинальные публикации.Что вы должны знать:
- Что такое пространство-время.
- Правильное использование определенных терминов, связанных с пространством-временем.
- Что такое световые конусы и как они делят пространство-время на различных регионах по отношению к каждому событию.
Авторское право Джон Д. Нортон. январь 2001 г., сентябрь 2002 г.; июль 2006 г.; 3 февраля 2007 г .; 23 января, 24 сентября 2008 г.; 3 февраля 2012 г.; 9 февраля 2013 г.; 27 января, 9 февраля 2015 г. Январь 28, 2022. 1 февраля, 2022.
Основы конуса и цветовое пространство LMS
В прошлой статье мы показали, как необработанные данные, захваченные цифровой камерой, связаны с наукой о цвете. В моем следующем трюке я покажу, что CIE 2012 2 deg XYZ Color Matching Functions, , показанные на рисунке 1, являются точным линейным преобразованием Stockman & Sharpe (2000) 2 deg Cone Fundamentals, , показанного на рисунке 29.
 0003
0003(1)
с CMF и CF в формате 3xN, матрицей 3×3 и умножением матриц. Et voilà: [1]
Рис. 1. Сплошные линии: CIE (2012) 2° XYZ «физиологически релевантные» функции согласования цветов и фотопическая функция светоотдачи (V) от cvrl.org, Исследовательской лаборатории цвета и зрения в ЛЧ. Пунктирные линии: Основы конуса на рисунке 2 после линейного преобразования с помощью матрицы 3×3 Mlx ниже. Источник: cvrl.org.Я также могу выполнить обратный трюк, от CMF к CF, используя обратную матрицу ,
(2)
Re-voilà:
Рисунок 2. Сплошные линии: Stockman & Sharpe (2000) 2-градусные основные принципы на основе 10-градусных CMF Стайлза и Берча (с поправкой на 2 градуса), cvrl.org . Пунктирные линии: CMF на рисунке 1 после линейного преобразования матрицей Mxl. Источник: cvrl.org.Все кривые и матрицы рассчитываются благодаря магии линейной алгебры и предположению, что линейность применима к свету. Базовые данные получены из Исследовательской лаборатории цвета и зрения в UCL: [2]
Основы колбочек — функции сопоставления цветов
У большинства людей в сетчатке есть три типа рецепторов дневного света, называемых колбочками, каждый тип обозначается как Длинный, Средний и Короткий (или, альтернативно, , ) в зависимости от длины волны, которую они поглощают.
 более эффективно. Таким образом,
более эффективно. Таким образом,, , являются конусообразными фундаментальными кривыми, которые производят трехцветные значения в пространстве, точно так же, как , , делают то же самое в — эти два являются просто линейным преобразованием друг от друга. Другими словами, Основы конуса — это функции сопоставления цветов, видимые из цветового пространства, которое лучше соответствует зрительной системе человека.
Используя эти матрицы для перемещения информации о цвете, мы делаем прыжок из всех других стандартных цветовых пространств, таких как ProPhotoRGB или sRGB, до которых легко добраться с помощью хорошо известных проекционных матриц, собранных на таких красивых сайтах, как сайт Брюса Линдблума. [3]
Почему XYZ?
Таким образом, вы можете задаться вопросом: почему CIE вообще придумала воображаемое цветовое пространство и — когда мы пытаемся извлечь лучший цвет из наших цифровых камер — почему мы пытаемся сделать их функции спектральной чувствительности похожими на , , , с двумя- пиковые красные вместо более качественных и похожих однопиковых конусных основ? Вот, например, два набора SSF из нескольких статей назад для сравнения с кривыми на рис.
Рис. 3. Пунктирные линии: функции спектральной чувствительности для Nikon D5100 и неизвестного объектива, измеренные Darrodi et al. в НПЛ. Сплошные линии: SSF камеры и объектива со спектральными составляющими, описанными несколько статей назад. 2.9.0952 [4]
2.9.0952 [4] Хороший вопрос. Однако ответ заключается в том, что в идеале не должно быть разницы, пытаемся ли мы имитировать один набор кривых (CIE 2 градуса CMF) или другой (CF), потому что они двойственны друг другу. [5]
И точно так же, как 5 умножить на 3 умножить на 7 равно 5 умножить на 7 умножить на 3, при условии, что мы придерживаемся правил линейной алгебры, для конечного результата не должно быть никакой разницы, вычисляем ли мы матрицу компромиссного цвета как описанный в предыдущей статье путем сведения к минимуму разницы между SSF и CMF нашей камеры, что приведет нас к XYZ; или вычислить эквивалентную, минимизировав разницу с CF, что вместо этого доставит нас в космос; или используйте функции согласования цветов sRGB в качестве эталона и приземлитесь там.
 Затем мы можем спроецировать на XYZ (или куда-либо еще в этом отношении) совершенно точно, применив соответствующую матрицу — без каких-либо штрафов, предполагая, что используется математика с плавающей запятой, что в наши дни в основном и происходит.
Затем мы можем спроецировать на XYZ (или куда-либо еще в этом отношении) совершенно точно, применив соответствующую матрицу — без каких-либо штрафов, предполагая, что используется математика с плавающей запятой, что в наши дни в основном и происходит.Кому нужны ответные конусы?
На самом деле, пока мы знаем кривые в заданном цветовом пространстве, например , мы фактически знаем их везде. А поскольку физически и этически сложно измерить мощность колбочек в сетчатке глаза человека, мы могли бы также измерить их чувствительность в другом цветовом пространстве, связанном с ним линейным преобразованием. Введите эксперименты по сопоставлению цветов, которые составляют основу науки о цвете, в основном выполняемые в физическом цветовом пространстве, которое в идеале представляет собой всего лишь матричное умножение 3 × 3, отличное от всех других, включая .
Интуитивно понятно, что в экспериментах по сопоставлению цветов они измеряют реакцию не на самих колбочках, а на реакцию дальше по цепочке обработки изображений зрительной системы человека, по крайней мере, после того, как сигнал уже был обнаружен тремя типами колбочек и кодируется нейронами в канал яркости (сумма) и два канала цветности (разность) для передачи через зрительный нерв в мозг:
Первая стадия представлена ро-, гамма- и бета-конусами (плюс палочки, которыми мы пренебрегаем при дневном свете) и в основном ведет себя радиометрически. Второй этап выполняется нейронами, которые кодируют сигнал, пропорциональный количеству фотонов, в противоположные цветовые каналы, которые затем передаются в мозг по нервным волокнам. Из «Измерение цвета, четвертое издание, Wiley, 2011» Р. В. Г. Ханта, М. Р. Пойнтера.
Второй этап выполняется нейронами, которые кодируют сигнал, пропорциональный количеству фотонов, в противоположные цветовые каналы, которые затем передаются в мозг по нервным волокнам. Из «Измерение цвета, четвертое издание, Wiley, 2011» Р. В. Г. Ханта, М. Р. Пойнтера.И даже тогда. Таким образом, это может привести к некоторым нелинейностям и играм в системе, которые, тем не менее, в обычной практике часто остаются незаметными.
Получение данных о чувствительности путем сопоставления цветов указывает на причину, по которой до сих пор ведутся споры о точных кривых физического отклика HVS, полученных, например, в результате физиологических экспериментов с колбочковыми фотопигментами [*] , в то время как существует гораздо лучшее согласие в отношении точности Стандартные кривые Observer CMF. И это прекрасно подходит для науки о цвете.
Другими словами, мы, возможно, не смогли точно измерить спектральный отклик HVS напрямую, но его косвенное измерение с помощью сопоставления цветов работает так же хорошо, потому что два набора кривых предположительно являются линейным преобразованием друг друга.
 То, что мы пока не смогли удовлетворительно определить, — это относительная матрица проекции 3 × 3, о которой выше — лишь одно из последних и лучших предположений. Это означает, что «основы конуса» и «LMS» могут быть немного неправильными названиями кривых и пространства, показанных на рисунке 2, и более подходящим может быть более общее пространство «отклик HVS» и «HVS».
То, что мы пока не смогли удовлетворительно определить, — это относительная матрица проекции 3 × 3, о которой выше — лишь одно из последних и лучших предположений. Это означает, что «основы конуса» и «LMS» могут быть немного неправильными названиями кривых и пространства, показанных на рисунке 2, и более подходящим может быть более общее пространство «отклик HVS» и «HVS».Хроматическая адаптация?
На самом деле может быть преимуществом перейти непосредственно от необработанного демозаики к тому, что глаз имеет тенденцию адаптироваться к основному освещению, в котором он купается, поэтому практически все сцены требуют некоторой формы хроматической компенсации, которая кажется похожей на специфичную для конуса Усиление в идеале применяется ближе всего к тому, где это происходит физиологически, к пространству в текущей простой модели.
Это типичная последовательность того, как линейный цвет применяется коммерческим преобразователем необработанных данных, причем практически каждый шаг требует линейного преобразования с умножением матрицы 3×3:
- необработанные данные баланса белого, демозаичные, с серой карты ()
- выберите компромиссную матрицу для данной сцены и источника света
- используйте его для проецирования в цветовое пространство подключения (обычно) Проект
- через подходящую стандартную матрицу (часто Брэдфорд)
- компенсировать хроматическую адаптацию просмотра путем масштабирования основных цветов (или более сложным методом)
- вернуться к использованию обратной матрицы на шаге 4
- из проекта в рабочее/выходное цветовое пространство (или аналогичное), используя соответствующую стандартную матрицу.

Поскольку эти шаги выполняются путем линейного умножения, их все можно свернуть в одну матрицу 3×3, чтобы, например, за один раз преобразовать захваченные демозаичные необработанные данные (шаг 1) в (шаг 7). Или различные шаги могут быть смещены и/или объединены по желанию, исходя из удобства и правил линейной алгебры. Мы могли бы даже забыть о существовании космоса, если бы не требовалась адаптация, но она практически всегда требуется.
Почему Брэдфорд?
Однако, вернемся немного назад, зачем использовать матрицу Брэдфорда для проецирования в (шаг 4) вместо той, которая использовалась для создания рис. 2 выше, ?
Ну, мы сказали, что линейное преобразование в все еще немного свободно, поэтому в зависимости от приложения может быть удобно растягивать его больше в одном направлении, чем в другом. В конкретном случае хроматической адаптации к основному источнику света — поскольку процедура обычно включает в себя круговой обход () только для выполнения того, что обычно представляет собой простую операцию масштабирования — выбор еще более широк.
 Преобразование Брэдфорда предполагает, что хроматическая адаптация к доминирующему источнику света в зрительной системе человека происходит не на стадии обнаружения как есть, на колбочках, а после некоторого сужения относительных ответов. По этой причине его иногда называют спектрально «заостренным» преобразованием.
Преобразование Брэдфорда предполагает, что хроматическая адаптация к доминирующему источнику света в зрительной системе человека происходит не на стадии обнаружения как есть, на колбочках, а после некоторого сужения относительных ответов. По этой причине его иногда называют спектрально «заостренным» преобразованием.Он работает довольно хорошо и в своей линейной форме стал стандартом для хроматической адаптации в необработанном преобразовании за последние двадцать лет, хотя ничто не идеально. [7]
Вкратце
- Нет никаких причин для того, чтобы быть стандартным пространством соединения , кроме как в 1931 году было круто иметь цветовое пространство без отрицательных значений в видимом диапазоне
- Любое пространство, являющееся линейным преобразованием любого колориметрического цветового пространства, так же хорошо с точки зрения науки о цвете
- Таким образом, мы можем получить абсолютно достоверные цветовые матрицы компромисса из функций спектральной чувствительности наших цифровых камер и объективов, сводя к минимуму ошибки по сравнению с функциями согласования цветов в любом пространстве, в том числе там, где они упоминаются как основы конуса .
- Спектральные отклики физиологических колбочек слабо связаны с основами колбочек Стокмана и Шарпа (2000), поскольку последние представляют собой просто линейное преобразование CMF, полученное в результате экспериментов по сопоставлению цветов в каком-то другом пространстве
- Поскольку координаты пространства не были полностью зафиксированы, на данный момент мы можем проецироваться в него и из него, когда и как мы сочтем удобным — до тех пор, пока мы согласны с относительными матрицами
- За последние 100 лет или около того в Пространстве подключения к профилю было сгенерировано так много справочных данных, что, если нет действительно веской причины поступать иначе, мы могли бы пока придерживаться его.

Примечания и ссылки
1. Код Matlab/Octave, использованный для создания рисунка 1, можно загрузить, нажав здесь.
2. Страница Лаборатории цвета и зрения Института офтальмологии UCL находится здесь.
3. На сайт Брюса Линдблума можно перейти, нажав здесь.
4. Спектральным откликам, показанным на рис. 3, около 10 лет, и они отражают красители CFA, использовавшиеся в то время. Более современные красители, такие как Color Mosaic нового поколения Fuji, создают спектры, которые пытаются устранить утечку красного канала в более низких длинах волн, см., например, «Технология материалов цветных фильтров для датчика изображения», Хироши Тагучи, Масаси Энокидо, FUJIFILM Electronic Materials Co. , ООО (2011)
5. «Точный цвет», Бертольд К. П. Хорн, Массачусетский технологический институт, 1983
6. «Основы конуса — это неправильное название», Джеймс Т. Фултон, 2009.
7. «Спектральная резкость и преобразование Брэдфорда», Грэм Д. Финлейсон и Сабин. Süsstrunk, CIS 2000.Нормальный конус погружения — проект The Stacks
Пусть $S$ — схема. Пусть $i : Z \to X$ — замкнутое погружение алгебраических пространств над $S$. Пусть $\mathcal{I} \subset \mathcal{O}_ X$ — соответствующий квазикогерентный пучок идеалов, см.
 {n + 1}$ аннулируется $\mathcal{I}$, эта градуированная алгебра соответствует квазикогерентному пучку градуированных $\mathcal {0}_Z$-алгебры морфизмами пространств, лемма 66.14.1. Эта квазикогерентная градуированная $\mathcal{O}_ Z$-алгебра называется 9*(\mathcal{C}_{Z/X}) \longrightarrow \mathcal{C}_{Z/X, *} \end{уравнение}
{n + 1}$ аннулируется $\mathcal{I}$, эта градуированная алгебра соответствует квазикогерентному пучку градуированных $\mathcal {0}_Z$-алгебры морфизмами пространств, лемма 66.14.1. Эта квазикогерентная градуированная $\mathcal{O}_ Z$-алгебра называется 9*(\mathcal{C}_{Z/X}) \longrightarrow \mathcal{C}_{Z/X, *} \end{уравнение}квазикогерентных градуированных $\mathcal{O}_ Z$-алгебр, являющийся изоморфизмом в степенях $0$ и $1$.
Лемма 75.6.2. Пусть $S$ — схема. Пусть $i : Z \to X$ — погружение алгебраических пространств над $S$. Пусть $\varphi : U \to X$ —этальный морфизм, где $U$ — схема. Положим $Z_ U = U \times _ X Z$, которая является локально замкнутой подсхемой в $U$. Затем
\[ \mathcal{C}_{Z/X, *}|_{Z_ U} = \mathcal{C}_{Z_ U/U, *} \] 9*\mathcal{C}_{Z’/X’, *} \longrightarrow \mathcal{C}_{Z/X, *} \]
Доказательство. Сначала найдите открытые подпространства $U’ \subset X’$ и $U \subset X$ такие, что $g(U) \subset U’$ и такие, что $i(Z) \subset U$ и $i(Z’) \subset U’$ замкнуты (доказательство существования опущено).
 Заменив $X$ на $U$ и $X’$ на $U’$, мы можем считать, что $i$ и $i’$ — замкнутые погружения. Пусть $\mathcal{I}’ \subset \mathcal{O}_{X’}$ и $\mathcal{I} \subset \mathcal{O}_ X$ — квазикогерентные пучки идеалов, ассоциированные с $i ‘$ и $i$, см. Морфизмы пространств, лемма 66.13.1. Рассмотрим состав
9*\mathcal{C}_{Z’/X’, *} \to \mathcal{C}_{Z/X, *}$ из леммы 75.6.3 сюръективно. Если $g$ плоский, то это изоморфизм.
Заменив $X$ на $U$ и $X’$ на $U’$, мы можем считать, что $i$ и $i’$ — замкнутые погружения. Пусть $\mathcal{I}’ \subset \mathcal{O}_{X’}$ и $\mathcal{I} \subset \mathcal{O}_ X$ — квазикогерентные пучки идеалов, ассоциированные с $i ‘$ и $i$, см. Морфизмы пространств, лемма 66.13.1. Рассмотрим состав
9*\mathcal{C}_{Z’/X’, *} \to \mathcal{C}_{Z/X, *}$ из леммы 75.6.3 сюръективно. Если $g$ плоский, то это изоморфизм.Доказательство. Мы можем проверить утверждение после этальной локализации $X’$. В этом случае можно считать, что $X’ \to X$ — морфизм схем, следовательно, $Z$ и $Z’$ — схемы, и результат следует из случая схем, см. Дивизоры, лемма 31.19.4. $\квадрат$
Мы используем те же соглашения для конусов и векторных расслоений над алгебраическими пространствами, что и для схем (где мы используем соглашения EGA), см. конструкции, разделы 27.7 и 27.6. В частности, векторное расслоение — это очень общий гаджет (и не локально изоморфное аффинному пространственному расслоению).

- θ=Θ.

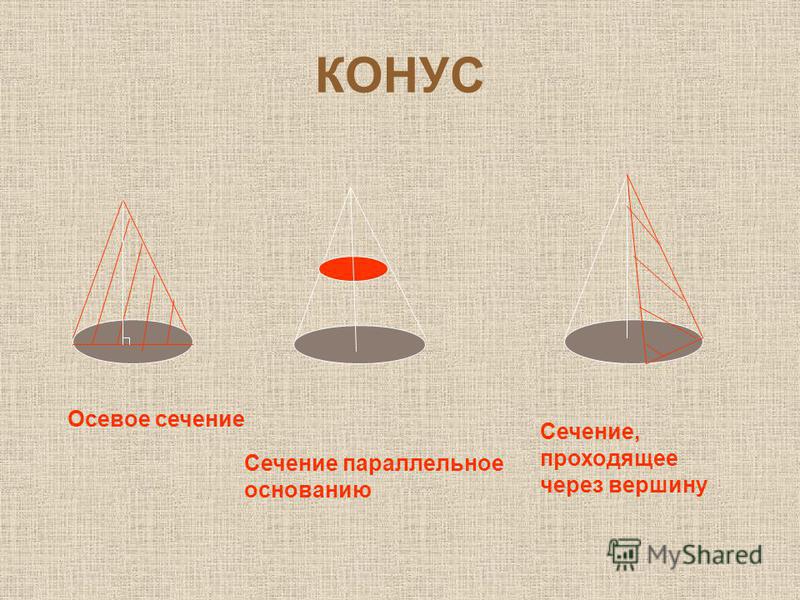

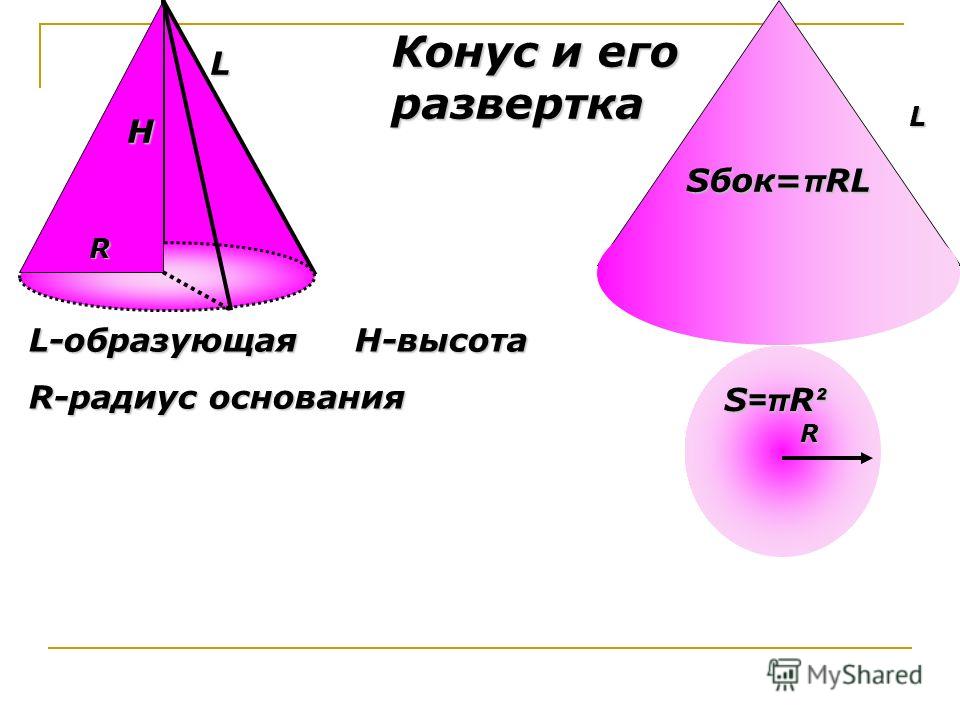 50)
50)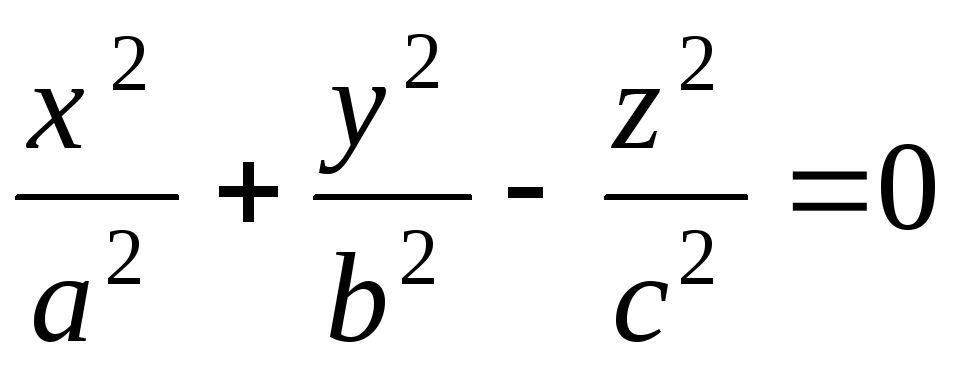

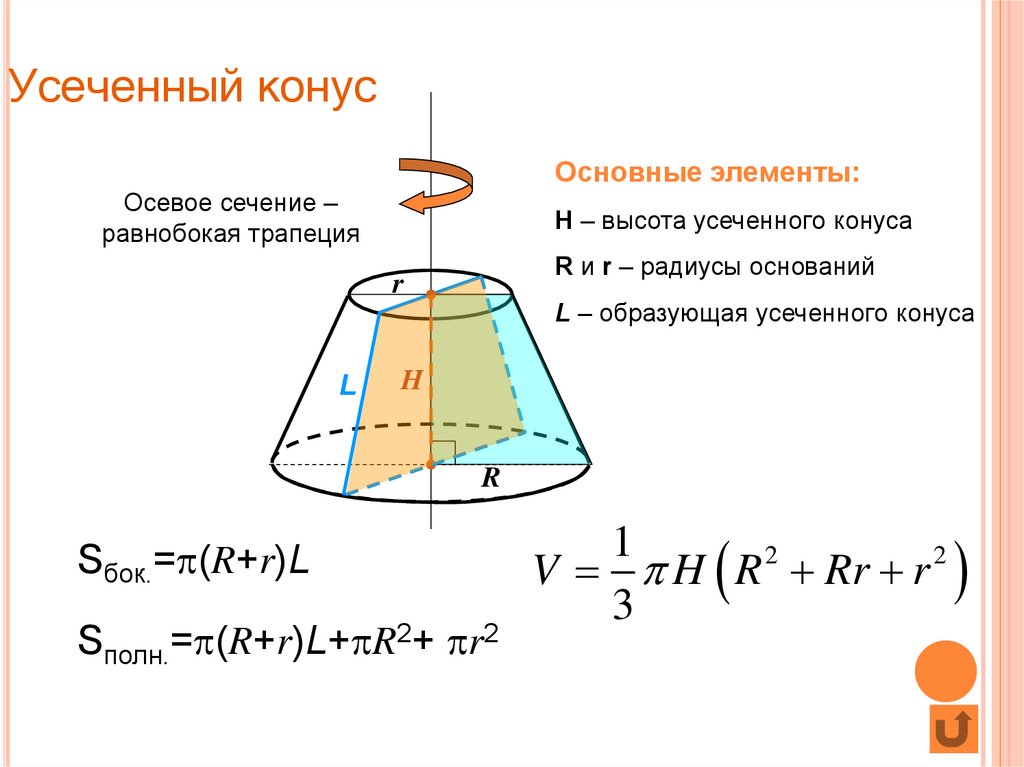
 53)
53) В этом случае поверхность называется двуполостным
гиперболоидом вращения.
В этом случае поверхность называется двуполостным
гиперболоидом вращения. Через каждую точку поверхности проходит одна прямолинейная образующая.
Неподвижная кривая, по которой скользит образующая, называется направляющей.
Если направляющая линия является кривой второго порядка, то и цилиндрическая
поверхность – второго порядка.
Через каждую точку поверхности проходит одна прямолинейная образующая.
Неподвижная кривая, по которой скользит образующая, называется направляющей.
Если направляющая линия является кривой второго порядка, то и цилиндрическая
поверхность – второго порядка.
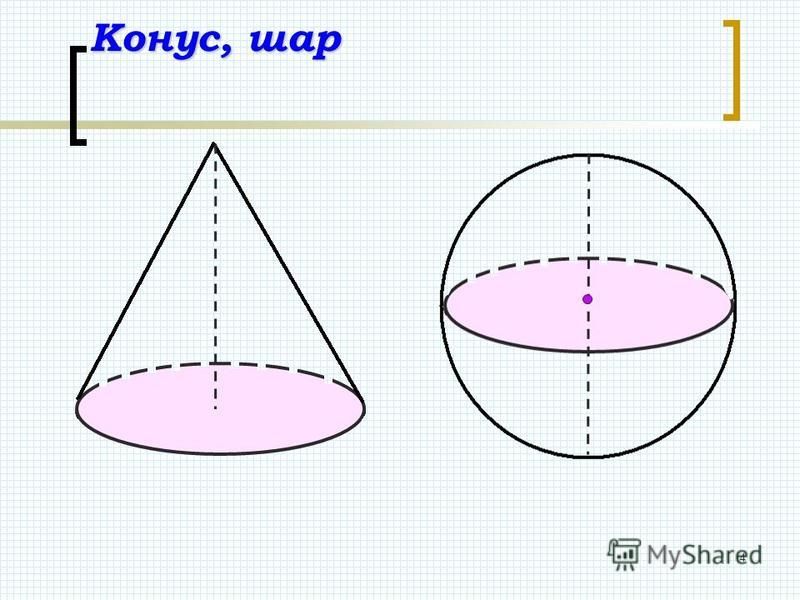 55)
55) Наклонные
сечения прямого эллиптического цилиндра в общем случае – эллипсы. Однако его
всегда можно пересечь плоскостью, наклонной к его образующим, таким образом,
что в сечении получится круг.
Наклонные
сечения прямого эллиптического цилиндра в общем случае – эллипсы. Однако его
всегда можно пересечь плоскостью, наклонной к его образующим, таким образом,
что в сечении получится круг. Такой конус можно рассматривать
как тело, происходящее от вращения прямоугольного треугольника, вокруг
катета как оси. При этом гипотенуза описывает боковую поверхность, а
катет – основание конуса.
Такой конус можно рассматривать
как тело, происходящее от вращения прямоугольного треугольника, вокруг
катета как оси. При этом гипотенуза описывает боковую поверхность, а
катет – основание конуса.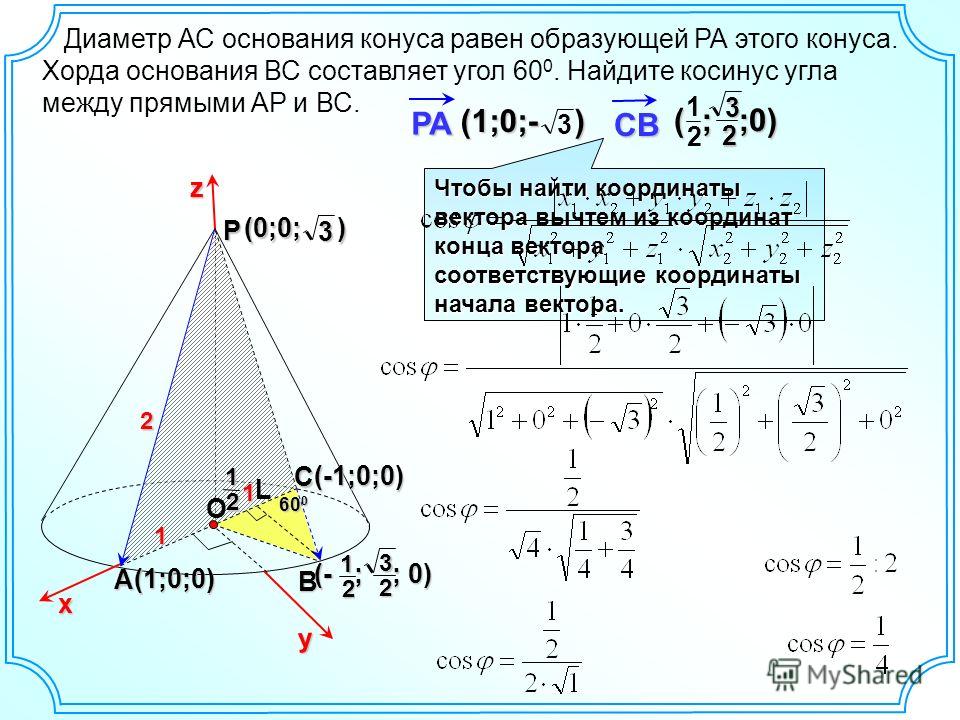 Так, уравнением второго порядка x2 = 0
описывается пара совпадающих плоскостей, уравнением x2 = 1 –
пара параллельных плоскостей, уравнением x2 – y2 = 0 – пара пересекающихся
плоскостей. Уравнение x2 + y2 + z2 = 0
описывает точку с координатами (0;0;0). Существуют и другие вырожденные случаи.
Полная теория поверхностей второго порядка рассматривается в курсе
аналитической геометрии
Так, уравнением второго порядка x2 = 0
описывается пара совпадающих плоскостей, уравнением x2 = 1 –
пара параллельных плоскостей, уравнением x2 – y2 = 0 – пара пересекающихся
плоскостей. Уравнение x2 + y2 + z2 = 0
описывает точку с координатами (0;0;0). Существуют и другие вырожденные случаи.
Полная теория поверхностей второго порядка рассматривается в курсе
аналитической геометрии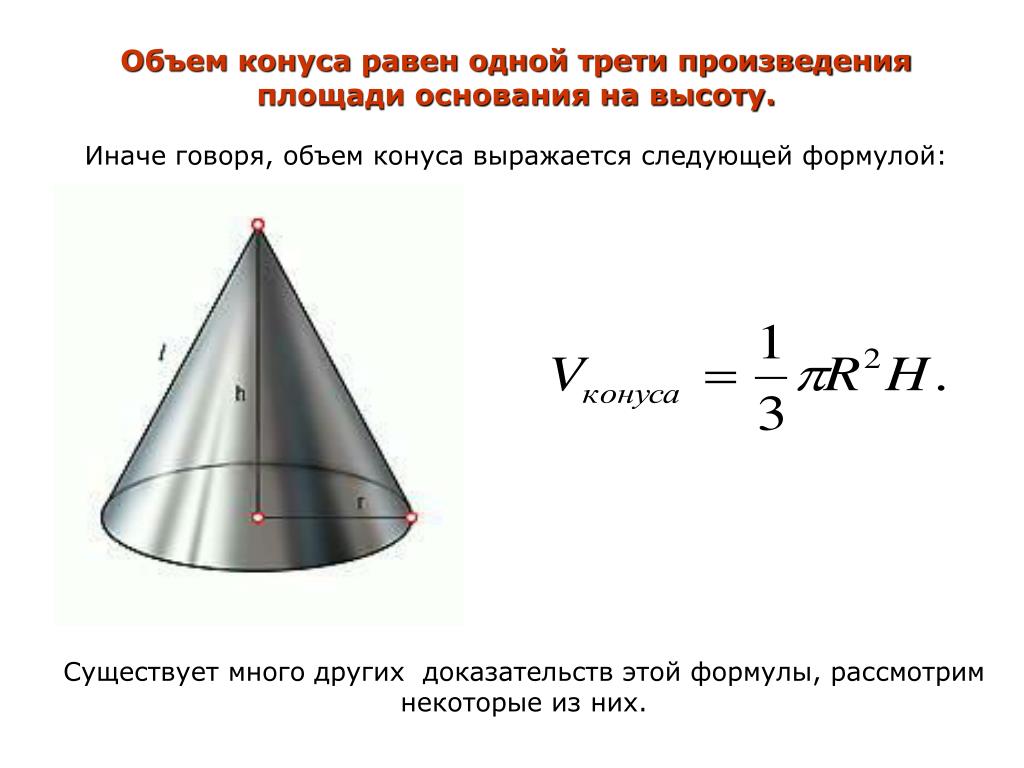 Поверхность, которая в декартовой системе координат определяется уравнением: (12.7)
Поверхность, которая в декартовой системе координат определяется уравнением: (12.7)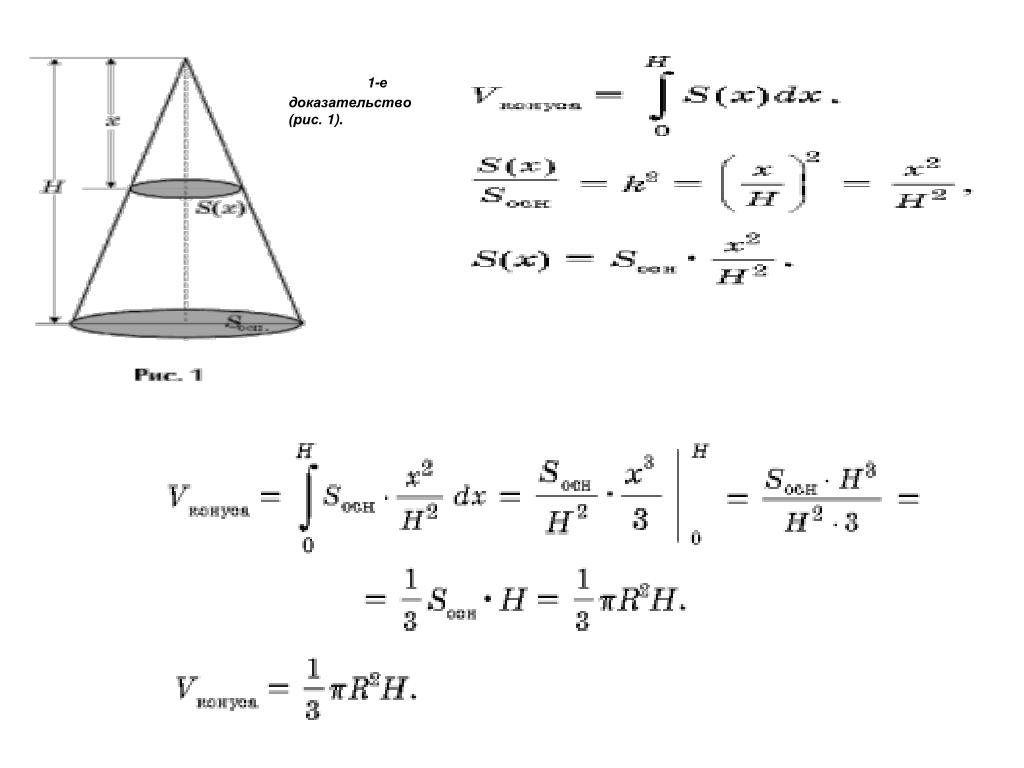
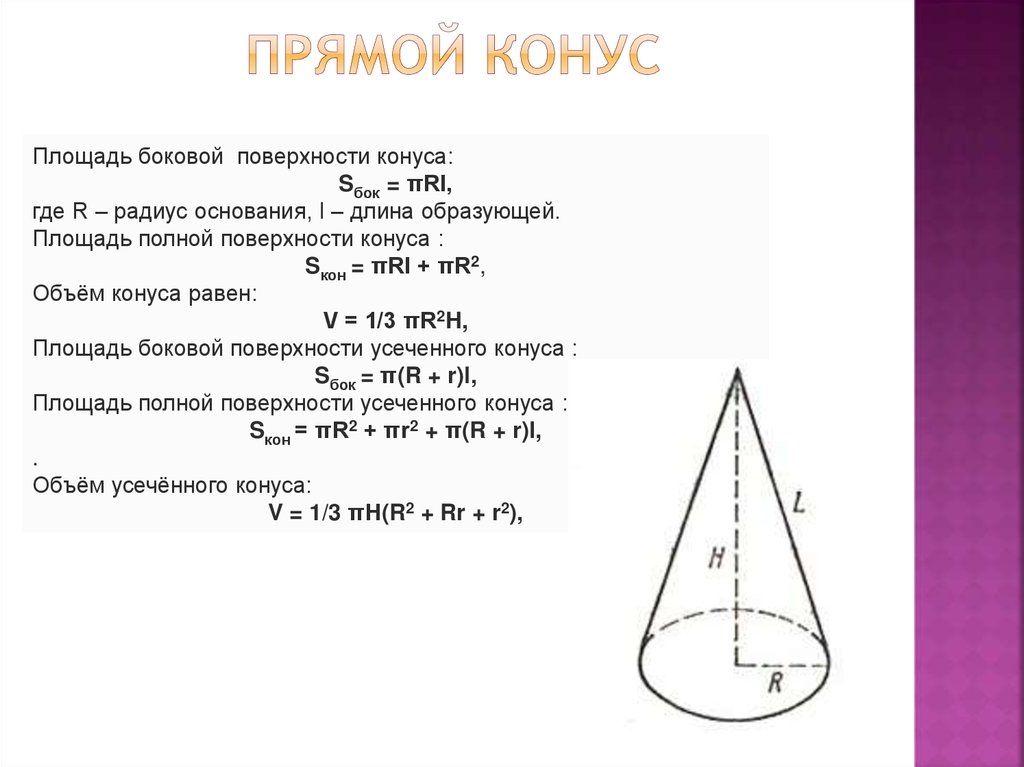 Прямая в пространстве»
Прямая в пространстве»



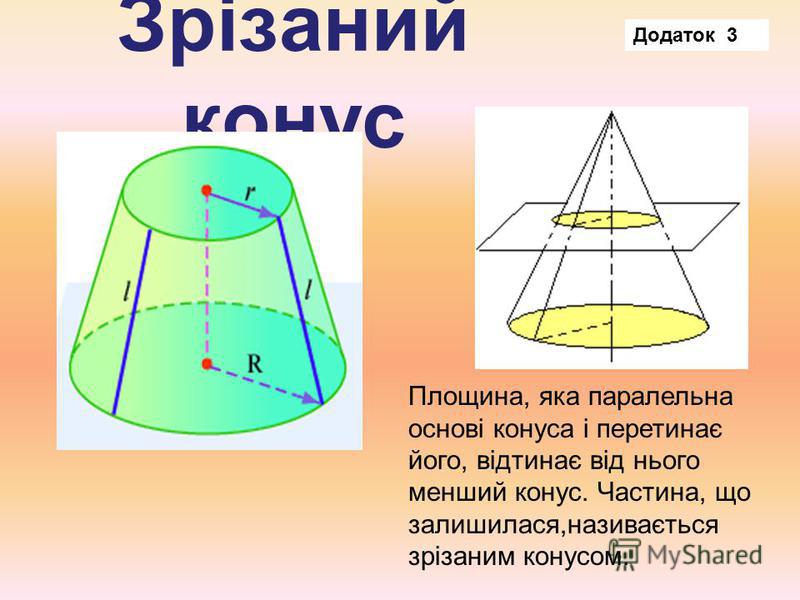
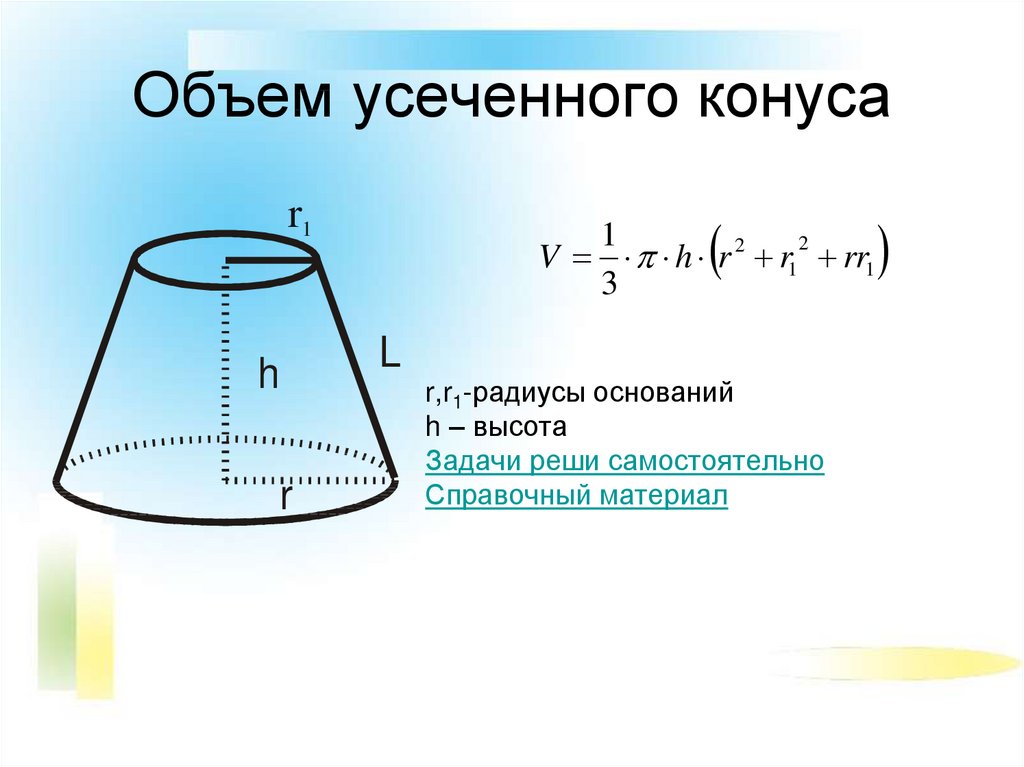
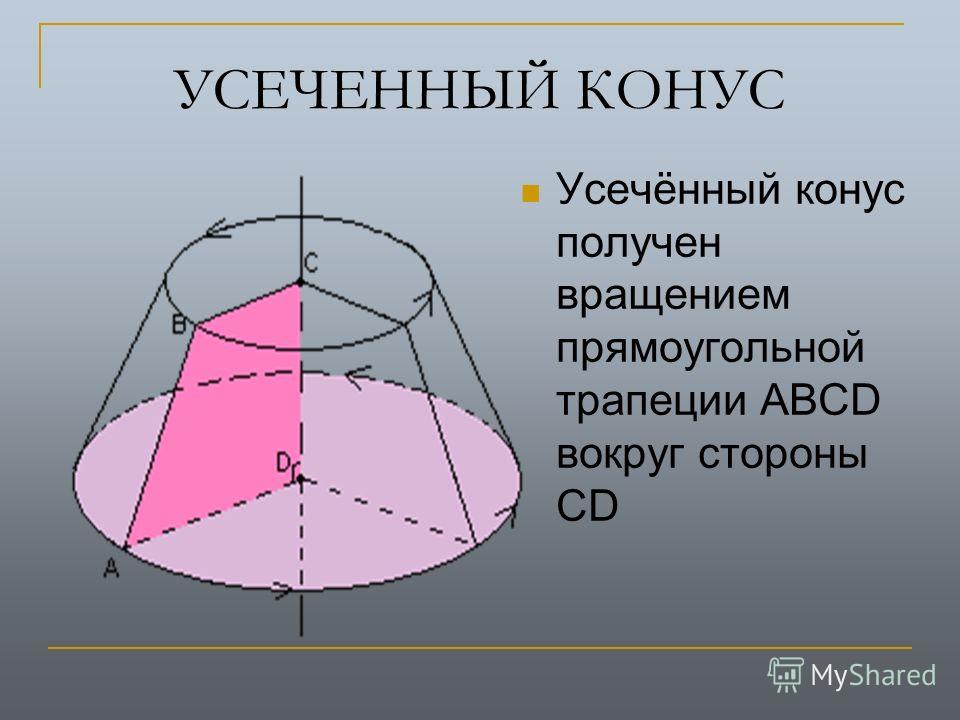
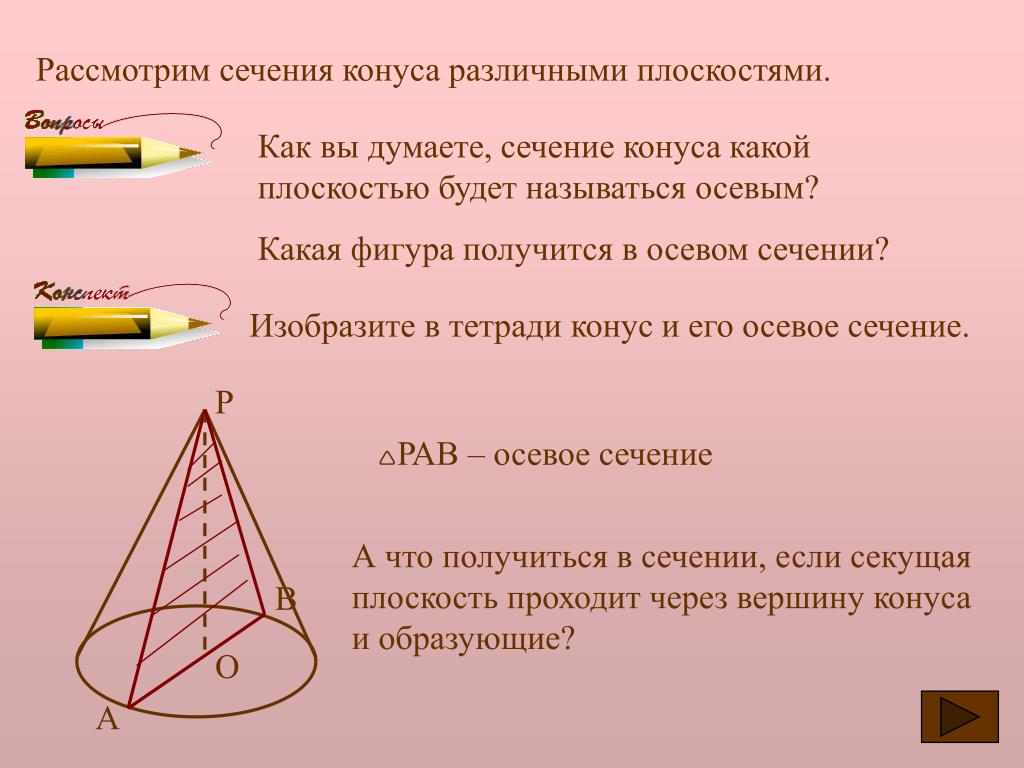 {2}),}
{2}),}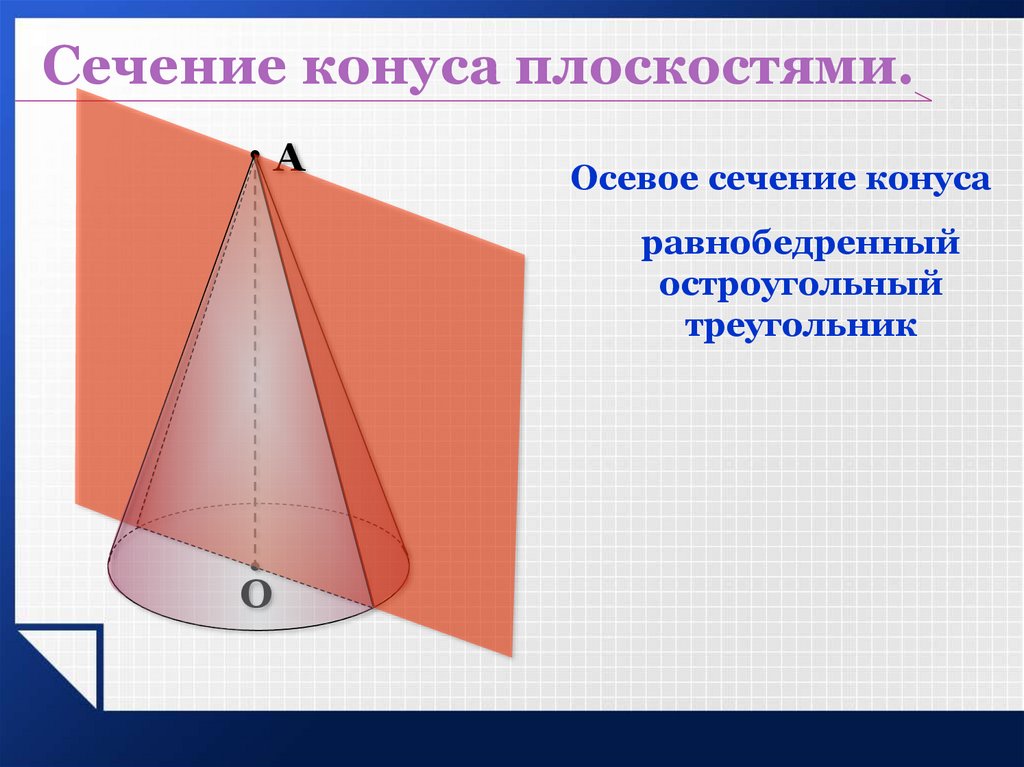 {n}f(x,y,z)} для любого действительного числа α.
{n}f(x,y,z)} для любого действительного числа α.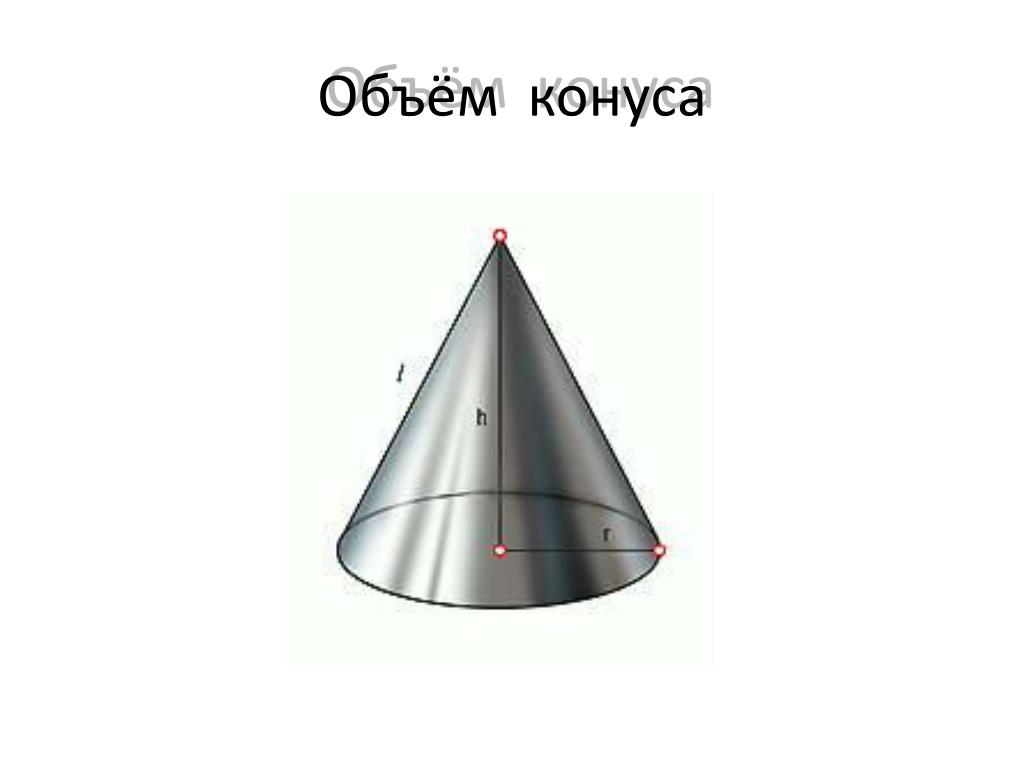
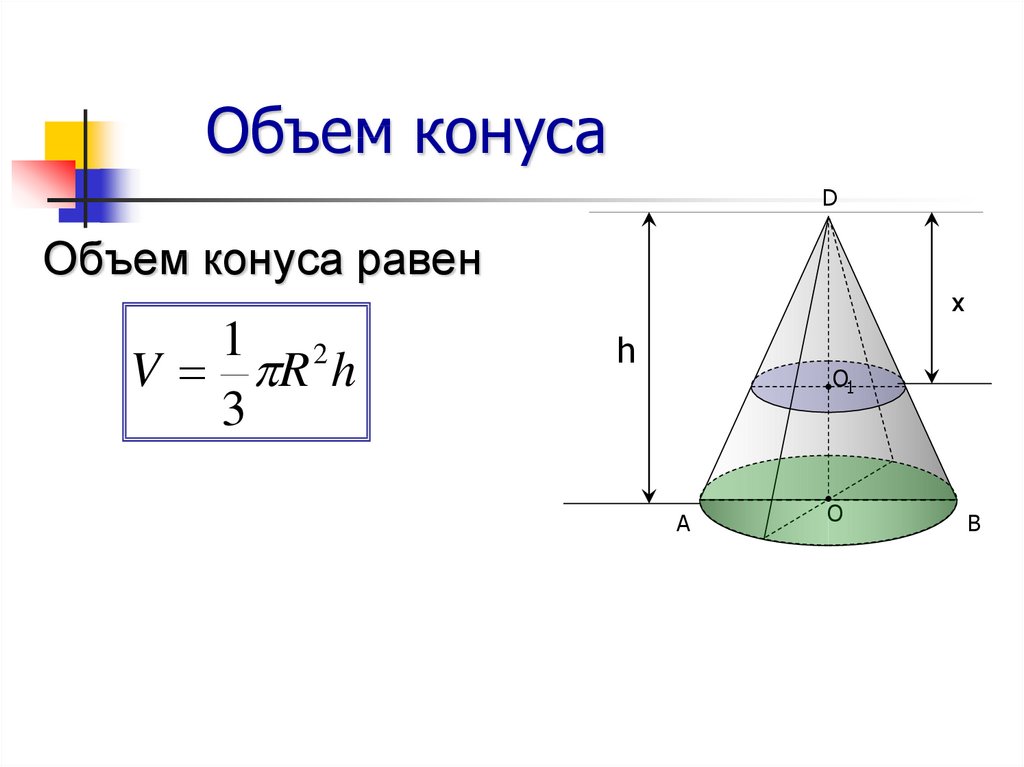 : Советская энциклопедия, 1988. — С. . — 847 с.
: Советская энциклопедия, 1988. — С. . — 847 с.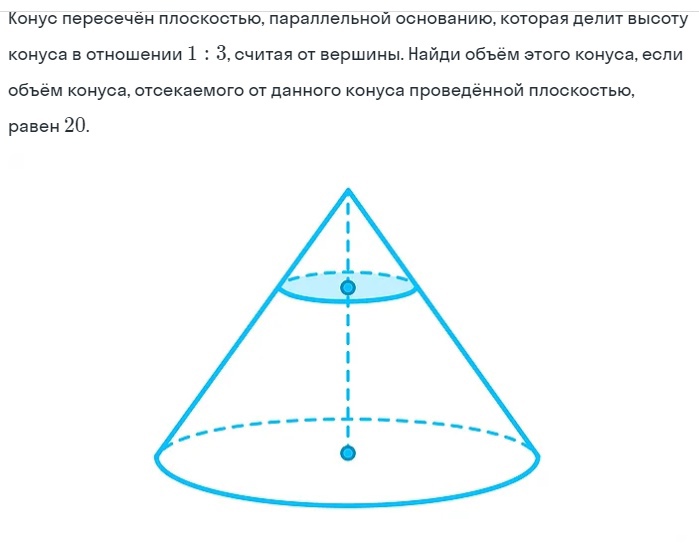 1, а II — стандартный интервал [0,1][0,1]. Тогда декартово произведение X×IX \times I действительно является цилиндром, и конус XX также является конусом.
1, а II — стандартный интервал [0,1][0,1]. Тогда декартово произведение X×IX \times I действительно является цилиндром, и конус XX также является конусом.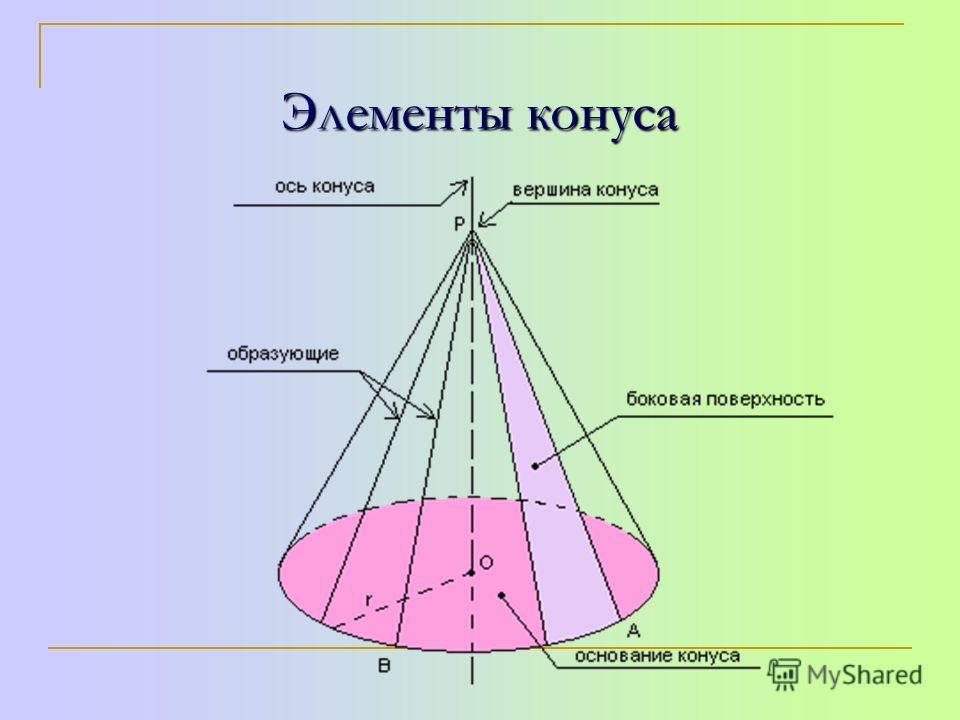 Коконус в этом смысле, который является универсальным, является копределом. Однако следует помнить, что в гомотопической теории слово кокон используется для обозначения другой дуализации.
Коконус в этом смысле, который является универсальным, является копределом. Однако следует помнить, что в гомотопической теории слово кокон используется для обозначения другой дуализации.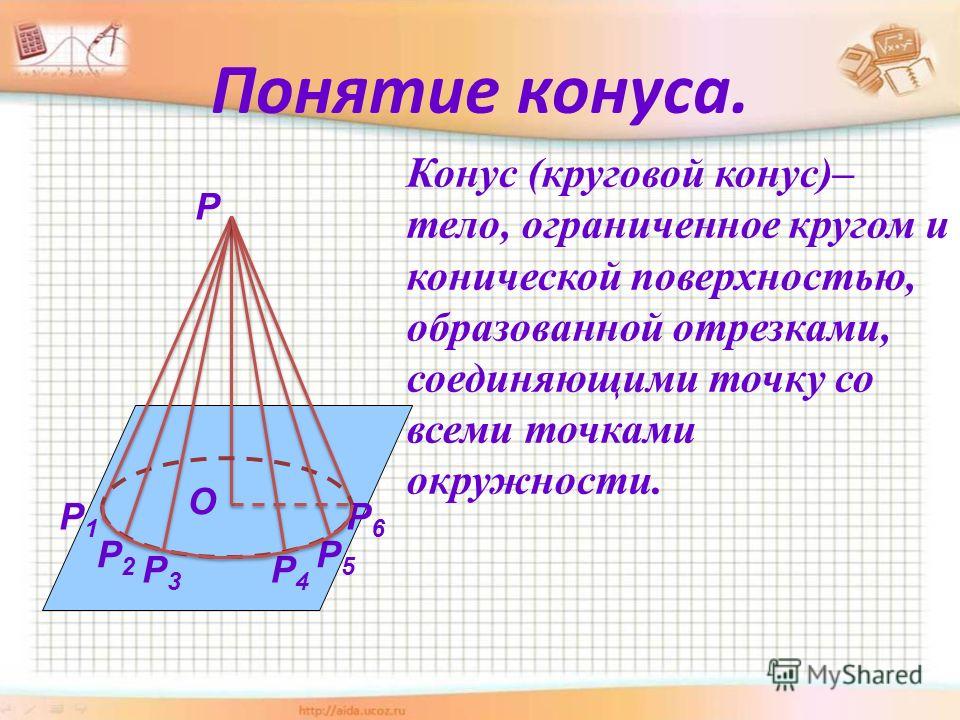
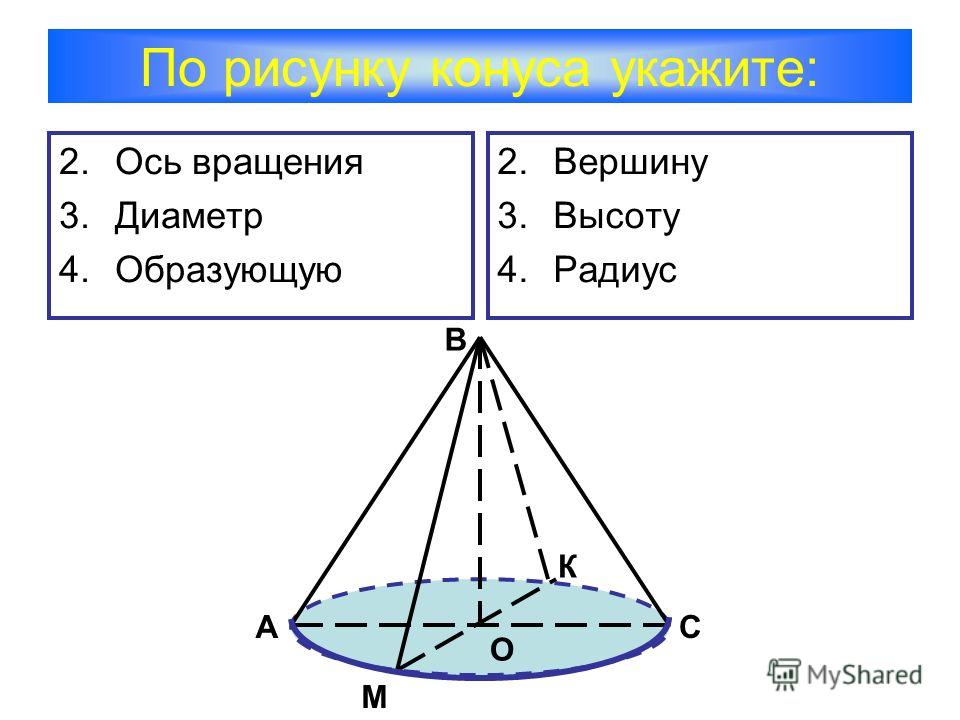 I & \stackrel{eval_0}{\to} & X.
}
I & \stackrel{eval_0}{\to} & X.
} По универсальному свойству категории козапятой, чтобы дать такой функтор должен дать объект cc из CC, функтор F:J→CF \colon J \to C и естественное преобразование
По универсальному свойству категории козапятой, чтобы дать такой функтор должен дать объект cc из CC, функтор F:J→CF \colon J \to C и естественное преобразование

 высота h цилиндра — это перпендикулярное расстояние между этими основаниями, а радиус r цилиндра — это просто радиус круглых оснований.
высота h цилиндра — это перпендикулярное расстояние между этими основаниями, а радиус r цилиндра — это просто радиус круглых оснований. Если основания не находятся прямо друг над другом, у нас есть косой цилиндр . Основания по-прежнему параллельны, но стороны как бы «наклоняются» под углом, отличным от 90°.
Если основания не находятся прямо друг над другом, у нас есть косой цилиндр . Основания по-прежнему параллельны, но стороны как бы «наклоняются» под углом, отличным от 90°. Вы можете попробовать это сами, например, сняв этикетку с банки с едой.
Вы можете попробовать это сами, например, сняв этикетку с банки с едой.
 Представьте себе, что нарисован цилиндр вокруг конуса с тем же основанием и высотой — это называется описанным цилиндром . Теперь конус будет занимать в точности объем цилиндра:
Представьте себе, что нарисован цилиндр вокруг конуса с тем же основанием и высотой — это называется описанным цилиндром . Теперь конус будет занимать в точности объем цилиндра: Как и прежде, мы можем распутать конус в свою сеть. Переместите ползунок, чтобы увидеть, что произойдет: в этом случае мы получим один кружок и один .
Как и прежде, мы можем распутать конус в свою сеть. Переместите ползунок, чтобы увидеть, что произойдет: в этом случае мы получим один кружок и один .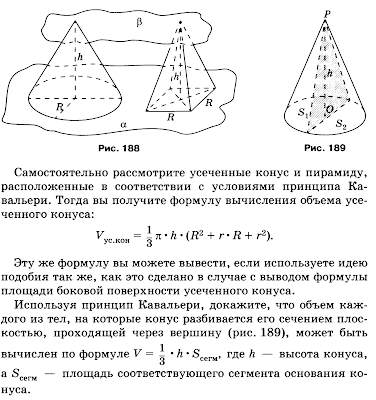 Это расстояние называется радиусом r сферы.
Это расстояние называется радиусом r сферы.

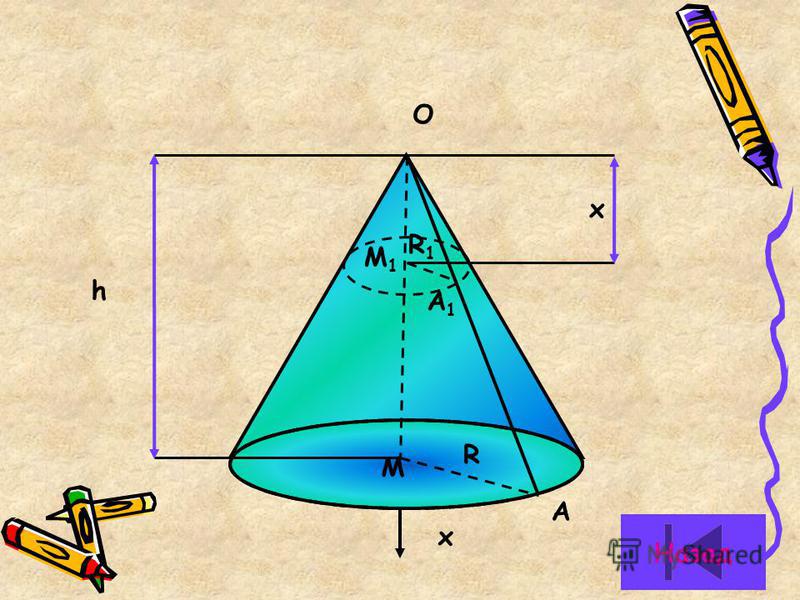 Одна из причин заключается в том, что мы не можем открыть и «сгладить» поверхность сферы, как мы делали раньше для конусов и цилиндров.
Одна из причин заключается в том, что мы не можем открыть и «сгладить» поверхность сферы, как мы делали раньше для конусов и цилиндров.
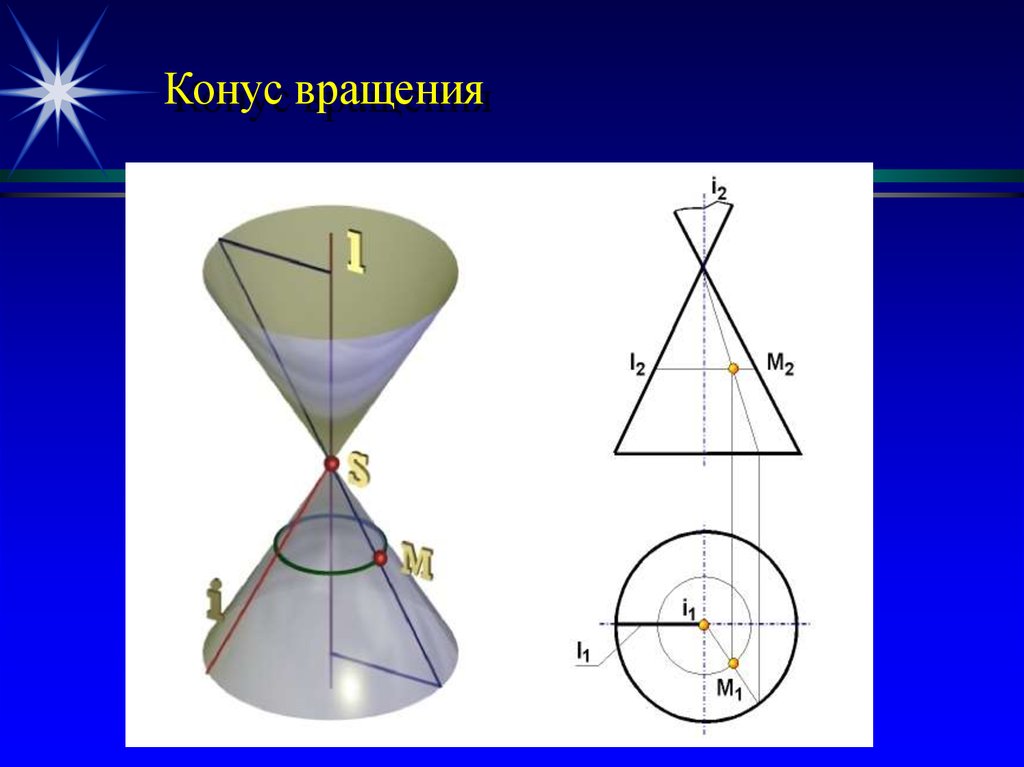 Если вы еще не
заметил, эти движения могут стать довольно сложными
визуализировать. Возьмем простой случай жезла со световым сигналом.
прыгает взад и вперед между его концами.
Если вы еще не
заметил, эти движения могут стать довольно сложными
визуализировать. Возьмем простой случай жезла со световым сигналом.
прыгает взад и вперед между его концами.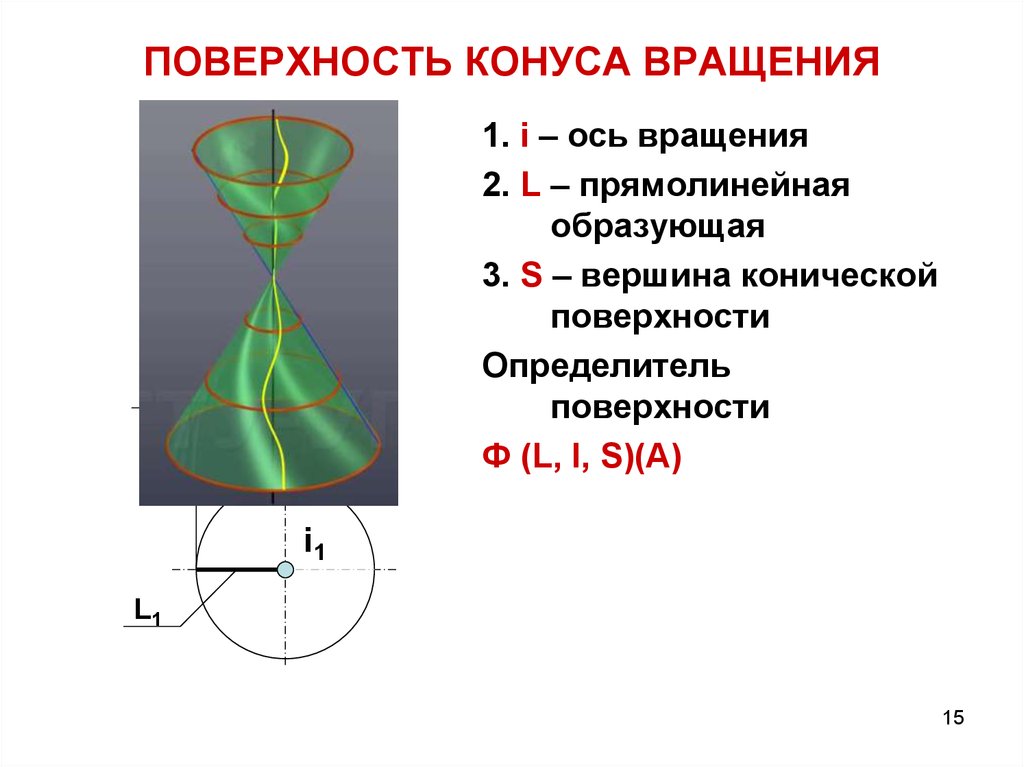 Это было их представление в пространстве-времени.
Довольно загадочные релятивистские эффекты можно понять с помощью
легкость в представлении пространства-времени и работа в теории
теория относительности стала превращаться в работу по геометрии
пространство-время.
Это было их представление в пространстве-времени.
Довольно загадочные релятивистские эффекты можно понять с помощью
легкость в представлении пространства-времени и работа в теории
теория относительности стала превращаться в работу по геометрии
пространство-время. Вертикальная линия сделает это. Если он движется, то
будет пересекать каждое мгновенное пространство в другом месте; а
движущееся тело изображают линией, наклоненной к вертикали.
Вертикальная линия сделает это. Если он движется, то
будет пересекать каждое мгновенное пространство в другом месте; а
движущееся тело изображают линией, наклоненной к вертикали. 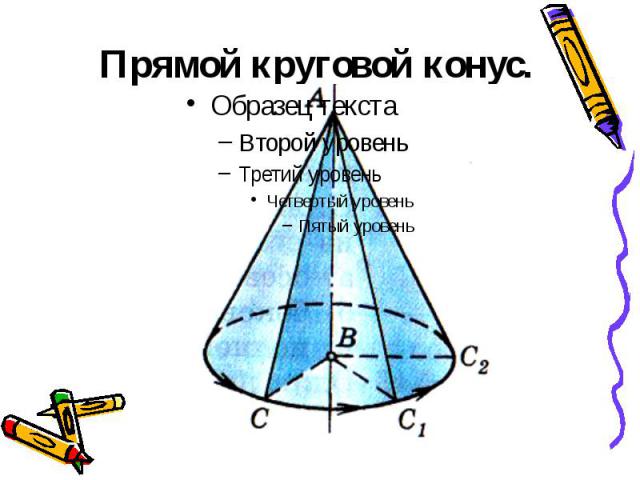 Делайте снимки земли
вращается вокруг Солнца в трехмерном пространстве вокруг Солнца в
течение года, которое будет иметь вид:
Делайте снимки земли
вращается вокруг Солнца в трехмерном пространстве вокруг Солнца в
течение года, которое будет иметь вид: Визуализация
это может быть очень тяжело. Но это не делает его загадочным.
Это просто другой вид пространства, которое выходит за рамки простого
визуализация. В физике четыре измерения на самом деле довольно
скромный. В статистической механике мы обычно имеем дело с фазой
места в 6 раз больше числа молекул в пробе газа. Даже для небольших
пробы газа, которые могут достигать 10 25 —место с
10000000000000000000000000 размеров. Так что мы не должны слишком бояться
математическим пространством всего с четырьмя измерениями!
Визуализация
это может быть очень тяжело. Но это не делает его загадочным.
Это просто другой вид пространства, которое выходит за рамки простого
визуализация. В физике четыре измерения на самом деле довольно
скромный. В статистической механике мы обычно имеем дело с фазой
места в 6 раз больше числа молекул в пробе газа. Даже для небольших
пробы газа, которые могут достигать 10 25 —место с
10000000000000000000000000 размеров. Так что мы не должны слишком бояться
математическим пространством всего с четырьмя измерениями!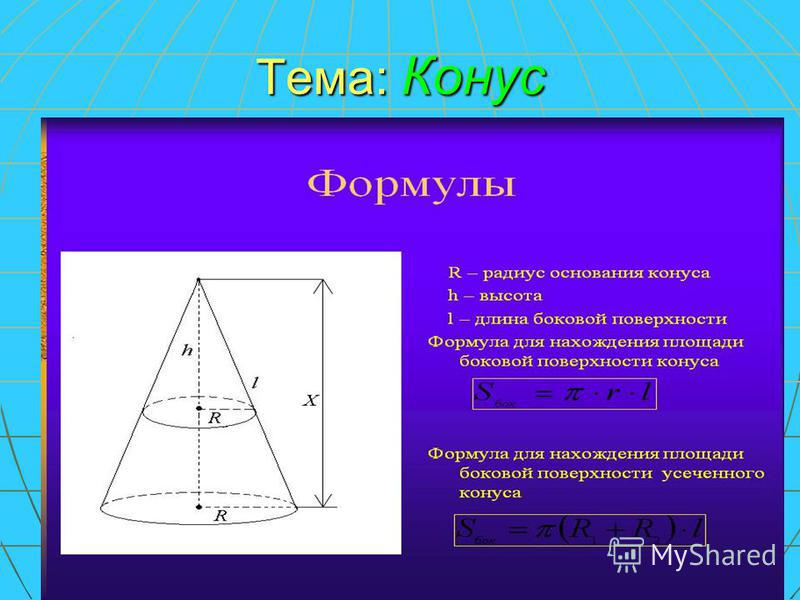
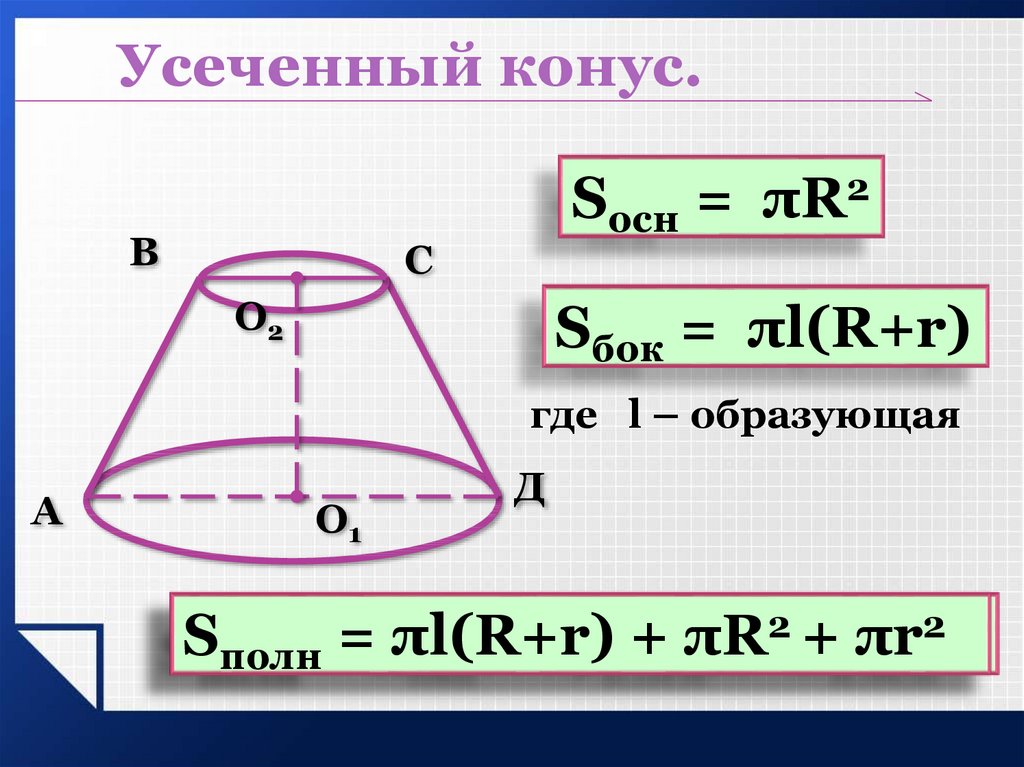 Каждый
пересечение конуса с пространством будет окружностью.
Каждый
пересечение конуса с пространством будет окружностью. в распространении через это событие. Мы могли бы выбрать
любое событие в пространстве-времени. Мы бы нашли световые конусы в
каждый из них. Это означает, что пространство-время полностью заполнено
легкие конусы. Он есть на каждом мероприятии.
в распространении через это событие. Мы могли бы выбрать
любое событие в пространстве-времени. Мы бы нашли световые конусы в
каждый из них. Это означает, что пространство-время полностью заполнено
легкие конусы. Он есть на каждом мероприятии. (Примечание
на потом: когда мы посмотрим на общую теорию относительности, мы встретимся
пространства-времени, которые являются релятивистскими, но не пространства-времени Минковского.)
(Примечание
на потом: когда мы посмотрим на общую теорию относительности, мы встретимся
пространства-времени, которые являются релятивистскими, но не пространства-времени Минковского.)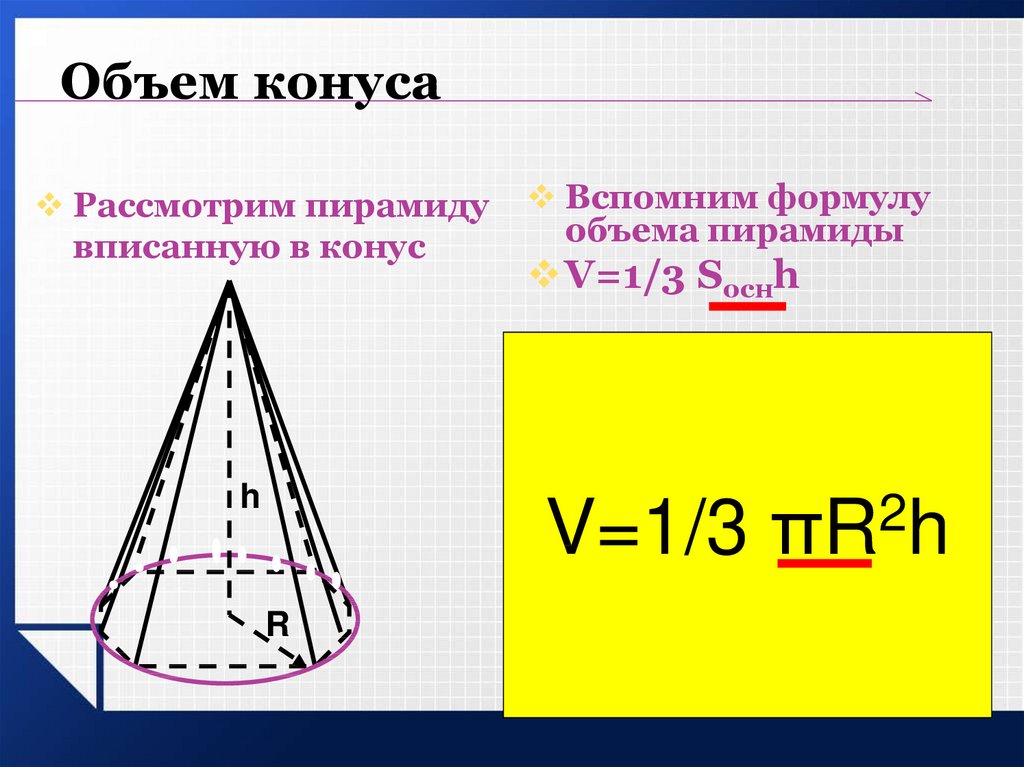
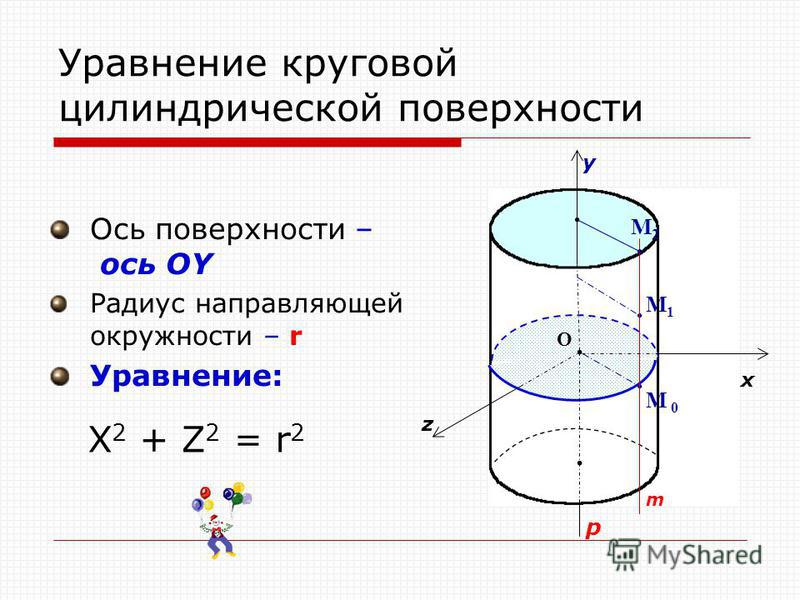 Они есть
прямые линии, лежащие внутри светового конуса. Этот технический термин
«геодезический» будет объяснен позже.
Они есть
прямые линии, лежащие внутри светового конуса. Этот технический термин
«геодезический» будет объяснен позже.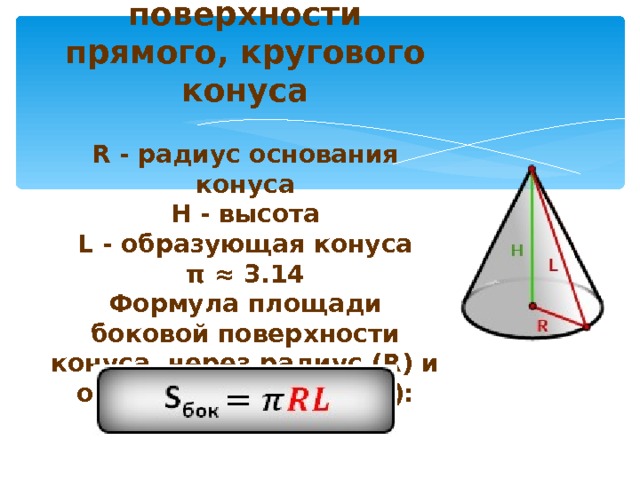 Это
раскрывает его самую основную географию.
Это
раскрывает его самую основную географию.
 То есть его события «пространственноподобны
отделены» от O.
То есть его события «пространственноподобны
отделены» от O.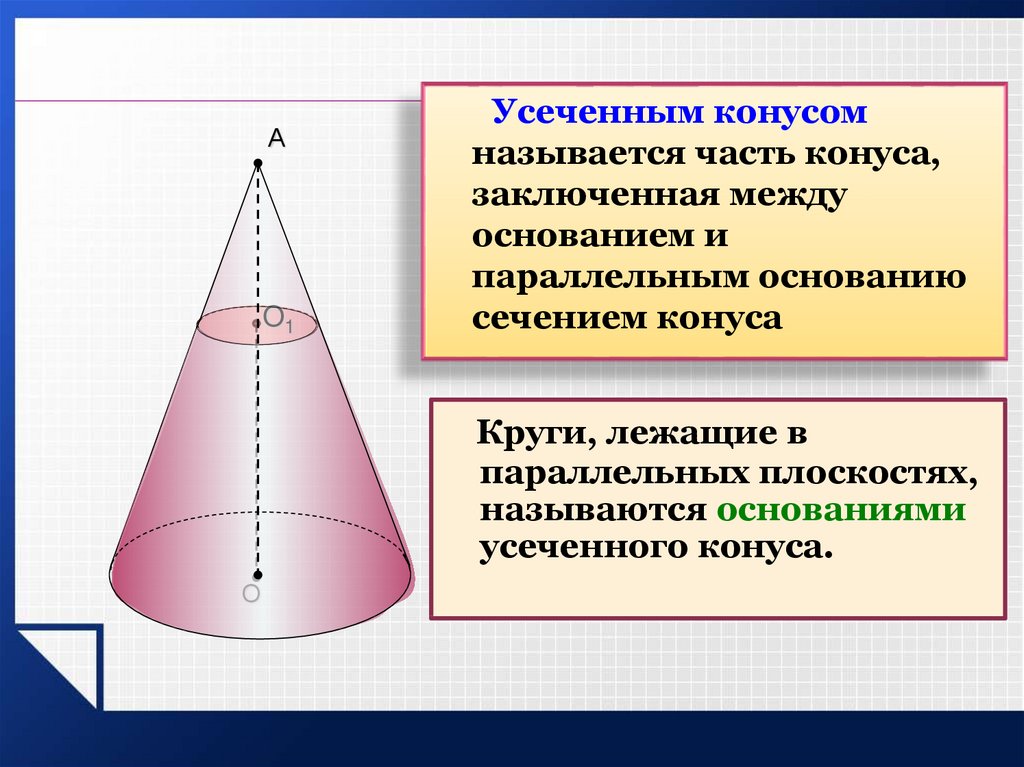

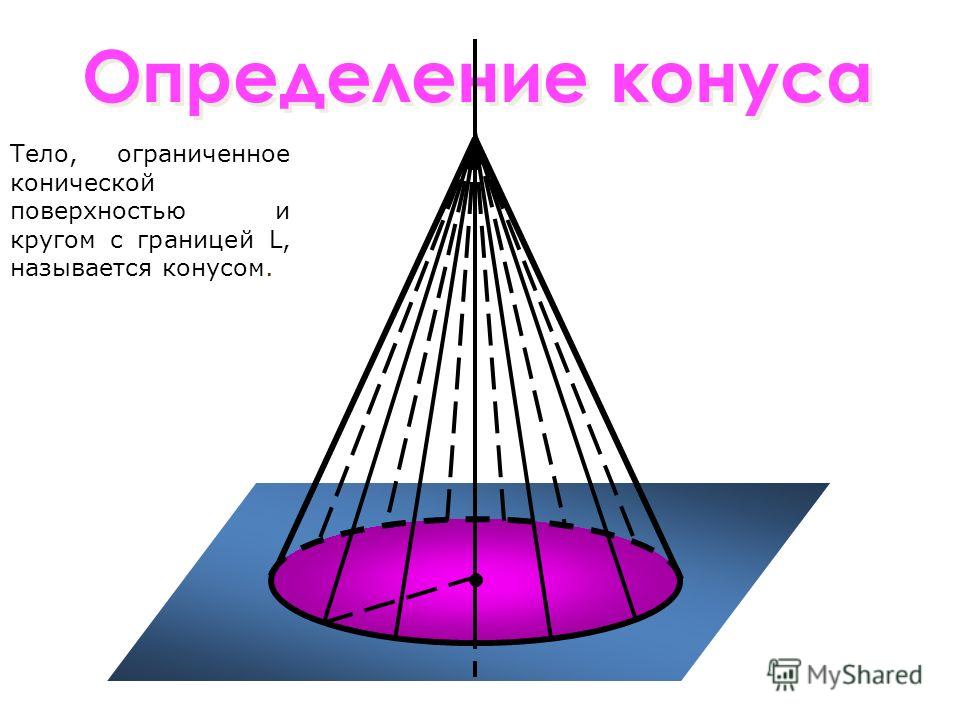 В Минковски
пространство-время, есть три типа расстояния, вместе известные как «интервал»
или «пространственно-временной интервал».
В Минковски
пространство-время, есть три типа расстояния, вместе известные как «интервал»
или «пространственно-временной интервал».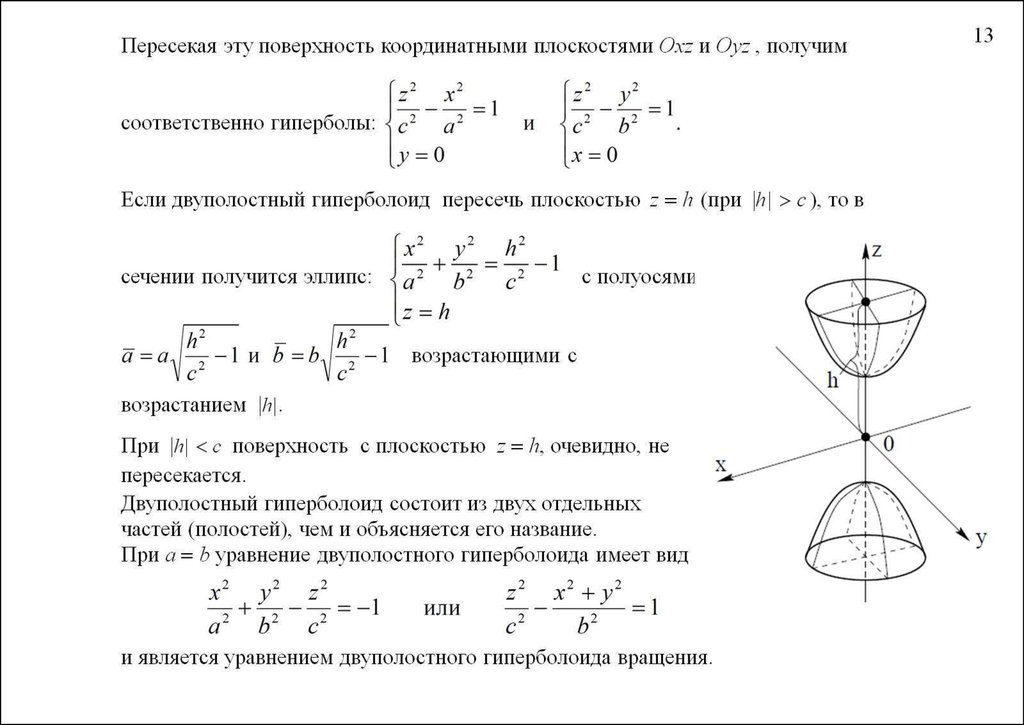 Время читается на часах
дает нам пространственно-временной интервал между двумя событиями. Его также называют
«подходящее время.»
Время читается на часах
дает нам пространственно-временной интервал между двумя событиями. Его также называют
«подходящее время.» Это гиперболы,
приближаться к световому конусу сколь угодно близко.
Это гиперболы,
приближаться к световому конусу сколь угодно близко.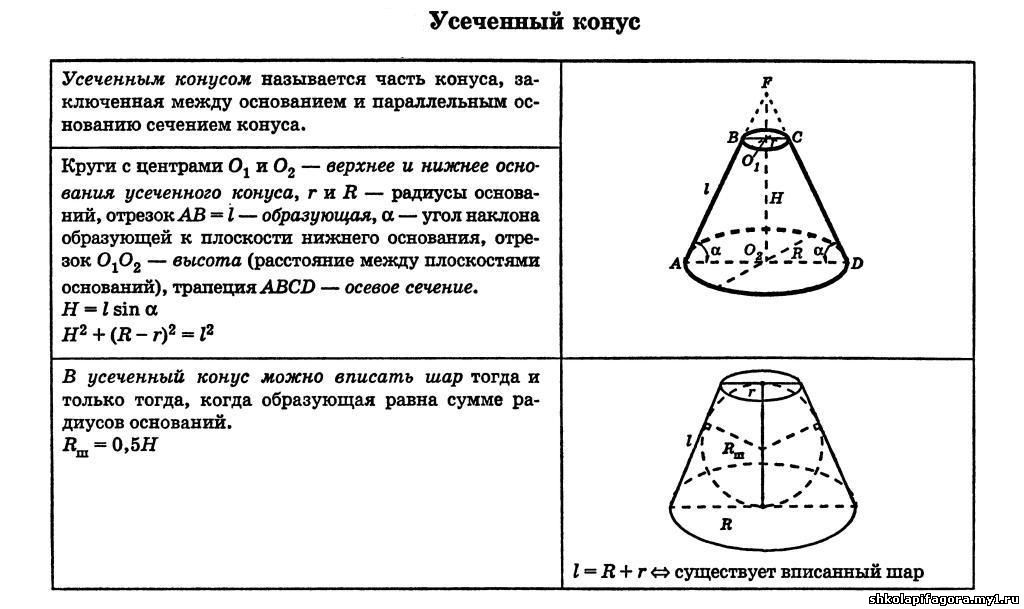
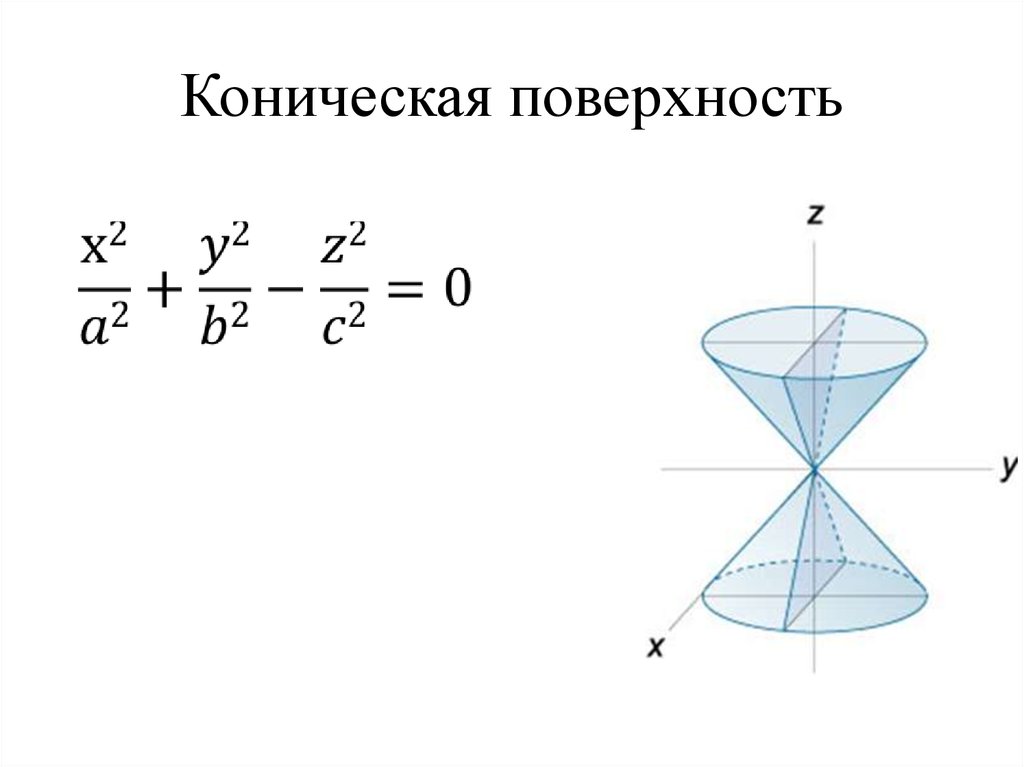 теория. Вот как они появились у Минковского.
оригинальные публикации.
теория. Вот как они появились у Минковского.
оригинальные публикации.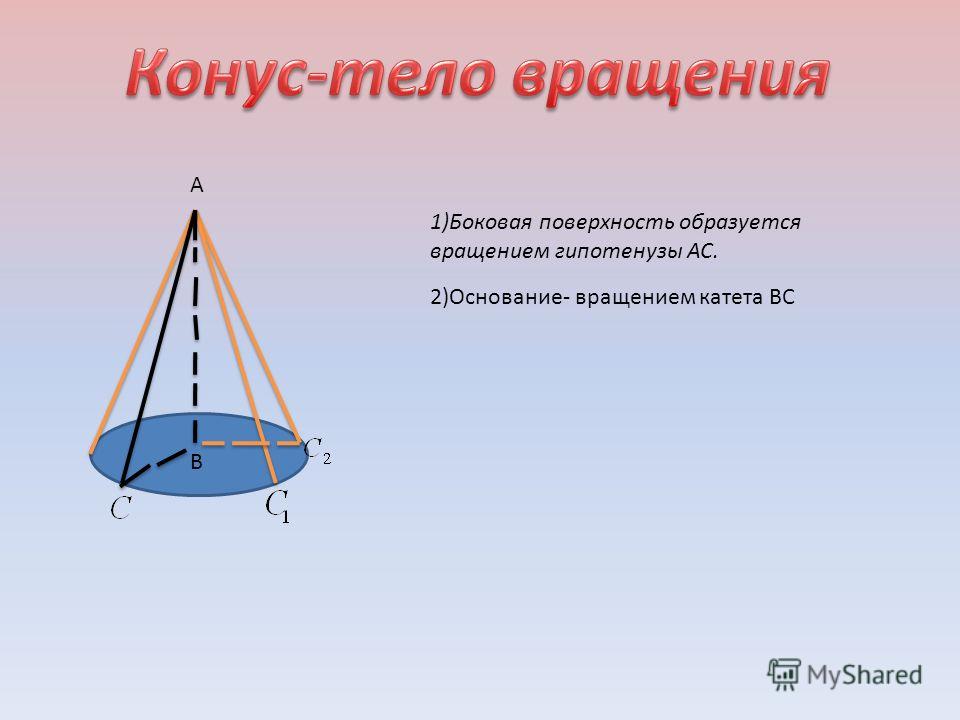 0003
0003 более эффективно. Таким образом,
более эффективно. Таким образом,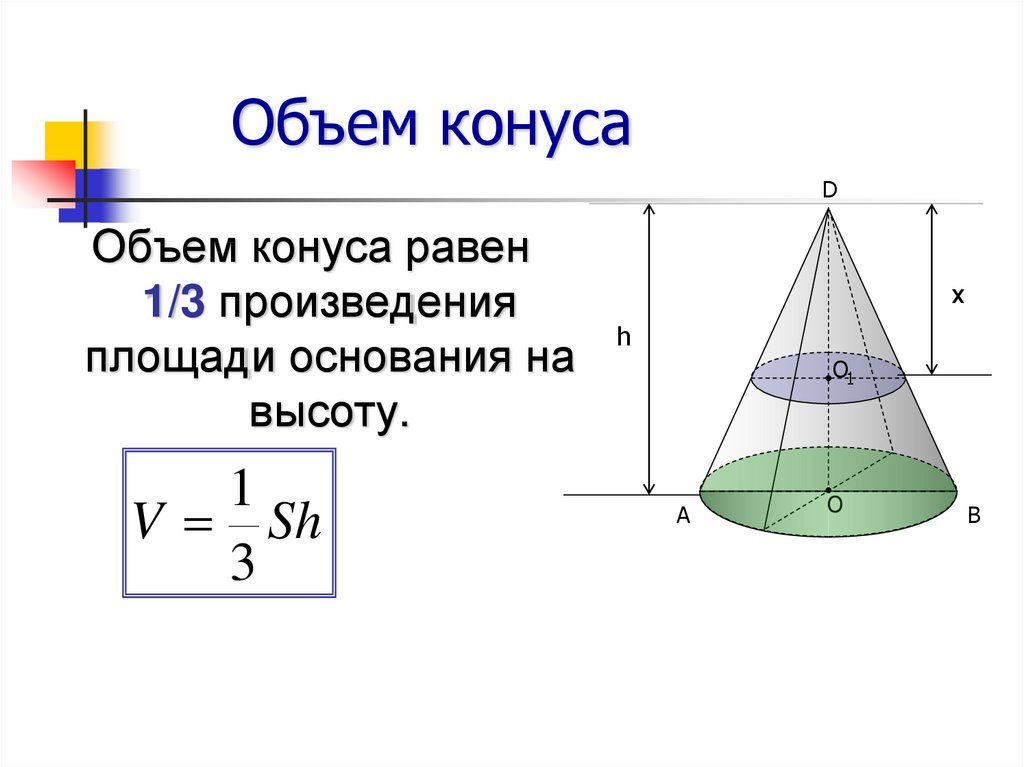 2.9.0952 [4]
2.9.0952 [4]  Затем мы можем спроецировать на XYZ (или куда-либо еще в этом отношении) совершенно точно, применив соответствующую матрицу — без каких-либо штрафов, предполагая, что используется математика с плавающей запятой, что в наши дни в основном и происходит.
Затем мы можем спроецировать на XYZ (или куда-либо еще в этом отношении) совершенно точно, применив соответствующую матрицу — без каких-либо штрафов, предполагая, что используется математика с плавающей запятой, что в наши дни в основном и происходит.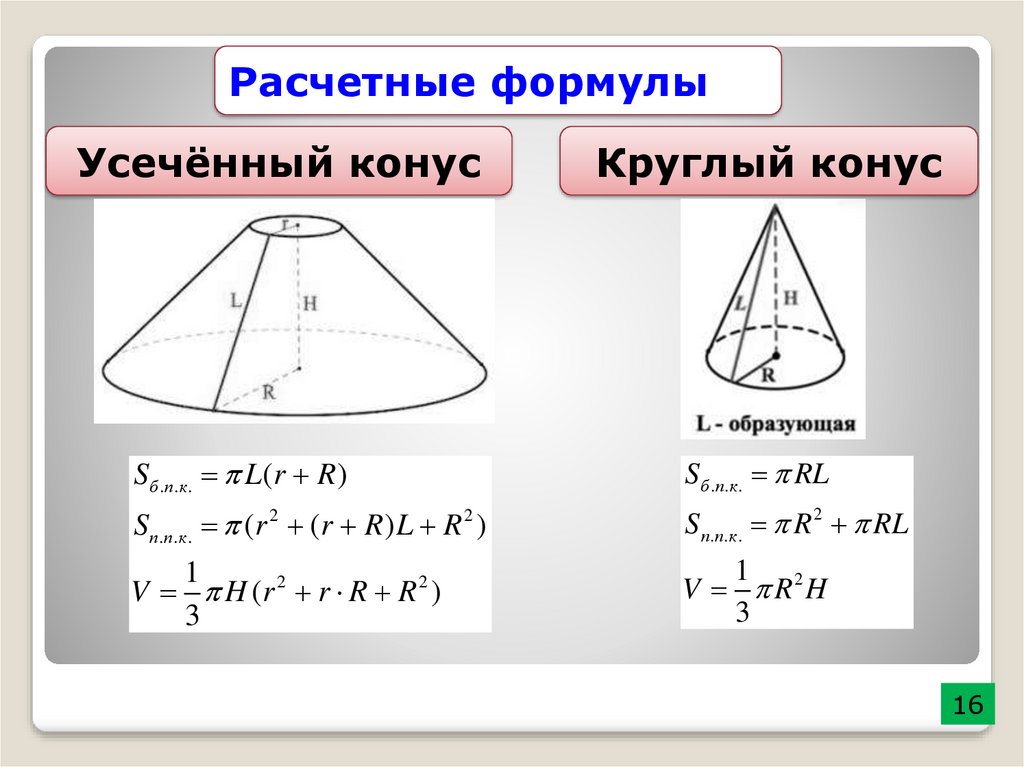 Второй этап выполняется нейронами, которые кодируют сигнал, пропорциональный количеству фотонов, в противоположные цветовые каналы, которые затем передаются в мозг по нервным волокнам. Из «Измерение цвета, четвертое издание, Wiley, 2011» Р. В. Г. Ханта, М. Р. Пойнтера.
Второй этап выполняется нейронами, которые кодируют сигнал, пропорциональный количеству фотонов, в противоположные цветовые каналы, которые затем передаются в мозг по нервным волокнам. Из «Измерение цвета, четвертое издание, Wiley, 2011» Р. В. Г. Ханта, М. Р. Пойнтера.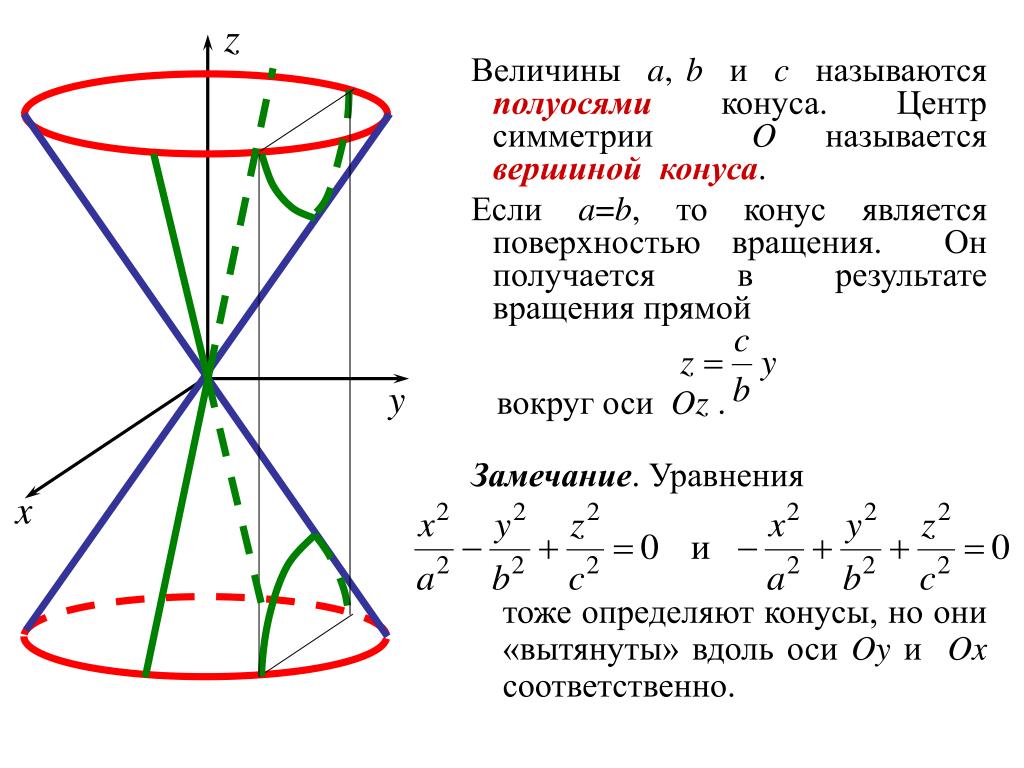 То, что мы пока не смогли удовлетворительно определить, — это относительная матрица проекции 3 × 3, о которой выше — лишь одно из последних и лучших предположений. Это означает, что «основы конуса» и «LMS» могут быть немного неправильными названиями кривых и пространства, показанных на рисунке 2, и более подходящим может быть более общее пространство «отклик HVS» и «HVS».
То, что мы пока не смогли удовлетворительно определить, — это относительная матрица проекции 3 × 3, о которой выше — лишь одно из последних и лучших предположений. Это означает, что «основы конуса» и «LMS» могут быть немного неправильными названиями кривых и пространства, показанных на рисунке 2, и более подходящим может быть более общее пространство «отклик HVS» и «HVS».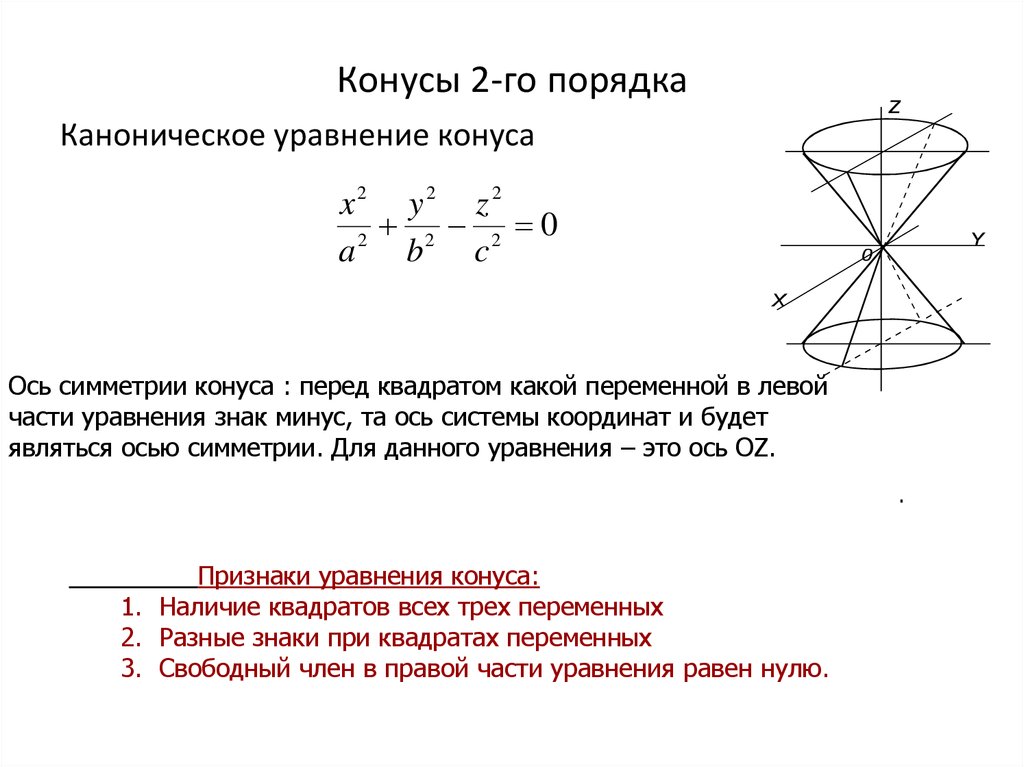
 Преобразование Брэдфорда предполагает, что хроматическая адаптация к доминирующему источнику света в зрительной системе человека происходит не на стадии обнаружения как есть, на колбочках, а после некоторого сужения относительных ответов. По этой причине его иногда называют спектрально «заостренным» преобразованием.
Преобразование Брэдфорда предполагает, что хроматическая адаптация к доминирующему источнику света в зрительной системе человека происходит не на стадии обнаружения как есть, на колбочках, а после некоторого сужения относительных ответов. По этой причине его иногда называют спектрально «заостренным» преобразованием.
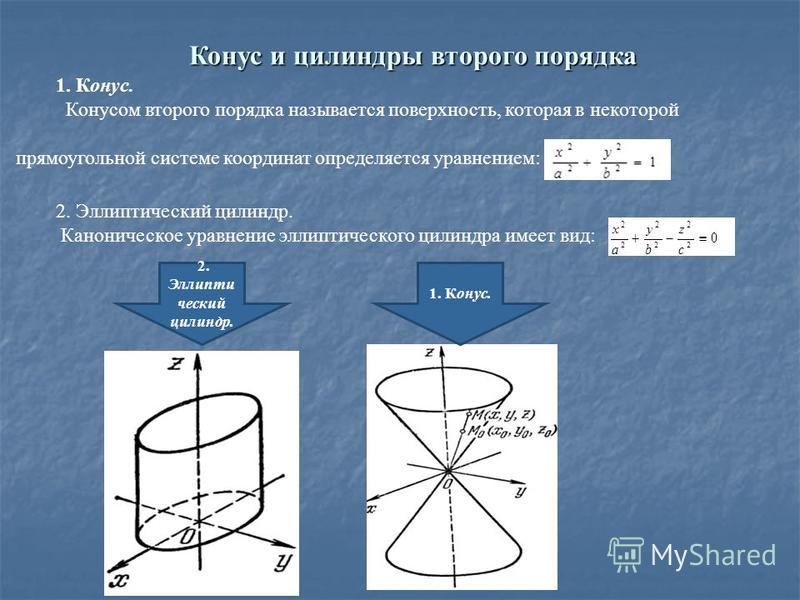
 {n + 1}$ аннулируется $\mathcal{I}$, эта градуированная алгебра соответствует квазикогерентному пучку градуированных $\mathcal {0}_Z$-алгебры морфизмами пространств, лемма 66.14.1. Эта квазикогерентная градуированная $\mathcal{O}_ Z$-алгебра называется 9*(\mathcal{C}_{Z/X}) \longrightarrow \mathcal{C}_{Z/X, *} \end{уравнение}
{n + 1}$ аннулируется $\mathcal{I}$, эта градуированная алгебра соответствует квазикогерентному пучку градуированных $\mathcal {0}_Z$-алгебры морфизмами пространств, лемма 66.14.1. Эта квазикогерентная градуированная $\mathcal{O}_ Z$-алгебра называется 9*(\mathcal{C}_{Z/X}) \longrightarrow \mathcal{C}_{Z/X, *} \end{уравнение} Заменив $X$ на $U$ и $X’$ на $U’$, мы можем считать, что $i$ и $i’$ — замкнутые погружения. Пусть $\mathcal{I}’ \subset \mathcal{O}_{X’}$ и $\mathcal{I} \subset \mathcal{O}_ X$ — квазикогерентные пучки идеалов, ассоциированные с $i ‘$ и $i$, см. Морфизмы пространств, лемма 66.13.1. Рассмотрим состав
9*\mathcal{C}_{Z’/X’, *} \to \mathcal{C}_{Z/X, *}$ из леммы 75.6.3 сюръективно. Если $g$ плоский, то это изоморфизм.
Заменив $X$ на $U$ и $X’$ на $U’$, мы можем считать, что $i$ и $i’$ — замкнутые погружения. Пусть $\mathcal{I}’ \subset \mathcal{O}_{X’}$ и $\mathcal{I} \subset \mathcal{O}_ X$ — квазикогерентные пучки идеалов, ассоциированные с $i ‘$ и $i$, см. Морфизмы пространств, лемма 66.13.1. Рассмотрим состав
9*\mathcal{C}_{Z’/X’, *} \to \mathcal{C}_{Z/X, *}$ из леммы 75.6.3 сюръективно. Если $g$ плоский, то это изоморфизм.