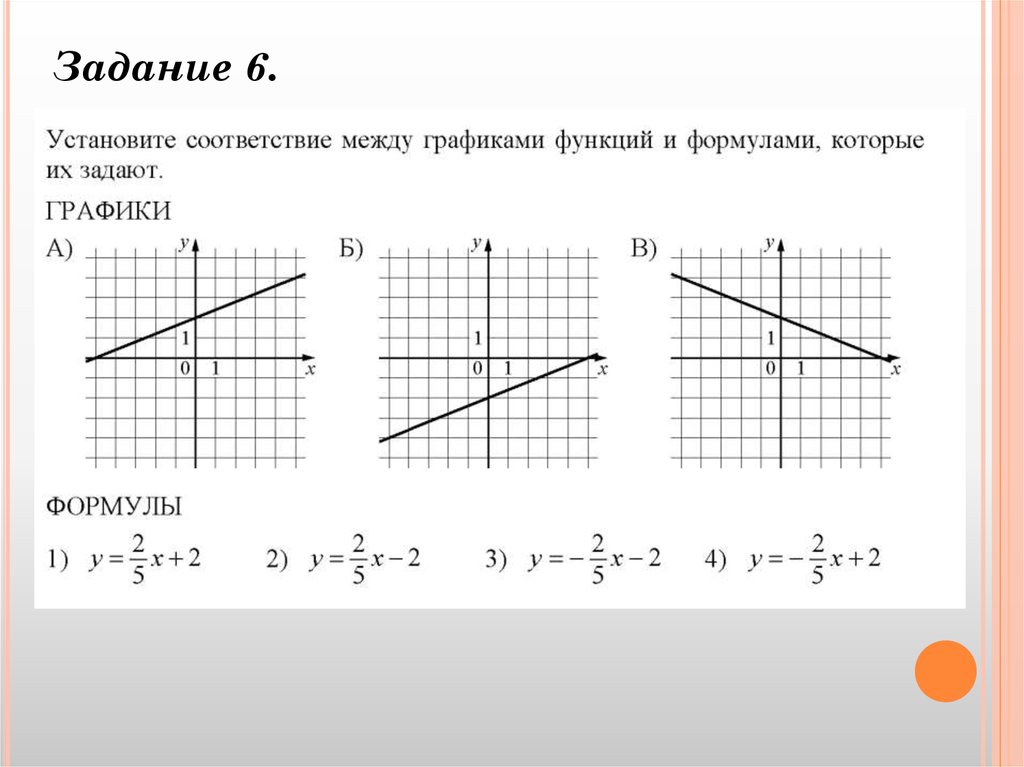
Взаимное расположение графиков линейной функции — что это, определение и ответ
График линейной функции представляет собой прямую. Если на одной координатной прямой существуют две прямые, то они, как и любые прямые на плоскости, могут пересекаться, быть параллельными друг другу или совпадать.
Рассмотрим две линейные функции:
\(y = k_{1}x + b_{1\ }\) и \(y = k_{2}x + b_{2}\)
И их возможные расположения на одной координатной плоскости.
СОВПАДЕНИЕ ГРАФИКОВ ЛИНЕЙНОЙ ФУНКЦИИ:
Графики линейных функций совпадают при:
\(k_{1} = k_{2}\)
\(b_{1} = b_{2}\)
Например:
Графики функций \(y = 3x–2\) и \(y = 3x–2\) совпадают, так как
\(k_{1} = k_{2} = 3\ \) и \(\ b_{1} = b_{2} = \ –2\)
ПАРАЛЛЕЛЬНОСТЬ ГРАФИКОВ ЛИНЕЙНОЙ ФУНКЦИИ:
Графики линейных функций параллельны при:
\(k_{1} = k_{2}\)
\(b_{1} \neq b_{2}\)
Например:
Графики функций \(y = –2x\) и \(y = –2x + 5\) параллельны, так как
\(k_{1} = k_{2} = \ –2\)
\(b_{1} = 0;\ b_{2} = 5 \Longrightarrow b_{1} \neq b_{2}\ \)
ПЕРЕСЕЧЕНИЕ ГРАФИКОВ ЛИНЕЙНОЙ ФУНКЦИИ:
Графики линейных функций пересекаются при:
\(k_{1} \neq k_{2}\ \) и \(\ b_{1} \neq b_{2}\)
Например:
Графики функций \(y = 2x–5\) и\(\ y = \frac{1}{4}x + 2\) пересекаются, так как
\(k_{1} = 2,\ k_{2} = \frac{1}{4} \Longrightarrow k_{1} \neq k_{2}\)
\(и\)
\(b_{1} = \ –5,\ b_{2} = 2 \Longrightarrow b_{1} \neq b_{2}\)
При этом по определению пересекающихся прямых, они должны иметь одну общую точку.
Эта будет такая точка с координатами \((x;\ y)\), которая будет принадлежать как первому, так и второму графику функций.
То есть для функций:
\(y_{1} = k_{1}x_{1} + b_{1}\)
\(y_{2} = k_{2}x_{2} + b_{2}\)
Будут соблюдаться условия:
\(k_{1} \neq k_{2}\ \) и \(\ b_{1} \neq b_{2}\)
Поэтому будет существовать точка пересечения этих графиков с координатами:
\(x = x_{1} = x_{2}\)
\(y = y_{1} = y_{2}\)
В таком случае, чтобы найти точку пересечения графиков функций без построения для функций \(\mathbf{y}_{\mathbf{1}} = k_{1}x = b_{1}\) нужно:
1. Приравнять \(y_{1}\ и\ y_{2},\) а значит приравнять\(\ k_{1}x_{1} + b_{1}\ и\ k_{2}x_{2} + b_{2}.\)
2. Так как \(x_{1} = x_{2} = x\), решим уравнение
\(k_{1}x + b_{1} = k_{2}x + b_{2}.\)
3. Подставить найденный аргумент в любую из функций и найти её значение y. Найденная пара (x; y) будет являться координатой общей точки для данных графиков функций.
Рассмотрим данный алгоритм на примере функций, заданных на графике выше.
Пример №1:
Найти без построений точку пересечения для графиков
\(y = 2x\ –\ 5\ \) и \(\ y = \frac{1}{4}x + 2\)
1. Игреки данных функций равны, следовательно:
\(2x\ –\ 5 = \frac{1}{4}x + 2\)
2. Иксы в данном уравнении равны, значит можем решить уравнение:
\(\frac{7}{4}x = 7\)
\(x = 4\)
3. Подставим x = 4 в первое уравнение, получим:
\(y = 2x\ –\ 5\)
\(y\ = \ 2 \bullet 4\ –\ 5\)
\(y = 3\)
Следовательно, точкой пересечения данных графиков является точка с координатами \((4;3)\), что и подтверждает наш график выше.
ЧАСТНЫЙ СЛУЧАЙ ПЕРЕСЕЧЕНИЯ ЛИНЕЙНЫХ ФУНКЦИЙ
Графики линейных функций пересекаются под прямым углом, если
\(k_{1} \bullet k_{2} = \ –1\)
\(k_{1} = \ –\frac{1}{k_{2}}\)
Например:
Графики функций \(y = 3x–2\) и \(y = \ –\frac{1}{3}x + 1\) перпендикулярны друг дугу, так как
\(k_{1} \bullet k_{2} = 3 \bullet (–\frac{1}{3}) = \ –1\)
ОглавлениеВВЕДЕНИЕЧасть первая. АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА 2. Простые и составные числа. Признаки делимости. 3. Наибольший общий делитель и наименьшее общее кратное.  4. Целые числа. Рациональные числа. 5. Десятичные дроби. Представление рациональных чисел десятичными дробями. 6. Иррациональные числа. Действительные числа. 7. Действия с приближенными числами. 8. Числовая ось. Координаты точки на плоскости. § 2. Степени и корни 9. Степени с натуральными показателями. 10. Степени с целыми показателями. 11. Корни. 12. Степени с рациональными показателями. Степени с действительными показателями. 13. Алгоритм извлечения квадратного корня. § 3. Комплексные числа 14. Основные понятия и определения. 15. Рациональные действия с комплексными числами. 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа. 17. Действия с комплексными числами, заданными в тригонометрической форме. Формула Муавра. 18. Извлечение корня из комплексного числа. Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ 19. Алгебраические выражения. Одночлены и многочлены. 20. Формулы сокращенного умножения.  n.41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени. 42. Показательная функция. 43. Логарифмическая функция. § 3. Преобразование графиков 44. Параллельный сдвиг графика. 45. График квадратного трех члена. 46. График дробно-линейной функции. 47. Преобразование симметрии. Сжатие и растяжение графика. 48. Построение графиков функций. 49. Сложение графиков. § 4. Некоторые сведения о рациональных функциях 50. Целые и дробные рациональные функции. Деление многочленов. 52. Нули многочлена. Разложение многочлена на множители. Глава V. УРАВНЕНИЯ 53. Уравнение. Корни уравнения. 54. Равносильные уравнения. 55. Системы уравнений. 56. Графическое решение уравнений. §. 2. Алгебраические уравнения с одной неизвестной 57. Число и кратность корней. 58. Уравнения первой степени (линейные уравнения). 59. Уравнения второй степени (квадратные уравнения).  60. Формулы Виета. Разложение квадратного трехчлена на множители. 61. Исследование квадратного уравнения. 62. Уравнения высших степеней. Целые корни. 63. Двучленные уравнения. 64. Уравнения, сводящиеся к квадратным. 65. Возвратные уравнения. § 3. Системы алгебраических уравнений 66. Линейные системы. 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными. 68. Системы, состоящие из уравнения второй степени и линейного уравнения. 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней. § 4. Иррациональные, показательные и логарифмические уравнения 70. Иррациональные уравнения. 71. Показательные уравнения. 72. Логарифмические уравнения. 73. Разные уравнения. Системы уравнений. Глава VI. НЕРАВЕНСТВА 74. Свойства неравенств. Действия над неравенствами. 75. Алгебраические неравенства. § 2. Решение неравенств 76. Множество решений неравенства.  Равносильные неравенства.77. Графическое решение неравенств. 79. Квадратные неравенства. 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х. 81. Иррациональные, показательные и логарифмические неравенства. 82. Неравенства с двумя неизвестными. Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ 84. Предел числовой последовательности. 85. Бесконечно малые. Правила предельного перехода. § 2. Арифметическая прогрессия 86. Арифметическая прогрессия. Формула общего члена. 87. Свойства арифметической прогрессии. 88. Формула для суммы n членов арифметической прогрессии. § 3. Геометрическая прогрессия 89. Геометрическая прогрессия. Формула общего члена. 90. Свойства геометрической прогрессии. 91. Формулы для суммы n членов геометрической прогрессии. 92. Бесконечно убывающая геометрическая прогрессия. Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ) 93. Вектор, проекция вектора. 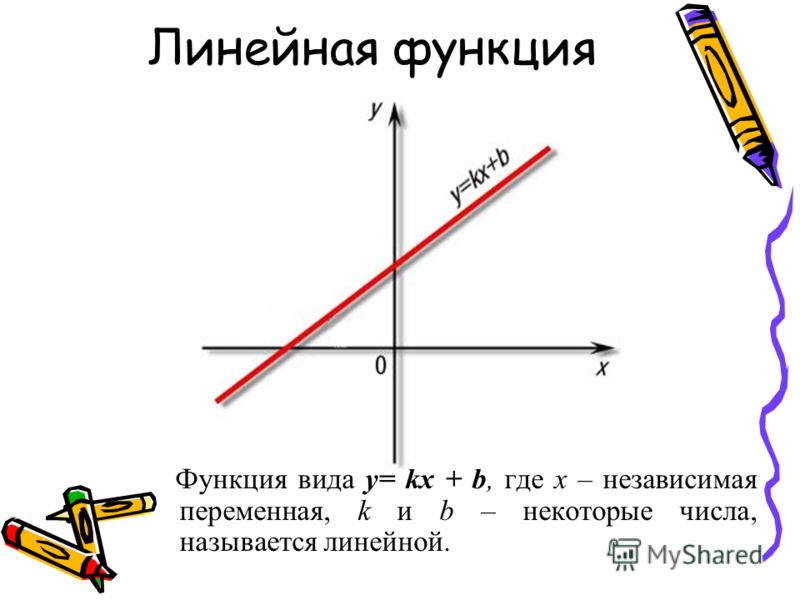 94. Положительные углы и дуги, меньшие 360°. 95. Углы и дуги, большие 360°. 96. Отрицательные углы. Сложение и вычитание углов. § 2. Тригонометрические функции произвольного угла 97. Определение основных тригонометрических функций. 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi. § 3. Соотношения между тригонометрическими функциями одного и того же угла 99. Основные тригонометрические тождества. 100. Вычисление значений тригонометрических функций по значению одной из них. 101. Значения тригонометрических функций некоторых углов. § 4. Четность, нечетность и периодичность тригонометрических функций 102. Четность и нечетность. 103. Понятие периодической функции. 104. Периодичность тригонометрических функций. § 5. Формулы приведения 105. Зависимость между тригонометрическими функциями дополнительных углов. 106. Формулы приведения. Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ § 1.  Тригонометрические функции числового аргумента108. Области определения и области изменения значений тригонометрических функций. § 2. Графики тригонометрических функций 110. Первоначальные сведения о таблицах тригонометрических функций. 111. Основные графики. 112. Примеры построения графиков некоторых других тригонометрических функций. 113. Дальнейшие примеры построения графиков функций. Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ 114. Расстояние между двумя точками на плоскости. 115. Косинус суммы и разности двух аргументов. 116. Синус суммы и разности двух аргументов. 117. Тангенс суммы и разности двух аргументов. 118. О формулах сложения для нескольких аргументов. § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a 119. Тригонометрические функции двойного аргумента. 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n. 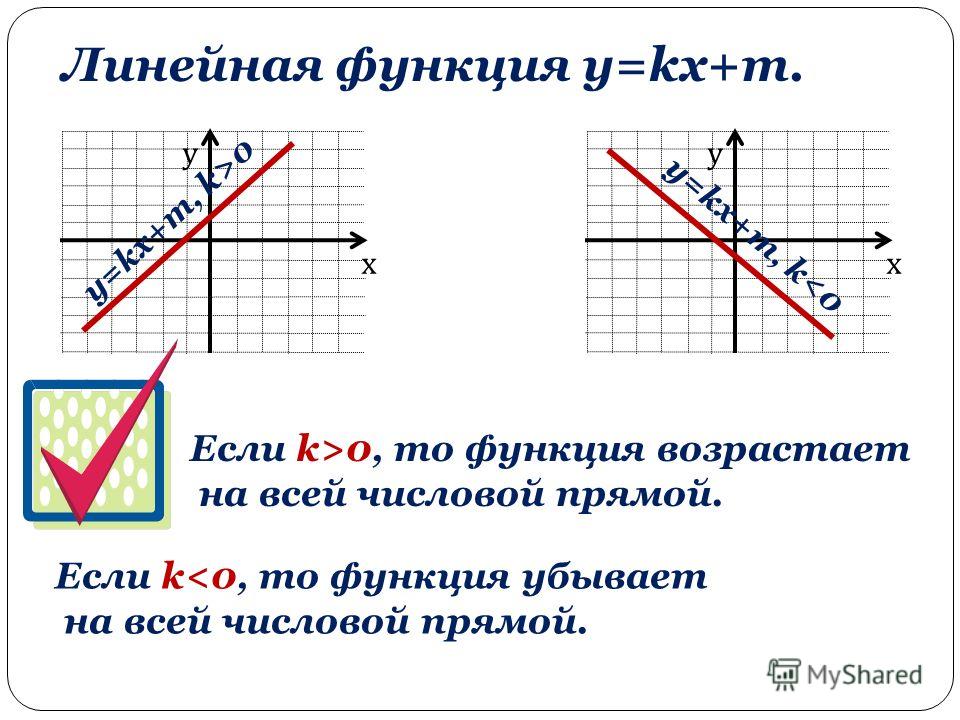 121. Тригонометрические функции половинного аргумента. 122. Выражение основных тригонометрических функций аргумента а через tg(a/2). § 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb § 4. Преобразование в произведение сумм вида § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента 127. Преобразование в произведение выражения a•sina + b•cosa. 128. Преобразование в произведение выражений a•sina+b и a•cosa+b 129. Преобразование в произведение выражения a•tga+b. Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ 130. Функция у = arcsin x (арксинус). 131. Функция y = arccos x (арккосинус). 132. Функция y = arctg x (арктангенс). 133. Функция y = arcctg x (арккотангенс). 134. Пример. § 2. Операции над обратными тригонометрическими функциями 135. Тригонометрические операции. 136. Операции сложения (вычитания). § 3. Обратные тригонометрические операции над тригонометрическими функциями 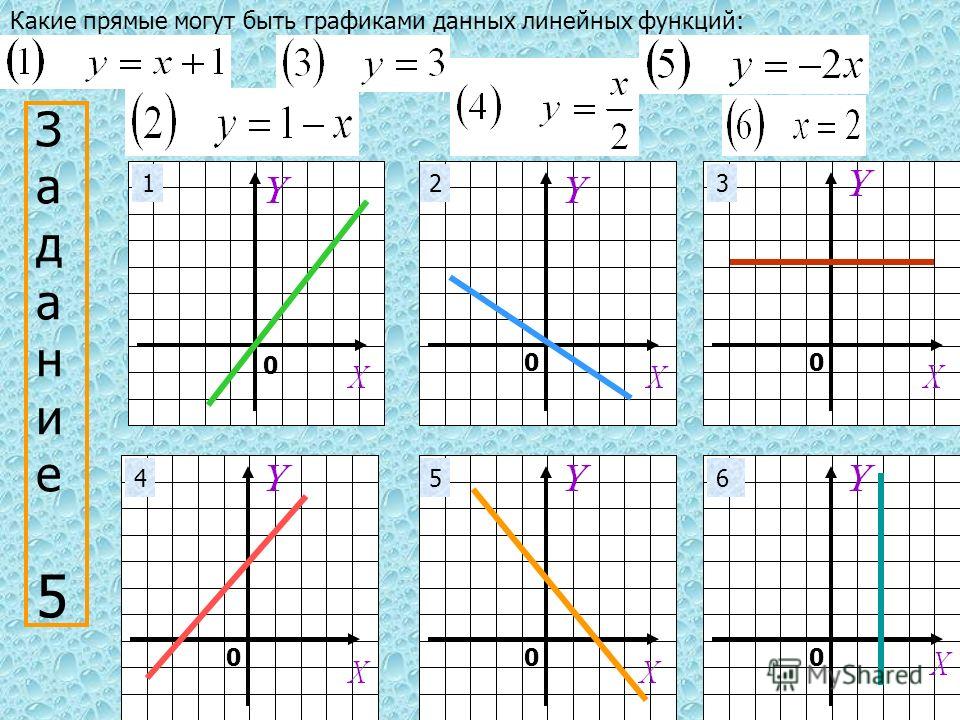 Функция у = arcsin (sin x).138. Функция y = arctg (tg x). Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 139. Уравнение sin х = а. 140. Уравнение cos х = a. 141. Уравнение tg x = a. 142. Уравнение ctg x = a. 143. Некоторые дополнения. § 2. Способ приведения к одной функции одного и того же аргумента 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента. 146. Способ разложения на множители. 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t. § 3. Некоторые частные приемы решения тригонометрических уравнений и систем 148. Введение вспомогательного аргумента. 149. Преобразование произведения в сумму или разность. 150. Переход к функциям удвоенного аргумента. 151. Решение уравнения типа… 152. Применение подстановок sinx ± соsx = y. § 4. Решение тригонометрических неравенств 154. Простейшие тригонометрические неравенства. 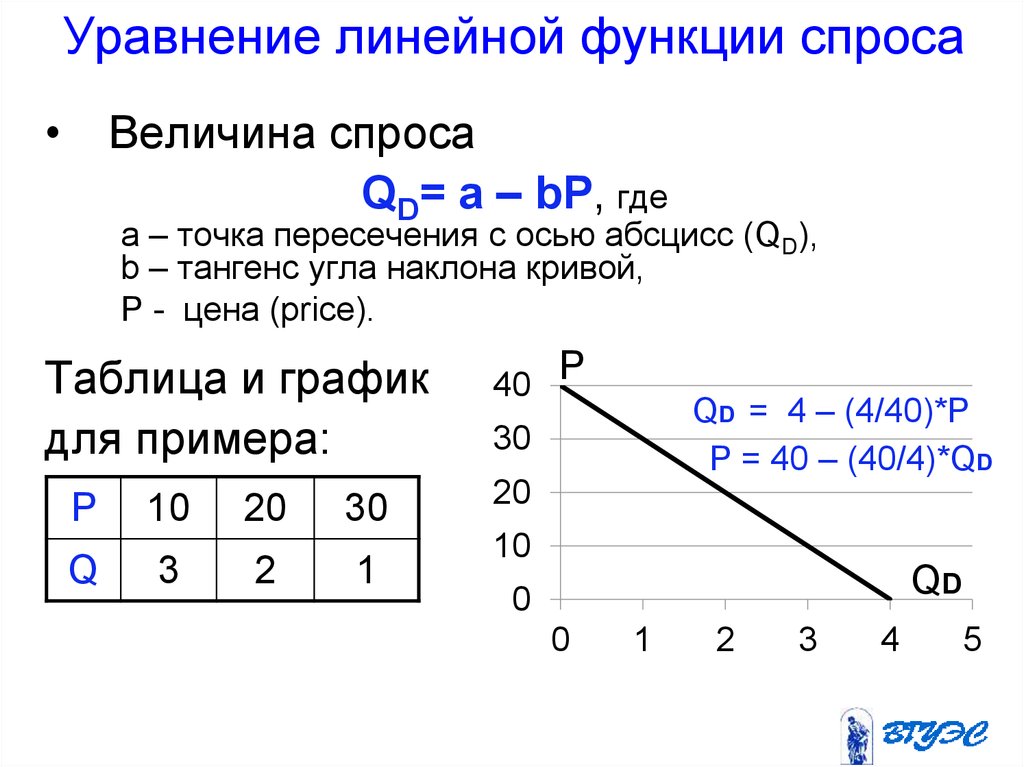 155. Примеры тригонометрических неравенств, сводящихся к простейшим. Часть вторая. ГЕОМЕТРИЯ 156. Точка. Прямая. Луч. Отрезок. 157. Плоскость. Фигуры и тела. 160. Равенство фигур. Движение. 161. Равенство тел. § 2. Измерение геометрических величин 162. Сложение отрезков. Длина отрезка. 163. Общая мера двух отрезков. 164. Сравнительная длина отрезков и ломаных. 165. Измерение углов. 166. Радианная мера угла. 167. Измерение площадей. 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда. Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ 169. Перпендикуляр и наклонные. 170. Свойство перпендикуляра, проведенного к отрезку в его середине. 172. Углы, образованные двумя параллельными прямыми и секущей. 173. Углы с параллельными или перпендикулярными сторонами. § 2. Геометрические места точек. Окружность 174. Геометрическое место точек. 175. Свойство биссектрисы угла. 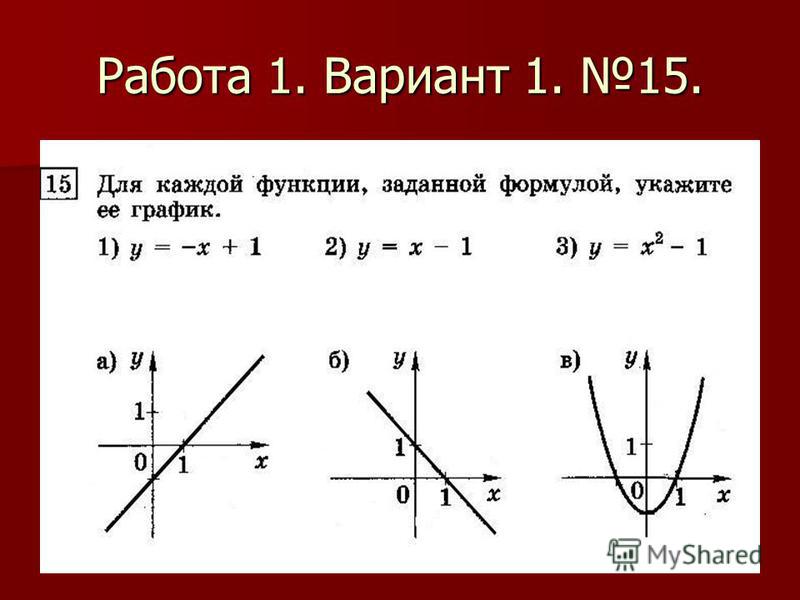 176. Окружность. 177. Взаимное расположение прямой и окружности. Касательная и секущая. 178. Хорда и диаметр. Сектор и сегмент. 179. Взаимное расположение двух окружностей. § 3. Основные задачи на построение 181. Деление отрезка пополам. Построение перпендикуляров. 182. Построение углов. 183. Другие задачи на построение. Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ 184. Стороны и углы треугольника. 185. Биссектрисы треугольника. Вписанная окружность. 186. Оси симметрии сторон треугольника. Описанная окружность. 187. Медианы и выcоты треугольника. 188. Равенство треугольников. 189. Построение треугольников. 190. Равнобедренные треугольники. 191. Прямоугольные треугольники. § 2. Параллелограммы 192. Четырехугольники. 193. Параллелограмм и его свойства. 194. Прямоугольник. § 3. Трапеция 196. Трапеция. 197. Средняя линия треугольника. 198. Средняя линия трапеции. 199. Деление отрезка на равные части.  § 4. Площади треугольников и четырехугольников 200. Площадь параллелограмма. 201. Площадь треугольника. 202. Площадь трапеции. Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР 203. Пропорциональные отрезки. 204. Свойства биссектрис внутреннего и внешнего углов треугольника. § 2. Подобное преобразование фигур (гомотетия) 205. Определение гомотетичных фигур. 206. Свойства преобразования подобия. § 3. Общее подобное соответствие фигур 207. Подобные фигуры. 208. Периметры и площади подобных треугольников. 209. Применение подобия к решению задач на построение. Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ 210. Углы с вершиной на окружности. 211. Углы с вершиной внутри и вне круга. 212. Угол, под которым виден данный отрезок. 213. Четырехугольники, вписанные в окружность. 214. Пропорциональные отрезки в круге. 215. Задачи на построение. § 2. Метрические соотношения в треугольнике 216. Пропорциональные отрезки в прямоугольном треугольнике.  Теорема Пифагора.218. Теорема синусов. Формула Герона. 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов. 218. Теорема синусов. Формула Герона. 219. Радиусы вписанной и описанной окружностей. § 3. Решение треугольников 220. Таблицы функций. 221. Решение треугольников. Сводка основных формул. 222. Решение прямоугольных треугольников. 223. Решение косоугольных треугольников. Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА 224. Выпуклые многоугольники. 225. Правильные многоугольники. 226. Соотношения между стороной, радиусом и апофемой. 227. Периметр и площадь правильного n-угольника. 228. Удвоение числа сторон правильного многоугольника. § 2. Длина окружности. Площадь круга и его частей 229. Длина окружности. 230. Площадь круга и его частей. Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ 231. Взаимное расположение двух прямых в пространстве.  232. Взаимное расположение прямой линии и плоскости. 233. Взаимное расположение двух плоскостей. 234. Свойства параллельных прямых и плоскостей. 235. Построения в стереометрии. § 2. Перпендикулярность прямых и плоскостей 236. Перпендикуляр к плоскости. 237. Перпендикуляр и наклонные. 238. Угол между прямой и плоскостью. 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей. 240. Общий перпендикуляр двух скрещивающихся прямых. § 3. Двугранные и многогранные углы 241. Двугранный угол. 242. Взаимно перпендикулярные плоскости. 243. Трехгранные углы. 244. Многогранные углы. § 4. Многогранники 245. Многогранники. 246. Правильные многогранники. Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА 247. Цилиндры и призмы. 248. Параллелепипеды. 249. Объемы призм и цилиндров. 250. Площадь боковой поверхности призмы. 251. Площадь поверхности цилиндра. § 2. Пирамида. Конус 252. Свойства пирамиды и конуса. 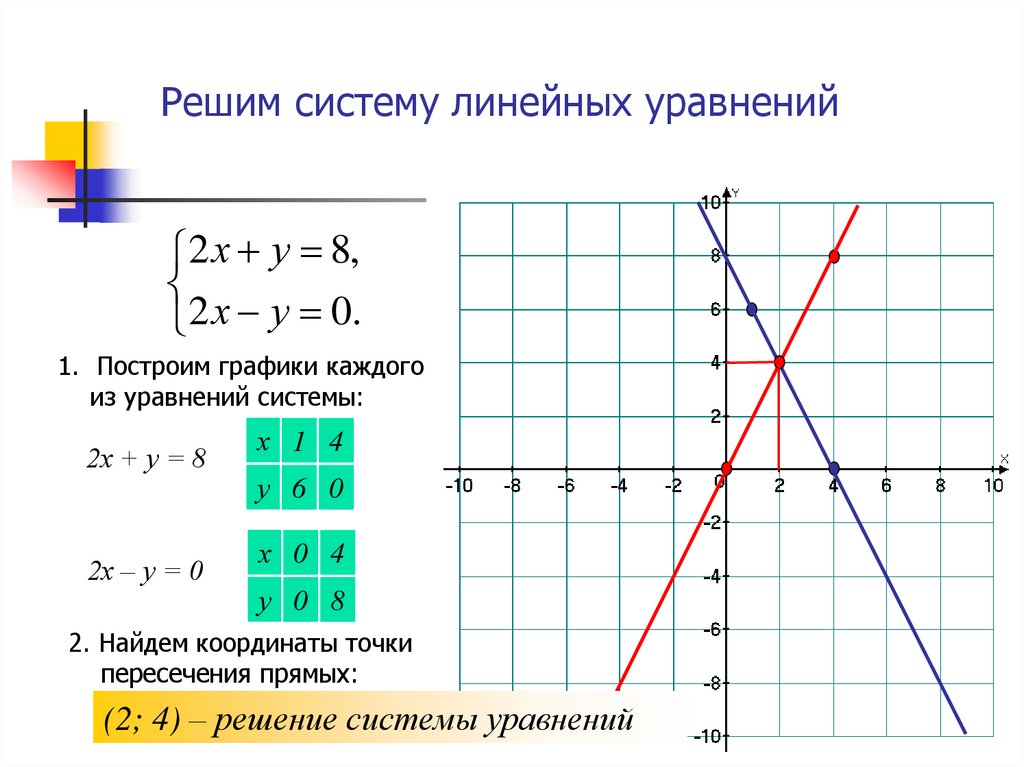 253. Объем пирамиды и конуса. 254. Площадь боковой поверхности правильной пирамиды и конуса. 255. Усеченный конус и усеченная пирамида. § 3. Шаровая поверхность. Шар 256. Шар и шаровая поверхность. 257. Объем шара и его частей. 258. Площадь поверхности шара и ее частей. 259. Понятие телесного угла. Ответы к упражнениям Приложения |
И. Элементарная математика. 2-е изд., перераб. и доп., М.: 1974г. — 592с.
Линейная функция — определение, уравнение, график, примеры
Линейные функции
В математике функция — это отношение со свойством, в котором каждый вход связан ровно с одним выходом. Линейные функции имеют большое значение из-за их универсального характера. Они могут быть реализованы во многих ситуациях. Более того, они появляются в разных формах уравнений. Итак, что такое линейная функция? Линейная функция — это функция с одной или двумя переменными без показателей степени. Эта функция представляет собой прямую линию на координатной плоскости. Если функция имеет больше переменных, то они должны быть постоянными, чтобы оставаться в одном и том же состоянии линейной функции.
В этой статье мы подробно узнаем о:
- Что такое линейная функция?
- Уравнение линейных функций
- Характеристики линейной функции
- Скорость изменения линейной функции
- График линейной функции
- Таблица линейных функций
- Примеры линейных функций из реальной жизни
- Решенные задачи на линейные функции
Определение линейной функции: Линейная функция — это алгебраическая функция, которая образует прямую линию в координатной плоскости. Как правило, это полиномиальная функция с максимальной степенью 1 или 0. Линейные функции также выражаются в терминах исчисления и линейной алгебры. Основное отличие заключается в обозначении функции. Необходимо знать упорядоченную пару, записанную в функциональной записи. Например, функция записывается так:
f(2) = 3 и f(5) = 2
Упорядоченная пара будет (2, 3) (5, 2)
Линейная функция может быть записана как;
y = f(x) = mx + b
Это уравнение выглядит как форма пересечения наклона линии, которая задается как y = mx + b, потому что линейная функция представляет собой горизонтальную линию.
т. е. его график представляет собой прямую.
Наоборот, нелинейная функция не является линейной, т. е. не образует на графике прямой линии. Показательная функция является примером нелинейной функции.
Уравнение линейных функцийЛинейную функцию можно представить следующим выражением:
y = f(x) = mx + b (форма пересечения наклона) m» и «b» — действительные числа, где «m» — наклон линии, а «b» — точка пересечения линии по оси y.
«x» — независимая переменная
«y» или f(x) — зависимая переменная
Линейная функция также может быть представлена в виде точка-наклон формы как
y−y 1 =m(x−x 1 )
В то время как в стандартной форме записывается как
4 Ax0 + By0 = C линейной функции
Вот некоторые важные характеристики линейных функций:
- Переменная — это символ, который показывает количество в выражении.
- Скорость, с которой линейная функция отклоняется от эталона, представлена крутизной.
- Направление линейных функций может быть возрастающим, убывающим, горизонтальным или вертикальным.
- Убывающая линейная функция с отрицательным наклоном. Итак, если m<0, то f(x) = mx + b убывает.
- Возрастающая линейная функция — это функция с положительным наклоном. Итак, когда m>0, то f(x)=mx+b увеличивается.
- Y-отрезок — это значение функции, а ноль — это входное значение. Оно известно как начальное значение.
- Когда m=0, линейная функция f(x) = mx + b представляет собой горизонтальную линию и называется постоянной функцией.
Скорость изменения линейной функции также называется наклоном. Уравнение прямой линии в форме пересечения наклона. Он включает наклон и начальное значение функции. Y-отрезок или начальное значение является выходным значением, когда ноль является входом линейной функции.
Например, скорость — это скорость изменения расстояния во времени. Если мы знаем два момента времени и общее пройденное расстояние, мы можем определить скорость изменения, также известную как наклон. Используя информацию, мы можем составить линейное уравнение и делать прогнозы на основе линейного уравнения.
График линейной функцииЧтобы представить любое линейное уравнение на графике, выполните три простых шага:
- Сначала найдите две точки (x 1 , x 2 ) и (y 1 0 , y 2 ), которые удовлетворяют уравнению y = mx+b.
- Нанесите эти точки на график или оси X-Y.
- Соедините две точки на плоскости прямой линией.
Кроме того, формула для наклона линейной функции : m= y 2 -y 1 /x 2 -x 1
Получив наклон, мы можем использовать одну из известных точек и формулу пересечения наклона, чтобы найти b.
Табличные данные, содержащие значения x и y, могут помочь проверить линейную функцию.
Чтобы определить, удовлетворяют ли заданные табличные данные линейной функции, мы вычислим разницу в значениях x. Далее мы определим различия в значениях y. Теперь каждый раз проверяйте отношение (разница в y)/(разница в x). Если отношение является константой, то данные представляют собой линейную зависимость.
Кроме того, в линейной функции скорость изменения y относительно переменной x остается постоянной. Как указывалось выше, эта скорость изменения представляет собой наклон линии при графическом представлении.
Let us consider the following table with x and y values,
| x | y |
| 0 | 4 |
| 1 | 5 |
| 2 | 6 |
| 3 | 7 |
| 4 | 8 |
Из приведенной выше таблицы видно, что скорость изменения между x и y равна 4.
Чтобы представить эти данные с помощью линейной функции, мы можем написать так как у = х+4.
Существует множество реальных примеров линейных функций, включая задачи о расстоянии и скорости, вычисления размерностей, задачи ценообразования, смешение процентов решений и многое другое. Приведенные ниже примеры линейных функций из реальных приложений помогают нам понять концепцию линейных функций.
- Игровой сервис взимает ежемесячную плату в размере 5,50 долларов США и дополнительную плату в размере 0,45 долларов США за каждую игру. Тогда общая ежемесячная плата может быть представлена линейной функцией f(x) = 0,45x + 5,50, где x — количество игр, которые пользователь загружает в месяц.
- Пакет печенья стоит 20 долларов. Существует линейная зависимость между деньгами, которые вы тратите, и количеством упаковок печенья, которые вы покупаете. Итак, согласно стандартной форме, A=20x, где A — сумма потраченных денег, а x — количество купленных пакетов печенья.
- Пекарня зарабатывает 150 долларов в месяц, в то время как их единовременные начальные затраты составляли 200 долларов. Линейная функция, представляющая эту ситуацию, будет y=150x−200.
В этом уравнении переменная x представляет количество месяцев, в течение которых они получали прибыль. Переменная y представляет собой общий доход пекарни за месяц после первого месяца. Это уравнение линейной функции помогает пекарному комитету прогнозировать будущие доходы. Например, через 6 месяцев они могут рассчитывать на доход: 150(6)−200=700 долларов.
Решенные задачи на линейные функции
| Пример 1: Перепишите следующую функцию в виде упорядоченных пар, чтобы успешно построить график. f(3) = -2 и f(-8) = -4 Ответ: Вышеупомянутая функция может быть записана как (3, -2) и (-8, -4) |
Пример 2: Найдите наклон графика для следующей функции. f(1) = -1 и f(-4) = -6 Ответ: Вышеупомянутая функция может быть записана в упорядоченной парной форме как (1, -1) и (-4, -6) Итак, m= -6-(-1)/-4-1 m= -5/-5 Итак, m = 1, т.е. наклон функции . |
| Пример 3: Найдите уравнение линейной функции (-1, 15) и (2, 27). Ответ: Используя формулу наклона, мы можем оценить наклон. (-1, 15) и (2, 27) соответствуют (x 1 , y 1 ) и (x 2 , y 2 ) m = y 2 -y 1 /x 2 -x 1 m= 27-(15)/2-(-1) m=12/3 m= 4 наклон равен 4. Теперь мы можем написать уравнение для линейной функции, подставив значения х +1) у – 15= 4х +4 y= 4x +19 Итак, y= 4x +19 — это уравнение для данной функции.  |
Определение уравнения линейной функции
Все ресурсы для предварительного исчисления
12 Диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept
Precalculus Help » Графические функции » Линейные функции » Определите уравнение линейной функции
Каково уравнение прямой, проходящей через точки и ?
Выразите свой ответ в форме.
Возможные ответы:
Ни один из других ответов.
Правильный ответ:
Объяснение:
Во-первых, нам нужно вычислить наклон. Мы можем сделать это с помощью формулы наклона
, иногда называемой «подъем над пробегом». Неважно, какую точку мы используем, поэтому мы будем использовать .
Тогда мы имеем:
Что становится .
Следовательно, мы берем найденное значение для и подставляем его обратно, чтобы получить
.
Сообщить об ошибке
Найдите уравнение прямой с наклоном, которая проходит через точку.
Выразите свой ответ в форме.
Возможные ответы:
Ни один из других ответов.
Правильный ответ:
Объяснение:
Так как наш склон есть, то мы можем подключить его сразу давая.
Чтобы решить для , мы подставляем данную точку к значениям и дающего.
Это упростит до или после вычитания дроби.
Следовательно, наш ответ будет после подстановки наших значений для и .
Сообщить об ошибке
Предположим, у Боба 4 конфеты. Затем он зарабатывает конфеты из расчета 14 конфет в неделю.
Какая из следующих формул является наиболее разумной, чтобы узнать, сколько конфет у Боба в любой конкретный день?
Возможные ответы:
Правильный ответ:
Пояснение:
Боб начинает игру с 4 конфетами. Напишите уравнение.
Каждую неделю он зарабатывает 14 конфет. В каждой неделе всего 7 дней. Разделите количество конфет на количество дней, чтобы определить, сколько конфет Боб заработает за день.
Затем Боб зарабатывает 2 конфеты в день. Обозначим количество конфет в день. Закончите неполное уравнение.
Сообщить об ошибке
После часа работы у Билли есть три доллара. Через восемь часов у Билли пятьдесят долларов. Выберите наиболее правильную линейную функцию, представляющую этот сценарий, если представляет время и представляет доллары.
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы решить уравнение этой задачи, нам понадобится 2 очка.
Пусть точка определяется как , где – это время в часах, – доллары, которые заработал Билли.
Билли начинает с трех долларов в первый час. Напишите суть.
По истечении восьми часов у Билли будет пятьдесят долларов. Напишите второй пункт.
Напишите формулу пересечения наклона.
Запишите формулу наклона.
Подставьте точку и заданный наклон к формуле пересечения наклона, чтобы найти точку пересечения по оси Y.
Подставьте это и наклон обратно в уравнение пересечения наклона.
Поскольку заработок Билли зависит от времени, которое он работает, перепишите уравнение так, чтобы время было независимой переменной, а заработанная сумма — зависимой.
Сообщить об ошибке
Определите уравнение прямой, проходящей через точки и .
Возможные ответы:
Правильный ответ:
Объяснение:
Линейные функции имеют вид , где m — наклон, а b — точка пересечения по оси y.
Мы можем определить уравнение линейной функции, когда у нас есть наклон и точка пересечения y, которая является отправной точкой для рисования нашей линии. Если нам нужно уравнение линии, проходящей через две точки, мы используем уравнение наклона точки:
, где переменные с номерами рядом с ними соответствуют местам, где вы вводите x и y из одной (одной и той же) пары координат.
Поскольку у нас есть две точки, мы можем вычислить наклон линии, проходящей между ними. .
.
Теперь используйте формулу наклона точек:
распределите правую сторону
добавьте 6 к обеим сторонам
, что является окончательным ответом.
Посмотрите на пары координат. Нужно ли было использовать формулу точечного наклона? Ответ отрицательный, так как пара координат (0,5) уже является точкой пересечения y. Так что все, что было необходимо, это вычислить наклон.
Сообщить об ошибке
Какое уравнение перпендикулярно и проходит через ?
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала найдите обратную величину наклона заданной функции.
Функция перпендикуляра:
Теперь мы должны найти константу , используя заданную точку, которую пересекает перпендикуляр.
решить для :
Сообщить об ошибке
Какое уравнение перпендикулярно и проходит через него ?
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала найдите обратную величину наклона заданной функции.
Перпендикулярная функция:
Теперь мы должны найти константу , используя данную точку, которую пересекает перпендикуляр.
решить для :
Сообщить об ошибке
Какое уравнение перпендикулярно и проходит через него ?
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала найдите обратную величину наклона заданной функции.