Уравнение методом гаусса: Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса

Содержание

65.Система линейных уравнений. Метод Гаусса.

Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Решить систему уравнений методом Гаусса:

x + y — 3z = 2,

3x — 2y + z = — 1,

2x + y — 2z = 0.

Решение. Выпишем расширенную матрицу данной системы

и произведем следующие элементарные преобразования над ее строками:

а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:

~ ;

б) третью строку умножим на (-5) и прибавим к ней вторую:

В результате всех этих преобразований данная система приводится к треугольному виду:

x + y — 3z = 2,

-5y + 10z = -7,

— 10z = 13.

Из последнего уравнения находим z = -1,3. Подставляя это значение во второе уравнение, имеем y = -1,2. Далее из первого уравнения получим x = — 0,7.

Рангом матрицы А называется наивысший порядок минора матрицы А , отличного от нуля.

Вычисляется:

1)Умножение строки(столбца) на числ, отличное от нуля.

2)Прибавление к одной строке(столбцу) другой, умножение на любое число.

3)Перемена местами двух строк(столбцов)

4)Вычёркивание нулевой строки

Первую строку умножим на и прибавим ко второй. Получим строку. Первую строку умножим наи прибавим к третьей. Получим строку. Первую строку умножим наи прибавим к четвертой.

Получим строку. В итоге имеем матрицу

Вторую строку оставляем без изменений. К третьей строке прибавляем вторую, умноженную на 2. Получим строку . К четвертой строке прибавляем вторую. Получим нулевую строку. Преобразованная матрица имеет вид

Поменяем местами третий и четвертый столбцы:

Базисный минор матрицы стоит в первых трех столбцах и первых трех строках,. Следовательно,.

67.Теорема Кронекера – Капели

Теорема Кронекера — Капе́лли —Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Доказательство (условия совместности системы)

Необходимость

Пусть система совместна. Тогда существуют числа такие, что. Следовательно, столбец b является линейной комбинацией столбцовматрицы A. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (соответственно столбец), которая является линейной комбинацией других строк (соответственно столбцов) следует, что.

Достаточность

Пусть . Возьмем в матрице A какой-нибудь базисный минор. Так как, то он же и будет базисным минором и матрицы B. Тогда согласно теореме о базисномминоре последний столбец матрицы B будет линейной комбинацией базисных столбцов, то есть столбцов матрицы A. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы A.

Решение уравнений методом Гаусса онлайн калькулятор

Карл Фридрих Гаусс — немецкий математик, механик, физик, астроном и геодезист. Он считается одним из величайших математиков всех времён, «королём математиков». И даже избирался иностранным почетным членом Петербургской академии наук. Для творчества Гаусса характерна органическая связь между теоретической и прикладной математикой, широта проблематики.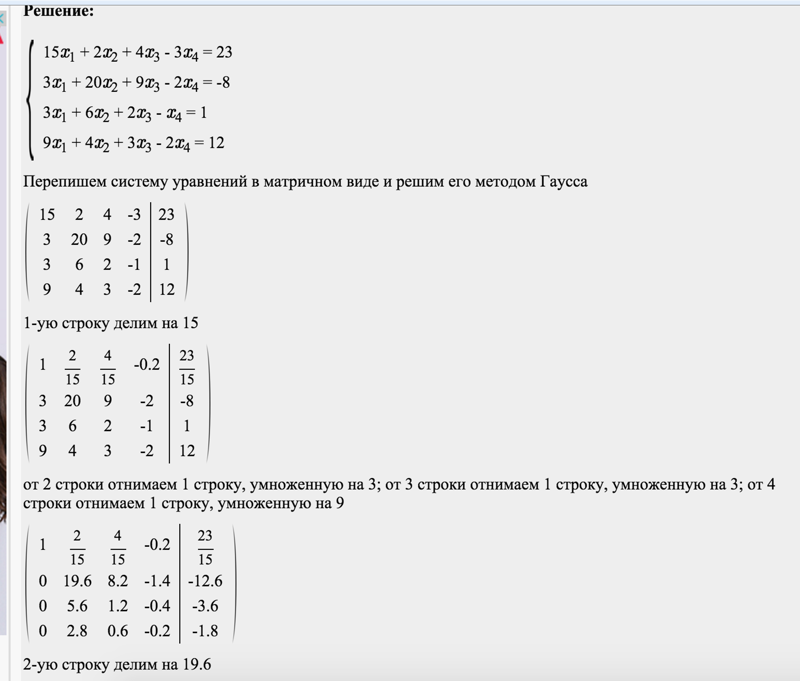

Труды Гаусса оказали большое влияние на развитие алгебры, теории чисел, дифференциальной геометрии, математической физики, теории электричества и магнетизма, геодезии и многих разделов астрономии. Метод Гаусса позволяет максимально легко и быстро решить систему линейных алгебраических уравнений (СЛАУ). Успех данного метода заключается в последовательном исключении неизвестных из уравнений. Сегодня решить систему алгебраических уравнений онлайн методом Гаусса можно с помощью специальных решательов, но ниже мы разберем решение системы линейных уравнений, чтобы наглядно на примере увидеть все его достоинства.

Так же читайте нашу статью «Решить уравнение матричным способом онлайн решателем»

Допустим, дана система линейных уравнений:

\[\left\{\begin{matrix} 2\cdot x_1+4\cdot x_2+1\cdot x_3 = 36\\ 5\cdot x_1 + 2 \cdot x_2 +1 \cdot x_3 =47\\ 2\cdot x_1 + 3\cdot x_2 + 4 \cdot x_3 = 37 \end{matrix}\right. \]

Представим ее в матричной форме:

\[\begin{bmatrix} 2 & 4 & 1\\ 5 & 2 & 1\\ 2 & 3 & 4 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 36\\ 47\\ 37 \end{bmatrix}\]

Выберем строку с максимальным коэффициентом \[a_i1\] и меняем ее с первой.

\[\begin{bmatrix} 5 & 2 & 1\\ 2 & 4 & 1\\ 2 & 3 & 4 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 47\\ 36\\ 37 \end{bmatrix}\]

Нормируем уравнения относительно коэффициента при \[x_1\]:

\[\begin{bmatrix} 1 & \frac{2}{5} & \frac{1}{5}\\ 2 & \frac{4}{2} & \frac{1}{2}\\ 2 & \frac{3}{2} & \frac{4}{2} \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} \frac{47}{5}\\ \frac{36}{2}\\ \frac{37}{2} \end{bmatrix} \]

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 1 & 2 & 1\\ 1 & 1.5 & 2 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9. 4\\ 9.6\\ 9.1 \end{bmatrix}\]

Вычитаем 1 уравнение из 2 и 3:

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1.6 & 0.3\\ 0 & 1.1 & 1.8 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 8.6\\ 9.1 \end{bmatrix}\]

Выбираем строку с наибольшим коэффициентом при \[a_i2\] (уравнение 1 не рассматривается) и перемещаем ее на место 2.

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1.6 & 0.3\\ 0 & 1.1 & 1.8 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 8.6\\ 9.1 \end{bmatrix}\]

Нормируем 2 и 3 уравнения относительно коэффициента при \[x_2\]

\[\begin{bmatrix} 1 & 0.4 & 0.2\\ 0 & 1 & 0.1875\\ 0 & 1 & 1.636 \end{bmatrix}\cdot\begin{bmatrix} x_1 \\ x_2\\ x_3 \end{bmatrix}=\begin{bmatrix} 9.4\\ 5.375\\ 8.272 \end{bmatrix}\]

Вычитаем уравнение 2 из 3

\[\begin{bmatrix} 1 & 0.4 & 0. T\].

Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Распределение Гаусса / функция кривой нормального распределения

Определения расчетов >

Содержание:

Определение распределения Гаусса
Квадратура Гаусса
Функция Гаусса

Гауссово семейство кривых. Красный — это стандартное нормальное среднее значение 0 и стандартное отклонение 1.

Что такое кривая нормального распределения или распределение Гаусса?

Колоколообразная кривая — это другое название распределения Гаусса или кривой нормального распределения (иногда ее просто сокращают до «нормальной кривой»). Название происходит от того факта, что он выглядит в форме колокола.

Термин «кривая нормального распределения» обычно используется в социальных науках; в статистике это называется нормальным распределением, а в физике — распределением Гаусса. Однако все они относятся к одному и тому же: распределению вероятностей, имеющему определенные характеристики, в том числе тот факт, что оно имеет форму колокола.

Почему разные имена для одного и того же дистрибутива?

Хотя де Муавр впервые описал нормальное распределение как приближение к биномиальному, Карл Фридрих Гаусс использовал его в 1809 году.для анализа астрономических данных о позициях, отсюда и термин распределение Гаусса.

Характеристики кривых нормального распределения, нормальных кривых

Среднее арифметическое (среднее) всегда находится в центре кривой нормального распределения или кривой нормального распределения.
Колоколообразная кривая/распределение Гаусса имеет только одну моду или пик. Режим здесь означает «пик»; кривая с одним пиком унимодальна; два пика бимодальны, и так далее.
Гауссовая кривая имеет предсказуемые стандартные отклонения, следующие за 68 9Правило 5 99,7 (см. ниже).
Колоколообразная кривая симметрична. Ровно половина точек данных находится слева от среднего и ровно половина — справа от среднего.

Распределение вероятности многих явлений представляет собой кривую нормального распределения, в том числе:

Высота
Гири
баллов IQ
Темпы роста
Экзаменационные баллы
Температура связана с глобальным потеплением

Стандартные отклонения кривой нормального распределения

А — это единица измерения, которая может помочь вам выяснить, куда могут попасть элементы данных. Например, 68% всех измерений находятся в пределах одного стандартного отклонения по обе стороны от среднего значения. Другими словами, основная часть ваших данных будет находиться в пределах от -1 до +1 стандартных отклонений от среднего значения. Если вы дойдете до двух стандартных отклонений, этот процент возрастет до 95; почти все (99,7%) ваших данных будут находиться в пределах трех стандартных отклонений.

Семейство кривых

Распределение Гаусса представляет собой непрерывное семейство кривых, имеющих форму колокола. Другими словами, существуют бесконечные возможности для количества возможных распределений, учитывая безграничные возможности измерения стандартного отклонения (которое может быть от 0 до бесконечности). Стандартное распределение Гаусса имеет среднее значение 0 и стандартное отклонение 1. Чем больше стандартное отклонение, тем более пологая кривая. Чем меньше стандартное отклонение, тем выше пик кривой.

Что такое функция распределения Гаусса?

Функцию распределения Гаусса можно использовать для описания физических событий, если число событий очень велико. Проще говоря, центральная предельная теорема (из вероятности и статистики) говорит, что, хотя вы не можете предсказать, что будет делать один элемент, если у вас есть целая куча элементов, вы можете предсказать, что они будут делать в целом.

Например, если у вас есть сосуд с газом при постоянной температуре, распределение Гаусса позволит вам вычислить вероятность того, что одна частица будет двигаться с определенной скоростью.

Приблизительно 68% событий находятся в пределах одного стандартного отклонения от среднего значения.
95% находятся в пределах двух стандартных отклонений от среднего значения.
99% находятся в пределах трех стандартных отклонений от среднего значения.

Квадратура Гаусса — это способ интегрирования с использованием взвешенных сумм. Основная идея заключается в том, что вы используете кривую Гаусса в качестве накладывающейся формы вместо прямоугольников или трапеций.

Сравнение методов гауссовского и трапециевидного численного интегрирования. Двухточечное квадратурное правило Гаусса дает точный результат, потому что площадь светло-серых областей равна площади темно-серых областей.

Это может привести к большей точности, чем другие методы, такие как правило трапеций. Оптимальные узлы (расстояния) в квадратуре Гаусса обычно неравномерны.

Пример квадратуры Гаусса

Пример вопроса : Выполните квадратуру Гаусса для = 2 и интервала [ ] = [−1, 1].

Контекст:
Наивысшая степень точности с квадратурой Гаусса составляет 2n -1. Цель процедуры состоит в том, чтобы найти значения для интегрирования, которые достигают этого уровня точности. Формула точна для функций f(x) = 1, x, x ² , х ³ ,…, х _п . Чтобы проинтегрировать функцию на интервале [-1, 1], вам нужно найти значения x (x _i) и веса (w _i), чтобы:

, когда f является полиномиальной функцией степени 2n – 1 = 2(2) – 1 = 3 или меньше (т.е. степень точности 3).

Решение :
Шаг 1: Интегрируйте для различных значений x. Нам нужно 2 n параметров, поэтому для этого примера мы интегрируем следующие (2 n = 2 * 2 = 4) значения:

f(x) = 1: w ₁ + w ₂ = 1 dx = 2
f(x) = x: w ₁ + w ₂ = x dx = 0
f(x) = x ² : w ₁ + w ₂ = x ² dx = 2/3
f(x) = x ³ : w ₁ + w ₂ = x ³ dx = 1

Solving for ₁ , ₂ , w ₁ and w ₂ дает:

Использование технологии

В MATLAB квадратурное правило Гаусса реализовано с помощью quadl .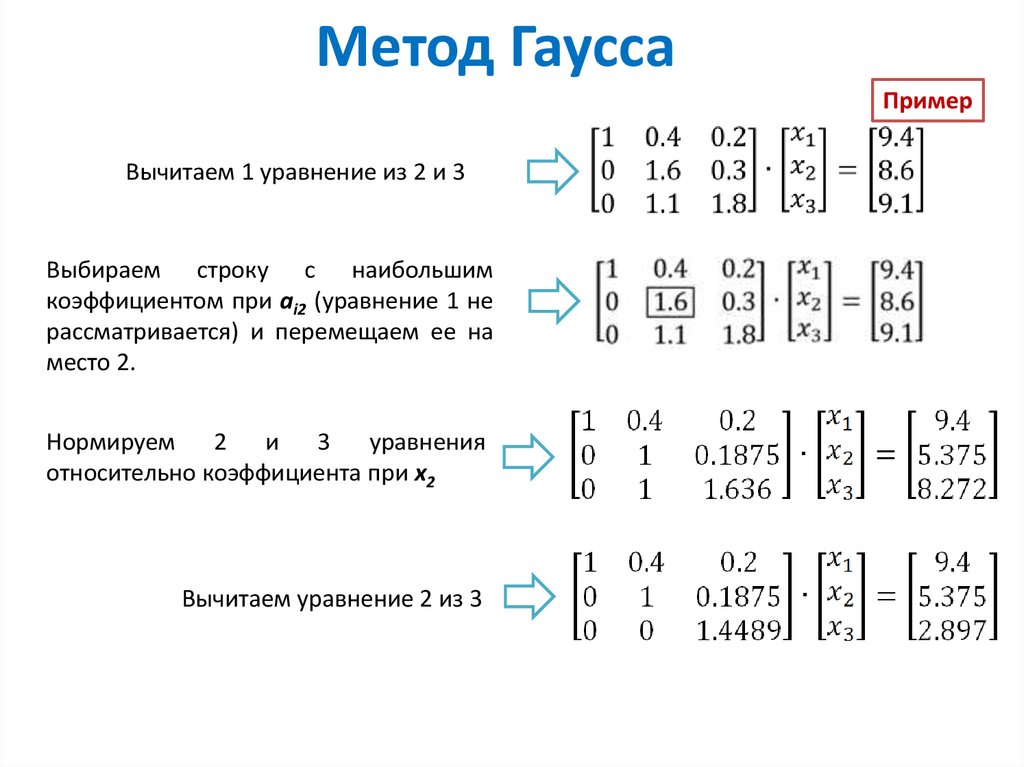

Функция Гаусса (названная в честь Карла Фридриха Гаусса) — это функция, которая дает классическую колоколообразную кривую. Обычно он определяется как:

Где:

exp означает «экспоненциальный» (т.е. e ^x),
a, b и c (ненулевые) являются регулируемыми константами:
- а (высота пика),
- б (положение пика),
- c (стандартное отклонение или «разброс»).

Приведенная выше формула используется, когда константа a является временем. Гауссиана также может быть указана со стандартным отклонением (σ или S), где 2 * S * S появляется в знаменателе показателя степени (Hahn, 1995).

Глобальный максимум и точки перегиба

Функция имеет глобальный максимум (т. е. максимальную высоту) при x = b, где наклон равен нулю. На следующем графике показано, как манипулирование значением «b» перемещает график по оси X:
Две кривые Гаусса. Красная функция имеет максимальную высоту при x = 2, синяя — при x = 3.

График имеет две точки перегиба: x = b ± √( с /2).

Производные

Первая производная функции Гаусса:

Вторая производная:

Практическое использование функции Гаусса обучение, физика и биомедицинские науки. Например, это обычный выбор для нейронной сети с радиальной базисной функцией (RBF), поскольку она обобщает глобальное отображение и уточняет локальные признаки без изменения изученного отображения (Sundararajan & Lu, 19).99). В физике гауссов пучок описывается функцией Гаусса. Гауссиан — единственная функция, которая обеспечивает минимально возможное произведение времени на пропускную способность среди всех гладких (аналитических) функций (Смит, 2020). Распределение Бирнбаума-Сондерса, используемое при тестировании срока службы компонентов, представляет собой смесь обратного распределения Гаусса и обратного обратного распределения Гаусса (Shakti, 2022).

Ссылки

4. 7 Квадратура Гаусса. Получено 13 января 2019 г. с: https://www3.nd.edu/~zxu2/acms4039.0F15/Lec-4.7.pdf
Абрамовиц М. и Стегун И. А. (ред.). Справочник по математическим функциям с формулами, графиками и математическими таблицами, 9-е издание. Нью-Йорк: Довер, стр. 887–888, 1972.
Актон, Ф. С. Численные методы, которые работают, 2-е издание. Вашингтон, округ Колумбия: математика. доц. амер., с. 103, 1990.
Арфкен, Г. «Приложение 2: Квадратура Гаусса». Математические методы для физиков, 3-е изд. Орландо, Флорида: Academic Press, стр. 968–974, 1985.
Хан, Л. (1995). Функция Гаусса. Получено 22 июля 2020 г. с: http://retina.anatomy.upenn.edu/~rob/lance/gaussian.html
Хильдебранд, Ф. Б. Введение в численный анализ. Нью-Йорк: McGraw-Hill, стр. 319–323, 1956.
Kurzweg, U. (2020). Свойства функции Гаусса. Получено 22 июля 2020 г. с: https://mae.ufl.edu/~uhk/GAUSSIAN-NEW.pdf
Shakti, P. (2022). Распределение Бирнбаума-Сондерса. P-Distribution.com
Смит, Дж. (2011). Спектральная обработка аудиосигнала. Издательство W3K.
Страуд А. Х. и Секрест Д. Квадратурные формулы Гаусса. Englewood Cliffs, NJ: Prentice-Hall, 1966.
Sundararajan, N. & Lu, Y. (1999). Радиальные базисные нейронные сети с последовательным обучением. MRAN и его приложения. Всемирная научная.

График: Desmos.com

УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Распределение Гаусса / Функция кривой Белла» Из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/gaussian-distribution-bell-curve/

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

Модели Гаусса — MATLAB & Simulink

Модели Гаусса

О моделях Гаусса

Модель Гаусса соответствует пикам и задается как

y=∑i=1naie[−(x−bici)2]

амплитуда, b – это центроид (местоположение), c относится к ширине пика, n — количество пиков, которые должны соответствовать, и 1 ≤ n ≤ 8,

Пики Гаусса встречаются во многих областях науки и техники. За Например, пики Гаусса могут описывать линейчатые спектры излучения и химические вещества. анализы концентрации.

Подгонка моделей Гаусса в интерактивном режиме

Откройте приложение Curve Fitter, введя curveFitter в командной строке MATLAB ^®. В качестве альтернативы, на вкладке Приложения в Математика, статистика и оптимизация щелкните Curve Fitter .
В приложении Curve Fitter выберите данные кривой. На Вкладка Curve Fitter в Данные раздел, нажмите Выбрать Данные . В разделе выберите фитинг Данные 9диалоговое окно 0006, выберите X данные и Y данные или просто Y данные по индексу.
Щелкните стрелку в разделе Fit Type , чтобы откройте галерею и нажмите Gaussian в Группа моделей регрессии .

Вы можете указать следующие параметры в Подходит Панель параметров :

Укажите количество терминов в виде положительного целого числа в диапазон [1 8]. Просмотрите панель результатов . увидеть условия модели, значения коэффициентов и статистика соответствия.
Опционально, в дополнительных параметрах укажите начальные значения коэффициентов и ограничения или изменить настройки алгоритма. Приложение рассчитывает оптимизированные начальные точки для Gaussian подходит, исходя из набор данных. Вы можете переопределить начальные точки и указать ваши собственные значения в Fit Options панель.
Подгонка по Гауссу имеет параметр ширины c1 ограничено нижней границей 0 . Нижние границы по умолчанию для большинства библиотечные модели -Инф , который указывает, что коэффициенты не ограничены.

Дополнительные сведения о настройках см. в разделе «Указание параметров подгонки и оптимизированных начальных точек».

Подгонка гауссовских моделей с использованием функции подгонки

Открыть Live Script

В этом примере показано, как использовать функцию подгонки для подгонки гауссовой модели к данным.

Библиотечная модель Гаусса является входным аргументом для подгонки 92) Коэффициенты (с доверительной вероятностью 95%): а1 = 1,47 (1,426, 1,515) b1 = 897,7 (897, 898,3) с1 = 27,08 (26,08, 28,08) а2 = 0,6994 (0,6821, 0,7167) b2 = 810,8 (790, 831,7) с2 = 592,9 (500,1, 685,7)

 plot(f,x,y)

`См. также`

`Приложения`

Curve Fitter

`Функции`

fit | фиттип | фитопций

`Связанные темы`

Гауссовская аппроксимация с экспоненциальным фоном
Укажите параметры аппроксимации и оптимизированные начальные точки

У вас есть модифицированная версия этого примера.