Таблица локальная теорема лапласа: Локальная теорема Лапласа

Локальная теорема Лапласа

Пусть в каждом из n одинаковых независимых испытаний вероятность появления некоторого события А равна p (p0 и p1), тогда вероятность того, что событие А наступит ровно k раз в n испытаниях Р_n(k) может быть приближенно (тем точнее, чем больше n) вычислена по формуле.

Р_n(k) =  (х), (13)

где функция

, (14)

а .

В каждом учебнике по теории вероятностей имеется таблица значений функции (х), однако значение функции (х) можно вычислять и непосредственно по формуле (14). При этом следует помнить свойства функции (х). Эта функция четная, т.е. (-х) = (х), и значения функции для х4 столь малы, что их принято считать равным нулю. Следует учитывать также, что применение локальной теоремы Лапласа вместо формулы Бернулли, целесообразно (не приводят к существенным погрешностям) в случае, если npq 10.

Покажем, как работает локальная теорема Лапласа при решении предыдущей задачи.

Поскольку n = 400, p = 0,2, q = 1-p = 0,8, k = 80, то согласно теореме (поскольку npq = 4000,20,8 = 64  10)

P₄₀₀(80) = .(х) = (х).

При этом х = = = 0.

По таблице находим (0) = 0,3989, и стало быть искомая вероятность

Р₄₀₀(80) = 0,3989 = 0,04986.

Пример

Найти вероятность того, что в результате 405 бросаний игральной кости ровно 30 раз выпадает 6 очков.

Поскольку вероятность выпадения 6 очков в одном бросании кости р = , а вероятность не выпадения 6 очков q = 1-p =1 — = , npq = 405  = 10, то, используя локальную теорему Лапласа, получим:

Р₄₀₅(30)  (х),

При этом

= = = = .

Согласно свойствам функции (х), (-5) = (5) и поскольку значение аргумента х = =54, то можно считать (5)  0, а, следовательно, искомая вероятность

Р₄₀₅(30)   (5) = 0 = 0.

Интегральная теорема Лапласа

Во многих случаях возникает необходимость в условиях ранее сформулированного эксперимента из n независимых одинаковых испытаний определить вероятность того, что интересующее нас событие появится не менее k₁ и не более k₂ раз (такая вероятность обычно обозначается Р_n(k₁, k₂)). Ответ на этот вопрос позволяет получить интегральная теорема Лапласа.

Интегральная теорема Лапласа. Пусть проводятся n независимых одинаковых испытания, в каждом из которых вероятность появления события А равна р (р 0 и р 1). Тогда вероятность Р_n(k

1, k₂) того, что событие А появится в n испытаниях не менее k₁ и не более k₂ раз приближенно равна

Р_n(k_1, k₂) = Ф(х»)-Ф(х’), (15)

где Ф(х) = — функция Лапласа. Вычисление функции Лапласа может быть произведено почленным интегрированием ряда .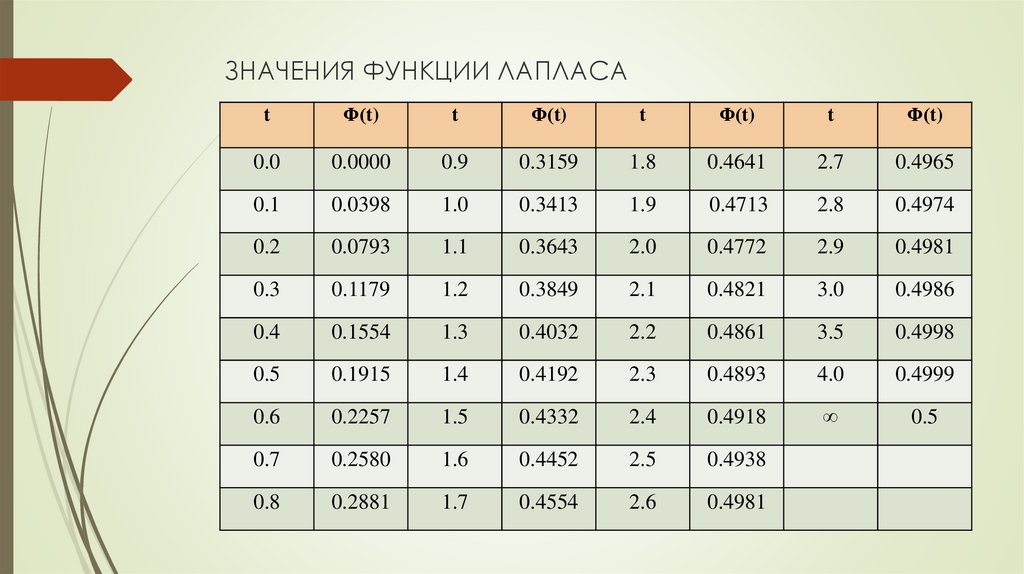 Для упрощения вычислений применяются таблицы функции Лапласа, которые имеются в каждом учебнике по теории вероятностей. В таблицах функции Лапласа x меняется от 0 до 5. Если x отрицательно, то нужно воспользоваться нечетностью функции, т. е. Ф(-x) = -Ф(x), а при значениях х > 5 функция Лапласа с большой степенью точности равна 0,5.

Значения х’ и х» в формуле (15) определяется отношениями

х’ = , х» = . (16)

Пример 1. Партия деталей содержит 20% брака. Найти вероятность того, что среди 400 проверенных изделий попадется не менее 50 и не более 90 бракованных.

Поскольку n достаточно велико, а npq = 4000,20,8  10, используют интегральную теорему Лапласа n = 100, p = 0,2, q = 0,8, k₁ = 50, k₂ = 90 по формулам (16)

k’ = = = -3,75,

k» = = = 1,25,

следовательно, искомая вероятность найдется по формуле (15)

Р₄₀₀(50; 90)  Ф(1,25)- Ф(-3,75) = Ф(1,25)+ Ф(3,75)

и по таблице функции Лапласа

Р₄₀₀(50; 90)  0,3944+ 0,4970 = 0,8924.

статистика — Как получить значение функции лапласа? Python

Здравствуйте!

Подскажите, пожалуйста, как получить значение функции Лапласа (функции стандартного нормального распределения) в python?

Функция laplace.pdf() из scipy дает не то значение. Значения не совпадают с табличными значениями интегральной функции Лапласа:

• python
• статистика
• scipy

10

Нашёл: значения упомянутой таблицы даёт функция scipy.stats.norm.cdf(x) - 0.5. Только вот по-моему к Лапласу она никакого отношение не имеет, ибо это интеграл от обычного гауссового распределения.

4

Гугль подсказывает, что math.erf(x)

1

scipy.stats.norm.cdf(x)

Дает интеграл плотности распределения. По сути оно и есть функция Лапласа. Это интеграл от минус бесконечности до х. Оно же зовется cdf.

В таблицах используется нормированная функция Лапласа, которая (как уже отмечалось) равна обычной функции минус 0,5. Она представляет интеграл от 0 до х.

Вот вывод из книги Письменный Д.Т. Конспект лекций по теории вероятностей, математической статистике и случайным процессам:

Отсюда и понятно, почему нужно вычитать 0,5. Ведь интеграл всей плотности вероятности равен единице. А он симметричен. И именно отрицательная часть равна 0,5.

Так же вы можете использовать erf. Она связана с cdf (см статью на википедии).

А вот этот ответ дал мне возможность ускорить cdf еще сильнее чем scipy.

В своем проекте я вешаю еще jit компиляцию. И это выходит в два раза быстрее чем cdf.(Normal(0,1),x) на Julia. В итоге ускорение в сравнении с scipy было в 10 раз.

Моя реализация представлена ниже. Но к сожалению у неё отсутствует проверка входных данных, так что обеспечьте её сами.

@nb.njit(cache=True)
def cdf(x):
    """
    Расчет функции Лапласа.
    Внимание! Отключена проверка по границам
    """
    x = x / 1.414213562
    a1 = 0.254829592
    a2 = -0.284496736
    a3 = 1.421413741
    a4 = -1.453152027
    a5 = 1.061405429
    p = 0.3275911
    s = np.sign(x)
    t = 1 / (1 + s * p * x)
    b = np.exp(-x * x)
    y = (s * s + s) / 2 - \
        s * (((((a5 * t + a4) * t) + a3) * t + a2) * t + a1) * t * b / 2
    return y

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

pr.

probability — Количественная теорема де Муавра–Лапласа (запрос ссылки)

спросил 11 лет, 4 месяца назад

Изменено 8 лет, 3 месяца назад

Просмотрено 2к раз

$\begingroup$

Классическая теорема де Муавра-Лапласа утверждает, что мы можем аппроксимировать нормальное распределение дискретным биномиальным распределением: 92 / (2npq)}.$$

У меня такой вопрос: существуют ли в литературе более точные количественные версии этой теоремы? Есть ли хорошие оценки, как измерить ошибку? К сожалению, я не знаком с предметом, но мне нужен результат такого типа.

Конечно, всегда есть возможность просмотреть существующие доказательства и проверить детали, а также превратить их из «мягких» в «жесткие», но я подозреваю, что это уже должно быть сделано. А может это и не оптимально, может есть хорошие доступные способы.

Может ли кто-нибудь указать мне хорошую ссылку в этом направлении?

• ссылка-запрос
• пр.вероятность
• на.численный-анализ

$\endgroup$

6

$\begingroup$

Во-первых, я думаю, что под «качественным» вы подразумеваете «количественный». Во-вторых, хотя по количественным версиям центральной предельной теоремы имеется огромная литература, канонические результаты можно найти в томе 2 Феллера. Для центра распределения есть теорема Берри-Эссеена, для хвостов — большие теория отклонений, введение в которую также охвачено Феллером.

РЕДАКТИРОВАТЬ Если вас действительно волнует конкретная аппроксимация бинома нормальным (или наоборот ), вы просто говорите о более высоких членах в приближении Стирлинга к факториалу (и, следовательно, к биномиальным коэффициентам). Вы можете прочитать все об этом, например, в Concrete Math Грэма/Кнута/Паташника.

$\endgroup$

4

$\begingroup$

Вас может заинтересовать эта статья (очень точная оценка, очевидно, упущенная из виду большинством людей!)

Дж. Э. Литтлвуд, О вероятности хвоста двучлена дистрибьюция, админ. заявл. Проб. 1 (1969) 43–72.

пересмотрено и исправлено Маккеем

Брендан Д. Маккей, Об оценке Литтлвуда для бинома Распространение, Достижения в области прикладной теории вероятностей, Vol. 21, № 2 (июнь, 1989), стр. 475-478

$\endgroup$

$\begingroup$

Вам просто нужна локальная предельная теорема для суммы i.i.d. Случайные величины Бернулли.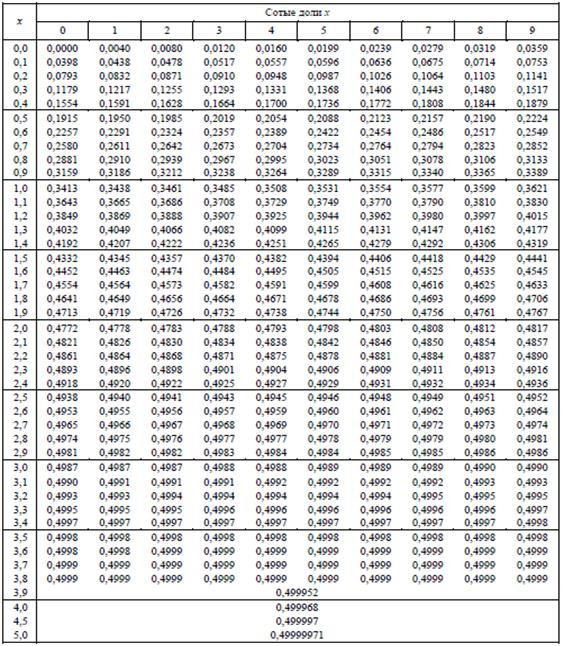 Стандартным справочником (не только по Бернулли с.в.!) являются «Суммы независимых случайных величин» Петрова, в частности глава VII, §3.

$\endgroup$

$\begingroup$

http://www.johndcook.com/normal_ приблизительно_to_binomial.html

$\endgroup$

2

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

[PDF] Использование локальных аппроксимаций PHS+poly для преобразования преобразования Лапласа с помощью алгоритма Гавера-Штефеста

• Идентификатор корпуса: 228082266

 @article{Campagna2020UsingLP,
  title={Использование локальных аппроксимаций PHS+poly для преобразования преобразования Лапласа по алгоритму Гавера-Штефеста},
  автор={Розанна Кампанья, Виктор Байона и Сальваторе Куомо},
  journal={Примечания об исследованиях Доломитовых Альп},
  год = {2020},
  громкость={13}
} 

• R. Campagna, V. Bayona, S. Cuomo
• Published 2020
• Mathematics
• Dolomites Research Notes on Approximation

Обращение преобразования Лапласа — хорошо известная плохо обусловленная задача, и во многих численных схемах в литературе исследовано, как ее решить. В этой статье мы пересматриваем метод Гавера-Штефеста, используя полигармонические сплайны, дополненные полиномами, для аппроксимации преобразования Лапласа в формулу численного обращения. Даны теоретические границы точности подгоночной модели. Дискуссии об эффективности алгоритма инверсии производятся и подтверждаются числовыми… 

drna.padovauniversitypress.it

Greedy algorithms for exponential-polynomial splines reduced models

• R. Campagna, S. D. Marchi, E. Perracchione, G. Santin

• Computer Science, Mathematics

• 2021

This В работе представлены два алгоритма, которые выполняют адаптивный выбор точек сплайновой интерполяции на основе минимизации либо невязок выборки (f-жадный), либо верхней границы ошибки аппроксимации на основе сплайн-функции Лебега (λ-жадный).

жадные алгоритмы для обучения с помощью экспоненциальных полиномиальных сплайнов

• R. Campagna, S. D. Marchi, E. Perracchione, G. Santin

• Commergy Science

  Arxiv

• 20211199

999910 2

0

110

0

11110

110

10 29002

1111110 29002

11111110 29002

1111110 29002

1111110 29002

1111110. EXTER EXTERENGENT EXTERNESE AR на основе жадных алгоритмов к экспоненциально-полиномиальным сплайнам, основной недостаток которых состоит в возможном переобучении и, как следствие, осцилляции аппроксиманта.

Стабильная интерполяция с экспоненциально-полиномиальными сплайнами и выбором узлов с помощью жадных алгоритмов

Эта работа расширяет некоторые представления о жадных алгоритмах, которые являются хорошо зарекомендовавшими себя инструментами, например, для ядерных базисов и экспоненциально-полиномиальных сплайнов, главный недостаток которых состоит в возможном переобучении и последующих осцилляциях аппроксимации, и развивает некоторые результаты по теоретически оптимальным точки интерполяции.

Управляемая данными экстраполяция посредством увеличения характеристик на основе сплайнов тонкой пластины с переменным масштабом

Ориентируясь на полигармонические сплайны, предлагаемый численный метод использует так называемые ядра с переменным масштабированием (VSK), которые вводятся для реализации увеличения характеристик. как стратегия, основанная на дискретных данных, для поиска регуляризованного решения с помощью гребневой регрессии.

с показателем 1-10 из 33 ссылок

Сорт Byrelevancemost, поддержанный Papercersercess,

Численные методы для инверсии преобразования Лапласа

• A. M. Cohen

• Mathematics

• 2007

• Mathematics

• 2007

Mathematics

2007

Mathematics

2007

. такие задачи, как обыкновенные дифференциальные уравнения и уравнения в частных производных. При решении таких задач во многих случаях достаточно просто получить…

Вычисление обратного преобразования Лапласа на основе метода коллокации, использующего только действительные значения

• S. Cuomo, L. D’Amore, A. Murli, M. Rizzardi

• Mathematics

• 2007

Multi -Precision Laplace Inversion

• J. Abate, P. P. Valksion Laplace
  • J. Abate, P. P. Valkision Laplace
    • J. Abate, P. P. Valkision Laplace
      • J. Abate, P. P. valkision
      • J. Abate, P. valkision
      • J. Математика

      • 2004

      Для численного обращения преобразований Лапласа мы предлагаем использовать мультиточные вычисления с уровнем точности, определяемым алгоритмом. Приведем две такие процедуры. …

      Границы вычислительной погрешности для инверсии преобразования Лапласа на основе сглаживающих сплайнов

      • Р. Кампанья, К. Конти, С. Куомо

      • Математика, информатика

        Прил. Мат. вычисл.

      • 2020

      Сравнение акселераторов последовательностей для метода GAVER Инверсии преобразования Лапласа

      • P. Valko, J. Abate

      • Математика

      • 2004
      29007 8. Регулирование NIMERSISTARIS ARSERITIARISIS ARSERISIS ARSERALIS ARSERALIS ARSERALIS ARSERALIS ARSERALIS ARSERALIS ARSERISISARISIS ARSERALIS ARSERISISARISIARISIARISIARISTIARIGIS Разложение по собственной функции преобразования Лапласа обратной функции
      • А. Мурли, С. Куомо, Л. Д’Аморе, А. Галлетти

      • Математика

      • 2007

      Мы опишем численное приближение обратной функции Лапласа на основе преобразования Лапласа по собственной функции обратная функция в реальном случае. Анализ ошибок позволяет нам…

      Функции Лагерра в обращении преобразования Лапласа

      • К. Кунья, Фермин Вилош

      • Математика

      • 1993

      Авторы представляют метод численного обращения преобразования Лапласа, основанный на рядах Фурье функций Лагерра.

      No related posts.