Уравнение нормали и касательной: Как составить уравнение касательной и нормали к кривой в точке: формула, примеры решений

alexxlab / / Разное

Содержание

Краткий курс высшей математики

Краткий курс высшей математики
  

Шнейдер В. Е. и др. Краткий курс высшей математики. Учеб. пособие для втузов. М., «Высш. школа», 1972. 640 с.

Данное учебное пособие предназначено для студентов вечерних факультетов втузов и заводов-втузов. Оно в основном охватывает весь материал, предусмотренный обязательной программой. Достаточное количество решенных примеров и задач способствует лучшему усвоению теоретического материала.



Оглавление

ПРЕДИСЛОВИЕ
ГЛАВА I. МЕТОД КООРДИНАТ. ПОНЯТИЕ ФУНКЦИИ
§ 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. КООРДИНАТЫ ТОЧКИ НА ПРЯМОЙ
2. Геометрическое изображение действительных чисел. Координаты точки на прямой
3. Абсолютная величина действительного числа
4. Расстояние между двумя точками на прямой
§ 2. КООРДИНАТЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
2. Расстояние между двумя точками на плоскости
3. Деление отрезка в данном отношении
4. Координаты точки в пространстве
5. Расстояние между двумя точками в пространстве
§ 3. УГОЛ МЕЖДУ ДВУМЯ ОСЯМИ. ПОЛЯРНЫЕ КООРДИНАТЫ
2. Полярные координаты
3. Зависимость между декартовыми и полярными координатами
§ 4. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ
2. Понятие функции
3. График функции
4. Способы задания функций
5. Основные элементарные функции и их графики
6. Сложные функции. Элементарные функции
7. Целые и дробно-рациональные функции
8. Функции четные и нечетные. Периодические функции
§ 5. УРАВНЕНИЕ ЛИНИИ
2. Нахождение уравнения линии по ее геометрическим свойствам
§ 6 ПРЕОБРАЗОВАНИЕ КООРДИНАТ
2. Поворот осей координат
ГЛАВА II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
§ 1. ПРЯМАЯ
2. Уравнение прямой с угловым коэффициентом
3. Уравнение прямой, параллельной оси ординат
4. Общее уравнение прямой и его частные случаи
5. Точка пересечения прямых. Построение прямой по ее уравнению
6. Вычисление угла между двумя прямыми. Условия параллельности и перпендикулярности двух прямых
7. Уравнение прямой, проходящей через данную точку в заданном направлении
8. Пучок прямых
9. Уравнение прямой, проходящей через две данные точки
10. Расстояние от точки до прямой
§ 2. КРИВЫЕ ВТОРОГО ПОРЯДКА
2. Окружность
3. Эллипс
4. Гипербола
5. Парабола
6. Окружность, эллипс, гипербола и парабола как конические сечения
7. Упрощение уравнения кривой второго порядка. График квадратного трехчлена
8. Уравнение равносторонней гиперболы, асимптоты которой приняты за оси координат
9. График дробно-линейной функции
10. Преобразование уравнения кривой второго порядка, не содержащего члена с произведением координат
ГЛАВА III. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ И ВЕКТОРНОЙ АЛГЕБРЫ
§ 1. ЭЛЕМЕНТЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ
2. Определитель третьего порядка
3. Понятие об определителях высших порядков
§ 2. СИСТЕМЫ УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ
2. Однородная система двух уравнений первой степени с тремя неизвестными
3. Система трех уравнений первой степени с тремя неизвестными
4. Однородная система трех уравнений первой степени с тремя неизвестными
§ 3. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
2. Линейные операции над векторами
4. Проекция вектора на ось и составляются вектора по оси
5. Разложение вектора на составляющие по осям координат
6. Направляющие косинусы вектора
7. Условие коллинеарности двух векторов
8. Скалярное произведение
9. Выражение скалярного произведения через проекции перемножаемых векторов
10. Косинус угла между двумя векторами
11. Векторное произведение
12. Выражение векторного произведения через проекции перемножаемых векторов
13. Смешанное произведение трех векторов
14. Геометрический смысл смешанного произведения
15. Условие компланарности трех векторов
§ 4. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
2. Равенство матриц. Действия над матрицами
3. Обратная матрица
4. Матричная запись и матричное решение системы уравнений первой степени
§ 5. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ
2. Преобразование координат
3. Приведение квадратичной формы к каноническому виду
4. Упрощение общего уравнения кривой второго порядка
ГЛАВА IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
§ 1. ПЛОСКОСТЬ
2. Нормальный вектор плоскости. Уравнение плоскости, проходящей через данную точку
3. Общее уравнение плоскости и его частные случаи
4. Построение плоскости по ее уравнению
5. Угол между плоскостями. Условия параллельности и перпендикулярности двух плоскостей
6. Точка пересечения трех плоскостей
§ 2. ПРЯМАЯ В ПРОСТРАНСТВЕ
2. Общие уравнения прямой
3. Векторное уравнение прямой. Параметрические уравнения прямой
4. Канонические уравнения прямой
5. Уравнения прямой, проходящей через две точки
6. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых
§ 3. Прямая и плоскость в пространстве
2. Точка пересечения прямой с плоскостью
3. Расстояние от точки до плоскости
4. Пучок плоскостей
§ 4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
2. Цилиндрические поверхности
3. Конические поверхности
4. Поверхность вращения
6. Гиперболоиды
7. Параболоиды
ГЛАВА V. ТЕОРИЯ ПРЕДЕЛОВ
§ 1. ПРЕДЕЛ ФУНКЦИИ
2. Предел функции при х -> -оо
3. Предел функции при х->х0
4. Бесконечно малые функции. Ограниченные функции
5. Бесконечно большие функции и их связь с бесконечно малыми функциями
6. Основные теоремы о пределах
7. Предел функции при x -> 0
8. Последовательность. Число e
9. Натуральные логарифмы
10. Сравнение бесконечно малых функций
§ 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ
2. Операции над непрерывными функциями. Непрерывность элементарных функций
3. Свойства функций, непрерывных на сегменте
4. Понятие об обратной функции
5. Обратные тригонометрические функции
6. Показательная и логарифмическая функции
7. Понятие о гиперболических функциях
ГЛАВА VI. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
1. Приращение аргумента и приращение функции
2. Определение непрерывности функции с помощью понятии приращения аргумента и приращения функции
3. Задачи, приводящие к понятию производной
4. Определение производной и ее механический смысл
5. Дифференцируемость функции
6. Геометрический смысл производной
7. Производные некоторых основных элементарных функций
8. Основные правила дифференцирования
9. Производная обратной функции
10. Производные обратных тригонометрических функций
11. Производная сложной функции
§ 12. Производные гиперболических функций
13. Производная степенной функции с любым показателем
14. Сводная таблица формул дифференцирования
15. Неявные функции и их дифференцирование
16. Уравнения касательной а нормали к кривой
17. Графическое дифференцирование
§ 2. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
1. Нахождение производных высших порядков
2. Механический смысл второй производной
§ 3. ДИФФЕРЕНЦИАЛ ФУНКЦИИ
2. Производная как отношение дифференциалов
3. Дифференциал суммы, произведения и частного функций
4. Дифференциал сложной функции. Инвариантность формы дифференциала
5. Применение дифференциала к приближенным вычислениям
6. Дифференциалы высших порядков
§ 4. ФУНКЦИИ, ЗАДАННЫЕ ПАРАМЕТРИЧЕСКИ, И ИХ ДИФФЕРЕНЦИРОВАНИЕ
2. Дифференцирование функций, заданных параметрически
§ 5. ВЕКТОРНАЯ ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
2. Векторная функция скалярного аргумента и ее производная
3. Уравнения касательной прямой и нормальной плоскости к пространственной кривой
4. Механический смысл первой и второй производных векторной функции скалярного аргумента
§ 6. НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
2. Теорема Ролля
3. Теорема Лагранжа
4. Правило Лопиталя
§ 7. ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ПОСТРОЕНИЮ ГРАФИКОВ
2. Максимум и минимум функции
3. Достаточный признак существования экстремума, основанный на знаке второй производной
4.
Отыскание наибольшего и наименьшего значений функции
5. Применение теории максимума и минимума к решению задач
6. Выпуклость и вогнутость графика функции. Точки перегиба
7. Асимптоты графика функции
8. Общая схема исследования функции и построение ее графика
§ 8. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
2. Уточнение найденных значений корней методом хорд и касательных
§ 9. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА
ГЛАВА VII. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА
2. Геометрический смысл неопределенного интеграла
3. Таблица основных интегралов
4. Основные свойства неопределенного интеграла
§ 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
2. Интегрирование методом замены переменной
3. Интегрирование по частям
§ 3. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
2. Рациональные дроби. Выделение правильной рациональной дроби
3. Интегрирование простейших рациональных дробей
4. Разложение правильной рациональной дроби на простейшие дроби
5. Метод неопределенных коэффициентов
6. Интегрирование рациональных дробей
§ 4. Интегрирование тригонометрических функций
2. Рациональные функции двух переменных
3. Интегралы вида
§ 5. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ
2. Интеграл вида
3. Интегралы видов
4. Интегралы вида
§ 6. ОБЩИЕ ЗАМЕЧАНИЯ О МЕТОДАХ ИНТЕГРИРОВАНИЯ. ИНТЕГРАЛЫ, НЕ БЕРУЩИЕСЯ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
2. Понятие об интегралах, не берущихся в элементарных функциях
ГЛАВА VIII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. ЗАДАЧИ, ПРИВОДЯЩИЕ К ОПРЕДЕЛЕННОМУ ИНТЕГРАЛУ
2. Задача о работе переменной силы
§ 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
2. Свойства определенного интеграла
3. Производная интеграла по переменной верхней границе
4. Формула Ньютона—Лейбница
5. Замена переменной в определенном интеграле
6. Интегрирование по частям в определенном интеграле
§ 3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
2. Вычисление площади в полярных координатах
3. Вычисление объема тела по известным поперечным сечениям
4. Объем тела вращения
5. Длина дуги кривой
6. Дифференциал дуги
7. Площадь поверхности вращения
8. Общие замечания о решении задач методом интегральных сумм
§ 4. КРИВИЗНА ПЛОСКОЙ КРИВОЙ
2. Вычисление кривизны
3. Радиус кривизны. Круг кривизны. Центр кривизны
4. Эволюта и эвольвента
§ 5. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
2. Интегралы от разрывных функций
3. Признаки сходимости несобственных интегралов
§ 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
2. Метод трапеций
3. Метод параболических трапеций (метод Симпсона)
ГЛАВА IX. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
2. График функции двух переменных
3. Функции трех и большего числа переменных
§ 2. Предел функции нескольких переменных. Непрерывность функции. Точки разрыва
2. Непрерывность функции нескольких переменных
3. Понятие области
4. Точки разрыва
5. Свойства функций, непрерывных в ограниченной замкнутой области
§ 3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ
2. Геометрический смысл частных производных функции двух переменных
3. Частные производные высших порядков
§ 4. ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
2. Полный дифференциал функции
3. Приложение полного дифференциала к приближенным вычислениям
§ 5. Дифференцирование сложных и неявных функций
2. Инвариантность формы полного дифференциала
3. Дифференцирование неявных функций
§ 6. СКАЛЯРНОЕ ПОЛЕ
2. Производная по направлению
3. Градиент
4. Касательная плоскость а нормаль к поверхности
5. Геометрический смысл полного дифференциала функции двух переменных
§ 7. ЭКСТРЕМУМ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ
2. Наибольшее и наименьшее значения функции двух переменных
ГЛАВА X. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
§ 1. ДВОЙНОЙ ИНТЕГРАЛ
2. Двойной интеграл. Теорема существования
3. Свойства двойного интеграла
4. Вычисление двойного интеграла в декартовых координатах
5. Вычисление двойного интеграла в полярных координатах
6. Приложения двойного интеграла
§ 2. ТРОЙНОЙ ИНТЕГРАЛ
2. Тройной интеграл и его свойства
3. Вычисление тройного интеграла в декартовых координатах
4. Вычисление тройного интеграла в цилиндрических координатах
5. Приложения тройного интеграла
§ 3. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
2. Задача о работе. Криволинейный интеграл
3. Вычисление криволинейного интеграла
4. Формула Остроградского — Грина
5. Независимость криволинейного интеграла от пути интегрирования
6. Отыскание первообразной по полному дифференциалу
7. Криволинейный интеграл по длине дуги
ГЛАВА XI. РЯДЫ
§ 1. ЧИСЛОВЫЕ РЯДЫ
2. Геометрическая прогрессия
3. Простейшие свойства числовых рядов
4. Необходимый признак сходимости ряда
5. Достаточные признаки сходимости знакоположительных рядов
6. Знакопеременные ряды
7. Остаток ряда и его оценка
§ 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
2. Правильно сходящиеся функциональные ряды и их свойства
§ 3. СТЕПЕННЫЕ РЯДЫ
2. Свойства степенных рядов
3. Ряды по степеням разности х-а
4. Разложение функций в степенные ряды. Ряд Тейлора
5. Разложение некоторых элементарных функций в ряды Тейлора и Маклорена
§ 4. ПРИЛОЖЕНИЕ РЯДОВ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
2. Приближенное вычисление интегралов
§ 5. ПОНЯТИЕ О ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ. СТЕПЕННЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
2. Числовые ряды с комплексными членами
3. Степенные ряды в комплексной области
§ 6. РЯДЫ ФУРЬЕ
2. Ряд Фурье
3. Сходимость ряда Фурье
4. Ряды Фурье для четных и нечетных функций
5. Разложение в ряд Фурье функций с периодом 2l
ГЛАВА XII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
§ 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
2. Дифференциальные уравнения первого порядка
3. Уравнения с разделяющимися переменными
4. Однородные уравнения
5. Линейные уравнения
6. Уравнение в полных дифференциалах
7. Особые решения
8. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера
§ 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
2. Простейшие уравнения второго порядка, допускающие понижение порядка
3. Понятие о дифференциальных уравнениях высших порядков
§ 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
2. Линейные однородные дифференциальные уравнения второго порядка
3. Линейные неоднородные дифференциальные уравнения второго порядка
4. Метод вариации произвольных постоянных
§ 4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
2. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
3. Приложение линейных дифференциальных уравнений второго порядка к изучению механических и электрических колебаний
§ 5. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
2. Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами
§ 6. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ РЯДОВ
§ 7. ПОНЯТИЕ О СИСТЕМАХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
2. Системы линейных дифференциальных уравнений с постоянными коэффициентами
ПРИЛОЖЕНИЕ 1. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА
ПРИЛОЖЕНИЕ 2. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

Как найти уравнение нормали к графику функции в заданной точке?

На данном уроке мы узнаем, как найти уравнение нормали к графику функции в точке и разберём многочисленные

примеры, которые касаются этой задачи. Для качественного усвоения материала нужно понимать геометрический смысл производной и

уметь их находить хотя бы на уровне следующих статей:

Как найти производную? Производная сложной функции

и

Простейшие задачи с производными.

Перечисленные уроки позволят «чайникам» быстро сориентироваться в теме и поднять свои навыки дифференцирования практически с полного нуля. По существу, сейчас последует развёрнутое продолжение параграфа об уравнении касательной 3-й статьи из вышеприведенного списка. Почему продолжение? Уравнение нормали тесно связано с уравнением касательной. Помимо прочего я рассмотрю задачи о том, как построить уравнения этих линий в ситуациях, когда функция задана неявно либо параметрически.

Но сначала освежим воспоминания: если функция дифференцируема в точке (т.е. если существует конечная производная ), то уравнение касательной к графику функции в точке можно найти по следующей формуле:

Это самый распространенный случай, с которым мы уже столкнулись на уроке Простейшие задачи с производными. Однако дело этим не

ограничивается: если в точке существует бесконечная производная: , то касательная будет параллельна оси и её уравнение примет вид . Дежурный пример: функция с

производной , которая обращается в бесконечность

вблизи критической точки . Соответствующая касательная выразится уравнением:

(ось ординат).

Если же производной не существует (например, производной от в точке ), то, разумеется, не существует и общей касательной.

Как различать последние два случая, я расскажу чуть позже, а пока что вернёмся в основное русло сегодняшнего урока:

Что такое нормаль? Нормалью к графику функции в точке называется прямая, проходящая через данную точку перпендикулярно касательной к графику функции в этой точке

(понятно, что касательная должна существовать). Если совсем коротко, нормаль – это перпендикулярная к касательной прямая, проходящая через точку касания.

Как найти уравнение нормали? Из курса аналитической геометрии напрашивается очень простой алгоритм: находим

уравнение касательной и представляем его в общем виде

. Далее «снимаем» нормальный вектор и составляем уравнение нормали по точке и направляющему вектору .

Этот способ применять можно, но в математическом анализе принято пользоваться готовой формулой, основанной на взаимосвязи угловых коэффициентов перпендикулярных прямых. Если

существует конечная и отличная от нуля производная , то уравнение нормали к графику функции в точке выражается следующим уравнением:

Особые случаи, когда равна нулю либо бесконечности мы обязательно рассмотрим, но сначала «обычные» примеры:

Пример 1 Составить уравнения касательной и нормали к графику кривой

в точке, абсцисса которой равна .

В практических заданиях часто требуется найти и касательную тоже. Впрочем, это очень только нА руку – лучше будет «набита рука» =)

Решение: Первая часть задания хорошо знакома, уравнение касательной составим по формуле:

В данном случае:

Найдём производную:

Здесь на первом шаге вынесли константу за знак производной, на втором – использовали правило дифференцирования сложной функции.

Теперь вычислим производную в точке :

Получено конечное число и это радует. Подставим и в формулу

:

Перебросим наверх левой части, раскроем скобки и представим уравнение касательной в общем виде:

Вторая часть задания ничуть не сложнее. Уравнение нормали составим по формуле:

Избавляемся от трёхэтажности дроби и доводим уравнение до ума:

– искомое уравнение.

Ответ:

Здесь можно выполнить частичную проверку. Во-первых, координаты точки должны удовлетворять каждому уравнению:

– верное равенство.

– верное равенство.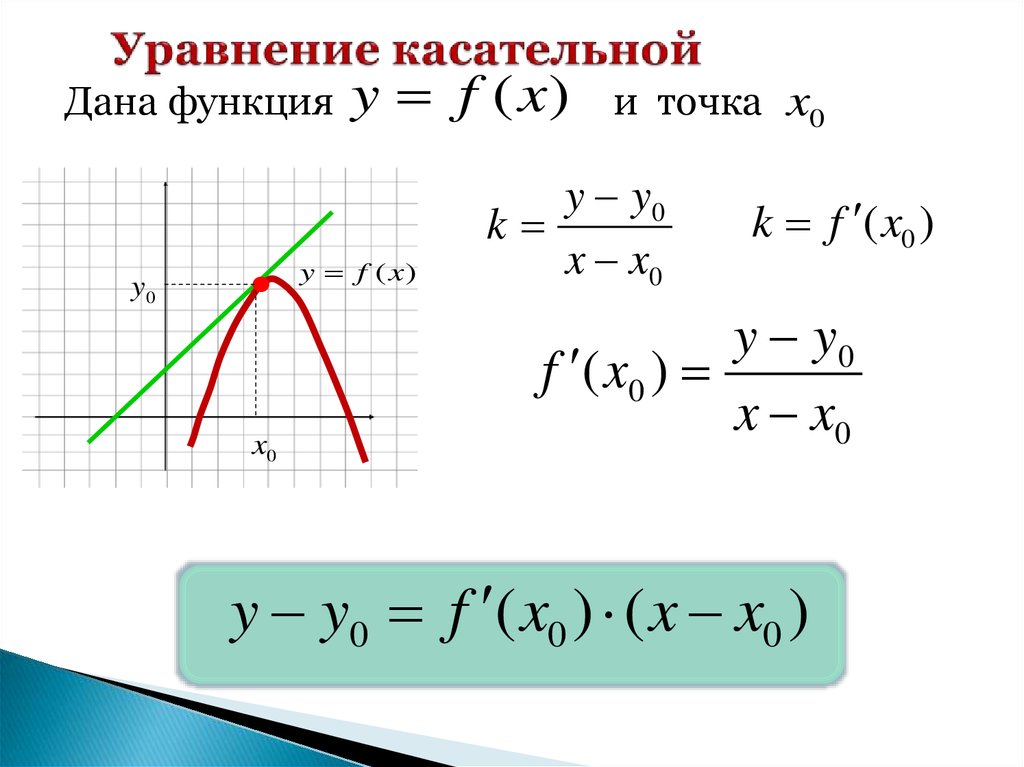

И, во-вторых, векторы нормали должны быть

ортогональны. Это элементарно проверяется с помощью скалярного произведения:

, что и требовалось проверить.

Как вариант, вместо нормальных векторов можно использовать

направляющие векторы прямых.

! Данная проверка оказывается бесполезной, если неверно найдена производная и/или производная в точке . Это «слабое звено» задания – будьте предельно внимательны!

Чертежа по условию не требовалось, но полноты картины ради:

Забавно, но фактически получилась и полная проверка, поскольку чертёж выполнен достаточно точно =) Кстати, функция

задаёт верхнюю дугу эллипса. Следующая задача для самостоятельного решения:

Пример 2 Составить уравнения касательной и нормали к графику функции

в точке .

Примерный образец чистового оформления задания в конце урока. Теперь разберём два особых случая:

1) Если производная в точке равна нулю: , то уравнение касательной упростится:

То есть, касательная будет параллельна оси . Соответственно, нормаль будет проходить через точку

параллельно оси , а значит её уравнение примет вид .

2) Если производная в точке существует, но бесконечна: , то, как отмечалось в самом начале статьи, касательная станет вертикальной: . И поскольку нормаль проходит через точку параллельно оси , то её уравнение выразится «зеркальным» образом: Всё просто:

Пример 3

Составить уравнения касательной и нормали к параболе в точке . Сделать чертёж.

Требование выполнить чертёж я не добавлял – так было сформулировано задание в оригинале. Хотя это редкость.

Решение: составим уравнение касательной .

В данном случае

Казалось бы, расчёты пустяковые, а в знаках запутаться более чем реально:

Таким образом:

Поскольку касательная параллельна оси (Случай №1), то нормаль, проходящая через ту же точку , будет параллельна оси ординат:

Чертёж – это, конечно же, дополнительные хлопоты, но зато добротная проверка аналитического решения:

Ответ: ,

В школьном курсе математики распространено упрощённое определение касательной, которое формулируется примерно так:

«Касательная к графику функции – это прямая, имеющая с данным графиком единственную общую точку». Как видите, в общем случае это утверждение некорректно. Согласно геометрическому смыслу производной, касательной является именно зелёная, а не синяя прямая.

Следующий пример посвящён тому же Случаю №1, когда : Пример 4

Написать уравнение касательной и нормали к кривой в точке .

Краткое решение и ответ в конце урока

Случай №2, в котором на практике встречается редко, поэтому начинающие могут особо не волноваться и с лёгким сердцем пропустить пятый пример. Информация, выделенная курсивом, предназначена для читателей с высоким уровнем подготовки, которые хорошо разобрались с определениями производной и касательной, а также имеют опыт нахождения производной по определению:

Пример 5 Найти уравнения касательной и нормали к графику функции

в точке

Решение: в критической точке знаменатель производной обращается в ноль, и поэтому здесь нужно

вычислить односторонние производные с помощью определения производной (см. конец статьи Производная по определению):

Обе производные бесконечны, следовательно, в точке

существует общая вертикальная касательная:

Ну, и очевидно, что нормалью является ось абсцисс. Формально по формуле:

Для лучшего понимания задачи приведу чертёж:

Ответ:

Я рад, что вы не ушли бороздить просторы Интернета, потому что всё самое интересное только начинается! Чтобы осилить материал следующего параграфа, нужно уметь находить производную от неявно заданной функции:

Касательные и нормали — определение, формула, примеры, часто задаваемые вопросы

Касательные и нормали — это линии, связанные с кривыми. Касательная — это линия, касающаяся кривой в отдельной точке, и каждая точка кривой имеет касательную. Нормаль – это линия, перпендикулярная касательной в точке касания. Уравнение таланта в точке (x 1 , y 1 ) имеет вид (y — y 1 ) = m(x — x 1 ), а уравнение нормали, проходящей через эта же точка есть (y — y 1 ) = -1/м. (х — х 1 ).

Давайте узнаем больше о том, как найти уравнение касательных и нормалей для различных кривых, таких как окружность, парабола, эллипс, гипербола, и их свойствах с помощью примеров, часто задаваемых вопросов.

1. Что такое касательные и нормали?
2. Как найти касательные и нормали?
3. Касательные и нормали для различных кривых
4. Свойства касательных и нормалей
5. Примеры касательных и нормалей
6. Практические вопросы
7. Часто задаваемые вопросы по касательным и нормалям

Что такое касательные и нормали?

Касательные и нормали — это линии, связанные с такими кривыми, как окружность, парабола, эллипс, гипербола. Касательная — это линия, касающаяся кривой в одной отдельной точке, и эта отдельная точка называется точкой касания. Нормаль – это линия, перпендикулярная касательной, в точке касания. Нормаль также проходит через фокус кривой.

Существует множество касательных, которые можно провести к кривой в каждой из отдельных точек, лежащих на кривой.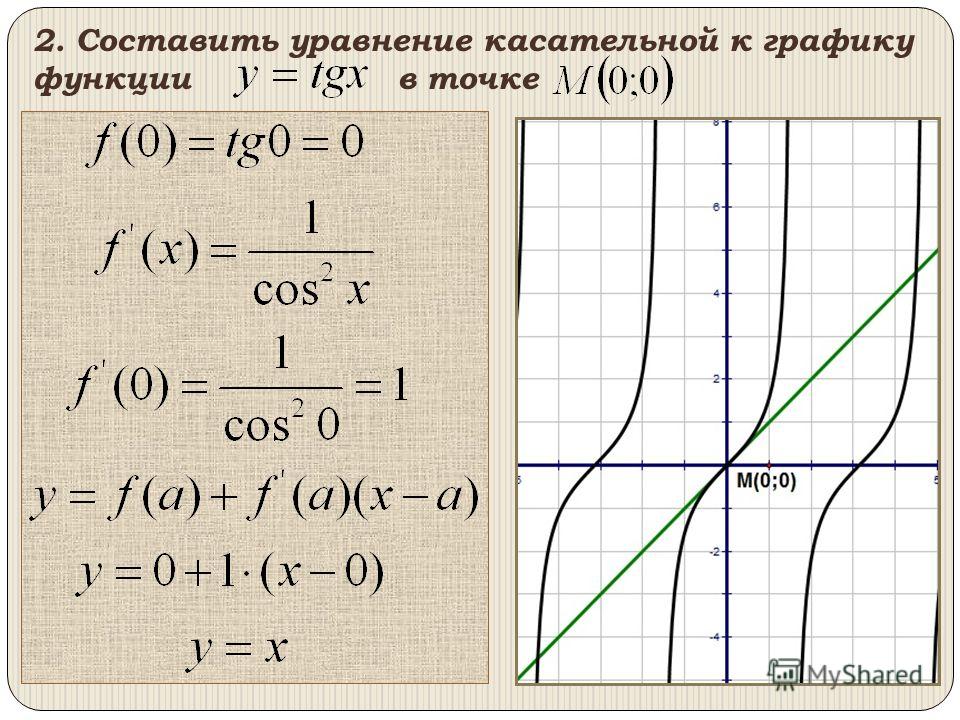 Касательные и нормали являются прямыми линиями и, следовательно, они представлены в виде линейного уравнения относительно x и y. Общая форма уравнения касательной и нормали: ax + by + c = 0. Точка касания удовлетворяет уравнению касательной и уравнению кривой.

Как найти касательные и нормали?

Касательная и нормаль могут быть вычислены с помощью уравнения кривой. Уравнение касательной и нормали можно вычислить дифференцированием уравнения кривой. Дифференцирование кривой по независимой переменной x равно dy/dx и дает наклон касательной, а отрицательное значение, обратное дифференцированию -dx/dy, дает наклон нормали к кривой.

Этот наклон представляется как m = dy/dx, а уравнение касательной и нормали можно рассчитать с помощью точечно-наклонной формы уравнения прямой — (y — y 1 ) = m (х — х 1 ).

Касательная и нормаль перпендикулярны друг другу, а произведение наклона касательной и наклона нормали равно -1. Общая форма уравнения касательной, проходящей через точку (x 1 , y 1 ) и имеющей наклон m: \((y — y_1) = m(x — x_1)\). А уравнение нормали, проходящей через эту же точку, имеет вид \((y — y_1) = \dfrac{-1}{m}(x — x_1)\)

Касательные и нормали для различных кривых

Касательные и нормали могут быть сформированы для следующего ниже набора кривых. Касательные и нормали можно рисовать для окружности, параболы, гиперболы эллипса соответственно.

  • Окружность: Уравнение касательной к окружности x 2 + y 2 + 2gx + 2fy + c = 0 в точке (x 1 , y 1 ) равно xx 1 + 030 900 1 + г(х + х 1 ) + f(y + y 1 ) + c = 0,

  • Парабола: Уравнение касательной к параболе y 2 = 4ax в точке (x 1 , y 1 ) равно yy 1 = 2a(x + x 1 ).

  • Эллипс: Уравнение касательной к эллипсу х 2 /а 2 + у 2 /b 2 = 1 в точке0004 /a 2 + yy 1 /b 2 = 1.

  • Гипербола: уравнение касательной к гиперболе x 2 /a 2 — y 2 /b 2 = 1 в точке (x 1 , y 1 90 x 304 1 0) /a 2 — yy 1 /b 2 = 1.

Уравнение нормали в точке (x 1 , y 1 ) для каждой кривой можно рассчитать, взяв обратное отрицательное дифференцирование кривой в точке в качестве наклона, а затем образуя уравнение нормали.

Свойства касательных и нормалей

Следующие свойства касательных и нормалей помогают лучше понять касательные и нормали.

  • Касательная и нормали перпендикулярны друг другу.
  • Произведение наклонов касательной и нормали равно -1.
  • Касательные лежат вне кривой, а нормали лежат внутри кривой.
  • С каждым тангенсом кривой связана нормаль.
  • Нормаль к кривой наверняка не проходит через фокус или центр кривой.
  • Касательные и нормали представляют собой прямые линии и представляются в виде линейных уравнений.
  • К кривой можно провести бесконечное количество касательных.

Связанные темы

Следующие темы помогают лучше понять касательные и нормали.

  • Общие касательные
  • Копланарная
  • Линейная симметрия
  • Конгруэнтные линии
  • Самолет Арганда

Часто задаваемые вопросы по касательным и нормалям

Что такое касательные и нормали?

Касательные и нормали — это линии, связанные с такими кривыми, как окружность, парабола, эллипс, гипербола. Касательная — это линия, касающаяся кривой в одной отдельной точке, и эта отдельная точка называется точкой касания. Нормаль – это линия, перпендикулярная касательной, в точке касания. Нормаль также проходит через фокус кривой.

Как найти касательные и нормали?

Касательные и нормали могут быть найдены с помощью точечно-наклонной формы уравнения прямой — (y — y 1 ) = m(x — x 1 ). Наклон касательной можно вычислить, взяв производную уравнения кривой по независимой переменной x, которая равна m = dy/dx, а наклон нормали равен отрицательной обратной величине дифференцирование m = -dx/dy.

Что такое уравнение касательных и нормалей?

Уравнение касательной и нормали можно вычислить с помощью формальной геометрии координат формы точка-наклон. Уравнение касательной имеет вид (y — y 1 ) = m(x — x 1 ), а уравнение нормали, проходящей через эту же точку и перпендикулярной касательной, имеет вид (y — y 1 ) = -1/м. (х — х 1 ).

Что говорят нам касательные и нормали?

Касательные говорят нам направление, в котором сила, действующая на тело, движущееся по кругу, действовала бы наружу, а та же удерживающая сила, действующая на тело во внутреннем направлении, отождествляется с нормалью.

Какая связь между касательными и нормалями?

Касательные и нормы — это набор прямых, перпендикулярных друг другу. Произведение наклонов касательных и нормалей равно -1. Наклон касательной равен m = dy/dx, а наклон нормали равен m = -dx/dy.

Нахождение уравнения нормали к кривой — Криста Кинг Математика

Что такое нормальная линия и шаги, которые мы предпринимаем, чтобы найти ее уравнение

В каждой точке функции функция имеет наклон, который мы можем вычислить. Если наша функция представляет собой прямую линию, она будет иметь одинаковый наклон в каждой точке. Но для любой функции, которая не является прямой линией, наклон функции будет меняться по мере изменения значения функции.

Чтобы найти наклон функции в определенной точке, мы можем взять производную функции, а затем вычислить ее в интересующей нас точке. Это дает нам наклон функции в точке, но также наклон касательной к функции в этой точке.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Нормальная линия — это линия, перпендикулярная касательной в точке, где касательная пересекает функцию. Это означает, что если наклон касательной равен ???m???, то наклон нормальной линии является отрицательной обратной величиной ???m???, или ???-1/m?? ?.

Итак, выполните следующие действия, чтобы найти уравнение нормальной линии.

  1. Возьмите производную исходной функции и оцените ее в заданной точке. Это наклон касательной, которую мы назовем ???m???.

  2. Найдите отрицательную обратную величину ???m???, другими словами, найдите ???-1/m???. Это наклон нормальной линии, которую мы назовем ???n???. Итак, ???n=-1/m???.

  3. Вилка ???n??? и данную точку в формулу наклона точки для уравнения линии, ???(y-y_1)=n(x-x_1)???.

  4. Упростите уравнение, найдя ???y???.

Как именно найти уравнение нормали к кривой в определенной точке (плюс как найти касательную в той же точке)

Пройти курс

Хотите узнать больше об исчислении 1? У меня есть пошаговый курс для этого.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *