Матрицу разложить по строке онлайн: Определитель матрицы онлайн

Содержание

Матрицы и определители — презентация онлайн

Похожие презентации:

Матрицы и определители

Определители матриц. Обратная матрица, ранг матрицы

Определители и их свойства

Матрицы и определители. (Тема 1)

Определители. Свойства определителей

Матрицы и определители. (Лекция 1)

Определители. Свойства определителей и методы их вычисления

Определители. Свойства определителей

1. Математика Тема 1. Матрицы и определители. Лекция 2

Данчул Александр Николаевич
зав. кафедрой информационных
технологий в управлении,
д.т.н., профессор
436-03-23, каб.2125 (2 корп.)
[email protected]
2012 г.

2. Минор и алгебраическое дополнение элемента квадратной матрицы

Опр. 14. Минором Мij элемента a ij квадратной матрицы А
n-го порядка называется определитель матрицы,
полученной из A удалением i-ой строки и j-го столбца.

Опр. 15. Алгебраическим дополнением Аij элемента a ij
квадратной матрицы А называется минор этого элемента
со знаком, определяемым по «шахматному правилу»
Аij=(-1)i+j Мij
+-+-+-+
+-+1 0 2
1 0
2 3
A 1 3 4 ; A23 ( 1)
(1 1 0 ( 2)) 1
2 1
2 1 5

3. Вычисление определителя квадратной матрицы разложением по строке (столбцу)

Теорема Лапласа
1. Определитель квадратной матрицы равен сумме
произведений элементов любой строки (столбца)
матрицы А на их алгебраические дополнения.
разложение по i-ой строке
n
i A aij Aij ai1 Ai1 ai 2 Ai 2 ain Ain
j 1
разложение по j-ому столбцу
n
j A aij Aij a1 j A1 j a2 j A2 j anj Anj
i 1

4. Вычисление определителя квадратной матрицы разложением по строке (столбцу)

1
0 2
3 4
1 4
1 3
1 3 4 1
0 ( 1)
2
1 5
2 5
2 1
2 1 5
1 (3 5 1 4) 0 2 (( 1) 1 3 ( 2)) 11 10 21
Теорема Лапласа
2. Сумма произведений элементов любой строки
(столбца) матрицы А на алгебраические дополнения
соответствующих элементов любой другой строки
(столбца) матрицы А равно 0.

n
i k aij Akj ai1 Ak1 ai 2 Ak 2 ain Akn 0
k i
j 1
n
j l aij Ail a1 j A1l a2 j A2l anj Anl 0
l j
i 1

5. Вычисление определителей

Определитель удобно вычислять по строке или столбцу,
содержащему наибольшее число нулей.
Определитель диагональной и треугольной матрицы равен
произведению элементов, принадлежащих главной диагонали.
1
*
i
0
n
n
l 1
l 2
A ai1 Ai1 a11 A11 ai1 A11
a11
A11
1 3 0
0 2 5
0 0 1
a11 A11
n
0 A
l 1, l j
i1
a11 A11
3
A a11 A11 0 Ai1 1 A11
l 2
1 ( 2 1 5 0) 1 2 1 2
Определитель единичной матрицы равен 1
1 0 0
E 0 1 0
0 0 1

6. Свойства определителей

Можно доказать, используя теорему Лапласа
i A
n
a
j 1
ij
Aij ;
j A
n
a
i 1
ij
Aij
1. При транспонировании матрицы ее определитель не меняется.
Свойства строк и столбцов одинаковы.
2.

Если все элементы какой-либо строки матрицы равны 0, то ее
определитель тоже равен 0.
3. Если все элементы какой-либо строки матрицы умножить на
число λ, то ее определитель тоже умножится на λ.
4. При перестановке любых двух строк матрицы ее определитель
меняет знак на противоположный.
5. Если матрица содержит две одинаковые строки, то ее
определитель равен 0.
6. Если элементы двух строк матрицы пропорциональны, ее
определитель равен 0.
7. Определитель матрицы не изменится, если к элементам какойлибо строки прибавить соответствующие элементы другой
строки, предварительно умноженные на одно и то же число λ.
8. det (A·B) = det (A) · det (B)

7. Элементарные преобразования матриц

№ Преобразование
Характеристика
изменения
1 Транспонирование матрицы
Определитель не меняется
2 Перестановка двух строк
(столбцов)
Определитель меняет знак
3 Сложение одной строки с
другой строкой, умноженной
на число
Определитель не меняется
4 Умножение одной строки на
число
Определитель умножается
на это число
5 Вычеркивание нулевой
строки
Меняется размер матрицы

8.

Обратная матрицаЧисло а-1 называется обратным к числу а, отличному от 0, если
а-1· а = а· а-1 =1.
-1
Опр. 16. Матрица А называется обратной квадратной
матрице А порядка n, если
-1 ·
-1
А А = А · А =Е.
(1)
Очевидно,
что по правилам умножения матриц матрицы
-1
А и Е должны быть квадратными порядка n.
Так как умножение матриц некоммутативно, докажем
совпадение левой и правой обратных матриц, умножаемых
слева и справа на А в формуле (1).
Aл 1 Aл 1 E Aл 1 ( A Aп 1 ) ( Aл 1 A) Aп 1 E Aп 1 Aп 1
Опр. 17. Квадратная матрица А называется вырожденной,
если ее определитель равен 0.

9. Вычисление обратной матрицы

Необходимым и достаточным условием существования
для А обратной матрицы является ее невырожденность.
1
~
A
A
det A
1
(2)
~
где A — присоединенная матрица, элементы a~ij которой
получаются транспонированием матрицы алгебраических
дополнений исходной матрицы .

i j a~ij A ji
Пример:
1 2
1 2
; det A
A
1 5 3 2 1;
3 5
3 5
A11 5;
A12 3;
A21 2; A22 1;
~ 5 2
;
A
3 1
1 5 2 5 2
A
( 1) 3 1 3 1
1

10. Ранг матрицы

Опр. 18. Минором порядка k матрицы А размера m n
называется определитель матрицы, полученной из А
выделением произвольных k ее строк и k столбцов.
Очевидно, что 1 ≤ k ≤ min (m, n)
Опр. 19. Рангом матрицы А называется наивысший
порядок отличного от нуля минора этой матрицы.
Ранг нулевой матрицы равен 0.
Очевидно, что 0 ≤ r(A) ≤ min (m, n)
0 0 0
A 1 3 4 ;
2 1 5
3 4
det A 0;
3 5 4 1 11; r ( A) 2
1 5
При элементарных преобразованиях матрицы ее
ранг не меняется.

11. Вычисление ранга матрицы

1. Ранг диагональной матрицы равен числу элементов
диагонали, отличных от нуля.
0
0
0
0
В ненулевой минор выделяем строки и столбцы, где стоят
ненулевые элементы диагонали.

Все миноры большего
порядка будут содержать нулевую строку.
0
r(A)=2
2. Ранг верхней треугольной матрицы, в которой
все элементы главной диагонали, не равны 0,
равен числу строк.
0
*
3. Ранг прямоугольной матрицы удобно вычислить, приведя ее
элементарными преобразованиями к ступенчатому виду:
верхние строки представляют собой треугольную или
трапециедальную матрицу, в которой все элементы главной
диагонали не равны 0, а нижние строки – нулевые.
Тогда ранг будет равен числу ненулевых строк в этой матрице.

12. Геометрический смысл ранга квадратной матрицы 2-го и 3-го порядка

a1 a2
b1
b2
3 1
1 2
2
3 2 1 1 5 S ; r 2
b 2 a (6 2)
2
3 1
3 2 6 1 0; r 1
6 2
1
0
b
S
1
ā
3
1
Если ранг матрицы равен 1, то векторы a и b — коллинеарны
(находятся на одной линии).
Если ранг матрицы А3 равен 2, то векторы a , b и c — компланарны
(находятся в одной плоскости), а если равен 1, то коллинеарны.

Ранг матрицы равен размерности фигуры (тела), построенной
на векторах, координаты которых записаны в строках
матрицы.

English Русский Правила

Расширяемые заголовки строк в матрицах

Power BI теперь позволяет расширять заголовки строк, как и в сводной таблице Excel:

Вы можете нажать на символы +, чтобы развернуть содержимое строки.

Два сюрприза для меня с этой функцией: она не работает для заголовков столбцов, и символы + не включены по умолчанию (предположительно из соображений совместимости).

Когда доступны заголовки строк

Чтобы иметь возможность расширять заголовки строк, необходимо иметь более одного поле. Вот пример поля подходящей матрицы:

С помощью этой матрицы вы сможете расширяйте регионы, чтобы увидеть их города, и города, чтобы увидеть их торговые центры. Однако вы не сможете сделать то же самое для заголовков столбцов.

Расширение/свертывание с помощью правой кнопки мыши

Microsoft постепенно начинает больше полагаться на правую кнопку мыши в Power BI, и это лучший способ развернуть/свернуть строки:

Если щелкнуть строку правой кнопкой мыши, вы можете развернуть ее (или, при необходимости, свернуть) на Выбор , Весь уровень или Все . Ниже показано, что означают различные варианты.

Вот что покажут первые два варианта выше:


Выбор	Весь уровень

Выбор Все расширит не только все регионы, но и все их города, чтобы показать свои торговые центры.

Включение кнопок «плюс» и «минус»

Если вам нужен более графический способ расширения или свертывания, включите + / — кнопки:

Вы можете нажать на кнопку +/- значки свойство в нижней части заголовков строк , чтобы включить значки, а затем настроить их размер и цвет (этот пример показан ниже).

Вот что показал бы приведенный выше пример:

Yuk! Размер и цвет значка по умолчанию были намного лучше…

Подробнее о том, как работает расширение и свертывание строк

Вот еще несколько заметок о том, как работает эта новая функция:

Район	Примечания
Сохранение состояния	Если вы сохраните и закроете файл отчета Power BI, Power BI запомнит ваше расширение. /свернуть настройки и восстановить их при повторном открытии файла отчета.
Условное форматирование	Любое условное форматирование будет применяться только к самый низкий уровень детализации, показанный в матрице.
Старое программное обеспечение	Эта функция не работает с табличными моделями SSAS до версии 2016 или с Многомерные модели ССОО.

Чтобы проиллюстрировать второй пункт, вот что мы увидим для нашего примера, если мы применил правило к цветным ячейкам, где общее количество было более 50:

Цветными являются только ячейки на уровне торгового центра (вероятно, именно так вы и хотели бы, чтобы это работало).

Вопрос о таблице матриц

Вопросы о таблицах матриц

Матричные вопросы-таблицы позволяют комбинировать несколько вопросов с одинаковыми ответами. Это наиболее полезно, когда вам нужно задать несколько вопросов, которые должны оцениваться по одной шкале.

Есть несколько вариантов ответа на вопрос о таблице матриц. Каждый вариант имеет уникальные параметры и уникальный формат.

Операторы

и точки шкалы

Операторы — это строки матричной таблицы. Это утверждения, которые вы хотели бы, чтобы респондент оценил.

Точки шкалы — это столбцы матричной таблицы. Это рейтинги, которые вы хотите, чтобы респонденты выбирали для каждого утверждения.

Когда вы устанавливаете в матричной таблице один ответ, вы можете выбрать одну точку шкалы для каждого утверждения. Это то же самое, даже если вы транспонируете таблицу так, что операторы становятся столбцами, а точки шкалы становятся строками.

Добавление и удаление операторов и точек шкалы

Используйте кнопки плюс ( + ) и минус ( – ) под Операторы и Масштабные точки для настройки количества операторов и масштабных точек.

Вы также можете щелкнуть непосредственно имя оператора или точки шкалы и нажать . Введите для каждого параметра, который вы хотите добавить, или используйте Редактировать несколько

для изменения текста. Дополнительные сведения см. в разделе Добавление и редактирование вопросов.

Совет: При добавлении утверждений или точек шкалы у вас есть возможность выбрать один из предложенных вариантов. Это может быть быстрый способ добавить общие варианты выбора, такие как шкала «согласен или не согласен», одним щелчком мыши.

Подсказка: Вы можете настроить ширину столбца, содержащего ваши утверждения, щелкнув и перетащив вертикальную линию слева от ваших утверждений.

Вариации

Для доступа к вариантам таблицы матриц используйте Тип матрицы выпадающее меню. Обратите внимание, что в каждом варианте будет отображаться свой набор параметров редактирования вопроса.

Лайкерт

Вариант Likert отображает список утверждений (строк) и точек шкалы (столбцы) в формате таблицы. Затем вы можете определить, как респонденты отвечают на вопрос, используя раскрывающийся список

Тип ответа :

Разрешить один ответ : Респондент может выбрать один балл шкалы для каждого утверждения.
Разрешить несколько ответов: Респондент может выбрать несколько точек шкалы для каждого утверждения.
Раскрывающийся список : Респондент выбирает один балл шкалы для каждого утверждения, используя раскрывающееся меню.
Перетаскивание : Респондент выбирает одну точку шкалы для каждого утверждения, перетаскивая точки шкалы в сегменты отчетов.

Биполярный

Вариант Bipolar отображает два крайних значения шкалы. Респонденты выбирают точку между двумя крайностями.

Ранг Орден

Вариант Порядок ранжирования позволяет респондентам ранжировать набор баллов по шкале, вводя число для каждого из них.

Вы можете включить несколько утверждений и позволить респонденту ранжировать баллы по шкале для нескольких разных тем (например, «Пожалуйста, оцените следующие темы от 1 до 5 для каждого из следующих ресторанов»).

Постоянная сумма

Вариант Постоянная сумма позволяет респондентам распределять ресурсы между элементами в каждой строке. По мере того как респондент дает ответы, респонденту могут отображаться общие ресурсы.

Таблицы матрицы с постоянной суммой имеют следующие уникальные параметры, которые помогут вам настроить процесс проведения опроса:

Добавить итоговое поле : Добавляет итоговое поле, которое суммирует введенные значения. Вы можете расположить прямоугольник либо на операторах, либо на точках шкалы.
Добавить символ : Добавляет символ до или после каждого поля. Это полезно для добавления символов валюты.
Добавить требуемый диапазон : Позволяет указать минимальное и максимальное значение для каждого поля.

Подсказка: В приведенном выше примере вы заметите, что вы также можете расположить в матрице место, где вы хотите, чтобы итоговое поле отображалось. Здесь итоги отображаются внизу, суммируя значения в столбцах (точки шкалы).

Ввод текста

В варианте Текстовая запись каждая строка содержит набор полей для ввода текста. Этот вариант выглядит и действует аналогично текстовой записи — тип вопроса формы. Вы можете указать размер текстовых полей (короткий, средний, длинный) с помощью Текстовое поле Размер

вариант.

Можно использовать параметры Добавить проверку , чтобы указать, какой тип содержимого разрешается в полях. Вы можете ограничить диапазоны символов, максимальную и минимальную длину символов и пользовательскую проверку.

Профиль

Вариант Profile позволяет отдельно помечать каждую точку шкалы в матричной таблице, чтобы каждая строка могла иметь свои собственные точки шкалы. Чтобы включить изменение профиля, выберите l ikert матричная таблица и изменить формат на p rofile.

Варианты вопросов могут быть с одним ответом, несколькими ответами или раскрывающимся списком.

MaxDiff

MaxDiff — это специализированный вариант матричной таблицы, позволяющий респондентам выбирать по одному варианту в каждой из двух категорий.

Qtip: Заинтересованы в запуске проекта MaxDiff? Посетите наши страницы поддержки по решению MaxDiff XM.

Qtip: Если вам нужно добавить более одной шкалы к одному и тому же набору утверждений, попробуйте вместо этого использовать параллельный вопрос.

Просмотр карусели

Карусельное представление позволяет участникам опроса просматривать матричные таблицы по одному утверждению за раз. В редакторе они выглядят так же, как обычные таблицы матрицы Лайкерта, но при прохождении опроса выглядят так:

Qtip: Независимо от того, включен ли в опросе автоматический переход по вопросам, ответ на утверждение автоматически переводит респондента к следующему утверждению. Если респонденты хотят вернуться назад или пропустить вперед, они могут использовать стрелки по обе стороны от утверждений.

Чтобы включить просмотр карусели:

Выберите матричную таблицу.
Убедитесь, что тип матрицы установлен на Likert .
В разделе Тип ответа выберите либо Разрешить один ответ , либо Разрешить несколько ответов (в зависимости от того, должны ли респонденты выбрать один ответ или несколько ответов).
Для Формат выберите Карусель .
Выберите выравнивание текста вашего заявления. Вы можете выбрать один из следующих вариантов:
- Вертикально : Ответы выстраиваются вертикально под утверждением.
- Горизонтальный : Ответы выстраиваются горизонтально под утверждением.
- Столбец : Разбить ответы на столбцы. Вы можете установить, сколько столбцов.
Выберите Показать ход выполнения , чтобы добавить в карусель индикатор выполнения. Эта полоса заполняется цветом по мере того, как респондент отвечает на утверждения.

Qtip: Опция M obile-friendly гарантирует, что вопрос всегда находится в вертикальном представлении на мобильных устройствах.

Подсказка: В отличие от других матричных таблиц, вы можете добавить текстовую запись для точек шкалы карусельной матрицы.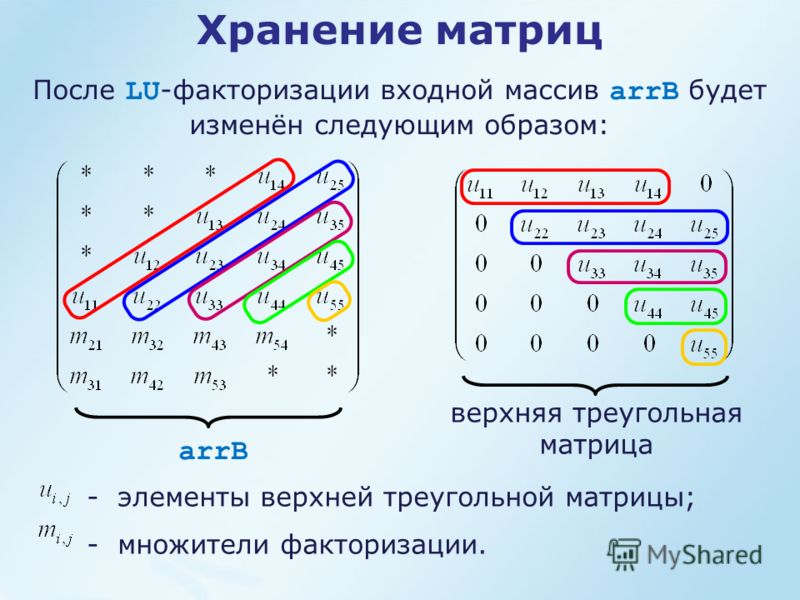

Вот как это выглядит в опросе:

Дополнительные опции для матричных таблиц

В зависимости от варианта таблицы матрицы, который вы выбрали выше, вы можете увидеть некоторые из следующих дополнительных настроек при редактировании вашего вопроса.

Типы ответов

Если вы настроили свою матричную таблицу в формате Likert, вы можете изменить формат ответа.

Разрешить один ответ: Респонденты могут выбрать один балл шкалы для каждого утверждения.
Разрешить несколько ответов: Респонденты могут выбрать несколько точек шкалы для каждого утверждения. Если вы это сделаете, вы получите дополнительные параметры в разделе Добавить подтверждение:
- Выбрано минимальное количество баллов: Требовать от респондентов выбрать определенное количество ответов, прежде чем они смогут продолжить оставшуюся часть опроса. В этом случае нет максимального количества ответов, есть только минимум.
- Диапазон ответов: Укажите минимальное и максимальное количество ответов, которые может дать респондент.
- Пользовательский: Требовать от респондентов выбора конкретных вариантов, прежде чем они смогут продолжить. См. пользовательскую проверку и сообщения пользовательской проверки.
Раскрывающийся список: Респонденты могут выбрать одну точку шкалы для каждого утверждения из раскрывающегося списка. Вы должны выбрать Нажмите здесь, чтобы изменить точки шкалы , чтобы изменить имена точек шкалы.
Перетаскивание: Респонденты могут перетаскивать утверждения в поле одной точки шкалы.

Данные для раскрывающегося списка и перетаскивания имеют тот же формат, что и таблицы с одним ответом Likert.

Подходит для мобильных устройств

При просмотре на мобильных устройствах или при уменьшенном размере экрана матричные таблицы часто требуют от респондентов прокрутки, чтобы увидеть вопрос полностью. Опция , дружественная к мобильным устройствам, форматирует операторы матричных таблиц в аккордеон, чтобы все они могли удобно разместиться на одном экране.

Для получения дополнительной информации о совместимости ваших опросов с мобильными устройствами посетите нашу страницу оптимизации опросов для мобильных устройств.

Транспонировать таблицу

Таблица транспонирования перемещает точки шкалы слева, а утверждения вверху. Однако важно отметить, что выбор работает так же, как если бы таблица не транспонировалась, поэтому для матрицы лайкерта с одним ответом вы можете выбрать только одну точку шкалы для каждого оператора, а экспорт данных будет иметь столбцы, организованные по операторам.

Позиция над текстом

Для более компактного отображения операторы для каждой строки располагаются вверху шкалы, а не слева.

Повторяющиеся заголовки

Повторять заголовки полезно для респондентов, когда матричные таблицы длиннее. Строка заголовка периодически повторяется на протяжении всего вопроса.

Повторить точки шкалы вдоль среднего ряда операторов ( Средний ).

Повторить точки шкалы вдоль нижнего ряда ( Нижний ).

Повторить точки шкалы как в среднем, так и в нижнем ряду ( Оба ).

Повторить точки шкалы над каждой строкой операторов ( Все ).

Добавить пробел

Добавить пробел полезно для респондентов, работающих с более длинными матричными таблицами. Если этот параметр включен, пробелы периодически добавляются по всему вопросу.

Рандомизация выбора

Вы можете рандомизировать варианты в своей матричной таблице в Вопрос Поведение Раздел:

Нажмите Рандомизация операторов , чтобы рандомизировать операторы.
Нажмите Рандомизация точек шкалы , чтобы рандомизировать точки шкалы.

Подробную информацию см. в разделе Рандомизация выбора.

Загруженный формат данных

После того, как ваши ответы будут собраны, Qualtrics предлагает различные методы создания отчетов как внутри платформы, так и вне ее. На вкладке «Данные и анализ» вы можете просматривать ответы на опросы и управлять ими на индивидуальной основе.

При экспорте данных ответа способ форматирования данных таблицы матрицы зависит от формата вопроса. Например, ответ таблицы матрицы текстового ввода может отображаться как строки буквенно-цифровых символов при загрузке, тогда как ответ таблицы матрицы Likert отображается как одно число; каждый формат вопроса имеет другой формат загружаемых данных.

Аналогично всем экспортным товарам

Первые три строки каждого экспорта являются заголовками столбцов. Каждая последующая строка — это ответы разных респондентов.

Подсказка: Если вы добавили теги экспорта в матричную таблицу, имена столбцов экспорта могут отличаться. Подробнее о том, как эта функция влияет на экспорт, см. на связанной странице тегов экспорта.

Таблица матрицы Лайкерта с одним ответом

Для одного ответа вариантов матричной таблицы Лайкерта, где участник может выбрать один ответ для каждого утверждения в вашей матричной таблице, вы найдете один столбец в своем наборе данных для каждого утверждения в вашей матричной таблице.

Как правило, каждый оператор матричной таблицы получает свой собственный отдельный столбец данных. Каждый столбец имеет заголовок в формате «Текст вопроса — Текст утверждения», чтобы уточнить, к какой конкретной матричной таблице и к какому утверждению она относится.

Пример: В приведенном ниже примере экспорта данных столбец данных для первого оператора помечен как «Насколько вы были удовлетворены следующим во время вашего визита? – Количество собак в офисе».

В зависимости от того, экспортировали ли вы данные в выбранном текстовом или числовом формате, вы увидите либо точку шкалы, выбранную респондентом (например, Крайне недоволен), либо значение перекодирования, присвоенное точке шкалы (например, 1).

Матрица Лайкерта с несколькими ответами Таблица

Для вариантов с несколькими вариантами ответов это зависит от того, решили ли вы разделить поля с несколькими значениями на столбцы. Если вы этого не сделали (что используется по умолчанию), каждое утверждение получает свой собственный столбец, и каждый ответ, выбранный респондентом, перечисляется через запятую в том же столбце.

Пример: Обратите внимание, что заголовок имеет формат «Вопрос – Заявление», а ответы разделены запятыми в одном и том же столбце.

Если вы выбрали разделение столбцов, то каждая точка шкалы будет иметь свой собственный столбец в наборе данных. В строке каждого участника будет «1» или текст ответа в столбцах выбранных вариантов.

Пример: Обратите внимание, что формат заголовка теперь «Вопрос — Утверждение — Шкала», а столбцы теперь пусты или содержат только один ответ.

Таблица матрицы ввода текста

Для этого варианта матрицы столбец будет включен в набор данных для каждого текстового поля в таблице. В этом столбце вы увидите текст, который каждый участник ввел в текстовое поле. В приведенном ниже примере текстовая запись была ограничена числовым типом содержимого , поэтому при экспорте отображаются числа, введенные респондентами в текстовые поля.

Каждый столбец помечен в соответствии со следующей схемой нумерации: [Номер вопроса]_[Номер строки]_[Номер столбца].

Матрица максимальных различий

Для этого варианта матрицы вы увидите столбец в электронной таблице для каждого элемента, который участник может оценить в вашей таблице MaxDiff. Эти столбцы отсортированы таким образом, что первый столбец в наборе данных относится к первому оператору в вашей матричной таблице, второй столбец в наборе данных — к второму оператору в вашей матричной таблице и т. д.

В зависимости от того, экспортировали ли вы данные в выбранном текстовом или числовом формате, вы увидите:

Текст выбора: Уровень предпочтения, выбранный респондентом (например, «Любимый» или «Наименее любимый»).
Числовое значение: Для каждой строки матричной таблицы вы увидите «1» в столбце, представляющем элемент, указанный слева от операторов, и «0» в столбце, представляющем элемент, указанный в право заявлений. В показанном здесь примере «Наименее любимому» будет присвоен код «1», а «Избранному» будет присвоен код 0.

Таблица матрицы постоянных сумм

Для этого варианта матрицы загруженный файл данных будет включать по одному столбцу для каждого текстового поля в таблице матрицы. Столбцы маркируются в соответствии со следующей схемой нумерации: (номер вопроса)_(номер столбца)_(номер строки). В каждой ячейке этих столбцов будет число, которое респондент ввел в текстовое поле постоянной суммы.

Подсказка: Вопросы с постоянной суммой не экспортируют данные для итогов автоматически. Чтобы включить эти данные в экспорт, вы можете создать переменную формулы в любой момент сбора данных. Если вы хотите, чтобы эта сумма отображалась для респондентов, то перед сбором данных вам нужно будет создать встроенные данные, эквивалентные математическим операциям, путем добавления переданного текста для соответствующих столбцов или строк.

Биполярный матричный стол

Для этого варианта матрицы загруженный файл данных будет включать по одному столбцу для каждой строки в таблице матрицы. В каждой ячейке этих столбцов будет число, соответствующее одному из переключателей в этой конкретной строке. Для получения дополнительной информации о числах, прикрепленных к переключателям в вопросе, посетите нашу страницу значений перекодирования.

Экспорт будет выглядеть таким образом, независимо от того, в текстовом или числовом формате он выбран.

Таблица матрицы порядка рангов

Для этого варианта матрицы загруженный файл данных будет включать по одному столбцу для каждого текстового поля в таблице матрицы. Столбцы маркируются в соответствии со следующей схемой нумерации: (номер вопроса)_(номер столбца)_(номер строки). В каждой ячейке этих столбцов будет рейтинг (в числовом формате), который респондент присвоил этой конкретной теме.

Таблица матрицы профилей

Для этого варианта матрицы загруженный файл данных будет включать по одному столбцу для каждого оператора в таблице матрицы.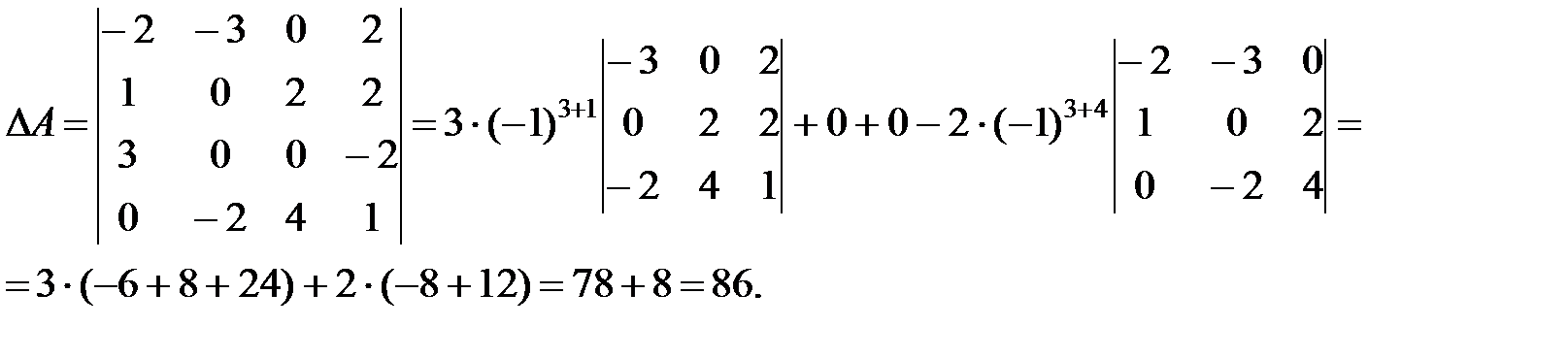 В зависимости от того, экспортировали ли вы данные в выбранном текстовом или числовом формате, вы увидите либо точку шкалы, выбранную респондентом (например, Крайне недоволен), либо значение перекодирования, присвоенное точке шкалы (например, 1).

Отчет по матричным таблицам

После того, как ваши ответы будут собраны, Qualtrics предлагает различные методы создания отчетов как внутри платформы, так и вне ее. На вкладке «Отчеты» вы можете просматривать сводные данные с готовыми отчетами, а также создавать свои собственные.

Типы визуализации, доступные для вашей матричной таблицы, зависят от выбранного вами формата матричной таблицы.

Например, матрицы Лайкерта, как правило, имеют те же параметры визуализации, что и вопросы с несколькими вариантами ответов, вплоть до того, как ведут себя форматы с одним и несколькими ответами.

Между тем, матричные таблицы ввода текста лучше всего работают с визуализациями, созданными для открытых данных в стиле обратной связи.