| 1 | Оценить с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень из 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
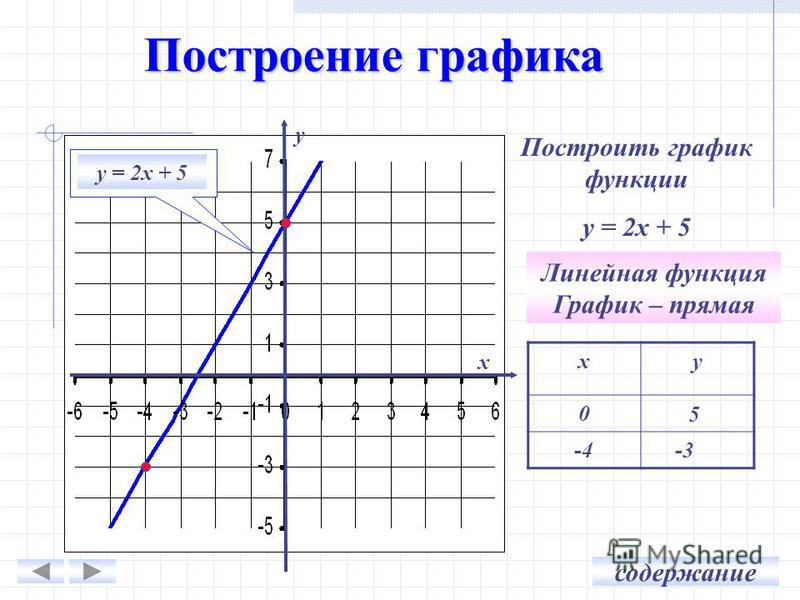
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | y=x+4 | |
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
3D график по x,y,z
← →
shkeeper
(2004-04-22 22:33) [0]
Очень нужно! Есть ли какой нибудь спрособ «малой кровью» построить 3Д график (по x,y,z)?
Вариант строить в Excel слишком банален и неудобен.
Может кто подскажет где что мона взять?
← →
shkeeper
(2004-04-22 22:33) [0]
Очень нужно! Есть ли какой нибудь спрособ «малой кровью» построить 3Д график (по x,y,z)?
Вариант строить в Excel слишком банален и неудобен. Может кто подскажет где что мона взять?
← →
shkeeper
(2004-04-22 23:15) [1]
ну и… что никто не сталкивался… это ужасно..
← →
shkeeper
(2004-04-22 23:15) [1]
ну и… что никто не сталкивался… это ужасно..
← →
Yegorchic ©
(2004-04-22 23:19) [2]
Посмотри программу в кладовке.
..
как называется не помню… вроде «Математика 0.5″…
там есть построение 3D графика…
← →
Yegorchic ©
(2004-04-22 23:19) [2]
Посмотри программу в кладовке…
как называется не помню… вроде «Математика 0.5″…
там есть построение 3D графика…
← →
SergLight ©
(2004-04-23 10:26) [3]
TChart
← →
SergLight ©
(2004-04-23 10:26) [3]
TChart
← →
Курдль ©
(2004-04-23 11:30) [4]
> Очень нужно! Есть ли какой нибудь спрособ «малой кровью»
> построить 3Д график (по x,y,z)?
А что Вы называете «малой кровью»? Такие проги писать — одно сплошное эстетическое удовольствие (жаль, что их редко заказывают).
Все проще пареной репы — берете TImage и на его Canvas-е строите все, что заблагорассудится!
← →
Курдль ©
(2004-04-23 11:30) [4]
> Очень нужно! Есть ли какой нибудь спрособ «малой кровью»
> построить 3Д график (по x,y,z)?
А что Вы называете «малой кровью»? Такие проги писать — одно сплошное эстетическое удовольствие (жаль, что их редко заказывают). Все проще пареной репы — берете TImage и на его Canvas-е строите все, что заблагорассудится!
← →
Algol
(2004-04-23 12:09) [5]
> одно сплошное эстетическое удовольствие
Я б так не сказал. Создание интерактивных графиков произвольного типа, с шаблонами, с поддержкой внедрения, да еще и 3D — задача не тривиальная, и довольно сложная.
← →
Algol
(2004-04-23 12:09) [5]
> одно сплошное эстетическое удовольствие
Я б так не сказал. Создание интерактивных графиков произвольного типа, с шаблонами, с поддержкой внедрения, да еще и 3D — задача не тривиальная, и довольно сложная.
← →
Курдль ©
(2004-04-23 12:12) [6]
> Я б так не сказал. Создание интерактивных графиков произвольного
> типа, с шаблонами, с поддержкой внедрения, да еще и 3D
> — задача не тривиальная, и довольно сложная.
Но для меня приятнее, чем создание каких-нить бухгалтерских интерактивных отчетов произвольного типа, с шаблонами, с поддержкой внедрения 🙂
← →
Курдль ©
(2004-04-23 12:12) [6]
> Я б так не сказал.
Создание интерактивных графиков произвольного
> типа, с шаблонами, с поддержкой внедрения, да еще и 3D
> — задача не тривиальная, и довольно сложная.
Но для меня приятнее, чем создание каких-нить бухгалтерских интерактивных отчетов произвольного типа, с шаблонами, с поддержкой внедрения 🙂
← →
shkeeper
(2004-04-23 15:20) [7]
После того как я обрал весь Инет в поисках удобного и НОРМАЛЬНОГО компонента я зациклился на TChart Pro 6.0. Но он выдает все время ошибки, избавится от них никак не могу. А посему пришел к выводу, что еще никто такого компонента не придумал, а те что есть не могут построить диаграмму по 3-м осям, если записей например больше 5000.
.. 🙁← →
shkeeper
(2004-04-23 15:20) [7]
После того как я обрал весь Инет в поисках удобного и НОРМАЛЬНОГО компонента я зациклился на TChart Pro 6.0. Но он выдает все время ошибки, избавится от них никак не могу. А посему пришел к выводу, что еще никто такого компонента не придумал, а те что есть не могут построить диаграмму по 3-м осям, если записей например больше 5000.
← →
Курдль ©
(2004-04-23 15:26) [8]
> а все грамотные, пока по делу не начнем говорить… 🙁
Я Вам абсолютно грамотно подсказал, как грамотно пстроить диаграмму по 3-м осям! Надо брать и строить, а не компоненты искать!
Если медленно работает — переходите на ассемблер!
Как сделаете лучший и менее глючный, чем есть — напишите мне — я куплю за большие деньги!
← →
Курдль ©
(2004-04-23 15:26) [8]
> а все грамотные, пока по делу не начнем говорить.
.. 🙁
Я Вам абсолютно грамотно подсказал, как грамотно пстроить диаграмму по 3-м осям! Надо брать и строить, а не компоненты искать!
Если медленно работает — переходите на ассемблер!
Как сделаете лучший и менее глючный, чем есть — напишите мне — я куплю за большие деньги!
← →
WebErr ©
(2004-04-23 16:41) [9]
Всё оч. просто:
Дано: исходный вектор P = (x, y, z), найти простейший вариант отображения на плоскость экрана.
Решение:
Пусть некий объект расположен неподалёку от точки O = (0, 0, 0).
(Иначе делаем перенос координат!)
Пусть «камера» направлена в эту точку и имеет сферические координаты с углами (a, b).
Поворачиваем P, используя матрицу поворота T(a, b) =
|| sin(a)*cos(b) cos(a)*cos(b) -sin(b) ||
|| sin(a)*sin(b) cos(a)*sin(b) cos(b) ||
Q = T*P.
Q = (X, Y, Z).
Итак мы отобразили (непроективно — это посложнее!) P на плоскость экрана.
Теперь можно сделать косметическое преобразование:
xs = X*k + x0
ys = Y*k + y0
И всё! :))))
← →
WebErr ©
(2004-04-23 16:41) [9]
Всё оч. просто:
Дано: исходный вектор P = (x, y, z), найти простейший вариант отображения на плоскость экрана.
Решение:
Пусть некий объект расположен неподалёку от точки O = (0, 0, 0).
(Иначе делаем перенос координат!)
Пусть «камера» направлена в эту точку и имеет сферические координаты с углами (a, b).
|| cos(a) -sin(a) 0 ||
|| sin(a)*cos(b) cos(a)*cos(b) -sin(b) ||
|| sin(a)*sin(b) cos(a)*sin(b) cos(b) ||
Q = T*P.
Q = (X, Y, Z).
Итак мы отобразили (непроективно — это посложнее!) P на плоскость экрана.
Теперь можно сделать косметическое преобразование:
xs = X*k + x0
ys = Y*k + y0
И всё! :))))
← →
WebErr ©
(2004-04-23 17:03) [10]
Z координату мы используем для Z-буффера, если надо.
А при проективном преобразовании нужно знать ещё и 3-ю сферическую координату «камеры» r, т.е. C = (r, a, b) в сферических координатах.
Также надо знать длину до фокуса камеры = d.
xr = X*p
yr = Y*p
zr = r-d-Z
R = (xr, yr, zr).
Т.е. проекция применяется после поворота и перед «косметическим» масштабированием. :))))
Литература: «Программирование компьютерной графики» Виктора Порева.
← →
WebErr ©
(2004-04-23 17:03) [10]
Z координату мы используем для Z-буффера, если надо.
А при проективном преобразовании нужно знать ещё и 3-ю сферическую координату «камеры» r, т.е. C = (r, a, b) в сферических координатах.
Также надо знать длину до фокуса камеры = d.
Получаем преобразование R = R(Q), при некоем p = r/(r-Z).
xr = X*p
yr = Y*p
zr = r-d-Z
R = (xr, yr, zr).
Т.е. проекция применяется после поворота и перед «косметическим» масштабированием. :))))
Литература: «Программирование компьютерной графики» Виктора Порева.
← →
WebErr ©
(2004-04-23 17:06) [11]
Разумеется точки, которые после поворота получили координату Z >= r-d не отображаются на экран, т.к. находятся за камерой! :))))
Прошу послать данный материал автору сабжа! :))))
← →
WebErr ©
(2004-04-23 17:06) [11]
Разумеется точки, которые после поворота получили координату Z >= r-d не отображаются на экран, т.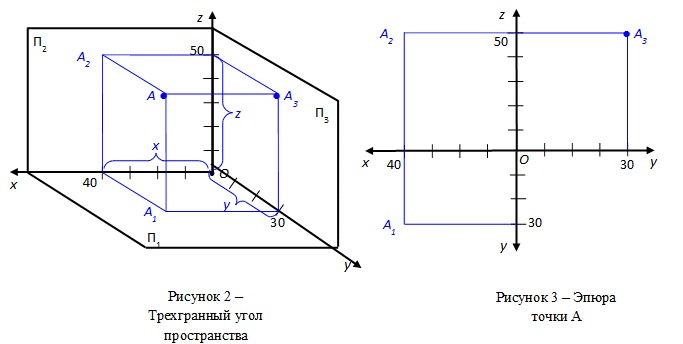
к. находятся за камерой! :))))
Прошу послать данный материал автору сабжа! :))))
← →
WebErr ©
(2004-04-23 17:17) [12]
Могу ещё про вертексное построение с закраской Гуро или Фонга рассказать, но лучше сами почитайте книжку — она того стоит!!! :))))
← →
WebErr ©
(2004-04-23 17:17) [12]
Могу ещё про вертексное построение с закраской Гуро или Фонга рассказать, но лучше сами почитайте книжку — она того стоит!!! :))))
← →
Дмитрий
(2004-04-23 17:27) [13]
Компоненты есть… И очень даже хорошие.
.. Просто искать надо уметь… Я бы тебе выслал одну, да она на домашнем компе висит… А его я увижу, ой, как нескоро… К сожалению не помню как зовётся…
Ещё вариант — OpenGl… Малой крови не обещаю, зато надёжно и со вкусом…
← →
Дмитрий
(2004-04-23 17:27) [13]
Компоненты есть… И очень даже хорошие… Просто искать надо уметь… Я бы тебе выслал одну, да она на домашнем компе висит… А его я увижу, ой, как нескоро… К сожалению не помню как зовётся…
Ещё вариант — OpenGl… Малой крови не обещаю, зато надёжно и со вкусом…
← →
WebErr ©
(2004-04-23 17:27) [14]
Если что-то непонятно спрашивайте!
← →
WebErr ©
(2004-04-23 17:27) [14]
Если что-то непонятно спрашивайте!
← →
WebErr ©
(2004-04-23 17:29) [15]
> Дмитрий (23.
04.04 17:27) [13]
Это всё здорово, но всегда нужно знать как это всё работает! Это касается не только OpenGL & DirectX, но и всеми любимой VCL — WinAPI знать надо не хуже родных библиотек! :))))
← →
WebErr ©
(2004-04-23 17:29) [15]
> Дмитрий (23.04.04 17:27) [13]
Это всё здорово, но всегда нужно знать как это всё работает! Это касается не только OpenGL & DirectX, но и всеми любимой VCL — WinAPI знать надо не хуже родных библиотек! :))))
← →
WebErr ©
(2004-04-23 18:14) [16]
Кстати, если неизвесны сферические координаты камеры, а только декартовы (xc, yc, zc), то это даже лучше, тогда оператор T(a, b) считается быстрее, т.
к.
< пусть rxy = sqrt(sqr(xc)+sqr(yc)),
тогда r = sqrt(sqr(r0)+sqr(zc)) >
cos(a) = yc/rxy, sin(a) = xc/rxy
cos(b) = zc/r, sin(b) = rxy/r
С уважением, Керимов Владимир. (с) :)))) (спец по 3D графике)
← →
WebErr ©
(2004-04-23 18:14) [16]
Кстати, если неизвесны сферические координаты камеры, а только декартовы (xc, yc, zc), то это даже лучше, тогда оператор T(a, b) считается быстрее, т.к.
< пусть rxy = sqrt(sqr(xc)+sqr(yc)),
тогда r = sqrt(sqr(r0)+sqr(zc)) >
cos(a) = yc/rxy, sin(a) = xc/rxy
cos(b) = zc/r, sin(b) = rxy/r
С уважением, Керимов Владимир. (с) :)))) (спец по 3D графике)
← →
WebErr ©
(2004-04-23 18:16) [17]
Где r = sqrt(sqr(rxy)+sqr(zc)) — расстояние от начала координат, до камеры! :))))
← →
WebErr ©
(2004-04-23 18:16) [17]
Где r = sqrt(sqr(rxy)+sqr(zc)) — расстояние от начала координат, до камеры! :))))
← →
WebErr ©
(2004-04-23 18:50) [18]
Если rxy < eps (rxy близко к нулю), то можно взять любые (a, b), в том числе и (0, 0).
:))))
← →
WebErr ©
(2004-04-23 18:50) [18]
Если rxy < eps (rxy близко к нулю), то можно взять любые (a, b), в том числе и (0, 0). :))))
← →
csr ©
(2004-04-24 12:32) [19]
Давай, я те такую прогу напишу гы 😉 Это ж проще пареной репы! Математику надо было учить :). Естессно за вознаграждение! 😉
← →
csr ©
(2004-04-24 12:32) [19]
Давай, я те такую прогу напишу гы 😉 Это ж проще пареной репы! Математику надо было учить :). Естессно за вознаграждение! 😉
← →
Piter ©
(2004-04-24 14:01) [20]
22.
04.04 22:33
Очень нужно! …
22.04.04 23:15
ну и… что никто не сталкивался
нда..
← →
Piter ©
(2004-04-24 14:01) [20]
22.04.04 22:33
Очень нужно! …
22.04.04 23:15
ну и… что никто не сталкивался
нда..
Как отображать данные XYZ в 3D в Microsoft Excel
Пару лет назад мы опубликовали сообщение в блоге о том, как графически отображать данные XYZ в MESH в Excel, Как отображать данные XYZ в MESH в Microsoft Excel . Сегодня мы хотели бы развить этот пост немного дальше и объяснить различные варианты того, как вы можете отображать данные XYZ в 3D в Excel; со сторонними приложениями и самостоятельно.
Во-первых, имейте в виду, что Microsoft Excel, хотя и является отличным приложением для работы с электронными таблицами, не предлагает удобных для пользователя вариантов построения графиков, кроме стандартных графиков.
Это не означает, что Excel не может работать со сложными графиками, Excel, безусловно, может, но это далеко не так просто. Однако есть несколько доступных приложений, которые значительно упрощают эту задачу. Конечно, мы будем рассматривать эти продукты, а также самый экономичный метод, сделать это самостоятельно.
Как отображать данные XYZ в 3D — линии, сплайны и разброс с надстройкой Excel,
Cel Tools . Cel Tools — это набор инструментов, полный функций, которые упрощают работу с Excel для обычного пользователя. Такие функции, как скрытие и защита контента паролем, изменение порядка списков, отправка рабочих листов или книг по электронной почте, экспорт страниц, случайный выбор и многие другие. Интересующая нас функция связана с графическим разделом Cel Tools. На вкладке графиков инструментов ячейки вы найдете множество опций для построения графиков. На чем мы сосредоточимся, находится в разделе «3D XYZ Tools». Эта надстройка упрощает графическое отображение ваших данных в 3D: выберите, нажмите «3D-линия», «3D-сплайн» или «3D-рассеяние», и ваш график будет создан.
Cel Tools создает расчеты на основе выбранных данных XYZ, полос прокрутки для настройки поворота по оси X, поворота по оси Y, масштабирования и панорамирования и, наконец, выводит их на чистую диаграмму, которую можно настроить в соответствии со своими потребностями. Еще одна замечательная особенность этого — возможность отправить свой график кому угодно. Поскольку все это содержится в документе Excel, вы можете отправить этот документ по электронной почте любому, у кого есть Excel, и они смогут вращать, масштабировать и панорамировать так же, как вы можете с помощью Cel Tools.
Метод 2: Сделай сам – Используйте впечатляющие формулы! Этот метод очень сложен, и мы кратко объясним его сложности. Проще говоря, нам очень не хочется воссоздавать колесо. Джордж Лунгу проделал потрясающую работу по объяснению математических уравнений, лежащих в основе построения трехмерных графиков, в Microsoft Excel.
Он предлагает множество руководств по этому вопросу, и мы настоятельно рекомендуем вам посетить его страницу, если вы заинтересованы в создании удивительных графиков с помощью Excel; Excel Необычный .
Существует несколько различных уравнений, необходимых для построения графика данных XYZ в Excel. Excel может отображать только две точки данных одновременно (X и Y). Поэтому вам нужно преобразовать XYZ в просто XY. Это сложная часть, и уравнение разбито для вас справа:
С помощью приведенного выше уравнения вы можете отобразить значения XYZ на 2D-графике в X и Y. Необходимые числа — это ваши исходные X, Y и значения Z (OX, OY, OZ), азимут (поворот X) и высота (поворот Y). После того, как ваши формулы размещены, вы настраиваете повороты и наблюдаете, как графические значения X и Y автоматически обновляются.
Опять же, не так просто и ясно, как с Cel Tools, но это работает. И снова спасибо Джорджу Лунгу за формулы.
Данные XYZ, преобразованные в данные XY для расчетов 3D графики
Высота = градусы вращения от 1 до 360 (Y)
Azimuth = Degrees 1 до 360 (x)
Alpha.
= (3,1415926535/180)*АзимутБЕТА = (3,1415926535/180)*Высота 92)
(equations above were modified from linked Excel Unusual URL XLS document download) How to plot XYZ data in 3D – MESH, Surface Plot, Wireframe, Grid Frame
Теперь мы вернемся к нашему предыдущему сообщению о том, как строить графики 3D MESH в Excel с использованием данных XYZ .
Если вы пропустили эту статью, вы можете посетить ее по ссылкам, доступным здесь, но я вскоре подытожу этот пост.
Проще говоря, очень легко создать чертеж MESH в 3D, используя только значения XYZ. Однако это чрезвычайно утомительно, если вы не пользуетесь помощью форматированного расчета для размещения и усреднения точек. Как и раньше, я покажу вам два метода. Во-первых, стороннее приложение, а во-вторых, метод, который вы можете сделать сами.
Метод 1: Применение — сетка XYZ Существует несколько методов преобразования XYZ в макет MESH, который может прочитать Excel, однако доступна только одна программа, которая преобразует эти данные в правильный макет и заполняют пустые точки данных. Этот метод заполнения недостающих данных называется изгибом. Изгиб — это очень сложная цепочка вычислений, которая усредняет переменные по расстояниям и создает среднюю кривую значений в зависимости от расстояния. По сути, он делает расчетное предположение о том, какие числа должны быть в этой отсутствующей точке данных.
Почему отсутствующие точки данных являются такой большой проблемой? Microsoft Excel рассматривает эти пустые точки данных как данные, а не как пропущенные значения. Это означает, что вместо того, чтобы просто пропускать эти значения (как это сделали бы большинство графических движков), Excel считает их нулевыми «0», а в ответ вводит ложные данные в графическое изображение.
XYZ Mesh В настоящее время является единственным доступным программным обеспечением, которое будет принимать данные XYZ и преобразовывать их непосредственно в формат Excel MESH с кривизной данных. Просто вставьте свои значения в соответствующие столбцы X, Y и Z, выберите нужные параметры и нажмите «Преобразовать».
В мгновение ока данные преобразуются и отображаются для вас в окне предварительного просмотра, отображая каркасную сетку преобразованных данных. Отсюда данные можно экспортировать в Excel. Быстрые и простые преобразования с изгибом и никаких хлопот, связанных со следующей частью этого поста….
Как упоминалось ранее, Excel имеет неприятную привычку думать, что никакие значения не равны нулю. Хотя в некоторых случаях это может быть правдой (где ноль ничего не значит), что касается чисел, ноль — это фактическое число. Это превышение может привести к неправильному отображению данных, поэтому использование XYZ Mesh очень важно для создания сглаженных данных.
Но в этом разделе мы научим вас, как сделать это самостоятельно. Первое, что вам нужно понять, это то, что данные XYZ наносятся на график в трех столбцах, X, Y и Z. Чтобы Excel мог отображать их в 3D-графике поверхности, данные должны быть в формате MESH. Формат MESH — это структура, содержащая строки и столбцы, очень похожая на электронную таблицу. Значения X устанавливаются стационарными в первом столбце каждой строки, значения Y устанавливаются стационарными в первой строке каждого столбца, а значения Z размещаются точно там, где X означает Y для соответствующего значения Z.
Чтобы лучше понять это, посмотрите изображение, представленное ниже:
Как показано на изображении выше, значения X и Y достаточно легко разместить, однако значения Z требуют времени. Причина в том, что вам нужно будет отследить и вставить каждое значение Z в нужное место, чтобы правильно построить этот график формата MESH. Но подождите, это была самая легкая часть. Далее идет вызов. Вам нужно рассчитать разницу между значениями, чтобы получить правильное изгибание данных. Если вы пропустите эту часть, Excel будет считать, что ваши пустые точки данных равны нулю, и ваш график будет выглядеть так (изображение справа ->). Что, если вы не можете сказать, неверно.
Расчет данных кривых в MESH
Существует несколько различных способов расчета разницы между значениями и расстояниями, но все они имеют один и тот же процесс.
- Выберите понравившийся метод расчета; Лично я предпочитаю метод VALUE = A [+/-] ((B – A) / C ).
- Поместите вычисление в пустую ячейку.
- Перетаскивайте, пока не дойдете до следующего значения.
Это может показаться простым, но на это уходит очень много времени, и если ваши расчеты несовершенны, график будет неправильным.
К сожалению, нет другого способа сформулировать или скопировать и вставить эти значения самостоятельно, если только вы не воспользуетесь помощью стороннего приложения. Если вы решите использовать стороннее приложение для упрощения процесса, знайте, что доступно несколько вариантов. Некоторые преобразуют XYZ в MESH, а другие берут данные MESH и заполняют пустые точки данных. Если вы идете по этому пути, почему бы не использовать приложение, которое будет и то, и другое? Сетка XYZ .
Я надеюсь, что этот пост был вам полезен. Если вы хотите поговорить с нами о своих чувствах к этому посту, пожалуйста, оставьте комментарий ниже. Мы рады услышать от наших читателей!
Помощь в Интернете — Учебные пособия — XYZ Contour
Все книгиКниги, не связанные с программированием Руководство пользователя Учебники Быстрая справка Справка OriginКниги по программированию X-Function Origin C LabTalk Programming Python Python (внешний) Automation Server LabVIEW VI Приложения Разработка приложений Code Builder Лицензия 0lab0GMOCA | |||
Содержание
Резюме В этом руководстве показано, как создать контур из данных XYZ и добавить границы X и Y. Требуемая минимальная версия Origin: 2020
Чему вы научитесьЭтот туториал покажет вам, как
шаговЭтот учебник связан с образцом встроенного графика Contour Plots — XYZ Contour .
| |||
Вы получите образец, указанный ниже: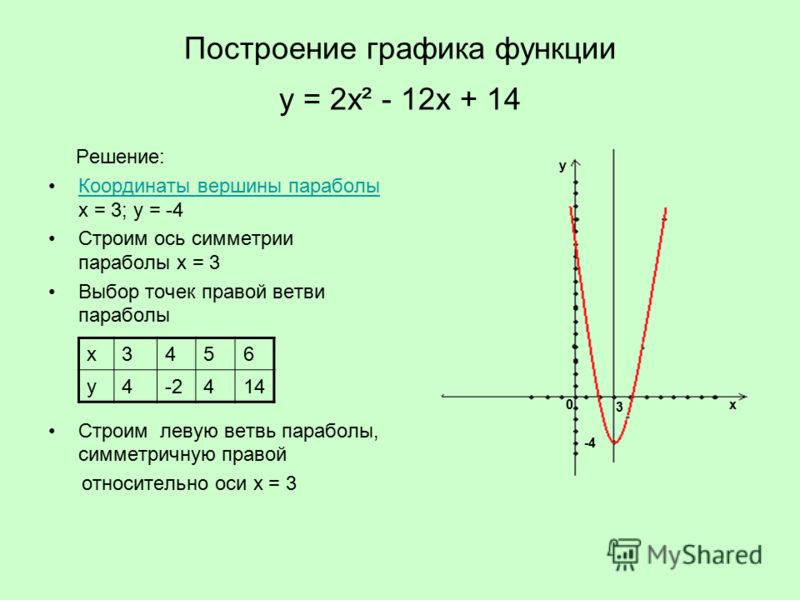
Нажмите кнопку ОК.
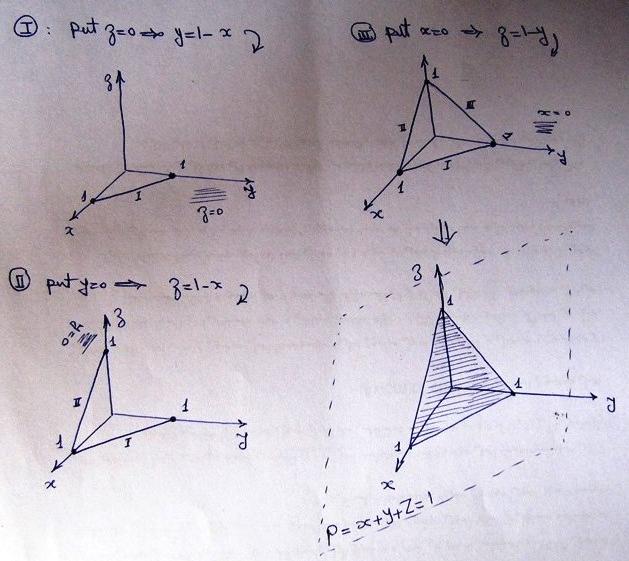Щелкните заголовок Lines , убедитесь, что выбран параметр Show on Major Levels Only . Выберите 9Установите флажок 0274 Color под Apply to All и выберите LT Grey из раскрывающегося списка в качестве цвета контурной линии. Нажмите OK , чтобы закрыть диалоговое окно.