Выражение подынтегрально — Энциклопедия по экономике
Операция вычисления определенного интеграла по заданной подынтегральной функции и заданному интервалу интегрирования выполняется по стандартной программе, заложенной в память машины. В этой связи задача сводится лишь к построению подынтегральных выражений, которые зависят от вида функции или модели факторной системы. [c.134]Для облегчения решения задачи построения подынтегральных выражений в зависимости от вида модели факторной системы (мультипликативные или кратные) предложим матрицы исходных значений для построения подынтегральных выражений элементов структуры факторной системы. Принцип, заложенный в матрицах, позволяет построить подынтегральные выражения элементов структуры факторной системы для любого набора элементов модели конечной факторной системы. В основном построение подынтегральных выражений элементов структуры факторной системы — процесс индивидуальный, и в случае, когда число элементов структуры измеряется большим количеством, что в экономической практике является редкостью, исходят из конкретно заданных условий.
При формировании рабочих формул расчета влияния факторов в условиях применения ЭВМ пользуются следующими правилами, -отражающими механику работы с матрицами подынтегральные выражения элементов структуры факторной системы для мультипликативных моделей строятся путем произведения полного набора элементов значений, взятых по каждой строке матрицы, отнесенных к определенному элементу структуры факторной системы с последующей расшифровкой [c.134]
Приведем примеры построения подынтегральных выражений. [c.135]
Построение подынтегральных выражений [c.136]
Формирование рабочих формул интегрального метода для кратных моделей. Подынтегральные выражения элементов структуры факторной системы для- кратных моделей строятся путем ввода под знак интеграла исходного значения, полученного на пересечении строк в зависимости от вида модели и элементов структуры факторной системы с последующей расшифровкой значений, приведенных справа и в низу матрицы исходных значений.
Матрица исходных значений для построения подынтегральных выражений элементов структуры [c.137]
Построение подынтегральных выражений [c.138]
В том случае, когда усредненная задача о минимуме а при условии (2.208) выпукла вниз, она имеет стационарное решение и, на котором подынтегральное выражение в (2.208) равно нулю. [c.110]
Величина D характеризует необратимые потери прибыльности ресурса. Действительно, для того, чтобы вернуть систему в прежнее состояние, т.е. закупить ресурс NQ на рынке по цене р+ и продать его подсистеме по цене i(7V) [c.295]
Использование переменной состояния в качестве независимой переменной. Для многих задач оптимального управления характерно то обстоятельство, что независимая переменная t не входит явно в функцию /о — подынтегральное выражение критерия оптимальности — ив правые части дифференциальных уравнений / (у — 1,…, п). Считая для простоты, что FQ (а (Т)) = 0, запишем постановку такой задачи как
[c.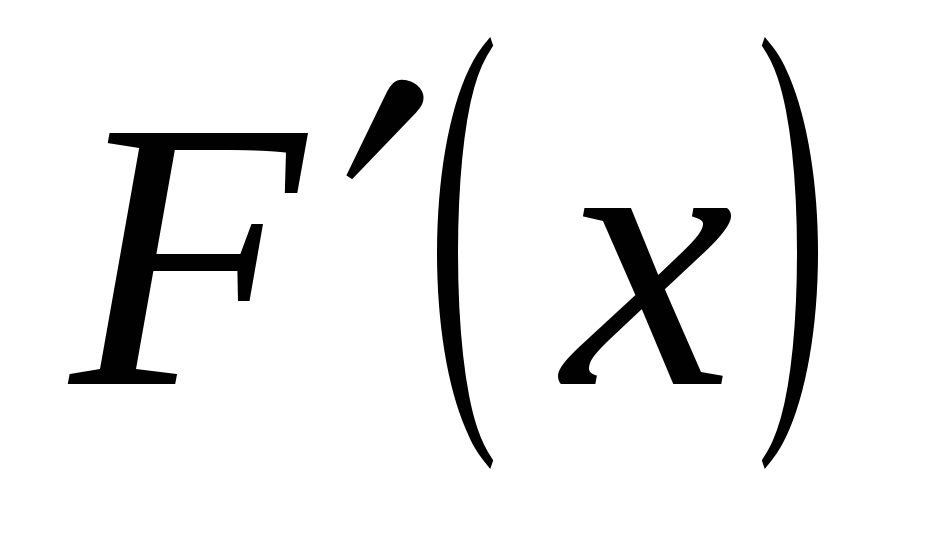
Метод трансформации фазового пространства может быть использован и в том случае, когда в подынтегральное выражение функционала (9.271) входит слагаемое /02( 5 z v. В этом случае удобно увеличить [c.401]
Знак f называется знаком интеграла, функция f(x) — подынтегральной функцией, выражение /(ж) dx — подынтегральным выражением, переменная х — переменной интегрирования. [c.203]
Дифференциал неопределенного интеграла равен подынтегральному выражению [c.204]
Решение. Числитель данного подынтегрального выражения напоминает дифференциал для подкоренного выражения 3 х2 + 5 в самом деле, d (3 ж2 + 5) = (3 х1 + 5) dx = 6 х dx. Это наводит на мысль о целесообразности подстановки t = [c.211]
Заметим, что в простых случаях нет нужды вводить новую переменную. Так, предыдущий пример можно решить следующим образом. Находим в уме дифференциал от подкоренного выражения 3 ж + 4 d (3 ж + 4) = 3 dx. Вводим в подынтегральное [c.211]
Эта формула называется формулой интегрирования по частям.
Ею обычно пользуются в тех случаях, когда подынтегральное выражение v du проще, чем подынтегральное выражение udv.
[c.214]
В данном примере формулу интегрирования по частям была применена дважды после первого интегрирования по частям степень переменной ж в подынтегральном выражении уменьшилась на единицу. Второе применение формулы интегрирования по частям привело уже к табличному интегралу. А [c.215]
Эта запись читается интеграл от а до бэ эф от икс дэ икс . При этом число а называется нижним пределом, число 6 — его верхним пределом ( пределы интегрирования не имеют ничего общего с термином предел функции ) функция /(ж) — подынтегральной функцией, выражение f(x dx — подынтегральным [c.226]
Переходная или импульсная характеристики определяются экспериментально. При их использовании по методу суперпозиции осуществляется сначала разложение выбранной модели входного воздействия на элементарные» функции времени, а затем суммирование откликов на них. Последнюю операцию называют иногда свертыванием, а интегралы в выражениях (24).
. . (29) — интегралами свертки. Из них выбирается тот, у которого проще подынтегральная функция.
[c.176]
Когда большинство людей думает о шуме, они думают о «белом» или случайном шуме. Этот тип шума — шипение, которое слышно на чистых магнитофонных лентах. Поскольку оно не имеет свойственного масштаба, шипение кажется одинаковым, независимо от скорости ленты. Его подынтегральное выражение называют «коричневым» шумом, или броуновским движением. Коричневый шум — это просто текущая сумма белого шума. Он звучит так, как будто там что-то есть, но в действительности в коричневом шуме нет никакой информации. [c.166]
Так как подынтегральное выражение само по себе является р-распределением, то этот интеграл равен 1, и мы получаем [c.184]
Сравнивая подынтегральное выражение с формулой, задающей р-распределение, можно найти значение интеграла. В результате получаем для безусловного распределения величины г выражение [c.186]
Основываясь на асимптотических результатах относительно J и Y (формулы 9.
1.7,9 и 9.2.1,2 в [1]), можно показать, что знаменатель в подынтегральном выражении в (26) асимптотически является константой при у -> 0 и ведет себя как у 1/2 при у — оо. Отсюда авторы [127] заключают, что плотность меры Леви
[c.269]
Величины дик и (5 к) — зависимы, так как (5ик) — полностью определяются по 6м». Для приведения выражения (1.15) в форме, содержащей только независимые вариации, проинтегрируем второй член подынтегрального количества по частям [c.14]
Подынтегральное выражение во втором слагаемом —— ds есть не [c.398]
Определение. Функция Дх) называется подынтегральной функцией, j(x)dx- подынтегральным выражением, х — переменной интегрирования, символ J — знаком неопределенного интеграла, С -постоянной интегрирования. [c.57]
Пользуясь формулой Тейлора, разложим подынтегральное выражение, выделяя линейную часть разложения Имеем [c.219]
Заметим, что все рассмотренные формулы позволяют корректно обрабатывать особенность в подынтегральном выражении, возникающую при
[c.
Поскольку подынтегральное выражение положительно, то нижний предел интегрирования не может превышать верхний yi > у». [c.482]
Это равенство противоречит условию, что v (x) 0, (подынтегральное выражение справа всегда меньше, чем подынтегральное выражение слева). Здесь предполагается, что хЪ Ф xl, что читателю предлагается установить самостоятельно. Таким образом, для решения задачи выполняется соотношение [c.501]
Достигается максимум подынтегрального выражения в (2.109) в одном или двух базовых значенияхб зависит от тогоб выпукла ли вверх [c.80]
Решение. В данное подынтегральное выражение входит множитель osxdx, являющийся дифференциалом функции sin ж. [c.210]
Подынтегральные выражения не превосходят 4/г2г2 в первом и третьем интегралах и 82 — во втором. Поэтому [c.224]
В последнем выражении первое, четвертое и шестое слагаемые образуют основную часть формулы (14), а лишние второе, третье, пятое и седьмое слагаемые оцениваются величинами типа О (s)f (s), так как подынтегральные выражения имеют величину О (s), а меры множеств, по которым они интегрируются, не превосходят к) (s).
Поскольку величина ftqdt постоянна, график производства q(t), при котором V максимально, должен быть таким, чтобы единичное приращение в q увеличивало подынтегральную функцию одинаково как в одно, так и в другое время. Таким образом, выражение [c.269]
Дифференциал неопределенного интеграла равен подынтегральному выражению. Имеем d(jf(x)dx) = (lf(x)dxydx=f(x)dx. [c.57]
2.4. Интегрирование рациональных функций
Дробно-рациональной функцией (дробью) называется выражение видагде и — многочлены степени и , не имеющие общих корней, т.е.
Дробь называется
правильной если ;
неправильной в противном случае.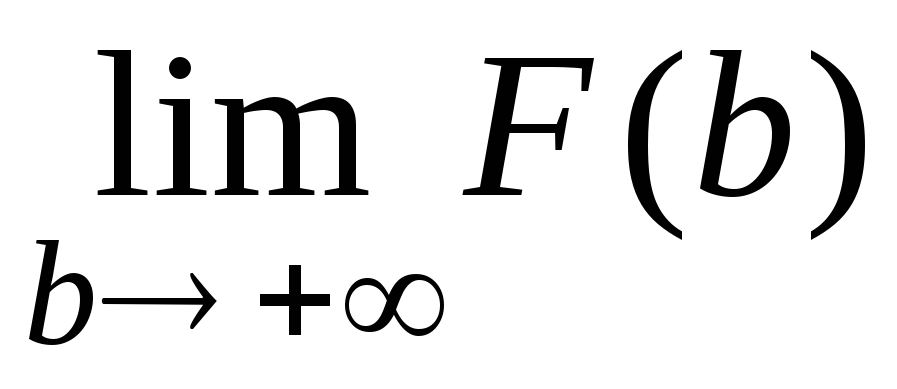
Каждую
неправильную дробь можно привести к
правильной путем исключения целой
части, интегрирование которой не
представляет сложностей.
В курсе высшей алгебры доказывается теорема, о том, что любая правильная дробь может быть представлена в виде конечного числа простых дробей.
Если — корни уравнения , а — их соответствующие кратности, так что
то дробь представляется в виде
где числители отдельных дробей определяются из системы линейных уравнений после приведения к общему знаменателю и приравнивания коэффициентов при одинаковых степенях с (метод неопределенных коэффициентов).
Если — простые корни уравнения , т.е. , то
Если некоторые корни уравнения мнимы, то, соединяя вместе элементарные дроби, соответствующие сопряженным корням, можно после некоторых преобразований соответствующие пары дробей представить в виде действительных дробей вида
.
и методом неопределенных коэффициентов найти неизвестные и
Таким образом, интегрирование правильной рациональной дроби приводится к интегралам вида
и
рассмотренных в предыдущем п.3.
Примеры:
2.4.1. Найти интеграл: .
1. В подынтегральном выражении
максимальная степень при переменной в числителе равна максимальной степени при переменной в знаменателе. Поэтому подынтегральная дробь – неправильная. Выполняя деление на , получаем
следовательно,
.
2. Так как подынтегральная функция — правильная рациональная дробь, а корни её знаменателя являются вещественными и простыми (их кратность равна единице), то
,
откуда
.
Сравнивая коэффициенты при , , (свободные члены) в тождестве, получаем систему
решение которой , , .
Тогда,
.
2.4.2. Найти интеграл:
Так как подынтегральная функция — правильная рациональная дробь, а корни её знаменателя являются вещественными, то представляя в виде суммы простых дробей
,
откуда
.()
Сравнивая коэффициенты при , , , (свободные члены) в тождестве, получаем систему
решение которой .
Тогда
.
2.4.3. Найти интеграл:
Подынтегральная функция — правильная дробь и представляя её в виде суммы простых дробей
,
откуда
,
и приравнивая коэффициенты при одинаковых степенях, получаем систему
решение которой .
Тогда
2.
4.4. Найти интеграл:
■ Подынтегральная функция – правильная рациональная дробь, знаменатель которой имеет различные действительные корни.
Представим её в виде суммы элементарных дробей:
.
Откуда: ;
Приравняем коэффициенты при одинаковых степенях и решим систему линейных уравнений:
Первоначальный интеграл примет вид:
.◄
2.5.1. Интегралы вида
где — рациональные числа, приводятся к интегралам от рациональных функций подстановкой
где общий знаменатель дробей .
Примеры.
2.5.1.1. Найти интеграл:
Положим , тогда , т. е. ;
Представляя рациональную функцию как сумму простsх дробей, получим:
2. 5.1.2. Найти интеграл:
Положим , тогда , т. е. . Первоначальный интеграл примет вид:
.
2.5.1.3. Найти интеграл:
Подынтегральную функцию преобразуем к виду:
.
Полагая , имеем:
, , ,
тогда:
2.5.2. Интегралы вида
(интегралы от биномиальных дифференциалов), где — действительные числа, а — рациональные, выражаются в элементарных функциях только в следующих случаях:
(а) когда — целое число; тогда этот интеграл рационализируется подстановкой , где — наименьшее общее кратное знаменателей дробей и .
(б) когда — целое число, то подстановкой этот интеграл преобразуется к виду
В этом случае рационализация подынтегрального выражения осуществляется подстановкой
,
где — знаменатель дроби
.
(в) когда — целое число, то при помощи той же подстановки данный интеграл приводится к
Здесь мы будем использовать подстановку
.
Примеры:
2.5.2.1. Найти интеграл: .
■ В подынтегральном выражении – целое число.
Здесь случай (а). Применим подстановку:
; . Тогда ; . Здесь 6 – наименьшее общее кратное чисел 2 и 3.
Первоначальный интеграл примет вид:
.
И, наконец, переходя к первоначальной переменной , получим:
.◄
2.5.2.2. Найти интеграл: .
■ Преобразуем подынтегральную функцию следующим образом:
.
Тогда первоначальный интеграл примет вид:
.
— целое число. Имеем место случай (a). Применим подстановку: ; т. е. , получим: . Откуда
; .
Следовательно, .
С учётом подстановки первоначальный интеграл примет вид:
Знаменатель подынтегральной дроби имеет действительные корни.
Разложим подынтегральную функцию: на сумму простых дробей:
.
Приведём к общему знаменателю и приравняем числители обеих частей уравнения:
;
Сгруппируем слагаемые при одинаковых степенях :
;
Приравняем коэффициенты при одинаковых степенях и решим систему уравнений:
Тогда исходный интеграл примет вид:
=
.◄
2.5.2.3. Найти интеграл:
.
■ Преобразуем подынтегральную функцию: .
В интеграле — целое число.
Имеем случай (б). Применим подстановку Чебышева или .
Тогда ; ; ; ;
.
Тогда исходный интеграл примет вид:
.◄
2.5.2.4. Найти интеграл:
Перепишем подынтегральное выражение в виде:
.
При , , и . Очевидно, имеет место случай (в). Так как , то полагая , получаем , откуда
.
Следовательно,
.
2.5.2.5. Найти интеграл:
Перепишем подынтегральное выражение в виде:
.
При , , и .
Очевидно, имеет место случай (в). Так как
,
то полагая ,
получаем ,
откуда
.
Следовательно,
2.5.2.6. Найти интеграл:
■ Преобразуем подынтегральную функцию:
.
В интеграле — целое число. Имеем случай (б). Применим подстановку Чебышева: или . Тогда ;
Тогда исходный интеграл примет вид:
.
Перейдём к первоначальной переменной :
Так как , то
.◄
2.5.2.7. Найти интеграл: .
■ Преобразуем подынтегральную функцию:
.
Тогда исходный интеграл примет вид:
.
В интеграле —
целое число. Имеем случай (б). Положим или .
Дифференцируя последнее равенство,
получаем: . Откуда: .
С учётом замены первоначальный интеграл
примет вид:
.
Подынтегральная функция — рациональная дробь. Разложим знаменатель дроби на множители: .
Так как один корень знаменателя – действительный, а другой не является действительным, представим подынтегральную дробь в виде суммы простых дробей:
.
Приведём к общему знаменателю и приравняем числители обеих частей уравнения:
;
;
Сгруппируем слагаемые при одинаковых степенях :
.
Приравняем коэффициенты при одинаковых степенях .
.
Получим систему уравнений:
Следовательно,
.
Введём новую
переменную , .
Тогда интеграл примет вид:
.◄
2.5.2.8. Рационализация подынтегрального выражения в интегралах вида
достигается с помощью, по крайней мере, одной из следующих трех подстановок, называемых подстановками Эйлера
(а) при ;
(б) при ;
(в) при условии, что корни и уравнения действительны.
Следует иметь в виду, что подстановки (а) – (в) часто приводят к громоздким вычислениям. Поэтому обычно применяют другие способы.
Заметим, что подынтегральную функцию можно представить в виде
,
где и — рациональные дроби. Записывая в виде суммы многочлена и суммы простых дробей, сведем интеграл к линейной комбинации интегралов следующих трех типов:
(а) ;
(б) , ;
(в)
, , .
При нахождении интеграла (а), где — многочлен степени , удобно использовать формулу
.
В этой формуле — многочлен степени не выше , — некоторое число. Дифференцируя тождество и умножая затем обе части получаемого соотношения на , находим
.
Приравнивая коэффициенты при одинаковых степенях , вычислим коэффициенты многочлена и число . Интеграл в правой части сводится к табличному с помощью линейной подстановки.
Рассмотрим случай (б). Подстановкой этот интеграл сводится к интегралу (а).
Рассмотрим интеграл (в). Пусть существует число такое, что для всех выполняется равенство , т.е. , , то интеграл (в) можно представить в виде линейной комбинации интегралов
и .
Интеграл сводится к табличному, а интеграл подстановкой Абеля
сводится к интегралу
от многочлена.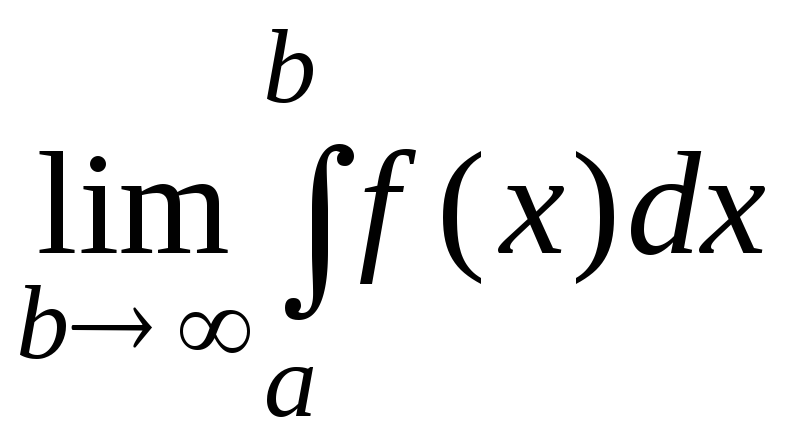
Если , то используется подстановка
,
где числа и подбираются такими, чтобы коэффициенты при в квадратных трехчленах подынтегральной функции обратились в нуль. При этом интеграл (в) примет вид
, ()
где — многочлен степени , .
Если , но , то можно применить подстановку .
Чтобы найти интеграл, разложим правильную рациональную дробь на простые дроби и представим интеграл в виде линейной комбинации интегралов вида
и .
Интеграл вычисляется с помощью подстановки , а интеграл — с помощью подстановки Абеля .
Примеры:
2.5.1. Найти интеграл:
Данный интеграл относится к случаю (а).
Полагаем
.
Продифференцируем это тождество. Получим:
,
Откуда получаем:
Для нахождения неопределённых коэффициентов получим систему уравнений:
Откуда: .
Следовательно,
2.5.2. Найти интеграл:
Данный интеграл относится к случаю (б). Введём подстановку .
Тогда интеграл приводится к виду, рассмотренному в предыдущей задаче.
Положим тогда и для имеем:
,
2.5.3. Найти интеграл:
Данный интеграл относится к случаю (в).
Полагаем
,
Тогда:
,
Откуда:
.
Дифференцируя равенство , получим:
,
Откуда:
.
Итак,
.
Поэтому:
.
2.5.4. Найти интеграл .
Данный интеграл относится к (в), причём . Положим . Подберём числа и так, чтобы коэффициенты при в квадратных трехчленах подынтегральной функции обратились в нуль. Так как
,
,
то, приравнивая к нулю коэффициенты при в числителях этих дробей, получаем систему
решение которой , .
Следовательно, искомая замена . Тогда имеем
, ,
числитель преобразуется как
, ,
а сам интеграл
,
где
и .
Интеграл вычисляется при помощи замены . Тогда, , . То есть, вычисление интеграла сводится к табличному
.
Для вычисления сделаем подстановку или . Дифференцируя, получаем
,
а с учётом подстановки
или .
Кроме того, из следует . Таким образом, вычисление сводится к табличному
.
Объединяя вычисления, окончательно получаем
, где .
Integrand: простое определение, примеры, функция
Определения вычислений >
Содержание:
- Определение
- Нечетный и четный Интегранд
- Определение интегральной функции
Подынтегральная функция — это функция, которую вы хотите интегрировать.
Это расчетный эквивалент дивиденда в базовой математике, который представляет собой количество, которое вы хотите разделить. С подынтегральным выражением это количество, которое вы хотите проинтегрировать.
Примеры
В интеграле
∫ x 2 sin 4 x dx ,
подынтегральная функция равна x 2 .
Для (x + 4) 3 dx подынтегральная функция равна (x + 4) 3 .
Термины «нечетный» и «четный» здесь не относятся к положительным (+) или отрицательным (-) величинам; они относятся к нечетным функциям или четным функциям. Нечетные функции симметричны относительно начала координат, а четные функции симметричны относительно оси Y (вертикальной оси). Эти факты важны, потому что они могут помочь вам решать уродливые интегралы, просто рассматривая форму графика.
Например, следующий график представляет собой функцию x log(2,125 + x 2 ) e -x 2 , нечетную функцию (поскольку она симметрична относительно начала координат):
График x. Область под кривой выделена синим цветом, область выше заштрихована оранжевым цветом.
Допустим, вы хотели вычислить подынтегральную функцию (x log(2,125 + x 2 ) e -x 2 ) в интервале от -2 до 2. Вы можете использовать калькулятор, но проще посмотреть на график. Интеграл на самом деле представляет собой просто площадь под кривой, поэтому общая площадь этого интеграла равна нулю (потому что вы вычитаете площадь под кривой из площади выше, и они обе равны). Этот факт будет выполняться для всех нечетных подынтегральных выражений, если вы оцениваете их на равном расстоянии от начала координат (например, от -2 до 2, от -9 до 9 или от -1000 до 1000).
Термин обычно относится к функции, интегрируемой при численном интегрировании, хотя иногда он неофициально используется при общем интегрировании как ответ на простой вопрос « какая функция интегрируется ?».
Например, вы можете захотеть проинтегрировать функцию косинуса f(x) = cos (x) от π2 до π:
- Подынтегральная функция (т.
е. интегрируемая здесь функция) равна f(x) = cos (Икс). - Интервал от π/2 до π.
е. интегрируемая здесь функция) равна f(x) = cos (Икс).Вместе эти две части информации сообщают вам, что вы интегрируете, и где находятся ограничения или интегрирование.
Интегральная функция в программном обеспечении
Вы также можете встретить эту функцию в MATLAB или R.
Например, Yang et al. (2018) ссылаются на следующее при обсуждении символических линейных интегралов/поверхностных интегралов в MATLAB:
f = векторная или скалярная подынтегральная функция в x, y и z
Смысл здесь тот же, за исключением того, что авторы заявляют, что функция может быть скалярной или векторной.
В своей книге Mastering Scientific Computing with R Джеррард и Джонсон (2015) впервые показали, как решить задачу с помощью функции R интегрировать() . Эта функция позволяет вычислять интегралы с помощью адаптивных квадратур для функций одной переменной на заданном интервале.
Чтобы использовать функцию интегрировать () , вы должны сначала определить ее и сохранить как подынтегральная функция объект. Для простого примера вы должны ввести функцию x 2 как:
> подынтегральное выражение
Вы можете комбинировать это с функцией подынтегрального выражения , установив нижний и верхний пределы и интервал [a, b]:
>интегрировать(подынтегральное выражение, нижнее = 0, верхнее = 4)
21,33333 с абсолютной ошибкой 3 / 3.
Ссылки
Джеррард, П. и Джонсон, Р. (2015). Освоение научных вычислений с R. Packt Publishing
Хоффман, Дж. и Франкель, С. (2001). Численные методы для инженеров и ученых, второе издание. КПР Пресс.
Ян, В. и др. (2018). Инженерная математика с MATLAB. КПР Пресс.
Графический калькулятор Desmos.
Джон Д. Кук Консалтинг. Сохранено Симметрией. Получено 5 декабря 2019 г. с: https://www.johndcook.com/blog/2011/03/31/saved-by-symmetry/
Open University.
3.3.3 Математические термины умножения и деления. Получено 5 декабря 2019 г. с: https://www.open.edu/openlearncreate/mod/oucontent/view.php?id=605§ion=4.3
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Integrand: простое определение, примеры, функция» от StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/integrand-simple-definition-examples/
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Математические слова: Интеграл
Математические слова: Интеграл
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
