| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | ||
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | загар((5pi)/3) | ||
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
2 Sin a Cos a Формула — вывод, применение, пример
2 sin a cos a — это тригонометрическая формула, равная синусу угла 2a, т.
е. она определяется как 2 sin a cos a = sin 2a. Это одно из важных тригонометрических тождеств, которое используется для решения различных тригонометрических и интегральных задач. 2 sin a cos формула также называется формулой двойного угла функции синуса, так как она равна sin 2a, где 2a — это удвоенный угол a. Эта формула также может быть выражена через тангенс а.
Давайте рассмотрим формулу 2 sin a cos a, выведем формулу, используя формулу sin (a + b), и поймем ее применение для решения различных математических задач. Мы также приведем несколько примеров с использованием формулы 2 sin a cos для лучшего понимания ее применения.
| 1. | Что такое 2 Sin a Cos Formula? |
| 2. | Вывод 2 Sin a Cos Формула |
| 3. | 2 Sin a Cos a Формула загара a |
| 4. | Как применить формулу 2 Sin a Cos? |
5. | Часто задаваемые вопросы о формуле 2 Sin a Cos a |
Что такое 2 Sin a Cos Formula?
2 sin a cos формула — важная тригонометрическая формула, равная sin 2a. Математически это записывается как sin 2a = 2 sin a cos a. Это также может быть выражено через tan a. Формула 2 sin a cos может быть записана двумя способами:
- 2 sin a cos a = sin 2a
- 2 sin a cos a = (2 тангенс а)/(1 + тангенс 2 а)
Первая форма этой формулы является наиболее часто используемой и используется для упрощения сложных тригонометрических функций и решения задач. Мы также можем выразить 2 sin как формулу, используя sin 2 a + cos 2 a = 1 формула:
- 2 sin a cos a = 2 √(1 — cos 2 a) cos a
- 2 sin a cos a = 2 sin a √(1 — sin 2 a)
Получение 2 Sin a Cos формулы
Теперь мы докажем формулу 2 sin a cos a, используя формулу суммы углов функции синуса, т.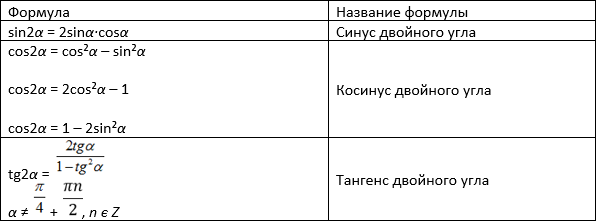
е. sin (a + b) = sin a cos b + sin b cos a. Предположим, что a = b в этой формуле, и давайте выведем формулу 2 sin a cos a пошагово. У нас есть,
sin (a + b) = sin a cos b + sin b cos a
⇒ sin (a + a) = sin a cos a + sin a cos a [Предположим, что a = b]
⇒ sin a cos a + sin a cos a = sin (a + a)
⇒ 2 sin a cos a = sin (2a)
Таким образом, мы доказали, что 2 sin a cos a равно sin 2a.
2 Sin a Cos a Формула загара
Далее мы выведем формулу 2 sin a cos a через tan a. Мы получили, что 2 sin a cos a = sin (2a). Теперь, если мы умножим и разделим 2 sin a cos a на cos a, то мы получим
2 sin a cos a = (2 sin a cos a) × (cos a)/(cos a)
= 2 (sin a/cos a) (cos 2 a)
Теперь мы знаем, что sin x/cos x = tan x и 1/cos x = sec x или 1/sec x = cos x. Следовательно, мы имеем
2 sin a cos a = (2 tan a)/(sec 2 a)
= (2 tan a)/(1 + tan 2 a) [используя тригонометрическую формулу 1 + tan 2 x = sec 2 x]
Следовательно, формула 2 sin a cos a в терминах тангенса a задается следующим образом: 2 sin a cos a = (2 tan a)/(1 + tan 2 а)
Как применить формулу 2 Sin a Cos a?
Итак, мы получили формулу для 2 sin a cos a.
Далее давайте разберемся с применением этих формул при решении различных задач. Давайте решим несколько примеров, чтобы научиться применять формулу 2 sin a cos.
Пример 1: Найдите значение sin 120°, используя формулу 2 sin a cos.
Решение: Нам известны значения тригонометрических функций для конкретных углов. Итак, у нас
sin 120° = sin (2 × 60°)
⇒ sin 120° = 2 sin 60° cos 60° (Потому что 2 sin a cos a = sin (2a))
⇒ sin 120° = 2 × √ 3/2 × 1/2
⇒ sin 120° = √3/2
Эту формулу можно использовать и наоборот, чтобы найти значение 2 sin a cos a, используя sin 2a.
Пример 2: Определите значение 2 sin 15° cos 15°.
Решение: Поскольку мы знаем значения функции синуса для конкретных углов и 2 sin a cos a = sin (2a), мы имеем
2 sin 15° cos 15° = sin (2 × 15°)
⇒ 2 sin 15° cos 15° = sin 30°
⇒ 2 sin 15° cos 15° = 1/2
Важные примечания на 2 sin a cos a
- 2 sin a cos формула также широко известна как формула sin 2a.
- 2 sin a cos a = sin (2a)
- 2 sin a cos a = (2 тангенс а)/(1 + тангенс 2 а)
- 2 sin a cos a = 2 √(1 — cos 2 a) cos a
- 2 sin a cos a = 2 sin a √(1 — sin 2 а)
Похожие темы по 2 sin a cos a
- Cos a Cos b
- Кос 2x
- Кос 3а
Часто задаваемые вопросы о формуле 2 Sin a Cos a
Что такое формула 2 Sin a Cos a в тригонометрии?
2 sin a cos a формула — важная тригонометрическая формула, равная sin 2a. Математически это записывается как sin 2a = 2 sin a cos a. Это также может быть выражено через tan a.
Формулы Sin 2a и 2 Sin a Cos a одинаковы?
Да, Sin 2a Formula и 2 Sin a Cos a Formula совпадают с sin 2a = 2 sin a cos a. На самом деле формула 2 sin a cos a также широко известна как формула sin 2a.
Как вывести формулу 2 Sin a Cos?
2 Sin a Cos a можно получить, используя формулу суммы углов функции синуса sin (a + b), учитывая, что a = b.