Уравнение прямой проходящей через точку параллельно прямой калькулятор: Онлайн калькулятор. Уравнение прямой проходящей через две точки

Содержание

Уравнение прямой с угловым коэффициентом на плоскости

Прямая, проходящая через данную точку в направлении, заданном угловым коэффициентом
Прямая, проходящая через две данные точки
Прямая, проходящая через данную точку параллельно данной прямой

Пусть на плоскости xOy задана прямая, непараллельная оси Oy. Углом между прямой и осью Ox называется тот угол между прямой и положительным направлением оси, который расположен в верхней полуплоскости (рисунок снизу, прямая обозначена красным цветом).

Если прямая параллельна оси или совпадает с нею, то угол считается равным нулю.

Для того, чтобы составить уравнение прямой, достаточно, чтобы были заданы точка , лежащая на этой прямой, и угол наклона прямой к оси Ox.

Угловым коэффициентом прямой называется тангенс угла наклона этой прямой к оси Ox.

Уравнение прямой с угловым коэффициентом в случае нашей задачи составляется по формуле

, (1)

где — координаты точки , — угловой коэффициент прямой.

После подстановки указанных выше величин в формулу должно получиться уравнение вида

. (2)

Пример 1. Составить уравнение прямой с угловым коэффициентом, если угловой коэффициент и прямая проходит через точку .

Решение. Используя формулу (1), получаем:

Получили уравнение вида (2).

Проверяем — подставляем координаты точки в полученное уравнение, в нашем случае получается верное равенство:

Пример 2. Составить уравнение прямой с угловым коэффициентом, если угол наклона прямой и прямая проходит через точку .

Решение. Находим угловой коэффициент, то есть тангенс угла наклона прямой:

Теперь, используя формулу (1), получаем:

Получили уравнение вида (2).

Решая задачи контрольных работ, надо стараться сделать проверку (для себя), даже если этого не требует условие задачи.

Как видно на примерах 1 и 2, из возможности проверки верного равенства следует возможность установить, принадлежит ли прямой, заданной уравнением с угловым коэффициентом, любая точка плоскости с заданными координатами. Проиллюстрируем это следующим примером.

Пример 3. Установить, принадлежит ли прямой, заданной уравнением с угловым коэффициентом точки и .

Решение. Подставляя координаты точки в уравнение прямой, получаем:

Получили верное равенство, следовательно точка принадлежит заданной прямой.

Подставляя координаты точки в уравнение прямой, получаем:

Получили неверное равенство, следовательно точка не принадлежит заданной прямой.

Нет времени вникать в решение? Можно заказать работу!

Применяя соотношение (1), легко решить следующую задачу: составить уравнение прямой, которая проходит через две данные точки и .

В аналитической геометрии доказано, что угловой коэффициент искомой прямой можно вычислить по формуле:

. (3)

Нам остаётся лишь применять эту формулу.

Пример 4. Составить уравнение прямой с угловым коэффициентом, если она проходит через точки и .

Решение. По формуле (3) находим угловой коэффициент:

Теперь, используя формулу (1), получаем:

Итак, получили уравнение вида (2).

Проверяем — подставляем координаты точек в полученное уравнение, получаются верные равенства:

Для того, чтобы составить уравнение прямой, проходящей через данную точку параллельно данной прямой, следует использовать следующее условие параллельности прямых.

Для параллельности прямых необходимо и достаточно, чтобы их угловые коэффициенты были равны.

Следовательно, эта задача просто обращается в задачу из примера 1. В формулу (1) следует подставить угловой коэффициент заданной прямой.

Пример 5. Составить уравнение прямой, проходящей через точку параллельно прямой, проведённой через две данные точки и .

Решение. Используя условия параллельности прямых. Требуется сначала найти угловой коэффициент прямой, проходящей через точки B и C, а затем воспользоваться этим угловым коэффициентом. Угловой коэффициент находим по формуле (3):

Угловой коэффициент искомой прямой также равен -5.

Теперь остаётся лишь составить уравнение прямой по угловому коэффициенту и точке, как в примере 1:

Итак, получили уравнение вида (2).

Аналогично решается задача, если задано, что прямая перпендикулярна данной прямой. Для её решения следует воспользоваться условием перпендикулярности прямых:

для перпендикулярности двух прямых необходимо и достаточно, чтобы их угловые коэффициенты были обратны по величине и противоположны по знаку.

Назад

Листать

Вперёд>>>

К началу страницы

Пройти тест по теме Прямая и плоскость

Всё по теме «Прямая на плоскости

Уравнение прямой с угловым коэффициентом

Общее уравнение прямой на плоскости

Уравнение прямой в отрезках

Каноническое уравнение прямой на плоскости

Параметрические уравнения прямой на плоскости

Нормальное уравнение прямой на плоскости, расстояние от точки до прямой

Примеры

1. Прямая задана общими уравнениями Написать ее канонические уравнения, а также уравнение ее проекций на координатные плоскости.

Решение. Т. к. то для нахождения точки прямой приведем исходные уравнения к виду

Полагая z равным произвольному числу , например из данной системы найдем , , т. е. .

В качестве направляющего вектора прямой может быть взят вектор , где , – нормальные векторы плоскостей, линией пересечения которых является заданная прямая. Таким образом,

По формуле (1.30) записываем искомые канонические уравнения

или .

Полученная пропорция эквивалентна системе трех уравнений описывающих три плоскости, проектирующие прямую на координатные плоскости и соответственно (уравнения прямой в проекциях).

2. Составить параметрическое уравнение прямой, проходящей через точку перпендикулярно плоскости .

Решение. Нормальный вектор плоскости параллелен искомой прямой и, значит, его можно взять в качестве направляющего вектора этой прямой. Согласно соотношениям (1.31), параметрические уравнения искомой прямой есть

3. Дан треугольник с вершинами . Составить уравнение прямой, на которой лежит медиана, проведенная из вершины В.

Решение. Используя формулы деления отрезка пополам, находим середину отрезка АС – точку Cоставим уравнение прямой, проходящей через две точки В и D, используя формулу (1.33): или .

4. Из начала координат опустить перпендикуляр на прямую

Решение. Используя условие (1.41) перпендикулярности прямой и плоскости и полагая составим уравнение плоскости, проходящей через начало координат и перпендикулярной заданной прямой. Это уравнение имеет вид .

Найдем точку пересечения этой плоскости и данной прямой. Параметрические уравнения прямой запишутся так: ; ; . Для определения t подставим выражения для в уравнение плоскости: откуда Координаты точки пересечения

Остается составить уравнение прямой, проходящей через начало координат и через точку М.

Используя соотношение (1.33), получим или

5. Составить уравнение прямой, проходящей через точку и пересекающей ось под прямым углом.

Решение. Так как прямая перпендикулярна оси и пересекает ее, то она проходит через точку Составив уравнение прямой, проходящей через точки и по формуле (1.33), получаем

6. Найти точку , симметричную точке относительно плоскости

Решение. Искомая точка принадлежит прямой , проведенной из точки перпендикулярно плоскости Р. Уравнения прямой , параллельной вектору и проходящей через точку имеют вид или в параметрическом виде:

Найдем точку пересечения прямой и плоскости, подставляя выражения для в уравнение плоскости. Найдем , откуда

Воспользовавшись формулами деления отрезка пополам, найдем координаты симметричной точки: откуда , , Следовательно, .

7. Дана прямая и вне ее точка . Найти точку , симметричную точке относительно данной прямой.

Решение. Уравнение плоскости, проецирующей точку на данную прямую, имеет вид .

В качестве нормального вектора плоскости, перпендикулярной прямой, можно взять направляющий вектор данной прямой

Тогда получим или

Найдем проекцию точки на прямую, для чего совместно решим систему уравнений (параметрические уравнения прямой). Найдем , отсюда Тогда координаты симметричной точки можно найти, используя формулы для координат середины отрезка, т. е. откуда

8. Через прямую провести плоскость, параллельную прямой

Решение. Запишем уравнения первой из заданных прямых с помощью уравнений двух плоскостей, проецирующих ее соответственно на плоскости и : или или

Уравнение пучка плоскостей, проходящих через эту прямую, имеет вид

или

Используя условие параллельности прямой и плоскости, определим так, чтобы соответствующая плоскость пучка была параллельна второй из заданных прямых.

Имеем или откуда Таким образом, искомая плоскость определяется уравнением .

9. Найти уравнение проекции прямой на плоскость

Решение. Запишем уравнения заданной прямой в виде уравнений двух плоскостей, проецируюших ее соответственно на плоскости и

или или

Уравнение пучка плоскостей, проходящих через данную прямую, запишется в виде: или

Используя условие перпендикулярности плоскостей, выберем из этого пучка плоскость, проецирующую данную прямую на заданную плоскость. Имеем или откуда Итак, уравнение проецирующей плоскости имеет вид или

Искомую проекцию можно определить как линию пересечения двух плоскостей – заданной и проецирующей:

Приведя эти уравнения прямой к каноническому виду, окончательно получим

10. Заданы скрещивающиеся прямые

Найти расстояние между прямыми и написать уравнения общего перпендикуляра L к этим прямым.

Решение. Найдем уравнение плоскости Р, проходящей через прямую параллельно прямой . Точка лежит на прямой и, следовательно, принадлежит искомой плоскости Р. В качестве нормального вектора к этой плоскости возьмем вектор

Уравнение плоскости Р: или

Расстояние равно расстоянию от любой точки прямой , например, точки , до плоскости Р. Нормальное уравнение плоскости имеет вид откуда

Для того чтобы составить уравнения общего перпендикуляра L, найдем уравнения плоскостей и , проходящих через заданные прямые и соответственно и перпендикулярных плоскости Р.

Имеем и откуда : Аналогично, и откуда : Cледовательно,

– общие уравнения прямой

11. Найти угол между прямыми и

Решение. Направляющий вектор прямой а где Откуда следует, что . Так как то

12. Дан треугольник с вершинами , , . Составить параметрические уравнения прямой, на которой лежит его высота, проведенная из точки В.

Решение. Эту прямую можно рассматривать как линию пересечения двух плоскостей: плоскости, проходящей через три точки , и плоскости, проходящей через точку В перпендикулярно к вектору . Составим их уравнения:

Следовательно, данная прямая определяется уравнениями:

Приведем эти уравнения к параметрическому виду. Нам известна точка В, через которую проходит данная прямая. Найдем координаты направляющего вектора Так как , , то или . Следовательно, параметрические уравнения прямой имеют вид:

Калькулятор параллельных линий

Создано Bogna Szyk

Отзыв от Adena Benn

Последнее обновление: 27 декабря 2022 г.

Содержание:

Как найти наклон параллельной линии?
Уравнение параллельных прямых
Нахождение расстояния между двумя параллельными прямыми
Вычисления параллельных прямых: пример
Часто задаваемые вопросы

Если вы ломаете голову, когда пытаетесь решить некоторые уравнения параллельных прямых , не беспокойтесь: этот калькулятор параллельных линий — именно то, что вам нужно. Всего за несколько секунд он определит уравнение прямой, параллельной данной прямой и проходящей через данную точку. Но это еще не все. наш калькулятор также может определить расстояние между двумя линиями.

Читайте дальше, чтобы узнать, как найти наклон параллельной линии или что такое точка пересечения по оси Y.

🙋 Вас интересуют другие подобные калькуляторы? Проверьте наш калькулятор перпендикулярных линий!

Как найти наклон параллельной линии?

Каждая прямая линия в двумерном пространстве может быть описана простым уравнением прямой:

y=ax+b,y = ax + b,y=ax+b,

, где a и b — коэффициенты, x — координата x, y — координата y. Каждая строка определяется однозначно, если известны значения a и b .

Предположим, вы знаете следующую информацию:

Уравнение данной прямой y = mx + r . Вы знаете значения м и r и ищете прямую, параллельную этой.
Вы также знаете координаты точки, через которую должна проходить ваша линия. Это x₀ и y₀ .

Наклон любой линии равен значению коэффициента . Если две прямые параллельны, то они должны иметь одинаковый наклон. Отсюда мы можем сделать такой вывод.

a = m

Мы также рекомендуем воспользоваться нашим калькулятором средней скорости изменения.

💡 Чтобы рассчитать наклон любой линии, используйте наш калькулятор наклона.

Уравнение параллельной линии

После того, как вы узнали коэффициент a линии, все, что осталось сделать, это определить коэффициент b (также известный как точка пересечения по оси y).

Метод прост: нужно подставить координаты (x₀, y₀) и значение a в уравнение вашей линии.

y=ax+by = ax + by=ax+b

y₀=mx₀+by₀ = mx₀ + by₀=mx₀+b

b=y₀−mx₀b = y₀ — mx₀b=y₀−mx₀3 900 между двумя параллельными линиями

Теперь, когда вы знаете уравнение новой линии, вы можете легко использовать его для определения расстояния между ней и первой линией. В этом случае расстояние определяется как длина кратчайшего возможного отрезка, соединяющего две линии вместе.

Наш калькулятор параллельных линий автоматически находит это расстояние . Однако, если вы хотите проверить правильность результата, вы можете использовать формулу расстояния:

D=∣b−r∣m²+1 D = \frac{|b — r|}{\sqrt{m² + 1}}D=m²+1

∣b−r∣

Вычисление параллельных прямых: пример

Если вы все еще не уверены как найти уравнение параллельной прямой , посмотрите на примере ниже!

Запишите уравнение первой строки. Допустим, это:
у = 3х — 5
Запишите координаты заданной точки P , через которую будет проходить вторая линия. Предположим, что это (1,6). Другими словами, x₀ = 1 и y₀ = 6,
.
Запишите уравнение новой линии: y = ax + b . Вы попытаетесь определить значения коэффициентов a и b .
Коэффициент а равно м . Следовательно,
а = м = 3 .
Подставьте координаты точки P в уравнение новой линии, чтобы определить b :
у₀ = ах₀ + б
6 = 3 × 1 + б
б = 6 — 3 × 1 = 3
Зная значения наклона и точки пересечения с осью y, теперь вы можете записать полное уравнение новой линии: y = 3x + 3 .
Вы также можете рассчитать расстояние между двумя линиями:
D = |b — r| / √(м² + 1)
Д = |3 — 6| / √(3² + 1) = |-3| / √(10) = 2,53

Расстояние между двумя линиями равно 2,53.

Часто задаваемые вопросы

Как рассчитать расстояние между двумя параллельными линиями?

Чтобы найти расстояние между двумя параллельными прямыми на декартовой плоскости, выполните следующие простые шаги:

Найдите уравнение первой строки: y = m1 × x + c1 .
Найдите уравнение второй прямой y = m2 × x + c2 .
Вычислить разницу между точками пересечения : (c2 − c1) .
Разделите этот результат на следующее количество: sqrt(m² − 1) :
d = (c2 − c1) / √(m² − 1)

Это расстояние между двумя параллельными линиями.

Как определить две параллельные линии на декартовой плоскости?

Две параллельные прямые на декартовой плоскости имеют одинаковый угловой коэффициент . Зная это, можно исключить тривиальный случай, когда точка пересечения одинакова (две линии совпадают).

Сложнее определить параллелизм в трех измерениях: две линии могут быть непараллельными, но никогда не пересекаться!

Как найти параллельную прямую, проходящую через точку?

Параллель прямой y = m × x + b , проходящей через точку (p, q) можно найти с помощью следующих шагов:

Найдите наклон параллельной линии — это м !
Найдите точку пересечения уравнения параллельной прямой, подставив координаты точки в уравнение исходной прямой:
q = m × p + b
Отсюда:
b = q / (m × p)

Какие есть примеры параллельных линий?

Стороны дороги являются прекрасным примером параллельных линий: перед перекрестком две стороны никогда не встречаются! Другими примерами являются параллели (но не меридианы!) на земном шаре: это трехмерные параллельные линии . Вы можете найти параллельные линии на многих человеческих творениях, но редко в природе: зорким глазом вы можете увидеть их в некоторых геологических образованиях и на коротких участках в деревьях и других растениях.

Bogna Szyk

Уравнение первой прямой y = mx + r

Вторая прямая проходит через точку…

Уравнение параллельной прямой y = ax + b

Расстояние между прямыми

Расстояние

2 Координата 3 калькуляторы геометрии 📈

Средняя скорость измененияБилинейная интерполяцияКатенарная кривая… Еще 35

Уравнения прямых: параллельные и перпендикулярные линии перпендикулярные линии. Вот общий формат упражнений на эту тему:

Дана линия 2
x − 3 y = 9и точку (4, −1), найдите линии в форме пересечения наклона, проходящие через заданную точку, такие, что две линии соответственно равны: 90 307

(а) параллельно данной линии, а

(б) перпендикулярно ему.

Мне дали ориентир, а именно, 2 x − 3 y = 9; это линия, на наклон которой я буду ссылаться позже в своей работе.

Содержимое продолжается ниже

MathHelp.com

Типы чисел: рациональные или иррациональные

Эта линия имеет некоторое значение наклона (хотя, конечно, не значение «2», потому что это уравнение прямой не решено для » у =»).

Сначала мне нужно найти наклон опорной линии. Я мог бы использовать метод двойной подстановки значений x в опорную линию, нахождения соответствующих значений y , а затем подстановки двух найденных точек в формулу наклона, но я бы предпочел просто решить для y =». (Это только мое личное предпочтение. Если ваши предпочтения отличаются, то используйте любой метод, который вам больше нравится.) Итак:

Первое, что я сделаю, это решу «2 x − 3 y = 9″ для « y =», так что я могу найти опорный наклон:

2 x — 3 y = 9

-3 y = -2 0 x 901

y = (² / ₃ ) x − 3

Таким образом, базовый наклон от базовой линии равен

м = ² / ₃ .

Теперь мне нужно найти два новых склона и использовать их с точкой, которую они мне дали; а именно, с точкой (4, −1). Они хотят, чтобы я нашел прямую через (4, −1), параллельную 2 x − 3 y = 9; то есть через заданную точку они хотят, чтобы я нашел линию, которая имеет тот же наклон, что и исходная линия. Затем они хотят, чтобы я нашел прямую, проходящую через (4, −1), которая перпендикулярна 2 х — 3 у = 9; то есть через данную точку они хотят, чтобы я нашел линию, имеющую наклон, который является отрицательной обратной величиной наклона базовой линии.

Поскольку параллельная прямая имеет одинаковый наклон, то параллельная прямая, проходящая через (4, −1), будет иметь наклон

м = ² / ₃ . Эй, теперь у меня есть точка и наклон! Поэтому я буду использовать форму точка-наклон, чтобы найти линию:

y − (−1) = ( ² / ₃ )( x − 4)

y + 1 = ( ² / ₃ ) x − ⁸ / ₃

y = ( ² / ₃ ) x − ⁸ / ₃ − ³ / ₃

y = ( ² / ₃ ) x − ¹¹ / ₃

Это параллельная линия, о которой они просили, и она имеет форму пересечения наклона, которую они указали.

Для перпендикулярной линии я должен найти перпендикулярный уклон. Базовый уклон равен

м = ² / ₃ . Для перпендикулярного уклона я переверну эталонный уклон и изменю знак. Тогда перпендикулярный уклон равен м = − ³ / ₂ .

Опять же, у меня есть точка и наклон, поэтому я могу использовать форму точка-наклон, чтобы найти свое уравнение. Обратите внимание, что единственное изменение, которое следует из вычислений, которые я только что сделал выше (для параллельной линии), заключается в том, что наклон отличается, теперь он является наклоном перпендикулярной линии.

y − (−1) = ( − ³ / ₂ )( x − 4)

y + 1 = ( − ³ / ₂ ) х + 6

y = ( − ³ / ₂ ) x + 5

Then the full solution to this exercise is:

parallel:

y = ( ² / ₃) x — ¹¹ /₃

Перпендикуляр:

Y = ( — ³ /₂) x + 5 /₂) x + 5 ^{95555550555055055505}

5505

505

55505

05 _{/₂). две заданные линии «параллельны, перпендикулярны или ни то, ни другое», вы должны ответить на этот вопрос, найдя их наклоны, не рисуя картинку! Фотографии могут дать вам только приблизительное представление о том, что происходит.}

Например, вы просто не смогли бы сказать, просто «взглянув» на картинку, что нарисованные линии с уклонами, скажем, м ₁ = 1,00 и м ₂ = 0,99 являются НЕ параллельно — и они будут чертовски уверены, что выглядят параллельно на картинке. Но поскольку 1,00 не равно 0,99, прямые не могут быть параллельными.

Другими словами, чтобы ответить на такое упражнение, всегда находите численные наклоны; не пытайтесь просто нарисовать несколько красивых картинок.

Вы можете использовать приведенный ниже виджет Mathway, чтобы попрактиковаться в поиске параллельной линии, проходящей через заданную точку. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Следующий виджет предназначен для поиска перпендикулярных линий.) Или перейдите к двум сложным примерам, которые следуют ниже.

Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.

(Нажав «Нажмите, чтобы просмотреть шаги» на экране ответов виджета, вы перейдете на сайт Mathway для платного обновления.)

Вы можете использовать приведенный ниже виджет Mathway, чтобы попрактиковаться в поиске перпендикулярной линии, проходящей через заданную точку. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.

Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.

(Щелкнув «Нажмите для просмотра шагов» на экране ответов виджета, вы перейдете на сайт Mathway для платного обновления.)

Почти все упражнения по нахождению уравнений параллельных и перпендикулярных линий будут аналогичны приведенным ниже. , или точно так же, как тот, что выше. Вот два примера более сложных типов упражнений:

Поскольку наклон представляет собой значение, умноженное на » x » при решении уравнения для » y =», тогда значение » a » будет значением наклона перпендикулярной линии. Другими словами, они просят у меня перпендикулярный уклон, но немного замаскировали свою цель. Я должен заметить связь.

Первое, что мне нужно сделать, это найти наклон опорной линии. Я решу для » y =»:

(2/3) y − 6 x = 3

2 y − 18 x = 9

y − 9 x = 9/2

y = 9 x + 9/2

Тогда эталонный уклон равен м = 9. Перпендикулярный уклон (будучи значением « a «, о котором меня спросили) будет отрицательная величина, обратная эталонному наклону.

Я начинаю с преобразования «9» в дробную форму, поместив его над «1». Затем я переворачиваю и меняю знак. Результат:

a = -1/9

Единственный способ, которым эти две линии могут иметь расстояние между ними, если они параллельны. (В противном случае они должны встретиться в какой-то точке, и в этой точке расстояние между прямыми, очевидно, будет равно нулю.) Параллельны ли эти прямые? :

3 х + 2 у = 15

2 y = −3 x + 15

Y ₁ = (−3/2) x + 15/2

… и:

9012 + 15/2

… и:

9012

0 + 15/2

… y + 6 x = 3

4 y = −6 x + 3

y = (−6/4) x + 3/4

y ₂ = (−3/2) x + 3/4

Линии имеют одинаковый наклон, поэтому они действительно параллельны.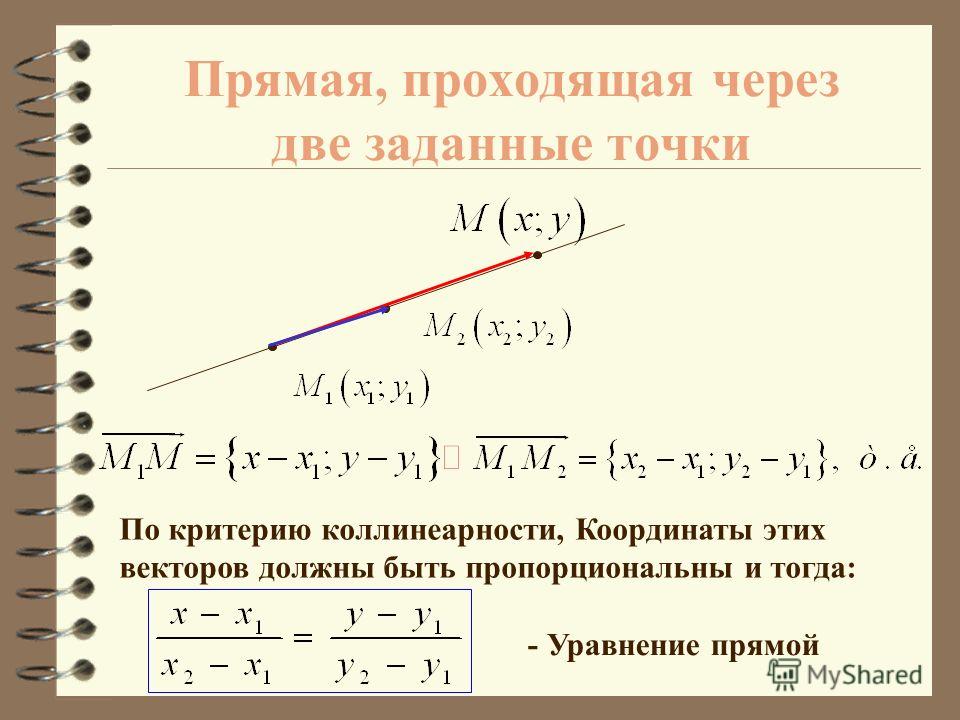 И у них разные и — перехваты, так что это не одна и та же линия. Следовательно, между этими двумя линиями действительно есть некоторое расстояние. Но как найти это расстояние? Это будет перпендикулярное расстояние между двумя линиями, но как мне его найти?

Я знаю, что могу найти расстояние между двумя точками; Я подставляю две точки в формулу расстояния. Но у меня нет двух точек. Ах; но я могу выбрать любую точку на одной из прямых, а затем найти перпендикулярную прямую, проходящую через эту точку. Поскольку исходные прямые параллельны, то эта перпендикулярная прямая также перпендикулярна второй из исходных прямых. Тогда я могу найти, где перпендикулярная линия и вторая линия пересекается. Эта точка пересечения будет второй точкой, которая мне понадобится для формулы расстояния.

Я знаю, что эталонный уклон равен

м = −3/2. Тогда мой перпендикулярный уклон будет м = 2/3. Теперь мне нужна точка, через которую я проведу перпендикулярную линию. Я выберу x = 1 и подставлю это в уравнение первой строки, чтобы найти соответствующее значение y :

y = (−3/2)(1) + 15/2

= −3/2 + 15/2

= 12/2 = 6

Итак, моя точка зрения (в первой строке мне дали) это (1, 6). С помощью этой точки и моего перпендикулярного наклона я могу найти уравнение перпендикулярной линии, которое даст мне расстояние между двумя исходными линиями:

y — 6 = (2/3)( x — 1 )

у — 6 = (2/3) х — 2/3

y = (2/3) x − 2/3 + 18/3

y = (2/3) x + 16/3

3 90; теперь у меня есть уравнение перпендикуляра. Расстоянием будет длина отрезка вдоль этой линии, который пересекает каждую из исходных линий.

Где эта линия пересекает вторую из данных линий? Он будет пересекаться там, где уравнения двух прямых равны, поэтому я приравняю стороны, отличные от y экватора второй исходной линии, и уравнения перпендикулярной линии, и решу:

(-3/2) х + 3/4 = (2/3) х + 16/3

9/2 — 32 = 13 x

(−55/2)/13 = x

x = -55/26

. Линейно-уравнение часть упражнения. Я оставлю остальную часть упражнения для вас, если вам интересно.

(Чтобы закончить, вам нужно подключить последние x -значение в уравнение перпендикулярной линии, чтобы найти соответствующее y -значение. Это даст вам второе очко. [Оказывается,

(-55/26, 51/13) , если вы посчитаете.