Уравнение прямой на плоскости. Примеры решения типовых задач. Часть 3
Высшая математика / Практикум по аналитической геометрии
Задача № 1. Составить уравнение прямой, если известно, что ее расстояние от начала координат равно 13, а угол, образованный перпендикуляром, опущенным с начала координат на прямую, и осью Ох, равен 225°.
Решение этой задачи подробно изложено в следующем видео
Задача № 2. Провести прямую через точку Р (3;-4), являющуюся основанием перпендикуляра, опущенного из начала координат на прямую.
Решение этой задачи подробно изложено в следующем видео
Задача № 3.
Найти геометрическое место точек, отклонение которых от прямой 6х-8y+5=0, равно 5.
Задача № 4. Найти геометрическое место точек, расстояние которых от прямой 5х-12у-13=0 равно 3.
Решения этих двух задач подробно объясняются в следующем видео:
Задача № 5. Две стороны квадрата лежат на прямых 4х-Зу+15=0 и 8х-6y+25=0. Вычислить его площадь.
Задача № 6. Доказать, что через точку Р(2;7) можно провести две прямые так, чтобы их расстояния от точки Q(1;2) были равны 5. Составить уравнения этих прямых.
Решения этих двух задач подробно объясняются в следующем видео:
Задача № 7. Составить уравнения прямых, перпендикулярных к прямой 2х+6y-3=0 и отстоящих от точки (5;4) на расстоянии V10 ед.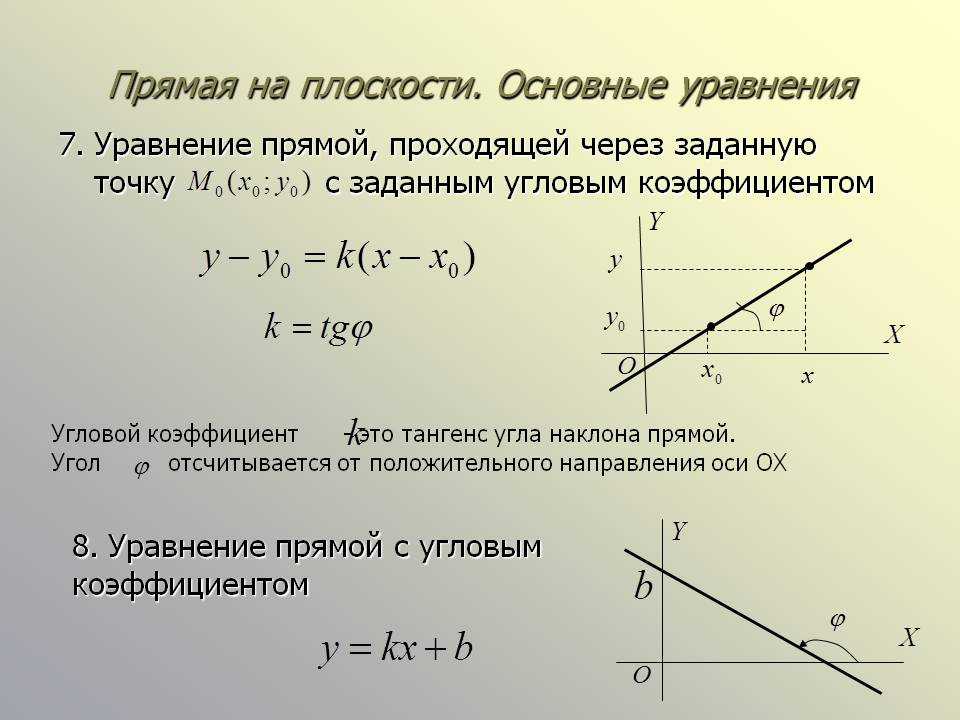
Решение этой задачи подробно изложено в следующем видео
Задача № 8. На прямой х+у-8=0 найти точки, равноудаленные от точки (2;8) и от прямой х-Зy+2=0.
Решение этой задачи подробно изложено в следующем видео
Задача № 9. Найти биссектрисы углов между прямыми Зх+4у-1=0 и 4х-Зy+5=0.
Решение этой задачи подробно изложено в следующем видео
Задача № 10. Даны вершины треугольника А (2; —2), В (3; -5) и С (5; 1). Составить уравнение перпендикуляра, опущенного из вершины С на биссектрису внутреннего угла при вершине В.
Рис. 1
Решение. Чтобы составить уравнение перпендикуляра CD (рис.
1), опущенного на биссектрису BD, необходимо знать угловой коэффициент BD. Для этого достаточно найти координаты точки L, которая согласно свойству биссектрисы внутреннего угла треугольника делит сторону АС в отношении
Для определения λ необходимо найти длины сторон АВ и ВС, которые находим по формуле расстояния между двумя точками.
Таким образом,
Координаты точки L найдем по формулам деления отрезка в заданном отношении:
Угловой коэффициент BD найдем по формуле
Следовательно, биссектриса BD перпендикулярна к оси Ох.
В таком случае прямая CD будет параллельна оси Ох, ее уравнение у = b, где b — ордината точки, через которую проходит прямая. b=1.
Таким образом, уравнением перпендикуляра CD будет уравнение у = 1, или у —1=0.
Ответ: у —1=0.
Решение этой задачи подробно изложено в следующем видео
Уравнение прямой, проходящей через две точки
Пусть
прямая проходит через точки М1 (х1;
у1)
и М2 (х2;
у2).
Уравнение прямой, проходящей через
точку М1,
имеет вид у— у1 = k (х — х1),
(10.6)
где k — пока неизвестный коэффициент.
Так как прямая проходит через точку М2(х2 у2), то координаты этой точки должны удовлетворять уравнению (10.6): у2—у1 = k (х2—х1).
Отсюда находим Подставляя найденное значениеk в уравнение (10.6), получим уравнение прямой, проходящей через точки М1 и М2:
Предполагается,
что в этом уравнении х1 ≠ х2,
у
Если
х1 = х2,
то прямая, проходящая через точки М1 (х1 ,уI)
и М2 (х2,у2)
параллельна оси ординат. Ее уравнение
имеет вид х
= х1.
Если у2 = уI, то уравнение прямой может быть записано в виде у = у1, прямая М1 М2 параллельна оси абсцисс.
Уравнение прямой в отрезках
Пусть прямая пересекает ось Ох в точке М1(а;0), а ось Оу – в точке М2(0;b). Уравнение примет вид: т.е.. Это уравнение называетсяуравнением прямой в отрезках, т.к. числа а и b указывают, какие отрезки отсекает прямая на осях координат.
Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
Найдем уравнение прямой, проходящей через заданную точку Мо (х О; уо) перпендикулярно данному ненулевому вектор n = (А; В).
Возьмем на прямой произвольную точку М(х; у) и рассмотрим вектор М0М (х — х0; у — уо) (см. рис.1). Поскольку векторы n и МоМ перпендикулярны, то их скалярное произведение равно нулю: то есть
А(х
— хо) + В(у — уо) = 0.
(10.8)
Уравнение (10.8) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору.
Вектор n= (А; В), перпендикулярный прямой, называется нормальным нормальным вектором этой прямой.
Уравнение (10.8) можно переписать в виде Ах + Ву + С =0, (10.9)
где
А и В координаты нормального вектора,
С = —Ах
Рис.1 Рис.2
Канонические уравнения прямой
,
Где — координаты точки, через которую проходит прямая, а- направляющий вектор.
Кривые второго порядка Окружность
Окружностью
называется множество всех точек
плоскости, равноотстоящих от данной
точки, которая называется центром.
Каноническое уравнение круга радиуса R с центром в точке :
В частности, если центр кола совпадает с началом координат, то уравнение будет иметь вид:
Эллипс
Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух заданных точек и, которые называются фокусами, есть величина постоянная, большая чем расстояние между фокусами.
x
Каноническое уравнение эллипса, фокусы которого лежат на оси Ох, а начало координат посредине между фокусами имеет видгдеa длина большой полуоси; b– длина малой полуоси (рис. 2).
Зависимость между параметрами эллипса ивыражается соотношением:
(4)
Эксцентриситетом эллипса называется отношение межфокусного расстояния 2с к большой оси 2а:
Директрисами эллипса называются прямые, параллельные
оси Оу, которые находятся от этой оси
на расстоянии.
Если в уравнении эллипса , тогда фокусы эллипса находятся на оси Оу.
Итак,
Калькулятор перпендикулярных линий — MathCracker.com
Инструкции: Используйте этот калькулятор, чтобы найти перпендикулярную линию к предоставленной вами линии, которая проходит через заданную точку, со всеми показанными шагами. С этой целью вам нужно предоставить информацию для определения линии, и вам нужно указать точку, в которой вы хотите провести перпендикулярную линию. пройти через.
Вы можете определить данную линию, указав: (1) как наклон, так и точку пересечения с осью y, (2) линейное уравнение (пример: \(x + 3y = 2 + \frac{2}{3}x\ ))
(3) наклон и точка, через которую проходит линия, или (4) две точки, через которые проходит линия.
Узнайте больше об этом калькуляторе перпендикулярных линий.
Линии в значительной степени определяются их наклоном (наклоном). Горизонтальные линии — это линии с нулевым наклоном, вертикальные — линии, где наклон не определен (отрицательная или положительная бесконечность).
Перпендикулярные линии – это линии, которые пересекаются, образуя прямой угол. Существует особое условие для наклона и перпендикулярного уклона, когда наклоны определены, чтобы линии были перпендикулярны, то есть произведение наклонов равно -1.
Заметьте, что к одной заданной прямой перпендикулярно бесконечное количество прямых.
Для того, чтобы найти тот, который вы ищете, вам нужно исправить
точка, через которую он проходит.
Как найти перпендикуляр к прямой?
Стратегия проста. Шаг состоит в том, чтобы найти наклон данной линии. Если вам предоставлены наклон и точка пересечения, чтобы определить линию то у вас уже есть наклон.
В противном случае, возможно, у вас есть две точки, через которые проходит линия, и в этом случае вы можете вычислить склон прямо.
В конечном счете, если вы определяете заданную линию уравнением, вам нужно преобразовать это уравнение в форму пересечения наклона, чтобы получить наклон.
Получив наклон заданной линии, вы используете формулу для перпендикулярного наклона, умножая на минус один обратный исходному наклону.
Что такое перпендикуляр к горизонтальной линии
Перпендикуляр к горизонтальной линии является вертикальной линией.
Что такое перпендикуляр к вертикальной линии
Перпендикуляр к вертикальной линии является горизонтальной линией.
Можете ли вы вычислить перпендикулярную линию без точек
Если у вас есть линия, то существует не одна, а множество (бесконечных) перпендикулярных линий к данной линии. Для определения одного конкретного перпендикуляра линии, вам нужно указать одну точку, через которую проходит линия.
Как правило, вы указываете точку на исходной линии, где вы хотите перпендикулярная линия, через которую нужно пройти.
Пример расчета перпендикуляра для заданной линии:
Рассмотрим прямую с уравнением \(2x + 3y = 5)\). Найдите уравнение перпендикуляра, проходящего через \((1, 1)\).
Решение: Сначала мы получаем уравнение пересечения наклона для ДАННОЙ линии, если это возможно
Мы получили следующее уравнение:
\[\displaystyle 2x+3y=5\]
Подставив \(y\) в левую часть, а \(x\) и константу в правую, получим
\[\displaystyle 3y = -2x +5\]
Тогда, решив \(y\), разделив обе части уравнения на \(3\), получим следующее
\[\displaystyle y=-\frac{2}{3}x+\frac{5}{3}\]
Формула перпендикулярного уклона
В общем, формула, необходимая для вычисления перпендикулярного уклона, \(m_{\perp}\), выглядит следующим образом:
\[m_{\perp} = \displaystyle -\frac{1}{ m}\]
Подставляя значение \(m = \) в формулу, мы находим, что перпендикулярный наклон равен
\[m_{\perp} = \displaystyle -\frac{1}{m} = \displaystyle -\frac{1}{} = \frac{3}{2}\]
Построение перпендикулярной линии
Теперь мы подсчитали, что перпендикулярный наклон равен \(m_{\perp} = \frac{3 {2}\) the и мы знаем, что перпендикуляр проходит через точку \((1, 1)\).
Следовательно, с имеющейся у нас информацией мы можем напрямую построить форму точки-наклона линии, которая равна
\[\displaystyle y — y_1 = m_{\perp} \left(x — x_1\right)\]
, а затем подставить известные значения \(\displaystyle m_{\perp} = \frac{3}{2}\) и \(\displaystyle \left( x_1, y_1 \right) = \left( 1, 1 \справа)\), получаем, что
\[\displaystyle y-1 = \frac{3}{2} \left(x-1\right)\]
Теперь нам нужно расширить правую часть уравнения, распределив наклон, так что мы получим \[\displaystyle y = \frac{3}{2} x + \frac{3}{2} \left(-1\right) + 1\]
и упрощая получаем что \[\displaystyle y=\frac{3}{2}x-\frac{1}{2}\]
Таким образом, мы заключаем, что уравнение данной прямой есть \(\displaystyle y=-\frac{2}{3}x+\frac{5}{3}\), а уравнение перпендикулярной линии есть \(\displaystyle y=\frac{3}{2}x-\frac{1}{2}\).
Если вы хотите сделать вещи более прямыми, используйте этот калькулятор перпендикулярного уклона и используйте
формула перпендикулярной линии, чтобы получить непосредственно наклон линии, которая является перпендикулярной линией.
Это на тот случай, если вы ищете только наклон в контексте того, что вы делаете.
Калькулятор перпендикулярных линий
Создано Bogna Szyk
Отзыв от Adena Benn
Последнее обновление: 19 декабря 2022 г.
Содержание:- Как найти перпендикулярную линию?
- Уравнение перпендикулярной линии: пример
- Поиск точки пересечения
- Часто задаваемые вопросы
Если вы хотите быстро решить задачу по геометрии, попробуйте этот калькулятор перпендикулярных линий. Находит уравнение (еще не определенной) прямой, перпендикулярной заданной прямой и проходящей через заданную точку.
Дополнительно рассчитывает координаты точки пересечения двух линий. Все, что вам нужно сделать, это ввести координаты любой точки и коэффициенты, описывающие заданную линию, а наш калькулятор уравнения перпендикулярной линии сделает все за вас!
В этой статье объясняется, как найти перпендикулярную линию, используя основные математические принципы.
Он также предоставит простой пример, чтобы проиллюстрировать, как работает метод.
Не забудьте также воспользоваться калькулятором параллельных линий!
Как найти перпендикуляр?
Каждая прямая линия в двумерном пространстве может быть описана простым уравнением прямой:
y = ax + b
где a и b коэффициенты, x — это координата x, а y — это координата y. Каждая строка определяется однозначно, если известны значения a и b .
Предположим, что вы знаете следующую информацию:
- Уравнение данной прямой y = mx + r . Вы знаете значения m и r и ищете прямую, перпендикулярную этой.
- Вы также знаете координаты точки, через которую должна пройти ваша линия. их x₀ и y₀ .
Наклон любой линии равен значению коэффициента a .
Если две прямые перпендикулярны, произведение их наклонов равно -1. Следовательно,
a × m = -1
a = -1 / m
,y₀) и значение a в уравнение вашей линии:
y = ax + b
y₀ = -1 × x₀ / m + b
b = y₀ + 1 × x₀ / m
💡 .
Уравнение перпендикулярной линии: пример
Как эти расчеты выглядят на практике? Предположим, вы хотите, чтобы ваша линия проходила через точку (3, 5) и была перпендикулярна линии y = 2x - 2 . Вы можете найти уравнение перпендикулярной линии, выполнив следующие шаги:
Определите уклон ( м ) и точку пересечения с осью Y ( r ) данной линии. В этом случае
m = 2иr = -2.Рассчитайте наклон вашей линии. Он равен
а = -1 / м = -1/2 = -0,5Введите это значение в линейное уравнение
y = ax + b:у = -0,5х + бПодставить координаты (3,5) вместо значений х и у :
5 = -0,5 × 3 + b5 = -1,5 + бб = 6,5В качестве последнего шага введите коэффициент b в линейное уравнение:
у = -0,5х + 6,5
Не верите? Проверьте результат с помощью этого калькулятора перпендикулярных линий!
Поиск точки пересечения
Как только вы узнаете уравнение новой линии, найти точку пересечения между ней и первой (данной) линией несложно.
Все, что вам нужно сделать, это найти точку с координатами (xₐ,yₐ) такое, что оно лежит на каждой из двух строк.
Рассмотрим пример, который мы только что проанализировали. Мы нашли две перпендикулярные линии: y = 2x — 2 и y = -0,5x + 6,5 . Эти два уравнения образуют систему уравнений с двумя неизвестными — координатами точки пересечения.
Решим эту систему уравнений:
yₐ = 2xₐ — 2
yₐ = -0,5xₐ + 6,5
Умножая второе уравнение на 9 4, получаем 9 4,0005
yₐ = 2xₐ — 2
4yₐ = -2xₐ + 26
Adding the two equations together,
5yₐ = 24
From there,
yₐ = 4.8
xₐ = 0,5yₐ + 1 = 2,4 + 1 = 3,4
Координаты точки пересечения (3.4, 4.8).
Конечно, вам не нужно выполнять эти утомительные расчеты самостоятельно — наш калькулятор перпендикулярных линий сделает то же самое всего за несколько секунд! И не забудьте проверить наши другие калькуляторы координатной геометрии, такие как калькулятор средней скорости изменения.
Часто задаваемые вопросы
Что такое перпендикулярные линии?
Мы говорим, что две прямые перпендикулярны, если они пересекают друг друга под прямым углом (90°) . Вы можете найти перпендикулярные линии во многих геометрических фигурах, таких как квадраты, прямоугольники и треугольники. Мы также можем использовать их для описания ориентации линий, плоскостей и поверхностей в трехмерном пространстве.
Как проверить, перпендикулярны ли две линии?
Чтобы проверить, перпендикулярны ли две линии, выполните следующие действия:
- Запишите наклонов этих линий. (Напомним, наклон — это коэффициент a , стоящий рядом с переменной x в формуле y = ax + b .)
- Умножьте два наклона вместе.
- Если произведение равно -1 , ваши линии перпендикулярны. Если нет, то они не перпендикулярны.
