Уравнение разложение на множители: Решение уравнений методом разложения на множители

Содержание

описание метода, примеры решения уравнений

В этой статье мы разберем метод разложения на множители и с теоретической, и с практической стороны. Материал теоретической части объясняет, в каких случаях применяется метод разложения на множители, в чем он состоит и как обосновывается. Материал практической части содержит алгоритм решения уравнений методом разложения на множители и решение характерного примера с подробными пояснениями.

Когда применяется метод разложения на множители и в чем он состоит

Метод разложения на множители применяется для решения уравнений, в левой части которых находится произведение конечного числа выражений, а в правой – нуль, то есть, для решения уравнений f₁(x)·f₂(x)·…·f_n(x)=0, где f₁(x), f₂(x),…, f_n(x) – некоторые выражения. Например, он подходит для решения уравнений x³·(x²−4)=0, и т. п.

Метод разложения на множители состоит в переходе от решения уравнения f

1(x)·f₂(x)·…·f_n(x)=0 к решению совокупности уравнений f₁(x)=0, f₂(x)=0, …, f_n(x)=0 на области допустимых значений переменной x для исходного уравнения. Поясним на примерах. Согласно методу разложения на множители от решения уравнения x·(x+1)·(x+2)=0 следует перейти к решению совокупности трех уравнений x=0, x+1=0, x+2=0 на ОДЗ для исходного уравнения, которая в данном примере, очевидно, есть множество всех действительных чисел R. Еще пример: решение уравнения можно заменить решением совокупности двух уравнений , на ОДЗ переменной x для исходного уравнения, которая здесь определяется условиями .

Все сказанное в двух предыдущих абзацах полностью согласуется с информацией по теме из школьных учебников, например, с [1, с. 212-213].

В основе метода разложения на множители лежит следующее утверждение:

Утверждение

Решение уравнения f₁(x)·f₂(x)·…·f_n(x)=0 составляют все решения совокупности , принадлежащие ОДЗ для уравнения f₁(x)·f₂(x)·…·f_n(x)=0.

Докажем его в следующем пункте.

К началу страницы

Обоснование

Обоснуем метод разложения на множители. Для этого достаточно доказать, что любой корень уравнения f₁(x)·f₂(x)·…·f_n(x)=0 является корнем совокупности уравнений f₁(x)=0, f₂(x)=0, …, f_n(x)=0 и что любой корень совокупности уравнений f₁(x)=0, f₂(x)=0, …, f_n(x)=0, принадлежащий ОДЗ для исходного уравнения, является корнем уравнения f₁(x)·f₂(x)·…·f

n(x)=0.

Начнем с доказательства первой части. Пусть x₀ – корень уравнения f₁(x)·f₂(x)·…·f_n(x)=0. Докажем, что x₀ является корнем совокупности уравнений f₁(x)=0, f₂(x)=0, …, f_n(x)=0.

Так как x₀ – корень уравнения f₁(x)·f₂(x)·…·f_n(x)=0, то f₁(x₀)·f₂(x₀)·…·f_n(x₀)=0 — верное числовое равенство. Известно, что произведение нескольких чисел равно нулю тогда и только тогда, когда хотя бы одно из них равно нулю. Значит, из равенства f₁(x₀)·f₂(x₀)·…·f_n(x₀)=0 следует, что f₁(x₀)=0, и/или f₂(x₀)=0, и/или …, f_n(x₀)=0. А это означает, что x

0 является корнем хотя бы одного из уравнений f₁(x)=0, f₂(x)=0, …, f_n(x)=0, а значит, является корнем совокупности уравнений f₁(x)=0, f₂(x)=0, …, f_n(x)=0.

Переходим к доказательству второй части. Пусть x₀ – корень совокупности уравнений f₁(x)=0, f₂(x)=0, …, f_n(x)=0, причем x₀ принадлежит ОДЗ переменной x для уравнения f₁(x)·f₂(x)·…·f_n(x)=0. Докажем, что x₀ – корень уравнения f₁(x)·f₂(x)·…·f_n(x)=0.

Так как x₀ принадлежит ОДЗ переменной x для уравнения f₁(x)·f₂(x)·…·f_n(x)=0, то запись f₁(x₀)·f₂(x

0)·…·f_n(x₀)=0 имеет смысл. А так как x₀ – корень совокупности уравнений f₁(x)=0, f₂(x)=0, …, f_n(x)=0, то x₀ – корень хотя бы одного из уравнений совокупности, значит, хотя бы одно из числовых равенств f₁(x₀)=0, f₂(x₀)=0, …, f_n(x₀)=0 является верным. Следовательно, f₁(x₀)·f₂(x₀)·…·f_n(x₀)=0 — верное числовое равенство. Из этого вытекает, что x₀ – корень уравнения f₁(x)·f₂(x)·…·f_n(x)=0.

К началу страницы

Алгоритм решения уравнений методом разложения на множители

Сформулированное и доказанное в предыдущих пунктах утверждение позволяет записать алгоритм решения уравнений методом разложения на множители.

Чтобы решить уравнение f₁(x)·f₂(x)·…·f_n(x)=0 методом разложения на множители, нужно

Перейти к совокупности уравнений f₁(x)=0, f₂(x)=0, …, f_n(x)=0 и найти ее решение,
Оставить корни, принадлежащие ОДЗ для исходного уравнения, остальные отсеять как посторонние корни.

Стоит кратко пояснить второй шаг алгоритма. Переход от уравнения f₁(x)·f₂(x)·…·f_n(x)=0 к совокупности уравнений f₁(x)=0, f₂(x)=0, …, f_n(x)=0 в общем случае не является равносильным, то есть, среди корней совокупности могут быть корни, посторонние для исходного уравнения. Посторонними корнями для исходного уравнения являются все корни совокупности, выходящие за пределы ОДЗ для исходного уравнения. Именно поэтому алгоритм решения уравнений методом разложения на множители содержит второй шаг, предписывающий оставить лишь корни, принадлежащие ОДЗ для исходного уравнения.

Заметим, что в данной ситуации отсеивание посторонних корней целесообразно проводить либо по ОДЗ (когда ОДЗ несложно найти в виде числового множества), либо по условиям ОДЗ (когда по этим условиям сложно или невозможно найти ОДЗ в виде числового множества).

К началу страницы

Решение характерного примера

Обычно первое знакомство с методом разложения на множители происходит при изучении целых рациональных уравнений. Если в левой части целого рационального уравнения произведение нескольких выражений с переменной, а в правой части – нуль, то оно решается методом разложения на множители. С решением таких уравнений все обстоит особо просто: достаточно перейти к совокупности уравнений и найти ее решение. При этом даже не приходится заботиться об отсеивании посторонних корней, ведь ОДЗ для целых рациональных уравнений есть множество всех действительных чисел. Например, решение уравнения (x−2)·(x+1)=0 сводится к решению совокупности двух уравнений x−2=0 и x+1=0.

Решив эти линейные уравнения и объединив их решения, имеем решение исходного уравнения: 2, −1.

Позже изучаются иррациональные уравнения, и обязательно рассматривается решение иррациональных уравнений методом разложения на множители. Дальше идут тригонометрические, показательные, логарифмические уравнения, и там вновь всплывает метод разложения на множители. Решения соответствующих примеров Вы без труда найдете на данном сайте. Наконец, к концу изучения школьного курса математики мы начинаем понимать, что метод разложения на множители позволяет справляться с уравнениями, в записи которых одновременно присутствуют самые разнообразные функции. Главное, чтобы уравнение имело вид f

1(x)·f₂(x)·…·f_n(x)=0. Давайте решим подобное уравнение.

Пример

Решите уравнение

Смотреть решение

В заключение заметим, что часто метод разложения на множители требует предварительной подготовки, то есть, приведения уравнения к виду f₁(x)·f₂(x)·…·f_n(x)=0. Например, уравнение сначала нужно привести к виду , а уже после этого действовать по методу разложения на множители. Впрочем, это скорее вопрос преобразования уравнений.

Квадратное уравнение на множители — примеры, квадратичное уравнение на множители

Квадратное уравнение на множители представляет собой метод выражения многочлена как произведения его линейных множителей. Это процесс, который позволяет нам упрощать квадратные выражения, находить их корни и решать уравнения. Квадратичный многочлен имеет форму ax

2 + bx + c, где a, b, c — действительные числа. Факторирование квадратичных уравнений — это метод, который помогает нам найти нули квадратного уравнения ax ² + bx + c = 0,

В этом мини-уроке давайте узнаем об увлекательной концепции факторизации квадратичных уравнений, формуле факторизации квадратных уравнений и некоторых решенных примерах для лучшего понимания.

1.	Что такое Факторинг Квадратичные?
2.	Методы факторизации квадратичных уравнений
3.	Тождества для факторинга квадратичных уравнений
4.	Формула факторизации квадратичных чисел
5.	Часто задаваемые вопросы по факторинговым квадратикам

Что такое факторинг Квадратичные?

Квадратичная факторизация — это метод выражения квадратного уравнения ax ² + bx + c = 0 в виде произведения его линейных множителей как (x — k)(x — h), где h, k — корни квадратное уравнение ax ² + bx + c = 0. Этот метод также называют методом факторизации квадратных уравнений. Факторизация квадратных уравнений может быть выполнена с использованием различных методов, таких как расщепление среднего члена, использование квадратной формулы, заполнение квадратов и т. д.

Факторизация квадратичных чисел Значение

Факторная теорема связывает линейные множители и нули любого многочлена. Каждое квадратное уравнение имеет два корня, например $\alpha$ и $\beta$. Это нули квадратного уравнения. Рассмотрим квадратное уравнение f(x) = 0, где f(x) — многочлен степени 2. Предположим, что x = $\alpha$ — один из корней этого уравнения. Это означает, что x = $\alpha$ является нулем квадратного выражения f(x). Таким образом, (x — $\alpha$) должно быть фактором f(x).

Аналогично, если x = $\beta$ является вторым корнем f(x) = 0, то x = $\beta$ является нулем f(x). Таким образом, (x — $\beta$) должно быть фактором f(x). Следовательно, факторизация квадратичных уравнений — это метод выражения квадратных уравнений в виде произведения их линейных множителей, то есть f (x) = (x — \ (\ alpha \)) (x — \ (\ beta \)). Рассмотрим несколько примеров факторизации квадратичных уравнений:

Примеры факторизации квадратичных чисел

1. Рассмотрим квадратное уравнение x ² + 5x + 6 = 0

-3 и -2 являются корнями уравнения. Подставьте корни в данное уравнение и проверьте, равно ли значение 0.

Коэффициент 1: (x + 3)

LHS = x ² + 5x + 6 = (-3) ² + 5 × -3 + 6 = 9 -15 + 6 = 0 = RHS

Коэффициент 2: (x + 2)

LHS = x ² + 5x + 6 = (-2) ² + 5 × -2 + 6 = 4 -10 + 6 = 0 = RHS

Таким образом, уравнение имеет 2 множителя (x + 3) и (x + 2)

2. Рассмотрим x ² — 9 = 0

3 и -3 два корня уравнения. Подставьте корни в данное уравнение и проверьте, равно ли значение 0.

3 ² — 9 = 9 — 9 = 0

(-3) ² — 9 = 9 — 9 = 0

Таким образом, уравнение имеет 2 множителя (x+3) и (x-3)

Методы факторизации квадратичных уравнений

Факторизация квадратного уравнения дает нам корни квадратного уравнения. Существуют различные методы, которые можно использовать для факторизации квадратных уравнений. Разложение квадратичных чисел на множители осуществляется четырьмя способами:

Факторизация НОД
Разделение среднего члена
Использование алгебраических тождеств (заполнение квадратов)
Использование квадратичной формулы

Разложение квадратичных чисел на множители путем исключения НОД

Разложение на множители квадратичных чисел можно выполнить, найдя общий числовой множитель и алгебраические множители, общие для членов квадратного уравнения, а затем вычтя их. Давайте решим пример, чтобы понять факторинг квадратных уравнений, убрав НОД.

Рассмотрим это квадратное уравнение: 3x ² + 6x = 0

Численный множитель равен 3 (коэффициент x ² ) в обоих выражениях.
Общий алгебраический делитель равен x в обоих терминах.
Общие делители 3 и x. Поэтому мы их выносим.
Таким образом, 3x ² + 6x = 0 факторизуется как 3x(x + 2) = 0

Разделение среднего члена для факторизации квадратичных уравнений

Сумма корней квадратного уравнения по оси ² + bx + c = 0 определяется выражением $\alpha + \beta$ = -b/a
Произведение корней квадратного уравнения ax ² + bx + c = 0 равно $\alpha\beta$ = c/a

Мы разделяем средний член b квадратного уравнения на ax ² + bx + c = 0, когда пытаемся факторизовать квадратные уравнения. Определим пары факторов произведения a и c, сумма которых равна b.

Пример: f(x) = x ² + 8x + 12

Разделите средний член 8x таким образом, чтобы множители произведения 1 и 12 в сумме составляли 8. Пары множителей 12: (1, 12), (2, 6), ( 3, 4). Теперь мы можем видеть, что пара факторов (2, 6) удовлетворяет нашей цели, поскольку сумма 6 и 2 равна 8, а произведение равно 12. Следовательно, мы разделяем средний член и записываем квадратное уравнение как:

x ² + 8x + 12 = 0

⇒ x ² + 6x + 2x + 12 = 0

Теперь разбейте термины на пары следующим образом:

(x ² + 6x) + (2x + 12) = 0

⇒ x(x + 6) + 2(x + 6) = 0

Вычитая общий множитель (x + 6), мы имеем

(x + 2) (x + 6) = 0

Таким образом, (x + 2) и (x + 6) являются множителями x ² + 8x + 12 = 0

Тождества для факторинга квадратичных уравнений

Процесс факторизации квадратичных чисел можно выполнить, заполнив квадраты, которые требуют использования алгебраических тождеств. Основные алгебраические тождества, которые используются для заполнения квадратов:

(а + б) ² = а ² + 2аб + б ²
(а — б) ² = а ² — 2аб + б ²

Шаги для факторизации квадратного уравнения ax ² + bx + c = 0 с использованием метода квадратов:

Шаг 1: Разделите обе части квадратного уравнения ax ² + bx + c = 0 на а. Теперь полученное уравнение равно x ² + (b/a) x + c/a = 0
Шаг 2: Вычесть c/a из обеих частей квадратного уравнения x ² + (b/a) x + c/a = 0. Полученное уравнение равно x ² + (b/a) x = -к/а
Шаг 3: Добавьте квадрат (b/2a) к обеим частям квадратного уравнения x ² + (b/a) x = -c/a. Полученное уравнение: x ² + (b/a) x + (b/2a) ² = -c/a + (b/2a) ²
Шаг 4: Теперь левая сторона квадратного уравнения x ² + (b/a) x + (b/2a) ² = -c/a + (b/2a) ² можно записать в виде полного квадрата и при необходимости упростить RHS. Полученное уравнение: (x + b/2a) ² = -c/a + (b/2a) ²
Шаг 5: Корни данного квадратного уравнения могут быть получены и, следовательно, мы можем составить множители уравнения.

Другим алгебраическим тождеством, которое используется для факторизации квадратичных уравнений, является a ² — b ² = (а + б)(а — б). Давайте посмотрим на пример, чтобы понять.

Пример 1: f(x) = 9x ² — 4 (разность 2 полных квадратов)

9x ² — 4 = (3x) ² — 7 002 9 9

4 2 Заметим, что это имеет вид a

² — b ² = (a + b)(a — b)

Следовательно, мы факторизуем уравнение 9x ² — 4 = 0 как (3x+2) (3x- 2)

9x ² — 4 = (3x+2) (3x-2)

Пример 2: f(x) = 4x ² + 12x + 9

4x ² + 12x + 9 = (2x) ² + 2(2x)(3) + (3) ²
Заметим, что это имеет вид (a+b) ² = a ² + 2ab + b ²
(2x) ² + 2(2x)(3) + (3) ² = (2x + 3) ²
Следовательно, мы имеем (2x + 3), (2x + 3) как линейные множители f(x) = 4x ² + 12x + 9

Формула факторизации квадратичных чисел 92-4\times 1 \times 4}}{2\times 1}\\\\&= \dfrac{-5\pm \sqrt{25 -16}}{2}\\\\&= \dfrac{ -5\pm \sqrt{9}}{2}\\\\&= \dfrac{-5\pm 3}{2}\\&= \dfrac{-5+3}{2}\text{ и } \dfrac{-5-3}{2}\\\\&=\dfrac{-2}{2}\text{ и }\dfrac{-8}{2}\\\\x &=(- 1)\text{ and} (-4)\end{align}\]
Таким образом, множители равны (x + 1) и (x + 4).
Связанные темы по факторингу Квадратичные уравнения
Факторная теорема
Факторы
Методы факторинга
Важные примечания по факторингу квадратичных чисел
Линейные коэффициенты имеют форму ax + b, и их нельзя разложить на множители.
Квадратичный многочлен — это многочлен второй степени.
Сумма корней квадратного уравнения ax ² + bx + c = 0 определяется выражением $\alpha + \beta$ = -b/a
Произведение корней квадратного уравнения ax ² + bx + c = 0 равно $\alpha\beta$ = c/a
Часто задаваемые вопросы по факторинговым квадратикам
Что такое факторизация квадратичных чисел в алгебре?
Квадратичная факторизация — это метод выражения многочлена как произведения его линейных множителей. Это процесс, который позволяет нам упрощать квадратные выражения, находить их корни и решать уравнения.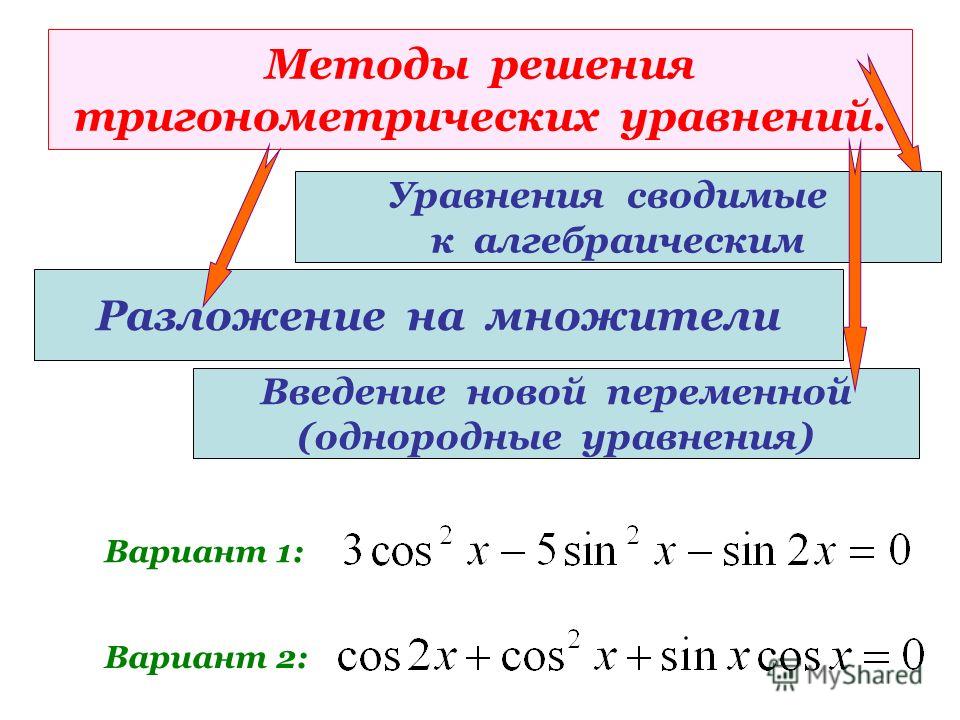
Как решать квадратные уравнения, разлагая квадратные уравнения на множители?
Факторизация квадратного уравнения дает нам корни квадратного уравнения. Существуют различные методы, которые можно использовать для факторизации квадратных уравнений. Разложение квадратичных чисел на множители осуществляется четырьмя способами:
Факторизация НОД
Разделение среднего члена
Использование алгебраических тождеств (заполнение квадратов)
Использование квадратичной формулы
Определив коэффициенты, мы можем получить корни квадратного уравнения и, следовательно, решение.
Какие методы используются для факторизации квадратных уравнений?
Методы факторизации квадратных уравнений: разделение среднего члена, использование алгебраических тождеств, использование квадратной формулы и вынесение НОД на множители.
Что такое метод факторизации квадратных уравнений?
Разделение среднего члена и использование квадратной формулы являются наиболее эффективными методами факторизации квадратных уравнений.
Является ли факторинг квадратичных уравнений таким же, как и их решение?
Когда мы факторизуем квадратное уравнение, мы получаем линейные множители, которые делят квадратный полином нацело. Следующим шагом является нахождение нулей уравнения путем приравнивания множителей к нулю.
Как кратчайшим образом разложить на множители любое квадратное уравнение?
Использование формулы квадратного уравнения является кратчайшим способом разложения квадратного уравнения на множители.
Какие есть хитрости для факторинга квадратичных уравнений?
Найдите сумму корней и произведение корней или, определив любое известное алгебраическое тождество, мы можем факторизовать квадратные уравнения.
Что такое факторизованная форма квадратного уравнения?
(x — $\alpha$) (x — $\beta$) — факторизованная форма квадратного уравнения, где $\alpha$ и $\beta$ — корни квадратного уравнения уравнение.
Как решить квадратное уравнение?
Существуют различные методы факторизации квадратных уравнений и решения квадратных уравнений. Факторинг квадратичных чисел осуществляется четырьмя способами:
Факторизация НОД
Разделение среднего члена
Использование алгебраических тождеств (заполнение квадратов)
Использование квадратичной формулы
Как легко разложить квадратные уравнения на множители?
Мы разделяем средний член b квадратного уравнения ax ² + bx + c = 0, когда пытаемся факторизовать квадратные уравнения. Определим пары факторов произведения a и c, сумма которых равна b. Убрав общие множители, мы можем легко факторизовать квадратные уравнения.
Почему мы факторизуем уравнения? – BetterExplained
О чем алгебра? При изучении переменных ($x, y, z$) они как бы «скрывают» число:
Какое число может скрываться внутри $x$? 2, в данном случае. 92$ — это компонент, взаимодействующий сам с собой
$x$ является самостоятельным компонентом
6 — желаемое состояние, которое мы хотим, чтобы вся система стала
. 2$, $x$ и 6 летают повсюду. 92 + x — 6$) как набор связанных систем меньшего размера.
Представьте, что вы берете кучу палок (наша беспорядочная, неорганизованная система) и ставите их так, чтобы они поддерживали друг друга, как вигвам:
/\
(Это двумерный пример с двумя палками).
Убери любую палку, и вся конструкция рухнет. Если мы сможем переписать нашу систему:
как серию умножений:
, мы сложим палочки в «типи». Если Компонент А или Компонент Б становится равным 0, структура разрушается, и в результате мы получаем 0.
Чисто! Это и есть причина разложения камней на множители: мы преобразуем нашу систему ошибок в хрупкий вигвам, чтобы мы могли сломать его. Мы найдем то, что стирает наши ошибки и приводит нашу систему в идеальное состояние.
Помните: мы ломаем ошибку в системе, а не в самой системе.
На Факторинг
Обучение «факторизации уравнения» — это процесс упорядочивания вашего вигвама. В этом случае:
Если $x = -3$, то Компонент А падает. Если $x = 2$, компонент B падает. Любое значение приводит к краху ошибки, что означает, что наши 92 + х — 6$)
Фактор ошибки: Перепишите ошибку как взаимосвязанные компоненты: $(x + 3)(x — 2)$
Уменьшить ошибку до нуля: Обнулить один или другой компонент ($x = -3$ или $x = 2$).
Когда ошибка = 0, наша система должна быть в желаемом состоянии. Были сделаны!
Алгебра чертовски полезна:
Наша система — это траектория, «желаемое состояние» — цель. По какой траектории попадает в цель?
Наша система — это продажи наших виджетов, «желаемое состояние» — это наша цель по доходам. Какая сумма заработка достигает цели?
Наша система — это вероятность победы в нашей игре, «желаемое состояние» — это 50-50 (справедливый) исход. Какие настройки делают игру честной?
Идея «приведения системы в желаемое состояние» — это просто одна из интерпретаций того, почему факторинг полезен.
No related posts.