Уравнение с параметром квадратное: Квадратные уравнения с параметром. Задание 18 в ЕГЭ

Квадратные уравнения с параметрами — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Квадратные уравнения с параметрами (8класс)

Первый урок

2. Квадратные уравнения с параметрами

ax2+bx+c=0 (a ≠ 0) — квадратное уравнение
Формула корней:
D – дискриминант квадратного уравнения
Если D < 0, то уравнение не имеет корней,
Если D = 0, то уравнение имеет один корень,
Если D > 0, то уравнение имеет два различных
корня.
Матчина Надежда Егоровна, школа №258, СПБ.

3. Квадратные уравнения с параметрами

Решить уравнение с параметром b – это
значит установить соответствие, с
помощью которого для каждого значения
параметра b указывается множество
корней данного уравнения.
Допустимым значением параметра b
считаются все те значения b, при
которых выражения, входящие в
уравнение, имеют смысл.
Матчина Надежда Егоровна, школа №258, СПБ.
Квадратные уравнения с параметрами
Задача 1. Решите относительно x уравнение x2-bx+9=0
Решение:
x2-bx+9=0
D = b2 — 36.
1) Если
уравнение имеет два корня:
2) Если
уравнение имеет один корень
3) Если
уравнение корней не имеет.
Матчина Надежда Егоровна, школа №258, СПБ.
Квадратные уравнения с параметрами
Задача 1. Решите относительно x уравнение x2-bx+9=0
Ответ:
при -6<b<6 уравнение корней не имеет;
при b=-6 или b=6 уравнение имеет
единственный корень
,
при b<-6 или b>6 уравнение имеет два
различных корня:
Матчина Надежда Егоровна, школа №258, СПБ.
.
Квадратные уравнения с параметрами
Задача 2. При каких значениях параметра b уравнение
x2+bx+4=0:
1) имеет один из корней, равный 3;
2) имеет действительные различные корни;
3) имеет один корень;
4) не имеет действительных корней?
Ответы:
;
1) при
2) при b<-4 или b>4 уравнение имеет два корня:
;
3) при b=-4 или b=4 уравнение имеет
;
единственный корень
4) при -4<b<4 уравнение корней не имеет .
Матчина Надежда Егоровна, школа №258, СПБ.
Квадратные уравнения с параметрами
Задача 3.
Решите относительно x уравнение
Решение: Приведем к целому виду:
ax2 – (6a–3)x+(5a–15)=0
если a=0, то 3x=15 (линейное уравнение)
x=5.
если a≠0, то ax2 – (6a–3)x+(5a–15)=0 квадратное
уравнение.
ax2 – 3(2a–1)x+5(a–3)=0
D = 9(2a–1)2–4∙5a(a–3) = … = (4a+3)2 ≥ 0
Матчина Надежда Егоровна, школа №258, СПБ.
Квадратные уравнения с параметрами
Задача 3.
Решите относительно x уравнение
Решение (продолжение):
при 4a+3=0, т. е.
уравнение имеет единственный
корень
,
при 4a+3≠0, т.е.
уравнение имеет два корня:
.
Матчина Надежда Егоровна, школа №258, СПБ.
Квадратные уравнения с параметрами
Задача 3.
Решите относительно x уравнение
Ответ:
при a ≠ -0,75 и a ≠0 уравнение имеет два корня:
;
при a = -0,75 или a=0 уравнение имеет
единственный корень x=5.
Матчина Надежда Егоровна, школа №258, СПБ.
Квадратные уравнения с параметрами
Задача 4. При каких значениях a уравнение
(a+2)x2 +2(a+2)x+2=0
имеет один корень?
Ответ:
Д/З
при a=0 уравнение имеет один корень x = -1.
Решите относительно x уравнение:
1) bx2 – 6 x+1=0
2) x2 – ax =0
3) 6×2 – 5bx+b2 = 0
4) (n2 – 5)x + n = n(n – 4x)
Матчина Надежда Егоровна, школа №258, СПБ.

English     Русский Правила

Методика обучения решению квадратных уравнений с параметром

Решение задач с параметром вызывает затруднения у учащихся, так как практических заданий по данной теме в школьных учебниках недостаточно.

Цели разработки темы

• формирование устойчивого интереса к познавательному процессу при изучении математики и оценка возможности овладения предметом с точки зрения дальнейшей перспективы;
• обеспечение прочного и сознательного усвоения учащимися системой математических знаний, умений и навыков;
• формирование качества мышления, характерного для математической деятельности и необходимые человеку для жизни в современном обществе;
• выявление и развитие математических способностей учащихся.
• Задачи разработки темы:
• показать универсальные алгоритмы для решения квадратных уравнений с параметром;
• научить приемам решения различного класса задач с параметром, способствовать овладению технических и интеллектуальных математических умений на уровне свободного их использования;
• использование новых современных педагогических технологий обучения.

В математике параметр – это постоянная величина, выраженная буквой, сохраняющая свое постоянное значение лишь в условиях данной задачи (“параметр” с греческого “parametron” – отмеривающий)..

Если ставится задача для каждого значения параметра а из некоторого числового множества А решить уравнение F(х;а)= 0 относительно х, то это уравнение называют уравнением с переменной х и параметром а, а множество А – областью изменения параметра. Под областью определения уравнения F(х;а)=0 с параметром а понимаются такие системы значений х и а, при которых F(х;а) имеет смысл. Все значения параметра а, при которых F(

х;а) не имеет смысла, включать в число значений параметра, при которых уравнение не имеет решений. Под областью изменения параметра (если не сделано специальных оговорок) берется множество всех действительных чисел, а задачу решения уравнения с параметром формулировать следующим образом: решить уравнение F(х;а)=0 (с переменной х и параметром а) – это значит на множестве действительных чисел решить семейство уравнений, получающихся из данного уравнения при всех действительных значениях параметра или установить, что решений нет.

В связи с тем, что выписать каждое уравнение из бесконечного семейства уравнений невозможно, но каждое уравнение семейства должно быть решено, следовательно, необходимо по некоторому целесообразному признаку разбить множество всех значений параметра на подмножества и решить затем заданное уравнение на каждом из этих подмножеств. Для разбиения множества значений параметра на подмножества, удобно пользоваться теми значениями параметра, при которых или при переходе через которые происходят качественные изменения уравнения. Такие значения параметра называются контрольными.

1. КВАДРАТНЫЕ УРАВНЕНИЯ С ПАРАМЕТРОМ

Задачи с параметрами можно разделить на два больших класса:

• задачи, в которых необходимо при всех значениях параметра из некоторого множества решить уравнение;
• задачи, в которых требуется найти все значения параметра, при каждом из которых решение уравнения удовлетворяют некоторым условиям.

В зависимости от типа задачи изменяется и вид ответа. В первом случае в решении и ответе должны быть рассмотрены все возможные значения параметров. Если хотя бы одно значение какого-либо параметра не исследовано, решение задачи не может быть признано полным.

Во втором случае в ответе перечисляются только те значения параметра, при которых выполнены условия задачи, а при решении подобных задач обычно решать заданное уравнение нет необходимости.

Уравнение вида Ах² + Вх + С= 0 , где А, В, С — выражения, зависимые от параметра, х – переменная — называется квадратным уравнением с параметром.

Уравнение вида ах²+вх+с=0, где , а, в, с – действительные числа, называют квадратным уравнением. D=в²-4ас называется дискриминантом квадратного уравнения (“дискриминант” по – латыни “различитель”).

В зависимости от значения дискриминанта возможны три случая:

D > 0.

Данное квадратное уравнение имеет два действительных корня

D=0. Данное уравнение имеет корень двойной кратности

D<0. Данное уравнение не имеет действительных корней.

Для уравнения ах²+2кх+с=0 со вторым коэффициентом (в=2к) четным, для нахождения корней удобно пользоваться формулами: , где D₁= =к²-ас.

№ 1.1. Определите все значения параметра а при которых уравнение ах²+2(а+1)х+а+3=0 имеет два неравных корня.

Решение.

Если а=0, то имеем 0·х²+2(0+1)х+0+3=0, 2х+3=0 — данное уравнение является линейным, х=-1,5 – единственный корень. Итак, а=0 не удовлетворяет условию задачи.

Если а?0, то уравнение имеет два различных корня, когда дискриминант >0.

Найдем=(а+1)²-а(а+3)=-а+1,-а+1>0, а<1. С учетом а 0 ответ: .

№ 1.2. Определите все значения параметра а, при котором уравнение 2ах²-4(а+1)х+4а+1=0 имеет один корень.

Решение.

Если а=0, то имеем 2·0·х²-4(0+1)х+4·0+1=0, -4х+1=0 - данное уравнение является линейным, х=0,25 – единственный корень. Итак, а=0 удовлетворяет условию задачи.

Если а 0, то исходное уравнение является квадратным и имеет единственный корень при =0. Найдем =(2(a+1))²-2a(4а+1) = -4a²+6a+4,4a²+6a+4=0,   а₁=2, а₂=-0,5.

С учетом а=0, запишем ответ: а=-0,5, а=0, а=2.

№ 1.3. При каких значениях параметра а квадратное уравнение (5а-1)х²-(5а+2)х+3а-2=0  не имеет корней?

Решение.

Если 5а-1=0,а=0,2, то имеем (5*0,2-1)х²-(5*0,2+2)х+3*0,2-2=0,

-3х-1,4=0 — данное уравнение является линейным, х = — единственный корень.

Итак, а=0,2 не удовлетворяет условию задачи.

Если а 0,2, то квадратное уравнение не имеет корней, если дискриминант квадратного уравнения D<0. Найдем D=(5а+2)²-4(5a-1)(3а-2)=-35a²+72a-4,-35a²+72a-4<0,

35a²-72a+4>0, а₁=2, а₂=, (а-2)(а-)>0. С учетом а 0,2 ответ:

№ 1.4. Определите все значения параметра а при которых уравнение (2а-1)х² +ах+2а-3=0 имеет не более одного решения.

Решение.

Если 2а-1=0,а=0,5, то имеем (2·0,5-1)х²+0,5·х+2·0,5-3=0, 0,5х-2=0 — данное уравнение является линейным, х=4 - единственный корень.

Итак, а=0,5 удовлетворяет условию задачи.

Если а 0,5, то квадратное уравнение имеет не более одного решения, если дискриминант квадратного уравнения D0.

Найдем D=а²-4(2a-1)(2а-3)=-15a²+32a-12, -15a²+32a-120,

15a²-32a+12?0, а₁=, а₂=, (а-)(а-) 0.

С учетом а 0,5, имеем .

С учетом а=0,5, запишем ответ: .

2. НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ С ПАРАМЕТРОМ.

Квадратное уравнение ах²+вх+с=0, где а 0 называется неполным, если хотя бы один из коэффициентов в или с равен 0.

Общая схема решения неполных квадратных уравнений с параметрами.

ах²=0, где а 0, в=0, с=0. Если а 0 ,то уравнение примет вид: х²=0, х=0.

Следовательно, уравнение имеет два совпадающих корня, равных нулю.

Если а=0, то х — любое действительное число.

ах²+с=0, где а0, в=0, с0. Если а0,то уравнение примет вид: следовательно, уравнение имеет корни, то они равны по абсолютной величине, но противоположны по знаку; < 0, то , следовательно, уравнение корней не имеет. Если а=0 и с0, то уравнение действительных корней не имеет.

ах²+вх=0, где а0, в0, с=0. Если а0,то уравнение примет вид: х(а+в)=0,или Если а=0, то вх=0, х=0.

№ 2.1. При каких значениях параметра а оба корня уравнения 2х²+(3а²-|а|)х-а²-3а=0 равны нулю?

Решение.

Оба корня квадратного уравнения равны нулю, когда

№ 2.2. При каких значениях параметра а, корни уравнения 2 х²-(5а-3)х+1=0 равны по модулю, но противоположны по знаку?

Решение.

Корни квадратного уравнения равны по модулю, но противоположны по знаку, когда 5а-3=0,а=0,6, но с учетом того, что имеем уравнение 2х²+1=0, х²=-0,5, которое корней не имеет. Ответ: .

№ 2.3. При каких значениях параметра а один из двух различных корней уравнения 3х²+х+2а-3=0 равен нулю?

Решение.

Параметр должен удовлетворять условию: 2а-3=0, а=1,5. Ответ: а=1,5.

№ 2.4. При каких значениях параметра а корни уравнения 3х²+(а²-4а)х+а-1=0 равны по модулю, но противоположны по знаку?

Решение.

Корни квадратного уравнения равны по модулю, но противоположны по знаку, когда:

Ответ: а=0.

№ 2.5. Решить относительно х неполное квадратное уравнение х²-2а+1=а.

Решение.

х²=а+2а-1; х²=3а-1.

Если 3а-1=0, а= ,то уравнение имеет два совпадающих корня, равных нулю.

Если 3а-1<0, а<, то уравнение корней не имеет.

Если 3а-1>0. а>, то уравнение имеет два корня .

Ответ: при арешений нет; при а= х=0; при

3. ИССЛЕДОВАНИЕ И РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ С ПАРАМЕТРОМ.

№ 3.1. Исследовать и решить уравнение с параметром х² –2(а-1)х+2а+1=0.

Решение.

Найдем дискриминант: D=(а — 1)² -2а – 1= а² -2а+1-2а-1= а² — 4а.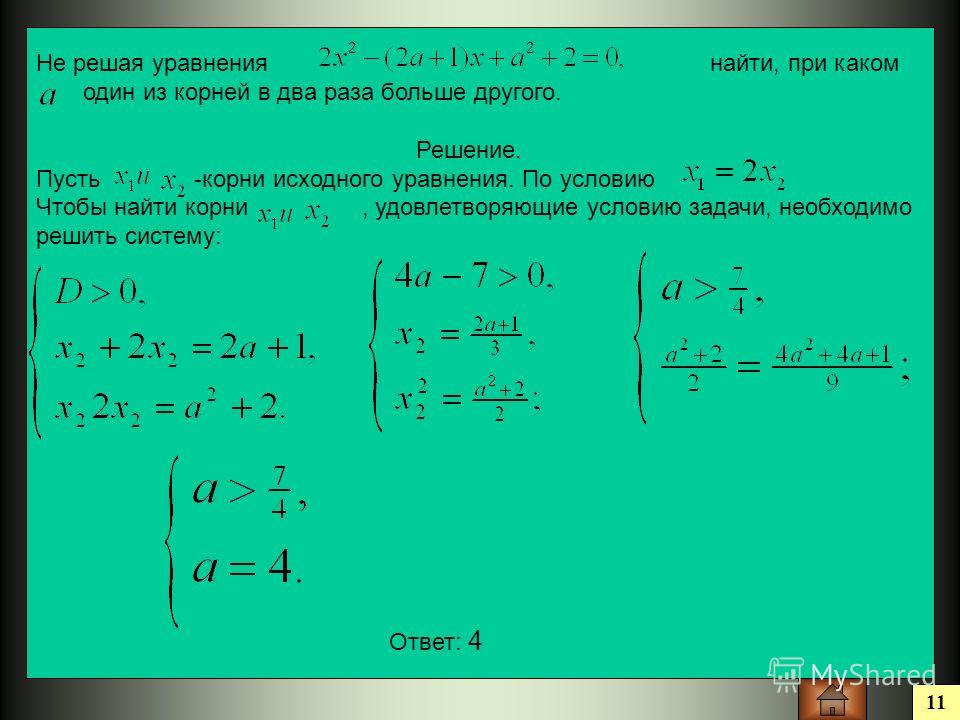

D > 0, а² - 4а > 0, а (а -4) > 0, а < 0 или а > 4, то уравнение имеет два действительных корня ;

D =0, а (а-4)=0, а=0, то х=а-1, х=0-1, х=-1, а=4,то х=а-1, х=4-1, х=3;

D < 0, а(а-4) < 0, 0 < а < 4, то уравнение не имеет корней.

Ответ: при а; при а=0 х=-1;

при а=4 х=3; при а корней нет.

№ 3.2. Исследовать и решить уравнение с параметром (а–1)х² +2(а+1)х+а–2= 0.

Решение.

1) При а-1=0, а=1 имеем линейное уравнение 4х-1=0, х=– единственное решение.

2) При а 1 уравнение является квадратным, найдем дискриминант:

D₁ = (а+1)²-(а–1)(2а-2)=а²+2а+1-а² +2а+а-2=5а-1.

D₁>0. 5а-1>0, а>, а 1, то уравнение имеет два корня .

D₁=0. 5а-1=0, а=, то уравнение имеет два равных корня .

D₁ < 0. 5а-1< 0, а<, то уравнение не имеет действительных корней.

Ответ: при а корней нет; при а = х=1,5; при а=1 х =;

при а.

№ 3.3. Исследовать и решить уравнение с параметром х² +2х- 8–а(х–4)=0.

Решение.

х² +2х-8–ах+4а=0; х² +(2-а)х+4а-8=0. Уравнение является квадратным.

Найдем дискриминант: D=(2-а)²-4(4а-8)=4-4а+а² -16а+32= а² -20а+36.

D>0. а² 20а+36>0, (а-18)(а -2)>0, а <2 или а >18, то уравнение имеет два действительных корня .

D=0. (а-18)(а-2)=0, а=2, то ; а=18, то ;

D < 0. (а-18)(а-2)< 0, 2< а <18, то уравнение не имеет действительных корней.

Ответ: при а; при а=2 х=0; при а=18 х=8; при а корней нет.

4. РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ С ПРИМЕНЕНИЕМ теоремы ВИЕТА.

Если в квадратном уравнении коэффициент при х² равен 1, то уравнение принимает вид х²+px+q, где p и q — некоторые числа называется приведенным квадратным уравнением.

Теорема Виета: Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

х²+px+q=0, где х₁ и х₂ – корни квадратного уравнения, то х₁ + х₂=-p; х₁ х₂=q.

ах²+вх+с=0, где х₁ и х₂ – корни квадратного уравнения, то

Справедливо утверждение, обратное теореме Виета.

Теорема: Если числа p и q таковы, что их сумма равна -p, а произведение равно q. то эти числа являются корнями уравнения х²+px+q=0.

№ 4.1. При каком значении параметра а сумма обратных величин действительных корней уравнения 2х² -2ах+а²-2=0 равна ?

Решение

Пусть х₁ и х₂ – корни квадратного уравнения, по условию _.

По теореме Виета: Используя соотношения между корнями и условие задачи, имеем:

Найдем дискриминант квадратного уравнения:

Имеем: Ответ: при

№ 4.2. В уравнении (а²-5а+3)х² +(3а-1)х+2=0 определите а так, чтобы один из корней был вдвое больше другого.

Решение.

Пусть х₁ и х₂ – корни квадратного уравнения, по условию х₁ =2 х_2. Заметим, что кратное сравнение выполняется только для положительных чисел.

По теореме Виета и условию задачи имеем систему:

Составим и решим уравнение:

Можно вычислить дискриминант данного уравнения, а затем проверить, удовлетворяет ли данное значение параметра а условию, что дискриминант неотрицателен, а так же, что корни положительны. Однако в данной задаче значительно проще сделать проверку, подставив это значение а в исходное уравнение.

При Корни отрицательны и кратно не сравниваются, поэтому задача решений не имеет. Ответ: решений нет.

№ 4.3. Найти все значения параметра а, при которых квадратное уравнение (а+2)х² –ах-а=0 имеет два корня, расположенных на числовой прямой симметрично относительно точки х=1.

Решение.

При а+2=0, а=-2, то 2х+2=0, х=-1 – единственное решение, следовательно данное значение а не удовлетворяет условию задачи.

При а-2. Пусть х₁ и х₂ – корни квадратного уравнения, по условию х₁ =1-у, х_2.=1+у, где у – некоторое действительное число.

По теореме Виета имеем:

Решим первое уравнение системы: 2(а+2)=а, а=-4.

Найдем дискриминант данного квадратного уравнения:

Данное значение а=-4 удовлетворяет полученным значениям. Ответ: а=-4.

Ответ: при а = — 4.

1. ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА.
2. Азаров А.И., Барвенов С.А., Федосенко В.С. Методы решения задач с параметрами. Минск; “Аверсэв”. 2005.
3. Амелькин В. В., Рабцевич В. Л. Задачи с параметрами. Минск; “Асар”. 1996.
4. Данкова И. Н., Бондаренко Т. Е., Емелина Л. Л., Плетнева О. К.Предпрофильная подготовка учащихся 9 классов по математике. Москва; “5 за знания”.2006.
5. Литвиненко В. Н., Мордкович А. Г.. Практикум по элементарной математике. Москва; “Просвещение”.1991.
6. Родионов Е. М. Решение задач с параметрами. Москва; “Русь – 90”. 1995.
7. Студенецкая В. Н., Сагателова Л. С. Математика 8 – 9классы: сборник элективных курсов. Волгоград; “Учитель”. 2006.
8. Шарыгин И. Ф. Решение задач. Москва; “Просвещение”. 1994.
9. Шахмейстер А. Х. Уравнения и неравенства с параметрами. Санкт-Петербург; “Петроглиф”. 2006.

101 использование квадратного уравнения

Март 2004

Нечасто математическое уравнение делает национальную прессу, гораздо менее популярной радио или, что самое поразительное, предметом дебатов в парламенте Великобритании. Однако в 2003 году старое доброе квадратное уравнение, о котором мы все учили в школе, было всем этим.

С чего мы начинаем

Все началось на собрании Национального союза учителей. Квадратное уравнение превозносили перед народом как пример жестокой пытки, которой математики подвергали бедных ничего не подозревающих школьников. Заинтригованное этим обвинением, квадратное уравнение взяло на себя главную роль на радио в прайм-тайм, где оно было допрошено грозным интервьюером, более привыкшим браться за прайм-тайм. Министр. The (London) Times заняла место в своей первой колонке, обычно предназначенное для весомых дискуссий о моральном (или ином) здоровье современного мира, чтобы объявить, что квадратное уравнение бесполезно, математика бесполезна и что никто не хочет ее изучать. математика в любом случае, так что заморачиваться. Обеспокоенный тем, чтобы опасные допущения, сделанные квадратным уравнением, не оспаривались, жизненно важное значение Уравнение выживания Соединенного Королевства обсуждалось (было принято положительное мнение, возможно, вам будет приятно узнать) в британской палате общин.

Чем все это закончится? Действительно ли квадратное уравнение мертво? Кто-нибудь заботился? Являются ли математики действительно злыми монстрами, которые хотят навязывать квадратные уравнения молодому поколению только для того, чтобы развратить их бессмертные души?

Может и так, но на самом деле это не ошибка квадратного уравнения. На самом деле, квадратное уравнение сыграло ключевую роль не только во всей человеческой цивилизации, какой мы ее знаем, но и в возможном обнаружении других инопланетных цивилизаций и даже в таких жизненно важных видах современной деятельности, как просмотр спутникового телевидения. Что еще, кроме природы божественного откровения, можно считать такое влияние на жизнь, какой мы ее знаем? Действительно, в самом прямом смысле квадратные уравнения могут спасти вам жизнь.

Вавилоняне

Вавилонские клинописные таблички с таблицами умножения 9

Все началось около 3000 г. до н.э. с вавилонян. Они были одной из первых цивилизаций в мире и придумали некоторые великие идеи, такие как сельское хозяйство, ирригация и письменность. Они начертили пути Солнца, Луны и планет и записали их на глиняных табличках (которые до сих пор можно увидеть в Британском музее). Вавилонянам мы обязаны современными представлениями об угле, в том числе и тем, как круг разбит на 360 градусов (из-за небольшого просчета, по одному в день). Мы также обязаны вавилонянам гораздо менее приятным изобретением (ужасного) сборщика налогов. И это было одной из причин, по которой вавилонянам нужно было решать квадратные уравнения.

Предположим, вы вавилонский фермер. Где-то на вашей ферме у вас есть поле площадью квадратных , на котором вы выращиваете какой-то урожай. Какое количество урожая вы можете вырастить на поле? Удвойте длину каждой стороны поля, и вы обнаружите, что можете вырастить в четыре раза больше урожая, чем раньше. Причина этого в том, что количество урожая, которое вы можете вырастить, пропорционально площади поля, что, в свою очередь, пропорционально квадратам 9.0024 длины стороны. С математической точки зрения, если длина стороны поля, количество урожая, которое вы можете вырастить на квадратном поле со стороной 1, и количество урожая, которое вы можете вырастить, то

Это наше первое квадратное уравнение, голое и мерцающее на солнце. Квадратные уравнения и области связаны друг с другом, как братья и сестры в одной семье. Однако в данный момент нам не нужно ничего решать — пока не приедет налоговая! Весело он говорит фермеру: «Я хочу, чтобы ты дал мне урожай, чтобы заплатить налоги с твоей фермы». Теперь перед фермером стоит дилемма: какого размера поле ему нужно, чтобы вырастить такое количество урожая? Мы можем легко ответить на этот вопрос, на самом деле

Находить квадратные корни с помощью калькулятора для нас несложно, но для вавилонян это было большой проблемой. На самом деле они разработали метод последовательного приближения к ответу, который идентичен алгоритму (так называемый метод Ньютона-Рафсона ), используемому современными компьютерами для решения гораздо более сложных задач, чем квадратные уравнения.

Теперь не все поля квадратные. Давайте теперь предположим, что у фермера есть поле более странной формы с двумя треугольными секциями, как показано справа.

Соответствующие значения и количество урожая, которое фермер может вырастить на этом поле, определяется как

Это больше похоже на квадратное уравнение, к которому мы привыкли, и даже под дурным взглядом налогового инспектора решить его намного сложнее. И все же вавилоняне снова нашли ответ. Сначала мы делим на, чтобы получить

Теперь мы заполним квадрат , используя тот факт, что

Объединив это с исходным уравнением, мы получим

Теперь это уравнение, которое мы можем решить, взяв квадратный корень. В результате получается знаменитая «формула»:

, который можно переписать как

(Формула обычно имеет «-4ac», потому что квадратное уравнение чаще записывается в форме «».)

Тот факт, что извлечение квадратного корня может дать положительный или отрицательный ответ, приводит к замечательному результату, который квадратное уравнение имеет два раствора . Вот вам и математические головоломки, имеющие только одно решение!

На этом обучение квадратным уравнениям часто останавливается. Мы достигли любимой всеми журналистами цели, когда они берут интервью у математиков, — формулы . Можно составить бесконечные вопросы, которые включают в себя подстановку значений и в формулу, чтобы дать (два) ответа. Но дело вовсе не в математике. Найти формулу — это только первый шаг на долгом пути. Мы должны спросить, что означает формула означает ; что это говорит нам о вселенной; Имеет ли значение формула? Давайте теперь посмотрим, куда нас приведет эта формула.

Сюрприз для греков, немного математического оригами и чувство меры

Теперь мы перенесемся на 1000 лет вперед к древним грекам и посмотрим, что они сделали с квадратными уравнениями. Греки были превосходными математиками и открыли большую часть математики, которой мы пользуемся до сих пор. Одним из уравнений, которое им было интересно решить, было (простое) квадратное уравнение 9.0003

Они знали, что это уравнение имеет решение. На самом деле это длина гипотенузы прямоугольного треугольника, длина стороны которого равна единице.

Из теоремы Пифагора следует, что если прямоугольный треугольник имеет более короткие стороны и гипотенузу, то

Положить и потом . Таким образом

Итак, что в этом случае? Или, если задать вопрос, который задавали греки, что такое рода числа? Причина, по которой это имело значение, заключалась в греческом смысле пропорции к . Они считали, что все числа пропорциональны друг другу. Если быть точным, это означало, что все числа были дробями вида где и являются целыми числами . Такие числа, как 1/2, 3/4 и 355/113, являются примерами дробей. Естественно было ожидать, что это тоже дробь. Огромным сюрпризом было то, что это не так. На самом деле

, где точки означают, что десятичное расширение продолжается до бесконечности без какой-либо различимой закономерности. (Мы еще встретимся с этой ситуацией позже, когда узнаем о хаосе.)

было первым иррациональным числом (то есть числом, которое не является дробью или рациональным), которое было признано таковым. Другие примеры включают , и фактически «большинство» чисел. Прошло до 1910-м веке до того, как у нас был хороший способ думать об этих числах. Открытие, которое не было рациональным числом, вызвало как большое волнение (в результате было принесено в жертву 100 быков), так и большой шок, поскольку первооткрывателю пришлось покончить жизнь самоубийством. (Пусть это будет ужасным предупреждением для любителей математики!) В этот момент греки бросили алгебру и обратились к геометрии.

Далеко не неизвестный номер, мы встречаемся регулярно: всякий раз, когда используем лист бумаги формата А4. В Европе размеры бумаги измеряются в размерах A, причем A0 является самым большим размером с площадью . Размеры А имеют особое соотношение между собой. Если теперь сделать немного оригами, взяв лист бумаги формата А1, а затем сложив его пополам (по самой длинной стороне), то получится лист формата А2. Если снова сложить его пополам, получится А3, снова А4 и т. д. Однако бумага устроена так, что пропорции каждого из размеров А одинаковы, то есть каждый лист бумаги имеет одинаковую форму.

Можно задать вопрос, какова эта пропорция. Начните с листа бумаги со сторонами х и х с х самой длинной стороны. Теперь разделите это пополам, чтобы получить еще один лист бумаги со сторонами х и х/2 , где теперь х является самой длинной стороной. Это показано справа.

Пропорции первого листа бумаги, а второго — или . Мы хотим, чтобы эти две пропорции были равны. Это означает, что

или

Еще одно квадратное уравнение! К счастью, это тот, который мы уже встречали. Решая его, находим, что

Этот результат легко проверить. Просто возьмите лист бумаги формата А4 (или А3, или А5) и измерьте стороны. Мы также можем определить размер каждого листа. площадь листа бумаги формата А0 определяется как

Но мы это знаем, поэтому у нас есть еще одно квадратное уравнение для наибольшей стороны A0, заданное как

Это означает, что самая длинная сторона A равна (почему?), а самая длинная сторона A равна . Проверьте это на своих листах бумаги.

Бумага, используемая в Соединенных Штатах, называемая Foolscap , имеет другую пропорцию. Чтобы понять, почему, вернемся к грекам и другому квадратному уравнению. Вызвав такое горе, квадратное уравнение искупает себя в поисках идеальных пропорций: поиск, который продолжается и сегодня в дизайне съемочных площадок, и его можно увидеть во многих аспектах природы.

Начнем с прямоугольника, а затем удалим из него квадрат с той же длиной стороны, что и самая короткая сторона прямоугольника. Если самая длинная сторона прямоугольника имеет длину 1, а самая короткая сторона имеет длину , то у квадрата есть стороны длины . Удаление его из прямоугольника дает меньший прямоугольник с наибольшей стороной и наименьшей стороной. Пока так абстрактно. Однако греки считали, что прямоугольник, имеющий наиболее эстетичные пропорции (т. н. «золотой прямоугольник»), — это тот, у которого большие и малые прямоугольники, построенные выше, имеют одинаковые пропорции. Для этого необходимо иметь

Это еще одно квадратное уравнение : очень важное, которое встречается во всех видах приложений. Он имеет (положительное) решение

Число называется золотым сечением и часто обозначается греческой буквой .

Золотой прямоугольник можно увидеть в форме окон, особенно в георгианских домах. В последнее время золотое сечение также можно найти как «идеальную форму» для фотографий и киноизображений. Квадратное уравнение возникает также при изучении популяций кроликов и при изучении закономерностей расположения семян подсолнечника и листьев на стеблях растений. Все они связаны с золотым сечением через 9.0023 Последовательность Фибоначчи , которая задается как

Семена подсолнуха, упорядоченные с помощью чисел Фибоначчи

Парфенон, воплощающий золотое сечение

В этой последовательности каждый член является суммой двух предыдущих членов. Фибоначчи открыл его в 15 веке, пытаясь предсказать будущую популяцию кроликов. Если вы возьмете отношение каждого члена к следующему за ним, вы получите последовательность чисел

и эти числа все ближе и ближе (как вы уже догадались) к золотому сечению.

Найдя оба корня приведенного выше квадратного уравнения, мы действительно можем найти формулу для n-го члена последовательности Фибоначчи. Если это th такое число с и то задается формулой

Коники связывают квадратные уравнения со звездами

Греки также очень интересовались формой конусов. на картинке слева показан типичный конус.

Половину конуса можно представить как распространение света, исходящего от факела. Теперь, если вы посветите факелом на плоскую поверхность, например на стену, вы увидите различные формы, когда будете перемещать факел. Эти формы называются коническими сечениями и представляют собой кривые, которые вы получите, если сделаете срез конуса под разными углами. Именно эти кривые изучались греками, и они признали, что существует в основном четыре типа конического сечения. Если вы сделаете горизонтальный разрез через конус, вы получите круг . Сечение под небольшим углом к ​​горизонтали дает эллипс . Если взять вертикальное сечение, то получится гипербола , а если взять сечение, параллельное одной стороне конуса, то получится парабола . Эти кривые показаны ниже.

Поперечное сечение конуса может быть кругом…	… эллипс…	… парабола…	… или гипербола.

Конические сечения входят в наш рассказ, потому что каждое из них описывается квадратным уравнением. В частности, если представляет собой точку на каждой кривой, то квадратное уравнение связывает и . Имеем:

Круг : ;

Эллипс : ;

Гипербола : ;

Парабола :

Эти кривые были известны и изучались со времен греков, но, кроме круга, они, похоже, не имели никакого практического применения. Однако, как мы увидим в следующем выпуске « Plus », связь между квадратными уравнениями и кониками вкупе с могучей счастливой случайностью привели к пониманию того, как устроена Вселенная, и в 16 веке пришло время чтобы коники менялись мир.

---

Крис Бадд — профессор прикладной математики на факультете математических наук Университета Бата и заведующий кафедрой математики в Королевском институте в Лондоне.

Крис Сангвин — сотрудник Школы математики и статистики Бирмингемского университета. Он является научным сотрудником Центра сети поддержки обучения и преподавания по математике, статистике и операционным исследованиям.

Недавно они написали популярную книгу по математике Математика в изобилии! , опубликованном Oxford University Press.

Эта статья была частично вдохновлена ​​замечательными дебатами в британской палате общин по вопросу о квадратных уравнениях. Запись этих дебатов можно найти в Hansard, Палата общин Соединенного Королевства, 26 июня 2003 г. , колонки 1259–1269, 2003 г., которая доступна в Интернете в Палате общин. Веб-сайт дебатов Commons Hansard.

Квадратное уравнение — математика GCSE

Что такое квадратное уравнение?

Рабочий лист квадратного уравнения

Как решать квадратные уравнения

Практика квадратного уравнения вопросы

Вопросы квадратного уравнения для GCSE

Вы знали?

Контрольный список обучения

Следующие уроки

Все еще застряли?

Индивидуальные занятия по математике, созданные для успеха KS4

Еженедельные онлайн-уроки повторения математики GCSE теперь доступны

Узнать больше

Что такое квадратное уравнение?

Рабочий лист квадратного уравнения

Как решать квадратные уравнения

Практика квадратного уравнения вопросы

Вопросы квадратного уравнения для GCSE

Вы знали?

Контрольный список обучения

Следующие уроки

Все еще застряли?

Здесь мы узнаем о квадратном уравнении и о том, как решать квадратные уравнения, используя четыре метода: факторизация , использование формулы квадратного уравнения , завершение квадрата и использование графика .

Существуют также рабочие листы с квадратными уравнениями, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.

Что такое квадратное уравнение?

Квадратное уравнение — это квадратное выражение, равное чему-либо.

Квадратные алгебраические уравнения – это уравнения, содержащие члены до x 92+bx+c=0\]

a – коэффициент (число впереди) x ² члена

b – коэффициент (число впереди) x члена

c – постоянный член (число на свой собственный)

В GCSE решения полиномиальных уравнений, таких как квадратные уравнения, всегда будут давать действительные числа, но они могут быть как иррациональными, так и рациональными числами.

Что такое квадратное уравнение?

Рабочий лист квадратного уравнения

Получите бесплатный рабочий лист квадратного уравнения, содержащий более 20 вопросов и ответов. {2}-2х-24=0\] 9{2}-2x-24=0\]

Коэффициенты
1, 24
2, 12
3, 8
4, 6

\[\begin{align} -6+4&=-2\\ -6\умножить на 4&=-24 \end{aligned}\]

\[(x-6)(x+4)=0\]

2 Установить каждую скобку равной 0.

\[x-6=0\qquad \qquad x+4=0\]

3 Решите каждое уравнение, чтобы найти x.

\[\begin{выровнено} х-6&=0 \квадратный &х+4&=0\\ х&=6 \квадратный &х&=-4 \end{aligned}\]

Мы можем проверить правильность нашего решения, подставив его в исходное уравнение. 9{2}-25=0\]

2 Измените уравнение, чтобы найти неизвестную переменную (x).

Противоположность − 25 равна + 25, поэтому + 25 к обеим частям уравнения.

Противоположностью возведения в квадрат является квадратный корень, поэтому возьмите квадратный корень из левой и правой частей.

Помните, что квадратный корень имеет положительное и отрицательное решение, поэтому используйте знак ±.

3 Квадратный корень имеет + и — ответ, запишите обе версии вычисления, чтобы найти два решения x.

\[\begin{выровнено} x&=\sqrt{25}+1 \quad &x&=-\sqrt{25}+1\\ х&=5+1 \квадратный &х&=-5+1\\ х&=6 \квадратный &х&=-4 \end{aligned}\]

Мы можем проверить правильность нашего решения, подставив его в исходное уравнение.

Пример 4: квадратное уравнение – решение путем построения графика

Мы можем построить квадратное уравнение, чтобы построить квадратный график, который поможет нам решить его.

Мы можем подставить значения для x в квадратичную функцию, чтобы получить значения для y. Когда мы наносим эти значения на сетку x, y, мы получаем специальную кривую в форме буквы «U», называемую 9.{2}-2x-24=0\]

нам нужно:

1. Нарисовать квадратичный график

2 Решения/корни уравнения находятся там, где график пересекает ось x (когда y =0)

Мы знаем, что для решения квадратного уравнения должно быть равно 0 .

Поскольку x ² – 2x – 24 = 0, мы ищем значения x, которые при подстановке в уравнение дадут нам значение y, равное 0 9{2}-2 x-24=0\]

равно

\[x=6 \quad and \quad x=-4\]

Мы можем проверить правильность нашего решения, подставив его в исходное уравнение .

Пошаговое руководство: Графическое решение квадратных уравнений

Вопросы по квадратным уравнениям

Решите следующие вопросы, используя факторизацию, квадратную формулу или завершение квадрата. Как будет выглядеть квадратичный граф?

x=-2 \quad x=-3

x=2 \quad x=-3 92+х-6=0

 

можно разложить как

 

(х+3)(х-2)=0

 

Приравняв каждую скобку к нулю и решив, получим требуемые решения.

 

х=-0,236 \; (3 с.ф) \quad x=-4,23\; (3 с.ф)

х=0,236 \; (3 с.ф) \quad x=4,23 \; (3 с.ф)

х=-0,236 \; (3 с.ф) \quad x=4,23 \; (3 с.