Уравнение синуса: Арксинус и уравнение sin x = a — урок. Алгебра, 10 класс.

Решение основных тригонометрических уравнений.

• Существуют 4 вида основных тригонометрических уравнений:
• sin x = a; cos x = a
• tg x = a; ctg x = a
• Решение основных тригонометрических уравнений подразумевает рассмотрение различных положений «х» на единичной окружности, а также использование таблицы преобразования (или калькулятора).
• Пример 1. sin x = 0,866. Используя таблицу преобразования (или калькулятор), вы получите ответ: х = π/3. Единичная окружность дает еще один ответ: 2π/3. Запомните: все тригонометрические функции являются периодическими, то есть их значения повторяются. Например, периодичность sin x и cos x равна 2πn, а периодичность tg x и ctg x равна πn. Поэтому ответ записывается следующим образом:
• x1 = π/3 + 2πn; x2 = 2π/3 + 2πn.
• Пример 2. соs х = -1/2. Используя таблицу преобразования (или калькулятор), вы получите ответ: х = 2π/3. Единичная окружность дает еще один ответ: -2π/3.
• x1 = 2π/3 + 2π; х2 = -2π/3 + 2π.
• Пример 3. tg (x — π/4) = 0.
• Ответ: х = π/4 + πn.
• Пример 4. ctg 2x = 1,732.
• Ответ: х = π/12 + πn.

Преобразования, используемые при решении тригонометрических уравнений.

• Для преобразования тригонометрических уравнений используются алгебраические преобразования (разложение на множители, приведение однородных членов и т.д.) и тригонометрические тождества.
• Пример 5. Используя тригонометрические тождества, уравнение sin x + sin 2x + sin 3x = 0 преобразуется в уравнение 4cos x*sin (3x/2)*cos (x/2) = 0. Таким образом, нужно решить следующие основные тригонометрические уравнения: cos x = 0; sin (3x/2) = 0; cos (x/2) = 0.

• Нахождение углов по известным значениям функций.

  • Перед изучением методов решения тригонометрических уравнений вам необходимо научиться находить углы по известным значениям функций. Это можно сделать при помощи таблицы преобразования или калькулятора.
  • Пример: соs х = 0,732.
    Калькулятор даст ответ х = 42,95 градусов. Единичная окружность даст дополнительные углы, косинус которых также равен 0,732.

• Отложите решение на единичной окружности.

  • Вы можете отложить решения тригонометрического уравнения на единичной окружности. Решения тригонометрического уравнения на единичной окружности представляют собой вершины правильного многоугольника.
  • Пример: Решения x = π/3 + πn/2 на единичной окружности представляют собой вершины квадрата.
  • Пример: Решения x = π/4 + πn/3 на единичной окружности представляют собой вершины правильного шестиугольника.

• Методы решения тригонометрических уравнений.

  • Если данное тригонометрическое уравнение содержит только одну тригонометрическую функцию, решите это уравнение как основное тригонометрическое уравнение. Если данное уравнение включает две или более тригонометрические функции, то существуют 2 метода решения такого уравнения (в зависимости от возможности его преобразования).
    • Метод 1.
  • Преобразуйте данное уравнение в уравнение вида: f(x)*g(x)*h(x) = 0, где f(x), g(x), h(x) — основные тригонометрические уравнения.
  • Пример 6. 2cos x + sin 2x = 0. (0
  • Решение. Используя формулу двойного угла sin 2x = 2*sin х*соs х, замените sin 2x.
  • 2соs х + 2*sin х*соs х = 2cos х*(sin х + 1) = 0. Теперь решите два основных тригонометрических уравнения: соs х = 0 и (sin х + 1) = 0.
  • Пример 7. cos x + cos 2x + cos 3x = 0. (0
  • Решение: Используя тригонометрические тождества, преобразуйте данное уравнение в уравнение вида: cos 2x(2cos x + 1) = 0. Теперь решите два основных тригонометрических уравнения: cos 2x = 0 и (2cos x + 1) = 0.
  • Пример 8. sin x — sin 3x = cos 2x . (0
  • Решение: Используя тригонометрические тождества, преобразуйте данное уравнение в уравнение вида: -cos 2x*(2sin x + 1) = 0. Теперь решите два основных тригонометрических уравнения: cos 2x = 0 и (2sin x + 1) = 0.
    • Метод 2. 2 — 1) = 0. Теперь найдите t, а затем найдите х для t = tg х.

Простейшие тригонометрические уравнения решаются, как правило, по формулам. Напомню, что простейшими называются вот такие тригонометрические уравнения:

sinx = а

cosx = а

tgx = а

ctgx = а

х — угол, который нужно найти,
а — любое число.

А вот и формулы, с помощью которых можно сразу записать решения этих простейших уравнений.

Для синуса:

Для косинуса:

х = ± arccos a + 2π n, n ∈ Z

Для тангенса:

х = arctg a + π n, n ∈ Z

Для котангенса:

х = arcctg a + π n, n ∈ Z

Собственно, это и есть теоретическая часть решения простейших тригонометрических уравнений. Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона. Почему?

Да потому, что масса народу записывает эти буковки, не понимая их смысла совершенно! С опаской записывает, как бы чего не вышло…) С этим надо разобраться. Тригонометрия для людей, или люди для тригонометрии, в конце концов!?)

Разберёмся?

Один угол у нас будет равен arccos a, второй: -arccos a.

И так будет получаться всегда. При любом а.

Если не верите, наведите курсор мышки на картинку, или коснитесь рисунка на планшете.) Я изменил число а на какое-то отрицательное. Всё равно, один угол у нас получился

arccos a, второй: -arccos a.

Следовательно, ответ можно всегда записать в виде двух серий корней:

х 1 = arccos a + 2π n, n ∈ Z

х 2 = — arccos a + 2π n, n ∈ Z

Объединяем эти две серии в одну:

х= ± arccos а + 2π n, n ∈ Z

И все дела. Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом.

Если вы понимаете, что это не какая-то сверхнаучная мудрость, а просто сокращённая запись двух серий ответов, вам и задания «С» будут по плечу. С неравенствами, с отбором корней из заданного интервала… Там ответ с плюсом/минусом не катит. А если отнестись к ответу делово, да разбить его на два отдельных ответа, всё и решается.) Собственно, для этого и разбираемся. Что, как и откуда.

В простейшем тригонометрическом уравнении

sinx = а

тоже получается две серии корней. Всегда. И эти две серии тоже можно записать одной строчкой. Только эта строчка похитрее будет:

х = (-1) n arcsin a + π n, n ∈ Z

Но суть остаётся прежней. Математики просто сконструировали формулу, чтобы вместо двух записей серий корней, сделать одну. И всё!

Проверим математиков? А то мало ли…)

В предыдущем уроке подробно разобрано решение (безо всяких формул) тригонометрического уравнения с синусом:

В ответе получились две серии корней:

х 1 = π /6 + 2π n, n ∈ Z

х 2 = 5π /6 + 2π n, n ∈ Z

Если мы будем решать это же уравнение по формуле, получим ответ:

х = (-1) n arcsin 0,5 + π n, n ∈ Z

Вообще-то, это недоделанный ответ. ) Ученик обязан знать, что arcsin 0,5 = π /6. Полноценный ответ будет:

х = (-1) n π /6 + π n, n ∈ Z

Тут возникает интересный вопрос. Ответ через х 1 ; х 2 (это правильный ответ!) и через одинокий х (и это правильный ответ!) — одно и то же, или нет? Сейчас узнаем.)

Подставляем в ответ с х 1 значения n =0; 1; 2; и т.д., считаем, получаем серию корней:

х 1 = π/6; 13π/6; 25π/6 и так далее.

При такой же подстановке в ответ с х 2 , получаем:

х 2 = 5π/6; 17π/6; 29π/6 и так далее.

А теперь подставляем значения n (0; 1; 2; 3; 4…) в общую формулу для одинокого х . Т.е возводим минус один в нулевую степень, затем в первую, вторую, и т.д. Ну и, разумеется, во второе слагаемое подставляем 0; 1; 2 3; 4 и т.д. И считаем. Получаем серию:

х = π/6; 5π/6; 13π/6; 17π/6; 25π/6 и так далее.

Вот всё и видно.) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)

Формулы для решения тригонометрических уравнений с тангенсом и котангенсом тоже можно проверить. Но не будем.) Они и так простенькие.

Я расписал всю эту подстановку и проверку специально. Здесь важно понять одну простую вещь: формулы для решения элементарных тригонометрических уравнений есть, всего лишь, краткая запись ответов. Для этой краткости пришлось вставить плюс/минус в решение для косинуса и (-1) n в решение для синуса.

Эти вставки никак не мешают в заданиях, где нужно просто записать ответ элементарного уравнения. Но если надо решать неравенство, или далее нужно что-то делать с ответом: отбирать корни на интервале, проверять на ОДЗ и т.п, эти вставочки могут запросто выбить человека из колеи.

И что делать? Да либо расписать ответ через две серии, либо решать уравнение/неравенство по тригонометрическому кругу. Тогда исчезают эти вставочки и жизнь становится легче.)

Можно подвести итоги.

Для решения простейших тригонометрических уравнений существуют готовые формулы ответов. Четыре штуки. Они хороши для мгновенной записи решения уравнения. Например, надо решить уравнения:

sinx = 0,3

Легко: х = (-1) n arcsin 0,3 + π n, n ∈ Z

cosx = 0,2

Без проблем: х = ± arccos 0,2 + 2π n, n ∈ Z

tgx = 1,2

Запросто: х = arctg 1,2 + π n, n ∈ Z

ctgx = 3,7

Одной левой: x= arcctg3,7 + π n, n ∈ Z

cos x = 1,8

Если вы, блистая знаниями, мгновенно пишете ответ:

х= ± arccos 1,8 + 2π n, n ∈ Z

то блистаете вы уже, это… того… из лужи.) Правильный ответ: решений нет. Не понимаете, почему? Прочитайте, что такое арккосинус. Кроме того, если в правой части исходного уравнения стоят табличные значения синуса, косинуса, тангенса, котангенса, — 1; 0; √3; 1/2; √3/2 и т. п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.

А если уж вам попалось неравенство, типа

то ответ в виде:

х πn, n ∈ Z

есть редкая ахинея, да…) Тут надо по тригонометрическому кругу решать. Чем мы и займёмся в соответствующей теме.

Для тех, кто героически дочитал до этих строк. Я просто не могу не оценить ваши титанические усилия. Вам бонус.)

Бонус:

При записи формул в тревожной боевой обстановке, даже закалённые учёбой ботаны частенько путаются, где πn, а где 2π n. Вот вам простой приёмчик. Во всех формулах стоит πn. Кроме единственной формулы с арккосинусом. Там стоит 2πn. Два пиэн. Ключевое слово — два. В этой же единственной формуле стоят два знака в начале. Плюс и минус. И там, и там — два.

Так что, если вы написали два знака перед арккосинусом, легче вспомнить, что в конце будет два пиэн. А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Основными методами решения тригонометрических уравнений являются: сведение уравнений к простейшим (с использованием тригонометрических формул), введение новых переменных, разложение на множители. Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.

Необходимым условием успешного решения тригонометрических уравнений является знание тригонометрических формул (тема 13 работы 6).

Примеры.

1. Уравнения, сводящиеся к простейшим.

1) Решить уравнение


Решение:

Ответ:

2) Найти корни уравнения

(sinx + cosx) 2 = 1 – sinxcosx, принадлежащие отрезку .

Решение:

Ответ:

2. Уравнения, сводящиеся к квадратным.

1) Решить уравнение 2 sin 2 x – cosx –1 = 0.

Решение: Используя формулу sin 2 x = 1 – cos 2 x, получаем

Ответ:

2) Решить уравнение cos 2x = 1 + 4 cosx.

Решение: Используя формулу cos 2x = 2 cos 2 x – 1, получаем

Ответ:

3) Решить уравнение tgx – 2ctgx + 1 = 0

Решение:

Ответ:

3. Однородные уравнения

1) Решить уравнение 2sinx – 3cosx = 0

Решение: Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1. Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим

Ответ:

2) Решить уравнение 1 + 7 cos 2 x = 3 sin 2x

Решение:

Используем формулы 1 = sin 2 x + cos 2 x и sin 2x = 2 sinxcosx, получим

sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0

Пусть cosx = 0, тогда sin 2 x = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1.
Значит cosx ≠ 0 и можно поделить уравнение на cos 2 x. Получим

tg 2 x – 6 tgx + 8 = 0
Обозначим tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y 2 = 2
а) tgx = 4, x= arctg4 + 2 k , k
б) tgx = 2, x= arctg2 + 2 k , k .

Ответ: arctg4 + 2 k , arctg2 + 2 k, k

4. Уравнения вида a sinx + b cosx = с, с ≠ 0.

1) Решить уравнение .

Решение:

Ответ:

5. Уравнения, решаемые разложением на множители.

1) Решить уравнение sin2x – sinx = 0.

Корнем уравнения f ( х ) = φ ( х ) может служить только число 0. Проверим это:

cos 0 = 0 + 1 – равенство верно.

Число 0 единственный корень данного уравнения.

Ответ: 0.

Простейшие тригонометрические уравнения




Нам будет достаточно повторить уравнения  , где  – константа. Ну и чуть более сложные, когда аргумент равен  и т.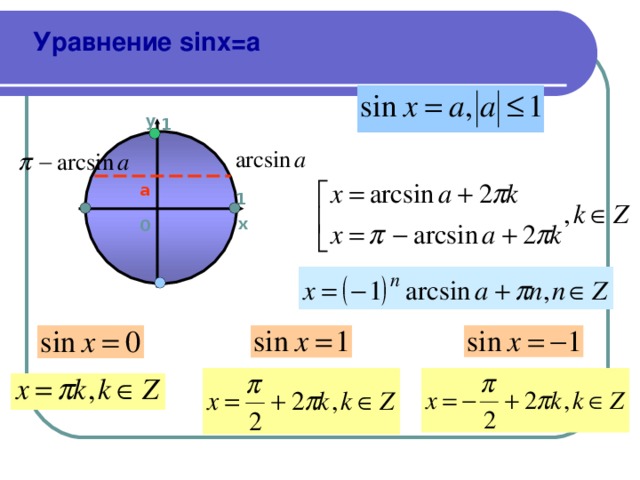 п. В силу периодичности тригонометрических функций эти уравнения имеют бесконечно много решений, а синус с косинусом могут не иметь их вовсе. И в самом деле, уравнению  или  соответствует бесконечно много углов, а вот с  – печаль.

С синуса и начнём: . Поскольку синус ограничен, то это уравнение имеет корни только в том случае, если .

И эти корни таковы, общая формула: , где  принимает все целые значения, сокращённо будем писать: .
Так решением уравнения  являются углы:


Распишем несколько штук для

Довольно часто в задачах требуется найти какой-то конкретный угол (или углы), так, если по условию угол должен быть тупым, то следует выбрать корень .

А теперь важный вопрос: откуда взялась общая формула? В школьном курсе формулы выводятся с помощью единичной окружности, но сейчас нам гораздо полезнее вспомнить графический метод решения уравнений. Строим синусоиду  и прямую , например,  (малиновый цвет). После чего определяем «иксовые» координаты их точек пересечения (малиновые отметки на оси ):

Это и есть корни. Осталось уловить периодичность расположения корней и сконструировать формулу. Отработаем этот принцип на важных частных случаях:

Решим графически уравнение . Из чертежа следует, что прямая  пересекает синусоиду  через каждые радиан, начиная от значения  (выбираем самое маленькое). Таким образом, уравнение имеет корни (синие точки):
.  Легко видеть, что решением уравнения  является множество углов  (красные точки), а решением  – углы .

Все формулы справедливы не только для переменной , но и для сложного аргумента, например,  (самые популярные) и других. Решим, например, уравнение . Используем только что выведенную частную формулу, только ВМЕСТО «икс» у нас «два икс»: . Но это ещё не всё, ведь нам нужно выразить «икс»:  .

Готово.

Разумеется, встречаются и «плохие» решения, рассмотрим уравнение . Приведём его к виду , и по общей формуле: . Этот арксинус можно вычислить лишь приближенно:  и поэтому ответ лучше оставить с арксинусом.

Решим уравнение . Как и в случае с синусом, оно имеет корни, только если . Изобразим на чертеже графики функций  и определим «иксовые» координаты их точек пересечения. Во-первых, обращаем внимание на самые близкие к нулю значения:  (красная и синяя точки вблизи нуля):

И анализируя точки пересечения графиков, легко понять, что «красные» корни повторяются через каждые  радиан:  и «синие» корни тоже повторяются через этот же период: . Обе ветки решения можно объединить в общую формулу:
Решим, например, уравнение . Уловка здесь детская: избавляемся от иррациональности в знаменателе: , после чего записываем «хороший» ответ:
. Именно это случай я изобразил на схематическом чертеже выше и желающие могут ещё раз осмыслить общую формулу, используя конкретные значения углов.

И в качестве задания я предложу вам вывести три частные формулы для уравнений  . Уже скоро на экранах ваших мониторов! 🙂 Разумеется, аргумент может быть сложным: . Формула та же самая: . Единственное, не забываем выразить «икс», разделив всё семейство углов на три: .

Осталось два более простых уравнения.

Уравнение  имеет решения при любом значении , и ситуация здесь прозрачна, даже чертежа особо не нужно: «главная» ветка тангенса расположена на интервале , берём отсюда угол:  и добавляем периоды тангенса:
 – общая формула.

В качестве примера решим приятное уравнение :
    Готово!

И всё же приведу чертёж для этого и двух других частных случаев:
Решением уравнения  является множество углов .
Решением уравнения  – множество:

Эти формулы легко получить как аналитически (по общей формуле), так и графически.

Уравнение  предлагаю для самостоятельного изучения, в числе других заданий, которые уже нет сил – не могу не предложить:

Задание 10

а) Перевести из градусов в радианы или наоборот: .

б) Вычислить, не пользуясь калькулятором: .

в) Упростить:
, ; понизить степень до первой:
.

г) Графическим методом решить уравнения .

д) Вывести (аналитически или графически) общую формулу для решения  уравнения   и получить частные формулы для .

е) Решить аналитически: .

Решения и ответы в конце книги, и ещё будет пункт ж) (в хорошем смысле :)), который я предложу вам после изучения следующего параграфа:

5.8. Тригонометрические неравенства

5. 6. Обратные тригонометрические функции

| Оглавление |



Проверка синусоидальной функции (Назначение 1) Функция синуса

(назначение 1)

по

____________________________________________________________________

Дайте нам осмотреть функцию Sine Fund as the Coepaitafit T. изменить, чтобы увидеть влияние этих изменений на различные графики.

 

Дан график y = a sin (bx + c) с переменными a, b и c.

 

Наш первый шаг:

 

            Смотреть На базовом синусоидальном графике, когда a = 1, b = 1 и c = 0

Обратите внимание, что

. это множество действительных чисел, а Диапазон : [-1,1]. Период для функции синуса равен 2. График функции синуса продолжается бесконечно.

 

Амплитуда — это расстояние от оси до самого высокого или самого низкого точка. Или это половина расстояния от самой высокой до самой низкой точки. В этом случае амплитуда равна 1. Давайте использовать в этом примере переменную a в демонстрируя амплитуду . В настоящее время а = 1,

 

Период — это время, за которое график совершает один полный цикл , или, другими словами, количество времени, которое требуется для график, чтобы начать повторяться. Давайте используем переменную b в сочетании с корректировка периода . В таком случае 2.

 

В нашем примере синусоида фаза управляется переменной c, первоначально пусть c = 0.

 

Продолжайте использовать базовый график синусоиды как наша система отсчета. Посмотрим, что происходит с графом под следующие рекомендации.

 

Шаг 1: a sin (bx +c)

 

Пусть b=1, c=0 и варьируются значения а. Наше новое уравнение становится y=a sin(x).

 

Воспользуемся графическим калькулятором исследовать эффекты изменения значений для a, не забывая использовать оба положительные и отрицательные значения.

 

Синий график: y=sin x. Y = sin (x), основной график синусов в будущем всегда будет синим примеры для сравнения.

 

 

 

 

 

переменная a положительна, амплитуда увеличивается в кратном размере абсолютного значения a, и график имитирует y=sin x исходный график продемонстрировано выше. Это известно как вертикальное растяжение . Точно так же, когда переменная a отрицательна, амплитуда по-прежнему увеличивается на тот же коэффициент, абсолютное значение а.

 

Однако отрицательное значение заставляет график быть отражением по оси X.

 

 

 

Шаг 2: Теперь мы исследуем влияние переменной b. Пусть а=1, и c=0 и измените значения переменной b. Наше новое уравнение теперь    y = sin (bx).

 

 

 

 

 

Обратите внимание, что амплитуда графиков не меняется, хотя значение переменная b варьировалась. Когда b>1, период графика изменяется на 2/b, в результате при горизонтальном сжатии графика. Когда 0 < b < 1, период  по-прежнему изменено на 2/b, однако график теперь растянут.

 

Остается вопрос: что происходит, когда отрицательные значения заменяются переменной b?

 

Путем замены отрицательных значений для переменной b, уведомление есть отражение по оси x для наших двух графиков, а также горизонтальное изменение основной синусоидальный график.

 

Шаг 3: Давайте снова начнем с уравнения y= asin(bx+c). Пусть а=1, b=1 и варьировать c, в результате чего y = sin(x+c)

 

 

 

Значение переменной c перемещается синусоидальный график вправо или влево. При c > 0 график переходит в оставил. Когда c < 0, график смещается вправо.

 

Это горизонтальное движение называется фазовый сдвиг . Фазовый сдвиг оказывается равным значению c. Для уверенности давайте проверьте, что с изменением переменной b одновременно.

 

Это показывает, что на фазовый сдвиг влияет b. Таким образом, фазовый сдвиг на самом деле является результатом -с/б.

 

 

 

Таким образом, учитывая уравнение y = a sin (bx +c) верно следующее:

 

• Изменения в значении переменной a влияет на высоту график синуса.

 

• Изменения в значении переменной b эффекты период графика.

 

• Изменения в значении переменной c в в сочетании со значением переменной b вместе влияет на фаза сдвиг граф.

 

 

 

Вернуться на главную страницу Robins

 

Функция синуса

Тригонометрическая функция синуса тесно связана с греческой функцией аккорда (если вы не знакомы с функцией аккорда, вы можете прочитать страницу, озаглавленную «Аккорды»). На самом деле функция синуса, иногда известная как функция полухорды , имеет такую ​​же связь с радиусом окружности, как функция хорды имеет диаметр окружности. Первое появление функции синуса (в отличие от функции аккорда) появляется в Surya Siddhanta (слово Siddhanta означает доктрина или традиция ), иногда описываемая как учебник индуистской астрономии и, вероятно, самый известный из ряда сиддхант. О точном происхождении этих сочинений можно только догадываться. Считается, что на Сурья-сиддханту повлияли труды греческих астрономов, санскритские переводы которых были доступны в Индии к третьему веку нашей эры, хотя они могли быть намного старше.

Свойства функции синуса (или полукорда ) были наверняка известны индийскому математику и астроному Арьябхате . Его знаменитая работа под названием « Арьябхатива » содержала собрание учений, содержащихся в различных сиддхантах. Эта работа, написанная примерно в конце пятого века нашей эры, включала определение синуса как отношения между половиной хорды и половиной центрального угла, образуемого хордой. Он также включал таблицы значений синуса из ноль градусов (0°) до девяносто градусов (90°) с двадцатью четырьмя шагами по три с четвертью градуса (3,75°). Считается, что они являются старейшими сохранившимися примерами таблиц синусов и имеют точность до четырех знаков после запятой. Связь между полухордой и центральным углом 90 290 θ 90 291, который она стягивает, показана ниже.




Угол θ — это центральный угол, опирающийся на полухорду 9029. 0 г. н.э.




Как видно из диаграммы, полухорда AD является одной стороной прямоугольного треугольника ADC. Другой отрезок представляет собой отрезок CD , который является серединным перпендикуляром хорды AB . Гипотенуза AC прямоугольного треугольника является радиусом окружности. Здесь мы использовали окружность единиц (т. е. окружность с радиусом одна единица ), что означает, что по определению полухорда AD равно синусу угла θ . Для окружности произвольного радиуса r длина полухорды н.э. будет равна sin ( θ  )  r . Связь между хордовой функцией и синусоидальной функцией задается уравнением:

crd ( α )  =  2 sin (	α	)  =  2 sin ( θ  )
	2

где α — центральный угол, опирающийся на хорду. Точно так же, как хордовая функция, используемая греческими астрономами и математиками, связана со свойствами прямоугольного треугольника, вписанного в полуокружность 90 290 , функция синуса, которой отдают предпочтение индийские ученые, полностью описывает свойства прямоугольного треугольника в квадрант .

В течение следующих нескольких столетий индийские ученые продолжали развивать свои знания в области тригонометрии, составляя таблицы синусов с точностью до двенадцати знаков после запятой. Однако к восьмому веку нашей эры большая часть астрономических и математических знаний греков, китайцев и индийцев была переведена на арабский язык. Исламские ученые ассимилировали и расширили эти накопленные знания, и к десятому веку н.э. тригонометрия стала самостоятельным разделом математики и составила всеобъемлющие и точные тригонометрические таблицы, в том числе таблицы значений синусов. Хотя исламское влияние начало ослабевать к двенадцатому веку нашей эры, многие труды исламских ученых попали в Европу, в основном через Пиренейский полуостров, который оставался под властью мавров до пятнадцатого века нашей эры.

Синус на санскрите звучит как джия , что означает тетива . Считается, что арабские ученые использовали слово jiba , которое на самом деле бессмысленно на арабском языке, а затем позже перевели (или, возможно, неправильно) слово как jaib , что на арабском языке означает раз . Европейские ученые перевели арабское слово на латынь как sinus (что также означает fold ), откуда мы получили англизированное слово 9.0290 синус . Более значительным вкладом европейских ученых стала разработка представления функции синуса в виде суммы бесконечного числа членов (иногда называемого бесконечным рядом ). Не вдаваясь в подробности, мы просто рассмотрим один пример такого представления, который дает синус угла x (выраженный в радианах) как:

sin ( x )  =   x —

x 3

+

x 5

—

x 7 9

X 7

x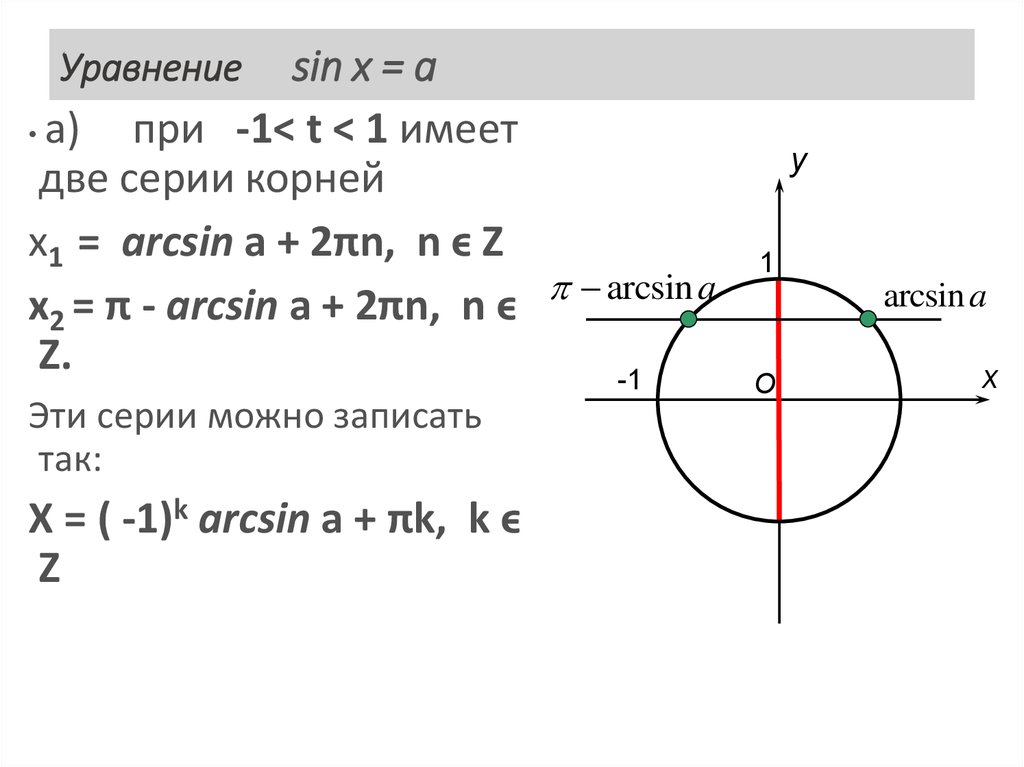

.

5!

7!

Очевидно, что нецелесообразно или даже невозможно выполнять вычисления с использованием бесконечного числа терминов. Количество фактически используемых терминов будет зависеть от степени точности, необходимой для значения синуса.

Еще одна разработка, приписываемая европейским ученым, — это определение тригонометрических функций только с точки зрения прямоугольного треугольника, а не с точки зрения прямоугольного треугольника, вписанного в полукруг или квадрант. Ниже показано, как функция синуса относится к прямоугольному треугольнику. В любом прямоугольном треугольнике один из внутренних углов всегда будет девяносто градусов (90°). Так как сумма внутренних углов любого треугольника всегда равна сто восемьдесят градусов (180°), два других внутренних угла должны быть равны острым углам (т.е. меньше девяноста градусов). Сторона, противоположная прямому углу, всегда является самой длинной стороной и называется гипотенузой .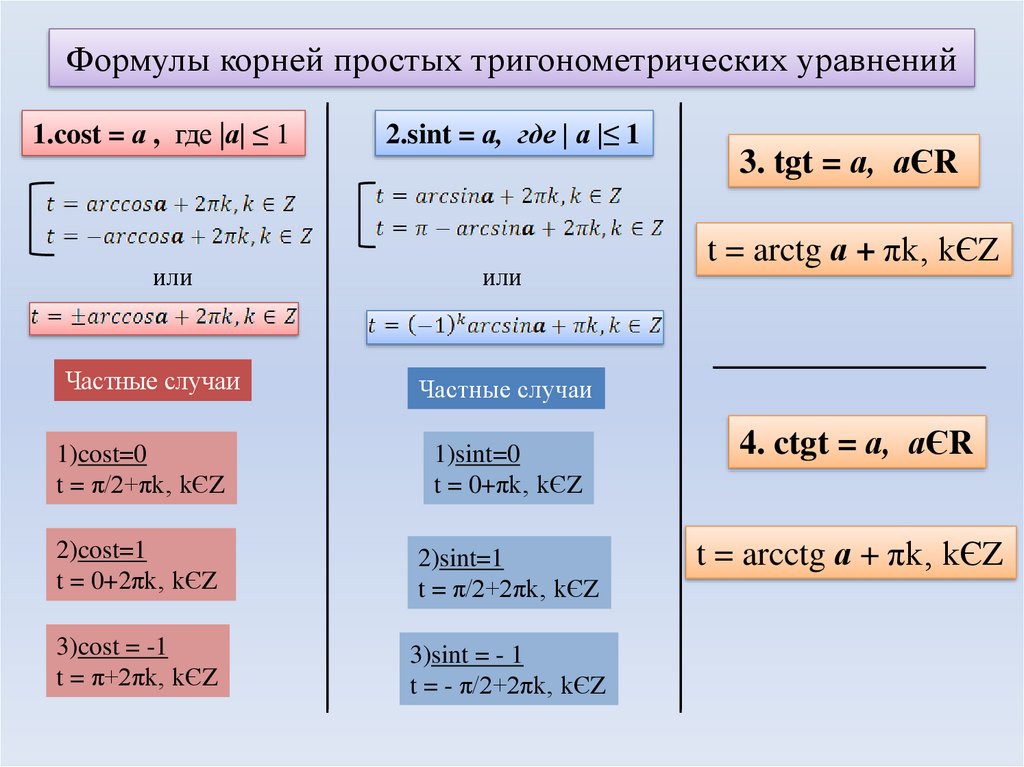 По отношению к любому из острых углов сторона, противоположная углу, называется 90 290, противоположной 90 291. Оставшаяся сторона (сторона, общая как для интересующего нас угла, так и для прямого угла) называется рядом .




В треугольнике ABC sin ( θ  ) = a/c




В треугольнике ABC нас интересует угол θ . Мы использовали условное обозначение каждой вершины символом верхнего регистра, а сторону напротив каждой вершины соответствующим символом нижнего регистра. Сторона напротив относительно угла θ является стороной a . рядом с — это сторона b , а гипотенуза — это сторона c . Синус угла прямоугольного треугольника определяется как частное длин противоположной стороны и гипотенузы. Таким образом, в треугольнике ABC синус угла θ задается как:


На иллюстрации ниже, используя тот же прямоугольный треугольник, мы показываем часть окружности с центром в точке А и радиусом р = с . Мы продлили отрезок BC до точки D на периметре окружности, так что отрезок BD стал хордой окружности. По отношению к треугольнику ABC сторона a ( напротив ) становится полукордом стягивающим углом θ . Сторона b (, примыкающая к ) становится серединным перпендикуляром хорды , а угол θ составляет половину центрального угла, стягиваемого хордой. Мы включили эту диаграмму, чтобы подчеркнуть взаимосвязь между прямоугольными треугольниками и окружностями.



Угол θ составляет половину центрального угла, опирающегося на хорду BD .




Надеюсь, вы понимаете, что, несмотря на то, что тригонометрию часто называют разделом математики, изучающим отношения между сторонами и углами треугольников , она также жизненно важна для изучения окружностей и циклических явлений . Заметим, кстати, что если бы нас интересовал синус угла ABC сторона b была бы противоположной, а сторона a соседней. Круг был бы того же размера (то есть радиус r = c ), но на этот раз точка B была бы центром круга, а окружность проходила бы через точку A.

На данный момент, хотя на данный момент нас действительно интересует только функция синуса, стоит упомянуть, что каждая из трех основных тригонометрических функций ( синус , косинус и тангенс ) описывает отношение двух сторон прямоугольного треугольника по отношению к одному его острых углов. Определения функций синуса, косинуса и тангенса по отношению к прямоугольным треугольникам очень просты. Проблема для многих изучающих тригонометрию, по-видимому, заключается в запоминании каких двух сторон прямоугольного треугольника, используемых для вычисления каждой из тригонометрических функций для рассматриваемого угла. Англоговорящие студенты часто используют относительно легко запоминающуюся мнемонику SOH-CAH-TOA , который должен напоминать им, что:

S ine  =   O pposite over H ypotenuse

C osine  =   A djacent over H ypotenuse

T angent  =   O pposite over A djacent

В те дни, когда я ходил в школу, у нас не было калькуляторов. Нахождение синуса угла (или угла, соответствующего заданному значению синуса) требовало использования тригонометрических таблиц, и я должен признаться, что использование таких таблиц оказалось чем-то, к чему у меня не было абсолютно никаких способностей, хотя они кажутся совершенно прямо для меня сейчас. Я также смутно помню короткий период, в течение которого я изо всех сил пытался понять тайны логарифмической линейки, которая якобы несколько облегчала использование тригонометрических функций. Сегодня, к счастью, у нас есть сложные калькуляторы, которые могут мгновенно найти синус угла (или, наоборот, угол, соответствующий значению синуса), если, конечно, вы знаете, как пользоваться калькулятором. Использование Microsoft Excel , мы составили собственную таблицу синусов для углов от ноль градусов (0°) до триста шестьдесят градусов (360°) с шагом в одну десятую градуса. Чтобы увидеть таблицу, нажмите здесь .

Нахождение синуса угла с помощью встроенного калькулятора, предусмотренного в Microsoft Windows , относительно просто. Предположим, мы хотим найти синус угла пятьдесят градусов (50°). На приведенном ниже снимке экрана показана научная версия встроенного калькулятора Microsoft Windows. Вы можете найти это, нажав кнопку «Пуск» в Windows 7 и выбрав «Все программы»> «Стандартные»> «Калькулятор» (в других версиях Windows может потребоваться другая последовательность нажатий клавиш). Научную версию калькулятора можно выбрать в меню приложения View .




Встроенный калькулятор Microsoft Windows




Чтобы найти синус пятидесяти градусов с помощью калькулятора Windows (если он у вас есть, в противном случае используйте любой доступный калькулятор), введите следующие нажатия клавиш:




Введите эти нажатия клавиш, чтобы найти синус пятидесяти градусов




Убедитесь, кстати, что у вас установлен режим калькулятора градусов (если только вы не планируете вводить значение угла в радианах или градах). Если вы правильно ввели нажатия клавиш, вы должны увидеть следующий экран:




Калькулятор отображает значение sin (50°)




Предположим, что вы хотите найти размер острого угла в прямоугольном треугольнике, сначала найдя частное противоположного угла и гипотенузы (т.е. синус угла ). Если у вас есть значения длин сторон треугольника, вы можете достаточно легко найти значение синуса угла. Нахождение угла — это просто случай применения к результату функции арксинуса (обратной функции синуса). Найдем значение угла θ для прямоугольного треугольника, показанного ниже.




Мы хотим найти величину угла θ




Для угла θ стороны a и c являются противоположностью и гипотенузой соответственно. На самом деле мы можем найти размер угла за одну операцию на калькуляторе Windows. Мы делаем это, используя скобки во введенной последовательности клавиш, чтобы заставить калькулятор сначала найти частное противоположного и гипотенузы (т. е. синуса угла). Затем мы применяем арксинус (обратная функция синуса) к результату. Вот последовательность клавиш для использования:




Введите эти нажатия клавиш, чтобы найти размер угла θ




Если вы правильно ввели комбинации клавиш, вы должны увидеть следующий экран:




Калькулятор отображает значение угла θ




Возможно, вас интересовало значение синуса для угла, превышающего девяносто градусов (90°). Чтобы увидеть интерактивную демонстрацию того, как значения синуса изменяются по мере того, как центральный угол, образуемый полухордой, превышает девяносто градусов, щелкните здесь (примечание: ваш браузер должен поддерживать Java, чтобы интерактивная страница работала). Здесь интересно отметить, что когда угол поворота увеличивается за пределы 90 градусов, полухорда перемещается в новый квадрант. центральный угол опирается на полухорду, поэтому фактически снова начинает уменьшаться. Приведенная ниже серия снимков экрана дополнительно иллюстрирует это положение (для ясности мы добавили к снимкам экрана числа квадранта ). В демонстрации используется модуль Unit Circle . Это окружность, центр которой (обозначенный здесь как точка O) находится в начале декартовой системы координат. Круг имеет радиус в одну единицу, поэтому длина полухорды в любой точке равна (абсолютному) значению синуса центрального угла, стягиваемого полухордой.




Полуаккорд в квадранте I





Полуаккорд в квадранте II





Полуаккорд в квадранте III





Полуаккорд в квадранте IV




Угол поворота в первом квадранте составляет 90 290 сорок пять градусов 90 291 (45 °) и, следовательно, равен углу, образуемому полухордой. На втором скриншоте мы увеличили угол поворота на девяносто градусов до сто тридцать пять градусов (135°). Полухорда теперь находится во втором квадранте, но центральный угол, стягиваемый полухордой, снова равен сорока пяти градусам. То же самое мы видим в третьем и четвертом квадрантах. Угол поворота продолжает увеличиваться по мере того, как мы перемещаем точку P против часовой стрелки по окружности круга, но центральный угол, образуемый полухордой в каждом квадранте, никогда не превышает девяноста градусов.

Это поднимает интересный вопрос как о определение функции синуса и ее знак по отношению к единичной окружности. И функция синуса, и функция косинуса могут быть определены в терминах точки, лежащей на окружности единичного круга. Эта точка — это точка, в которой полухорда касается окружности единичного круга (точка P на диаграммах, показанных выше). Угол θ , которому соответствует синус, представляет собой угол между положительной осью x и точкой соединения радиуса P и центром окружности O, измеренный против часовой стрелки . Синус этого угла определяется как y -координата точки P. Мы можем выразить это просто как:

sin ( θ  )  =   y

Таким образом, по определению синусоидальная функция имеет значения в диапазоне от до минус один (от 1 до -1). В первых двух квадрантах (два квадранта над осью x ) эти значения всегда будут между нулем и единицей, поскольку y всегда будет больше или равно нулю. В третьем и четвертом квадрантах (два квадранта ниже по оси x ) значения всегда будут между нулем и минус один , поскольку y всегда будет равно или меньше нуля . . Синусы углов ноль градусов (0°), девяносто градусов (90°), сто восемьдесят градусов (180°) и двести семьдесят градусов (270°) будут равны ноль (0), единица (1), ноль (0) и минус единица (-1) соответственно.

Функция синуса часто используется в различных научных, инженерных и даже деловых приложениях для моделирования поведения циклических явлений. Синусоида (один полный цикл которой показан ниже) используется для представления плавных повторяющихся колебаний.




Один цикл синусоиды




Синусоида — это, по сути, график того, как значение y изменяется во времени. Цикл начинается под углом θ из ноль градусов (0°), в этой точке как sin( θ  ), так и y равны нулю. Угол θ плавно увеличивается в положительном направлении, пока не достигнет девяносто градусов (90°), в этой точке sin( θ  ) равен 1 (1), а y имеет максимальное положительное значение. По мере увеличения угла от девяноста градусов до сто восемьдесят градусов (180°), оба sin( θ  ) и y вернутся к нулю. Как только угол превышает сто восемьдесят градусов, sin( θ  ) и y становятся отрицательными. При двести семьдесят градусов (270°) sin( θ  ) равен минус один (-1), а y имеет максимальное отрицательное значение. По мере увеличения угла от двухсот семидесяти градусов до трехсот шестидесяти градусов (360°), оба sin( θ  ) и y вернутся к нулю. Простая анимация ниже иллюстрирует, как это работает.




Синусоидальная анимация




Обратите внимание, что хотя угол в триста шестьдесят градусов отмечает конец одного полного цикла, его положение на синусоиде также можно определить как начальную точку для следующего полного цикла (т. е. ноль градусов ). Синусоидальные волны могут описывать многочисленные виды циклических явлений, таких как звуковые или электромагнитные волны, движение маятника или вращение колеса. В своей основной форме синусоида представляет собой функцию времени, которая описывается формулой:

y ( t )  =   A   ·  sin ( ωt + φ )

куда:

A   =  the amplitude of the function (the maximum absolute value of y )

ω   =  the angular frequency (usually measured in in radians per second )

t   =  the истекшее время

φ   =  фаза , то есть угол (в радианах), когда t  = 0

Электропитание, которое входит в ваш дом, является хорошим примером синусоиды.

No related posts.

Добавить комментарий Отменить ответ

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Комментарий *

Имя *

Email *

Сайт

sin ( θ  )  =	a
	c