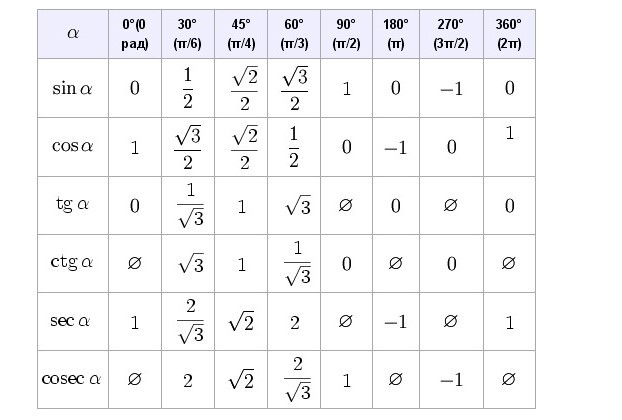
2+n-72)=1/(n+9)sine of pi/2 — Translation into Russian — examples English
Premium History Favourites
Advertising
Download for Windows It’s free
Download our free app
Advertising
Advertising
No ads with Premium
English
Arabic German English Spanish French Hebrew Italian Japanese Dutch Polish Portuguese Romanian Russian Swedish Turkish Ukrainian Chinese
Russian
Synonyms Arabic German English Spanish French Hebrew Italian Japanese Dutch Polish Portuguese Romanian Russian Swedish Turkish Ukrainian Chinese Ukrainian
These examples may contain rude words based on your search.
These examples may contain colloquial words based on your search.
sine
синус sine синусоидальной синусоидальную синусоидальные
returns 1, the sine of PI/2 radians.
возвращает значение 1, т.е. синус пи/2 радиан.
Plus sine of pi/2, for the same reason, we’re pointing straight up on the unit circle, so the y-coordinate, or the sine coordinate, is 1, right on the unit — is essentially at the point 0, 1 on the unit circle.
Плюс sin π/2, где таким же образом мы укажем прямо вверх на единичной окружности, потому y-координата, или координата синуса, равна 1, по сути — это в точке (0,1) на единичной окружности.
This could have been 90 degrees instead, if we wanted to be in degrees.
Это было бы 90º, если бы нам захотелось выражать в градусах… sin π/2 cos a), правильно?
Other results
So we know that — so let’s see, if we have sine — what’s sine of a plus pi/2? a plus pi/2.
Посмотрим, если у нас есть синус — чему равен sin (а + π/2)? а + π/2.
It’s also interesting to sometimes actually draw the graph on the x-y plane of, say, you know, cosine of x plus pi/2, or sine of x plus pi/2, or sine of x.
Также интересно иногда построить графики в плоскости х-у, допустим, cos (x+ π/2), или sin (x+π/2), или sin x.
In general, cosine of x is actually sine of x shifted to the left by pi/2.
Вообще, cos х — это sin х, смещенный влево на π/2.
And another way to rewrite this exact same thing is the sine of a is equal to the cosine of a minus pi/2, right?
А другой способ переписать точно такое же равенство: sin a = cos (а — π/2), правильно?
So we know that A sine of beta is equal to x, which is also equal to B sine of beta — sorry, B sine of alpha.
Итак, мы знаем, что А
And so if where it intersects the unit circle is at 1 comma 0, then sine of theta is just the sine of theta is 0.
Поэтому если координаты точки, в которой радиус пересекает единичную окружность — (1,0), то sinθ равен Y-координате, т.е. sinθ=0.
And that minus will cancel that out, so it’ll be plus sine of a times the sine of b.
И эти два минуса сокращаются, поэтому здесь будет плюс sin a*sin b.
And I want you to sit and think about why sine of 2x has 1/2 the period of sine of x.
И я хочу, чтоб вы сели и подумали о том, почему синус 2х имеет половину периода синуса х.
So this is sine of beta.
Значит, sinβ — это ВЕ/АВ…
In the last problem we said sine of 0 is 0 and cosine of 0 is 1.
В предыдущей задаче мы говорили, что sin0=0, а cos0=1. f(0) для этой функции, какой бы она ни была — это 0.
So sine of theta is equal to 0.625.
Итак, синус тетта равняется 0,625.
So its speed in the vertical direction is s
Итак, скорость в вертикальном направлении равна произведению s на синус тета.
Let’s see if we can do anything with the sine of 2a.
Посмотрим, можем ли мы что-нибудь сделать с sin2а. Выберу новый цвет, который еще не использовал.
So sine of 2a is equal to that.
Итак, sin2а равен вот этому.
So we know that it is sine of 4x.
Мы знаем, что это sin4х.
And Archimedes’ theorem on broken chords is equivalent to formulas for sines of sums and differences of angles.
Теорема Архимеда для деления хорд эквивалентна формулам для синусов суммы и разности углов.
Most computers only perform basic arithmetic operations and cannot directly calculate the sine of a given value.
Большинство компьютеров поддерживают только основные арифметические операции и не могут вычислить значение синуса напрямую.
Possibly inappropriate content
Examples are used only to help you translate the word or expression searched in various contexts.
They are not selected or validated by us and can contain inappropriate terms or ideas. Please report examples to be edited or not to be displayed. Rude or colloquial translations are usually marked in red or orange.
Register to see more examples It’s simple and it’s free
Register Connect
No results found for this meaning.More features with our free app
Voice and photo translation, offline features, synonyms, conjugation, learning games
Results: 181. Exact: 3. Elapsed time: 158 ms.
Documents Corporate solutions Conjugation Synonyms Grammar Check Help & aboutWord index: 1-300, 301-600, 601-900
Expression index: 1-400, 401-800, 801-1200
Phrase index: 1-400, 401-800, 801-1200
3
Функция обратного синуса — формула, производная и решение Пример
Функция обратного синуса — это одна из обратных тригонометрических функций, которая определяет обратную функцию синуса и обозначается как sin -1 или арксинус.
Например: Если значение синуса 90 градусов равно 1, то значение обратного sin 1 или sin -1 (1) будет равно 90°. Каждая тригонометрическая функция, такая как косинус, тангенс, косеканс, котангенс, имеет свою обратную в ограниченной области. Формулы обратной функции используются для расчета измерения углов с помощью тригонометрических соотношений из прямоугольного треугольника. Обычно функция, обратная синусу, представляется как sin -1 . Он не утверждает, что синус нельзя возводить в отрицательную степень.
Вы можете легко вывести формулу обратной функции синуса. Студенты также могут вычислить обратную тригонометрическую функцию с помощью калькуляторов. Вы можете легко найти обратную функцию, если знаете шесть основных тригонометрических функций. В этой статье вы узнаете, что такое обратный синус, функция обратного синуса, график обратного синуса, вывод обратного синуса, примеры обратного синуса, формулы обратного синуса и т. Д.
Функция обратного синуса
Чтобы четко понять концепцию функции обратного синуса, мы должны сначала узнать о функции синуса.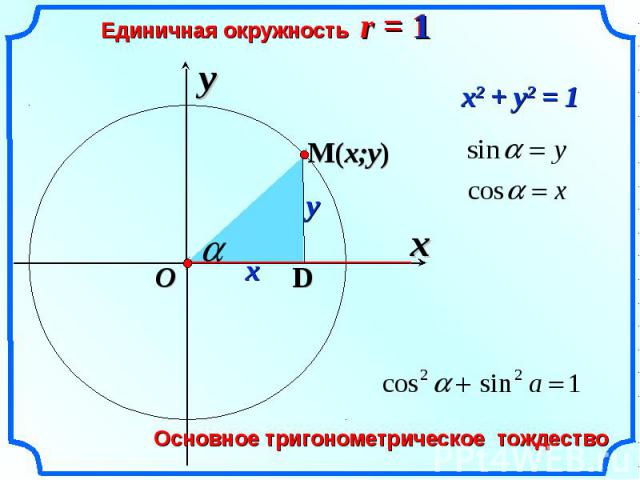
Функция синуса. Функция синуса угла ϴ в прямоугольном треугольнике определяется как отношение противоположной стороны угла ϴ к стороне гипотенузы.
Sin\[\theta = \frac{\text{Противоположная сторона}}{\text{Сторона гипотенузы}}\]
Обратная функция sin или sin -1 , также известная как arcsin или asine, дает угол ϴ, если он принимает соотношение \[\frac{\text{Противоположная сторона}}{\text{Сторона гипотенузы}}\]
Обратный синус представлен sin -1 или arcsin.
Sin Обратный пример
В треугольнике PQR, PQ = 4,9 см, QR = 4,0 см, PR = 2,8 см и угол Q = 35°
(изображение скоро будет загружено)
Решение: Sin 35° = \ [\frac{\text{Противоположная сторона}}{\text{Сторона гипотенузы}}\]
Sin 35° = \[\frac{2.8}{4.9}\]
Sin 35° = 0,57
Итак, sin -1 \[\frac{\text{Противоположная сторона}}{\text{Сторона гипотенузы}}\] = 35°
Sin -1 (0,57)= 35°
Давайте разберемся с формулой обратного синуса на примере: , и даны следующие две спецификации:
Функция синуса помогает вам рассчитать расстояние или глубину корабля от глубокого морского дна с помощью следующего метода.
Если длина троса равна 40 м, а угол равен 39°, то
(Изображение будет загружено в ближайшее время)
Sin 39° = \[\frac{\text{Противоположная сторона}}{\text{Сторона гипотенузы}}\]
Sin 39° = \[\frac{d} {40}\]
Глубина (d) = Sin 39° x 40
Глубина (d) = 0,6293 x 40
Глубина (d) = 25,172
Следовательно, глубина морского дна составляет 25,17 см.
Тригонометрическая функция синуса и формула, обратная синусу Сводка
Формула для тригонометрической функции синуса для угла ϴ записывается как
Sin\[\theta = \frac{\text{Противоположная сторона}}{\text{Гипотенуза}} \] 9{-1}\] = \[\frac{\text{Противоположная сторона}}{\text{Сторона гипотенузы}}\] = \[\theta\]
График арксинуса
Функция арксинуса, также известная как функция, обратная синусу, представлена как sin⁻¹ x.
Это представлено на графике, как показано ниже: (изображение будет загружено в ближайшее время)
Производная обратного синуса
Представим функцию в виде ϴ = sin⁻¹ k. Мы будем использовать неявное дифференцирование для вычисления производной этой функции.
Исключение обратной функции
ϴ = sin⁻¹ k → sin ϴ = k
Новая функция будет записана в виде k = sin ϴ
Где область определения ϴ ограничена диапазоном главных значений, которые sin⁻¹ функция может выбрать.
Продифференцируем обе части уравнения по ϴ
\[\frac{dk}{d\theta }=\frac{d}{\theta}\left ( sin\theta \right )\]
\ [\frac{dk}{d\theta }=\left ( cos \theta \right )\]
Из тригонометрического тождества sin²ϴ + cos²ϴ = 1 получаем, 9{2} }\]
Через обратные производные мы получаем
\[\frac{dk}{d\theta }=\frac{1}{\frac{dk}{d\theta }}\]
Здесь вы можете увидеть значения обратного синуса в виде таблицы.
Обратное значение синусации Таблица
ө | SIN⁻⁻ ө | SIN⁻⁻⁻ ө ө | . — \[\frac{\pi }{2}\] | -90° | ||||||||||||||||||||||
— \[\frac{\sqrt{3}}{2}\] | — \[\frac{\pi} {3}\]
Производная от Sin, обратная x w. r.t. Cos Inverse √(1- x²)Существует еще один способ проверки производной sin, обратной x. Теперь мы вычислили производную от sin, обратную x, как 1/√(1- x²), где -1 < x < 1. Теперь мы приступим к дифференцированию sin⁻¹ x относительно другой функции. Эта функция равна cos-1√(1-x²). Чтобы продолжить наши расчеты, предположим, что cos-1√(1-x²) равен некоторой переменной, например z. Предположим, что y = sin-1x Отсюда следует, что sin y = x Используя cos² θ + sin² θ = 1, мы теперь имеем cos θ = √(1 — sin² θ) Это означает, что cos y = √ (1 — sin² y) = √(1- x²) После дифференцирования sin y = x по x мы получим cos y (dy/dx) = 1 ⇒ dy/dx = 1/cos у ⇒ dy/dx = 1/√(1-x²). Пусть это будет уравнение 1. Теперь предположим, что z = cos-1√(1- x²) ⇒ sin z = x и cos z = √(1-x²) Теперь, дифференцируя cos z = √(1- x² ) в. ⇒ -x(dz/dx) = -x/√(1-x²) ⇒ dz/dx = 1/√(1-x²) ⇒ dx/dz = √(1-x²). Пусть это будет уравнение 2. Теперь, чтобы определить значение d(sin⁻¹ x)/d(cos⁻¹ √(1- x²)) = dy/dz, Мы видим, что dy/ dz = dy/dx × dx/dz = [1/√(1-x²)] × √(1-x²) = 1 Таким образом, производная sin, обратная x, относительно cos, обратная √(1 — x²) равно 1. Доказательство производной sin, обратной xТеперь мы знаем, что производная sin, обратная x, равна 1/√(1 — x²), где x лежит между -1 и 1. Эта производная sin, обратная x можно легко получить, используя некоторые формулы дифференцирования. Давайте посмотрим, как именно мы можем достичь этого вывода. Мы знаем, cos 2 θ + sin 2 θ= 1, Цепное правило утверждает, что (f(g(x)))’ = f'(g(x)).g'(x ) Таким образом, d(sin x)/dx = cos x Предположим, что y = sin⁻¹ x ⇒ sin y = x Дифференцируя обе части sin y = x по x, мы получаем cos y dy/dx = 1 Отсюда следует, что dy/dx = 1/cos y ⇒ dy/dx = 1/√(1 — sin² y) (использование cos² θ + sin² θ равно 1) ⇒ dy /dx = 1/√(1 — x²) (поскольку sin y равен x) ⇒ d(sin⁻¹ x)/dx = 1/√(1 — x²) Следовательно, d(sin⁻¹ x)/dx = 1/√(1 — x²). |
р.т. x, имеем -sin z (dz/dx) = -2x/2√(1- x²)