Уравнений решений: Решение уравнений с дробями онлайн · Как пользоваться Контрольная Работа РУ

18. Нахождение решений общей системы уравнений.

Пусть дана неоднородная система m линейных уравнений с n неизвестными

Предположим, что система совместна, т.е. r(A)==r. Следовательно, существует минор порядка rматрицы А, отличный от нуля. Предположим, что он расположен в левом верхнем углу матрицы. Если это не так, то можно переставить уравнения и перенумеровать неизвестные.

.

Первые r уравнений системы линейно независимы. Остальные выражаются через них. Следовательно, их можно отбросить.

Определение 1. Переменные, коэффициенты при которых образуют минор, отличный от нуля (базисный минор), называются базисными переменными (x₁, x₂, …, x_r). Остальные переменные x_r+1, …, x_n называются свободными.

Дадим свободным переменным произвольные числовые значения 

x_r+1=с_r+1, x_r+2=с_r+2, …, x_n=c_n.

Запишем систему в виде

Мы получили систему из r линейных уравнений с r неизвестными, определитель которой отличен от нуля. Она имеет единственное решение.

 — общее решение.

Определение 2. Выражение базисных переменных через свободные называется общим решением системы.

Определение 3. Решение системы, полученное из общего при конкретных значениях свободных переменных, называется частным решением. Частных решений у системы бесконечно много, все они содержатся в общем решении.

Определение 4. Частное решение, полученное из общего, когда свободные переменные равны нулю, называется базисным решением системы.

Определение 5. Базисное решение, координаты которого неотрицательны, называется опорным решением системы.

19. Метод Гаусса. Нахождение опорных решений

 

Определение 1.  Элементарными преобразованиями системы называются:

1)     умножение уравнения на число, отличное от нуля;

2)     прибавление к одному уравнению другого уравнения, умноженного на некоторое число, отличное от нуля.

3)     перестановка двух уравнений;

4)     отбрасывание уравнения 0=0.

Если получено уравнение 0=k, то система несовместна.

Метод Гаусса состоит в приведении системы к диагональному виду путем последовательного исключения неизвестных. Количество исключенных неизвестных равно числу линейно независимых уравнений. Переменная считается исключенной, если она содержится только в одном уравнении с коэффициентом 1.

Метод Гаусса удобно применять к расширенной матрице системы, левую часть которой с помощью элементарных преобразований матрицы нужно привести к единичной матрице.

20. Совместность однородной системы.

Рассмотрим однородную систему

.

Однородная система всегда совместна, так как всегда имеет тривиальное (нулевое) решение . Выясним, когда данная система имеет нетривиальное решение.

Теорема 1. Однородная система имеет нетривиальное решение тогда и только тогда, когда ранг матрицы, составленной из коэффициентов при неизвестных, меньше числа неизвестных.

Доказательство. Пусть система совместна. Это может быть тогда и только тогда, когда найдутся числа с₁, с₂, …, с_n, при подстановке которых в систему мы получим m тождеств. Эти 

m тождеств можно записать в виде

.

Следовательно, система векторов-столбцов матрицы А линейно зависима. А это может быть тогда и только тогда, когда ранг системы векторов-столбцов меньше n, т.е. r(A)<n.

Следствие.  Квадратная однородная система имеет нетривиальное решение тогда и только тогда, когда определитель матрицы, составленной из коэффициентов при неизвестных, равен нулю.

Доказательство. Так как r(A)<n, то столбцы матрицы линейно зависимы и, следовательно, определитель матрицы равен нулю.

Число решений системы двух линейных уравнений с двумя переменными

Репетиторы ❯ Математика ❯ Число решений системы двух линейных уравнений с двумя переменными

Автор: Владимир Л., онлайн репетитор по математике

●

23.10.2011

●

Раздел: Математика

Предположим, требуется найти все пары значений переменных х и у, которые удовлетворяют уравнение
ху – 6 = 0 и уравнение у – х – 1 = 0, то есть необходимо найти пересечение множеств решений этих уравнений. В таких случаях говорят, что надо решить систему уравнений ху – 6 = 0 и у – х – 1 = 0.

Систему уравнений принято записывать с помощью фигурной скобки. Например, рассматриваемую систему уравнений можно записать так:

{ху – 6 = 0,
{у – х – 1 = 0.

Пара значений переменных, обращающая в истинное равенство каждое уравнение системы, называется решением системы уравнений с двумя переменными.

Решить систему уравнений – значит найти множество её решений.

Рассмотрим системы двух линейных уравнений с двумя переменными, в которых в каждом уравнении хотя бы один из коэффициентов отличен от нуля.

Графическое решение систем такого вида сводится к отысканию координат общих точек двух прямых.

Как известно, две прямые на плоскости могут быть пересекающимися или параллельными. В случае параллельности прямые либо не имеют общих точек, либо совпадают.

Рассмотрим каждый из этих случаев.

Пример 1.

Решим систему уравнений:

{2х + у = -11,
{х – 2у = 8.

Решение.

Выразив из каждого уравнения у через х, получим систему:

{у = -3х – 11,
{у  = 0,5х – 4.

Угловые коэффициенты прямых – графиков уравнений системы различны (-3 и 0,5), значит, прямые пересекаются.

Координаты точки их пересечения являются решением этой системы, единственным решением.

Пример 2.

Решим систему уравнений:

{3х – 2у = 12,
{6х – 4у = 11.

Решение.

Выразив из каждого уравнения у через х, получим систему:

{у = 1,5х – 6,
{у = 1,5х – 2,75.

Прямые  у = 1,5х – 6 и у = 1,5х – 2,75 имеют равные угловые коэффициенты, значит эти прямые параллельны, причём прямая  у = 1,5х – 6 пересекает ось у в точке (0; -6), а прямая у = 1,5х – 2,75 – в точке (0; -2,75), следовательно, прямые не имеют общих точек. Поэтому система уравнений не имеет решений.

В том, что данная система не имеет решений можно убедиться рассуждая следующим образом.

Умножив все члены первого уравнения на 2, получим уравнение 6х – 4у = 24.

Сравнивая это уравнение со втором уравнением системы, видим, что левые части уравнений одинаковы, поэтому при тех же значениях х и у они не могут принимать различных значений (24 и 11). Следовательно, система

{6х – 4у = 24,
{6х – 4у = 11.

не имеет решений, значит, не имеет решений и система

{3х – 2у = 12,
{6х – 4у = 11.

Пример 3.

Решим систему уравнений:

{5х – 7у = 16,
{20х – 28у = 64.

Решение.

Разделив каждый член второго уравнения на 4, получим систему:

{5х – 7у = 16,
{5х – 7у = 16,

состоящую из двух одинаковых уравнений. Графики этих уравнений совпадают, поэтому координаты любой точки графика будут удовлетворять каждому из уравнений системы, то есть являться решением системы. Значит, данная система имеет бесконечное множество решений.

Если в каждом уравнении системы двух линейных уравнений с двумя переменными хотя бы один из коэффициентов при переменной не равен нулю, то система либо имеет единственное решение, либо имеет бесконечно много решений.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Задать вопрос

Математика

Курсы по математике 10 класс

Математика

Курсы по математике 9 класс

Математика

Математика 11 класс

Математика

Курсы по геометрии 7 класс

Математика

Курсы по алгебре 7 класс

Математика

Алгебра 8 класс

Математика

Курсы по геометрии 8 класс

Французский язык

Курсы французского языка для начинающих

Решение уравнения | Encyclopedia.

com

Методы решения простых уравнений

Решение более сложных уравнений

Решение уравнений с несколькими переменными

Решение уравнений второй степени и выше

Ресурсы

Решением уравнения является множество всех значений, которые при подстановке неизвестных, сделайте уравнение верным. Для уравнений с одним неизвестным, возведенным в одну степень, для определения его решений используются два основных правила алгебры, в том числе свойство аддитивности и свойство мультипликативности. Решения для уравнений с несколькими неизвестными переменными находятся с использованием принципов системы уравнений. Уравнения с членами, возведенными в степень большую, могут быть решены с помощью факторизации, а в некоторых частных случаях — с помощью квадратного уравнения.

Идея решения уравнений существовала еще со времен древних египтян и вавилонян. В то время они использовали простые алгебраические методы для решения практических проблем, связанных с их повседневной жизнью. Методы, использовавшиеся древними, сохранились в трактате, написанном арабским математиком Аль-Коваризми (825 г. н.э.). В эту работу он включает методы решения линейных уравнений, а также уравнений второй степени. Решения некоторых уравнений высших степеней были найдены в шестнадцатом веке итальянским математиком Джероламо Кардано (1501–1576).

Уравнение — это алгебраическое выражение, которое обычно связывает неизвестные переменные с другими переменными или константами. Например, x + 2 = 15 — это уравнение, как и y ² = 4. Решением или корнем уравнения является любое значение или набор значений, которые можно подставить в уравнение, чтобы сделать его верным утверждением. . В первом примере решение для x равно 13. Во втором примере есть два значения, которые сделают утверждение верным, а именно 2 и –2. Эти значения составляют набор решений уравнения.

Используя два фундаментальных правила алгебры, можно получить решения многих простых уравнений. Первое правило гласит, что к обеим частям уравнения можно добавить одну и ту же величину без изменения решения уравнения. Например, уравнение x + 4 = 7 имеет решение x = 3. Согласно первому правилу, можно прибавить любое число к обеим частям уравнения и все равно получить одно и то же решение. При добавлении 4 к обеим частям уравнение становится x + 8 = 11, но решение остается x = 3. Это правило известно как аддитивное свойство равенства. Чтобы использовать это свойство для поиска решения уравнения, все, что требуется, — это выбрать правильное число для добавления. Решение предыдущего примера x + 4 = 7 можно найти, добавив -4 к обеим частям уравнения. Если это сделать, уравнение упрощается до x + 4 – 4 = 7 – 4orx = 3, и уравнение решается.

Второе фундаментальное правило, известное как мультипликативное свойство равенства, гласит, что каждый член в обеих частях уравнения можно умножить или разделить на одно и то же число без изменения решения уравнения. Например, решение уравнения y – 2 = 10 равно y = 12. Используя правило умножения, можно получить эквивалентное уравнение с тем же набором решений, умножив обе части на любое число, например 2. Таким образом, уравнение становится 2y– 4= 20, но решение остается y = 12. Это свойство также можно использовать для решения алгебраических уравнений. В случае уравнения 2x = 14 решение получается путем деления обеих частей на 2. Когда это делается 2x/2 = 14/2, уравнение упрощается до x = 7,9.0003

Часто оба этих правила необходимо использовать для решения одного уравнения, например, уравнения 4x + 7 = 23. В этом уравнении к обеим частям уравнения добавляется -7, и получается 4x = 16. Оба части этого уравнения затем делятся на 4, и оно упрощается до решения, x = 4.

Большинство уравнений дается в более сложной форме, которую можно упростить. Рассмотрим уравнение 4x – x – 5 = 2x + 7. Первым шагом в решении этого уравнения является объединение одинаковых членов с каждой стороны уравнения. В правой части нет одинаковых терминов, но 4x и -x в левой части являются подобными терминами. Это уравнение при упрощении принимает вид 3x – 5 = 2x + 7. Следующий шаг – исключить неизвестное из одной части уравнения. В данном примере это достигается добавлением -2x к обеим частям уравнения, что дает x — 5 = 7. Используя аддитивное свойство, решение получается добавлением 5 к обеим частям уравнения, поэтому x = 12.

Весь процесс решения алгебраических уравнений с одной переменной можно описать следующими шагами. Во-первых, удалите все скобки, умножив множители. Во-вторых, добавьте похожие термины с каждой стороны. В-третьих, исключите неизвестное из одной части уравнения, используя мультипликативные или аддитивные свойства. В-четвертых, исключить постоянный член со стороны неизвестного с помощью аддитивного свойства. Наконец, устраните любой коэффициент при неизвестном, используя мультипликативное свойство.

Многие алгебраические уравнения содержат более одной переменной, поэтому полный набор решений не может быть найден с помощью описанных выше методов. Уравнения с двумя неизвестными называются линейными уравнениями и могут быть представлены общей формулой ax + by = c; где a, b и c — константы, а x и y — переменные. Решением этого типа уравнения будет упорядоченная пара x и y, которая делает уравнение верным. Например, набор решений для уравнения x + y = 7 будет содержать все пары значений x и y, которые удовлетворяют уравнению, такие как (2,5), (3,4), (4,3), и т. д. В общем случае для определения решения линейного уравнения с двумя переменными уравнение переписывается и решается с одной переменной. Тогда решением уравнения x + y = 7 становится любая пара значений, которая делает x = 7 – y верным.

Часто существует несколько линейных уравнений, связывающих две переменные в одной и той же системе. Все уравнения, связанные с переменными, известны как система уравнений, а их решение представляет собой упорядоченную пару, которая делает каждое уравнение верным. Эти уравнения решаются методами построения графиков, замены и исключения.

Уравнения, содержащие неизвестные, возведенные в степень единицы, называются уравнениями первой степени. Существуют также уравнения второй степени, включающие

КЛЮЧЕВЫЕ ТЕРМИНЫ

Аддитивное свойство — Свойство уравнения, в котором указано число, может быть добавлено к обеим частям уравнения, не влияя на его решение.

Факторинг — Метод сведения уравнения более высокой степени к произведению уравнений более низкой степени.

Уравнение первой степени —Алгебраическое выражение, содержащее неизвестное, возведенное в первую степень.

Мультипликативное свойство — Свойство уравнения, состоящее в том, что все члены уравнения могут быть умножены на одно и то же число, не влияя на окончательное решение.

Уравнение второй степени —Алгебраическое выражение, содержащее неизвестное, возведенное во вторую степень.

хотя бы одна переменная, возведенная в квадрат или возведенная в степень двойки. Уравнения также могут быть третьей степени, четвертой степени и так далее. Наиболее известным уравнением второй степени является квадратное уравнение, имеющее общий вид ах ² +bx +c = 0; где a, b и c являются константами, а a не равно 0. Решение для этого типа уравнения часто можно найти с помощью метода, известного как факторинг.

Поскольку квадратное уравнение является произведением двух уравнений первой степени, его можно включить в эти уравнения. Например, произведение двух выражений (x + 2)(x – 3) дает одно с квадратным выражением x ² – x – 6. Два выражения (x + 2) и (x – 3) называются множители квадратного выражения x ² – x – 6. Приравнивая каждый множитель квадратного уравнения к нулю, можно получить решения. В этом квадратном уравнении решения x = –2 и x = 3,

Найти коэффициенты квадратного уравнения не всегда просто. Для решения этой задачи была придумана квадратная формула, позволяющая решить любое квадратное уравнение. Квадратное уравнение формулируется следующим образом для общего уравнения: .

См. также Системы уравнений.

КНИГИ

Биттингер, Марвин Л. и Дэвик Элленбоген. Алгебра среднего уровня: концепции и приложения . 7-е изд. Рединг, Массачусетс: Addison-Wesley Publishing, 2006.

Ларсон, Рон. Предварительный расчет . 7-е изд. Бостон, Массачусетс: Houghton Mifflin, 2007.

Лоренц, Фалько. Алгебра. Нью-Йорк: Springer, 2006.

Сетек, Уильям М. Основы математики . Река Аппер-Сэдл, Нью-Джерси: Pearson Prentice Hall, 2005.

Perry Romanowski

Системы линейных уравнений с одним решением (3 способа сказать) – JDM Educational

При работе с системами линейных уравнений мы часто видим бесконечно много решений или вообще одно. Однако также возможно, что линейная система будет иметь ровно одно решение.

Итак, когда система линейных уравнений имеет одно решение? Система двух линейных уравнений с двумя переменными имеет одно решение, если две линии имеют разные наклоны. С точки зрения алгебры это означает, что при решении системы мы получаем единственное значение. Визуально линии пересекаются на графике ровно один раз, так как имеют разный наклон.

Конечно, система из трех уравнений с тремя переменными имеет одно решение, если существует ровно одна точка, в которой пересекаются все три плоскости.

В этой статье мы поговорим о том, как можно сказать, что система линейных уравнений имеет одно решение. Мы также рассмотрим некоторые примеры линейных систем с одним решением с 2 переменными и с 3 переменными.

Начнем.

Системы линейных уравнений с одним решением

Система линейных уравнений может иметь одно решение, если существует единственная точка, которая делает каждое уравнение в системе верным. Это означает, что существует одна точка, которая может удовлетворять всем уравнениям одновременно.

На изображении ниже показаны 3 возможных случая решения системы из 2 линейных уравнений с 2 ​​переменными.

Система из двух линейных уравнений с двумя переменными имеет одно решение, если две линии имеют разные наклоны.

Система уравнений с 2, 3 и более переменными может иметь одно решение. Начнем с линейных уравнений с двумя переменными и одним решением.

Что не может быть многочленом?

Пожалуйста, включите JavaScript

Что не может быть многочленом?

Когда линейная система имеет одно решение? (Система линейных уравнений с двумя переменными)

Есть несколько способов узнать, имеет ли линейная система с двумя переменными одно решение:

• так как x = 2 и y = 5), то есть одно решение.
• Посмотрите на график – если две линии имеют разный наклон (они пересекаются ровно один раз), то решение системы одно.
• Посмотрите на наклон и точку пересечения по оси y – решите оба уравнения для y, чтобы получить форму зависимости от угла наклона, y = mx + b. Если два уравнения имеют разные наклоны, то две линии различны и не параллельны, поэтому есть только одно решение (вы можете узнать, как определить, что две линии параллельны, в моей статье здесь).

Рассмотрим несколько примеров для каждого случая, начиная с решения системы.

Решение линейной системы одним решением

Когда мы решим линейную систему одним решением, мы получим результат, который даст нам одно значение x и одно значение y. Например, после решения мы получим что-то вроде x = 2 и y = 5.

Давайте рассмотрим несколько примеров, чтобы увидеть, как это может произойти.

Пример 1. Использование исключения для демонстрации того, что линейная система имеет одно решение

Допустим, мы хотим решить следующую систему линейных уравнений:

• 2x + 4y = 3
• -6x – 8y = 11

Для решения воспользуемся методом исключения. Попробуем исключить переменную «x».

Начнем с умножения первого уравнения на 3, чтобы получить:

• 3(2x + 4y) = 3(3)   [умножить первое уравнение на 3 с обеих сторон]
• 6x + 12y = 9 [распределите 3 через круглые скобки]

Теперь добавим это модифицированное уравнение ко второму:

6x + 12y = 9

+

-6x -8y = 11

___________

0x + 4y = 20

Это подразумевает Y = 5. Подменить Y = 5 в первое уравнение. 2x + 4y = 3

2x + 4(5) = 3

2x + 20 = 3

2x = -17

x = -8.5

So the solution is (-8,5, 5). Мы можем проверить это, подставив x = -8,5, y = 5 в оба исходных уравнения, чтобы убедиться, что мы получили правильные значения.

Поскольку существует только одна упорядоченная пара, которая делает оба уравнения верными, существует только одно решение этой системы линейных уравнений. График ниже подтверждает, что линии имеют разный наклон и пересекаются ровно один раз.

Две линии 2x + 4y = 3 (синяя) и -6x – 8y = 11 (красная) имеют разные наклоны, поэтому они пересекаются в одной точке, и существует одно решение линейной системы.

Пример 2. Использование подстановки для демонстрации того, что линейная система имеет одно решение

Допустим, мы хотим решить следующую систему линейных уравнений:

• y = 2x + 5
• 3x + 4y = 9

Для решения воспользуемся подстановкой. Подставим y из первого уравнения в y во втором уравнении:

• 3x + 4y = 9   [начнем со второго уравнения]
• 3x + 4(2x + 5) = 9   [ подставьте y = 2x + 5 из первого уравнения]
• 3x + 8x + 20 = 9  [распределите 4 через круглые скобки]
• 11x = -11   [объединить одинаковые члены на противоположных сторонах]
• x = -1  [разделить на 11 с обеих сторон]

Теперь мы можем подставить x = -1 в первое уравнение, чтобы получить:

• y = 2 (-1) + 5
• y = -2 + 5
• y = 3

Итак, решение (-1, 3).

Поскольку существует только одна упорядоченная пара, которая делает оба уравнения верными, у этой системы линейных уравнений есть только одно решение. График ниже подтверждает, что линии имеют разный наклон и пересекаются ровно один раз.

Две линии y = 2x + 5 (синяя) и 3x + 4y = 9 (красная) имеют разные наклоны, поэтому они пересекаются в одной точке, и существует одно решение линейной системы.

Глядя на график линейной системы с одним решением

Когда мы рисуем линейную систему с одним решением, мы получаем две разные линии, которые не параллельны (то есть они будут иметь разные наклоны).

Давайте рассмотрим несколько примеров, чтобы увидеть, как это может произойти.

Пример 1. График двух пересекающихся линий линейной системы с одним решением

Нарисуем следующую систему линейных уравнений:

• y = 2x + 4
• y = -4x – 2

Линии имеют разные наклоны (2 и -4), как вы можете видеть. на графике ниже:

Две линии y = 2x + 4 (синяя) и y = -4x – 2 (красная) имеют разные наклоны, поэтому они пересекаются в одной точке, и существует одно решение линейной системы.

Поскольку наклоны разные, линии будут пересекаться ровно в одной точке. Это означает, что существует единственная упорядоченная пара (x, y) = (-1, 2), которая является решением линейной системы, с которой мы начали (это единственная точка, которая лежит на обеих прямых).

Пример 2. График двух пересекающихся линий из линейной системы с одним решением

Построим график следующей системы линейных уравнений:

• x = 2
• y = -3

  2

  2 Первая линия имеет неопределенный наклон (это вертикальная линия), а вторая линия имеет нулевой наклон. Это говорит нам о том, что наклоны разные, как вы можете видеть на графике ниже:
  Две линии y = -3 (синяя) и x = 2 (красная) имеют разные наклоны, поэтому они пересекаются в одной точке, и есть одно решение линейной системы.

  Поскольку наклоны разные, линии будут пересекаться ровно в одной точке. Это означает, что существует единственная упорядоченная пара (x, y) = (2, -3), которая является решением линейной системы, с которой мы начали (это единственная точка, которая лежит на обеих прямых).

  Глядя на наклон и точку пересечения Y, чтобы показать, что существует одно решение системы двух линейных уравнений

  Когда мы решаем линейное уравнение для y, мы получаем форму точки пересечения наклона. Если мы сделаем это для обоих уравнений в линейной системе, мы сможем сравнить наклон и точку пересечения по оси y.

  Если два наклона разные, то у нас есть две разные прямые, которые не параллельны, то есть пересекаются в одной точке, и существует ровно одно решение линейной системы.

  Давайте рассмотрим несколько примеров, чтобы увидеть, как это может произойти.

  Пример 1. Сравнение наклона и точки пересечения Y, чтобы показать, что существует одно решение системы двух линейных уравнений0102

• 3y = -12x + 6

Мы найдем y в обоих уравнениях, чтобы получить форму пересечения наклона, y = mx + b.

Решив первое уравнение относительно y, получим:

• 4x = – 2y + 8
• 4x + 2y = 8   [прибавить 2y к обеим частям] вычесть 4x с обеих сторон]
• y = -2x + 4  [разделить на 2 с обеих сторон]

Решив второе уравнение относительно y, получим:

• 3y = -12x + 6
• y = -4x + 2  [разделить на 3 с обеих сторон]

Итак, два уравнения в форме наклона-отрезка:

8

2: -2x + 4

y = -4x + 2

Поскольку эти два уравнения имеют разные наклоны (-2 и -4), мы знаем, что это две разные линии, которые не параллельны. Поскольку прямые пересекаются ровно один раз, у системы есть одно решение: точка (-1, 6), лежащая на обеих прямых.

Две линии y = -2x + 4 (синяя) и y = -4x + 2 (красная) имеют разные наклоны, поэтому они пересекаются в одной точке, и существует одно решение линейной системы.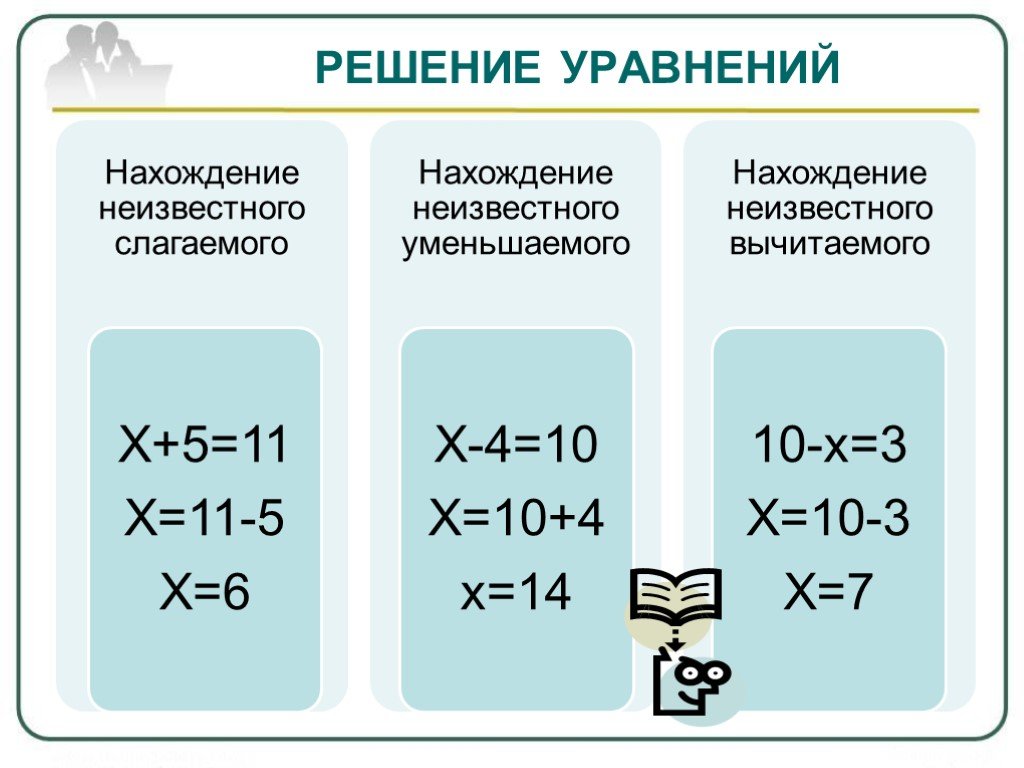

Пример 2. Сравнение наклона и точки пересечения Y, чтобы показать, что существует одно решение системы двух линейных уравнений

Допустим, у нас есть следующая система линейных уравнений: – 32x + 5 = 13

Мы найдем y в обоих уравнениях, чтобы получить форму пересечения наклона, y = mx + b.

Решение первого уравнения для Y, мы получаем:

• 30x = 6y — 18
• 30x + 18 = 6y [Добавить 18 к обеим сторонам]
• 5x + 3 = y [Divide. 6 с обеих сторон]

Решив второе уравнение относительно y, получим:

• 4y – 32x + 5 = 13
• 4y – 32x = 13 – 5 2 90 90 5 с обеих сторон 4y – 32x = 8   [объединить подобные члены: константы]
• 4y = 32x + 8   [прибавьте 32x к обеим сторонам]
• y = 8x + 2  [делите на 4 с обеих сторон]

Итак, два уравнения в форме наклона-отрезка: y = 5x + 3

y = 8x + 2

Поскольку эти два уравнения имеют разные наклоны (5 и 8), мы знаем, что это две разные линии, которые не параллельны. Поскольку прямые пересекаются ровно один раз, у системы есть одно решение: точка (1/3, 14/3), лежащая на обеих прямых.

Две линии y = 5x + 3 (синяя) и y = 8x + 2 (красная) имеют разные наклоны, поэтому они пересекаются в одной точке, и существует одно решение линейной системы.

Как создать систему линейных уравнений с одним решением

Чтобы создать систему линейных уравнений с одним решением, мы можем использовать несколько подходов:

• Один из методов заключается в том, чтобы начать с выбора значений «а» и « b” для любого выражения ax + by. Затем выберите значения x и y для решения (x, y). Затем вычислите значение ax + by, которое является значением c. Уравнение ax + by = c является нашим первым уравнением. Повторите шаги для другой пары значений «e» и «f», того же решения (x, y) и найдите значение «g», чтобы получить второе уравнение ex + fy = g.
• Другой метод состоит в том, чтобы построить график решения (x, y), а затем провести две линии с разными наклонами, которые проходят через (x, y). Найдите уравнение обеих линий, и у вас будет система с решением (x, y).

Давайте попробуем каждый метод по очереди.

Пример 1. Создание системы линейных уравнений с одним решением

Выберем значения a = 2 и b = 3. Тогда наше уравнение будет выглядеть так:

• ax + by = c
• 2x + 3y = c

Все, что нам нужно сделать, это найти c для заданной точки (x, y). Выберем x = 1, y = 4, чтобы получить:

• 2x + 3y = c
• 2(1) + 3(4) = c
• 2 + 12 = c
02 90 = c

Таким образом, наше первое уравнение

• 2x + 3y = 14 (a = 2, b = 3, c = 14)

Теперь мы повторяем шаги для нашего второго уравнения.

Выберем значения e = 5 и f = 4. Тогда наше уравнение будет выглядеть так:

• ex + fy = g
• 5x + 4y = g

Все, что нам нужно сделать, это найти g для той же точки x = 1, y = 4:

4 y G
• 5 (1) + 4 (4) = G
• 5 + 16 = G
• 21 = G

Таким образом (e = 5, f = 4, g = 21)

Тогда система линейных уравнений:

• 2x + 3y = 14
• 5x + 4y = 21

Мы можем решить подстановкой или исключением, чтобы убедиться, что решением является точка (1, 4).

Две линии 2x + 3y = 14 (синяя) и 5x + 4y = 21 (красная) имеют разные наклоны, поэтому они пересекаются в одной точке, и существует одно решение линейной системы.

Пример 2. Создание системы линейных уравнений с одним решением

Допустим, нам нужна линейная система с решением (3, 7). Через эту точку проведем две прямые:

[график из 2 линий ниже и точки (3, 7)]

Первая линия имеет наклон 4 и точку пересечения с осью Y -5. Его уравнение y = 4x – 5.

Вторая линия имеет наклон -2 и точку пересечения y 13. Ее уравнение y = -2x + 13.

Итак, наша система линейного уравнения:

• y = 4x – 5
• y = -2x + 13

Мы можем решить подстановкой или исключением, чтобы убедиться, что решением является точка (3, 7).

Две линии y = 4x – 5 (синяя) и y = -2x + 13 (красная) имеют разные наклоны, поэтому они пересекаются в одной точке, и существует одно решение линейной системы.

Система линейных уравнений с тремя переменными и одним решением

Система уравнений с тремя переменными будет иметь одно решение, если существует единственная точка, в которой пересекаются все три плоскости. Вот пример:

• x + y + z = 1
• x + y + 2z = 2
• x + 2y + 3z = 3

Мы можем легко исключить переменную x, вычитая уравнения:

• y + 2z = 2   [вычесть первое уравнение из третьего]
• z = 1 1 Используя [904 1 из второго 32] 901 z = 1 в уравнении y + 2z = 2 дает нам y = 0.

  Использование z = 1 и y = 0 в первом уравнении дает нам x = 0.

  Таким образом, решение представляет собой упорядоченную тройку (0, 0, 1).

  Когда система линейных уравнений имеет решение?

  Система линейных уравнений с двумя переменными имеет решение, если две прямые пересекаются хотя бы в одном месте.

  • Если две линии имеют одинаковый наклон и одинаковую точку пересечения по оси Y, то эти два уравнения эквивалентны и представляют одну и ту же прямую (поэтому существует бесконечно много решений, поскольку каждая точка на прямой является решением) .
  • Если две линии имеют разные наклоны, то они пересекаются ровно в одной точке.

  Когда система линейных уравнений не имеет решения?

  Система двух линейных уравнений с двумя переменными не имеет решения, если две прямые параллельны.

  С точки зрения алгебры это означает, что мы получаем ложное уравнение при решении системы.

  Визуально линии никогда не пересекаются на графике, так как они имеют одинаковый наклон, но разные точки пересечения по оси Y.

  Подробнее об этом случае (и некоторых примерах) можно узнать из моей статьи здесь.

  Вывод

  Теперь вы знаете, когда система линейных уравнений имеет одно решение. Вы также знаете, на что обращать внимание с точки зрения наклона, точки пересечения по оси Y и графика линий в этих системах.

  Вам также может быть полезно прочитать мою статью о системах линейных уравнений с бесконечными решениями.

  Подробнее о наклоне можно узнать в этой статье.

  No related posts.