исчисление — Найти уравнение касательной к кривой $x=\cos(t) + \cos(2t)$, $y= \sin(t) + \sin(2t)$ в точке $(-1 ,1)$.
спросил
Изменено 7 лет, 11 месяцев назад
Просмотрено 16 тысяч раз
$\begingroup$
Я получаю уравнение для наклона в виде $\frac{\cos(t) + 2\cos(2t)}{-\sin(t) -2\sin(2t)}$, но не знаю, как найти значение $t$. Я знаю, что мне нужно заменить $-1$ и $1$ на $x$ и $y$, но уравнения трудно решить.
- исчисление
- параметрическое
$\endgroup$
1
$\begingroup$
Дана кривая: $$\begin{собран} x(t) = \cos(t) + \cos(2t)\hfill\\ y(t) = \sin(t) + \sin(2t)\hfill\\ \end{собрано}$$
$$\начало {собрано} \varphi (t) = \left( {\begin{массив}{*{20}{c}} {х(т)} \\ {г(т)} \end{массив}} \right) = \left( {\begin{массив}{*{20}{c}} {\ соз (т) + \ соз (2т)} \\ {\ грех (т) + \ грех (2т)} \end{массив}} \right) \hfill \\ \ frac {{d \ varphi}} {{dt}} (t) = \ left ( {\ begin {array} {* {20} {c}} { — \sin(t) — 2\sin(2t)} \\ {\ соз (т) + 2 \ соз (2т)} \end{массив}} \right) \hfill \\ \end{gathered}$$
Из графиков sin и cos находим: $$\begin{собран} \cos (\frac{\pi }{2}) = 0 \клин \cos (\pi ) = — 1 \hfill \\ \sin (\frac{\pi }{2}) = 1 \клин \sin (\pi ) = 0 \hfill \\ \end{собрано} $$
$$\начало {собрано} \ varphi (\ frac {\ pi} {2}) = \ left ( {\ begin {array} {* {20} {c}} {- 1} \\ 1 \end{массив}} \right) \hfill \\ \ frac {{d \ varphi}} {{dt}} (\ frac {\ pi} {2}) = \ left ( {\ begin {array} {* {20} {c}} {- 1} \\ {- 2} \end{массив}} \right) \hfill \\ \end{gathered}$$
и рассчитаем наклон: $$\frac{{dy}}{{dx}} = \frac{{dy}}{{dt}} \cdot \frac{{dt}}{{dx}} = \frac{{dy}}{ {dt}} \cdot \frac{1}{{\frac{{dx}}{{dt}}}} = — 2 \cdot \frac{1}{{ — 1}} = 2$$
Примечание: Наш касательный вектор нормирован и поэтому имеет длину, равную единице.
Так что это
$$\frac{{d\varphi}}{{dt}} = \frac{1}{{\sqrt 5}}\left( {\begin{array}{*{20}{c}}
{- 1} \\
{- 2}
\end{массив}} \right)$$
Наклон не меняется, потому что $\frac{1}{{\sqrt 5 }}$ сокращается при делении. 92t-1+\cos t=-1\iff\cos t(2\cos t+1)=0$$
Если $\cos t=0,\sin2t=2\cos t\sin t=0\ подразумевает\sin t=1\имплицит t=2n\pi+\dfrac\pi2$
Теперь значение наклона можно легко определить
Если $2\cos t+1=0,1=\sin t+\sin2t= \sin t(1+2\cos t)=\sin t\cdot0$ что невозможно
$\endgroup$
1
$\begingroup$
Я не уверен, но подозреваю, что у вас опечатка в заголовке.
Найдите уравнение касательной к кривой $x=\cos(t)+\cos(2t), y=\sin(t)+\sin(2t) $ в точке $ (−1 ,0)$ .
Вопрос о двойном наклоне кривой класса Cardoid, для которой дана параметризация, включающая двойную точку в $(-1,0)$.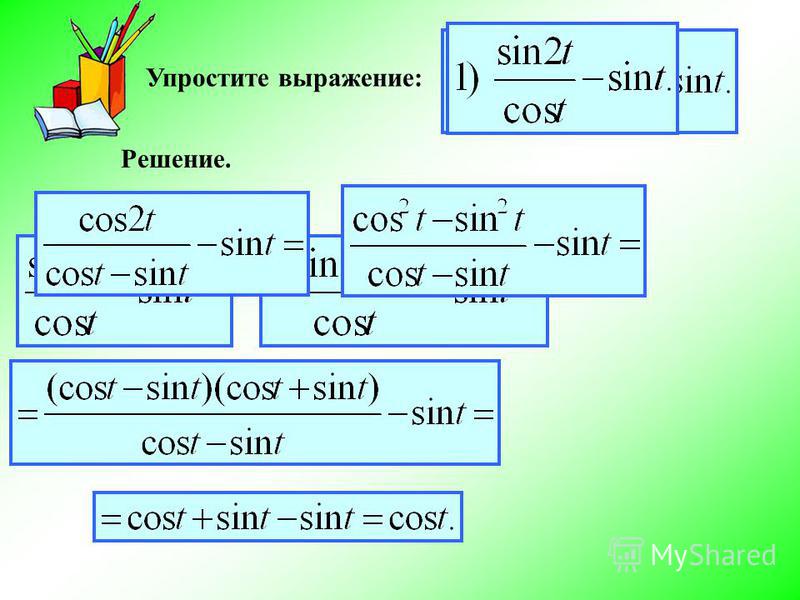
(можно также увидеть в посте Фридера).
Я предлагаю найти два $t$ в двойной точке $ (x,y)= (-1,0)$ и соответствующие им два наклона согласно соотношению $t$, которое вы уже получили.
$\endgroup$
0
$\begingroup$
Я не уверен, но подозреваю, что у вас опечатка в заголовке.
Найдите уравнение касательной к кривой $x=\cos(t)+\cos(2t), y=\sin(t)+\sin(2t) $ в точке $ (−1 ,0)$ .
Вопрос касается двойного наклона кривой класса Cardoid, для которой дана параметризация, включающая двойную точку $(-1,0)$, соответствующую $t=\pi$. (Двойная точка самопересечения также видна в посте Фридера).Я предлагаю вам найти два $t$ в двойной точке $ (x,y)= (-1,0)$ и соответствующие им два наклона в соответствии с соотношением $t$, которое вы уже получили.
$\endgroup$
1
РЕШЕНО: Пусть cos( 2t) 2 sin (2t) 91(t) = 1 J 92 (t) = (sin(2t)) 2 cos(2t) Вычислите вронскиан, чтобы определить, являются ли функции 11 (t) и 32 (t) линейно независимыми.
Вронскиан дет
Эти функции являются линейно независимыми решениями 91(t) и %z(t) в систему
потому что вронскиан отличен от нуля
для всех т. Следовательно
1′ =
образуют фундаментальное множество (т. е. линейно независимое множество) решений:Вопрос
Пошаговый ответ
Пусть cos( 2t) 2 sin (2t) 91(t) = 1 J 92 (t) = (sin(2t)) 2 cos(2t) Вычислите вронскиан, чтобы определить, являются ли функции 11 (t) и 32 (t) линейно независимыми. Неправильно…
Пусть cos( 2t) 2 sin (2t) 91(t) = 1 J 92 (t) = (sin(2t)) 2 cos(2t) Вычислите вронскиан, чтобы определить, являются ли функции 11 (t) и 32 (t) линейно независимыми. Вронскиан дет Эти функции являются линейно независимыми решениями 92}
Рекомендация видео с лучшим совпадением:
Решено проверенным экспертом
У нас нет заданного вами вопроса, но вот рекомендуемое видео, которое может помочь.
Лучшее совпадение Вопрос:
балла) Это вторая часть задачи из четырех частей:
Позволять
91 (т) =
2t 2] 92() = [t
Вычислите вронскиан, чтобы определить, являются ли функции 91 (t) и 32 (t) линейно независимым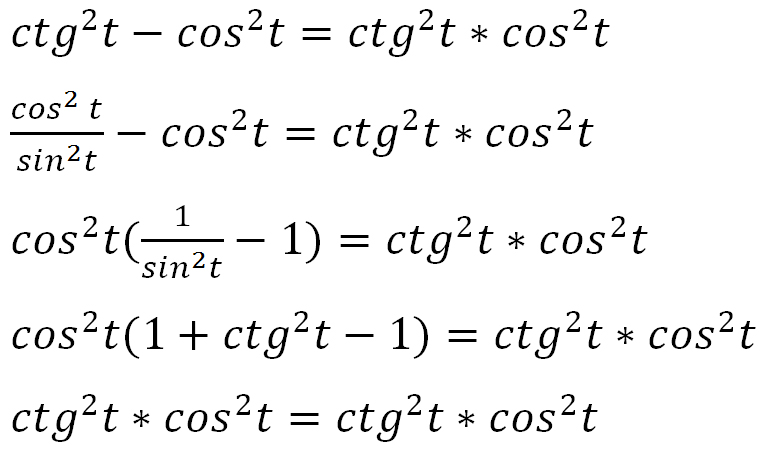и.
Вронскиан дет
Эти функции линейно. Выберите 91(t) и 9z(t) для системы
потому что вронскиан выбирает
при условии 7 0. Поэтому решения
2т 2 2т
1 _ 2т 1 + 2т 2 2т 1 _ 2т 2
Выбирать
образуют фундаментальное множество (т. е. линейно независимое множество) решений:
Рекомендуемые видео
Стенограмма
Давайте посмотрим на решения уравнений. Мы собираемся посмотреть, независимы ли они. Для этого. Мы собираемся найти кожу Рона. Скин Рона состоит из одного раствора в первой колонке и другого во 2-й колонке. Мы собираемся решить этот определитель и не забудьте добавить этот член в уравнение. Когда мы движемся вниз по диагонали. Это будет t в квадрате минус два T, затем мы вычтем и умножим следующие два члена. Итак, мы смотрим на то, что у нас есть, и замечаем, что два T. S отменяются. Но я получаю минус Т в квадрате. Это не равно нулю. Scan не равно нулю, если T не равно нулю. Хорошие новости, вот что это значит. Два решения являются линейными и независимыми. Так что это правильно.