Уравнения 4 степени решение онлайн: Уравнение четвертой степени | Онлайн калькулятор

Содержание

Онлайн калькулятор: Решение уравнения 4-й степени

Калькулятор ниже решает уравнение 4-й степени степени с одной неизвестной. В общем виде уравнение выглядит следующим образом: . В результате получается четыре комплексных или вещественных корня. Формулы, использующиеся для решения описаны сразу под калькулятором.

Уравнение 4-й степени

Точность вычисления

Знаков после запятой: 2

save Сохранить extension Виджет

Первым шагом разделим все коэффициенты уравнения на a и получим эквивалентное уравнение следующего вида:

Далее решаем кубическое уравнение вида:

Это уравнение можно решить, например, способом описанным тут: Кубическое уравнение.
Один вещественный корень этого уравнения u₁ мы будем использовать далее для вычисления корней квадратных уравнений. Если вещественных корней уравнения несколько, то нужно выбрать среди них один u

1 таким образом, чтобы p и q в следующих выражениях были тоже вещественными:

Вычислив p₁, p₂,q₁,q₂, подставляем их в квадратные уравнения в правой части следующего выражения:
^{Четыре корня двух квадратных уравнений в правой части будут соответствовать корням исходного уравнения. Знаки в выражениях для p_i и q_i выбираются таким образом, чтобы выполнялись условия:
Фактически можно проверить только третье условие и если оно не выполняется — поменять q₁ и q₂ местами.
Решение можно проверить, получив значение полинома при помощи этого калькулятора: Вычисление значения полинома с комплексными числами.
Найти корни уравнения, многочлена 4 степени онлайн

Данный калькулятор позволяет высчитывать корни произвольного полинома четвертой степени. Коэффициенты могут быть как вещественными так и комплексными числами.

Использовалась определенная методика, которая нигде не описана и не разобрана.

Формулами Феррари не стал пользоваться — не интересно.

Несмотря на свой собственный путь, все равно утыкаешься в задачу решения вспомогательного уравнения третьей степени, так называемой кубической резольвенты.

И по всей видимости избежать её никак не получится.

Но дальше все идет по другому.

По любому значения корня резольвенты, мы высчитываем три вспомогательный параметра.

Зная эти три параметра, мы можем легко найти все четыре корня исходного уравнения.

Есть только один нюанс с которым сталкивались предшественники, мне тоже надо иногда каким то определять знак + или — для одного вспомогательного параметра.

Теперь в виде формул

Заменой   мы получаем так называемый приведенный многочлен

Решение данного уравнения ищем в виде сумм двух функций

Три вспомогательных параметра связаны к коэффициентами приведенного полинома через следующие соотношения

Выражая любой из вспомогательных параметров мы получаем, в том или ином виде кубическую резольвенту

Например, если выразим F₂

Это кубическое уравнение которое подстановкой  превращается к классическую кубическую резольвенту.

Теперь о нюансе о котором говорил раньше. Какой же знак брать когда высчитываем корни?

Критерий оказывается очень простой. Берем любой корень резольвенты и сравниваем его

если это условие верное то ставится +(плюс), если условие неверное то -(минус)

Дальше все эти параметры подставляются в формулу

и определяются корни уравнения 4 степени.

Еще хотелось бы поговорить про критерий. Вдумчивый читатель спросит: «А что если любой корень резольвенты является комплексным числом? Какой в этом случае критерий?»

Лучшим способом, я посчитал для подстановка корня в исходное уравнение. Для этого есть простой алогритический способ описанный в статье Значение производной многочлена по методу Горнера. Если выражение обращается в ноль, то есть является верным, то знак не меняется. Если иначе то знак ставим минус.

Решать комплексные уравнения 4 степени теперь можно достаточно легко и быстро. В онлайн сервисах Вы такого не найдете.

Попробуйте решить уравнение

Один из корней равен

Кто считает что действительной частью можно принебречь и отбросить как «почти ноль» глубоко ошибается. Отбросив его у нас значение функции будет , а не ноль.

И только с учетом «такой маленькой» действительной части уравнение становиться тождественным.

Поэтому точность в вычислениях очень важны.

Если Вы вдруг заметили ошибку в расчетах ( а вдруг?) , просьба сообщить. Но я надеюсь, что такого не произойдет.

Несколько примеров:

Найти число по остатку от деления >>
Уравнения 4 степени с помощью решателя онлайн
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве
сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только
возрастает. Решения данного рода уравнений можно выполнять по общей схеме решения уравнений высших степеней.
Данного рода уравнения имеют решения в радикалах благодаря методу Феррари, позволяющему свести решения к
кубическому уравнению. Однако в большинстве случаев с помощью разложения многочлена на множители удается
быстро найти решение уравнения.

Так же читайте нашу статью «Решить уравнения онлайн по алгебре
решателем»
Допустим, дано двучленное уравнение четвертой степени:
\[4x^4 + 1 = 0\]
Выполним разложение \[4x^4+1\] на множители многочлена:
\[4x^4+1=4x^4+4x^2-4x^2+1=(2x^2+1)^2-4x^2=(2x^2-2x+1)(2x^2+2x+1)\]
Определяем корни первого квадратного трехчлена:
\[2x^2-2x+1=0\]
\[D=(-2)^2-4 \cdot2 \cdot1=-4\]
\[x_1= \frac{2+ \sqrt D}{2 \cdot 2}=\frac{1}{2} +i\]
\[x_2=\frac{2- \sqrt D}{2 \cdot 2}=\frac{1}{2} -i\]
Определяем корни второго трехчлена:
\[2x^2+2x+1=0\]
\[D=2^2-4\cdot2\cdot1=-4\]
\[x_3= \frac{-2+ \sqrt D}{2 \cdot 2}=-\frac{1}{2} +i\]
\[x_4= \frac{-2- \sqrt D}{2 \cdot 2}=-\frac{1}{2} -i\]
В результате, исходное уравнение имеет четыре комплексных корня:
\[x=\frac{1}{2}\pm i\]
\[x=-\frac{1}{2}\pm i\]
Где можно решить уравнения 4 степени онлайн?
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель
позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это
просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию
и узнать, как решить уравнение на нашем сайте.А если у вас остались вопросы, то вы можете задать их в нашей
групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда
рады помочь вам.
Калькулятор уравнения четвертой степени | BBF.RU
Решить
{$ main.types[data.type] $}
Введите уравнение
* x +
=
Введите уравнение
* x² +
* x +
=
Введите уравнение * x³ +
* x² +
* x +
=
Введите уравнение * x⁴ +
* x³ +
* x² +
* x +
=
Введите уравнения
* x +
* y +
=
* x +
* y +
=
Введите уравнения
* x +
* y +
* z =
* x +
* y +
* z =
* x +
* y +
* z =
Рассчитать
{$ error $}!
Результаты расчёта
A^-1 {$ result.IA[0][0]|number $} {$ result.IA[0][1]|number $} {$ result.IA[0][2]|number $} * {$ result.B[0][0]|number $} = {$ result.x|number $}
{$ result.IA[1][0]|number $} {$ result.IA[1][1]|number $} {$ result.IA[1][2]|number $} {$ result.B[1][0]|number $} {$ result.y|number $}
{$ result.IA[2][0]|number $} {$ result.IA[2][1]|number $} {$ result.IA[2][2]|number $} {$ result.B[2][0]|number $} {$ result.z|number $}
x = {$ result.x|number $}
y = {$ result.y|number $}
z = {$ result.z|number $}
Результаты расчёта
x1 = {$ main.FormatResult(result.x1) $}
x2 = {$ main.FormatResult(result.x2) $}
x3 = {$ main.FormatResult(result.x3) $}
x4 = {$ main.FormatResult(result.x4) $}
Значение дискриминанта: b² − 4 * a * c = {$ result.d|number $}
Решение кубических уравнений онлайн · Как пользоваться Контрольная Работа РУ
Рассмотрим два примера кубических уравнений, которые калькулятор уравнений умеет без проблем решать с подробным решением:
Пример простого кубического уравнения
Первый пример будет простым:
49*x^3 — x = 0
После того, как вы нажмёте «Решить уравнение!», то вы получите ответ с подробным объяснением:
Дано уравнение:
преобразуем
Вынесем общий множитель x за скобки
получим:
тогда:
и также
получаем ур-ние
Это уравнение вида
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:

___
\/ D - b
x2 = ---------
2*a

___
-b - \/ D
x3 = ----------
2*a
где D = b^2 — 4*a*c — это дискриминант.
Т.к.
, то

(0)^2 - 4 * (49) * (-1) = 196
Т.к. D > 0, то уравнение имеет два корня.

x2 = (-b + sqrt(D)) / (2*a)

x3 = (-b - sqrt(D)) / (2*a)
или
Получаем окончательный ответ для -x + 49*x^3 = 0:

x3 = -1/7

Второй простой пример кубического уравнения будет таким:
8 = (1/2 + 3*x)^3
Получим подробное решение:
Дано уравнение:
преобразуем:
Вынесем общий множитель за скобки

/ 2\
-9*(-1 + 2*x)*\7 + 12*x + 12*x /
-------------------------------- = 0
8
Т.к. правая часть ур-ния равна нулю, то решение у ур-ния будет, если хотя бы один из множителей в левой части ур-ния равен нулю.
Получим ур-ния
решаем получившиеся ур-ния:
1.
Переносим свободные слагаемые (без x)
из левой части в правую, получим:
Разделим обе части ур-ния на -9/4
Получим ответ: x1 = 1/2
2.
Это уравнение вида
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:

___
\/ D - b
x2 = ---------
2*a

___
-b - \/ D
x3 = ----------
2*a
где D = b^2 — 4*a*c — это дискриминант.
Т.к.
, то

(12)^2 - 4 * (12) * (7) = -192
Т.к. D < 0, то уравнение
не имеет вещественных корней,
но комплексные корни имеются.

x2 = (-b + sqrt(D)) / (2*a)

x3 = (-b - sqrt(D)) / (2*a)
или

___
1 I*\/ 3
x2 = - - + -------
2 3

___
1 I*\/ 3
x3 = - - - -------
2 3
Тогда, окончательный ответ:

___
1 I*\/ 3
x2 = - - + -------
2 3

___
1 I*\/ 3
x3 = - - - -------
2 3
Пример сложного кубического уравнения
Третьим примером будет более сложный — возвратное кубическое уравнение онлайн.
5*x^3 -8*x^2 — 8*x + 5 = 0
Чтобы решить такое возвратное кубическое уравнение, то введите данное уравнение в калькулятор:
Дано уравнение:

2 3
5 - 8*x - 8*x + 5*x = 0
преобразуем

3 2
5*x + 5 - 8*x + 8 - 8*x - 8 = 0
или

3 3 2 2
5*x - 5*(-1) - 8*x - -8*(-1) - 8*x - 8 = 0

/ 3 3\ / 2 2\
5*\x - (-1) / - 8*\x - (-1) / - 8*(x + 1) = 0

/ 2 2\
5*(x + 1)*\x - x + (-1) / + -8*(x + 1)*(x - 1) - 8*(x + 1) = 0
Вынесем общий множитель 1 + x за скобки
получим:

/ / 2 2\ \
(x + 1)*\5*\x - x + (-1) / - 8*(x - 1) - 8/ = 0
или

/ 2\
(1 + x)*\5 - 13*x + 5*x / = 0
тогда:
и также
получаем ур-ние
Это уравнение вида
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:

___
\/ D - b
x2 = ---------
2*a

___
-b - \/ D
x3 = ----------
2*a
где D = b^2 — 4*a*c — это дискриминант.
Т.к.
, то

(-13)^2 - 4 * (5) * (5) = 69
Т.к. D > 0, то уравнение имеет два корня.

x2 = (-b + sqrt(D)) / (2*a)

x3 = (-b - sqrt(D)) / (2*a)
или

____
13 \/ 69
x2 = -- + ------
10 10

____
13 \/ 69
x3 = -- - ------
10 10
Получаем окончательный ответ для 5 — 8*x — 8*x^2 + 5*x^3 = 0:

____
13 \/ 69
x2 = -- + ------
10 10

____
13 \/ 69
x3 = -- - ------
10 10
Решить кубические уравнения онлайн
Часто при решении математических, статистических, инженерных задач приходится решать разные уравнения.
Уравнение 3-й степени — это кубическое уравнение вида ax³ + bx² + cx + d = 0, где а не равно 0. Число х считается корнем уравнения, если при его подстановке получается верное равенство.
Для графического анализа уравнения используется кубическая парабола.
Имеются разные способы решения кубических уравнений, среди них: теорема Безу, формулы Кардано, Виета, метод возвратного уравнения.
Кубические уравнения вида: х³ = а имеют корень x = ³√a
В некоторых случаях при решении уравнений:
в левой части уравнения можно сгруппировать слагаемые;
разложить ее на множители;
найти корни.
Решение уравнения методом Кардано начинается с приведения исходного кубического уравнения ax³ + bx² + cx + d = 0 к более простому виду: y³ + py + q = 0, если заменить х неизвестным у при условии х = у — b / 3а.
В данном уравнении: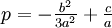
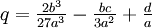Кубическое уравнение имеет 3 корня, разберем их с помощью дискриминанта:
Δ = — 4b³d + b²c² — 4ac³ + 18abcd — 27a²d²
если дискриминант больше 0, уравнение имеет 3 вещественных корня;
если меньше 0, 1 — вещественный корень и 2 комплексных;
если меньше 0, тогда хотя бы 2 корня совпадают.
С помощью онлайн калькулятора можно намного быстрее решить кубическое уравнение, найти его корни.

Онлайн калькулятор: Кубическое уравнение
Сегодня выполняем запрос пользователя Решение кубического уравнения.
Канонический вид кубического уравнения:
Решать кубическое уравнение мы будем по формуле Виета.
Формула Виета — способ решения кубического уравнения вида

Соответственно, чтобы привести к этому виду оригинальное уравнение первым шагом все введенные коэффициенты делятся на коэффициент а:
Калькулятор ниже, а описание формулы Виета — под ним
Кубическое уравнение
Точность вычисленияЗнаков после запятой: 2
save Сохранить extension Виджет
Кстати сказать, на других сайтах почему-то для решения кубических уравнений используют формулу Кардано, однако я согласен с Википедией в том, что формула Виета более удобна для практического применения. Так что почему везде формула Кардано — непонятно, разве что лень людям Гиперболические функции и Обратные гиперболические функции реализовывать. Ну мне не лень было.
Итак, формула Виета (из Википедии)
Обратите внимание, что по представлению формулы Виета а — второй коэффициент, а коэффициент перед x3 всегда считается равным 1. Калькулятор позволяет ввести а как коэффициент перед х3, но сразу же на него и делит уравнение, чтобы получить 1
Вычисляем:
Вычисляем:
Если S > 0, то вычисляем:

и имеем три действительных корня:
Если S < 0, то заменяем тригонометрические функции гиперболическими. Здесь возможны два случая в зависимости от знака Q
Q > 0:

(действительный корень)

(пара комплексных корней)
Q < 0:

(действительный корень)

(пара комплексных корней)
Если S = 0, то уравнение вырождено и имеет меньше 3 различных решений (второй корень кратности 2):
По этим формулам калькулятор и работает. Решает вроде правильно, хотя решения с мнимой частью не проверял. Если что, пишите.
Калькулятор квадратичных формул
Использование калькулятора
Этот онлайн-калькулятор представляет собой программа решения квадратного уравнения , которая решает полиномиальное уравнение второго порядка, такое как ax ² + bx + c = 0 для x, где a 0, используя квадратная формула .
Решение калькулятора покажет работу с использованием формулы квадратного уравнения для решения введенного уравнения для действительных и комплексных корней.2 — 4ac> 0 \) Итак, есть два действительных корня.
Упростите радикал:
\ (x = \ dfrac {8 \ pm 2 \ sqrt {11} \,} {2} \)
\ (x = \ dfrac {8} {2} \ pm \ dfrac {2 \ sqrt {11} \,} {2} \)
Упростить дроби и / или знаки:
\ (x = 4 \ pm \ sqrt {11} \, \)
, который становится
\ (х = 7.2 — 4ac
Упростите радикал:
\ (x = \ dfrac {-20 \ pm 4 \ sqrt {15} \, i} {10} \)
\ (x = \ dfrac {-20} {10} \ pm \ dfrac {4 \ sqrt {15} \, i} {10} \)
Упростить дроби и / или знаки:
\ (x = -2 \ pm \ dfrac {2 \ sqrt {15} \, i} {5} \)
, который становится
\ (х = -2 + 1,54919 \, я \)
\ (х = -2 — 1.54919 \, и \)
В калькулятор добавлено полное решение для действительных и сложных корней
. Решатель уравнений — Решите для x Калькулятор
Поиск инструмента
Решатель уравнений
Инструмент / решатель для решения одного или нескольких уравнений. Уравнение — это математическое выражение, представленное как равенство двух элементов с неизвестными переменными.
Результаты
Решатель уравнений — dCode

Тег (и): Символическое вычисление
Поделиться
dCode и вы
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Калькулятор для расчета уравнений
Инструмент / решатель для решения одного или нескольких уравнений.Уравнение — это математическое выражение, представленное как равенство двух элементов с неизвестными переменными.
Ответы на вопросы
Как решить уравнение?
Калькулятор dCode может решать уравнения (или неравенства или другие математические формулы) и находить неизвестные переменные. Уравнения должны содержать символ сравнения, например, равно, т.е. = (или или>).
Пример: $ 2x = 1 $ возвращает решение $ x = 1/2 $
dCode возвращает точные решения (целые числа, дроби и т. Д.) по умолчанию, если уравнение содержит числа-запятые, то dCode вернет решение с десятичными числами.
Пример: $ 2x = 1.0 $ возврат для решения $ x = 0.5 $
Чтобы решить шифрование (заменяя буквы несколькими значениями от 0 до 9), используйте решатель шифровальных кодов dCode.
Как решить несколько уравнений?
Уравнения можно комбинировать с оператором и (логическое соединение): && или ⋀ или с возвратом строки между каждым уравнением .2 + 1 = 3 && 3x-1 = 2 дает x = 1
Как решить несколько уравнений с несколькими переменными?
Чтобы решить систему уравнений , необходимо разделить уравнения с помощью && или ⋀. Переменные должны быть перечислены и разделены в поле ввода переменных.
Как проверить равенство?
Введите уравнение
и нажмите «Решить», решающая программа ответит «Истина», если равенство проверяется независимо от переменной.
Пример: 2n + 18n + 4 = 2 (n + 9n + 2) ИСТИНА для любого значения n
Как добавить домен определения?
Добавьте дополнительную строку, которая будет действовать как дополнительное уравнение .2-2 = 0 \ \ & \ & \ x> 0 $, если , уравнение действительно только для строго положительных чисел $ x> 0 $.
Как пошагово решить уравнение?
Шаги вычислений решателя не показаны, потому что они не соответствуют шагам, которые сделал бы человек. Операции, выполняемые решателем, представляют собой двоичные вычисления, бит за битом сильно отличающиеся от тех, которые выполняются вручную математиком.
Задайте новый вопрос Исходный код
dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Решатель уравнений».За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любой алгоритм, апплет или фрагмент (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любая функция (преобразование, решение, дешифрование / encrypt, decipher / cipher, decode / encode, translate) написано на любом информатическом языке (PHP, Java, C #, Python, Javascript, Matlab и т. д.), доступ к данным, скриптам или API не будет бесплатным, то же самое для Equation Solver скачать для автономного использования на ПК, планшете, iPhone или Android!
Нужна помощь?
Пожалуйста, заходите в наше сообщество в Discord для получения помощи!
Вопросы / комментарии
Сводка
Инструменты аналогичные
Поддержка
Форум / Справка
Рекламные объявления
Ключевые слова
уравнение, равенство, равенство, неизвестное, переменная, x, число, калькулятор
Ссылки

Источник: https: // www.dcode.fr/equation-solver
© 2020 dCode — Идеальный «инструментарий» для решения любых игр / загадок / геокэшинга / CTF. . Графические уравнения с программой «Пошаговое решение математических задач»
Введите уравнение, которое вы хотите построить, при необходимости установите зависимую переменную и нажмите кнопку «График».
Язык математики особенно эффективен для представления отношений
между двумя или более переменными. В качестве примера рассмотрим пройденное расстояние
через определенный промежуток времени автомобилем, движущимся с постоянной скоростью 40 миль в час.Мы можем представить эту взаимосвязь как
. 1. Словесное предложение:
Пройденное расстояние в милях равно сороккратному количеству пройденных часов.
2. Уравнение:
d = 40r.
3. Таблица значений.
4. График, показывающий зависимость между временем и расстоянием.
Мы уже использовали словесные предложения и уравнения для описания таких отношений;
в этой главе мы будем иметь дело с табличным и графическим представлениями.
7.1 РЕШЕНИЕ УРАВНЕНИЙ ОТ ДВУХ ПЕРЕМЕННЫХ
ЗАКАЗАННЫЕ ПАРЫ
Уравнение d = 40f объединяет расстояние d для каждого момента времени t. Например,

, если t = 1, то d = 40
, если t = 2, то d = 80
, если t = 3, то d = 120
и так далее.
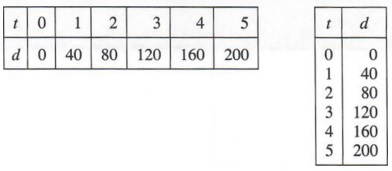
Пара чисел 1 и 40, рассматриваемая вместе, называется решением
уравнение d = 40r, потому что когда мы подставляем 1 вместо t и 40 вместо d в уравнении,
мы получаем верное утверждение. Если мы согласны ссылаться на парные номера в указанном
порядок, в котором первое число относится ко времени, а второе число относится к
расстояния, мы можем сократить приведенные выше решения как (1, 40), (2, 80), (3, 120) и
скоро.Мы называем такие пары чисел упорядоченными парами и ссылаемся на первую и
вторые числа в парах как компоненты. При этом соглашении решения
Уравнение d — 40t — это упорядоченные пары (t, d), компоненты которых удовлетворяют уравнению.
Некоторые упорядоченные пары для t, равного 0, 1, 2, 3, 4 и 5, равны
(0,0), (1,40), (2,80), (3,120), (4,160) и (5,200)
Такие пары иногда отображаются в одной из следующих табличных форм.

В любом конкретном уравнении, включающем две переменные, когда мы присваиваем значение одной
переменных определяется значение другой переменной и, следовательно,
зависит от первого.Удобно говорить о переменной, связанной с
первый компонент упорядоченной пары как независимая переменная и переменная
связанный со вторым компонентом упорядоченной пары как зависимая переменная. Если в уравнении используются переменные x и y, подразумевается, что заменить —
элементы для x являются первыми компонентами и, следовательно, x — независимая переменная и
замены y являются вторыми компонентами и, следовательно, y является зависимой переменной.
Например, мы можем получить пары для уравнения

, подставив конкретное значение одной переменной в уравнение (1) и решив для
другая переменная.
Пример 1
Найдите недостающий компонент, чтобы заказанная пара стала решением для
2х + у = 4
а. (0 ,?)
г. (1 ,?)
г. (2 ,?)
Решение
, если x = 0, то 2 (0) + y = 4
y = 4
если x = 1, то 2 (1) + y = 4
y = 2
, если x = 2, то 2 (2) + y = 4
y = 0
Теперь три пары могут отображаться как три упорядоченные пары
(0,4), (1,2) и (2,0)
или в табличной форме

ЯВНО ВЫРАЖАЮЩИЙ ПЕРЕМЕННУЮ
Мы можем добавить -2x к обоим членам 2x + y = 4, чтобы получить
-2x + 2x + y = -2x + 4
y = -2x + 4
В уравнении (2), где y есть само по себе, мы говорим, что y явно выражается через
из х.Часто бывает проще получить решения, если сначала выразить уравнения в такой форме
поскольку зависимая переменная явно выражается через независимые
переменная.
Например, в уравнении (2) выше
, если x = 0, то y = -2 (0) + 4 = 4
, если x = 1, то y = -2 (1) + 4 = 2
, если x = 2, то y = -2 (2) + 4 = 0
Мы получаем те же самые пары, которые мы получили с помощью уравнения (1)
(0,4), (1,2) и (2,0)
Мы получили уравнение (2) добавлением одинаковой величины -2x к каждому члену
уравнения (1), получая таким образом y отдельно.В общем, мы можем написать эквивалент
уравнения с двумя переменными, используя свойства, которые мы ввели в главе 3,
где мы решали уравнения первой степени с одной переменной.
Уравнения эквивалентны, если:
Одно и то же количество прибавляется к равным количествам или вычитается из них.
Равные количества умножаются или делятся на одинаковое ненулевое количество.
Пример 2
Решите 2y — 3x = 4 явно для y через x и получите решения для x = 0,
х = 1 и х = 2.
Решение
Во-первых, добавляя 3x к каждому члену, мы получаем
2y — 3x + 3x = 4 + 3x
2y = 4 + 3x (продолжение)
Теперь, разделив каждый член на 2, получаем

В этой форме мы получаем значения y для заданных значений x следующим образом:

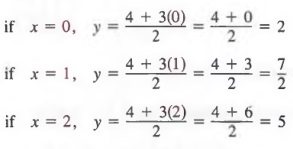
В этом случае три решения: (0, 2), (1, 7/2) и (2, 5).
ОБОЗНАЧЕНИЕ ФУНКЦИЙ
Иногда мы используем специальные обозначения для наименования второго компонента заказанного
пара, которая связана с указанным первым компонентом.Символ f (x), который часто
используется для обозначения алгебраического выражения в переменной x, также может использоваться для обозначения
значение выражения для конкретных значений x. Например, если
f (x) = -2x + 4
, где f (x) играет ту же роль, что и y в уравнении (2) на странице 285, тогда f (1)
представляет значение выражения -2x + 4, когда x заменяется на 1
f (l) = -2 (1) + 4 = 2
Аналогично
f (0) = -2 (0) + 4 = 4
и
f (2) = -2 (2) + 4 = 0
Символ f (x) обычно называют обозначением функции.
Пример 3
Если f (x) = -3x + 2, найти f (-2) и f (2).
Решение
Замените x на -2, чтобы получить
f (-2) = -3 (-2) + 2 = 8
Замените x на 2, чтобы получить
f (2) = -3 (2) + 2 = -4
7.2 ГРАФИК ЗАКАЗАННЫХ ПАР
В разделе 1.1 мы увидели, что каждое число соответствует точке на линии. Simi-
Как правило, каждая упорядоченная пара чисел (x, y) соответствует точке на плоскости. Чтобы
граф упорядоченной пары чисел, мы начинаем с построения пары перпендикулярных
числовые линии, называемые осями.Горизонтальная ось называется осью x, вертикальная ось
называется осью Y, а точка их пересечения называется началом координат. Эти топоры
разделите плоскость на четыре квадранта, как показано на рисунке 7.1.

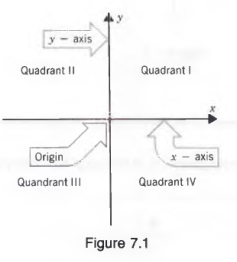
Теперь мы можем присвоить упорядоченную пару чисел точке на плоскости, указав
на перпендикулярное расстояние точки от каждой из осей. Если первый
составляющая положительная, точка лежит правее вертикальной оси; если отрицательный, это
лежит слева.Если второй компонент положительный, точка находится выше
Горизонтальная ось; если отрицательный, он находится внизу.
Пример 1
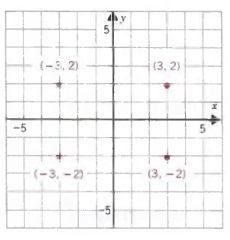
График (3, 2), (-3, 2), (-3, -2) и (3, -2) в прямоугольной системе координат.
Решение
График (3, 2) находится на 3 единицы правее
ось y и на 2 единицы выше оси x;
график (-3,2) лежит на 3 единицы слева от
ось y и на 2 единицы выше оси x;
график (-3, -2) лежит на 3 единицы слева от
ось y и на 2 единицы ниже оси x;
график (3, -2) лежит на 3 единицы правее
по оси Y и на 2 единицы ниже оси X.

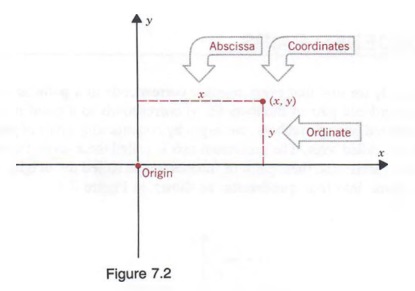
Расстояние y, на котором точка расположена от оси x, называется ординатой.
точки, а расстояние x, на котором точка расположена от оси y, называется
абсцисса точки. Абсцисса и ордината вместе называются прямоугольником.
Гулярные или декартовы координаты точки (см. рисунок 7.2).

7.3 ИЗОБРАЖЕНИЕ УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ
В разделе 7.1 мы увидели, что решение уравнения с двумя переменными является упорядоченным
пара.В разделе 7.2 мы видели, что компонентами упорядоченной пары являются
координаты точки на плоскости. Таким образом, чтобы построить уравнение с двумя переменными, мы
Изобразите набор упорядоченных пар, которые являются решениями уравнения. Например, мы
может найти некоторые решения уравнения первой степени
у = х + 2
, положив x равным 0, -3, -2 и 3. Затем
для x = 0, y = 0 + 2 = 2
для x = 0, y = -3 + 2 = -1
для x = -2, y = -2 + 2-0
для x = 3, y = 3 + 2 = 5
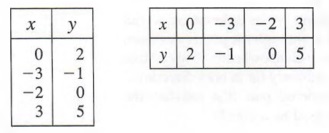
и получаем решения
(0,2), (-3, -1), (-2,0) и (3,5)
, который может отображаться в табличной форме, как показано ниже.

Если мы изобразим точки, определенные этими
упорядоченные пары и проведите прямую через
их, мы получаем график всех решений
y = x + 2, как показано на рисунке 7.3. То есть,
каждое решение y = x + 2 лежит на прямой,
и каждая точка на линии является решением
у = х + 2.

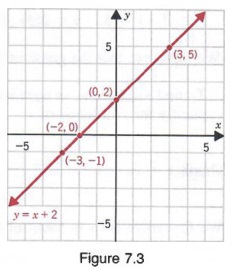
Графики уравнений первой степени в двух
переменные всегда прямые; следовательно,
такие уравнения также называются линейными
уравнения.
В приведенном выше примере значения, которые мы использовали для
x были выбраны случайным образом; мы могли бы использовать
любые значения x, чтобы найти решения уравнения.
Графики любых других упорядоченных пар, которые являются решениями уравнения, также будут
быть на линии, показанной на рисунке 7.3. Фактически, каждое линейное уравнение с двумя переменными
имеет бесконечное количество решений, график которых лежит на прямой. Однако мы только
нужно найти два решения, потому что для определения
прямая линия. Третий балл можно получить как проверку.
Чтобы построить уравнение первой степени:
Постройте набор прямоугольных осей, показывающих масштаб и переменную, представляющую
отправляется каждой осью.
Найдите две упорядоченные пары, которые являются решениями уравнения для построения графика
присвоение любого удобного значения одной переменной и определение соответствующего
значение другой переменной.
Изобразите эти упорядоченные пары.
Проведите прямую линию через точки.
Проверьте, построив третью упорядоченную пару, которая является решением уравнения и
убедитесь, что он лежит на линии.
Пример 1
Постройте уравнение y = 2x — 6.
Решение
Сначала мы выбираем любые два значения x, чтобы найти соответствующие значения y.
Мы будем использовать 1 и 4 для x.
Если x = 1, y = 2 (1) — 6 = -4
, если x = 4, y = 2 (4) — 6 = 2
Таким образом, два решения уравнения:
(1, -4) и (4, 2).
Затем мы строим график этих упорядоченных пар и проводим прямую линию через точки, как показано
на рисунке. Мы используем стрелки, чтобы показать, что
линия тянется бесконечно далеко в обоих направлениях.Любая третья упорядоченная пара, удовлетворяющая
уравнение можно использовать в качестве проверки:
, если x = 5, y = 2 (5) -6 = 4
Затем отметим, что график (5, 4) также лежит на линии
. Чтобы найти решения уравнения, как мы уже отмечали, часто проще всего сначала решить
явно для y через x.

Пример 2
График x + 2y = 4.
Решение
Сначала мы решаем y через x, чтобы получить

Теперь мы выбираем любые два значения x, чтобы найти соответствующие значения y.Мы будем использовать
2 и 0 для x.

Таким образом, два решения уравнения: (2, 1) и (0, 2).
Затем мы графически отображаем эти упорядоченные пары и
проведите через точки прямую, как
показано на рисунке.
Любая третья упорядоченная пара, удовлетворяющая
уравнение можно использовать как проверку:

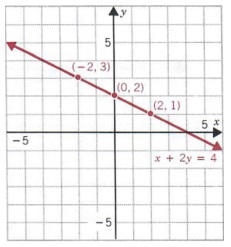
Затем отметим, что график (-2, 3) также
лежит на линии.
ОСОБЫЕ СЛУЧАИ ЛИНЕЙНЫХ УРАВНЕНИЙ
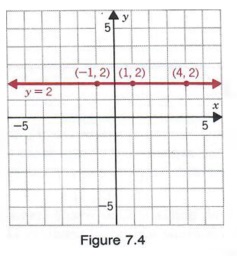
Уравнение y = 2 можно записать как
0x + y = 2
и может рассматриваться как линейное уравнение в двух
переменные, у которых коэффициент при x равен 0.Некоторые
решения 0x + y = 2 равны
(1,2), (-1,2) и (4,2)
Фактически, любая упорядоченная пара вида (x, 2) является
решение (1). Графическое изображение решений
дает горизонтальную линию, как показано на рисунке
7.4.

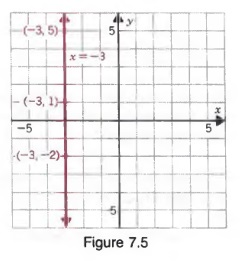
Точно так же уравнение, такое как x = -3, может
можно записать как
х + 0у = -3
и может рассматриваться как линейное уравнение в двух
переменные, у которых коэффициент при y равен 0.
Некоторые решения x + 0y = -3 являются
(-3, 5), (-3, 1) и (-3, -2).Фактически любой
упорядоченная пара вида (-3, y) является решением
из (2). Построение графика решений дает вертикальную
линии, как показано на рисунке 7.5.

Пример 3
График
а. у = 3
б. х = 2
Решение
а. Мы можем записать y = 3 как Ox + y = 3.
Некоторые решения: (1, 3), (2,3) и (5, 3).

б. Мы можем записать x = 2 как x + Oy = 2.
Некоторые решения: (2, 4), (2, 1) и (2, -2).

7.4 МЕТОД ПЕРЕСЕЧЕНИЯ ГРАФИКА
В Разделе 7.3 мы присвоили значения x в уравнениях с двумя переменными, чтобы найти
соответствующие значения y. Решения уравнения с двумя переменными, равные
как правило, легче всего найти те, в которых первый или второй компонент
0. Например, если мы заменим 0 на x в уравнении
3x + 4y = 12
у нас
3 (0) + 4y = 12
y = 3
Таким образом, решением уравнения (1) является (0, 3).Мы также можем найти упорядоченные пары, которые
решения уравнений с двумя переменными путем присвоения значений y и определения
соответствующие значения x. В частности, если мы подставим 0 вместо y в уравнение (1), мы
получить
3x + 4 (0) = 12
x = 4
и второе решение уравнения (4, 0). Теперь мы можем использовать упорядоченные пары
(0, 3) и (4, 0) для построения графика уравнения (1). График представлен на рисунке 7.6. Уведомление
что линия пересекает ось x в точке 4 и ось y в точке 3. По этой причине число
4 называется пересечением по оси x графа, а число 3 — точкой пересечения по оси y.

Такой способ построения графика линейного уравнения называется перехватом.
метод построения графиков. Обратите внимание, что когда мы используем этот метод построения графиков линейного
уравнение, нет никакого преимущества в том, чтобы сначала явно выразить y через x.
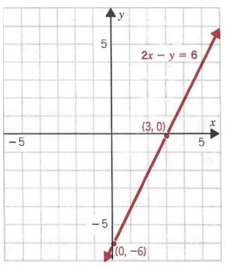
Пример 1
График 2x — y = 6 методом пересечения.
Решение
Мы находим точку пересечения с x, подставляя 0 вместо y в уравнение, чтобы получить
2x — (0) = 6
2x = 6
x = 3
Теперь мы находим точку пересечения по оси Y, подставляя
для x в уравнении, чтобы получить
2 (0) — y = 6
-y = 6
y = -6
Упорядоченные пары (3, 0) и (0, -6) являются решениями 2x — y = 6.Графическое изображение этих
точки и соединяя их прямой линией, получаем график 2x — y = 6.
Если график пересекает оси в или около начала координат, метод перехвата не работает.
удовлетворительно. Затем мы должны построить график упорядоченной пары, которая является решением уравнения
и чей график не является началом координат или не слишком близок к началу координат.

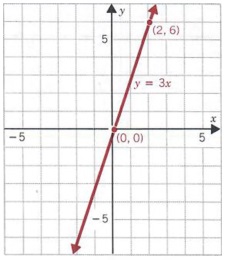
Пример 2
График y = 3x.
Решение
Мы можем заменить 0 на x и найти
y = 3 (0) = 0
Аналогичным образом, заменив 0 на y, мы получим
0 = 3.x, x = 0
Таким образом, 0 является и точкой пересечения по оси x, и точкой пересечения по оси y.
Так как одной точки недостаточно для графического = 3x, мы прибегаем к методам, описанным в
Раздел 7.3. Выбирая любое другое значение для x, скажем 2, получаем
у = 3 (2) = 6
Таким образом, (0, 0) и (2, 6) являются решениями
уравнение. График y = 3x показан на
право.

7,5 НАКЛОН ЛИНИИ
ФОРМУЛА НАКЛОНА
В этом разделе мы изучим важное свойство линии.Мы назначим
число к линии, которую мы называем уклоном, что даст нам меру «крутизны»
или «направление» линии.
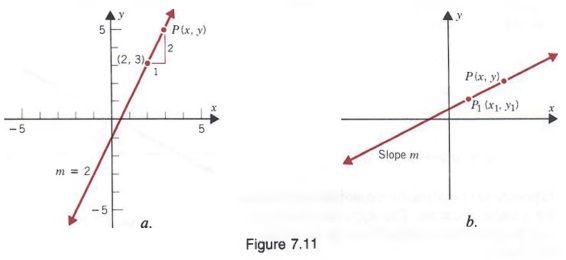
Часто бывает удобно использовать специальные обозначения для различения прямоугольников.
Гулярные координаты двух разных точек. Мы можем обозначить одну пару координат
на (x ₁, y ₁ (читается «x sub one, y sub one»), связанный с точкой P ₁, и второй
пара координат по (x ₂, y ₂), связанная со второй точкой P ₂, как показано на рисунке
7.7. Обратите внимание на рис. 7.7, что при переходе от P ₁ к P ₂ вертикальное изменение (или
расстояние по вертикали) между двумя точками составляет y ₂ — y ₁, а изменение по горизонтали (или
расстояние по горизонтали) составляет x ₂ — x ₁.

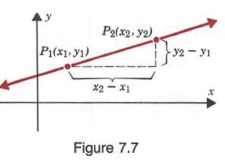
Отношение вертикального изменения к горизонтальному называется крутизной
линия, содержащая точки P ₁ и P ₂. Это соотношение обычно обозначают m.Таким образом,

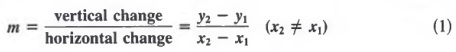
Пример 1 Найдите наклон прямой, содержащей два
точки с координатами (-4, 2) и (3, 5) как
показано на рисунке справа.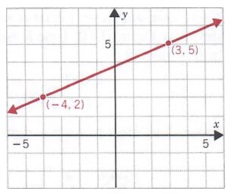
Решение
Мы обозначаем (3, 5) как (x ₂, y ₂) и (-4, 2)
как (x ₁, y ₁). Подставляя в уравнение (1)
дает

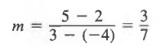
Обратите внимание, что мы получим тот же результат, если подставим -4 и 2 вместо x ₂ и y ₂ и 3 и
5 для x ₁ и y ₁

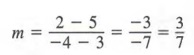
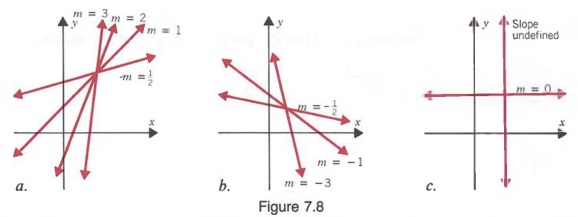
Линии с различным уклоном показаны на рисунке 7.8 ниже. Наклоны линий, которые
вверх вправо положительны (рис. 7.8а), а наклон линий, идущих вниз
справа отрицательны (рис. 7.8b). Обратите внимание (рис. 7.8c), поскольку все
точки на горизонтальной линии имеют одинаковое значение y, y ₂ — y ₁ равно нулю для любых двух
точек, а наклон линии просто

Также обратите внимание (рисунок 7.8c), что, поскольку все точки на вертикали имеют одинаковое значение x,
x ₂ — x ₁ равняется нулю для любых двух точек.Однако

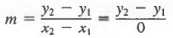
не определено, поэтому вертикальная линия не имеет наклона.

ПАРАЛЛЕЛЬНЫЕ И ПЕРПЕНДИКУЛЯРНЫЕ ЛИНИИ
Рассмотрим линии, показанные на рисунке 7.9. Линия l ₁ имеет наклон m ₁ = 3, а линия l ₂ имеет
уклон м ₂ = 3. В данном случае

Эти линии никогда не пересекаются и называются параллельными линиями. Теперь рассмотрим строки
показано на рисунке 7.10. Линия l ₁ имеет наклон m ₁ = 1/2, а линия l ₂ имеет наклон m ₂ = -2.В данном случае

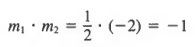
Эти линии пересекаются, образуя прямой угол, и называются перпендикулярными линиями.

Как правило, если две линии имеют уклон и м2:
а. Линии параллельны, если они имеют одинаковый наклон, то есть
если m ₁ = m ₂.
г. Линии перпендикулярны, если произведение их уклонов
равно -1, то есть если m ₁ * m ₂ = -1.
7.6 УРАВНЕНИЯ ПРЯМЫХ ЛИНИЙ
ФОРМА POINT-SLOPE
В разделе 7.5, мы нашли наклон прямой по формуле

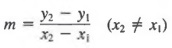
Допустим, мы знаем, что линия проходит через точку (2, 3) и имеет наклон 2.
Если мы обозначим любую другую точку на прямой как P (x, y) (см. Рис. 7.1а), наклоном
формула

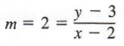
Таким образом, уравнение (1) — это уравнение прямой, проходящей через точку (2, 3), и
имеет уклон 2.

В общем, допустим, мы знаем, что линия проходит через точку P ₁ (x ₁, y ₁ и имеет
уклон м.Если мы обозначим любую другую точку на прямой как P (x, y) (см. Рисунок 7.11 b), то через
формула наклона

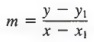
Уравнение (2) называется формой точечного уклона для линейного уравнения. В уравнении (2),
m, x ₁ и y ₁ известны, а x и y — переменные, которые представляют координаты
любая точка на линии. Таким образом, если нам известен наклон линии и точки на
линии, мы можем найти уравнение линии, используя уравнение (2).
Пример 1
Линия имеет наклон -2 и проходит через точку (2, 4).Найдите уравнение прямой.
Решение
Замените -2 вместо m и (2, 4) вместо (x ₁, y ₁) в уравнении (2)

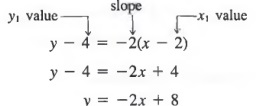
Таким образом, прямая с наклоном -2, проходящая через точку (2, 4), имеет уравнение
y = -2x + 8. Мы могли бы также записать уравнение в эквивалентной форме y + 2x = 8,
2x + y = 8 или 2x + y — 8 = 0.
ФОРМА НАКЛОНА
Теперь рассмотрим уравнение прямой с наклоном m и точкой пересечения оси y b, как показано на
Рисунок 7.12. Подставляя 0 вместо x ₁ и b вместо y ₁ в форме точечного наклона линейного
уравнение, имеем
y — b = m (x — 0)
y — b = mx
или
y = mx + b

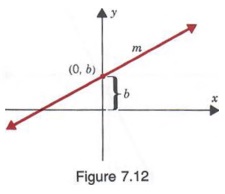
Уравнение (3) называется формой пересечения наклона
для линейного уравнения. Наклон и пересечение по оси Y
можно получить непосредственно из уравнения в
эта форма.
Пример 2 Если линия имеет уравнение

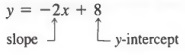
, то наклон линии должен быть -2, а точка пересечения оси Y — 8.Точно так же
график
г = -3x + 4
имеет наклон -3 и точку пересечения по оси Y 4; и график

имеет наклон 1/4 и точку пересечения по оси Y -2.
Если уравнение не записано в форме x = mx + b, и мы хотим знать наклон
и / или точку пересечения с y, мы переписываем уравнение, решая относительно y через x.
Пример 3
Найдите наклон и точку пересечения оси Y 2x — 3y = 6.
Решение
Сначала мы решаем y в терминах x, добавляя -2x к каждому члену.
2x — 3y — 2x = 6 — 2x
— 3y = 6 — 2x
Теперь, разделив каждого члена на -3, мы получим

Сравнивая это уравнение с формой y = mx + b, отметим, что наклон m (величина
коэффициент при x) равен 2/3, а точка пересечения оси y равна -2.
7.7 ПРЯМОЕ ИЗМЕНЕНИЕ
Частный случай уравнения первой степени с двумя переменными дается
y = kx (k — постоянная)
Такая связь называется прямой вариацией.Мы говорим, что переменная y изменяется
прямо как x.
Пример 1
Мы знаем, что давление P в жидкости изменяется прямо пропорционально глубине d ниже
поверхность жидкости. Мы можем обозначить это соотношение в символах как
P =
кД В прямом варианте, если мы знаем набор условий для двух переменных, и если
мы также знаем другое значение для одной из переменных, мы можем найти значение
вторая переменная для этого нового набора условий.
В приведенном выше примере мы можем решить для константы k, чтобы получить

Поскольку отношение P / d является постоянным для каждого набора условий, мы можем использовать соотношение
для решения задач, связанных с прямым изменением.
Пример 2
Если давление P напрямую зависит от глубины d и P = 40, когда d = 10, найдите P, когда
d = 15.
Решение
Поскольку отношение P / d является постоянным, мы можем подставить значения для P и d и получить
пропорция

Таким образом, P = 60 при d = 15.
7.8 НЕРАВЕНСТВА В ДВУХ ПЕРЕМЕННЫХ
В разделах 7.3 и 7.4 мы построили уравнения для двух переменных. В этом разделе мы
построит график неравенств по двум переменным. Например, рассмотрим неравенство
у ≤ -x + 6
Решения — это упорядоченные пары чисел, которые «удовлетворяют» неравенству.То есть,
(a, b) является решением неравенства, если неравенство является истинным утверждением после того, как мы
заменим a на x и b на y.
Пример 1
Определите, является ли данная упорядоченная пара решением y = -x + 6.
а. (1, 1)
б. (2, 5)
Решение
Упорядоченная пара (1, 1) является решением, потому что, когда 1 заменяется на x, а 1
подставляем вместо y, получаем
(1) = — (1) + 6, или 1 = 5
, что является правдой. С другой стороны, (2, 5) не является решением, потому что когда
2 заменяется на x и 5 заменяется на y, мы получаем
(5) = — (2) + 6, или 5 = 4
, что является ложным заявлением.
Чтобы изобразить неравенство y = -x + 6, сначала построим уравнение y = -x + 6
показано на рисунке 7.13. Обратите внимание, что (3, 3), (3, 2), (3, 1), (3, 0) и т. Д., Связанные
с точками, находящимися на линии или под ней, являются решениями неравенства
y = -x + 6, тогда как (3,4), (3, 5) и (3,6) связаны с остроумием
. Калькулятор уравнений 2-й степени — Бесплатный онлайн-калькулятор
Классы Класс 1-3
Класс 4-5
Класс 6-10
Класс 11-12
КОНКУРСНЫЙ ЭКЗАМЕН BNAT 000 NC 000 NC Книги Книги NCERT для класса 5
Книги NCERT для класса 6
Книги NCERT для класса 7
Книги NCERT для класса 8
Книги NCERT для класса 9
Книги NCERT для класса 10
Книги NCERT для класса 11
Книги NCERT для класса 12
NCERT Exemplar NCERT Exemplar Class 8
NCERT Exemplar Class 9
NCERT Exemplar Class 10
NCERT Exemplar Class 11
NCERT 9000 9000
NCERT Exemplar Class Решения RS Aggarwal, класс 12
Решения RS Aggarwal, класс 11
Решения RS Aggarwal, класс 10
90 003 Решения RS Aggarwal класса 9 Решения RS Aggarwal класса 8
Решения RS Aggarwal класса 7
Решения RS Aggarwal класса 6
Решения RD Sharma RD Sharma Class 6 Решения
Решения RD Sharma
Решения RD Sharma Class 8 Решения RD Sharma Class 9
Решения RD Sharma Class 10
Решения RD Sharma Class 11
Решения RD Sharma Class 12
PHYSICS Механика
Оптика
Термодинамика Электромагнетизм
ХИМИЯ Органическая химия
Неорганическая химия
Периодическая таблица
MATHS Теорема Пифагора
0004000300030004
Простые числа
Взаимосвязи и функции
Последовательности и серии
Таблицы умножения
Детерминанты и матрицы
Прибыль и убыток
Полиномиальные уравнения
Деление фракций
000
000
000
000
000
000 Microology
000
000 Microology
000 BIOG3000 FORMULAS Математические формулы
Алгебраические формулы
Тригонометрические формулы
Геометрические формулы
КАЛЬКУЛЯТОРЫ Математические калькуляторы
0003000 PBS4000
000300030002 Примеры калькуляторов химии
Класс 6 Образцы документов CBSE для класса 7
Образцы документов CBSE для класса 8
Образцы документов CBSE для класса 9
Образцы документов CBSE для класса 10
Образцы документов CBSE для класса 11
Образцы документов CBSE чел для класса 12
CBSE Контрольный документ за предыдущий год CBSE Контрольный документ за предыдущий год Класс 10
Контрольный документ за предыдущий год CBSE, класс 12
HC Verma Solutions HC Verma Solutions Class 11 Physics
Решения HC Verma, класс 12, физика
Решения Лакмира Сингха Решения Лакмира Сингха, класс 9
Решения Лакмира Сингха, класс 10
Решения Лакмира Сингха, класс 8
Заметки CBSE
, класс CBSE Notes Примечания CBSE класса 7 Примечания CBSE класса 8
Примечания CBSE класса 9
Примечания CBSE класса 10
Примечания CBSE класса 11
Примечания CBSE класса 12
Примечания к редакции CBSE Примечания к редакции
CBSE
Примечания к редакции класса 10 CBSE
Примечания к редакции класса 11 CBSE 9000 4
Примечания к редакции класса 12 CBSE
Дополнительные вопросы CBSE Дополнительные вопросы по математике класса 8 CBSE
Дополнительные вопросы по науке 8 класса CBSE
Дополнительные вопросы по математике класса 9 CBSE
Дополнительные вопросы по науке класса 9 CBSE
Дополнительные вопросы по математике для класса 10 Дополнительные вопросы по науке, класс 10 по CBSE
CBSE, класс, класс 3
, класс 4
, класс 5
, класс 6
, класс 7
, класс 8
, класс 9 Класс 10
Класс 11
Класс 12
Учебные решения
Решения NCERT Решения NCERT для класса 11 Решения NCERT для класса 11 по физике
Решения NCERT для класса 11 Химия
Решения для биологии класса 11 Решения NCERT для математики класса 11
9 0003 NCERT Solutions Class 11 Accountancy NCERT Solutions Class 11 Business Studies
NCERT Solutions Class 11 Economics
NCERT Solutions Class 11 Statistics
NCERT Solutions Class 11 Commerce
NCERT Solutions For Class 12 NCERT Solutions For Класс 12 по физике
Решения NCERT для химии класса 12
Решения NCERT для класса 12 по биологии
Решения NCERT для класса 12 по математике
Решения NCERT Класс 12 Бухгалтерия
Решения NCERT, класс 12, бизнес-исследования
Решения NCERT, класс 12 Экономика
NCERT Solutions Class 12 Accountancy Part 1
NCERT Solutions Class 12 Accountancy Part 2
NCERT Solutions Class 12 Micro-Economics
NCERT Solutions Class 12 Commerce
NCERT Solutions Class 12 Macro-Economics
NCERT Solutions For Класс 4 Решения NCERT для математики класса 4
Решения NCERT для класса 4 EVS
Решения NCERT для класса 5 Решения NCERT для математики класса 5
Решения NCERT для класса 5 EVS
Решения NCERT для класса 6 Решения NCERT для математики класса 6
Решения NCERT для науки класса 6
Решения NCERT для социальных наук класса 6
Решения NCERT для класса 6 Английский
Решения NCERT для класса 7 Решения NCERT для класса 7 Математика
Решения NCERT для класса 7 Наука
Решения NCERT для класса 7 по социальным наукам
Решения NCERT для класса 7 Английский
Решения NCERT для класса 8 Решения NCERT для класса 8 Математика
Решения NCERT для класса 8 Science
Решения NCERT для социальных наук 8 класса
Решение NCERT ns для класса 8 Английский
Решения NCERT для класса 9 Решения NCERT для социальных наук класса 9
Решения NCERT для математики класса 9 Решения NCERT для математики класса 9 Глава 1
Решения NCERT для Математика класса 9 Глава 2
Решения NCERT для математики класса 9 Глава 3
Решения NCERT для математики класса 9 Глава 4
Решения NCERT для математики класса 9 Глава 5
Решения NCERT для математики класса 9 Глава 6
Решения NCERT для Математика класса 9 Глава 7
Решения NCERT для математики класса 9 Глава 8
Решения NCERT для математики класса 9 Глава 9
Решения NCERT для математики класса 9 Глава 10
Решения NCERT для математики класса 9 Глава 11
Решения NCERT для Математика класса 9 Глава 12
Решения NCERT для математики класса 9 Глава 13
Решения NCERT для математики класса 9 Глава 14
Решения NCERT для математики класса 9 Глава 15
Решения NCERT для науки класса 9 Решения NCERT для науки класса 9 Глава 1
Решения NCERT для науки класса 9 Глава 2
Решения NCERT для класса 9 Наука Глава 3
Решения NCERT для Науки Класса 9 Глава 4
Решения NCERT для Науки Класса 9 Глава 5
Решения NCERT для Науки Класса 9 Глава 6
Решения NCERT для Науки Класса 9 Глава 7
Решения NCERT для Класса 9 Наука Глава 8
Решения NCERT для Науки Класса 9 Глава 9
Решения NCERT для Науки Класса 9 Глава 10
Решения NCERT для Науки Класса 9 Глава 12
Решения NCERT для Науки Класса 9 Глава 11
Решения NCERT для Класса 9 Наука Глава 13
Решения NCERT для класса 9 Наука Глава 14
Решения NCERT для класса 9 по науке Глава 15
Решения NCERT для класса 10 Решения NCERT для класса 10 по социальным наукам
Решения NCERT для математики класса 10 Решения NCERT для математики класса 10 Глава 1
Решения NCERT для математики класса 10 Глава 2
Решения NCERT для математики класса 10 Глава 3
Решения NCERT для математики класса 10 Глава 4
Решения NCERT для математики класса 10 Глава 5
Решения NCERT для математики класса 10 Глава 6
Решения NCERT для математики класса 10 Глава 7
Решения NCERT для математики класса 10 Глава 8
Решения NCERT для математики класса 10 Глава 9
Решения NCERT для математики класса 10 Глава 10
Решения NCERT для математики класса 10 Глава 11
Решения NCERT для математики класса 10 Глава 12
Решения NCERT для математики класса 10 Глава 13
NCERT Sol Решения NCERT для математики класса 10 Глава 14
Решения NCERT для математики класса 10 Глава 15
Решения NCERT для науки класса 10 Решения NCERT для науки класса 10 Глава 1
Решения NCERT для науки класса 10 Глава 2
Решения NCERT для науки класса 10, глава 3
Решения NCERT для науки класса 10, глава 4
Решения NCERT для науки класса 10, глава 5
Решения NCERT для науки класса 10, глава 6
Решения NCERT для науки класса 10, глава 7
Решения NCERT для науки 10 класса, глава 8
Решения NCERT для науки класса 10 Глава 9
Решения NCERT для науки класса 10 Глава 10
Решения NCERT для науки класса 10 Глава 11
Решения NCERT для науки класса 10 Глава 12
Решения NCERT для науки 10 класса Глава 13
Решения NCERT для науки 10 класса Глава 14
Решения NCERT для науки класса 10 Глава 15
Решения NCERT для науки класса 10 Глава 16
Учебный план NCERT
NCERT
Commerce Class 11 Commerce Syllabusancy Account
Учебная программа по бизнесу 11 класса
Учебная программа по экономике 11 класса
Учебная программа по коммерции 12 класса Учебная программа по бухгалтерии 12 класса
Учебная программа по бизнесу 12 класса
Учебная программа по экономике
9000
Образцы документов по коммерции класса 11
Образцы документов по коммерции класса 12
TS Grewal Solutions TS Grewal Solutions Class 12 Accountancy
TS Grewal Solutions Class 11 Accountancy
Отчет о движении денежных средств
Что такое Entry eurship
Защита прав потребителей
Что такое основные средства
Что такое баланс
Формат баланса
Что такое обыкновенные акции
.No related posts.}