- имеет два решения, если \(\displaystyle {\rm D}>0{\small ;}\)
- имеет одно решение (два совпадающих решения), если \(\displaystyle {\rm D}= 0{\small ;}\)
- не имеет решений, если \(\displaystyle {\rm D}<0{\small .}\)
Значит, так как \(\displaystyle {\rm D}=-55<0{ \small ,} \) то уравнение не имеет решений.
Задание 9 ОГЭ по математике. Уравнения, неравенства, системы уравнений и неравенств
Джамиля Агишева
При выполнении задания 9 ОГЭ по математике необходимо:
уметь решать линейные и квадратные уравнения, системы уравнений и неравенств.
Пример 1. Решите уравнение .
Решение. Уравнение линейное. Раскрываем скобки, приводим подобные слагаемые, все «иксы» переносим в левую часть равенства, всё без «иксов» – вправо:
Ответ: — 2.
Пример 2. Решите уравнение .
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение. Уравнение является квадратным , , . Вычисляем дискриминант и корни:
Ответ: .
Пример 3. Решите уравнение . Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Решение. В левой части данного уравнения произведение двух множителей-скобок, и это произведение равно нулю. Это возможно тогда и только тогда, когда хотя бы один из множителей равен нулю. Значит, получаем два уравнения:
Тогда меньший из корней уравнения равен -0,75.
Ответ: -0,75.
Пример 4. Решите систему уравнений
В ответе запишите значение .
Решение. Используем метод подстановки: из второго уравнения можно выразить y и подставить в первое уравнение.
Таким образом, .
Пример 5.
На рисунке изображены графики функций и . Вычислите ординату точки B.
Решение. Для нахождения координат точек пересечения графиков заданных функций необходимо решить систему уравнений.
Найдём корни первого уравнения системы.
̶ абсцисса точка B.
Тогда ордината точки В:
Ответ: -5.
Пример 6. Найдите наибольшее значение x, удовлетворяющее системе неравенств:
Решение. Выразим из каждого неравенства переменную x. Не забываем, что при делении обеих частей неравенства на положительное число знак неравенства не меняется, при делении на отрицательное число ̶ знак неравенства меняется на противоположный.
Используем числовую прямую. Решение первого неравенства отметим штриховкой («ёлочкой») с наклоном вправо, второго неравенства ̶ штриховкой с наклоном влево. При этом точка -2 будет «закрашенной», т.
Решением системы неравенств является тот промежуток, на котором пересеклись две «ёлочки», то есть две штриховки. Это промежуток . «Выколотой» точке соответствует круглая скобка, «закрашенной» ̶ квадратная.
Ответим на вопрос задачи. Наибольшее значение
Ответ: .
2 + bx + c, где a не равно 0. Выберите все утверждения, которые должны быть верными относительно графика f.A. Y-пересечение графика находится в точке (0,c).
B. На графике есть точка пересечения с точкой x (c, 0).
C.При a<0 график открывается вниз.
D.График имеет две точки пересечения.
E. Если b=0, то вершина находится на оси y.
Подписаться І 1
Подробнее
Отчет
1 ответ эксперта
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Раймонд Б.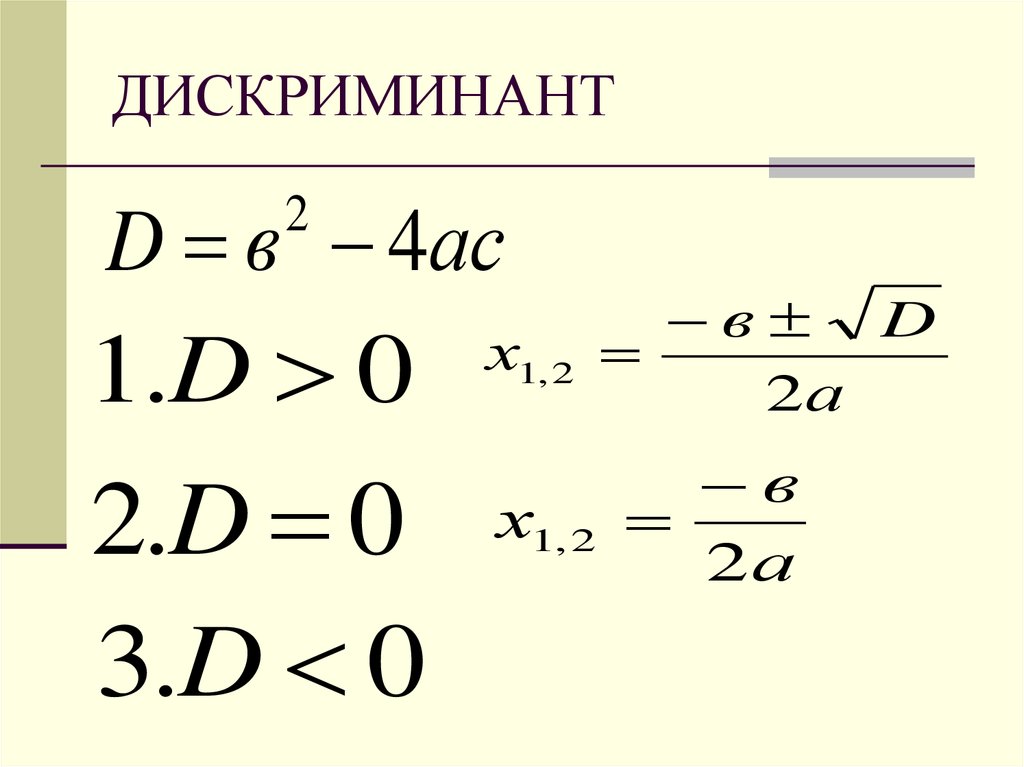
2 -4ac), что не равно (c,0), хотя координата y верна
когда a<0, парабола направлена вниз, C истинно
D ложно. квадратичный может иметь 2, 1 или 0 x точек пересечения. Если дискриминант <0, то действительных решений нет, и график никогда не пересекает ось x. Если дискриминант = 0, то решение одно, и график не «пересекает» ось x, а касается ее при одном значении x
E Верно: если b = 0, ось симметрии x= 0, а вершина имеет координату x = 0, поэтому вершина находится на оси y
A,C, E верны
B,D ложны
ACE да, BD нет
Голосовать за 0 голос против
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.
901:00 Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Как найти дискриминант квадратного уравнения?
Дискриминант является частью квадратной формулы ниже квадратного корня. Прочтите эту статью, чтобы узнать, как найти дискриминант квадратного уравнения.
Дискриминант в математике определяется для полиномов и является функцией коэффициентов полиномов. Выражает природу корней или, другими словами, различает корни.
Связанные темы- Как решить квадратное уравнение
Дискриминант представляет собой математическую функцию полинома от полинома.
2+bx+c = 0\) выражается его коэффициентами \(a, b\) и \(c\) . то есть 92+bx+c = 0\) — значения \(x\), удовлетворяющие уравнению. Их можно найти по квадратичной формуле: \(x=\frac{-b\pm \sqrt{D}}{2a}\). Хотя мы не можем найти корни, просто используя дискриминант, мы можем определить природу корней следующим образом.
Если \(D>0\), квадратное уравнение имеет два различных действительных корня. Это связано с тем, что, когда \(D>0\), корни задаются как \(x=\frac{-b\pm \sqrt{Positive\:number}}{2a}\), а квадратный корень из a положительное число всегда дает действительное число. Таким образом, когда дискриминант квадратного уравнения больше \(0\), оно имеет два корня, которые являются различными и действительными числами.
Если дискриминант отрицательный : Если \(D<0\), квадратное уравнение имеет два разных комплексных корня. Это связано с тем, что, когда \(D<0\), корни задаются как \(x=\frac{-b\pm \sqrt{Negative\:number}}{2a}\), а квадратный корень из отрицательного число всегда приводит к мнимому числу.