Уравнение касательной к графику функции
Чтобы закрепить предыдущий параграф, рассмотрим задачу нахождения касательной к графику функции в данной точке. Это задание встречалось нам в школе, и оно же встречается в курсе высшей математики.
Рассмотрим «демонстрационный» простейший пример.
Составить уравнение касательной к графику функции в точке с абсциссой . Я сразу приведу готовое графическое решение задачи (на практике этого делать в большинстве случаев не надо):
Строгое
определение касательной дается с помощью
определения самой производной функции,
и с этим пока повременим. Наверняка
практически всем интуитивно понятно,
что такое касательная. Если объяснять
«на пальцах», то касательная к графику
функции – этопрямая,
которая касается графика функции
в единственной точке.
При этом все близлежащие точки прямой
расположены максимально близко к графику
функции.
Применительно к нашему случаю: при касательная (стандартное обозначение) касается графика функции в единственной точке .
И наша задача состоит в том, чтобы найти уравнение прямой .
Как составить уравнение касательной в точке с абсциссой ?
Общая формула знакома нам еще со школы:
Значение нам уже дано в условии.
Теперь нужно вычислить, чему равна сама функция в точке :
На следующем этапе находим производную:
Находим производную в точке (задание, которое мы недавно рассмотрели):
Подставляем значения , и в формулу :
Таким образом, уравнение касательной:
Это «школьный» вид уравнения прямой с угловым коэффициентом. В высшей математике уравнение прямой принято записывать в так называемой общей форме , поэтому перепишем найденное уравнение касательной в соответствии с традицией:
Очевидно,
что точка
должна
удовлетворять данному уравнению: –
верное равенство.
Следует отметить, что такая проверка является лишь частичной. Если мы неправильно вычислили производную в точке , то выполненная подстановка нам ничем не поможет.
Рассмотрим еще два примера.
Пример 5
Составить уравнение касательной к графику функции в точке с абсциссой
Уравнение касательной составим по формуле
1) Вычислим значение функции в точке :
2) Найдем производную. Дважды используем правило дифференцирования сложной функции:
3) Вычислим значение производной в точке :
Готово.
Выполним частичную проверку: Подставим точку в найденное уравнение: – верное равенство.
Пример 6
Составить уравнение касательной к графику функции в точке с абсциссой
Полное решение и
образец оформления в конце урока.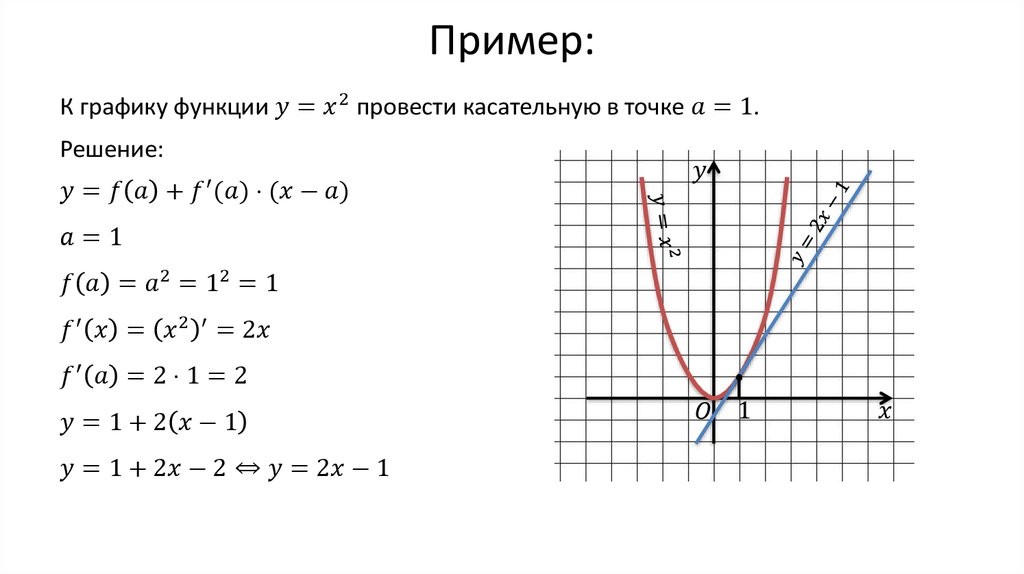
В задаче на нахождение уравнения касательной очень важно ВНИМАТЕЛЬНО и аккуратно выполнить вычисления, привести уравнение прямой к общему виду.
Коль скоро я не объяснил (на данный момент), что такое производная функции, то не имеет смысла объяснять, и что такое дифференциал функции. В самой примитивной формулировке дифференциал – это «почти то же самое, что и производная».
Производная функции чаще всего обозначается через .
Дифференциал функции стандартно обозначается через (так и читается – «дэ игрек»)
Дифференциал функции одной переменной записывается в следующем виде:
Другой вариант записи:
Простейшая задача: Найти дифференциал функции
1) Первый этап. Найдем производную:
2) Второй этап. Запишем дифференциал:
Готово.
Дифференциал
функции одной или нескольких переменных
чаще всего используют дляприближенных
вычислений.
Помимо других задач с дифференциалом время от времени встречается и «чистое» задание на нахождение дифференциала функции. Кроме того, как и для производной, для дифференциала существует понятие дифференциала в точке. И такие примеры мы тоже рассмотрим.
Пример 7
Найти дифференциал функции
Перед тем, как находить производную или дифференциал, всегда целесообразно посмотреть, а нельзя ли как-нибудь упростить функцию (или запись функции) ещё додифференцирования? Смотрим на наш пример. Во-первых, можно преобразовать корень:
(корень пятой степени относится именно к синусу).
Во-вторых, замечаем, что под синусом у нас дробь, которую, очевидно, предстоит дифференцировать. Формула дифференцирования дроби очень громоздка. Нельзя ли избавиться от дроби? В данном случае – можно, почленно разделим числитель на знаменатель:
Функция
сложная.
В ней два вложения: под степень
вложен синус, а под синус вложено
выражение
.
Найдем производную, используя правило
дифференцирования сложной функции
два
раза:
Запишем дифференциал, при этом снова представим в первоначальном «красивом» виде:
Готово.
Когда производная представляет собой дробь, значок обычно «прилепляют» в самом конце числителя (можно и справа на уровне дробной черты).
Пример 8
Найти дифференциал функции
Это пример для самостоятельного решения.
Следующие два примера на нахождение дифференциала в точке.
Пример 9
Вычислить дифференциал функции в точке
Найдем производную:
Опять, производная вроде бы найдена. Но в эту бодягу еще предстоит подставлять число, поэтому результат максимально упрощаем:
Труды были не напрасны, записываем дифференциал:
Теперь вычислим дифференциал в точке :
В
значок дифференциала
единицу
подставлять не нужно, он немного из
другой оперы.
Ну и хорошим тоном в математике считается устранение иррациональности в знаменателе. Для этого домножим числитель и знаменатель на . Окончательно:
Пример 10
Вычислить дифференциал функции в точке . В ходе решения производную максимально упростить.
Это пример для самостоятельного решения. Примерный образец оформления и ответ в конце урока.
Публикация не была найдена — Студопедия
Поделись с друзьями:
Из курса геометрии известно, что в прямоугольной декартовой системе координат уравнение прямой с угловым коэффициентом , проходящем через точку имеет вид:
. (1)
Поэтому, подставив в уравнение (1) , получим уравнение касательной к кривой в точке :
. (2)
Как известно, условием перпендикулярности прямых, задаваемых уравнениями с угловыми коэффициентами и , является условие . Следовательно, уравнение нормали к кривой в точке имеет вид:
.
(3)
Замечание: Уравнение (3) задает нормаль к графику функции в точке , если существует отличная от нуля производная .
Если , то касательная к кривой в такой точке будет параллельна оси , а ее уравнение будет иметь вид: . Из определения же нормали следует, что нормаль к кривой в такой точке будет перпендикулярна оси , а ее уравнение имеет вид .
Если же , то касательная к кривой в такой точке параллельна оси и ее уравнение имеет вид , а нормаль параллельна оси и ее уравнение имеет вид
Примеры: Найти уравнения касательной и нормали к кривым:
в точке с абсциссой
в точке с абсциссой
в точке с абсциссой
Решение:
1) Найдем значение функции в точке с : .
Далее найдем производную этой функции: . Теперь найдем
Составим уравнение касательной, для этого подставим найденные значения в уравнение (2):
– уравнение касательной
Составим уравнение нормали, для этого подставим найденные значения в уравнение (3):
– уравнение нормали.
2) Найдем значение функции в точке с абсциссой :
.
Найдем значение производной в точке :
.
Так как , то по замечанию уравнение касательной примет вид , то есть , а уравнение нормали , то есть .
3) Найдем значение функции в точке с абсциссой
.
Теперь найдем значение производной:
,
.
Подставив найденные значения в уравнение (2) получим уравнение касательной:
– уравнение касательной.
Подставив найденное значение в уравнение (3) получим уравнение нормали:
– уравнение нормали.
Упражнения:
1) В какой точке касательная к кривой параллельна прямой .
2) В какой точке касательная к кривой перпендикулярна прямой .
3) Кривая задана уравнением . Определить углы наклона касательных к положительному направлению оси , проведенных к кривой в точках с абсциссами .
4) Найти угловой коэффициент касательной, проведенной к кривой в точке .
5) Составить уравнение касательной и нормали к кривым в данных точках с абсциссами:
а)
б)
в)
г)
д) .
6) Найти координаты точки, в которой касательная к параболе образует угол в 135о с осью .
7) Найти скорость тела, движущегося по закону .
8) Тело движется прямолинейно по закону . Найти скорость тела в моменты , и .
9) Найти скорость движения тела в момент времени , если закон движения задан формулой: .
10) Когда скорость точки, движущейся прямолинейно по закону , равна нулю?
11) Какой угол образует с осью абсцисс касательная к параболе , проведенная в точке ? Составить уравнение этой касательной.
12) Найти угол наклона касательной к кубической параболе в точках с абсциссами , и .
13) Какой угол образует с осью абсцисс касательная к кривой в точке ?
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Уравнение касательной
В этой статье вы узнаете, что такое касательная и как найти уравнение касательной.
Вы часто будете сталкиваться с задачами в исчислении, где вас попросят найти уравнение прямой, касательной к кривой. Находим это уравнение касательной с помощью первой производной. При решении задач, связанных с уравнениями касательной, следует помнить следующее:
- Линия, касающаяся кривой только в одной точке, называется касательная .
- Форма наклон-пересечение уравнения линии есть y = mx + b. Здесь м представляет наклон линии, а b изображает точку пересечения y .
- Уравнение линии в форме точка-наклон: . Эта форма уравнения использует точку на линии, которая отражается . Наклон линии представлен m.
- Наклон означает среднюю скорость изменения функции в данной точке. Для расчета наклона нам нужно подставить значения и в следующую формулу наклона:
Наклон =
Наклон касательной
Наклон касательной к кривой в точке является производной функции в этой точке, как показано на графике выше.
Касательной к кривой в точке называется линия, проходящая через точку (a, f(a)) и наклон которой равен f ‘(a).
Лучшие репетиторы по математике
Поехали
Что такое производная?
Что касается производной функции, вы должны знать, что производная представляет собой мгновенную скорость изменения функции в данной точке. Геометрически первая производная представляет наклон линии. Другими словами, мы можем сказать, что наклон линии, касательной к кривой, представляет собой первую производную.
Обозначим производную функции следующими способами:
Формула для вычисления производной функции с использованием предела приведена ниже:
Мы можем найти даже высшие производные функции, то есть производную от производной. Эти производные известны как вторая производная, третья производная и четвертая производная соответственно. Мы можем найти производные, используя определенные правила дифференцирования, такие как правило суммы/разности, правило произведения, правило степени, правило отношения, правило цепочки и т.
д.
Шаги, чтобы найти уравнение касательной линии к кривой шаги, чтобы найти уравнение касательной линии к кривой:
- Найдите первую производную функции
- Подставьте значение точки в производную, чтобы получить наклон линии
- Найдите координату y уравнения, подставив точку, в которой линия касается кривой в исходное уравнение.
- Теперь у вас есть обе координаты x-y, поэтому вы можете легко подставить эти значения в форму уравнения «точка-наклон» и преобразовать ее в форму «наклон-отрезок».
В следующем разделе мы решим несколько примеров, в которых найдем уравнение касательной.
Пример 1
Найдите уравнение касательной к точке
Решение
Сначала нам нужно найти производную функции, используя правила суммы/разности и степени. Производная равна 2x, а производная 3 равна нулю.
Теперь следующим шагом является вычисление наклона касательной через производную функции.
В примере дано, что линия касается в точке x = 3. Следовательно, мы подставим 3 в приведенную выше производную, чтобы получить наклон касательной линии:
Следовательно, наклон касательной равен 6.
Чтобы составить уравнение касательной, мы должны знать ее точки. Дано, что прямая касается в точке х = 3. Следовательно, у нас есть x-координата линии. Чтобы найти координату y, мы подставим в уравнение
Следовательно, мы получили точки . Следовательно, мы можем легко сформулировать уравнение линии, используя следующую форму наклона точки:
Подставьте в приведенное выше уравнение:
Следовательно, уравнение линии , где 6 — это наклон, а -6 — точка пересечения линии по оси Y.
Пример 2
Найдите уравнение касательной к параболе в точке
Решение
Сначала нам нужно найти производную квадратичной функции в этом примере, которая задана в стандартной форме, используя сумму/разность и правила питания.
Производная равна 2x, производная 3x равна 3, а производная константы 4 равна нулю.
Теперь следующим шагом является вычисление наклона касательной через производную функции. В примере показано, что линия касается точки x = -1. Следовательно, мы подставим -1 в приведенную выше производную, чтобы получить наклон касательной:
Следовательно, наклон касательной равен 1.
Чтобы составить уравнение касательной , мы должны знать точки прямой. Дано, что прямая касается в точке x = -1. Следовательно, у нас есть x-координата линии. Чтобы найти координату y, подставим в уравнение
Итак, мы получили очки. Следовательно, мы можем легко сформулировать уравнение линии, используя следующую форму наклона точки:
Подставьте в приведенное выше уравнение:
наклон, а 3 — точка пересечения линии по оси Y.
Пример 3
Найдите уравнение касательной к точке
Решение
Во-первых, нам нужно найти производную функции, используя правила суммы/разности и степени.
Производная равна 2х. производная -4x равна -4, а производная константы 1 равна 0.
Теперь следующим шагом является вычисление наклона касательной через производную функции. В примере дано, что линия касается в точке x = 4. Следовательно, мы подставим 4 в приведенную выше производную, чтобы получить наклон касательной:
Следовательно, наклон касательной равен 4.
Чтобы составить уравнение касательной, мы должны знать точки этой линии. Дано, что прямая касается в точке x = 4. Следовательно, мы имеем x-координату прямой. Чтобы найти координату y, мы подставим в уравнение
Следовательно, мы получили точки . Следовательно, мы можем легко сформулировать уравнение линии, используя следующую форму наклона точки:
Подставьте в приведенное выше уравнение:
Следовательно, уравнение прямой имеет вид , где 4 — наклон, а -15 — точка пересечения линии по оси Y.
Окружность — Касательная: Примеры
В этом уроке будет рассмотрено несколько примеров, иллюстрирующих уравнения касательных к окружностям и точки их касания.