определение, алгоритм и методы решения, примеры
В математике большая часть задач ориентирована на решение стандартных уравнений, в которых представлена одна переменная. Однако, некоторые из них, помимо числовых выражений, содержат одновременно две неизвестные. Перед тем как приступить к решению такого уравнения, стоит изучить его определение.
Определение
Итак, уравнением с двумя неизвестными называют любое равенство следующего типа:
a*x + b*y =с, где a, b, c — числа, x, y — неизвестные переменные.
Ниже приведены несколько примеров:
- 10x + 25y = 180.
- x — y = 6.
- -6x + y = 7.
Уравнение с двумя неизвестными точно так же, как и с одной, имеет решение. Однако такие выражения, как правило, имеют бесконечное множество разных решений, поэтому в алгебре их принято называть неопределенными.
Решение задач
Чтобы решить подобные задачи, необходимо отыскать любую пару значений x и y, которая удовлетворяла бы его, другими словами, обращала бы уравнение с неизвестными x и y в правильное числовое равенство. Найти удовлетворяющую пару чисел можно при помощи метода подбора.
Для наглядности объяснений подберем корни для выражения: y-x = 6.
При y=5 и x=-1 равенство становится верным тождеством 5- (-1) = 6. Поэтому пару чисел (-1; 5) можно считать корнями выражения y-x = 6. Ответ: (-1; 5).
Необходимо отметить, что записывать полученный ответ по правилам необходимо в скобках через точку с запятой. Первым указывается значение х, вторым — значение y.
У равенств такого вида может и не быть корней. Рассмотрим такой случай на следующем примере: x+y = x+y+9
Приведем исходное равенство к следующему виду:
В результате мы видим ошибочное равенство, следовательно, это выражение не имеет корней.
При решении уравнений можно пользоваться его свойствами. Первое их них: каждое слагаемое можно вынести в другую часть выражения. Вместе с этим обязательно нужно поменять знак на обратный. Получившееся равенство будет равнозначно исходному.
Например, из выражения 20y — 3x = 16 перенесем неизвестное y в другую его часть.
- 20y — 3x = 16;
- -3x = 16−20y.
Оба равенства равносильны.
Второе свойство: допустимо умножать или делить части выражения на одинаковое число, не равное нолю. В итоге получившиеся равенства будут равнозначны.
Пример:
- y — x = 6*2;
- 2y — 2x = 12.
Оба уравнения также равносильны.

Система уравнений с двумя неизвестными
Система уравнений представляет собой некоторое количество равенств, выполняющихся одновременно. В большинстве задач приходится находить решение системы, состоящей из двух равенств с двумя переменными.
Для решения системы уравнений необходимо найти
Решить подобные системы уравнений можно, применяя следующие методы.
Метод подстановки
Последовательность действий:
- Выражаем неизвестное из любого равенства через вторую переменную.
- Подставляем получившееся выражение неизвестного во второе равенство и решаем его.
- Делаем подстановку полученного значения неизвестного и вычисляем значение второго неизвестного.
Метод сложения
Этапы решения:
- Приводим к равенству модули чисел при каком-либо неизвестном.
- Производим вычисление одной из переменных, произведя сложение или вычитание полученных выражений.
- Подставляем найденное значение в какое-либо уравнение в первоначальной системе и вычисляем вторую переменную.
Графический метод
- Выражаем в каждом равенстве одну переменную через другую.
- Строим графики двух имеющихся уравнений в одной координатной плоскости.
- Определяем точку их пересечения и ее координаты. На этом шаге у вас может получиться три варианта: графики пересекаются — у системы единственно верный вариант решения; прямые параллельны друг другу — система решений не имеет; графики совпадают — у системы бесконечно много решений.
- Делаем проверку, подставив полученные значения в исходную систему равенств.
При нахождении корней у одной системы всеми этими способами у вас обязательно должен получиться одинаковый результат, если вы, конечно, все сделали правильно.
В настоящее время есть возможность решения подобных задач с помощью встроенных средств офисной программы Excel, а также на специализированных онлайн-ресурсах и калькуляторах. С помощью них вы легко можете проверить правильность своих вычислений и результатов.
Надеемся, что наша статья помогла вам в освоении этой базовой темы школьной математики. Если же вы пока не можете справиться с решением уравнений такого вида, не расстраивайтесь. Для понимания и закрепления изученной темы рекомендуется как можно больше практиковаться, и тогда у вас без труда получится решать задачи любой сложности. Желаем вам удачи в покорении математических вершин!
Видео
Из этого видео вы узнаете, как решать уравнения с двумя неизвестными.
Способы решения систем уравнений с двумя неизвестными
Линейные системы уравнений
Системы линейных уравнений. Метод подстановки
+ показать
• Выражаем одну переменную через другую.
• Выраженную из одного уравнения переменную подставляем во второе уравнение. Получаем уравнение относительно одной переменной, которое и решаем.
• Опираясь на найденное значение одной переменной, находим значение второй, подставляя в оставшееся уравнение.
Решить систему уравнений: 
Решение: + показать
Системы линейных уравнений. Метод сложения
+ показать
• Добиваемся, путем равносильных преобразований, наличия равных (или противоположных) коэффициентов при одной из неизвестных переменных в уравнениях.
• Вычитаем (или складываем) полученные уравнения с целью выхода на уравнение с одной неизвестной.
• Решаем полученное уравнение с одной неизвестной.
• Найденное значение одной переменной подставляем в любое из уравнений системы, находим значение второй.
1. Решить систему уравнений: 
Решение: + показать Складываем уравнения системы, заменяя результатом одно из уравнений, оставляя другое. Ответ: 



2. Решить систему уравнений: 
Решение: + показать
Нелинейные системы уравнений
Системы уравнений, сводящихся к линейным
1. Решить систему уравнений: 
Решение: + показать Можно сделать замену  и
и 

Систему можно решить методом сложения, например.
Но приведем решение без замены.
Умножим первое уравнение системы на  , второе – на
, второе – на  и произведем сложение полученных уравнений, оставим при этом в системе, например, первое уравнение исходной системы.
и произведем сложение полученных уравнений, оставим при этом в системе, например, первое уравнение исходной системы.





Ответ: 
2. Решить систему уравнений: 
Решение: + показать Можно сделать замену Приведем решение без замены. Выражаем Ответ:  и выйти на систему линейных уравнений:
и выйти на систему линейных уравнений:
 из второго уравнения системы и подставляем в первое.
из второго уравнения системы и подставляем в первое.




Нелинейные системы уравнений. Метод подстановки
Решить систему уравнений: 
Решение: + показать Выражаем Ответ:  из первого уравнения системы и подставляем во второе.
из первого уравнения системы и подставляем во второе.




Нелинейные системы уравнений. Метод сложения
Решить систему уравнений: 
Решение: + показать Складываем уравнения системы, заменяя результатом одно из уравнений, оставляя другое. Ответ: 




Нелинейные системы уравнений. Метод почленного умножения (деления)
1. Решить систему уравнений: 
Решение: + показать Производим деление первой строки на вторую, оставляем в системе вторую строку без изменений. Ответ: 






Симметрические системы. Метод введения переменной
Симметрическая система – система, все уравнения которой симметрические. Симметрическое уравнение от двух переменных  и
и  – уравнение, которое не изменяется при замене
– уравнение, которое не изменяется при замене  на
на  и
и  на
на  .
.
Для таких систем удобно использовать замену 
Решить систему уравнений: 
Решение: + показать При замене которую будем решать способом подстановки: Производим обратную замену: Ответ: 
 приходим к следующей системе
приходим к следующей системе







Системы однородных уравнений и приводящиеся к ним системы
Однородным уравнением с двумя неизвестными  будем называть уравнение вида
будем называть уравнение вида 
1. Решить систему уравнений: 
Решение: + показать
2. Решить систему уравнений: 
Решение: + показать Применим прежде к системе метод сложения. После чего выйдем на однородное уравнение. Ответ: 





Графический метод решения систем уравнений
1. Решите графически систему уравнений: 
Решение: + показать Выразим в обеих строках системы Первое уравнение системы задает прямую, второе – гиперболу. Строим графики в одной системе координат, находим координаты точек пересечения графиков. Ответ:  через
через  :
:


2. Решите графически систему уравнений: 
Решение: + показать
3. Решите графически систему уравнений: 
Решение: + показать
Задания для самостоятельной работы
+ показать Решите системы уравнений: 1. Ответ: 2. Ответ: 3. Ответ: 4. Ответ: 5. Ответ: 6. Ответ: 7. Ответ: 8. Ответ: Решите графически системы уравнений: 9. Ответ: 10. Ответ: 



















Решение уравнений с двумя неизвестными онлайн калькулятор
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Наверняка многие знают, что уравнение представляет собой некое тождество с неизвестной, которую необходимо определить, чтобы решить уравнение и получить равные значения левой и правой частей. Чтобы решить данного рода уравнения необходимо перенести в левую сторону все известные значения, а в правую все неизвестные. Решить данные уравнения можно с помощью 3 методов:
1) подстановки;
2) сложения;
3) построения графиков.
Выбор метода зависит от целевого уравнения. Решить онлайн уравнение с двумя неизвестными можно на многих сайтах, однако слепо доверять полученному результату не стоит.

Так же читайте нашу статью «Решить уравнение с 3 неизвестными онлайн»
Ниже приведен пример решения уравнения с 2 неизвестными методом сложения.
\[2x — 5y = 61\]
\[-9x + 5y = -40\]
Первое, с чего стоит начать решение — сложить каждое слагаемое с учетом их знаков:
\[2x + (-9x) = -7x\]
\[-5y + 5y = 0\]
\[61 + (-40) = 21\]
В большинстве случаев, одна из сумм, включающая в себя неизвестную будет содержать величину, равную нулю. На следующем этапе решения уравнения нам необходимо составить уравнение из полученных данных:
\[-7x + 0 = 21\]
Найти неизвестное:
\[-7x = 21, x = 21 \div (-7) = -3\]
Вставить полученное значение в любое из исходных уравнений и получить 2 неизвестное с помощью решения уравнения линейного типа:
\[2x — 5y = 61\]
\[2(-3) — 5y = 61\]
\[-6 — 5y = 61\]
\[-5y = 61 + 6\]
\[-5y = 67\]
\[y = -13,4\]
Конечный результат:
\[x = -3, y = -13,4\]
Где можно решить уравнение с 2 неизвестными онлайн?
Решить уравнение с двумя неизвестными онлайн решателем можно на сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Нелинейные уравнения с двумя неизвестными
Определение 1. Пусть A – некоторое множество пар чисел (x ; y) . Говорят, что на множестве A задана числовая функция z от двух переменных x и y , если указано правило, с помощью которого каждой паре чисел из множества A ставится в соответствие некоторое число.
Задание числовой функции z от двух переменных x и y часто обозначают так:
причем в записи (1) числа x и y называют аргументами функции, а число z – значением функции, соответствующим паре аргументов (x ; y) .
Определение 2. Нелинейным уравнением с двумя неизвестными x и y называют уравнение вида
где f (x , y) – любая функция, отличная от функции
f (x , y) = ax +by + c ,
где a , b , c – заданные числа.
Определение 3. Решением уравнения (2) называют пару чисел (x ; y) , для которых формула (2) является верным равенством.
Пример 1. Решить уравнение
| x2 – 4xy + 6y2 – – 12 y +18 = 0 . | (3) |
Решение. Преобразуем левую часть уравнения (3):
x2 – 4xy + 6y2 – 12 y +18 =
= (x2 – 4xy + 4y2) +
+ (2y2– 12y +18) =
= (x – 2y)2 + 2(y – 3)2 .
Таким образом, уравнение (3) можно переписать в виде
| (x – 2y)2 + 2(y – 3)2 = 0 . | (4) |
Поскольку квадрат любого числа неотрицателен, то из формулы (4) вытекает, что неизвестные x и y удовлетворяют системе уравнений

решением которой служит пара чисел (6 ; 3) .
Ответ: (6 ; 3)
Пример 2. Решить уравнение
Решение. Из неравенства
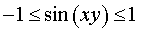
вытекает, что уравнение (5) решений не имеет.
Ответ: Решений нет.
Пример 3. Решить уравнение
Решение. В соответствии с определением логарифма из формулы (6) получаем

Следовательно, решением уравнения (6) является бесконечное множество пар чисел вида
(1 + y ; y) ,
где y – любое число.
Системы из двух уравнений, одно из которых линейное
Определение 4. Решением системы уравнений
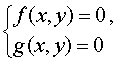
называют пару чисел (x ; y) , при подстановке которых в каждое из уравнений этой системы получается верное равенство.
Системы из двух уравнений, одно из которых линейное, имеют вид
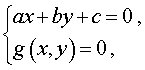
где a , b , c – заданные числа, а g(x , y) – функция двух переменных x и y .
Пример 4. Решить систему уравнений
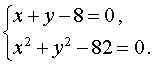 | (7) |
Решение. Выразим из первого уравнения системы (7) неизвестное y через неизвестное x и подставим полученное выражение во второе уравнение системы:
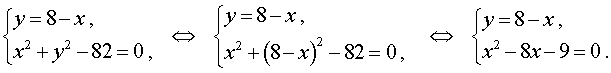
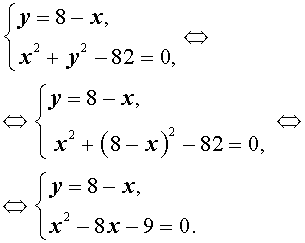
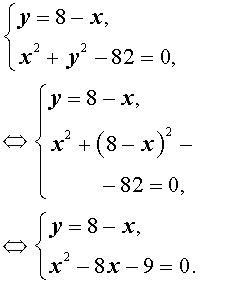
Решая уравнение
x2 – 8x – 9 = 0 ,
находим корни
x1 = – 1 , x2 = 9 .
Следовательно,
y1 = 8 – x1 = 9 ,
y2 = 8 – x2 = – 1 .
Таким образом, решениями системы (7) являются две пары чисел
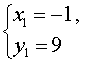 и
и 
Ответ: (– 1 ; 9) , (9 ; – 1)
Однородные уравнения второй степени с двумя неизвестными
Определение 5. Однородным уравнением второй степени с двумя неизвестными x и y называют уравнение вида
ax2 + bxy + cy2 = 0 .
где a , b , c – заданные числа.
Пример 5. Решить уравнение
| 3x2 – 8xy + 5y2 = 0 . | (8) |
Решение. Для каждого значения y рассмотрим уравнение (8) как квадратное уравнение относительно неизвестного x . Тогда дискриминант D квадратного уравнения (8) будет выражаться по формуле
D = (8y)2 – 60y2 = 4y2 ,
откуда с помощью формулы для корней квадратного уравнения найдем корни уравнения (8):

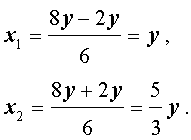
Ответ. Решениями уравнения (8) являются все пары чисел вида
( y ; y) или 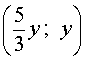
где y – любое число.
Следствие. Левую часть уравнения (8) можно разложить на множители

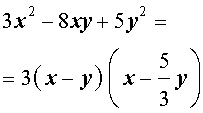
Системы из двух уравнений, одно из которых однородное
Системы из двух уравнений, одно из которых однородное, имеют вид
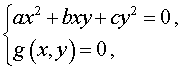
где a , b , c – заданные числа, а g(x , y) – функция двух переменных x и y .
Пример 6. Решить систему уравнений
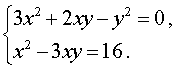 | (9) |
Решение. Решим однородное уравнение
3x2 + 2xy – y2 = 0 ,
рассматривая его как квадратное уравнение относительно неизвестного x :
 .
.
В случае, когда x = – y , из второго уравнения системы (9) получаем уравнение
4y2 = 16 ,
корнями которого служат числа y1 = 2 , y2 = – 2 . Находя для каждого из этих значений y соответствующее ему значение x , получаем два решения системы: (– 2 ; 2) , (2 ; – 2) .
В случае, когда
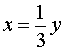 ,
,
из второго уравнения системы (9) получаем уравнение
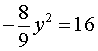
которое корней не имеет.
Ответ: (– 2 ; 2) , (2 ; – 2)
Системы из двух уравнений, сводящиеся к системам, в которых одно из уравнений однородное
Пример 7. Решить систему уравнений
 | (10) |
Решение. Совершим над системой (10) следующие преобразования:
- второе уравнение системы оставим без изменений;
- к первому уравнению, умноженному на 5 , прибавим второе уравнение, умноженное на 3 , и запишем полученный результат вместо первого уравнения системы (10).
В результате система (10) преобразуется в равносильную ей систему (11), в которой первое уравнение является однородным уравнением:
 | (11) |
Решим однородное уравнение
3x2 + 17xy + 10y2 = 0 ,
рассматривая его как квадратное уравнение относительно неизвестного x :
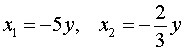 .
.
В случае, когда x = – 5y , из второго уравнения системы (11) получаем уравнение
5y2 = – 20 ,
которое корней не имеет.
В случае, когда
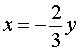 ,
,
из второго уравнения системы (11) получаем уравнение
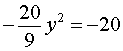 ,
,
корнями которого служат числа y1 = 3 , y2 = – 3 . Находя для каждого из этих значений y соответствующее ему значение x , получаем два решения системы: (– 2 ; 3) , (2 ; – 3) .
Ответ: (– 2 ; 3) , (2 ; – 3)
Примеры решения систем уравнений других видов
Пример 8. Решить систему уравнений (МФТИ)
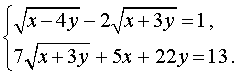 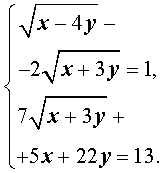 | (12) |
Решение. Введем новые неизвестные u и v , которые выражаются через x и y по формулам:
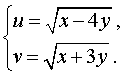 | (13) |
Для того, чтобы переписать систему (12) через новые неизвестные, выразим сначала неизвестные x и y через u и v . Из системы (13) следует, что
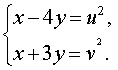 | (14) |
Решим линейную систему (14), исключив из второго уравнения этой системы переменную x . С этой целью совершим над системой (14) следующие преобразования:
- первое уравнение системы оставим без изменений;
- из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.
В результате система (14) преобразуется в равносильную ей систему

из которой находим
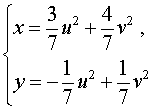 | (15) |
Воспользовавшись формулами (13) и (15), перепишем исходную систему (12) в виде
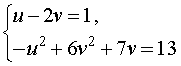 | (16) |
У системы (16) первое уравнение – линейное, поэтому мы можем выразить из него неизвестное u через неизвестное v и подставить это выражение во второе уравнение системы:
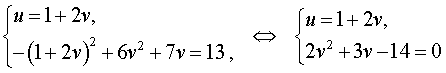
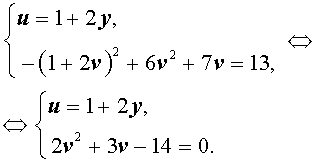
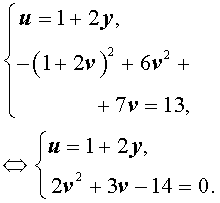
Решая уравнение
2v2 + 3v – 14 = 0 ,
находим корни
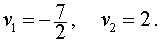
Следовательно, решениями системы (16) являются две пары чисел
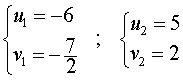
Из формул (13) вытекает, что  , поэтому первое решение должно быть отброшено. В случае u2 = 5, v2 = 2 из формул (15) находим значения x и y :
, поэтому первое решение должно быть отброшено. В случае u2 = 5, v2 = 2 из формул (15) находим значения x и y :
x = 13, y = – 3 .
Ответ: (13 ; – 3)
Определение 6. Решением системы из двух уравнений с тремя неизвестными называют тройку чисел (x ; y ; z) , при подстановке которых в каждое уравнение системы получается верное равенство.
Пример 9. Решить систему из двух уравнений с тремя неизвестными
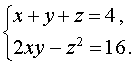 | (17) |
Решение. У системы (17) первое уравнение – линейное, поэтому мы можем выразить из него неизвестное z через неизвестные x и y и подставить это выражение во второе уравнение системы:
 | (18) |
Перепишем второе уравнение системы (18) в другом виде:
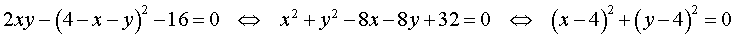
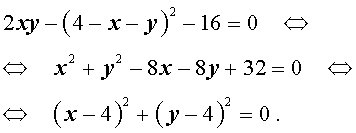
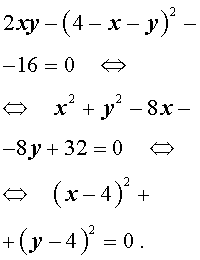
Поскольку квадрат любого числа неотрицателен, то выполнение последнего равенства возможно лишь в случае x = 4, y = 4 .
Следовательно,
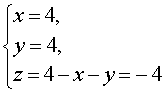
Ответ: (4 ; 4 ; – 4)
Замечание. Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы линейных уравнений» и нашим учебным пособием «Системы уравнений».

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
2.1.8 Простейшие системы уравнений с двумя неизвестными
Видеоурок 1: Системы двух уравнений с двумя неизвестнымиВидеоурок 2: Решение систем уравнений
Лекция: Простейшие системы уравнений с двумя неизвестными
 Уравнения с двумя неизвестными
Уравнения с двумя неизвестнымиВ этой теме мы рассмотрим с Вами уравнения, которые содержат две неизвестных. Зачастую, чтобы решить подобного рода уравнения, нам необходимо иметь столько уравнений, сколько содержится неизвестных.
Уравнения с двумя неизвестными имеют следующий вид:

a, b, c, d — это числа, стоящие рядом в переменными (х, у).
Решить систему уравнения — это означает найти такое значение переменных, которые приведут оба уравнения в верное равенство.
Каждое из уравнений может иметь несколько ответов, однако ответом на систему уравнений будет та пара чисел, которая будет подходить обоим уравнениям.
Трактовать решение системы уравнений можно аналитическим способом, некоторые из которых мы рассмотрим позднее, и графическим способом.
 Графический способ решения системы уравнений
Графический способ решения системы уравненийДля каждого из заданных уравнений можно построить свой график на плоскости — это может быть любой из известных графиков функции. Решением системы уравнений будет считаться точка, в которой будут пересекаться графики. Данная точка будет иметь свою координату, которой будет соответствовать ордината и абсцисса, которые будут являться решением.
На графике можно получить несколько видов решений:
1. Множество решений. Например, если одно уравнение будет представлять тригонометрическую функцию, а вторая — это прямая, например, параллельная оси ОХ, то данная прямая будет пересекать график второй функции во множестве точек с некой периодичностью.
2. Одно решение. В таком случае графики функций будут пересекаться в одной точке. Обычно такая картина наблюдается, если графиками уравнений являются прямые.
3. Два решения. То есть графики уравнений будут пересекаться в двух точках. Обычно такое наблюдается в том случае, если графиком одной из функций является парабола.
4. Не иметь решений. Некоторые графики функций и вовсе могут не пересекаться, в таком случае решений система иметь не будет.
 Основные способы аналитического решения
Основные способы аналитического решенияРешать с помощью графика не всегда удобно, поскольку точка пересечения функций может находиться достаточно далеко от начала координат, или же она будет иметь дробные координаты. Чтобы наиболее точно найти решение системы, лучше воспользоваться аналитическими способами решения.
1. Подстановка
Чтобы решить систему методом подстановки, необходимо в одном из уравнений выразить одну из неизвестных и подставить её во второе уравнение.

x = ( c – by ) / a
d ( c – by ) / a + ey = f
После данной подстановки одно из уравнений будет иметь одну неизвестную, после чего уравнение решается известным способом. Когда одна из переменных найдена, её значение подставляется в первое уравнение и, таким образом, находится и вторая переменная.
2. Метод сложения или вычитание уравнений
Данный метод позволяет избавиться от одной из неизвестных. Итак, давайте представим, что вы желаете избавиться от переменной «х». Чтобы данный способ имел место, Вам необходимо первое уравнение почленно домножить на d, а второе почленно домножить на a. После этого Вы получите одинаковые коэффициенты при переменной «х». Если вычтите одно уравнение из другого, у Вас получится избавиться от одной неизвестной. Дальше уравнение известными способами.
Линейные диофантовы уравнения с двумя переменными
Сначала калькулятор, теория под ним.

Линейные диофантовы уравнения с двумя переменными
Множество всех х
Множество всех y
save Сохранить extension Виджет
Диофантово уравнение с двумя неизвестными имеет вид:
,
где a, b, c — заданные целые числа, x и y — неизвестные целые числа.
Для нахождения решений уравнения используется Расширенный алгоритм Евклида (исключая вырожденный случай, когда a = b = 0 и уравнение имеет либо бесконечно много решений, либо же не имеет решений вовсе).
Если числа a и b неотрицательны, тогда с помощью расширенного алгоритма Евклида мы можем найти их наибольший общий делитель g, а также такие коэффициенты и , что:
.
Утверждается, что если число c делится на g, то диофантово уравнение имеет решение; в противном случае диофантово уравнение решений не имеет. Это следует из очевидного факта, что линейная комбинация двух чисел по-прежнему должна делиться на их общий делитель.
То есть если c делится на g, тогда выполняется соотношение:
,
т. е. одним из решений диофантова уравнения являются числа:
Если одно из чисел a и b или они оба отрицательны, то можно взять их по модулю и применить к ним алгоритм Евклида, как было описано выше, а затем изменить знак найденных коэффициентов и в соответствии с настоящим знаком чисел a и b соответственно.
Если мы знаем одно из решений, мы можем получить выражение для всех остальных решений, которых бесконечное множество.
Итак, пусть g = НОД (a,b), выполняется условие:
.
Тогда, прибавив к число и одновременно отняв от , мы не нарушим равенства:
Этот процесс можно повторять сколько угодно, т. е. все числа вида:
,
где k принадлежит множеству целых чисел, являются множеством всех решений диофантова уравнения.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Линейные уравнения (уравнения первой степени) с двумя неизвестными
Определение 1. Линейным уравнением (уравнением первой степени) с двумя неизвестными x и y называют уравнение, имеющее вид
где a , b , c – заданные числа.
Определение 2. Решением уравнения (1) называют пару чисел (x ; y) , для которых формула (1) является верным равенством.
Пример 1. Найти решение уравнения
Решение. Выразим из равенства (2) переменную y через переменную x :
 | (3) |
Из формулы (3) следует, что решениями уравнения (2) служат все пары чисел вида

где x – любое число.
Замечание. Как видно из решения примера 1, уравнение (2) имеет бесконечно много решений. Однако важно отметить, что не любая пара чисел (x ; y) является решением этого уравнения. Для того, чтобы получить какое-нибудь решение уравнения (2), число x можно взять любым, а число y после этого вычислить по формуле (3).
Системы из двух линейных уравнений с двумя неизвестными
Определение 3. Системой из двух линейных уравнений с двумя неизвестными x и y называют систему уравнений, имеющую вид
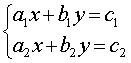 | (4) |
где a1 , b1 , c1 , a2 , b2 , c2 – заданные числа.
Определение 4. В системе уравнений (4) числа a1 , b1 , a2 , b2 называют коэффициентами при неизвестных, а числа c1 , c2 – свободными членами.
Определение 5. Решением системы уравнений (4) называют пару чисел (x ; y) , являющуюся решением как одного, так и другого уравнения системы (4).
Определение 6. Две системы уравнений называют равносильными (эквивалентными), если все решения первой системы уравнений являются решениями второй системы, и все решения второй системы являются решениями первой системы.
Равносильность систем уравнений обозначают, используя символ « »
»
Системы линейных уравнений решают с помощью метода последовательного исключения неизвестных, который мы проиллюстрируем на примерах.
Пример 2 . Решить систему уравнений
 | (5) |
Решение. Для того, чтобы решить систему (5) исключим из второго уравнения системы неизвестное х.
С этой целью сначала преобразуем систему (5) к виду, в котором коэффициенты при неизвестном x в первом и втором уравнениях системы станут одинаковыми.
Если первое уравнение системы (5) умножить на коэффициент, стоящий при x во втором уравнении (число 7 ), а второе уравнение умножить на коэффициент, стоящий при x в первом уравнении (число 2 ), то система (5) примет вид
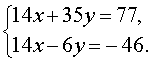 | (6) |
Теперь совершим над системой (6) следующие преобразования:
- первое уравнение системы оставим без изменений;
- из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.
В результате система (6) преобразуется в равносильную ей систему

Из второго уравнения находим y = 3 , и, подставив это значение в первое уравнение, получаем
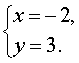
Ответ. (–2 ; 3) .
Пример 3. Найти все значения параметра p , при которых система уравнений
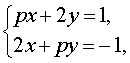 | (7) |
а) имеет единственное решение;
б) имеет бесконечно много решений;
в) не имеет решений.
Решение. Выражая x через y из второго уравнения системы (7) и подставляя полученное выражение вместо x в первое уравнение системы (7), получим
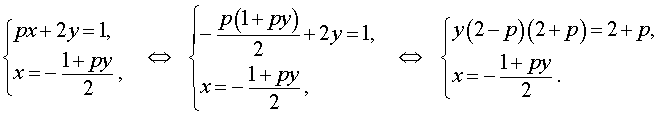
Следовательно, система (7) равносильна системе
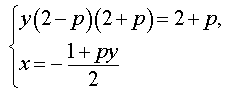 | (8) |
Исследуем решения системы (8) в зависимости от значений параметра p . Для этого сначала рассмотрим первое уравнение системы (8):
| y (2 – p) (2 + p) = 2 + p | (9) |
Если 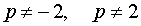 , то уравнение (9) имеет единственное решение
, то уравнение (9) имеет единственное решение

Следовательно, система (8) равносильна системе

Таким образом, в случае, когда 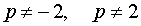 , система (7) имеет единственное решение
, система (7) имеет единственное решение
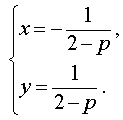
Если p = – 2 , то уравнение (9) принимает вид
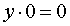 ,
,
и его решением является любое число 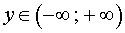 . Поэтому решением системы (7) служит бесконечное множество всех пар чисел
. Поэтому решением системы (7) служит бесконечное множество всех пар чисел
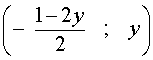 ,
,
где y – любое число.
Если p = 2 , то уравнение (9) принимает вид
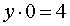
и решений не имеет, откуда вытекает, что и система (7) решений не имеет.
Системы из трех линейных уравнений с тремя неизвестными
Определение 7. Системой из трех линейных уравнений с тремя неизвестными x , y и z называют систему уравнений, имеющую вид
 | (10) |
где a1 , b1 , c1 , d1 , a2 , b2 , c2 , d2 , a3 , b3 , c3 , d3 – заданные числа.
Определение 8. В системе уравнений (10) числа a1 , b1 , c1 , a2 , b2 , c2 , a3 , b3 , c3 называют коэффициентами при неизвестных, а числа d1 , d2 , d3 – свободными членами.
Определение 9. Решением системы уравнений (10) называют тройку чисел (x ; y ; z) , при подстановке которых в каждое из трех уравнений системы (10) получается верное равенство.
Пример 4 . Решить систему уравнений
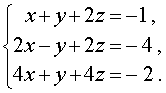 | (11) |
Решение. Будем решать систему (11) при помощи метода последовательного исключения неизвестных.
Для этого сначала исключим из второго и третьего уравнений системы неизвестное y , совершив над системой (11) следующие преобразования:
- первое уравнение системы оставим без изменений;
- ко второму уравнению прибавим первое уравнение и заменим второе уравнение системы на полученную сумму;
- из третьего уравнения вычтем первое уравнение и заменим третье уравнение системы на полученную разность.
В результате система (11) преобразуется в равносильную ей систему
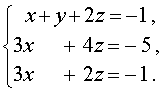 | (12) |
Теперь исключим из третьего уравнения системы неизвестное x , совершив над системой (12) следующие преобразования:
- первое и второе уравнения системы оставим без изменений;
- из третьего уравнения вычтем второе уравнение и заменим третье уравнение системы на полученную разность.
В результате система (12) преобразуется в равносильную ей систему
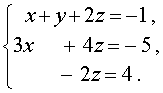 | (13) |
Из системы (13) последовательно находим
z = – 2 ; x = 1 ; y = 2 .
Ответ. (1 ; 2 ; –2) .
Пример 5. Решить систему уравнений
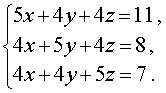 | (14) |
Решение. Заметим, что из данной системы можно получить удобное следствие, сложив все три уравнения системы:
Если числа (x ; y ; z) являются решением системы (14), то они должны удовлетворять и уравнению (15). Однако в таком случае числа (x ; y ; z) должны также быть решением системы, которая получается, если из каждого уравнения системы (14) вычесть уравнение (15):

Поскольку мы использовали следствие из системы (14), не задумываясь о том, являются ли сделанные преобразования системы (14) равносильными, то полученный результат нужно проверить. Подставив тройку чисел (3 ; 0 ; –1) в исходную систему (14), убеждаемся, что числа (3 ; 0 ; –1) действительно являются ее решением.
Ответ: (3 ; 0 ; –1) .
Замечание. Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы с нелинейными уравнениями» и нашим учебным пособием «Системы уравнений».

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
