|
Алгебра 7-9 классы. 9. Решение линейных уравнений с двумя неизвестными
Алгебра 7-9 классы. 9. Решение линейных уравнений с двумя неизвестными
- Подробности
- Категория: Алгебра 7-9 классы
УРАВНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ И ЕГО ГРАФИК
Пусть требуется найти два числа» разность которых равна 5. Если первое число обозначить буквой х, а второе буквой у, то соотношение между ними можно записать в виде равенства .
Если первое число обозначить буквой х, а второе буквой у, то соотношение между ними можно записать в виде равенства .
Равенство содержит две переменные. Такие равенства называют уравнениями с двумя переменными или уравнениями с двумя неизвестными.
При уравнение обращается в верное равенство 8 — 3 = 5. Говорят, что пара значений переменных является решением этого уравнения. Пара х = 3, у = 8 не обращает уравнение в верное равенство, значит, не является его решением.
Определение. Решением уравнения с двумя переменными называется пара значений,переменных, обращающая это уравнение в верное равенство.
Пару , являющуюся решением уравнения , можно записать так: (8; 3). При такой записи необходимо знать, значение какой из переменных стоит на первом месте, а какой — на втором. В записи решений уравнений с переменными х и у на первое место ставят значения х, а на второе место — значения у. Например, решениями уравнения служат также пары: (12; 7), (5,2; 0,2), ( — 2; —7), (3,8; -1,2).’
Например, решениями уравнения служат также пары: (12; 7), (5,2; 0,2), ( — 2; —7), (3,8; -1,2).’
Уравнения с двумя переменными, имеющие одни и те же решения, называются равносильными.
Уравнения с двумя переменными обладают такими же свойствами, как и уравнения с одной переменной. В уравнении слагаемые можно переносить из одной его части в другую, изменив знаки этих слагаемых; обе части уравнения можно умножать или делить на одно и то же число, отличное от нуля. При этом получаются уравнения, равносильные исходному. Чтобы найти решения уравнения
можно подставить в него вместо х произвольное число, например 3. Получим уравнение с одной переменной у: . Решив его, найдем, что у = —0,5. Пара (3; —0,5) — решение уравнения .
Для отыскания решений уравнения (1) удобно выразить одну переменную через другую. Выразим, например, переменную у через х. Для этого перенесем слагаемое Зх в правую часть уравнения, изменив его знак:
Для этого перенесем слагаемое Зх в правую часть уравнения, изменив его знак:
Разделив обе части этого уравнения на 2, получим:
Уравнение (3) равносильно уравнению (2), а уравнение (2) — уравнению (1). Поэтому уравнение (3) равносильно уравнению(1).
По формуле можно найти сколько угодно решений уравнения . Например, если х = 2
, то ;если x = —0,4, то . Значит, уравнение (1) имеет бесконечно много решений.
Каждое решение вида, уравнения с двумя переменными можно изобразить в координатной плоскости точкой с координатами х и у. Все такие точки образуют график уравнения. На рисунке 55 показан график уравнения
Этот график — парабола. Действительно, уравнение равносильно уравнению , а формулой задается функция, графиком которой является парабола.
Графики уравнений весьма разнообразны. На рисунках 56 и 57 изображены графики уравнений
На рисунках 56 и 57 изображены графики уравнений
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ
Каждое из уравнений с двумя переменными , имеет вид , где
Определение. Линейным уравнением с двумя переменными называется уравнение вида , где х и у — переменные, а, b и с — числа.
Числа а и b называют коэффициентами при переменных, число с — свободным членом.
Выясним, что представляет собой график линейного уравнения.
Если в линейном уравнении коэффициент при у не равен нулю, то из этого уравнения можно выразить у через х. Возьмем, например, уравнение. Имеем:
Имеем:
Формулой задается линейная функция, графиком которой служит прямая. Та же самая прямая является и графиком уравнения , так как это уравнение равносильно уравнению
Если в линейном уравнении коэффициент при у равен нулю, а коэффициент при х отличен от нуля, то графиком такого уравнения также является прямая. Рассмотрим, например, уравнение . Его решениями служат все пары чисел (х ; у), в которых x = 6, а у — любое число. Изобразив эти пары точками, получим прямую, параллельную оси ординат (рис. 59).
Итак, графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.
Уравнение , в котором а = О и b = 0, имеет вид . При с = 0 любая пара чисел является решением этого уравнения, а его графиком — вся координатная плоскость. При уравнение не имеет решений, и его график не содержит ни одной точки.
При уравнение не имеет решений, и его график не содержит ни одной точки.
Приведем примеры построения графиков линейных уравнений.
Пример 1. Построим график уравнения .
В линейном уравнении коэффициенты при переменных отличны от нуля. Поэтому его графиком является прямая. Прямая определяется двумя точками. Найдем координаты двух каких-либо точек прямой:
Отметим точки (0; —3) и (2; —1,5) и проведем через них прямую (рис. 60). Эта прямая — график уравнения
Пример 2. Построим график уравнения х= — 3. Это уравнение можно записать в виде . графиком служит прямая, параллельная оси у (рис. 61).
Понятие системы уравнений. |
|||||
|
|||||
Свойства систем уравнений: |
|||||
Линейные системы уравнений с двумя неизвестными: |
|||||
|
Линейные системы уравнений с двумя переменными — это система вида: |
|||||
|
Прямые — графики уравнений системы пересекаются в одной точке. |
|||||
| Прямые — графики уравнений системы — параллельны. Система не имеет решений. | |||||
|
Прямые — графики уравнений системы совпадают. Система имеет бесконечно много решений: |
|||||
Основные методы решения систем уравнений: |
|||||
| Графический метод: | |||||
| 1. Построить в одной системе координат графики обоих уравнений: | |||||
| 2. Найти координаты точек пересечения графиков. | |||||
| Метод подстановки: | |||||
1. Выразить одну переменную через другую в одном из уравнений. |
|||||
| 2. Подставить это выражение в другое уравнение и получить уравнение с одной переменной. | |||||
| 3. Найти корни уравнения с одной переменной. | |||||
| 4. Подставить найденные корни в выражение для первой переменной и получить ее значение. | |||||
| Метод сложения (вычитания): | |||||
|
1. Сложить почленно уравнения системы, предварительно умножив каждое из уравнений на такой множитель: |
|||||
| 2. Найти корни уравнения с одной переменной. | |||||
| 3. Подставить найденные корни в любое из уравнений системы и получить уравнение с одной неизвестной. | |||||
4. Найти корни этого уравнения. Найти корни этого уравнения. |
|||||
| Метод введения новых переменных: | |||||
|
1. Вместо исходных переменных x и y ввести такие новые переменные: чтобы система с ними стала проще. |
|||||
| 2. Решить систему с новыми переменными. | |||||
| 3. Найти значения исходных переменных. | |||||
7 класс. Алгебра. Линейная функция. — Решение линейных уравнений с двумя неизвестными.
Комментарии преподавателяНа данном уроке мы рассмотрим уравнение с двумя переменными, дадим его определение и построим график.Тема: Линейная функция
Урок: Линейное уравнение с двумя переменными и его график
Опредепение
Мы познакомились с понятиями координатной оси и координатной плоскости. Мы знаем, что каждая точка плоскости однозначно задает пару чисел (х; у), причем первое число есть абсцисса точки, а второе – ордината.
Мы знаем, что каждая точка плоскости однозначно задает пару чисел (х; у), причем первое число есть абсцисса точки, а второе – ордината.
Мы будем очень часто встречаться с линейным уравнением с двумя переменными, решением которого и есть пара чисел, которую можно представить на координатной плоскости.
Уравнение вида:
, где a, b, с – числа, причем
Называется линейным уравнением с двумя переменными х и у. Решением такого уравнения будет любая такая пара чисел х и у, подставив которую в уравнение мы получим верное числовое равенство.
Пара чисел будет изображаться на координатной плоскости в виде точки.
У таких уравнений мы увидим много решений, то есть много пар чисел, и все соответствующие точки будут лежать на одной прямой.
Построение графика
Пример 1:
; ; ;
Чтобы найти решения данного уравнения нужно подобрать соответствующие пары чисел х и у:
Пусть , тогда исходное уравнение превращается в уравнение с одной неизвестной:
,
То есть, первая пара чисел, являющаяся решением заданного уравнения (0; 3). Получили точку А(0; 3)
Получили точку А(0; 3)
Пусть . Получим исходное уравнение с одной переменной: , отсюда , получили точку В(3; 0)
Занесем пары чисел в таблицу:
Построим на графике точки и проведем прямую:
Отметим, что любая точка на данной прямой будет решением заданного уравнения. Проверим – возьмем точку с координатой и по графику найдем ее вторую координату. Очевидно, что в этой точке . Подставим данную пару чисел в уравнение. Получим 0=0 – верное числовое равенство, значит точка, лежащая на прямой, является решением.
Пока доказать, что любая точка, лежащая на построенной прямой является решением уравнения, мы не можем, поэтому принимаем это за правду и докажем позже.
Пример 2 – построить график уравнения:
Составим таблицу, нам достаточно для построения прямой двух точек, но возьмем третью для контроля:
В первой колонке мы взяли удобный , найдем у:
, ,
Во втором столбике мы взяли удобный , найдем х:
, , ,
Возьмем для проверки и найдем у:
, ,
Построим график:
Умножим заданное уравнение на два:
От такого преобразования множество решений не изменится и график останется таким же самым.
Вывод:
мы научились решать уравнения с двумя переменными и строить их графики, узнали, что графиком подобного уравнения есть прямая и что любая точка этой прямой является решением уравнения
Урок: Линейное уравнение с двумя переменными и его график (более сложные случаи)
Напомним, что линейным уравнением с двумя переменными называется уравнение вида
Мы научились строить графики подобных уравнений и узнали, что они имеют бесчисленное множество решений – пар чиселх и у, которые на графике отображаются в виде точек.
В предыдущих задачах нам было задано уравнение, но как и все другие – линейное уравнение с двумя переменными это математическая модель некоторой реальной ситуации. Теперь рассмотрим такие задачи, в которых нужно для простейшей задачи составить уравнение – математическую модель, а затем его решить.
Пример 1:
Сумма двух чисел равна четырем. Построить математическую модель, то есть соответствующее линейное уравнение, и его график.
Пусть искомые числа это х и у, сумма их равна четырем:
– линейное уравнение с двумя переменными. Построим график, для этого составим таблицу, для контроля возьмем три точки, а не две:
Решение задачи сведено в таблицу:
|
Словесная модель |
Сумма двух чисел равна четырем |
|
Алгебраическая модель |
, |
|
Геометрическая модель |
Следующая группа задач связана с тем, что в одной задаче могут участвовать два линейных уравнения.
Пример 2:
Графически найти точку пересечения прямых и
Обе прямые являются графиками соответствующих уравнений, построим их. Для этого составим таблицы. Для удобства представим уравнение в следующем виде:
Графически найдена точка пересечения А(1; 2)
Чтобы проверить, что точка А(1; 2) удовлетворяет обоим уравнениям, нужно подставить ее координаты в уравнения:
;
точка А удовлетворяет обоим уравнениям, значит, точка пересечения прямых найдена верно.
Уравнение с параметрами
Следующий тип задач – это задачи с параметрами.
Пример 3:
Найдите значение коэффициента в уравнении , если известно, что решением уравнения является пара чисел (3; 2)
Ранее у нас было задано или мы сами составляли линейное уравнение с известными коэффициентами, в данном случае один из коэффициентов неизвестен, но дано одно из решений уравнения, то есть пара значений х и у, удовлетворяющих уравнению. Чтобы найти параметр подставим данные значения в уравнение:
Чтобы найти параметр подставим данные значения в уравнение:
итак, исходное уравнение имеет вид:
Итак, мы рассмотрели линейное уравнение с двумя неизвестными:
Отметим, что в случае, если , мы получаем частный случай данного уравнения – уравнение с одной переменной:
Аналогично если мы получим линейное уравнение с одной переменной:
Вывод: в данном уроке мы рассмотрели более сложные задачи на линейные уравнения с двумя переменными, в частности текстовые задачи, уравнения с параметрами, задачи на два уравнения. Кроме того мы закрепили знание понятий и терминов.
Источники конспекта: http://interneturok.ru/ru/school/algebra/7-klass/glava-2-lineynaya-funktsiya/lineynoe-uravnenie-s-dvumya-peremennymi-i-ego-grafik?konspekt&chapter_id=8
http://interneturok.ru/ru/school/algebra/7-klass/glava-2-lineynaya-funktsiya/lineynoe-uravnenie-s-dvumya-peremennymi-i-ego-grafik-bolee-slozhnye-sluchai?konspekt&chapter_id=8
Источник видео: https://www. youtube.com/watch?v=8WdpbeZFy_c
youtube.com/watch?v=8WdpbeZFy_c
Системы уравнений. Способы решения систем уравнений
Система уравнений — это группа уравнений, в которых одни и те же неизвестные обозначают одни те же числа. Чтобы показать, что уравнения рассматриваются как система, слева от них ставится фигурная скобка:
| x — 4y = 2 | |
| 3x — 2y = 16 |
Решить систему уравнений — это значит, найти общие решения для всех уравнений системы или убедиться, что решения нет.
Чтобы решить систему уравнений, нужно исключить одно неизвестное, то есть из двух уравнений с двумя неизвестными составить одно уравнение с одним неизвестным. Исключить одно из неизвестных можно тремя способами: подстановкой, сравнением, сложением или вычитанием.
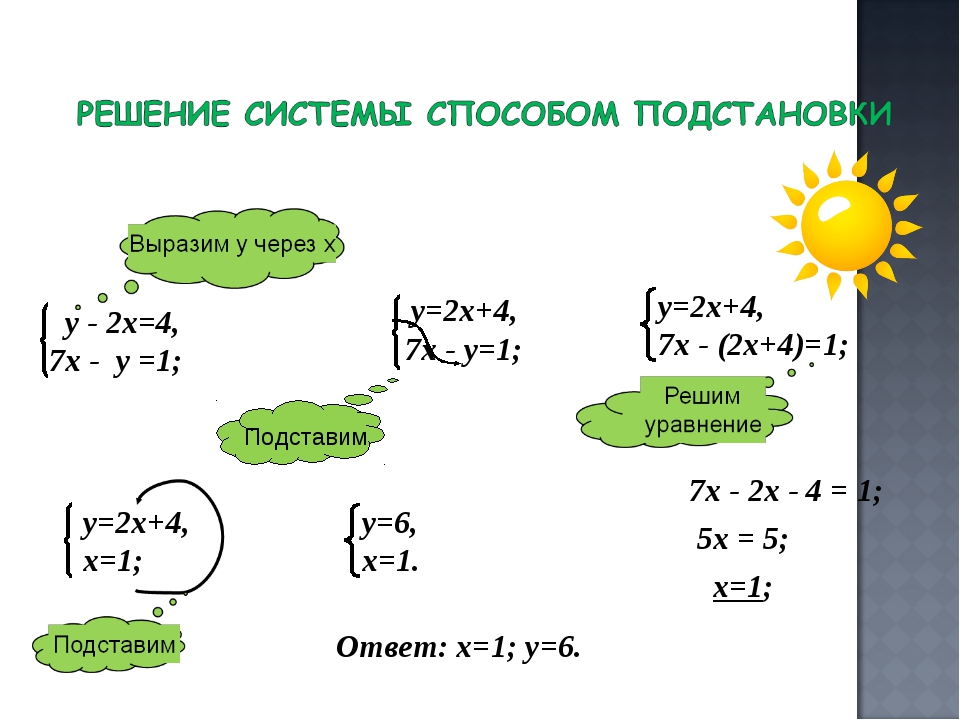
Способ подстановки
Чтобы решить систему уравнений способом подстановки, нужно в одном из уравнений выразить одно неизвестное через другое и результат подставить в другое уравнение, которое после этого будет содержать только одно неизвестное. Затем находим значение этого неизвестного и подставляем его в первое уравнение, после этого находим значение второго неизвестного.
Затем находим значение этого неизвестного и подставляем его в первое уравнение, после этого находим значение второго неизвестного.
Рассмотрим решение системы уравнений:
| x — 4y = 2 | |
| 3x — 2y = 16 |
Сначала найдём, чему равен x в первом уравнении. Для этого перенесём все члены уравнения, не содержащие неизвестное x, в правую часть:
x — 4y = 2;
x = 2 + 4y.
Так как x, на основании определения системы уравнений, имеет такое же значение и во втором уравнении, то подставляем его значение во второе уравнение и получаем уравнение с одним неизвестным:
| 3x | — 2y = 16; |
| 3(2 + 4y) | — 2y = 16. |
Решаем полученное уравнение, чтобы найти, чему равен y. Как решать уравнения с одним неизвестным, вы можете посмотреть в соответствующей теме.
| 3(2 + 4y) — 2y = 16; |
| 6 + 12y — 2y = 16; |
| 6 + 10y = 16; |
| 10y = 16 — 6; |
| 10y = 10; |
| y = 10 : 10; |
| y = 1. |
Мы определили что y = 1. Теперь, для нахождения численного значения x, подставим значение y в преобразованное первое уравнение, где мы ранее нашли, какому выражению равен x:
x = 2 + 4y = 2 + 4 · 1 = 2 + 4 = 6.
Ответ: x = 6, y = 1.
Способ сравнения
Способ сравнения — это частный случай подстановки. Чтобы решить систему уравнений способом сравнения, нужно в обоих уравнениях найти, какому выражению будет равно одно и то же неизвестное и приравнять полученные выражения друг к другу. Получившееся в результате уравнение позволяет узнать значение одного неизвестного. С помощью этого значения затем вычисляется значение второго неизвестного.
С помощью этого значения затем вычисляется значение второго неизвестного.
Например, для решение системы:
| x — 4y = 2 | |
| 3x — 2y = 16 |
найдём в обоих уравнениях, чему равен y (можно сделать и наоборот — найти, чему равен x):
| x — 4y = 2 | 3x — 2y = 16 |
| -4y = 2 — x | -2y = 16 — 3x |
| y = (2 — x) : — 4 | y = (16 — 3x) : -2 |
Составляем из полученных выражений уравнение:
Решаем уравнение, чтобы узнать значение x:
| ||||||
| 2 — x = 32 — 6x | ||||||
| —x + 6x = 32 — 2 | ||||||
| 5x = 30 | ||||||
| x = 30 : 5 | ||||||
| x = 6 |
Теперь подставляем значение x в первое или второе уравнение системы и находим значение y:
| x — 4y = 2 | 3x — 2y = 16 |
| 6 — 4y = 2 | 3 · 6 — 2y = 16 |
| -4y = 2 — 6 | -2y = 16 — 18 |
| -4y = -4 | -2y = -2 |
| y = 1 | y = 1 |
Ответ: x = 6, y = 1.
Способ сложения или вычитания
Чтобы решить систему уравнений способом сложения, нужно составить из двух уравнений одно, сложив левые и правые части, при этом одно из неизвестных должно быть исключено из полученного уравнения. Неизвестное можно исключить, уравняв при нём коэффициенты в обоих уравнениях.
Рассмотрим систему:
| x — 4y = 2 | |
| 3x — 2y = 16 |
Уравняем коэффициенты при неизвестном y, умножив все члены второго уравнения на -2:
(3x — 2y) · -2 = 16 · -2
-6x + 4y = -32
Получим:
| x — 4y = 2 | |
| -6x + 4y = -32 |
Теперь сложим по частям оба уравнения, чтобы получить уравнение с одним неизвестным:
| + | x — 4y = 2 |
| -6x + 4y = -32 | |
| -5x = -30 |
Находим значение x (x = 6). Теперь, подставив значение x в любое уравнение системы, найдём y = 1.
Теперь, подставив значение x в любое уравнение системы, найдём y = 1.
Если уравнять коэффициенты у x, то, для исключения этого неизвестного, нужно было бы вычесть одно уравнение из другого.
Уравняем коэффициенты при неизвестном x, умножив все члены первого уравнения на 3:
(x — 4y) · 3 = 2 · 3
3x — 12y = 6
Получим:
| 3x — 12y = 6 | |
| 3x — 2y = 16 |
Теперь вычтем по частям второе уравнение из первого, чтобы получить уравнение с одним неизвестным:
| — | 3x — 12y = 6 |
| 3x — 2y = 16 | |
| -10y = -10 |
Находим значение y (y = 1). Теперь, подставив значение y в любое уравнение системы, найдём x = 6:
| 3x — 2y = 16 |
| 3x — 2 · 1 = 16 |
| 3x — 2 = 16 |
| 3x = 16 + 2 |
| 3x = 18 |
| x = 18 : 3 |
| x = 6 |
Ответ: x = 6, y = 1.
Для решения системы уравнений, рассмотренной выше, был использован способ сложения, который основан на следующем свойстве:
Любое уравнение системы можно заменить на уравнение, получаемое путём сложения (или вычитания) уравнений, входящих в систему. При этом получается система уравнений, имеющая те же решения, что и исходная.
Уравнение первой степени с двумя неизвестными
x2 + y2 = 7.
Для уравнений с двумя неизвестными остаются справедливы все те свойства, которые были установлены для уравнений с одним неизвестным (§ 48).
Уравнением первой степени с двумя неизвестными называется уравнение вида
ax + by = c, (1)
где x и y – неизвестные, a и b (коэффициенты при неизвестных) — данные числа, не равные оба нулю, c (свободный член) — любое данное число.
Примеры уравнений первой степени:
5x – 2y = 1; 3x + y = 4.
Уравнения:
1) 5x – 2y + 3 = 2x + y – 1; 2) y = 1,7x;
3) y = 4x – 9; 4)
после переноса членов, содержащих неизвестные, в левую часть, а известных чисел — в правую часть, приводятся к виду (1), а потому эти уравнения также являются уравнениями первой степени.
Уравнение (1) называется нормальным видом уравнения первой степени с двумя неизвестными.
Из приведенных примеров видно (пример 2 и 3), что рассмотренные ранее равенства, выражающие прямо пропорциональную и линейную зависимости, являются уравнениями первой степени с двумя неизвестными.
Равенство, выражающее обратно пропорциональную зависимость, например xy = 8, уже не является уравнением первой степени.
Рассмотрим какое-нибудь уравнение с двумя неизвестными, например:
2x – y = 3.
Возьмем какую-либо пару чисел, например: x = 1, y = –1. Подставив эти числа в данное уравнение, получим верное равенство:
2 – (–1) = 3.
Говорят, что эта пара чисел удовлетворяет данному уравнению или что она (эта пара) есть решение данного уравнения.
Возьмем теперь такую пару чисел: x = 2, y = 4.
Подставив эти значения в данное уравнение, получим в его левой части 2 * 2 – 4 = 0. При этих значениях левая часть (нуль) оказалась не равной правой части (т. е. числу 3). Говорят, что пара чисел x = 2, у = 4 не удовлетворяет данному уравнению или что она не есть решение уравнения.
Каждая пара значений x и y, подстановка которых в уравнение с двумя неизвестными x и y обращает его в верное равенство, называется решением этого уравнения.
Решим такую задачу.
Задача. Сумма двух чисел равна 6. Чему равно каждое слагаемое?
Обозначим через x и y искомые слагаемые.
Задача приводит к уравнению:
x + y = 6.
Дадим x какое-либо значение, например x = 2, тогда для другого неизвестного y получим уравнение:
2 + y = 6,
из которого найдем у = 4. Пара чисел x = 2, y = 4 дает решение нашей задачи.
Однако вместо x = 2 мы могли бы взять какое-нибудь другое значение для x, например x = 1, и тогда мы нашли бы y = 5. Значит, мы получили еще одно решение уравнения: x = 1, y = 5.
В таблице приведено несколько решений данного уравнения: значения x и y записаны друг под другом, а в нижней строчке показано, что сумма этих значений равна 6.
Ясно, что одному из неизвестных (например, x) можно придать любое значение и, подставив его в данное уравнение, найти соответствующее значение другого неизвестного.
Как видим, задача имеет бесконечное множество решений.
Уравнение не дает определенного ответа на вопрос задачи. Оно лишь указывает на зависимость между двумя неизвестными. На основании этой зависимости, зная значение одного неизвестного, мы могли найти значение и другого.
Итак, уравнение первой степени, содержащее два неизвестных, имеет бесконечное множество решений.
Одному из неизвестных можно придать произвольное значение и из данного уравнения найти соответствующее значение другого неизвестного.
Мы уже видели, что в случае линейной (в частности, прямо пропорциональной) зависимости, выражающейся уравнением первой степени с двумя неизвестными, графиком является прямая линия. Докажем, что прямая линия будет графиком и любого уравнения первой степени с двумя неизвестными.
Начнем с примера. Возьмем уравнение:
19x – 6y = –4.
Выразив в нем неизвестное y через x, получим:
6y = 19x +4;
Мы видим, что это уравнение представляет собой не что иное, как линейную зависимость
y = kx + b при.
Значит, графиком этого уравнения является прямая линия (черт. 31).
Какое бы уравнение первой степени, содержащее два неизвестных x и y, мы ни взяли, всегда можно выразить одно из неизвестных, например y, через другое (через x) и получить уравнение (равносильное данному), выражающее линейную зависимость y = kx + b. Например, если 2x + 3y = 5, то.
Отсюда вывод:
Графиком уравнения первой степени с двумя неизвестными является прямая линия.
Примечание. Мы рассматривали выше уравнения, содержащие два неизвестных, однако может оказаться, что коэффициент при одном из неизвестных будет равен нулю, так что уравнение запишется в виде уравнения с одним неизвестным.
Возьмем, например, уравнение:
x + 2y – 3 = 2(x – y) + 5
Приведем это уравнение к нормальному виду:
3x + 0 * y = 8.
Это уравнение также имеет бесконечное множество решений; ему удовлетворяет любая пара чисел, y, где y – произвольное число. Обычно член 0 * y не пишут и уравнение записывают так: 3x = 8.
python — Sympy, как решить уравнение с 2 неизвестными в заданном диапазоне
Предположим, я определил два символа x и y.
import sympy as sp
x = sp.symbols('x', integer=True)
y = sp.symbols('y', integer=True)
Я знаю, что могу решать уравнения с одной переменной как таковой:
expr = 3*x**2 - 12
result = sp.solve(expr, x)
print(result)
[-2, 2]
И я могу ограничить диапазон решения с
result = sp.solve([expr, x>0], x)
print(result)
Уравнение (х, 2)
Теперь я хочу решить уравнение с двумя неизвестными в диапазоне (0, 10). Вот что я попробовал:
expr = 3*x - y - 10
result = sp.solve([expr, x>0, x<10, y>0, y<10], x, y)
Но это дает NotImplementedError
NotImplementedError:
inequality has more than one symbol of interest.
Это действительно не реализовано или я делаю что-то не так? Я знаю, что sympy — это мощная библиотека, поэтому я ожидаю, что sympy решит такие проблемы. Я ожидаю следующих решений:
(x=4, y=2), (x=5, y=5), (x=6, y=8)
Люди в Интернете предлагают использовать solveset, nonlinsolve, linsolve, но я не мог заставить их работать с этими методами.
1
Seljuk Gülcan 2 Дек 2019 в 14:19
2 ответа
Лучший ответ
Использование неравенств в solve часто сбивает с толку пользователей. Я думаю, что большинство пользователей хотят использовать неравенства для фильтрации решений, как вы говорите. Однако solve на самом деле предполагает использовать неравенства для упрощения одномерной системы неравенств, которая является чем-то совершенно другим, например:
In [3]: solve([x**2+1<10, x>2])
Out[3]: 2 < x ∧ x < 3
Обратите внимание на то, что решение возвращает результат Boolean, а не список Expr, который он обычно возвращает. Я думаю, что из-за этого альтернативного использования функция solve со смесью уравнений и неравенств не вполне соответствует ожиданиям пользователей. Чтобы показать, почему это может быть полезно, я фактически использовал solve, как это ниже.
Ваш пример действительно является диофантовой проблемой, поскольку система уравнений недоопределена (1 уравнение на два неизвестных), но вам нужны только целочисленные решения. Я раньше не пользовался диофантовым солвером, но просто попробовал и придумал:
from sympy import *
x, y = symbols('x, y', integer=True)
eq = 3*x - y - 10
conds = [(0 < x), (x < 10), (0 < y), (y < 10)]
# Solve the diophantine equation for solutions in parameter t_0
t, t_0 = symbols('t, t_0', integer=True)
gensol = diophantine(eq, t, [x, y])
((xs, ys),) = gensol
# "Solve" the inequalities for constraints on t_0
conds_t = [cond.subs(x, xs).subs(y, ys) for cond in conds]
conds_t_sol = solve(conds_t, t_0)
# Find the finite set of values for t_0 and sub in to general solution
set_t0 = (conds_t_sol.as_set() & Integers)
sol_set = [(xs.subs(t_0, ti), ys.subs(t_0, ti)) for ti in set_t0]
print(sol_set)
На выходе
[(4, 2), (5, 5), (6, 8)]
3
Oscar Benjamin 2 Дек 2019 в 13:24
Рекурсивный подход к генерации целочисленных решений уравнения с более чем двумя переменными — кубические и более высокие случаи не реализованы в качестве диофантовых решателей — заключается в следующем (и вам придется фильтровать решения, как только они будут получены):
def make(e, t, quick=True):
"""Return True if t can be made as a linear combination of values in e
when quick is True, otherwise a list of all multiples of the elements
needed to make t (with respect to the sorted elements in e).
Examples
========
>>> make((6, 9, 20), 43) # c.f. the McNugget problem
False
>>> make((6, 9, 20), 50, quick=False)
[[2, 2, 1], [5, 0, 1]]
50 can be made as 2*6 + 2*9 + 1*20 or 5*6 + 0*9 + 1*20
"""
def _(e, t):
(m, r) = divmod(t, e[0])
if len(e) == 1:
if not r:
yield [t // e[0]]
else:
for m in range(m + 1):
for g in _(e[1:], t - m * e[0]):
yield [m] + g
e = list(sorted([i for i in e if i]))
if quick:
for i in _(e, t):
return True
else:
return [i for i in _(e, t)]
1
smichr 4 Дек 2019 в 18:19
Решение систем уравнений с двумя переменными (Алгебра 2, Как решить систему линейных уравнений) — Mathplanet
Система линейного уравнения состоит из двух или более уравнений, одно из которых ищет общее решение этих уравнений. В системе линейных уравнений каждому уравнению соответствует прямая линия, и каждый ищет точку, где две линии пересекаются.
Пример
Решите следующую систему линейных уравнений:
$$ \ left \ {\ begin {matrix} y = 2x + 4 \\ y = 3x + 2 \\ \ end {matrix} \ right.
$Поскольку мы ищем точку пересечения, мы можем изобразить уравнения:
Здесь мы видим, что линии пересекаются друг с другом в точке x = 2, y = 8. Это наше решение, и мы можем называть его графическим решением задачи.
Но как найти решение, если линии никогда не пересекаются? Нельзя, система уравнений не имеет решения.
Можно также прийти к правильному ответу с помощью метода исключения (также называемого методом сложения или методом линейной комбинации) или методом подстановки.
При использовании метода подстановки мы используем тот факт, что если два выражения y и x имеют одинаковое значение x = y, то x может заменить y или наоборот в другом выражении без изменения значения выражения.
Пример
Решите системы уравнений методом подстановки
$$ \ left \ {\ begin {matrix} y = 2x + 4 \\ y = 3x + 2 \\ \ end {matrix} \ right. $$
Подставляем y в верхнем уравнении выражением для второго уравнения:
$$ \ begin {array} {lcl} 2x + 4 & = & 3x + 2 \\ 4-2 & = & 3x-2x \\ 2 & = & x \\ \ end {array} $$
Чтобы определить значение y , мы можем продолжить, вставив наше значение x в любое из уравнений.Выбираем первое уравнение:
$$ y = 2x + 4 $$
Подключаем x = 2 и получаем
$$ y = 2 \ cdot 2 + 4 = 8 $$
Таким образом, мы пришли к тому же ответу, что и в графическом решении.
Метод исключения требует, чтобы мы добавляли или вычитали уравнения, чтобы исключить x или y , часто нельзя приступить к сложению напрямую, не умножив сначала первое или второе уравнение на некоторое значение.
Пример
$$ 2x-2y = 8 $$
$$ x + y = 1 $$
Теперь мы хотим сложить два уравнения, но это не приведет к исключению x или y .Следовательно, мы должны умножить второе уравнение на 2 с обеих сторон и получить:
$$ 2x-2y = 8 $$
$$ 2x + 2y = 2 $$
Теперь мы пытаемся добавить нашу систему уравнений. Мы начинаем с терминов x слева, а затем с терминов y и, наконец, с цифр справа:
$$ (2x + 2x) + (- 2y + 2y) = 8 + 2 $$
Термины и исключены, и теперь у нас есть уравнение только с одной переменной:
$$ 4x = 10 $$
$$ x = \ frac {10} {4} = 2.5 $$
После этого, чтобы определить значение y , мы вставляем x = 2,5 в одно из уравнений. Выбираем первое:
$$ \ begin {array} {lcl} 2 \ cdot 2.5-2y & = & 8 \\ 5-8 & = & 2y \\ -3 & = & 2y \\ \ frac {-3} {2} & = & y \\ y & = & -1,5 \\ \ end {array} $$
Видеоурок
Решите систему уравнений:
$$ \ left \ {\ begin {matrix} 2x-4y = 0 \\ -4x + 4y = -4 \ end {matrix} \ right.
$
Два уравнения с двумя неизвестными
У нас есть два ответа для вас
Привет Мэри.
Два уравнения могут находиться в одном из трех соотношений друг с другом:
- Это разные выражения одной и той же линии. Например, y = 2x и 2y = 4x на самом деле одна и та же линия. В этом случае существует «бесконечно много решений», потому что существует бесконечное количество значений x, которые дают значение для y, совпадающее в обоих уравнениях.Также обратите внимание, что в этом случае наклоны и точки пересечения по оси Y двух уравнений будут совпадать.
- Это параллельные линии. Например, y = 2x и y = 2x + 1 параллельны. Параллельные линии имеют одинаковый наклон, но разные точки пересечения по оси y. Поскольку нет точек (x, y), которые одновременно находятся на обеих линиях, мы говорим, что «нет решения».
- Они пересекаются в одной точке. Единственный момент — это «уникальное решение». Это может быть только в том случае, если два уравнения имеют разные склоны.Перехват y не имеет значения.
Чтобы определить, какой из этих случаев у вас есть для данной пары уравнений, часто проще всего написать оба уравнения в форме y = mx + b и сравнить наклоны, а затем, при необходимости, сравнить точки пересечения y. Однако это не скажет вам, что на самом деле представляет собой уникальное решение (если они пересекаются в одной точке, а не являются идентичными или параллельными линиями).
Вот как обстоят дела, когда вы используете метод подстановки для «решения» двух уравнений:
Пример 1:
2x + y = 1
-3x + 2y = 0Решите одно уравнение для одной переменной (какую? Просто выберите то, что выглядит проще всего!)
2x + y = 1
y = 1-2xЗатем подставьте это выражение (которое равно y) вместо y в другом уравнении.Таким образом,
-3x + 2y = 0
становится
-3x + 2 (1-2x) = 0И решите относительно x:
-3x + 2 — 4x = 0
-7x = -2
x = 2/7.Поскольку он дал нам единственное значение x, я знаю, что мы получим уникальное решение. Я использую это значение x, чтобы найти значение y. Просто выберите одно из исходных уравнений (неважно какое) и замените x на 2/7.
2x + y = 1
становится
2 (2/7) + y = 1
y = 3/7.Итак, единственное решение этой пары уравнений — (2/7, 3/7).
Давайте посмотрим на две другие ситуации, чтобы увидеть, что могло бы произойти.
Пример 2:
2x + y = 1
-2x — y = 2Решите первое относительно y:
y = 1-2xПодставим во второе уравнение:
-2x — (1 — 2x) = 2
-2x — 1 + 2x = 2
-1 = 2.Очевидно, противоречие! Значит, решения нет. Эти два уравнения представляют собой параллельные линии.
Пример 3:
2x + y = 1
6x + 3y = 3Решите первое относительно y:
y = 1-2xПодставляем во второе уравнение:
6x + 3 (1 — 2x) = 3
6x + 3 — 6x = 3
3 = 3.Это трюизм: это верно независимо от значения x, поэтому существует бесконечное количество решений. Эти два уравнения на самом деле являются всего лишь двумя способами выражения одного и того же уравнения (умножьте первое уравнение на 3 с обеих сторон, и вы убедитесь в этом).
Я надеюсь, что это объяснение и набор примеров помогут вам решить любые ваши проблемы с двумя линейными уравнениями.
Cheers,
Стивен Ла Рок.
Привет Мэри,
Фактически не решая эту систему уравнений, мы можем определить, что на самом деле будет ТОЛЬКО ОДНО решение. Первое уравнение имеет наклон -4 (мы можем изменить его так, чтобы читать y = -4x + 4), а второе уравнение имеет наклон -1/4 (мы можем изменить его так, чтобы читать y = -1 / 4x).Когда две линии имеют разные уклоны, они гарантированно пересекаются в одной точке, что дает нам одно решение.
Если бы эта система не имела решений или имела бы бесконечно много решений, уравнения должны были бы иметь одинаковый наклон. Кроме того, они должны были бы иметь разные точки пересечения по оси Y, чтобы не было решения, и одну точку пересечения по оси Y, чтобы иметь бесконечно много решений.
Надеюсь, это поможет.
Лиэнн
Как решить два уравнения с двумя неизвестными — I
Не могли бы вы напомнить, как решить два уравнения с двумя неизвестными? Если да или если вы никогда не знакомы с этой концепцией, я приглашаю вас посмотреть это видео и следующее видео, которое является второй частью этой серии.
Два уравнения с двумя переменными. До сих пор при изучении алгебраических уравнений мы рассматривали решение отдельных уравнений только с одной переменной. Например, что-то вроде 2x + 7 = 15.
Что произойдет, если в уравнении есть более одной переменной? Предположим, у нас есть что-то вроде 2x + 3y = 15.
Итак, что будет означать для кого-то прийти и сказать нам, решить это уравнение? Как нам найти значения, которые работают в этом уравнении? Ну, конечно, одно возможное значение, если x = 0, тогда y может быть равно 5, так что это было бы решением.Другими словами, если x = 3 и y = 3, x = 6 и y = 1, это также значения, которые заставляют его работать.
Конечно, нет никаких ограничений на то, что любая переменная должна быть положительной, поэтому другие решения включают (x = 9, y = -1) или (x = -3 и y = +7). Как вы понимаете, мы могли бы сделать x все более и более отрицательным, а y — все более и более положительным — или наоборот. Так что мы могли получить довольно много подобных решений. Также нет ограничений, что переменные должны быть целыми числами, поэтому другие решения включают такие вещи, как x = 7 1/2 y = 0 или x = 4 и y = 2 1/3.
Итак, только на этой странице обратите внимание, что у нас есть одно, два, три, четыре, пять, шесть, семь решений для этого. И, безусловно, ясно, что мы можем получить намного больше. Фактически, одно уравнение с двумя переменными обычно имеет бесконечное количество решений. Обратите внимание, что все эти решения, если их построить на графике x-y, лежали бы на прямой линии.
Чтение диаграммы
Итак, семь упомянутых нами решений — это семь точек на этой диаграмме. И все они лежат на прямой.Теперь по причинам, которые мы обсудим позже в модуле координатной геометрии, любое отдельное уравнение только с x и y (ни одна из переменных не возведена в степень или дробь) может быть представлено линией в плоскости x-y. Так что прямо сейчас вам не нужно беспокоиться об их графическом отображении. Вам не нужно беспокоиться о том, как вы найдете наклон линии или что-то в этом роде.
Все, что вам нужно сделать, это просто иметь эту идею, только эту ассоциацию — что уравнение с x и y представлено линией. Это все, что вам нужно знать для этого обсуждения.
Большая идея номер один
Итак, первая большая идея заключается в том, что никто не может попросить вас решить одно уравнение с двумя переменными, потому что у него будет бесконечное количество решений. Линия проходит через бесконечное количество точек, и каждая из этих точек является решением.
Таким образом, никто не может законно попросить вас решить, потому что они просят вас решить бесконечное количество вещей одновременно.
Теперь предположим, что у нас есть два уравнения, каждое с двумя переменными.Это называется системой уравнений. Значения x и y должны одновременно удовлетворять обоим уравнениям. Что ж, это интересно.
Если каждое уравнение представляет собой линию, то имеет смысл, что единственная точка, где эти две линии пересекаются, будет единственной точкой, которая удовлетворяет обоим уравнениям. Итак, вы выбираете одну случайную линию и выбираете другую случайную линию, очень велики шансы, что они собираются где-то пересекаться, и они пересекаются в одной точке, и эта одна точка будет решением.
Большая идея номер два
С алгебраической точки зрения, когда мы находим это решение, мы находим геометрическую точку, в которой они пересекаются. Итак, большая идея №2 состоит в том, что если у нас есть система из двух уравнений с двумя неизвестными, мы обычно можем решить для уникальных значений x и y. Как решить систему уравнений для этих значений? Есть две стратегии.
Один из них — это замена, а другой — либо исключение, некоторые источники также называют это линейной комбинацией.Я буду называть их замена и исключение . Цель обоих этих методов — свести ситуацию с двумя уравнениями и двумя неизвестными к ситуации с одним уравнением и одним неизвестным, в которой мы уже знаем, как найти решение.
Метод замещения
Итак, что мы делаем, и это часто верно в отношении математики, мы превращаем проблему, которую не знаем, как решить, в проблему, которую мы действительно знаем, как решить. Это очень типично для математики. Итак, метод подстановки.В этом методе мы сначала решаем одно уравнение, либо одно для одной из переменных.
Изображение с digitalconsumator
В этом уравнении мы получим одну переменную на одной стороне уравнения. Итак, есть два уравнения, которые я привел минуту назад, одно из них было x + 2y = 11. И это уравнение, в котором особенно легко получить x само по себе. Что я собираюсь сделать, так это вычесть 2y с обеих сторон, и я получу x = 11-2y. Так что задержитесь на секунду, x = 11-2y.Теперь давайте посмотрим на другое уравнение.
Мы можем заменить x в другом уравнении выражением, равным x. Это потому, что x = 11-2y означает, что везде, где есть x, мы можем удалить x и заменить его тем, что он равен. Итак, вот другое уравнение, и мы просто снова напишем то же уравнение, но мы заменим это x на 11 минус 2y. Где теперь у нас есть одно уравнение с y.
Итак, теперь мы просто используем наше обычное решение, мы распределим, объединим
Image by CLS Digital Art
как термины, мы вычтем 22 с обеих сторон, мы получим -y = -7 умножить на — 1 получаем y = 7.Итак, теперь мы решили для одного из двух значений, мы решили для y, нам все еще нужно решить для x. Теперь мы подставляем это значение для возврата y в уравнение, которое было решено для x.Итак, у нас было x = 11-2y, теперь мы знаем, что y = 7. Итак, мы просто вставим это, 11-14 равно -3. Таким образом, точка x равна -3, y равна положительному 7, что является решением. Обратите внимание, что метод подстановки наиболее полезен, когда в одном из двух уравнений коэффициенты одной из переменных равны положительной 1 или отрицательной 1.
Дроби и метод исключения
Если все коэффициенты при x и y в двух уравнениях не равны положительному или отрицательному, то решение для любой переменной приведет к получению дробей, что сделает решение более громоздким. Так, например, предположим, что это наша система. Предположим, мы пытаемся решить первое уравнение относительно x. Хорошо, если мы можем разложить 5y на обе стороны, то делим на 4.
Сразу попадаем на дроби. Заменить это было бы неинтересно.Да, математически мы могли бы решить уравнение таким образом — и после дробления, но мы предпочитаем не делать этого. В системах, в которых замена не удобна, мы будем использовать исключение. Мы рассмотрим метод исключения в следующем уроке.
Таким образом, система уравнений, два уравнения с двумя переменными, обычно имеют одно уникальное решение, и опять же, это место, где две линии пересекаются. Вот что мы находим. Мы можем решить либо заменой, либо устранением.Подстановка работает лучше всего, когда одна из переменных имеет коэффициент плюс или минус 1.
И снова, в следующем уроке мы поговорим об исключении.
О Майке МГарри
Майк создает экспертные уроки и практические вопросы, чтобы помочь студентам GMAT добиться успеха. У него есть степень бакалавра физики и магистра религии в Гарварде, а также более 20 лет опыта преподавания, специализирующегося на математике, естественных науках и стандартизированных экзаменах. Майк любит разбивать футбольные мячи на орбите, и, несмотря на отсутствие очевидной черепно-мозговой недостаточности, он настаивает на том, чтобы болеть за Нью-Йорк Метс.Линейные системы с двумя переменными
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с «узкой» шириной экрана (, то есть , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 7-1: Линейные системы с двумя переменными
Линейная система двух уравнений с двумя переменными — это любая система, которую можно записать в форме.
\ [\ begin {align *} ax + by & = p \\ cx + dy & = q \ end {align *} \], где любая из констант может быть равна нулю, за исключением того, что каждое уравнение должно содержать хотя бы одну переменную.
Также система называется линейной, если переменные указаны только в первой степени, присутствуют только в числителе и нет произведений переменных ни в одном из уравнений.
Вот пример системы с числами.
\ [\ begin {align *} 3x — y & = 7 \\ 2x + 3y & = 1 \ end {align *} \]Прежде чем мы обсудим, как решать системы, мы должны сначала поговорить о том, что такое решение системы уравнений. Решение системы уравнений — это значение \ (x \) и значение \ (y \), которые при подстановке в уравнения удовлетворяют обоим уравнениям одновременно.
В приведенном выше примере \ (x = 2 \) и \ (y = — 1 \) является решением системы. Проверить это достаточно легко.
\ [\ begin {align *} 3 \ left (2 \ right) — \ left ({- 1} \ right) & = 7 \\ 2 \ left (2 \ right) + 3 \ left ({- 1} \ вправо) & = 1 \ end {выровнять *} \]Итак, конечно, эта пара чисел является решением системы. Не беспокойтесь о том, как мы получили эти ценности. Это будет самая первая система, которую мы решим, когда перейдем к примерам.
Обратите внимание, что важно, чтобы пара чисел удовлетворяла обоим уравнениям. Например, \ (x = 1 \) и \ (y = — 4 \) удовлетворяют первому уравнению, но не второму, и поэтому не являются решением системы. Аналогично, \ (x = — 1 \) и \ (y = 1 \) будут удовлетворять второму уравнению, но не первому, и поэтому не могут быть решением системы.
Итак, что же представляет собой решение системы двух уравнений? Хорошо, если вы думаете об этом, оба уравнения в системе являются линиями.Итак, давайте построим их график и посмотрим, что мы получим.
Как видите, решение системы — это координаты точки пересечения двух линий. Итак, при решении линейных систем с двумя переменными мы действительно спрашиваем, где пересекаются две линии.
В этом разделе мы рассмотрим два метода решения систем.
Первый метод называется методом замены . В этом методе мы решим одно из уравнений для одной из переменных и подставим его в другое уравнение.Это даст одно уравнение с одной переменной, которую мы можем решить. Как только это решено, мы подставляем это значение обратно в одно из уравнений, чтобы найти значение оставшейся переменной.
На словах этот метод не всегда очень понятен. Давайте рассмотрим пару примеров, чтобы увидеть, как работает этот метод.
Пример 1 Решите каждую из следующих систем.- \ (\ begin {align *} 3x — y & = 7 \\ 2x + 3y & = 1 \ end {align *} \)
- \ (\ begin {align *} 5x + 4y & = 1 \\ 3x — 6y & = 2 \ end {align *} \)
Итак, это была первая система, которую мы рассмотрели выше.Мы уже знаем решение, но это даст нам возможность проверить значения, которые мы записали для решения.
Теперь метод говорит, что нам нужно решить одно из уравнений для одной из переменных. Какое уравнение мы выберем и какую переменную выбрать, зависит от вас, но обычно лучше выбрать уравнение и переменную, с которыми будет легко иметь дело. Это означает, что мы должны стараться избегать дробей, если это вообще возможно.
В этом случае, похоже, будет действительно легко решить первое уравнение для \ (y \), так что давайте сделаем это.
\ [3x — 7 = y \]Теперь подставьте это во второе уравнение.
\ [2x + 3 \ влево ({3x — 7} \ вправо) = 1 \]Это уравнение в \ (x \), которое мы можем решить, так что давайте сделаем это.
\ [\ begin {align *} 2x + 9x — 21 & = 1 \\ 11x & = 22 \\ x & = 2 \ end {align *} \]Итак, есть часть решения \ (x \).
Наконец, НЕ забудьте вернуться назад и найти часть решения \ (y \).Это одна из наиболее распространенных ошибок, которые студенты делают при решении систем. Для этого мы можем либо вставить значение \ (x \) в одно из исходных уравнений и решить для \ (y \), либо мы можем просто вставить его в нашу замену, которую мы нашли на первом шаге. Так будет легче, так что давайте.
\ [y = 3x — 7 = 3 \ left (2 \ right) — 7 = — 1 \]Итак, решение — \ (x = 2 \) и \ (y = — 1 \), как мы отметили выше.
b \ (\ begin {align *} 5x + 4y & = 1 \\ 3x — 6y & = 2 \ end {align *} \) Показать решение
С этой системой мы не сможем полностью избежать дробей.Однако похоже, что если мы решим второе уравнение для \ (x \), мы сможем их минимизировать. Вот эта работа.
\ [\ begin {align *} 3x & = 6y + 2 \\ x & = 2y + \ frac {2} {3} \ end {align *} \]Теперь подставьте это в первое уравнение и решите полученное уравнение относительно \ (y \).
\ [\ begin {align *} 5 \ left ({2y + \ frac {2} {3}} \ right) + 4y & = 1 \\ 10y + \ frac {{10}} {3} + 4y & = 1 \\ 14y & = 1 — \ frac {{10}} {3} = — \ frac {7} {3} \\ y & = — \ left ({\ frac {7} {3}} \ right) \ left ({\ frac {1} {{14}}} \ right) \\ y & = — \ frac {1} {6} \ end {align *} \]Наконец, подставьте это в исходную замену, чтобы найти \ (x \).
\ [x = 2 \ left ({- \ frac {1} {6}} \ right) + \ frac {2} {3} = — \ frac {1} {3} + \ frac {2} {3} = \ frac {1} {3} \]Итак, решение этой системы — \ (x = \ frac {1} {3} \) и \ (y = — \ frac {1} {6} \).
Как и в случае с отдельными уравнениями, мы всегда можем вернуться и проверить это решение, подключив его к обоим уравнениям и убедившись, что оно удовлетворяет обоим уравнениям. Также обратите внимание, что нам действительно нужно включить оба уравнения.Вполне возможно, что ошибка может привести к тому, что пара чисел будет удовлетворять одному из уравнений, но не другому.
Теперь перейдем к следующему методу решения систем уравнений. Как мы видели в последней части предыдущего примера, метод подстановки часто заставляет нас иметь дело с дробями, что увеличивает вероятность ошибок. У второго метода этой проблемы не будет. Что ж, это не совсем так. Если будут отображаться дроби, они будут отображаться только на последнем этапе, и они будут отображаться только в том случае, если решение содержит дроби.
Этот второй метод называется методом исключения . В этом методе мы умножаем одно или оба уравнения на соответствующие числа (, т.е. умножаем каждый член в уравнении на число), чтобы одна из переменных имела одинаковый коэффициент с противоположными знаками. Следующим шагом будет сложение двух уравнений. Поскольку одна из переменных имела одинаковый коэффициент с противоположными знаками, она будет удалена, когда мы сложим два уравнения.Результатом будет одно уравнение, которое мы можем решить для одной из переменных. Как только это будет сделано, замените этот ответ на одно из исходных уравнений.
Как и в случае с первым методом, гораздо легче увидеть, что здесь происходит, с помощью пары примеров.
Пример 2 Постановка задачи.- \ (\ begin {align *} 5x + 4y & = 1 \\ 3x — 6y & = 2 \ end {align *} \)
- \ (\ begin {align *} 2x + 4y & = — 10 \\ 6x + 3y & = 6 \ end {align *} \)
Это система из предыдущего набора примеров, которая заставила нас работать с дробями.Работа с ним здесь покажет различия между двумя методами, а также покажет, что любой метод может использоваться для получения решения для системы.
Итак, нам нужно умножить одно или оба уравнения на константы, чтобы одна из переменных имела одинаковый коэффициент с противоположными знаками. Итак, поскольку члены \ (y \) уже имеют противоположные знаки, давайте работать с этими терминами. Похоже, что если мы умножим первое уравнение на 3, а второе уравнение на 2, члены \ (y \) будут иметь коэффициенты 12 и -12, что нам и нужно для этого метода.
Вот работа для этого шага.
\ [\ begin {align *} 5x + 4y & = 1 & \ underrightarrow {\ times \, \, 3} \ hspace {0.5in} & 15x + 12y = 3 \\ 3x-6y & = 2 & \ underrightarrow {\ times \, \, 2} \ hspace {0,5 дюйма} & \ underline {\, \, 6x-12y = 4} \\ & & & 21x \ hspace {0,5 дюйма} = 7 \\ \ конец {выравнивание *} \]Итак, как и было обещано в описании метода, у нас есть уравнение, которое можно решить относительно \ (x \).Это дает \ (x = \ frac {1} {3} \), что мы и нашли в предыдущем примере. Обратите внимание, однако, что единственная дробь, с которой нам пришлось иметь дело до этого момента, — это сам ответ, который отличается от метода подстановки.
Теперь снова не забудьте найти \ (y \). В этом случае работы будет немного больше, чем метод подстановки. Чтобы найти \ (y \), нам нужно подставить значение \ (x \) в любое из исходных уравнений и решить относительно \ (y \).Поскольку \ (x \) является дробью, заметим, что в этом случае, если мы подставим это значение во второе уравнение, мы потеряем дроби, по крайней мере, временно. Обратите внимание, что часто этого не происходит, и нам придется иметь дело с дробями, хотим мы этого или нет.
\ [\ begin {align *} 3 \ left ({\ frac {1} {3}} \ right) — 6y & = 2 \\ 1 — 6y & = 2 \\ — 6y & = 1 \\ y & = — \ frac {1} {6} \ end {align *} \]Опять же, это то же значение, которое мы нашли в предыдущем примере.
b \ (\ begin {align *} 2x + 4y & = — 10 \\ 6x + 3y & = 6 \ end {align *} \) Показать решение
В этой части все переменные положительны, поэтому нам придется принудительно установить противоположный знак, умножив где-нибудь на отрицательное число. Также заметим, что в этом случае, если мы просто умножим первое уравнение на -3, то коэффициенты при \ (x \) будут -6 и 6.
Иногда нам нужно только умножить одно из уравнений, а другое можно оставить в покое.Вот эта работа по этой части.
\ [\ begin {align *} 2x + 4y & = -10 & \ underrightarrow {\ times \, \, — 3} \ hspace {0,5 дюйма} & -6x-12y = 30 \\ 6x + 3y & = 6 & \ underrightarrow {\ text {same}} \ hspace {0,5 дюйма} & \ underline {\ hspace {0,35 дюйма} 6x + 3y = 6} \\ & & & \ hspace {0,5 дюйма} -9y = 36 \\ & & & \ hspace {0,85 дюйма} y = -4 \\ \ конец {выравнивание *} \]Наконец, подставьте это в любое из уравнений и решите относительно \ (x \).На этот раз мы воспользуемся первым уравнением.
\ [\ begin {align *} 2x + 4 \ left ({- 4} \ right) & = — 10 \\ 2x — 16 & = — 10 \\ 2x & = 6 \\ x & = 3 \ end {align *} \]Итак, решение этой системы — \ (x = 3 \) и \ (y = — 4 \).
Существует третий метод, который мы рассмотрим для решения систем из двух уравнений, но он немного сложнее и, вероятно, более полезен для систем, по крайней мере, с тремя уравнениями, поэтому мы рассмотрим его в следующем разделе.
Перед тем, как покинуть этот раздел, мы должны рассмотреть несколько частных случаев решения систем.
Пример 3 Решите следующие системы уравнений. \ [\ begin {align *} x — y & = 6 \\ — 2x + 2y & = 1 \ end {align *} \] Показать решениеЗдесь мы можем использовать любой метод, но похоже, что замена будет немного проще. Мы решим первое уравнение относительно \ (x \) и подставим его во второе уравнение.
\ [\ begin {align *} x & = 6 + y \\ & \\ — 2 \ left ({6 + y} \ right) + 2y & = 1 \\ — 12 — 2y + 2y & = 1 \\ — 12 & = 1 \, \, \, ?? \ end {align *} \]Итак, это явно неправда, и, похоже, нигде в нашей работе нет ошибки. Так в чем проблема? Чтобы увидеть, давайте изобразим эти две линии и посмотрим, что мы получим.
Похоже, что эти две линии параллельны (можете ли вы проверить это с помощью наклона?), И мы знаем, что две параллельные линии с разными пересечениями \ (y \) (что важно) никогда не пересекутся.
Как мы видели в начале обсуждения этого раздела, решения представляют собой точку пересечения двух линий. Если две линии не пересекаются, у нас не будет решения.
Итак, когда мы получаем такой бессмысленный ответ в результате нашей работы, у нас есть две параллельные линии и нет решения этой системы уравнений.
Система в предыдущем примере называется несовместимая .Также обратите внимание, что если бы мы использовали исключение в этой системе, мы бы получили аналогичный бессмысленный ответ.
Пример 4 Решите следующую систему уравнений. \ [\ begin {align *} 2x + 5y & = — 1 \\ — 10x — 25y & = 5 \ end {align *} \] Показать решениеВ этом примере кажется, что устранение было бы самым простым методом.
\ [\ begin {align *} 2x + 5y & = -1 & \ underrightarrow {\ times \, \, 5} \ hspace {0.5in} & \, \, \, \, 10x + 25y = -5 \\ -10x-25y & = 5 & \ underrightarrow {\ text {same}} \ hspace {0,5 дюйма} & \ underline {-10x-25y = 5} \\ & & & \ hspace {0.9in} 0 = 0 \\ \ конец {выравнивание *} \]На первый взгляд может показаться, что это та же проблема, что и в предыдущем примере. Однако в этом случае мы пришли к равенству, которое просто не соответствовало действительности. В этом случае мы имеем 0 = 0, и это истинное равенство, и в этом смысле в этом нет ничего плохого.
Однако это явно не тот ответ, который мы ожидали здесь, и поэтому нам нужно определить, что именно происходит.
Мы предоставим вам проверить это, но если вы найдете наклон и \ (y \) — точки пересечения для этих двух линий, вы обнаружите, что обе линии имеют точно такой же наклон, и обе линии имеют одинаковые \ ( y \) — перехват. Итак, что это значит для нас? Хорошо, если две линии имеют одинаковый наклон и одинаковые \ (y \) — точки пересечения, тогда графики этих двух линий являются одним и тем же графиком.Другими словами, графики этих двух линий — это один и тот же график. В этих случаях любой набор точек, удовлетворяющий одному из уравнений, также будет удовлетворять другому уравнению.
Также напомним, что график уравнения — это не что иное, как набор всех точек, удовлетворяющих уравнению. Другими словами, существует бесконечный набор точек, которые удовлетворяют этой системе уравнений.
В этих случаях мы действительно хотим записать что-нибудь для решения.Итак, что мы сделаем, так это решим одно из уравнений для одной из переменных (неважно, что вы выберете). Решим первую относительно \ (y \).
\ [\ begin {align *} 2x + 5y & = — 1 \\ 5y & = — 2x — 1 \\ y & = — \ frac {2} {5} x — \ frac {1} {5} \ end {выровнять*}\]Затем для любого \ (x \) мы можем найти \ (y \), и эти два числа образуют решение системы уравнений. Обычно мы обозначаем это, записывая решение следующим образом:
\ [\ begin {array} {* {20} {c}} \ begin {align} x & = t \\ y & = — \ frac {2} {5} t — \ frac {1} {5} \ конец {выровненный} & {\ hspace {0.25in} {\ mbox {где}} \, t {\ mbox {- любое действительное число}}} \ end {array} \]Чтобы показать, что они дают решения, давайте рассмотрим несколько значений \ (t \).
\ (t = 0 \)
\ [x = 0 \ hspace {0,25 дюйма} y = — \ frac {1} {5} \]Чтобы показать, что это решение, нам нужно вставить его в оба уравнения системы.
\ [\ begin {align *} 2 \ left (0 \ right) + 5 \ left ({- \ frac {1} {5}} \ right) & \ mathop = \ limits ^? — 1 & \ hspace {0.? 5 \\ — 1 & = — 1 & \ hspace {0,25 дюйма} 5 & = 5 \ end {align *} \]Итак, \ (x = 0 \) и \ (y = — \ frac {1} {5} \) является решением системы. Давай быстро сделаем еще один.
\ (t = — 3 \)
\ [x = — 3 \ hspace {0,25 дюйма} y = — \ frac {2} {5} \ left ({- 3} \ right) — \ frac {1} {5} = \ frac {6} {5 } — \ frac {1} {5} = 1 \]И снова нам нужно вставить его в оба уравнения системы, чтобы показать, что это решение.? 5 \\ — 1 & = — 1 & \ hspace {0,25 дюйма} 5 & = 5 \ end {align *} \]
Конечно, \ (x = — 3 \) и \ (y = 1 \) — это решение.
Итак, поскольку существует бесконечное количество возможных \ (t \) ‘, должно быть бесконечное количество решений для этой системы, и они даются как,
\ [\ begin {array} {* {20} {c}} \ begin {align} x & = t \\ y & = — \ frac {2} {5} t — \ frac {1} {5} \ конец {выровненный} & {\ hspace {0.25in} {\ mbox {где}} \, t {\ mbox {- любое действительное число}}} \ end {array} \]Системы, подобные тем, что в предыдущих примерах, называются зависимыми .
Теперь мы увидели все три возможности решения системы уравнений. Система уравнений не будет иметь решения, ровно одно решение или бесконечно много решений.
Решение линейных уравнений с двумя неизвестными
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Всегда ли будет решение $ 2 $ линейных уравнений с $ 2 $ неизвестными?
Есть три возможных случая для $ 2 $ линейных уравнений с $ 2 $ неизвестными (наклон и пересечение):
$ \ qquad $ $ \ mathbf {0} $ точек решения $ \ qquad $ $ \ qquad $ $ \ mathbf {1} $ точка решения $ \ qquad $ $ \ qquad $ $ \ mathbf {\ infty} $ точек решения
$ \ qquad \ quad $ $ \ nexists $ не существует $ \ qquad $ $ \ qquad $ $ \ exists! $ уникальность $ \ qquad $ $ \ qquad $ $ \ exists $ нет уникальности
Строки имеют вид $ y (x) = mx + b $.
Случай 1: параллельные линии
Решение не существует.
Линии параллельны: у них одинаковый наклон.
$$ % \ begin {align} % y_ {1} (x) & = m x + b_ {1} \\ % y_ {2} (x) & = m x + b_ {2} \\ % \ end {align} %
$Случай 2: пересекающиеся линии
Имеем наличие и уникальность.
Склоны четкие.
$$ m_ {1} \ ne m_ {2} $$
$$ % \ begin {align} % y_ {1} (x) & = m_ {1} x + b_ {1} \\ % y_ {2} (x) & = m_ {2} x + b_ {2} \\ % \ end {align} %
$Случай 3: совпадающие линии
У нас наличие , но не уникальность .Есть бесконечное количество решений. Каждая точка решает систему уравнений.
Обе строки одинаковы.
$$ % \ begin {align} % y_ {1} (x) & = m x + b \\ % y_ {2} (x) & = m x + b \\ % \ end {align} % $$
С точки зрения линейной алгебры, посмотрите на проблему в терминах пробелов $ \ color {blue} {range} $ и $ \ color {red} {null} $.
Линейная система для двух уравнений имеет вид $$ % \ begin {align} % m_ {1} x — y & = b_ {1} \\ % m_ {2} x — y & = b_ {1} \\ % \ end {align} $$ которая имеет матричный вид $$ % \ begin {align} % \ mathbf {A} x & = b \\ % \ left [\ begin {array} {cc} м_ {1} & -1 \\ м_ {2} & -1 \\ \ end {array} \ right] % \ left [\ begin {array} {cc} Икс \\ у \\ \ end {array} \ right] % знак равно % \ left [\ begin {array} {cc} б_ {1} \\ Би 2} \\ \ end {array} \ right] % \ end {align} %
$Основная теорема обеспечивает естественную основу для классификации данных и решений.{*} \верно)} % \ end {align}
$Случай 1: не существует
Матрица $ \ mathbf {A} $ имеет дефект ранга $ (m_ {1} = m_ {2}) $ и $ b_ {1} \ ne b_ {2} $. $$ b = \ color {синий} {b _ {\ mathcal {R}}} + \ color {красный} {b _ {\ mathcal {N}}} $$ Это компонент пространства $ \ color {red} {null} $, который препятствует прямому решению. (Интересно, что существует решение методом наименьших квадратов. {*} \ right)} = % \ text {span} \ left \ {\, \красный цвет}{ \оставил[ \ begin {array} {r} -1 \ м \ end {массив} \верно] } \, \верно\} $$
Постскриптум: здесь полезны теоретические основы.Путешествие к пониманию начинается с простых примеров, таких как комментарий @ Nick.
линейной алгебры — неизвестное решение с 3 уравнениями и 2 неизвестными
линейная алгебра — неизвестное решение с 3 уравнениями и 2 неизвестными — Mathematics Stack ExchangeСеть обмена стеков
Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange- 0
- +0
- Авторизоваться Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 12к раз
$ \ begingroup $Рассмотрим систему с 3 уравнениями и 2 неизвестными, у которой нет решений.Перечислите все возможные варианты расположения трех уравнений в виде линий на плоскости x-y.
Я знаю, что для системы, у которой нет решения, определитель должен быть 0. Но я не понимаю, какие возможные варианты у меня могут быть.
задан 24 мая ’17 в 22: 542017-05-24 22:54
ХолодныйОгоньХолодныйОгонь3711 золотой знак11 серебряный знак44 бронзовых знака
$ \ endgroup $ 4 $ \ begingroup $Пример трех (линейных) уравнений с двумя неизвестными: \ begin {eqnarray *} x + 2y & = & 3 \\ 4x-5y & = & 6 \\ -7x + 8y & = & 9 \ end {eqnarray *} Каждое из этих уравнений дает прямую на плоскости.Три уравнения дают три линии на плоскости.
Как три линии могут расположиться на плоскости?
У вас может быть три разные параллельные линии. У вас могут быть две разные параллельные линии и поперечная. Вы можете иметь две параллельные линии и третью параллельную. У вас может быть три непараллельных линии, которые пересекаются в одной точке. Есть много разных возможностей.
Создан 24 мая ’17 в 23: 372017-05-24 23:37
Летать ночью, летать ночью29.7k33 золотых знака4040 серебряных знаков8888 бронзовых знаков
$ \ endgroup $ $ \ begingroup $Учитывая, что уравнения с двумя переменными (предположим, $ x, y \ in \ mathbb {R} $) графически представляют собой линии на плоскости $ XY $, то порядок следующий:
- Если есть одно решение: три линии пересекаются в одной точке, которая является решением системы.(Система совместима и определяется)
- Нет решения: в этом случае три линии как-то не пересекаются в одной и той же точке. Так что всякий раз, когда у них нет общей точки, это будет несовместимая система.
- Все они — одна и та же линия: в этом случае они пересекаются в бесконечном количестве точек, так что существует бесконечное количество решений для вашей системы. (Система совместима и не определена).
Создан 24 мая ’17 в 23: 412017-05-24 23:41
BBC3BBC346533 серебряных знака1313 бронзовых знаков
$ \ endgroup $ Mathematics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.

 Я их отразил в виде схем для наглядности.
Я их отразил в виде схем для наглядности.