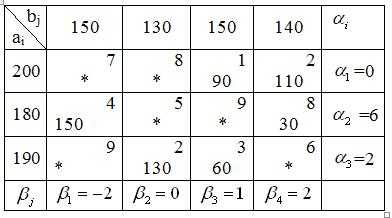Решение транспортной задачи распределительным методом на примерах
Если запасы груза равны суммарным потребностям, то транспортная задача называется замкнутой. Если же существует профицит (запасы превышают потребности) или дефицит (запасы меньше потребностей) груза, то транспортная задача называется открытой.
Пример 1. Решить транспортную задачу распределительным методом, составив первоначальный план перевозок по правилу минимального элемента.
Из трёх пунктов отправления нужно отправить груз в четыре пункта потребления.
В пункте A1 в наличии 40 единиц груза, в пункте A2 — 60 единиц, в пункте A3 — 100. Пункту потребления B1 требуются 35 единиц груза, пункту B2 — 35, пункту B3 — 80, пункту B4 — 50.
Решение. Строим таблицу, в которой в последний столбец записываем количества грузов
в пунктах отправления, а в последнюю строку — количества грузов, которые требуются в пунктах потребления.
В клетки пересечения пункта отправления
Таблица 1. Условие транспортной задачи в примере 1
| Пункт отправления | Пункт назначения | Запас груза | |||
| B1 | B2 | B3 | B4 | ||
| A1 | 2 | 5 | 6 | 4 | 40 |
| A2 | 2 | 4 | 5 | 2 | 60 |
| A3 | 2 | 3 | 4 | 1 | 100 |
| Потребность в грузе | 35 | 35 | 80 | 50 | |
Строим первоначальный план перевозок, применяя правило минимального элемента
Из всех клеток таблицы выбираем клетку с минимальной стоимостью перевозок. Это клетка A3B4. Ей соответствует стоимость c34 = 1. Это клетка, соответствующая пункту отправления A3 и пункту потребления B4. Запас груза в пункте A3 равен 100 единицам, а потребность в грузе в пункте B4 — 50 единицам.
Удовлетворим потребность пункта B4 за счёт пункта A3: впишем в правый нижний угол клетки A3B4 число 50, а стоимость, равную 1, возьмём в кружок.
Теперь по правилу минимального элемента следующую клетку с минимальным элементом
следует искать или в столбце, или в строке, в которой находится пройденная клетка
Далее следует двигаться или по столбцу, или по строке, в которой находится кретка A3B1. В пункте отправления A3 осталось неизрасходовано 15 единиц груза. Поэтому вновь движемся по строке и находим клетку A3B2 с минимальной стоимостью c32 = 3. Оставшиеся в пункте A3 15 единиц груза отправляем в пункт потребления B2, в правый нижний угол клетки A3B2 впишем число 15, а стоимсть 3 возьмём в кружок.
Вновь нам предстоит двигаться или по столбцу, или по строке, в которой находится
пройденная клетка. В пройденной клетке A3B2
запасы груза в пункте отправления A3
были израсходованы, поэтому дальше двигаемся уже по столбцу. Приходим на строку, соответствующую
пункту отправления A2, в клетку
A2B2,
с минимальной в данном столбце стоимостью перевозок c22 = 4.
У пункта потребления B2 остались
неудовлетворённые потребности в 20 единицах груза. Удовлетворим эти потребности за счёт пункта отправления
A2: в правый нижний угол клетки
Как двигаться дальше — по строке или по столбцу? Угадайте с одного раза! Правильно, по строке, потому что в пункте отправления A2 остались неизрасходованы 40 единиц груза. Попадаем в клетку A2B3. Куда направим оставшиеся 40 единиц груза? Потребности пунктов потребления B1, B2 и B4 уже удовлетворены, поэтому 40 единиц груза, требующиеся пункту потребления B3, направим в этот пункт, в правый нижний угол клетки A2B3 вписываем число 40, а стоимость 5 берём в кружок.
Таблица 2. Первоначальный план перевозок в примере 1
Все запасы груза, находившиеся в пункте отправления A2, израсходованы, поэтому дальше двигаемся по столбцу и попадаем в клетку A1B3, соответствующую пункту отправления A1. Запасы груза в этом пункте составляют 40 единиц, а неудовлетворённые потребности в грузе в пункте потребления B3 — также 40 единиц. Удовлетворим потребности пункта B3 за счёт пункта A1, впишем в правый нижний угол клетки A1B3 число 40, а стоимость перевозки 6 возьмём в кружок.
На этом потребности в грузе во всех пунктах потребления удовлетворены, а запасы груза во всех пунктах отправления израсходованы.
Найдём значение линейной формы, соответствующей первоначальному плану перевозок:
z(x1) = 6⋅40 + 4⋅20 + 5⋅40 + 2⋅35 + 3⋅15 + 1⋅50 = 685.
Клетки таблицы, содержащие кружочки, будем называть «занятыми местами», а клетки, не содержащие кружочков — «свободными местами». Первоначальный план перевозок составлен. Но мы ещё не решили всю транспортную задачу!
Оценка «свободных мест» и оптимальности плана перевозок
Следующий этап решения транспортной задачи после составления плана перевозок — исследование этого плана на минимум. Для этого исследуются знаки «свободных мест». Если во всех «свободных местах» имеются знаки «плюс», то транспортная задача решена, то есть план перевозок по стоимости является минимальным. Если же хотя бы одно из «свободных мест» имеет знак «минус», то план не даёт мимимума стоимости и его нужно улучшить.
Знаки «свободных мест» определяются следующим образом: начиная с любого «свободного места», двигаемся по ломаной линии, шагая только по «занятым местам». После каждого кружочка поворот делается только под прямым углом. Затем двигаемся до второго кружочка (не обязательно соседнего) и опять поворачиваем под прямым углом.
Таким образом, на пути по строке или столбцу в строке или столбце не могут встретиться больше двух кружков. Такое движение продолжается до тех пор, пока поворот от последнего кружочка не приведёт к исходному пункту, то есть исходному «свободному месту». Каждое движение должно быть или вертикальным, или горизонтальным, то есть перемещение по диагонали не допускается. Идя от исходной точки, то есть «свободного места», не обязательно брать первый встретившийся на пути кружок. Иногда можно пропустить один или несколько кружков, если через них невозможно кратчайшим путём вернуться к исходной точке. Путь, пройденный по вышеизложенным правилам, называется циклом.
Составим цикл для свободного места A1B1.
В первой клетке, то есть A1B1,
в правом верхнем углу ставим знак «плюс» (и так делаем всегда в начальной клетке цикла). Идём к «занятому
месту» — к клетке
Получаем следующий цикл:
A1B1 → A1B3 → A2B3 → A2B2 → A3B2 → A3B1.
Значение «свободного места» получаем так: составляем ряд из стоимостей перевозки в каждой клетке цикла, взятых со знаком «плюс» или «минус», в зависимости от того, какой знак поставлен в правом верхнем углу соответствующей клетки. По этому правилу получаем оценку свободного места A1B1:
Δ11 = 2 − 6 + 5 − 4 + 3 − 2 = −2.
Точно так же составляем циклы для «свободных мест» A1B2, A1B4, A2B1, A2B4, A3B
3 и вычисляем их оценки:Δ12 = 5 − 6 + 5 − 4 = 0,
Δ14 = 4 − 1 + 3 − 4 + 5 − 6 = 1,
Δ21 = 2 − 4 + 3 − 2 = −1,
Δ24 = 2 − 1 + 3 − 4 = 0,
Δ33 = 4 − 3 + 4 − 5 = 0.
Так как оценки Δ11 и Δ21 отрицательны, первоначальный план перевозок — не оптимальный и его нужно улучшить. Таким образом, решение транспортной задачи ещё не получено.
Улучшение плана перевозок
Среди оценок «свободных мест» две отрицательные: Δ11 = −2 и Δ21 = −1. Выберем наименьшее из этих отрицательных значений: Δ11 = −2. Вдоль цикла для соответствующего ему «свободного места» A1B1 выбираем наименьшее из чисел в кружочке, отмеченных знаком «минус». Это число 20, обозначим его буквой θ («тэта»):
θ = min{40, 20, 35} = 20.
Смотрим в первоначальный план перевозок. Найденное число «тэта» прибавляется ко всем «кружочкам» в клетках с положительными знаками и вычитается из всех «кружочков» в клетках с отрицательными знаками, включая само наименьшее число.
Таким образом, получаем перенаправление единиц груза для нового плана перевозок:
x’11 = x11 + θ = 0 + 20 = 20,
x’23 = x23 + θ = 40 + 20 = 60,
x’32 = x32 + θ = 15 + 20 = 35,
x’13 = x13 − θ = 40 − 20 = 20,
x’31 = x31 − θ = 35 − 20 = 15,
x’34 = x34 = 50.
Так как x’22 = x22 − θ = 20 − 20 = 0, то в новой таблице клетка A2B2 становится «свободным местом». Значение в клетке A3B4 остаётся прежним: x’34 = x34 = 50, так как эта клетка не входит в цикл.
Таблица 3. Второй план перевозок в примере 1
Значение линейной формы для нового плана перевозок вычисляется следующим образом. Вычисляется «экономия»: наименьшее число «тэта» умножается на число, стоящее в кружочке в соответствующей клетке. Получается отрицательное число, так как «тэта» — отрицательное число. К значению линейной формы предыдущего плана прибавляется «экономия», то есть отрицательное число (фактически вычитается «экономия», если удобнее смотреть на неё «экономически», то есть считать положительным числом).
Вычислим значение линейной формы для плана перевозок x2:
z(x2) = z(x1) + θ⋅Δ21 = 685 + 20⋅(−2) = 645.
Для новой таблицы, как уже было показано, составляем циклы от «свободных мест» и вычисляем оценки «свободных мест»:
Δ12 = 5 − 3 + 2 − 2 = 2,
Δ14 = 4 − 1 + 2 − 2 = 3,
Δ21 = 2 − 2 + 6 − 5 = 1,
Δ22 = 4 − 3 + 2 − 2 + 6 − 5 = 2,
Δ24 = 2 − 1 + 2 − 2 + 6 − 5 = 2,
Δ33 = 4 − 2 + 2 − 6 = −2.
Среди оценок свободных мест — одна отрицательная: Δ33 = −2, поэтому план x2 — не оптимальный.
Рассмотрим цикл, соответствующий «свободному месту» с отрицательной оценкой:
A3B3 → A3B1 → A1B1 → A1B3.
Точно так же, как было сделано в случае первоначального плана, вдоль этого цикла выбираем наименьшее из чисел в кружочке, отмеченных знаком «минус». Это число 15:
θ = min{15, 20} = 15.
Это число прибавляем ко всем «кружочкам» в клетках с положительными знаками и вычитаем из всех «кружочков» в клетках с отрицательными знаками и получаем перенаправление единиц груза для нового плана перевозок:
x’11 = x11 + θ = 20 + 15 = 35,
x’33 = x33 + θ = 0 + 15 = 15,
x’13 = x13 − θ = 20 − 15 = 5,
x’31 = x13 − θ = 15 − 15 = 0.
Таблица 4. Третий план перевозок в примере 1
Вычислим значение линейной формы для плана перевозок x3:
z(x3) = z(x2) + θ⋅Δ33 = 645 + 15⋅(−2) = 615.
Составим циклы для «свободных мест» плана x3 и вычислим оценки:
Δ12 = 5 − 6 + 4 − 3 = 0,
Δ14 = 4 − 1 + 4 − 6 = 1,
Δ21 = 2 − 2 + 6 − 5 = 1,
Δ22 = 4 − 5 + 4 − 3 = 0,
Δ24 = 2 − 1 + 4 − 5 = 0,
Δ31 = 2 − 2 + 6 − 4 = 2.
Так как оценки всех «свободных мест» неотрицательны, план x3 — оптимальный, он даёт минимум линейной формы z = 615.
Так как оценки Δ12, Δ22 и Δ24 равны нулю, то эта транспортная задача имеет бесконечное множество оптимальных планов (решений).
Пример 2. Решить транспортную задачу распределительным методом, составив первоначальный план перевозок по правилу северо-западного угла.
Из трёх пунктов отправления нужно отправить груз в три пункта потребления.
В пункте A1 в наличии 20 единиц груза, в пункте A2 — 40 единиц, в пункте A3 — 40. Пункту потребления B1 требуются 20 единиц груза, пункту B2 — 20, пункту B3 — 60.
Строим таблицу, руководствуясь теми же соображениями, что в примере 1.
Таблица 5. Условие транспортной задачи в примере 2
| Пункт отправления | Пункт назначения | Запас груза | ||
| B1 | B2 | B3 | ||
| A1 | 3 | 4 | 3 | 20 |
| A2 | 1 | 1 | 2 | 40 |
| A3 | 1 | 5 | 4 | 40 |
| Потребность в грузе | 20 | 20 | 60 | |
Применение правила северо-западного угла начинается с составления плана перевозок для первого пункта отправления (для A1), то есть с левого верхнего (северо-западного) угла таблицы. Далее, как и по правилу минимального элемента, нужно двигаться вперёд по строке или столбцу, в которых находится пройденная клетка, но, в отличие от правила минимального элемента, не требуется искать в этих строке или столбце минимальный элемент (клетку с минимальной стоимостью), а можно двигаться последовательно от соседнего элемента к соседнего до тех пор, пока все запасы груза в пунктах отправления не будут распределены по всем пунктам потребления.
Если при применении правила северо-западного угла на каком-либо шаге, кроме последнего, окажется, что все имеющиеся запасы груза в одном соответствующем пункте отправления передаются одному пункту потребления (потребности одного пункта потребления удовлетворены за один шаг за счёт одного пункта отправления), то транспортная задача имеет вырожденный (сингулярный) план перевозок. В этом случае в соседнюю клетку — вправо или вниз — от пройденной следует вписать нуль. Рекомендуется вписывать нуль в ту соседнюю клетку, которой соответствуют меньшие транспортные расходы.
Итак, начинаем движение с клетки A1B1. Запас груза в пункте отправления A1 равен 20. Потребность в грузе в пункте потребления B1 составляет также 20. Удовлетворяем потребность пункта потребления B1 за счёт пункта отправления A1 и в правый нижний угол клетки A1B1 вписываем 20. Видим, что мы получаем вырожденный (сингулярный) план перевозок. Поэтому в правый нижний угол соседней клетки с меньшими транспортными расходами (A2B1) вписываем нуль.
Далее, соответственно правилу северо-западного угла, движемся по клеткам A2B2, A2B3, A3B3 и получаем план перевозок x1.
Таблица 6. Первый план перевозок в примере 2
Значение линейной формы плана x1:
z(x1) = 3⋅20 + 1⋅20 + 2⋅40 + 4⋅40 = 280.
Знаки «свободных мест» (для установления оптимальности плана) определяются точно так же, как и в случае применения правила минимального элемента (пример 1) — составляются циклы для каждого «свободного места». В нашем случае получаем следующие циклы:
A1B2 → A2B2 → A2B1 → A1B1,
A1B3 → A2B3 → A2B1 → A1B1,
A3B1 → A2B1 → A2B3 → A3B3,
A3B2 → A2B2 → A2B3 → A3B3.
Вычисляем оценки «свободных мест»:
Δ12 = 4 − 1 + 1 − 3 = 1,
Δ13 = 3 − 2 + 1 − 3 = −1,
Δ31 = 1 − 1 + 2 − 4 = −2,
Δ32 = 5 − 1 + 2 − 4 = 2.
Так как два свободных места имеют отрицательные оценки, план x1 — не оптимальный и его нужно улучшить. Решение транспортной задачи ещё не получено.
Выбираем «свободную» клетку A3B1, у которой минимальная отрицательная оценка: Δ31 = −2. Вдоль цикла, соответствующего этой клетке, выбираем наименьшее из чисел в кружочке, отмеченное знаком минус:
θ = min{0, 40} = 0.
В результате перенаправления грузов клетка A2B1 становится «свободным местом» в плане перевозок x2, а «свободное место» A3B1 становится «занятым местом», которому соответствует количество груза 0 единиц.
Таблица 7. Второй план перевозок в примере 2
Вычисляем значение линейной формы для плана x2:
z(x2) = z(x1) + θ⋅Δ31 = 280 + 0⋅(−2) = 280.
Для плана x2 вычисляем оценки «свободных мест»:
Δ12 = 4 − 1 + 2 − 4 + 1 − 3 = −1,
Δ13 = 3 − 4 + 1 − 3 = −3,
Δ21 = 1 − 2 + 4 − 1 = 2,
Δ32 = 5 − 1 + 2 − 4 = 2.
Среди оценок свободных мест две — отрицательные, поэтому план перевозок необходимо улучшить. В следующем плане перевозок «свободное место» A1B3 становится «занятым местом», так как его оценка Δ13 = −3 — наибольшая по модулю отрицательная оценка.
Вдоль цикла, соответствующего этой клетке, выбираем наименьшее из чисел в кружочке, отмеченное знаком минус:
θ = min{40, 20} = 20.
Таблица, соответствующая плану перевозок x3, будет следующей:
Таблица 8. Третий план перевозок в примере 2
Находим значение линейной формы для плана x3:
z(x3) = z(x2) + θ⋅Δ13 = 280 + 20⋅(−3) = 220.
Вычисляем оценки «свободных мест»:
Δ11 = 3 − 3 + 4 − 1 = 3,
Δ12 = 4 − 3 + 2 − 1 = 2,
Δ21 = 1 − 2 + 4 − 1 = 2,
Δ32 = 5 − 1 + 2 − 4 = 2.
Окончательное решение данной транспортной задачи получено. Поскольку все оценки «свободных мест» — неотрицательные, план x3 является оптимальным планом и ему соответствует минимум линейной формы z = 220.
Резюмируя выполненные выше решения, сформулируем алгоритм решения транспортной задачи распределительным методом (поиска оптимального плана транспортной задачи).
Эти шаги следует повторять до тех пор, пока оценки всех «свободных мест» не станут положительными.
Если в ходе решения транспортной задачи появились вырожденные (сингулярные) планы, то возможно, что число «тэта» равно нулю. Тогда на соответствующей итерации решения значение линейной формы не меняется (что и было показано в примере 2).
Продолжение темы «Линейное программирование»
function-x.ru
Транспортная задача — решение методом потенциалов
Одна из самых распространенных и востребованных оптимизационных задач в логистике – транспортная задача. В классическом виде она предполагает нахождение оптимального (т.е. сопряженного с минимальными затратами) плана грузоперевозок.
Например, у нас есть сеть розничных магазинов, которым требуется определенное количество товаров. Также имеется ряд складов поставщиков, где требуемые товары хранятся. При этом на каждом складе различный объем запасов этих товаров. Кроме этого нам известны тарифы – затраты на перевозку 1 товара от каждого склада к каждому магазину.
Возникает необходимость разработать такой план перевозок, чтобы магазины получили требуемое количество товаров с наименьшими затратами на транспортировку. Вот именно в таких случаях (и во множестве других) приходится решать транспортную задачу.
Теоретический материал по транспортной задаче
Транспортная задача (задача Монжа — Канторовича) — математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение.
Для простоты понимания рассматривается как задача об оптимальном плане перевозок грузов из пунктов отправления (например, складов) в пункты потребления (например, магазины), с минимальными общими затратами на перевозки.
Математическая модель транспортной задачи имеет следующий вид:
где: Z — затраты на перевозку грузов;
X — объем груза;
C — стоимость (тариф) перевозки единицы груза;
A — запас поставщика;
B — запрос потребителя;
m — число поставщиков;
n — число потребителей.
Общий план решения транспортной задачи методом потенциалов
Решить транспортную задачу можно различными методами, начиная от симплекс-метода и простого перебора, и заканчивая методом графов. Один из наиболее применяемых и подходящих для большинства случаев методов – итерационное улучшение плана перевозок.
Суть его в следующем: находим некий опорный план и проверяем его на оптимальность (Z → min). Если план оптимален – решение найдено. Если нет – улучшает план столько раз, сколько потребуется, пока не будет найден оптимальный план.
Ниже приведен алгоритм решения транспортной задачи в самом общем виде:
- Построение транспортной таблицы.
- Проверка задачи на закрытость.
- Составление опорного плана.
- Проверка опорного плана на вырожденность.
- Вычисление потенциалов для плана перевозки.
- Проверка опорного плана на оптимальность.
- Перераспределение поставок.
- Если оптимальное решение найдено, переходим к п. 9, если нет – к п. 5.
- Вычисление общих затрат на перевозку груза.
- Построение графа перевозок.
Подробная инструкция по решению транспортной задачи
1. Построение транспортной таблицы
Строим таблицу, где указываем запасы материалов, имеющиеся на складах поставщиков (Ai), и потребности заводов (Bj) в этих материалах.
В нижний правый угол ячеек таблицы заносим значение тарифов на перевозку груза (Cij).
2. Проверка задачи на закрытостьОбозначим суммарный запас груза у всех поставщиков символом A, а суммарную потребность в грузе у всех потребителей – символом B.
Тогда:
Транспортная задача называется закрытой, если A = B . Если же A ≠ B , то транспортная задача называется открытой. В случае закрытой задачи от поставщиков будут вывезены все запасы груза, и все заявки потребителей будут удовлетворены. В случае открытой задачи для ее решения придется вводить фиктивных поставщиков или потребителей.Проверим задачу на закрытость:
A = 10 + 20 + 30 = 60
B = 15 + 20 + 25 = 60
A = B, следовательно данная транспортная задача – закрытая.
3. Составление опорного плана
Составляет предварительный (опорный) план перевозок. Он не обязательно должен быть оптимальный. Это просто своеобразный «черновик», «набросок», улучшая который мы постепенно придем к плану оптимальному.
Есть разные методы нахождения опорного плана. Наиболее распространены следующие:
а) Метод Северо-Западного угла. Показать
Суть метода проста — ячейки транспортной таблицы последовательно заполняются максимально возможными объемами перевозок, в направлении сверху вниз и слева направо. То есть сперва заполняется самая верхняя левая ячейка («северо-западная» ячейка), потом следующая справа и т.д. Затем переходят на новую строку и вновь заполняют ее слева направо. И так пока таблица не будет заполнена полностью.
Подробное описание метода и пример можно посмотреть здесь.
б) Метод минимального элемента. Показать
Метод заключается в том, что для заполнения ячеек транспортной таблицы выбирается клетка с минимальным значением тарифа. Затем выбирается следующая клетка с наименьшим тарифом и так продолжается до тех пор, пока таблица не будет заполнена (все запасы и потребности при этом обнулятся).
Подробное описание метода и пример можно посмотреть здесь
в) Аппроксимация Фогеля. Показать
Основа метода в нахождении разности (по модулю) между парой минимальных тарифов в каждой строке и столбце. Затем в строке или столбце с наибольшей разностью заполняется клетка с наименьшим тарифом. Затем все эти действия повторяются заново, только при этом уже не учитываются заполненные клетки.
Подробное описание аппроксимации Фогеля и пример можно посмотреть онлайн
г) Метод двойного предпочтения. Показать
Суть метода в том, что отмечаются клетки с наименьшим тарифом по строкам, а затем по столбцам. Затем ячейки заполняются в следующей очередности: сначала клетки с двумя отметками, потом с одной, наконец без отметок.Подробное описание метода и пример можно посмотреть здесь
4. Проверка опорного плана на вырожденность
Клетки таблицы, в которые записаны отличные от нуля перевозки, называются базисными, а остальные (пустые) — свободными.
План называется вырожденным, если количество базисных клеток в нем меньше, чем m + n -1. Если во время решения задачи получился вырожденный план, то его необходимо пополнить, проставив в недостающем числе клеток нулевую перевозку и превратив, тем самым, эти клетки в базисные (общий баланс и суммарная стоимость перевозок плана при этом не изменятся). Однако проводить пополнение плана, выбирая клетки произвольно, нельзя. План должен быть ациклическим!
План называется ациклическим, если его базисные клетки не содержат циклов. Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией так, чтобы две соседние вершины ломаной были расположены либо в одной строке, либо в одном столбце. Ниже приведен пример цикла:
Ломаная линия может иметь точки самопересечения, но не в клетках цикла.Кол-во базисных клеток = 5
m + n – 1 = 3 + 3 – 1 = 5
Следовательно, первоначальный план перевозок – невырожденный.
5. Вычисление потенциалов для плана перевозки
Для анализа полученных планов и их последующего улучшения удобно ввести дополнительные характеристики пунктов отправления и назначения, называемые потенциалами.
Этот метод улучшения плана перевозок называется методом потенциалов. Есть другие методы итерационного улучшения плана перевозок, но здесь мы их рассматривать не будем.
Итак, сопоставим каждому поставщику Ai и каждому потребителю Bj величины Ui и Vj соответственно так, чтобы для всех базисных клеток плана было выполнено соотношение:
Ui + Vj = Cij
Добавим к транспортной таблице дополнительную строку и столбец для Ui и Vj.
Предположим, что U1 = 0.
Тогда мы сможем найти V3 = C13 – U1 = 1 – 0 = 1.
Зная V3, мы теперь можем найти U3:
По аналогии вычисляем все оставшиеся потенциалы:
6. Проверка плана на оптимальность методом потенциалов
Для каждой свободной клетки плана вычислим разности
ΔCij = Cij – (Ui + Vj )
и запишем полученные значения в левых нижних углах соответствующих ячеек.
План является оптимальным, если все разности ΔCij ≥ 0.
В данном случае план – неоптимальный (ΔC22 < 0), и его следует улучшить путем перераспределения поставок.
7. Перераспределение поставок
Найдем ячейку с наибольшей по абсолютной величине отрицательной разностью ΔCij и построим цикл, в котором кроме этой клетки все остальные являются базисными. Такой цикл всегда существует и единственен.
Отметим ячейку с отрицательной разностью ΔCij знаком «+», следующую знаком «-», и так далее, поочередно.
Затем находим минимальной значение груза в ячейках цикла имеющих знак «-» (здесь это 5) и вписываем его в свободную ячейку со знаком «+». Затем последовательно обходим все ячейки цикла, поочередно вычитая и прибавляя к ним минимальное значение (в соответствии со знаками, которыми эти ячейки помечены: где минус — вычитаем, где плюс — прибавляем).
Получим новый опорный план перевозок:
Так как базисных клеток стало больше, чем m + n – 1, то базисную клетку с нулевым значением делаем свободной:
Снова вычисляем значения потенциалов и разности ΔCij:
На этот раз все разности ΔCij ячеек положительные, следовательно, найдено оптимальное решение.8. Если оптимальное решение найдено, переходим к п. 9, если нет – к п. 5.
У нас оптимальное решение найдено, поэтому переходим к пункту 9.
9. Вычисление общих затрат на перевозку груза
Вычислим общие затраты на перевозку груза (Z), соответствующие найденному нами оптимальному плану, по формуле:
Zmin = 10 ∙ 1 + 15 ∙ 3 + 5 ∙ 2 + 15 ∙ 1 + 15 ∙ 2 = 110 ден. ед.
Общие затраты на доставку всей продукции, для оптимального решения, составляют 110 ден. ед.
10. Построение графа перевозок
Найдя оптимальный план перевозок, построим граф. Вершинами графа будут «склады» и «магазины». В вершинах укажем соответствующие объемы запасов и потребностей. Дугам, соединяющим вершины графа, будут соответствовать ненулевые перевозки. Каждую такую дугу подпишем, указав объем перевозимого груза.
В результате получится граф, аналогичный изображенному ниже:
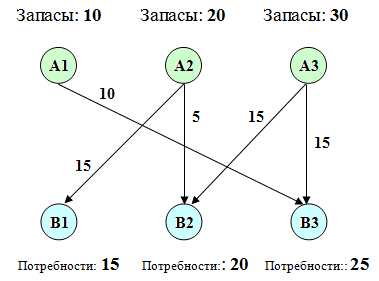
Все, транспортная задача решена. Поздравляю!
Практическое применение транспортной задачи
Транспортная задача применяется во многих случаях. Это оптимизация поставок сырья и материалов на производственные предприятия. Это оптимизация доставок товаров со складов в розничные магазины. Это оптимизация пассажирских перевозок, и много-многое другое.
Галяутдинов Р.Р.
© Копирование материала допустимо только при указании прямой гиперссылки на источник: Галяутдинов Р.Р.
galyautdinov.ru
Транспортная задача — пример и оформление
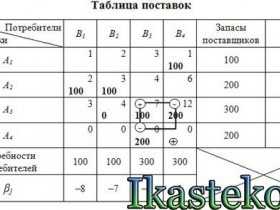
Пример. На три базы поступили ящики с заготовками деталей, которые необходимо доставить на четыре завода. Исходные данные представлены в нижеследующей транспортной таблице.
Таблица 10.3
Определите оптимальный план доставки заготовок на заводы с учетом минимизации совокупных транспортных затрат.
Решение
Обозначим искомые объемы поставок от i-ой базы-поставщика к j-му заводу-потребителю через .
Математическая модель данной задачи будет иметь вид:
I итерация:
1 этап: проверка сбалансированности запасов и потребностей.
Представленная транспортная задача является открытой, т.к. суммарная мощность баз-поставщиков меньше суммарной потребности заводов-потребителей на 200 ящиков:
,
,
.
Сведем данную транспортную задачу к закрытой: введем фиктивную базу А4 с недостающей мощностью а4 = 200 ящиков:
.
Зададим значения условных транспортных затрат на единицу груза от данной базы к заводам-потребителям равными нулю, результаты занесем в следующую таблицу.
Таблица 10.4
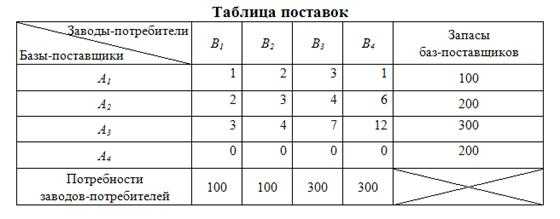
С учетом фиктивного поставщика математическая модель будет иметь вид:
2 этап: разработка исходного опорного плана.
Для отыскания исходного опорного плана воспользуемся методом минимальной стоимости. Согласно таблице поставок (таблица 10.4) минимальная стоимость соответствует клеткам строки фиктивного поставщика. Рассмотрим, к примеру, клетку «4-3». Объем поставок для данной пары поставщик-потребитель составит:
Запишем в клетку «4-3» объем поставок x43=200 (таблица 10.5). Запасы фиктивного поставщика исчерпаны (зачеркиваем остальные клетки данной строки, они в дальнейших рассмотрениях не участвуют).
Таблица 10.5
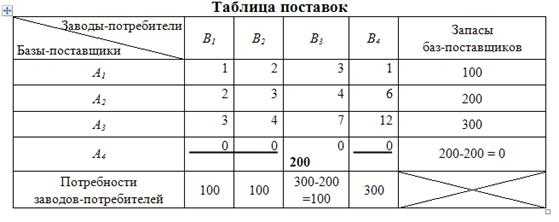
Из свободных клеток минимальная стоимость соответствует клеткам «1- 1» и «1-4» (cij=1), выберем, к примеру, клетку «1-4». Вписываем в данную клетку объем поставок x14=100 (таблица 10.6). Запасы первого поставщика исчерпаны (зачеркиваем остальные клетки данной строки, они в дальнейших рассмотрениях не участвуют).
Таблица 10.6
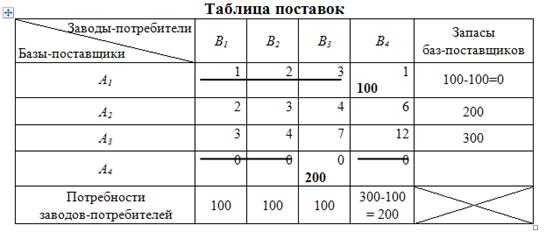
Следующая свободная клетка с наименьшей стоимостью поставок единицы груза – клетка «2-1» (c21=2). Объем поставок для данной пары поставщик-потребитель составит:
Запишем в клетку «2-1» объем поставок x21=100 (таблица 10.7). Потребность первого завода-потребителя полностью удовлетворена (зачеркиваем незадействованную клетку данной колонки – «3-1», она в дальнейших рассмотрениях не участвуют).
Таблица 10.7
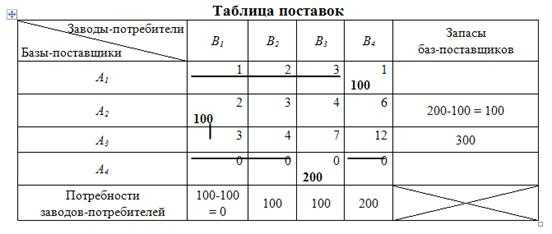
Оставшиеся запасы второго поставщика целесообразно направить для удовлетворения потребностей второго завода-потребителя, так как стоимость доставки единицы груза здесь наименьшая (c 22=3). Вписываем в соответствующую клетку объем поставок x22=100 (таблица 10.8).
Таблица 10.8

Таким образом, потребность второго завода-потребителя полностью удовлетворена и мощность второго поставщика полностью задействована, поэтому вычеркиваем незадействованные клетки «2-3», «2-4» и «3-2», в дальнейших рассмотрениях они не участвуют.
Продолжая данные рассуждения, в результате получим следующее распределение поставок:
Таблица 10.9
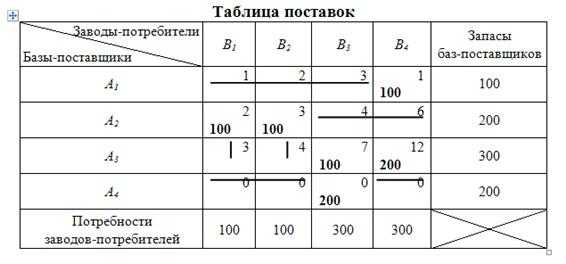
Совокупные транспортные издержки для данного плана поставок составят (усл. ден. ед.):
.
3 этап: проверка вырожденности опорного плана.
Количество задействованных клеток в таблице поставок (таблица 10.9): N=6. Ранг r системы ограничений транспортной задачи равен:
.
Так как, , следовательно, опорный план транспортной задачи вырожденный. Определим количество фиктивных поставок:
.
В любой свободной клетке таблицы поставок проектному параметру xij присвоим нулевое значение. Выберем, к примеру, клетку «3-2» (клетки для фиктивных поставок необходимо выбирать таким образом, чтобы в дальнейшем можно было корректно построить контур перераспределения поставок).
Таблица 10.10
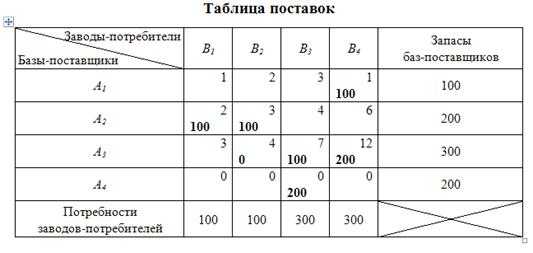
4 этап: расчет потенциалов.
Для первой строки принимаем ?1=0. Рассмотрим загруженную клетку «1-4»: .
Для загруженной клетки «3-4»: .
Аналогично последовательно находим потенциалы строк и колонок по остальным загруженным клеткам, результаты расчетов представлены в таблице 10.11.
Таблица 10.11
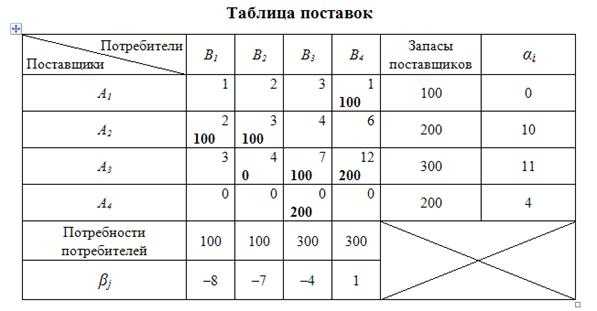
5 этап: проверка плана на оптимальность.
По таблице 10.11 для незагруженных клеток проверим условие оптимальности ():
«1-1»: ,
«1-2»: ,
«1-3»: ,
«2-3»: ,
«2-4»: ,
«3-1»: ,
«4-1»: ,
«4-2»: ,
«4-4»: .
Опорный план не оптимальный, так как имеются клетки, для которых условие оптимальности не выполняется: «2-3», «2-4», «4-4».
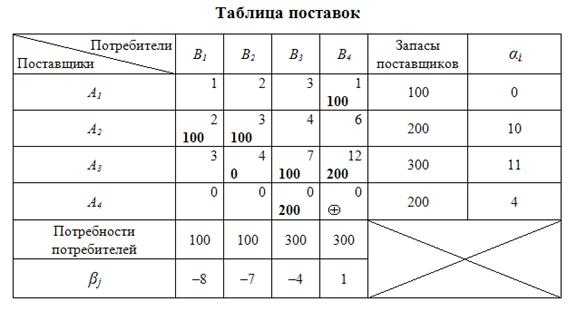
6 этап: поиск «вершины максимальной неоптимальности» (ВМН).
Для клеток «2-3», «2-4», «4-4» рассчитаем оценки: .
,
,
.
.
Выбор ВМН неоднозначен (можно выбрать любую), примем клетку «4-4» в качестве ВМН. Пометим ее в таблице поставок знаком (таблица 10.12).
Таблица 10.12
7 этап: построение контура перераспределения поставок.
Построим контур перераспределения поставок (таблица 10.13).
Таблица 10.13
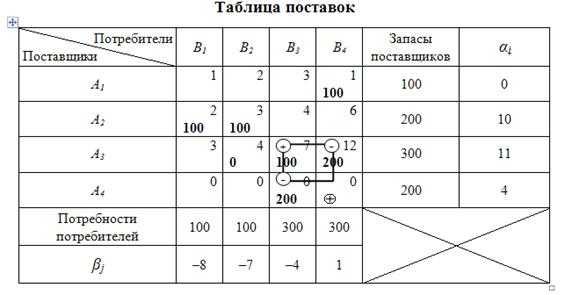
В таблице 10.13 начиная с ВМН разделим вершины на загружаемые
и разгружаемые.
8 этап: определение минимального элемента в контуре перераспределения и перераспределение поставок по контуру.
В рамках построенного контура из клеток со статусом «разгружаемые» выберем клетку с наименьшим объемом поставок (полностью разгружаемую клетку):
.
Выбор неоднозначен, полностью разгружаем, к примеру, клетку x34 и загружаем ВМН (x44=200). Для обеспечения соответствия объемов запасов и потребностей перераспределим поставки по контуру – разгрузим клетку «4-3» на 200 ящиков (x43=0) и загрузим на этот же объем клетку «3-3» (x33=100+200=300).
9 этап: получения нового опорного плана.
В результате перераспределения поставок по контуру получим новый опорный план (таблица 10.14).
Таблица 10.14
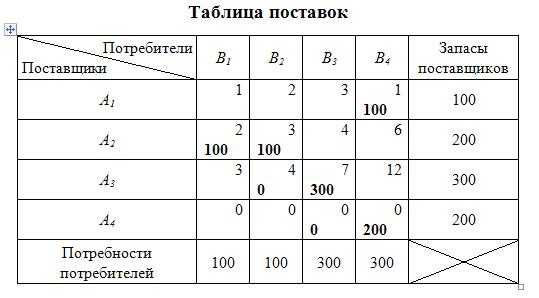
Совокупные транспортные издержки для данного плана поставок составят (усл. ден. ед.):
.
II итерация:
1 этап: проверка вырожденности опорного плана.
Опорный план условно невырожденный.
2 этап: расчет потенциалов.
Результаты расчета потенциалов приведены в таблице 10.15.
Таблица 10.15
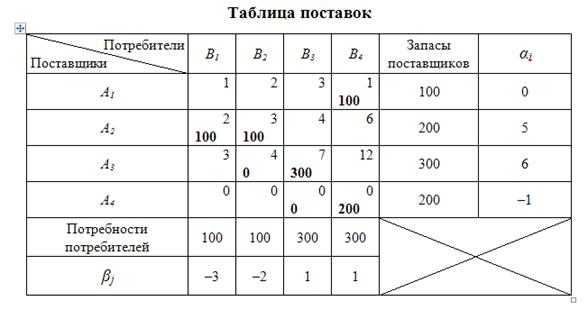
3 этап: проверка плана на оптимальность.
«1-1»: ,
«1-2»: ,
«1-3»: ,
«2-3»: ,
«2-4»: ,
«3-1»: ,
«3-4»: ,
«4-1»: ,
«4-2»: .
Опорный план не оптимальный, так как имеются клетка «2-3», для которой условие оптимальности не выполняется.
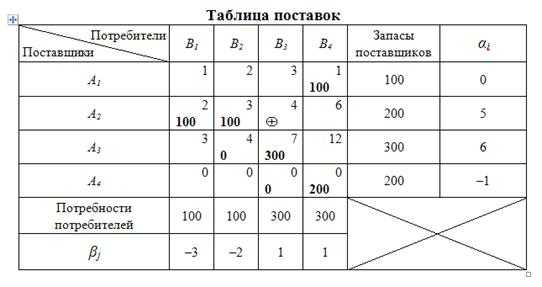
4 этап: поиск «вершины максимальной неоптимальности» (ВМН).
Клетку «2-3» примем в качестве ВМН. Пометим ее знаком (таблица 10.16).
Таблица 10.16
5 этап: построение контура перераспределения поставок.
Построим контур перераспределения поставок (таблица 10.17).
Таблица 10.17
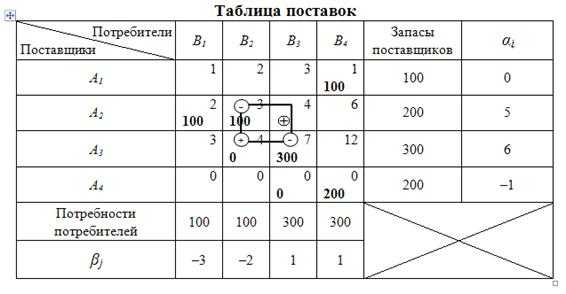
В таблице 10.17 начиная с ВМН разделим вершины на загружаемые
и разгружаемые.
6 этап: определение минимального элемента в контуре перераспределения и перераспределение поставок по контуру.
В рамках построенного контура из клеток со статусом «разгружаемые» выберем клетку с наименьшим объемом поставок (полностью разгружаемую клетку):
.
Полностью разгружаем клетку x22 и загружаем ВМН (x23=100). Для обеспечения соответствия объемов запасов и потребностей перераспределим поставки по контуру – разгрузим клетку «3-3» на 100 ящиков (x33=200) и загрузим на этот же объем клетку «3-2» (x32=100).
7 этап: получения нового опорного плана.
В результате перераспределения поставок по контуру получим новый опорный план (таблица 10.18).
Таблица 10.18
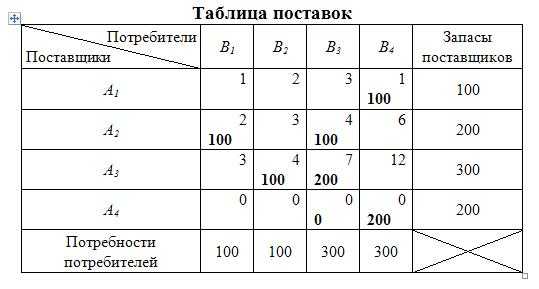
Совокупные транспортные издержки для данного плана поставок составят (усл. ден. ед.):
.
III итерация:
1 этап: проверка вырожденности опорного плана.
Опорный план невырожденный.
2 этап: расчет потенциалов.
Результаты расчета потенциалов приведены в таблице 10.19.
Таблица 10.19
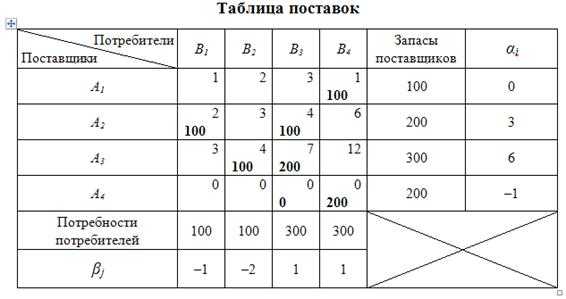
3 этап: проверка плана на оптимальность.
«1-1»: ,
«1-2»: ,
«1-3»: ,
«2-2»: ,
«2-4»: ,
«3-1»: ,
«3-4»: ,
«4-1»: ,
«4-2»: .
Опорный план не оптимальный, так как имеются клетка «3-1», для которой условие оптимальности не выполняется.
4 этап: поиск «вершины максимальной неоптимальности» (ВМН).
Клетку «3-1» примем в качестве ВМН. Пометим ее знаком (таблица 10.20).
Таблица 10.20
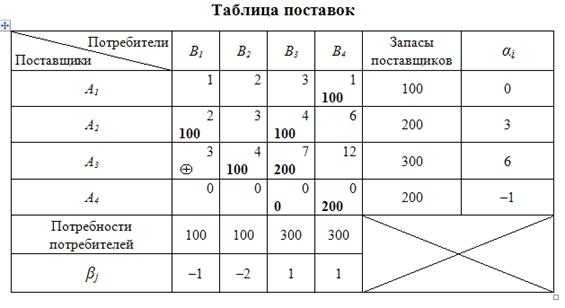
5 этап: построение контура перераспределения поставок.
Построим контур перераспределения поставок (таблица 10.21).
Таблица 10.21
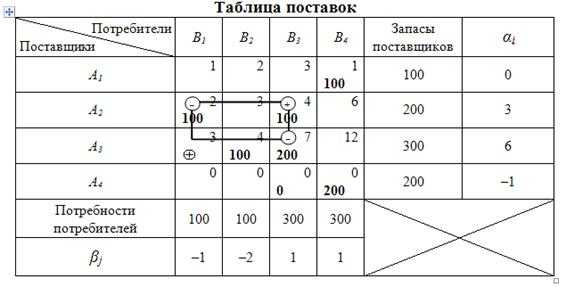
В таблице 10.21 начиная с ВМН разделим вершины на загружаемые
и разгружаемые .
6 этап: определение минимального элемента в контуре перераспределения и перераспределение поставок по контуру.
В рамках построенного контура из клеток со статусом «разгружаемые» выберем клетку с наименьшим объемом поставок (полностью разгружаемую клетку):
.
Полностью разгружаем клетку x21 и загружаем ВМН (x31=100). Для обеспечения соответствия объемов запасов и потребностей перераспределим поставки по контуру – разгрузим клетку «3-3» на 100 ящиков (x33=100) и загрузим на этот же объем клетку «2-3» (x23=200).
7 этап: получения нового опорного плана.
В результате перераспределения поставок по контуру получим новый опорный план (таблица 10.22).
Таблица 10.22
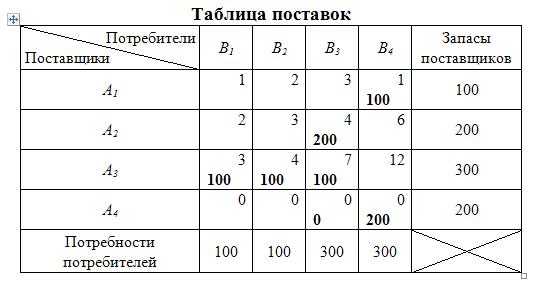
Совокупные транспортные издержки для данного плана поставок составят (усл. ден. ед.):
.
VI итерация:
1 этап: проверка вырожденности опорного плана.
Опорный план невырожденный.
2 этап: расчет потенциалов.
Результаты расчета потенциалов приведены в таблице 10.23.
Таблица 10.23
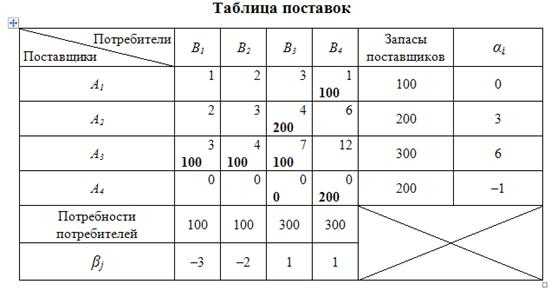
3 этап: проверка плана на оптимальность.
«1-1»: ,
«1-2»: ,
«1-3»: ,
«2-1»: ,
«2-2»: ,
«2-4»: ,
«3-4»: ,
«4-1»: ,
«4-2»: .
Найденный опорный план оптимальный, так как для всех незагруженных клеток выполняется условие оптимальности. Оптимальное решение является единственным, так как все неравенства строгие.
Ответ: оптимальное распределение поставок:
.
Данное распределение поставок обеспечит оптимальные транспортные издержки в размере 2300 усл. ден. ед.
СКАЧАТЬ методические указания к решению транспортной задачи: Транспортная задача с ограничениями на пропускную способность
Еще записи по теме
www.ikasteko.ru
|
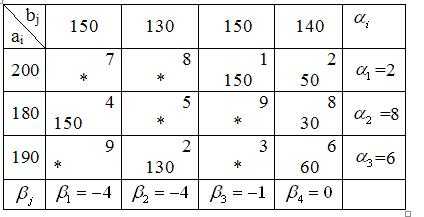
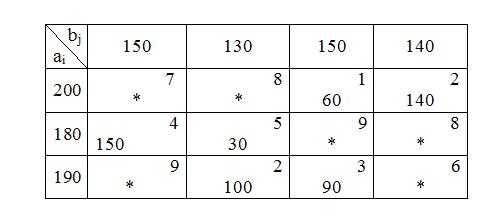
Пример. 1. Проверим, является ли данная задача замкнутой. Подсчитаем суммарные запасы груза и суммарные потребности заказчиков , . Поскольку , модель транспортной задачи замкнутая, и задача имеет оптимальный план. 2. Построим первый опорный план транспортной задачи методом северо-западного угла. Начинаем заполнение распределительной таблицы с верхней левой клетки, то есть построение исходного опорного плана начинаем с удовлетворения потребностей первого потребителя b1 за счет запасов первого поставщика a1. Для этого сравниваем запас a1 = 200 с потребностями b1 = 150. Так как a1 > b1, то потребности b1 полностью удовлетворяем за счет a1, и в первую клетку помещаем min (200, 150)=150. У первого поставщика осталось 50 единиц груза. Так как потребности первого получателя груза полностью удовлетворены, исключим из рассмотрения первый столбец, заполнив в нем оставшиеся клетки точками. Далее заполняем таблицу по строкам слева направо и сверху вниз. Следующая самая верхняя левая незаполненная клетка – (1,2). Потребителю b2 поставляем 50 единиц груза, оставшихся у первого поставщика. Поскольку от первого поставщика весь груз вывезен, заполняем оставшиеся клетки первой строки точками. Второму получателю, пока что, недопоставлено 80 единиц груза. Следующая незаполненная клетка – (2,2). Потребителю b2 отправляем недостающие 80 единиц груза, при этом его потребности полностью удовлетворены, поэтому оставшиеся клетки во втором столбце заполняем точками. У второго поставщика a2 осталось еще 100 единиц груза. Аналогичным образом заполняем оставшиеся клетки, пока не удовлетворим всех потребителей и не вывезем все запасы груза у поставщиков. В результате распределения груза получим первый опорный план, в котором x11 = 150, x12 = 50, x22 = 80, x23 = 100, x33 = 50, x34 = 140. Эти переменные соответствуют заполненным клеткам и являются базисными, остальные переменные, соответствующие клеткам с точками, являются свободными (значения свободных переменных равны нулю). Первый опорный план можно представить в матричном виде Число заполненных клеток k = 6. Это число должно равняться рангу системы ограничений r = m + n – 1 = 3 + 4 – 1 = 6. Так как k = r = 6, то построенный план является невырожденным. Подсчитаем затраты на перевозку по этому плану . 3. Построим первое опорное решение транспортной задачи методом минимальной стоимости (минимального тарифа). Найдем клетку с минимальным тарифом. Это клетка (1,3) с тарифом C13 =1. Построение исходного опорного плана начинаем с занесения поставки груза в клетку с наименьшей стоимостью c13. Заполняем клетку x13 = 150. Оставшиеся клетки третьего столбца заполняем точками, так как потребности третьего получателя полностью удовлетворены. У первого поставщика осталось 50 единиц груза. Ищем следующую клетку с минимальным тарифом. Таких клеток две: c14 =2, c32 =2. Заполним сначала клетку (3,2). Поставим в нее x32=min (190, 130)=130. Второй столбец заполняем точками. У третьего поставщика осталось 60 единиц груза. Ищем следующую клетку с наименьшим тарифом – это клетка (1,4). В нее помещаем 50 единиц груза, min(50,140)=50. Первую строку заполняем точками, так как от первого поставщика вывезен весь груз. Четвертому получателю недопоставлено 90 единиц. Аналогичным образом распределяем весь имеющийся груз и получаем первый опорный план перевозок. Подсчитаем затраты на перевозку по этому плану. . Итак, в каждой строке и в каждом столбце таблицы заполнена хотя бы одна клетка, циклов по заполненным клеткам нет, число заполненных клеток m+n-1=6, следовательно, план опорный и невырожденный. 4. Проверка первого опорного плана (решения) на оптимальность. Метод потенциалов После построения исходного опорного плана приступаем к проверке его на оптимальность методом потенциалов, который заключается в последовательном улучшении опорных планов транспортной задачи на основе информации, полученной с помощью чисел, называемых потенциалы поставщиков и потребителей (, — двойственные переменные, то есть переменные задачи, двойственной к транспортной). Потенциалы находим из условия , где cij — тарифы заполненных клеток. Будем проверять на оптимальность первый опорный план, построенный методом минимального тарифа. В двойственной задаче одна свободная переменная, поэтому возьмем одну любую из двойственных переменных и приравняем ее к нулю. Возьмем, например,(выгоднее брать в качестве нулевой переменной ту, которая соответствует строке или столбцу с наибольшим количеством заполненных клеток). В таблице в дополнительном столбце справа помещаем потенциалы отправителей , а в строке снизу – потенциалы получателей. Составим систему уравнений для определения потенциалов:
Из этой системы находим
Считаем оценки для свободных клеток: Запишем получившиеся оценки в левом верхнем углу свободных клеток.
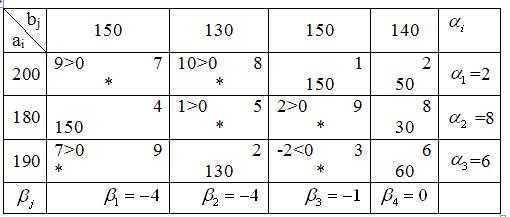
Так как среди оценок имеются отрицательные , то данный план не является оптимальным. Его можно улучшить перераспределением поставок. Для этого выбираем свободную клетку с наименьшим отрицательным значением (наибольшим по абсолютной величине). В данном случае это клетка (3,3).
Сроим цикл пересчета, начиная с клетки (3,3), в которую нужно поместить поставку груза (её отмечают знаком «+»), и двигаясь по занятым клеткам (в данном случае это клетки (3,4), (1,4), (1,3)), поочередно отмечая их знаками «-», «+». Если в клетку (3,3) добавили +, то в смежных по циклу клетках необходимо вычесть для сохранения баланса перевозок по третьей строке и третьему столбцу. Звенья цикла должны быть параллельны строкам или столбцам таблицы, причем в каждой вершине цикла встречаются ровно два звена, одно из которых находится в строке, а другое – в столбце. Количество вершин в цикле должно быть четно. В результате построения цикла в соответствующих строках и столбцах должно быть парное количество знаков «-», «+». Определяем величину поставки в клетку (3,3), как минимальную величину из поставок, стоящих в отрицательных клетках, то есть . Перераспределяем по циклу поставки на величину . Значение записываем в незанятую клетку (3,3), отмеченную знаком «+», двигаясь по циклу, прибавляем эту величину к поставкам в клетках со знаком «+», вычитаем в клетках со знаком «-». В результате получаем новое опорное решение или новый опорный план, в котором клетки с грузом, равным величине , становятся свободными. Если освобождается больше одной клетки, то есть число заполненных клеток меньше числа m + n — 1, то такой план называется вырожденными, и для определения потенциалов необходимо ввести недостающее количество нулевых элементов в число основных базисных переменных. Свободные клетки заполняют нулевыми поставками так, чтобы они не образовывали цикл по заполненным клеткам, и чтобы в каждой строке и в каждом столбце находилась хотя бы одна заполненная клетка. Проверим новый опорный план на оптимальность. Пусть =0. Тогда найдем все остальные потенциалы, рассматривая только заполненные клетки и помня, что для них , то есть что сумма потенциалов должна быть равна тарифу, стоящему на пересечении соответствующих потенциалам строки и столбца.
Число заполненных клеток k=m+n-1, следовательно, план невырожденный. Найдем оценки Для всех клеток с точками, где стоят свободные переменные. Данный опорный план не является оптимальным, так как не все оценки для свободных клеток , а именно, .
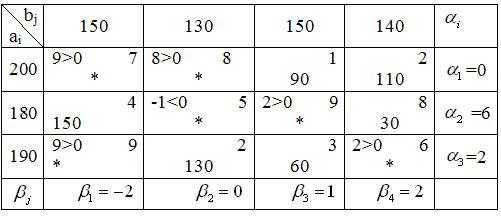
Возьмем клетку (2,2) за начало цикла пересчета. Цикл будет проходить по клеткам (2,2), (3,2), (3,3), (1,3), (1,4), (2,4) и опять вернется в (2,2).
Ищем количество единиц груза , перераспределяемых по циклу пересчета, как минимум по клеткам, помеченных знаком минус. Получаем новый опорный план
Проверяем данный опорный план на оптимальность
Полученный опорный план является оптимальным, так как все оценки для свободных клеток . Выписываем оптимальный план: x11 = 0; x12 = 0; x13 = 60; x14 =140; x21 = 150; x22 = 30; x23 = 0; x24 = 0; x31 = 0; x32 = 100; x33 = 90; x34 = 0. Или в матричной форме Высчитываем минимальные затраты на транспортировку продукции:
|
matica.org.ua