Системы уравнений с двумя переменными, способы решения
Используй поиск, чтобы найти научные материалы и собрать список литературы
База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны
Содержание статьи
1. Способ подстановки
2. Способ сложения.
3. Графический способ
4. Способ введения новых переменных
Напомним для начала определение решения системы уравнений с двумя переменными.
Определение 1
Пара чисел называется решением системы уравнений с двумя переменными, если при их подстановки в уравнение получается верное равенство.
В дальнейшем будем рассматривать системы из двух уравнений с двумя переменными.
Существуют четыре основных способа решения систем уравнений: способ подстановки, способ сложения, графический способ, способ ведения новых переменных.
Способ подстановки
Способ подстановки заключается в следующем: берется любое из данных уравнений и выражается $y$ через $x$, затем $y$ подставляется в уравнение системы, откуда и находится переменная $x.$ После этого мы легко можем вычислить переменную $y.$
Пример 1
\[\left\{ \begin{array}{c} {2x+3y=5} \\ {3x-y=-9} \end{array} \right.\]
Выразим из второго уравнения $y$ через $x$:
\[y=3x+9\]
Подставим в первое уравнение, найдем $x$:
\[2x+9x+27=5\] \[11x=-22\] \[x=-2\]
Найдем $y$:
\[y=-6+9=3\]
Ответ: $(-2,\ 3)$
Способ сложения.
Рассмотрим данный способ на примере:
Пример 2
\[\left\{ \begin{array}{c} {2x+3y=5} \\ {3x-y=-9} \end{array} \right. \]
\]
Умножим второе уравнение на 3, получим:
\[\left\{ \begin{array}{c} {2x+3y=5} \\ {9x-3y=-27} \end{array} \right.\]
Теперь сложим оба уравнения между собой:
\[2x+3y+9x-3y=5-27\] \[11x=-22\] \[x=-2\]
Найдем $y$ из второго уравнения:
\[-6-y=-9\] \[y=3\]
Ответ: $(-2,\ 3)$
Замечание 1
!!! Отметим, что в данном способе необходимо умножать одно или оба уравнения на такие числа, чтобы при сложении одна из переменных «исчезла».
Графический способ
Графический способ заключается в следующем: оба уравнения системы изображается на координатной плоскости и находится точка их пересечения.
Пример 3
\[\left\{ \begin{array}{c} {2x+3y=5} \\ {3x-y=-9} \end{array} \right.\]
Выразим из обоих уравнений $y$ через $x$:
\[\left\{ \begin{array}{c} {y=\frac{5-2x}{3}} \\ {y=3x+9} \end{array} \right. y=3} \end{array} \right.\]
y=3} \end{array} \right.\]
Получаем:
\[\left\{ \begin{array}{c} {x=0} \\ {y=1} \end{array} \right.\]
Ответ: ($0,1$).
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 08.04.2022
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
Система линейных уравнений с двумя переменными.
 Методы решения систем уравнений.
Методы решения систем уравнений.- Альфашкола
- Статьи
- Методы решения систем уравнений с двумя переменными
Решением системы линейных уравнений двух переменных является любая упорядоченная пара, удовлетворяющая каждому уравнению независимо. Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям.
Как можно решить систему уравнений с двумя переменными?
Системы уравнений с двумя переменными можно решить методом подстановки:
Системы уравнений с двумя переменными можно решить методом сложения:
Пример. Решить систему методом сложения: \(\begin{equation*} \begin{cases} x-y-4=0 \\ 3x+y-8=0 \end{cases} \end{equation*}\).
Решить систему методом сложения: \(\begin{equation*} \begin{cases} x-y-4=0 \\ 3x+y-8=0 \end{cases} \end{equation*}\).
Решение:
Ответ: \((3;-1).\)
Система уравнений состоящее из двух переменных должно удовлетворять всем решениям одновременно. Система линейных уравнений из двух переменных рассматривается одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти численное значение для каждой переменной в системе, которая будет удовлетворять всем уравнениям системы одновременно. Некоторые линейные системы могут не иметь решения, и это будет их решением, другие системы могут иметь бесконечное число решений. Для того чтобы линейная система имела единственное решение, должно быть не меньше уравнений, чем переменных. Тем не менее, это не гарантирует уникальное решение.
Выводы:
- Система линейных уравнений из двух переменных решается совместно методом подстановки или методом сложения.
- Чтобы найти решение системы линейных уравнений, мы должны найти численное значение для каждой переменной в системе, которая будет удовлетворять всем уравнениям в системе одновременно.

- Для того чтобы линейная система имела единственное решение, должно быть не меньше уравнений, чем переменных.
- Решить систему уравнений это значит найти численное значение для каждой переменной в системе либо доказать что решений нет.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Наталья Анатольевна Люфт
Репетитор по математике
Стаж (лет)
Образование:
Новосибирскй педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по химии 8-9 классов.
Лариса Александровна Новакова
Репетитор по математике
Стаж (лет)
Образование:
Амурский педагогический колледж, ООО «Издательство «Учитель»
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-8 класса. Люблю математику за то, что она воспитывает человека, приучая его к точности , учит логично мыслить, и в какой-то степени она способна привести ум в порядок. В своей работе использую не только традиционные формы и методы преподавания математики, но и новые современные технологии. Моя цель прежде всего, усилить мотивацию ребенка к познанию окружающего мира, продемонстрировать ему, что занятия математикой – это не получение отвлеченных от жизни знаний, а необходимая подготовка к жизни, поиск полезной информации и навыки ее применения в реальной жизни. Учитель пения, музыки.
Люблю математику за то, что она воспитывает человека, приучая его к точности , учит логично мыслить, и в какой-то степени она способна привести ум в порядок. В своей работе использую не только традиционные формы и методы преподавания математики, но и новые современные технологии. Моя цель прежде всего, усилить мотивацию ребенка к познанию окружающего мира, продемонстрировать ему, что занятия математикой – это не получение отвлеченных от жизни знаний, а необходимая подготовка к жизни, поиск полезной информации и навыки ее применения в реальной жизни. Учитель пения, музыки.
Юрий Алексеевич Алексеенко
Репетитор по математике
Стаж (лет)
Образование:
Кубанский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 5-11 классов. Подготовка к ОГЭ, ЕГЭ, ВПР и олимпиадам. Средний балл подготовки к ЕГЭ у моих учеников выше 70 баллов и нет тех, кто не сдал. Жду на занятиях.
Подготовка к ОГЭ, ЕГЭ, ВПР и олимпиадам. Средний балл подготовки к ЕГЭ у моих учеников выше 70 баллов и нет тех, кто не сдал. Жду на занятиях.
Похожие статьи
- Задачи на проценты
- Как перевести квадратные метры в квадратные километры
- Как перевести граммы в миллиграммы?
- Факультет Мировой Экономики НИУ ВШЭ
- МИФИ: Информационная безопасность
- Финансовый Университет | Международная Экономика
- ЕГЭ по математике, базовый уровень. Простейшие уравнения (вариант 2)
- ЕГЭ по математике, базовый уровень. Преобразование алгебраических выражений
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Уравнение с двумя переменными и его график
Урок 15.
 Алгебра 9 класс ФГОС
Алгебра 9 класс ФГОСНа этом уроке вводиться понятие решения уравнения с двумя переменными. Рассматриваются примеры отыскания некоторых решений уравнений с двумя переменными, а так же изображения множества всех решений на координатной плоскости, то есть изображение графика. Происходит знакомство с уравнением окружности и рассматриваются всевозможные примеры.
Конспект урока «Уравнение с двумя переменными и его график»
Цель:
· уравнения с двумя переменными;
· решения уравнения с двумя переменными;
· степень уравнения с двумя переменными;
· график уравнения с двумя переменными.
Перед вами записаны уравнения:
Все они являются уравнениями с двумя переменными, так как в каждом из них есть две переменные. Возьмём, например, первое уравнение и подставим в него x=3 и y=5:
Получили
неверное равенство. А если подставим x=3
и y=3,
то получим верное числовое равенство.
А если подставим x=3
и y=3,
то получим верное числовое равенство.
Определение:
Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное числовое равенство.
Пара чисел (3; 3) является решением данного уравнения. Но это не единственное решение.
Для определения степени уравнения с двумя переменными, нужно преобразовать его так, чтобы в левой части стоял многочлен стандартного вида, а справа ноль. Тогда степень уравнения считают равной степени данного многочлена.
Чтобы определить степень многочлена с двумя переменными, нужно определить степень каждого одночлена, входящего в состав многочлена, и выбрать из них наибольшую. Степень данного уравнения равна 1.
Пример.
Определить степени уравнений и найти любых два решения.
1. Рассмотрим уравнение:
Преобразуем его:
Степень
данного уравнения равна 2.
Найдём два любых решения:
Решением данного уравнения будут пары чисел (0; 2) и (0; -2).
2. Решить уравнение:
Степень уравнения равна 2.
Найдём два решения уравнения:
Получили две пары чисел: (-1; -6) и (3; 2).
3. Решить уравнение:
Преобразуем его:
Степень данного уравнения равна 3.
Найдём любые два решения:
Получили две пары: (1; 2) и (1; -2).
В ходе выполнения заданий стало понятно, что уравнения с двумя переменными имеют много решений. И указать все решения достаточно сложно. Если решением является пара значений, то его можно изобразить на координатной плоскости в виде точки. Так все решения и образуют график уравнения с двумя переменными.
Определение:
Графиком
уравнения с двумя переменными является множество точек
координатной плоскости, координаты которых обращают уравнение в верное
равенство.
Пример.
1. Построить график уравнения:
Так как произведение равно нулю, то каждый из множителей также равен нулю. Решим каждое из полученных уравнений:
Изобразим график данного уравнения:
Решением являются две прямые: х=7 и у=-3.
2. Построить график уравнения:
Так как произведение равно нулю, то каждый из множителей также равен нулю. Решим каждое из полученных уравнений:
Изобразим график данного уравнения:
Решением являются две прямые: х=-5 и х=2.
Пример.
Составить уравнения, графиками которых являются пары прямых, изображённых на рисунках.
Посмотрим на первый рисунок:
Получили, что прямые являются графиком уравнения.
Обратимся ко второму случаю:
Получили, что эти прямые являются графиком уравнения.
Рассмотрим уравнение:
Графиком
уравнения является окружность с центром в точке начала координат и радиусом r.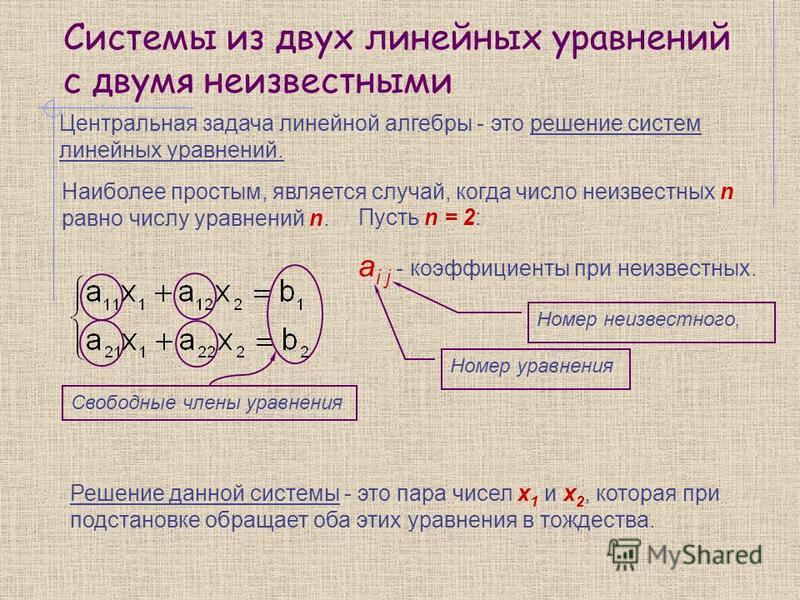
Например, графиком уравнения:
является окружность с r=4.
Пример.
Записать уравнение окружности с центром в точке начала координат и r=6.
Получим уравнение окружности:
Если центром окружности не является точка начала координат, то уравнение окружности будет выглядеть так:
Центр окружности имеет координаты (a; b).
Например,
Выполним обратное действие. Но для записи уравнения окружности уже не достаточно только координат центра, необходимо знать и радиус. Например:
Предыдущий урок 14 Решение неравенств методом интервалов
Следующий урок 16 Графический способ решения систем уравнений
Получите полный комплект видеоуроков, тестов и презентаций Алгебра 9 класс ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Основные определения, примеры системы двух уравнений 9 класс онлайн-подготовка на Ростелеком Лицей
Рациональное уравнение, примеры
Рациональным уравнением с двумя переменными называется уравнение вида где рациональное выражение (т.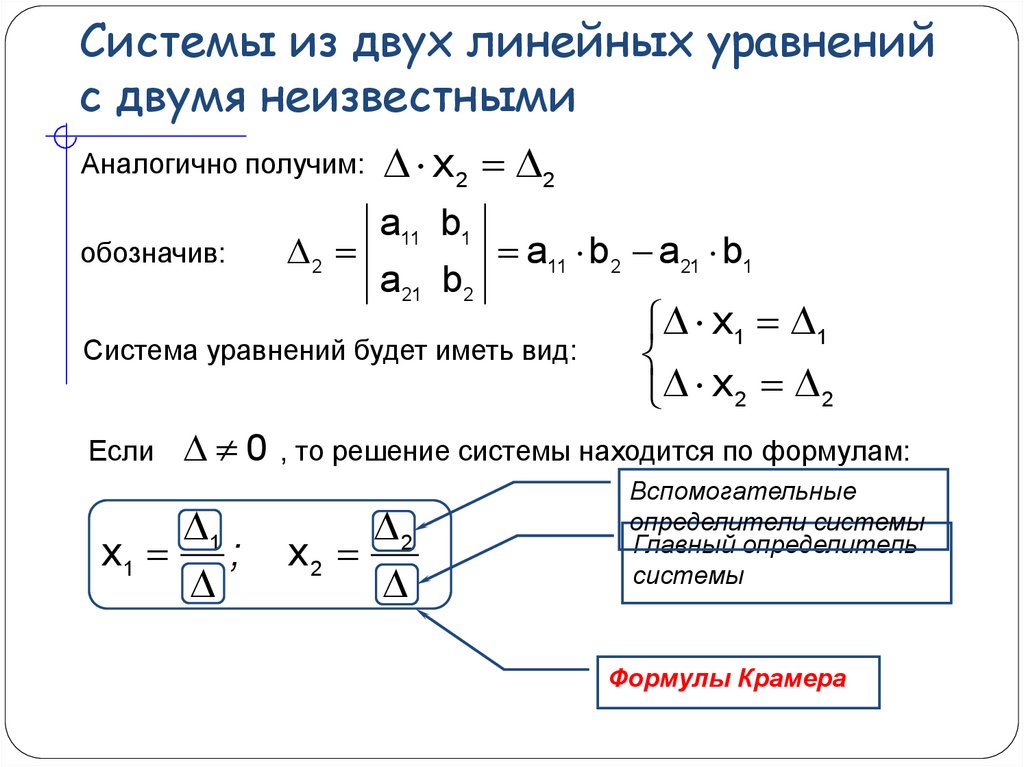 е. алгебраическое выражение, составленное из чисел и переменных с помощью операций сложения, вычитания, умножения, деления и возведения в натуральную степень).
е. алгебраическое выражение, составленное из чисел и переменных с помощью операций сложения, вычитания, умножения, деления и возведения в натуральную степень).
Например:
Решением уравнения с двумя переменными называется пара чисел, которая обращает уравнение в верное числовое равенство.
Пример линейного уравнения
Ранее мы рассматривали линейное уравнение с двумя переменными Линейное уравнение имеет бесчисленное множество решений, график линейного уравнения – прямая линия.
Рассмотрим пример:
Найти хотя бы одно решение уравнения
Зададим – решение уравнения
Если задана одна переменную, то вторую можно найти.
Итак, основные понятия сводятся к следующему:
называется уравнением с двумя переменными. Частным решением такого уравнения называется любая пара чисел , которая удовлетворяет уравнению. Но наша задача – найти все решения этого уравнения, т.е. множество всех пар чисел, которые удовлетворяют уравнению.
Пример уравнения окружности
Мы рассмотрели линейное уравнение, теперь рассмотрим уравнение
Вспомним, что уравнение окружности с центром в т.(0;0) и радиусом 1 (Рис. 1).
Любая точка на этой окружности имеет две координаты – x и y, и эти координаты удовлетворяют уравнению, значит, координаты любой точки на окружности являются решением данного уравнения.
Например,
является решением уравнения. также является решением уравнения.
Основные понятия
Иногда удается перейти к геометрической (графической) модели уравнения с двумя переменными, т. е. построить график уравнения. Графиком уравнения с двумя переменными называется множество всех точек координатной плоскости, координаты которых удовлетворяют данному уравнению.
Мы рассматриваем одно уравнение с двумя переменными. Частным решением этого уравнения является любая пара чисел, ему удовлетворяющая.
Геометрический образ этой пары – точка на плоскости. Множество всех пар называется решением данного уравнения.
Графиком уравнения называется такая линия, координаты всех точек которой удовлетворяют данному уравнению.
Графиком уравнения является окружность. Графиком линейного уравнения является прямая линия.
Уравнение окружности и линейное в общем виде
Рассмотрим уравнение окружности и линейное уравнение в общем виде.
Уравнение окружности в общем виде: Это окружность с центром в и радиусом R.
Дадим геометрическую интерпретацию данного уравнения (Рис. 2).
Координаты любой точки на этой окружности – это пара чисел, которые удовлетворяют уравнению окружности.
Методы решения уравнений с двумя переменными
Далее вспомним линейное уравнение с двумя переменными в общем виде:
Графиком данного уравнения является прямая. Мы неоднократно строили графики линейных уравнений, отметим только, что каждая точка данной прямой дает пару чисел, являющихся решением уравнения.
Каким образом решаются уравнения с двумя переменными ? Как правило, сложное заменяется более простым, но равносильным ему. Два уравнения с двумя переменными называются равносильными, если они имеют одинаковые решения. Замена данного уравнения более простым, но равносильным ему, называется равносильным преобразованием уравнения. Два основных равносильных преобразования – это перенос членов одной части в другую с противоположным знаком, умножение или деление обеих частей уравнения на одно и то же отличное от нуля число или выражение.
Неравносильные преобразования – это освобождение от знаменателя, возведение в квадрат.
Система уравнений с двумя переменными
Если поставлена задача найти такие пары чисел , которые одновременно удовлетворяют уравнению и уравнению , то получаем систему уравнений с двумя переменными
Решением данной системы уравнений называется такая пара чисел, которая является одновременно решением и первого уравнения, и второго. Решить систему уравнений – это значит найти все ее решения или установить, что решений нет.
Решить систему уравнений – это значит найти все ее решения или установить, что решений нет.
Иногда удается решить систему уравнений графическим методом: построить график первого уравнения, построить график второго уравнения, найти точки пересечения графиков; координаты каждой точки пересечения являются решением системы.
Графический способ решения системы уравнений
Рассмотрим графики некоторых уравнений.
1. Построить график уравнения:
Графиком является парабола, ветви направлены вверх (Рис. 3).
2. Построить график уравнения:
Необходимо выделить y, для этого нужно обе части уравнения поделить на x. Но мы не можем это сделать, если Поэтому рассмотрим два случая – для
График уравнения гипербола, координаты любой ее точки дают пару чисел – решений исходного уравнения (Рис. 4).
3. Теперь рассмотрим систему и решим ее графически.
Поместим график первого уравнения и график второго уравнения, построенные в предыдущем примере, в одну координатную плоскость (Рис. 5).
5).
Рис. 5.
единственное решение системы уравнений. Подставим для проверки в систему:
Верно.
Ответ:
Графический метод позволяет решить систему уравнений, но он не всегда удобен.
Заключение
Мы рассмотрели основные понятия, связанные с системой двух уравнений с двумя переменными. Мы рассмотрели одно рациональное уравнение, график этого уравнения, решение системы, графический метод решения системы.
Нужны другие методы решения систем, к которым мы перейдем на следующих уроках.
Список литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Раздел College.ru по математике (Источник).
2. Интернет-проект «Задачи» (Источник).
3. Образовательный портал «РЕШУ ЕГЭ» (Источник).
Домашнее задание
1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 90 – 94, 103, 104.
Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 90 – 94, 103, 104.
Алгебра 7-9 классы. 9. Решение линейных уравнений с двумя неизвестными
- Подробности
- Категория: Алгебра 7-9 классы
УРАВНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ И ЕГО ГРАФИК
Пусть требуется найти два числа» разность которых равна 5. Если первое число обозначить буквой х, а второе буквой у, то соотношение между ними можно записать в виде равенства .
Равенство содержит две переменные. Такие равенства называют уравнениями с двумя переменными или уравнениями с двумя неизвестными.
При уравнение обращается в верное равенство 8 — 3 = 5. Говорят, что пара значений переменных является решением этого уравнения. Пара х = 3, у = 8 не обращает уравнение в верное равенство, значит, не является его решением.
Определение. Решением уравнения с двумя переменными называется пара значений,переменных, обращающая это уравнение в верное равенство.
Пару , являющуюся решением уравнения , можно записать так: (8; 3). При такой записи необходимо знать, значение какой из переменных стоит на первом месте, а какой — на втором. В записи решений уравнений с переменными х и у на первое место ставят значения х, а на второе место — значения у. Например, решениями уравнения служат также пары: (12; 7), (5,2; 0,2), ( — 2; —7), (3,8; -1,2).’
Уравнения с двумя переменными, имеющие одни и те же решения, называются равносильными.
Уравнения с двумя переменными обладают такими же свойствами, как и уравнения с одной переменной. В уравнении слагаемые можно переносить из одной его части в другую, изменив знаки этих слагаемых; обе части уравнения можно умножать или делить на одно и то же число, отличное от нуля. При этом получаются уравнения, равносильные исходному. Чтобы найти решения уравнения
можно подставить в него вместо х произвольное число, например 3. Получим уравнение с одной переменной у: . Решив его, найдем, что у = —0,5. Пара (3; —0,5) — решение уравнения .
Для отыскания решений уравнения (1) удобно выразить одну переменную через другую. Выразим, например, переменную у через х. Для этого перенесем слагаемое Зх в правую часть уравнения, изменив его знак:
Разделив обе части этого уравнения на 2, получим:
Уравнение (3) равносильно уравнению (2), а уравнение (2) — уравнению (1). Поэтому уравнение (3) равносильно уравнению(1).
Поэтому уравнение (3) равносильно уравнению(1).
По формуле можно найти сколько угодно решений уравнения . Например, если х = 2, то ;
если x = —0,4, то . Значит, уравнение (1) имеет бесконечно много решений.
Каждое решение вида, уравнения с двумя переменными можно изобразить в координатной плоскости точкой с координатами х и у. Все такие точки образуют график уравнения. На рисунке 55 показан график уравнения
Этот график — парабола. Действительно, уравнение равносильно уравнению , а формулой задается функция, графиком которой является парабола.
Графики уравнений весьма разнообразны. На рисунках 56 и 57 изображены графики уравнений
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ
Каждое из уравнений с двумя переменными , имеет вид , где а, b и с — некоторые числа. Такие уравнения называют линейными уравнениями с двумя переменными.
Такие уравнения называют линейными уравнениями с двумя переменными.
Определение. Линейным уравнением с двумя переменными называется уравнение вида , где х и у — переменные, а, b и с — числа.
Числа а и b называют коэффициентами при переменных, число с — свободным членом.
Выясним, что представляет собой график линейного уравнения.
Если в линейном уравнении коэффициент при у не равен нулю, то из этого уравнения можно выразить у через х. Возьмем, например, уравнение. Имеем:
Формулой задается линейная функция, графиком которой служит прямая. Та же самая прямая является и графиком уравнения , так как это уравнение равносильно уравнению
Если в линейном уравнении коэффициент при у равен нулю, а коэффициент при х отличен от нуля, то графиком такого уравнения также является прямая.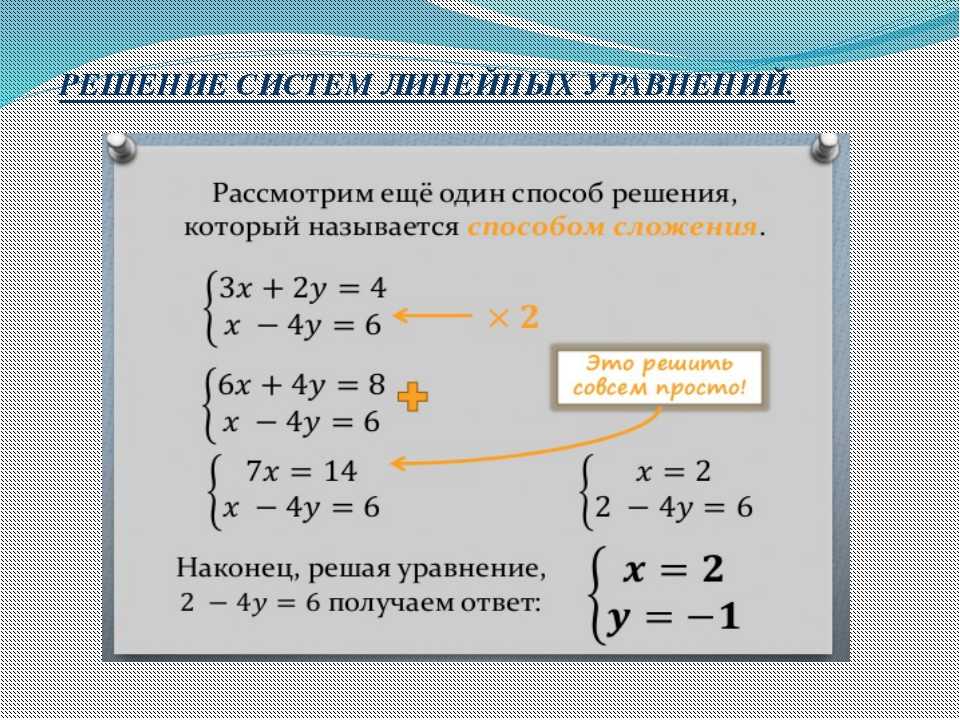 Рассмотрим, например, уравнение . Его решениями служат все пары чисел (х ; у), в которых x = 6, а у — любое число. Изобразив эти пары точками, получим прямую, параллельную оси ординат (рис. 59).
Рассмотрим, например, уравнение . Его решениями служат все пары чисел (х ; у), в которых x = 6, а у — любое число. Изобразив эти пары точками, получим прямую, параллельную оси ординат (рис. 59).
Итак, графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.
Уравнение , в котором а = О и b = 0, имеет вид . При с = 0 любая пара чисел является решением этого уравнения, а его графиком — вся координатная плоскость. При уравнение не имеет решений, и его график не содержит ни одной точки.
Приведем примеры построения графиков линейных уравнений.
Пример 1. Построим график уравнения .
В линейном уравнении коэффициенты при переменных отличны от нуля. Поэтому его графиком является прямая. Прямая определяется двумя точками. Найдем координаты двух каких-либо точек прямой:
Найдем координаты двух каких-либо точек прямой:
Отметим точки (0; —3) и (2; —1,5) и проведем через них прямую (рис. 60). Эта прямая — график уравнения
Пример 2. Построим график уравнения х= — 3. Это уравнение можно записать в виде . графиком служит прямая, параллельная оси у (рис. 61).
Уравнения с двумя переменными. Решение биквадратных уравнений Решение уравнений с параметром
Представление об уравнениях с двумя переменными впервые формируется в курсе математики за 7 класс. Рассматриваются конкретные задачи, процесс решения которых приводит к такому виду уравнений.
При этом они изучаются довольно поверхностно. В программе главный акцент делается на системах уравнений с двумя неизвестными.
Это стало причиной того, что задачи, в которых на коэффициенты уравнения накладываются определенные ограничения, практически не рассматриваются. Недостаточно внимания уделено методам решения заданий типа «Решить уравнение в натуральных или целых числах». Известно, что материалы ЕГЭ и билеты вступительных экзаменов часто содержат такие упражнения.
Недостаточно внимания уделено методам решения заданий типа «Решить уравнение в натуральных или целых числах». Известно, что материалы ЕГЭ и билеты вступительных экзаменов часто содержат такие упражнения.
Какие именно уравнения определяются как уравнения с двумя переменными?
ху = 8, 7х + 3у = 13 или х 2 + у = 7 – примеры уравнений с двумя переменными.
Рассмотрим уравнение х – 4у = 16. Если х = 4, а у = -3, оно будет правильным равенством. Значит, эта пара значений – решение данного уравнения.
Решение любого уравнения с двумя переменными – множество пар чисел (х; у), которые удовлетворяют это уравнение (превращают его в верное равенство).
Часто уравнение преобразовывают так, чтобы из него можно было получить систему для нахождения неизвестных.
Примеры
Решить уравнение: ху – 4 = 4х – у.
В данном примере можно воспользоваться методом разложения на множители. Для этого нужно сгруппировать слагаемые и вынести общий множитель за скобки:
ху – 4 = 4х – у;
ху – 4 – 4х + у = 0;
(ху + у) – (4х + 4) = 0;
у(х + 1) – 4(х + 1) = 0;
(х + 1)(у — 4) = 0.
Ответ: Все пары (х; 4), где х – любое рациональное число и (-1; у), где у – любое рациональное число.
Решить уравнение: 4х 2 + у 2 + 2 = 2(2х — у).
Первый шаг – группирование.
4х 2 + у 2 + 2 = 4х – 2у;
4х 2 + у 2 + 1 — 4х + 2у + 1 = 0;
(4х 2 – 4х +1) + (у 2 + 2у + 1) = 0.
Применив формулу квадрата разности, получим:
(2х — 1) 2 + (у + 1) 2 = 0.
При суммировании двух неотрицательных выражений ноль получится только в том случае, если 2х – 1 = 0 и у + 1 = 0. Отсюда следует: х = ½ и у = -1.
Ответ: (1/2; -1).
Решить уравнение (х 2 – 6х + 10)(у 2 + 10у + 29) = 4.
Рационально применить оценочный метод, выделив полные квадраты в скобках.
((х — 3) 2 + 1)((у + 5) 2 + 4) = 4.
При этом (х — 3) 2 + 1 ≥ 1, а (у + 5) 2 + 4 ≥ 4. Тогда левая часть уравнения всегда не меньше 4. Равенство возможно в случае
(х — 3) 2 + 1 = 1 и (у + 5) 2 + 4 = 4. Следовательно, х = 3, у = -5.
Ответ: (3; -5).
Решить уравнение в целых числах: х 2 + 10у 2 = 15х + 3.
Можно записать это уравнение в таком виде:
х 2 = -10у 2 + 15х + 3. Если правую часть равенства делить на 5, то 3 – остаток. Из этого следует, что х 2 не делится на 5. Известно, что квадрат числа, которое не делится на 5, должен дать в остатке или 1, или 4. Значит, уравнение корней не имеет.
Ответ: Решений нет.
Не стоит расстраиваться из-за трудностей в поиске верного решения для уравнения с двумя переменными. Упорство и практика обязательно принесут свои плоды.
Цели:
- Систематизировать и обобщить знания и умения по теме: Решения уравнений третьей и четвертой степени.
- Углубить знания, выполнив ряд заданий, часть из которых не знакома или по своему типу, или способу решения.
- Формирование интереса к математике через изучение новых глав математики,
воспитание графической культуры через построение графиков уравнений.

Тип урока : комбинированный.
Оборудование: графопроектор.
Наглядность: таблица «Теорема Виета».
Ход урока
1. Устный счет
а) Чему равен остаток от деления многочлена р n (х) = а n х n + а n-1 х n-1 + … + а 1 х 1 + a 0 на двучлен х-а?
б) Сколько корней может иметь кубическое уравнение?
в) С помощью чего мы решаем уравнение третьей и четвертой степени?
г) Если b четное число в квадратном уравнение, то чему равен Д и х 1 ;х 2
2. Самостоятельная работа (в группах)
Составить уравнение, если известны корни (ответы к заданиям закодированы) Используется «Теорема Виета»
1 группа
Корни: х 1 = 1; х 2 = -2; х 3 = -3; х 4 = 6
Составить уравнение:
B=1 -2-3+6=2; b=-2
с=-2-3+6+6-12-18= -23; с= -23
d=6-12+36-18=12; d= -12
е=1(-2)(-3)6=36
х 4 — 2 х 3 — 23х 2 — 12 х + 36 = 0 (это уравнение решает потом 2 группа на доске)
Решение .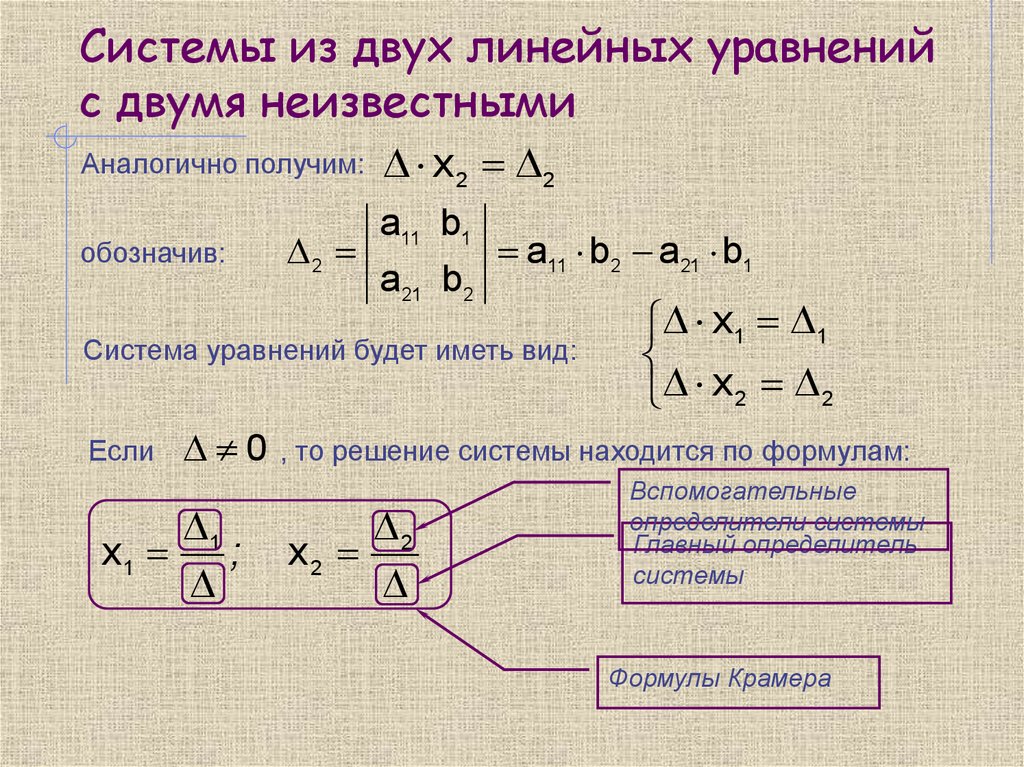 Целые корни ищем среди делителей числа 36.
Целые корни ищем среди делителей числа 36.
р = ±1;±2;±3;±4;±6…
р 4 (1)=1-2-23-12+36=0 Число 1 удовлетворяет уравнению, следовательно, =1 корень уравнения. По схеме Горнера
р 3 (x) = х 3 -х 2 -24x -36
р 3 (-2) = -8 -4 +48 -36=0, х 2 =-2
р 2 (x) = х 2 -3х -18=0
х 3 =-3, х 4 =6
Ответ: 1;-2;-3;6 сумма корней 2 (П)
2 группа
Корни: х 1 = -1; х 2 = х 3 =2; х 4 =5
Составить уравнение:
B=-1+2+2+5-8; b= -8
с=2(-1)+4+10-2-5+10=15; с=15
D=-4-10+20-10= -4; d=4
е=2(-1)2*5=-20;е=-20
8+15+4х-20=0 (это уравнение решает на доске 3 группа)
р = ±1;±2;±4;±5;±10;±20.
р 4 (1)=1-8+15+4-20=-8
р 4 (-1)=1+8+15-4-20=0
р 3 (x) = х 3 -9х 2 +24x -20
р 3 (2) = 8 -36+48 -20=0
р 2 (x) = х 2 -7х +10=0 х 1 =2; х 2 =5
Ответ: -1;2;2;5 сумма корней 8(Р)
3 группа
Корни: х 1 = -1; х 2 =1; х 3 =-2; х 4 =3
Составить уравнение:
В=-1+1-2+3=1;в=-1
с=-1+2-3-2+3-6=-7;с=-7
D=2+6-3-6=-1; d=1
е=-1*1*(-2)*3=6
х 4 — х 3 — 7х 2 + х + 6 = 0 (это уравнение решает потом на доске 4 группа)
Решение. Целые корни ищем среди делителей числа 6.
Целые корни ищем среди делителей числа 6.
р = ±1;±2;±3;±6
р 4 (1)=1-1-7+1+6=0
р 3 (x) = х 3 — 7x -6
р 3 (-1) = -1+7-6=0
р 2 (x) = х 2 -х -6=0; х 1 =-2; х 2 =3
Ответ:-1;1;-2;3 Сумма корней 1(О)
4 группа
Корни: х 1 = -2; х 2 =-2; х 3 =-3; х 4 =-3
Составить уравнение:
B=-2-2-3+3=-4; b=4
с=4+6-6+6-6-9=-5; с=-5
D=-12+12+18+18=36; d=-36
е=-2*(-2)*(-3)*3=-36;е=-36
х 4 + 4х 3 – 5х 2 – 36х -36 = 0 (это уравнение решает потом 5 группа на доске)
Решение. Целые корни ищем среди делителей числа -36
р = ±1;±2;±3…
р(1)= 1 + 4-5-36-36 = -72
р 4 (-2) = 16 -32 -20 + 72 -36 = 0
р 3 (х) = х 3 +2х 2 -9х-18 = 0
р 3 (-2)= -8 + 8 + 18-18 = 0
р 2 (х) = х 2 -9 = 0; x=±3
Ответ: -2; -2; -3; 3 Сумма корней-4 (Ф)
5 группа
Корни: х 1 = -1; х 2 =-2; х 3 =-3; х 4 =-4
Составить уравнение
х 4 + 10х 3 + 35х 2 + 50х + 24 = 0 (это уравнение решает потом 6группа на доске)
Решение . Целые корни ищем среди делителей числа 24.
Целые корни ищем среди делителей числа 24.
р = ±1;±2;±3
р 4 (-1) = 1 -10 + 35 -50 + 24 = 0
р 3 (х) = x- 3 + 9х 2 + 26x+ 24 = 0
p 3 (-2) = -8 + 36-52 + 24 = О
р 2 (х) = x 2 + 7x+ 12 = 0
Ответ:-1;-2;-3;-4 сумма-10 (И)
6 группа
Корни: х 1 = 1; х 2 = 1; х 3 = -3; х 4 = 8
Составить уравнение
B=1+1-3+8=7;b=-7
с=1 -3+8-3+8-24= -13
D=-3-24+8-24= -43; d=43
х 4 — 7х 3 — 13х 2 + 43 x — 24 = 0 (это уравнение решает потом 1 группа на доске)
Решение . Целые корни ищем среди делителей числа -24.
р 4 (1)=1-7-13+43-24=0
р 3 (1)=1-6-19+24=0
р 2 (x)= х 2 -5x — 24 = 0
х 3 =-3, х 4 =8
Ответ: 1;1;-3;8 сумма 7 (Л)
3. Решение уравнений с параметром
1. Решить уравнение х 3 + 3х 2 + mх — 15 = 0; если один из корней равен (-1)
Ответ записать в порядке возрастания
R=Р 3 (-1)=-1+3-m-15=0
х 3 + 3х 2 -13х — 15 = 0; -1+3+13-15=0
По условию х 1 = — 1; Д=1+15=16
Р 2 (х) = х 2 +2х-15 = 0
х 2 =-1-4 = -5;
х 3 =-1 + 4 = 3;
Ответ:- 1;-5; 3
В порядке возрастания: -5;-1;3. (Ь Н Ы)
(Ь Н Ы)
2. Найти все корни многочлена х 3 — 3х 2 + ах — 2а + 6, если остатки от его деления на двучлены х-1 и х +2 равны.
Решение: R=Р 3 (1) = Р 3 (-2)
Р 3 (1) = 1-3 + а- 2а + 6 = 4-а
Р 3 (-2) = -8-12-2а-2а + 6 = -14-4а
x 3 -Зх 2 -6х + 12 + 6 = х 3 -Зх 2 -6х + 18
x 2 (x-3)-6(x-3) = 0
(х-3)(х 2 -6) = 0
3) а=0, х 2 -0*х 2 +0 = 0; х 2 =0; х 4 =0
а=0; х=0; х=1
а>0; х=1; х=а ± √а
2. Составить уравнение
1 группа . Корни: -4; -2; 1; 7;
2 группа . Корни: -3; -2; 1; 2;
3 группа . Корни: -1; 2; 6; 10;
4 группа . Корни: -3; 2; 2; 5;
5 группа . Корни: -5; -2; 2; 4;
6 группа . Корни: -8; -2; 6; 7.
Предлагаем вам удобный бесплатный онлайн калькулятор для решения квадратных уравнений. Вы сможете быстро получить и разобраться, как они решаются, на понятных примерах.
Чтобы произвести решение квадратного уравнения онлайн , вначале приведите уравнение к общему виду:
ax 2 + bx + c = 0
Заполните соответственно поля формы:
| Как решить квадратное уравнение: | Виды корней: |
1. Привести квадратное уравнение к общему виду: Привести квадратное уравнение к общему виду: Общий вид Аx 2 +Bx+C=0 Пример: 3х — 2х 2 +1=-1 Приводим к -2х 2 +3х+2=0 2. Находим дискриминант D. 3. Находим корни уравнения. | 1. Действительные корни. Причем. x1 не равно x2 Ситуация возникает, когда D>0 и A не равно 0. 2. Действительные корни совпадают. x1 равно x2 3. Два комплексных корня. x1=d+ei, x2=d-ei, где i=-(1) 1/2 5. Уравнение имеет бесчисленное множество решений. 6. Уравнение решений не имеет. |
Для закрепления алгоритма, вот еще несколько показательных примеров решений квадратных уравнений .
Пример 1. Решение обычного квадратного уравнения с разными действительными корнями.
x 2 + 3x -10 = 0
В этом уравнении
А=1, B = 3, С=-10
D=B 2 -4*A*C = 9-4*1*(-10) = 9+40 = 49
квадратный корень будем обозначать, как число 1/2 !
x1=(-В+D 1/2)/2А = (-3+7)/2 = 2
x2=(-В-D 1/2)/2А = (-3-7)/2 = -5
Для проверки подставим:
(x-2)*(x+5) = x2 -2x +5x – 10 = x2 + 3x -10
Пример 2. Решение квадратного уравнения с совпадением действительных корней.
х 2 – 8x + 16 = 0
А=1, B = -8, С=16
D = k 2 – AC = 16 – 16 = 0
X = -k/A = 4
Подставим
(x-4)*(x-4) = (x-4)2 = X 2 – 8x + 16
Пример 3. Решение квадратного уравнения с комплексными корнями.
Решение квадратного уравнения с комплексными корнями.
13х 2 – 4x + 1 = 0
А=1, B = -4, С=9
D = b 2 – 4AC = 16 – 4*13*1 = 16 — 52 = -36
Дискриминант отрицательный – корни комплексные.
X1=(-В+D 1/2)/2А = (4+6i)/(2*13) = 2/13+3i/13
x2=(-В-D 1/2)/2А = (4-6i)/(2*13) = 2/13-3i/13
, где I – это квадратный корень из -1
Вот собственно все возможные случаи решения квадратных уравнений.
Надеемся, что наш онлайн калькулятор окажется весьма полезным для вас.
Если материал был полезен, вы можете
Использование предлога in в английском языке
Употребление и произношение in
Решение линейных уравнений с двумя неизвестными
Все математические ресурсы GMAT
22 диагностических теста 693 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
GMAT Math Help » Проблемные вопросы » Алгебра » Линейные уравнения, два неизвестных » Решение линейных уравнений с двумя неизвестными
Какое уравнение является линейным?
Возможные ответы:
ни один из них не является линейным
Пояснение:
Давайте рассмотрим все варианты ответов.
1. : и являются константами, поэтому уравнение на самом деле является линейным.
2. 5x + 7y — 8yz = 16: Это нелинейно из-за члена yz.
3. : можно преобразовать в y + 8 = (x + 6)(x — 2). Ясно, что когда это расширится, будет член, так что это нелинейно.
4. : Это тоже нелинейно, в том числе из-за терма.
Сообщить об ошибке
Решить.
Возможные ответы:
Правильный ответ:
Объяснение:
Найдите в первом уравнении:
Подставьте во второе уравнение:
4
40004 Решите для . Отчет о ошибке
Что является
Возможные ответы:
Правильный ответ:
. Пояснение:
Пояснение:
Решите первое уравнение, чтобы получить
Подставьте его во второе уравнение и получите
Решите уравнение, чтобы получить , затем подставьте его в первое уравнение, чтобы получить .
Подключение этих двух значений, дает
Отчет о ошибке
Решить систему уравнений:
Возможные ответы:
. Система не имеет решения.
Правильный ответ:
Система не имеет решения.
Объяснение:
Умножьте обе части первого уравнения на 12:
Теперь сложите обе части двух уравнений:
Поскольку это невозможно, система уравнений несовместима и, следовательно, не имеет решения.
Сообщить об ошибке
Дайте набор решений для .
Возможные ответы:
Недостаточно информации для ответа на вопрос.
Правильный ответ:
Объяснение:
Выражение на левых факторах. Разница в квадратах:
С тех пор мы можем заменить:
У нас есть система линейных уравнений для Solve:
Сообщить об ошибке
Компания хочет отправить некоторые виджеты. Если вес коробки плюс один предмет равен 6 фунтам, а вес ящика плюс два предмета равен 10 фунтам, то каковы вес коробки и вес предмета? Поместите ответ в упорядоченную пару так, чтобы упорядоченная пара была (вес коробки, вес виджета).
Возможные ответы:
Правильный ответ:
Объяснение:
Пусть вес коробки будет представлен как , а вес виджета будет представлен как . Поскольку вес коробки плюс вес одного предмета составляет 6 фунтов, это можно представить уравнением
Поскольку вес коробки плюс вес одного предмета составляет 6 фунтов, это можно представить уравнением
Поскольку вес коробки плюс два предмета составляет 10 фунтов, это можно представить уравнением
Теперь у нас есть два уравнения и два неизвестных, и теперь мы можем решить для и . Для этого решаем первое уравнение для и подставляем его во второе уравнение. Решая первое уравнение, мы получаем
. Подставляя это во второе уравнение, мы получаем
Используя и подставляя его в первое уравнение, мы получаем
. виджет 4 фунта. Это дает нам упорядоченную пару.
Отчет о ошибке
Решайте, когда
Возможные ответы:
Правильный ответ:
.
Объяснение:
Подставьте заданное значение и затем изолируйте .
Сообщить об ошибке
Какое значение когда :
0004 Возможные ответы:
Правильный ответ:
Объяснение:
Отчет о ошибке
Решение для:
Возможные ответы:
Правильный ответ:
959959959959959995959995999595999959 9005 .
Объяснение:
Сообщить об ошибке
Что такое ?
Возможные ответы:
Правильный ответ:
Explanation:
From the second equation:
Substitute into the first, then solve:
Сообщить об ошибке
← Назад 1 2 3 Далее →
Уведомление об авторских правах
Все математические ресурсы GMAT
22 Диагностические тесты
693 практических теста
Вопрос дня
Карточки
Learn by Concept
Два линейных уравнения с двумя неизвестными Практические онлайн-задачи
Чтобы начать изучение линейной алгебры, мы рассмотрим простой случай: систему двух линейных уравнений с двумя неизвестными. Хотя решить эту систему довольно легко, все же есть немало интересных концепций и идей, которые возникают, когда мы глубоко задумываемся о процессе. Эти концепции и идеи играют большую роль, когда мы позже рассмотрим более общие системы линейных уравнений.
Хотя решить эту систему довольно легко, все же есть немало интересных концепций и идей, которые возникают, когда мы глубоко задумываемся о процессе. Эти концепции и идеи играют большую роль, когда мы позже рассмотрим более общие системы линейных уравнений.
Итак, начнем с системы
х-2у=63х+у=4.
\begin{выровнено}
х-2у &= 6 \\
3x+y &= 4.
\end{выровнено}
х−2y3x+y=6=4.
Первая идея, которая у нас может возникнуть, — найти одну из переменных. Давайте выделим xxx в первом уравнении и используем его для решения yyy во втором. После выделения xxx в первом уравнении мы получаем x=6+2y.x = 6+2y.x=6+2y. Теперь мы можем подставить это во второе уравнение и решить:
3(6+2у)+у=418+7у=4у=-2.
\begin{выровнено}
3(6+2у)+у &= 4 \\
18+7лет &= 4\\
у &= -2.
\end{выровнено}
3(6+2у)+у18+7уу=4=4=−2.
Решение для xxx дает x=2,x=2,x=2, поэтому мы получили единственное решение, x=2,y=-2.x=2,y=-2.x=2,y=-2 .
В следующих нескольких задачах это упражнение будет рассмотрено с разных точек зрения: поиск другого способа решения, геометрическая интерпретация и представление того, что может произойти, если мы изменим некоторые числа.
Другой стандартный способ решения задачи аналогичен тому, что его целью является удаление переменной, но достигается эта цель несколько иначе. То есть мы можем умножить обе части одного из уравнений на константу, а затем сложить или вычесть два уравнения.
х-2у=63х+у=4.
\begin{выровнено}
х-2у &= 6 \\
3x+y &= 4.
\end{выровнено}
x−2y3x+y=6=4.
Например, если мы хотим исключить x,x,x, мы можем взять первое уравнение, умноженное на 333, минус второе уравнение:
3x−6y=183x+y=4
\begin{выровнено}
3х-6у &=18\
3x+y &= 4
\end{выровнено}
3x−6y3x+y=18=4
так
(3x−6y)−(3x+y)=18−4−7y=14y=−2
\begin{выровнено}
(3х-6у)-(3х+у) &= 18-4\\
-7г&=14\\
у &= -2
\end{выровнено}
(3x−6y)−(3x+y)−7yy=18−4=14=−2
как прежде. (Кроме того, подставив y=-2 y = -2 y=-2 обратно в одно из исходных уравнений и решив, получим x=2.) x = 2 .)x=2.)
Просто чтобы убедиться, что мы обращаем внимание, предположим, что вместо этого мы хотим исключить yyy. Какая комбинация приведенных ниже уравнений позволит это сделать?
Уравнение 1: x−2y=6Уравнение 2: 3x+y=4. \begin{выровнено}
\text{Уравнение 1: }x-2y &= 6 \\
\text{Уравнение 2: }3x+y &= 4.
\end{выровнено}
Уравнение 1: x−2yУравнение 2: 3x+y=6=4.
\begin{выровнено}
\text{Уравнение 1: }x-2y &= 6 \\
\text{Уравнение 2: }3x+y &= 4.
\end{выровнено}
Уравнение 1: x−2yУравнение 2: 3x+y=6=4.
Какие изменения в исходной системе уравнений изменят количество решений?
Помните, мы начали с
х-2у=63х+у=4.
\begin{выровнено}
х-2у &= 6 \\
3x+y &= 4.
\end{выровнено}
х−2y3x+y=6=4.
Давайте изменим число «333» во втором уравнении на другое и посмотрим, как это повлияет на количество решений. Помните, что наша исходная система имеет ровно одно решение: x=2,y=-2.x=2,y=-2.x=2,y=-2.
На какое число нужно заменить «333», чтобы составить систему уравнений, не имеющую ровно одного решения?
Вскоре мы вернемся к алгебре, но давайте сделаем паузу, чтобы подумать о том, что пара линейных уравнений означает геометрически.
Каждое из двух уравнений, содержащих xxx и yyy, вырезает линию в координатной плоскости. Например, рассмотрим систему x+y=0, y−12x=−3. x+y = 0 \ , \ y — \frac{1}{2} x = — 3.x+y=0 , y−21x=−3.
y=−xy=12x−3\begin{выровнено} y &= -x \\ y &= \frac{1}{2}x-3 \end{выровнено}yy=-x=21x−3
Решением этой системы (как и исходной) является пересечение этих двух прямых, то есть точка (2,−2). (2,-2).(2,−2).
(2,-2).(2,−2).
Теперь подумайте обо всех различных способах пересечения любых двух линий. Используйте это, чтобы ответить на следующий вопрос:
Предположим, у нас есть система двух линейных уравнений с действительными коэффициентами при двух действительных неизвестных. Какой из следующих вариантов невозможен ?
Теперь, когда у нас есть геометрическая интуиция, попробуем обобщить. Скажем, у нас есть система двух уравнений вида
2x+by=m3x+dy=n.
\begin{выровнено}
2x+by &= м \\
3x+dy &= п.
\end{выровнено}
2x+by3x+dy=m=n.
Какое условие гарантирует, что система будет иметь ровно одно решение?
Предположим, что у него есть по крайней мере одно решение.
Если говорить еще шире, то можно рассмотреть систему уравнений
топор+by=mcx+dy=n.
\begin{выровнено}
топор+по &=м \\
сх+dy &= п.
\end{выровнено}
ax+bycx+dy=m=n.
Выражено в форме пересечения наклона:
y=-abx+mby=-cdx+nd\begin{aligned} y&=-\frac{a}{b} x+\frac{m}{b} \\\\ y&=-\frac{c}{d}x+\frac{n}{d} \end{aligned}yy=−bax+bm=− dcx+dn
Система двух линейных уравнений имеет единственное решение, если наклоны разные:
ab≠cd ⟹ ad-bc≠0. \frac{a}{b}\neq \frac{c}{d} \ подразумевает ad-bc\neq 0.ba=dc⟹ad-bc =0.
\frac{a}{b}\neq \frac{c}{d} \ подразумевает ad-bc\neq 0.ba=dc⟹ad-bc =0.
Система не имеет решений, если наклоны равны (ad-bc=0),(ad-bc=0 ),(ad-bc=0), но точки пересечения yyy различны:
mb≠nd ⟹ dm−bn≠0\frac{m}{b}\neq\frac{n}{d} \ подразумевает dm-bn\neq 0 bm=dn⟹dm−bn=0
Система имеет бесконечные решения, если наклоны равны (ad-bc=0),(ad-bc=0 ),(ad-bc=0) и yyy-отрезки равны (dm-bn=0).( дм-бн=0).(дм-бн=0).
Итак, есть как минимум два важных вывода: один из них — полезный факт, что «вырождение» системы уравнений можно свести к рассмотрению определенного алгебраического выражения в коэффициентах, ad-bcad-bcad-bc в этой случае и решить, отличен ли он от нуля. Оказывается, это можно обобщить на более крупные системы уравнений.
Второй вывод — это наше интуитивное представление о поведении этих систем. Поскольку «случайно» выбранное действительное число почти всегда не равно нулю, следует ожидать, что «случайная» система из двух уравнений с двумя неизвестными будет иметь единственное решение. (Геометрически говоря, две «случайные» прямые почти всегда не будут параллельны и, следовательно, будут пересекаться ровно в одной точке.) Эта интуиция также будет сопровождать нас, когда мы будем исследовать более крупные системы уравнений.
(Геометрически говоря, две «случайные» прямые почти всегда не будут параллельны и, следовательно, будут пересекаться ровно в одной точке.) Эта интуиция также будет сопровождать нас, когда мы будем исследовать более крупные системы уравнений.
Линейные уравнения с двумя неизвестными — примеры и практические задачи
Мы можем решить линейные уравнения с двумя неизвестными, если знаем значение одной из переменных. В противном случае, если мы не знаем значения одной переменной, можно сделать вывод, что уравнение имеет бесконечное число решений.
В этой статье мы кратко рассмотрим процесс, используемый для решения примеров линейных уравнений с двумя неизвестными. Кроме того, мы рассмотрим несколько примеров с ответами, чтобы освоить процесс.
АЛГЕБРА
Актуально для …
Решение примеров линейных уравнений с двумя неизвестными.
См. примеры
Содержание
АЛГЕБРА
Актуально для …
Решение примеров линейных уравнений с двумя неизвестными.
См. примеры
Сводка линейных уравнений с двумя неизвестными
Чтобы уравнение имело первую степень, все его переменные должны иметь максимальную степень 1. В этом случае две неизвестные должны иметь степень 1. Например, уравнения $latex 3x+2y=5$ и $latex 3y=2x-4$ являются уравнениями первой степени с двумя неизвестными. Чтобы решить эти типы уравнений, мы можем выполнить следующие шаги:
Шаг 1: Подставьте известное значение одной переменной. Если у нас нет значения переменной, уравнение автоматически имеет бесконечные решения.
Шаг 2: Упрощение: мы удаляем знаки группировки (например, скобки), удаляем дроби и упрощаем аналогичные термины.
Шаг 3: Найти переменную. Переносим все переменные в одну часть уравнения, а константы — в другую.
Шаг 4: Решаем делением или умножением.
Примеры с ответами линейных уравнений с двумя неизвестными
На следующих примерах вы можете попрактиковаться в решении линейных уравнений с двумя неизвестными. В каждом примере показан соответствующий процесс, используемый для поиска решения. Попробуйте сначала решить проблемы, прежде чем смотреть на решение.
ПРИМЕР 1 Если значение y равно 5, найдите значение x в уравнении $latex 3x-4y=10$.
Решение
Шаг 1: Замена: у нас есть $латекс y=5$, следовательно:
$латекс 3x-4y=10$
$латекс 3x-4(5)=10$
$ латекс 3x-20=10$
Шаг 2: Упрощаем: Нам нечего упрощать:
Шаг 3: Решите для переменной: Прибавляем 20 к обеим частям:
$latex 3x-20=10 $
$латекс 3x-20+20=10+20$
$latex 3x=30$
Шаг 4: Решение: Делим обе части на 3:
$latex \frac{3x}{3}=\frac{30}{3}$
$latex x=10$
ПРИМЕР 2 Мы имеем, что значение y равно -3. Решите уравнение $latex -3x+5y=-6$ для x .
Решите уравнение $latex -3x+5y=-6$ для x .
Решение
Шаг 1: Замена: у нас есть этот $латекс y=-3$, следовательно:
$латекс -3x+5y=-6$
$латекс -3x+5(-3)= -6$
$latex -3x-15=-6$
Шаг 2: Упрощение: у нас нет подобных терминов.
Шаг 3: Решите для переменной: мы добавляем 15 к обеим частям:
$latex -3x-15+15=-6+15$
$latex -3x=9$
Шаг 4: Решение: делим обе части на -3:
$latex \frac{-3x}{-3}=\frac{9}{-3}$
$latex x=-3$
ПРИМЕР 3 Если значение x равно -2, решите уравнение $latex 4y+2(2y+3)=3x-4$ для и .
Решение
Шаг 1: Замена: у нас есть $латекс x=-2$, поэтому:
$латекс 4y+2(2y+3)=3(-2)-4$
$латекс 4y+2(2y+3)=-6-4$
Шаг 2: Упрощение: мы раскрываем круглые скобки и объединяем одинаковые термины:
$латекс 4y+2(2y+3)=-6-4$
$latex 4y+4y+6=-10$
$latex 8y+6=-10$
Шаг 3: Решение для переменной: вычитаем 6 из обеих частей:
$latex 8y+6 -6=-10-6$
$latex 8y=-16$
Шаг 4: Решение: Делим обе части на 8:
$latex \frac{8y}{8}=\frac{16}{-8}$
$latex y=-2$
Начните прямо сейчас: Изучите наши дополнительные ресурсы по математике
ПРИМЕР 4 У нас есть значение x равно 5. Решите уравнение $latex 3x+2 -4x+5)=3y+6$ для y .
Решите уравнение $latex 3x+2 -4x+5)=3y+6$ для y .
Решение
Шаг 1: Подстановка: мы подставляем $латекс x=5$ в уравнение:
$латекс 3x+2(-4x+5)=3y+6$
$латекс 3(5)+2(-4(5)+5)=3y+6$
$латекс 15+2( -20+5)=3y+6$
Шаг 2: Упрощение: Раскрываем скобки и объединяем одинаковые термины:
$latex 15+2(-20+5)=3y+6$
$latex 15+2(-15)=3y+6$
$latex 15-30=3y+6$
$latex -15=3y+6$
Шаг 3: Найти переменную: вычесть 6 с обеих сторон:
$латекс -15-6=3у+6-6$
$латекс -21=3у$
Шаг 4: Решение: Делим обе части на 3:
$latex \frac{-21}{3}=\frac{3y}{3}$
$latex -7=y$
ПРИМЕР 5 Если значение z равно 5, решите уравнение $latex 4y+2z=2(3y+10)+z-11$ для y .
Решение
Шаг 1: Подстановка: подставляем $latex z=5$ в уравнение:
$latex 4y+2(5)=2(3y+10)+5-11$
$latex 4г+10=2(3г+10)+5-11$
Шаг 2: Упрощение: Раскрываем скобки и объединяем одинаковые термины:
$latex 4y+10=6y+20+5-11$
$latex 4y+10=6y+14$
Step 3: Решите для переменной: мы вычитаем 10 и 6 y с обеих сторон:
$latex 4y+10-10=6y+14-10$
$latex 4y=6y+4$
$latex 4y-6y=6y+4-6y$
$latex -2y=4$
Шаг 4: Решение: делим обе части на -2:
$latex \frac{-2y}{-2} =\frac{4}{-2}$
$latex y=-2$
ПРИМЕР 6 Если значение y равно -3, решите уравнение $latex \frac{y+1}{2}+2x= 2(2y+6)+x+2$ для x .
Решение
Шаг 1: Замена: у нас есть $latex y=-3$, поэтому:
$latex \frac{-3+1}{2}+2x=2(2(-3) +6)+x+2$
$latex \frac{-3+1}{2}+2x=2(-6+6)+x+2$
Шаг 2: Упрощение: комбинируем подобное термины и упростить:
$latex \frac{-2}{2}+2x=2(0)+x+2$
$latex -1+2x=x+2$
Шаг 3: Найти переменную: Прибавляем 1 и вычитаем x с обеих сторон:
$latex -1+2x+1=x+2+1$
$latex 2x=x+3$
$latex 2x-x=x+3-x $
$latex x=3$
Шаг 4: Решение: Мы уже нашли решение:
$latex x=3$
ПРИМЕР 7 90 уравнение $04xve 90 2y=3x+10$ за и . Решение
Шаг 1: Замена: В этом случае у нас нет заданного значения, поэтому автоматически уравнение имеет бесконечное число решений . Например, предположим, что у нас есть $латекс x = 0$, тогда у нас будет:
$латекс 2x+2y=3x+10$
$латекс 2(0)+2y=3(0)+10$
$latex 2y=10$
$latex y=5$
Если теперь у нас есть $latex x = 1$, мы имеем:
$latex 2x+2y=3x+10$
$latex 2(1) +2г=3(1)+10$
$latex 2+2y=3+10$
$latex 2+2y=13$
$latex 2y=15$
$latex y=15/2$
Мы могли бы продолжить с другими значениями и каждым время мы получили бы разные результаты, поэтому, не имея определенного значения переменной, уравнение имеет бесконечные решения.
Линейные уравнения с двумя неизвестными. Практические задачи
Используйте следующие практические задачи, чтобы попрактиковаться в решении линейных уравнений с двумя неизвестными. Просто выберите ответ и проверьте его, нажав «Проверить». Вы можете внимательно просмотреть приведенные выше примеры, если у вас возникли проблемы с решением этих упражнений.
Если у нас есть $latex y=-2$, каково значение x в $latex 2x+4y=-4$?.
Выберите ответ
$латекс x=1$
$латекс x=2$
$латекс x=3$
$latex x=4$
Решите уравнение $latex 4x+2y=2x-2$, если у нас есть $latex y=5$.
Выберите ответ
$латекс x=-3$
$латекс x=3$
$латекс x=6$
$латекс x=-6$
У нас есть $латекс z=10$. Найдите значение x в уравнении $latex 4x+3(z-10)=z+10$.
Выберите ответ
$латекс x=2$
$латекс x=4$
$латекс x=5$
$latex x=6$
Решите уравнение $latex 2x-2y+5=x+3$.

Выберите ответ
$латекс x=0$
$латекс x=1$
$латекс x=3$
Бесконечное количество решений
Решите уравнение $latex \frac{x+1}{3}+5=\frac{y+2}{2}+x+4$, если $latex y=-2$.
Выберите ответ
$латекс x=2$
$латекс x=-2$
$латекс x=3$
$latex x=-3$
См. также
Хотите узнать больше о решении уравнений? Взгляните на эти страницы:
- Упражнения с уравнениями первой степени
- 20 Упражнения с уравнениями первой степени
- Уравнения первой степени с дробями Упражнения
- Упражнения на линейные уравнения
Изучайте математику с помощью наших дополнительных ресурсов по различным темам
УЗНАТЬ БОЛЬШЕ
Линейные системы с двумя переменными
Онлайн-заметки Пола
Главная
/
Алгебра
/
Системы уравнений
/ Линейные системы с двумя переменными
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 7-1: Линейные системы с двумя переменными
Линейная система двух уравнений с двумя переменными — это любая система, которую можно записать в виде.
\[\begin{align*}ax + by & = p\\ cx + dy & = q\end{align*}\]
, где любая константа может быть равна нулю, за исключением того, что каждое уравнение должно содержать хотя бы одну переменную.
Также система называется линейной, если переменные стоят только в первой степени, входят только в числитель и ни в одном из уравнений нет произведений переменных.
Вот пример системы с числами.
\[\begin{align*}3x — y & = 7\\ 2x + 3y & = 1\end{align*}\]
Прежде чем мы обсудим, как решать системы, мы должны сначала поговорить о том, что такое решение системы уравнений. Решением системы уравнений является значение \(x\) и значение \(y\), которые при подстановке в уравнения удовлетворяют обоим уравнениям одновременно.
В приведенном выше примере \(x = 2\) и \(y = — 1\) является решением системы. Это достаточно легко проверить.
\[\begin{align*}3\left( 2 \right) — \left( { — 1} \right) & = 7\\ 2\left( 2 \right) + 3\left( { — 1} \ справа) & = 1\end{align*}\]
Итак, конечно же, эта пара чисел является решением системы. Не беспокойтесь о том, как мы получили эти значения. Это будет самая первая система, которую мы решим, когда приступим к примерам.
Обратите внимание, что важно, чтобы пара чисел удовлетворяла обоим уравнениям. Например, \(x = 1\) и \(y = — 4\) удовлетворяют первому уравнению, но не второму, и поэтому не являются решением системы. Точно так же \(x = — 1\) и \(y = 1\) будут удовлетворять второму уравнению, но не первому, и поэтому не могут быть решением системы.
Например, \(x = 1\) и \(y = — 4\) удовлетворяют первому уравнению, но не второму, и поэтому не являются решением системы. Точно так же \(x = — 1\) и \(y = 1\) будут удовлетворять второму уравнению, но не первому, и поэтому не могут быть решением системы.
Что представляет собой решение системы двух уравнений? Ну, если подумать, оба уравнения в системе являются линиями. Итак, давайте нарисуем их и посмотрим, что у нас получится.
Как видите, решением системы являются координаты точки пересечения двух прямых. Итак, при решении линейных систем с двумя переменными мы действительно спрашиваем, где пересекаются две линии.
В этом разделе мы рассмотрим два метода решения систем.
Первый метод называется методом подстановки . В этом методе мы решим одно из уравнений для одной из переменных и подставим его в другое уравнение. Это даст одно уравнение с одной переменной, которое мы можем решить. Как только это решено, мы подставляем это значение обратно в одно из уравнений, чтобы найти значение оставшейся переменной.
На словах этот метод не всегда очень понятен. Давайте рассмотрим пару примеров, чтобы увидеть, как работает этот метод.
Пример 1. Решите каждую из следующих систем.
- \(\begin{align*}3x — y & = 7\\ 2x + 3y & = 1\end{align*}\)
- \(\begin{align*}5x + 4y & = 1\\ 3x — 6y & = 2\end{align*}\)
Показать все решения Скрыть все решения
a \(\begin{align*}3x — y & = 7\\ 2x + 3y & = 1\end{align*}\) Показать решение
Итак, это была первая система, которую мы рассмотрели выше. Мы уже знаем решение, но это даст нам возможность проверить значения, которые мы записали для решения.
Теперь метод говорит, что нам нужно решить одно из уравнений для одной из переменных. Какое уравнение мы выберем и какую переменную выберем, зависит от вас, но обычно лучше выбрать уравнение и переменную, с которыми будет легко работать. Это означает, что мы должны стараться избегать дробей, если это вообще возможно.
Это означает, что мы должны стараться избегать дробей, если это вообще возможно.
В этом случае будет очень просто решить первое уравнение для \(y\), так что давайте сделаем это.
\[3x — 7 = у\]
Теперь подставьте это во второе уравнение.
\[2x + 3\влево( {3x — 7} \вправо) = 1\]
Это уравнение относительно \(x\), которое мы можем решить, так что давайте сделаем это.
\[\begin{align*}2x + 9x — 21 & = 1\\ 11x & = 22\\ x & = 2\end{align*}\]
Итак, есть \(x\) часть решения.
Наконец, НЕ забудьте вернуться и найти \(y\) часть решения. Это одна из наиболее частых ошибок, которую студенты допускают при решении систем. Для этого мы можем либо подставить значение \(x\) в одно из исходных уравнений и найти \(y\), либо просто подставить его в нашу замену, которую мы нашли на первом шаге. Так будет проще, так что давайте.
Так будет проще, так что давайте.
\[y = 3x — 7 = 3\влево( 2 \вправо) — 7 = — 1\]
Итак, решение есть \(x = 2\) и \(y = — 1\), как мы отметили выше.
b \(\begin{align*}5x + 4y & = 1\\ 3x — 6y & = 2\end{align*}\) Показать решение
С этой системой мы не сможем полностью избежать дробей. Однако похоже, что если мы решим второе уравнение относительно \(x\), мы сможем их минимизировать. Вот эта работа.
\[\begin{align*}3x & = 6y + 2\\ x & = 2y + \frac{2}{3}\end{align*}\]
Теперь подставьте это в первое уравнение и решите полученное уравнение относительно \(y\).
\[\begin{align*}5\left( {2y + \frac{2}{3}} \right) + 4y & = 1\\ 10y + \frac{{10}}{3} + 4y & = 1\\ 14y & = 1 — \frac{{10}}{3} = — \frac{7}{3}\\ y & = — \left( {\frac{7}{3}} \right) \left( {\frac{1}{{14}}} \right)\\ y & = — \frac{1}{6}\end{align*}\]
Наконец, подставьте это в исходную замену, чтобы найти \(x\).
\[x = 2\left( { — \frac{1}{6}} \right) + \frac{2}{3} = — \frac{1}{3} + \frac{2}{3} = \фракция{1}{3}\]
Итак, решением этой системы является \(x = \frac{1}{3}\) и \(y = — \frac{1}{6}\).
Как и в случае с отдельными уравнениями, мы всегда можем вернуться и проверить это решение, подставив его в оба уравнения и убедившись, что оно удовлетворяет обоим уравнениям. Обратите также внимание, что нам действительно нужно было бы подключиться к обоим уравнениям. Вполне возможно, что в результате ошибки может получиться пара чисел, удовлетворяющая одному из уравнений, но не удовлетворяющая другому.
Теперь перейдем к следующему методу решения систем уравнений. Как мы видели в последней части предыдущего примера, метод подстановки часто вынуждает нас иметь дело с дробями, что увеличивает вероятность ошибок. Этот второй метод не будет иметь этой проблемы. Ну, это не совсем так. Если будут появляться дроби, они появятся только на последнем шаге и только в том случае, если решение содержит дроби.
Этот второй метод называется метод ликвидации . В этом методе мы умножаем одно или оба уравнения на соответствующие числа (, т.е. , умножаем каждый член уравнения на число), так что одна из переменных будет иметь одинаковый коэффициент с противоположными знаками. Затем следующим шагом будет сложение двух уравнений вместе. Поскольку одна из переменных имеет одинаковый коэффициент с разными знаками, она будет исключена при сложении двух уравнений. Результатом будет одно уравнение, которое мы можем решить для одной из переменных. Как только это будет сделано, подставьте этот ответ обратно в одно из исходных уравнений.
Как и в случае с первым методом, гораздо проще понять, что здесь происходит, на паре примеров.
Пример 2 Постановка задачи.
- \(\begin{align*}5x + 4y & = 1\\ 3x — 6y & = 2\end{align*}\)
- \(\begin{align*}2x + 4y & = — 10\\ 6x + 3y & = 6\end{align*}\)
Показать все решения Скрыть все решения
a \(\begin{align*}5x + 4y & = 1\\ 3x — 6y & = 2\end{align*}\) Показать решение
Это система из предыдущего набора примеров, которая заставила нас работать с дробями. Работа здесь покажет различия между двумя методами, а также покажет, что любой метод можно использовать для получения решения системы.
Работа здесь покажет различия между двумя методами, а также покажет, что любой метод можно использовать для получения решения системы.
Итак, нам нужно умножить одно или оба уравнения на константы так, чтобы одна из переменных имела одинаковый коэффициент с разными знаками. Итак, поскольку члены \(y\) уже имеют противоположные знаки, давайте работать с этими членами. Похоже, что если мы умножим первое уравнение на 3, а второе уравнение на 2, члены \(y\) будут иметь коэффициенты 12 и -12, что нам и нужно для этого метода.
Вот работа для этого шага.
\[\начать{выравнивать*}
5x+4y & = 1 & \underrightarrow{\times \,\,3} \hspace{0.5in} & 15x+12y=3 \\
3x-6y & = 2 & \underrightarrow{\times \,\,2} \hspace{0.5in} & \underline{\,\,6x-12y=4} \\
& & & 21x \hspace{0.5in} =7 \\
\конец{выравнивание*}\]
Итак, как и обещало описание метода, мы имеем уравнение, которое можно решить относительно \(x\). Это дает \(x = \frac{1}{3}\), что в точности соответствует тому, что мы нашли в предыдущем примере. Обратите внимание, однако, что единственная часть, с которой нам приходилось иметь дело до этого момента, — это сам ответ, который отличается от метода подстановки.
Это дает \(x = \frac{1}{3}\), что в точности соответствует тому, что мы нашли в предыдущем примере. Обратите внимание, однако, что единственная часть, с которой нам приходилось иметь дело до этого момента, — это сам ответ, который отличается от метода подстановки.
Теперь снова не забудьте найти \(y\). В этом случае работы будет чуть больше, чем метод подстановки. Чтобы найти \(y\), нам нужно подставить значение \(x\) в любое из исходных уравнений и найти \(y\). Поскольку \(x\) является дробью, заметим, что в этом случае, если мы подставим это значение во второе уравнение, мы потеряем дроби, по крайней мере временно. Обратите внимание, что часто этого не происходит, и нам приходится иметь дело с дробями, хотим мы этого или нет.
\[\begin{align*}3\left( {\frac{1}{3}} \right) — 6y & = 2\\ 1 — 6y & = 2\\ — 6y & = 1\\ y & = — \frac{1}{6}\end{align*}\]
Опять же, это то же самое значение, которое мы нашли в предыдущем примере.
b \(\begin{align*}2x + 4y & = — 10\\ 6x + 3y & = 6\end{align*}\) Показать решение
В этой части все переменные положительны, так что нам придется поставить противоположный знак, умножив где-нибудь на отрицательное число. Заметим также, что в этом случае, если мы просто умножим первое уравнение на -3, то коэффициенты при \(x\) будут равны -6 и 6.
Иногда нам нужно умножить только одно из уравнений, а другое можно не трогать. Вот эта работа по этой части.
\[\начать{выравнивать*}
2x+4y & =-10 & \underrightarrow{\times\,\,-3} \hspace{0.5in} & -6x-12y=30 \\
6x+3y & =6 & \underrightarrow{\text{тот же}} \hspace{0,5in} &\underline{\hspace{0,35in}6x+3y=6} \\
& & & \hspace{0.5in} -9y=36 \\
& & & \hspace{0.85in} y=-4 \\
\конец{выравнивание*}\]
Наконец, подставьте это в любое из уравнений и найдите \(x\). На этот раз мы будем использовать первое уравнение.
На этот раз мы будем использовать первое уравнение.
\[\begin{align*}2x + 4\left( { — 4} \right) & = — 10\\ 2x — 16 & = — 10\\ 2x & = 6\\ x & = 3\end{align *}\]
Итак, решением этой системы является \(x = 3\) и \(y = — 4\).
Существует третий метод, который мы рассмотрим для решения систем из двух уравнений, но он немного сложнее и, вероятно, более полезен для систем, состоящих как минимум из трех уравнений, поэтому мы рассмотрим его в следующем разделе. .
Прежде чем покинуть этот раздел, мы должны рассмотреть пару частных случаев решения систем.
Пример 3. Решите следующие системы уравнений.
\[\begin{align*}x — y & = 6\\ — 2x + 2y & = 1\end{align*}\]
Показать решение
Здесь можно использовать любой метод, но похоже, что замена будет немного проще. Мы решим первое уравнение относительно \(x\) и подставим его во второе уравнение.
Мы решим первое уравнение относительно \(x\) и подставим его во второе уравнение.
\[\begin{align*}x & = 6 + y\\ & \\ — 2\left( {6 + y} \right) + 2y & = 1\\ — 12 — 2y + 2y & = 1\\ — 12 & = 1\,\,\,??\end{align*}\]
Итак, это явно неправда и нигде в нашей работе нет ошибки. Так в чем проблема? Чтобы увидеть, давайте нарисуем эти две линии и посмотрим, что мы получим.
Похоже, что эти две прямые параллельны (можете ли вы проверить это по наклонам?), и мы знаем, что две параллельные прямые с разными \(y\)-перехватами (это важно) никогда не пересекутся.
Как мы видели во вступительном обсуждении этого раздела, решения представляют собой точку пересечения двух линий. Если две линии не пересекаются, у нас не может быть решения.
Итак, когда мы получаем такой бессмысленный ответ от нашей работы, мы имеем две параллельные линии и нет решения этой системы уравнений.
Система в предыдущем примере называется непоследовательной . Обратите также внимание, что если бы мы использовали исключение в этой системе, мы бы получили такой же бессмысленный ответ.
Пример 4. Решите следующую систему уравнений.
\[\begin{align*}2x + 5y & = — 1\\ — 10x — 25y & = 5\end{align*}\]
Показать решение
В этом примере кажется, что удаление будет самым простым методом.
\[\начать{выравнивать*}
2x+5y & =-1 & \underrightarrow{\times \,\,5} \hspace{0.5in} & \,\,\,\,10x+25y=-5 \\
-10x-25y & =5 & \underrightarrow{\text{тот же}} \hspace{0.5in} & \underline{-10x-25y=5} \\
& & & \hspace{0.9в} 0=0 \\
\конец{выравнивание*}\]
На первый взгляд может показаться, что это та же проблема, что и в предыдущем примере. Однако в этом случае мы получили равенство, которое просто не соответствовало действительности. В этом случае мы имеем 0=0, и это истинное равенство, и в этом смысле в этом нет ничего плохого.
Однако в этом случае мы получили равенство, которое просто не соответствовало действительности. В этом случае мы имеем 0=0, и это истинное равенство, и в этом смысле в этом нет ничего плохого.
Однако это явно не тот ответ, которого мы ожидали здесь, и поэтому нам нужно определить, что именно происходит.
Мы предоставим вам проверить это, но если вы найдете наклон и \(y\)-отрезки для этих двух линий, вы обнаружите, что обе линии имеют точно такой же наклон, и обе линии имеют точно такое же \ (у\)-перехват. Итак, что это значит для нас? Хорошо, если две линии имеют одинаковый наклон и одинаковую \(y\)-пересечение, то графики этих двух линий являются одним и тем же графиком. Другими словами, графики этих двух линий представляют собой один и тот же график. В этих случаях любой набор точек, удовлетворяющий одному из уравнений, будет удовлетворять и другому уравнению.
Также напомню, что график уравнения — это не что иное, как множество всех точек, удовлетворяющих уравнению. Другими словами, существует бесконечное множество точек, удовлетворяющих этому набору уравнений.
Другими словами, существует бесконечное множество точек, удовлетворяющих этому набору уравнений.
В этих случаях мы хотим записать что-нибудь для решения. Итак, что мы будем делать, так это решать одно из уравнений для одной из переменных (неважно, какую вы выберете). Мы решим первое для \(y\).
\[\begin{align*}2x + 5y & = — 1\\ 5y & = — 2x — 1\\ y & = — \frac{2}{5}x — \frac{1}{5}\end {выровнять*}\]
Тогда по любому \(x\) мы можем найти \(y\), и эти два числа составят решение системы уравнений. Обычно мы обозначаем это, записывая решение следующим образом:
\[\begin{array}{*{20}{c}}\begin{aligned}x & = t\\ y & = — \frac{2}{5}t — \frac{1}{5}\ end{выровнено}&{\hspace{0,25 дюйма}{\mbox{где}}\,t{\mbox{любое действительное число}}}\end{массив}\]
Чтобы показать, что они дают решения, давайте проработаем пару значений \(t\). 9? 5\\ — 1 & = — 1 & \hspace{0.25in} 5 & = 5\end{align*}\]
9? 5\\ — 1 & = — 1 & \hspace{0.25in} 5 & = 5\end{align*}\]
Итак, \(x = 0\) и \(y = — \frac{1}{5}\) является решением системы. Давайте сделаем еще один очень быстро.
\(t = — 3\)
\[x = — 3\hspace{0,25 дюйма}y = — \frac{2}{5}\left( { — 3} \right) — \frac{1}{5} = \frac{6}{5 } — \frac{1}{5} = 1\]
Нам снова нужно подставить его в оба уравнения системы, чтобы показать, что это решение. 9? 5\\ — 1 & = — 1 & \hspace{0.25in}5 & = 5\end{align*}\]
Действительно, \(x = — 3\) и \(y = 1\) — решение.
Таким образом, поскольку существует бесконечное число возможных \(t\), должно быть бесконечное число решений этой системы, и они задаются как
\[\begin{array}{*{20}{c}}\begin{aligned}x & = t\\ y & = — \frac{2}{5}t — \frac{1}{5}\ end{выровнено}&{\hspace{0,25 дюйма}{\mbox{где}}\,t{\mbox{любое действительное число}}}\end{массив}\]
Системы, такие как в предыдущих примерах, называются зависимыми .
Теперь мы рассмотрели все три возможности решения системы уравнений. Система уравнений либо не имеет решения, либо имеет ровно одно решение, либо бесконечно много решений.
4.1: Решение систем линейных уравнений с двумя переменными
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 30838
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Определять, является ли упорядоченная пара решением системы уравнений
- Решите систему линейных уравнений, построив график
- Решите систему уравнений подстановкой
- Решите систему уравнений методом исключения
- Выберите наиболее удобный способ решения системы линейных уравнений
Прежде чем приступить к работе, пройдите этот тест на готовность.
- Для уравнения \(y=\frac{2}{3}x−4\),
ⓐ Является ли \((6,0)\) решением? ⓑ Является ли \((−3,−2)\) решением?
Если вы пропустили эту проблему, просмотрите [ссылка] . - Найдите наклон и y -точку пересечения линии \(3x−y=12\).
Если вы пропустили эту проблему, просмотрите [ссылка] . - Найдите x- и y пересечений прямой \(2x−3y=12\).
Если вы пропустили эту проблему, просмотрите [ссылка] .
Определить, является ли упорядоченная пара решением системы уравнений
В разделе Решение линейных уравнений мы научились решать линейные уравнения с одной переменной. Теперь мы будем работать с двумя или более линейными уравнениями, сгруппированными вместе, что известно как система линейных уравнений .
СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ
Когда два или более линейных уравнения группируются вместе, они образуют систему линейных уравнений .
В этом разделе мы сосредоточим нашу работу на системах двух линейных уравнений с двумя неизвестными. Мы будем решать более крупные системы уравнений позже в этой главе.
Ниже показан пример системы двух линейных уравнений. Мы используем фигурную скобку, чтобы показать, что два уравнения сгруппированы вместе, чтобы сформировать систему уравнений.
\[ \left\{ \begin{выровнено} 2x+y & = 7 \\ x−2y & = 6 \end{выровнено} \right. \nonumber \]
Линейное уравнение с двумя переменными, такое как \(2x+y=7\), имеет бесконечное число решений. Его график представляет собой линию. Помните, что каждая точка на прямой — это решение уравнения, а каждое решение уравнения — это точка на прямой.
Чтобы решить систему двух линейных уравнений, мы хотим найти значения переменных, являющихся решениями обоих уравнений. Другими словами, мы ищем упорядоченные пары \((x,y)\), которые делают оба уравнения верными. Их называют решения системы уравнений .
РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ
решений системы уравнений являются значениями переменных, которые делают все уравнений истинными. Решение системы двух линейных уравнений представлено упорядоченной парой \((x,y)\).
Чтобы определить, является ли упорядоченная пара решением системы двух уравнений, мы подставляем значения переменных в каждое уравнение. Если упорядоченная пара делает оба уравнения верными, это решение системы.
Пример \(\PageIndex{1}\)
Определить, является ли упорядоченная пара решением системы \(\left \{ \begin{array} {l} x−y = −1 \\ 2x−y = −5 \end{массив} \right. \).
ⓐ \((−2,−1)\) ⓑ \((−4,−3)\)
- Ответ
ⓐ
ⓑ
Пример \(\PageIndex{2}\)
Определить, является ли упорядоченная пара решением системы \(\left \{ \begin{array} 3x+y = 0 \\ x+2y = −5 \ конец{массив} \справа. \).
\).
ⓐ \((1,−3)\) ⓑ \((0,0)\)
- Ответ
ⓐ да ⓑ нет
Пример \(\PageIndex{3}\)
Определить, является ли упорядоченная пара решением системы \(\left \{ \begin{array} x−3y = −8 \\ −3x−y = 4 \end{массив} \right. \).
ⓐ \((2,−2)\) ⓑ \((−2,2)\)
- Ответ
ⓐ нет ⓑ да
Решение системы линейных уравнений с помощью графика
В этом разделе мы будем использовать три метода для решения системы линейных уравнений. Первый метод, который мы будем использовать, — это построение графика.
График линейного уравнения представляет собой линию. Каждая точка на прямой является решением уравнения. Для системы двух уравнений мы начертим две линии. Тогда мы сможем увидеть все точки, являющиеся решениями каждого уравнения. И, найдя, что общего у линий, мы найдем решение системы.
Большинство линейных уравнений с одной переменной имеют одно решение, но мы видели, что некоторые уравнения, называемые противоречиями, не имеют решений, а для других уравнений, называемых тождествами, решениями являются все числа.
Аналогичным образом, когда мы решаем систему двух линейных уравнений, представленную графиком из двух линий на одной плоскости, возможны три случая, как показано.
Рисунок \(\PageIndex{1}\) Каждый раз, когда мы демонстрируем новый метод, мы будем использовать его для одной и той же системы линейных уравнений. В конце раздела вы решите, какой метод был наиболее удобным для решения этой системы.
Пример \(\PageIndex{4}\): как решить систему уравнений с помощью графика
Решить систему с помощью графика \( \left\{ \begin{array} {l} 2x+y = 7 \\ x−2y = 6 \end{array} \right. \).
- Ответить
Пример \(\PageIndex{5}\)
Решите систему графически: \( \left\{ \begin{array} {l} x−3y = −3 \\ x+y = 5 \end{ массив} \справа.\).
- Ответить
\((3,2)\)
Пример \(\PageIndex{6}\)
Решите систему графически: \( \left\{ \begin{array} {l} −x+y = 1 \\ 3x+2y = 12 \end{ массив} \справа. \)
\)
- Ответить
\((2,3)\)
Здесь показаны шаги, необходимые для решения системы линейных уравнений с помощью графика.
РЕШИТЬ СИСТЕМУ ЛИНЕЙНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ ГРАФИКА.
- Нарисуйте первое уравнение.
- Нарисуйте график второго уравнения в той же прямоугольной системе координат.
- Определите, пересекаются ли линии, параллельны или являются одной и той же линией.
- Определите решение системы.
- Если линии пересекаются, определите точку пересечения. Это решение системы.
- Если прямые параллельны, система не имеет решения.
- Если линии одинаковые, система имеет бесконечное число решений.
- Проверьте решение обоих уравнений.
В следующем примере мы сначала перепишем уравнения в форме наклон-пересечение, так как это облегчит нам быстрое построение линий.
Пример \(\PageIndex{7}\)
Решите систему графически: \(\left\{ \begin{array} {l} 3x+y = −1 \\ 2x+y = 0 \end{ массив}\право.\)
- Ответ
Мы решим оба этих уравнения относительно \(y\), чтобы мы могли легко построить их график, используя их наклоны и \(y\)-отрезки.
Решите первое уравнение для y .
Найти наклон и у -пересечение. Решите второе уравнение для y . Найти наклон и у -пересечение. Нарисуйте линии. : Определить точку пересечения. Линии пересекаются в точке \((−1,2)\).
Проверьте решение обоих уравнений. Решение: \((−1,2)\).
Пример \(\PageIndex{8}\)
Решите систему графически: \(\left\{ \begin{array} {l} −x+y = 1 \\2x+y = 10 \end{ массив}\справа.\).
- Ответить
\((3,4)\)
Пример \(\PageIndex{9}\)
Решите систему графически: \(\left\{ \begin{array} {l} 2x+y = 6 \\x+y = 1 \end{array }\Правильно. \).
- Ответить
\((5,−4)\)
Пока что во всех системах линейных уравнений линии пересекались, а решением была одна точка. В следующих двух примерах мы рассмотрим систему уравнений, не имеющую решения, и систему уравнений, имеющую бесконечное число решений.
Пример \(\PageIndex{10}\)
Решите систему графически: \(\left\{ \begin{array} {l} y = \tfrac{1}{2}x-3 \\ x -2y = 4 \end{array}\right. \).
- Ответить
Для построения графика первого уравнения мы будем использовать его наклон
и точку пересечения y .
Для построения графика второго уравнения мы будем использовать
перехватов. Нарисуйте линии. Определите точки пересечения. Линии параллельны.
Поскольку на обеих линиях нет точек, не существует
упорядоченной пары, которая делает оба уравнения
верными. У этой системы нет решения.
Пример \(\PageIndex{11}\)
Решите систему графически: \(\left\{ \begin{array} {l} y = -\tfrac{1}{4}x+2 \\ x+4y = 4 \end{массив}\right. \).
\).
- Ответить
нет решения
Пример \(\PageIndex{12}\)
Решите систему графически: \(\left\{ \begin{array} {l} y = 3x-1 \\ 6x-2y = 6 \end{array }\Правильно. \).
- Ответить
нет решения
Иногда уравнения в системе представляют одну и ту же прямую. Поскольку каждая точка на прямой делает оба уравнения верными, существует бесконечно много упорядоченных пар, которые делают оба уравнения верными. Система имеет бесконечно много решений.
Пример \(\PageIndex{13}\)
Решите систему графически: \(\left\{ \begin{array} {l} y = 2x-3 \\ -6x+3y = 9 \end{ массив}\справа.\).
- Ответ
In the second equation, when x is 0, y is minus 3 and when y is 0, x is 3 by 2. We use these points for graphing the lines to determine the point of intersection. The lines are the same. Since every point on the line makes both equations true, there are infinite many ordered pairs that make both equations true. There are infinite many solutions to this system.»> Найдите наклон и y -пересечение первого уравнения. Найдите точки пересечения второго уравнения. Нарисуйте линии.
Линии одинаковые!
Поскольку каждая точка на прямой делает оба уравнения
верными, существует бесконечно много
упорядоченных пар, которые делают оба уравнения верными.
У этой системы бесконечно много решений. Если вы запишете второе уравнение в форме наклон-пересечение, вы можете заметить, что уравнения имеют один и тот же наклон и одно и то же y -пересечение.
Пример \(\PageIndex{14}\)
Решите систему графически: \(\left\{ \begin{array} {l} y = -3x-6 \\ 6x+2y = -12 \end {массив}\справа.\).
- Ответить
бесконечно много решений
Пример \(\PageIndex{15}\)
Решите систему графически: \(\left\{ \begin{array} {l} y = \tfrac{1}{2}x-4 \\ 2x -4y = 16 \end{array}\right. \).
\).
- Ответить
бесконечно много решений
Когда мы рисовали вторую линию в последнем примере, мы нарисовали ее прямо над первой линией. Мы говорим, что две строки совпадают с . Совпадающие линии имеют одинаковый наклон и одинаковую точку пересечения y-.
СОВПАДАЮЩИЕ ЛИНИИ
Совпадающие прямые имеют одинаковый наклон и одинаковую точку пересечения и .
Системы уравнений в Пример и Пример каждый имел две пересекающиеся линии. Каждая система имела одно решение.
В Пример уравнения давали совпадающие прямые, поэтому система имела бесконечно много решений.
Системы в этих трех примерах имели по крайней мере одно решение. Система уравнений, имеющая хотя бы одно решение, называется -непротиворечивой системой .
Система с параллельными прямыми, например Пример , не имеет решения. Мы называем такую систему уравнений несовместимой. Нет решения.
Мы называем такую систему уравнений несовместимой. Нет решения.
НЕСОВМЕСТИМЫЕ И НЕСОВМЕСТИМЫЕ СИСТЕМЫ
непротиворечивая система уравнений — это система уравнений, имеющая хотя бы одно решение.
Несовместимая система уравнений — это система уравнений, не имеющая решения.
Мы также классифицируем уравнения в системе уравнений, называя уравнения независимыми или зависимыми . Если два уравнения независимы, то каждое из них имеет собственный набор решений. Пересекающиеся прямые и параллельные прямые независимы.
Если два уравнения являются зависимыми, то все решения одного уравнения также являются решениями другого уравнения. Когда мы рисуем два зависимых уравнения, мы получаем совпадающие линии.
Подведем итоги, взглянув на графики трех типов систем. См. ниже и Таблица .
Parallel lines have no solution and are inconsistent and independent. Coincident lines have infinitely many solutions and are consistent and dependent.»> Линии Пересечение Параллельный Совпадение Количество растворов 1 балл Нет решения Бесконечно много Последовательный/непоследовательный Последовательный Несоответствие Последовательный Зависимый/ независимый Независимый Независимый Зависимый Пример \(\PageIndex{16}\)
Без построения графика определите количество решений, а затем классифицируйте систему уравнений.
ⓐ \( \left\{ \begin{array} {l} y = 3x−1 \\ 6x−2y = 12 \end{array}\right. \) ⓑ \( \left\{ \begin{array } {l} 2x+y=−3 \\ x−5y=5 \end{массив} \right.\)
- Ответ
ⓐ Сравним наклоны и точки пересечения двух линий.
\(\begin{array} {lll} {} &{} &{ \left\{ \begin{array} {l} {y=3x-1} \\ {6x−2y=12} \end{array } \right.} \\ {} &{} &{y = 3x-1} \\ {\text{Первое уравнение уже находится в форме пересечения наклона.}} &{} &{} \\ {\text {Запишите второе уравнение в форме пересечения наклона.}} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \ \ {} &{} &{6x-2y=12} \\ {} &{} &{-2y=-6x+12} \\ {} &{} &{\frac{-2y}{-2} =\frac{-6x+12}{-2}} \\ {} &{} &{y=3x-6} \\ {} &{y=3x-1} &{y=3x-6} \ \ {} &{m=3} &{m=3} \\ {} &{b=-1} &{b=-6} \\ {\text{Найдите наклон и точку пересечения каждой линии.}} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{\text{Поскольку наклоны одинаковы, а y-перехваты}} &{} \\ {} &{\text{различны, линии параллельны. }} &{} \\ \end{массив}\)
}} &{} \\ \end{массив}\)
ⓑ Сравним наклон и точки пересечения двух линий.
\(\begin{array} {lll} {} &{} &{} \\ {} &{ \left\{ \begin{array} {l} 2x+y=-3 \\ x-5y=5 \\ \end{массив} \right. } &{} \\ {\text{Запишите оба уравнения в форме наклона–отрезка.}} &{} &{} \\ {} &{} &{} \\ { } &{} &{} \\ {} &{} &{} \\ {} &{2x+y=-3} &{x-5y=5} \\ {} &{y=-2x-3 } &{-5y=-x+5} \\ {} &{} &{\frac{-5y}{-5}=\frac{-x+5}{-5}} \\ {} &{ } &{y=\frac{1}{5}-1} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {\text{Найти наклон и точку пересечения каждой прямой.}} &{} &{} \\ {} &{} &{} \\ {} &{y=-2x- 3} &{y=\frac{1}{5}-1} \\ {} &{m=-2} &{m=\frac{1}{5}} \\ {} &{b=- 3} &{b=-1} \\ {} &{} &{} \\ {} &{\text{Поскольку наклоны разные, линии пересекаются.}} &{} \\ \end{массив} \)
Система уравнений, графики которой пересекаются, имеет 1 решение, непротиворечива и независима.
Пример \(\PageIndex{17}\)
Без построения графика определите количество решений, а затем классифицируйте систему уравнений.
ⓐ \(\left\{ \begin{array} {l} y=−2x−4 \\ 4x+2y=9 \end{array} \right. \) ⓑ \(\left\{ \begin{ array} {l} 3x+2y=2 \\ 2x+y=1 \end{array} \right.\)
- Ответ
ⓐ нет решения, противоречивое, независимое ⓑ одно решение, последовательное, независимое
Пример \(\PageIndex{18}\)
Без построения графика определите количество решений, а затем классифицируйте систему уравнений.
ⓐ \(\left\{ \begin{array} {l} y=\frac{1}{3}x−5 \\ x−3y=6 \end{array} \right. \) ⓑ \( \left\{ \begin{array} {l} x+4y=12 \\ −x+y=3 \end{array} \right. \)
- Ответ
ⓐ нет решения, противоречивое, независимое ⓑ одно решение, последовательное, независимое
Решение систем линейных уравнений с помощью графика — хороший способ визуализировать возможные решения. Однако во многих случаях решение системы с помощью графика неудобно или неточно. Если графики выходят за пределы маленькой сетки с x и y между \(−10\) и 10, графическое изображение линий может быть громоздким. И если решения системы не являются целыми числами, может быть трудно точно прочитать их значения по графику.
И если решения системы не являются целыми числами, может быть трудно точно прочитать их значения по графику.
Решить систему уравнений методом подстановки
Теперь мы будем решать системы линейных уравнений методом подстановки.
Мы будем использовать ту же систему, которую использовали для построения графика.
\[ \left\{ \begin{массив} {l} 2x+y=7 \\ x−2y=6 \end{массив} \right. \nonumber \]
Сначала мы решим одно из уравнений либо для x , либо для y . Мы можем выбрать любое уравнение и найти решение для любой переменной, но мы постараемся сделать такой выбор, который облегчит нам работу.
Затем мы подставляем это выражение в другое уравнение. В результате получается уравнение только с одной переменной, и мы знаем, как его решить!
После того, как мы найдем значение одной переменной, мы подставим это значение в одно из исходных уравнений и найдем другую переменную. Наконец, мы проверяем наше решение и убеждаемся, что оба уравнения верны.
Пример \(\PageIndex{19}\): как решить систему уравнений подстановкой
Решить систему подстановкой: \( \left\{ \begin{array} {l} 2x+y=7 \ \ x−2y=6 \end{массив} \right.\)
- Ответить
Пример \(\PageIndex{20}\)
Решите систему подстановкой: \( \left\{ \begin{array} {l} −2x+y=−11 \\ x+3y=9 \end {массив} \право.\)
- Ответ
\((6,1)\)
Пример \(\PageIndex{21}\)
Решите систему подстановкой: \( \left\{ \begin{array} {l} 2x+y=−1 \\ 4x+3y=3 \end{ массив} \справа.\)
- Ответить
\((−3,5)\)
РЕШИТЕ СИСТЕМУ УРАВНЕНИЙ ПОДСТАВКОЙ.
- Решите одно из уравнений для любой переменной.
- Подставьте выражение из шага 1 в другое уравнение.
- Решите полученное уравнение.
- Подставьте решение шага 3 в одно из исходных уравнений, чтобы найти другую переменную.

- Запишите решение в виде упорядоченной пары.
- Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
Будьте очень осторожны со знаками в следующем примере.
Пример \(\PageIndex{22}\)
Решите систему подстановкой: \( \left\{ \begin{array} {l} 4x+2y=4 \\ 6x−y=8 \end{array } \справа.\)
- Ответ
Нам нужно решить одно уравнение для одной переменной. Решим первое уравнение для y .
The ordered pair is 5 by 4, minus 1 by 2. Check the ordered pair in both equations. Both hold true. Hence, that is the solution.»> Решите первое уравнение для y .
Подставьте \(−2x+2\) вместо y во втором уравнении. Замените y на \(−2x+2\). Решите уравнение для x . Подставьте \(x=54\) в \(4x+2y=4\), чтобы найти y .
Упорядоченная пара равна \((54,−12)\). Проверьте упорядоченную пару в обоих уравнениях. Решение: \((54,−12)\).
Пример \(\PageIndex{23}\)
Решите систему подстановкой: \( \left\{ \begin{array} {l} x−4y=−4 \\ −3x+4y=0 \end{ массив} \справа.\)
- Ответ
\((2,32)\)
Пример \(\PageIndex{24}\)
Решите систему подстановкой: \( \left\{ \begin{array} {l} 4x−y=0 \\ 2x−3y=5 \end{array } \справа.\)
- Ответ
\((−12,−2)\)
Решение системы уравнений методом исключения
Мы решали системы линейных уравнений путем построения графиков и замены. Графики хорошо работают, когда переменные коэффициенты малы, а решение имеет целые значения. Подстановка работает хорошо, когда мы можем легко решить одно уравнение для одной из переменных и не иметь слишком много дробей в результирующем выражении.
Графики хорошо работают, когда переменные коэффициенты малы, а решение имеет целые значения. Подстановка работает хорошо, когда мы можем легко решить одно уравнение для одной из переменных и не иметь слишком много дробей в результирующем выражении.
Третий метод решения систем линейных уравнений называется методом исключения. Когда мы решали систему подстановкой, мы начинали с двух уравнений и двух переменных и сводили ее к одному уравнению с одной переменной. То же самое мы сделаем и с методом исключения, но у нас будет другой способ добраться туда.
Метод исключения основан на свойстве сложения равенства. Свойство сложения равенства говорит о том, что, когда вы добавляете одно и то же количество к обеим частям уравнения, вы все равно получаете равенство. Мы расширим свойство равенства сложения, чтобы сказать, что когда вы добавляете равные количества к обеим частям уравнения, результаты равны.
Для любых выражений a, b, c, и d .
\[\begin{array} {ll} {\text{if}} &{a=b} \\ {\text{and}} &{c=d} \\ {\text{then}} & {a+c=b+d.} \\ \nonumber \end{массив}\]
Чтобы решить систему уравнений методом исключения, мы начинаем с обоих уравнений в стандартной форме. Затем мы решаем, какую переменную будет проще всего исключить. Как мы решаем? Мы хотим, чтобы коэффициенты одной переменной были противоположными, чтобы мы могли сложить уравнения и исключить эту переменную.
Обратите внимание, как это работает, когда мы складываем эти два уравнения вместе:
\[\left\{ \begin{array} {l} 3x+y=5 \\ \underline{2x−y=0} \end{array } \Правильно. \номер\]
\[5x=5 \nonumber\]
y прибавляются к нулю, и мы получаем одно уравнение с одной переменной.
Попробуем еще:
\[ \left\{ \begin{array} x+4y=2 \\ 2x+5y=−2 \end{array} \right. \nonumber\]
На этот раз мы не видим переменную, которую можно сразу исключить, если добавить уравнения.
Но если мы умножим первое уравнение на \(−2\), мы сделаем коэффициенты x противоположными. Мы должны умножить каждый член в обеих частях уравнения на \(−2\).
Мы должны умножить каждый член в обеих частях уравнения на \(−2\).
Тогда перепишите систему уравнений.
Теперь мы видим, что коэффициенты членов x являются противоположными, поэтому x будут исключены, когда мы сложим эти два уравнения.
Получив уравнение только с одной переменной, мы решаем его. Затем мы подставляем это значение в одно из исходных уравнений, чтобы найти оставшуюся переменную. И, как всегда, мы проверяем наш ответ, чтобы убедиться, что он является решением обоих исходных уравнений.
Теперь мы посмотрим, как использовать исключение для решения той же системы уравнений, которую мы решали с помощью графика и подстановки.
Упражнение \(\PageIndex{25}\): Как решить систему уравнений методом исключения
Решить систему методом исключения: \(\left\{ \begin{array} {l} 2x+y=7 \ \ x−2y=6 \end{массив} \right. \)
- Ответ
Упражнение \(\PageIndex{26}\)
Решите систему методом исключения: \(\left\{ \begin{array} {l} 3x+y=5 \\ 2x−3y=7 \end{array } \право. \)
\)
- Ответить
\((2,−1)\)
Упражнение \(\PageIndex{27}\)
Решите систему методом исключения: \(\left\{ \begin{array} {l} 4x+y=−5 \\ −2x−2y=−2 \ end{массив} \right.\)
- Ответ
\((−2,3)\)
Шаги перечислены здесь для удобства.
РЕШИТЬ СИСТЕМУ УРАВНЕНИЙ ИСКЛЮЧЕНИЕМ.
- Запишите оба уравнения в стандартной форме. Если какие-либо коэффициенты являются дробями, очистите их.
- Сделайте коэффициенты одной переменной противоположными.
- Решите, какую переменную вы удалите.
- Умножьте одно или оба уравнения так, чтобы коэффициенты этой переменной были противоположны.
- Добавьте уравнения, полученные на шаге 2, чтобы исключить одну переменную.
- Найдите оставшуюся переменную.
- Подставьте решение шага 4 в одно из исходных уравнений.
 Затем найдите другую переменную.
Затем найдите другую переменную. - Запишите решение в виде упорядоченной пары.
- Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
Теперь сделаем пример, где нам нужно умножить оба уравнения на константы, чтобы сделать коэффициенты одной переменной противоположными.
Упражнение \(\PageIndex{28}\)
Решите систему методом исключения: \(\left\{ \begin{array} {l} 4x−3y=9 \\ 7x+2y=−6 \end{ массив} \справа.\)
- Ответ
В этом примере мы не можем умножить только одно уравнение на любую константу, чтобы получить противоположные коэффициенты. Поэтому мы стратегически умножим оба уравнения на разные константы, чтобы получить противоположные значения.
We get 2 open parentheses 4x minus 3y close parentheses equals 2 times 9 and 3 open parentheses 7x plus 2y close parentheses equals 3 times minus 6. Simplifying both, we get 8x minus 6y equals 18 and 21x plus 6y equals minus 18. Adding the two equations to eliminate y, and solving for x, we get x equal to 0. Substituting this into one of the original equations and solving for y, we get y equal to minus 3. The ordered pair of the solution is 0, minus 3. Check that the ordered pair is a solution to both original equations.»> Оба уравнения имеют стандартную форму.
Чтобы получить противоположные коэффициенты y , мы умножим
первое уравнение на 2 и
второе уравнение на 3. Упрощение.
Добавьте два уравнения, чтобы исключить y . Решить для x . Подставьте x=0x=0 в одно из исходных уравнений. Решить на г . Запишите решение в виде упорядоченной пары. Упорядоченная пара равна \((0,−3)\).
Убедитесь, что упорядоченная пара является решением
обоих исходных уравнений. Решение: \((0,−3)\).
Упражнение \(\PageIndex{29}\)
Решите систему методом исключения: \(\left\{ \begin{array} {l} 3x−4y=−9 \\ 5x+3y=14\end{ массив} \справа.\)
- Ответ
\((1,3)\)
Упражнение \(\PageIndex{30}\)
Решите каждую систему методом исключения: \(\left\{ \begin{array} {l} 7x+8y=4 \\ 3x−5y=27 \end{array } \право.\)
- Ответ
\((4,−3)\)
Когда система уравнений содержит дроби, мы сначала очистим дроби, умножив каждое уравнение на ЖК-дисплей всех дробей в уравнении.
Упражнение \(\PageIndex{31}\)
Решите систему методом исключения: \(\left\{ \begin{array} {l} x+\tfrac{1}{2}y=6 \\ \tfrac {3}{2}x+\tfrac{2}{3}y=\tfrac{17}{2} \end{массив} \right.\)
- Ответ
В этом примере оба уравнения содержат дроби. Нашим первым шагом будет умножение каждого уравнения на ЖК-дисплей всех дробей в уравнении, чтобы очистить дроби.
The ordered pair is 3, 6. It is a solution to both original equations.»> Чтобы очистить дроби, умножьте каждое уравнение
на его ЖК-дисплей. Упрощение. Теперь мы готовы исключить одну из
переменных. Обратите внимание, что оба уравнения имеют стандартную форму
. Мы можем исключить y, умножив первое уравнение на \(−4\). Упростить и добавить.
Подставьте \(x=3\) в одно из исходных уравнений.
Решите для y.
Запишите решение в виде упорядоченной пары. Упорядоченная пара: \((3,6)\). Убедитесь, что упорядоченная пара является решением
обоих исходных уравнений. Решение: \((3,6)\).
Упражнение \(\PageIndex{32}\)
Решите каждую систему методом исключения: \(\left\{ \begin{array} {l} \tfrac{1}{3}x−\tfrac{1}{ 2}y=1 \\ \tfrac{3}{4}x−y=\tfrac{5}{2} \end{массив} \right. \)
\)
- Ответить
\((6,2)\)
Упражнение \(\PageIndex{33}\)
Решите каждую систему методом исключения: \(\left\{ \begin{array} {l} x+\tfrac{3}{5}y=−\tfrac{1 {5} \\ −\tfrac{1}{2}x−\tfrac{2}{3}y=\tfrac{5}{6} \end{массив} \right.\)
- Ответ
\((1,−2)\)
Когда мы решили систему с помощью графика, мы увидели, что не все системы линейных уравнений имеют в качестве решения одну упорядоченную пару. Когда два уравнения действительно представляли собой одну прямую, решений было бесконечно много. Мы назвали это последовательной системой. Когда два уравнения описывали параллельные прямые, решения не было. Мы назвали это непоследовательной системой.
То же самое верно для замены или исключения. Если уравнение в конце подстановки или исключения является верным утверждением, мы имеем непротиворечивую, но зависимую систему, а система уравнений имеет бесконечно много решений. Если уравнение в конце подстановки или исключения является ложным утверждением, мы имеем противоречивую систему, и система уравнений не имеет решения.
Если уравнение в конце подстановки или исключения является ложным утверждением, мы имеем противоречивую систему, и система уравнений не имеет решения.
Упражнение \(\PageIndex{34}\)
Решите систему методом исключения: \(\left\{ \begin{array} {l} 3x+4y=12 \\ y=3−\tfrac{3} {4}x \end{массив} \right. \)
- Ответить
\(\begin{array} {ll} {} &{ \left\{ \begin{array} {l} 3x+4y=12 \\ y=3−\frac{3}{4}x \end{ array} \right.} \\ {} &{} \\ {\text{Запишите второе уравнение в стандартной форме.}} &{\left\{ \begin{array} {l} 3x+4y=12 \\ \frac{3}{4}x+y=3 \end{array} \right.} \\ {} &{} \\ {\text{Очистить дроби, умножив } \\ \text{второе уравнение на 4.}} &{\left\{ \begin{array} {l} 3x+4y=12 \\ 4(\frac{3}{4}x+y)=4(3) \end{array} \ справа. } \\ {} &{} \\ {\text{Упрощение}} &{\left\{ \begin{array} {l} 3x+4y=12 \\ 3x+4y=12 \end{array } \right.} \\ {} &{} \\ {\text{Чтобы исключить переменную, мы умножаем} \\ \text{второе уравнение на −1. Упрощаем и складываем.}} &{\begin{массив } {l} {\left\{ \begin{array} {l} 3x+4y=12 \\ \underline{-3x-4y=-12 } \end{array} \right.} \\ {\hspace{ 16 мм} 0=0} \end{массив}} \\ \end{массив} \)
Упрощаем и складываем.}} &{\begin{массив } {l} {\left\{ \begin{array} {l} 3x+4y=12 \\ \underline{-3x-4y=-12 } \end{array} \right.} \\ {\hspace{ 16 мм} 0=0} \end{массив}} \\ \end{массив} \)
Это верное утверждение. Уравнения непротиворечивы, но зависимы. Их графики были бы одной линией. Система имеет бесконечно много решений.
После того, как мы очистили дроби во втором уравнении, вы заметили, что два уравнения были одинаковыми? Это означает, что у нас есть совпадающие линии.
Упражнение \(\PageIndex{35}\)
Решите систему методом исключения: \(\left\{ \begin{array} {l} 5x−3y=15 \\ 5y=−5+\tfrac{5 {3}x \end{массив} \right. \)
- Ответить
бесконечно много решений
Упражнение \(\PageIndex{36}\)
Решите систему методом исключения: \(\left\{ \begin{array} {l} x+2y=6 \\ y=-\tfrac{1}{ 2}x+3\end{массив} \right. \)
- Ответ
бесконечно много решений
Выберите наиболее удобный метод решения системы линейных уравнений
Когда вы решаете систему линейных уравнений в приложении, вам не сообщают, какой метод использовать. Вам нужно будет принять это решение самостоятельно. Таким образом, вы захотите выбрать метод, который проще всего сделать и сводит к минимуму вероятность ошибок.
Вам нужно будет принять это решение самостоятельно. Таким образом, вы захотите выбрать метод, который проще всего сделать и сводит к минимуму вероятность ошибок.
\[ \textbf{Выберите наиболее удобный метод решения системы линейных уравнений} \\ \begin{array} {lll} {\underline{\textbf{График}}} &{\underline{\textbf{Подстановка }}} &{\underline{\textbf{Исключение}}} \\ {\text{Используйте, когда вам нужно}} &{\text{Используйте, когда одно уравнение}} &{\text{Используйте, когда уравнения }} \\ {\text{картина ситуации.}} &{\text{уже решена или может быть}} &{\text{соответствует стандартной форме.}} \\ {\text{}} &{\text {легко решается за один}} &{\text{}} \\ {\text{}} &{\text{переменная.}} &{\text{}} \\ \end{массив} \nonumber \]
Пример \(\PageIndex{37}\)
Для каждой системы линейных уравнений решите, как удобнее решать ее подстановкой или исключением. Поясните свой ответ.
ⓐ \(\left\{ \begin{array} {l} 3x+8y=40 \\ 7x−4y=-32 \end{array} \right.\) ⓑ \(\left\{ \begin{ array} {l} 5x+6y=12 \\ y=\tfrac{2}{3}x−1 \end{array} \right. \)
\)
- Ответ
ⓐ
\[\left\{ \begin{array} {l} 3x+8y=40 \\ 7x−4y=-32 \end{array} \right.\nonumber\]
Поскольку оба уравнения имеют стандартную форму, наиболее удобным будет использование метода исключения.
ⓑ
\[\left\{ \begin{array} {l} 5x+6y=12 \\ y=\tfrac{2}{3}x−1 \end{array} \right.\nonumber \]
Поскольку одно уравнение уже решено для y , наиболее удобным будет использование подстановки.
Пример \(\PageIndex{38}\)
Для каждой системы линейных уравнений решить, будет ли удобнее решать ее подстановкой или исключением. Поясните свой ответ.
ⓐ \(\left\{ \begin{array} {l} 4x−5y=−32 \\ 3x+2y=−1 \end{array} \right.\) ⓑ \(\left\{ \begin {массив} {l} x=2y−1 \\ 3x−5y=−7 \end{массив} \right.\)
- Ответ
ⓐ Поскольку оба уравнения имеют стандартную форму, наиболее удобным будет использование метода исключения. ⓑ Так как одно уравнение уже решено для x , наиболее удобным будет использование подстановки.
ⓑ Так как одно уравнение уже решено для x , наиболее удобным будет использование подстановки.
Пример \(\PageIndex{39}\)
Для каждой системы линейных уравнений решите, как удобнее решать ее подстановкой или исключением. Поясните свой ответ.
ⓐ \(\left\{ \begin{array} {l} y=2x−1 \\ 3x−4y=−6 \end{array} \right.\) ⓑ \(\left\{ \begin{ массив} {l} 6x−2y=12 \\ 3x+7y=−13 \end{массив} \right.\)
- Ответ
ⓐ Поскольку одно уравнение уже решено для y , наиболее удобным будет использование подстановки. ⓑ Так как оба уравнения имеют стандартную форму, наиболее удобным будет использование метода исключения.
Ключевые понятия
- Как решить систему линейных уравнений с помощью графика.
- Нарисуйте первое уравнение.
- Нарисуйте график второго уравнения в той же прямоугольной системе координат.

- Определите, пересекаются ли линии, параллельны или являются одной и той же линией.
- Определите решение системы.
Если линии пересекаются, определите точку пересечения. Это решение системы.
Если прямые параллельны, система не имеет решения.
Если линии одинаковые, система имеет бесконечное число решений. - Проверьте решение обоих уравнений.
- Как решить систему уравнений подстановкой.
- Решите одно из уравнений для любой переменной.
- Подставьте выражение из шага 1 в другое уравнение.
- Решите полученное уравнение.
- Подставьте решение шага 3 в одно из исходных уравнений, чтобы найти другую переменную.
- Запишите решение в виде упорядоченной пары.
- Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
- Как решить систему уравнений методом исключения.

- Запишите оба уравнения в стандартной форме. Если какие-либо коэффициенты являются дробями, очистите их.
- Сделайте коэффициенты одной переменной противоположными.
Решите, какую переменную вы удалите.
Умножьте одно или оба уравнения так, чтобы коэффициенты этой переменной были противоположны. - Добавьте уравнения, полученные на шаге 2, чтобы исключить одну переменную.
- Найдите оставшуюся переменную.
- Подставьте решение шага 4 в одно из исходных уравнений. Затем найдите другую переменную.
- Запишите решение в виде упорядоченной пары.
- Убедитесь, что упорядоченная пара является решением обоих исходных уравнений. \[ \textbf{Выберите наиболее удобный метод решения системы линейных уравнений} \\ \begin{array} {lll} {\underline{\textbf{График}}} &{\underline{\textbf{Подстановка}} } &{\underline{\textbf{Исключение}}} \\ {\text{}} &{\text{Используйте, когда одно уравнение}} &{\text{}} \\ {\text{Используйте, когда вам нужно a}} &{\text{уже решено или может быть}} &{\text{Используйте, когда уравнения a}} \\ {\text{картина ситуации.
 }} &{\text{легко решается за один} } &{\text{соответствует стандартной форме.}} \\ {\text{}} &{\text{переменная.}} &{\text{}} \\ \end{массив} \nonumber \]
}} &{\text{легко решается за один} } &{\text{соответствует стандартной форме.}} \\ {\text{}} &{\text{переменная.}} &{\text{}} \\ \end{массив} \nonumber \]
Глоссарий
- совпадающие строки
- Совпадающие линии имеют одинаковый наклон и одинаковую точку пересечения и .
- непротиворечивые и непротиворечивые системы
- Непротиворечивая система уравнений – это система уравнений, имеющая хотя бы одно решение; несовместная система уравнений – это система уравнений, не имеющая решения.
- решения системы уравнений
- Решениями системы уравнений являются значения переменных, которые делают все уравнений истинными; решение представлено упорядоченной парой (x,y).(x,y).
- система линейных уравнений
- Когда два или более линейных уравнения группируются вместе, они образуют систему линейных уравнений.

- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Показать страницу Содержание
- да
- Включено
- да
- Теги
- источник[1]-math-5138
Системы линейных уравнений: две переменные
Результаты обучения
- Решайте системы уравнений с помощью графиков, подстановок и сложений.

- Найдите несовместимые системы уравнений, содержащие две переменные.
- Выразите решение системы зависимых уравнений с двумя переменными, используя стандартные обозначения.
Производитель скейтбордов представляет новую линейку досок. Производитель отслеживает свои затраты, которые представляют собой сумму, которую он тратит на производство плат, и свой доход, который представляет собой сумму, которую он зарабатывает на продаже своих плат. Как компания может определить, получает ли она прибыль от своей новой линии? Сколько скейтбордов нужно произвести и продать, чтобы можно было получить прибыль? В этом разделе мы рассмотрим линейные уравнения с двумя переменными, чтобы ответить на эти и подобные вопросы.
(кредит: Томас Сёренес)
Введение в системные решения
Чтобы исследовать такие ситуации, как ситуация с производителем скейтбордов, нам нужно признать, что мы имеем дело с более чем одной переменной и, вероятно, с более чем одним уравнением. Система линейных уравнений состоит из двух или более линейных уравнений, составленных из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти числовое значение для каждой переменной в системе, которое будет удовлетворять всем уравнениям в системе одновременно. Некоторые линейные системы могут не иметь решения, а другие могут иметь бесконечное число решений. Чтобы линейная система имела единственное решение, в ней должно быть не меньше уравнений, чем переменных. Тем не менее, это не гарантирует уникальности решения.
Система линейных уравнений состоит из двух или более линейных уравнений, составленных из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти числовое значение для каждой переменной в системе, которое будет удовлетворять всем уравнениям в системе одновременно. Некоторые линейные системы могут не иметь решения, а другие могут иметь бесконечное число решений. Чтобы линейная система имела единственное решение, в ней должно быть не меньше уравнений, чем переменных. Тем не менее, это не гарантирует уникальности решения.
В этом разделе мы рассмотрим системы линейных уравнений с двумя переменными, которые состоят из двух уравнений, содержащих две разные переменные. Например, рассмотрим следующую систему линейных уравнений с двумя переменными.
[латекс]\begin{align}2x+y&=15\\[1mm] 3x-y&=5\end{align}[/latex]
Решение системы линейных уравнений с двумя переменными: любая упорядоченная пара, удовлетворяющая каждому уравнению независимо. В этом примере упорядоченная пара [латекс](4,7)[/латекс] является решением системы линейных уравнений. Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям. Вскоре мы исследуем методы нахождения такого решения, если оно существует.
В этом примере упорядоченная пара [латекс](4,7)[/латекс] является решением системы линейных уравнений. Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям. Вскоре мы исследуем методы нахождения такого решения, если оно существует.
[латекс]\begin{align}2\left(4\right)+\left(7\right)&=15 &&\text{True} \\[1mm] 3\left(4\right)-\ left(7\right)&=5 &&\text{True} \end{align}[/latex]
Помимо учета количества уравнений и переменных, мы можем классифицировать системы линейных уравнений по количеству решений. непротиворечивая система уравнений имеет хотя бы одно решение. Непротиворечивая система считается независимой системой , если она имеет единственное решение, как в примере, который мы только что рассмотрели. Две линии имеют разные наклоны и пересекаются в одной точке плоскости. Непротиворечивая система считается зависимая система , если уравнения имеют одинаковый наклон и одинаковые и -перехваты. Другими словами, прямые совпадают, поэтому уравнения представляют одну и ту же прямую. Каждая точка на прямой представляет собой пару координат, удовлетворяющую системе. Таким образом, существует бесконечное множество решений.
Другими словами, прямые совпадают, поэтому уравнения представляют одну и ту же прямую. Каждая точка на прямой представляет собой пару координат, удовлетворяющую системе. Таким образом, существует бесконечное множество решений.
Другим типом системы линейных уравнений является противоречивая система , в которой уравнения представляют две параллельные линии. Линии имеют одинаковый наклон и разные г- перехватов. Нет общих точек для обеих прямых; следовательно, система не имеет решения.
A Общее примечание: Типы линейных систем
Существует три типа систем линейных уравнений с двумя переменными и три типа решений.
- Независимая система имеет ровно одну пару решений [латекс]\лево(х,у\право)[/латекс]. Точка пересечения двух прямых является единственным решением.
- противоречивая система не имеет решения. Обратите внимание, что две линии параллельны и никогда не пересекаются.
- зависимая система имеет бесконечно много решений.
 Линии совпадают. Это одна и та же линия, поэтому каждая пара координат на линии является решением обоих уравнений.
Линии совпадают. Это одна и та же линия, поэтому каждая пара координат на линии является решением обоих уравнений.
Ниже приведено сравнение графических представлений каждого типа системы.
Как: Имея систему линейных уравнений и упорядоченную пару, определить, является ли упорядоченная пара решением.
- Подставьте упорядоченную пару в каждое уравнение в системе.
- Определить, верны ли утверждения в результате замены в обоих уравнениях; если да, то упорядоченная пара является решением.
Пример: Определение того, является ли упорядоченная пара решением системы уравнений
Определить, является ли упорядоченная пара [латекс]\лево(5,1\право)[/латекс] решением данной системы уравнений.
[латекс]\begin{align}x+3y&=8\\ 2x-9&=y \end{align}[/latex]
Показать решение
Попробуйте
Определите, является ли упорядоченная пара [латекс]\левый(8,5\правый)[/латекс] решением следующей системы.
[латекс]\begin{align}5x-4y&=20\\ 2x+1&=3y\end{align}[/latex]
Показать решение
Решение систем уравнений с помощью графика
Существует несколько методов решения систем линейных уравнений. Для системы линейных уравнений с двумя переменными мы можем определить как тип системы, так и решение, построив график системы уравнений на одном и том же наборе осей.
Пример. Решение системы уравнений с двумя переменными с помощью графика
Решите следующую систему уравнений с помощью графика. Определите тип системы.
[латекс]\begin{align}2x+y&=-8\\ x-y&=-1\end{align}[/latex]
Показать решение
Попробуйте
Решите следующую систему уравнений с помощью графика.
[латекс]\begin{gathered}2x — 5y=-25 \\ -4x+5y=35 \end{gathered}[/latex]
Показать решение
Вопросы и ответы
Можно ли использовать графику, если система непоследовательна или зависима?
Да, в обоих случаях мы все еще можем построить график системы, чтобы определить тип системы и решения. Если две прямые параллельны, то система не имеет решений и несовместна. Если две линии идентичны, система имеет бесконечные решения и является зависимой системой.
Если две прямые параллельны, то система не имеет решений и несовместна. Если две линии идентичны, система имеет бесконечные решения и является зависимой системой.
Попробуйте
Постройте график трех различных систем с помощью онлайн-графического инструмента. Классифицируйте каждое решение как последовательное или непоследовательное. Если система непротиворечива, определите, зависима она или независима. Возможно, вам будет проще построить каждую систему по отдельности, а затем очистить свои записи, прежде чем строить следующую.
1)
[латекс]5x-3y = -19[/латекс]
[латекс]x=2y-1[/латекс]
2)
[латекс]4x+y=11[/латекс]
[латекс ]-2y=-25+8x[/латекс]
3)
[латекс]у = -3х+6[/латекс]
[латекс]-\frac{1}{3}у+2=х[/ латекс]
Показать решение
Решение систем уравнений путем подстановки
Решение линейной системы с двумя переменными с помощью графика хорошо работает, когда решение состоит из целых значений, но если наше решение содержит десятичные дроби или дроби, это не самый точный метод. Рассмотрим еще два метода решения система линейных уравнений более точная, чем графическая. Одним из таких методов является решение системы уравнений методом подстановки , в котором мы решаем одно из уравнений для одной переменной, а затем подставляем результат во второе уравнение для решения для второй переменной. Напомним, что мы можем решать только для одной переменной за раз, поэтому метод подстановки ценен и практичен.
Рассмотрим еще два метода решения система линейных уравнений более точная, чем графическая. Одним из таких методов является решение системы уравнений методом подстановки , в котором мы решаем одно из уравнений для одной переменной, а затем подставляем результат во второе уравнение для решения для второй переменной. Напомним, что мы можем решать только для одной переменной за раз, поэтому метод подстановки ценен и практичен.
Как: Имея систему из двух уравнений с двумя переменными, решите ее методом подстановки.
- Решите одно из двух уравнений для одной из переменных относительно другой.
- Подставьте выражение для этой переменной во второе уравнение, затем найдите оставшуюся переменную.
- Подставьте это решение в любое из исходных уравнений, чтобы найти значение первой переменной. Если возможно, запишите решение в виде упорядоченной пары.
- Проверьте решение обоих уравнений.
Пример.
 Решение системы уравнений с двумя переменными путем замены
Решение системы уравнений с двумя переменными путем замены Решите следующую систему уравнений путем замены.
[латекс]\begin{align}-x+y&=-5 \\ 2x-5y&=1 \end{align}[/latex]
Показать решение
Попробуйте
Решите следующую систему уравнений методом замены.
[латекс]\begin{align}x&=y+3 \\ 4&=3x — 2y \end{align}[/latex]
Показать решение
Вопросы и ответы
Можно ли использовать метод подстановки для решения любой линейной системы с двумя переменными?
Да, но метод работает лучше всего, если одно из уравнений содержит коэффициент 1 или –1, чтобы нам не приходилось иметь дело с дробями.
Следующее видео длится около 10 минут и представляет собой мини-урок по использованию метода подстановки для решения системы линейных уравнений. Мы представляем три разных примера, а также используем инструмент построения графиков, чтобы обобщить решение для каждого примера.
Решение систем уравнений с двумя переменными методом сложения
Третий метод решения систем линейных уравнений — это метод сложения, этот метод также называется методом исключения . В этом методе мы добавляем два слагаемых с одной и той же переменной, но с противоположными коэффициентами, так что сумма равна нулю. Конечно, не во всех системах два члена одной переменной имеют противоположные коэффициенты. Часто нам приходится корректировать одно или оба уравнения путем умножения, чтобы исключить одну переменную путем сложения.
Как: Имея систему уравнений, решить ее методом сложения.
- Напишите оба уравнения с x – и y – переменными слева от знака равенства и константами справа.

- Напишите одно уравнение над другим, выстраивая соответствующие переменные. Если одна из переменных в верхнем уравнении имеет противоположный коэффициент той же переменной в нижнем уравнении, сложите уравнения вместе, исключив одну переменную. Если нет, используйте умножение на ненулевое число, чтобы одна из переменных в верхнем уравнении имела коэффициент, противоположный той же переменной в нижнем уравнении, затем добавьте уравнения, чтобы исключить переменную.
- Решите полученное уравнение для оставшейся переменной.
- Подставьте это значение в одно из исходных уравнений и найдите вторую переменную.
- Проверьте решение, подставив значения в другое уравнение.
Пример: Решение системы методом сложения
Решите данную систему уравнений методом сложения.
[латекс]\begin{align}x+2y&=-1 \\ -x+y&=3 \end{align}[/latex]
Показать решение
Попробуйте IT
Пример: Использование метода сложения при необходимости умножения одного уравнения
Решите данную систему уравнений методом сложения .
[латекс]\begin{align}3x+5y&=-11 \\ x — 2y&=11 \end{align}[/latex]
Показать решение
Попробуйте
Решите систему уравнений сложением.
[латекс]\begin{align}2x — 7y&=2\\ 3x+y&=-20\end{align}[/latex]
Показать решение
Пример: Использование метода сложения, когда требуется умножение обоих уравнений
Решите данную систему уравнений с двумя переменными методом сложения.
[латекс]\begin{align}2x+3y&=-16 \\ 5x — 10y&=30\end{align}[/latex]
Показать решение
Пример: Использование метода сложения в системах уравнений, содержащих дроби
Решите данную систему уравнений с двумя переменными методом сложения.
[латекс]\begin{align}\frac{x}{3}+\frac{y}{6}&=3 \\[1 мм] \frac{x}{2}-\frac{y}{ 4}&=1 \end{выравнивание}[/latex]
Показать решение
Попробуйте
Решите систему уравнений сложением.
[латекс]\begin{align}2x+3y&=8\\ 3x+5y&=10\end{align}[/latex]
Показать решение
в следующем видео мы представляем больше примеров того, как использовать метод сложения (исключения) для решения системы двух линейных уравнений.
Классификация решений систем
Теперь, когда у нас есть несколько методов решения систем уравнений, мы можем использовать эти методы для выявления несогласованных систем. Напомним, что несогласованная система состоит из параллельных прямых, имеющих одинаковый наклон, но разные [латекс]у[/латекс] -перехваты. Они никогда не пересекутся. При поиске решения для несогласованной системы мы придем к ложному утверждению, например [латекс]12=0[/латекс].
Пример. Решение противоречивой системы уравнений
Решите следующую систему уравнений.
[латекс]\begin{gathered}&x=9 — 2y \\ &x+2y=13 \end{gathered}[/latex]
Показать решение
Попробуйте
Решите следующую систему уравнений с двумя переменными.
[латекс]\начало{собрано}2y — 2x=2\\ 2y — 2x=6\конец{собрано}[/латекс]
Показать решение
Выражение решения системы зависимых уравнений с двумя переменными
Напомним, что зависимая система уравнений с двумя переменными — это система, в которой два уравнения представляют одну и ту же прямую. Зависимые системы имеют бесконечное число решений, потому что все точки на одной прямой находятся также и на другой прямой. После использования подстановки или сложения результирующее уравнение будет тождеством, например [латекс]0=0[/латекс].
Пример: поиск решения зависимой системы линейных уравнений
Найдите решение системы уравнений методом сложения .
[латекс]\начало{собрано}x+3y=2\\ 3x+9y=6\конец{собрано}[/латекс]
Показать решение
Написание общего решения
В предыдущем примере мы представили анализ решения следующей системы уравнений:
[латекс]\начало{собрано}x+3y=2\\ 3x+9y=6\ конец {собрано}[/латекс]
После недолгих вычислений мы обнаружили, что эти два уравнения совершенно одинаковы. Затем мы записали общее решение как [латекс]\влево(х, -\фракция{1}{3}х+\фракция{2}{3}\право)[/латекс]. Почему мы должны писать решение таким образом? В некотором смысле это представление говорит нам о многом. Он говорит нам, что x может быть чем угодно, x — это x . Это также говорит нам, что y будет зависеть от x , точно так же, как когда мы пишем функциональное правило. В этом случае, в зависимости от того, что вы положили на x , y будет определено через x как [латекс]-\frac{1}{3}x+\frac{2}{3}[/latex].
Затем мы записали общее решение как [латекс]\влево(х, -\фракция{1}{3}х+\фракция{2}{3}\право)[/латекс]. Почему мы должны писать решение таким образом? В некотором смысле это представление говорит нам о многом. Он говорит нам, что x может быть чем угодно, x — это x . Это также говорит нам, что y будет зависеть от x , точно так же, как когда мы пишем функциональное правило. В этом случае, в зависимости от того, что вы положили на x , y будет определено через x как [латекс]-\frac{1}{3}x+\frac{2}{3}[/latex].
Другими словами, существует бесконечно много ( x , y ) пар, удовлетворяющих этой системе уравнений, и все они попадают на прямую [latex]f(x)-\frac{1}{3 }x+\frac{2}{3}[/latex].
Попробуйте
Решите следующую систему уравнений с двумя переменными.
[латекс]\begin{собран}y — 2x=5 \\ -3y+6x=-15 \end{собран}[/latex]
Показать решение
Использование систем уравнений для исследования прибыли Используя то, что мы узнали о системах уравнений, мы можем вернуться к проблеме производства скейтбордов в начале раздела. Функция дохода производителя скейтбордов — это функция, используемая для расчета суммы денег, поступающей в бизнес. Его можно представить уравнением [латекс]R=xp[/латекс], где [латекс]х=[/латекс] количество и [латекс]р=[/латекс] цена. Функция дохода показана оранжевым цветом на графике ниже.
Функция дохода производителя скейтбордов — это функция, используемая для расчета суммы денег, поступающей в бизнес. Его можно представить уравнением [латекс]R=xp[/латекс], где [латекс]х=[/латекс] количество и [латекс]р=[/латекс] цена. Функция дохода показана оранжевым цветом на графике ниже.
Функция затрат — это функция, используемая для расчета затрат на ведение бизнеса. Он включает постоянные затраты, такие как арендная плата и заработная плата, и переменные затраты, такие как коммунальные услуги. Функция стоимости показана синим цветом на графике ниже. Ось x представляет количество в сотнях единиц. Ось y представляет либо стоимость, либо доход в сотнях долларов.
Точка, в которой пересекаются две линии, называется точкой безубыточности . Из графика видно, что при производстве 700 единиц стоимость составляет 3300 долларов, а выручка также составляет 3300 долларов. Другими словами, компания безубыточна, даже если она произведет и продаст 700 единиц. Они не зарабатывают и не теряют деньги.
Они не зарабатывают и не теряют деньги.
Заштрихованная область справа от точки безубыточности представляет объемы, при которых компания получает прибыль. Заштрихованная область слева представляет объемы, по которым компания несет убытки. Функция прибыли представляет собой функцию дохода минус функция затрат, записанную как [латекс]Р\влево(х\вправо)=R\влево(х\вправо)-С\влево(х\вправо)[/латекс]. Очевидно, что знание количества, при котором затраты равны выручке, имеет большое значение для бизнеса.
Пример: нахождение точки безубыточности и функции прибыли с помощью подстановки
Учитывая функцию затрат [латекс]C\влево(х\вправо)=0,85x+35{,}000[/латекс] и функцию дохода [латекс]R\влево(х\вправо)=1,55x[/ латекс], найти точку безубыточности и функцию прибыли.
Показать решение
Написание системы линейных уравнений с учетом ситуации
Редко можно получить уравнения, которые точно моделируют поведение, с которым вы сталкиваетесь в бизнесе, скорее, вы столкнетесь с ситуацией, для которой вам известна ключевая информация, как в примере выше. Ниже мы суммируем три ключевых фактора, которые помогут вам преобразовать ситуацию в систему.
Ниже мы суммируем три ключевых фактора, которые помогут вам преобразовать ситуацию в систему.
Как сделать: Дана ситуация, представляющая систему линейных уравнений, напишите систему уравнений и найдите решение.
- Определите вход и выход каждой линейной модели.
- Определите наклон и y — точку пересечения каждой линейной модели.
- Найдите решение, установив две линейные функции равными другой и найдя x , или найдите точку пересечения на графике.
Теперь давайте попрактикуемся в применении этих ключевых факторов. В следующем примере мы определяем, сколько различных типов билетов продано, учитывая информацию об общем доходе и количестве билетов, проданных на мероприятие.
Пример: Написание и решение системы уравнений с двумя переменными
Стоимость билета в цирк составляет 25 долларов США для детей и 50 долларов США для взрослых. В определенный день посещаемость цирка составляет 2000 человек, а общий доход от продажи билетов составляет 70 000 долларов. Сколько детей и сколько взрослых купили билеты?
Сколько детей и сколько взрослых купили билеты?
Показать решение
Попробуйте
Билеты в цирк стоят 4 доллара для детей и 12 долларов для взрослых. Если было куплено 1650 талонов на питание на общую сумму 14 200 долларов, сколько детей и сколько взрослых купили талоны на питание?
Показать решение
Иногда решение может принимать система уравнений. В нашем следующем примере мы помогаем ответить на вопрос: «Какая компания по аренде грузовиков даст наибольшую ценность?»
Пример: построение системы линейных моделей для выбора компании по аренде грузовиков
Джамал выбирает между двумя компаниями по аренде грузовиков. Первый, Keep on Trucking, Inc., взимает авансовый платеж в размере 20 долларов, а затем 59 центов за милю. Второй, Move It Your Way, взимает авансовый платеж в размере 16 долларов, а затем 63 цента за милю. [1] Когда компания Keep on Trucking, Inc. станет лучшим выбором для Джамала?
станет лучшим выбором для Джамала?
Показать решение
Применение систем кажется почти бесконечным, но мы покажем еще одно. В следующем примере мы определяем количество 80% раствора метана, которое нужно добавить к 50% раствору, чтобы получить окончательный раствор 60%.
Пример. Решение задачи о химической смеси
У химика есть 70 мл 50%-го раствора метана. Какое количество 80%-ного раствора она должна добавить, чтобы конечный раствор состоял из 60%-ного метана?
Показать решение
Try IT
Основные понятия
- Система линейных уравнений состоит из двух или более уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно.
- Решением системы линейных уравнений с двумя переменными является любая упорядоченная пара, удовлетворяющая каждому уравнению независимо.
- Системы уравнений классифицируются как независимые с одним решением, зависимые с бесконечным числом решений и несовместные без решения.

- Одним из методов решения системы линейных уравнений с двумя переменными является построение графика. В этом методе мы наносим уравнения на один и тот же набор осей.
- Другой метод решения системы линейных уравнений — подстановка. В этом методе мы находим одну переменную в одном уравнении и подставляем результат во второе уравнение.
- Третий метод решения системы линейных уравнений — сложение, в котором мы можем исключить переменную, добавляя противоположные коэффициенты соответствующих переменных.
- Часто бывает необходимо умножить одно или оба уравнения на константу, чтобы облегчить исключение переменной при сложении двух уравнений.
- Любой метод решения системы уравнений приводит к ложному утверждению о несовместимых системах, поскольку они состоят из параллельных линий, которые никогда не пересекаются.
- Решение системы зависимых уравнений всегда будет верным, поскольку оба уравнения описывают одну и ту же прямую.
- Системы уравнений можно использовать для решения реальных задач, включающих более одной переменной, например связанных с доходом, затратами и прибылью.

Глоссарий
метод сложения алгебраический метод, используемый для решения систем линейных уравнений, в котором уравнения складываются таким образом, что исключается одна переменная, что позволяет решить полученное уравнение для оставшейся переменной; Затем подстановка используется для определения первой переменной
точки безубыточности точки, в которой функция затрат пересекает функцию дохода; где прибыль равна нулю
непротиворечивая система система, для которой существует единственное решение всех уравнений в системе, и она является независимой системой, или если существует бесконечное число решений, и это зависимая система
функция стоимости функция, используемая для расчета затраты на ведение бизнеса; обычно состоит из двух частей: постоянных затрат и переменных затрат
зависимая система система линейных уравнений, в которой два уравнения представляют одну и ту же прямую; существует бесконечное число решений зависимой системы
несовместная система система линейных уравнений, не имеющая общего решения, поскольку они представляют собой параллельные прямые, не имеющие общих точек и прямых
независимая система система линейных уравнений, имеющая ровно одно решение, пара [латекс]\слева (x,y\right)[/latex]
функция прибыли функция прибыли записывается как [latex]P\left(x\right)=R\left(x\right)-C\left(x\ справа)[/latex], доход минус стоимость
функция дохода функция, используемая для расчета дохода, просто записывается как [latex]R=xp[/latex], где [latex]x=[/latex] количество и [latex]p=[/latex] цена
замена метод алгебраический метод, используемый для решения систем линейных уравнений, в котором одно из двух уравнений решается для одной переменной, а затем подставляется во второе уравнение для решения второй переменной
система линейных уравнений набор из двух или несколько уравнений с двумя или более переменными, которые необходимо рассматривать одновременно.
 Пояснение:
Пояснение:
 Поскольку вес коробки плюс вес одного предмета составляет 6 фунтов, это можно представить уравнением
Поскольку вес коробки плюс вес одного предмета составляет 6 фунтов, это можно представить уравнением
 Хотя решить эту систему довольно легко, все же есть немало интересных концепций и идей, которые возникают, когда мы глубоко задумываемся о процессе. Эти концепции и идеи играют большую роль, когда мы позже рассмотрим более общие системы линейных уравнений.
Хотя решить эту систему довольно легко, все же есть немало интересных концепций и идей, которые возникают, когда мы глубоко задумываемся о процессе. Эти концепции и идеи играют большую роль, когда мы позже рассмотрим более общие системы линейных уравнений.
 \begin{выровнено}
\text{Уравнение 1: }x-2y &= 6 \\
\text{Уравнение 2: }3x+y &= 4.
\end{выровнено}
Уравнение 1: x−2yУравнение 2: 3x+y=6=4.
\begin{выровнено}
\text{Уравнение 1: }x-2y &= 6 \\
\text{Уравнение 2: }3x+y &= 4.
\end{выровнено}
Уравнение 1: x−2yУравнение 2: 3x+y=6=4. (2,-2).(2,−2).
(2,-2).(2,−2). \frac{a}{b}\neq \frac{c}{d} \ подразумевает ad-bc\neq 0.ba=dc⟹ad-bc =0.
\frac{a}{b}\neq \frac{c}{d} \ подразумевает ad-bc\neq 0.ba=dc⟹ad-bc =0. (Геометрически говоря, две «случайные» прямые почти всегда не будут параллельны и, следовательно, будут пересекаться ровно в одной точке.) Эта интуиция также будет сопровождать нас, когда мы будем исследовать более крупные системы уравнений.
(Геометрически говоря, две «случайные» прямые почти всегда не будут параллельны и, следовательно, будут пересекаться ровно в одной точке.) Эта интуиция также будет сопровождать нас, когда мы будем исследовать более крупные системы уравнений.

 Решите уравнение $latex -3x+5y=-6$ для x .
Решите уравнение $latex -3x+5y=-6$ для x .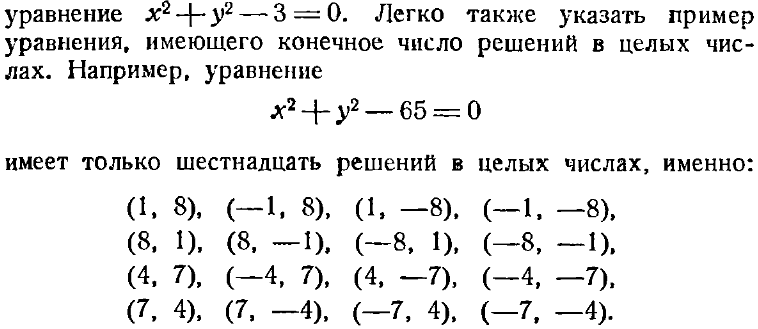 Решите уравнение $latex 3x+2 -4x+5)=3y+6$ для y .
Решите уравнение $latex 3x+2 -4x+5)=3y+6$ для y .

Главная / Алгебра / Системы уравнений / Линейные системы с двумя переменными
 е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
 Например, \(x = 1\) и \(y = — 4\) удовлетворяют первому уравнению, но не второму, и поэтому не являются решением системы. Точно так же \(x = — 1\) и \(y = 1\) будут удовлетворять второму уравнению, но не первому, и поэтому не могут быть решением системы.
Например, \(x = 1\) и \(y = — 4\) удовлетворяют первому уравнению, но не второму, и поэтому не являются решением системы. Точно так же \(x = — 1\) и \(y = 1\) будут удовлетворять второму уравнению, но не первому, и поэтому не могут быть решением системы.
 Это означает, что мы должны стараться избегать дробей, если это вообще возможно.
Это означает, что мы должны стараться избегать дробей, если это вообще возможно. Так будет проще, так что давайте.
Так будет проще, так что давайте.

 Работа здесь покажет различия между двумя методами, а также покажет, что любой метод можно использовать для получения решения системы.
Работа здесь покажет различия между двумя методами, а также покажет, что любой метод можно использовать для получения решения системы. Это дает \(x = \frac{1}{3}\), что в точности соответствует тому, что мы нашли в предыдущем примере. Обратите внимание, однако, что единственная часть, с которой нам приходилось иметь дело до этого момента, — это сам ответ, который отличается от метода подстановки.
Это дает \(x = \frac{1}{3}\), что в точности соответствует тому, что мы нашли в предыдущем примере. Обратите внимание, однако, что единственная часть, с которой нам приходилось иметь дело до этого момента, — это сам ответ, который отличается от метода подстановки.
 На этот раз мы будем использовать первое уравнение.
На этот раз мы будем использовать первое уравнение. Мы решим первое уравнение относительно \(x\) и подставим его во второе уравнение.
Мы решим первое уравнение относительно \(x\) и подставим его во второе уравнение.
 Однако в этом случае мы получили равенство, которое просто не соответствовало действительности. В этом случае мы имеем 0=0, и это истинное равенство, и в этом смысле в этом нет ничего плохого.
Однако в этом случае мы получили равенство, которое просто не соответствовало действительности. В этом случае мы имеем 0=0, и это истинное равенство, и в этом смысле в этом нет ничего плохого. Другими словами, существует бесконечное множество точек, удовлетворяющих этому набору уравнений.
Другими словами, существует бесконечное множество точек, удовлетворяющих этому набору уравнений. 9? 5\\ — 1 & = — 1 & \hspace{0.25in} 5 & = 5\end{align*}\]
9? 5\\ — 1 & = — 1 & \hspace{0.25in} 5 & = 5\end{align*}\]
- Последнее обновление
- Идентификатор страницы
- 30838

ⓐ Является ли \((6,0)\) решением? ⓑ Является ли \((−3,−2)\) решением?
Если вы пропустили эту проблему, просмотрите [ссылка] .
Если вы пропустили эту проблему, просмотрите [ссылка] .
Если вы пропустили эту проблему, просмотрите [ссылка] .


ⓐ
ⓑ
 \).
\).ⓐ да ⓑ нет
ⓐ нет ⓑ да

\((3,2)\)
 \)
\)\((2,3)\)
- Если линии пересекаются, определите точку пересечения. Это решение системы.
- Если прямые параллельны, система не имеет решения.
- Если линии одинаковые, система имеет бесконечное число решений.

Мы решим оба этих уравнения относительно \(y\), чтобы мы могли легко построить их график, используя их наклоны и \(y\)-отрезки.
Решите первое уравнение для y . | |
| Найти наклон и у -пересечение. | |
| Решите второе уравнение для y . | |
| Найти наклон и у -пересечение. | |
| Нарисуйте линии. | |
| : Определить точку пересечения. | Линии пересекаются в точке \((−1,2)\). |
| Проверьте решение обоих уравнений. | |
| Решение: \((−1,2)\). |
\((3,4)\)
\((5,−4)\)

| Для построения графика первого уравнения мы будем использовать его наклон и точку пересечения y .  | |
| Для построения графика второго уравнения мы будем использовать перехватов. | |
| Нарисуйте линии. | |
| Определите точки пересечения. | Линии параллельны. Поскольку на обеих линиях нет точек, не существует упорядоченной пары, которая делает оба уравнения верными. У этой системы нет решения. |
 \).
\).нет решения
нет решения

Поскольку каждая точка на прямой делает оба уравнения
верными, существует бесконечно много
упорядоченных пар, которые делают оба уравнения верными.
У этой системы бесконечно много решений.
Если вы запишете второе уравнение в форме наклон-пересечение, вы можете заметить, что уравнения имеют один и тот же наклон и одно и то же y -пересечение.
бесконечно много решений
 \).
\).бесконечно много решений
 Мы называем такую систему уравнений несовместимой. Нет решения.
Мы называем такую систему уравнений несовместимой. Нет решения.
ⓐ Сравним наклоны и точки пересечения двух линий.
\(\begin{array} {lll} {} &{} &{ \left\{ \begin{array} {l} {y=3x-1} \\ {6x−2y=12} \end{array } \right.} \\ {} &{} &{y = 3x-1} \\ {\text{Первое уравнение уже находится в форме пересечения наклона.}} &{} &{} \\ {\text {Запишите второе уравнение в форме пересечения наклона.}} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \ \ {} &{} &{6x-2y=12} \\ {} &{} &{-2y=-6x+12} \\ {} &{} &{\frac{-2y}{-2} =\frac{-6x+12}{-2}} \\ {} &{} &{y=3x-6} \\ {} &{y=3x-1} &{y=3x-6} \ \ {} &{m=3} &{m=3} \\ {} &{b=-1} &{b=-6} \\ {\text{Найдите наклон и точку пересечения каждой линии.}} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{\text{Поскольку наклоны одинаковы, а y-перехваты}} &{} \\ {} &{\text{различны, линии параллельны. }} &{} \\ \end{массив}\)
}} &{} \\ \end{массив}\)
ⓑ Сравним наклон и точки пересечения двух линий.
\(\begin{array} {lll} {} &{} &{} \\ {} &{ \left\{ \begin{array} {l} 2x+y=-3 \\ x-5y=5 \\ \end{массив} \right. } &{} \\ {\text{Запишите оба уравнения в форме наклона–отрезка.}} &{} &{} \\ {} &{} &{} \\ { } &{} &{} \\ {} &{} &{} \\ {} &{2x+y=-3} &{x-5y=5} \\ {} &{y=-2x-3 } &{-5y=-x+5} \\ {} &{} &{\frac{-5y}{-5}=\frac{-x+5}{-5}} \\ {} &{ } &{y=\frac{1}{5}-1} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {\text{Найти наклон и точку пересечения каждой прямой.}} &{} &{} \\ {} &{} &{} \\ {} &{y=-2x- 3} &{y=\frac{1}{5}-1} \\ {} &{m=-2} &{m=\frac{1}{5}} \\ {} &{b=- 3} &{b=-1} \\ {} &{} &{} \\ {} &{\text{Поскольку наклоны разные, линии пересекаются.}} &{} \\ \end{массив} \)
Система уравнений, графики которой пересекаются, имеет 1 решение, непротиворечива и независима.

ⓐ нет решения, противоречивое, независимое ⓑ одно решение, последовательное, независимое
ⓐ нет решения, противоречивое, независимое ⓑ одно решение, последовательное, независимое
 И если решения системы не являются целыми числами, может быть трудно точно прочитать их значения по графику.
И если решения системы не являются целыми числами, может быть трудно точно прочитать их значения по графику.
\((6,1)\)
\((−3,5)\)

Нам нужно решить одно уравнение для одной переменной. Решим первое уравнение для y .
Подставьте \(−2x+2\) вместо y во втором уравнении.

\((2,32)\)
\((−12,−2)\)
 Графики хорошо работают, когда переменные коэффициенты малы, а решение имеет целые значения. Подстановка работает хорошо, когда мы можем легко решить одно уравнение для одной из переменных и не иметь слишком много дробей в результирующем выражении.
Графики хорошо работают, когда переменные коэффициенты малы, а решение имеет целые значения. Подстановка работает хорошо, когда мы можем легко решить одно уравнение для одной из переменных и не иметь слишком много дробей в результирующем выражении.
 Мы должны умножить каждый член в обеих частях уравнения на \(−2\).
Мы должны умножить каждый член в обеих частях уравнения на \(−2\). \)
\)\((2,−1)\)
\((−2,3)\)
- Решите, какую переменную вы удалите.
- Умножьте одно или оба уравнения так, чтобы коэффициенты этой переменной были противоположны.
 Затем найдите другую переменную.
Затем найдите другую переменную.В этом примере мы не можем умножить только одно уравнение на любую константу, чтобы получить противоположные коэффициенты. Поэтому мы стратегически умножим оба уравнения на разные константы, чтобы получить противоположные значения.
Чтобы получить противоположные коэффициенты y , мы умножим
первое уравнение на 2 и
второе уравнение на 3.

Упорядоченная пара равна \((0,−3)\).
обоих исходных уравнений.
\((1,3)\)
\((4,−3)\)

В этом примере оба уравнения содержат дроби. Нашим первым шагом будет умножение каждого уравнения на ЖК-дисплей всех дробей в уравнении, чтобы очистить дроби.
на его ЖК-дисплей.
переменных. Обратите внимание, что оба уравнения имеют стандартную форму
.

Подставьте \(x=3\) в одно из исходных уравнений.
обоих исходных уравнений.
 \)
\)\((6,2)\)
\((1,−2)\)
 Если уравнение в конце подстановки или исключения является ложным утверждением, мы имеем противоречивую систему, и система уравнений не имеет решения.
Если уравнение в конце подстановки или исключения является ложным утверждением, мы имеем противоречивую систему, и система уравнений не имеет решения. \(\begin{array} {ll} {} &{ \left\{ \begin{array} {l} 3x+4y=12 \\ y=3−\frac{3}{4}x \end{ array} \right.} \\ {} &{} \\ {\text{Запишите второе уравнение в стандартной форме.}} &{\left\{ \begin{array} {l} 3x+4y=12 \\ \frac{3}{4}x+y=3 \end{array} \right.} \\ {} &{} \\ {\text{Очистить дроби, умножив } \\ \text{второе уравнение на 4.}} &{\left\{ \begin{array} {l} 3x+4y=12 \\ 4(\frac{3}{4}x+y)=4(3) \end{array} \ справа. } \\ {} &{} \\ {\text{Упрощение}} &{\left\{ \begin{array} {l} 3x+4y=12 \\ 3x+4y=12 \end{array } \right.} \\ {} &{} \\ {\text{Чтобы исключить переменную, мы умножаем} \\ \text{второе уравнение на −1. Упрощаем и складываем.}} &{\begin{массив } {l} {\left\{ \begin{array} {l} 3x+4y=12 \\ \underline{-3x-4y=-12 } \end{array} \right.} \\ {\hspace{ 16 мм} 0=0} \end{массив}} \\ \end{массив} \)
Упрощаем и складываем.}} &{\begin{массив } {l} {\left\{ \begin{array} {l} 3x+4y=12 \\ \underline{-3x-4y=-12 } \end{array} \right.} \\ {\hspace{ 16 мм} 0=0} \end{массив}} \\ \end{массив} \)
Это верное утверждение. Уравнения непротиворечивы, но зависимы. Их графики были бы одной линией. Система имеет бесконечно много решений.
После того, как мы очистили дроби во втором уравнении, вы заметили, что два уравнения были одинаковыми? Это означает, что у нас есть совпадающие линии.
бесконечно много решений
бесконечно много решений
 Вам нужно будет принять это решение самостоятельно. Таким образом, вы захотите выбрать метод, который проще всего сделать и сводит к минимуму вероятность ошибок.
Вам нужно будет принять это решение самостоятельно. Таким образом, вы захотите выбрать метод, который проще всего сделать и сводит к минимуму вероятность ошибок. \)
\)ⓐ
\[\left\{ \begin{array} {l} 3x+8y=40 \\ 7x−4y=-32 \end{array} \right.\nonumber\]
Поскольку оба уравнения имеют стандартную форму, наиболее удобным будет использование метода исключения.
ⓑ
\[\left\{ \begin{array} {l} 5x+6y=12 \\ y=\tfrac{2}{3}x−1 \end{array} \right.\nonumber \]
Поскольку одно уравнение уже решено для y , наиболее удобным будет использование подстановки.
ⓐ Поскольку оба уравнения имеют стандартную форму, наиболее удобным будет использование метода исключения. ⓑ Так как одно уравнение уже решено для x , наиболее удобным будет использование подстановки.
ⓑ Так как одно уравнение уже решено для x , наиболее удобным будет использование подстановки.
ⓐ Поскольку одно уравнение уже решено для y , наиболее удобным будет использование подстановки. ⓑ Так как оба уравнения имеют стандартную форму, наиболее удобным будет использование метода исключения.
- Нарисуйте первое уравнение.
- Нарисуйте график второго уравнения в той же прямоугольной системе координат.

- Определите, пересекаются ли линии, параллельны или являются одной и той же линией.
- Определите решение системы.
Если линии пересекаются, определите точку пересечения. Это решение системы.
Если прямые параллельны, система не имеет решения.
Если линии одинаковые, система имеет бесконечное число решений. - Проверьте решение обоих уравнений.
- Решите одно из уравнений для любой переменной.
- Подставьте выражение из шага 1 в другое уравнение.
- Решите полученное уравнение.
- Подставьте решение шага 3 в одно из исходных уравнений, чтобы найти другую переменную.
- Запишите решение в виде упорядоченной пары.
- Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.

- Запишите оба уравнения в стандартной форме. Если какие-либо коэффициенты являются дробями, очистите их.
- Сделайте коэффициенты одной переменной противоположными.
Решите, какую переменную вы удалите.
Умножьте одно или оба уравнения так, чтобы коэффициенты этой переменной были противоположны. - Добавьте уравнения, полученные на шаге 2, чтобы исключить одну переменную.
- Найдите оставшуюся переменную.
- Подставьте решение шага 4 в одно из исходных уравнений. Затем найдите другую переменную.
- Запишите решение в виде упорядоченной пары.
- Убедитесь, что упорядоченная пара является решением обоих исходных уравнений. \[ \textbf{Выберите наиболее удобный метод решения системы линейных уравнений} \\ \begin{array} {lll} {\underline{\textbf{График}}} &{\underline{\textbf{Подстановка}} } &{\underline{\textbf{Исключение}}} \\ {\text{}} &{\text{Используйте, когда одно уравнение}} &{\text{}} \\ {\text{Используйте, когда вам нужно a}} &{\text{уже решено или может быть}} &{\text{Используйте, когда уравнения a}} \\ {\text{картина ситуации.
 }} &{\text{легко решается за один} } &{\text{соответствует стандартной форме.}} \\ {\text{}} &{\text{переменная.}} &{\text{}} \\ \end{массив} \nonumber \]
}} &{\text{легко решается за один} } &{\text{соответствует стандартной форме.}} \\ {\text{}} &{\text{переменная.}} &{\text{}} \\ \end{массив} \nonumber \]

- Тип изделия
- Раздел или страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Показать страницу Содержание
- да
- Включено
- да
- Теги
- источник[1]-math-5138

 Система линейных уравнений состоит из двух или более линейных уравнений, составленных из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти числовое значение для каждой переменной в системе, которое будет удовлетворять всем уравнениям в системе одновременно. Некоторые линейные системы могут не иметь решения, а другие могут иметь бесконечное число решений. Чтобы линейная система имела единственное решение, в ней должно быть не меньше уравнений, чем переменных. Тем не менее, это не гарантирует уникальности решения.
Система линейных уравнений состоит из двух или более линейных уравнений, составленных из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти числовое значение для каждой переменной в системе, которое будет удовлетворять всем уравнениям в системе одновременно. Некоторые линейные системы могут не иметь решения, а другие могут иметь бесконечное число решений. Чтобы линейная система имела единственное решение, в ней должно быть не меньше уравнений, чем переменных. Тем не менее, это не гарантирует уникальности решения. В этом примере упорядоченная пара [латекс](4,7)[/латекс] является решением системы линейных уравнений. Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям. Вскоре мы исследуем методы нахождения такого решения, если оно существует.
В этом примере упорядоченная пара [латекс](4,7)[/латекс] является решением системы линейных уравнений. Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям. Вскоре мы исследуем методы нахождения такого решения, если оно существует. Другими словами, прямые совпадают, поэтому уравнения представляют одну и ту же прямую. Каждая точка на прямой представляет собой пару координат, удовлетворяющую системе. Таким образом, существует бесконечное множество решений.
Другими словами, прямые совпадают, поэтому уравнения представляют одну и ту же прямую. Каждая точка на прямой представляет собой пару координат, удовлетворяющую системе. Таким образом, существует бесконечное множество решений. Линии совпадают. Это одна и та же линия, поэтому каждая пара координат на линии является решением обоих уравнений.
Линии совпадают. Это одна и та же линия, поэтому каждая пара координат на линии является решением обоих уравнений.
 Если две прямые параллельны, то система не имеет решений и несовместна. Если две линии идентичны, система имеет бесконечные решения и является зависимой системой.
Если две прямые параллельны, то система не имеет решений и несовместна. Если две линии идентичны, система имеет бесконечные решения и является зависимой системой. 1)
[латекс]5x-3y = -19[/латекс]
[латекс]x=2y-1[/латекс]
[латекс]4x+y=11[/латекс]
[латекс ]-2y=-25+8x[/латекс]
[латекс]у = -3х+6[/латекс]
[латекс]-\frac{1}{3}у+2=х[/ латекс]
 Рассмотрим еще два метода решения система линейных уравнений более точная, чем графическая. Одним из таких методов является решение системы уравнений методом подстановки , в котором мы решаем одно из уравнений для одной переменной, а затем подставляем результат во второе уравнение для решения для второй переменной. Напомним, что мы можем решать только для одной переменной за раз, поэтому метод подстановки ценен и практичен.
Рассмотрим еще два метода решения система линейных уравнений более точная, чем графическая. Одним из таких методов является решение системы уравнений методом подстановки , в котором мы решаем одно из уравнений для одной переменной, а затем подставляем результат во второе уравнение для решения для второй переменной. Напомним, что мы можем решать только для одной переменной за раз, поэтому метод подстановки ценен и практичен.




 Затем мы записали общее решение как [латекс]\влево(х, -\фракция{1}{3}х+\фракция{2}{3}\право)[/латекс]. Почему мы должны писать решение таким образом? В некотором смысле это представление говорит нам о многом. Он говорит нам, что x может быть чем угодно, x — это x . Это также говорит нам, что y будет зависеть от x , точно так же, как когда мы пишем функциональное правило. В этом случае, в зависимости от того, что вы положили на x , y будет определено через x как [латекс]-\frac{1}{3}x+\frac{2}{3}[/latex].
Затем мы записали общее решение как [латекс]\влево(х, -\фракция{1}{3}х+\фракция{2}{3}\право)[/латекс]. Почему мы должны писать решение таким образом? В некотором смысле это представление говорит нам о многом. Он говорит нам, что x может быть чем угодно, x — это x . Это также говорит нам, что y будет зависеть от x , точно так же, как когда мы пишем функциональное правило. В этом случае, в зависимости от того, что вы положили на x , y будет определено через x как [латекс]-\frac{1}{3}x+\frac{2}{3}[/latex]. Функция дохода производителя скейтбордов — это функция, используемая для расчета суммы денег, поступающей в бизнес. Его можно представить уравнением [латекс]R=xp[/латекс], где [латекс]х=[/латекс] количество и [латекс]р=[/латекс] цена. Функция дохода показана оранжевым цветом на графике ниже.
Функция дохода производителя скейтбордов — это функция, используемая для расчета суммы денег, поступающей в бизнес. Его можно представить уравнением [латекс]R=xp[/латекс], где [латекс]х=[/латекс] количество и [латекс]р=[/латекс] цена. Функция дохода показана оранжевым цветом на графике ниже. Они не зарабатывают и не теряют деньги.
Они не зарабатывают и не теряют деньги. Ниже мы суммируем три ключевых фактора, которые помогут вам преобразовать ситуацию в систему.
Ниже мы суммируем три ключевых фактора, которые помогут вам преобразовать ситуацию в систему. Сколько детей и сколько взрослых купили билеты?
Сколько детей и сколько взрослых купили билеты? станет лучшим выбором для Джамала?
станет лучшим выбором для Джамала?





 Уравнение становиться линейным.
Уравнение становиться линейным.