Решение уравнений с модулем презентация, доклад
Решение уравнений с модулем
Учителя МОУ СОШ №23
Сурмалян Л.М.
Кущевский район.
Обучение- это ремесло, использующее бесчисленное количество маленьких трюков.
Задание 1. IХ-3I=5 Отметьте точки, координаты которых удовлетворяют указанному условию. Запишите их координаты.
Отметим точки, удаленные от точки А на 5 единичных отрезков. Запишем их координаты.
0
3
А
B
-2
C
8
x
Геометрическая интерпретация
Уравнение Iх – аI = b, где b > 0, допускает простую геометрическую интерпретацию.
Решить уравнение Iх – 1I = 3 – значит найти все точки числовой оси, которые отстоят от точки с координатой (1) на расстоянии 3.
Ответ: -2 ; 4.
1
— 2
4
x
Геометрическая интерпретация
Решить уравнение Iх + 2I = 3 – значит найти все точки числовой оси, которые отстоят от точки с координатой (-2) на расстоянии 3.
Ответ: -5 ; 1.
— 2
1
-5
x
Задание 2. Решите уравнения
IХ – 4I = 3
I х + 2 I= 7
ответ 1; 7
5; -9
Метод интервалов
Уравнение вида:
b1I x – a1I + … + bnI x – anI = b,
где a1 Суть: точки a1 , a2 , …, an числовую ось делят на непересекающиеся промежутки знакопостоянства. Решаем уравнение на каждом промежутке; совокупность решений на всех промежутках и составит решение исходного уравнения.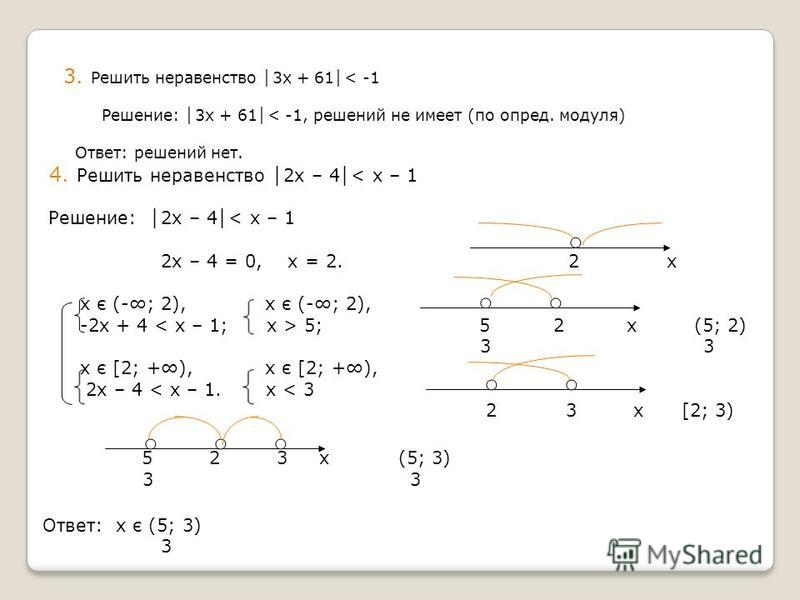
Решение уравнений.
Iх — 2I + Iх + 3I = 7
Ⅰ Ⅱ Ⅲ
x 2
-x+2-x-3=7 -x+2+x+3=7 x-2+x+3=7
X=-4 решений нет x=3
Ответ: -4; 3.
-3
2
x
Решение уравнений.
Iх — 5I — Iх — 2I = 3
Ⅰ Ⅱ Ⅲ
x 5
-x+5+x-2=3 -x+5-x+2=3 x-5-x+2=3
XОтвет: x
2
5
x
Геометрическая интерпретация
Уравнения
Ix – aI + Ix – bI =c и Ix – aI — Ix – bI =c
имеют простую геометрическую интерпретацию. Вернемся к предыдущим уравнениям.
Пример 1.
Решить уравнение Iх — 2I + Iх + 3I = 7 – это значит найти все точки на числовой оси Ох, для каждой из которых сумма расстояний до точек с координатами (2) и (-3) равна 7. Внутри отрезка таких точек нет, так как длина меньше семи, значит точки вне отрезка.
Ответ: -4; 3.
-3
2
-4
3
x
Пример 2.
Решить уравнение Iх — 5I — Iх — 2I = 3 – это значит найти все точки на числовой оси Ох, для каждой из которых разность расстояний от нее до точки с координатой (5) и расстояний от нее до точки с координатой (2) равнялось 3. Длина отрезка равна 3 следовательно любая точка левее (2) будет решением уравнения.
Ответ: x
2
-4
5
x
Пример 3.
IX — 1I + IX — 2I + IX — 3I =2
Построим графики функций:
Y=IX — 1I + IX — 3I и Y= 2 — IX — 2I
пересечение графиков
точка (2;2)
Ответ: 2.
1
2
3
х
Обобщение.
Если в уравнении Ix – aI + Ix – bI =c,
Iа – bI а если Ia – bI=c, то отрезок [a;b] будет решением уравнения;
если Ia – bI>c, то уравнение решений иметь не будет.
Обобщение.
Если в уравнении Ix – aI — Ix – bI =c,
Iа – bI = c, то при a b
a > b, x если Ia – bI если Ia – bI>c, то решение лежит внутри отрезка [a;b].
Домашняя работа.
IX + 3I + IX — 3I =6 IX — 3I + 2IX + 1I =4
IX — 1I + IXI = 9 IX — 4I + IX — 2I = IX+ 1I
IX — 3I + IX — 1I =3 IX+1I +IX-2I+IX-5I=6
IX + 6I + IX + 4I =5
IX — 1I – IX + 1I = 3
I5 + XI – Iх – 8I = 13
Скачать презентацию
Алгебраическое и графическое решение уравнений, содержащих модуль Исследовательская работа по математике Тема: Алгебраическое и графическое решение уравнений, содержащих модули ученика 10 класса Палдиской Русской гимназии Гаврилова Александра учитель: Сокольская Т. |
Блог учителя математики: Упражнения с модулями
«Модули – это интересно и доступно»
Основная цель курса — создать необходимый запас знаний
и способов их получения при решении различных видов уравнений и неравенств с
модулями. Как можно полнее развить потенциальные творческие способности каждого
ученика, не ограничивая заранее уровень сложности используемого задачного
материала, сформировать у учащихся потребность в продолжении математического
образования.
Как можно полнее развить потенциальные творческие способности каждого
ученика, не ограничивая заранее уровень сложности используемого задачного
материала, сформировать у учащихся потребность в продолжении математического
образования.
Данный курс для подготовки учащихся 9 классов вплотную примыкает к основному курсу алгебры, этот курс является развитием ранее приобретенных знаний, углубляет и расширяет курс математики основной школы. К сожалению, в основной школе, где задачи, содержащие абсолютную величину, рассматриваются лишь в дополнительных главах, трудно поддерживать интерес учащихся из-за ограниченности приобретенных знаний. Важные свойства и алгоритмы, необходимые для решения задач, отсутствуют. Такое положение создает определенные трудности для дальнейшего изучения математики и на вступительных экзаменах (подготовка к ЕГЭ).
Решение
задач с модулями является трудным для
большинства учащихся и вызывает у них страх, поэтому на каждом занятии предлагается тот минимум, который достаточен
для формирования основных представлений о модулях.
Любая тема может быть дополнена в различных учебных направлениях в старших классах профильной школы.
Учебный материал курса образует, своего рода, фундамент, опираясь на который можно в дальнейшем формировать систему знаний учащихся, а также их подготовку к ЕГЭ.
Содержание программы.
1. Решение уравнений, содержащих знак модуля.
На первом занятии учащимся сообщается цель и значение элективного курса. Учащиеся знакомятся с определением модуля, уравнением с модулем, им объясняется, что значит решить уравнение с модулем. Далее рассматриваются свойства модулей, а также различные методы решения уравнений с модулями. Применение полученных знаний на практике решения задач полезно организовать в малых группах. Лучшему осмыслению учебного материала послужит составление справочной таблицы.
2. Решение неравенств, содержащих знак модуля.
Программа (для общеобразовательных школ) не
акцентирует внимание на вопросе решения неравенств с модулем, не нашел он
достойного отражения и в материале действующих учебников.
Ожидаемый результат.
По окончании изучения данного курса ученик должен:
a) знать определение модуля и его свойства;
b) знать методы решения уравнений и неравенств, содержащих знак модуля;
c) уметь применять методы при решении уравнений и неравенств.
На изучение двух блоков отводится 15 часов, из них 2
часа – на определение успешности
освоения материала. Итоговые работы можно организовать в виде контрольной
работы (теста), в форме зачета. А также можно организовать игровой вариант.
Итоговые работы можно организовать в виде контрольной
работы (теста), в форме зачета. А также можно организовать игровой вариант.
Учебно — тематический план курса по выбору по математике «Модули – это доступно и интересно»; 9 класс.
№ | Наименование разделов и тем. | Количество часов |
I | Решение уравнений, содержащих знак модуля. | 9 |
1 | Определение и свойства модуля. Решение уравнений с использованием определений модуля | 2 |
2 | Уравнения вида ½f(x) ½=g(x) с использованием системы и совокупности. Решение уравнений методом интервалов. | 3 |
3 | Уравнения вида ½f(x) ½=½g(x)½. | 2 |
4 | Уравнения вида ½ax+b ½=cx+d. | 1 |
5 | Проверка усвоения знаний учащимися. | 1 |
II | 6 | |
1. | Решение неравенств вида ½f(x) ½<g(x) | 2 |
2 | Решение неравенств вида ½f(x) ½>g(x) | 2 |
3 | Решение неравенств вида½f(x)½<½g(x)½. | 1 |
4 | Проверка усвоения знаний
учащимися. | 1 |
III | Построение графиков функций, содержащих знак модуля | 4 |
Контрольная работа
(выполнить задания, используя определение модуля)
№ | I вариант | II вариант |
1 | Раскрыть модуль ½p-2½ | Раскрыть модуль ½3-p½ |
a) p-2 b) 2-p | a) 3-p b) p-3 | |
2 | ½x-x+¼½ | ½x+2x+1½ |
a) –x+x-¼ b) x-x+¼ c) x-x+¼ d) ¼-x-x | a) x+2x+1 b) –x-2x-1 c) x-2x-1 d) x-2x+1 | |
3 | Решить уравнение ½x-7½=-2 | Решить уравнение ½2x-3½=1 |
a) 7 c) 9 d) нет решений e) x – любое число | a) 2 b) 1 c) 1,2 d) нет решений | |
4 | ½x-1,5½=3,5 | ½125x-1,4½=-2 |
a) 2;5 b) –5;-2 c) –5;2 d) 2;-5 | a) 8;2 b) нет решений c) 2 d) 0;2 | |
5 | ½x-x½=0 | ½x+x½=0 |
a) 0;1 b) -1;0 c) x – любое число d) 1 | a) 1;0 b) нет решений c) –1;0 d) 0 |
Зачетный урок по теме «Решение уравнений с модулями»
«Лестница трудностей»
Система заданий составляется на два варианта от легкого к сложному
(сверху вниз). Каждый ученик, решив задание проверяет ответы у учителя, если
ответ правильный, то ученик «движется по лестнице» дальше, а если ученик
допустил ошибку, то учитель объясняет решение данного задания, а потом
предлагает аналогичное. Если ученик добрался до конца лестницы, значит, тему он
усвоил.
Каждый ученик, решив задание проверяет ответы у учителя, если
ответ правильный, то ученик «движется по лестнице» дальше, а если ученик
допустил ошибку, то учитель объясняет решение данного задания, а потом
предлагает аналогичное. Если ученик добрался до конца лестницы, значит, тему он
усвоил.
x-2½x½+1=0 | x-4½x½+4=0 | ||||||||||
½-x+2½=2x+1 | ½4-x½+½x-2½=2 | ||||||||||
½ x +3½+½2x-1½=8 | ½x-3½+2½x+1½=4 | ||||||||||
½ x +5½=½10+x½ | ½2x+1½=x | ||||||||||
½x-5½=3 | ½ x +5½=-3 | ||||||||||
Итоговое занятие по теме « Решение неравенств с модулями»
«Умники и умницы»
Три варианта выполнения работы: зеленая дорожка – более долгий путь
достижения цели, включает 4 задания, но можно 2 раза попросить помощь учителя;
желтая дорожка – «золотая середина», содержит 3 задания, можно 1 раз попросить помощь учителя; красная дорожка —
ученик решает без помощи учителя; этот путь содержит 2 задания. Для каждой
дорожки можно составить несколько вариантов заданий.
Для каждой
дорожки можно составить несколько вариантов заданий.
Зеленая дорожка | Желтая дорожка | Красная дорожка | |
1 | ½x½<3 | ½x-3½<2 | ½3+x½³x |
2 | ½x+2½>-2 | 5x-7£½x+2½ | ½2x-1½+½x-3½£4 |
3 | 3x+½2-x½£5 | ½x-2½+½x+2½£4 | |
4 | ½x-1½+½x+2½£3 |
Итоговое занятие по всему курсу можно провести в форме аукциона. Класс
делится на команды. Каждое задание имеет определенное количество баллов.
Команды знакомятся с заданиями и предлагают свои баллы, но не больше
первоначальных ( как в настоящем аукционе), а меньше, если они уверены, что
решат задание. Если команда решила задания правильно, то баллы складываются,
если неправильно – баллы вычитаются. Победила та команда, которая набрала
больше баллов.
Класс
делится на команды. Каждое задание имеет определенное количество баллов.
Команды знакомятся с заданиями и предлагают свои баллы, но не больше
первоначальных ( как в настоящем аукционе), а меньше, если они уверены, что
решат задание. Если команда решила задания правильно, то баллы складываются,
если неправильно – баллы вычитаются. Победила та команда, которая набрала
больше баллов.
1 | ½5-x½+½x-1½=10 | 3 балла |
2 | ½x+2½=2/(3-x) | 4 балла |
3 | ½2x-9x+15½³2 | 5 баллов |
4 | ½x-6½=½x-5x+9½ | 5 баллов |
5 | ½x½+½x+3½<5 | 7 баллов |
Уравнения
с модулями.
Абсолютной величиной числа a (обозначается |а| ) называется расстояние ( в единичных отрезках) от начала координат до точки с координатой (а).
|а|= а, если а≥0, (1)
-а, если а<0.
Некоторые основные свойства модуля:
1. |а| ≥ 0
2. |а| = |-а|
3. |а| ≥ а
4. |ab| = |a|•|b|
5.
, b≠0
Полезны упражнения, при решении которых следует воспользоваться одним важным правилом, которое непосредственно следует из соотношения (1): чтобы раскрыть модуль, надо знать знак выражения, стоящего под знаком модуля.
Примеры.
Раскрыть модуль:
1) |
-3|. Решение:
3,14,
-3=3,14-3=0,14, 0,14>0; (
-3) >0, следовательно |
-3|=
-3. Ответ:
Ответ:
-3.
2) |1-
|. Решение: 1-
=1-3,14= — 2,14; -2,14 <0, т.е. (1-
)<0, следовательно |1-
| = — (1-
) =
-1. Ответ:
-1.
3)
. Решение:
Определим знак выражения, стоящего под знаком модуля, для этого упростим его:
x² — x +
= x² — 2•
,
≥0 для любого x
. Ответ: x² — x +
.
Дополнительные примеры.
Раскрыть модули:
· |x²|
· |x4 + 1|
· |x² + 2x + 2|
Очень
часто встречаются случаи, в которых нет необходимости раскрывать модуль. Достаточно лишь воспользоваться свойствами 1-3 и соотношением (1).
Достаточно лишь воспользоваться свойствами 1-3 и соотношением (1).
Решить уравнение:
1) |x — 7| = — 2
Решение:
Левая часть: |x — 7| ≥ 0 по определению модуля.
Правая часть: – 2 < 0
Левая и правая части имеют разные знаки, следовательно, уравнение не имеет решений. Ответ: нет решений.
2) |2x — 3| = 1
Решение:
По определению модуля имеем:
2x – 3=1, 2x – 3 = -1,
2x = 4, 2x = 2,
x = 2. x = 1.
Ответ: 1; 2.
Дополнительные примеры.
Решите уравнение:
· | 1001x + 14| = — 1 Ответ: нет решений.
· | 125x – 1,4| = — 2 Ответ: нет решений.
· | x + 1,5 | = 3,5 Ответ: — 5; 2.
· | x ² — x | = 0 Ответ: 0; 1.
· | x ² + x | = 0 Ответ: — 1;0.
·
| | x – 1 | — 4 | = 3 Ответ: -6; 0; 2; 8.
· | | x + 3 | — 4 | = 1 Ответ: -8; -6; 0; 2.
· | | | x — 3 | — 3 | — 3 | = 0 Ответ: — 6;0; 6; 12.
· | | | x — 3 | + 3 | — 3 | = 3 Ответ: 0; 6.
· | 8 — | x + 2|| = 7 Ответ: — 17; -3; -1; 13.
· | 10 — | x — 1|| = 8 Ответ: — 17; -1; 3; 14.
Уравнения с модулем решались способом перехода от исходного уравнения к исходной системе:
g(x) ≥0f(x)=g(x)
f(x)= — g(x)
Этот способ удобнее использовать, если выражение для функции g(x) не сложное ( для удобства изложения материала назовем этот способ первым).
Второй способ, стандартный, основан на раскрытии модуля, исходя из его определения, и заключается в переходе к совокупности двух систем:
|
f(x) | = g(x)
С понятием
совокупности можно познакомить учащихся при решении уравнения вида f1(x) •f2(x) = 0.
Решение данного уравнения сводится к задаче об отыскании значений “x”, удовлетворяющих хотя бы одному из уравнений вида f1(x)=0 или f2(x)=0.
Если поставлена такая задача, то говорят, что задана совокупность уравнений. Обозначается это так:
Второй способ рациональнее применять в случае сложного выражения для функции g(x) и не очень сложного для функции f(x).
Необходимо обратить внимание, что первый способ применим только для уравнений, содержащих один модуль.
Решите уравнение:
3) |x-2| +| 2x-3|=5. Решение:
Рассмотрим четыре случая раскрытия модулей.
Первый случай: оба подмодульных выражения неотрицательны, тогда оба модуля раскрываются со знаком «+». Получим систему:
Решением системы является 3
Ответ: 3
Второй случай: первый модуль раскрывается со знаком “-“, т. к. подмодульное выражение
отрицательно, а второй модуль – со знаком «+», т. к. подмодульное выражение
неотрицательно. Имеем систему:
к. подмодульное выражение
неотрицательно. Имеем систему:
Система не имеет решений.
Решение уравнения системы x=6 не удовлетворяет условиям раскрытия модулей.
Ответ 2: нет решений.
Третий случай (первый модуль раскрывается со знаком «+», а второй со знаком “-“) приводит к системе:
Первое и второе неравенства системы противоречивы, следовательно, система не имеет решений. Ответ 3: решений нет.
Четвертый случай приводит к системе:
Следовательно, x=0. Ответ 4: 0.
Окончательный ответ исходного уравнения x=0 и x=3
. Ответ: 0; 3
.
Раскрывая последовательно все модули, входящие в рассмотренное уравнение, мы рассмотрели 4 случая, причем третий случай можно было бы опустить.
Решение
линейных неравенств с модулями.
Неравенства, содержащие переменную под знаком
модуля, решают различными способами; рассмотрим достаточно простой пример:
№1.Решить неравенство:
>4.
Первый способ: Имеем:
>4,
>4,
>2.
Геометрически выражение
означает расстояние на координатной прямой
между точками х и 2,5. Значит, нам нужно найти все такие точки х,
которые удалены от точки 2,5 более чем на 2, — это точки из промежутков х<0,5 и х>4,5.
Второй способ: Поскольку обе части заданного неравенства
неотрицательны, то возведем обе части этого неравенства в квадрат:
2>42 .
(2х–5)2>42,
(2х–5)2–16>0,
(2х–5–4)(2х–5+4)>0,
2(х–4,5) 2(х–0,5)>0,
(х–4,5)(х–0,5)>0.
Применив метод интервалов, получим: х<0,5
и х>4,5.
Третий способ: Выражение 2х–5 может быть неотрицательным или
отрицательным. Т.е. имеем совокупность двух систем:
Откуда: х<0,5 и х>4,5.
Рассмотрим еще несколько примеров.
Пример №2.Решить неравенство:
<3.
Данное неравенство равносильно совокупности
двух систем:
Из первой системы получаем 2х<5, из второй -1<х<2.
Объединяя эти два решения, получаем: -1<х<5.
Пример №3. Решить неравенство: 3
х+3.
Данное неравенство равносильно двойному
неравенству -х-33х–3х+3 или системе
Имеем: 0х3.
Упражнения для самостоятельной работы:
Решить неравенства:
1. <3х+1,
2. +>2,
3. ->-2.
->-2.
Решение квадратных неравенств с модулями.
Рассмотрим пример №1. Решите неравенство: +х–2<0.
Данное неравенство можно решить методом
интервалов. Рассмотрим иное решение, основанное на следующем утверждении: при
любом значении а неравенство равносильно системе неравенств:
, а неравенство
равносильно совокупности неравенств
.
Поэтому наше неравенство равносильно системе
неравенств:
решая которые, получим:
Запишем ответ: (1-
;2-
).
Пример №2. Найти целые решения неравенства:
2х–х2 . Задача сводится к решению совокупности двух систем неравенств:
Решим первую систему: из первого неравенства
имеем: х1; х2.
из второго: 2х2–5х+20, или 0,5х2.
Отметив найденные решения первого и второго
неравенств первой системы на координатной прямой, находим пересечение решений.
Т.о. 0,5х1 и х=2. Это решение первой
системы.
Решим вторую систему: из первого неравенства
имеем: 1<х<2, из второго: -(х2 -3х+2)2х–х2, или – х2+3х–2–2х+
х20, или х2.
Отметив найденные решения первого и второго
неравенств второй системы на координатной прямой, получим: 1<х<2.
Это решение второй системы.
Объединив найденные решения систем неравенств 0,5×1; х=2; 1<x<2, получаем: 0,5×2 и т.о. целыми решениями будут х=1 и х=2.
Упражнения для самостоятельной работы:
Решите неравенства:
1. <6,
2. <х,
3. <3х–3,
4. х2-3+2>0,
5. х2-х<3,
6. х2-6х+7-<0,
х2-6х+7-<0,
7. 3+х2–7>0,
8. >.
Метод интервалов решения уравнений и
неравенств, содержащих модуль.
Рассмотрим метод интервалов на примере
решения уравнения
-+3-2=х+2.
Чтобы решить данное неравенство, необходимо
раскрыть модули. Для этого выделим интервалы, на каждом из которых выражения,
стоящие под знаком модуля, принимают только положительные или отрицательные
значения. Отыскание таких интервалов основано на теореме: если на интервале
(а; в) функция f непрерывна и не обращается в нуль, то она на этом интервале
сохраняет постоянный знак.
Чтобы выделить интервалы знакопостоянства,
найдем точки, в которых выражения, записанные под модулем, обращаются в нуль:
х+1=0, х=-1; х=0; х–1=0, х=1; х–2=0, х=2.
Полученные точки разобьют прямую на искомые
интервалы. Определим знаки выражений
х+1, х, х–1, х–2 на этих интервалах:
Учитывая знаки, раскроем модули. В результате
получим совокупность систем, равносильную данному уравнению:
Последняя совокупность приводится к виду:
Решение совокупности систем и данного уравнения: -2; х
2.
Использованный прием называется методом
интервалов. Он применяется и при решении неравенств.
Решить неравенство:
+х–2<0.
1) Найдем нули выражения: х2-3х.
х1=0, х2=3.
2) Разобьем координатную прямую на интервалы
и установим знак выражения х2-3х на каждом интервале:
3) Раскроем модуль:
Решение первой системы:
, решение второй
. Решение данного неравенства:
.
Упражнения для самостоятельной работы:
№1
№2
№3
Решение неравенств вида , посредством равносильных переходов.
Рассмотрим неравенства вида
и
. Примем без доказательства следующую теорему: при любом значении а неравенство
равносильно системе неравенств а неравенство
равносильно совокупности неравенств
Рассмотрим пример: решить неравенство:
>х+2.
Пользуясь сформулированной теоремой, перейдем
к совокупности неравенств:
Система
и неравенство 0х>2 не имеют
решений. Следовательно, решением совокупности (и данного неравенства) является х.
Упражнения для самостоятельной работы:
1. <6,
2.1,
3.>х+3,
4. <х+3.
Применение свойств абсолютной величины при
решении уравнений и неравенств.
При решении некоторых заданий находят
применение свойства модуля. (При необходимости повторить их, см. занятие № 1).
Проиллюстрируем применение свойств модуля при
решении следующих примеров.
Пример №1: решить уравнение:
=1.
Заметим, что
=1, значит,
. Следовательно, по свойству 5: (х3-1)(2–х3)0, решением которого является числовой отрезок
Пример №2. Решите
систему уравнений:
Решите
систему уравнений:
Заметим, что
Следовательно, по свойству 5 ху
0, т.е. х и у принимают значения одного знака. Тогда данная система равносильна совокупности систем:
или
Решением первой системы является любая пара
неотрицательных чисел, сумма которых равна 1. Например, (0,5; 0,5), (1/6;
5/6).Решением второй системы является пара неположительных чисел, сумма которых
равна – 1. Например, (0,8;-0,2).
Пример №3.Запишите при помощи знака модуля,
что по крайней мере одно из чисел а, в, с, d отлично от нуля.
Ответ:
Пример №4. Дано:
<1,<10, <10.
Докажите неравенство:
<20.
Доказательство:
10=20.
Упражнения для самостоятельной работы:
1. Решите систему:
2.
При каких значениях х справедливы равенства:
а)
,
б)
3. Найдите числа х и у такие, что
=0;
4. Найдите наименьшее значение суммы:
а)
б)
5. Решите уравнение:
Решение уравнений и неравенств с модулями
на координатной прямой.
При изучении расстояния между двумя точками
А(х1) и В(х2) координатной прямой выводится
формула, согласно которой АВ=
. Используя эту формулу, можно решать уравнения и неравенства вида =в, , <в, , , а также уравнения и неравенства, к ним приводимые.
Рассмотрим
примеры.
1. Решите уравнение:
=1.
Переводя запись данного уравнения на “язык расстояний”, получим предложение “расстояние от точки с координатой х до точки с координатой 3 равно
1”.
Следовательно, решение уравнения сводится к отысканию точек, удаленных от точки
с координатой 3 на расстояние 1.
Корнями уравнения являются числа 2 и 4.
2.
= 3.
Приводя данное уравнение к виду
=1,5, используем формулу расстояния:
Ответ: — 2; 1.
3.
.
Запишем данное уравнение в виде:
. Исходя из геометрических представлений,
нетрудно понять, что корнем последнего уравнения
является координата точки, равноудаленной от точек с координатами 1 и – 2, т. е.
число – 0,5.
е.
число – 0,5.
Упражнения для самостоятельной работы:
Решите уравнения и неравенства:
1. =0,4;
2. =0,7;
3. <0,5;
4. <7;
5.
6.
7.
8.
Литература для учащихся:
2. Н.Я. Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И. Жохов. Математика: Учебник 6 класса средней школы., Москва, Просвещение. 1991г.
3. Ю.Н. Макарычев, Н.Г. Миндюк, и др. Алгебра: Учебник 7 (8,9) классов средней школы. Под ред. С. А. Теляковского, Москва, просвещение, 1993г.
4. Г. В. Дорофеев, С.Б. Суворова, Е. А. Бунимович, Л. В. Минаева. Алгебра: Учебник 7 (8,9) классов средней школы. Москва, Просвещение.
5. А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. Агебраический тренажер. Москва — Харьков: Импса, Гимназия, 1998г.
6. В. Гольдич, С. Злотин. Три тысячи задач по алгебре 5-9 класс, С.П.: Мир и семья-95, 1998г.
7. А. П. Ершова,
В.В. Голобородько, А.С. Ершова. Математика: Самостоятельные и контрольные
работы (разноуровневые дидактические материалы). Москва – Харьков: Импса,
Гимназия, 1998г.
А. П. Ершова,
В.В. Голобородько, А.С. Ершова. Математика: Самостоятельные и контрольные
работы (разноуровневые дидактические материалы). Москва – Харьков: Импса,
Гимназия, 1998г.
Литература для учителя:
1. И. Ф. Шарыгин. Факультативный курс по математике:Решение задач: — М.:Просвещение, 1989г.
2. И.М. Гельфонд. Функции и графики. Москва, Наука, 1968г.
3. О. Ю. Черкасов, И. Г. Якушев. Математика для поступающих в вузы. Москва. Московский лицей, 1996г.
4. И. С. Петраков. Математические кружки. – Москва. Просвещение. 1987г.
5. Е. Л. Мельникова. Проблемный урок. – М., 2002г.
6. Н.Я. Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И. Жохов. Математика: Учебник 6 класса средней школы., Москва, Просвещение. 1991г.
7. Ю.Н. Макарычев, Н.Г. Миндюк, и др. Алгебра: Учебник 7 (8,9) классов средней школы. Под ред. С. А. Теляковского, Москва, просвещение, 1993г.
8.
Г. В. Дорофеев,
С.Б. Суворова, Е. А. Бунимович, Л. В. Минаева. Алгебра: Учебник 7 (8,9) классов средней школы. Москва,
Просвещение.
В. Минаева. Алгебра: Учебник 7 (8,9) классов средней школы. Москва,
Просвещение.
9. А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. Агебраический тренажер. Москва — Харьков: Импса, Гимназия, 1998г.
10. В. Гольдич, С. Злотин. Три тысячи задач по алгебре 5-9 класс, С.П.: Мир и семья-95, 1998г.
11. А. П. Ершова, В.В. Голобородько, А.С. Ершова. Математика: Самостоятельные и контрольные работы (разноуровневые дидактические материалы). Москва – Харьков: Импса, Гимназия, 1998г.
Прохождение модулей 7 класса | Великие умы | Eureka Math
Ответ на часто задаваемые вопросы
В этом блоге рассматриваются модули 7 класса в История пропорций. Рассмотрим следующий пример преднамеренной траектории модулей 7 класса.
Модуль 1: На протяжении 6 класса учащиеся приобретают прочные знания о соотношениях, коэффициентах и единицах измерения. В первом модуле 7-го класса учащиеся опираются на эти знания, чтобы формально определить пропорциональные отношения и константу пропорциональности. Эта концепция развивается еще дальше, когда учащиеся знакомятся со ставками с рациональными числами. Например, учащиеся используют ставки, чтобы определить лучшую покупку между 3 1/3 фунта индейки, которая стоит 10,50 долларов, или 2 1/2 фунта индейки, которая стоит 6,25 долларов. Создание прочной основы с рациональными числами в младших классах имеет решающее значение, поскольку сложность возрастает в 7 классе. Учащиеся используют модели, такие как ленточные диаграммы и двойные числовые линии (показаны ниже), чтобы помочь в понимании и решении этих сложных задач. Наконец, учащиеся связывают пропорциональные отношения с контекстом чертежей в масштабе, поскольку они связывают удельные цены и константу пропорциональности с коэффициентом масштабирования.
Эта концепция развивается еще дальше, когда учащиеся знакомятся со ставками с рациональными числами. Например, учащиеся используют ставки, чтобы определить лучшую покупку между 3 1/3 фунта индейки, которая стоит 10,50 долларов, или 2 1/2 фунта индейки, которая стоит 6,25 долларов. Создание прочной основы с рациональными числами в младших классах имеет решающее значение, поскольку сложность возрастает в 7 классе. Учащиеся используют модели, такие как ленточные диаграммы и двойные числовые линии (показаны ниже), чтобы помочь в понимании и решении этих сложных задач. Наконец, учащиеся связывают пропорциональные отношения с контекстом чертежей в масштабе, поскольку они связывают удельные цены и константу пропорциональности с коэффициентом масштабирования.
Во втором модуле учащиеся знакомятся с операциями с целыми числами и другими рациональными числами. Хотя учащиеся познакомились с целыми числами в модуле 3 6 класса, их работа с целочисленными операциями начинается только в 7 классе. Благодаря использованию числовой прямой и целочисленной игры учащиеся развивают понимание того, как вычислять выражения с рациональными числами. Обратите внимание, что стрелки показывают длину и направление, а длина стрелки на числовой прямой представляет собой абсолютное значение (рассматривается в Модуле 3 6 класса) целого числа. Кроме того, добавление нескольких стрелок аналогично объединению целых чисел в игре с целыми числами. Работа с рациональными числами, которую учащиеся выполняют в Модуле 1, будет продолжена, когда учащиеся начнут работать с отрицательными рациональными числами позже в Теме A.
Благодаря использованию числовой прямой и целочисленной игры учащиеся развивают понимание того, как вычислять выражения с рациональными числами. Обратите внимание, что стрелки показывают длину и направление, а длина стрелки на числовой прямой представляет собой абсолютное значение (рассматривается в Модуле 3 6 класса) целого числа. Кроме того, добавление нескольких стрелок аналогично объединению целых чисел в игре с целыми числами. Работа с рациональными числами, которую учащиеся выполняют в Модуле 1, будет продолжена, когда учащиеся начнут работать с отрицательными рациональными числами позже в Теме A.
Ближе к концу модуля учащиеся кратко знакомятся с утверждениями «если-то» с помощью целочисленной игры. Они исследуют, как внесение одного и того же изменения в две одинаковые суммы карт приводит к истинному числовому предложению. Это введение в выражения и уравнения в теме D этого модуля является важной основой для следующего модуля, поскольку операторы «если-то» важны при решении алгебраических уравнений.
Используя свои предыдущие знания об ассоциативных, коммутативных и дистрибутивных свойствах, учащиеся учатся писать выражения как в стандартной форме, так и в факторизованной форме. Студенты продолжают накапливать свои знания о написании и решении уравнений с помощью задач с неизвестными углами и других концепций геометрии. По мере того, как их уверенность в решении уравнений продолжает расти, учащиеся знакомятся с неравенствами и тем, как отрицательные числа влияют на сохранение или изменение знака неравенства. Без знаний, полученных в Модуле 2, учащиеся не могут оценивать выражения или решать уравнения, представленные в этом модуле. Ближе к концу модуля учащиеся знакомятся с площадью и окружностью кругов, а также расширяют свои знания о выражениях и уравнениях при решении задач, связанных с круговыми областями.
7 класс, модуль 3, урок 10 В оставшейся части модуля основное внимание уделяется геометрии с использованием выражений и уравнений для вычисления площади, периметра, объема и площади поверхности различных двумерных и трехмерных фигур.
После ознакомления с пропорциональными отношениями в Модуле 1 учащиеся продолжают работу с пропорциональными отношениями в Модуле 4. В начале этого модуля учащиеся опираются на свои знания о соотношениях между дробями, десятичными знаками, и проценты из модуля 1 6 класса. Учащиеся учатся распознавать 100% как целое и использовать эти знания для написания уравнений для решения многоэтапных задач на проценты. Учащиеся используют знания, полученные в предыдущих модулях, для использования и решения уравнения 9.0007 Количество = Проценты x Всего . Учащиеся применяют это уравнение для решения задач как на процентное увеличение, так и на процентное уменьшение.
7 класс, модуль 3, урок 3 По мере увеличения сложности учащиеся применяют свои предыдущие знания о пропорциональных отношениях и абсолютных значениях для решения различных типов задач, включая наценки, уценки, простые проценты, налог с продаж, комиссионные, сборы и процентную ошибку. Учащимся предлагается использовать модели, отработанные в предыдущих модулях, чтобы помочь разработать план решения этих более сложных задач. В Модуле 1 учащиеся строили чертежи в масштабе, определяли масштабные длины и площади с учетом фактических величин и масштабного коэффициента (и наоборот). Работа Модуля 4 добавляет новую сложность, поскольку коэффициент масштабирования представлен в виде процентов, показывая учащимся эту связь и еще больше укрепляя их понимание пропорциональных отношений.
Учащимся предлагается использовать модели, отработанные в предыдущих модулях, чтобы помочь разработать план решения этих более сложных задач. В Модуле 1 учащиеся строили чертежи в масштабе, определяли масштабные длины и площади с учетом фактических величин и масштабного коэффициента (и наоборот). Работа Модуля 4 добавляет новую сложность, поскольку коэффициент масштабирования представлен в виде процентов, показывая учащимся эту связь и еще больше укрепляя их понимание пропорциональных отношений.
Учащиеся продолжают наблюдать взаимосвязь между дробями, десятичными знаками и процентами в Модуле 5, когда они знакомятся с вероятностью. Учащиеся узнают, как рассчитать теоретическую вероятность различных событий и чем она отличается от предполагаемой вероятности. В случаях, когда сбор данных невозможен, учащиеся учатся создавать симуляции, чтобы собирать данные для принятия обоснованных решений. Учащиеся также используют свои знания о рациональных числах для вычисления вероятности сложных событий с помощью списков, таблиц и древовидных диаграмм. Во второй половине модуля учащиеся продолжают развивать свои знания в области статистики, которые начались в конце 6-го класса. С помощью случайной выборки учащиеся могут делать неформальные выводы и оценивать среднее значение генеральной совокупности. Модуль завершается тем, что учащиеся сравнивают две популяции с одинаковой изменчивостью.
Во второй половине модуля учащиеся продолжают развивать свои знания в области статистики, которые начались в конце 6-го класса. С помощью случайной выборки учащиеся могут делать неформальные выводы и оценивать среднее значение генеральной совокупности. Модуль завершается тем, что учащиеся сравнивают две популяции с одинаковой изменчивостью.
Последний модуль 7 класса обобщает знания, полученные в течение всего года. Он начинается с дальнейшего развития у учащихся способности вычислять неизвестные углы, используя новые отношения углов и их знания уравнений, расширяя изучение Модуля 3. После неизвестных углов учащиеся используют линейку, циркуль и транспортир для построения геометрических фигур. С помощью этих построений учащиеся создают список условий, определяющих уникальные треугольники. Следуя этим построениям, учащиеся определяют, какие двухмерные фигуры получаются в результате разрезания трехмерных фигур. В последних двух темах на уровне класса учащиеся продолжают развивать свое понимание площади, площади поверхности и объема, снова основываясь на изучении Модуля 3. По мере того, как уровень сложности увеличивается на последних уроках, учащиеся должны использовать их знания, полученные в течение всего года, чтобы испытать успех.
По мере того, как уровень сложности увеличивается на последних уроках, учащиеся должны использовать их знания, полученные в течение всего года, чтобы испытать успех.
На первый взгляд может показаться, что изменение порядка модулей не повлияет на успеваемость учащихся. Тем не менее, важно признать преднамеренность в порядке каждого модуля и отдельного урока. Подобно сборникам рассказов, где очень важно читать каждую главу по порядку, История отношений была написана с намерением следовать последовательно.
Автором этой записи в блоге является Криста Гиббс , учитель-писатель средней школы Eureka Math .
© Great Minds 2016
Математический сайт г-на Миллера / Модуль 3
7 класс Модуль 3: Выражения и уравнения
Этот модуль объединяет и расширяет понимание учащимися эквивалентных выражений по мере того, как они применяют свойства операций для записи выражений как в стандартной форме, так и в факторизованной форме. Они используют линейные уравнения для решения задач с неизвестными углами и других задач, представленных в контексте, чтобы понять, что решение алгебраических уравнений связано с числами. Учащиеся используют числовую прямую, чтобы понять свойства неравенства и понять, когда сохранить неравенство, а когда обратить неравенство при решении задач, ведущих к неравенству. Они интерпретируют решения в контексте проблем. Учащиеся расширяют свое изучение геометрических фигур и взаимосвязей между ними в шестом классе, применяя свою работу с выражениями и уравнениями для решения задач, связанных с площадью круга и составной площадью на плоскости, а также объемом и площадью поверхности прямых призм.
Они используют линейные уравнения для решения задач с неизвестными углами и других задач, представленных в контексте, чтобы понять, что решение алгебраических уравнений связано с числами. Учащиеся используют числовую прямую, чтобы понять свойства неравенства и понять, когда сохранить неравенство, а когда обратить неравенство при решении задач, ведущих к неравенству. Они интерпретируют решения в контексте проблем. Учащиеся расширяют свое изучение геометрических фигур и взаимосвязей между ними в шестом классе, применяя свою работу с выражениями и уравнениями для решения задач, связанных с площадью круга и составной площадью на плоскости, а также объемом и площадью поверхности прямых призм.
(выдержка взята с веб-сайта NYS Engage)
NYS Engage Module 3 — link to all things related to Module 3, provided by NYS
Khan academy sorted by lessons
NEW Khan Academy On Grade Support для Модуля 3
Рабочие листы и видеоуроки Engage для всех уроков, описанных в Модуле
http://www. onlinemathlearning.com/common-core-math-worksheets-grade7.html
onlinemathlearning.com/common-core-math-worksheets-grade7.html
Important Vocabulary (taken from lesson 1 of the module):
Переменная : Переменная – это символ (например, буква), представляющий число, т. е. заполнитель для числа.
Числовое выражение : A числовое выражение является числом или любой комбинацией сумм, разностей, произведений или делений чисел, результатом которой является число.
Значение числового выражения : Значение числового выражения – это число, найденное путем вычисления выражения.
Выражение : Выражение – это числовое выражение или результат замены некоторых (или всех) чисел в числовом выражении переменными.
Эквивалентные выражения : Два выражения эквивалентны , если оба выражения дают одно и то же число при каждой замене цифр на все буквы в обоих выражениях.
Выражение в развернутой форме : Выражение , записанное как суммы (и/или разности) произведений, коэффициенты которых являются числами, переменными или переменными, возведенными в целые степени, называется быть в расширенная форма. Единичное число, переменная или единичное произведение чисел и/или переменных также считается представленным в развернутой форме. Примеры выражений в расширенной форме включают: 324, 3x, 5x + 3 — 40 и т. д. Например, выражение 2x + 3x + 5 состоит из 3 элементов: 2x, 3x и 5.
Коэффициент термина : Число, полученное путем умножения только чисел в термине вместе. Например, если произведение 2 * x * 4, его эквивалент равен 8x. Число 8 называется коэффициентом при члене 8x.
Выражение в стандартной форме : Выражение в развернутой форме со всеми сходными с ним элементами называется стандартной формой . Например, 2x + 3x + 7 — это выражение, записанное в расширенной форме; однако, чтобы быть записанными в стандартной форме, подобные термины 2x и 3x должны быть объединены. Эквивалентное выражение 5x + 7 записывается в стандартной форме .
Например, 2x + 3x + 7 — это выражение, записанное в расширенной форме; однако, чтобы быть записанными в стандартной форме, подобные термины 2x и 3x должны быть объединены. Эквивалентное выражение 5x + 7 записывается в стандартной форме .
Важный словарь (взят из урока 7 модуля):
Уравнение : Уравнение является утверждением равенства между двумя выражениями.
Если A и B — два выражения с переменной x, то A = B — уравнение с переменной x.
Иногда учащимся трудно понять, что такое выражение, а что уравнение. Выражение никогда не включает знак равенства (=) и может рассматриваться как часть предложения. Выражение 3 + 4, прочитанное вслух, — это «три плюс четыре», что является всего лишь фразой в возможном предложении. Уравнения, с другой стороны, всегда имеют знак равенства, который является символом глагола «есть». Уравнение 3 + 4 = 7, прочитанное вслух, звучит так: «Три плюс четыре равно семи», которое выражает законченную мысль, т. е. предложение.
е. предложение.
Числовые предложения — уравнения только с числами — являются особыми среди всех уравнений.
Числовое предложение : Числовое предложение является утверждением о равенстве (или неравенстве) между двумя числовыми выражениями.
Числовое предложение — наиболее конкретная версия уравнения. Оно также обладает очень важным свойством: оно всегда истинно или всегда ложно, и именно это свойство отличает его от общего уравнения. Например, 3 + 4 = 7 (верно) и 3 + 3 = 7 (ложно). Это важное свойство гарантирует возможность проверить, является ли число решением уравнения с переменной: просто подставьте число в переменную. В результате числовое предложение является либо истинным, либо ложным. Если числовое предложение верно, то число является решением уравнения. По этой причине числовые предложения являются первым и наиболее важным типом уравнений, которые учащиеся должны понять.
Математика 7 класс — Красная комета
Математика 7 класс — Красная кометаМатематика 7 класс
Рекомендуемый уровень обучения:
7Цена курса:
$350.00Сведения о курсе:
Учащимся, которые любят интерактивное обучение, понравится курс математики M/J 7 класса. Они испытывают интригу и веселье, когда входят в этот курс. Это практический курс, полный слайд-шоу, приложений, видео и реальных сценариев. Обучение в этом курсе сосредоточено на четырех важнейших областях: (1) развитие понимания и применение пропорциональных отношений; (2) развитие понимания операций с рациональными числами и работы с выражениями и линейными уравнениями; (3) решение задач, связанных с чертежами в масштабе и неформальными геометрическими построениями, а также работа с двух- и трехмерными формами для решения задач, связанных с площадью, площадью поверхности и объемом; и (4) делать выводы о популяциях на основе выборок.
Необходимые материалы:
Для прохождения этого курса вам потребуются следующие предметы:
- Текущий минимальный Flash Player, требуемый вашей школой.
- Место на диске вашего компьютера, а также внешнее устройство для резервного копирования ваших файлов (флэш-накопитель, внешний жесткий диск, компакт-диск и т. д.)
- Принтер
Программа:
Сегмент I
Модуль 1: Рациональные числа
- 00 Первый модуль Контрольный список и предварительное тестирование
- 01 Числовая линия
- 02 Сложение и вычитание рациональных чисел
- 03 Проверка среднего модуля
- 04 Умножение рациональных чисел
- 05 Стратегии для рациональных чисел
- 06A Иррациональные числа
- 07A Аппроксимация рациональных чисел
- 08 Практический тест первого модуля
- 09 Оценка на основе обсуждения
- 10 Тестовый модуль 1
- 11A Расширенный тест модуля 1
Модуль 2: Применение рациональных чисел
- 00 Второй модуль Контрольный список и предварительное тестирование
- 01 Деление рациональных чисел
- 02 Преобразование рациональных чисел
- 03 Рациональные числа в реальном мире
- 04A Экспоненты
- 05A Операции с корнями
- 06A Научное обозначение
- 07A Операции с экспоненциальной записью
- 08 Модуль 2.
 Практический тест
Практический тест - 09 Оценка на основе обсуждения
- 10 Второй модуль теста
- Модуль 11A 2 Расширенный тест
Модуль 3: Уравнения и неравенства
- 00 Контрольный список модуля 3 и предварительное тестирование
- 01 Расширение и упрощение выражений
- 02 Применение выражений
- 03 Проверка среднего модуля
- 04 Уравнения
- 05 Неравенства
- 06A Линейные уравнения
- 07A Системы уравнений
- 08 Модуль 3. Практический тест
- 09 Оценка на основе обсуждения
- 10 Тестовый модуль 3
- Расширенный тест третьего модуля 11A
Модуль 4: Пропорции
- 00 Модуль 4 Контрольный список и предварительное тестирование
- 01 Удельные ставки
- 02 Характеристики пропорции
- 03 Пропорциональность и уравнения
- 04 Применение соотношений
- 05 Применение процентов
- 06A Графики пропорциональных отношений
- 07A Форма пересечения уклонов
- 08 Практический тест четвертого модуля
- 09 Оценка на основе обсуждения
- 10 Четырехмодульный тест
- Расширенный тест модуля 11A 4
- 12 практических тестов первого сегмента
- 13 Первый сегмент экзамена
- 14A Сегмент 1 Расширенный экзамен
Сегмент II
Модуль 5: Геометрия
- 00 Контрольный список пятого модуля и предварительное тестирование
- 01 Чертежи в масштабе
- 02 Углы и треугольники
- 03 Проверка среднего модуля
- 04 Круги
- 05 Трехмерные фигуры и сечения
- 06А Трансформации
- 07A Конгруэнтность
- 08A Преобразования и координатная плоскость
- 09A Поперечины и уголки
- 10 Практический тест пятого модуля
- 11 Оценка на основе обсуждения
- 12 Тестовый модуль 5
- Расширенный тест модуля 13A Five
Модуль 6: Вероятность простых событий
- 00 Модуль 6 Контрольный список и предварительное тестирование
- 01 Понимание вероятности
- 02 Приближенная вероятность
- 03 Проверка среднего модуля
- 04 Вероятностные модели
- 05 Наблюдение за данными
- 06A Теорема Пифагора
- 07A Применение теоремы Пифагора
- 08A Теорема Пифагора на координатной плоскости
- 09A Формулы
- 10 Практический тест модуля 6
- 11 Оценка на основе обсуждения
- 12 Тестовый модуль 6
- Расширенный тест модуля 13A Six
Модуль 7.

 Н. Палдиски 2003 год.Содержание:1.Введение………………………………………………………….42.Понятия и определения………………………………………….43.Доказательство теорем…………………………………………..54.Способы решение уравнений, содержащих модуль……………64.1.Решение при помощи зависимостей между числами a и b, их модулями иквадратами…………………………………………………………124.2.Использование геометрической интерпритации модуля для решенияуравнений…………………………………………………………..144.3.Графики простейших функций, содержащих знак абсолютной величины.………………………………………………………………………154.4.Решение нестандартных уравнения, содержащие модуль….165.Заключение……………………………………………………….226.Список использованной литературы……………………………23 Цель работы: хотя уравнения с модулями ученики начинают изучать уже с 6-го – 7-го класса, где они проходят самые азы уравнений с модулями. Я выбрал именно эту тему, потому что считаю, что она требует более глубокого и досканального исследования. Я хочу получить более широкие знания о модуле числа, различных способах решения уравнений, содержащих знак абсолютной величины.
Н. Палдиски 2003 год.Содержание:1.Введение………………………………………………………….42.Понятия и определения………………………………………….43.Доказательство теорем…………………………………………..54.Способы решение уравнений, содержащих модуль……………64.1.Решение при помощи зависимостей между числами a и b, их модулями иквадратами…………………………………………………………124.2.Использование геометрической интерпритации модуля для решенияуравнений…………………………………………………………..144.3.Графики простейших функций, содержащих знак абсолютной величины.………………………………………………………………………154.4.Решение нестандартных уравнения, содержащие модуль….165.Заключение……………………………………………………….226.Список использованной литературы……………………………23 Цель работы: хотя уравнения с модулями ученики начинают изучать уже с 6-го – 7-го класса, где они проходят самые азы уравнений с модулями. Я выбрал именно эту тему, потому что считаю, что она требует более глубокого и досканального исследования. Я хочу получить более широкие знания о модуле числа, различных способах решения уравнений, содержащих знак абсолютной величины. 1. Введение: Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это многозначное слово(омоним), которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, програмировании и других точных науках. В архитектуре-это исходная еденица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов. В технике-это термин, применяемый в различных облостях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости и .т.п. Модуль объемного сжатия( в физике)-отношение нормального напряжения в материале к относительному удлинению. 2. Понятия и определения Чтобы глубоко изучать данную тему, необходимо познакомиться с простейшими определениями, которые мне будут необходимы: Уравнение-это равенство, сродержащее переменные. Уравнение с модулем-это уравнение, содержащие переменную под знаком абсолютной величины(под знаком модуля).
1. Введение: Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это многозначное слово(омоним), которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, програмировании и других точных науках. В архитектуре-это исходная еденица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов. В технике-это термин, применяемый в различных облостях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости и .т.п. Модуль объемного сжатия( в физике)-отношение нормального напряжения в материале к относительному удлинению. 2. Понятия и определения Чтобы глубоко изучать данную тему, необходимо познакомиться с простейшими определениями, которые мне будут необходимы: Уравнение-это равенство, сродержащее переменные. Уравнение с модулем-это уравнение, содержащие переменную под знаком абсолютной величины(под знаком модуля). Например: |x|=1 Решить уравнение-это значит найти все его корни, или доказать, что корней нет. В математике модуль имеет несколько значений, но в моей исследовательской работе я возьму лишь одно: Модуль-абсолютная величина числа, равная расстоянию от начала отсчетадо точки на числовой прямой. 3. Доказательство теорем Определение. Модуль числа a или абсолютная величина числа a равна a,если a больше или равно нулю и равна -a, если a меньше нуля: [pic] Из определения следует, что для любого действительного числа a, [pic] Теорема 1. Абсолютная величина действительного числа [pic] равнабольшему из двух чисел a или -a. Доказательство 1. Если число a положительно, то -a отрицательно, т. е. -a Объединяя последние дванеравенства в одно, получаем: [pic] Теорема 2. Абсолютная величина любого действительного числа a равнаарифметическому квадратному корню из [pic] [pic] В самом деле, если [pic] то, по определению модуля числа, будем иметь[pic] С другой стороны, при [pic] [pic] значит |a| = [pic] Если a 0 ?уравнение имеет 2 различных корня.
Например: |x|=1 Решить уравнение-это значит найти все его корни, или доказать, что корней нет. В математике модуль имеет несколько значений, но в моей исследовательской работе я возьму лишь одно: Модуль-абсолютная величина числа, равная расстоянию от начала отсчетадо точки на числовой прямой. 3. Доказательство теорем Определение. Модуль числа a или абсолютная величина числа a равна a,если a больше или равно нулю и равна -a, если a меньше нуля: [pic] Из определения следует, что для любого действительного числа a, [pic] Теорема 1. Абсолютная величина действительного числа [pic] равнабольшему из двух чисел a или -a. Доказательство 1. Если число a положительно, то -a отрицательно, т. е. -a Объединяя последние дванеравенства в одно, получаем: [pic] Теорема 2. Абсолютная величина любого действительного числа a равнаарифметическому квадратному корню из [pic] [pic] В самом деле, если [pic] то, по определению модуля числа, будем иметь[pic] С другой стороны, при [pic] [pic] значит |a| = [pic] Если a 0 ?уравнение имеет 2 различных корня. x1=(11 – 7 )/3=11/3 x2=(11 + 7 )/3=6Как показывает решение, корнями данного уравнения также являются числа 11/3и 6 Ответ: x1=6, x2=11/3Пример 5. Решим уравнение (2x + 3)2=(x – 1)2.Учитывая соотношение (2), получим, что |2x + 3|=|x – 1|, откуда по образцупредыдущего примера(и по соотношению (1)):2х + 3=х – 1 или 2х + 3=-х + 12х – х=-1 – 3 2х+х=1 – 3 х=-4 х=-0,(6)Таким образом корнями уравнения являются х1=-4, и х2=-0,(6)Ответ: х1=-4, х2=0,(6)Пример 6. Решим уравнение |x – 6|=|x2 – 5x + 9|Пользуясь соотношением (1), получим:х – 6=х2 – 5х + 9 или х – 6 = -(х2 –5х + 9)-х2 + 5х + х – 6 – 9=0 |(-1) x – 6=-x2 + 5x- 9×2 — 6x + 15=0 x2 – 4x +3=0D=36 – 4 * 15=36 – 60= -24 0?2 р.к.? корней нет.x1=(4- 2 ) /2=1×2=(4 + 2 ) /2=3Проверка: |1 – 6|=|12 – 5 * 1 + 9| |3 – 6|=|32 – 5 * 3 + 9| 5 = 5(И) 3 =|9 – 15 + 9|3 = 3(И)Ответ: x1=1; x2=34.2.Использование геометрической интерпритации модуля для решенияуравнений.Геометрический смысл модуля разности величин-это расстояние между ними.Например, геометрический смысл выражения |x – a | -длина отрезкакоординатной оси, соединяющей точки с абсцисами а и х .
x1=(11 – 7 )/3=11/3 x2=(11 + 7 )/3=6Как показывает решение, корнями данного уравнения также являются числа 11/3и 6 Ответ: x1=6, x2=11/3Пример 5. Решим уравнение (2x + 3)2=(x – 1)2.Учитывая соотношение (2), получим, что |2x + 3|=|x – 1|, откуда по образцупредыдущего примера(и по соотношению (1)):2х + 3=х – 1 или 2х + 3=-х + 12х – х=-1 – 3 2х+х=1 – 3 х=-4 х=-0,(6)Таким образом корнями уравнения являются х1=-4, и х2=-0,(6)Ответ: х1=-4, х2=0,(6)Пример 6. Решим уравнение |x – 6|=|x2 – 5x + 9|Пользуясь соотношением (1), получим:х – 6=х2 – 5х + 9 или х – 6 = -(х2 –5х + 9)-х2 + 5х + х – 6 – 9=0 |(-1) x – 6=-x2 + 5x- 9×2 — 6x + 15=0 x2 – 4x +3=0D=36 – 4 * 15=36 – 60= -24 0?2 р.к.? корней нет.x1=(4- 2 ) /2=1×2=(4 + 2 ) /2=3Проверка: |1 – 6|=|12 – 5 * 1 + 9| |3 – 6|=|32 – 5 * 3 + 9| 5 = 5(И) 3 =|9 – 15 + 9|3 = 3(И)Ответ: x1=1; x2=34.2.Использование геометрической интерпритации модуля для решенияуравнений.Геометрический смысл модуля разности величин-это расстояние между ними.Например, геометрический смысл выражения |x – a | -длина отрезкакоординатной оси, соединяющей точки с абсцисами а и х . Перевод алгеб-раической задачи на геометрический язык часто позволяет избежать громоздкихрешений.Пример7. Решим уравнение |x – 1| + |x – 2|=1 с использованиемгеометрической интерпритации модуля.Будем рассуждать следующим образом: исходя из геометрической интерпри-тациимодуля, левая часть уравнения представляет собой сумму расстояний отнекторой точки абсцисс х до двух фиксированных точек с абсциссами 1 и 2.Тогда очевидно, что все точки с абсциссами из отрезка [1; 2] обладаюттребуемым свойством, а точки, расположенные вне этого отрезка- нет. Отсюдаответ: множеством решений уравнения является отрезок [1; 2].Ответ: х ? [1; 2]Пример8. Решим уравнение |x – 1| — |x – 2|=1 1 с использованиемгеометрической интерпритации модуля.Будем рассуждать аналогично предыдущему примеру, при этом получим, чторазность расстояний до точек с абсциссами 1 и 2 равна единице только дляточек, расположенных на координатной оси правее числа 2. Следовательнорешением данного уравнения будет являтся не отрезок, заключенный междуточками 1 и 2, а луч, выходящий из точки 2, и направленный в положительномнаправлении оси ОХ.
Перевод алгеб-раической задачи на геометрический язык часто позволяет избежать громоздкихрешений.Пример7. Решим уравнение |x – 1| + |x – 2|=1 с использованиемгеометрической интерпритации модуля.Будем рассуждать следующим образом: исходя из геометрической интерпри-тациимодуля, левая часть уравнения представляет собой сумму расстояний отнекторой точки абсцисс х до двух фиксированных точек с абсциссами 1 и 2.Тогда очевидно, что все точки с абсциссами из отрезка [1; 2] обладаюттребуемым свойством, а точки, расположенные вне этого отрезка- нет. Отсюдаответ: множеством решений уравнения является отрезок [1; 2].Ответ: х ? [1; 2]Пример8. Решим уравнение |x – 1| — |x – 2|=1 1 с использованиемгеометрической интерпритации модуля.Будем рассуждать аналогично предыдущему примеру, при этом получим, чторазность расстояний до точек с абсциссами 1 и 2 равна единице только дляточек, расположенных на координатной оси правее числа 2. Следовательнорешением данного уравнения будет являтся не отрезок, заключенный междуточками 1 и 2, а луч, выходящий из точки 2, и направленный в положительномнаправлении оси ОХ. Ответ: х ?[2; +?)Обобщением вышеприведенных уравнений являются следующие равносильныепереходы: |x – a| + |x – b|=b – a, где b ? a ? a ? x ? b |x – a| — |x – b|=b – a, где b ? a ? x ? b4.3. Графики простейших функций, содержащих знак абсолютной величиныПод простейшими функциями понимают алгебраическую сумму модулей линейныхвыражений. Сформулируем утверждение, позволяющее строить графики такихфункций, не раскрывая модули ( что особенно важно, когда модулей достаточномного ): «Алгебраическая сумма модулей n линейных выражений представляетсобой кусочно- линейную функцию, график которой состоит из n +1прямолинейного отрезка. Тогда график может быть построен по n +2 точкам, nиз которых представляют собой корни внутримодульных выражений, ещё одна —произвольная точка с абсциссой, меньшей меньшего из этих корней и последняя— с абсциссой, большей большего из корней.Например:1)f(x)=|x — 1| Вычисляя функции в точках 1, 0 и 2, получаем график,состоящий из двух отрезков(рис.1)2) f(x)=|x — 1| + |x – 2| Вычисляя значение функиции в точках с абсциссами1, 2, 0 и 3, получаем график, состоящий из двух отрезков прямых.
Ответ: х ?[2; +?)Обобщением вышеприведенных уравнений являются следующие равносильныепереходы: |x – a| + |x – b|=b – a, где b ? a ? a ? x ? b |x – a| — |x – b|=b – a, где b ? a ? x ? b4.3. Графики простейших функций, содержащих знак абсолютной величиныПод простейшими функциями понимают алгебраическую сумму модулей линейныхвыражений. Сформулируем утверждение, позволяющее строить графики такихфункций, не раскрывая модули ( что особенно важно, когда модулей достаточномного ): «Алгебраическая сумма модулей n линейных выражений представляетсобой кусочно- линейную функцию, график которой состоит из n +1прямолинейного отрезка. Тогда график может быть построен по n +2 точкам, nиз которых представляют собой корни внутримодульных выражений, ещё одна —произвольная точка с абсциссой, меньшей меньшего из этих корней и последняя— с абсциссой, большей большего из корней.Например:1)f(x)=|x — 1| Вычисляя функции в точках 1, 0 и 2, получаем график,состоящий из двух отрезков(рис.1)2) f(x)=|x — 1| + |x – 2| Вычисляя значение функиции в точках с абсциссами1, 2, 0 и 3, получаем график, состоящий из двух отрезков прямых. (рис.2)3) f(x)=|x — 1| + |x – 2| + |x – 3| Для построения графика вычислимзначения функции в точках 1, 2, 3, 0 и 4 (рис.3)4) f(x)=|x — 1| — |x – 2| График разности строится аналогично графикусуммы, тоесть по точкам 1, 2, 0 и 3.[pic]рис1. рис2. рис3. рис4.4.4.Решение нестандартных уравнений, содержащих модули.Пример9. Решить уравнение 3| x + 2 | + x2 + 6x + 2 = 0. Решение. Рассмотрим два случая. [pic]Ответ: (– 4; – 1).Пример10. Решить уравнение | 4 – x | + | (x – 1)(x – 3) | = 1. Решение.Учитывая, что | 4 – x | = | x – 4 |, рассмотрим четыре случая. [pic]так как [pic]2) [pic]3) 4) [pic]4) [pic]Ответ: 3. Графический способ.Построим графики функций y = |(x–1)(x–3)| и y=1–|x–4 |1)в Гy = |(x–1)(x–3)| подставим значение х=1 и х=3. Мы получим у=0,тоесть пересечение графика с осью ОХ. При х равном нулю у=3, тоесть графикпересекается с осью ОУ в точке (0 ;3). И при х=4 у также равен 3- мыполучили первый график.2) y=1–|x–4 | Найдем пересечение с осью ОХ, для этого решим простоеуравнение: 1-|x-4|=0 |x-4|=1 x — 4=1 или x — 4=-1 x=5 x=3Следовательно данный график пересекает ось ОХ в точках 5 и 3.
(рис.2)3) f(x)=|x — 1| + |x – 2| + |x – 3| Для построения графика вычислимзначения функции в точках 1, 2, 3, 0 и 4 (рис.3)4) f(x)=|x — 1| — |x – 2| График разности строится аналогично графикусуммы, тоесть по точкам 1, 2, 0 и 3.[pic]рис1. рис2. рис3. рис4.4.4.Решение нестандартных уравнений, содержащих модули.Пример9. Решить уравнение 3| x + 2 | + x2 + 6x + 2 = 0. Решение. Рассмотрим два случая. [pic]Ответ: (– 4; – 1).Пример10. Решить уравнение | 4 – x | + | (x – 1)(x – 3) | = 1. Решение.Учитывая, что | 4 – x | = | x – 4 |, рассмотрим четыре случая. [pic]так как [pic]2) [pic]3) 4) [pic]4) [pic]Ответ: 3. Графический способ.Построим графики функций y = |(x–1)(x–3)| и y=1–|x–4 |1)в Гy = |(x–1)(x–3)| подставим значение х=1 и х=3. Мы получим у=0,тоесть пересечение графика с осью ОХ. При х равном нулю у=3, тоесть графикпересекается с осью ОУ в точке (0 ;3). И при х=4 у также равен 3- мыполучили первый график.2) y=1–|x–4 | Найдем пересечение с осью ОХ, для этого решим простоеуравнение: 1-|x-4|=0 |x-4|=1 x — 4=1 или x — 4=-1 x=5 x=3Следовательно данный график пересекает ось ОХ в точках 5 и 3.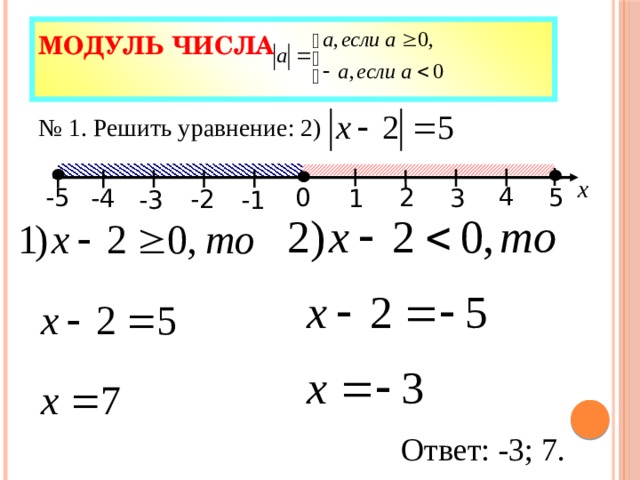 При х=4 у=1 и ак видно из графика: графики обеих функций пересекаются водной точке 3[pic]Ответ: 3Пример11. Решить уравнение | x2 + 3x | = 2(x + 1). Решение. Уравнение равносильно системе [pic]Ответ: [pic]Пример12.Решить уравнение х2 — 4х +|x — 3| +3=0Для освобождения от знака абсолютной величины разобьем числовую прямую надве области и будем искать решения исходного уравнения в каждой из этихобластей отдельно:__________x ?3__________________|____________x0?два различ. корняx=0 –посторонний корень, так как x1= (5- 1 )/2 =2не удовлетворяет промежутку. x2=(5 + 1)/2=3 x=3 -посторонний корень, так как неудовлетворяет промежутку.Значит, исходное уравнение имеет два решения х1=2 и х2=3Ответ: х1=2, х2=3Пример13. Решить уравнение | 2x + 8 | – | x – 5 | = 12. Решение. Раскрытие пары модулей приводит к трем случаям (без x + 4 ? 0, x – 5 ? 0).[pic]Ответ: – 25; 3. Пример 14. Решить уравнение . [pic] Решение:Напишем равносильную смешанную систему: [pic]Ответ: х=-4 Пример 15 Решить графически уравнение |1 – x| — |2x + 3| + x + 4=0 Решение:Представим уравнение в виде |1 – x| — |2x + 3| =-х – 4Построим два графика у=|1 – x| — |2x + 3| и у=-х – 41) у=|1 – x| — |2x + 3|Критические точки: х=1, х=-1.
При х=4 у=1 и ак видно из графика: графики обеих функций пересекаются водной точке 3[pic]Ответ: 3Пример11. Решить уравнение | x2 + 3x | = 2(x + 1). Решение. Уравнение равносильно системе [pic]Ответ: [pic]Пример12.Решить уравнение х2 — 4х +|x — 3| +3=0Для освобождения от знака абсолютной величины разобьем числовую прямую надве области и будем искать решения исходного уравнения в каждой из этихобластей отдельно:__________x ?3__________________|____________x0?два различ. корняx=0 –посторонний корень, так как x1= (5- 1 )/2 =2не удовлетворяет промежутку. x2=(5 + 1)/2=3 x=3 -посторонний корень, так как неудовлетворяет промежутку.Значит, исходное уравнение имеет два решения х1=2 и х2=3Ответ: х1=2, х2=3Пример13. Решить уравнение | 2x + 8 | – | x – 5 | = 12. Решение. Раскрытие пары модулей приводит к трем случаям (без x + 4 ? 0, x – 5 ? 0).[pic]Ответ: – 25; 3. Пример 14. Решить уравнение . [pic] Решение:Напишем равносильную смешанную систему: [pic]Ответ: х=-4 Пример 15 Решить графически уравнение |1 – x| — |2x + 3| + x + 4=0 Решение:Представим уравнение в виде |1 – x| — |2x + 3| =-х – 4Построим два графика у=|1 – x| — |2x + 3| и у=-х – 41) у=|1 – x| — |2x + 3|Критические точки: х=1, х=-1. 5(1 – х) ________+________|______ +____________|_____-______ >(2х +3) — -1.5 + 1 +а) х0 и (2х + 3)0 и (2x +3) ?0, т.е функция примет виду=1 – х – 2х -3, у=-3х – 2 –графиком является прямая, проходящая через дветочки (0; -2), (-1; 1).в)При х ?1, (1 – х) ?0 и (2х + 3)>0, т.е. функция примет вид у= -1 + х – 2х– 3,у= -х – 4 –графиком является прямая, проходящая через две точки (0; -4),(-4; 0).График функции у= — х – 4 совпадает с графиком у=|1 – x| — |2x + 3|, при х?1,Поэтому решением являются все х ?1 и х= -4[pic]Ответ: х ?1,х= -4 Аналитическое решение.y=|1 – x| — |2x + 3|y=-x – 4Построим числовую прямую так, чтобы по определению модуля знак абсолютнойвеличины числа можно будет снять. Для этого найдем критические точки: 1-х=0 и 2х – 3 =0, х=1 х=-1,5___________х
5(1 – х) ________+________|______ +____________|_____-______ >(2х +3) — -1.5 + 1 +а) х0 и (2х + 3)0 и (2x +3) ?0, т.е функция примет виду=1 – х – 2х -3, у=-3х – 2 –графиком является прямая, проходящая через дветочки (0; -2), (-1; 1).в)При х ?1, (1 – х) ?0 и (2х + 3)>0, т.е. функция примет вид у= -1 + х – 2х– 3,у= -х – 4 –графиком является прямая, проходящая через две точки (0; -4),(-4; 0).График функции у= — х – 4 совпадает с графиком у=|1 – x| — |2x + 3|, при х?1,Поэтому решением являются все х ?1 и х= -4[pic]Ответ: х ?1,х= -4 Аналитическое решение.y=|1 – x| — |2x + 3|y=-x – 4Построим числовую прямую так, чтобы по определению модуля знак абсолютнойвеличины числа можно будет снять. Для этого найдем критические точки: 1-х=0 и 2х – 3 =0, х=1 х=-1,5___________х

 Практический тест
Практический тест