Тригонометрические уравнения исключения. Решение тригонометрических уравнений
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей.
Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Вы можете заказать подробное решение вашей задачи !!!
Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.
Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число. Запишем для каждого из них формулы корней.
1. Уравнение `sin x=a`.
При `|a|>1` не имеет решений.
При `|a| \leq 1` имеет бесконечное число решений.
Формула корней: `x=(-1)^n arcsin a + \pi n, n \in Z`
2.
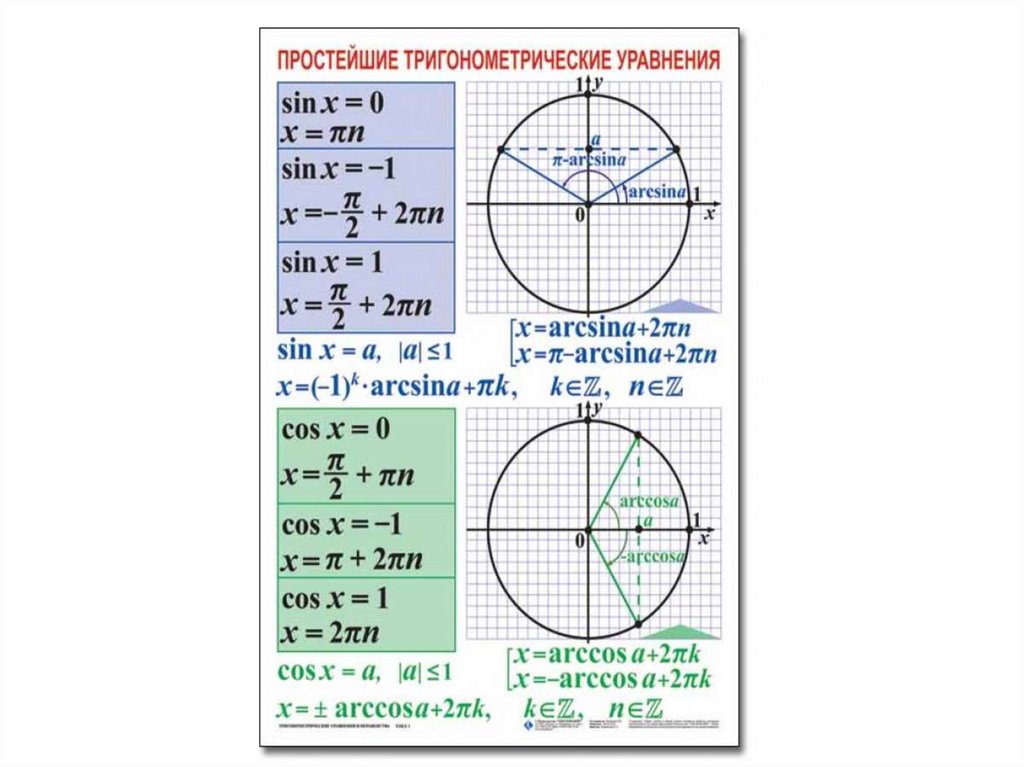Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`
Формулы корней тригонометрических уравнений в таблице
Для синуса:
Для косинуса:
Для тангенса и котангенса:
Формулы решения уравнений, содержащих обратные тригонометрические функции:
Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Простейшие тригонометрические уравнения решаются, как правило, по формулам. Напомню, что простейшими называются вот такие тригонометрические уравнения:
sinx = а
cosx = а
tgx = а
ctgx = а
х — угол, который нужно найти,
а — любое число. А вот и формулы, с помощью которых можно сразу записать решения этих простейших уравнений.
Для синуса:
Для косинуса:
х = ± arccos a + 2π n, n ∈ Z
Для тангенса:
х = arctg a + π n, n ∈ Z
Для котангенса:
х = arcctg a + π n, n ∈ Z
Собственно, это и есть теоретическая часть решения простейших тригонометрических уравнений. Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона. Почему?
Да потому, что масса народу записывает эти буковки, не понимая их смысла совершенно! С опаской записывает, как бы чего не вышло…) С этим надо разобраться. Тригонометрия для людей, или люди для тригонометрии, в конце концов!?)
Разберёмся?
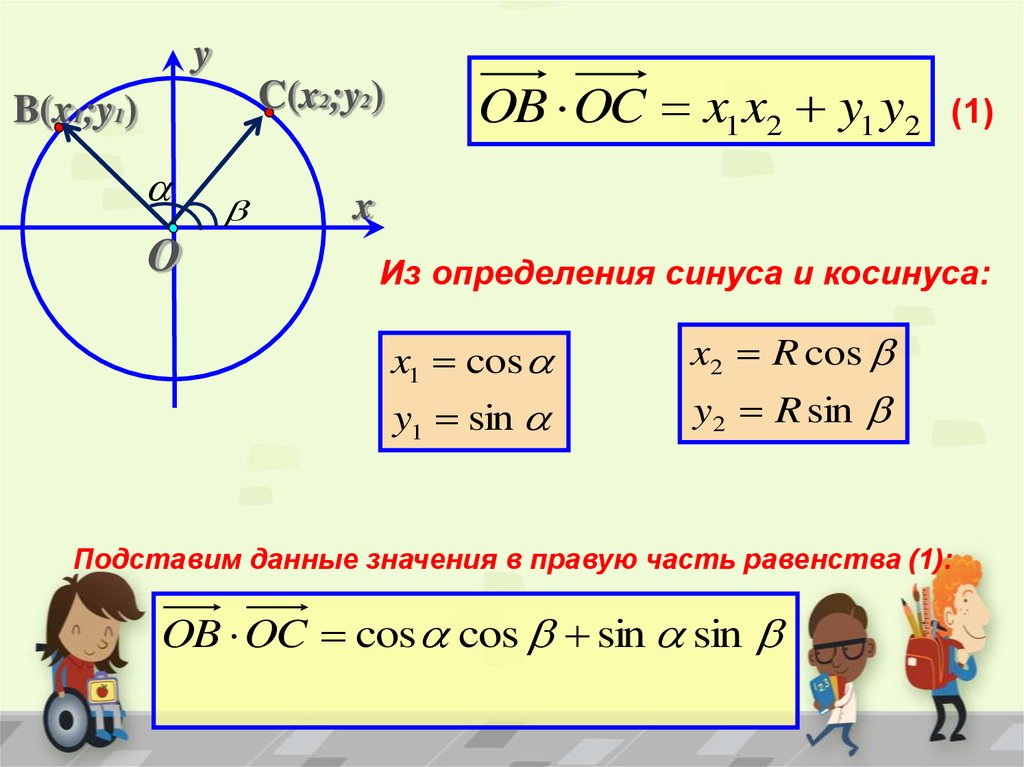
Один угол у нас будет равен arccos a, второй: -arccos a.
И так будет получаться всегда. При любом а.
Если не верите, наведите курсор мышки на картинку, или коснитесь рисунка на планшете.) Я изменил число а на какое-то отрицательное. Всё равно, один угол у нас получился arccos a, второй: -arccos a.
Следовательно, ответ можно всегда записать в виде двух серий корней:
х 1 = arccos a + 2π n, n ∈ Z
х 2 = — arccos a + 2π n, n ∈ Z
Объединяем эти две серии в одну:
х= ± arccos а + 2π n, n ∈ Z
И все дела. Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом.
Если вы понимаете, что это не какая-то сверхнаучная мудрость, а просто сокращённая запись двух серий ответов, вам и задания «С» будут по плечу. С неравенствами, с отбором корней из заданного интервала… Там ответ с плюсом/минусом не катит. А если отнестись к ответу делово, да разбить его на два отдельных ответа, всё и решается.) Собственно, для этого и разбираемся.
Что, как и откуда.В простейшем тригонометрическом уравнении
sinx = а
тоже получается две серии корней. Всегда. И эти две серии тоже можно записать
х = (-1) n arcsin a + π n, n ∈ Z
Но суть остаётся прежней. Математики просто сконструировали формулу, чтобы вместо двух записей серий корней, сделать одну. И всё!
Проверим математиков? А то мало ли…)
В предыдущем уроке подробно разобрано решение (безо всяких формул) тригонометрического уравнения с синусом:
В ответе получились две серии корней:
х 1 = π /6 + 2π n, n ∈ Z
х 2 = 5π /6 + 2π n, n ∈ Z
Если мы будем решать это же уравнение по формуле, получим ответ:
х = (-1) n arcsin 0,5 + π n, n ∈ Z
Вообще-то, это недоделанный ответ.) Ученик обязан знать, что arcsin 0,5 = π /6. Полноценный ответ будет:
х = (-1) n π /6 + π n, n ∈ Z
Тут возникает интересный вопрос.
Ответ через х 1 ; х 2 (это правильный ответ!) и через одинокий х (и это правильный ответ!) — одно и то же, или нет? Сейчас узнаем.)Подставляем в ответ с х 1 значения n =0; 1; 2; и т.д., считаем, получаем серию корней:
х 1 = π/6; 13π/6; 25π/6 и так далее.
При такой же подстановке в ответ с х 2 , получаем:
х 2 = 5π/6; 17π/6; 29π/6 и так далее.
А теперь подставляем значения n (0; 1; 2; 3; 4…) в общую формулу для одинокого х . Т.е возводим минус один в нулевую степень, затем в первую, вторую, и т.д. Ну и, разумеется, во второе слагаемое подставляем 0; 1; 2 3; 4 и т.д. И считаем. Получаем серию:
х = π/6; 5π/6; 13π/6; 17π/6; 25π/6 и так далее.
Вот всё и видно.) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.
)Формулы для решения тригонометрических уравнений с тангенсом и котангенсом тоже можно проверить. Но не будем.) Они и так простенькие.
Я расписал всю эту подстановку и проверку специально. Здесь важно понять одну простую вещь: формулы для решения элементарных тригонометрических уравнений есть, всего лишь, краткая запись ответов. Для этой краткости пришлось вставить плюс/минус в решение для косинуса и (-1) n в решение для синуса.
Эти вставки никак не мешают в заданиях, где нужно просто записать ответ элементарного уравнения. Но если надо решать неравенство, или далее нужно что-то делать с ответом: отбирать корни на интервале, проверять на ОДЗ и т.п, эти вставочки могут запросто выбить человека из колеи.
И что делать? Да либо расписать ответ через две серии, либо решать уравнение/неравенство по тригонометрическому кругу. Тогда исчезают эти вставочки и жизнь становится легче.)
Можно подвести итоги.
Для решения простейших тригонометрических уравнений существуют готовые формулы ответов.
Четыре штуки. Они хороши для мгновенной записи решения уравнения. Например, надо решить уравнения:sinx = 0,3
Легко: х = (-1) n arcsin 0,3 + π n, n ∈ Z
cosx = 0,2
Без проблем: х = ± arccos 0,2 + 2π n, n ∈ Z
tgx = 1,2
Запросто: х = arctg 1,2 + π n, n ∈ Z
ctgx = 3,7
Одной левой: x= arcctg3,7 + π n, n ∈ Z
cos x = 1,8
Если вы, блистая знаниями, мгновенно пишете ответ:
х= ± arccos 1,8 + 2π n, n ∈ Z
то блистаете вы уже, это… того… из лужи.) Правильный ответ: решений нет.
А если уж вам попалось неравенство, типа
то ответ в виде:
х πn, n ∈ Z
есть редкая ахинея, да.
..) Тут надо по тригонометрическому кругу решать. Чем мы и займёмся в соответствующей теме.Для тех, кто героически дочитал до этих строк. Я просто не могу не оценить ваши титанические усилия. Вам бонус.)
Бонус:
При записи формул в тревожной боевой обстановке, даже закалённые учёбой ботаны частенько путаются, где πn, а где 2π n. Вот вам простой приёмчик. Во всех
формулах стоит πn. Кроме единственной формулы с арккосинусом. Там стоит 2πn. Два пиэн. Ключевое слово — два. В этой же единственной формуле стоят два знака в начале. Плюс и минус. И там, и там — два.Так что, если вы написали два знака перед арккосинусом, легче вспомнить, что в конце будет два пиэн. А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.
Если Вам нравится этот сайт… )Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Основными методами решения тригонометрических уравнений являются: сведение уравнений к простейшим (с использованием тригонометрических формул), введение новых переменных, разложение на множители. Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.
Необходимым условием успешного решения тригонометрических уравнений является знание тригонометрических формул (тема 13 работы 6).
Примеры.
1. Уравнения, сводящиеся к простейшим.
1) Решить уравнение
Решение:
Ответ:
2) Найти корни уравнения
(sinx + cosx) 2 = 1 – sinxcosx, принадлежащие отрезку .
Решение:
Ответ:
2.
Уравнения, сводящиеся к квадратным.1) Решить уравнение 2 sin 2 x – cosx –1 = 0.
Решение: Используя формулу sin 2 x = 1 – cos 2 x, получаем
Ответ:
2) Решить уравнение cos 2x = 1 + 4 cosx.
Решение: Используя формулу cos 2x = 2 cos 2 x – 1, получаем
Ответ:
3) Решить уравнение tgx – 2ctgx + 1 = 0
Решение:
Ответ:
3. Однородные уравнения
1) Решить уравнение 2sinx – 3cosx = 0
Решение: Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1. Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим
Ответ:
2) Решить уравнение 1 + 7 cos 2 x = 3 sin 2x
Решение:
Используем формулы 1 = sin 2 x + cos 2 x и sin 2x = 2 sinxcosx, получим
sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0Пусть cosx = 0, тогда sin 2 x = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1.
Значит cosx ≠ 0 и можно поделить уравнение на cos 2 x. Получимtg 2 x – 6 tgx + 8 = 0
Обозначим tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y 2 = 2
а) tgx = 4, x= arctg4 + 2 k , k
б) tgx = 2, x= arctg2 + 2 k , k .Ответ: arctg4 + 2 k , arctg2 + 2 k, k
4. Уравнения вида a sinx + b cosx = с, с ≠ 0.
1) Решить уравнение .
Решение:
Ответ:
5. Уравнения, решаемые разложением на множители.
1) Решить уравнение sin2x – sinx = 0.
Корнем уравнения f ( х ) = φ ( х ) может служить только число 0. Проверим это:
cos 0 = 0 + 1 – равенство верно.
Число 0 единственный корень данного уравнения.
Ответ: 0.
”Тригонометрические уравнения. Решение простейших тригонометрических уравнений вида sinx = a. “
Тема: ”Тригонометрические уравнения. Решение простейших тригонометрических уравнений вида sinx = a.
“Эпиграф урока: ”Изучать что-либо и не задумываться над
выученным — абсолютно бесполезно.
Задумываться над чем-либо, не изучив
предварительно предмет раздумий-
опасно.”
Конфуций.
Основные цели: 1) Повторить с учащимися определение и свойства функции
у = sinx и ее график.
2) Сформировать умение решать простейшие
тригонометрические уравнения, а также уравнения,
сводящиеся к простейшим в результате преобразования
тригонометрических выражений.
Оборудование урока:
1. Учебная литература:
1) Алгебра: Учеб. для 9 кл. общеобразоват. учреждений/
Ю.Н.Макарычев, Н. Г. Миндюк, К. И.Нешков, С. Б.Суворова;
Под ред. С. А. Теляковского. – 4-е изд. – М.: Прсвещение,1997. –
272 с.: ил. – ISBN 5-09-007514-X.
2) Галицкий М.Л. и др.
Сборник задач по алгебре для 8-9 классов. Учебное пособие для
учащихся школ и классов с углубленным изучением математики/
М.Л. Галицкий, А.М.Гольдман, Л.И.Звавич. – 3-е изд. – М.: 1996. –
271 с.: ил. —
2. Плакаты.
Ход урока.
1.Вводная беседа (о программе, тетрадях, требованиях).
Фронтально проверить домашнее задание.
2.Повторение материала по вопросам.
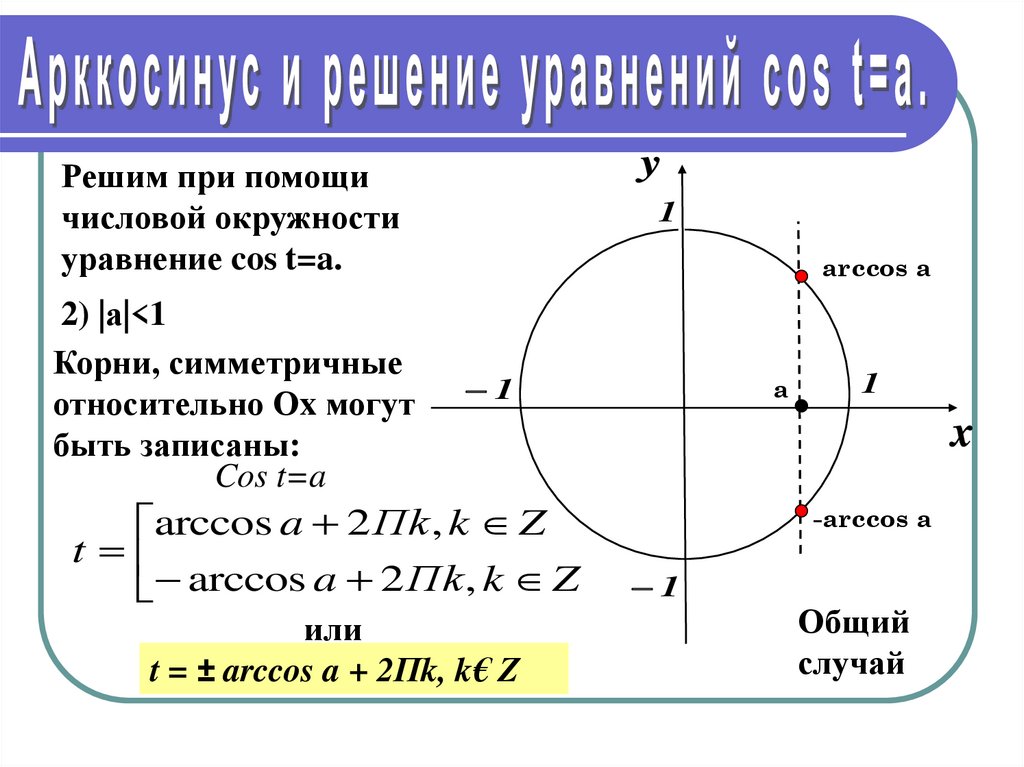
Q(a; b)
a) Дать определение sinx.
Чтобы определить понятия тригонометрических функций, рассматривают круг с центром, расположенным в начале координат, и радиусом равным единице (это так называемый тригонометрический круг). Для любого действительного числа х можно провести радиус OQ этого круга, образующий с осью абсцисс угол, радианная мера которого равна числу х (положительным считается направление поворота против хода часовой стрелки).
Пусть конец единичного радиуса OQ, соответствующего углу х,
совпадает с точкой Q(a;b) окружности; тогда координаты (a;b) точки Q называют координатами конца радиуса, соответствующего углу х.
Определение. Число, равное ординате конца единичного радиуса, соответствующего углу х, называется синусом угла х и обозначается sinx.
Поскольку каждому значению величины угла х на тригонометрическом круге соответствует единственная точка Q(a;b) такая, что радиус OQ образует угол х с осью абсцисс, то введенное отображение y = sinx является функцией.
б) Область определения функции. Так как для любого значения угла однозначно определена точка, являющаяся концом соответствующего радиуса, то область определения функции y = sinx – множество действительных чисел. Пишут D(sin) = R.
в) Область значений функции. E(sin) = [-1;1]. Действительно, ордината всякой точки, являющейся концом радиуса тригонометрического круга, может принимать лишь значения на отрезке [-1;1]. С другой стороны, для каждого значения ординаты b из этого отрезка можно указать хотя бы одну точку на окружности, имеющую эту ординату. Следовательно, это значение b будет синусом угла, образованного положительным направлением оси абсцисс и радиусом, соединяющим центр окружности и построенную точку.
г) Периодичность. Наименьший положительный период функции равен 2π . Докажем это. Поскольку центральный угол, опирающийся на дугу, совпадающую со всей окружностью, равен 2π , то точки, соответствующие углам х, (х+2π), (х -2π), изображаются на тригонометрическом круге одной и той же точкой, следовательно, синусы этих углов равны.
Это означает, что число T=2π является периодом рассматриваемой
функции. Докажем, что это наименьший положительный период. Рассмотрим значение
функции y = sinx, равное единице. Оно достигается, только если х = π/2 + 2πn,
n є Ζ. Следовательно, никакое число, меньшее 2π не может быть периодом.M(a,b)
д) Четность или нечетность. Рассмотрим (рис.2) точки M и N, соответствующие на тригонометрическом круге углам х и –х. Поскольку всякий круг симметричен относительно любой прямой, проходящей через его центр (а ось Оx является такой прямой), и равные по величине углы при симметрии переходят в равные углы, то точки M и N симметричны относительно оси Оx, следовательно, их ординаты противоположны. Это означает, что для любого значения х выполнено
sin(-x) = -sinx, т.
е. функция y = sinx является нечетной.N(a;-b)
е) Точки пересечения графика с осями координат. График пересекает ось Ох в точках с абсциссами, определяемыми уравнением sinx=0, т. е.
х = πn, n є Ζ; график пересекает ось Оу в точке с ординатой,
определяемой равенством y = sin0, т.е. у = 0.
ж) Промежутки знакопостоянства функции. Так как ординаты точек, лежащих в верхней полуплоскости, положительны, а точек, расположенных в нижней полуплоскости, отрицательны, то sinx > 0 при
х є (2πk; π + 2πk), k є Ζ; sin x < 0 при х є (π + 2πk; 2π + 2πk ), k є Ζ;
з) Наибольшее и наименьшее значение. Наибольшее значение, равное 1, достигается при х = π/2 + 2πn, n є Ζ ; наименьшее значение, равное -1, достигается при х = — π/2 + 2πn, n є Ζ ;
и) Интервалы возрастания и убывания.
Функция не является монотонной на всей области
определения; она является монотонной на отрезках: возрастает при х є ( — π /2
+2πk; π /2 + 2πk), k є Ζ; убывает прих є (π /2+ 2πk; 3π /2 + 2πk ), k є Ζ .
Для исследования функции на возрастание и убывание воспользуемся признаком возрастания и убывания, то есть найдем производную
f ́ (x) = (sinx) ́= cosx. Так как абсциссы точек, лежащих в правой полуплоскости положительны, то cos x >0 при х є ( — π /2 +2πk; π /2 + 2πk),
k є Ζ, следовательно, функция y = sinx будет возрастать на каждом промежутке вида ( — π /2 +2πk; π /2 + 2πk), k є Ζ . Абсциссы точек, лежащих в левой полуплоскости, отрицательны, т.е. cos x < 0 при
х є (π /2+ 2πk; 3π /2 + 2πk ), k є Ζ ; следовательно, на этих промежутках производная отрицательна и функция y = sinx будет убывать на промежутках вида (π /2+ 2πk; 3π /2 + 2πk ), k є Ζ.
к) Асимптоты. График функции асимптот не имеет.
3.
Изложение нового
материала.Решение уравнения sin х = а.
Поскольку по определению синусом угла называется ордината точки, лежащей на окружности единичного радиуса, то для решения уравнения
sin x =a надо найти на окружности все точки имеющие ординату a, т.е. лежащие на прямой y = a, см. рис.4
По теореме о взаимном расположении прямой и окружности на плоскости заключаем, что при |a| > 1 прямая и окружность общих точек не имеют, следовательно и рассматриваемое уравнение не имеет решений. Если |a| = 1, то прямая
y = a касается окружности, т.е. имеет с ней ровно одну общую точку C. Наконец, если |a| < 1, то имеются две точки пересечения (они располагаются симметрично относительно оси Oy). Для завершения решения задачи остается заметить, что каждой полученной точке соответствует бесконечное множество точек на числовой прямой, отстоящих друг от друга на расстояние 2π. Все они и являются решениями рассматриваемого уравнения.
Для записи решения уравнения sin x = a вводят понятие арксинуса числа a.
Чтобы
однозначно определить угол х0 , соответствующий числу а,
приходится требовать выполнения дополнительного условия, например, чтобы этот
угол принадлежал интервалу [-π /2; π /2].Определение. Арксинусом числа а, а є [-1;1], называется такое число х0, принадлежащее отрезку [-π /2; π /2], синус которого равен а. Это число обозначается arcsin a.
Из определения следует, что для каждого числа а, |a| ≤ 1, выполнено
sin(arcsin a) = a и −π /2 ≤ arcsin a ≤ π /2;
и наоборот, если выполнены условия
sinx = a и −π /2 ≤ a ≤ π /2 ,
то x = arcsin a.
С помощью введенного понятия удобно записать решение уравнения. По определению, точке пересечения A соответствует угол х1 = arcsin a, см. рис.4. Учитывая периодичность функции y = sin x, получим серию решений
x = arcsin a + 2πk, k є Ζ .
Точка В, как отмечалось, симметрична точке А относительно оси Оу, поэтому ей соответствует угол х2 = π − arcsin a, поэтому можно записать вторую серию решений
x = π − arcsin a + 2πk, k є Ζ .
Других решений рассматриваемое уравнение иметь не может, поскольку противное означало бы, что окружность и прямая пересекаются более чем в двух точках.
Для сокращения записи две полученные серии решений обычно объединяют в одну
x = (-1) arcsin a + πk, k є Ζ .
При четных значениях k эта формула соответствует первой серии решений; при нечетных — второй.
4. Решение нескольких примеров на доске.
Пример 1. Решить уравнение sin(π /6 – 2x) = √3 /2.
□ Имеем π /6 – 2x = ( — 1) arcsin √3 /2 + πk. Так как arcsin √3 /2 = π /3, то
π /6 – 2x = ( — 1) π /3 + πk, откуда х = — ( — 1) π /6 + π /12 + πk /2, или
х = (-1) π /6 + π /12 (6k + 1), k є Ζ.
■Если уравнение не является простейшим, то с помощью тождественных преобразований его нужно свести к одному или нескольким простейшим уравнениям, совокупность которых равносильна заданному.
При решении тригонометрических уравнений часто используются разложение на множители и введение новой переменной (метод подстановки).
Пример 2. Решить уравнение sin x = sin 2x cos 3x.
□ Применив к sin 2x формулу синуса двойного аргумента, получим
sin x = 2 sin x cos x cos 3x; sin x (1 — 2 cos x cos 3x) = 0.
Так как множители в левой части этого уравнения имеют смысл при любых значениях х, то оно равносильно совокупности двух уравнений: sin x = 0 и
1 — 2 cos x cos 3x = 0.
Первому уравнению удовлетворяют значения x = πn, n є Ζ.
Для решения второго уравнения преобразуем произведение косинусов в сумму; имеем 1 – (cos 4x + cos 2x) = 0. Поскольку 1- cos 4x = 2 sin2x, уравнение принимает вид 2sin2x – cos 2x = 0, или 2(1-cos 2x)-cos 2x = 0, откуда получим 2cos2x + cos 2x – 2 = 0— квадратное уравнение относительно cos 2x.
Полагая cos 2x = z , имеем 2z + z – 2 = 0. Решив это уравнение, находим z1
= (-1 + √17) /4, z2 = (-1-√17) /4. Так как|z2| =|(-1-√17) /4| >1, то уравнение cos 2x = z2 не имеет решений. Остается решить уравнение cos 2x = (-1 + √17) /4. Имеем 2х = ± arccos(√17-1) /4 + 2πk, k є Ζ. Итак получаем ответ: x = πn; х = ± (1 /2)arccos(√17 -1) /4 + πk, k,n є Ζ. ■
При решении уравнения методом разложения на множители оно может не быть равносильным полученной совокупности уравнений, так как возможно появление посторонних корней. Чтобы избежать ошибки в ответе, нужно исключить из найденных значений неизвестного те, для которых заданное уравнение не имеет смысла.
Пример 3. Решить уравнение (1-sinx)(tg x-3) = 0.
□ Найдем значения х, удовлетворяющие каждому из уравнений 1-sinx = 0 и tg x-3 = 0; если sinx = 1,то получим
x = π /2 + 2πk, k є Ζ; (1)
если tg x = 3, т.
е. tgx = ±√3,
тоx = ±π /3 + πn, n є Ζ. (2)
Однако было бы ошибочным считать ответом объединение решений (1) и (2). Дело в том, что исходное уравнение не имеет смысла для значений
x = π /2 +πn (n є Ζ), поэтому первое из предполагаемых решений непригодно и ответом является только второе решение x = ±π /3 + πn, n є Ζ.■
Пример 4. Решить уравнение cosx cos2x cos4x = 1/8.
□ Наиболее быстрый способ решения – умножение правой и левой частей равенства на 8sinx, хотя при этом возможно появление посторонних корней. Чтобы избежать этого, следует учитывать, что в окончательное решение не должны входить значения х, для которых sinx = 0, т.е. значения x = πn (nєΖ), так как они не удовлетворяют исходному уравнению.
После умножения на 8sinx уравнение примет вид
8sinx cosx cos2x cos4x = sinx.
Последовательно трижды применив формулу sin2x = 2 sinx cosx, получим сначала 4sin2x cos2x cos4x = sinx, затем 2sin4x cos4x = sinx и далее
sin8x = sinx, или sin8x — sinx = 0.
Преобразуя по формулеsinx-siny = 2cos(x+y)/2 sin(x-y)/2 разность синусов в произведение, получаем
Пусть sin 7x/2 = 0, тогда 7х/2 = πk (k є Ζ), откуда х = 2πk /7, k є Ζ, причем следует исключить значения х = 2πn (n є Ζ), получающиеся при k = 7n, как посторонние для исходного уравнения. Пусть теперь cos 9x/2 = 0;
тогда 9х/2 = π /2 + πm (m є Ζ), откуда х = π (2m +1) /9 (m є Ζ), причем следует исключить значения х = π(2n +1) (n є Ζ), получающиеся при m=9n+4 (nєΖ),как посторонние для исходного уравнения.
Итак, получаем ответ: х = 2πk /7, где целое k ≠ 7n, n є Ζ; х = π (2m + 1) /9, где целое m ≠ 9n + 4, n є Ζ. ■
5. Заключение урока.
1) теоретико-прикладные итоги урока; дифференцированная оценка
уровня ментального опыта учащихся: уровня усвоения ими темы,
компетентности, качества устной и письменной математической речи;
уровня проявленного творчества; уровня самостоятельности и рефлексии; уровня инициативы, познавательного интереса к отдельным методам математического мышления; уровней сотрудничества, интеллектуальной состязательности, стремления к высоким показателям учебно-математической деятельности и др.
;2) объявление аргументированных отметок, поурочного балла;
3) сбор тетрадей с домашней работой на выборочную или сплошную
проверку.
Спасибо за урок!
Тригонометрическая функция | Определение, формула и факты
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Этот день в истории
- Викторины
- Подкасты
- Словарь
- Биографии
- Резюме
- Популярные вопросы
- Обзор недели
- Инфографика
- Демистификация
- Списки
- #WTFact
- Товарищи
- Галереи изображений
- Прожектор
- Форум
- Один хороший факт
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Britannica объясняет
В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы. - Britannica Classics
Посмотрите эти ретро-видео из архивов Encyclopedia Britannica. - #WTFact Видео
В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти. - На этот раз в истории
В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории. - Demystified Videos
В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
- Студенческий портал
Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д. - Портал COVID-19
Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня. - 100 женщин
Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю. - Britannica Beyond
Мы создали новое место, где вопросы находятся в центре обучения. Вперед, продолжать. Просить. Мы не будем возражать. - Спасение Земли
Британника представляет список дел Земли на 21 век. Узнайте об основных экологических проблемах, стоящих перед нашей планетой, и о том, что с ними можно сделать! - SpaceNext50
Britannica представляет SpaceNext50. От полёта на Луну до управления космосом — мы изучаем широкий спектр тем, которые подпитывают наше любопытство к космосу!
Содержание
- Введение
Краткие факты
- Факты и сопутствующий контент
Викторины
- Числа и математика
6.
\circ \) и \(9\circ k \quad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(…\)}
\nonumber \]Это наиболее общее решение уравнения. Часто часть, которая говорит «for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(…\)» опускается, так как обычно понял, что \(k \) варьируется для всех целых чисел.Общее решение в радианах будет:
\[ А ~=~ 0,6435 \;+\; \pi k \quad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(…\)}
\nonumber \]Пример 6.1
\;\theta ~=~ \frac{1}{2} \quad\Rightarrow\quad \cos\;\theta ~=~ \pm\,\frac{1}{\sqrt{2}}
\quad \Rightarrow\quad \theta ~=~ \frac{\pi}{4}\;,~\frac{3\pi}{4}\;,~\frac{5\pi}{4}\;,~
\frac{7\pi}{4}~,
\nonumber \]и, поскольку период косинуса равен \(2\pi \), мы должны добавить \(2\pi k \) к каждому из этих углы, чтобы получить общее решение. Но обратите внимание, что приведенные выше углы отличаются кратно \(\frac{\pi}{2} \). Итак, поскольку каждое кратное \(2\pi \) также кратно \(\frac{\pi}{2} \), мы можем объединить эти четыре отдельных ответа в один:
\[ \boxed{\theta ~=~ \frac{\pi}{4} \;+\; \frac{\pi}{2}\,k}
\qquad\text{для \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \( . ..\)}
\nonumber \]Пример 6.3
Решите уравнение \(\;2\,\sec\;\theta ~=~ 1 \).
Решение:
Изоляция \(\;\sec\;\theta \) дает нам
\[ \sec\;\theta ~=~ \frac{1}{2} \quad\Rightarrow\quad \cos\;\theta ~=~ \frac{1}{\sec\;\theta} ~=~ 2~,
\nonumber \]что невозможно. Таким образом, существует \(\fbox{нет решения}\). 92 \;+\; Икс \;-\; 1 ~=~ 0 \quad\Rightarrow\quad x ~=~ \frac{-1 \;\pm\; \sqrt{1 — (4)\,(-1)}}{
2\,(1)} ~=~ \frac{-1 \;\pm\; \sqrt{5}}{2} ~=~ -1,618\;,~0,618
\nonumber \]по квадратичной формуле элементарной алгебры. Но \(-1,618 < -1 \), поэтому невозможно, чтобы \(\;\sin\theta = x = -1,618 \). Таким образом, мы должны иметь \(\;\sin\;\theta = x = 0,618 \). Следовательно, возможны два решения: \(\theta = 0,666\) рад в QI и его отражение \(\pi - \theta = 2,475\) рад вокруг оси \(y\) в QII. Добавление к ним кратных \(2\pi \) дает нам общее решение:
\[ \boxed{\theta ~=~ 0,666 \;+\; 2\pi k \quad\text{and}\quad 2.
475 \;+\; 2\pi k}
\qquad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(…\)}
\ nonumber \]Пример 6.5
Решите уравнение \(\;\sin\;\theta ~=~ \tan\;\theta \).
Решение:
Попробовав тот же метод, что и в предыдущем примере, мы получим
\[\nonumber \begin{align*}
\sin\;\theta ~&=~ \tan\;\theta\ \\nonumber
\sin\;\theta ~&=~ \frac{\sin\;\theta}{\cos\;\theta}\\ \nonumber
\sin\;\theta~\cos\;\theta ~&=~ \sin\;\theta\\ \nonumber
\sin\;\theta~\cos\;\theta \;-\; \sin\;\theta ~&=~ 0\\ \nonumber
\sin\;\theta~(\cos\;\theta \;-\; 1) ~&=~ 0\\ \nonumber
&\Rightarrow \quad \sin\;\theta ~=~ 0 \quad\text{or}\quad \cos\;\theta ~=~ 1\\ \nonumber
&\Стрелка вправо\quad \theta ~=~ 0\;, ~\pi \quad\text{or}\quad \theta ~=~ 0\\ \nonumber
&\Стрелка вправо\quad \theta ~=~ 0\;,~\pi~,
\end{align*} \ нечисло \]плюс кратные \(2\pi \). Итак, поскольку приведенные выше углы кратны \(\pi \), а каждое кратное \(2\pi \) кратно \(\pi \), мы можем объединить два ответа в один для общего решения: 9{-1} \frac{1}{2} = \frac{\pi}{3} \), есть два возможных решения для \(3\theta\): \(3\theta = \frac{\pi {3} \) в QI и его отражение \(-3\theta = -\frac{\pi}{3} \) вокруг оси \(x\) в QIV.
Добавление к ним кратных \(2\pi \) дает нам:\[ 3\theta ~=~ \pm\,\frac{\pi}{3} \;+\; 2\pi k \qquad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(…\)}
\nonumber \ ]Итак, разделив все на \(3 \), мы получим общее решение для \(\theta\):
\[ \boxed{\theta ~=~ \pm\,\frac{\pi}{9} \;+\; \frac{2\pi}{3} k}
\qquad\text{для \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(. ..\)}
\nonumber \]Пример 6.7
Решите уравнение \(\;\sin\;2\theta ~=~ \sin\;\theta \).
Решение:
Здесь мы используем формулу двойного угла для синуса:
\[\nonumber \begin{align*}
\sin\;2\theta ~&=~ \sin\;\theta\ \\nonumber
2\,\sin\theta~\cos\;\theta ~&=~ \sin\;\theta\\ \nonumber
\sin\;\theta~(2\,\cos\;\theta \;-\;1) ~&=~ 0\\ \номер
&\Rightarrow\quad \sin\;\theta ~=~ 0 \quad\text{or}\quad \cos\;\theta ~=~ \frac{1}{2}\\ \nonumber
&\Rightarrow \quad \theta ~=~ 0\;,~\pi \quad\text{or}\quad \theta ~=~ \pm\,\frac{\pi}{3}\\ \nonumber
&\Rightarrow\ quad \ boxed {\ theta ~ = ~ \ pi k \ quad \ text {and} \ quad \ pm \, \ frac {\ pi} {3} \; + \; 2\pi k}
\qquad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(. ..\)}
\ end{align*}
\nonumber \]Пример 6.8
Решить уравнение \(\;2\,\sin\;\theta \;-\; 3\,\cos\;\theta ~=~ 1 \).
Рисунок 6.1.1: Скопируйте и вставьте заголовок сюда. (Авторское право; автор через источник)Решение
Мы будем использовать технику, которую обсуждали в главе 5, для нахождения амплитуды комбинации функций синуса и косинуса. Возьмите коэффициенты \(2\) и \(3\) при \(\;\sin\;\theta\) и \(\;-\cos\;\theta\) соответственно в приведенном выше уравнении и сделайте на них стороны прямоугольного треугольника, как на рис. 6.1.1. Пусть \(\phi \) будет углом, показанным в прямоугольном треугольнике. Участок длины \(3 >0 \) означает, что угол \(\phi \) находится над осью \(x\), а участок длины \(2>0 \) означает, что \(\phi \) находится справа от оси \(y\). Следовательно, \(\phi \) должен быть в QI. Гипотенуза имеет длину \(\sqrt{13} \) по теореме Пифагора, и, следовательно, \(\;\cos\;\phi = \frac{2}{\sqrt{13}} \) и \(\; \sin\;\theta = \frac{3}{\sqrt{13}} \).
Мы можем использовать это, чтобы преобразовать уравнение, чтобы решить его следующим образом:\[\nonumber \begin{align*}
2\,\sin\;\theta \;-\; 3\,\cos\;\theta ~&=~ 1\\ \nonumber
\sqrt{13}\,\left( \tfrac{2}{\sqrt{13}}\,\sin\;\theta \ ;-\; \tfrac{3}{\sqrt{13}}\,\cos\;\theta
\right) ~&=~ 1\\ \nonumber
\sqrt{13}\,( \cos\; \phi\;\sin\;\theta \;-\;\sin\;\phi\;\cos\;\theta ) ~&=~ 1\\ \nonumber
\sqrt{13}\,\sin\ ;(\theta — \phi) ~&=~ 1\quad\text{(по формуле вычитания синусов)}\\ \nonumber
\sin\;(\theta — \phi) ~&=~ \tfrac{1 }{\sqrt{13}}\\ \номер
&\Rightarrow\quad \theta — \phi ~=~ 0,281 \quad\text{or}\quad \theta — \phi ~=~ \pi — 0,281 = 2,861\\ \nonumber
&\Rightarrow\quad \theta ~=~ \фи \;+\; 0,281 \quad\text{or}\quad \theta ~=~ \phi \;+\; 2.861
\end{align*} \nonumber \]Теперь, поскольку \(\;\cos\;\phi = \frac{2}{\sqrt{13}} \) и \(\phi \) равно в QI наиболее общим решением для \(\phi\) является \(\phi = 0,983 + 2\pi k \) для \(k=0 \), \(\pm\,1 \), \(\ ч\,2 \), \(.
.. \). Итак, поскольку нам нужно было добавить кратные \(2\pi \) к решениям \(0,281 \) и \(2,861 \) в любом случае, наиболее общее решение для \(\theta \):\[\begin{align*}
\тета ~&=~ 0,983 \;+\; 0,281 \;+\; 2\pi k\quad\text{and}\quad 0,983 \;+\; 2,861 \;+\; 2\pi k\\
&\Стрелка вправо\четверка \boxed{\theta ~=~ 1,264 \;+\; 2\pi k\quad\text{and}\quad 3.844 \;+\; 2\pi k}
\quad\text{для \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(…\)}
\ end{align*} \nonumber \]Примечание: в примере 6.8, если уравнение было \(\;2\,\sin\;\theta \;+\; 3\,\cos\;\theta ~= ~ 1 \), то мы все равно использовали бы прямоугольный треугольник с длинами сторон \(2\) и \(3\), но вместо формулы вычитания использовали бы формулу сложения синусов.
Эта страница под названием 6.1: Решение тригонометрических уравнений распространяется в соответствии с лицензией GNU Free Documentation License 1.3 и была создана, изменена и/или курирована Майклом Корралом посредством исходного контента, отредактированного в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.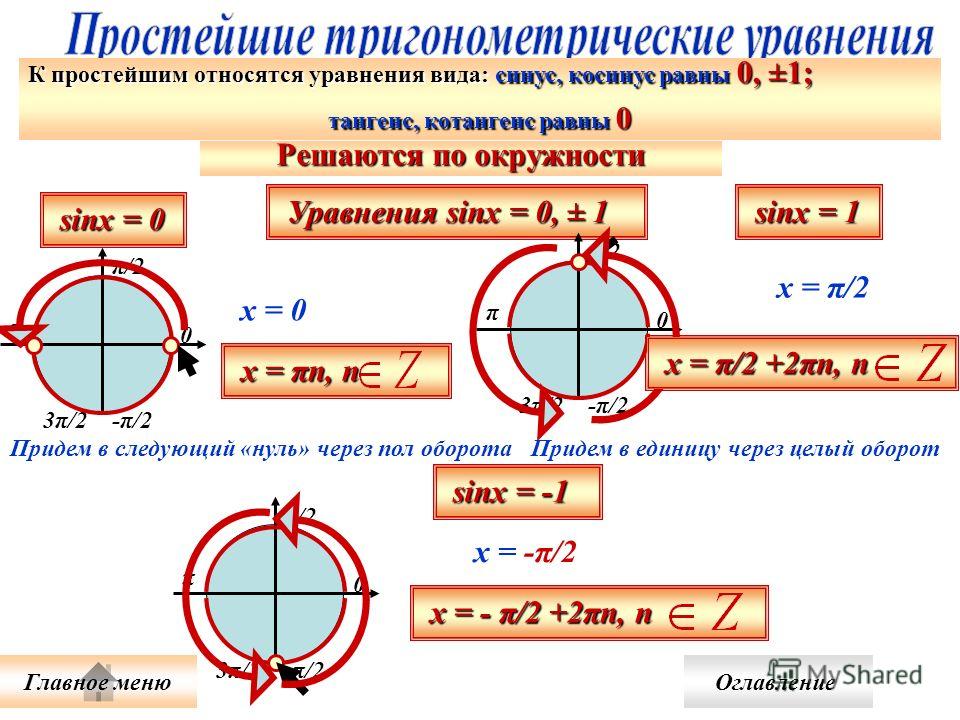
Что, как и откуда.
Четыре штуки. Они хороши для мгновенной записи решения уравнения. Например, надо решить уравнения:
..) Тут надо по тригонометрическому кругу решать. Чем мы и займёмся в соответствующей теме.
)
Уравнения, сводящиеся к квадратным.
“
Это означает, что число T=2π является периодом рассматриваемой
функции. Докажем, что это наименьший положительный период. Рассмотрим значение
функции y = sinx, равное единице. Оно достигается, только если х = π/2 + 2πn,
n є Ζ. Следовательно, никакое число, меньшее 2π не может быть периодом.
е. функция y = sinx является нечетной.
Функция не является монотонной на всей области
определения; она является монотонной на отрезках: возрастает при х є ( — π /2
+2πk; π /2 + 2πk), k є Ζ; убывает при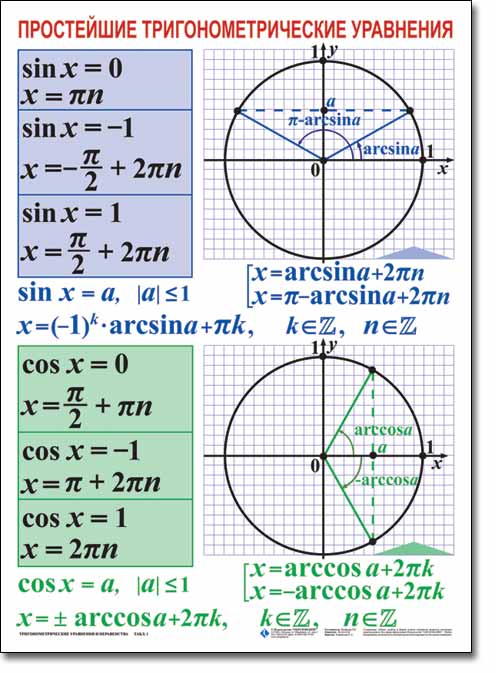
Изложение нового
материала.
Чтобы
однозначно определить угол х0 , соответствующий числу а,
приходится требовать выполнения дополнительного условия, например, чтобы этот
угол принадлежал интервалу [-π /2; π /2].
■
Полагая cos 2x = z , имеем 2z + z – 2 = 0. Решив это уравнение, находим z1
= (-1 + √17) /4, z2 = (-1-√17) /4. Так как
е. tgx = ±√3,
то
Преобразуя по формуле
;
\circ \) и \(9\circ k \quad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(…\)} 
..\)} 
475 \;+\; 2\pi k} 
Добавление к ним кратных \(2\pi \) дает нам:
..\)} 
Мы можем использовать это, чтобы преобразовать уравнение, чтобы решить его следующим образом:
.. \). Итак, поскольку нам нужно было добавить кратные \(2\pi \) к решениям \(0,281 \) и \(2,861 \) в любом случае, наиболее общее решение для \(\theta \):