Медиана к гипотенузе прямоугольного треугольника: свойства, задача
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Определение и свойства медианы прямоугольного треугольника
В данной статье мы рассмотрим определение и свойства медианы прямоугольного треугольника, проведенной к гипотенузе. Также разберем пример решения задачи для закрепления теоретического материала.
- Определение медианы прямоугольного треугольника
- Свойства медианы прямоугольного треугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Пример задачи
Определение медианы прямоугольного треугольника
Медиана – это отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
Прямоугольный треугольник – это треугольник, в котором один из углов является прямым (90°), а два остальных – острыми (<90°).
Свойства медианы прямоугольного треугольника
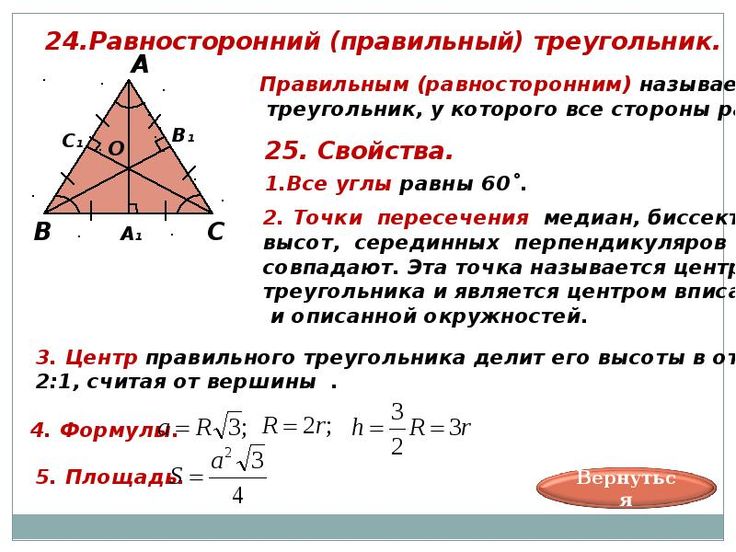
Свойство 1
Медиана (AD) в прямоугольном треугольнике, проведенная из вершины прямого угла (∠
- BC = 2AD
- AD = BD = DC
Следствие: Если медиана равняется половине стороны, к которой она проведена, то данная сторона является гипотенузой, а треугольник – прямоугольным.
Свойство 2
Медиана, проведенная к гипотенузе прямоугольного треугольника, равняется половине квадратного корня из суммы квадратов катетов.
Для нашего треугольника (см. рисунок выше):
Это следует из теоремы Пифагора и Свойства 1.
Свойство 3
Медиана, опущенная на гипотенузу прямоугольного треугольника, равна радиусу описанной вокруг треугольника окружности.
Т.е. BO – это одновременно и медиана, и радиус.
Примечание: К прямоугольному треугольнику также применимы общие свойства медианы, независимо от вида треугольника.
Пример задачи
Длина медианы, проведенной в гипотенузе прямоугольного треугольника, составляет 10 см. А один из катетов равен 12 см. Найдите периметр треугольника.
Решение
Гипотенуза треугольника, как следует из Свойства 1, в два раза больше медианы. Т.е. она равняется: 10 см ⋅ 2 = 20 см.
Воспользовавшись теоремой Пифагора находим длину второго катета (примем его за “b”, известный катет – за “a”, гипотенузу – за “с”):
b2 = с2 – a2 = 202 – 122 = 256.
Следовательно, b = 16 см.
Теперь мы знаем длины всех сторон и можем посчитать периметр фигуры:

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
ее определение, свойства, функции, формула нахождения
Что такое медиана
В геометрии понятие «медианы» рассматривается с позиции линии, разделяющей треугольник на две части. Многие задачи опираются на ее свойство и требуют знаний профильных теорем.
Многие задачи опираются на ее свойство и требуют знаний профильных теорем.
Медианой называется отрезок, который берет свое начало в вершине треугольника, а заканчивается на середине противоположной стороны.
Для равнобедренного треугольника медиана совпадает с его биссектрисой и высотой.
Определение 2Равнобедренным называется треугольник, у которого две стороны одинаковой длины. Эти две стороны считаются боковыми, а третья — основанием.
Определение 3Равносторонним (правильным) называется треугольник, который имеет три стороны одинаковой длины.
Определение 4Прямоугольным называется треугольник, имеющий угол 90°. В таком треугольнике сторона, противоположная прямому углу, называется гипотенузой, а две другие — катетами.
Определение 5Треугольник с тремя острыми углами называется остроугольным, а тот, у которого один угол тупой — тупоугольным.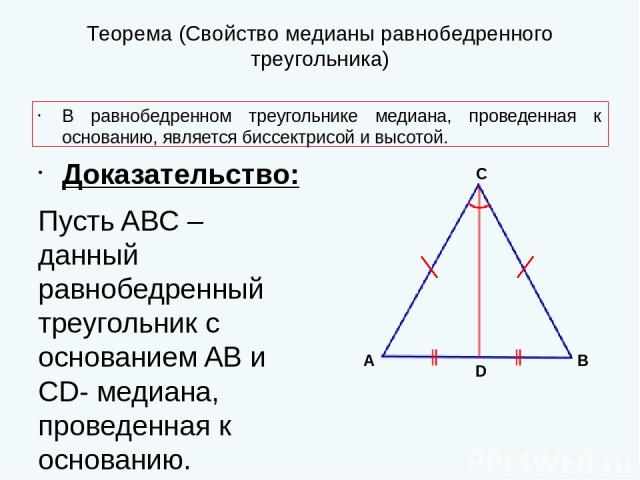
Биссектрисой угла называется луч, начинающийся в вершине угла и делящий его пополам. Биссектриса треугольника — часть (отрезок) биссектрисы угла, который соединяет вершину и точку, расположенную на стороне, противоположной стороне.
Определение 7Высотой в треугольнике принято называть отрезок, соединяющий вершину треугольника и его противоположную сторону, таким образом, что является к ней перпендикуляром.
Определение 8Отрезок, который соединяет середины сторон в треугольнике, носит название средней линии.
Определение 9Прямая, которая проходит через середину выбранного отрезка, образуя с ним прямой угол, — серединный перпендикуляр.
Функции медианы в треугольниках
Существует несколько теорем, дающих характеристику функций медианы.
Теорема 1Правильно построенная медиана делит треугольник на два, равных по площади.
Источник: fmclass.ru
Теорема 2Центроид — точка, в которой пересекаются медианы треугольника. Центроид делит медианы на две части 2:1, считая от вершины.
Центроид делит медианы на две части 2:1, считая от вершины.
Источник: fmclass.ru
Теорема 3Отрезками медиан, заключенными между вершинами и центроидом, треугольник делится на три одинаковых.
Источник: fmclass.ru
Теорема 4Когда медианы пересекаются, они делят треугольник на шесть одинаковых по площади.
Источник: fmclass.ru
Теорема 5Для вычисления длины медианы, которую провели из угла к стороне с (рисунок), пользуются формулой:
Источник: fmclass.ru
Схематически выглядит так:
Источник: fmclass.ru
Примеры заданий с объяснениями
Приведенные функции медианы находят свое применение при решении геометрических и прочих заданий.
Задача 1Дан равнобедренный треугольник. Его характеристики: длина боковой стороны — 5 см, проведенная медиана имеет длину 4 см. Необходимо посчитать площадь этого треугольника.
Решение
Для нахождения искомой величины рассмотрим чертеж:
Источник: ru.solverbook.com
Зная правило медианы, делить треугольник на два одинаковых, получаем следующее равенство: SΔABC=2SΔABL
Значит нужно определить SΔABL
По условию следует, что для равнобедренного треугольника медиана является высотой.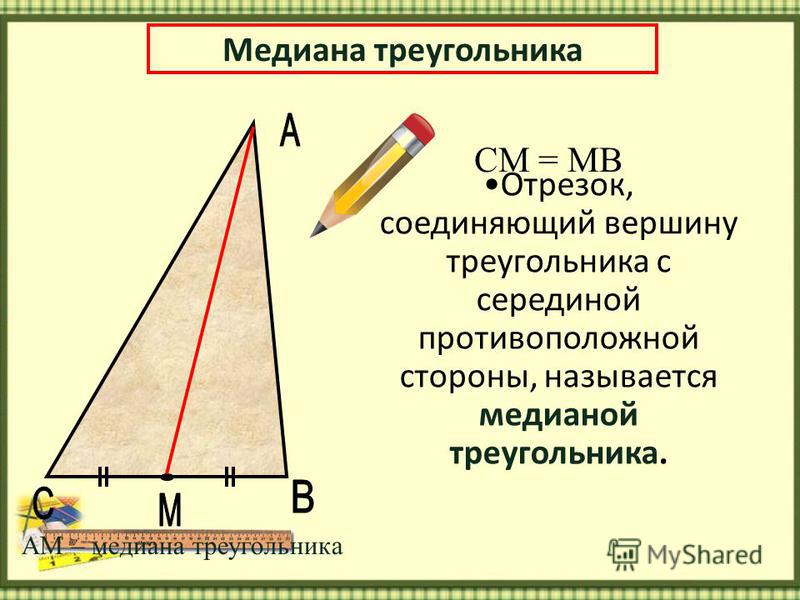 Поэтому справедлива формула: SΔABL= 1/2*AL*BL
Поэтому справедлива формула: SΔABL= 1/2*AL*BL
Катет AL по теореме Пифагора равен:
Источник: ru.solverbook.com
Теперь подставляем в формулу значения: SΔABL =6см2 .
Настало время определить площадь ΔABC: SΔABC=2SΔABL=6*2=12 см2.
Рассмотрим другой пример.
Задача 2Дан треугольник со сторонами: АВ=4 см, АС=6 см и углом А — 60о.
В примере проведено две медианы:
Источник: ru.solverbook.com
AL=LC=1/2AC=3см
Рассматривая треугольник ABL, используем теорему косинусов и получаем уравнение:
Источник: ru.solverbook.com
Дальнейшее объяснение опирается на свойство двух пересекающихся медиан, которые в этой точке делятся на отрезки с соотношением 2:1. Тогда:
Источник: ru.solverbook.com
Задачи для самостоятельной работы
Задача 3Источник: shkolkovo.net
Решение
Источник: shkolkovo.net
Задача 4Источник: shkolkovo.net
Решение:
Источник: shkolkovo.net
Задача 5Источник: https://shkolkovo.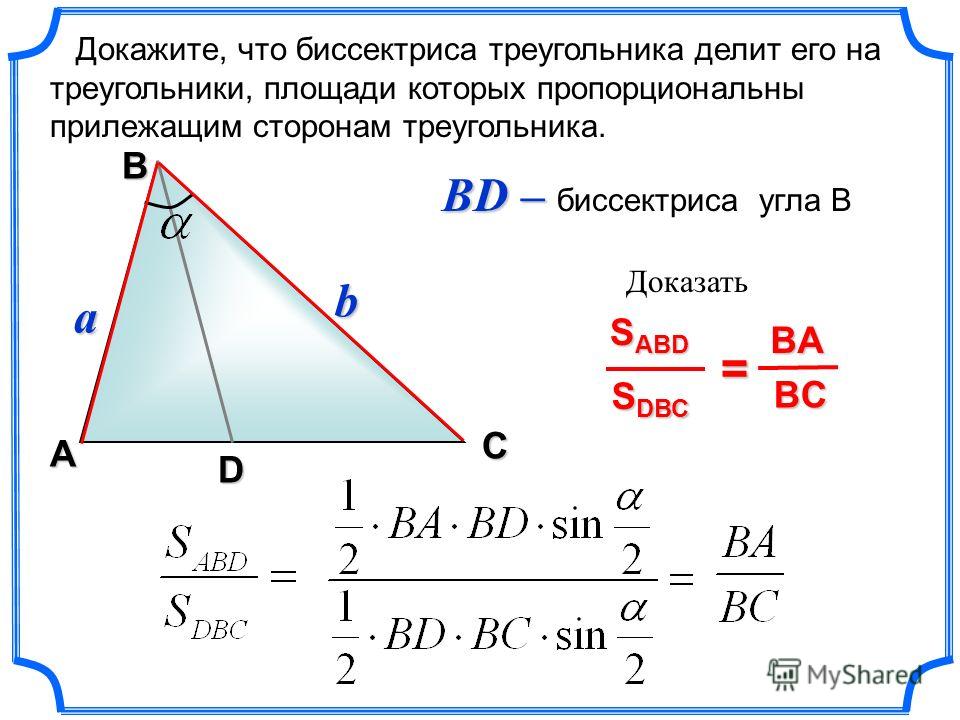 net/catalog/planimetriya_chast_i/treugolnik_fakty_o_vysote_bissektrise_i_mediane
net/catalog/planimetriya_chast_i/treugolnik_fakty_o_vysote_bissektrise_i_mediane
Решение
Рисунком к задаче является треугольник:
Источник: shkolkovo.net
Источник: shkolkovo.net
Урок Длина медианы треугольника
Этот Урок (Длина медианы треугольника) создан пользователем ikleyn(46855) : Просмотр исходного кода, Показать
О ikleyn :
00 0
Этот урок посвящен формуле, выражающей длину медианы треугольника.
раздел Алгебра-II на этом сайте). Также приведены примеры, показывающие, как использовать эту формулу.
Теорема 1
В треугольнике со сторонами a , b и c медиана, проведенная к стороне c , имеет длину
= . Доказывать.
Доказывать.
| Доказательство На рисунке 1 показан треугольник ABC со сторонами a (BC) , b (AC) и c (AB) и медиана м ( c 9 0 0 сторона 9.004 0 ) Пусть d будет длиной отрезка AD и e будет длиной отрезка DB как и углы при пересечении медианы CD и стороны АБ . Применить Закон косинусов , чтобы выразить длину стороны AC треугольника ADC | Рисунок 1 . К теореме 1 |
Теперь возьмем сумму двух последних равенств. Обратите внимание, что , поскольку углы и являются дополнительными углами.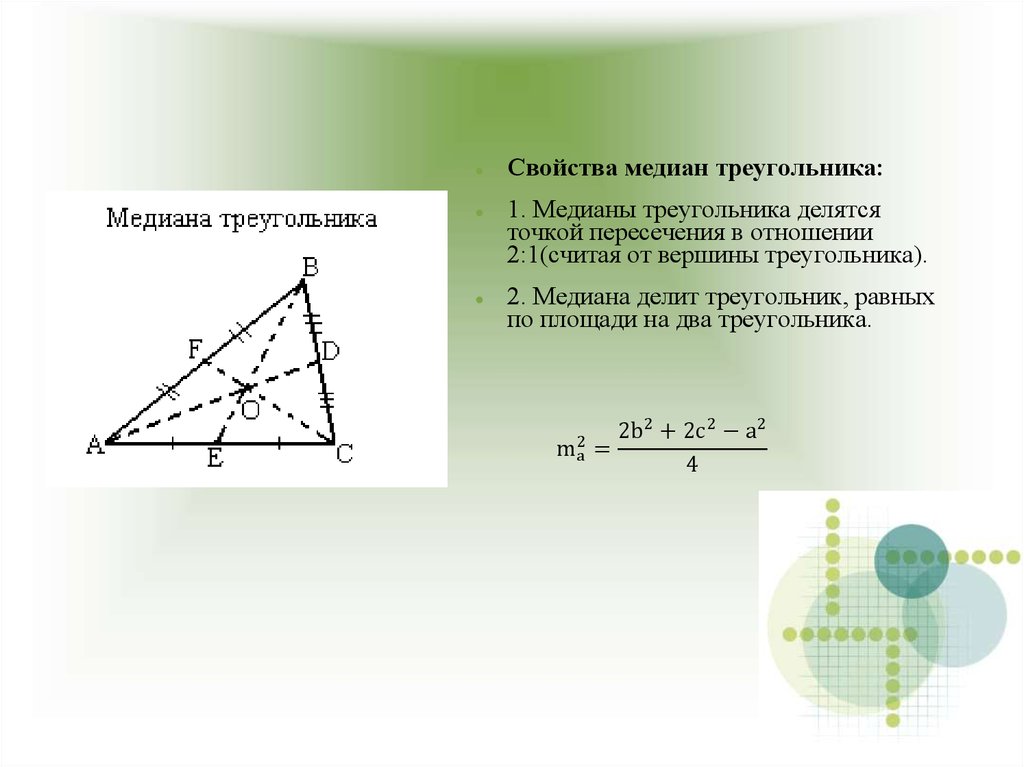 Также обратите внимание, что, поскольку CD — это
Также обратите внимание, что, поскольку CD — это
медиана. Следовательно, при взятии суммы условия и взаимно компенсируют друг друга. Итак, после суммирования получаем
+ = + + .
Замените здесь, используя тот факт, что CD является медианой. Получаем
+ = + + ,
или
= ( + — )/4.
Вот что нужно продемонстрировать. Доказательство завершено.
Теорема 2
В треугольнике со сторонами a , b и c длины медиан , и , проведенные к сторонам a , b и c соответственно удовлетворяют тождеству
= . Доказывать.
Доказательство
На основании Теоремы 1 имеем три равенства
= ,
= , и
= .
Суммируя эти равенства, получаем тождество
= .
Это именно то, что нужно продемонстрировать. Теорема 2 доказана.
| Пример 1 В треугольнике длины сторон равны a = 5 , b = 6 и c = 4 ( рис. 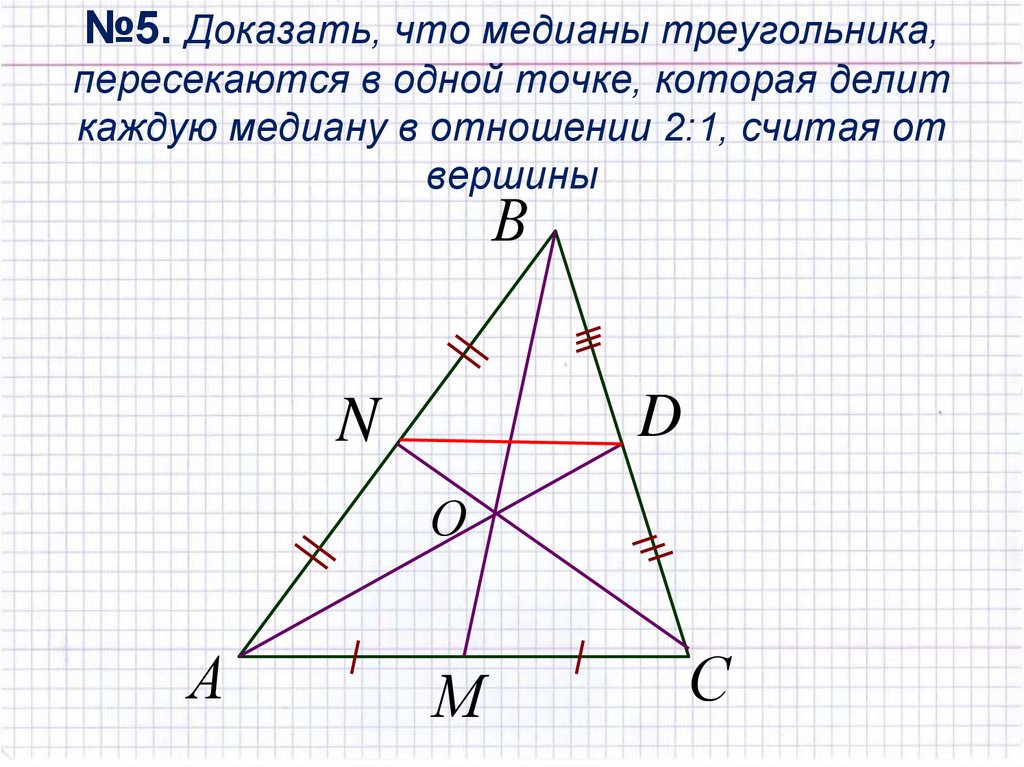 2 ). 2 ). Найдите длину медианы, проведенной к стороне Раствор = = = = = . Ответить . = =~ 5,148 (приблизительно). | Рисунок 2 . К Пример 1 |
| Пример 2 В равнобедренном треугольнике боковая сторона имеет длину 4 . Медиана, проведенная к боковой стороне, имеет длину 3 ( Рисунок 3 ). Найдите длину основания треугольника. Раствор . Упростите это уравнение шаг за шагом, как показано ниже: , , , , , . Ответить . Основание треугольника имеет длину . | Рисунок 3 . 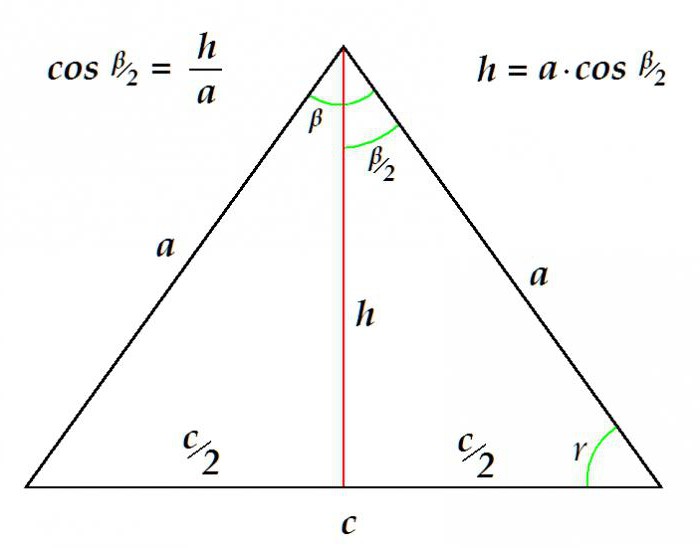 К Пример 2 К Пример 2 |
Для навигации по урокам по свойствам треугольников используйте этот файл/ссылку Свойства треугольников.
Для навигации по всем темам/урокам онлайн-учебника по геометрии используйте этот файл/ссылку ГЕОМЕТРИЯ — ВАШ ОНЛАЙН-УЧЕБНИК.
Центроид треугольника, значение, определение, свойства, формула и примеры
В этой статье мы узнаем о центроиде формулы треугольника с выводом, а также приведем несколько примеров с решениями.
В координатной геометрии центр тяжести треугольника часто используется для измерения точки совпадения медианы или середины треугольника. Медиана или середина треугольника — это точка, в которой сходятся все точки после разделения треугольника на более мелкие части. Медиана треугольника разрезает треугольник на два меньших треугольника и проходит через середину треугольника.
Содержание
- 1 Что такое центр тяжести треугольника?
- 2 Свойства центра тяжести треугольника
- 3 Формула для нахождения координат центра тяжести треугольника
Что такое центр тяжести треугольника?
Центр тяжести треугольника образуется путем трехкратного разрезания треугольника и проведения на нем трех медиан.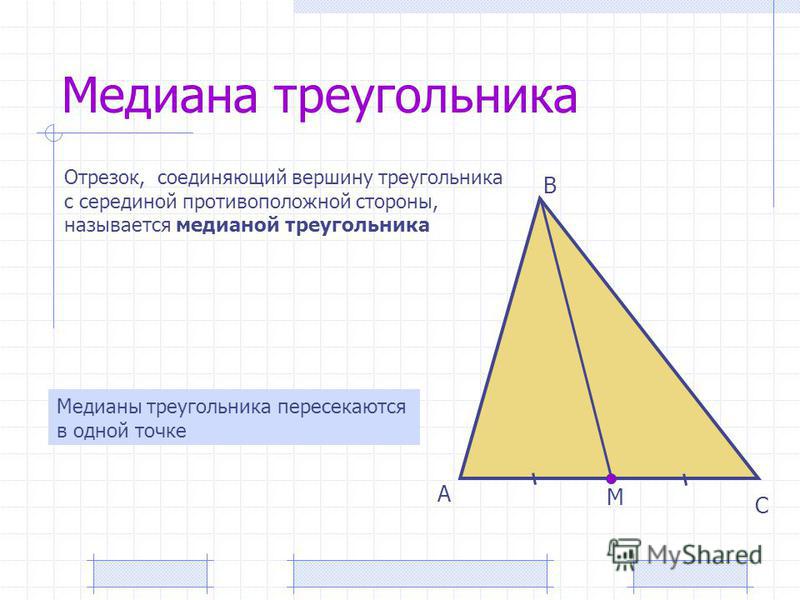 Центральная точка, где пересекаются все три медианы, называется центром тяжести треугольника. Медиана образуется, когда каждая вершина треугольника встречается с противоположной вершиной треугольника.
Центральная точка, где пересекаются все три медианы, называется центром тяжести треугольника. Медиана образуется, когда каждая вершина треугольника встречается с противоположной вершиной треугольника.
Место, где все точки медианы пересекаются с центром тяжести треугольника, также известно как точка параллелизма. Каждая медиана имеет точки от начального до конечного пути в треугольнике. Эти точки медиан используются для вычисления центра тяжести треугольника.
Свойства центра тяжести треугольника
1) Геометрический центр объекта также можно использовать вместо центра тяжести.
2) Центроид всегда находится внутри треугольника, потому что каждая вершина проводит медиану внутри треугольника к противоположной вершине.
3) Центроид находится на расстоянии 2/3 от вершины до середины и делит медиану в соотношении 2:1.
4) Центроид – это точка, полученная путем взятия середины всех трех медиан.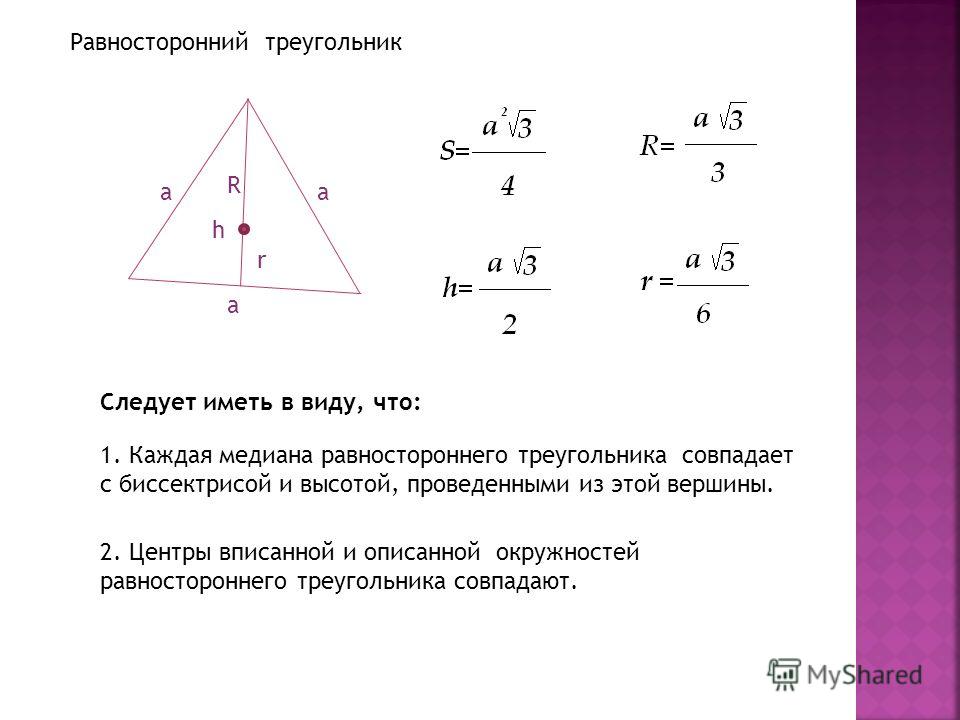
5) Для расчета длины срединного сегмента можно использовать расстояние от центра тяжести до вершины треугольника.
Формула для определения координат центра тяжести треугольника
Центром тяжести треугольника является точка пересечения его медиан. Для нахождения координат центроида треугольника необходимы координаты вершин треугольника.
В приведенном выше P(x1, y1), Q(x2, y2) и R(x3, y3) вершины треугольника △ PQR. Здесь PU — медиана, делящая пополам основание QR.
Таким образом, центральная точка основания QR — это U. Координаты центра «U»
Теперь точка V на PU, которая делит его внутри в соотношении 2 : 1, является центроидом, и мы уже знаем координаты P и U
Пусть (x, y) — координаты V, тогда мы используем формулу
Следовательно, координаты центроида V треугольник приведен ниже
Рассмотрим несколько примеров нахождения координат центра тяжести треугольника. ) и (2, 3)?
) и (2, 3)?
Решение
Шаг 1: Возьмите заданные вершины и дайте имя каждой точке.
(12, 34), (13, 23), (2, 3)
х 1 = 12, у 1 = 34
х 2 = 13, у 2 = 23
x 3 = 2, y 3 = 3
Шаг 2: Теперь возьмите общую формулу, чтобы рассчитать
Шаг 3: . формула выше.
= [(12 + 13+ 2)/3, (34 + 23 + 3)/3]
= (27/3, 60/3)
= (9, 20)
Следовательно, центр тяжести есть (9, 20) с использованием заданных вершин.
Пример 2. Найти центр тяжести треугольника, используя заданные вершины (21, 41), (-3, -13) и (-12, -17)?
Решение
Шаг 1: Возьмите заданные вершины и дайте имя каждой точке.
(21, 41), (-3, -13), (-12, -17)
x 1 = 21, у 1 = 41
x 2 = -3, у 2 = -13
x 3 = -12, y 3 = -17
Шаг 2: Теперь воспользуемся общей формулой для вычисления
392 значений вершин Шаг 1
902: в приведенной выше формуле.
= [ (21 + (-3) + (-12)/3, 41 + (-13) + (-17)/3]
= [ (21 – 3 – 12)/3, (41 – 13 – 17)/3]
= [ (21 – 15)/3, (41 – 30)/3]
= (6/3, 11/3)
= (2, 11/3)
Следовательно, центр тяжести равен (2, 11/3) при использовании заданных вершин
Пример 3 : Найти центр тяжести треугольника при использовании заданных вершин, (-2, -4), (13, 43), и (31, 17)?
Решение
Шаг 1: Возьмем заданные вершины и назовем каждую точку.
(-2, -4), (13, 43), (31, 17)
x 1 = -2, у 1 = -4
x 2 = 13, у 2 = 43
x 3 = 31, Y 3 = 17
Шаг 2: Теперь возьмите общую формулу, чтобы рассчитать
Центоид треуулерия = (x 1 + x 2 2 2 2 2 2 2 2 2 2 6 2 6 2 6 2 2 2 2 2 2 2 2 x 3 /3, y 1 + y 2 + y 3 /3) Шаг 3: Подставьте значения вершин в приведенную выше формулу. =[ (-2 + 13 + 31)/3, (-4 + 43 + 17)/3] = [(-2 + 44)/3, (-4 + 60)/3] = (14, 56/3) Следовательно, центроид равен (14, 56/3) при использовании заданных вершин. Пример 4. Найти центр тяжести треугольника, используя заданные вершины (12, 4), (-33, 3) и (-1, -7)? Решение Шаг 1: Возьмите заданные вершины и дайте имя каждой точке. (12, 4), (-33, 3), (-1, -7) x 1 = 12, у 1 = 4 x 2 = -33, y 2 = 3 x 3 = -1, y 3 = -7 Теперь вычислите общую формулу 2. Центрад треугольника = (x 1 + x 2 + x 3 /3, y 1 + y 2 + y 3 /3) 
+ y 3 /3)
+ y 3 /3)
111191 2 2: 3 /3) 11191 .