Уравнения в степени с неизвестным: Показательные уравнения (с неизвестной в показателе степени)

Алгебра. Учебник для 6-8 классов

Алгебра. Учебник для 6-8 классов

Барсуков А.Н. Алгебра. Учебник для 6-8 классов. 11-е изд., стер. — М.: Просвещение, 1966. — 296 с. Учебник для средних общеобразовательных школ СССР в 50-60-е годы. Шестое издание „Алгебры» А.Н. Барсукова переработано и приведено в соответствие с новой программой. Переработка учебника и изложение вопросов, вновь включенных в программу восьмилетней школы, выполнены С.И. Новоселовым. Главу „Счётная (логарифмическая) линейка* и о возвышении в квадрат и куб, извлечении квадратного и кубического корней при помощи счётной линейки написал учитель математики школы № 315 Москвы И. Б. Вейцман. Одиннадцатое издание печатается с десятого без изменений. Оглавление ГЛАВА ПЕРВАЯ АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ. § 2. Алгебраические выражения. § 3. Допустимые значения букв. § 4. Порядок действий. § 5. Основные законы сложения и умножения. § 6. Краткие исторические сведения. ГЛАВА ВТОРАЯ. РАЦИОНАЛЬНЫЕ ЧИСЛА. § 7. Положительные и отрицательные числа. § 8. Числовая ось. § 9. Противоположные числа. § 10. Абсолютная величина числа. § 11. Сравнение рациональных чисел. § 12. Сложение рациональных чисел. § 13. Сложение нескольких чисел. § 14. Законы сложения. § 15. Вычитание рациональных чисел. § 16. Алгебраическая сумма. § 17. Умножение. § 18. Умножение нескольких чисел. § 19. Законы умножения. § 20. Деление. § 21. Свойства деления. § 22. Возведение в степень. § 23. Порядок выполнения действий. § 24. Уравнения. § 25. Решение задач с помощью уравнений. § 26. Графики. § 27. Краткие исторические сведения. (Из истории отрицательных чисел.) ГЛАВА ТРЕТЬЯ. ДЕЙСТВИЯ НАД ЦЕЛЫМИ АЛГЕБРАИЧЕСКИМИ ВЫРАЖЕНИЯМИ. § 28. Одночлен и многочлен. § 29. Тождества и тождественные преобразования. § 30. Коэффициент. § 31. Расположенные многочлены. § 32. Приведение подобных членов. § 33. Сложение одночленов и многочленов. § 34. Противоположные многочлены. § 35. Вычитание одночленов и многочленов § 36. Умножение одночленов. § 37. Умножение многочлена на одночлен. § 38. Умножение многочленов. § 39. Умножение расположенных многочленов. § 40. Возведение одночленов в степень. § 41. Формулы сокращённого умножения. § 42. Общие замечания о делении целых алгебраических выражений. § 43. Деление одночленов. § 44. Деление многочлена на одночлен § 45. Примеры решения уравнений. ГЛАВА ЧЕТВЁРТАЯ. УРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ С ОДНИМ НЕИЗВЕСТНЫМ. § 47. Равносильные уравнения. § 48. Два основных свойства уравнений. § 49. Уравнения, содержащие неизвестное в обеих частях. § 50. Уравнение первой степени с одним неизвестным. § 51. Общие указания к решению уравнений. § 52. Решение задач с помощью уравнений. § 53. Краткие исторические сведения. (Из истории уравнений.) ГЛАВА ПЯТАЯ. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ. § 54. Понятие о разложении на множители. § 55. Вынесение за скобки общего множителя. § 56. Способ группировки. § 57. Применение формул сокращённого умножения. § 58. Применение нескольких способов. § 59. Деление многочленов при помощи разложения на множители. ГЛАВА ШЕСТАЯ. АЛГЕБРАИЧЕСКИЕ ДРОБИ. § 60. Понятие об алгебраической дроби. § 61. Основное свойство дроби и сокращение дробей. § 62. Перемена знака у членов дроби. § 63. Целая отрицательная и нулевая степени числа. § 64. Приведение дробей к общему знаменателю. § 65. Сложение дробей. § 66. Вычитание дробей. § 67. Умножение дробей. § 68. Деление дробей. § 69. Возведение дроби в натуральную степень. § 70. Дробные уравнения. § 71. Примеры решения уравнений с буквенными коэффициентами. ГЛАВА СЕДЬМАЯ. КООРДИНАТЫ И ПРОСТЕЙШИЕ ГРАФИКИ. § 72. Координаты точки на плоскости. § 73. Прямо пропорциональная зависимость. § 74. График прямо пропорциональной зависимости. § 75. Линейная зависимость. § 76. Обратно пропорциональная зависимость. ГЛАВА ВОСЬМАЯ. СИСТЕМА УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ С ДВУМЯ НЕИЗВЕСТНЫМИ. § 77. Уравнение первой степени с двумя неизвестными. § 78. Система двух уравнений первой степени с двумя неизвестными. § 79. Равносильные системы. § 80. Решение систем уравнений. § 81. Графическое решение системы двух уравнений. § 82. Решение задач. § 83. Уравнение с тремя неизвестными. § 84. Система трёх уравнений с тремя неизвестными. ГЛАВА ДЕВЯТАЯ. СЧЁТНАЯ (ЛОГАРИФМИЧЕСКАЯ) ЛИНЕЙКА. § 85. Равномерные и неравномерные шкалы. § 86. Устройство счётной (логарифмической) линейки. § 87. Основная шкала. § 88. Умножение и деление с помощью счётной линейки. ГЛАВА ДЕСЯТАЯ. КВАДРАТНЫЙ КОРЕНЬ. § 89. Построение графика зависимости y = x^2 § 90. (1/3) § 130. Примеры графического решения уравнений и систем уравнений.

Как решать показательные уравнения

• Альфашкола
• Статьи
• Как решать показательные уравнения

Мы уже неоднократно писали о том, как научиться решать показательные уравнения. Вопрос всегда сводится к знанию и умению применять алгоритм. Давайте еще раз повторим основные теоретические положения этой важной темы.

 

Если в уравнении неизвестное содержится в показателе степени, то такое уравнение называется показательным. Простейшее показательное уравнение имеет вид: а^х = а^b, где а>0, а≠1, х — неизвестное. {x2}\) ⇔  x1=x2.

 

Для представления числа в виде степени используют  

a > 0, a≠1, b > 0.

 

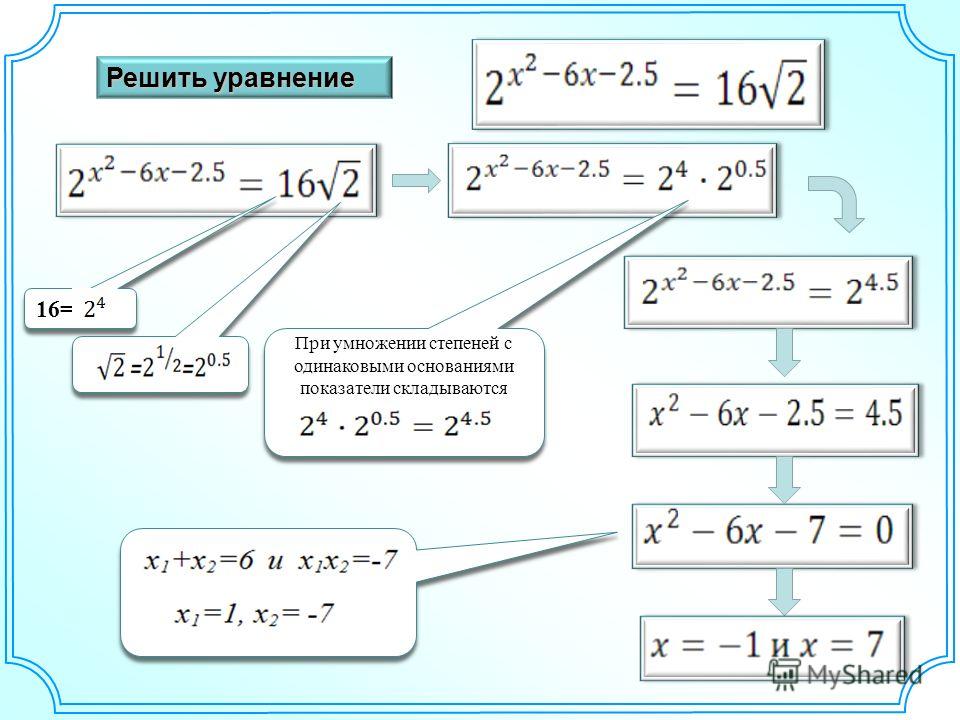
1. Решение уравнений вида а^f(x)=a^q(x) сводится к решению уравнения f(x)=q(x). Иногда в таких уравнениях требуется привести обе части к одинаковому основанию степени, как правило, это разные степени одного основания.
2. Решение уравнений вида  а^f(x)=b. Для решения используем логарифмирование по основанию а, т.е. решаем уравнение f(x)=log_a^b.
3. Уравнения, решаемые с помощью вынесения за скобки общего множителя.
4. Уравнения, решаемые с помощью замены переменной.
5. Уравнения, содержащие степени с двумя различными (не сводящимися друг к другу) основаниями, a^f(x)=b^f(x). Решением является решения уравнения f(x)=0.
6. Уравнения, однородные относительно a^x и b^x.

Успехов!

 

Автор — Дмитрий Айстраханов

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Ольга Викторовна Смольская

Репетитор по математике

Стаж (лет)

Образование:

Белорусский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Роман Михайлович Мясников

Репетитор по математике

Стаж (лет)

Образование:

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Павел Андреевич Демин

Репетитор по математике

Стаж (лет)

Образование:

Южно-Уральский Государственный Гуманитарно Педагогичесий Университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

• Математика
• Репетитор по физике
• Репетитор по химии
• Репетитор по русскому языку
• Репетитор по английскому языку
• Репетитор по обществознанию
• Репетитор по истории России
• Репетитор по биологии
• Репетитор по географии
• Репетитор по информатике

Специализации

• Репетитор по алгебре
• Подготовка к олимпиадам по химии
• Репетитор для подготовки к ОГЭ по физике
• Репетитор по русскому языку для подготовки к ЕГЭ
• Репетитор для подготовки к сочинению ЕГЭ по русскому
• Репетитор по английскому языку для подготовки к ЕГЭ
• Репетитор по английскому языку для подготовки к ОГЭ
• Репетитор по биологии для подготовки к ЕГЭ
• Подготовка к ОГЭ по литературе
• Программирование Pascal

Похожие статьи

• Объем куба
• Радикальные уравнения: примеры решения
• Как перевести тонны в килограммы?
• Факультет Социологии (НИУ ВШЭ)
• Теорема косинусов
• ЕГЭ по математике, базовый уровень. Задачи на координатной решетке
• Первая школьная любовь и как помочь подростку пережить ее?
• Как использовать материнский капитал на образование: полная инструкция для родителей

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Текст с ошибкой:

Расскажите, что не так

x = 5

Уравнение экспоненциальное, потому что неизвестное находится в экспоненциальной степени 625

Правильный ответ:

x =  0,25

Пошаговое объяснение:

625x=5 625 = 54 (54)x = 5 x ln625 = ln5 x=ln5/ln625=0,25

Нашли ошибку или неточность? Не стесняйтесь

пишите нам

. Спасибо!

Советы для связанных онлайн-калькуляторов

У вас есть линейное уравнение или система уравнений и вы ищете ее решение? Или у вас есть квадратное уравнение?

You need to know the following knowledge to solve this word math problem:

• algebra
• equation
• exponential equation
• expression of a variable from the formula
• arithmetic
• square root
• возведение в степень
• основные функции
• логарифм
• экспоненциальная функция

Уровень задачи:

• средняя школа

• ГП последовательность
  Найдите оставшиеся неизвестные характеристики в конечной геометрической последовательности, если она задана: a1 = 5, an = 320, sn = 635, n =?, q =?
• Экспоненциальная 3858
  Определить m (решить показательное уравнение — неизвестно в показателе степени): 0,25 мкм = 0,5
• Конечная геометрическая последовательность
  Найти остальные неизвестные характеристики в конечной геометрической последовательности, если даны: a1 = 18, an = 13122 , sn = 19674, n =?, q =?
9-1)=36. Неизвестный y — натуральное число больше нуля.
• Одна треть
  Одна треть неизвестного числа в пять раз больше разности между тем же неизвестным числом и числом 28. Найдите неизвестное число.
• Геометрическая прогрессия
  В геометрической прогрессии a1 = 7, q = 5. Найдите условие, при котором n суммирует первые n членов: sn≤217.
• Последовательность
  Найти n-й член прогрессии 2,6,12,20…
• Определить 3840 9z = 1/144
• Найти x
  Решить: если 2(x-1)=14, то x= (решить уравнение с одним неизвестным)
• Уравнение: 4386
  Решить уравнение мощности: 2,1463 = 0,4179x ^0,419
• Степени 3
  2 в степени n разделить на 4 в степени -3 равно 4. Каково значение n?
• Неизвестно 2881
  Найти неизвестное число: (9 + y) x 6 = 12 x 7 y =?
• Точки OPQ
  Точка P находится на отрезке OQ. Учитывая OP = 6, OQ = 4x — 3 и PQ = 3x, найдите числовую длину OQ.
• Середина 6
  Для длины отрезка дана: FM=8a+1, FG=42. Точка M является серединой FG. Найдите неизвестное а.
• 5 раз
  Найти неизвестный номер; если 110 в пять раз больше, чем 1/2 от какого числа? Кинематические уравнения и решение задач0003

  В приведенных выше уравнениях символ d обозначает смещение объекта. Символ t обозначает время, в течение которого объект перемещался. Символ a обозначает ускорение объекта. А символ v обозначает мгновенную скорость объекта; нижний индекс i после v (как в v _i ) указывает, что значение скорости является начальным значением скорости, а нижний индекс f (как в v _f ) указывает, что значение скорости является конечным значением скорости.

  
  

   

  Стратегия решения проблем

  В этой части урока 6 мы исследуем процесс использования уравнений для определения неизвестной информации о движении объекта. Процесс включает в себя использование стратегии решения проблем, которая будет использоваться на протяжении всего курса. Стратегия включает следующие шаги:

  1. Построить информативную диаграмму физической ситуации.
  2. Определите и перечислите данную информацию в переменной форме.
  3. Определите и перечислите неизвестную информацию в переменной форме.
  4. Определите и перечислите уравнение, которое будет использоваться для определения неизвестной информации из известной.
  5. Подставьте известные значения в уравнение и используйте соответствующие алгебраические шаги для поиска неизвестной информации.
  6. Проверьте свой ответ, чтобы убедиться, что он разумен и математически верен.

  Использование этой стратегии решения проблемы при решении следующей задачи моделируется в примерах A и B ниже.

   

  Пример Задача A

  Има Торопится приближается к светофору, движущемуся со скоростью +30,0 м/с. Свет загорается желтым, и Има нажимает на тормоза и останавливается. Если ускорение Имы равно -8,00 м/с ² , то определить перемещение автомобиля в процессе заноса. (Обратите внимание, что направления векторов скорости и ускорения обозначены знаком + и -. )

  Решение этой задачи начинается с построения информативной диаграммы физической ситуации. Это показано ниже. Второй шаг включает идентификацию и перечисление известной информации в переменной форме. Обратите внимание, что версия

  f можно сделать вывод, что это 0 м/с, так как машина Имы останавливается. Начальная скорость (v _i ) автомобиля равна +30,0 м/с, так как это скорость в начале движения (занос). А ускорение (а) автомобиля определяется как — 8,00 м/с ² . (Всегда обращайте особое внимание на знаки + и — для данных величин.) Следующий шаг стратегии включает перечисление неизвестной (или желаемой) информации в переменной форме. В этом случае задача запрашивает информацию о водоизмещении автомобиля. Итак, d — неизвестная величина. Результаты первых трех шагов представлены в таблице ниже.
  

  Схема:	Дано:	Найти:
  	v i = +30,0 м/с v f = 0 м/с a = — 8,00 м/с 2	д = ??

  Следующий шаг стратегии включает определение кинематического уравнения, которое позволит вам определить неизвестную величину. На выбор предлагается четыре кинематических уравнения. В общем, вы всегда будете выбирать уравнение, содержащее три известные и одну неизвестную переменную. В этом конкретном случае три известные переменные и одна неизвестная переменная равны v _f , v _i , a и d. Таким образом, вы будете искать уравнение, в котором перечислены эти четыре переменные. Проверка четырех приведенных выше уравнений показывает, что уравнение в правом верхнем углу содержит все четыре переменные.

   v _f ² = v _i ² + 2 • a • d
  

  Как только уравнение определено и записано, следующий шаг стратегии включает подстановку известных значений в уравнение и использование соответствующих алгебраических шагов для поиска неизвестной информации. Этот шаг показан ниже.

  (0 м/с) ² = (30,0 м/с) ² + 2 • (-8,00 м/с ² ) • d

  0 м ² /с 2 м ² /с ² + (-16,0 м/с ² ) • d

  (16,0 м/с ² ) • d = 900 м ² /с ² /с ²

  (16,0 м /с ² )*D = 900 м ² /S ²

  D = (900 м ² /с ² ) /(16,097 2 /с ² ) /(16. 0097 2 /с ² ) /(16.0. м/с ² )

  d = (900 м ² /с ² )/ (16,0 м/с ² )

  d = 56,3 м

  Приведенное выше решение показывает, что расстояние 5 6,3 м автомобиля будет скользить. . (Обратите внимание, что это значение округлено до третьего знака.)

  Последний шаг стратегии решения проблем включает проверку ответа, чтобы убедиться, что он является разумным и точным. Стоимость кажется достаточно разумной. Автомобилю требуется значительное расстояние, чтобы занести от 30,0 м / с (примерно 65 миль / ч) до остановки. Рассчитанное расстояние составляет примерно половину футбольного поля, что делает его очень разумным расстоянием для заноса. Проверка точности включает подстановку вычисленного значения обратно в уравнение для смещения и обеспечение того, чтобы левая часть уравнения была равна правой части уравнения. В самом деле!

   

  
  

  Пример задачи B

  Бен Рашин ждет на светофоре. Когда он, наконец, стал зеленым, Бен разогнался из состояния покоя со скоростью 6,00 м/с ² за время 4,10 секунды. Определите перемещение автомобиля Бена за этот период времени.

  Еще раз, решение этой проблемы начинается с построения информативной диаграммы физической ситуации. Это показано ниже. Второй шаг стратегии включает идентификацию и перечисление известной информации в переменной форме. Обратите внимание, что версия 9Можно сделать вывод, что значение 0121 i равно 0 м/с, поскольку изначально автомобиль Бена находится в состоянии покоя. Ускорение (а) автомобиля равно 6,00 м/с ² . А время (t) равно 4,10 с. Следующий шаг стратегии включает перечисление неизвестной (или желаемой) информации в переменной форме. В этом случае задача запрашивает информацию о водоизмещении автомобиля. Итак, d — неизвестная информация. Результаты первых трех шагов представлены в таблице ниже.

  Диаграмма:	Дано:	Найти:
  	v i = 0 м/с t = 4,10 с а = 6,00 м/с 2	д = ??

  Следующий шаг стратегии включает определение кинематического уравнения, которое позволит вам определить неизвестную величину. На выбор предлагается четыре кинематических уравнения. Опять же, вы всегда будете искать уравнение, содержащее три известные переменные и одну неизвестную переменную. В этом конкретном случае три известные переменные и одна неизвестная переменная равны t, v _и , а и г. Проверка четырех приведенных выше уравнений показывает, что уравнение в левом верхнем углу содержит все четыре переменные.
  

   d = v _i • t + ½ • a • t ²

  
  Как только уравнение определено и записано, следующий шаг стратегии включает подстановку известных значений в уравнение и использование соответствующих алгебраических шагов для поиска неизвестной информации. Этот шаг показан ниже.

  d = (0 м/с) • (4,1 с) + ½ • (6,00 м/с ² ) • (4,10 с) ²

  d = (0 м) + ½ • (6,00 м/с ² ) • (16,81 с ² )

  м3 =

  d0

  d = 50,4 м

  Приведенное выше решение показывает, что автомобиль проедет расстояние 50,4 метра. (Обратите внимание, что это значение округлено до третьего знака.)

  Последний шаг стратегии решения проблем включает проверку ответа, чтобы убедиться, что он является разумным и точным. Стоимость кажется достаточно разумной. Автомобиль с ускорением 6,00 м/с/с достигнет скорости примерно 24 м/с (примерно 50 миль/ч) за 4,10 с. Расстояние, на которое такой автомобиль переместится за этот период времени, составит примерно половину футбольного поля, что делает это расстояние вполне разумным. Проверка точности включает подстановку вычисленного значения обратно в уравнение для смещения и обеспечение того, чтобы левая часть уравнения была равна правой части уравнения. В самом деле!

  Приведенные выше два примера задач иллюстрируют, как кинематические уравнения могут быть объединены с простой стратегией решения задач для прогнозирования неизвестных параметров движения движущегося объекта. При условии, что известны три параметра движения, можно определить любое из оставшихся значений.

  No related posts.