В чем измеряется площадь треугольника: Как найти площадь треугольника, формула 🔺

Содержание

Площадь прямоугольного треугольника — формула, пример расчета, калькулятор

Прямоугольным треугольником называется треугольник, у которого один из углов равняется 90°. Его площадь можно найти, если известны два катета. Можно, конечно, пойти и длинным путем – найти гипотенузу и просчитать площадь по формуле Герона, но в большинстве случаев это только займет лишнее время. Именно поэтому формула площади прямоугольного треугольника выглядит так:

Площадь прямоугольного треугольника равняется половине произведения катетов.

Пример расчета площади прямоугольного треугольника.
Дан прямоугольный треугольник с катетами a = 8 см, b = 6 см.
Вычисляем площадь:
Площадь равна: 24 см²

Также в прямоугольном треугольнике применяется теорема Пифагора. – сумма квадратов двух катетов равняется квадрату гипотенузы.
Формула площади равнобедренного прямоугольного треугольника вычисляется также как и обычного прямоугольного треугольника.

Пример расчета площади равнобедренного прямоугольного треугольника:
Дан треугольник с катетами a = 4 см, b = 4 см. Вычисляем площадь:
Вычисляем площадь:=8 см²

Формула площади прямоугольного треугольника по гипотенузе может использоваться, если в условии дан один катет. Из теоремы Пифагора находим длину неизвестного катета. К примеру, дана гипотенуза c и катет a, катет b будет равен:
Далее вычисляем площадь по обычной формуле. Пример расчета формулы площади прямоугольного треугольника по гипотенузе идентичен описанному выше.

Рассмотрим интересную задачу, которая поможет закрепить знания формул для решения треугольника.

Задача

: площадь прямоугольного треугольника равняется 180 кв. см. найдите меньший катет треугольника, если он меньше второго на 31 см.

Решение

: обозначим катеты a и b. Теперь подставим данные в формулу площади:, еще мы знаем, что один катет меньше другого a – b = 31 см
Из первого условия получаем, что
Подставляем данное условие во второе уравнение:

Так как мы находили стороны, то знак минус убираем.
Получается, что катет a = 40 см, а b = 9 см.

Калькулятор нахождения площади прямоугольного треугольника:
Катет a=	Катет b=
Ответ: Площадь треугольника= 10.000

Найдите площадь треугольника изображённого

Бизнес с Oriflame — рост и РАЗВИТИЕ!

ЗАМУЧИЛИ БОЛИ В СПИНЕ?

Александр | 2012-09-13

Здравствуйте! В этой статье мы разберём задачи на нахождение площади треугольника построенного на листке в клетку (масштаб клетки 1×1).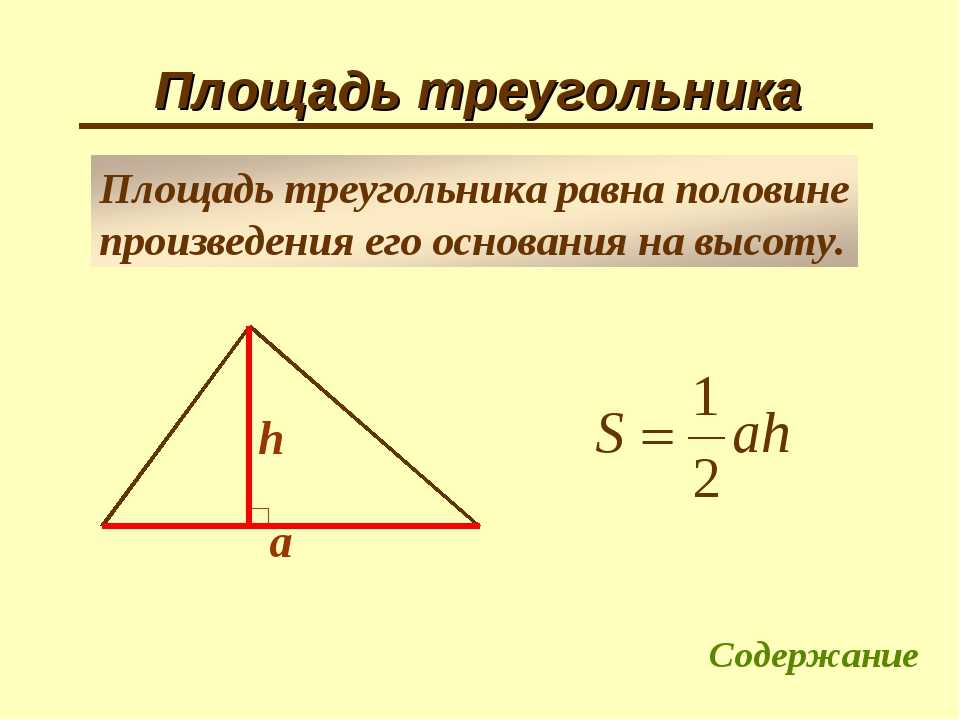 Фигуры на листе в клетку с вычислением их площади — это целая группа типов задач входящая в экзамен по математике. Кроме треугольника рассматриваются следующие фигуры — трапеция, параллелограмм, ромб, квадрат.

Решение заданий с треугольником труда не представляет, относятся они к простейшим. Для решения необходимо знать формулу площади треугольника и знать один приём, о котором я вам расскажу ниже.

Вообще, способов нахождения площади любой фигуры, построенной на листе в клетку существует более пяти. Все здесь рассматривать не будем, в интернете вы без труда найдёте их описание. Уверен, что тех рекомендаций, которые представлены будет вполне достаточно для решения.

Итак! Вам необходимо знать и понимать одну из основных формул площади треугольника, она наиболее часто используется при решении:

Длину основания и высоту считаем по клеткам. В задаче 27545 это наглядно показано. То есть, если перед вами задача, где треугольник построен именно таким образом, то считаем оговоренным способом.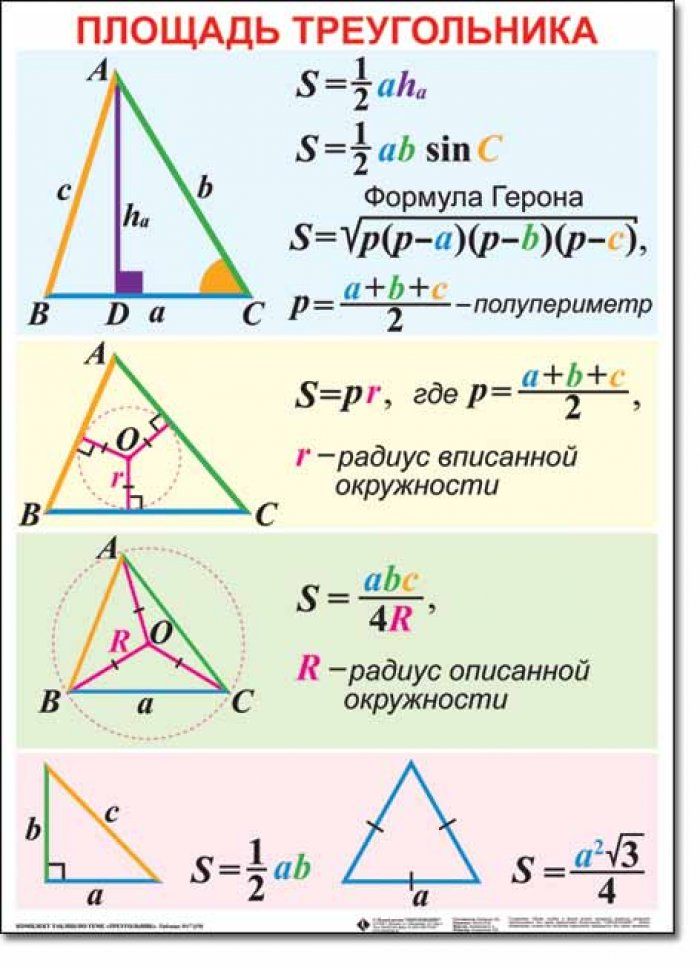 Например, рассмотрим треугольники:

У всех этих треугольников можно по клеткам установить длину основания и высоту. У первого основание равно 3, высота 5; у второго основание 6, высота 2; у третьего основание 6, высота 2; у четвертого основание равно 3, высота 8; у пятого основание равно 6, высота 2. Подставив их в формулу, остаётся только вычислить площадь (без ошибки).

Есть задачи, в которых треугольники расположены так, что по клеткам длину основания и высоту посчитать неудобно (но можно), вот примеры:

В задачах, где будут даны подобные треугольники, используйте способ, который по моему мнению универсален, его достоинство объясню в одной из следующих статей: «заключите» такой треугольник в прямоугольник, вычислите площадь прямоугольника, затем из его площади вычтите площади треугольников. Пример:

Найти площадь треугольника, изображённого на рисунке:

Заключим данный треугольник в прямоугольник:

Теперь вычислим площадь прямоугольника. Уверен, всем известно, что она равна произведению его соседних сторон:

Далее из его площади вычитаем площади трёх треугольников:

Ответ: 26

Есть ещё подобные задачи, но в них иначе представлено условие. Также нужно найти площадь треугольника, он построен на координатной плоскости, например:

Решения аналогичны: если можем установить длину основания и высоту треугольника по координатам, то далее площадь вычисляем просто по формуле:

В треугольнике на рисунке 1 этого сделать нельзя, поэтому советую построить данный треугольник по координатам на листе в клетку, и использовать уже рассмотренный нами метод, а именно описать около треугольника прямоугольник.

В будущем мы рассмотрим нахождения площадей параллелограммов, трапеций, четырёхугольников, элементов круга, а так же «сложных» фигур, не пропустите!

Спасибо за внимание, учитесь с удовольствием!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Категория: Площади фигур | ЕГЭ-№1Треугольник

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

Площадь треугольника: формула и примеры

Треугольник представляет собой трехстороннюю фигуру с высотой , которая перпендикулярна его основанию . Существуют различные типы треугольников, такие как разносторонний, равнобедренный и равносторонний. Формулы нахождения площади и периметра треугольника одинаковы для всех его видов.

Вот иллюстрация , показывающая формулы для нахождения площади и периметра треугольника.

Хотите узнать, как найти периметр треугольника?
Связанное чтение: Периметр треугольника – формулы и примеры

Как найти площадь треугольника

Площадь треугольника равна половине его основания, умноженной на его высоту.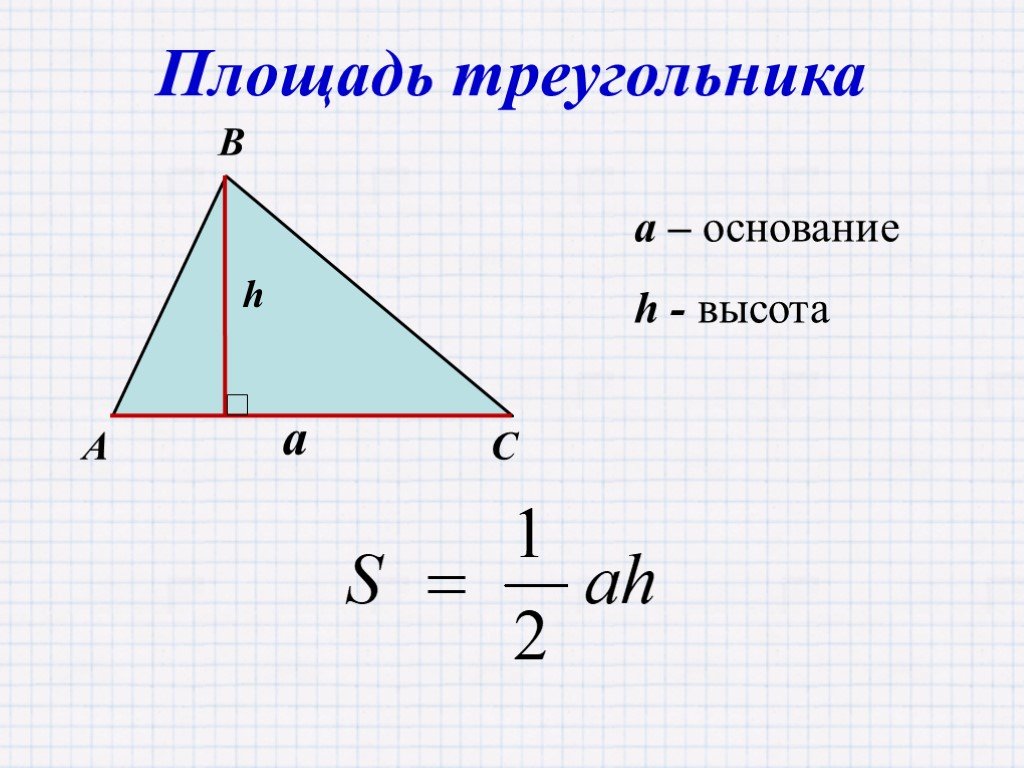 Обратите внимание, что площадь всегда выражается в квадратных единицах (например, ² , м ² или см ² ). Найдите площадь треугольника по формуле:

A = 1/2 ( bh )
где b = основание треугольника и h = высота треугольника

Пример. Найдите площадь , если даны следующие размеры: b = 20 см; h =12 см

A = 1/2 ( bh )
Подставьте данные измерения в уравнение.
A = 1/2 [(20 см) (12 см)] = 1/2 (240 см ² )
A = 120 см ²

Следовательно, площадь равна 120см ² .

Пример №1: Найдите площадь треугольника со следующими размерами:

b = 12 см; ч = 10 см.

Решение для примера № 1:

Подставьте данные измерения в формулу площади: A = 1/2 ( bh ) .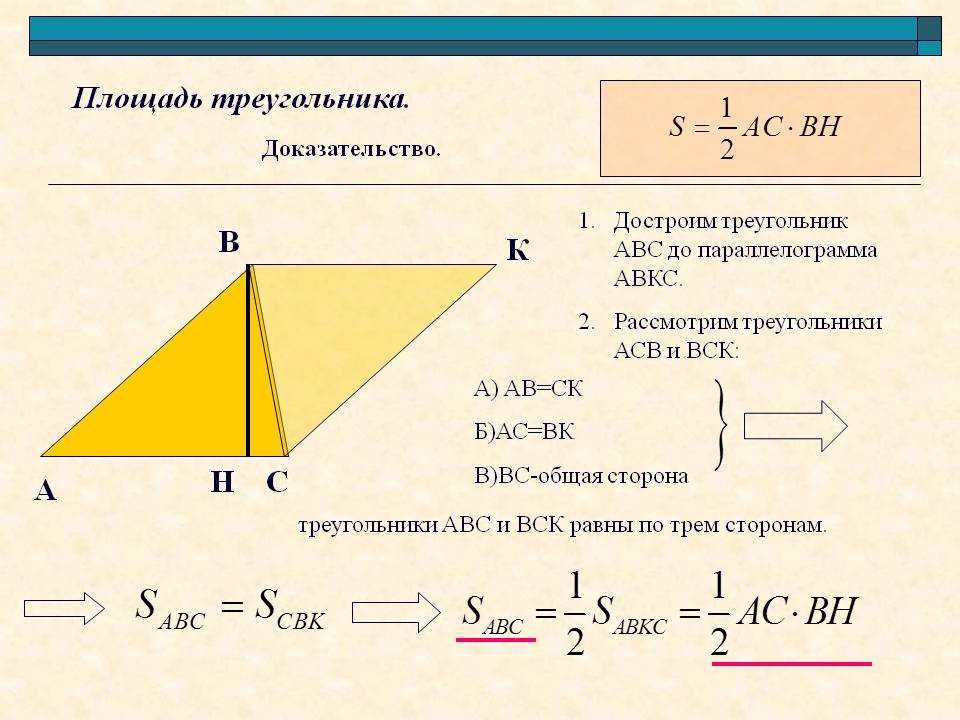 База ( b ) равна 12 см , а высота ( h ) равна 10 см .

A = 1/2 [(12 см) (10 см)] = 1/2 (120 см ² )
A = 60 см ²

Следовательно, площадь это 60 см ² .

Пример №2: Найдите площадь треугольника со следующими размерами:

b = 0,7 км; ч = 0,9 км.

Решение для примера № 2:

Подставьте данные измерения в формулу площади, A = 1/2 ( bh ) .
Основание ( b ) равно 0,7 k м , а высота ( h ) равна 0,9 k м .

A = 1/2 [(0,7 км) (0,9 км)] = 1/2 (0,63 км ² )
A = 0,315 км ²

900 02 Следовательно, область равна 0,315 км ² .

Спасибо, что прочитали. Мы надеемся, что это эффективно! Всегда не стесняйтесь возвращаться на эту страницу, если у вас когда-либо возникнут вопросы о площадь треугольника.

Ознакомьтесь с некоторыми из наших других сообщений в блоге или инвестируйте в свое будущее с помощью одного из наших курсов самообучения!

Щелкните здесь, чтобы ознакомиться с руководством по подготовке к экзамену AP по программе Calculus AB 2021 г. !

Что такое площадь и периметр треугольника? Определение, примеры

Треугольник

Треугольник – это трехсторонняя замкнутая фигура. Это одна из основных геометрических фигур, которая имеет 3 стороны и 3 вершины 9.0004 . Треугольник можно классифицировать как равносторонний, равнобедренный или разносторонний в зависимости от длины его сторон.

Родственные игры

Каков периметр треугольника?

Периметр многоугольника равен общей длине границы . Для треугольника мы можем найти его, сложив длины трех его сторон.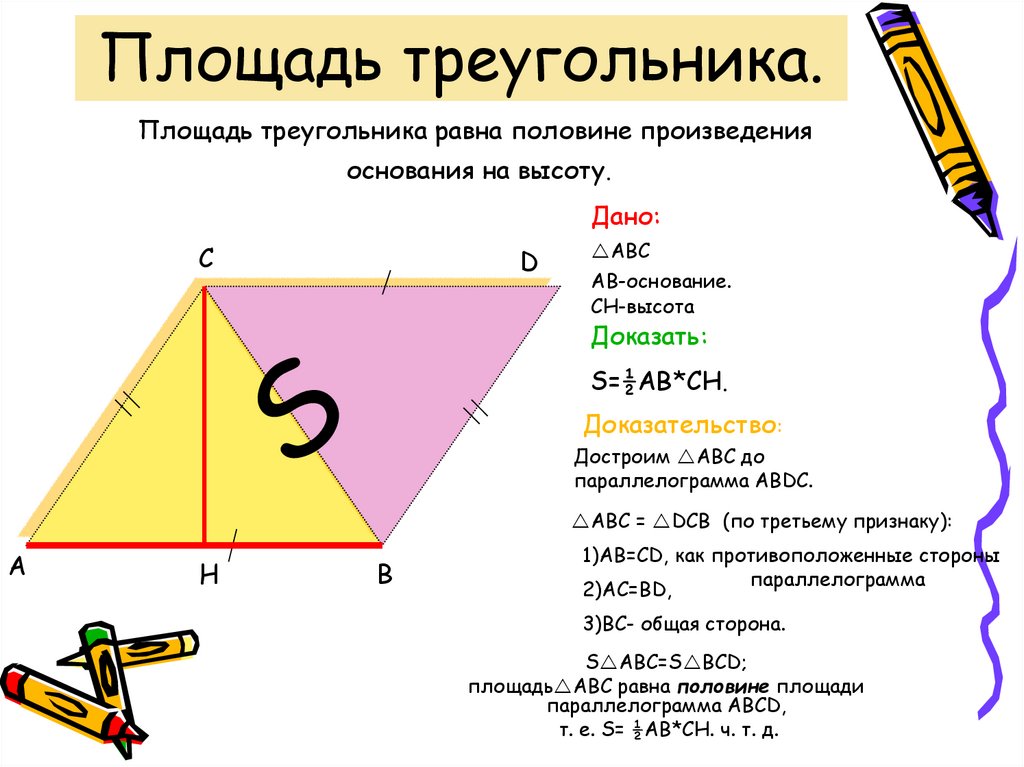

Итак, если ABC — треугольник. Найдем периметр треугольника ABC, сложив длины всех трех сторон.

Периметр △ABC = AB + BC + CA = a + b + c

Давайте разберемся в этом на примере из реальной жизни.

Предположим, у нас есть треугольный парк. Нам нужно найти длину забора, необходимого для покрытия парка. Как мы это находим?

Длину ограждения, необходимого для треугольного парка, можно найти, найдя периметр треугольника.

Возьмем другой пример.

Сервировочный поднос, как показано, образует равносторонний треугольник, то есть треугольник с тремя равными сторонами. Пусть каждая сторона будет 20 см в длину.

Чтобы найти общую длину декоративного шнурка, который нужно наклеить на внешние края, нужно найти периметр треугольника. Поскольку все три стороны треугольника имеют одинаковую длину, мы можем найти периметр, умножив длину каждой стороны на 3.

20 + 20 + 20 = 3 × 20 = 60 см.

Итак, мы видим, что периметр равностороннего треугольника в 3 раза больше длины каждой стороны.

Связанные рабочие листы

Какова площадь треугольника?

Площадь двумерной фигуры — это пространство, занимаемое фигурой. Эту площадь можно найти, разделив фигуру на единичные квадраты и определив количество единичных квадратов в фигуре, поскольку каждый единичный квадрат занимает одну квадратную единицу пространства .

Рассмотрим прямоугольник длиной 4 см и шириной 3 см. Его можно заполнить 3 строками и 4 столбцами единичных квадратов, поэтому площадь равна 3 умножить на 4 или 12 квадратных сантиметров. То есть площадь прямоугольника равна произведению его длины на ширину.

Прямоугольник можно разделить на два равных треугольника.

Итак, площадь каждого треугольника равна половине площади прямоугольника. Это 12 × l × w, где l обозначает длину прямоугольника, а w обозначает ширину прямоугольника.

Рассмотрим разносторонний треугольник △ABC. Обратите внимание: чтобы записать площадь треугольника как половину площади прямоугольника, нам нужно, чтобы высота была перпендикулярна основанию. Итак, проведите перпендикуляр из вершины в противоположную сторону.

Здесь BD — перпендикуляр, проведенный из вершины B на противоположную сторону AC.

Таким образом, площадь треугольника равна половине произведения его основания на высоту.

Площадь треугольника = ½ × основание × высота.

Интересные факты

Треугольник — это простейший многоугольник с тремя сторонами. Все остальные многоугольники имеют более трех сторон.
Слово «периметр» происходит от греческих слов, означающих «вокруг меры».
Площадь A равностороннего треугольника со стороной s см можно рассчитать по формуле A=34×s2. Значение 3 составляет около 1,73. Таким образом, приблизительное значение становится равным A = 0,4325 с2.

Решенные примеры площади и периметра треугольника

Стороны треугольника имеют следующие длины:

10 см, 14 см и 12 см

Найдите периметр треугольника.

Раствор. Мы знаем, что периметр треугольника равен сумме всех его сторон. Отсюда

периметр = 10 см + 14 см + 12 см = 36 см.
У равностороннего треугольника одна сторона имеет длину 6 см. Найдите периметр треугольника.
Раствор. Поскольку все стороны равностороннего треугольника равны по длине, его периметр можно рассчитать следующим образом:
Периметр = 6 см + 6 см + 6 см = 18 см
Периметр треугольника равен 25 см. Две его стороны равны 4 см и 10 см. Найдите длину третьей стороны.
Раствор. Периметр — это сумма всех сторон. Мы можем найти третью сторону, вычитая размеры двух других сторон из заданного периметра.
Длина третьей стороны = 25 см – (4 см + 10 см) = 11 см
Высота треугольника 4 см, а его основание 5 см. Найдите его площадь.
Раствор.
Мы знаем, что площадь треугольника равна 12 x основание x высота. Следовательно,
Площадь = 12 × 4 × 5 = 10 см кв. ?
32 см
13 см
12 см
16 см
Правильный ответ: 13 см
Периметр = 3 см + 6 см + 4 см = 13 см
2
Сторона равностороннего треугольника равна 3 см в длину. Найдите периметр треугольника.
9 см
13 см
12 см
16 см
Правильный ответ: 9 см
Периметр = 3 см + 3 см + 3 см = 9 см
3
Периметр треугольника равен 15 см. Длины двух сторон равны 5 см и 4 см. Найдите длину третьей стороны.
6 см
5 см
3 см
4 см
Правильный ответ: 6 см
Длина третьей стороны = 15 см – 5 см – 4 см = 6 см
4 9 0011
Стороны треугольника 4 см, 4 см и 3 см. Найдите периметр.
9 см
11 см
12 см
16 см
Правильный ответ: 11 см
4 см + 4 см + 3 см = 11 см.
5
Основание треугольника 8 см. Его высота составляет 6 см. Что такое площадь?
24 см кв.
44 см кв.
12 см кв.
16 см кв.
Правильный ответ: 24 см кв. умножить на 6$ = 24 см кв.
Часто задаваемые вопросы о площади и периметре треугольника
Какова формула периметра треугольника?
Формула периметра треугольника представляет собой сумму длин всех сторон треугольника. Например, если длины сторон треугольника равны 3 см, 4 см и 5 см, то периметр треугольника будет равен 3 + 4 + 5 = 12 см.
Увеличивается ли площадь по мере увеличения периметра?
Увеличение периметра фигуры всегда увеличивает площадь фигуры.
Чему равен периметр равнобедренного треугольника?
Периметр равнобедренного треугольника равен 2х сторона + основание.

Как определить площадь треугольника?
Площадь треугольника — это пространство, занимаемое внутри его границы.
No related posts.