S (б.п.) = hP = 2πrh
— Если известна площадь бок. поверхности S (б.п.) и высота h цилиндра, радиус будет равен частному от деления S (б.п.) на произведение 2пи на высоту:
Формула вычисления объема цилиндра
1. Через площадь основания и высоту
Объем (V) цилиндра равняется произведению его высоты и площади основания.
V = S ⋅ H
2. Через радиус основания и высоту
Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R2. Следовательно, формулу для вычисления объема цилиндра можно представить в виде:
V = π ⋅ R2 ⋅ H
Примечание: в расчетах значение числа π округляется до 3,14. 2.
2.
Расшифровать формулу просто:
- V – объем цилиндра;
- π – 3,14;
- R – радиус цилиндра;
- D – диаметр.
То есть получается, что, если разделить объем на площадь основания, получится высота цилиндра.
Можно поступить проще. Для этого нам придется вычислить площадь боковой поверхности искомого цилиндра. Это легко сделать по формуле: S=2πRH. Слегка изменив формулу, получаем: H=S/2πR.
Таким образом, есть уже два способа, которые помогли вспомнить, как найти высоту цилиндра. Это нетрудно, когда перед глазами стройные формулы.
Способ расчета радиуса цилиндра:
Высота: Объем:
Высота: Площадь боковой поверхности:
Высота: Площадь полной поверхности:
Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее.
Формула радиуса цилиндра:
где V – объем цилиндра, h – высота
Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где Sb – площадь боковой поверхности, h – высота
Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее.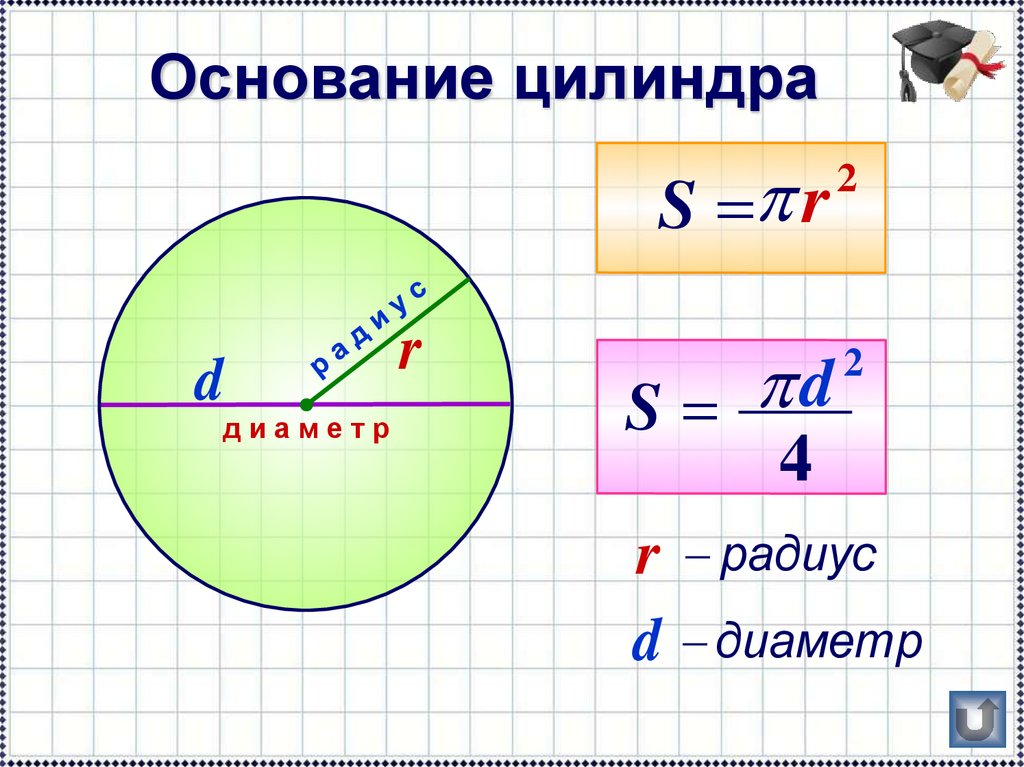
Формула радиуса цилиндра:
где S – площадь полной поверхности, h – высота
S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr2=πr (2h+r)
Площадь боковой поверхности равняется длине окружности основания умноженной на высоту:
R = √V / πh
где V — объем цилиндра, h — высота.
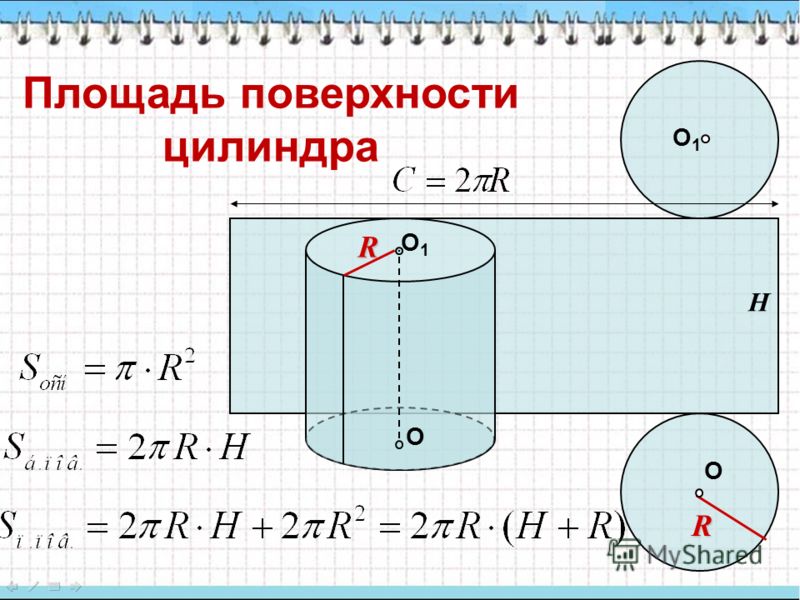
Полная площадь поверхности цилиндра складывается из сумм площадей его боковой поверхности и двух оснований:
Примеры задач
Задание 1
Высота цилиндра равняется 5 см, а объем – 141,3 см3. Вычислите его радиус.
Решение:
Воспользуемся соответствующей формулой, подставив в нее известные по условиям задачи значения:
Задание 2
Найдите радиус цилиндра, если площадь его боковой поверхности равна 175,84 см2, а высота составляет 7 см.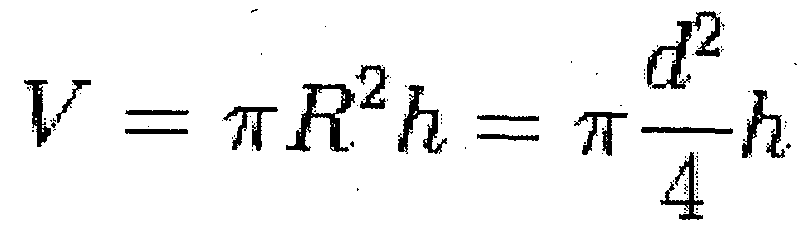
Решение:
Применим формулу, в которой задействованы заданные величины:
Задание 3
Рассчитайте радиус цилиндра, если полная площадь его поверхности – 602,88 см2, а высота – 10 см.
Решение:
Используем третью формулу для нахождения неизвестной величины:
Через площадь боковой поверхности
Радиус цилиндра считается таким образом:
Sбок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2πR), являющейся основанием фигуры, на его высоту:
S = 2πRh
Площадь полной поверхности цилиндра через радиус основания и высоту
{S = 2pi r (h+r)}
Формула для нахождения полной поверхности цилиндра через высоту и радиус основания:
{S = 2pi r (h+r)}, где π — число Пи (3,14159…), r — радиус основания цилиндра, h — высота цилиндра.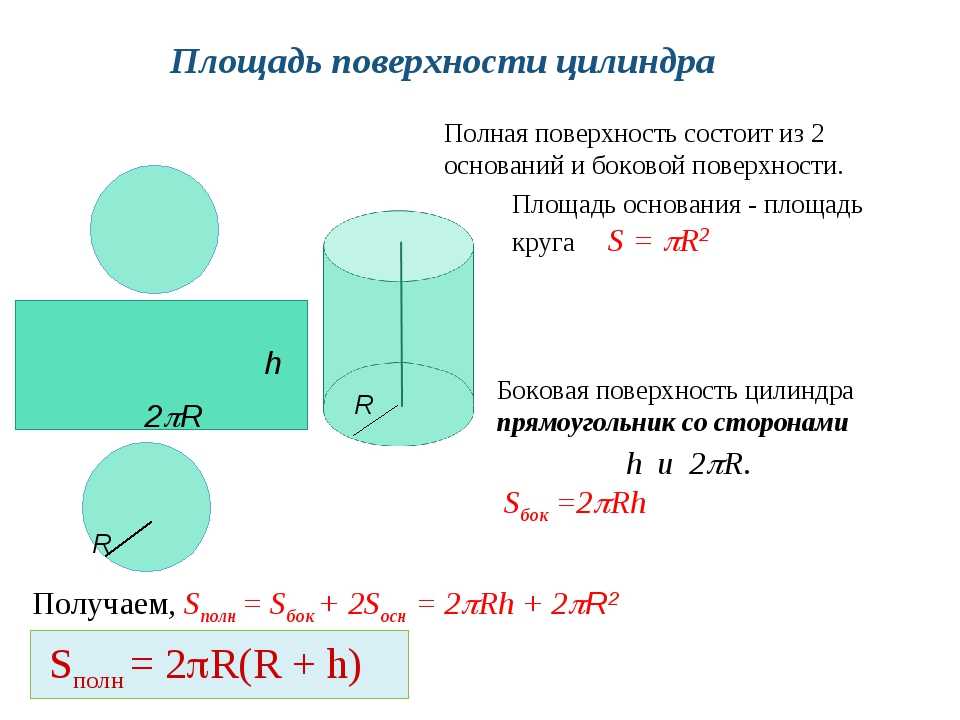
Источники
- https://mnogoformul.ru/obem-cilindra
- https://infofaq.ru/radius-cilindra.html
- https://MicroExcel.ru/obyom-tsilindra/
- https://www.calc.ru/radius-tsilindra.html
- https://MicroExcel.ru/radius-tsilindra/
- https://mnogoformul.ru/ploshhad-poverkhnosti-cilindra
Объем цилиндра
Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.
Объем правильного цилиндра через радиус и высоту цилиндра
— Вычисления (показано) (скрыто)
— примечания (показано) (скрыто)
r — радиус основания цилиндра
h — высота цилиндра
… вычисление …
Площадь основания цилиндра
… вычисление …
Площадь боковой поверхности
.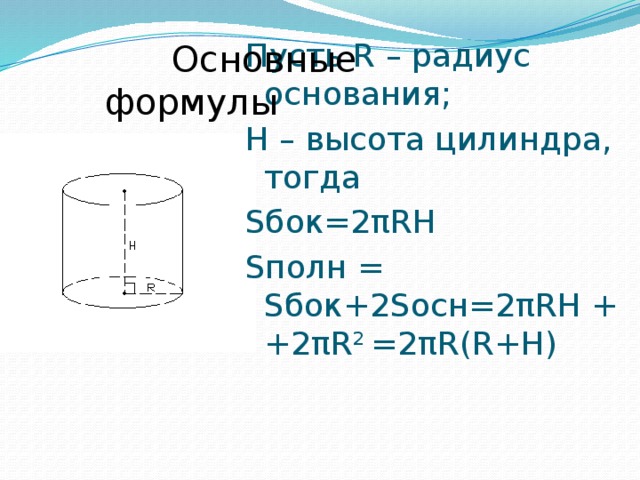 .. вычисление …
.. вычисление …
Общая площадь
… вычисление …
Упрощение формулы:
Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра
S — площадь основания цилиндра
h — высота цилиндра
… вычисление …
Площадь боковой поверхности
… вычисление …
Общая площадь
… вычисление …
Формулы и калькулятор для вычисления объема цилиндра через диаметр основания
d — диаметр основания цилиндра
h — высота цилиндра
… вычисление …
Площадь основания цилиндра
… вычисление …
Площадь боковой поверхности
… вычисление …
Общая площадь
. .. вычисление …
.. вычисление …
Объем цилиндрической полости
Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.
На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.
Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
Теория
Цилиндр может быть правильным или наклонным.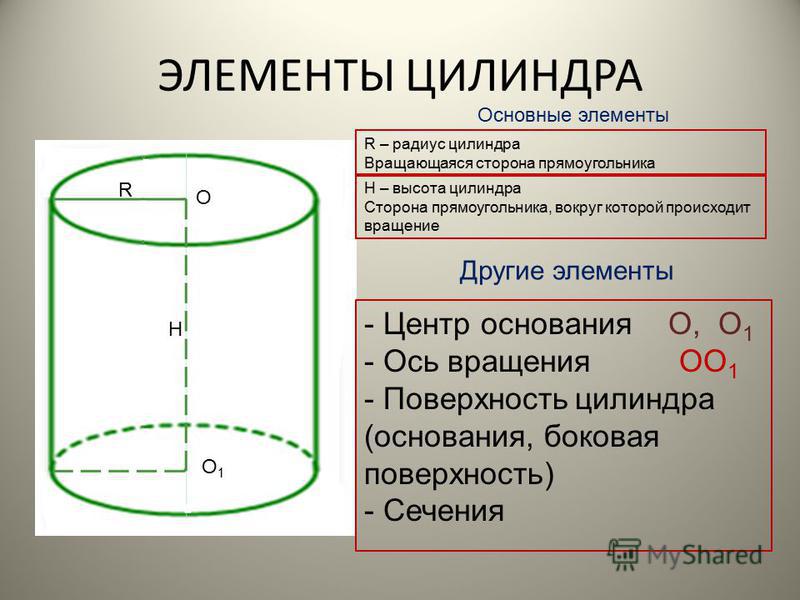
Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.
Рассмотрим правильный цилиндр.
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра
.Радиус основания цилиндра, является радиусом цилиндра.
Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.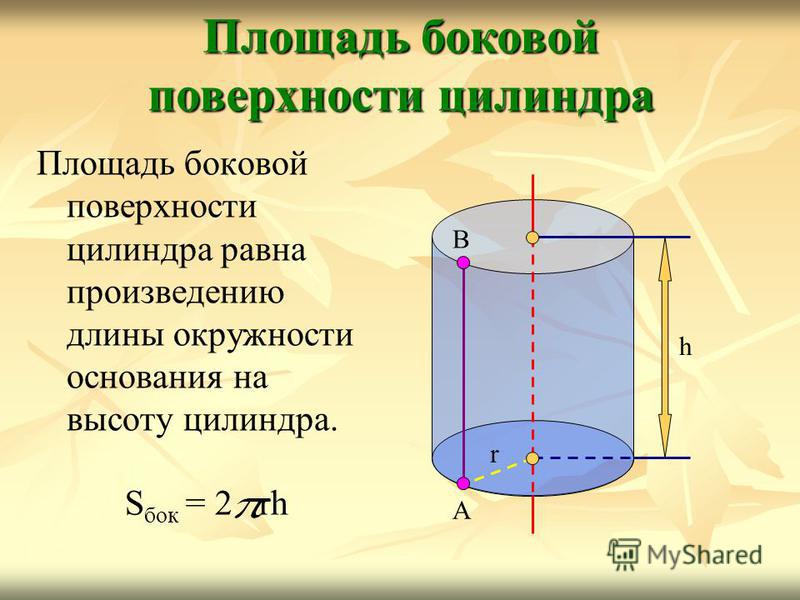
Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.
Поверхности цилиндра
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.
Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.
Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).
Сечения цилиндра
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник, но две боковые стороны которого будут являться кривыми линиями.
Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг.
Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс.
Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса.
Что такое объем
Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм3, см3, мл3.
Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.
Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость).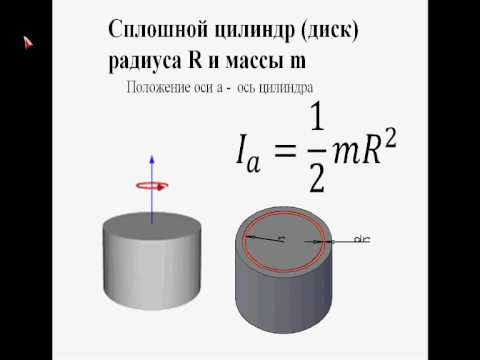 В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.
В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.
Объем и площадь других видов цилиндров рассмотрен в статьях:
Объем полого цилиндра
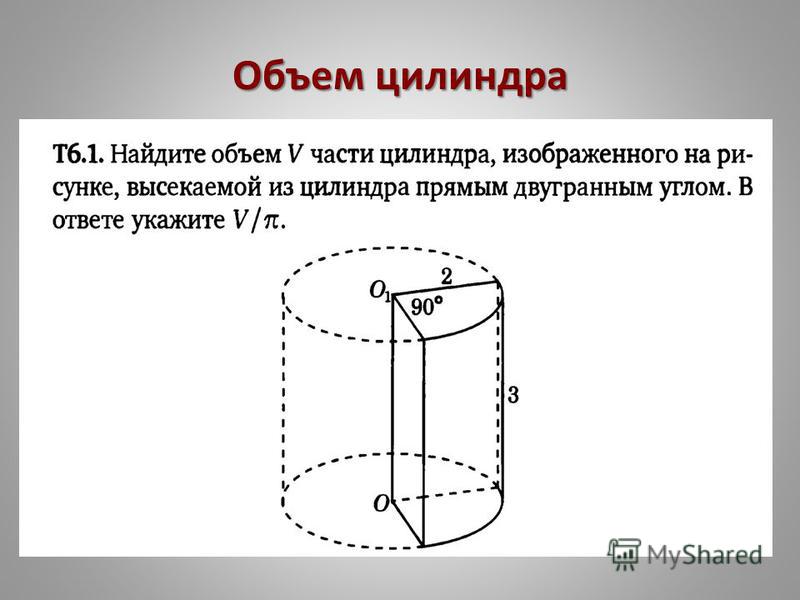
Объем части цилиндра
Объем части полого цилиндра
Вы можете скачать формулы объема и площади поверхностей правильного цилиндра в виде картинки
Объем цилиндра: формула, калькулятор — 24СМИ
Содержание
- Расчет объема цилиндра
- Где применяется расчет объема цилиндра
Как отличить человека технической специальности от человека с гуманитарным складом ума? Спросите каждого, что такое цилиндр. Первый скажет, что это геометрическое тело, второй вспомнит мужской головной убор 19 века. Оба будут правы, да и шляпа получила такое название благодаря особенной форме, основой которой являлась та самая фигура из геометрии. Итак, каковы особенности цилиндра и как рассчитать его объем.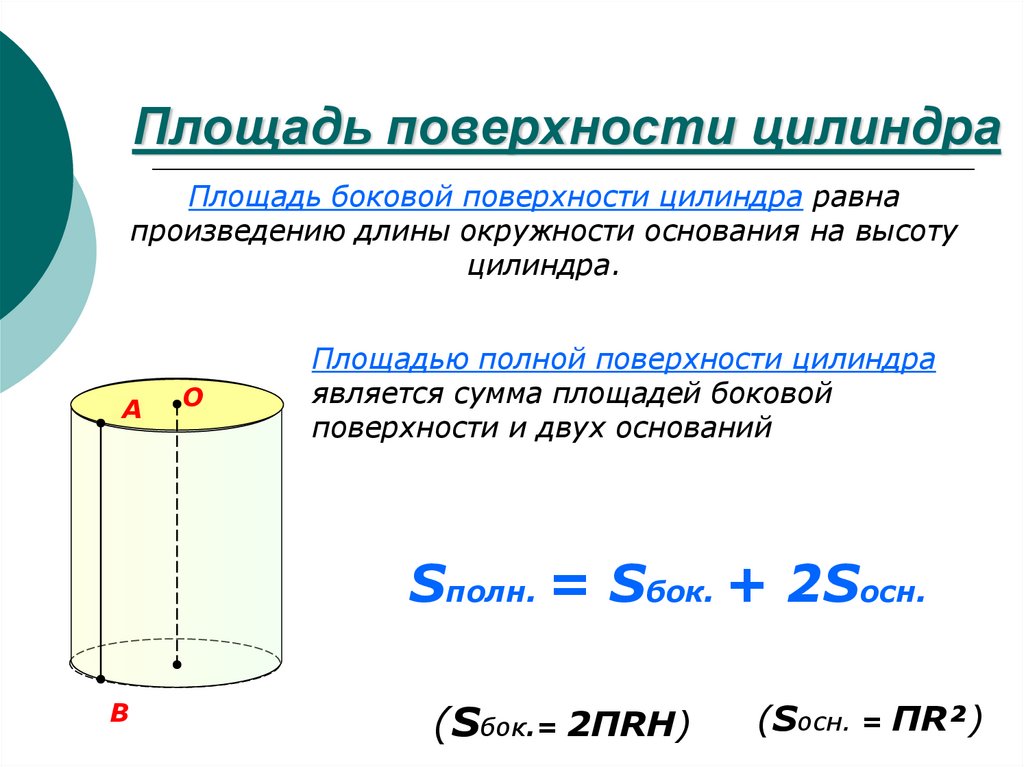
Расчет объема цилиндра
Слово «цилиндр» произошло от древнегреческого kylindros, означающего «валик». Математики дают несколько определений цилиндру:
- Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее под прямым углом.
- Цилиндр — это тело вращения, которое получается при вращении прямоугольника вокруг его стороны.
- Цилиндр — геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одной из его сторон.
Все эти определения верны. Также стоит отметить основные части цилиндра:
- Основания — плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями.
- Боковая поверхность цилиндра — поверхность между плоскостями оснований.
Если в основании цилиндра лежит круг, то его называют круговым. Существуют и другие виды цилиндров, в зависимости от формы основания — эллиптический, гиперболический, параболический и т. д.
д.
Также все цилиндры делятся на прямые и наклонные. У каждого цилиндра есть образующие — это отрезки, соединяющие соответствующие точки оснований. Если образующие перпендикулярны основаниям, то цилиндр называется прямым, а если образующие расположены под углом — цилиндр наклонный или косой.
Рисунок цилиндраЕсть и другие общие понятия для цилиндров:
- Основания цилиндра равны и лежат в параллельных плоскостях. У цилиндра образующие параллельны и равны.
- Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих.
- Радиусом цилиндра называется радиус его основания.
- Высотой цилиндра называется расстояние между плоскостями оснований.
- Осью цилиндра называется прямая, проходящая через центры оснований.
- Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.
- Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра.

Итак, как же вычислить объем цилиндра. Посчитать объем прямого кругового цилиндра можно на калькуляторе. Он равен произведению площади основания на высоту.
V = πR2h,
где V — объем цилиндра, R — радиус основания, h — высота цилиндра, а «пи» — константа, равная 3,14.
Объем цилиндрТаким же образом вычисляется объем прямого кругового цилиндра через диаметр окружности основания — d.
V = πhd2/4
Если цилиндр прямой, но не круговой, то формула вычисления объема представляет произведение длины образующей – n на площадь сечения цилиндра плоскостью, перпендикулярной образующей — S.
V = n * S
Наклонный цилиндрЕсли цилиндр наклонный, то в формуле участвует и синус угла наклона (альфа) образующей к основанию. В этом случае объем вычисляется по формуле:
V = S * n * sin α
Исчисляется объем цилиндра в кубических единицах.
Если стоит задача найти объем описанного вокруг сферы цилиндра, то расчеты будут такими:
Цилиндр и сфераРадиус цилиндра равен радиусу сферы — R.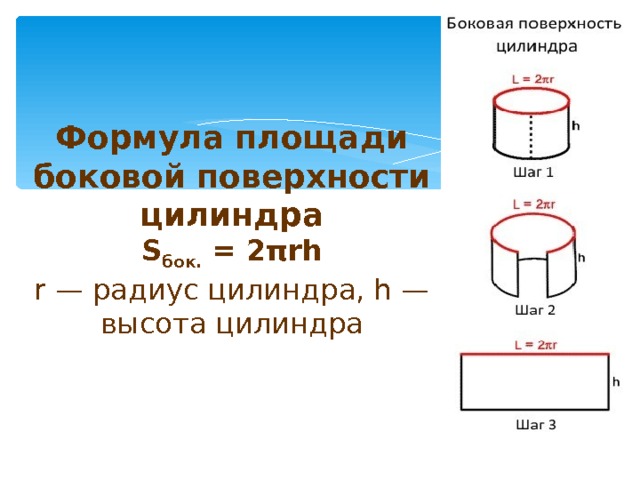 Высота цилиндра равна диаметру сферы. Диаметр есть удвоенный радиус — 2R. Таким образом объем прямого описанного цилиндра равен произведению площади основания πR2 («пи» умножить на радиус в квадрате) на высоту, т. е. 2R.
Высота цилиндра равна диаметру сферы. Диаметр есть удвоенный радиус — 2R. Таким образом объем прямого описанного цилиндра равен произведению площади основания πR2 («пи» умножить на радиус в квадрате) на высоту, т. е. 2R.
V = 2R * πR2
Приведя формулу к должному виду получим:
V = 2πR3
Если цилиндр вписан в прямоугольный параллелепипед, то, зная длину стороны его основания и высоту, можно найти объем.
Цилиндр, вписанный в параллелепипедВ этом случае радиус основания цилиндра равен половине длины стороны основания параллелепипеда — а. Высота цилиндра и параллелепипеда совпадают, обозначим h. Тогда объем вычисляется по формуле:
V = πh(a/2)2
Где применяется расчет объема цилиндра
Расчет объема цилиндра учащиеся проходят в средней школе. Во взрослой жизни эти знания применяют в своей работе инженеры и конструкторы различных машин и механизмов, потребительских товаров, а также архитекторы.
Из товаров народного потребления форму цилиндра имеют стаканы, кружки, бокалы, кастрюли, термосы и прочая посуда, а также некоторые вазы, банки и упаковки напитков либо средств бытовой химии. Объем таких цилиндрических предметов исчисляется в литрах.
Объем таких цилиндрических предметов исчисляется в литрах.
Рассчитывается объем цилиндра при производстве медицинских шприцов. От полученного объема зависит точное количество медикаментов, вводимое пациенту при инъекциях. Лекарства в жидкой форме, суспензии, растворы помещаются в стеклянные или пластиковые бутылочки цилиндрической формы, а на бирке указывается объем средства.
Распространены цилиндры и в технике: такой вид имеют валы и их отдельные составные части, используемые в двигателях внутреннего сгорания. К тому же, расчет объема цилиндра – задача, которую приходится решать конструкторам при проектировании современных бензиновых и дизельных силовых агрегатов, ведь от этого параметра зависят характеристики, в первую очередь, мощность. Двигатели внутреннего сгорания снабжаются поршнями, которые также имеют цилиндрическую форму.
Расчет цилиндрического валаАрхитекторам приходится рассчитывать объем цилиндра при проектировании зданий, снабженных колоннами. Правда, эти архитектурные элементы в классическом варианте (вместе с базой и капителем) встречаются редко, но упрощенные разновидности, состоящие из одного ствола (который и представляет собой цилиндр) используются часто.
Правда, эти архитектурные элементы в классическом варианте (вместе с базой и капителем) встречаются редко, но упрощенные разновидности, состоящие из одного ствола (который и представляет собой цилиндр) используются часто.
Чрезвычайно распространенные детали, которые присутствуют в конструкциях технических устройств — роликовые подшипники. Как нетрудно догадаться по названию, главный компонент — прочные и износостойкие металлические цилиндрические ролики. Благодаря такой геометрии, эти детали обладают большой несущей способностью и способны выдерживать нагрузки. Роликовые подшипники — высокоточные детали, и поэтому при их создании правильный расчет объема цилиндра (ролика) играет немаловажную роль.
формулы и задача :: SYL.ru
Вопрос, как найти объем цилиндра, может возникнуть не только у школьника. Ведь такую форму имеет, к примеру, кастрюля, емкость которой иногда срочно нужно узнать. Вот тогда потребуется знание специальной формулы.
Что нужно знать о цилиндре?
Геометрическое тело, о котором мы говорим, образуется в результате вращения прямоугольника вокруг одной из его сторон, и всегда будет прямым.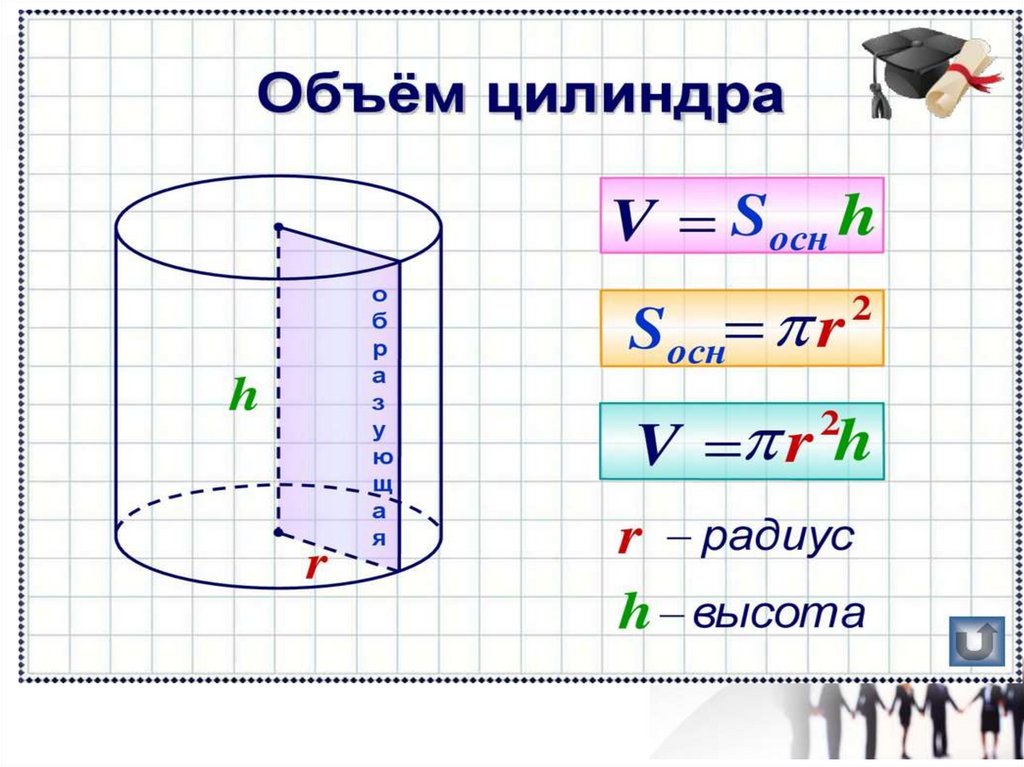 То есть угол между образующей цилиндра и его основанием в данном случае равен 90 градусам. Если выполнить это простое движение не удается, и угол уже не 90 градусов, то идет речь о наклонном цилиндре.
То есть угол между образующей цилиндра и его основанием в данном случае равен 90 градусам. Если выполнить это простое движение не удается, и угол уже не 90 градусов, то идет речь о наклонном цилиндре.
Каким бы ни был вид тела, все равно нужно знать о том, как найти объем цилиндра. Но сначала нужно определиться с некоторыми теоретическими данными.
Как называются отдельные элементы цилиндра и что о них известно?
Отрезки, которые соединяют попарно соответствующие точки на двух основаниях, называются образующими. У любого цилиндра они равны и параллельны друг другу. Если он прямой, то длина образующей совпадает с высотой тела.
В основании может лежать окружность или эллипс, тогда цилиндр будет круговым или эллиптическим соответственно. В формулах этот факт потребуется учесть. Потому что чаще всего они даются для кругового цилиндра. В эллиптическом, до того как вычислить объем цилиндра, нужно будет узнать, по какой формуле определить площадь овала.
Формулы объема для прямого и наклонного цилиндров
Здесь и далее приняты такие обозначения.
| Буква-обозначение | математическая величина |
| V | объем |
| S | площадь основания |
| h | высота |
| r | радиус окружности |
| l | длина образующей |
| α | угол между образующей и основанием |
В любом случае потребуется формула, в которой высота тела, умножается на площадь основания. Она выглядит так:
V = Sh
Если требуется узнать, как найти объем цилиндра прямого, то здесь высота по длине полностью совпадает с образующей. Основанием чаще всего является круг, тогда его площадь будет сосчитана по формуле:
S = πr2.
Когда в задаче идет речь об эллиптическом цилиндре, то потребуется такая формула площади основания:
S = π ab, здесь буквами a и b обозначены малая и большая полуоси овала.
При решении задач о наклонном цилиндре потребуется ввести некоторые дополнения в формулу. Например, если не известна высота, но идет речь об образующей и угле между ней и основанием. Тогда букву h потребуется заменить таким выражением:
Например, если не известна высота, но идет речь об образующей и угле между ней и основанием. Тогда букву h потребуется заменить таким выражением:
h = l * sin α.
Как быть, если нужно определить объем на практике?
В задачах обычно уже известны значения угла или высоты с образующей. А возможно, какие-то другие элементы, через которые их можно найти. В жизни приходится делать измерения самостоятельно.
Тогда вопрос о том, как определить объем цилиндра, сводится к тому, чтобы правильно сделать измерения его высоты и радиуса. Для этого потребуются: линейка, карандаш и прямоугольный лист бумаги.
Чаще всего в быту нас окружают прямые круговые цилиндры. Измерить их высоту обычно не составляет труда. Нужно просто приложить линейку сбоку и измерить расстояние от низа до верха тела. Это будет высота — h.
С радиусом окружности все не так легко. Нужно немного вспомнить геометрию. Здесь потребуется лист бумаги с прямым углом и карандаш.
Что дает теория по геометрии? Вокруг прямоугольного треугольника можно описать окружность. Причем его прямой угол окажется на ней, а гипотенуза совпадет с диаметром.
Причем его прямой угол окажется на ней, а гипотенуза совпадет с диаметром.
Нужно взять лист бумаги и положить его так, чтобы прямой угол касался края основания. Тогда две его стороны, которые образуют этот угол, в некоторых точках пересекутся с окружностью. В этих местах потребуется сделать метки. По ним провести отрезок. Он окажется гипотенузой и искомым диаметром основания цилиндра.
Как найти объем цилиндра, в нашем случае? В формуле фигурирует радиус. Он равен половине диаметра. То есть длину получившегося отрезка нужно разделить на два.
Осталось только подставить результаты измерений в формулу объема и сосчитать. Причем учесть, что ответ получится в см3. Если объем нужно узнать в кубических метрах, то число нужно будет разделить на миллион. Чтобы получить объем в литрах, делителем окажется тысяча.
Задача
Условие. Даны два цилиндра. Высота первого в два раза больше второго. Радиус второго вдвое больше, чем у первого. Необходимо узнать, во сколько раз объем первого цилиндра больше или мегьше объема второго.
Решение. Сначала потребуется ввести обозначения. Пусть высота и радиус первого тела будут иметь индекс 1, а второго — 2.
Теперь можно записать данные в условии значения в виде выражений:
h1 = 2h2 и r2 = 2r1.
Формулы объемов обоих цилиндров примут такой вид:
v1 = π r12 h1 и v2 = π r22 h2.
В задаче требуется найти:
v1 : v2 = (π r12 h1) : (π r22 h2).
После сокращения πи замены h1 и r2введенными выражениями, получается:
v1 : v2 = (r12 2h2) : (4r12 h2).
То есть v1 : v2 = 1 : 2. Это означает, что объем первого цилиндра в два раза меньше.
Ответ. v1 = v2 : 2.
Объём цилиндра.
 Калькулятор объёма цилиндра онлайн
Калькулятор объёма цилиндра онлайн- Главная
- Справочник
- Геометрия
- Формулы объема
- Формула объема цилиндра
- Объем прямого цилиндра
- Объем цилиндра через радиус основания и высоту цилиндра
- Объем цилиндра через площадь основания и высоту цилиндра
- Объем цилиндра через диаметр основания и высоту цилиндра
- Калькулятор объёма цилиндра
Цилиндр – это геометрическое тело, которое имеет цилиндрическую поверхность, называемое еще как боковая поверхность цилиндра и имеет две поверхности, которые носят название оснований цилиндра. Круговым цилиндр называют, если у него в основании лежит круг.
Высота цилиндра — это отрезок, соединяющий две любые точки оснований но обязательно расположенный перпендикулярно к ним обоим.
Объем прямого цилиндра
Цилиндр — это геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одним из его сторон. 3 $$
3 $$
Уровень5 класс ПредметМатематика СложностьПростая
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Формула объема конуса
Объем конуса равен одной трети произведения площади основания на высоту
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Формула объема куба
Объем куба равен кубу его ребра
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Формула объема шара
Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Формула объема пирамиды
Объем пирамиды равен одной трети произведения площади основания на высоту
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Формула объёма параллелепипеда
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту
Формулы объема Расчёт Объем Тригонометрия Формулы Геометрия Фигуры
Что такое Ватт
1 ватт определяется как мощность, при которой за 1 секунду времени совершается работа в 1 джоуль.

Электротехника Формулы Физика Теория Электричество
Калькулятор для ЕГЭ. Как отличить непрограммируемый калькулятор от программируемого?
ЕГЭ Экзамены
Сколько должен весить человек?
Чтобы узнать вес человека, достаточно знать его рост в сантиметрах, из этой цифры вычесть 100, а к полученному числу либо прибавить 10, если речь идет о мужчине, либо отнять 10, если вычисляется вес женщины.
Масса и вес Масса Теория Единицы измерения
Сложение и вычитание векторов
Суммой двух векторов a и b называется третий вектор c, проведенный из начала a к концу b, если начало вектора b совпадает с концом вектора a. Разностью двух векторов a и b называется вектор c при условии: c = a − b, если c + b =a.
Вектора Формулы Геометрия Алгебра Теория Обозначения
Округление чисел
Числа Формулы Алгебра Числа
Возведение экспоненты в степень
Алгебра Калькулятор Расчёт
Конвертер текста в цифровой код
Онлайн калькулятор преобразует символы в их цифровые коды.

Работа с текстом Калькулятор Расчёт Конвертер Преобразовать Текст
Как перевести число из десятичной системы в двоичную
Основы Расчёт Справочник Информатика Программирование
Калькулятор для расчета рабочего объема цилиндров двигателя автомобиля
Рабочий объем цилиндра представляет собой объем находящийся между крайними позициями движения поршня.
Формула расчета цилиндра известна еще со школьной программы – объем равен произведению площади основания на высоту. И для того чтобы вычислить объем двигателя автомобиля либо мотоцикла, также нужно воспользоваться этими множителями. Рабочий объём любого цилиндра двигателя рассчитывается так:
где,
h — длина хода поршня мм в цилиндре от ВМТ до НМТ (Верхняя и Нижняя мёртвая точка)
r — радиус поршня мм
π — 3,14 постоянная величина.
Или по формуле: V=(πD²/4)h, где вместо радиуса используется D диаметр цилиндра. Для примера, чтобы рассчитать какой объем двигателя Уаз Патриот с двигателем ЗМЗ 40906, мы возьмем данные:
- Диаметр цилиндра 95.
 5 мм (R — 47.75 мм).
5 мм (R — 47.75 мм). - Ход поршня 94 мм.
- Количество цилиндров — 4 шт.
Вставляем данные в калькулятор и получаем объем 2693 куб.см.
Для сравнения рассчитаем какой объем двигателя ВАЗ 2114 с двигателем ВАЗ-11183. Согласно характеристикам:
- Диаметр цилиндра — 82 мм (радиус = 41 мм).
- Ход поршня — 75.6 мм.
- Количество цилиндров — 4 шт.
Получаем в калькуляторе объем 1596 куб.см. Согласно технических характеристик, полученный результат сходится с заводскими данными.
Как узнать объем двигателя
Для расчета рабочего объема двигателя вам будет нужно посчитать объем одного цилиндра и затем умножить на их количество у ДВС. И того получается:
Vдвиг = число Пи умноженное на квадрат радиуса (диаметр поршня) умноженное на высоту хода и умноженное на кол-во цилиндров.
Поскольку, как правило, параметры поршня везде указываются в миллиметрах, а объем двигателя измеряется в см. куб., то для перевода единиц измерения, результат придется разделить еще на 1000.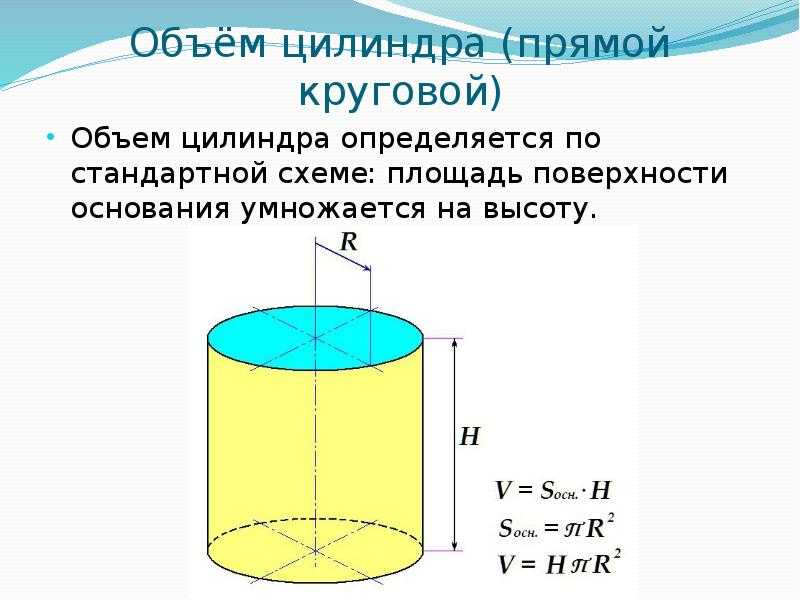
Заметьте, что полный объем и рабочий, отличаются, так как поршень имеет выпуклости и выточки под клапана и в него также входить объем камеры сгорания. Поэтому не стоит путать эти два понятия. И чтобы рассчитать реальный (полный) объем цилиндра, нужно суммировать объем камеры и рабочий объем.
Определить объем двигателя можно обычным калькулятором, зная параметры цилиндра и поршня, но посчитать рабочий объем в см³ нашим, в режиме онлайн, будет намного проще и быстрее, тем более, если вам расчеты нужны, дабы узнать мощность двигателя, поскольку эти показатели напрямую зависят друг от друга.
Объем двигателя внутреннего сгорания очень часто также могут называть литражом, поскольку измеряется как в кубических сантиметрах (более точное значение), так и литрах (округленное), 1000 см³ равняется 1 л.
Расчет объема ДВС калькулятором
Чтобы посчитать объем интересующего вас двигателя нужно внести 3 цифры в соответствующие поля, — результат появится автоматически. Все три значения можно посмотреть в паспортных данных автомобиля или тех. характеристиках конкретной детали либо же определить, какой объем поршневой поможет штангенциркуль.
характеристиках конкретной детали либо же определить, какой объем поршневой поможет штангенциркуль.
Таким образом, если к примеру у вас получилось что объем равен 1598 см³, то в литрах он будет обозначен как 1,6 л, а если вышло число 2429 см³, то 2,4 литра.
Длинноходный и короткоходный поршень
Также замете, что при одинаковом количестве цилиндров и рабочем объеме двигателя могут иметь разный диаметр цилиндров, ход поршней и мощность таких моторов так же будет разной. Движок с короткоходными поршнями очень прожорлив и имеет малый КПД, но достигает большой мощности на высоких оборотах. А длинноходные стоят там, где нужна тяга и экономичность.
Следовательно, на вопрос «как узнать объем двигателя по лошадиным силам» можно дать твердый ответ – никак. Ведь лошадиные силы хоть и имеют связь с объемом двигателя, но вычислить его по ним не получится, поскольку формула их взаимоотношения еще включает много разных показателей. Так что определить кубические сантиметры двигателя можно исключительно по параметрам поршневой.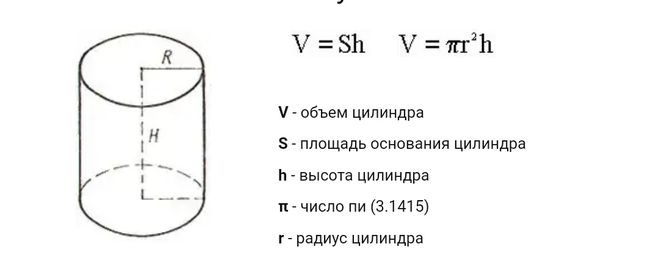
Зачем нужно проверять объем двигателя
Чаще всего узнают объем двигателя когда хотят увеличить степень сжатия, то есть если хотят расточить цилиндры с целью тюнинга. Поскольку чем больше степень сжатия, тем больше будет давление на поршень при сгорании смеси, а следовательно, двигатель будет более мощным. Технология изменения объема в большую сторону, дабы нарастить степень сжатия, очень выгодна — ведь порция топливной смеси такая же, а полезной работы больше. Но всему есть свой предел и чрезмерное её увеличение грозит самовоспламенением, вследствие чего происходит детонация, которая не только уменьшает мощность, но и грозит разрушением мотора.
Часто задаваемые вопросы
В чем измеряется объем двигателя?
Объем двигателя измеряется в кубических сантиметрах (см3), но в документации часто пишется именно в литрах (л.
 ). 1000 кубических сантиметров равны 1 литру. Единица самого точного измерения объема именно куб сантиметры, поскольку, когда объем двигателя автомобиля указывается в литрах, то производится округление до целого числа после запятой. Например, объем 2,4 л. равны 2429 см3.
). 1000 кубических сантиметров равны 1 литру. Единица самого точного измерения объема именно куб сантиметры, поскольку, когда объем двигателя автомобиля указывается в литрах, то производится округление до целого числа после запятой. Например, объем 2,4 л. равны 2429 см3.Какая формула рабочего объем цилиндра двигателя?
Рабочий объем цилиндра двигателя равен произведению числа Пи (3.1415) на квадрат радиуса основания и на высоту хода в нем поршня. Сама формула объема цилиндра ДВС в куб. сантиметрах выглядит так: Vраб = π⋅r²⋅h/1000. Или по альтернативной формуле: V=(πD²/4)h.
Как измерить объем двигателя автомобиля?
Объем двигателя – это сумма рабочих объемов всех его цилиндров, соответственно, необходимо сначала узнать какой объем одного цилиндра, а затем умножить на их количество.
 Объем цилиндра вычисляют, умножив высоту на квадрат радиуса и число «Пи». Но, чтобы измерить именно рабочий объем цилиндра в двигателе, за высоту нужно брать длину хода поршня от НМТ до ВМТ, а радиус можно померить также линейкой, узнав сначала диаметр цилиндра. Такой метод измерения возможен только при снятой головке либо заведомо известных параметрах.
Объем цилиндра вычисляют, умножив высоту на квадрат радиуса и число «Пи». Но, чтобы измерить именно рабочий объем цилиндра в двигателе, за высоту нужно брать длину хода поршня от НМТ до ВМТ, а радиус можно померить также линейкой, узнав сначала диаметр цилиндра. Такой метод измерения возможен только при снятой головке либо заведомо известных параметрах.Объем двигателя 1.8 л. в см3
При конверсии метрической единица объема равной 1,8 литра, то в куб. см это будет 1800 см³, но если это касается именно объема двигателя, то он может варьироваться так как производитель, указывая объем 1.8, округляет значение от того что измеряется в см3. То есть это может быть, как 1799, так и 1761, и даже 1834. Следовательно, какой объем двигателя 1.8 в см³, можно узнать лишь из технической характеристики конкретного автомобиля.
Объем цилиндра: определение, формула, примеры
Сталкиваетесь ли вы с трудностями при нахождении объема цилиндра, если его форма искажена? Задумывались ли вы над тем, как найти объем таких цилиндров? Это то, что вы узнаете через мгновение.
Объем цилиндра означает пространство внутри цилиндра, которое может вместить определенное количество материала. Проще говоря, способность цилиндра удерживать предмет — это его объем. Внутри пространства цилиндра вы можете удерживать любой из трех типов материи — твердое, жидкое или газообразное. Эту емкость можно наблюдать только в трехмерном цилиндре, т. е. вы не можете удержать ни жидкость, ни твердое тело, ни газ в двумерном цилиндре.
Совершенный трехмерный цилиндр имеет два конгруэнтных и параллельных одинаковых основания. Это известно как правильный круговой цилиндр. В прямом круговом цилиндре основания круглые, а каждый отрезок является частью боковой криволинейной поверхности, перпендикулярной основаниям. Вы могли видеть правильные круглые цилиндры в своей повседневной жизни. Формы банок, формы рулонов бумаги, прямое стекло и многое другое.
Однако, если форма стакана совершенно прямая, он будет называться правильным круглым цилиндром. Если форма нелинейна, то какой она будет?
Если две конгруэнтные и идентичные параллельные стороны каким-то образом станут непараллельными или деформируются, вы получите любой из следующих цилиндров:
- Наклонный цилиндр — это цилиндр, стороны которого наклонены к основанию под углом, не равным равен прямому углу.
 Это будет форма искаженного стекла, о которой говорилось выше.
Это будет форма искаженного стекла, о которой говорилось выше. - Эллиптический цилиндр – это цилиндр, основания которого представляют собой эллипсы.
- Прямой круглый полый цилиндр – имеет форму правильного круглого цилиндра. Однако в конце нет замкнутых кругов.
Найти объем цилиндра проще, чем вы думали. Если вам все еще интересно, как найти объем цилиндра, все, что вам нужно, это ведро с водой, весы и пустая плоская поверхность, на которую можно поставить ведро.
Поставьте ванну на ровную пустую поверхность и начните наполнять ее водой. Вы должны убедиться, что вода заполнена до краев. Как только ванна наполнится водой, поместите цилиндр, объем которого вам нужно найти, внутрь ванны. Вы увидите, как вода начнет выходить из ванны.
Соберите выпавшую воду в стакан. Убедитесь, что вода не падает, пока вы делаете преобразование. Поставьте стакан на весы и запишите вес воды. Не забудьте вычесть вес стакана. Вы должны иметь только вес воды.
Согласно закону Архимеда, вес воды, падающей из ванны, будет равен весу цилиндра.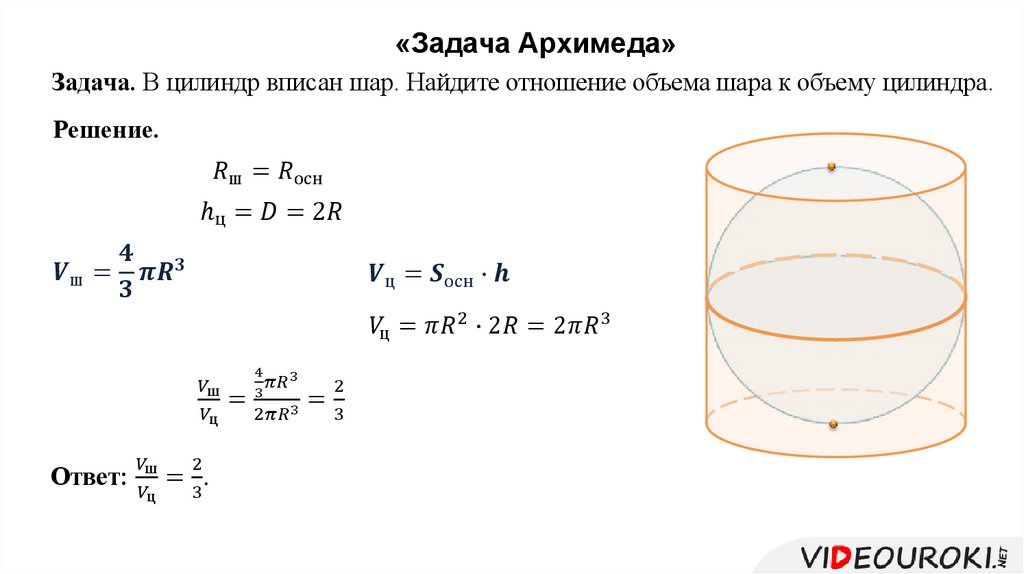 Следовательно, вес полученной воды будет равен весу цилиндра. Вам может быть интересно, как найти объем цилиндра?
Следовательно, вес полученной воды будет равен весу цилиндра. Вам может быть интересно, как найти объем цилиндра?
Согласно физике, если вы находитесь в помещении с комнатной температурой, вес будет равен объему. Это означает, что 1 кг будет эквивалентен 1 литру и так далее. Следовательно, вы получите объем цилиндра из объема воды.
Но что, если вы живете в холодном или жарком регионе? Тогда вам придется использовать другой метод.
Формула для нахождения объема цилиндраВы можете найти объем цилиндра, используя формулу. Это универсально и может применяться независимо от вашего региона. Единицами объема являются кубические сантиметры, кубические дюймы или любые стандартные единицы с префиксом «кубический».
Объем цилиндра можно найти двумя способами. Вот они:
- Используя площадь и высоту
- Используя размеры
- Нахождение объема цилиндров по площади и высоте есть не что иное, как произведение площади и высоты любой формы.
 Это правило справедливо для всех трехмерных фигур, известных в математике. Например, в кубоиде, если вы знаете площадь одной его стороны, а затем умножаете ее на высоту или ширину, то есть на оставшуюся сторону, вы получите объем.
Это правило справедливо для всех трехмерных фигур, известных в математике. Например, в кубоиде, если вы знаете площадь одной его стороны, а затем умножаете ее на высоту или ширину, то есть на оставшуюся сторону, вы получите объем.
В цилиндрах V = площадь x высота
- Нахождение площади с известными размерами – Универсальная формула для нахождения объема цилиндра: π r 2 ч, где значение π (пи) равно 3,14. или 22/7, r — радиус верха или низа цилиндра, а h — высота. Используя формулу, можно найти объемы прямых круговых цилиндров и косых цилиндров.
Однако для эллиптических цилиндров формула другая. Поскольку эллиптические цилиндры имеют различные радиусы, формула для нахождения их объемов имеет вид: V = π abh, где π = 22/7 или 3,14, a и b — радиусы основания эллиптического цилиндра, а h — высота .
Кроме того, формула также отличается для полых прямоугольных цилиндров. Объем полого прямоугольного цилиндра определяется формулой: V = π (R 2 — r 2 ) h, где R — внешний радиус круглого основания, r — внутренний радиус, а h — высота цилиндра.
Если вы ищете формулу площади поверхности цилиндра, то вот она: A = 2πr 2 + 2πrh, где r и h — радиус и высота цилиндра соответственно. Единицами площади поверхности будут квадратные единицы.
Шаги для расчета объема цилиндраСледуя приведенным ниже методам, вы можете найти объем цилиндра.
Шаг 1: Определите тип цилиндра, данный вам в вопросе или в реальной жизни.
Шаг 2: Когда у вас есть тип цилиндра, вам нужно выяснить формулу, по которой можно найти объем цилиндра.
Шаг 3: Теперь у вас есть и формула. Проверьте, какие размеры вам нужны, чтобы найти объем. Убедитесь, что все размеры имеют одинаковые единицы измерения.
Шаг 4: Разместите их на своих местах и рассчитайте объем.
Шаг 5: Сохраните единицы измерения после расчетного значения как «кубические единицы». Используйте соответствующую единицу измерения, такую как метр, сантиметр или любую другую, вместо слова единица измерения.
Примеры для нахождения объема цилиндра
Пример 1. Цилиндр имеет радиус 50 см и высоту 100 см. Как найти объем цилиндра?
Решение: Мы знаем, что объем цилиндра находится по формуле – π r 2 h, где r — радиус цилиндра, а h — высота.
Таким образом, подставив значения, получим
Пример 2: Как найти объем цилиндра, у которого один из радиусов равен 40 см, а другой — 60 см? Цилиндр имеет высоту 200 см.
Решение: Из приведенных данных видно, что цилиндр эллиптический, так как радиусы разные. Чтобы найти объем эллиптического цилиндра, используется формула V = π abh, где a и b — радиусы, а h — высота.
Следовательно, объем цилиндра = V = π abh
= π x 40 x 60 x 200 = 1507200 см 3 .
Пример 3: Как найти объем полого цилиндра изнутри и имеет внешний и внутренний радиусы единиц 6 и 8 соответственно? Высота этого полого цилиндра составляет 15 единиц.
Решение: Мы знаем, что формула объема полого цилиндра имеет вид V = π (R 2 – r 2 ) h.
Следовательно, ставя значения, получаем,
V = π (R 2 – r 2 ) ч
= π (8 2 – 6 2 ) 15 = 1318,8 ед. 2 .
Пример 4. Однажды Алекс задался вопросом: «Как мне найти объем цилиндра, высота которого равна 6 дюймам, а радиус — 3 дюймам». Можете ли вы помочь ей найти объем этого цилиндра?
Ответ: Да, можно! Вы знаете формулу для нахождения объема цилиндра: V = π r 2 h.
Таким образом, подставив значения, вы получите V = π r 2 ч
= π x 3 2 x 6 = 169,56 в 3 .
Вы можете сказать Алексу, что объем цилиндра равен 169,56 в 3 .
Калькулятор объема цилиндра
Автор: Ханна Памула, кандидат наук
Отзыв от Богны Шик и Джека Боуотера
Последнее обновление: 06 сентября 2022 г.
Содержание:- Как рассчитать объем цилиндра?
- Объем полого цилиндра
- Объем наклонного цилиндра
- Часто задаваемые вопросы
Наш калькулятор объема цилиндра позволяет рассчитать объем этого твердого тела.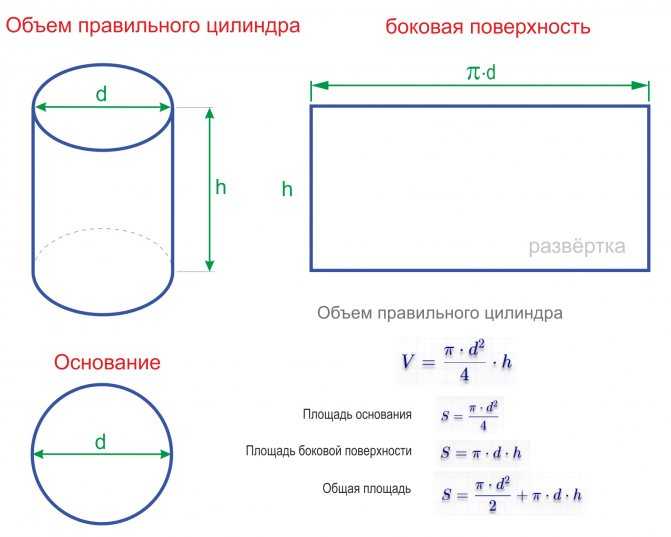 Если вы хотите выяснить, сколько воды помещается в банку, кофе в вашу любимую кружку или даже объем соломинки для питья — вы находитесь в правильном месте. Другим вариантом является расчет объема цилиндрической оболочки (полого цилиндра).
Если вы хотите выяснить, сколько воды помещается в банку, кофе в вашу любимую кружку или даже объем соломинки для питья — вы находитесь в правильном месте. Другим вариантом является расчет объема цилиндрической оболочки (полого цилиндра).
Как рассчитать объем цилиндра?
Начнем с самого начала – что такое цилиндр? Это твердое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями. Мы можем представить его как твердую физическую банку с крышками сверху и снизу. Для расчета его объема нам нужно знать два параметра – радиус (или диаметр) и высоту:
объем цилиндра = π × радиус цилиндра² × высота цилиндра
Калькулятор объема цилиндра помогает найти объем прямого, полого и наклонного цилиндра: оболочка, представляет собой трехмерную область, ограниченную двумя прямыми круговыми цилиндрами, имеющими одну ось и два параллельных кольцевых основания, перпендикулярных общей оси цилиндров.
Легче понять это определение, представив, например, соломинку для питья или трубку – полый цилиндр – это пластик, металл или другой материал.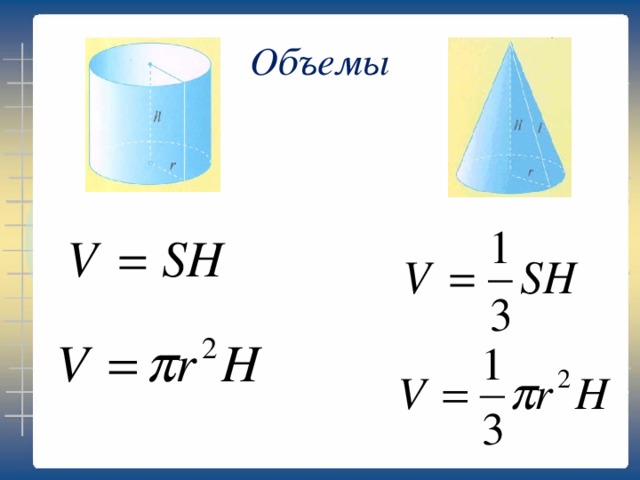 Формула объема полого цилиндра:
Формула объема полого цилиндра:
объем_цилиндра = π × (R² - r²) × высота_цилиндра
где R – внешний радиус, а r – внутренний радиус
Чтобы вычислить объем цилиндрической оболочки, возьмем реальный пример , может… рулон туалетной бумаги, а почему бы и нет? 😀
Введите внешний радиус цилиндра . Стандарт равен примерно 5,5 см.
Определить внутренний радиус цилиндра . Это внутренний радиус картонной детали около 2 см.
Узнать высоту цилиндра ; для нас это 9 см.
Тадаам! Объем полого цилиндра равен 742,2 см³.
Помните, что результатом является объем бумаги и картона. Если вы хотите посчитать, сколько пластилина можно положить внутрь картонного рулона, воспользуйтесь стандартной формулой объема цилиндра — калькулятор посчитает в мгновение ока!
Объем косого цилиндра
Косой цилиндр – это тот, который «наклоняется» – стороны не перпендикулярны основаниям, в отличие от стандартного «прямого цилиндра».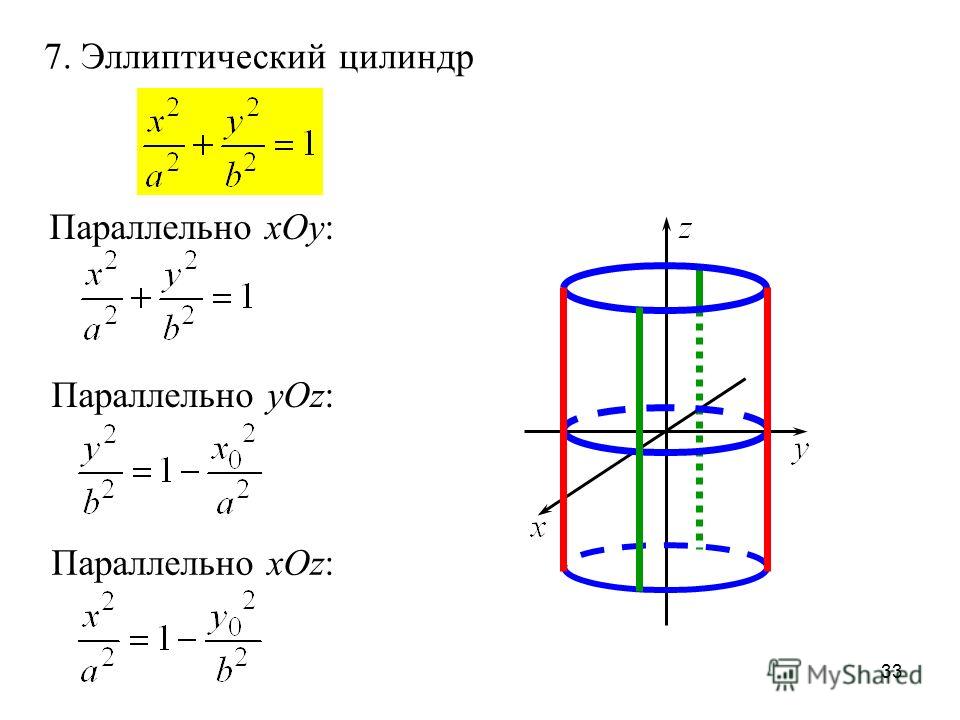 Как рассчитать объем косого цилиндра? Формула такая же, как и для прямого. Только помните, что высота должна быть перпендикулярна основаниям.
Как рассчитать объем косого цилиндра? Формула такая же, как и для прямого. Только помните, что высота должна быть перпендикулярна основаниям.
Теперь, когда вы знаете, как рассчитать объем цилиндра, возможно, вы захотите определить объемы других трехмерных тел? Используйте этот общий калькулятор объема!
Если вам интересно, сколько чайных ложек или чашек поместится в ваш контейнер, воспользуйтесь нашим конвертером объема.
Для расчета объема грунта, необходимого для цветочных горшков различной формы, в том числе для цилиндрического, воспользуйтесь калькулятором грунта.
Часто задаваемые вопросы
Где можно найти цилиндры в природе?
Цилиндры вокруг нас , и мы говорим не только о банках Pringles. Хотя вещи в природе редко бывают идеальными цилиндрами, некоторые примеры стволы деревьев и стебли растений, некоторые кости (и, следовательно, тела) и жгутики микроскопических организмов. Они составляют большое количество природных объектов на Земле!
Они составляют большое количество природных объектов на Земле!
Как нарисовать цилиндр?
Чтобы нарисовать цилиндр, выполните следующие действия:
Нарисуйте слегка приплюснутый круг. Чем более он сплющен, тем ближе вы смотрите на сторону цилиндра на .
Начертить две равные параллельные линии с дальних сторон вашего круга спускается вниз.
Соедините концы двух линий полукруглой линией, которая выглядит так же, как нижняя половина вашего верхнего круга.
При необходимости добавьте тень и штриховку.
Как рассчитать вес баллона?
Для расчета веса баллона:
Возведение в квадрат радиуса цилиндра .
Умножьте квадрат радиуса на число пи и высоту цилиндра .
Умножьте объем на плотность цилиндра.
 Результат — вес цилиндра.
Результат — вес цилиндра.
Как рассчитать отношение площади поверхности к объему цилиндра?
Найдите объем цилиндра по формуле πr²h .
Найдите площадь поверхности цилиндра по формуле 2πrh + 2πr² .
Из двух формул составьте отношение , т. е. πr²h : 2πrh + 2πr².
В качестве альтернативы упростите его до rh : 2(h+r) .
Разделите с обеих сторон на одну из сторон, чтобы получить соотношение в его простейшей форме.
Как найти высоту цилиндра?
Если у вас объем и радиус цилиндра:
- Убедитесь, что объем и радиус указаны в тех же единицах , что и (например, см³ и см), а радиус — в радианах .
- Квадрат радиус.
- Разделите объем на квадрат радиуса и число Пи, чтобы получить высоту в тех же единицах, что и радиус.

Если у вас есть площадь поверхности и радиус (r):
- Убедитесь, что поверхность и радиус указаны в тех же единицах , а радиус указан в радианах.
- Вычтите 2πr² из площади поверхности.
- Разделите результат шага 1 на 2πr.
- Результат — высота цилиндра.
Как найти радиус цилиндра?
Если у вас есть объем и высота цилиндра:
- Убедитесь, что объем и высота указаны в тех же единицах (например, см³ и см), а радиус указан в радианах .
- Разделить объем на пи и высоту.
- Квадрат корень результата.
Если у вас есть площадь поверхности и высота (h):
- Подставьте высоту, h и площадь поверхности в уравнение, площадь поверхности = πr²h : 2πrh + 2πr².
- Разделите с обеих сторон на 2π.

- Вычтите площади поверхности/2π с обеих сторон.
- Решите полученное квадратное уравнение.
- Положительный корень это радиус.
Как найти объем прямоугольного трапециевидного цилиндра?
Правильный трапециевидный цилиндр, , также известный как прямоугольная призма , может быть решен следующим образом:
- Сложите вместе две параллельные стороны (основания) трапеции.
- Разделить результат на 2.
- Умножьте результат шага 2 на высоту трапеции (т.е. расстояние, разделяющее две стороны).
- Умножьте результат на длину цилиндра.
- Результатом является площадь правильного трапециевидного цилиндра.
Как найти объем овального цилиндра?
Чтобы найти объем овального цилиндра:
- Умножьте наименьший радиус овала (малая ось) на его наибольший радиус (большая ось).

- Умножьте это новое число на пи .
- Разделите результат шага 2 на 4. Результатом будет площадь овала.
- Умножьте площадь овала на высоту цилиндра.
- Результат — объем овального цилиндра.
Как найти объем наклонного цилиндра?
Чтобы вычислить объем наклонного цилиндра:
- Найдите радиус , длину стороны и угол наклона цилиндра.
- Квадрат радиус.
- Умножьте результат на число пи.
- Возьмем грех угла .
- Умножьте sin на длину стороны.
- Умножьте результат шагов 3 и 5 вместе.
- В результате получился наклонный объем.
Как рассчитать рабочий объем цилиндра?
Чтобы вычислить рабочий объем цилиндра:
- Разделите диаметр отверстия на 2, чтобы получить радиус отверстия .

- Квадрат радиус отверстия.
- Умножьте радиус квадрата на число пи.
- Умножьте результат шага 3 на длину штриха . Убедитесь, что единицы измерения диаметра и длины хода совпадают.
- Результатом является рабочий объем одного цилиндра.
Ханна Памула, кандидат наук
Прямой/наклонный полный цилиндр
Высота
Радиус
Диаметр
Том
Полый цилиндр
Высота
Диаметр Внешний
Диаметр внутренний
Том
Проверьте 20 аналогичных 3D -калькуляторов 📦
Область гемисферекубе.
Объем цилиндра – формула, определение, решенные примеры
Объем цилиндра – это емкость цилиндра, которая вычисляет количество материала, которое он может вместить. В геометрии есть формула определенного объема цилиндра, которая используется для измерения того, какое количество любой величины, будь то жидкость или твердое тело, может быть погружено в него равномерно. Цилиндр – это трехмерная фигура с двумя конгруэнтными и параллельными одинаковыми основаниями. Существуют разные типы цилиндров. Их:
Цилиндр – это трехмерная фигура с двумя конгруэнтными и параллельными одинаковыми основаниями. Существуют разные типы цилиндров. Их:
- Прямой круговой цилиндр: Цилиндр, основания которого представляют собой окружности, а каждый отрезок, являющийся частью боковой криволинейной поверхности, перпендикулярен основаниям.
- Наклонный цилиндр: Цилиндр, стороны которого опираются на основание под углом, не равным прямому углу.
- Эллиптический цилиндр: Цилиндр, основания которого представляют собой эллипсы.
- Прямой круглый полый цилиндр: Цилиндр, состоящий из двух правильных круглых цилиндров, заключенных один внутри другого.
| 1. | Объем цилиндра |
| 2. | Объем цилиндра Формула |
| 3. | Как рассчитать объем цилиндра? |
4.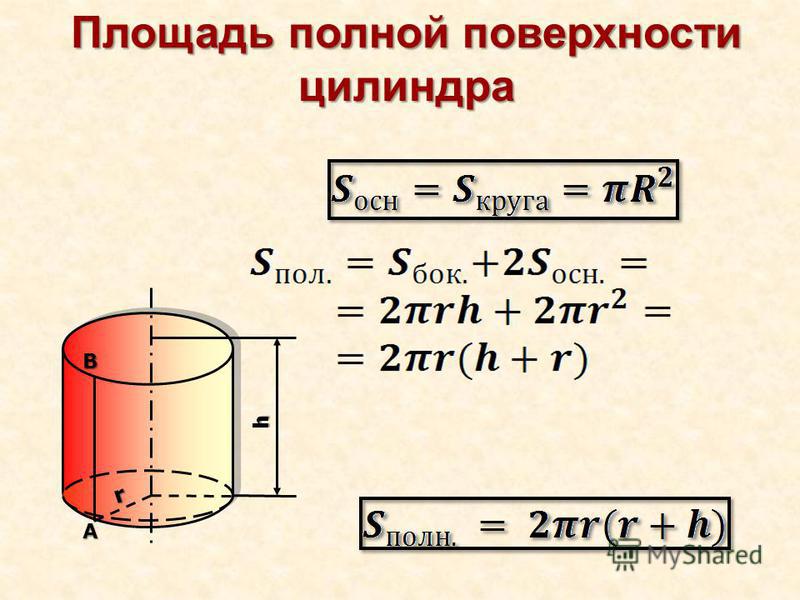 | Часто задаваемые вопросы об объеме цилиндра |
Каков объем цилиндра?
Объем цилиндра – это количество единичных кубов (кубов единичной длины), которые можно в него поместить. Это пространство, занимаемое цилиндром, поскольку объем любой трехмерной формы — это пространство, занимаемое им. Объем цилиндра измеряется в кубических единицах, таких как см 3 , м 3 , в 3 и т. д. Посмотрим формулу, используемую для расчета объема цилиндра.
Определение цилиндра
Цилиндр представляет собой трехмерное твердое тело, состоящее из двух параллельных оснований, соединенных изогнутой поверхностью. Эти основания имеют форму круглого диска. Линия, проходящая из центра или соединяющая центры двух круговых оснований, называется осью цилиндра.
Объем цилиндра Формула
Мы знаем, что цилиндр похож на призму (но обратите внимание, что цилиндр не является призмой, так как имеет изогнутую боковую грань), мы используем ту же формулу объема призмы, чтобы вычислить объем цилиндра.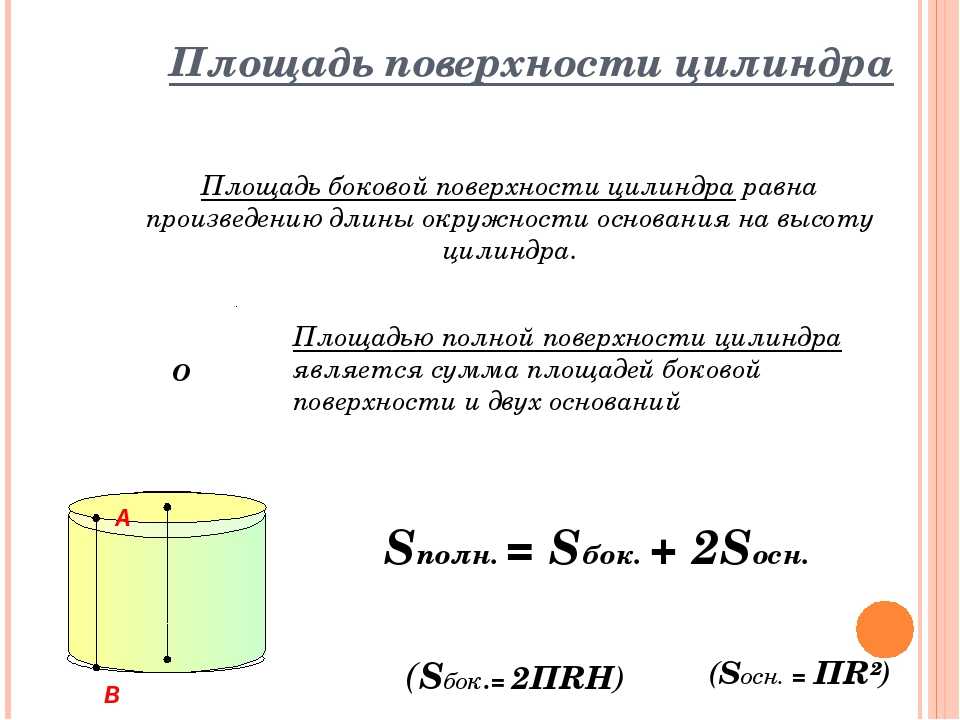 Мы знаем, что площадь призмы рассчитывается по формуле
Мы знаем, что площадь призмы рассчитывается по формуле
V = A × h, где
- A = площадь основания
- ч = высота
Теперь применим эту формулу для расчета объема различных типов цилиндров.
Объем прямого круглого цилиндра
Мы знаем, что основанием правильного круглого цилиндра является окружность, а площадь окружности радиуса ‘r’ равна πr 2 . Таким образом, объем (V) прямого кругового цилиндра по приведенной выше формуле равен
V = πr 2 h
Здесь
- цилиндр
- ‘h’ — высота цилиндра
- π — это константа, значение которой равно 22/7 (или) 3,142.
Таким образом, объем цилиндра прямо зависит от его высоты и прямо зависит от квадрата его радиуса. т. е. если радиус цилиндра удвоится, то его объем удвоится.
Объем наклонного цилиндра
Формула для расчета объема цилиндра (наклонного) такая же, как и у прямого кругового цилиндра. Таким образом, объем (V) наклонного цилиндра с радиусом основания «r» и высотой «h» равен
V = πr 2 h
Объем эллиптического цилиндра
Мы знаем, что эллипс имеет два радиуса.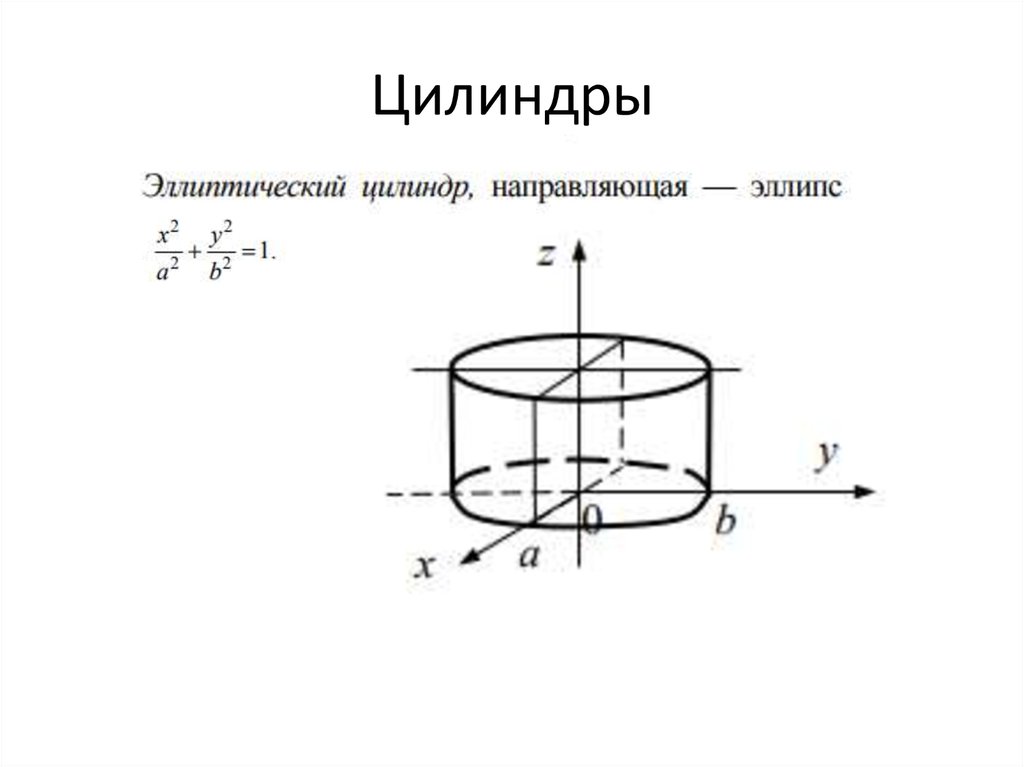 Кроме того, мы знаем, что площадь эллипса, радиусы которого равны «а» и «b», равна πab. Таким образом, объем эллиптического цилиндра равен
Кроме того, мы знаем, что площадь эллипса, радиусы которого равны «а» и «b», равна πab. Таким образом, объем эллиптического цилиндра равен
V = πabh
Здесь
- ‘a’ и ‘b’ — радиусы основания (эллипса) цилиндра.
- ‘h’ — высота цилиндра.
- π — это константа, значение которой равно 22/7 (или) 3,142.
Объем прямого кругового полого цилиндра
Так как правильный круговой цилиндр представляет собой цилиндр, состоящий из двух правильных круговых цилиндров, заключенных один внутри другого, его объем получается путем вычитания объема внутреннего цилиндра из объема внешнего цилиндра. . Таким образом, объем (V) прямого круглого полого цилиндра равен
V = π(R 2 — r 2 )h
Здесь
- ‘R’ — радиус основания внешнего цилиндра. .
- ‘r’ — радиус основания внутреннего цилиндра.
- ‘h’ — высота цилиндра.
- π — это константа, значение которой равно 22/7 (или) 3,142.

Как рассчитать объем цилиндра?
Вот шага для вычисления объема цилиндра:
- Определите радиус как ‘r’ и высоту как ‘h’ и убедитесь, что они имеют одинаковые единицы измерения.
- Подставить значения в формулу объема V = πr 2 ч.
- Запишите единицы измерения в кубических единицах.
Пример: Найдите объем прямоугольного цилиндра радиусом 50 см и высотой 1 метр. Используйте π = 3,142.
Решение:
Радиус цилиндра равен r = 50 см.
Высота: h = 1 метр = 100 см.
Его объем V = πr 2 h = (3,142)(50) 2 (100) = 785 500 см 3 .
Примечание: Нам нужно использовать формулу, чтобы найти объем цилиндра в зависимости от его типа, как мы обсуждали в предыдущем разделе. Кроме того, предположим, что цилиндр является правильным круговым цилиндром, если не указан тип, и примените формулу объема: V = πr 2 ч.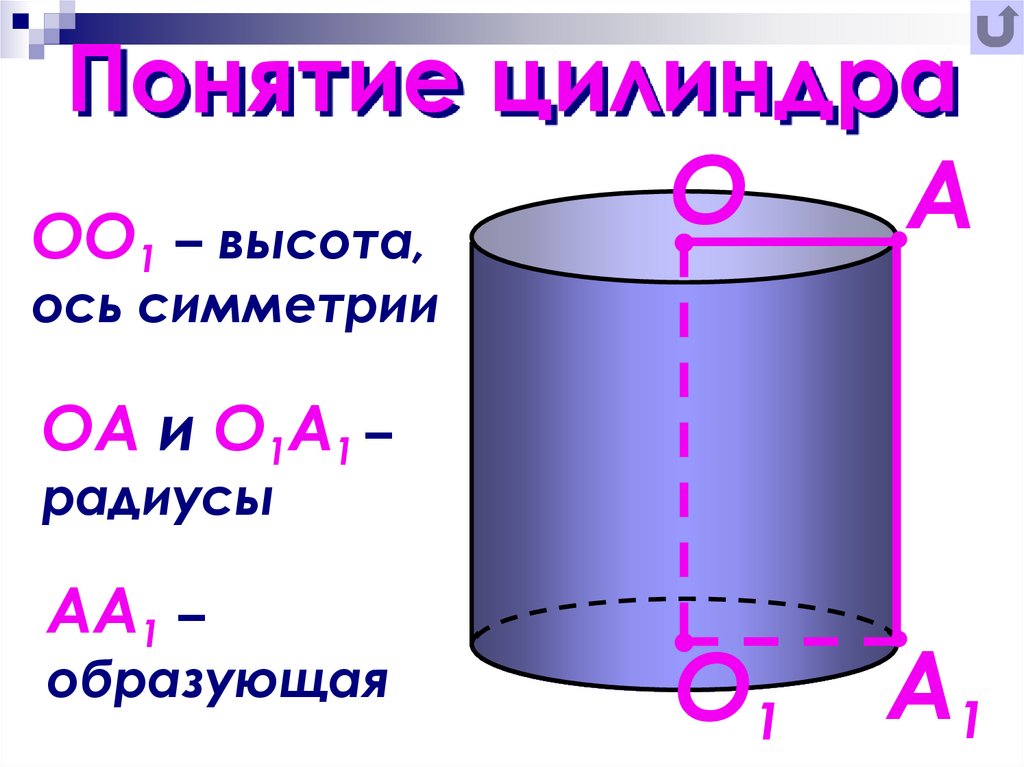
Объем цилиндра Примеры
Пример 1: Найдите объем цилиндрического резервуара для воды с радиусом основания 25 дюймов и высотой 120 дюймов. Используйте π = 3,14.
Решение:
Радиус цилиндрического резервуара r = 25 дюймов.
Его высота h = 120 дюймов.
Используя формулу объема цилиндра, объем резервуара равен
V = πr 2 ч
V = (3,14)(25) 2 (120) = 235500 кубических дюймов.
Ответ: Объем данного цилиндрического резервуара составляет 235 500 кубических дюймов.
Пример 2: Найдите объем эллиптического цилиндра, радиусы основания которого 7 дюймов и 10 дюймов, а высота 15 дюймов. Используйте π = 22/7.
Решение:
Радиусы основания данного эллиптического цилиндра равны
a = 7 дюймов и b = 10 дюймов.
Его высота h = 15 дюймов.
Используя формулу объема цилиндра, объем данного эллиптического цилиндра равен
V = πabh
V = (22/7) × 7 × 10 × 15 = 3300 кубических дюймов.

Ответ: Объем данного цилиндра составляет 3300 кубических дюймов.
Пример 3: Каков объем цилиндра с радиусом 4 единицы и высотой 6 единиц?
Решение:
Радиус,r = 4 единицы Высота,h = 6 единиц
Объем цилиндра, V = πr 2 h кубических единиц.
В = (22/7) × (4) 2 × 6 В = 22/7 × 16 × 6
В = 301,71 кубических единиц.
Следовательно, объем цилиндра равен 301,71 куб.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.
Записаться на бесплатный пробный урок
Практические вопросы по объему цилиндра
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об объеме цилиндра
Каков объем цилиндра?
Объем цилиндра – это количество свободного места в нем. Его можно получить, умножив площадь основания на высоту. Объем цилиндра с радиусом основания ‘r’ и высотой ‘h’ равен V = πr 2 ч.
Его можно получить, умножив площадь основания на высоту. Объем цилиндра с радиусом основания ‘r’ и высотой ‘h’ равен V = πr 2 ч.
Какая формула для расчета объема цилиндра?
Формула для расчета объема цилиндра: V = πr 2 h, где
- ‘r’ — радиус основания цилиндра
- ‘h’ — высота цилиндра
- π — это константа, значение которой равно 22/7 (или) 3,142.
Каков объем цилиндра с диаметром?
Рассмотрим цилиндр радиуса «r», диаметра «d» и высоты «h». Объем цилиндра с радиусом основания ‘r’ и высотой ‘h’ равен V = πr 2 ч. Мы знаем, что r = d/2. Подставив это в приведенную выше формулу, V = πd 2 ч/4.
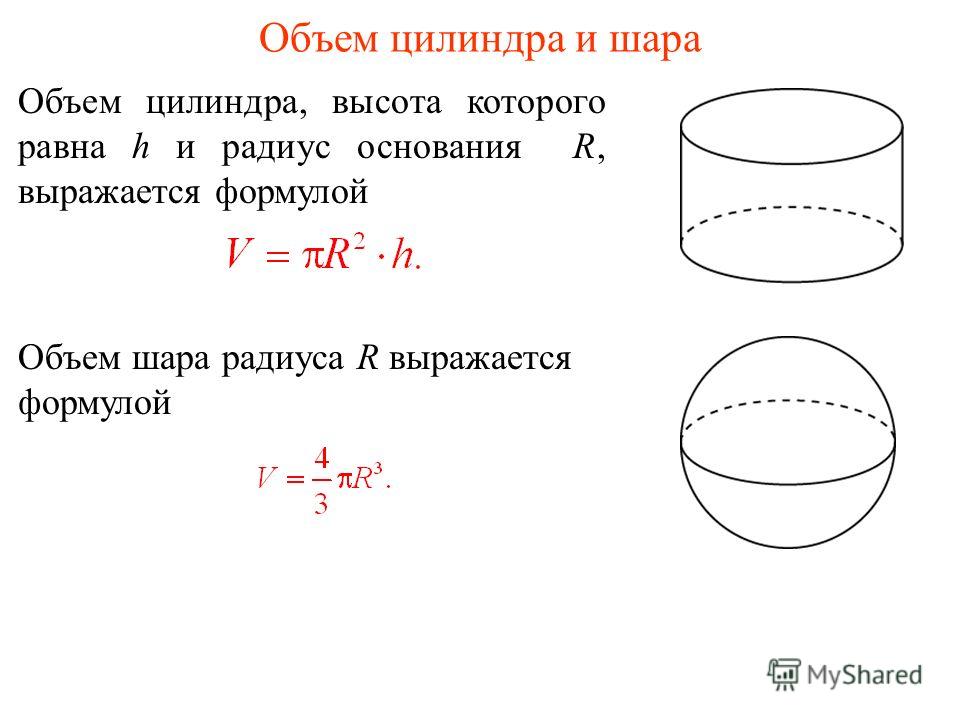
Каково соотношение объемов цилиндра и конуса?
Рассмотрим цилиндр и конус, каждый из которых имеет радиус основания ‘r’ и высоту ‘h’. Мы знаем, что объем цилиндра равен πr 2 ч, а объем конуса равен 1/3 πr 2 ч. Таким образом, требуемое соотношение равно 1:(1/3) (или) 3:1.
Как найти объем цилиндра по диаметру и высоте?
Объем цилиндра с радиусом основания ‘r’ и высотой ‘h’ равен, V = πr 2 h. Если диаметр основания равен d, то d = r/2. Подставляя это в приведенную выше формулу, мы получаем V = πd 2 ч/4. Таким образом, формула для нахождения объема цилиндра с диаметром (d) и высотой (h) имеет вид V = πd 2 h/4.
Как найти объем цилиндра по окружности и высоте?
Мы знаем, что длина окружности радиуса r равна C = 2πr. Таким образом, когда длина окружности основания цилиндра (C) и его высота (h) заданы, мы сначала решаем уравнение C = 2πr для ‘r’, а затем применяем формулу объема цилиндра, то есть V = πr 2 ч.
Как рассчитать объем цилиндра в литрах?
Мы можем использовать следующие формулы преобразования, чтобы преобразовать объем цилиндра из м 3 (или) см 3 в литры.
- 1 м 3 = 1000 литров
- 1 см 3 = 1 мл (или) 0,001 литра
☛ Чек:
- Преобразование в метрическую систему
- Преобразование единиц измерения
Что произойдет с объемом цилиндра, если его радиус уменьшить вдвое?
Объем цилиндра прямо пропорционален квадрату его радиуса. Таким образом, когда его радиус уменьшается вдвое, объем становится равным 1/4 th .
Таким образом, когда его радиус уменьшается вдвое, объем становится равным 1/4 th .
Что происходит с объемом цилиндра, когда его радиус увеличивается вдвое?
Мы знаем, что объем цилиндра прямо пропорционален квадрату его радиуса. Таким образом, когда его радиус увеличивается вдвое, объем увеличивается в четыре раза.
Как найти объем цилиндра с помощью калькулятора?
Калькулятор объема цилиндра — это машина для расчета объема цилиндра. Чтобы рассчитать объем цилиндра с помощью калькулятора, нам нужно предоставить необходимые данные для инструмента калькулятора, такие как требуемые размеры, такие как радиус, диаметр, высота и т. д. Попробуйте теперь вычислить объем цилиндра, введите радиус и высоту цилиндра. в данном ящике объема цилиндра калькулятор. Нажмите на кнопку «Рассчитать», чтобы найти объем цилиндра. Нажав кнопку «Сбросить», вы можете легко очистить ранее введенные данные и найти объем цилиндра для разных значений.
☛ Чек:
- Калькулятор цилиндров
- Калькулятор площади поверхности цилиндра
- Калькулятор высоты цилиндра
Что такое площадь и объем цилиндра?
Площадь поверхности цилиндра – это общая площадь или область, покрываемая поверхностью цилиндра. Площадь поверхности цилиндра определяется двумя следующими формулами:
Площадь поверхности цилиндра определяется двумя следующими формулами:
- Площадь криволинейной поверхности цилиндра = 2πrh
- Общая площадь поверхности цилиндра = 2πr 2 +2πrh = 2πr(h+r)
Площадь цилиндра выражается в квадратных единицах, например, м 2 , in 2 , см 2 , ярд 2 и т. д. в цилиндре, который можно рассчитать по формуле объема цилиндра V = πr 2 ч. Объем цилиндра всегда измеряется в кубических единицах.
☛ Проверить:
- Площадь поверхности цилиндра Листы
- Объем цилиндра Рабочие листы
- Формулы площади поверхности
Как изменится объем полого цилиндра при удвоении высоты?
Формула объема полого цилиндра равна V = π(R 2 — r 2 )h кубических единиц. Из формулы объема видно, что объем прямо пропорционален высоте полого цилиндра. Следовательно, объем удваивается, когда высота полого цилиндра удваивается.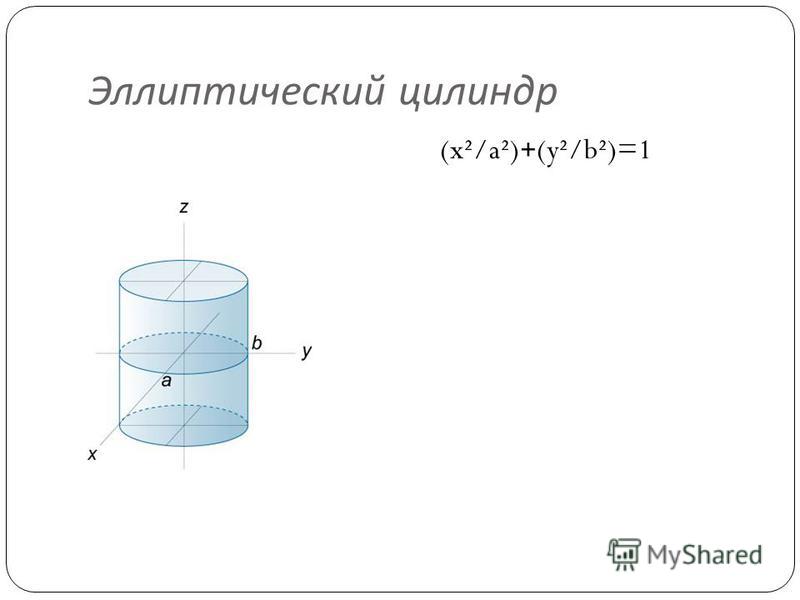
Каков объем цилиндра в единицах числа Пи?
Объем цилиндра определяется как вместимость цилиндра, выраженная в единицах пи. Объем цилиндра в единицах пи выражается в кубических единицах, где единицами измерения могут быть м 3 , см 3 , дюймы 3 или футы 3 .
Объем и площадь поверхности правильного круглого цилиндра (видео и практика)
Стенограмма FAQsPractice
Привет и добро пожаловать на это видео о цилиндрах! В этом видео мы рассмотрим, как найти объем и площадь поверхности любого цилиндра. Давайте узнаем о цилиндрах!
Цилиндры — одна из самых распространенных трехмерных фигур, которые мы видим вокруг себя. Большинство банок для еды и напитков имеют форму цилиндра.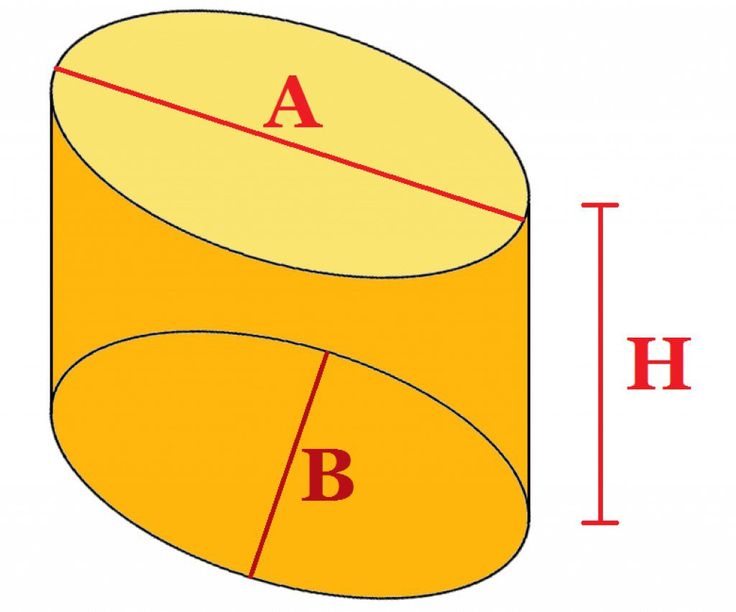 Еще один довольно распространенный элемент цилиндрической формы, который мы видим ежедневно, — это аккумулятор. Оглянитесь вокруг, видите ли вы какие-нибудь цилиндрические формы?
Еще один довольно распространенный элемент цилиндрической формы, который мы видим ежедневно, — это аккумулятор. Оглянитесь вокруг, видите ли вы какие-нибудь цилиндрические формы?
Как видите, все эти объекты имеют круглые верх и низ и изогнутую поверхность. Цилиндр — это трехмерная фигура с двумя круглыми основаниями, параллельными друг другу и соединенными криволинейной поверхностью. Перпендикулярное расстояние, соединяющее основания цилиндра, равно высотой и осью является линия, проходящая через центры круглых оснований.
Цилиндр, ось которого перпендикулярна основаниям, называется правым цилиндром . Цилиндр, ось которого не перпендикулярна основаниям, называется наклонным цилиндром .
Вспомним, что такое объем и площадь поверхности трехмерных фигур и как мы их находим.
Объем трехмерной фигуры — это количество жидкости, которое она может вместить, и измеряется в кубических единицах. {2}\)
{2}\)
изолят термин с переменной
\ (502,4 = 31,4H+157 \)
Комбинируйте, как термины
\ (502,4-157 = 31,4H+157-157 \)
\ (502,4-157 = 31,4H+157-157 \) \ (502,4-157 = 31,4H+157-157 \)\ (502,4-157 = 31,4H+157-157 \)
найти h
\(345,4=31,4h\)
разделить обе части на коэффициент, чтобы изолировать переменную
\(\frac{frac{3}{frac{100035}). 31.4}{31.4}h\)
Следовательно, высота цилиндра 11 футов.
\(11=h\)
У Джоан в магазине есть резервуар для воды высотой 34,8 дюйма и диаметром круглого основания 20,6 дюйма. Она хочет сделать этикетку с логотипом своей компании для боковой стороны резервуара и должна рассчитать площадь поперечного сечения , которая представляет собой площадь поверхности без площади оснований. Какова площадь этикетки? (Используйте 3.14 для \(\pi\))
Какова площадь этикетки? (Используйте 3.14 для \(\pi\))
Поскольку нам нужна только боковая площадь, мы можем удалить площадь кругов из нашей формулы. 93\)
Q
Каков радиус цилиндра?
A
Мы знаем, что радиус круга равен половине его диаметра, и мы знаем, что цилиндры имеют \(2\) (одинакового размера) круглые основания на каждом конце. Следовательно, радиус цилиндра равен радиусу его круговых оснований.
Каков радиус этого цилиндра?
\(r=8\text{ см}\)
Q
Как найти радиус цилиндра, зная только объем?
92h\), не зная хотя бы двух трех переменных. (Примечание: мы можем использовать любую комбинацию двух переменных, чтобы найти оставшуюся. Например, если мы хотим найти неизвестный радиус, нам нужно сначала знать объем и высоту этого цилиндра; для неизвестной высоты , нам потребуются радиус и объем и, конечно же, для неизвестного объема нам потребуются радиус и высота. )
) *Чтобы найти радиус цилиндра, когда нам даны оба высота и объем, нам просто нужно изменить уравнение объема, чтобы получить только r с одной стороны знака «равно». Смотри: 92}\)
\(h=\frac{36π}{9π}\)
\(h=4\text{дюймы}\)
Q
В чем разница между площадью криволинейной поверхности и общей площадью поверхности ?
A
Площадь изогнутой поверхности – это площадь средней части цилиндра. Общая площадь поверхности включает площадь криволинейной поверхности и площадь двух круглых оснований. Уравнение для общей площади поверхности цилиндра находится путем объединения площади основания 1, площади криволинейной поверхности и площади основания 2. Рассмотрим… 92\)
Q
По какой формуле определяется площадь криволинейной поверхности цилиндра?
A
Формула площади криволинейной поверхности цилиндра: \(2πrh\). Думайте об изогнутой части цилиндра как о прямоугольном листе, которым вы оборачиваете трехмерный объект. По сути, это прямоугольник, длина которого равна окружности круглого основания, которое он выравнивает (отсюда берется \(2πr\)) и чья ширина является высотой цилиндра (это где \(h\) происходит от).
По сути, это прямоугольник, длина которого равна окружности круглого основания, которое он выравнивает (отсюда берется \(2πr\)) и чья ширина является высотой цилиндра (это где \(h\) происходит от).
Q
Как иначе называется искривленная поверхность?
A
«Изогнутая поверхность» иногда упоминается как «боковая область». Следовательно, мы могли бы записать соответствующее уравнение в виде \(L=2πrh\). В случае открытого цилиндра (что означает: цилиндр без двух круглых оснований [Подумайте о пустом рулоне бумажных полотенец!]), общая площадь поверхности фактически будет просто боковой площадью.
Практические вопросы
Вопрос №1: 92+2(3,14)(1,5)(4)\). Это упрощается до \(SA=14,13+37,68\), что сокращается до 51,81. Площадь поверхности цилиндра составляет 51,81 ярда 2 .
Скрыть Ответ
Вопрос №2:
Вычислите объем следующего цилиндра.
202,9 см 3
302,3 см 3
402,6 СМ 3
502,4 СМ 3
Показать Ответ
.2(10)\). Когда аппроксимация пи (3.14) заменяется на символ \(π\), уравнение упрощается до 502,4. Объем цилиндра 502,4 см 3 .
Скрыть ответ
Вопрос №3:
Зерновой бункер состоит из цилиндра с куполом наверху. Фермеру Дженкису необходимо рассчитать объем зерна, содержащегося в силосе с высотой цилиндра 50 футов и диаметром цилиндра 10 футов. Купол останется пустым. Если цилиндрическая часть силоса для зерна полностью заполнена, каков общий объем зерна? 92(50)\). Это упрощается до 3925. Силос содержит 3925 футов 3 зерна.
Скрыть ответ
Вопрос №4:
Макс делает свечи для продажи на местном фермерском рынке. Свечи, которые он делает, имеют цилиндрическую форму. Он купил новую форму для свечей, и ему нужно выяснить, сколько расплавленного воска она может вместить. Цилиндрическая форма имеет высоту 10 дюймов и радиус 5 дюймов. Сколько расплавленного воска он может залить в форму, если хочет заполнить ее полностью? 92(10)\), что упрощается до 785. Форма для свечи может вместить 785 в 3 расплавленного воска.
Свечи, которые он делает, имеют цилиндрическую форму. Он купил новую форму для свечей, и ему нужно выяснить, сколько расплавленного воска она может вместить. Цилиндрическая форма имеет высоту 10 дюймов и радиус 5 дюймов. Сколько расплавленного воска он может залить в форму, если хочет заполнить ее полностью? 92(10)\), что упрощается до 785. Форма для свечи может вместить 785 в 3 расплавленного воска.
Скрыть ответ
Вопрос №5:
Джулия хочет переработать три старые банки из-под фруктов. Каждая банка имеет высоту 5 дюймов и радиус 2 дюйма. Она планирует покрасить банки и использовать их как цветочные горшки. Если она хочет покрасить только стороны цилиндров и днища, какова общая площадь поверхности, которую ей нужно будет покрасить?
426,08 дюйма 2 92+3(2(3.14)(2)(5))\), что упрощается до 226,08. Джулии нужно будет покрасить всего 226,08 в 2 .
Скрыть ответ
Вернуться к видео по геометрии
226463
Объем цилиндров – объяснение и примеры
Объем цилиндра – это мера объема цилиндра емкость цилиндра.
Эта статья покажет вам, как найти объем цилиндра, используя формулу объема цилиндра.
В геометрии цилиндр представляет собой трехмерную фигуру с двумя равными и параллельными окружностями, соединенными изогнутой поверхностью.
Расстояние между круглыми гранями цилиндра называется высотой цилиндра . Верх и низ цилиндра представляют собой две конгруэнтные окружности, радиус или диаметр которых обозначаются как « r » и « d » соответственно.
Чтобы рассчитать объем цилиндра, вам нужен радиус или диаметр круглого основания или вершины и высота цилиндра.
Объем цилиндра равен произведению площади круглого основания на высоту цилиндра.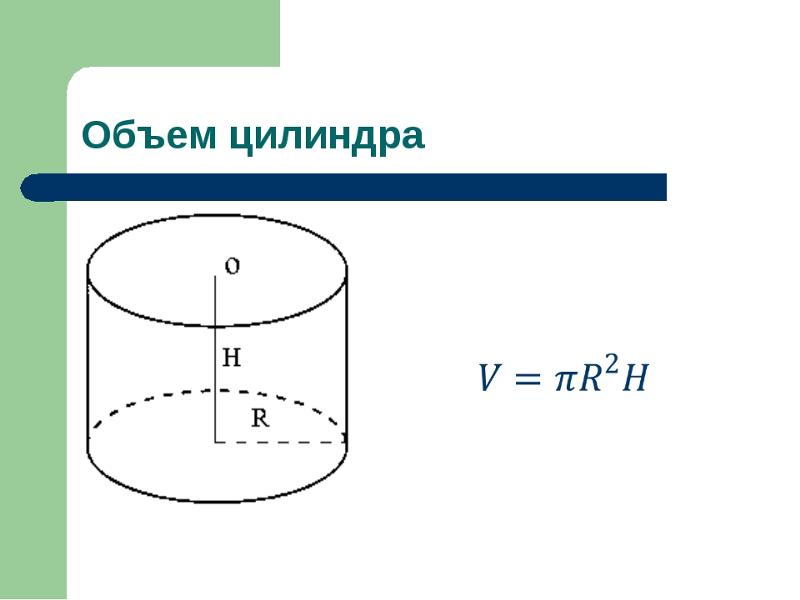 Объем цилиндра измеряется в кубических единицах.
Объем цилиндра измеряется в кубических единицах.
Расчет объема цилиндра полезен при проектировании цилиндрических объектов, таких как:
- Цилиндрические резервуары для водных батлов или лунки
- Culverts
- Pipums
- Cylindrical Coins и Pipes . химические лаборатории
Формула объема цилиндра
Формула объема цилиндра:
Объем цилиндра = πr 2 ч кубических единиц
Где πr 2 = площадь круга a;
π = 3,14;
r = радиус круглого основания и;
h = высота цилиндра.
Для полого цилиндра формула объема задается следующим образом:
Объем цилиндра = πh (r 1 2 – r 2 2 )
Где, r 1 = внешний радиус и r 2 = внутренний радиус цилиндра.
Разность внешнего и внутреннего радиусов образует толщину стенки цилиндра, т. е.
е.
Толщина стенки цилиндра = r 1 – r 2
Решим несколько примеров задач на объем цилиндров.
Пример 1
Диаметр и высота цилиндра 28 см и 10 см соответственно. Каков объем цилиндра?
Решение
Дано;
Радиус равен половине диаметра.
Диаметр = 28 см ⇒ радиус = 28/2
= 14 см
Высота = 10 см
По формуле объема цилиндра;
Том = πr 2 H
= 3,14 x 14 x 14 x 10
= 6154,4 см 3
СОСТОЯЩИЙ, объем цилиндра 6154,4 СМ 3
9000 2 3 Пример 2 3 9000 2 3 .Глубина воды в цилиндрическом резервуаре составляет 8 футов. Предположим, что радиус и высота резервуара равны 5 футам и 11,5 футам соответственно. Найдите объем воды, необходимый для заполнения бака до краев.
Раствор
Сначала рассчитайте объем цилиндрического резервуара
Объем = 3,14 x 5 x 5 x 11,5
= 902,75 куб. = 628 кубических футов.
= 628 кубических футов.
Объем воды, необходимый для заполнения бака = 902,75 – 628 кубических футов
= 274,75 кубических футов.
Пример 3
Объем цилиндра 440 м 3 , радиус основания 2 м. Рассчитайте высоту бака.
Решение
Объем цилиндра = πr 2 H
440 M 3 = 3,14 x 2 x 2 x ч
440 = 12,56H
на разделение 12,56 на обоих Стоу h = 35
Следовательно, высота резервуара 35 метров.
Пример 4
Радиус и высота цилиндрического резервуара для воды равны 10 см и 14 см соответственно. Найдите объем бака в литрах.
Решение
Объем цилиндра = πr 2 H
= 3,14 x 10 x 10 x 14
= 4396 см 3
.
Следовательно, разделите 4396 на 1000, чтобы получить
Объем = 4,396 литра
Пример 5
Внешний радиус пластиковой трубы равен 240 мм, а внутренний радиус равен 200 мм. Если длина трубы 100 мм, найдите объем материала, из которого изготовлена труба.
Если длина трубы 100 мм, найдите объем материала, из которого изготовлена труба.
раствор
Труба является примером полого цилиндра, поэтому мы имеем
объем цилиндра = πh (R 1 2 — R 2 2 ) 9003
= 3.1454 2 2 ) 9003
= 3.1454 2 2 ) 9003
= 3,1454 2 2 )
= 3.1454 2 2 )
= 3.1454 2 2 )
= 3.1454 2 2 ) — 100 x (240 2 – 200 2 )
= 3,14 x 100 x 17600
= 5,5264 x 10 6 мм 3
Пример 6
Цельный цилиндрический блок металла необходимо расплавить, чтобы сформировать кубы с ребром 20 мм. Предположим, что радиус и длина цилиндрического блока равны 100 мм и 49 мм.0 мм соответственно. Найдите количество кубиков, которые нужно составить.
Решение
Рассчитайте объем цилиндрического блока
Объем = 3,14 x 100 x 100 x 490
= 1,5386 x 10 7 мм 3
Объем CUBE = 20 x 20 x 20 x 20 x 20 x 20.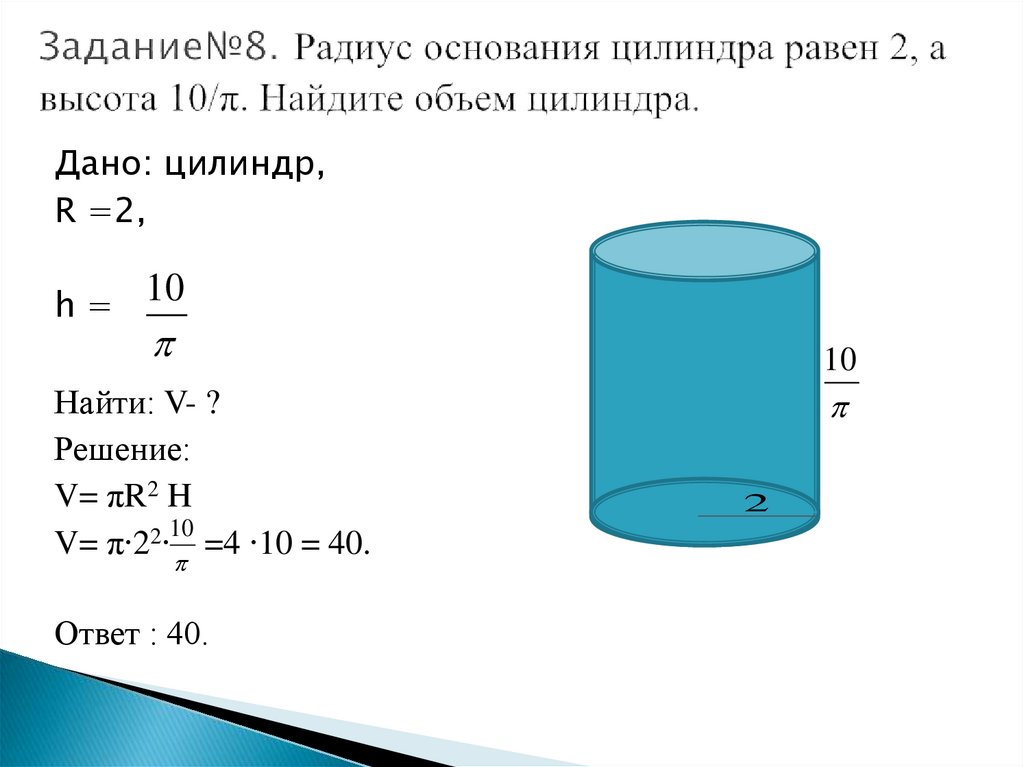
= 8000 мм 3
Количество кубов = объем цилиндрического блока/объем куба
= 1,5386 x 10 7 мм 3 / 8004 мм
55
= 1923 куба.
Пример 7
Найдите радиус цилиндра с той же высотой и объемом, что и у куба со стороной 4 фута. футов и,
объем куба = объем цилиндра
4 x 4 x 4 = 64 кубических фута
Но объем цилиндра = πr 2 h
3,14 x r 2 x 4 = 64 кубических фута
12,56r 2 = 64
Разделите обе стороны на 12,56
r 2 = 5,1 фута.
r = 1,72
Следовательно, радиус цилиндра будет 1,72 фута.
Пример 8
Сплошная шестиугольная призма имеет длину основания 5 см и высоту 12 см. Найдите высоту цилиндра такого же объема, что и призма. Возьмем радиус цилиндра равным 5 см.
Раствор
Формула объема призмы дается как;
Объем призмы = (h)(n) (s 2 )/ [4 tan (180/n)]
где n = количество сторон
s = длина основания призмы
h = высота призмы
Объем = (12) (6) (5 2 )/ (4tan 180/6)
=1800/2,3094
=779,42 см 3
Объем цилиндра 2 ч
779,42 = 3,14 х 5 х 5 х ч
ч = 9,93 см.
Значит, высота цилиндра будет 9,93 см.
Объем цилиндра: уравнение, формула и примеры
Вы когда-нибудь задумывались, какой формы выглядит контейнер Pringles? Или сколько сахара потребовалось бы, чтобы наполнить его, если бы он был очищен от всех чипсов Pringles?
Знание того, что такое цилиндры и как рассчитать их объем, может легко помочь вам в реальных измерениях, потому что очень много продуктов хранится в цилиндрических контейнерах.
В этой статье мы узнаем больше о цилиндрах и о том, как рассчитать их объемы.
Что такое цилиндр?
Цилиндр представляет собой твердое тело, имеющее два одинаковых круглых плоских конца, соединенных трубкой.
Цилиндр встречается во многих предметах повседневного использования, таких как туалетная бумага, контейнеры для конфет, жестяные контейнеры для молока, трубы и т. д.
д.
Типы цилиндров
Существует два основных типа цилиндров.
Правильные круговые цилиндры: Плоскости оснований этих цилиндров перпендикулярны отрезку, соединяющему центры окружностей цилиндра.
Изображение прямого кругового цилиндра, StudySmarter Originals
Наклонный круговой цилиндр — Плоскости оснований этих цилиндров не перпендикулярны отрезку, соединяющему центры окружностей цилиндра.
Изображение наклонного круглого цилиндра, StudySmarter Originals
Как рассчитать объем цилиндра?
Объем круглого цилиндра
Объем круглого цилиндра рассчитывается путем умножения его высоты на площадь его круглого основания.
Напомним, что площадь круга определяется выражением
Площадь окружности=πr2
Таким образом, объем круглого цилиндра определяется выражением
радиус основания 7 см, глубина 10 см. Найдите объем, если π=227
Решение:
Сначала отметим радиус и высоту цилиндра, r=7см,h=10см.
Объем круглого цилиндра рассчитывается как
Vcircularcylinder=πr2×h=227×72×10=220×7=1540 см3 если любые два тела имеют одинаковую высоту и таковы, что их соответствующие поперечные сечения на любом уровне имеют одинаковые площади, то они имеют одинаковый объем.
Принцип Кавальери очень важен при нахождении объемов наклонных объемных фигур. Это позволяет нам использовать ту же самую формулу для вычисления объемов этих твердых тел, даже если они не являются прямыми.
В соответствии с принципом Кавальери, рассматривая два круглых и наклонных цилиндра одинаковой высоты, имеющих одинаковый радиус основания, мы заключаем, что они будут иметь одинаковые площади поперечного сечения. Следовательно, мы можем сказать, что объем косого цилиндра равен объему прямого кругового цилиндра. Следовательно, объем косого цилиндра V o равно
V косой цилиндр = V круговой цилиндр = πr2 × h
Найдите объем фигуры ниже, приняв π = 227.
Решение:
Вспоминая принцип Кавалье,
Косоугольный цилиндр=Vкруговойцилиндр=πr2h
Из числа получаем, что r=9см,h=28см.
Таким образом, объем косого цилиндра, приведенный на рисунке выше, можно рассчитать как
V косогоцилиндра=227×92×28=22×81×4=7128см3.
В каких единицах измеряется объем цилиндра?
Объем цилиндра измеряется в кубических сантиметрах см 3 и кубических метрах м 3 . Также объем цилиндра измеряется в литрах л. Обратите внимание, что:
1000см3=1л1см3=0,001л
Объем полукруглого цилиндра
Полукруглый цилиндр имеет основание и вершину в виде полукруга. Также известно, что это половина правильного кругового цилиндра.
Изображение полукруглого цилиндра, StudySmarter Originals
Объем полукруглого цилиндра рассчитывается путем деления объема завершенного цилиндра на 2.
Представьте, что полукруглый цилиндр, завершенный, стал полным цилиндром. Таким образом,
Таким образом,
Объемполукруглого цилиндра=πr2×h
Тогда объем полукруглого цилиндра определяется выражением . Возьмем π=227.
Решение:
Объем полукруглого цилиндра определяется выражением,
Vsemicircularcylinder=πr2×h3
Запишем высоту и диаметр из заданных, h=6см,d=5см.
Выводим радиус из диаметра, r=диаметр2=52см.
Следовательно, объем полукруглого цилиндра равен
Vsemicircularcylinder=πr2×h3=π×522×62=227×254×62=3300282=58,93 см3.
Как рассчитать объем неправильной формы?
Знание объема правильных тел делает возможным расчет неправильных форм. Во-первых, вы должны разбить твердое тело неправильной формы на его правильные твердые компоненты, а затем определить его объем.
Давайте посмотрим, как это можно сделать на следующем примере.
Определите объем ларца внизу. Возьмем π=227.
Решение:
Сначала заметим, что верх шкатулки представляет собой полукруглый цилиндр, а основание — прямоугольную призму.
Найдем объем полукруглого цилиндрического волчка.
Vsemicircularcylinder=πr2×h3
Заметим, что диаметр полукруглого цилиндра равен d=14см. Таким образом, r=диаметр2=d2=142=7см.
Отсюда
Vполукруглыйцилиндр=πr2×h3=227×72×302=22×7×302=2310см3.
Объем прямоугольной призмы,
Vпрямоугольнаяпризма=длина×ширина×высотапризмы
Из рисунка делаем вывод, что длина = 30 см, ширина = 14 см и высота = 15 см.
Следовательно,
Vпрямоугольнаяпризма=30×14×15=6300см3.
Объем шкатулки рассчитывается как сумма объема полукруглого цилиндра и объема прямоугольной призмы.
Vшкаф=Vполукруглыйцилиндр+Vпрямоугольнаяпризма=2310+6300=8610см3.
Сколько рулонов салфеток нужно Бренде, чтобы перекрыть 40 425 кубических сантиметров проема в ее комнате, если высота рулона составляет 50 см? Возьмем π=227.
Решение:
Чтобы определить, сколько рулонов салфеток придется использовать Бренде, нам нужно найти объем салфетки Vtissue.
Объем ткани можно рассчитать путем вычитания объема полого пространства ткани, , из объема всего цилиндра.
Таким образом,
Vткань=Vцелый цилиндр-Vполое пространство
Сначала вычисляем объем всего цилиндра,
Vwholecylinder=π×r2×h=π×2822×50=227×142×50=30800 см3
Далее, чтобы вычислить объем полого пространства, нам сначала нужно вычислить его соответствующий радиус. Но диаметр полого пространства можно найти, вычитая диаметр всего цилиндра из диаметра непустого цилиндра, таким образом,
диаметр полого цилиндра = 28-7 = 21 см
Теперь объем полого пространства равен,
Vпустое пространство=π×r2×h=227×2122×50=17325 см3.
Таким образом, объем ткани равен
Vткани=Vцелого цилиндра-Vполого пространства=30800-17325=13475см3.
Поскольку объем помещения, которое Бренда должна заполнить, составляет 40 425 см 3 , то ей потребуется
(40425÷13475)тканей=3ткани.
Объем цилиндра – основные выводы
- Цилиндр представляет собой твердое тело, имеющее два одинаковых круглых плоских конца, соединенных трубкой.


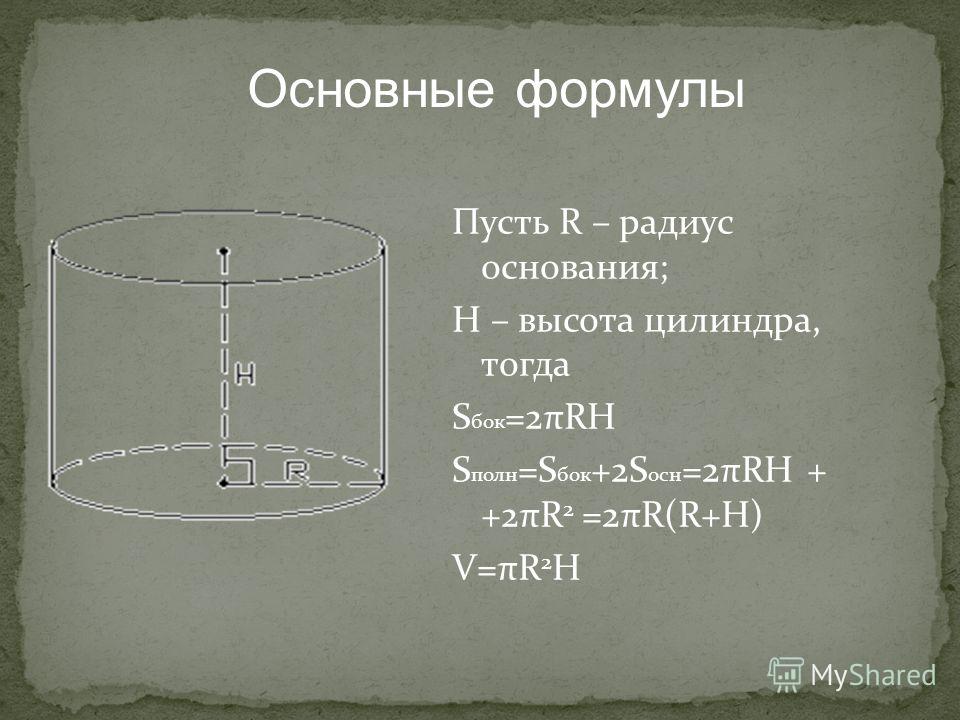

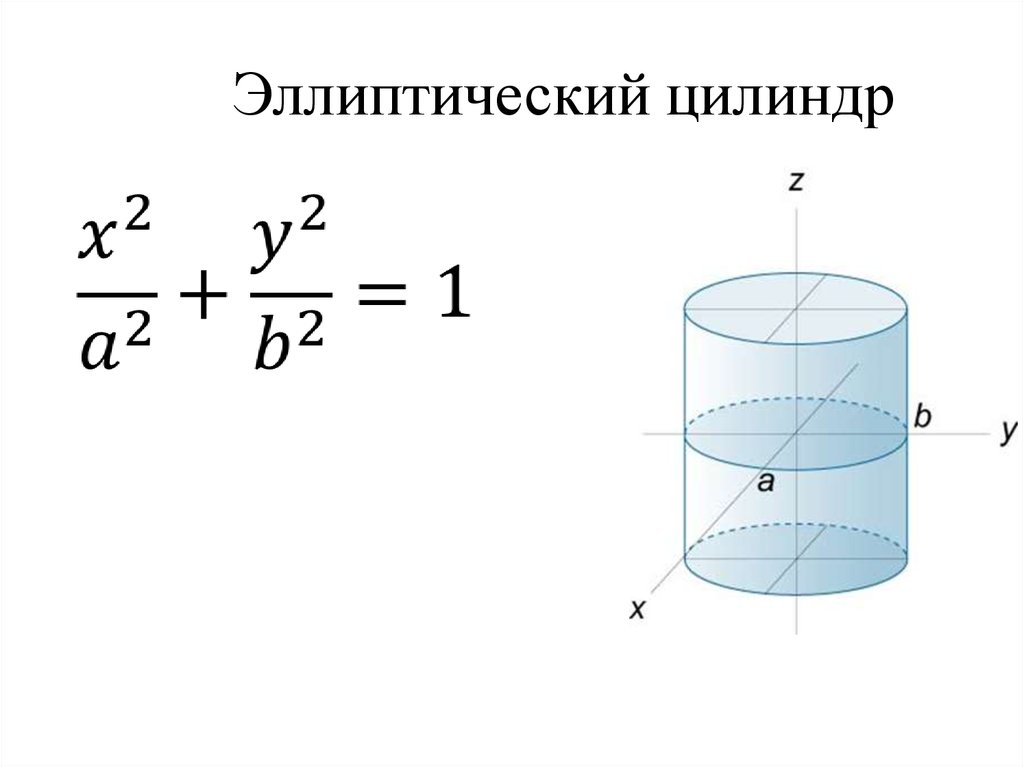
 5 мм (R — 47.75 мм).
5 мм (R — 47.75 мм).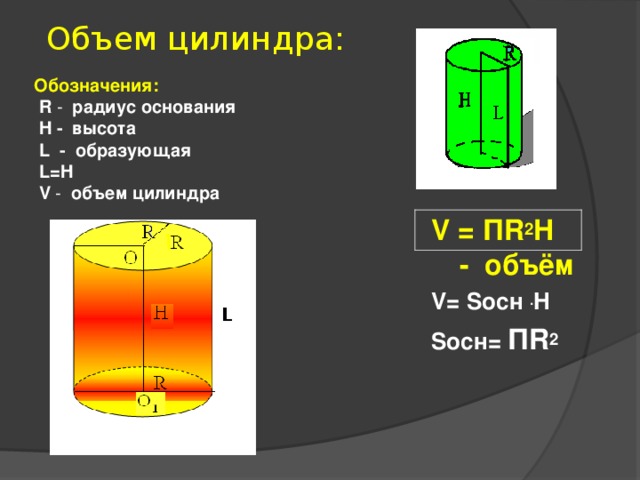 ). 1000 кубических сантиметров равны 1 литру. Единица самого точного измерения объема именно куб сантиметры, поскольку, когда объем двигателя автомобиля указывается в литрах, то производится округление до целого числа после запятой. Например, объем 2,4 л. равны 2429 см3.
). 1000 кубических сантиметров равны 1 литру. Единица самого точного измерения объема именно куб сантиметры, поскольку, когда объем двигателя автомобиля указывается в литрах, то производится округление до целого числа после запятой. Например, объем 2,4 л. равны 2429 см3.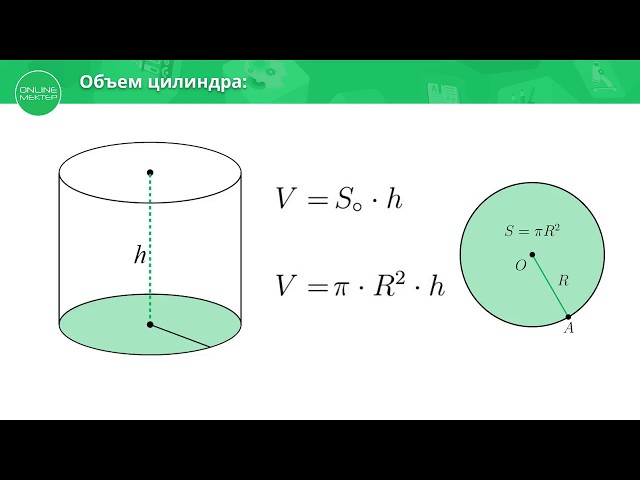 Это будет форма искаженного стекла, о которой говорилось выше.
Это будет форма искаженного стекла, о которой говорилось выше. Это правило справедливо для всех трехмерных фигур, известных в математике. Например, в кубоиде, если вы знаете площадь одной его стороны, а затем умножаете ее на высоту или ширину, то есть на оставшуюся сторону, вы получите объем.
Это правило справедливо для всех трехмерных фигур, известных в математике. Например, в кубоиде, если вы знаете площадь одной его стороны, а затем умножаете ее на высоту или ширину, то есть на оставшуюся сторону, вы получите объем. Результат — вес цилиндра.
Результат — вес цилиндра.