Межотраслевой баланс онлайн
Модель межотраслевого баланса:X = AX + Y
где A – матрица коэффициентов прямых материальных затрат; Y – уровень спроса на конечную продукцию, равновесный выпуск отраслей
X = B•Y.
С помощью сервиса в онлайн режиме можно:
- найти коэффициенты полных материальных затрат, определить вектор валовой продукции;
- составить межотраслевой баланс, составить схему межотраслевого баланса труда;
- проверить продуктивность матрицы.
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Для этого выберите размерность матрицы коэффициентов прямых материальных затрат. Полученное решение сохраняется в файле Word (см. примеры решений). Для проверки решения автоматически генерируется шаблон в Excel.
Размерность матрицы
2345678 Проводить анализ
Межотраслевой баланс отражает производство и распределение валового национального продукта в отраслевом разрезе, межотраслевые производственные связи, использование материальных и трудовых ресурсов, создание и распределение национального дохода.
Система уравнений X = AX + Y называется экономико-математической моделью межотраслевого баланса (МОБ) или моделью «затраты — выпуск». C помощью нее можно выполнить следующие расчеты:
- подставив в модель объемы валовой продукции каждой отрасли Xi, можно определить объем конечной продукции отрасли Yj:
Y = (E - A)X - задав величины конечной продукции всех отраслей Yj, можно определить величины валовой продукции каждой отрасли Xi:
X = (E - A)-1Y - установив для ряда отраслей величины валовой продукции, а для всех остальных отраслей задав объемы конечной продукции, можно найти объемы конечной продукции первых отраслей и объемы валовой продукции вторых.
Здесь A – матрица прямых затрат, коэффициенты которой, aij показывают затраты i-й отрасли на производство единицы продукции j-й отрасли. Введем обозначение B = (E — A)-1.
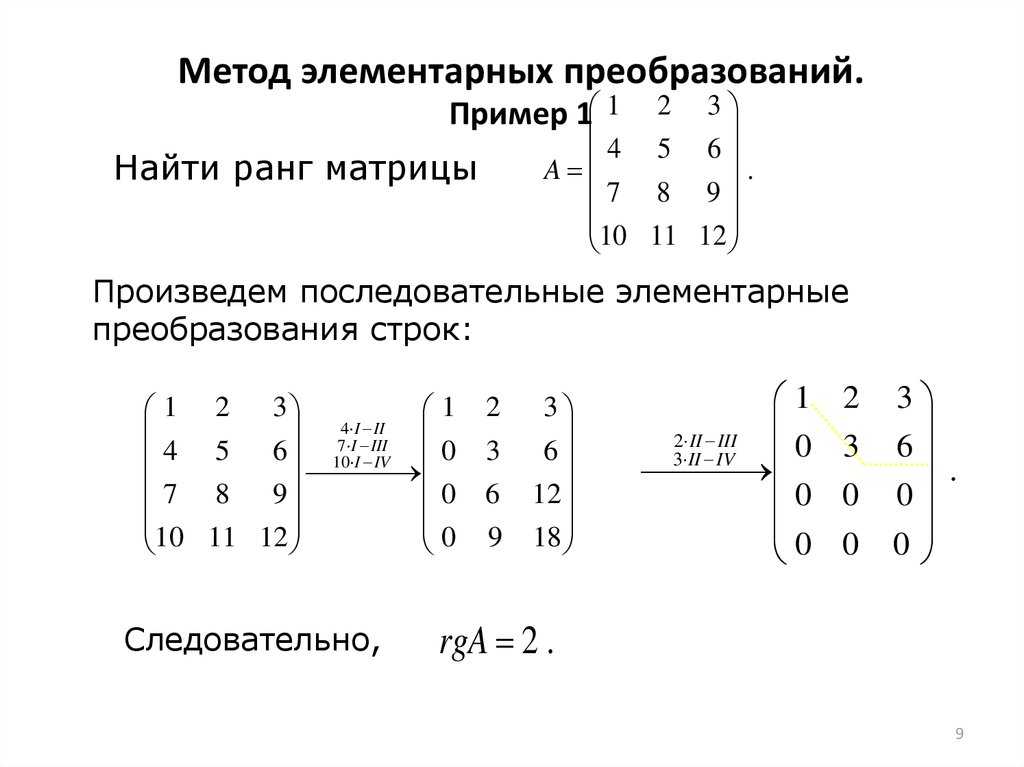Матрица B называется матрицей полных материальных затрат, коэффициенты которой, bij показывают полный объем продукции i-й отрасли, используемой для производства единицы продукции j-й отрасли. С учетом линейности соотношений эффект распространения спроса ΔX, вызванный изменением конечного спроса на величину ΔY рассчитывается как: ΔX = B·ΔY
Через C=A-B обозначают матрицу косвенных затрат.
Пример №1. Для трехотраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат
Пример №2. Дан межотраслевой баланс трехотраслевой модели хозяйства:
| № отрасли потребления | 1 | 2 | 3 | Конечный продукт | Валовый продукт | Y’ | |
| № отрасли | 1 | 20 | 20 | 60 | 100 | 200 | 150 |
| отрасли | 2 | 20 | 40 | 60 | 80 | 200 | 100 |
| производства | 3 | 20 | 0 | 10 | 70 | 100 | 100 |
Определить:
1) технологическую матрицу;
2) матрицу коэффициентов полных затрат;
3) дать экономический анализ каждого столбца матрицы коэффициентов полных затрат;
4) определить валовый выпуск X’ на новый ассортимент конечной продукции Y’;
Решение.
Находим валовой объем продукции xi;
x1 = 20 + 20 + 60 + 100 = 200
x2 = 20 + 40 + 60 + 80 = 200
x3 = 20 + 0 + 10 + 70 = 100
| Отрасль | Потребление | Конечный продукт | Валовой выпуск | ||
| Производство | 20 | 20 | 60 | 100 | 200 |
| 20 | 40 | 60 | 80 | 200 | |
| 20 | 0 | 10 | 70 | 100 | |
По формуле aij = xij / xj находим коэффициенты прямых затрат:
a11 = 20/200 = 0.
1; a12 = 20/200 = 0.1; a13 = 60/100 = 0.6; a21 = 20/200 = 0.1; a22 = 40/200 = 0.2; a23 = 60/100 = 0.6; a31 = 20/200 = 0.1; a32 = 0/200 = 0; a33 = 10/100 = 0.1;
| 0.1 | 0.1 | 0.6 |
| 0.1 | 0.2 | 0.6 |
| 0.1 | 0 | 0.1 |
Определим матрицу коэффициентов полных затрат с помощью формул обращения невырожденных матриц.
а) Находим матрицу (E-A):
| (E-A) = |
|
б) Вычисляем обратную матрицу (E-A)-1:
|
Найдем величины валовой продукции трех отраслей
| X’ = (B-1*Y’) = |
| * |
| = |
|
Пример №3.
В модели межотраслевого баланса
| Производство | Потребление | Конечная продукция | Валовая продукция | ||
| 1 | 2 | 3 | |||
| 1 | 10 | 5 | 15 | 70 | 100 |
| 2 | 20 | … | … | … | … |
| 3 | 30 | … | … | … | … |
| Оплата труда | 30 | … | … | … | … |
| Прибыль D | D | … | … | … | … |
прибыль
D = Валовая продукция – Затраты на производство – Оплата труда = 100 – (10+20+30) – 30 = 10.
Межотраслевой баланс. Примеры решений
Предположим, что рассматривается n отраслей промышленности, каждая из которых производит свою продукцию. Часть продукции идет на внутри производственное потребление данной отраслью и другими отраслями, а другая часть предназначена для целей конечного (вне сферы материального производства) личного и общественного потребления.Так как валовой объем продукции любой i-й отрасли равен суммарному объему продукции, потребляемой n отраслями и конечного продукта, то:
xi = (xi1 + xi2 + … + xin) + yi, (i = 1,2,…,n).
Эти уравнения (их n штук) называются соотношениями баланса. Будем рассматривать стоимостный межотраслевой баланс, когда все величины, входящие в эти уравнения, имеют стоимостное выражение.
Введем коэффициенты прямых затрат:
aij = xij/xj, (i,j = 1,2,…
,n),
показывающие затраты продукции i-й отрасли на производство единицы стоимости j-й отрасли.
Матрица потоков средств производства
Отрасль | Потребление | Конечный продукт | Валовой выпуск | |
Производство | 100 | 160 | 210 | 470 |
280 | 70 | 350 | 700 | |
Решение проводим с помощью калькулятора.
По формуле aij = xij / xj находим коэффициенты прямых затрат:
0. | 0.23 |
0.6 | 0.1 |
21
Коэффициент прямых затрат (aij) показывает, какое количество продукции i-й отрасли необходимо, учитывая только прямые затраты, для производства единицы продукции j-й отрасли.
Если ввести в рассмотрение матрицу коэффициентов прямых затрат A = (aij), вектор-столбец валовой продукции X = (Xi) и вектор-столбец конечной продукции Y = (Yi), то математическая модель межотраслевого баланса примет вид:
X = AX +Y
Идея сбалансированности лежит в основе всякого рационального функционирования хозяйства. Суть ее в том, что все затраты должны компенсироваться доходами хозяйства. В основе создания балансовых моделей лежит балансовый метод – взаимное сопоставление имеющихся ресурсов и потребностей в них.
Межотраслевой баланс отражает производство и распределение валового национального продукта в отраслевом разрезе, межотраслевые производственные связи, использование материальных и трудовых ресурсов, создание и распределение национального дохода.
Пусть экономика страны имеет n отраслей материального производства. Каждая отрасль выпускает некоторый продукт, часть которого потребляется другими отраслями (промежуточный продукт), а другая часть – идет на конечное потребление и накопление (конечный продукт).
Обозначим через Xi (i=1..n) валовый продукт i-й отрасли; xij – стоимость продукта, произведенного в i-й отрасли и потребленного в j-й отрасли для изготовления продукции стоимостью Xj; Yi – конечный продукт i-й отрасли.
Критерии продуктивности матрицы А
Существует несколько критериев продуктивности матрицы А.
1. Матрица А продуктивна, если максимум сумм элементов ее столбцов не превосходит единицы, причем хотя бы для одного из столбцов сумма элементов строго меньше единицы.
2. Для того чтобы обеспечить положительный конечный выпуск по всем отраслям необходимо и достаточно, чтобы выполнялось одно из перечисленных ниже условий:
3.
Определитель матрицы (E — A) не равен нулю, т.е. матрица (E- A) имеет обратную матрицу (E — A)-1.
4. Наибольшее по модулю собственное значение матрицы А, т.е. решение уравнения |λE — A| = 0 строго меньше единицы.
5. Все главные миноры матрицы (E — A) порядка от 1 до n, положительны.
Матрица A имеет неотрицательные элементы и удовлетворяет критерию продуктивности (при любом j сумма элементов столбца ∑aij ≤ 1.
I. Определим матрицу коэффициентов полных материальных затрат приближенно, учитывая косвенные затраты до 2-го порядка включительно.
а) Матрица коэффициентов косвенных затрат 1-го порядка равна:
б) Матрица коэффициентов косвенных затрат 2-го порядка равна:
Матрица коэффициентов полных затрат приближенно равна:
II. Определим матрицу коэффициентов полных затрат точно с помощью формул обращения невырожденных матриц.
Коэффициент полных затрат (bij) показывает, какое количество продукции i-й отрасли нужно произвести, чтобы с учетом прямых и косвенных затрат этой продукции получить единицу конечной продукции j-й отрасли.
Полные затраты отражают использование ресурса на всех этапах изготовления и равны сумме прямых и косвенных затрат на всех предыдущих стадиях производства продукции.
а) Находим матрицу (E-A):
б) Вычисляем обратную матрицу (E-A)-1:
Запишем матрицу в виде:
Главный определить
∆ = (0.79 • 0.9-(-0.6 • (-0.23))) = 0.57234043753495
Транспонированная матрица
Обратная матрица
Найдем величины валовой продукции двух отраслей
Для определения элементов первого квадранта материального межотраслевого баланса воспользуемся формулой xij = aij • Xj.
Составляющие третьего квадранта (условно-чистая продукция) находятся как разность между объемами валовой продукции и суммами элементов соответствующих столбцов найденного первого квадранта.
Межотраслевой баланс состоит из четырех квадрантов (табл.). Первый квадрант отражает межотраслевые потоки продукции.
Второй характеризует отраслевую материальную структуру национального дохода.
Третий представляет национальный доход как стоимость условно-чистой продукции (Zj), равной сумме амортизации (cj), оплаты труда (vj) и чистого дохода j-й отрасли (mj). Четвертый квадрант показывает конечное распределение и использование национального дохода.
Производящие отрасли | Потребляющие отрасли | Конечный продукт | Валовый продукт | |
1 | 2 | |||
1 | 100 | 160 | 210 | 470 |
2 | 280 | 70 | 350 | 700 |
Чистый доход | 90 | 470 | 560 | |
Валовый продукт | 470 | 700 | 1170 | |
1.
Для трехотраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат A и вектор конечной продукции Y. Найти вектор валовой продукции, составить межотраслевой баланс.
Пример №1,
Пример №2,
Пример №3,
Пример №4,
Пример №5,
Пример №6,
Пример №7,
Пример №8,
Пример №9,
Пример №10,
Пример №11
2. Рассматривается двухотраслевая модель экономики. Даны матрица прямых затрат A и вектор конечной продукции Y. Найти следующее:
- Проверить продуктивность матрицы A;
- Вектор валового выпуска;
- Межотраслевые поставки;
- Записать схему межотраслевого баланса.
3. В отчетном периоде имел место следующий баланс продукции (тыс. тонн). Рассчитайте коэффициенты прямых затрат, полных затрат и косвенных затрат первого порядка. Сделайте запись баланса в матричной форме.
Решение.
4.
В отчетном году натуральный баланс продукции выглядел следующим образом ( в тыс. тонн). На основе данного баланса:
- Составьте матрицу прямых затрат.
- Составьте матрицу полных затрат.
- Рассчитайте коэффициенты косвенных затрат первого и второго порядка.
- Запишите баланс в матричной форме.
- Рассчитайте объем валовой продукции, если конечное потребление составит: Y(140,120,280).
5. Два цеха предприятия выпускают продукцию двух видов: цех № 1 – продукцию В, цех № 2 – продукцию С. Часть производимой продукции направляется на внутреннее потребление, а остальная является конечным продуктом. Коэффициенты прямых затрат заданы матрицей.
Реализация продукции В на сторону составляет по плану 600 тонн, а продукции С – 300 тонн.
Составьте плановую модель выпуска продукции (валового и конечного продукта) с учетом внутреннего потребления.
Результаты расчетов запишите в таблицу.
Решение.
6. Каждый из трех цехов предприятия выпускает один вид продукции (изделие 1, изделие 2 и изделие 3 соответственно), часть которой направляется на внутрипроизводственное потребление. Коэффициенты прямых затрат и плановые объемы реализации продукции на сторону заданы матрицами. Рассчитайте план выпуска каждого изделия. Результаты расчетов оформите в таблице.
Пример.
7. В таблице приведены данные об исполнении баланса. Используя модель Леонтьева многоотраслевой экономики, вычислить необходимый объем валового выпуска каждой отрасли, если конечный выпуск энергетической отрасли увеличится вдвое, а машиностроительной сохранится на прежнем уровне.
Решение.
Задание. Пусть экономика условно разделена только на две отрасли, межотраслевой баланс которых с указанием коэффициентов прямых материальных затрат и конечной продукции приведен в таблице. По этим данным рассчитать валовую продукцию каждой отрасли и межотраслевые поставки.
Решение. Скачать решение
Найти максимальный технологический рост и магистраль в динамической модели Леонтьева, задаваемой матрицей затрат
A = (1/2; 1/4
1/16; 1/2)
Модель Леонтьева межотраслевого баланса. Матрицы затраты-выпуск, прямых и полных затрат. Матрица косвенных затрат. Экономико-математические модели
Пример решения задачи
Экономика представлена двумя отраслями производства: промышленностью и сельским хозяйством. За отчетный период получены следующие данные о межотраслевых поставках и векторе объемов конечного использования .
| Отрасли | Отрасли-потребители | Ресурсы | Нормы расхода | ||||||
| 1 | 2 | 1 | 2 | ||||||
| 1 | 66 | 46 | 106 | 256 | 156 | +16 | 1 |
1. 8
|
1.3 |
| 2 | 36 | 16 | 66 | 306 | 206 | -4 | 2 | 2.3 | 1.6 |
| 12 | 10 | 3 | 1.3 |
0. 6
|
|||||
Требуется:
- Определить матрицу коэффициентов прямых материальных затрат , матрицу «затраты-выпуск» и вектор конечного потребления для вектора валовых выпусков .
- Определить матрицу коэффициентов полных материальных затрат и валовые объемы выпуска для вектора конечного использования .
- Определить приросты валовых объемов выпуска, если конечное потребление должно измениться на по сравнению с .
- Определить матрицу полных затрат ресурсов для матрицы ее прямых затрат и суммарную потребность в ресурсах для вектора конечного использования (отчетного и планового).
- Определить
матрицы коэффициентов косвенных затрат первого
, второго
и третьего порядка
, сравнить сумму затрат
с полными затратами
, найти абсолютные
погрешности.
- Найти потребность в продукции всех отраслей материального производства для получения единицы конечного продукта i-го вида.
Указание: При вычислениях производить округление с точностью до тысячных.
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Матрица прямых затрат
Найдем валовые выпуски отраслей, просуммировав в каждой строке межотраслевые поставки и координату вектора :
Найдем матрицу прямых затрат. Ее элементы можно найти по формуле:
Подставляя числовые значения, получаем:
Матрица «Затраты — выпуск»
Найдем матрицу «Затраты — выпуск»
Вектор конечного использования Y для валового объема выпуска X
Вектор конечного использования Y для валового объема выпуска X определим на основе балансового соотношения:
Для этого выполним умножение двух матриц
Матрица полных затрат
Найдем матрицу коэффициентов полных материальных затрат -она будет равна обратной матрице :
Определитель матрицы :
Алгебраические дополнения:
Обратная матрица:
Вектор валового объема выпуска X для конечного использования Y
Вектор валового объема выпуска для конечного продукта определим формуле:
Приросты валовых объемов выпуска
Найдем приросты валовых объемов выпуска, если конечное потребление должно изменяться на по сравнению с :
Матрица полных затрат ресурсов S
Найдем матрицу полных затрат ресурсов S для заданной матрицы ее прямых затрат M:
Суммарная потребность в ресурсах
Суммарная потребность в ресурсах для вектора Y0:
Суммарная потребность в ресурсах для вектора Yn:
Матрицы косвенных затрат и сумма затрат
Найдем матрицы косвенных затрат первого, второго и третьего порядка
Сумма затрат:
Разность матриц:
Вектор потребности в продукции
Найдем
вектор потребности в продукции всех отраслей материального производства bij
для получения единицы конечного продукта bj вида.
Для этого
просуммируем столбцы матрицы полных затрат:
Это значит, что для производства единицы конечного продукта в первой отрасли во всех отраслях надо расходовать продукции на сумму 1,913 ден.ед., для производства единицы конечного продукта во второй отрасли -на 2,021 ден.ед.
Bloomington Tutors — Блог — Конечная математика
Сегодня давайте взглянем на всеми любимую задачу матричных приложений, Леонтьевские модели ввода-вывода. Вы можете знать их просто как проблемы «технологической матрицы», но на самом деле технологическая матрица — это только одна часть проблемы. Действительно интересная часть находится в выводе матричного уравнения — то, что большинство курсов конечной математики, кажется, замалчивают в конце семестрового безумия.
Итак, давайте взглянем на типичную проблему «технологической матрицы» и посмотрим, не сможем ли мы понять, как эта проблема на самом деле работает .
Надеюсь, это облегчит запоминание, чем произвольная формула.
Пример: Экономика состоит из двух взаимозависимых отраслей — сталелитейной и лесопромышленной. Для изготовления каждой единицы стали требуется 0,1 единицы стали и 0,5 единицы древесины. Для изготовления каждой единицы пиломатериала требуется 0,2 единицы стали и 0,0 единицы пиломатериала. В следующем месяце экономика будет экспортировать \(16\) единиц стали и 8 единиц пиломатериалов. Сколько единиц стали и пиломатериалов им потребуется произвести, чтобы удовлетворить этот внешний спрос?
Главное, что нужно понять в связи с этими проблемами, это то, что обе отрасли нуждаются в некотором количестве каждого продукта (возможно, включая их собственный), чтобы производить больше этого продукта. Это старая рутина «ты должен тратить деньги, чтобы делать деньги». Итак, чтобы производить сталь, сталелитейному заводу нужно немного стали (надеюсь, меньше, чем он производит) вместе с пиломатериалами.
Лесопилке также нужно немного стали и пиломатериалов, чтобы производить больше пиломатериалов. Это может быть особенно актуально, если вы когда-либо играли в игру, в которой нужно собирать и тратить ресурсы, например Age of Empires или Settlers of Catan.
Следующее, что нужно понять, это то, что проблема спрашивает нас, сколько каждого ресурса нам нужно, чтобы произвести , что будет больше, чем количество, которое мы экспортируем. Почему? Потому что часть производимой нами стали и пиломатериалов возвращается в две отрасли промышленности для удовлетворения производства (которое само по себе требует некоторого количества стали и пиломатериалов и т. д.).
Производство обоих ресурсов можно разделить на три части:
- Количество одного и того же ресурса, необходимого для производства большего количества ресурса;
- Количество другого ресурса, необходимого для производства большего количества ресурса;
- Количество ресурса, которое нам нужно оставить для экспорта .
В случае нашего производства стали и пиломатериалов мы можем написать два уравнения:
Теперь попробуем записать эти уравнения более математически. Задача говорит нам определить \(x\) и \(y\) так, чтобы:
Теперь давайте найдем выражения для всего единиц стали, необходимых для производства большего количества стали и пиломатериалов. Они будут зависеть от \(x\) и \(y\), поскольку \(x\) и \(y\) представляют количество стали и пиломатериалов, которые мы производим. Итак, задача говорит нам, что на каждую единицу стали требуется 0,1 единицы стали и на каждую единицу пиломатериала требуется 0,2 единицы стали: из стали .
Мы можем использовать тот же мыслительный процесс, чтобы найти количество пиломатериалов, необходимых для производства стали и пиломатериалов:
Подставляя эти выражения вместе с внешним спросом в наши общие уравнения производства, мы получаем:
Обратите внимание, что первое уравнение говорит, что общее количество стали, которое нам нужно произвести \((x)\) зависит от самого себя \((0,1x)\), а также от общего количества пиломатериалов, которое нам нужно произвести \((0,2y)\) и количества, которое нам нужно экспортировать (\(16)\).
Отлично, мы превратили нашу задачу в математику! Но как решить? ну это матрица проблемы с приложением, в конце концов. Итак, давайте перепишем эту систему уравнений в виде матричного уравнения:
Матрица \(A\) теперь является нашей печально известной «технологической матрицей», а вектор \(d\) является вектором спроса. Мы также можем определить производственный вектор:
Таким образом, мы можем записать наше уравнение более компактно:
, где нашей целью будет найти \(p\). как нам это сделать? Ну, это (почти) похоже на решение обычного нематричного уравнения — нам нужно сгруппировать одинаковые термины.
Вопрос только в том, как группировать подобные термины? Обычно мы выносим \(p\) из обоих терминов и получаем \((1-A)p\). Единственная проблема заключается в том, что мы не можем вычесть \(A\) (что является матрицей) из числа 1 (которое не является матрицей). Нам нужно использовать «матричный эквивалент» числа 1 — единичную матрицу!
Используя единичную матрицу 2×2, мы можем теперь написать:
Мы уже знаем \(A\), поэтому мы можем найти \((I-A)\), вычитая соответствующие элементы:
Мы также знаем \(d\), вектор спроса, поэтому мы можем создать расширенную матрицу, которая позволяет нам найти \(p\):
Мы умножим все это на 10, чтобы немного упростить арифметику.
Теперь мы можем начать выполнять операции со строками для решения расширенной матрицы:
И, наконец,
Итак, теперь в правом столбце есть решение для \(p\)!
Надеюсь, это имело смысл, и удачи в финале!
ЭКОНОМИЧЕСКАЯ ЗАДАЧА ЛЕОНТЬЕВА И ЕЕ МАТЕМАТИЧЕСКОЕ РЕШЕНИЕ (АНГЛИЙСКИЙ)
КТО БЫЛ ВАСИЛИЙ ЛЕОНТЬЕВ? Василий Васильевич Леонтьев родился в августе 1906 года в Санкт-Петербурге. Сын профессора экономики, он поступил в Ленинградский университет в 1921 году, изучал философию, социологию и экономику и продолжил обучение в Берлинском университете. Василий Леонтьев был известным русским экономистом, связанным с разработкой общей модели баланса и использованием межотраслевого анализа. Он также способствовал развитию других областей экономики. В 1919 году он получил Нобелевскую премию по экономике за работу над таблицами «затраты-выпуск». Таблицы «затраты-выпуск», которые мы объясним позже более подробно и которые сделали его достойным Нобелевской премии, анализируют отношение, существующее между входами и выходами, которые необходимы определенному сектору для его производства. Эти результаты могут стать конечным продуктом для общественного спроса или они могут стать ресурсами, которые потребуются другому финансовому сектору для производства своих собственных продуктов. Таким образом, различные сектора могут быть связаны с конечным спросом на определенный продукт. С помощью таблиц можно оценить возможное изменение спроса на один или несколько факторов производства при изменении спроса на конечные продукты. Следует исходить из того, что пропорции производства продукта фиксированы, поэтому межотраслевой анализ ограничивается подходами, а не прогнозами. В частности, он использовал эту модель для изучения характеристик коммерческого потока между Соединенными Штатами и другими странами. Это породило парадокс Леонтьева. МОДЕЛЬ ЗАПАС-ВЫПУСК Модель «затраты-выпуск», также известная как модель Леонтьева, количественно показывает взаимосвязь-зависимость между различными секторами экономики из разных стран или регионов. Эта модель была изначально не от Леонтьева, а от Кенэ, и была известна как «Экономическая таблица». На работу Леонтьева оказали влияние такие экономисты, как Маркс или Леонард де Сисмонди. Леонтьев упростил формулировку Варла, чтобы сделать ее полезной в реальных случаях. Анализ «затраты-выпуск» говорит о том, что пропорции затрат между различными секторами не меняются в действительности за короткий период времени. В противном случае, как было сказано, результаты будут приближенными. Отношение зависимости различных секторов экономики и потока продукции между ними выражается матрицей. Столбцы показывают входную денежную стоимость из определенного сектора, а строки показывают денежную стоимость каждого сектора. Они позволяют узнать степень зависимости между секторами, от секторов, производящих ресурсы, до тех, кто их включает. Эта модель очень полезна из-за ее гибкости и отсутствия сложности для расчета, что позволяет легко пересчитать влияние изменений спроса. Модель установлена матрицей: Производственный уровень = промежуточный спрос + внешний спрос x = I + D Leontife определил две модели: открытая модель и закрытая модель. ЗАКРЫТАЯ МОДЕЛЬ Закрытая модель Леонтьева предполагала, что внешнего спроса нет, то есть, что не будет ни покупать какие-либо ресурсы, ни продавать продукцию местной экономики. Это делает весь производственный цикл собственного рынка, следовательно, все входы и выходы тратятся на производство. CX = X CX-X=0 (C-I) X=0 Где C — матрица потребления, а X — массивы, n * 1 производство и внутренний спрос. ОТКРЫТАЯ МОДЕЛЬ Но об открытой модели поговорим подробнее. Открытая модель аналогична закрытой модели. большое различие между ними состоит в том, что в открытой модели существует внешний спрос на продукцию. Часть продукции будет использована другими отраслями экономики для своего производства. Другая часть будет направлена на удовлетворение внешнего спроса. Матрица будет иметь вид: 9-1d Матрица (I-C) является матрицей Леонтьева, и существует единственное возможное решение для матрицы X. Пока коэффициенты C положительны и сложение каждого столбца не превосходит 1, тогда обратная матрица (I-C) существуют. Следовательно, решение матрицы будет единственным. Матрица Леонтьева очень важна в модели «затраты-выпуск». не только потому, что она содержит матрицу X, но и потому, что она дает нам способ узнать, является ли матрица потребления продуктивной или нет. Леонтьев ставит экономическую задачу о группе из n отраслей или отраслей, каждая из которых производит один вид товара. Модель устанавливает связь между каждой отраслью и ее производством. Итак, мы определим x i как количество товаров (в единицах), произведенных i-м сектором в указанный период времени. Леонтьев распределяет производство по входным и выходным товарам в зависимости от того, должны ли они удовлетворять спрос (местный спрос, а также экспорт) или они должны покрывать потребности, необходимые отраслям в системе для продолжения работы. . Мы будем обозначать x ij как продукцию отрасли i , которая позже станет вкладом отрасли j . c i будет определяться как товары отрасли i , которые покроют выпуск продукции. Результирующий спрос будет суммой входа и выхода.
Следовательно, для промышленности j потребуется x ij единиц из i для производства x j товаров . Множитель x ij /x j будет оставаться постоянным и под названием a ij будет представлять необходимое количество продукта из i для производства 1 единицы дж. Теперь мы можем написать: , продлив его на секторы N, мы получаем систему матрицы: , которая также может быть записана таким образом: x = ax+c Где x — вектор «объема производства», A представляет собой матрицу коэффициентов (также называемую матрицей технических коэффициентов) , а c — вектор «конечного спроса». Клиринг: (I-A)x=c (I = единичная матрица). Назовем B=(I-A) и заменим: Bx=c Как решить? Мы собираемся написать систему с информацией, которую они нам предоставили: 0,2 x 11 +0,15x 12 +0,1×13 +1100=x1 0,35x 21 +0,25x 22 +0,1x 23 +600=x2 Нижний индекс 1 относится к фармацевтической промышленности, 2 – к химии, 3 – к транспортной службе. Это матрица:
Количество продукции, необходимое для удовлетворения конечного спроса, является решением матрицы. Запишем систему в виде матрицы и решим ее методом Гаусса-Жордана.
We divide 1th by 0.8
We divide 2th by 0.684375
We divide 3th by 2509/4380
В 1; 2 ряда вынимаем 3-ю изн, умноженную на -12/73; -46/219
Result:
Практические приложения ВНЕШНИЕ ССЫЛКИ Книги: -David C.Lay. (2006). Линейная алгебра и приложения. Эдо-де-Мексико: Pearson Education, Inc. Веб-сайты: — Педро Рамирес. (июль-декабрь 1992 г.). Эль система де Леонтьев у су решение matemática. 2000 г., Departamento de Maemáticas Facultad de Ciencias Económicas Universidad de Antioquia Sitio, веб-сайт: http://aprendeenlinea.udea.edu.co/revistas/index.php/lecturasdeeconomia/article/viewFile/509.2/4446 -Archivo del fundo de documentos de la Biblioteca del Ministryio (автор desconocido): http://www.magrama.gob.es/ministerio/pags/Biblioteca/fondo/pdf/18251_6.pdf — Jorge Маурисио Овьедо. (2002). Matriz де Insumo-Producto и ла Inversa Леонтьев-Cálculo por medio де Maple, Mathematica, Matlab у Macros en Excel. -, de — Sitio web: http://blogs.eco.unc.edu.ar/jorgeoviedo/files/2011/09/oviedo_matriz_de_insumo.pdf Таблицы ввода-вывода и обратная Леонтьева в R-часть I. 9-1) повсеместно. Названная в честь отца экономики «затраты-выпуск» Василия Леонтьева, матрица представляет собой компактное представление волновых эффектов в экономике, где отрасли взаимосвязаны. Отдельный матричный коэффициент передает все прямые и косвенные воздействия на выпуск в одном секторе, необходимые для единицы выпуска в другом секторе.Ниже приведена часть 1 двухчастного руководства по получению обратного Леонтьева с использованием R. Эта первая часть представляет собой «игрушечный» пример для мотивации частей анализа ввода-вывода и рабочего процесса в R. Часть 2 описывает, как вычислить Леонтьевская обратная из полномасштабной таблицы «затраты-выпуск». Игрушечная модель ввода-вывода.Рассмотрим пример с ребенком. Я буду использовать Таблицу 1 в качестве руководства для вычисления простой обратной Леонтьева с использованием R. В таблице представлены основные компоненты обычных таблиц «затраты-выпуск», использующих только два сектора. Таблица 1. Малая таблица «затраты-выпуск»
Приведенный выше пример заимствован из канонических примеров из главы 2 книги Миллера и Блэра « Анализ затрат-выпуска» (1985), а также из главы 2 книги Леонтьева 9. В основе таблицы лежит матрица два на два, представляющая промежуточные потоки товаров между двумя секторами: сектором 1 и сектором 2. Строка представляет стоимость продукции, отправленной из сектора товаров для производственного использования, в столбце сектор. Выше сектор-строка отправляет товары себе и сектору 2. После двух столбцов продаж промежуточных товаров столбец «Конечные товары» показывает стоимость продукции строки, используемой в качестве конечной продукции — продукции, не используемой в производстве. Если мы сложим выпуск строки, используемый как промежуточные товары и как конечные продукты, мы получим последний столбец: общий выпуск. Вычисление матрицы Обратное Леонтьева вычисляется следующим образом. Мы начнем с таблицы ввода-вывода, подобной приведенной выше. Используя эту базовую таблицу ввода-вывода, мы генерируем «матрицу технических коэффициентов», которую затем используем для решения обратной матрицы леонтии L. \[\textrm{Базовая таблица ввода/вывода: }~ X \Rightarrow \textrm{Техническая матрица: }~ A \Rightarrow \textrm{Матрица Леонтьева: }~ L\] Сначала мы построим таблицу «затраты-выпуск» в таблице 1, используя R. Мы создадим поток межотраслевых продаж два на два ( # Матрица промежуточного потока. таблица потоков <- rbind(c(150, 500), c(200, 100)) # Окончательный спрос. finaldemand <- rbind( c( 350 ), c( 1700 )) Мы объединили эти части в объект # Привязать к таблице ввода-вывода. inputoutputtable <- cbind(flowtable, finaldemand) # Преобразование объекта в data.frame. Теперь мы можем вывести матрицу технических коэффициентов , также называемую матрицей A . Столбец этой матрицы представляет промышленный рецепт, используемый для производства одного отраслевого товара. Матрица А рассчитывается путем деления межотраслевых потоков на общий объем производства каждого сектора столбца. В качестве альтернативы, мы можем использовать функцию R Используя R, мы сначала вычисляем | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
73.
Для Леонтьева основная структура торговли была основана на сравнительных преимуществах. Каждая страна специализируется на той экономической деятельности, для которой она лучше всего расположена, и торгует своей продукцией с другими странами с целью получения других товаров. Их первоначальное предложение состояло в том, что если брать ручной труд не как однородную массу, а как категории, то в промышленно развитых странах ручной труд лучше и более оформленный. Для Соединенных Штатов сравнительным преимуществом должны быть капитальные товары. Чтобы доказать это, он использовал матрицу сумма-произведение. Однако он обнаружил, что в Соединенных Штатах больше экспорта рабочей силы, чем капитала. Это, по Леонтьеву, обусловлено специализацией рабочей силы, более квалифицированной и производительной.
Также позволяет связать различные межрегиональные модели «затраты-выпуск» для исследования межрегионального коммерческого потока. По сути, он используется для измерения влияния, которое некоторые события оказали на экономический сектор и были введены во многих странах. По сути, это одна из экономических концептуальных моделей планового социалистического хозяйства, поскольку, зная количество продукции, которое необходимо для снабжения других отраслей и населения, можно обеспечить хорошее планирование экономики.
Поскольку это закрытая модель, матрица d будет равна 0, следовательно: 
Матрица С будет продуктивной, если матрица Леонтьева обратима. То есть, если существует инверсия (I-C) и ни один из его коэффициентов не является отрицательным. 
Соответственно запишем:
15
278125
Наконец, окончательный результат не может быть выражен дробно, потому что отрасль не может создать часть продукта, поэтому мы должны сделать следующую единицу больше, чем результат, чтобы уравнять отношения между спросом и производством. Итак, мы получили окончательные результаты x1 = 2029.,x2 = 2037, x3 = 2175.
.
0130 Экономика затрат-выпуска (1986). 
inputoutputtable <- as.data.frame( inputoutputtable )
# Имя столбца таблицы (dataframe)
имена (таблица ввода-вывода) <- c ("x1", "x2", "finaldemand")
# Рассчитайте общий выпуск, добавьте конечный спрос и промежуточные столбцы:
inputoutputtable$totaloutput <- inputoutputtable$x1 +
inputoutputtable$x2 +
inputoutputtable$finaldemand
# Показать небольшую таблицу ввода-вывода.
inputoutputtable
> x1 x2 конечный спрос общий объем производства
>1 150 500 350 1000
>2 200 100 1700 2000
# Сохранить общий выходной вектор как отдельный объект. Используйте позже.
totaloutput <- inputoutputtable$ totaloutput 
В частности, сектор 1 поставляет 500 долларов товара 1 в сектор 2, который производит 1000 долларов общего объема производства. Таким образом, один доллар товара 1 поглощается для производства 25 центов продукции сектора 2. 9-1 * диаг.( 2 )
A <- текучесть %*% z
# Показать А
А
[1] [2]
[1,] 0,15 0,25
[2,] 0,20 0,05 