Отношения в математике как решать: Отношение двух чисел — урок. Математика, 6 класс.

Содержание

Отношение ⭐ двух чисел 6 класс: объяснение, примеры решения задач

Понятие отношения двух чисел

Определение 1

Отношение чисел является частным данных чисел.

Запись отношения принято обозначать с помощью арифметического действия деления. Также допускается представление отношения в виде обыкновенной дроби:

a:b=ab

Здесь записано отношение чисел a и b. Число а может называться предыдущим членом, b играет роль последующего члена.

Пример 1

Запись отношения пары чисел таких, как 75 и 25, имеет вид:

75:25=7525=3

С помощью объяснения отношения можно выразить следующее:

во сколько раз первое число больше по сравнению со вторым;
какую часть первое число составляет от второго числа.

При решении задач на уроках по математике в шестом классе на тему «Отношение чисел» можно часто встретить примеры с процентами. Поэтому важно ознакомиться с особенностью понятия процентного соотношения и записать его в конспект.

Правило

Вычислить процентное отношение пары чисел можно путем деления одного числа на второе, а полученный результат следует умножить на 100.

Пример 2

Даны два числа: 52 и 400. Требуется определить, сколько процентов составляет первое число от второго числа. Воспользуемся правилом вычисления процентного соотношения и запишем:

52:400·100%=13%

Подобные отношения можно найти в заданиях, где по условию определены некие величины, и требуется вычислить их процентное соотношение. Знание определенных правил вычисления поможет значительно упростить решение. Среди вопросов могут быть такие:

на сколько процентов была перевыполнена работа;
на сколько процентов готов результат;
указать повышение или снижение цены товара в процентах

и другие вопросы, в которых присутствует понятие «процент».

Свойства отношения чисел

В том случае, когда имеется пара чисел или значений одинаковой величины, обозначенных как a и b, справедливы следующие соотношения:

отношение a к b является результатом частного a и b;
когда a>b, отношение a:b говорит о том, во сколько раз число a больше по сравнению с b;
когда a<b, отношение a:b говорит о том, что a является некой частью от b;
процентное отношение a к b представляет собой отношение a:b, которое умножили на 100%.

Определение 2

Ключевое свойство частного: частное сохраняется без изменений в том случае, когда делимое и делитель умножают или делят на одинаковое число.

Основное свойство частного позволяет вывести главное свойство отношения.

Определение 3

Основное свойство отношения: при умножении или делении членов какого-то отношения на одинаковое число, которое не равно нулю, данное отношение сохранится без изменений.

Примеры решения задач с пояснениями

Задача 1

Месячный план производства равен 1200 изделий. В результате предприятие произвело 2300 изделий. Требуется определить процент превышения плана.

Решение

Данную задачу можно решить двумя способами. Рассмотрим их по отдельности.

Способ 1. Запишем, что 1200 изделий являются планом, то есть составляют 100 %. Определим, количество изделий, изготовленных больше плана:

2300−1200=1100

Вычислим разницу между фактом и планом в процентах:

1100 от 1200 ⇒ 1100:1200·100%=91,7%.

Попробуем выполнить вычисления другим методом.

Способ 2. Сначала найдем разницу между планом и фактом в процентах:

2300 от 1200 ⇒ 2300:1200·100%=191,7%.

Далее определим процент перевыполнения плана:

191,7%-100%=91,7%.

Ответ: на 91,7 %.

Задача 2

Поставлена задача вспахать землю на участке поля площадью 500 га. В течение первого дня было обработано 150 га почвы. Требуется вычислить, сколько процентов удалось вспахать от общего запланированного объема.

Решение

Найдем отношение обработанной земли к общей площади поля и запишем результат в процентном выражении:

150:500·100%=150500·100%=310·100%=0,3·100%=30%.

Ответ: 30 %

Задача 3

Производительность мастера составила 45 деталей, а по плану требовалось изготовить 36 деталей. Нужно найти процент фактически проделанной работы от планируемого объема.

Решение

Здесь вычислим отношения чисел и запишем результат в процентном выражении:

45:36·100%=1,25·100%=125%

Ответ: 125 %

Задания для самостоятельной работы

Задача 4

Должность председателя желали занять два претендента. Явка на голосовании составила 120 человек. Распределение голосов соответствует пропорции 3:5. Требуется определить количество голосов, которые получил победитель.

Решение

3х+5х=120

х=15

15·5=75

Ответ: 75

Задача 5

Отношение количества хвойных деревьев к лиственным в лесу можно выразить как 1:4. Нужно вычислить процент лиственных деревьев.

Решение

4:5=0,8=80 %

Ответ: 80 %

Задача 6

Сельскохозяйственные растения высаживают на площади 24 Га. Зерновые культуры и овощные распределены в соответствии с отношением 5:3. Необходимо вычислить площадь в Га, которую занимают овощные культуры.

Решение

24·38=9

Ответ: 9 Га.

Как решать задачи на отношение

Что нужно знать об отношении двух чисел в математике за 6 класс

Отношение чисел является частным данных чисел.

Запись отношения пары чисел таких, как 75 и 25, имеет вид:

75 : 25 = 75 25 = 3

С помощью объяснения отношения можно выразить следующее:

во сколько раз первое число больше по сравнению со вторым;
какую часть первое число составляет от второго числа.

52 : 400 · 100 % = 13 %

на сколько процентов была перевыполнена работа;
на сколько процентов готов результат;
указать повышение или снижение цены товара в процентах

и другие вопросы, в которых присутствует понятие «процент».

Свойства отношения чисел

отношение a к b является результатом частного a и b;
когда a>b, отношение a:b говорит о том, во сколько раз число a больше по сравнению с b;
когда a<b, отношение a:b говорит о том, что a является некой частью от b;
процентное отношение a к b представляет собой отношение a:b, которое умножили на 100%.

Основное свойство частного позволяет вывести главное свойство отношения.

Примеры решения задач с пояснениями

Данную задачу можно решить двумя способами. Рассмотрим их по отдельности.

Вычислим разницу между фактом и планом в процентах:

1100 от 1200 ⇒ 1100 : 1200 · 100 % = 91 , 7 % .

Попробуем выполнить вычисления другим методом.

Способ 2. Сначала найдем разницу между планом и фактом в процентах:

2300 от 1200 ⇒ 2300 : 1200 · 100 % = 191 , 7 % .

Далее определим процент перевыполнения плана:

191 , 7 % — 100 % = 91 , 7 % .

Найдем отношение обработанной земли к общей площади поля и запишем результат в процентном выражении:

150 : 500 · 100 % = 150 500 · 100 % = 3 10 · 100 % = 0 , 3 · 100 % = 30 % .

Здесь вычислим отношения чисел и запишем результат в процентном выражении:

45 : 36 · 100 % = 1 , 25 · 100 % = 125 %

Задания для самостоятельной работы

Урок 21 Бесплатно Отношения

В этом уроке мы узнаем, что такое отношения. Также поймем, что нам показывает отношение двух чисел. И в завершение узнаем, как определить часть одного числа от другого.

Отношение

Начнем с определения:

Отношением двух чисел называют частное этих двух чисел.

Записать отношение числа a к числу b мы можем как $\mathbf$ или же через дробную черту: $\mathbf>$

У нас получается дробное выражение, поэтому возможны варианты во что оно преобразуется:

может получиться натуральное число
обыкновенная дробь
смешанное число

Посмотрим на разные примеры.

Пример 1

Найдем отношение чисел 256 и 8

По определению, отношением двух чисел будет являться их частное, что мы и посчитаем.

Ответом будет 32.

Иными словами, 256 относится к 8 как 32 к 1

В последней фразе была как раз упомянута суть отношения, мы акцентируем на этом внимание.

Отношение одного числа к другому показывает, как одно число соотносится с другим, иными словами, во сколько раз оно его больше или меньше:

если отношение получилось больше 1, значит, первое число больше второго
если меньше 1, то второе число больше первого
если отношение оказалось равно 1, значит, числа равны

Пример 2

Найдите отношение 15 к 12

По определению посчитаем частное, а далее посмотрим на полученный результат.

Данный пример иллюстрирует, в каких случая получается смешанное число.

Отношение равняется смешанному числу в тех случаях, когда первое число больше второго, и при этом первое на второе не делится.

Мы можем прочитать результат так: 15 больше 12 в $\mathbf>$ раза.

Пример 3

Найдем отношение 16 к 24.

Снова идем по алгоритму: делим первое число на второе.

В этом случае мы получили в ответе правильную дробь.

Нам это говорит о том, что первое число меньше второго.

А если мы хотим сказать, как именно первое число меньше второго, то это можно сделать так: первое число меньше второго в $\mathbf>$ раза.

Мы можем сформулировать вывод и так: 16 составляет $\mathbf>$ от 24-х, то есть мы отвечаем на вопрос, какой частью является первое число от второго.

Также важно отметить, что отношение числа a к числу b не всегда равно отношению числа b к числу a.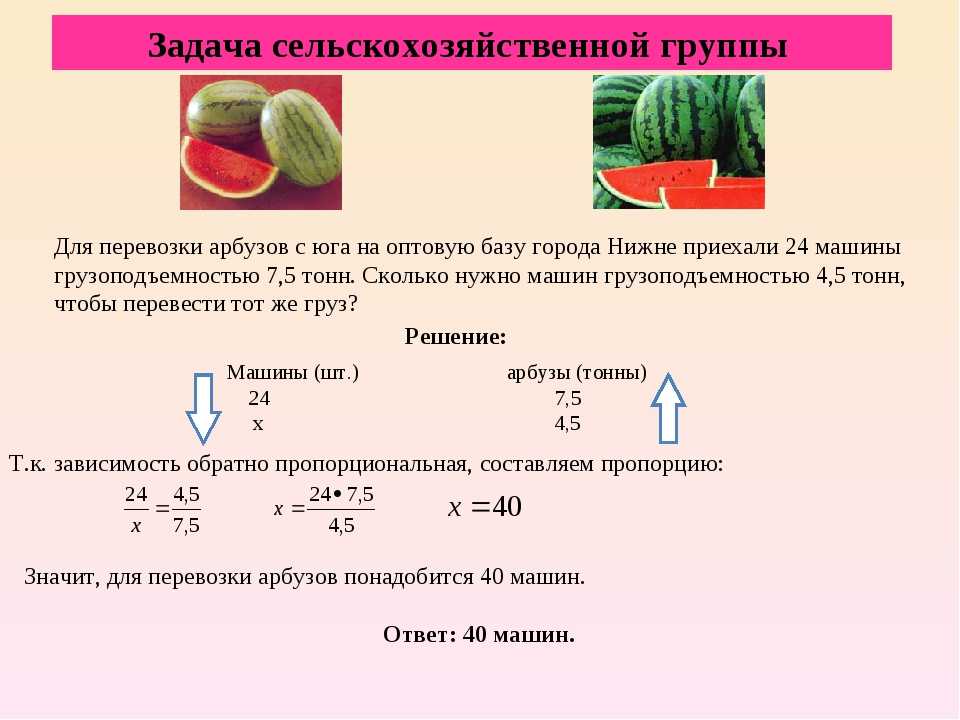

Пример 4

Есть два числа, 14 и 28

Посчитаем отношение 14 к 28

И посчитаем отношение 28 к 14

Как вы видите, получились разные значения.

Как можно заметить, это взаимно обратные числа.

Отметим еще одно свойство отношений: если есть два числа a и b, то отношение a к b взаимно обратно отношению b к a.

Если дано отношение первого числа ко второму, то мы без труда сможем найти отношение второго к первому, даже не зная самих чисел, просто посчитав обратное к отношению число.

Пример 5

Дано, что отношение числа a к числу b равно $\mathbf>$, найдем отношение b к a

Для этого надо найти обратное число к $\mathbf>$

Значит, отношение b к a равняется $\mathbf>$

В конце этой части добавим еще одно простое, но важное свойство.

Отношение двух чисел не изменится, если каждое из них домножить или разделить на одно и тоже число.

Это легко доказать, показав, что при делении этот множитель сократится.

Пример 6

Отношение числа 10 к числу 30 равно $\mathbf>$

Домножим каждое из чисел на 2 и заметим, что отношение 20 к 60 также равно $\mathbf>$

Пройти тест и получить оценку можно после входа или регистрации

Отношение и часть от числа

Посмотрим, какие еще можно сделать выводы, зная отношение.

Мы знаем, что, чтобы найти часть от числа (другими словами, дробь от числа), надо умножить число на эту дробь.

Так мы получим число, которое будет частью исходного.

Допустим, изначально у нас было число 4, и мы решили найти от него $\mathbf>$

Перемножив, мы получим:

А теперь найдите отношение полученного числа к изначальному.

Для этого разделите одно на другое:

То, что вы получили отношение, равное той дроби, которую мы находили, не совпадение.

Действительно, находя дробь от числа мы получаем число, чье отношение к исходному будет равно этой дроби.

Сформулируем еще более коротко и четко: отношение числа a к числу b обратно дроби, которую нужно взять от числа а, чтобы получить число b.

Пример 1

Известно, что некая дробь от числа 10 равна $\mathbf>$

Найдем, какая именно это дробь.

Решение:

Дробь от числа равна отношению полученного числа к изначальному.

Теперь разделим одно на другое и получим ответ.

Ответ: дробь, взяв которую от 10 получили $\mathbf>$, равняется $\mathbf>$

Пример 2

Отношение первого числа ко второму равно $\mathbf>$, также известно, что первое число равно 6.

Найдем второе число.

Решение:

Мы знаем, что отношение обратно дроби.

Найдем обратное число к $\mathbf>$

Теперь можно найти второе число, домножим первое на эту дробь:

Второе число равно 5

Проверка:

Найдем отношение первого числа ко второму, то есть 6 к 5

Получилось то же отношение, что и в условии.

Пример 3

Решим похожую задачу:

Отношение числа а к числу b равно $\mathbf>$

Известно, что число b равняется 8-ми, надо найти число а.

Решение:

Найдем, какую дробь число b составляет от числа a, то есть найдем обратное число от отношения:

Теперь, чтобы найти число по его дроби, надо разделить часть от числа на эту дробь.

В нашем случае на дробь надо делить число b :

Ответ: число a равняется 12

Пройти тест и получить оценку можно после входа или регистрации

Отношения в задачах

Теперь научимся находить отношения в задачах.

Сразу перейдем к примерам, чтобы посмотреть, за какими формулировками могут стоять отношения.

Задача 1

Длина улицы составляет 25 километров. Освещено 15 километров улицы.

а) Найдите, какая часть улицы освещена.

б) Во сколько раз вся улица длиннее ее освещенной части?

Решение:

В начале урока мы находили отношение меньшего числа к большему, тем самым определили, какую часть первое число составляет от второго.

Именно это и спрашивается в первом вопросе.

Для нахождения отношения длины освещенного участка к длине всей улицы поделим одну величину на другую:

Значит, длина освещенного участка составляет $\mathbf>$ от длины всей улицы.

Во втором вопросе нас спрашивают: «Во сколько раз больше?» — это соответствует отношению большего числа к меньшему.

Для нахождения этого отношения необходимо поделить длину всей улицы на длину ее освещенной части:

Что отвечает на вопрос второго пункта.

Также важно помнить, что если подаются какие-либо величины, то всегда надо следить, чтобы мера измерения была одинаковой.

То есть если нам подали что-то в тоннах и килограммах и мы хотим найти отношения этих величин, то надо либо тонны переводить в килограммы, либо наоборот.

Задача 2

Масса груза составляет 2 тонны. Известно, что часть груза- это одежда и ее масса 350 кг.

Найдите, какую часть от массы груза составляет масса одежды.

Решение:

Для начала преобразуем преобразуем тонны в килограммы. Получается, что масса груза равна 2000 кг.

Теперь найдем искомое отношение:

Теперь попробуйте порешать задачи самостоятельно, а если будет сложно, используйте подсказки.

Пройти тест и получить оценку можно после входа или регистрации

Интересная информация

Сегодня вы узнаете о математических фокусах!

Их идея в том, что можно запутать людей математическими преобразованиями, которые выдадут то, что нужно нам.

Фокус 1

Попросите зрителя загадать число и никому не говорить.

Теперь попросите его умножить это число на 2, прибавить к результату 8, разделить на 2 и вычесть задуманное число.

Теперь вы можете уверенно сказать, что у зрителя получилось число 4.

Так получается за счет того, что в процессе преобразований исходное число вообще уходит из цепочки вычислений и остается только четверка.

Попробуй доказать это на формулах, взяв за задуманное число Х

Фокус 2

В нем вы можете угадать День рождения человека.

Попросите зрителя умножить на 2 число дня его рождения, затем пусть он прибавит к результату 5 и умножит это все на 50, после этого попросите зрителя прибавить к этому числу номер месяца рождения (январь- 1, февраль- 2 и т. д.).

Для того чтобы сказать по полученному числу День рождения человека, надо вычесть из числа, названного зрителем, 250 — получится трехзначное или четырехзначное число, где первые одна или две цифры — это день рождения, а последние две — месяц.

Отношения

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока «Отношения»

Для решения практических задач человеку часто приходится сравнивать разные значения одной и той же величины – массы, расстояния, времени, скорости, стоимости, объёма, площади и т.д.

Для сравнения чисел и величин существуют, как вы знаете, два способа:

1-ый: вычисление разности и 2-ой: вычисление частного.

Оба этих способа используют часто при решении практических задач, но служат они для разных целей. К делению прибегают в тех случаях, когда хотят получить качественную оценку или относительную оценку той или иной ситуации.

Задача

На экране изображены два отрезка. Отрезок AB длиной 15 см и отрезок CD, длина которого 6 см. Во сколько раз отрезок АВ больше или длиннее отрезка CD?

Вторая задача: на экране изображены эти же два отрезка. Отрезок AB длиной 15 см и отрезок CD, длина которого 6 см. Но поставим вопрос по-другому: какую часть отрезок CD составляет от отрезка АВ?

Обе рассмотренные задачи решаются делением, и ответ даётся в виде частного. В таких случаях частное двух чисел называют их отношением.

Определение

Частное двух не равных нулю чисел (или двух величин) называют отношением.

Сами эти числа (величины) называют членами отношения.

Иными словами, отношение двух чисел – это другое название их частного. Отношение чисел записывают с помощью знака деления, а также с помощью черты обыкновенной дроби.

Частные чисел читают так:

Напомним, что отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого.

Черта дроби используется для записи отношения и тогда, когда его члены не являются натуральными числами.

Задача

Рост дяди Степы 2 м 10 см, а рост мальчика Васи – 105 см. Во сколько раз дядя степа выше мальчика Васи?

Но ведь дробную черту мы использовали для записи дробей! А сейчас записана не дробь. Верно. Но вы давно знаете, что при записи деления натуральных чисел вместо знака деления можно использовать дробную черту. Так вот, договариваются о том же и при записи деления любых чисел.

Итак, если а и b – любые числа, то

Сделаем важное замечание:

Если значения двух величин выражены разными единицами измерения, то для нахождения отношения этих величин надо предварительно перейти к одной единице измерения.

Отношение величин одного наименования (длин, скоростей, стоимостей и т.д., выраженных одинаковыми единицами измерения) есть число. Такие величины называют однородными.

Отношение величин разных наименований (пути и времени, стоимости товара и его количества, массы тела и его объема и т.д.) есть новая величина.

Вот, например, в предыдущей задаче мы находили во сколько раз дядя Степа выше мальчика Васи.

Рост Васи и рост дяди Степы – это однородные величины, т.е. длина. Поэтому отношение их роста выраженно натуральным числом.

А теперь давайте разберёмся, почему отношение разноимённых величин – это новая величина.

Задача

Муравей за 20 секунд пробегает 240 сантиметров. Определите скорость движения муравья.

Отметим, что обозначения км/ч, м/с и т.п. приняты именно потому, что расстояние делят на время. Их обычно записывают с наклонной чертой.

В виде отношений определяются и другие величины:

Из основного свойства частного следует свойство отношения.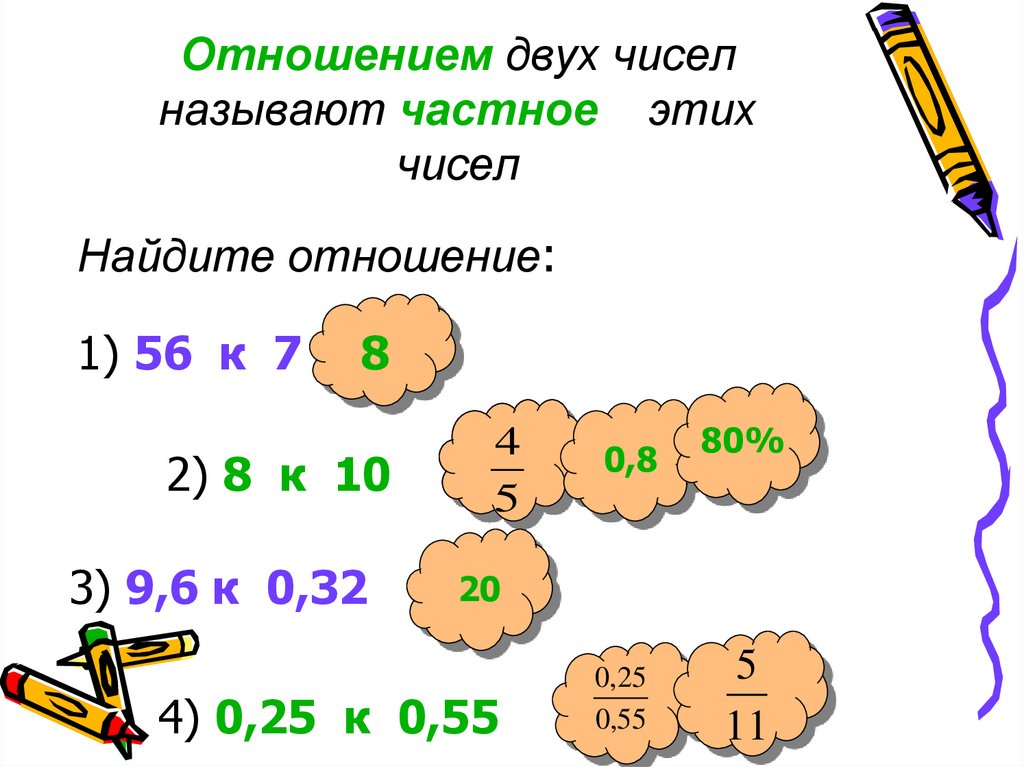

Давайте вспомним основное свойство частного:

если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Следовательно, получаем свойство отношения:

отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.

Пример

Мы с вами убедились, что свойство отношения действует. Мы умножили числитель и знаменатель дроби на одно и то же число, само же отношение не изменилось.

Итак, сегодня на уроке мы узнали, что частное двух не равных нулю чисел (или двух величин) называют отношением.

Сами эти числа (величины) называют членами отношения.

И свойство отношения: отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.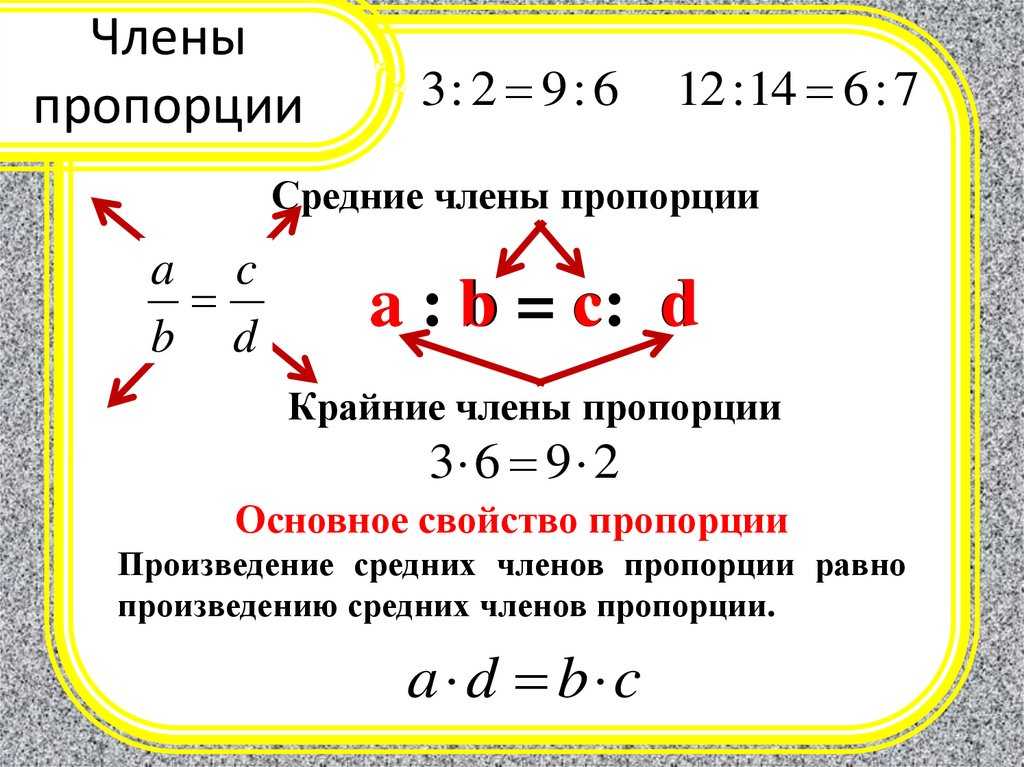

Отношения и пропорции

Используй поиск, чтобы найти научные материалы и собрать список литературы

База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны

Содержание статьи

1. Отношение двух чисел

2. Понятие пропорции

Отношение двух чисел

Определение 1

Отношением двух чисел является их частное.

Пример 1

отношение $18$ к $3$ может быть записано как:
$18\div 3=\frac{18}{3}=6$.
отношение $5$ к $15$ может быть записано как:
$5\div 15=\frac{5}{15}=\frac{1}{3}$.

С помощью отношения двух чисел можно показать:

во сколько раз одно число превышает другое;
какую часть представляет одно число от другого.

При составлении отношения двух чисел в знаменателе дроби записывают то число, с которым проводится сравнение.

Чаще всего такое число следует после слов «по сравнению с …» или предлога «к …».

Вспомним основное свойство дроби и применим его к отношению:

Замечание 1

При умножении или делении обоих членов отношения на одно и то же число, отличное от нуля, получаем отношение, которое равно исходному.

Рассмотрим пример, который иллюстрирует использование понятия отношения двух чисел.

Пример 2

Количество осадков в предыдущем месяце составляло $195$ мм, а в текущем месяце – $780$ мм. Во сколько раз увеличилось количество осадков в текущем месяце по сравнению с предыдущим месяцем?

Решение.

Составим отношение количества осадков в текущем месяце к количеству осадков в предыдущем месяце:

$\frac{780}{195}=\frac{780\div 5}{195\div 5}=\frac{156\div 3}{39\div 3}=\frac{52}{13}=4$.

Ответ: количество осадков в текущем месяце в $4$ раза больше, чем в предыдущем.

Пример 3

Найти сколько раз число $1 \frac{1}{2}$ содержится в числе $13 \frac{1}{2}$.

Решение.

$13 \frac{1}{2}\div 1 \frac{1}{2}=\frac{27}{2}\div \frac{3}{2}=\frac{27}{2} \cdot \frac{2}{3}=\frac{27}{3}=9$.

Ответ: $9$ раз.

Понятие пропорции

Определение 2

Пропорцией называется равенство двух отношений:

$a\div b=c\div d$

или

$\frac{a}{b}=\frac{c}{d}$.

Пример 4

$3\div 6=9\div 18$, $5\div 15=9\div 27$, $4\div 2=24\div 12$,

$\frac{8}{2}=\frac{36}{9}$, $\frac{10}{40}=\frac{9}{36}$, $\frac{15}{75}=\frac{1}{5}$.

В пропорции $\frac{a}{b}=\frac{c}{d}$ (или $a:b = с\div d$) числа a и d называются крайними членами пропорции, а числа $b$ и $c$ – средними членами

пропорции.

Правильную пропорцию можно преобразовать следующим образом:

Замечание 2

Произведение крайних членов правильной пропорции равно произведению средних членов:

$a \cdot d=b \cdot c$.

Данное утверждение является основным свойством пропорции.

Справедливо и обратное утверждение:

Замечание 3

Если произведение крайних членов пропорции равно произведению ее средних членов, то пропорция правильная.

Замечание 4

Если в правильной пропорции переставить средние члены или крайние члены, то пропорции, которые получатся, также будут правильными.

Пример 5

$6\div 3=18\div 9$, $15\div 5=27\div 9$, $2\div 4=12\div 24$,

$\frac{2}{8}=\frac{9}{36}$, $\frac{40}{10}=\frac{36}{9}$, $\frac{75}{15}=\frac{5}{1}$.

С помощью данного свойства легко из пропорции найти неизвестный член, если известны остальные три:

$a=\frac{b \cdot c}{d}$; $b=\frac{a \cdot d}{c}$; $c=\frac{a \cdot d}{b}$; $d=\frac{b \cdot c}{a}$.

Пример 6

$\frac{6}{a}=\frac{16}{8}$;

$6 \cdot 8=16 \cdot a$;

$16 \cdot a=6 \cdot 8$;

$16 \cdot a=48$;

$a=\frac{48}{16}$;

$a=3$.

Пример 7

$\frac{a}{21}=\frac{8}{24}$;

$a \cdot 24=21 \cdot 8$;

$a \cdot 24=168$;

$a=\frac{168}{24}$;

$a=7$.

Пример 8

Для пошива $7$ платьев понадобилось $21,7$ м шелка. Сколько нужно метров такого же шелка, чтобы пошить $18$ платьев?

Решение.

Пусть $x$ м – количество шелка, необходимого для пошива $18$ платьев. Тогда, по условию:

$7$ платьев – $21,7$ м;

$18$ платьев – $x$ м.

Составим пропорцию:

$\frac{7}{18}=\frac{21,7}{x}$.

Воспользуемся правилом нахождения неизвестного члена пропорции:

$d=\frac{b \cdot c}{a}$;

$x=\frac{18 \cdot 21,7}{7}$;

$x=18 \cdot 3,1$;

$x=55,8$.

Ответ: для пошива 18 платьев понадобится 55,8 м шелка.

Пример 9

$3$ садовника обрезают в день $108$ деревьев. Сколько нужно садовников, чтобы обрезать $252$ дерева?

Решение.

Пусть $x$ – количество садовников, необходимое для обрезки $252$ деревьев.

Тогда, по условию:

$3$ садовника – $108$ деревьев;

$x$ садовников – $252$ дерева.

Составим пропорцию:

$\frac{3}{x}=\frac{108}{252}$.

Воспользуемся правилом нахождения неизвестного члена пропорции:

$b=\frac{a \cdot d}{c}$;

$x=\frac{3 \cdot 252}{108}$;

$x=\frac{252}{36}$;

$x=7$.

Ответ: для обрезки $252$ деревьев потребуется $7$ садовников.

Чаще всего свойства пропорции используют на практике в математических вычислениях в случаях, когда необходимо вычислить значение неизвестного члена пропорции, если известны значения трех остальных членов.

Сообщество экспертов Автор24

Автор этой статьи Дата последнего обновления статьи: 20.06.2022

Выполнение любых типов работ по математике

Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами

Подбор готовых материалов по теме

Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы

Отношения в математике — определение, типы, графики, примеры

Отношения в математике помогают установить связь между любыми двумя объектами или вещами. Отношение описывает отношения между двумя объектами, которые обычно представляются в виде упорядоченной пары (вход, выход) или (x, y). Здесь x и y — элементы множеств.

Отношения имеют несколько применений, особенно в области информатики, для создания систем управления реляционными базами данных (RDBMS). В этой статье будут подробно описаны отношения, их типы, как связать элементы из двух наборов с помощью отношений и связанных примеров.

1.	Что такое отношения в математике?
2.	Представление отношений
3.	Типы отношений
4.	Графические отношения
5.	Часто задаваемые вопросы по отношениям в математике

Что такое отношения в математике?

Отношения в математике используются для описания связи между элементами двух множеств.

Они помогают отображать элементы одного набора (известного как домен) на элементы другого набора (называемого диапазоном), так что результирующие упорядоченные пары имеют форму (вход, выход). Кроме того, специальные типы отношений, которые можно использовать для установления соответствия между двумя величинами, известны как функции. Можно также сказать, что функция является подмножеством отношения.

Определение отношений в математике

Отношения в математике — это подмножество декартова произведения двух множеств. Предположим, что есть два множества, заданные X и Y. Пусть x ∈ X (x — элемент множества X) и y ∈ Y. Тогда декартово произведение X и Y, представленное как X × Y, задается набором все возможные упорядоченные пары (x, y). Другими словами, отношение говорит о том, что каждый вход будет производить один или несколько выходов.

Отношения в математике Пример

Предположим, что есть два набора X = {4, 36, 49, 50} и Y = {1, -2, -6, -7, 7, 6, 2}. Отношение, которое утверждает, что «(x, y) находится в отношении R, если x является квадратом y», может быть представлено с использованием упорядоченных пар как R = {(4, -2), (4, 2), (36, -6), (36, 6), (49, -7), (49, 7)}.

Представление отношений

Отношения могут быть представлены с использованием различных методов. Существует пять основных представлений отношений. Они представлены следующим образом:

Форма конструктора наборов: Это математическая запись, в которой четко указано правило, связывающее два набора X и Y. Если есть два набора X = {5, 6, 7} и Y = {25, 36, 49}. Правило состоит в том, что элементы X являются положительным квадратным корнем элементов Y. В форме построителя множеств это отношение может быть записано как R {(a, b): a — положительный квадратный корень из b, a ∈ X , b ∈ Y}.

Форма списка: В форме списка записываются все возможные упорядоченные пары двух наборов, которые следуют заданному отношению. Используя тот же пример, что упоминался выше, отношение элементы множества X являются положительными квадратными корнями элементов множества B представлено как R = {(5, 25), (6, 36), (7, 49)}.

Диаграмма-стрелка: Такая диаграмма используется для визуального представления отношения между элементами двух заданных наборов.

Стрелочная диаграмма вышеупомянутого примера представлена как

Табличная форма: Когда ввод и вывод отношения выражаются в форме таблицы, это известно как табличное представление отношения. При этом таблица рисуется с двумя столбцами. Первый обозначает вход, а второй выражает выход. Используя соотношение, согласно которому элементы X = {5, 6, 7} являются положительными квадратными корнями элементов Y = {25, 36, 49} таблица имеет следующий вид:

X	Д
5	25
6	36
7	49

Пятое представление, использующее графический метод, будет рассмотрено в следующих разделах.

Типы отношений

Два набора могут иметь разные типы соединений, поэтому для классификации этих соединений необходимы разные виды отношений. Основные типы отношений перечислены ниже:

Пустое отношение

Пустое отношение — это отношение, в котором любой элемент набора не отображается ни на элемент другого набора, ни на себя. Это соотношение обозначается как R = ∅. Например, P = {3, 7, 9} и соотношение на P, R = {(x, y), где x + y = 76}. Это будет пустое отношение, так как никакие два элемента P не суммируются до 76.

Универсальное отношение

Если все элементы, принадлежащие одному набору, отображаются на все элементы другого набора или на себя самого, то такое отношение известно. как универсальное отношение. Это записывается как R = X × Y, где каждый элемент X связан с каждым элементом Y. Пример, P = {3, 7, 9}, Q = {12, 18, 20} и R = {(x, y), где x < y}.

Отношение идентичности

Если все элементы в наборе связаны сами с собой, тогда оно становится отношением идентичности. Это записывается как I = {(x, x) : для всех x ∈ X}. Например, P = {3, 7, 9}, тогда I = {(3, 3), (7, 7), (9, 9)}

Обратное отношение

Если элементы одного множества являются обратными парами другой набор, то такое отношение известно как обратное отношение. Другими словами, обратное отношение является обратным отношением. Обратное отношение R обозначается как R ^-1 . т. е. R ^-1 = {(y, x) : (x, y) ∈ R}

Рефлексивное отношение

Если в наборе все элементы отображаются сами на себя, то это отношение является рефлексивным. Таким образом, если x ∈ X, то рефлексивное отношение определяется как (x, x) ∈ R. Например, P = {7, 1}, тогда R = {(7, 7), (1, 1)} является рефлексивным связь.

Симметричное отношение

Отношение называется симметричным отношением, если одно множество X содержит упорядоченные пары (x, y), а также противоположные этим парам (y, x). Другими словами, если (x, y) ∈ R, то (y, x) ∈ R для того, чтобы отношение было симметричным. Предположим, что P = {3, 4}, тогда симметричным отношением может быть R = {(3, 4), (4, 3)}.

Транзитивное отношение

Предположим, что (x, y) ∈ R и (y, z) ∈ R, тогда R является транзитивным отношением тогда и только тогда, когда (x, z) ∈ R. Например, P = {p, q, r}, то транзитивное отношение может быть R = {(p, q), (q, r), (p, r)}

Отношение эквивалентности

Отношение эквивалентности — это тип отношения, который является симметричным, транзитивным и рефлексивный.

Отношение «один к одному»

В отношении «один к одному» каждый элемент одного набора будет сопоставлен с отдельным элементом другого набора. Например, предположим, что есть два множества P = {1, 2, 3} и Q = {a, b, c}. Тогда отношение один к одному может быть R = {(1, a), (2, b), (3, c)}

Отношение «один ко многим»

В отношении «один ко многим» один элемент одного набора будет сопоставлен более чем с одним элементом другого набора. Например, для двух множеств P = {1, 2, 3} и Q = {a, b, c} отношение «один ко многим» записывается как R = {(2, a), (2, b), ( 2, c)}

Отношение «многие к одному»

Если более одного элемента одного множества отображаются в один отдельный элемент другого множества, то такое отношение называется отношением «многие к одному». Например, P = {1, 2, 3} и Q = {a, b, c}, тогда R = {(1, a), (2, a), (3, a)} является многими к одному связь.

Отношение «многие ко многим»

В отношении «многие ко многим» один или несколько элементов одного набора будут сопоставлены с тем же или другим элементом другого набора. Если P = {1, 2, 3} и Q = {a, b, c}, то R = {(2, a), (3, a), (2, c)} является примером множества для многие отношения.

Графические отношения

Отношения также могут быть представлены графически с использованием декартовой системы координат. Элемент отношения может быть либо выражен в виде упорядоченной пары (x, y), либо может быть задан в виде уравнения (или неравенства). Упорядоченная пара представляет положение точек на координатной плоскости. Предположим, что отношение задано как y = x — 2 на множестве всех действительных чисел, тогда шаги для построения графика следующие:0005

Замените x числовыми значениями; x = -1, 0, 2 (несколько случайных чисел) 90 180
Найдите соответствующие значения y, используя данное соотношение; у = -3, -2, 0,
Запишите эти контрольные точки как упорядоченные пары; {(-1, -3), (0, -2), (2, 0)}.
Нанесите эти точки на декартову плоскость. Если отношение уже задано в виде упорядоченных пар, то нанесите их на плоскость.
Соедините эти точки, чтобы получить график заданного отношения. Для данного примера график будет прямой линией.

Важные замечания по отношениям в математике:

Отношение используется для установления связи между элементами одного или разных наборов.
Упорядоченная пара вида (вход, выход) используется для обозначения элемента отношения.
Декартово произведение двух множеств можно описать с помощью соотношений.
Отношения могут быть представлены с использованием формы построения набора, формы реестра, стрелочной диаграммы, графической формы и табличной формы.
Существует множество различных типов отношений, таких как пустое отношение, универсальное отношение, отношение многие к одному и т. д.

☛ Связанные статьи:

Взаимосвязи и функции
Координатная геометрия
оси x и y

Часто задаваемые вопросы об отношениях в математике

Что такое определение отношения в математике?

Отношение в математике дает отношение между двумя множествами (скажем, A и B). Каждый элемент отношения представлен в виде упорядоченной пары (x, y), где x принадлежит A, а y принадлежит B. Другими словами, отношение — это подмножество декартова произведения A и B.

Что такое функции и отношения в математике?

Отношение помогает установить связь между элементами двух множеств так, что вход и выход образуют упорядоченную пару (вход, выход). Функция — это подмножество отношения, которое определяет результат при заданном входе. Все функции являются отношениями, но не все отношения являются функциями. Например, R = {(1, 2), (1, 3), (2, 3)} является отношением, но не функцией, поскольку 1 отображается дважды (и 2, и 3).

Какие существуют типы отношений в математике?

В математике существует девять различных типов отношений. Они даны следующим образом:

Пустое отношение
Универсальная связь
Отношение личности
Обратная зависимость
Рефлексивное отношение
Отношение симметрии
Переходное отношение
Отношение эквивалентности

Существует четыре других типа отношений, основанных на отображении.

Отношения один к одному
Отношение один ко многим
Отношение «многие к одному»
Отношение многие ко многим

Что такое уравнение отношения?

Когда отношение выражается в виде уравнения, оно называется уравнением отношения. y = x ² является примером уравнения отношения. График этой зависимости будет параболой.

Как представляются отношения в математике?

Существует 5 широко используемых способов представления отношения. Это форма построения набора, форма списка, табличная форма, стрелочная диаграмма и с использованием графика.

Как записать отношение на графике?

Если существует упорядоченная пара (x, y) такая, что x связано с y, то такое отношение можно изобразить на графике. Чтобы представить отношение на графике, просто отметьте на нем упорядоченные точки. Координата x представляет собой расстояние точки от оси y, а координата y обозначает расстояние от оси x.

Что такое симметричные отношения в математике?

Симметричное отношение в математике может быть определено как отношение, которое содержит упорядоченную пару (x, y), а также обратную эту пару (y, x). Таким образом, для симметричного отношения, если (x, y) ∈ R, то (y, x) ∈ R.

Все ли функции относятся к математике?

Все функции являются отношениями. Функция — это отношение, в котором каждый вход будет иметь только один выход. Таким образом, отношение «один к одному» и отношение «многие к одному» образуют функцию.

Какие существуют типы математических отношений?

Наклонная плоскость, используемая для демонстрации ускорения и квадратичной зависимости

Что такое математическая зависимость?

Математическое отношение — это отношение между наборами чисел или наборами элементов.

Часто взаимосвязи между переменными можно увидеть, просто изучив математическое уравнение. Многие физические соотношения в электростатике, электродинамике, термодинамике и т. д. выражаются математическими уравнениями. Следующие примеры математических взаимосвязей помогут вам в анализе данных для лабораторных работ в этом модуле.

Линейные отношения

Давайте посмотрим на следующее уравнение:

Y = 3X

По мере увеличения X Y будет увеличиваться пропорционально. Если мы построим график X-Y, будет сформирована прямая линия.

В природе данные не точны, поэтому точки не всегда попадают на линию. Ниже приведен график данных относительно удельной прочности на раздавливание в зависимости от давления (P). Точки падают достаточно близко к прямой линии, чтобы сделать вывод, что это линейная или прямая зависимость.

Что такое независимые и зависимые переменные на графике?

Независимая переменная — Независимая переменная — это именно то, на что это похоже. Это переменная, которая стоит особняком и не изменяется другие переменные, которые вы пытаетесь измерить . Например, если время является одной из ваших переменных , это независимая переменная . Время всегда независимая переменная . Ученые любят говорить, что « независимая » переменная идет по оси x (нижняя, горизонтальная), а « зависимая » переменная идет по оси y ( — ) левая сторона, вертикальная).

Зависимая переменная — Как и независимая переменная, зависимая переменная – это именно то, на что она похожа. Это то, что зависит от других факторов. Например, результат теста может быть зависимой переменной, потому что он может меняться в зависимости от нескольких факторов, например, от того, сколько вы учились, сколько вы спали в ночь перед сдачей теста или даже от того, насколько вы были голодны, когда сдавали его. Обычно, когда вы ищете взаимосвязь между двумя вещами, вы пытаетесь выяснить, что заставляет зависимую переменную изменяться так, как она это делает.

Обратная зависимость

Теперь рассмотрим следующее уравнение:

Y = 1/X

Если X=1, то Y = 1. Если X = 2, то Y = 0,5. Если X = 3, то Y = 0,33. Если X = 4, то Y = 0,25. Обратите внимание, что по мере увеличения X Y уменьшается нелинейным образом. Это обратная зависимость.

Пример обратной зависимости в науке: Когда более высокая вязкость приводит к уменьшению расхода, зависимость между вязкостью и расходом обратная. Обратные отношения следуют гиперболическому образцу. Ниже приведен график, показывающий гиперболическую форму обратной зависимости. 92

Примеры: Квадратичные отношения обнаруживаются во всех ускоряющихся объектах, например, падающих объектах. Ниже приведен график, демонстрирующий форму квадратного уравнения.

Закон обратных квадратов. силы. Например, объект, расположенный в трех футах от источника света, получит только одну девятую (1/9, обратное 3 в квадрате) столько же освещения, сколько объект находится на расстоянии одного фута от источника света.

В физике законом обратных квадратов называется любой физический закон, утверждающий, что определенная физическая величина или интенсивность обратно пропорциональна квадрату расстояния от источника этой физической величины. Фундаментальную причину этого можно понять как геометрическое разбавление, соответствующее излучению точечного источника, в трехмерном пространстве.

Один из известных законов обратных квадратов относится к притяжению двух масс. Две массы на заданном расстоянии притягивают друг друга равными и противоположными силами. Величина этой силы притяжения определяется выражением: 92), m1 — масса первого объекта в килограммах, m2 — масса второго объекта в килограммах, r — расстояние между центрами двух масс в метрах. График этого уравнения показан ниже.

Подробнее см.:

Гравитация: еще один пример закона 1/R2

Подробнее о яркости и законе обратных квадратов

Демпфирующее движение эффект уменьшения, ограничения или предотвращения его колебаний. В физических системах затухание вызывается процессами, которые рассеивают энергию, запасенную в колебаниях. Примеры включают вязкое сопротивление в механических системах, сопротивление в электронных генераторах, поглощение и рассеяние света в оптических генераторах. Демпфирование, не основанное на потерях энергии, может быть важным в других колебательных системах, например, в биологических системах.

Зависимость синусоиды

Графики функций синуса и косинуса представляют собой синусоиды разных фаз. Синусоида или синусоида — это математическая кривая, описывающая плавные повторяющиеся колебания. Он назван в честь функции синуса, графиком которой он является.

Математика, 7 класс, пропорциональные отношения, решение задач на пропорциональные отношения

CCSS.Math.Content.7.RP.A.2b 7 класс, Соотношения и пропорциональные отношения

Кластер: Анализ пропорциональных отношений и их использование для решения реальных и математических задач

Стандарт: Определение константы пропорциональности (единицы измерения) в таблицах, графиках, уравнениях, диаграммах и словесных описаниях пропорциональных отношений.