В корзине лежат белые и черные шары среди них 18: В корзине лежат белые и черные шары. Среди них 18 черных шаров. Сообщение о том, что из корзины достали белый шар, несет 2 бита информации. Сколько всего в корзине шаров?

ЕГЭ по информатике 2021 — Задание 8 (Супер-разбор!)

Сегодня на повестке дня 8 задание из ЕГЭ по информатике 2021. Данный тип заданий включает в себя нахождение количества вариантов, элементы комбинаторики и другие математические понятия.

Перейдём к практике решения задач задания 8 ЕГЭ по информатике 2021.

Задача (Классика)

Все 4-буквенные слова, составленные из букв А, Е, И, О записаны в алфавитном порядке и пронумерованы. Вот начало списка:

1. АААА
2. АААЕ
3. АААИ
4. АААО
5. ААЕА
…

Запишите слово, стоящее на 248-м месте от начала списка.

Решение:

Обозначим условно А — 0, Е — 1, И — 2, О — 3.

Важно: Нужно буквам присваивать цифры именно в том порядке, в котором они идут в самом правом столбце, потому что буквы могут дать в «перепутанном порядке» (например Е, А, И, О), и тогда ничего не получится.

Теперь запишем список с помощью цифр.
1. 0000
2. 0001
3. 0002
4. 0003
5. 0010
…

Получился обычный счёт в четверичной системе!! (всего используются 4 цифры: 0, 1, 2, 3). А слева нумерация показывает соответствие нашей десятичной системе. Но все числа десятичной системы в этой таблице соответствия сдвинуты на 1, ведь мы должны были начать с нуля.

Нас просят записать слово стоящее на 248, т.е. если была обычная таблица соответствия чисел десятичной системы и четверичной системы, слово стоящее на 248 месте, находилось бы на 247 (248 — 1) месте. Значит, наше искомое четверичное число соответствует 247 в десятичной системе.

Переведём число 247 в четверичную систему!

Получилось число 3313₄ в четверичной системе. Сделаем обратное декодирование в буквы.

Таким образом, ответ будет ООЕО.

Ответы: ООЕО

Ещё одна похожая задача 8 задания из примерных вариантов ЕГЭ по информатике, но другой вариации.

Задача (Классика, Другая вариация)

Все 5-буквенные слова, составленные из букв А, Р, У, К записаны в алфавитном порядке. Вот начало списка:

1. ААААА
2. ААААК
3. ААААР
4. ААААУ
5. АААКА
……
Укажите номер слова УКАРА

Решение:

Закодируем буквы цифрами: А — 0, К — 1, Р — 2, У — 3. Здесь как раз буквы даны не в том порядке, как они идут в самом правом столбце. Но мы должны кодировать именно в том порядке, как буквы идут в самом правом столбце.

У нас получилось четыре цифры! Значит снова можно слова превратить в таблицу соответствия между десятичной системой и четверичной системой. Но десятичная система смещена на 1 позицию.

1. 00000
2. 00001
3. 00002
4. 00003
5. 00010
……

Выписываем данное нам слово и посмотрим, какое число в четверичной системе было бы, если бы у нас были в место слов числа в четверичной системе!

Получили число в четверичной системе 31020₄. Узнаем, какое число в десятичной системе соответствовало этому числу, если бы была обычная таблица соответствия. Для этого переведём число 31020₄ из четверичной системы в десятичную. Перевод делаем по аналогии перевода из двоичной системы в десятичную.

Но помним, что у нас нумерация идёт на 1 быстрее, нежели мы бы поставили десятичные числа, как в таблице соответствия, потому что нумерация начинается не с нуля, а с 1. Поэтому к числу

840 нужно прибавить 1, и в ответе будет 841

Ответ: 841

Задача (Демонстрационный вариант ЕГЭ по информатике, 2020)

Все 4-буквенные слова, в составе которых могут быть буквы Н, О, Т, К, И, записаны в алфавитном порядке и пронумерованы, начиная с 1. Ниже приведено начало списка.

1. ИИИИ
2. ИИИК
3. ИИИН
4. ИИИО
5. ИИИТ
6. ИИКИ
…

Под каким номером в списке идёт первое слово, которое начинается с буквы О?

Решение:

Закодируем буквы цифрами.

Получилось 5 цифр ( 0, 1, 2, 3, 4 ), значит, будем работать в пятеричной системе.

Нужно найти номер первого слова, которое начинается с буквы О. Если говорить на языке пятеричных чисел, то нужно найти номер числа 3000₅. Мы «забиваем нулями», чтобы число было четырёхразрядное, т.к. слова 4-х буквенные. Именно нулями, потому что нужно именно первое слово найти.

Теперь, как в предыдущей задаче, переведём число 3000₅ из пятеричной системы в десятичную.

0 * 5 ⁰ + 0 * 5 ¹ + 0 * 5 ² + 3 * 5 ³ = 375 (в десят. системе)

Но опять же должны прибавить 1 к числу 375, т.к. нумерация отличается от десятичных чисел на 1 в большую сторону.

Ответ: 376

Задача (Досрочная волна 2020 ЕГЭ по информатике, вариант 1)

Вася составляет 5-буквенные слова, в которых есть только буквы В, О, Л, К, причём буква В используется в каждом слове ровно 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Вася?

Решение:

Для начала решим вводную подзадачу.

Пусть у нас есть те же буквы В, О, Л, К, каждая из букв может встречаться в слове любое количество раз или не встречаться совсем. Сколько можно составить 5-буквенных слов ?

Т.

е буквы могут повторяться!

Например

Такая конструкция сильно напоминает перебор чисел, где вместо цифр используются буквы.

Рассмотрим перебор трёхразрядных чисел. Вместо 5 букв теперь можно использовать 10 цифр ( 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ). Цифры так же могут повторяться. Сколько получится вариантов ?

Выведем общую формулу для количества вариантов, когда символы могут повторяться!

Для трёхразрядных чисел от 000 до 999:

N = 10³ = 1000 вариантов.

Вернёмся к пятибуквенным словам и нашей подзадаче. Здесь количество букв (разрядов) в слове равно 5, количество допустимых символов равно 4 ( В, О, Л, К ).

N = 4⁵ = 1024 вариантов.

Вернёмся к изначальной задаче.

Сначала найдём количество вариантов, когда буква В находится в самой левой ячейке!

Применим формулу! Здесь слово сократилось до четырёхразрядного. А количество букв для использования 3 (О, Л, К).

N = 3⁴ = 81 комбинация.

Но буква В так же может стоять во второй ячейке слева. Этот случай тоже даст 81 других комбинаций. Буква В может стоять в каждой из 5-ти ячеек, и везде будет получатся 81 комбинация.

Таким образом, окончательный ответ будет:

N = 81 * 5 = 405 различных вариантов.

Ответ: 405

Разобравшись с этой задачей, больше половины тренировочных задач десятого задания из различных книг и сайтов по подготовке к ЕГЭ по информатике будут решаться, как по маслу!

Задача(Закрепление формулы)

Рассматриваются символьные последовательности длины 5 в шестибуквенном алфавите {У, Ч, Е, Н, И, К}. Сколько существует таких последовательностей, которые начинаются с буквы У и заканчиваются буквой К?

Решение:

Применим главную формулу 8 задания из ЕГЭ по информатике

N = mⁱ = 6³ = 216

Здесь буквы могут изменяться на 3 ячейках! Значит, в формуле i=3. Количество допустимых символов, которые можно поставить в каждую ячейку равно 6. Значит, в формуле m=6.

В ответе будет 216.

Примечание: Здесь можно использовать все буквы в каждой ячейке, включая У и К. В некоторых задачах их уже использовать нельзя, т.е. сказано, что буквы

У и К используются один раз в слове. Тогда в формуле m, будет на 2 единицы меньше. Нужно внимательно читать задачу!

Ответ: 216

Задача (Демонстрационный вариант ЕГЭ по информатике, 2019)

Вася составляет 5-буквенные слова, в которых есть только буквы З, И, М, А, причём в каждом слове есть ровно одна гласная буква и она встречается ровно 1 раз. Каждая из допустимых согласных букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Вася?

Решение:

Рассмотрим количество вариантов, когда гласная И стоит в первом месте!

Подсчитаем количество слов с помощью супер-формулы

N = mⁱ = 2⁴ = 16

Длина изменяющихся ячеек равна 4, а количество допустимых букв равно 2.

Но буква И может стоять не только на первом месте. Она так же может стоять и на 2, и на 3, и на 4, и на 5 месте. Каждый такое случай добавляет столько же новых слов.

Значит, при использовании только буквы И будет количество слов 16 * 5 = 80. Ещё столько же слов добавится, если в словах вместо буквы И будет использоваться буква А. Поэтому окончательный ответ будет 80 * 2 = 160

Ответ: 160

Отработаем главную формулу 8 задания из ЕГЭ по информатике.

Задача (Развиваем понимание формулы!)

Сколько слов длины 5, начинающихся с согласной буквы и заканчивающихся гласной буквой, можно составить из букв З, И, М, А? Каждая буква может входить в слово несколько раз. Слова не обязательно должны быть осмысленными словами русского языка.

Решение:

Рассмотрим, какие варианты могут быть, если у нас на первом месте стоит согласная, а на последнем месте гласная

Получилось 4 разных случая. Подсчитаем, сколько слов можно составить при одном случае.

N = mⁱ = 4³ = 64

Длина изменяющихся ячеек равна 3, а количество возможных букв 4.

Но т.к. таких случая у нас четыре, то ответ будет 4 * 64 = 256

Ответ: 256

Рассмотрим важнейший «метод умножения» при решении 8 задания из ЕГЭ по информатике.

Задача (Другой метод решения!!)

Матвей составляет 6-буквенные коды из букв М, А, Т, В, Е, Й. Каждую букву нужно использовать ровно 1 раз , при этом код не может начинаться с буквы Й и не может содержать сочетания АЕ. Сколько различных кодов может составить Матвей?

Решение:

Эта задача отличается от уже разобранных тем, что каждую букву можно использовать один раз. В этой задаче удобнее воспользоваться немного другим методом решения! «Методом умножения»!

Решим вводную подзадачу (без дополнительных ограничений).

Сколькими способами можно составить 6-x буквенное слово из букв М, А, Т, В, Е, Й. Каждую букву нужно использовать ровно 1 раз .

Чтобы найти возможные варианты, перемножаем для каждой ячейки количество букв из которых у нас есть выбор!

N = 6 * 5 * 4 * 3 * 2 * 1 = 720

Вернёмся к изначальной задаче!

В начале подсчитаем «методом умножения» количество слов, не обращая внимание, на условие, в котором сказано, что слово не может содержать сочетание АЕ.

N = 5 * 5 * 4 * 3 * 2 * 1 = 600

В формуле стоят почти все те же самые числа, как и в вводном примере, только первый множитель не 6, а 5. Это произошло из-за того, что у нас в задаче слово не может начинаться на букву Й. Значит, выбор на первую позицию будет не из 6 букв, а из 5.

Но в 600 комбинаций входят и те случаи, когда в слове присутствует сочетание АЕ. Теперь найдём сколько таких слов, где присутствует сочетание АЕ

Узнаем количество вариантов в каждом таком случае.

N1 = 4 * 3 * 2 * 1 = 24

На первом месте мы не можем использовать букву Й, поэтому мы на первом месте выбираем из 3 букв.

N2 = 3 * 3 * 2 * 1 = 18

Аналогично предыдущему случаю.

N3 = 3 * 3 * 2 * 1 = 18

N4 = 3 * 3 * 2 * 1 = 18
N5 = 3 * 3 * 2 * 1 = 18

Всего слов с сочетанием АЕ будет

24 + 18 + 18 + 18 + 18 = 96

Значит, всего слов, которые удовлетворяют условию задаче будет

N = 600 — 96 = 504

Примечание: Метод умножения можно было использовать и в задачах, которые мы рассмотрели ранее. Например, в задаче «Закрепление формулы» в первой свободной ячейке выбираем из 6 букв, во второй свободной ячейке тоже из 6 букв, и в третий свободной ячейке тоже можно использовать 6 букв. Значит, по методу умножения получается N = 6 * 6 * 6 = 6³ = 216

Ответ: 504

Задача (Закрепления «метода умножения»)

Полина составляет 6-буквенные коды из букв П, О, Л, И, Н, А. Каждую букву нужно использовать ровно 1 раз, при этом нельзя ставить подряд две гласные или две согласные. Сколько различных кодов может составить Полина?

Решение:

Опять сказано, что каждая буква используется 1 раз, следовательно, нужно применять «метод умножения».

На первое место можно выбрать из 6 букв, предположим, мы выберем согласную. Тогда на второе место нужно выбирать из 3 гласных. Потом опять должна идти согласная, но их у нас осталось только 2. Далее, на следующее место выбираем из 2 гласных букв. И на предпоследнее место выбирается 1 согласная, а на последнее место остаётся 1 гласная.

Т.к. количество гласных букв и согласных одинаковое, и равно трём, то если мы бы начали делать «метод умножения» с гласной буквы, количество вариантов бы не поменялось.

N = 6 * 3 * 2 * 2 * 1 * 1 = 72

Ответ: 72

Задача (Азбука Морзе)

Азбука Морзе позволяет кодировать символы для сообщений по радиосвязи, задавая комбинацию точек и тире. Сколько различных символов (цифр, букв, знаков пунктуации и т.д.) можно закодировать, используя код Морзе длиной не менее трёх и не более четырёх сигналов (точек и тире) ?

Решение:

Зная формулу, без проблем решим данную примерную задачу из ЕГЭ по информатике.

У нас есть 2 символа, которые можно использовать: точка и тире. Фраза, что сообщение может иметь «не менее трёх и не более четырёх сигналов», означает, что сообщения могут быть длиною 3 символа и длиною 4 символа.

Подсчитаем общее количество вариантов.

N = 2³ + 2⁴ = 8 + 16 = 24 комбинаций.

Значит, для 24 различных символов (цифр, букв, знаков пунктуации и т.д.) мы найдём различные комбинации, чтобы их закодировать

Ответ: 24

Задача (Обратная предыдущей)

Световое табло состоит из цветных индикаторов. Каждый индикатор может окрашиваться в четыре цвета: белый, черный, желтый и красный. Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 300 различных сигналов?

Решение:

Нам нужно закодировать 300 различных вариантов! Имеются 4 различных лампочки! (Они имеют смысл, как количество допустимых символов!) На этот раз нужно узнать количество лампочек (количество разрядов, «длину слова»). Применяем формулу.

N = 4^x = 300

Не найдётся такое целое x, чтобы равенство стало верным. Поэтому берём целое минимальное x такое, чтобы 4^x больше 300.

4⁵ = 1024

Пять лампочек на табло хватит, чтобы закодировать 300 сигналов, но, к сожалению, много комбинаций просто не пригодится!

Ответ: 5

Задача (Важная!)

Нужно выбрать в подарок 3 книги из 5. Сколькими способами можно выбрать ?

Решение:

На рисунке показано две комбинации, как можно выбрать в подарок 3 книги из 5.

Данную задачку нужно решать используя формулу сочетаний из раздела комбинаторика.

n — количество книг, из которых мы выбираем подарок, m — количество книг, которое мы хотим выбрать, C — количество вариантов (способов).

Восклицательный знак — это факториал!

Факториалом числа «n» (условное обозначение n!- читается как «эн» — факториал) называется произведение чисел от 1 до «n»

Примечание: При использовании формулы сочетаний, не важен порядок, в котором мы выбираем одни и те же книги. Это будет один и тот же вариант.

Ответ: 10

Следующая задача часто встречается в книгах по подготовке к ЕГЭ по информатике.

Задача (Главная формула + сочетания)

Шифр кодового замка представляет собой последовательность из пяти символов, каждый из которых является цифрой от 1 до 5. Сколько различных вариантов шифра можно задать, если известно, что цифра 1 встречается ровно три раза, а каждая из других допустимых цифр может встречаться в шифре любое количество раз или не встречаться совсем?

Решение:

В начале нужно посчитать, сколькими способами на 5-ти ячейках можно расположить 3 единицы!

Обратите внимание, как будто мы выбираем 3 книги в подарок из 5 возможных! Значит, опять применяем формулу сочетаний из комбинаторики.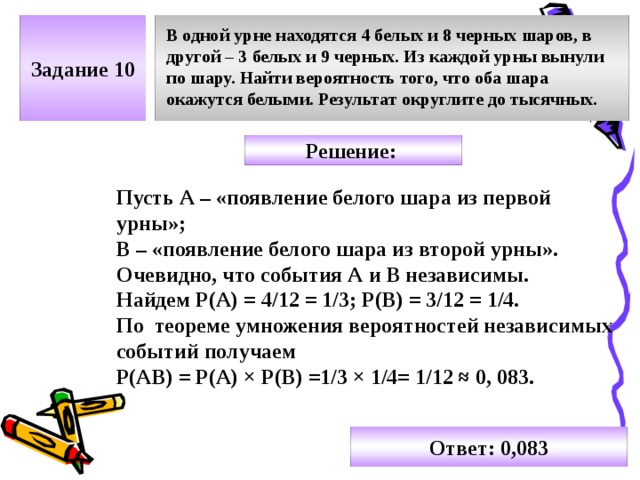 Мы вычисляли уже её точно с такими же числами в прошлой задаче, количество вариантов равно 10.

Подсчитаем, сколько вариантов кодового замка можно составить при одном определённом расположении трёх единиц.

Применим формулу, есть две ячейки, в которых изменяются цифры, а в каждой ячейке может быть одна из 4 цифр.

N = mⁱ = 4² = 16

Т.к. различных вариантов, как расположить единицы на 5 ячейках равно 10, то ответ будет 16 * 10 = 160

Ответ: 160

Ещё одна задача из примерных вариантов по подготовке к ЕГЭ по информатике.

Задача (Таблица соревнований)

Для записи результатов соревнований используется таблица, в которой для каждой из 20-ти команд по каждому из 10-ти видов состязаний записано 1, 2 или 3 (если команда заняла соответствующее место в этом состязании) или прочерк (если не заняла призовое место или не участвовала). Какое количество информации (бит) содержит таблица ?

Решение:

Есть таблица с 20 командами и для каждой команды есть результат по 10-ти видам состязаний.

	1 команда	2 команда	3 команда	…	20 команда
1 дисциплина	1	—	1	…	3
2 дисциплина	—	2	1	…	2
…	…	…	…	…	…
10 дисциплина	1	1	2	…	—

В каждой ячейке может быть 4 различных значения ( 1, 2, 3, — ). Нужно узнать, сколько бит занимает одна ячейка таблицы. Один бит может быть либо единицей, либо нулём.

Сделав рисунок, задача обрела привычные очертания.

Как будто мы решаем задачу с перебором слов. Но здесь длина слова неизвестна, а количество вариантов, которое должно получится уже дано и равно 4 (четырём). Применим главную формулу из 10 задания из ЕГЭ по информатике.

N = mⁱ = 2ⁱ = 4
i=2 бита (длина равна «2 буквам», если воспринимать задачу, как со словами.)

Одна ячейка таблицы весит 2 бита. Найдём количество ячеек во всей таблице соревнований.

Всего ячеек = 20 * 10 = 200

Тогда вся таблица будет весит:

V = 2 бита * 200 = 400 бит.

Ответ: 400

Формула Шеннона

Задача (Формула Шеннона)

В корзине лежат 8 черных шаров и 24 белых. Сколько бит информации несет сообщение о том, что достали черный шар?

Решение:

Данную задачу нужно решать по формуле Шеннона

Найдём вероятность p того, что вытащили чёрный шарик.

p = (количество чёрных шаров) / (количество всех шаров) = 8 / (24 + 8) = 8 / 32 = 1 /4
p = 1 / 4

Применим формулу Шеннона.

x = log₂(4)
2^x = 4
x = 2 бита

Ответ: 2

Информатика и ИКТ: 10 класс

10 класс

Домашнее задание 

Решить задачи

1.     

В мешке находятся 20 шаров. Из них 15 белых и 5 красных. Какое количество информации несет сообщение о том, что достали: а) белый шар; б) красный шар. Сравните ответы.

2.     

В коробке лежат кубики: 10 красных, 8 зеленых, 5 желтых, 12 синих. Вычислите вероятность доставания кубика каждого цвета и количество информации, которое при этом будет получено.

3.     

Мощность некоторого алфавита равна 64 символам. Каким будет объем информации в тексте, состоящем из 100 символов.

4. Сколько информации содержит сообщение, уменьшающее неопределенность знаний в 8 раз?
5. Вы подошли к светофору, когда горел желтый свет. После этого загорелся зеленый. Какое количество информации вы при этом получили?
6. Группа школьников пришла в бассейн, в котором 4 дорожки для плавания. Тренер сообщил, что группа будет плавать на дорожке номер 3. Сколько информации получили школьники из этого сообщения?
7. В корзине лежат 8 черных шаров и 24 белых. Сколько информации несет сообщение о том, что достали черный шар?
8. Известно, что в ящике лежат 20 шаров. Из них 10- синих, 5 – зеленых, 4 – желтых и 1 – красный. Какое количество информации несут сообщения о том, что из ящика случайным образом достали черный шар, белый шар, желтый шар, красный шар?
9. В корзине лежат белые и черные шары. Среди них 18 черных шаров. Сообщение о том, что из корзины достали белый шар, несет 2 бита информации. Сколько всего в корзине шаров?
10. В коробке лежат 64 цветных карандаша. Сообщение о том, что достали белый карандаш, несет 4 бита информации. Сколько белых карандашей было в корзине?
11. На железнодорожном вокзале 8 путей отправления поездов. Вам сообщили, что ваш поезд прибывает на четвертый путь. Сколько информации вы получили?
12. В коробке лежат 16 кубиков. Все кубики разного цвета. Сколько информации несет сообщение о том, что из коробки достали красный кубик?
13. Была получена телеграмма: «Встречайте, вагон 7». Известно, что в составе поезда 16 вагонов. Какое количество информации было получено?
14. В классе 30 человек. За контрольную работу по математике получено 15 пятерок, 6 четверок, 8 троек и 1 двойка. Какое количество информации в сообщении о том, что Андреев получил четверку?
15. За четверть ученик получил 100 оценок. Сообщение о том, что он получил пятерку, несет 2 бита информации. Сколько пятерок ученик получил за четверть?
16. При угадывании целого числа в диапазоне от 1 до N было получено 9 бит информации. Чему равно N?
17. Сообщение о том, что ваш друг живет на 10 этаже, несет 4 бита информации. Сколько этажей в доме?
18. В школьной библиотеке 16 стеллажей с книгами. На каждом стеллаже по 8 полок. Библиотекарь сообщил Пете, что нужная ему книга находится на пятом стеллаже на третьей сверху полке. Какое количество информации библиотекарь передал Пете?
19. Загадано слово из 10 букв. Вы просите открыть пятую букву. Вам ее открыли. Сколько информации вы получили?
20. В коробке лежат 6 разноцветных фломастеров. Какое количество информации содержит сообщение, что из коробки достали синий фломастер?
21. Какое количество информации несет сообщение: «Встреча назначена на май»?
22. Какое количество информации несет сообщение о том, что встреча назначена на 20 число?
23. В ящике лежат перчатки (черные и белые). Среди них – 2 пары черных. Сообщение о том, что из ящика достали пару черных перчаток, несет 4 бита информации. Сколько пар белых перчаток было в ящике?
24. Для ремонта школы использовали белую, синюю и коричневую краски. Израсходовали одинаковое количество банок белой и синей краски. Сообщение о том, что закончилась банка белой краски, несет 2 бита информации. Синей краски израсходовали 8 банок. Сколько банок коричневой краски израсходовали на ремонт школы?
25. На остановке останавливаются троллейбусы с разными номерами. Сообщение о том, что к остановке подошел троллейбус с номеров N1 несет 4 бита информации. Вероятность появления на остановке троллейбуса с номером N2  в два раза меньше, чем вероятность появления троллейбуса с номером N1. сколько информации несет сообщение о появлении на остановке троллейбуса с номером  N2?

Главная страница

Подписаться на: Сообщения (Atom)

4. Расчет вероятностей: риск

Жизнь полна неопределенности.

Иногда невозможно сказать, что произойдет через минуту. Но некоторые события происходят с большей вероятностью, чем другие, и именно здесь вступает в действие теория вероятности . Вероятность позволяет вам предсказывать будущее путем оценки возможных исходов, а знание того, что может произойти, помогает вам принимать обоснованные решения . В этой главе вы узнаете больше о вероятности и научитесь управлять будущим!

Казино Fat Dan’s — самое популярное казино в округе. Предлагаются всевозможные игры, от рулетки до игровых автоматов, от покера до блэкджека.

Так уж случилось, что сегодня твой счастливый день. Head First Labs предоставила вам целую стойку фишек, которые вы можете потратить в Fat Dan’s, и вы можете оставить себе любой выигрыш. Хотите попробовать? Продолжайте — вы знаете, что хотите.

У рулетки много активности, и вот-вот начнется еще одна игра. Давай посмотрим, как тебе повезло.

Вы наверняка видели, как люди играют в рулетку в кино, даже если сами никогда не пробовали играть. Крупье крутит колесо рулетки, затем вращает шарик в противоположном направлении, а вы делаете ставки на то, куда, по вашему мнению, приземлится шарик.

Колесо рулетки, используемое в казино Fat Dan’s, имеет 38 карманов, в которые может упасть шарик. Основные карманы пронумерованы от 1 до 36, и каждый карман окрашен в красный или черный цвет. Есть два дополнительных кармана с номерами 0 и 00. Оба эти кармана зеленого цвета.

В рулетке можно делать любые ставки. Например, вы можете сделать ставку на определенное число, независимо от того, четное оно или нечетное, или на цвет кармана. Вы узнаете больше о других ставках, когда начнете играть. Еще одна вещь, которую следует помнить: если мяч приземлится на зеленую лузу, вы проиграете.

Доски для рулетки облегчают отслеживание того, какие числа и цвета сочетаются друг с другом.

В этой главе вы будете делать много ставок в рулетке. Вот удобная доска для рулетки, которую вы можете вырезать и оставить себе. Вы можете использовать его для расчета вероятностей в этой главе.

Примечание

Будьте осторожны с этими ножницами.

Вы вырезали свою доску для рулетки? Игра только начинается. Как вы думаете, куда приземлится мяч? Выберите номер на доске для рулетки, и мы сделаем ставку.

Правильно, прежде чем делать какие-либо ставки, имеет смысл посмотреть, насколько велика вероятность того, что вы выиграете.

Возможно, некоторые ставки более вероятны, чем другие. Похоже, нам нужно посмотреть на некоторые вероятности…

Сила мозга

О чем нужно подумать, прежде чем делать ставки в рулетке? Если бы у вас был выбор, какую ставку вы бы сделали? Почему?

Были ли вы когда-нибудь в ситуации, когда вы задавались вопросом: «Каковы шансы, что или произойдут?» Возможно, друг позвонил вам именно в тот момент, о котором вы думали? их, или, может быть, вы выиграли какую-то лотерею или лотерею.

Вероятность — это способ измерения вероятности того, что что-то произойдет. Вы можете использовать его, чтобы указать, насколько вероятно событие (вероятность того, что вы ляжете спать где-нибудь на этой неделе), или насколько маловероятно (вероятность того, что койот попытается ударить вас наковальней, пока вы отдыхаете). прогулка по пустыне). Говоря статистикой, событие — это любое событие, с которым связана вероятность, другими словами, событие — это любой результат, о котором можно сказать, насколько вероятно, что оно произойдет.

Вероятность измеряется по шкале от 0 до 1. Если событие невозможно, его вероятность равна 0. Если это абсолютная уверенность, то вероятность равна 1. В большинстве случаев вы… будем иметь дело с вероятностями где-то посередине.

Вот несколько примеров по шкале вероятности.

Статистика естественного движения населения: событие

Исход или событие, которому присвоена вероятность

Вы видите, как вероятность связана с рулеткой?

Если вы знаете, какова вероятность того, что шарик приземлится на определенное число или цвет, у вас есть способ определить, следует ли вам делать конкретную ставку. Это полезное знание, если вы хотите выиграть в рулетку.

Давайте подробнее рассмотрим, как мы рассчитали эту вероятность.

Вот все возможные исходы вращения колеса рулетки. На самом деле нас интересует выигрыш по пари, то есть попадание шарика на 7.

Чтобы найти вероятность выигрыша, мы берем количество способов выиграть пари и делим на количество Возможные результаты:

Мы можем записать это и в более общем виде. Вероятность любого события A:

S известна как пространство возможностей или пространство выборки. Это сокращенный способ обозначить все возможные исходы. Все возможные события являются подмножествами S.

Вероятности могут быстро усложниться, поэтому часто очень полезно иметь какой-то способ их визуализации. Один из способов сделать это — нарисовать прямоугольник, представляющий пространство возможностей S , а затем нарисовать круги для каждого соответствующего события. Такая диаграмма известна как диаграмма Венна. Вот диаграмма Венна для нашей задачи с рулеткой, где — это событие получения 7.

Очень часто сами числа не показаны на диаграмме Венна. Вместо чисел у вас есть возможность использовать фактические вероятности каждого события на диаграмме. Все зависит от того, какая информация вам нужна, чтобы помочь вам решить проблему.

Существует сокращенный способ обозначения того, что событие А не происходит: A ^I . ^I известно как дополнительное событие к A.

Существует хитрый способ вычисления P(A ^I ). ^I охватывает все возможности, которых нет в событии A, поэтому между ними A и A ^I должны охватывать все возможности. Если что-то находится в A, оно не может быть в A ^I , а если что-то не в A, оно должно быть в A ^I . Это означает, что если вы сложите P(A) и P(A ^I ) вместе, вы получите 1. Другими словами, есть 100% вероятность того, что что-то будет либо в A, либо в A ^I . Это дает нам

P(A) + P(A ^I ) = 1

или

P(A ^I ) = 1 P(A)

Игра в рулетку вот-вот начнется.

Посмотрите события на предыдущей странице. Мы делаем ставку на то, что произойдет с наибольшей вероятностью, а именно на то, что шарик попадет в черную лузу.

О боже! Несмотря на то, что наша наиболее вероятная вероятность заключалась в том, что мяч приземлится в черную лузу, на самом деле он приземлился в зеленую лузу 0. Вы теряете часть своих фишек.

Вероятности — это только указания на то, насколько вероятны события; они не являются гарантиями.

Важно помнить, что вероятность указывает только на долгосрочный тренд. Если бы вы играли в рулетку тысячи раз, вы бы ожидали, что шарик попадет в черную лузу за 18/38 вращений, примерно в 47 % случаев, и в зеленую лузу через 2/38 вращений, или 5 % времени. . Даже если вы ожидаете, что мяч будет приземляться в зеленую лузу относительно редко, это не значит, что этого не может произойти.

Каким бы маловероятным ни было событие, если оно не невозможно, оно все равно может произойти.

Давайте посмотрим на вероятность события, которое должно произойти с большей вероятностью. Вместо того, чтобы делать ставку на то, что мяч попадет в черную лузу, давайте поспорим, что мяч попадет в черную или красную лузу. Чтобы вычислить вероятность, все, что нам нужно сделать, это посчитать, сколько карманов красные или черные, а затем разделить на количество карманов. Звучит достаточно легко?

Мы можем использовать уже известные нам вероятности, чтобы вычислить ту, которую мы не знаем.

Взгляните на свою рулетку. Есть только три цвета, на которые может приземлиться мяч: красный, черный или зеленый. Поскольку мы уже выяснили, что такое P(Green), мы можем использовать это значение, чтобы найти нашу вероятность, не считая всех этих черных и красных луз.

Есть еще один способ вычислить такую ​​вероятность. Если мы знаем P(черный) и P(красный), мы можем найти вероятность получения черного или красного, сложив эти две вероятности вместе. Давайте посмотрим.

В этом случае сложение вероятностей дает точно такой же результат, как подсчет всех красных или черных луз и деление на 38.

Статистика естественного движения населения: вероятность

Чтобы найти вероятность события A, используйте

A ^I — дополнительное событие к A. Это вероятность того, что событие A не произойдет.

P(A ^I ) = 1 P(A)

На этот раз шарик попал в красную лузу под номером 7, так что вы выиграли несколько фишек.

Теперь, когда вы научились вычислять вероятности, давайте попробуем кое-что еще. Какова вероятность того, что шар приземлится на черную или четную лузу?

Иногда можно сложить вероятности, но это работает не во всех случаях.

Возможно, мы не сможем рассчитывать на то, что сможем выполнить этот расчет вероятности точно так же, как предыдущий. Попробуйте выполнить упражнение на следующей странице и посмотрите, что получится.

Когда мы рассчитывали вероятность попадания мяча в черную или красную лузу, мы имели дело с двумя отдельными событиями: попадание мяча в черную лузу и попадание мяча в красную лузу. Эти два события взаимоисключающие, потому что шарик не может попасть в лузу, которая одновременно и черная, и красная.

Если два события являются взаимоисключающими, может произойти только одно из них.

Что насчет черных и даже событий? На этот раз события не исключают друг друга. Вполне возможно, что мяч упадет в лузу, которая одновременно является черной и четной . Два события пересекаются.

Если два события пересекаются, возможно, они могут произойти одновременно.

Сила мозга

Как вы думаете, какое влияние это пересечение могло оказать на вероятность?

Вычисление вероятности выпадения черного или даже не удалось, потому что мы дважды включили черное и четные лузы. Вот что произошло.

Прежде всего, мы нашли вероятность выпадения черного кармана и вероятность выпадения четного числа.

Когда мы сложили две вероятности вместе, мы дважды посчитали вероятность получить черную и четную лузу.

Чтобы получить правильный ответ, нам нужно вычесть вероятность получения как черного, так и четного. Это дает нам

P(черный или четный) = P(черный) + P(четный) — P(черный и четный)

Теперь мы можем подставить значения, которые мы только что вычислили, чтобы найти P(черный или четный):

P(черный или четный) = 18/38 + 18/38 ‒ 10/38 = 26/38 = 0,684

Существует более общий способ записи этого числа с использованием математических сокращений.

Прежде всего, мы можем использовать обозначение A → B для обозначения пересечения между A и B. Вы можете думать об этом символе как о значении «и». Он принимает общие элементы событий.

А — В, с другой стороны, означает союз А и В. Он включает в себя все элементы А, а также элементы В. Вы можете думать об этом как о значении «или».

Если A ª B = 1, то A и B называются исчерпывающими. Между ними они составляют все S. Они исчерпывают все возможности.

На самом деле это не так уж и отличается.

Взаимоисключающие события не имеют общих элементов друг с другом. Если у вас есть два взаимоисключающих события, вероятность получения A и B на самом деле равна 0, поэтому P(A → B) = 0. Давайте вернемся к нашему примеру с черным или красным. В этой ставке получение красного кармана на колесе рулетки и получение черного кармана являются взаимоисключающими событиями, поскольку карман не может быть одновременно красным и черным. Это означает, что P(черный → красный) = 0, так что часть уравнения просто исчезает.

Смотри!

Есть разница между исключительным и исчерпывающим.

Если события A и B исключающие, то

P(A → B) = 0

Если события A и B исчерпывающие, то B) = 1

Статистика естественного движения населения: A или B

Чтобы найти вероятность события A или B, используйте

P(A ≈ B) = P(A) + P(B) ✓ P(A ✓ B)

— означает ИЛИ

— означает И

Мы знаем, что вероятность того, что шарик приземлится на черное или четное, равна 0,684, но, к сожалению, шарик приземлился на 23, что является красным и странный.

Несмотря на то, что шансы были в нашу пользу, нам не повезло с результатами за столом рулетки. Крупье решает сжалиться над нами и предлагает немного инсайдерской информации. После того, как она покрутит рулетку, она даст нам подсказку о том, где приземлился шарик, и мы вычислим вероятность на основе того, что она нам скажет.

Должны ли мы принять эту ставку?

Как вероятность того, что мяч приземлится в черную лузу, зависит от нашей последней ставки на то, что шарик приземлится на черное или четное. Давайте разбираться.

Крупье говорит, что шар попал в черную лузу. Какова вероятность того, что лузы тоже четные?

Это немного другая задача

Мы не хотим найти вероятность того, что из всех возможных карманов будет одновременно черный и четный карман. Вместо этого мы хотим найти вероятность того, что луз четный, учитывая, что мы уже знаем, что он черный.

Другими словами, мы хотим узнать, сколько карманов четных из всех черных. Из 18 черных луз 10 четные, так что

Оказывается, даже с некоторой инсайдерской информацией наши шансы на самом деле ниже, чем раньше. Вероятность четного черного на самом деле меньше, чем вероятность черного или четного.

Однако вероятность 0,556 все же лучше, чем вероятность 50%, так что это все еще довольно хорошая ставка. Давайте пойдем на это.

Итак, как мы можем обобщить такого рода проблемы? Прежде всего, нам нужны дополнительные обозначения для представления условных вероятностей, которые измеряют вероятность появления одного события по отношению к другому.

Если мы хотим выразить вероятность того, что одно событие произойдет при условии, что другое уже произошло, мы используем символ «|» для обозначения «задано». Вместо того, чтобы говорить «вероятность событие A происходит при данном событии B, — мы можем сократить его до

P(A | B)

Примечание

Вероятность того, что A дает нам знать, что B произошло.

Теперь нам нужен общий способ вычисления P(A | B). Что нас интересует, так это количество исходов, в которых встречаются и A, и B, деленное на все исходы B. Глядя на диаграмму Венна, получаем:

Мы можем переписать это уравнение, чтобы найти способ нахождения P(A → B)

P(A → B) = P(A | B) → P(B)

Это не так. не заканчивается на этом. Другой способ записи P(A → B) – это P(B → A). Это означает, что мы можем переписать формулу как

P(B → A) = P(B | A) → P(A)

Другими словами, просто поменяйте местами A и B.

Диаграммы Венна — не всегда лучший способ визуализации условной вероятности.

Не волнуйтесь, вы можете использовать другой тип диаграммы — дерево вероятностей.

Не всегда легко визуализировать условные вероятности с помощью диаграмм Венна, но есть еще один тип диаграмм, которые действительно пригодятся в этой ситуации, — дерево вероятностей. Вот дерево вероятностей для нашей задачи с колесом рулетки, показывающее вероятности получения разноцветных и нечетных или четных ячеек.

Первый набор ветвей показывает вероятность каждого исхода, поэтому вероятность выпадения черного цвета составляет 18/38, или 0,474. Второй набор ветвей показывает вероятность исходов с учетом исхода ветки он связан с . Вероятность получить нечетный карман, если мы знаем, что он черный, составляет 8/18, или 0,444.

Деревья вероятностей не только помогают визуализировать вероятности; они также могут помочь вам вычислить их.

Давайте в общих чертах посмотрим, как это можно сделать. Вот еще одно дерево вероятностей, на этот раз с другим количеством ветвей. Он показывает два уровня событий: A и A ^I и B и B ^I . А ^I относится ко всем возможностям, не охватываемым A, а B ^I относится ко всем возможностям, не охватываемым B.

Вы можете найти вероятности пересечений, перемножая вероятности связанных ветвей. В качестве примера предположим, что вы хотите найти P(A → B). Вы можете найти это, перемножив P(B) и P(A | B) вместе. Другими словами, вы умножаете вероятность на первой ветви уровня B на вероятность на второй ветви уровня A.

Использование деревьев вероятностей дает те же результаты, что и ранее, и вам решать, будете вы их использовать или нет. На рисование деревьев вероятностей может уйти много времени, но они позволяют визуализировать условные вероятности.

Основные статистические данные: условия

Вы сделали ставку на то, что мяч попадет в четную лузу, поскольку нам сказали, что он черный. К сожалению, шарик попал в лузу 17, так что вы теряете еще несколько фишек.

Может быть, мы сможем отыграть немного фишек, сделав еще одну ставку. На этот раз крупье говорит, что мяч попал в четную лузу. Какова вероятность того, что карман тоже черный?

Примечание

Это ставка, противоположная предыдущей.

Мы можем повторно использовать расчеты вероятностей, которые мы уже сделали.

Наша предыдущая задача состояла в том, чтобы вычислить P(Четное | Черное), и мы можем использовать вероятности, которые мы нашли, решая эту задачу, чтобы вычислить P(Черное | Четное). Вот дерево вероятностей, которое мы использовали ранее:

Итак, как сделать и найти P(черное | четное)? Есть еще способ вычислить это, используя уже имеющиеся у нас вероятности, даже если это не сразу очевидно из дерева вероятностей. Все, что нам нужно сделать, это посмотреть на вероятности, которые у нас уже есть, и использовать их, чтобы каким-то образом рассчитать вероятности, которых мы еще не знаем.

Давайте начнем с общей вероятности, которую нам нужно найти, P(черный | четный).

Используя формулу для нахождения условных вероятностей, мы имеем

Если мы сможем определить, каковы вероятности P(черные ≈ четные) и P(четные), мы сможем использовать их в формуле для рассчитать P (черный | четный). Все, что нам нужно, — это какой-то механизм для нахождения этих вероятностей.

Звучит сложно? Не беспокойтесь, мы расскажем, как это сделать.

Используйте имеющиеся у вас вероятности, чтобы вычислить нужные вам вероятности

Давайте начнем с первой части формулы, P(черные — четные).

Мы хотим найти вероятность P(черный | четный). Мы можем сделать это, оценив

Сила мозга

Еще раз взглянем на дерево вероятностей в Итак, к чему это нас приведет?. Как вы думаете, как мы можем использовать его, чтобы найти P (четное)?

Следующим шагом является определение вероятности попадания шара в четную лузу, P(Even). Мы можем найти это, рассмотрев все способы, которыми это могло бы произойти.

Шарик может упасть в четную лузу, приземлившись либо в четную и черную лузу, либо в четную и красную лузу. Это все возможные способы попадания мяча в четную лузу.

Это означает, что мы находим P(Четный) путем сложения P(Черный-Четный) и P(Красный-Четный). Другими словами, мы добавляем вероятность того, что карман будет и черным, и четным, к вероятности того, что он будет и красным, и четным. Соответствующие ветви выделены на дереве вероятностей.

Вы помните нашу первоначальную задачу? Мы хотели найти P(черное | четное), где

Объединение этих значений означает, что мы можем вычислить P(черное | четное), используя вероятности из дерева вероятностей

Это означает, что теперь у нас есть способ найти новых условных вероятностей. с использованием вероятностей, которые мы уже знаем, — то, что может помочь с более сложными вероятностными задачами.

Давайте посмотрим, как это работает в целом.

Представьте, что у вас есть дерево вероятностей, показывающее события A и B, подобные этому, и предположим, что вы знаете вероятность каждой из ветвей.

Теперь представьте, что вы хотите найти P(A | B), и информация, показанная на ветвях выше, — это вся информация, которая у вас есть. Как вы можете использовать имеющиеся у вас вероятности для расчета P(A | B)?

Мы можем начать с формулы, которая у нас была раньше:

Теперь мы можем найти P(A → B), используя вероятности, которые у нас есть на дереве вероятностей. Другими словами, мы можем вычислить P(A → B), используя

P(A → B) = P(A) → P(B | A)

. Но как найти P(B) ?

Сила мозга

Внимательно посмотрите на дерево вероятностей. Как бы вы использовали его, чтобы найти P(B)?

Чтобы найти P(B), мы используем тот же процесс, который мы использовали для нахождения P(Even) ранее; нам нужно сложить вместе вероятности всех различных способов, которыми может произойти желаемое нами событие.

Даже B может произойти двумя способами: либо с событием A, либо без него. Это означает, что мы можем найти P(B), используя:

P(B) = P(A → B) + P(A ^I → B)

Примечание 9.0031

Сложите оба пересечения, чтобы получить P(B).

Мы можем переписать это в терминах вероятностей, которые мы уже знаем из дерева вероятностей. Это означает, что мы можем использовать:

P(A → B) = P(A) × P(B | A)

P(A ^I → B) = P(A ^I ) … P(B | A ^I )

Это дает нам:

P(B) = P(A) … P(B | A) + P(A ^I ) … P( B | A ^I )

Этот закон иногда называют законом полной вероятности, так как он позволяет найти общую вероятность конкретного события на основе условных вероятностей.

Теперь, когда у нас есть выражения для P(A → B) и P(B), мы можем сложить их вместе, чтобы получить выражение для P(A | B).

Мы начали с того, что хотели найти P(A | B) на основе вероятностей, которые мы уже знаем из дерева вероятностей. Мы уже знаем P(A), а также знаем P(B | A) и P(B | A ^I ). Что нам нужно, так это общее выражение для нахождения условных вероятностей, которые являются обратными того, что мы уже знаем, другими словами P(A | B).

Мы начали с:

Relax

Теорема Байеса – один из самых сложных аспектов теории вероятности.

Не беспокойтесь, если это покажется вам сложным — это настолько сложно, насколько это возможно. И хотя формула сложна, визуализация проблемы может помочь.

Это называется теоремой Байеса. Это дает вам средство нахождения обратных условных вероятностей, что очень полезно, если вы заранее не знаете всех вероятностей.

Статистика естественного движения населения: закон полной вероятности

Если у вас есть два события A и B, то

Закон полной вероятности является знаменателем теоремы Байеса.

Статистика естественного движения населения: теорема Байеса

Если у вас есть n взаимоисключающих и исчерпывающих событий, от A ¹ до A ⁿ , и B является другим событием, то

Поздравляем, на этот раз мяч приземлился на 10 , карман одновременно черный и ровный. Вы отыграли несколько фишек.

Перед тем, как вы покинете стол с рулеткой, крупье предлагает вам отличную цену за последнюю ставку, тройную или ничего. Если вы сделаете ставку на то, что шарик два раза подряд попадет в черную лузу, вы можете отыграть все свои фишки.

Вот дерево вероятностей. Обратите внимание, что вероятности попадания в две черные лузы подряд немного отличаются от тех, что были в нашем дереве вероятностей в «Неудача!», где мы пытались вычислить вероятность получения четной лузы, зная, что луз был черным. .

Вероятность того, что выпадет черное, а за ним еще одно черное, немного отличается от вероятности получить четную лузу, если мы уже знаем, что это черное. Взгляните на уравнение для этой вероятности:

P(четное | черное) = 10/18 = 0,556

Для P(четное | черное) на вероятность получения четной лузы влияет событие получения черного. Мы уже знаем, что мяч попал в черную лузу, поэтому используем это знание для определения вероятности. Смотрим, сколько ровных карманов из всех черных карманов.

Если бы мы не знали, что мяч попал в черную лузу, вероятность была бы другой. Чтобы вычислить P(Even), мы смотрим, сколько карманов четных из всех карманов 9.0005

P(Четное) = 18/38 = 0,474

Примечание

Эти две вероятности различны

P(Четное | Черное) дает результат, отличный от P(Четное). Другими словами, наше знание о том, что карман черный, изменяет вероятность. Эти два события называются зависимыми.

Вообще говоря, события A и B называются зависимыми, если P(A | B) отличается от P(A). Это способ сказать, что вероятности А и В зависят друг от друга.

Сила мозга

Еще раз посмотрите на дерево вероятностей на предыдущей странице. Что вы заметили в наборах ветвей? Зависят ли события получения черного в первой игре и получения черного во второй? Почему?

Не все события зависимы. Иногда события совершенно не зависят друг от друга, и вероятность наступления события остается неизменной независимо от того, произойдет другое событие или нет. В качестве примера взгляните на вероятности P (черное) и P (черное | черное). Что ты заметил?

P(черный) = 18/38 = 0,474

P(черный | черный) = 18/38 = 0,474

Примечание

Эти вероятности одинаковы. События независимы.

Эти две вероятности имеют одинаковое значение. Другими словами, событие получения черной лузы в этой игре не влияет на вероятность получения черной лузы в следующей игре. Эти события независимы.

Независимые события не влияют друг на друга. Они никак не влияют на вероятности друг друга. Если происходит одно событие, вероятность возникновения другого остается точно такой же.

Если события A и B независимы, то вероятность события A не зависит от события B. Другими словами,

P(A | B) = P(A)

для независимых событий.

Мы также можем использовать это как тест на независимость. Если у вас есть два события A и B, где P(A | B) = P(A), то события A и B должны быть независимыми.

Легче вычислить и другие вероятности для независимых событий, например P(A ≈ B).

Мы уже знаем, что

Если A и B независимы, то P(A | B) совпадает с P(A). Это означает, что

или

P(A → B) = P(A) → P(B)

Смотри!

Если A и B взаимоисключающие, они не могут быть независимыми, а если A и B независимые, они не могут быть взаимоисключающими.

Если А и В исключают друг друга, то если происходит событие А, событие В не может. Это означает, что результат А влияет на результат Б, и поэтому они зависимы.

Точно так же, если A и B независимы, они не могут быть взаимоисключающими.

для независимых мероприятий. Другими словами, если два события независимы, то вы можете вычислить вероятность наступления событий А и В, перемножив их индивидуальные вероятности вместе.

Статистика естественного движения населения: независимость

Если два события A и B независимы, то

P(A | B) = P(A)

Если это верно для любых двух событий, то события должны быть независимыми. Также

P(A → B) = P(A) x P(B)

При обоих вращениях колеса шарик приземлился на 30, красный квадрат, и вы удвоили свой выигрыш.

Вы многое узнали о вероятности за столом рулетки Толстяка Дэна, и вы обнаружите, что эти знания пригодятся вам в казино. Жаль, однако, что вы не выиграли достаточно фишек, чтобы забрать их домой.

Примечание

[Примечание от Толстяка Дэна: Это облегчение.]

Помимо шансов на выигрыш, вам также необходимо знать, сколько вы можете выиграть, чтобы решить, стоит ли ставка риска.

Ставки на событие с очень низкой вероятностью могут быть оправданы, если выигрыш достаточно высок, чтобы компенсировать риск. В следующей главе мы рассмотрим, как учесть эти выплаты в наших расчетах вероятности, чтобы помочь нам принимать более обоснованные решения о ставках.

Черно-белая круглая корзина с водорослями, 18 дюймов

1. Дом
2. Хранение и очистка
3. Корзины и ящики
4. Корзины
5. Черно-белая круглая корзина с водорослями, 18 дюймов

Зазор

Зазор

$34,99 Оригинал

$17,49 Сейчас

Оригинал $34,99

ноль ноль

Сейчас 17,49 $

Размеры 17,7 «Д х 10,6» В х 17,7 дюйма Вт Масса 10,4 фунта. Цвет Черный Материал Морская трава Форма Круглый Отделение Главная Организация Место нахождения Корзины СКП 191607503763 Идентификатор местоположения ОРГ29

Имя

Фамилия

Номер телефона

Почтовый индекс

День рождения

Так что мы можем дать вам купон на день рождения!

Адрес электронной почты

Требуется не менее 8 символов.

No related posts.