|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 9 из 19Следующая ⇒ И свойствами многогранников 1. Нарисуйте граф, у которого в каждой вершине сходится: а) два ребра; б) три ребра. 2. Граф имеет 5 вершин, в каждой из них сходится 3 ребра. Сколько у него ребер? 3. Какие из нижеприведенных фигур можно изобразить, не отрывая карандаша от бумаги и не проводя одну и ту же линию дважды (см. рис. 11)? Рис.11 4. Нарисуйте одним росчерком фигуры, изображенные на рисунке 12. Рис. 12 5. Может ли в пирамиде число ребер быть нечетным? 6. Верно ли, что в призме число ребер делится на три? 7. Гранями выпуклого многогранника являются только четырехугольники.
Подготовка к контрольной работе по теме «Способы решения комбинаторных задач» При написании этой работы проверяются следующие умения: — решать комбинаторные задачи методом перебора с использованием таблиц и графов; — решать несложные комбинаторные задачи с использованием правил и формул комбинаторики.
Задания для подготовки к контрольной работе 1. В алфавите племени УАУА есть только две буквы – а и у. Сколько различных трехбуквенных слов можно составить, пользуясь алфавитом этого племени? 2. В магазине продаются полотенца трех видов: белые, голубые и желтые. Из скольких вариантов покупки придется выбрать, если нужны два разных полотенца? 3. В школьной лотерее должно быть всего десять различных выигрышей. Есть ручки, блокноты, записные книжки, альбомы для рисования. 4. Сколько можно составить различных букетов из трех роз, если в продаже есть белые и красные розы? 5. Сколько получится двузначных чисел, если каждую из цифр 0, 1, 2 использовать не один раз? 6. Имеются ручки четырех цветов: красные, синие, зеленые, черные – и два вида записных книжек. Сколько различных наборов из ручки и записной книжки можно составить из этих предметов? 7. От турбазы к горному озеру ведут 4 тропы. Сколькими способами туристы могут отправиться в поход к озеру, если они не хотят спускаться по той же тропе, по которой поднимались? 8. Из четырех ребят надо выделить двоих для дежурства по классу. Сколькими способами это можно сделать? 9. У Портоса есть сапоги со шпорами и без шпор, 4 разные шляпы и 3 разных плаща. Сколько у него вариантов одеться по-разному? 10. 11. Концерт состоит из 5 номеров. Сколько имеется вариантов программы этого концерта? Тема 3. Методика обучения младших школьников решению комбинаторных задач(8 ч) Цель: освоение различных методических подходов к обучению младших школьников решению комбинаторных задач, направленных на развитие их математического мышления и формирование общего умения решать задачи.
Содержание занятий Литература из списка основной литературы: [ 2, 3, 4, 5, 8, 9, 10, 12] Вопросы для обсуждения 1. Требования к методике обучения младших школьников решению комбинаторных задач, вытекающие из возрастных особенностей детей 7–10 лет и задач развития их мышления. 2. Особенности методики обучения решению комбинаторных задач, предлагаемой Е. Е. Белокуровой. 3. Методика обучения решению комбинаторных задач, реализованная в тетрадях для учащихся 1–4 классов «Учимся решать комбинаторные задачи» (авторы Н. 4. Характеристика других подходов к обучению младших школьников решению комбинаторных задач, реализованных в учебниках математики для начальных классов.
Решение методических задач 1. Воспроизведите возможные рассуждения ученика при решении задачи. а) Какие двузначные числа можно составить из цифр 2, 3 и 4, если цифры в записи числа не повторяются? б) Какие трехзначные числа можно составить из цифр 3, 4 и 0, если цифры в записи числа не повторяются? в) Какие трехзначные числа можно составить из цифр 3, 4 и 0, если цифры в записи числа повторяются? 2. Решите задачу и расскажите, как вы будете на примере ее решения обучать детей систематическому перебору. а) Три поросенка хотят построить дом. Они еще не знают, будет ли в нем печка или камин, чем покрыть дом: соломой или черепицей, и какую в доме сделать дверь – дубовую или из простой фанеры. Сколько разных домиков они могут построить? б) От Бабы-Яги до Кощея ведут 3 дороги, а от Кощея до Кикиморы – 4 дороги. 3. Часто перебор комбинаторных соединений происходит с опорой на запись вариантов, в связи с этим возникает проблема обозначения рассматриваемых объектов. На каком этапе обучения младших школьников решению комбинаторных задач можно познакомить их с условными обозначениями рассматриваемых объектов? 4. Фридман Л. М. утверждает, что «задачи в школе решаются не для того, чтобы найти их ответы – они заранее известны. Важно четко представить себе для чего, с какой целью решается та или иная задача, какие знания, умения и навыки должны приобрести учащиеся в результате решения задачи, в том числе и умения поиска способа решения и осуществления самого процесса решения»[4]. На примере решения нижеприведенных комбинаторных задач покажите, как может быть реализовано это высказывание. а) Аня, Боря, Вера и Гена – лучшие лыжники школы. На соревнования надо выбрать из них троих. б) Круг разделили на две части и решили раскрасить их карандашами разных цветов. Сколькими способами можно это сделать, если имеются красный, зеленый и синий карандаши? в) За свои рисунки ученик получил две положительные отметки. Какими они могут быть? г) Имеется материя четырех цветов: красного, синего, белого и зеленого. Надо сшить трехцветный флаг (полосы располагаются горизонтально). Сколько различных флагов можно сшить, если верхняя полоса у каждого флага красная? Сколько всего различных трехцветных флагов можно сшить из материи четырех цветов? д) В соревнованиях участвуют 5 футбольных команд. Каждая команда играет один раз с каждой из остальных команд. Сколько матчей будет сыграно?
Задание для самостоятельной работы по теме 3: составить фрагмент занятия по теме «Обучение младших школьников решению комбинаторных задач». При разработке фрагмента учесть этап обучения.
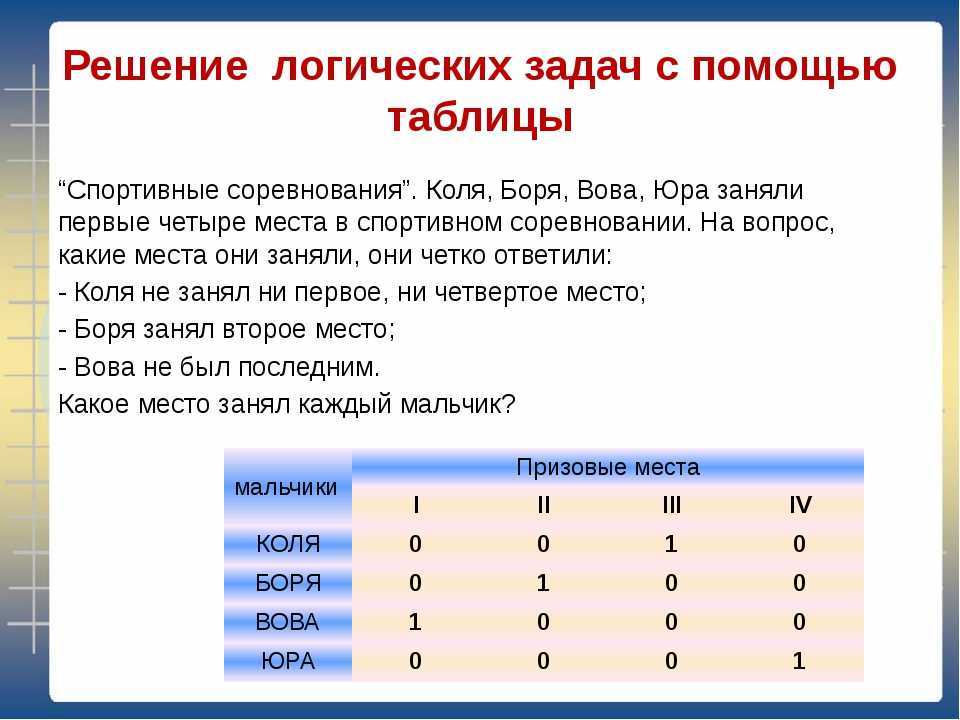
Тема 4. Цель: освоить способы решения основных видов логических задач: на упорядочивание множеств; на установление взаимно-однозначного соответствия между множествами; на доказательство, основанное на выявлении худшего случая и с использованием принципа Дирихле; на планирование действий (взвешивания, переливания, переправы).
Содержание занятий
⇐ Предыдущая45678910111213Следующая ⇒ Читайте также: Как правильно слушать собеседника Типичные ошибки при выполнении бросков в баскетболе Принятие христианства на Руси и его значение Средства массовой информации США |
Последнее изменение этой страницы: 2016-08-12; просмотров: 499; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Страница 47 №153-158 ГДЗ к учебнику «Математика» 5 класс Дорофеев, Шарыгин, Суворова
ГДЗ 1 класс
ГДЗ 10 класс
- Категория: ГДЗ Математика учебник 5 класс Дорофеев, Шарыгин, Суворова
Задание № 153. На поле пять игроков. Начал комбинацию игрок №1, продолжили игроки с другими номерами, а забил игрок № 5. Каждый хоккеист ударил по шайбе только один раз. На рисунке 2. 18 с помощью стрелок изображен один из возможных вариантов комбинации. Изобразите в тетради все другие варианты передачи шайбы между игроками в данной комбинации.
Решение
Ответ: 5 вариантов.
Задание № 154. В школьной лотерее должно быть всего десять различных выигрышей. Есть ручки, блокноты, записные книжки, альбомы для рисования. Можно ли из этих предметов составить десять различных выигрышей, по два разных предмета в каждом?
В школьной лотерее должно быть всего десять различных выигрышей. Есть ручки, блокноты, записные книжки, альбомы для рисования. Можно ли из этих предметов составить десять различных выигрышей, по два разных предмета в каждом?
Решение
Пусть:
ручки − Р;
блокноты − Б;
записные книжки − З;
альбомы − А.
РБ, РЗ, РА;
БЗ, БА;
ЗА.
Получается, что всего можно составить только 6 различных выигрышей по два разных предмета в каждом.
Ответ: десять различных выигрышей, по два разных предмета в каждом составить нельзя.
Задание № 155. Назовите все цифры, которые можно подставить вместо звездочки, чтобы получилось верное неравенство:
а) 7*38 > 7238;
б) 96*4 < 9614;
в) 1596 > 159*.
Решение
а) 7*38 > 7238 , при * = 3, 4, 5, 6, 7, 8, 9.
б) 96*4 < 9614, при * = 0.
в) 1596 > 159*, при * = 0, 1, 2, 3, 4, 5.
Задание № 156. Сравните:
Сравните:
а) 3 км 650 м и 3560 м;
б) 172 см и 17 дм 2 см;
в) 2 см 3 мм и 30 мм;
г) 35 км и 25000000 см.
Решение
а) 3 км 650 м > 3560 м, так как 3 км 560 м = 3 * 1000 + 650 = 3650 м
б) 172 см = 17 дм 2 см, так как 17 дм 2 см = 17 * 10 + 2 = 172 см
в) 2 см 3 мм < 30 мм, так как 2 см 3 мм = 2 * 10 + 3 = 23 мм
г) 35 км < 25000000 см, так как 25000000 см = 25000000 : 100000 = 250 км
Задание № 157. Выполните действия:
а) 524 + 2588;
б) 3000 − 1023;
в) 369 * 205;
г) 680 * 700;
д) 6675 : 5;
е) 10800 : 40.
Решение
Задание № 158. Начертите две окружности, каждую радиусом 3 см, так чтобы они пересекались. Обозначьте точки их пересечения буквами A и B. Начертите окружность, диаметром которого служит отрезок AB.
Ответ 7 гуру
- Назад
- Вперед
умножить наподелить на
Ответы к учебнику за пятый класс «Математика», авторы учебника: Г. В.Дорофеев, Шарыгин, С.Б.Суворова. Мы ни на минуту не сомневаемся, что вы и самостоятельно можете с легкостью выполнить все эти задания, найти ответы и решить все задачи без нашего решебника. Но ГДЗ на 7 гуру поможет вам очень быстро проверить, правильно ли выполнено домашнее задание.
В.Дорофеев, Шарыгин, С.Б.Суворова. Мы ни на минуту не сомневаемся, что вы и самостоятельно можете с легкостью выполнить все эти задания, найти ответы и решить все задачи без нашего решебника. Но ГДЗ на 7 гуру поможет вам очень быстро проверить, правильно ли выполнено домашнее задание.
ПЕРЕЙТИ К СПИСКУ ВСЕХ СТРАНИЦ УЧЕБНИКА МАТЕМАТИКА 5 КЛАСС ДОРОФЕЕВ >>
- ГДЗ
- ГДЗ по математике
- ГДЗ Математика учебник 5 класс Дорофеев, Шарыгин, Суворова
Вам может пригодиться:
Действительно ли лотереи приносят пользу государственным школам? Ответ туманный
В связи с безумием Mega Millions, охватившим страну в последние недели, какую пользу принесли государственные школы? Согласно рекламе лотереи, одним из преимуществ этой формы азартных игр является финансирование государственных школ. Хотя на бумаге это звучит хорошо, сколько пользы лотереи на самом деле приносят системам государственных школ? Оказывается, ответ на этот вопрос может быть гораздо сложнее, чем кажется на первый взгляд.
Хотя на бумаге это звучит хорошо, сколько пользы лотереи на самом деле приносят системам государственных школ? Оказывается, ответ на этот вопрос может быть гораздо сложнее, чем кажется на первый взгляд.
Обзор лотерей
Согласно веб-сайту системы лотерей Джорджии, лотерея — это «азартная игра, в которой игроки имеют равные возможности выиграть призы». Первая американская лотерея была проведена в Джеймстауне в 1612 году, и она составляла половину всего бюджета, необходимого первым поселенцам для строительства своей колонии. Лотереи использовались президентом Джорджем Вашингтоном для поддержки Войны за независимость, а Томас Джефферсон использовал их для финансирования различных общественных проектов.
Лотереи традиционно использовались для поддержки проектов общественных работ, таких как строительство зданий и улиц, а также образовательных и экологических проектов. В современных лотереях используются новейшие технологии, позволяющие игрокам выбирать между мгновенными билетами и онлайн-играми, а также стандартными розыгрышами лотереи. Призы в лотереях также стали более экстравагантными, о чем свидетельствует недавняя игра Mega Millions, которая попала в заголовки газет в таких штатах, как Вирджиния, Калифорния и Северная Каролина.
Призы в лотереях также стали более экстравагантными, о чем свидетельствует недавняя игра Mega Millions, которая попала в заголовки газет в таких штатах, как Вирджиния, Калифорния и Северная Каролина.
Куда идут лотерейные деньги?
Выручка от лотерей может направляться в различные места, установленные государством. Многие штаты хвастаются тем, что доходы от лотерей идут непосредственно в государственный бюджет образования, принося пользу в первую очередь детям, которые там живут. По большей части эти утверждения верны, хотя и могут вводить в заблуждение. Тем не менее, никто не может утверждать, что миллионы и даже миллиарды дополнительных долларов пошли в государственный бюджет образования в результате участия в лотерее.
Уборка в школах Вирджинии
Согласно отчету Washington Post, доход Вирджинии только от игры Mega Millions составил около 22 миллионов долларов. Сообщается, что все эти доходы идут непосредственно в бюджет штата на образование. Розничные продавцы Вирджинии также совершали лотерейные покупки, заработав более 2,4 миллиона долларов на комиссионных от продаж.
Сообщается, что все эти доходы идут непосредственно в бюджет штата на образование. Розничные продавцы Вирджинии также совершали лотерейные покупки, заработав более 2,4 миллиона долларов на комиссионных от продаж.
В отчете Washington Post говорится, что лотерея Вирджинии приносит до 1,2 миллиона долларов в день для системы государственных школ штата. В 2011 году лотерея принесла государственным школам более 444 миллионов долларов, что составляет около восьми процентов государственного финансирования школьной системы в целом. По крайней мере, на первый взгляд кажется, что школы Вирджинии действительно выигрывают в лотереях штата.
Северная Каролина преодолела рецессию благодаря доходам от лотереи
В Северной Каролине большие доходы от лотереи также поступали непосредственно в систему государственных школ. Согласно отчету Fay Observer, только округ Камберленд получил более 79,4 миллиона долларов дохода от государственной лотереи с момента ее запуска шесть лет назад. Образовательная лотерея Северной Каролины может похвастаться тем, что вложила в образование 2,2 миллиарда долларов, что помогло смягчить удар последней экономической рецессии.
Образовательная лотерея Северной Каролины может похвастаться тем, что вложила в образование 2,2 миллиарда долларов, что помогло смягчить удар последней экономической рецессии.
«Они будут в худшем состоянии, чем сейчас», — сказал Fay Observer член палаты представителей Билл Оуэнс (D-Элизабет-Сити). «У нас была бы дыра побольше, чем у нас есть».
Веб-сайт образовательной лотереи Северной Каролины показывает, как были потрачены деньги, начиная от зарплаты учителей и программ дошкольного образования и заканчивая финансовой помощью и финансированием стипендий. Законодательное собрание штата имеет право корректировать проценты распределения каждый год по мере необходимости.
Mega Millions приносит непредвиденную прибыль калифорнийским школам
Калифорния стала еще одним штатом, который добился больших доходов от лотерей, особенно благодаря недавней игре Mega Millions. ABC Local сообщает, что за каждый доллар, потраченный на лотерейные билеты Mega Millions, школы получают 32 цента. По некоторым оценкам, общая сумма выручки может превысить 100 миллионов долларов, что может сэкономить до 1000 преподавательских рабочих мест, которые в настоящее время находятся в стадии сокращения.
По некоторым оценкам, общая сумма выручки может превысить 100 миллионов долларов, что может сэкономить до 1000 преподавательских рабочих мест, которые в настоящее время находятся в стадии сокращения.
«С этим текущим розыгрышем Mega Millions мы будем довольно близки к нашему рекордному максимуму в том, что мы дали школам в любой данный год», — сказал ABC Алекс Траверсо, представитель Калифорнийской лотереи.
Покажите им деньги
Учитывая, что такие штаты могут похвастаться огромными непредвиденными доходами от лотерей, трудно поверить, что некоторые из этих штатов находятся в разгаре серьезного сокращения своих бюджетов на образование. Если лотереи процветают, почему не улучшаются и школы?
По данным Washington Post, одна из самых больших проблем заключается в том, что чем больше лотереи приносят школам, тем больше штаты сокращают бюджеты на образование в ожидании этих непредвиденных доходов. В статье Washington Post говорится: «Вместо того, чтобы использовать деньги в качестве дополнительного финансирования, законодательные органы использовали лотерейные деньги для оплаты бюджета образования и потратили деньги, которые были бы использованы, если бы не было лотерейных денег, на другие вещи».
В статье Washington Post говорится: «Вместо того, чтобы использовать деньги в качестве дополнительного финансирования, законодательные органы использовали лотерейные деньги для оплаты бюджета образования и потратили деньги, которые были бы использованы, если бы не было лотерейных денег, на другие вещи».
В штате Вирджиния деньги, выигранные в результате лотереи, теперь используются законодателями штата для оплаты обычных расходов на образование, а не для финансирования дополнительного образования.
«Это медленное и коварное движение, которое продолжается уже несколько лет, — сказала Washington Post Китти Бойтнотт, президент Образовательной ассоциации Вирджинии. «Это большая уловка, и я не думаю, что жители Вирджинии в целом знают об этом».
Руководители школ Северной Каролины согласны с тем, что лотерейные деньги теперь являются основным продуктом бюджета образования, а не глазурью на торте. Рики Лопес, помощник директора школ округа Камберленд, сказал Fay Observer, что финансирование лотереи не меняет соотношение расходов для улучшения текущих условий, а просто поддерживает статус-кво.
— Лотерейные деньги не прибавили учителей, — сказал Лопес. «Он заменил существующие позиции».
Хотя нет никаких сомнений в том, что доходы от лотереи действительно обеспечивают финансирование государственных школ, неясно, действительно ли школы продвигаются вперед.
Есть вопросы? Свяжитесь с нами на Facebook @publicschoolreview.
Пожалуйста, включите JavaScript для просмотра комментариев Disqus.comments на платформе Disqus
Лотерейные номера будут раскрыты в этом сезоне для учащихся средних и старших классов. — Помощь школы Нью-Йорка
Вопреки моим предположениям ранее в этом году (это случается), я получил окончательное подтверждение от директора по регистрации, что случайных чисел будут выпущены до истечения срока подачи заявок этой осенью. Я полагаю, что больше информации — это хорошая новость, но я чувствую, что эта информация полезна только для тех немногих людей, у которых исключительно хорошие номера, и для немногих людей, у которых исключительно плохие номера. Для большинства остальных это будет неубедительно, потому что у нас нет точных данных, которые могли бы сказать вам, что на самом деле будет означать ваш номер для какой-либо конкретной школы. Будет много паники (не паникуйте) и магического мышления. Будьте бдительны и будьте осмотрительны при составлении списков. И как всегда — РАНГ В ИСТИННОМ ПОРЯДКЕ ПРЕДПОЧТЕНИЯ. Причина, по которой мы не можем делать поспешных выводов, заключается в том, что это огромный процесс с множеством факторов и отсутствием исторических данных о том, что может означать отдельное число. Процесс старшей школы, например, включает около 65 000 учащихся, разбросанных по 5 районам, которые подают заявки на 700 программ средней школы с очень разными критериями приема.
Для большинства остальных это будет неубедительно, потому что у нас нет точных данных, которые могли бы сказать вам, что на самом деле будет означать ваш номер для какой-либо конкретной школы. Будет много паники (не паникуйте) и магического мышления. Будьте бдительны и будьте осмотрительны при составлении списков. И как всегда — РАНГ В ИСТИННОМ ПОРЯДКЕ ПРЕДПОЧТЕНИЯ. Причина, по которой мы не можем делать поспешных выводов, заключается в том, что это огромный процесс с множеством факторов и отсутствием исторических данных о том, что может означать отдельное число. Процесс старшей школы, например, включает около 65 000 учащихся, разбросанных по 5 районам, которые подают заявки на 700 программ средней школы с очень разными критериями приема.
Итак, давайте разберем это.
Есть одна «лотерея». Это случайное «число» является решающим в любых критериях приема. Иногда это единственный критерий для школы, как в средних школах D15 или в старших классах с «открытым» приемом.
 Из отличной статьи Амели Мариан, объясняющей все это, «использование единого лотерейного номера для всех школ — это то, что Министерство образования сделало правильно. Вопреки интуиции, литература показывает, что использование одного и того же числа для всех школ не наносит ущерба учащимся, а вместо этого немного увеличивает их шансы на совпадение с их лучшим выбором. В единой системе счисления учащиеся с хорошим лотерейным номером с большей вероятностью будут распределены в предпочитаемую ими школу, но если школы проводят отдельные лотереи, чтобы получить лучшую школу, учащиеся должны получить хороший лотерейный номер (с меньшими шансами) в своей школе. предпочитаемая школа.
Из отличной статьи Амели Мариан, объясняющей все это, «использование единого лотерейного номера для всех школ — это то, что Министерство образования сделало правильно. Вопреки интуиции, литература показывает, что использование одного и того же числа для всех школ не наносит ущерба учащимся, а вместо этого немного увеличивает их шансы на совпадение с их лучшим выбором. В единой системе счисления учащиеся с хорошим лотерейным номером с большей вероятностью будут распределены в предпочитаемую ими школу, но если школы проводят отдельные лотереи, чтобы получить лучшую школу, учащиеся должны получить хороший лотерейный номер (с меньшими шансами) в своей школе. предпочитаемая школа.Вы сможете найти свой номер в своем профиле МОИ ШКОЛЫ в какой-то момент после открытия сезона приема. Для старшей школы 12 октября и для средней школы 26 октября. Узнайте больше о случайных числах на веб-сайте DoE здесь.
Если в школе есть академический экран (например, оценки), если есть больше людей с одинаковой статистикой (тот же диапазон оценок, поэтому они считаются имеющими равный приоритет), то «лотерея» укажет, как они будут быть заказаны в этом приоритете.

Номер лотереи представляет собой шестнадцатеричное (удивительное слово) «число», содержащее 32 символа. Амели: «Числа сравниваются слева направо в порядке возрастания: от 0 до f (0–9, затем a-f). Это означает, что первого символа достаточно, чтобы дать вам приблизительное представление о том, насколько хорош ваш номер: номер лотереи, начинающийся с 0, находится в первой 1/16 (6,25%), номер, начинающийся с F, в последней 1/. 16-й».
Амели написала еще одну статью с результатами опросов, которые она провела в прошлом году, и ее всегда интересно читать, но результаты ее опроса не помогут в этом году из-за значительного год и в этом году. Что касается старших классов, то в прошлом году группа 1, проверенная Департаментом образования, оценивалась примерно в 60% учащихся этого класса (39,000). По оценкам, более узкий диапазон оценок в этом году включает, возможно, 20% от оценки (13 000). Это значительно повышает шансы учащихся со средними оценками 90 и выше, но это все еще огромная группа детей. Если вы подаете заявление в небольшую школу с соотношением абитуриентов и мест 50:1, в которой приоритет отдается 66% мест для учащихся FRPL (и вы не входите в эту когорту), считаете ли вы, что у вас хорошие шансы только потому, что ваша когорта группы 1 13000, а не 39000? Это не заставляет меня чувствовать себя намного лучше.
Если вы подаете заявление в небольшую школу с соотношением абитуриентов и мест 50:1, в которой приоритет отдается 66% мест для учащихся FRPL (и вы не входите в эту когорту), считаете ли вы, что у вас хорошие шансы только потому, что ваша когорта группы 1 13000, а не 39000? Это не заставляет меня чувствовать себя намного лучше.
Как вы можете себе представить, моя электронная почта была переполнена семьями, которые приходили на мои беседы и консультации, спрашивая, как новая проверенная информация и знания об их лотерейном номере должны изменить то, как они составляют свои списки. Мой совет остается прежним.
Для старшей школы изменение в диапазоне отбираемых оценок делает эту когорту относительно меньше, но когда соотношение приложений и мест настолько велико, на мой взгляд, это все еще дерьмовая съемка.
Если у вас СУПЕР хороший лотерейный номер, вы можете быть немного более амбициозным в своем списке. Если у вас СУПЕР плохое число, вы должны быть более осторожными, но для 80% чисел посередине мой совет остается прежним: составьте разнообразный список, а затем РАСЧИТАЙТЕ ШКОЛЫ В ИСТИННОМ ПОРЯДКЕ ПРЕДПОЧТЕНИЯ.
Для средней школы у вас может быть несколько небольших очень популярных общегородских или районных школ, но не сходите с ума и не заполняйте ими свой список. Удвойте свой выбор районов и займите как можно больше мест. В разных округах доступно разное количество школ, поэтому не каждый сможет найти 12 школ для ранжирования. Если вы находитесь в районе с большим количеством школ, таких как D15, занимайте 12-е место (в основном это районные школы, но, если хотите, также некоторые общегородские и районные школы). DoE не обязан помещать вас в школу из вашего списка, поэтому вы хотите, чтобы они знали ПОЛНЫЙ список школ, которые вы хотели бы рассмотреть. Если вам не повезло, и они не могут включить вас в свой список, они поместят вас в школу в вашем районе проживания. Не составляйте сумасшедший список, который позволяет им выбирать за вас.
Для старшей школы , программы 12 ранга. Есть некоторые достижения, но не слишком много. Имейте школы с разными критериями приема, некоторые просто отбираются по оценкам, некоторые эссе, некоторые прослушивания, если вы можете, возможно, некоторые варианты выбора для обучения, некоторые достойные школы с более низким соотношением приложений и мест.

 Все правила по сольфеджио
Все правила по сольфеджио
 Сколько у него вершин и граней, если число ребер равно 12? Нарисуйте такой многогранник.
Сколько у него вершин и граней, если число ребер равно 12? Нарисуйте такой многогранник.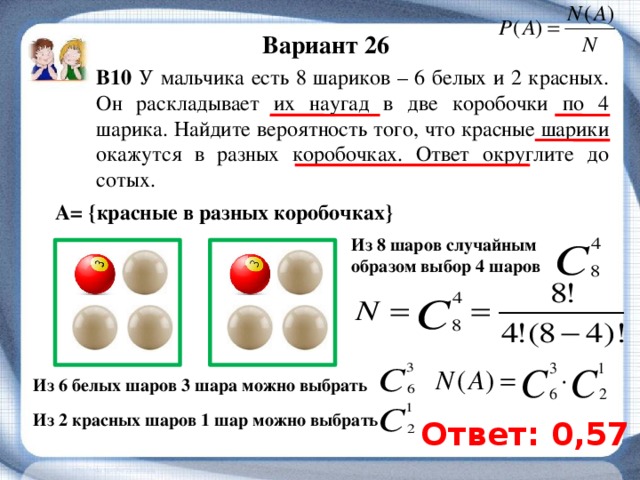
 Сколько существует четных трехзначных чисел?
Сколько существует четных трехзначных чисел? Б. Истомина, Е. П. Виноградова).
Б. Истомина, Е. П. Виноградова). Сколькими способами можно дойти от Бабы-Яги до Кикиморы, если надо зайти к Кощею?
Сколькими способами можно дойти от Бабы-Яги до Кикиморы, если надо зайти к Кощею? Сколькими способами можно это сделать?
Сколькими способами можно это сделать? Способы решения логических задач(12 ч)
Способы решения логических задач(12 ч) su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.004 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.004 с.) Из отличной статьи Амели Мариан, объясняющей все это, «использование единого лотерейного номера для всех школ — это то, что Министерство образования сделало правильно. Вопреки интуиции, литература показывает, что использование одного и того же числа для всех школ не наносит ущерба учащимся, а вместо этого немного увеличивает их шансы на совпадение с их лучшим выбором. В единой системе счисления учащиеся с хорошим лотерейным номером с большей вероятностью будут распределены в предпочитаемую ими школу, но если школы проводят отдельные лотереи, чтобы получить лучшую школу, учащиеся должны получить хороший лотерейный номер (с меньшими шансами) в своей школе. предпочитаемая школа.
Из отличной статьи Амели Мариан, объясняющей все это, «использование единого лотерейного номера для всех школ — это то, что Министерство образования сделало правильно. Вопреки интуиции, литература показывает, что использование одного и того же числа для всех школ не наносит ущерба учащимся, а вместо этого немного увеличивает их шансы на совпадение с их лучшим выбором. В единой системе счисления учащиеся с хорошим лотерейным номером с большей вероятностью будут распределены в предпочитаемую ими школу, но если школы проводят отдельные лотереи, чтобы получить лучшую школу, учащиеся должны получить хороший лотерейный номер (с меньшими шансами) в своей школе. предпочитаемая школа.