В случайном эксперименте симметричную монету бросают дважды найдите решка 1: В случайном эксперименте симметричную монету бросают дважды.найдите вероятность того,что решка выпадет ровно одинраз

В эксперименте симметричную монету бросают дважды. Математика и мы. Ршение задачи с симметричной монетой

Условие

В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет хотя бы один раза.

Решение

1. Данную задачу будем решать по формуле:

Где Р(А) – вероятность события А, m – число благоприятствующих исходов этому событию, n – общее число всевозможных исходов.

1. Применим данную теорию к нашей задаче:

А – событие, когда орел выпадет хотя бы 1 раза;

Р(А) – вероятность того, что орел выпадет хотя 1 раза.

1. Определим m и n:

m — число благоприятствующих этому событию исходов, то есть число исходов, когда орел выпадет 1 раза. В эксперименте бросают монету дважды, которая имеет 2 стороны: решка (Р) и орел (О). Нам необходимо, чтобы выпал орел хотя бы один раз, а это возможно тогда, когда выпадут следующее комбинации: ОР, РО и ОО, то есть получается, что

m = 3, так как возможно 3 варианта выпадения хотя бы 1-го орла;

n – общее число всевозможных исходов, то есть для определения n нам необходимо найти количество всех возможных комбинаций, которые могут выпасть при бросании монеты дважды.

Кидая первый раз монету может выпасть либо решка, либо орел, то есть возможно два варианта. При бросании второй раз монету возможны точно такие же варианты. Получается, что

В теории вероятностей существует группа задач, для решения которых достаточно знать классическое определение вероятности и наглядно представлять предлагаемую ситуацию. Такими задачами является большинство задач с подбрасыванием монеты и задачи с бросанием игрального кубика. Напомним классическое определение вероятности.

Вероятность события А (объективная возможность наступления события в числовом выражении) равна отношению числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов: Р(А)=m/n , где:

• m – число элементарных исходов испытания, благоприятствующих появлению события А;
• n – общее число всех возможных элементарных исходов испытания.

Число возможных элементарных исходов испытания и число благоприятных исходов в рассматриваемых задачах удобно определять перебором всех возможных вариантов (комбинаций) и непосредственным подсчетом.

Из таблицы видим, что число возможных элементарных исходов n=4. Благоприятные исходы события А = {орел выпадает 1 раз} соответствуют варианту №2 и №3 эксперимента, таких вариантов два m=2.
Находим вероятность события Р(А)=m/n=2/4=0,5

Задача 2 . В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел не выпадет ни разу.

Решение . Поскольку монету бросают дважды, то, как и в задаче 1, число возможных элементарных исходов n=4. Благоприятные исходы события А = {орел не выпадет ни разу} соответствуют варианту №4 эксперимента (см. таблицу в задаче 1). Такой вариант один, значит m=1.

Находим вероятность события Р(А)=m/n=1/4=0,25

Задача 3 . В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно 2 раза.

Решение . Возможные варианты трех бросаний монеты (все возможные комбинации орлов и решек) представим в виде таблицы:

Из таблицы видим, что число возможных элементарных исходов n=8.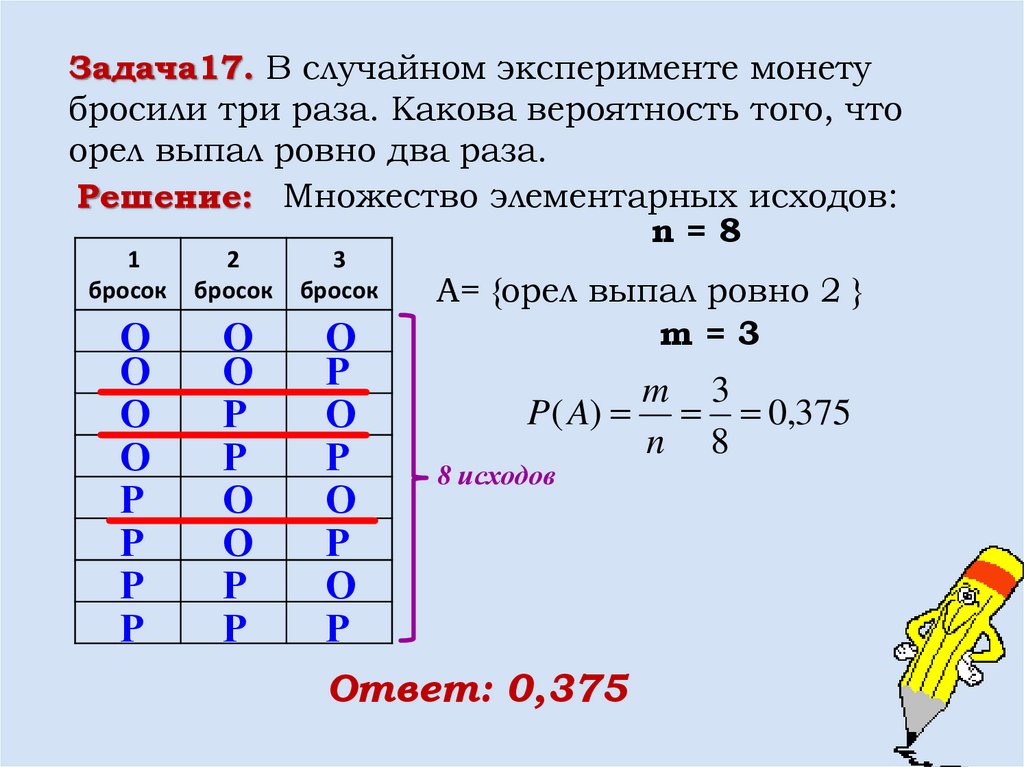 Благоприятные исходы события А = {орел выпадает 2 раза} соответствуют вариантам №5, 6 и 7 эксперимента. Таких вариантов три, значит m=3.
Находим вероятность события Р(А)=m/n=3/8=0,375

Задача 4 . В случайном эксперименте симметричную монету бросают четыре раза. Найдите вероятность того, что орёл выпадет ровно 3 раза.

Решение . Возможные варианты четырех бросаний монеты (все возможные комбинации орлов и решек) представим в виде таблицы:

№ варианта	1-й бросок	2-й бросок	3-й бросок	4-й бросок	№ варианта	1-й бросок	2-й бросок	3-й бросок	4-й бросок
1	Орел	Орел	Орел	Орел	9	Решка	Орел	Решка	Орел
2	Орел	Решка	Решка	Решка	10	Орел	Решка	Орел	Решка
3	Решка	Орел	Решка	Решка	11	Орел	Решка	Решка	Орел
4	Решка	Решка	Орел	Решка	12	Орел	Орел	Орел	Решка
5	Решка	Решка	Решка	Орел	13	Решка	Орел	Орел	Орел
6	Орел	Орел	Решка	Решка	14	Орел	Решка	Орел	Орел
7	Решка	Орел	Орел	Решка	15	Орел	Орел	Решка	Орел
8	Решка	Решка	Орел	Орел	16	Решка	Решка	Решка	Решка

Из таблицы видим, что число возможных элементарных исходов n=16.

Благоприятные исходы события А = {орел выпадет 3 раза} соответствуют вариантам №12, 13, 14 и 15 эксперимента, значит m=4.
Находим вероятность события Р(А)=m/n=4/16=0,25

Определение вероятности в задачах про игральную кость

Задача 5 . Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет более 3 очков.

Решение . При бросании игрального кубика (правильной кости) может выпасть любая из шести его граней, т.е. произойти любое из элементарных событий — выпадение от 1 до 6 точек (очков). Значит число возможных элементарных исходов n=6.
Событие А = {выпало более 3 очков} означает, что выпало 4, 5 или 6 точек (очков). Значит число благоприятных исходов m=3.
Вероятность события Р(А)=m/n=3/6=0,5

Задача 6 . Определите вероятность того, что при бросании игрального кубика выпало число очков, не большее 4. Результат округлите до тысячных.

Решение . При бросании игрального кубика может выпасть любая из шести его граней, т.е. произойти любое из элементарных событий — выпадение от 1 до 6 точек (очков). Значит число возможных элементарных исходов n=6.
Событие А = {выпало не более 4 очков} означает, что выпало 4, 3, 2 или 1 точка (очко). Значит число благоприятных исходов m=4.
Вероятность события Р(А)=m/n=4/6=0,6666…≈0,667

Задача 7 . Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, меньшее 4.

Решение . Так как игральную кость (игральный кубик) бросают дважды, то будем рассуждать следующим образом: если на первом кубике выпало одно очко, то на втором может выпасть 1, 2, 3, 4, 5, 6. Получаем пары (1;1), (1;2), (1;3), (1;4), (1;5), (1;6) и так с каждой гранью. Все случаи представим в виде таблицы из 6-ти строк и 6-ти столбцов:

1; 1	2; 1	3; 1	4; 1	5; 1	6; 1
1; 2	2; 2	3; 2	4; 2	5; 2	6; 2
1; 3	2; 3	3; 3	4; 3	5; 3	6; 3
1; 4	2; 4	3; 4	4; 4	5; 4	6; 4
1; 5	2; 5	3; 5	4; 5	5; 5	6; 5
1; 6	2; 6	3; 6	4; 6	5; 6	6; 6

Благоприятные исходы события А = {оба раза выпало число, меньшее 4} (они выделены жирным) подсчитаем и получим m=9.

Находим вероятность события Р(А)=m/n=9/36=0,25

Задача 8 . Игральную кость бросают дважды. Найдите вероятность того, что наибольшее из двух выпавших чисел равно 5. Ответ округлите до тысячных.

Решение . Все возможные исходы двух бросаний игральной кости представим в таблице:

1; 1	2; 1	3; 1	4; 1	5; 1	6; 1
1; 2	2; 2	3; 2	4; 2	5; 2	6; 2
1; 3	2; 3	3; 3	4; 3	5; 3	6; 3
1; 4	2; 4	3; 4	4; 4	5; 4	6; 4
1; 5	2; 5	3; 5	4; 5	5; 5	6; 5
1; 6	2; 6	3; 6	4; 6	5; 6	6; 6

Из таблицы видим, что число возможных элементарных исходов n=6*6=36.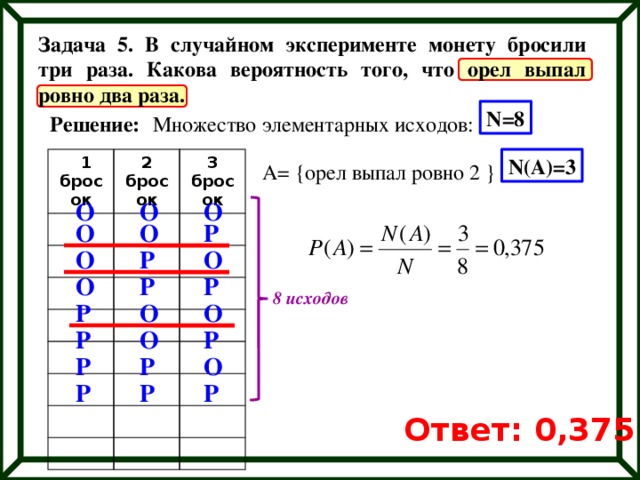
Благоприятные исходы события А = {наибольшее из двух выпавших чисел равно 5} (они выделены жирным) подсчитаем и получим m=8.
Находим вероятность события Р(А)=m/n=8/36=0,2222…≈0,222

Задача 9 . Игральную кость бросают дважды. Найдите вероятность того, что хотя бы раз выпало число, меньшее 4.

Решение . Все возможные исходы двух бросаний игральной кости представим в таблице:

1; 1	2; 1	3; 1	4; 1	5; 1	6; 1
1; 2	2; 2	3; 2	4; 2	5; 2	6; 2
1; 3	2; 3	3; 3	4; 3	5; 3	6; 3
1; 4	2; 4	3; 4	4; 4	5; 4	6; 4
1; 5	2; 5	3; 5	4; 5	5; 5	6; 5
1; 6	2; 6	3; 6	4; 6	5; 6	6; 6

Из таблицы видим, что число возможных элементарных исходов n=6*6=36.
Фраза «хотя бы раз выпало число, меньшее 4» означает «число меньшее 4 выпало один раз или два раза», тогда число благоприятных исходов события А = {хотя бы раз выпало число, меньшее 4} (они выделены жирным) m=27.
Находим вероятность события Р(А)=m/n=27/36=0,75

В задачах по теории вероятностей, которые представлены в ЕГЭ номером №4, кроме , встречаются задачи на подбрасывание монеты и о бросках кубика. Их сегодня мы и разберем.

Задачи о подбрасывании монеты

Задача 1. Симметричную монету бросают дважды. Найдите вероятность того, что решка выпадет ровно один раз.

В таких задачах удобно выписать все возможные исходы, записывая их при помощи букв Р (решка) и О (орел). Так, исход ОР означает, что при первом броске выпал орел, а при втором – решка. В рассматриваемой задаче возможны 4 исхода: РР, РО, ОР, ОО. Благоприятствуют событию «решка выпадет ровно один раз» 2 исхода: РО и ОР. Искомая вероятность равна .

Ответ: 0,5.

Задача 2. Симметричную монету бросают трижды, Найдите вероятность того, что орел выпадет ровно два раза.

Всего возможны 8 исходов: РРР, РРО, РОР, РОО, ОРР, ОРО, ООР, ООО. Благоприятствуют событию «орёл выпадет ровно два раза» 3 исхода: РОО, ОРО, ООР. Искомая вероятность равна .

Ответ: 0,375.

Задача 3. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнет игру с мячом. Команда «Изумруд» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Изумруд» выиграет жребий ровно один раз.

Эта задача аналогична предыдущей. Пусть каждый раз выпадение решки означает выигрыш жребия «Изумрудом» (такое предположение не влияет на вычисление вероятностей). Тогда возможны 8 исходов: РРР, РРО, РОР, РОО, ОРР, ОРО, ООР, ООО. Благоприятствуют событию «решка выпадет ровно один раз» 3 исхода: РОО,ОРО,ООР. Искомая вероятность равна .

Ответ: 0,375.

Задача 4 . Симметричную монету бросают трижды. Найдите вероятность того, что наступит исход РОО (в первый раз выпадает решка, во второй и третий — орёл).

Как и в предыдущих задачах, здесь имеется 8 исходов: РРР, РРО, РОР, РОО, ОРР, ОРО, ООР, ООО. Вероятность наступления исхода РОО равна .

Ответ: 0,125.

Задачи о бросках кубика

Задача 5. Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию «сумма очков равна 8»?

Задача 6 . Одновременно бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 4 очка. Результат округлите до сотых.

Вообще, если бросают игральных костей (кубиков), то имеется равновозможных исходов. Столько же исходов получается, если один и тот же кубик бросают раз подряд.

Событию «в сумме выпало 4» благоприятствуют следующие исходы: 1 – 3, 2 – 2, 3 – 1. Их количество равно 3. Искомая вероятность равна .

Для подсчёта приближённого значения дроби удобно воспользоваться делением уголком. Таким образом, приблизительно равна 0,083…, округлив до сотых имеем 0,08.

Ответ: 0,08

Задача 7 . Одновременно бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 5 очков. Результат округлите до сотых.

Исходом будем считать тройку чисел: очки, выпавшие на первой, второй и третьей игральной кости. Всего имеется равновозможных исходов. Событию «в сумме выпало 5» благоприятствуют следующие исходы: 1–1–3, 1–3–1, 3–1–1, 1–2–2, 2–1–2, 2–2–1. Их количество равно 6. Искомая вероятность равна . Для подсчёта приближённого значения дроби удобно воспользоваться делением уголком. Приблизительно получаем 0,027…, округлив до сотых, имеем 0,03.Источник “Подготовка к ЕГЭ. Математика. Теория вероятностей”. Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова

В качестве предисловия.
Все знают, что монета имеет две стороны — орёл и решку.
Нумизматы считают, что монета имеет три стороны — аверс, реверс и гурт.
И среди тех, и среди других, мало кто знает, что такое симметричная монета. Зато об этом знают (ну, или должны знать:), те, кто готовится сдавать ЕГЭ.

В общем, в этой статье речь пойдёт о необычной монете, которая, к нумизматике никакого отношения не имеет, но, при этом, является самой популярной монетой среди школьников.

Итак.
Симметричная монета — это воображаемая математически идеальная монета без размера, веса, диаметра и пр. Как следствие, гурта у такой монеты тоже нет, то есть вот она-то действительно имеет только две стороны. Главное свойство симметричной монеты в том, что при таких условиях вероятность выпадения орла или решки абсолютно одинакова. А придумали симметричную монету для проведения мысленных экспериментов.
Самая популярная задача с симметричной монетой звучит так — «В случайном эксперименте симметричную монету бросают дважды (трижды, четырежды и т.д.). Требуется определить вероятность того, что одна из сторон выпадет определённое количество раз.

Ршение задачи с симметричной монетой

Понятно, что в результате броска монета упадёт либо орлом, либо решкой. Сколько раз — зависит от того, сколько бросков совершить. Вероятность выпадения орла или решки вычисляется делением количества удовлетворяющих условию исходов на общее количество возможных исходов.

Одн бросок

Здесь всё просто. Выпадет либо орёл, либо решка. Т.е. имеем два возможных исхода, один из которых нас удовлетворяет — 1/2=50%

Дваброска

За два броска могут выпасть:
два орла
две решки
орёл, затем решка
решка, затем орёл
Т.е. возможны всего четыре варианта. Задачи с более, чем одним броском, проще всего решать составлением таблицы возможных вариантов. Для простоты, обозначим орла цифрой «0», а решку цифрой «1». Тогда таблица возможных исходов будет выглядеть так:
00
01
10
11
Если, например, нужно найти вероятность того, что орёл выпадет один раз, требуется просто подсчитать количество подходящих вариантов в таблице — т. е. тех строк, где орёл встречается один раз. Таких строк две. Значит, вероятность выпадения одного орла в двух бросках симметричной монеты равна 2/4=50%
Вероятность того, что орёл в двух бросках выпадет дважды равна 1/4=25%

Три роска

Составляем таблицу вариантов:
000
001
010
011
100
101
110
111
Те, кто знаком с двоичным исчислением, понимают, к чему мы пришли. 🙂 Да, это двоичные цифры от «0» до «7». Так проще не запутаться с вариантами.
Решим задачу из предыдущего пункта — вычислим вероятность того, что орёл выпадет один раз. Строк, где «0» встречается один раз имеется три. Значит, вероятность выпадения одного орла в трёх бросках симметричной монеты равна 3/8=37,5%
Вероятность того, что орёл в трёх бросках выпадет дважды равна 3/8=37,5%, т.е. абсолютно такая же.
Вероятность того, что орёл в трёх бросках выпадет трижды равна 1/8=12,5%.

Четыр броска

Составляем таблицу вариантов:
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
Вероятность того, что орёл выпадет один раз. Строк, где «0» встречается один раз имеется всего три, так же, как и в случае трёх бросков. Но, вариантов уже шестнадцать. Значит, вероятность выпадения одного орла в четырёх бросках симметричной монеты равна 3/16=18,75%
Вероятность того, что орёл в трёх бросках выпадет дважды равна 6/8=75%,.
Вероятность того, что орёл в трёх бросках выпадет трижды равна 4/8=50%.

Итак с увеличением количества бросков, принцип решения задачи совершенно не меняется — только, в соответствующей прогрессии, увеличивается количество вариантов.

Формулировка задачи: В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл (решка) не выпадет ни разу (выпадет ровно/хотя бы 1, 2 раза).

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 10 (Классическое определение вероятности).

Рассмотрим, как решаются подобные задачи на примерах.

Пример задачи 1:

В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу.

ОО ОР РО РР

Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых нет ни одного орла. Такая комбинация всего одна (РР).

P = 1 / 4 = 0.25

Ответ: 0.25

Пример задачи 2:

В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно два раза.

Рассмотрим все возможные комбинации, которые могут выпасть, если монету бросают дважды. Для удобства будем обозначать орла буквой О, а решку – буквой Р:

ОО ОР РО РР

Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых орел выпадает ровно 2 раза. Такая комбинация всего одна (ОО).

P = 1 / 4 = 0.25

Ответ: 0.25

Пример задачи 3:

В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно один раз.

Рассмотрим все возможные комбинации, которые могут выпасть, если монету бросают дважды. Для удобства будем обозначать орла буквой О, а решку – буквой Р:

ОО ОР РО РР

Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых орел выпал ровно 1 раз. Таких комбинаций всего две (ОР и РО).

Ответ: 0.5

Пример задачи 4:

В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет хотя бы один раз.

Рассмотрим все возможные комбинации, которые могут выпасть, если монету бросают дважды. Для удобства будем обозначать орла буквой О, а решку – буквой Р:

ОО ОР РО РР

Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых орел выпадет хотя бы 1 раз. Таких комбинаций всего три (ОО, ОР и РО).

P = 3 / 4 = 0.75

Задание № 3. Начала теории вероятностей. ЕГЭ. Математика. 1

1.  Планиметрия 

2.  Стереометрия 
3.  Начала теории вероятностей 

4.  Теория вероятностей

5.   Простейшие уравнения
6.  Преобразование выражений 
7.  Производная функции 
8.  Практические задачи 
9.  Текствые задачи 
10.  Графики функций 
11.  Исследование функций
12.  Уравнения 
13.  Стереометрия с доказ-вом
14.  Неравенства 
15.  Финансовая математика 
16.  Планиметрия с доказ-вом 
17.  Задачи с параметром 
18.  Задачи на логику 

      БАЗА ЗАДАНИЙ

Задание № 3. Начала теории вероятностей.

1. В среднем из 900 садовых насосов, поступивших в продажу, 27 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

Ответ: 0,97

2. В фирме такси в наличии 50 легковых автомобилей; 27 из них чёрного цвета с жёлтыми надписями на бортах, остальные — жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.

Ответ: 0,46

3. В чемпионате по гимнастике участвуют 70 спортсменок: 25 из США, 17 из Мексики, остальные из Канады. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Канады.

Ответ: 0,4

4. В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 — из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Швеции.

Ответ: 0,36

5. В сборнике билетов по истории всего 50 билетов, в 13 из них встречается вопрос про Александра Второго. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопрос про Александра Второго.

Ответ: 0,74

6. Вероятность того, что новый DVD-проигрыватель в течение года поступит в гарантийный ремонт, равна 0,045. В некотором городе из 1000 проданных DVD-проигрывателей в течение года в гарантийную мастерскую поступила 51 штука. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?

Ответ: 0,006

7. Фабрика выпускает сумки. В среднем 8 сумок из 100 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без дефектов.

Ответ: 0,92

8. Фабрика выпускает сумки. В среднем на 130 качественных сумок приходится 20 сумок, имеющих дефекты. Найдите вероятность того, что выбранная в магазине сумка окажется с дефектом. Результат округлите до сотых.

Ответ: 0,13

9. В некотором городе из 5000 появившихся на свет младенцев 2512 мальчиков. Найдите частоту рождения девочек в этом городе. Результат округлите до тысячных.

Ответ: 0,498

10. В кармане у Миши было четыре конфеты — «Грильяж», «Белочка», «Коровка» и «Ласточка», а также ключи от квартиры. Вынимая ключи, Миша случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Грильяж».

Ответ: 0,25

11. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной?

Ответ: 0,5

12. Из множества натуральный чисел от 10 до 24 выбирают одно число. Какова вероятность того, что оно делится на 5?

Ответ: 0,2

13. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 10, но не дойдя до отметки 1.

Ответ: 0,25

14. На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,35. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Ответ: 0,55

15. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу D.

Ответ: 0,0625
 

16. Вероятность того, что на тестировании по математике учащийся А. верно решит больше 9 задач, равна 0,63. Вероятность того, что А. верно решит больше 8 задач, равна 0,75. Найдите вероятность того, что А. верно решит ровно 9 задач.

Ответ: 0,12

17. Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже 36,8°C, равна 0,94. Найдите вероятность того, что в случайный момент времени у здорового человека температура тела окажется 36,8° C или выше.

Ответ: 0,06

18. Вероятность того, что новый тостер прослужит больше года, равна 0,93. Вероятность того, что он прослужит больше двух лет, равна 0,82. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

Ответ: 0,11

19. При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 66,99 мм, или больше, чем 67,01 мм.

Ответ: 0,035

20. На борту самолёта 12 кресел расположены рядом с запасными выходами и 18 — за перегородками, разделяющими салоны. Все эти места удобны для пассажира высокого роста. Остальные места неудобны. Пассажир В. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру В. достанется удобное место, если всего в самолёте 300 мест.

Ответ: 0,1

21. В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.

Ответ: 0,2

22. В группе туристов 8 человек. С помощью жребия они выбирают шестерых человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдёт в магазин?

Ответ: 0,75

23. Почти одновременно 8 человек, в том числе Андрей, заказали по телефону пиццу, все разных видов. Оператор перепутал 3 и 5 заказы. С какой вероятностью Андрею привезут его пиццу?

Ответ: 0,75

24. В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?

Ответ: 0,25

25. Перед началом первого тура чемпионата по теннису участников разбивают на игровые пары случайным образом с помощью жребия.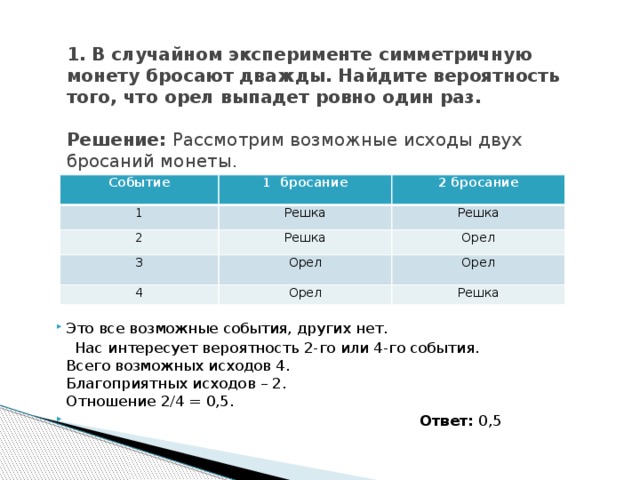 Всего в чемпионате участвует 76 теннисистов, среди которых 7 спортсменов из России, в том числе Анатолий Москвин. Найдите вероятность того, что в первом туре Анатолий Москвин будет играть с каким-либо теннисистом из России.

Ответ: 0,08

Главная

26. Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шахматистов, среди которых 5 спортсменов из России, в том числе Кирилл Черноусов. Найдите вероятность того, что в первом туре Кирилл Черноусов не будет играть с шахматистом из России.

Ответ: 0,84

27. В классе 16 учащихся, среди них два друга — Вадим и Сергей. Учащихся случайным образом разбивают на 4 равные группы. Найдите вероятность того, что Вадим и Сергей окажутся в одной группе.

Ответ: 0,2

28. В классе 21 шестиклассник, среди них два друга — Митя и Петя. Класс случайным образом делят на три группы, по 7 человек в каждой. Найдите вероятность того, что Митя и Петя окажутся в разных группах.

Ответ: 0,7

29. На олимпиаде по русскому языку 350 участников разместили в трёх аудиториях. В первых двух удалось разместить по 140 человек, оставшихся перевели в запасную аудиторию в другом корпусе. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.

Ответ: 0,2

30. Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений — по одному от каждой страны, участвующей в конкурсе. В первый день запланировано 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление исполнителя из России состоится в третий день конкурса?

Ответ:0,225

31. Дима, Марат, Петя, Надя и Света бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет мальчик.

Ответ: 0,6

32. Миша, Олег, Настя и Галя бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должна будет не Галя.

Ответ: 0,75

33. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу.

Ответ: 0,25

35. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно один раз.

Ответ: 0,5

34. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что в первый раз выпадет орёл, во второй решка.

Ответ: 0,25

36. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что количество выпавших орлов меньше 2.

Ответ: 0,75 

37. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что решка выпадет все три раза.

Ответ:  0,125

38. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орлов выпало больше, чем решек.

Ответ: 0,5

39. В случайном эксперименте бросают две игральные кости (кубика). Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.

Ответ: 0,17

40. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 5 или 6.

Ответ:  0,25

41. Игральный кубик бросают 2 раза. С какой вероятностью выпавшие числа будут отличаться на 3? Ответ округлите до сотых.

Ответ: 0,17

42. За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.

Ответ: 0,25

43. За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки не будут сидеть рядом.

Ответ: 0,5

44. На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.

Ответ: 0,33

45. Какова вероятность того, что последние две цифры случайного телефонного номера различны?

Ответ: 0,9

46. Какова вероятность того, что последние две цифры случайного телефонного номера одинаковы?

Ответ: 0,1

Эксперименты с подбрасыванием двух одинаковых монет

Бисерка Коларец

Студенты часто изучают классическое определение вероятности в самом начале процесса развития статистической грамотности. В этом определении говорится, что если шансы всех исходов или событий эксперимента равны, то вероятность конкретного события равна числу благоприятных исходов, деленному на число всех возможных исходов.

Простейшим примером классического вероятностного эксперимента является подбрасывание монеты: кто-то бросает монету и записывает, какой стороной она упадет — орлом (H) или решкой (T). Демонстрационное пространство состоит из двух событий {H, T}. Здесь предполагается, что монета симметрична. По классическому определению вероятности вероятности выпадения орла или решки одинаковы и равны 1/2. Классическая формула вероятности является естественной концепцией, и учащиеся сразу ее усваивают.

Поскольку количество всех возможных исходов в эксперименте с подбрасыванием одной монеты невелико, можно быстро перейти к более сложному эксперименту с подбрасыванием большего количества монет. Рассмотрим опыты с подбрасыванием двух монет. В большинстве книг по теории вероятностей подобные эксперименты приводятся без дополнительных объяснений. Например, в классической книге вероятностей Первый курс теории вероятностей дан следующий пример:

Если эксперимент состоит в подбрасывании двух монет, то выборочное пространство состоит из следующих четырех точек: S = {(H , Н), (Н, Т), (Т, Н), (Т, Т)}

Формулировка «подбрасывание двух монет» предполагает, что при одном подбрасывании выбрасываются две монеты. Так ли уж просты рассуждения в таком эксперименте? Не совсем. Студенты сомневаются в размере выборки, если им скажут, что мы подбрасываем две одинаковые монеты.

Задача

Рассмотрим эксперимент по подбрасыванию двух одинаковых монет за один бросок. Значительный процент студентов придерживается мнения, что возможны только три исхода этого эксперимента. А именно, студенты рассуждают, что можно получить две решки (H, H), две решки (T, T) или одну решку и одну решку (H, T). Ничего странного, поскольку именно это и можно наблюдать. На вопрос, какова вероятность выпадения одного орла и одной решки, учащиеся ответят, что она равна 1/3 (один благоприятный исход из трех возможных), что соответствует классическому определению вероятности. Такое рассуждение можно усилить, поставив следующую троичную задачу:

Рассмотрите следующие эксперименты и для каждого эксперимента запишите все возможные исходы, определите количество исходов и определите вероятность выпадения одного орла и одной решки.

Эксперимент 1: Один раз бросают монету дважды. Обозначим все возможные результаты как упорядоченные пары (-, -), где первая запись обозначает результат первого броска, а вторая — результат второго броска.

Эксперимент 2: За один бросок бросают две монеты разного типа.

Эксперимент 3: За один бросок бросают две одинаковые монеты.

Все три эксперимента были намеренно сформулированы как одна задача, чтобы заставить учащихся подозревать, что их выборочные пространства могут быть разными. Поскольку им были даны инструкции по маркировке результатов, почти всем учащимся удалось распознать четыре возможных результата эксперимента 1. Точно так же учащиеся пришли к выводу, что если существует соглашение о порядке маркировки результатов, то в эксперименте 2 есть четыре возможных результата, также.

Подводя итог, результаты первых двух экспериментов можно записать в виде упорядоченных пар: (H, H), (H, T), (T, H) и (T, T). По классическому определению вероятности студенты пришли к выводу, что вероятность выпадения одного орла и одной решки равна 2/4=1/2 в обоих экспериментах. Далее более 60% учащихся написали, что все три эксперимента имеют четыре исхода и вероятности выпадения одного орла и одной решки равны 1/2. Однако почти для 40% учащихся ответ был таким, как на рис. 19.0005

Рисунок 1: Одно из решений проблемы.

Противостояли две группы студентов с разными мнениями об общем количестве исходов в эксперименте 3. Главный вопрос заключался в том, нужно ли различать эксперименты по подбрасыванию двух разных или одинаковых монет за один бросок. Студентов попросили объяснить, почему, по их мнению, общее количество результатов в эксперименте 3 равно трем или четырем. Они обсудили этот вопрос в небольших группах в духе обучения сверстников, представленного Эриком Мазуром в книге «Обучение сверстников: научить учащихся думать в классе». Мы не вмешивались в обсуждение.

В конце концов, меньшинство убедило большинство изменить свое мнение! Причина заключалась в том, что, поскольку нет способа визуально различить результаты (H, T) и (T, H), можно выделить только три результата.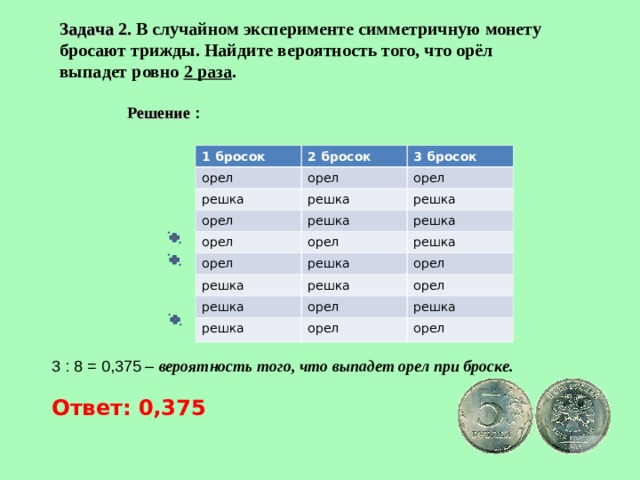 Это исходы H-H, H-T и T-T, и мы можем больше не записывать их как упорядоченные пары.

В эксперименте 3 студенты пришли к выводу, что исходов всего три, и, исходя из классического определения, вероятность выпадения одного орла и одной решки равна 1/3 (один благоприятный из трех возможных исходов). После обсуждения почти все студенты согласились с этим.

Наша цель активно и искренне вовлечь учащихся в проблему достигнута. Студенты взяли на себя ответственность за решение проблемы; пришло время направить их туда, где они должны быть.

Руководство к правильному заключению

Мы не занимались аксиоматическим определением вероятности, поэтому познакомили учащихся с тремя точками зрения на определение вероятности. Помимо классического определения, вероятность возникновения события можно рассматривать как относительное количество раз, которое мы ожидаем, что событие произойдет в большом количестве испытаний. Кроме того, можно говорить о субъективном понятии вероятности как меры веры. В эксперименте с одним подбрасыванием монеты, где есть два возможных исхода и при логическом предположении, что монета симметрична, все три определения совпадают. Субъективная, или эпистемическая, интерпретация вероятности предполагает (точно так же, как и классическая), что орел и решка появляются с одинаковой вероятностью с вероятностью 1/2 каждая. Определение через относительные частоты предполагает повторение эксперимента большое количество раз и нахождение вероятности события как предела результирующего отношения числа повторений события к количеству повторений эксперимента. Если кто-то сомневается в какой-то вероятности, подход относительной частоты — это просто средство для получения правильного ответа.

Студенты пришли к выводу, что существует способ проверить, равна ли вероятность выпадения одного орла и одной решки в двух одинаковых экспериментах с подбрасыванием монеты 1/3. Они экспериментировали с подбрасыванием двух одинаковых монет большое количество раз. Студенты были разделены на пары, и каждая пара считала, сколько раз выпадет один орел и одна решка, подбрасывая две одинаковые монеты 30 раз. Все результаты были объединены для расчета относительной частоты события.

Студенты были удивлены, когда оказалось, что это близко к 1/2, а не к 1/3! Это наблюдение привело к следующему выводу: хотя исходы H-T и T-H нельзя различить, они все равно случаются.

В заключение было обнаружено, что выборочное пространство в эксперименте по подбрасыванию двух одинаковых монет состоит из четырех исходов. Кроме того, вероятность выпадения одного орла и одной решки вдвое превышает вероятность выпадения либо двух орлов, либо двух решек. Мы заметили, что и те, кто был прав, и те, кто ошибался, кажется, убеждены в размере выборочного пространства.

Обсуждение задачи

Подбрасывание двух монет — простейший случайный эксперимент, упоминаемый практически во всех учебниках по статистике. В большинстве учебников предполагается прямое понимание того, что в экспериментах с подбрасыванием двух монет возможны четыре исхода. Авторы не комментируют, идентичны ли две монеты.

Согласно приведенному здесь случаю, учащиеся различают размер области выборки, если говорят, что подбрасывают две разные или две одинаковые монеты. Мы продолжаем сталкиваться с одной и той же проблемой год за годом, поколение за поколением: относительно большой процент студентов придерживался мнения, что в эксперименте с подбрасыванием двух одинаковых монет выборочное пространство состоит всего из трех событий. Даже те, кто думал, что есть четыре возможных исхода, не были достаточно уверены, чтобы настаивать на своем мнении, столкнувшись с другим.

Приведенная выше лекция, которая приводит студентов к правильному выводу о размере выборки, требует времени, которого может не хватать учителю. Было бы лучше, во-первых, убедиться, что нет недопонимания относительно пространства выборки. Есть простой способ сделать это: расскажите о монете, подброшенной два раза. В таких экспериментах результаты могут быть помечены как упорядоченные пары, и у студентов, вероятно, не будет проблем с записью всех четырех. Этот подход также можно найти в некоторых книгах по статистике, например 9.0009 Современное введение в теорию вероятностей и статистику: понимание того, почему и как .

Из нашей педагогической практики известно, что учащиеся легко обобщают и подсчитывают количество всех возможных исходов в эксперименте с подбрасыванием монеты более двух раз. Таким образом, в экспериментах, которые повторяются n раз, общее количество исходов равно 2 ⁿ . Единственная слабость таких экспериментов по сравнению с несколькими идентичными экспериментами с подбрасыванием монеты заключается в том, что если бы они действительно проводились, они заняли бы больше времени. Тем не менее, это небольшая цена, если таковая вообще имеется, поскольку большинство экспериментов, которые мы «выполняем», выполняются в уме (т.

Читатель может возразить против того, чтобы говорить о подбрасывании одной монеты дважды вместо одновременного подбрасывания двух одинаковых монет. Однако размышления о результатах эксперимента с двойным подбрасыванием одной монеты могут привести к лучшему пониманию того, что они такие же, как и в эксперименте с одновременным подбрасыванием двух монет. Действительно, независимо от того, брошены ли две одинаковые монеты одновременно, скорее всего, они не упадут в один и тот же момент. Это оправдывает рассмотрение экспериментов с подбрасыванием одной монеты дважды.

Математика и мы. В случайном эксперименте симметричная монета подбрасывается дважды В случайном эксперименте монета подбрасывается 4 раза

Загадки с подбрасыванием монеты считаются довольно сложными. И перед их решением требуется небольшое пояснение. Вдумайтесь, любая задача по теории вероятностей в итоге сводится к стандартной формуле:

, где p — искомая вероятность, k — количество устраивающих нас событий, n — общее количество возможных событий.

Большинство задач B6 решаются по этой формуле буквально одной строкой — достаточно прочитать условие. Но в случае подбрасывания монет эта формула бесполезна, так как из текста таких задач вообще не понятно, чему равны числа k и n. Вот в чем сложность.

Однако существует как минимум два принципиально разных метода решения:

1. Метод перебора комбинаций представляет собой стандартный алгоритм. Выписываются все комбинации орла и решки, после чего выбираются нужные;
2. Специальная формула вероятности — стандартное определение вероятности, специально переписанное так, чтобы было удобно работать с монетами.

Чтобы решить задачу B6, вам нужно знать оба метода. К сожалению, в школах преподается только первый. Не будем повторять школьных ошибок. Итак, начнем!

Метод комбинированного перебора

Этот метод также известен как «прорывное решение». Состоит из трех шагов:

1. Запишите все возможные комбинации орла и решки. Например: ИЛИ, РО, ОО, РР. Количество таких комбинаций равно n;
2. Среди полученных комбинаций отметим те, которые требуются по условию задачи. Считаем отмеченные комбинации — получаем число k;
3. Осталось найти вероятность: p = k : n .

К сожалению, этот метод работает только для небольшого количества бросков. Потому что с каждым новым броском количество комбинаций удваивается. Например, за 2 монеты вам придется выписать всего 4 комбинации. На 3 монеты их уже 8, а на 4 — 16, и вероятность ошибки приближается к 100%. Посмотрите примеры и сами все поймете:

Задача. В случайном эксперименте симметричную монету подбрасывают 2 раза. Найдите вероятность выпадения одинакового количества орлов и решек.

Итак, монета подбрасывается дважды. Запишем все возможные комбинации (О — решка, Р — решка):

Всего n = 4 варианта. Теперь выпишем те варианты, которые подходят по условию задачи:

Таких вариантов было k = 2. Находим вероятность:

Задача. Монету подбрасывают четыре раза. Найдите вероятность того, что никогда не выпадет решка.

Снова выписываем все возможные комбинации орла и решки:

OOOO OOOP OOPO OOPP OPOO OPOP OPPO OPPP
POOO POOP POPO POPP PPOO PPOP PPPO PPPP

Всего имеется n = 16 вариантов. Вроде ничего не забыл. Из этих вариантов нас устраивает только комбинация «ООООО», в которой вообще нет решек. Следовательно, k = 1. Осталось найти вероятность:

Как видите, в прошлой задаче мне пришлось выписать 16 вариантов. Вы уверены, что сможете написать их без единой ошибки? Лично я не уверен. Итак, давайте рассмотрим второе решение.

Специальная формула вероятности

Итак, у задач с монетами есть своя формула вероятности. Это настолько просто и важно, что я решил изложить это в виде теоремы. Взгляните:

Теорема. Пусть монета подброшена n раз. Тогда вероятность того, что орел выпадет ровно k раз, можно найти по формуле:

Где C n k — количество комбинаций n элементов по k , которое рассчитывается по формуле:

Таким образом, для решения задачи с монетами нужны два числа: количество подбрасываний и количество выпадений орла. Чаще всего эти цифры даются прямо в тексте задачи. При этом неважно, что именно считать: решку или орла. Ответ будет таким же.

На первый взгляд теорема кажется слишком громоздкой. Но стоит немного потренироваться — и к описанному выше стандартному алгоритму возвращаться уже не хочется.

Задача. Монету подбрасывают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза.

По условию задачи всего было n = 4 бросков. Необходимое количество головок: k = 3. Подставляем n и k в формулу:

Задача. Монета подбрасывается три раза. Найдите вероятность того, что никогда не выпадет решка.

Снова выписываем числа n и k. Так как монета подбрасывается 3 раза, то n = 3. А так как решки быть не должно, то k = 0. Осталось подставить числа n и k в формулу:

Напомню, что 0! = 1 по определению. Поэтому C 3 0 = 1,

Задача. В случайном эксперименте симметричную монету подбрасывают 4 раза. Найдите вероятность того, что орел выпадет чаще, чем решка.

Чтобы орла было больше, чем решки, они должны выпасть либо 3 раза (тогда будет 1 решка), либо 4 (тогда решки не будет вообще). Найдем вероятность каждого из этих событий.

Пусть p 1 — вероятность выпадения орла 3 раза. Тогда n = 4, k = 3. Имеем:

Теперь находим p 2 — вероятность того, что решка выпадет все 4 раза. В этом случае n = 4, k = 4. Имеем:

Чтобы получить ответ, осталось сложить вероятности p 1 и p 2 . Помните: вы можете добавлять вероятности только для взаимоисключающих событий. Имеем:

р = р 1 + р 2 = 0,25 + 0,0625 = 0,3125

В заданиях по теории вероятностей, которые представлены в ЕГЭ под номером № 4, кроме, есть задания на подбрасывание монеты и на бросок игральной кости. Сегодня мы их разберем.

Проблемы с подбрасыванием монеты

Задание 1. Симметричная монета подбрасывается дважды. Найдите вероятность того, что решка выпадет ровно один раз.

В таких задачах удобно записывать все возможные исходы, записывая их с помощью букв Р (решка) и О (орел). Таким образом, исход ИЛИ означает, что при первом броске выпал орел, а при втором — решка. В рассматриваемой задаче возможны 4 исхода: PP, RO, OR, OO. Благоприятствует событию «решка выпадает ровно один раз» 2 исхода: RO и OR. Искомая вероятность равна .

Ответ: 0,5.

Задание 2. Симметричную монету подбрасывают три раза. Найдите вероятность того, что орел выпадет ровно два раза.

Всего возможно 8 исходов: ПРР, РРО, РОР, РОО, ОРР, ОРО, ООР, ООО. Благоволить к событию «Выпадение орла ровно дважды» 3 исхода: РОО, ОРО, ООР. Искомая вероятность равна .

Ответ: 0,375.

Задание 3. Перед началом футбольного матча судья подбрасывает монету, чтобы определить, какая команда запустит мяч. Команда Emerald играет три матча с разными командами. Найти вероятность того, что в этих играх «Изумруд» ровно один раз выиграет жребий.

Эта задача аналогична предыдущей. Пусть каждый раз выпадение решки означает выигрыш лота «Изумрудом» (такое допущение не влияет на расчет вероятностей). Тогда возможны 8 исходов: ПРР, РРО, РОР, РОО, ОРР, ОРО, ООР, ООО. Есть 3 исхода в пользу события «решка выпадает ровно один раз»: POO, ORO, OOP. Искомая вероятность равна .

Ответ: 0,375.

Задача 4 . Симметричная монета подбрасывается три раза. Найти вероятность того, что выпадет исход РОО (в первый раз выпадет решка, во второй и третий — решка).

Как и в предыдущих заданиях, здесь 8 исходов: ППП, ППО, ПОП, ПОО, ОПП, ОРО, ООП, ООО. Вероятность исхода РОО равна .

Ответ: 0,125.

Проблемы с броском костей

Задание 5. Игральная кость подбрасывается дважды. Сколько элементарных исходов опыта благоприятствует событию «сумма очков равна 8»?

Задача 6 . Два игральных кубика бросают одновременно. Найдите вероятность того, что сумма будет равна 4. Округлите результат до сотых.

В общем случае, если бросить кости (кости), то исходы равновозможны. Одинаковое количество исходов получается, если один и тот же кубик бросают один раз подряд.

В пользу события «всего 4» благоприятствуют следующие исходы: 1 — 3, 2 — 2, 3 — 1. Их количество равно 3. Желаемая вероятность .

Для вычисления приблизительного значения дроби удобно использовать деление на угол. Таким образом, оно примерно равно 0,083…, округляя до сотых, имеем 0,08.

Ответ: 0,08

Задача 7 . Одновременно бросают три игральные кости. Найдите вероятность получить в сумме 5 очков. Округлите результат до сотых.

Исход будем рассматривать как тройку чисел: очки, выпавшие на первом, втором и третьем кубике. Итого равновозможные исходы. В пользу события «всего 5» говорят следующие исходы: 1-1-3, 1-3-1, 3-1-1, 1-2-2, 2-1-2, 2-2-1. Их количество равно 6. Искомая вероятность равна . Для вычисления примерного значения дроби удобно использовать деление на угол. Примерно получаем 0,027…, округляем до сотых, имеем 0,03. Источник «Подготовка к ЕГЭ. Математика. Теория вероятности». Под редакцией Ф. Ф. Лысенко, С.Ю. Кулабухов

В теории вероятностей существует группа задач, для решения которых достаточно знать классическое определение вероятности и наглядно представить предлагаемую ситуацию. К этим задачам относится большинство задач с подбрасыванием монеты и игральной кости. Вспомним классическое определение вероятности.

Вероятность события А (объективная возможность наступления события в числовом выражении) равно отношению числа исходов, благоприятных для этого события, к общему числу всех равновозможных несовместимых элементарных исходов: P(A)=m/n , где:

• m — количество результатов элементарного теста, благоприятствующих наступлению события A;
• n — общее количество всех возможных исходов элементарного теста.

Число возможных исходов элементарных тестов и число благоприятных исходов в рассматриваемых задачах удобно определять перебором всех возможных вариантов (комбинаций) и прямым вычислением.

Из таблицы видно, что количество возможных элементарных исходов равно n=4. Благоприятные исходы события А = (орел выпадает 1 раз) соответствуют варианту №2 и №3 эксперимента, таких вариантов два m=2.
Найти вероятность события Р(А)=m/n=2/4=0,5

Задача 2 . В случайном эксперименте дважды подбрасывают симметричную монету. Найдите вероятность того, что орел никогда не выпадет.

Раствор . Так как монета подбрасывается дважды, то, как и в задаче 1, количество возможных элементарных исходов равно n=4. Благоприятные исходы события А = (орел не выпадет ни разу) соответствуют варианту № 4 эксперимента (см. таблицу в задании 1). Такой вариант только один, поэтому m=1.
Найти вероятность события Р(А)=m/n=1/4=0,25

Задача 3 . В случайном эксперименте трижды подбрасывают симметричную монету. Найдите вероятность того, что орёл выпадет ровно 2 раза.

Раствор . Возможные варианты трех подбрасываний монеты (все возможные комбинации орла и решки) представлены в виде таблицы:

Из таблицы видно, что количество возможных элементарных исходов равно n=8. Благоприятные исходы события А = (выпадение орла 2 раза) соответствуют вариантам № 5, 6 и 7 опыта. Таких вариантов три, поэтому m=3.
Найти вероятность события Р(А)=m/n=3/8=0,375

Задача 4 . В случайном эксперименте симметричную монету подбрасывают четыре раза. Найдите вероятность того, что орёл выпадет ровно 3 раза.

Раствор . Возможные варианты четырех подбрасываний монеты (все возможные комбинации орла и решки) представлены в виде таблицы:

номер варианта	1-й бросок	2-й рулон	3-й рулон	4-й рулон	номер опции	1-й бросок	2-й рулон	3-й рулон	4-й рулон
1	Орел	Орел	Орел	Орел	9	Хвосты	Орел	Хвосты	Орел
2	Орел	Хвосты	Хвосты	Хвосты	10	Орел	Хвосты	Орел	Хвосты
3	Хвосты	Орел	Хвосты	Хвосты	11	Орел	Хвосты	Хвосты	Орел
4	Хвосты	Хвосты	Орел	Хвосты	12	Орел	Орел	Орел	Хвосты
5	Хвосты	Хвосты	Хвосты	Орел	13	Хвосты	Орел	Орел	Орел
6	Орел	Орел	Хвосты	Хвосты	14	Орел	Хвосты	Орел	Орел
7	Хвосты	Орел	Орел	Хвосты	15	Орел	Орел	Хвосты	Орел
8	Хвосты	Хвосты	Орел	Орел	16	хвосты	Хвосты	Хвосты	Хвосты

Из таблицы видно, что количество возможных элементарных исходов равно n=16. Благоприятные исходы события А = (орёл выпадает 3 раза) соответствуют вариантам № 12, 13, 14 и 15 опыта, что означает m=4.
Найти вероятность события Р(А)=m/n=4/16=0,25

Определение вероятности в задачах с костями

Задача 5 . Определить вероятность того, что при броске игральной кости (правильной кости) выпадет более 3 очков.

Раствор . При бросании игральной кости (обычной кости) может выпасть любая из шести его граней, т.е. произойти любое из элементарных событий — выпадение от 1 до 6 очков (очков). Таким образом, количество возможных элементарных исходов равно n=6.
Событие A = (выпало более 3 очков) означает, что выпало 4, 5 или 6 очков (баллов). Таким образом, число благоприятных исходов m=3.
Вероятность события Р(А)=m/n=3/6=0,5

Задача 6 . Определить вероятность того, что при броске игральной кости количество очков не превысит 4. Результат округлить до тысячных.

Раствор . При бросании игральной кости может выпасть любая из шести ее граней, т.е. произойти любое из элементарных событий — выпадение от 1 до 6 очков (баллов). Таким образом, количество возможных элементарных исходов равно n=6.
Событие A = (выпало не более 4 очков) означает, что выпало 4, 3, 2 или 1 очко (точка). Таким образом, число благоприятных исходов m=4.
Вероятность события Р(А)=m/n=4/6=0,6666…≈0,667

Задача 7 . Дважды подбрасывается игральная кость. Найдите вероятность того, что оба числа меньше 4.

Решение . Так как игральную кость (кости) бросают дважды, то будем рассуждать так: если на первом кубике выпало одно очко, то на втором может выпасть 1, 2, 3, 4, 5, 6. Получаем пары (1; 1), (1; 2), (1; 3), (1; 4), (1; 5), (1; 6) и так далее с каждой гранью. Представим все случаи в виде таблицы из 6 строк и 6 столбцов:

1; 1	2; 1	3; 1	4; 1	5; 1	6; 1
1; 2	2; 2	3; 2	4; 2	5; 2	6; 2
1; 3	2; 3	3; 3	4; 3	5; 3	6; 3
1; 4	2; 4	3; 4	4; 4	5; 4	6; 4
1; 5	2; 5	3; 5	4; 5	5; 5	6; 5
1; 6	2; 6	3; 6	4; 6	5; 6	6; 6

Подсчитаем благоприятные исходы события A = (оба раза выпало число меньше 4) (они выделены жирным шрифтом) и получим m=9.
Найти вероятность события Р(А)=m/n=9/36=0,25

Задача 8 . Дважды подбрасывается игральная кость. Найдите вероятность того, что наибольшее из двух выпавших чисел равно 5. Округлите ответ до тысячных.

Раствор . Все возможные исходы двух бросков костей представлены в таблице:

1; 1	2; 1	3; 1	4; 1	5; 1	6; 1
1; 2	2; 2	3; 2	4; 2	5; 2	6; 2
1; 3	2; 3	3; 3	4; 3	5; 3	6; 3
1; 4	2; 4	3; 4	4; 4	5; 4	6; 4
1; 5	2; 5	3; 5	4; 5	5; 5	6; 5
1; 6	2; 6	3; 6	4; 6	5; 6	6; 6

Из таблицы видно, что количество возможных элементарных исходов равно n=6*6=36.
Подсчитываются благоприятные исходы события A = (наибольшее из двух выпавших чисел равно 5) (они выделены жирным шрифтом) и получаем m=8.
Найти вероятность события Р(А)=m/n=8/36=0,2222…≈0,222

Задача 9 . Дважды подбрасывается игральная кость. Найти вероятность того, что число меньше 4 выпадет хотя бы один раз.

Раствор . Все возможные исходы двух бросков игральной кости представлены в таблице:

1; 1	2; 1	3; 1	4; 1	5; 1	6; 1
1; 2	2; 2	3; 2	4; 2	5; 2	6; 2
1; 3	2; 3	3; 3	4; 3	5; 3	6; 3
1; 4	2; 4	3; 4	4; 4	5; 4	6; 4
1; 5	2; 5	3; 5	4; 5	5; 5	6; 5
1; 6	2; 6	3; 6	4; 6	5; 6	6; 6

Из таблицы видно, что количество возможных элементарных исходов равно n=6*6=36.
Фраза «хотя бы один раз выпало число меньше 4» означает «число меньше 4 выпало один или два раза», тогда количество благоприятных исходов события А = (хотя бы один раз выпало число меньше 4 out) (они выделены жирным шрифтом) m=27.
Найти вероятность события Р(А)=m/n=27/36=0,75

Описание презентации на отдельных слайдах:

1 слайд

Описание слайда:

Решение задач по теории вероятностей. Учитель математики МБОУ Нивнянская СОШ, Нечаева Тамара Ивановна

2 слайд

Описание слайда:

Цели урока: рассмотреть различные типы задач теории вероятностей и методы их решения. Задачи урока: учить распознавать различные виды задач по теории вероятностей и совершенствовать логическое мышление школьников.

3 слайда

Описание слайда:

Задание 1. В случайном эксперименте симметричная монета подбрасывается 2 раза. Найдите вероятность выпадения одинакового количества орлов и решек.

4 слайда

Описание слайда:

Задание 2. Монету подбрасывают четыре раза. Найдите вероятность того, что никогда не выпадет решка.

5 слайдов

Описание слайда:

Задача 3. В случайном эксперименте дважды подбрасывают симметричную монету. Найдите вероятность того, что орел выпадет ровно один раз. Решение: Для того чтобы найти вероятность заданного события, необходимо рассмотреть все возможные исходы эксперимента, а затем выбрать из них благоприятные исходы (благоприятные исходы – это исходы, удовлетворяющие требованиям задачи). В нашем случае благоприятными будут те исходы, при которых при двух подбрасываниях симметричной монеты орел выпадет только один раз. Вероятность события рассчитывается как отношение числа благоприятных исходов к общему числу исходов. Следовательно, вероятность того, что при двукратном подбрасывании симметричной монеты орел выпадет только один раз, равна: Р = 2/4 = 0,5 = 50 % Ответ: вероятность того, что в результате проведенного опыта головки выпадут только один раз — это 50%. Номер эксперимента 1-й бросок 2-й бросок Количество раз, когда орел 1 орел орел 2 2 решка решка 0 3 орел решка 1 4 решка орел 1

6 слайдов

Описание слайда:

Задание 4. Один раз бросили игральную кость. Какова вероятность того, что количество выпавших очков больше 4. Решение: Случайный эксперимент — бросание игральной кости. Элементарное событие — это число на выпавшем ребре. Ответ: 1/3 Всего лиц: 1, 2, 3, 4, 5, 6 Элементарные события: N=6 N(A)=2

7 слайдов

Описание слайда:

Задание 5. Биатлонист пять раз стреляет по мишеням. Вероятность поражения цели одним выстрелом равна 0,8. Найти вероятность того, что биатлонист первые три раза попал в мишени, а два последних промахнулся. Округлите результат до сотых. Решение: Вероятность попадания = 0,8 Вероятность промаха = 1 — 0,8 = 0,2 А=(попал, попал, попал, промахнулся, промахнулся) 0,8 ∙ 0,2 ∙ 0,2 P(A) = 0,512 ∙ 0,04 = 0,02048 ≈ 0,02 Ответ: 0,02

8 слайдов

Описание слайда:

Задание 6. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 6. Округлите ответ до сотых. Решение: Элементарным результатом этого эксперимента является упорядоченная пара чисел. Первое число выпадет на первом кубике, второе — на втором. Набор элементарных исходов удобно представить в виде таблицы. Строки соответствуют количеству очков на первом кубике, столбцы — второму кубику. Всего n = 36 элементарных событий. Запишем в каждую ячейку сумму выпавших очков и раскрасим клетки, где сумма равна 6. Таких клеток 5. Следовательно, событию A = (сумма выпавших очков равна 6) благоприятствуют 5 элементарных исходов. Следовательно, m = 5. Следовательно, P(A) = 5/36 = 0,14. Ответ: 0,14. 2 3 4 5 6 7 3 4 5 6 7 8 4 5 6 7 8 95 6 7 8 9 10 6 7 8 9 10 11 7 8 9 10 11 12

9 слайд

Описание слайда:

Формула вероятности Теорема Пусть монета подброшена n раз. Тогда вероятность того, что орел выпадет ровно k раз, можно найти по формуле: Где Cnk – количество комбинаций из n элементов по k, которое вычисляется по формуле:

10 слайдов

Описание слайда:

Задача 7. Монету подбрасывают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза. Решение По условию задачи всего было n =4 бросков. Необходимое количество орлов: k =3. Подставляем n и k в формулу: С таким же успехом можно посчитать количество решек: k = 4 − 3 = 1. Ответ будет тот же. Ответ: 0,25

11 слайд

Описание слайда:

Задача 8. Монету подбрасывают три раза. Найдите вероятность того, что никогда не выпадет решка. Решение Снова запишем числа n и k. Так как монета подбрасывается 3 раза, то n = 3. А так как решки быть не должно, то k = 0. Осталось подставить числа n и k в формулу: Напомню, что 0! = 1 по определению. Следовательно, C30 = 1. Ответ: 0,125

12 слайдов

Описание слайда:

Задача 9. В случайном эксперименте симметричную монету подбрасывают 4 раза. Найдите вероятность того, что орел выпадет чаще, чем решка. Решение: Чтобы орла было больше, чем решки, они должны выпасть либо 3 раза (тогда будет 1 решка), либо 4 (тогда решки не будет вообще). Найдем вероятность каждого из этих событий. Пусть p1 — вероятность выпадения орла 3 раза. Тогда n = 4, k = 3. Имеем: Теперь найдем p2 — вероятность того, что решка выпадет все 4 раза. В этом случае n = 4, k = 4. Имеем: Чтобы получить ответ, осталось сложить вероятности p1 и p2. Помните: вы можете добавлять вероятности только для взаимоисключающих событий. Имеем: p = p1 + p2 = 0,25 + 0,0625 = 0,3125 Ответ: 0,3125

13 слайдов

Описание слайда:

Задание 10. Перед началом волейбольного матча капитаны команд жеребьевкой определяют, какая команда начнет игру с мячом. Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найти вероятность того, что Статор начнет только первую и последнюю игры. Решение. Требуется найти вероятность произведения трех событий: «Статор» начинает первую игру, не начинает вторую игру, начинает третью игру. Вероятность возникновения независимых событий равна произведению вероятностей этих событий. Вероятность каждого из них равна 0,5, откуда находим: 0,5 0,5 0,5 = 0,125.