В случайном эксперименте бросают монетку. В случайном эксперименте симметричную монету бросают дважды
Описание презентации по отдельным слайдам:
1 слайд
Описание слайда:
Решение задач по теории вероятностей. Учитель математики МБОУ Нивнянская СОШ, Нечаева Тамара Ивановна
2 слайд
Описание слайда:
Цели урока: рассмотреть разные виды задач по теории вероятностей и методы их решения. Задачи урока: обучить распознавать различные разновидности задач по теории вероятностей и совершенствовать логическое мышление школьников.
3 слайд
Описание слайда:
Задача 1.В случайном эксперименте симметричную монету бросают 2 раза. Найдите вероятность того, что орлов и решек выпадет одинаковое количество.
4 слайд
Описание слайда:
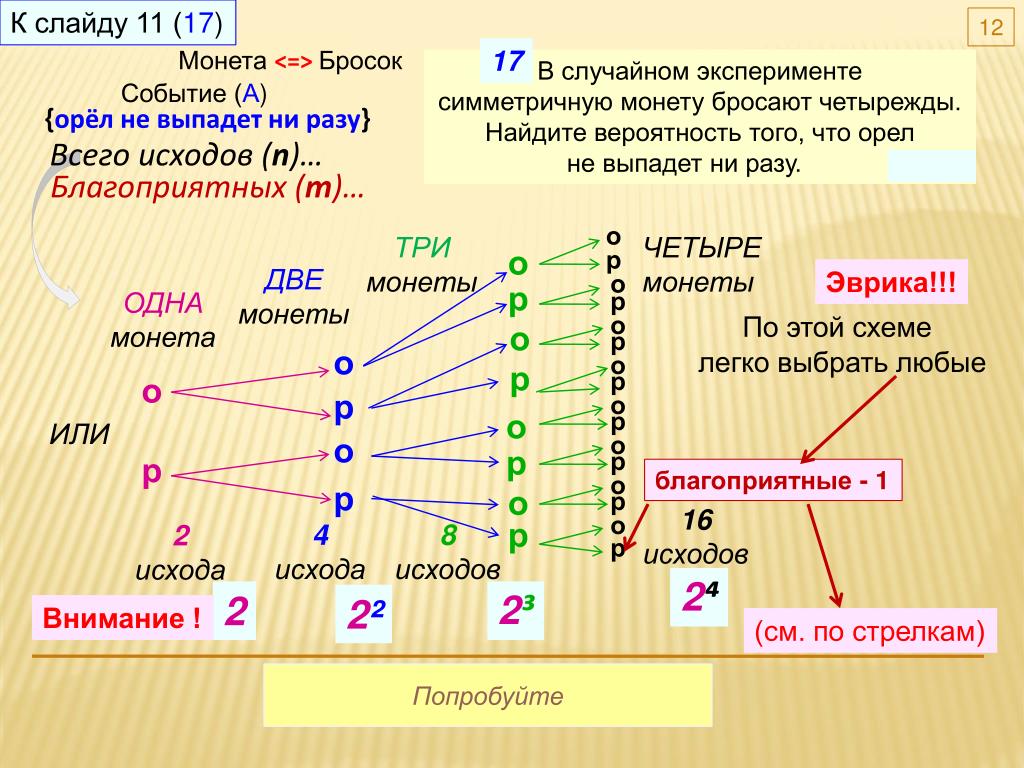
Задача 2.Монету бросают четыре раза. Найдите вероятность того, что решка не выпадет ни разу.
5 слайд
Описание слайда:
Задача 3.В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз. Решение: Для того чтобы найти вероятность указанного события, необходимо рассмотреть все возможные исходы эксперимента, а затем из них выбрать благоприятные исходы (благоприятные исходы – это исходы удовлетворяющие требованиям задачи). В нашем случае, благоприятными будут те исходы, в которых при двух бросаниях симметричной монеты, орел выпадет только один раз. Вероятность события вычисляется как отношение количества благоприятных исходов к общему количеству исходов. Следовательно, вероятность того, что при двух кратном бросании симметричной монеты орел выпадет только один раз, равна: Р=2/4=0,5=50% Ответ: вероятность того, что в результате проведения вышеописанного эксперимента орел выпадет только один раз равна 50%. Номер эксперимента 1-ый бросок 2-ой бросок Сколько раз выпал орел 1 Орел Орел 2 2 Решка Решка 0 3 Орел Решка 1 4 Решка Орел 1
6 слайд
Описание слайда:
Задача 4.
Игральный кубик бросили один раз. Какова вероятность того, что выпало число очков, большее чем 4. Решение: Случайный эксперимент – бросание кубика. Элементарное событие – число на выпавшей грани. Ответ:1/3 Всего граней: 1, 2, 3, 4, 5, 6 Элементарные события: N=6 N(A)=2
7 слайд
Описание слайда:
Задача 5. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два раза промахнулся. Результат округлите до сотых. Решение: Вероятность попадания = 0,8 Вероятность промаха = 1 — 0,8 = 0,2 А={попал, попал, попал, промахнулся, промахнулся} По формуле умножения вероятностей Р(А)= 0,8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2 Р(А)= 0,512 ∙ 0,04 = 0,02048 ≈ 0,02 Ответ: 0,02
8 слайд
Описание слайда:
Задача 6.В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 6.
Ответ округлите до сотых Решение: Элементарный исход в этом опыте – упорядоченная пара чисел. Первое число выпадет на первом кубике, второе – на втором. Множество элементарных исходов удобно представить таблицей. Строки соответствуют количеству очков на первом кубике, столбцы –на втором кубике. Всего элементарных событий п = 36. Напишем в каждой клетке сумму выпавших очков и закрасим клетки, где сумма равна 6. Таких ячеек 5. Значит, событию А = {сумма выпавших очков равна 6} благоприятствует 5 элементарных исходов. Следовательно, т = 5. Поэтому, Р(А) = 5/36 = 0,14. Ответ: 0,14. 2 3 4 5 6 7 3 4 5 6 7 8 4 5 6 7 8 9 5 6 7 8 9 10 6 7 8 9 10 11 7 8 9 10 11 12
9 слайд
Описание слайда:
Формула вероятности Теорема Пусть монету бросают n раз. Тогда вероятность того, что орел выпадет ровно k раз, можно найти по формуле: Где Cnk — число сочетаний из n элементов по k, которое считается по формуле:
10 слайд
Описание слайда:
Задача 7.
Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза. Решение По условию задачи, всего бросков было n =4. Требуемое число орлов: k =3. Подставляем n и k в формулу: С тем же успехом можно считать число решек: k = 4 − 3 = 1. Ответ будет таким же. Ответ: 0,25
11 слайд
Описание слайда:
Задача 8. Монету бросают три раза. Найдите вероятность того, что решка не выпадет ни разу. Решение Снова выписываем числа n и k. Поскольку монету бросают 3 раза, n = 3. А поскольку решек быть не должно, k = 0. Осталось подставить числа n и k в формулу: Напомню, что 0! = 1 по определению. Поэтому C30 = 1. Ответ: 0,125
12 слайд
Описание слайда:
Задача 9.В случайном эксперименте симметричную монету бросают 4 раза. Найдите вероятность того, что орел выпадет больше раз, чем решка. Решение: Чтобы орлов было больше, чем решек, они должны выпасть либо 3 раза (тогда решек будет 1), либо 4 (тогда решек вообще не будет).
Найдем вероятность каждого из этих событий. Пусть p1 — вероятность того, что орел выпадет 3 раза. Тогда n = 4, k = 3. Имеем: Теперь найдем p2 — вероятность того, что орел выпадет все 4 раза. В этом случае n = 4, k = 4. Имеем: Чтобы получить ответ, осталось сложить вероятности p1 и p2. Помните: складывать вероятности можно только для взаимоисключающих событий. Имеем: p = p1 + p2 = 0,25 + 0,0625 = 0,3125 Ответ: 0,3125
13 слайд
Описание слайда:
Задача 10.Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Статор» по очереди играет с командами «Ротор», «Мотор» и «Стартер». Найдите вероятность того, что «Статор» будет начинать только первую и последнюю игры. Решение. Требуется найти вероятность произведения трех событий: «Статор» начинает первую игру, не начинает вторую игру, начинает третью игру. Вероятность произведения независимых событий равна произведению вероятностей этих событий.
Вероятность каждого из них равна 0,5, откуда нахо дим: 0,5·0,5·0,5 = 0,125. Ответ: 0,125.
В теории вероятностей существует группа задач, для решения которых достаточно знать классическое определение вероятности и наглядно представлять предлагаемую ситуацию. Такими задачами является большинство задач с подбрасыванием монеты и задачи с бросанием игрального кубика. Напомним классическое определение вероятности.
Вероятность события А (объективная возможность наступления события в числовом выражении) равна отношению числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов: Р(А)=m/n , где:
- m – число элементарных исходов испытания, благоприятствующих появлению события А;
- n – общее число всех возможных элементарных исходов испытания.
Число возможных элементарных исходов испытания и число благоприятных исходов в рассматриваемых задачах удобно определять
перебором всех возможных вариантов (комбинаций) и непосредственным подсчетом.
Из таблицы видим, что число возможных элементарных исходов n=4. Благоприятные
исходы события А = {орел выпадает 1 раз} соответствуют варианту №2 и №3 эксперимента, таких
вариантов два m=2.
Находим вероятность события Р(А)=m/n=2/4=0,5
Задача 2 . В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел не выпадет ни разу.
Решение . Поскольку монету бросают дважды, то, как и в задаче 1, число
возможных элементарных исходов n=4. Благоприятные исходы события А = {орел не выпадет ни разу}
соответствуют варианту №4 эксперимента (см. таблицу в задаче 1). Такой вариант один, значит m=1.
Находим вероятность события Р(А)=m/n=1/4=0,25
Задача 3 . В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно 2 раза.
Решение . Возможные варианты трех бросаний монеты (все возможные комбинации орлов и решек) представим в виде таблицы:
Из таблицы видим, что число возможных элементарных исходов n=8.
Благоприятные
исходы события А = {орел выпадает 2 раза} соответствуют вариантам №5, 6 и 7 эксперимента.
Таких вариантов три, значит m=3.
Находим вероятность события Р(А)=m/n=3/8=0,375
Задача 4 . В случайном эксперименте симметричную монету бросают четыре раза. Найдите вероятность того, что орёл выпадет ровно 3 раза.
Решение . Возможные варианты четырех бросаний монеты (все возможные комбинации орлов и решек) представим в виде таблицы:
| № варианта | 1-й бросок | 2-й бросок | 3-й бросок | 4-й бросок | № варианта | 1-й бросок | 2-й бросок | 3-й бросок | 4-й бросок |
| 1 | Орел | Орел | Орел | Орел | 9 | Решка | Орел | Решка | Орел |
| 2 | Орел | Решка | Решка | Решка | 10 | Орел | Решка | Орел | Решка |
| 3 | Решка | Орел | Решка | Решка | 11 | Орел | Решка | Решка | Орел |
| 4 | Решка | Решка | Орел | Решка | 12 | Орел | Орел | Орел | Решка |
| 5 | Решка | Решка | Решка | Орел | 13 | Решка | Орел | Орел | Орел |
| 6 | Орел | Решка | Решка | 14 | Орел | Решка | Орел | Орел | |
| 7 | Решка | Орел | Орел | Решка | 15 | Орел | Орел | Решка | Орел |
| 8 | Решка | Решка | Орел | Орел | 16 | Решка | Решка | Решка | Решка |
Из таблицы видим, что число возможных элементарных исходов n=16.
Благоприятные
исходы события А = {орел выпадет 3 раза} соответствуют вариантам №12, 13, 14
и 15 эксперимента, значит m=4.
Находим вероятность события Р(А)=m/n=4/16=0,25
Задача 5 . Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет более 3 очков.
Решение . При бросании игрального кубика (правильной кости) может
выпасть любая из шести его граней, т.е. произойти любое из элементарных событий — выпадение
от 1 до 6 точек (очков). Значит число возможных элементарных исходов n=6.
Событие А = {выпало более 3 очков} означает, что выпало 4, 5 или 6 точек (очков). Значит
число благоприятных исходов m=3.
Вероятность события Р(А)=m/n=3/6=0,5
Задача 6 . Определите вероятность того, что при бросании игрального
кубика выпало число очков, не большее 4.
Результат округлите до тысячных.
Решение . При бросании игрального кубика может выпасть любая из шести
его граней, т.е. произойти любое из элементарных событий — выпадение от 1 до 6 точек (очков). Значит
число возможных элементарных исходов n=6.
Событие А = {выпало не более 4 очков} означает, что выпало 4, 3, 2 или 1 точка (очко).
Значит число благоприятных исходов m=4.
Вероятность события Р(А)=m/n=4/6=0,6666…≈0,667
Задача 7 . Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, меньшее 4.
Решение . Так как игральную кость (игральный кубик) бросают дважды, то будем рассуждать следующим образом: если на первом кубике выпало одно очко, то на втором может выпасть 1, 2, 3, 4, 5, 6. Получаем пары (1;1), (1;2), (1;3), (1;4), (1;5), (1;6) и так с каждой гранью. Все случаи представим в виде таблицы из 6-ти строк и 6-ти столбцов:
| 1; 1 | 2; 1 | 3; 1 | 4; 1 | 5; 1 | 6; 1 |
| 1; 2 | 2; 2 | 3; 2 | 4; 2 | 5; 2 | 6; 2 |
| 1; 3 | 2; 3 | 3; 3 | 4; 3 | 5; 3 | 6; 3 |
| 1; 4 | 2; 4 | 3; 4 | 4; 4 | 5; 4 | 6; 4 |
| 1; 5 | 2; 5 | 3; 5 | 4; 5 | 5; 5 | 6; 5 |
| 1; 6 | 2; 6 | 3; 6 | 4; 6 | 5; 6 | 6; 6 |
Благоприятные исходы события А = {оба раза выпало число, меньшее 4} (они выделены жирным)
подсчитаем и получим m=9.
Находим вероятность события Р(А)=m/n=9/36=0,25
Задача 8 . Игральную кость бросают дважды. Найдите вероятность того, что наибольшее из двух выпавших чисел равно 5. Ответ округлите до тысячных.
Решение . Все возможные исходы двух бросаний игральной кости представим в таблице:
| 1; 1 | 2; 1 | 3; 1 | 4; 1 | 5; 1 | 6; 1 |
| 1; 2 | 2; 2 | 3; 2 | 4; 2 | 5; 2 | 6; 2 |
| 1; 3 | 2; 3 | 3; 3 | 4; 3 | 5; 3 | 6; 3 |
| 1; 4 | 2; 4 | 3; 4 | 4; 4 | 5; 4 | 6; 4 |
| 1; 5 | 2; 5 | 3; 5 | 4; 5 | 5; 5 | 6; 5 |
| 1; 6 | 2; 6 | 3; 6 | 4; 6 | 5; 6 | 6; 6 |
Из таблицы видим, что число возможных элементарных исходов n=6*6=36.
Благоприятные исходы события А = {наибольшее из двух выпавших чисел равно 5} (они выделены жирным)
подсчитаем и получим m=8.
Находим вероятность события Р(А)=m/n=8/36=0,2222…≈0,222
Задача 9 . Игральную кость бросают дважды. Найдите вероятность того, что хотя бы раз выпало число, меньшее 4.
Решение . Все возможные исходы двух бросаний игральной кости представим в таблице:
| 1; 1 | 2; 1 | 3; 1 | 4; 1 | 5; 1 | 6; 1 |
| 1; 2 | 2; 2 | 3; 2 | 4; 2 | 5; 2 | 6; 2 |
| 1; 3 | 2; 3 | 3; 3 | 4; 3 | 5; 3 | 6; 3 |
| 1; 4 | 2; 4 | 3; 4 | 4; 4 | 5; 4 | 6; 4 |
| 1; 5 | 2; 5 | 3; 5 | 4; 5 | 5; 5 | 6; 5 |
| 1; 6 | 2; 6 | 3; 6 | 4; 6 | 5; 6 | 6; 6 |
Из таблицы видим, что число возможных элементарных исходов n=6*6=36.
Фраза «хотя бы раз выпало число, меньшее 4» означает «число меньшее 4 выпало один раз или два раза»,
тогда число благоприятных исходов события А = {хотя бы раз выпало число, меньшее 4} (они выделены жирным)
m=27.
Находим вероятность события Р(А)=m/n=27/36=0,75
Формулировка задачи: В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл (решка) не выпадет ни разу (выпадет ровно/хотя бы 1, 2 раза).
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 10 (Классическое определение вероятности).
Рассмотрим, как решаются подобные задачи на примерах.
Пример задачи 1:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу.
ОО ОР РО РР
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых нет ни одного орла. Такая комбинация всего одна (РР).
P = 1 / 4 = 0.25
Ответ:
0.
25
Пример задачи 2:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно два раза.
Рассмотрим все возможные комбинации, которые могут выпасть, если монету бросают дважды. Для удобства будем обозначать орла буквой О, а решку – буквой Р:
ОО ОР РО РР
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых орел выпадает ровно 2 раза. Такая комбинация всего одна (ОО).
P = 1 / 4 = 0.25
Ответ: 0.25
Пример задачи 3:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно один раз.
Рассмотрим все возможные комбинации, которые могут выпасть, если монету бросают дважды. Для удобства будем обозначать орла буквой О, а решку – буквой Р:
ОО ОР РО РР
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых орел выпал ровно 1 раз. Таких комбинаций всего две (ОР и РО).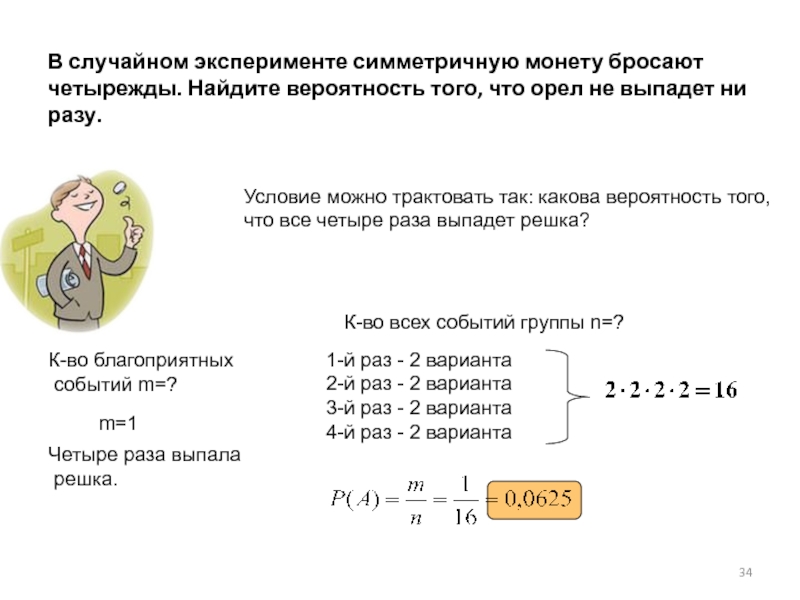
Ответ: 0.5
Пример задачи 4:
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет хотя бы один раз.
Рассмотрим все возможные комбинации, которые могут выпасть, если монету бросают дважды. Для удобства будем обозначать орла буквой О, а решку – буквой Р:
ОО ОР РО РР
Всего таких комбинаций получилось 4. Нас интересуют только те из них, в которых орел выпадет хотя бы 1 раз. Таких комбинаций всего три (ОО, ОР и РО).
P = 3 / 4 = 0.75
Задачи на подбрасывание монет считаются довольно сложными. И перед тем как решать их, требуется небольшое пояснение. Задумайтесь, любая задача по теории вероятностей в итоге сводится к стандартной формуле:
где p — искомая вероятность, k — число устраивающих нас событий, n — общее число возможных событий.
Большинство задач B6 решаются по этой формуле буквально в одну строчку — достаточно прочитать условие. Но в случае с подбрасыванием монет эта формула бесполезна, поскольку из текста таких задач вообще не понятно, чему равны числа k
и n
.
В этом и состоит вся сложность.
Тем не менее, существует как минимум два принципиально различных метода решения:
- Метод перебора комбинаций — стандартный алгоритм. Выписываются все комбинации орлов и решек, после чего выбираются нужные;
- Специальная формула вероятности — стандартное определение вероятности, специально переписанное так, чтобы было удобно работать с монетами.
Для решения задачи B6 надо знать оба метода. К сожалению, в школах изучают только первый. Не будем повторять школьных ошибок. Итак, поехали!
Метод перебора комбинаций
Этот метод еще называется «решение напролом». Состоит из трех шагов:
- Выписываем все возможные комбинации орлов и решек. Например: ОР, РО, ОО, РР. Число таких комбинаций — это n ;
- Среди полученных комбинаций отмечаем те, которые требуются по условию задачи. Считаем отмеченные комбинации — получаем число k ;
- Осталось найти вероятность: p = k : n .
К сожалению, этот способ работает лишь для малого количества бросков.
Потому что с каждым новым броском число комбинаций удваивается. Например, для 2 монет придется выписать всего 4 комбинации. Для 3 монет их уже 8, а для 4 — 16, и вероятность ошибки приближается к 100%. Взгляните на примеры — и сами все поймете:
Задача. В случайном эксперименте симметричную монету бросают 2 раза. Найдите вероятность того, что орлов и решек выпадет одинаковое количество.
Итак, монету бросают два раза. Выпишем все возможные комбинации (O — орел, P — решка):
Итого n = 4 варианта. Теперь выпишем те варианты, которые подходят по условию задачи:
Таких вариантов оказалось k = 2. Находим вероятность:
Задача. Монету бросают четыре раза. Найдите вероятность того, что решка не выпадет ни разу.
Снова выписываем все возможные комбинации орлов и решек:
OOOO OOOP OOPO OOPP OPOO OPOP OPPO OPPP
POOO POOP POPO POPP PPOO PPOP PPPO PPPP
Всего получилось n
= 16 вариантов. Вроде, ничего не забыл.
Из этих вариантов нас устраивает лишь комбинация «OOOO», в которой вообще нет решек. Следовательно, k
= 1. Осталось найти вероятность:
Как видите, в последней задаче пришлось выписывать 16 вариантов. Вы уверены, что сможете выписать их без единой ошибки? Лично я — не уверен. Поэтому давайте рассмотрим второй способ решения.
Специальная формула вероятности
Итак, в задачах с монетами есть собственная формула вероятности. Она настолько простая и важная, что я решил оформить ее в виде теоремы. Взгляните:
Теорема. Пусть монету бросают n раз. Тогда вероятность того, что орел выпадет ровно k раз, можно найти по формуле:
Где C n k — число сочетаний из n элементов по k , которое считается по формуле:
Таким образом, для решения задачи с монетами нужны два числа: число бросков и число орлов. Чаще всего эти числа даны прямо в тексте задачи. Более того, не имеет значения, что именно считать: решки или орлы. Ответ получится один и тот же.
На первый взгляд, теорема кажется слишком громоздкой. Но стоит чуть-чуть потренироваться — и вам уже не захочется возвращаться к стандартному алгоритму, описанному выше.
Задача. Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза.
По условию задачи, всего бросков было n = 4. Требуемое число орлов: k = 3. Подставляем n и k в формулу:
Задача. Монету бросают три раза. Найдите вероятность того, что решка не выпадет ни разу.
Снова выписываем числа n и k . Поскольку монету бросают 3 раза, n = 3. А поскольку решек быть не должно, k = 0. Осталось подставить числа n и k в формулу:
Напомню, что 0! = 1 по определению. Поэтому C 3 0 = 1.
Задача. В случайном эксперименте симметричную монету бросают 4 раза. Найдите вероятность того, что орел выпадет больше раз, чем решка.
Чтобы орлов было больше, чем решек, они должны выпасть либо 3 раза (тогда решек будет 1), либо 4 (тогда решек вообще не будет).
Найдем вероятность каждого из этих событий.
Пусть p 1 — вероятность того, что орел выпадет 3 раза. Тогда n = 4, k = 3. Имеем:
Теперь найдем p 2 — вероятность того, что орел выпадет все 4 раза. В этом случае n = 4, k = 4. Имеем:
Чтобы получить ответ, осталось сложить вероятности p 1 и p 2 . Помните: складывать вероятности можно только для взаимоисключающих событий. Имеем:
p = p 1 + p 2 = 0,25 + 0,0625 = 0,3125
Главная → Видеоуроки → ЕГЭ по математике. Профильный уровень. Задание 5. Описание видеоурока: Теория вероятностей ЕГЭ . Классическое определение вероятности. Решение задач без использования формул комбинаторики. Условие задачи: В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет не менее двух раз. 00:04:13 Валерий Волков
7
15. Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями! Новости образования | ЕГЭ по математике Профильный уровень Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 ГИА по математике Задача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 6 Задача 7 Задача 8 Задача 9 Задача 10 Задача 11 Задача 12 Задача 13 Задача 14 Задача 15 Задача 16 Задача 17 Задача 18 Задача 19 Задача 20 Задача 21 Задача 22 Задача 23 Задача 24 Задача 25 Задача 26 Демонстрационные варианты ОГЭ по математике Математика. Натуральные числа Обыкновенные дроби Десятичные дроби Проценты Математика. 6 класс. Делимость чисел Сложение и вычитание дробей с разными знаменателями Умножение и деление обыкновенных дробей Отношения и пропорции Положительные и отрицательные числа Измерение величин Математика. 7 класс. Преобразование выражений Многочлены Формулы сокращенного умножения Математика. 8 класс. Модуль числа. Уравнения и неравенства. Квадратные уравнения Квадратные неравенства Уравнения с параметром Задачи с параметром Математика. 9 класс. Функции и их свойства Прогрессии Векторы Комбинаторика, статистика и теория вероятностей Математика. Числовые функции Тригонометрические функции Тригонометрические уравнения Преобразование тригонометрических выражений Производная Степенные функции Показательная функция Логарифмические функции Первообразная и интеграл Уравнения и неравенства Комбинаторика Создаёте видеоуроки? Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала. Актуально Физкультминутки для школьников и дошкольников Подготовка к ЕГЭ Подготовка к ОГЭ |
07.2014
5 класс.
10 — 11 класс.
Эксперимент с подбрасыванием монеты
Эксперимент с подбрасыванием монеты всегда играет ключевую роль в концепции вероятности. Всякий раз, когда мы будем рассматривать вероятность вещей в статистике, у нас обязательно будут примеры с подбрасыванием монеты.
Пространство для проб
При подбрасывании монеты возможны два исхода.
Это «голова» и «хвост».
Итак, выборочное пространство S = {H, T}, n(s) = 2.
При подбрасывании двух монет
общее количество всех возможных исходов = 2 x 2 = 4
Таким образом, выборочное пространство S = {HH, TT, HT, TH}, n(s) = 4.
При подбрасывании трех монет
общее количество всех возможных исходов = 2 x 2 x 2 = 8.
Таким образом, пространство выборки равно
S = {HHH, TTT, HHT, HTH, THH, TTH, THT, HTT},
n(s) = 8
Таким образом, мы можем получить пространство выборки при подбрасывании монеты или монет.
Примечание:
В эксперименте с подбрасыванием монеты мы также можем получить пространство выборки с помощью древовидной диаграммы.
Формула вероятности
Мы можем использовать формулу из классического определения, чтобы найти вероятность в экспериментах с подбрасыванием монеты.
Пусть A — событие случайного эксперимента.
Тогда
n(A) = количество возможных исходов события A
n(S) = количество всех возможных исходов эксперимента
Возможные результаты случайного эксперимента.
Тогда приведенная выше формула станет.
Чтобы лучше понять приведенную выше формулу, давайте рассмотрим следующий эксперимент с подбрасыванием монеты.
Монета подбрасывается один раз.
S = {H, T} и n(S) = 2
Пусть A — событие получения орла.
A = {H} и n(A) = 1
Тогда
P(A) = n(A)/n(S)
= 1/2
Решенные задачи
Задача 1 :
Монета дважды. Какова вероятность головы?
Решение:
При подбрасывании двух монет
общее количество всех возможных исходов = 2 x 2 = 4.
И у нас есть следующее примерное пространство.
S = {HH, TT, HT, TH} и n(S) = 4
Согласно классическому определению вероятности,
P(B) = 2/4
P(B) = 0,50 или 50%.
Задача 2 :
Монета подбрасывается три раза. Какова вероятность получить :
(i) 2 орла
(ii) не менее 2 орлов
Решение:
Когда монету подбрасывают три раза, сначала нужно перечислить все элементарные события.
Это можно сделать с помощью «Деревовидной диаграммы», как показано ниже:
Таким образом, элементарными событиями являются HHH, HHT, HTH, HTT, THH, THT, TTH, TTT.
То есть,
S = { HHH, HHT, HTH, HTT, THH, THT, TTH, TTT }
Таким образом, количество элементарных событий n(s) = 8
(i) 2 орла :
Из этих 8 исходов 2 орла выпадают в трех случаях, а именно HHT, HTH и THH.
Если обозначить выпадение двух орлов событием A и предположить, что монета, как и исполнитель эксперимента, непредвзяты, то это предположение обеспечивает равновероятность всех восьми элементарных событий.
Тогда по классическому определению вероятности имеем
P(A) = n(A) / n(s)
P(A) = 3/8
P(A) 0,375 или 37,5%
(ii) не менее 2 головок :
Пусть B обозначает наличие не менее 2 головок, т. е. 2 головок или 3 головки.
Поскольку 2 головы встречаются в 3 случаях, а 3 головы встречаются только в 1 случае, B встречается в 3 + 1 или 4 случаях.
По классическому определению вероятности
P(B) = 4/8
P(B) = 0,50 или 50%
Задача 3 :
Четыре монеты подбрасываются один раз. Какова вероятность того, что выпадет хотя бы 2 решки?
Решение:
Когда четыре монеты подбрасываются один раз,
общее количество всех возможных исходов = 2 x 2 x 2 x 2 = 16
И у нас есть следующее примерное пространство.
S = {HHHH, TTTT, HHHT, HHTH, HTHH, THHH, TTTH, TTHT, THTT, HTTT, HHTT, TTHH, HTHT, THTH, HTTH, THHT}
и n(S) = 16
Пусть A — событие выпадения хотя бы двух решек.
Тогда A должно включать все события, в которых есть две решки и более двух решек.
A = {TTTT, TTTH, TTHT, THTT, HTTT, HHTT, TTHH, HTHT, THTH, HTTH, THHT}
и n(A) = 11
По классическому определению вероятности,
P( Б ) = 11/36
Пожалуйста, отправьте свой отзыв на [email protected]
Мы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all.com
Квантовый подбрасывание монеты – Почти уверен
Позвольте мне задать следующий очень простой вопрос. Предположим, что я подбрасываю пару одинаковых монет одновременно, тогда какова вероятность того, что обе они выпадут решкой? Здесь нет подвоха, обе монеты честные. Возможны три исхода: обе решки, одна решка и одна решка и обе решки. Предполагая, что это совершенно случайно, так что все исходы равновероятны, мы могли бы утверждать, что каждая возможность имеет шанс один к трем, так что ответ на вопрос состоит в том, что вероятность равна 1/3.
Конечно, это неправильно! Честная монета имеет вероятность 1/2 выпадения орла, и, по независимости, стандартная теория вероятностей говорит, что мы должны перемножить их вместе для каждой монеты, чтобы получить правильный ответ , который можно проверить экспериментально. В качестве альтернативы мы можем отметить, что исход одной решки и одной решки в действительности состоит из двух равновероятных возможностей.
Либо первая монета может быть орлом, а вторая решкой, либо наоборот. Таким образом, на самом деле существует четыре равновероятных исхода, только в одном из которых обе монеты выпадают решкой, что опять-таки дает вероятность 1/4.
Любой, кто имеет хотя бы базовые знания о вероятности, должен прийти к этому ответу, так почему же я вообще упоминаю ошибочный аргумент, приведенный выше? Ну, в наши дни у нас есть формализованная теория вероятности, так что такие свойства, как независимость подбрасывания монеты, легко обрабатываются. В прошлом это было не так, и даже уважаемые и известные математики приводили неправильные аргументы, подобные приведенным выше, чтобы прийти к неправильному ответу. Например, один из самых выдающихся математиков всех времен Готфрид Вильгельм Лейбниц (1646–1716) утверждал, что
…с двумя костями одинаково вероятно выпадение двенадцати очков, чем одиннадцати; потому что одно или другое может быть сделано только одним способом.
Ошибка здесь та же, что и с монетами выше.
Выпадение одиннадцати на самом деле может быть выполнено двумя способами, когда первая кость дает пять, а вторая шесть, или наоборот. Следовательно, у нас в два раза больше шансов выбросить одиннадцать, чем двенадцать. В качестве другого примера, Жан ле Рон д’Аламбер (1717–1783) рассматривал вопрос:
Какова вероятность того, что при двух подбрасываниях правильной монеты хотя бы один раз выпадет орёл?
Правильный ответ, как известно, должен быть 3/4. Ясно, что она равна единице минус вероятность того, что обе монеты выпадут решкой, что из-за произвольности обозначения сторон монет «орлом» и «решкой» равносильно единице минус вероятность того, что обе монеты выпадут орлом. На самом деле Даламбер дал ответ 2/3. Ошибка, приведенная в его аргументе, похожа на ошибку в приведенном выше ошибочном аргументе, но немного отличается от нее. Он полагал, что если первая монета выпадет орлом, то вторую монету можно даже не рассматривать. Итак, есть только три исхода, когда первая монета выпадает орлом, первая монета — решкой, а вторая — решкой, и обе они выпадают решкой.
Даламбер считал эти три исхода равновероятными. На самом деле случай, когда первая монета выпадает орлом, фактически состоит из двух возможностей, зависящих от результата второй монеты, что указывает на источник ошибки. Эти примеры и различные другие ошибки, допущенные в элементарной вероятности до полного развития теории, описаны в статье 9.0206 Ошибки вероятности в историческом контексте , Пракаш Горручурн (The American Statistician, ноябрь 2011 г., том 65, № 4).
Ошибки в неправильном вычислении вероятности в начале этого поста и в рассуждениях Лейбница легко объяснимы. Две монеты или игральные кости предполагались идентичными. Это означает, что мы не можем отличить какой-либо конкретный исход от альтернативного исхода с обменом их состояниями. Таким образом, ошибка состоит в том, чтобы рассматривать эти два неразличимых исхода как одно и то же событие. Это приводит к недооценке пространства возможных исходов и вместе с предположением, что все исходы имеют одинаковую вероятность, дает неверные результаты.
Взяв пример подбрасывания двух монет, мы всегда можем заранее пометить одну из них маркером, чтобы их можно было различить. Это не должно повлиять на результаты, но позволяет нам различать два способа, при которых одна монета выпадает орлом, а другая решкой. Таким образом, вероятности должны соответствовать ситуации, когда монеты действительно можно отличить друг от друга. Это фактически то, что мы делали в исправленном аргументе выше, где мы неявно пометили одну из монет как первую, а другую как вторую.
Для развлечения мы можем рассмотреть, как бы обстояли дела, если бы вероятность действительно вела себя так, как в приведенных выше неверных рассуждениях. Мы подбрасываем несколько одинаковых монет, где каждый результат равновероятен, и, кроме того, обмен любой пары монет дает не просто неразличимое событие, а на самом деле является точно таким же результатом. Результаты довольно интересные, как я объясню, и, кроме того, это не просто абстрактное и бесполезное занятие. Говорят, что объекты, которые ведут себя таким образом, следуют Бозе-Эйнштейна статистики и является наблюдаемым поведением определенных частиц на квантовом уровне.
Такие частицы известны как бозоны и включают фотоны, глюоны, W- и Z-бозоны и бозон Хиггса, а также различные составные частицы. Удивительно, но эти статистические свойства были фактически обнаружены в результате совершения ошибки, аналогичной ложному аргументу выше, показывающему, что вероятность двух орлов равна 1/3. Цитата из докторской диссертации 2007 г. диссертация Алессандро Микеланджели, Конденсация Бозе-Эйнштейна: анализ проблем и строгие результаты ,
Читая лекцию в Университете Дакки о фотоэлектрическом эффекте и ультрафиолетовой катастрофе, Бозе намеревался показать своим студентам, что существующая теория неадекватна, потому что она предсказанные результаты не соответствуют экспериментальным результатам. Во время этой лекции Бозе допустил ошибку в применении теории, которая неожиданно дала предсказание, совпадающее с экспериментами. Ошибка была простой ошибкой — похожей на утверждение, что при подбрасывании двух одинаковых монет выпадет две решки в одной трети случаев — что могло бы показаться совершенно неверным любому, кто хоть немного разбирается в статистике.
Однако предсказанные результаты совпали с экспериментом, и Бозе понял, что это может быть вовсе не ошибка.
Однако предсказанные результаты совпали с экспериментом, и Бозе понял, что это может быть вовсе не ошибка.Другие элементарные частицы, такие как электроны, протоны и нейтроны, известны как фермионов и подчиняются статистике Ферми-Дирака, которая не позволяет ни одной идентичной паре частиц находиться в одном и том же состоянии. В этом посте я рассматриваю только бозоны, которые более интересны для примеров с подбрасыванием монеты.
Если подбросить идентичную пару бозонных монет, то аргумент в начале этого поста теперь верен, и пара орлов выпадет с вероятностью 1/3, а не 1/4 для «классических» монет. Этот аргумент по-прежнему требует некоторых дополнительных предположений, а именно, что две монеты находятся в одном и том же состоянии, помимо того, являются ли они орлом или решкой, иначе их можно было бы отличить друг от друга. В качестве реального физического примера рассмотрим фотоны, составляющие стоячую волну электромагнитного поля или света, заключенного в камеру.
Поскольку все они имеют одинаковый импульс, определяемый длиной волны, их можно будет различить только по их поляризации (или, что то же самое, по спину), которая может находиться только в одном из двух состояний. Фотоны могут иметь круговую поляризацию по или против часовой стрелки.
Затем подбросьте число N одинаковых бозонных монет. Каково распределение вероятностей доли выпавших орлов? Рассмотрим случай m головок для любого . Поскольку любая конфигурация из 90 236 m 90 237 орлов и решек может быть преобразована в любую другую подобную конфигурацию путем перестановки монет, для этого существует только один способ. Следовательно, существуют ровно исходы, соответствующие каждому возможному числу выпавших орлов, каждый из которых выпадает с вероятностью . Интересно сравнить это с классическим случаем для стандартных неквантовых монет. Разница в поведении разительна, особенно в пределе N становится большим. Для бозонов доля голов приближается к равномерному распределению на единичном интервале, в отличие от классического случая, когда доля голов приближается к 1/2 (по закону больших чисел).
Точнее, классические монеты следуют биномиальной статистике, так что вероятность выпадения 90 236 m 90 237 решек равна . Доля головок имеет среднее значение и стандартное отклонение, которое стремится к нулю, когда N стремится к бесконечности. Кроме того, по центральной предельной теореме оно хорошо аппроксимируется нормальным распределением как N становится большим. Это поведение показано на рисунке 1 ниже, на котором вероятности масштабируются, чтобы аппроксимировать непрерывную плотность вероятности.
Такое поведение классических монет, когда пропорция решек приближается к половине, точно такое, к которому мы привыкли как математически, так и на практике. В результате, когда мы имеем систему, состоящую из очень большого числа микроскопических компонентов, случайные свойства отдельных компонентов не наблюдаются в больших масштабах. Индивидуальное движение атомов, например, не проявляется на макроскопическом уровне, остается только тепло, исходящее от их усредненной кинетической энергии.
Точно так же движение цен на акции управляется чистым поведением большого числа отдельных участников, покупающих и продающих, которые обычно в значительной степени компенсируются, оставляя небольшое количество остаточного случайного шума.
Со статистикой Бозе-Эйнштейна дела обстоят совершенно иначе. Общее количество орлов одинаково, независимо от того, насколько большое количество монет используется. Так, например, будет 20% вероятность того, что по крайней мере 90% монет окажутся одинаковыми. Микроскопические случайные эффекты больше не усредняются, поэтому они также вызывают случайное макроскопическое поведение.
Далее предположим, что мы подбросили очень большое количество N одинаковых монет, выбираем их одну за другой и смотрим, выпадут ли они орлом или решкой. По симметрии первая монета выпадет орлом с вероятностью 1/2. Тогда какова будет вероятность выпадения орла для второй монеты, для третьей и так далее? Для классических монет вероятность всегда равна 1/2, независимо от того, что наблюдалось до сих пор.
Однако эта независимость не распространяется на бозонные монеты. Так как доля решек равномерно распределена на единичном интервале, вероятность выпадения первых n все головы есть. Тогда, взяв соотношения, вероятность того, что n-я монета выпадет орлом, при условии, что первая монета выпадет орлом, равна . Ибо это 1/2, как и ожидалось, но увеличивается до 1 по мере увеличения n . Таким образом, чем больше орла мы видим, тем больше вероятность того, что следующий тоже будет орлом.
Для получения дополнительной информации о квантовых монетах, игральных костях (и детях!), см. статью Чи-Кеунг Чоу и Томаса Д. Коэна Quantum Coins, Dice and Children: Probability and Quantum Statistics 1999 года.
Неверные монеты
Все становится еще интереснее, если мы рассмотрим необъективные монеты, где один бросок монеты дает решку с вероятностью . Также считаем, что p находится строго между 0 и 1, иначе это не интересно, и устанавливаем для вероятности выпадения решки.
Для классических монет N ситуация очень похожа на беспристрастный случай выше. Количество орлов распределено биномиально со средним значением и дисперсией. Значит, разделив на N , пропорция головок имеет среднее значение p и стандартное отклонение , которое стремится к нулю, когда N стремится к бесконечности. Как и прежде, случайность исчезает в пределе больших N , и мы получаем фиксированную пропорцию p голов.
Совсем другая ситуация с бозонными монетами со смещением. Поскольку у нас больше нет простого аргумента симметрии, использованного выше, согласно которому все исходы имеют одинаковую вероятность, не сразу становится очевидным, каковы вероятности. Подумайте о том, чтобы бросить N монет и посмотрите на результаты, соответствующие m голов. Классически количество способов, которыми это может произойти, равно количеству способов выбора 90 236 m 90 237 из набора 90 236 N 90 237 объектов, определяемому биномиальным коэффициентом .
Каждый из этих исходов имеет вероятность. Суммируя все исходы с 90 236 m 90 237 головами, получаем биномиальную вероятность . Для бозонных монет каждую из этих возможностей следует интерпретировать как один и тот же результат, поэтому мы не масштабируем биномиальный коэффициент и можем ожидать, что вероятность будет просто равна . К сожалению, это не работает. Если просуммировать все такие «вероятности», мы получим
, что строго меньше единицы. Чтобы исправить это, мы нормализуем распределение, масштабируя эту константу, давая вероятность 90 236 m 90 237 голов как , что действительно согласуется с наблюдениями за бозонами. Для , чтобы решка выпадала чаще, чем орёл, можно записать это как для нормировочной константы . У этого есть удобное свойство, состоящее в том, что, кроме постоянного множителя, вероятность не зависит от N и имеет конечную сумму по m . Таким образом, при увеличении N до бесконечности вероятность выпадения m голов сходится к пределу с нормировочной константой .