PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
- 2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
- 3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
- 4 Электродинамика
- 4.
 1 Электростатика
1 Электростатика - 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
- 4.
- 5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.
 6 СТО
6 СТО
- 6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
Физические основы механики
Как известно, бывают величины скалярные, не имеющие направления, а бывают векторные, которым кроме величины приписывается некое направление. Время — величина скалярная, а положение в пространстве надо задавать векторами. Недостаточно сказать, что лекция состоится в 860 км от Таллинна. Этой информации не хватит, чтобы узнать, где именно: в Москве или, скажем, в Копенгагене. Отсюда ясно, что векторы должны играть важную роль в физике. Недаром векторное исчисление получило современный вид именно благодаря работам физиков (Дж. Гиббс). Кроме длины и направления, для векторов определяются операция умножения вектора на действительное число и операция сложения векторов, то есть задается векторная алгебра.
Время — величина скалярная, а положение в пространстве надо задавать векторами. Недостаточно сказать, что лекция состоится в 860 км от Таллинна. Этой информации не хватит, чтобы узнать, где именно: в Москве или, скажем, в Копенгагене. Отсюда ясно, что векторы должны играть важную роль в физике. Недаром векторное исчисление получило современный вид именно благодаря работам физиков (Дж. Гиббс). Кроме длины и направления, для векторов определяются операция умножения вектора на действительное число и операция сложения векторов, то есть задается векторная алгебра.
Использование векторного исчисления удобно тем, что многие соотношения получаются в общем компактном виде и без особого труда могут быть трансформированы в соответствующие соотношения для любой системы координат. Соотношения между векторами остаются неизменными при смене начала отсчета или выборе иной системы координат. В этом разделе мы напомним некоторые правила векторной алгебры. Занимаясь сейчас физикой, мы не стремимся к точным математическим доказательствам.
Пусть нам дана какая-то декартова прямоугольная система координат. Любой вектор A можно задать тремя компонентами — проекциями вектора на оси , , .В дальнейшем мы используем обе общепринятых записи векторов, выделяя соответствующую букву жирным шрифтом, либо ставя над ней вектор:
Модулем вектора А (или его длиной) называется число:
Длина вектора не меняется при поворотах системы координат.
Произведение вектора А на число является вектором
проекции которого определяются как
Отсюда следует, во-первых, что длина вектора B равна длине вектора A, умноженной на абсолютное значение числа
Во-вторых, векторы A и A коллинеарны и имеют одно направление, если >0, и противоположное, если <0.
Суммой двух векторов A и B называется вектор с
чьи компоненты определяются как сумма компонент слагаемых
Отсюда следует геометрическое представление суммы векторов — правило параллелограмма либо правило треугольника (рис. 1.12).
1.12).
Рис. 1.12. Сложение двух векторов
Аналогично для вычитания векторов
где
Правило вычитания векторов иллюстрируется на рис. 1.13.
Рис. 1.13. Вычитание векторов
Единичный вектор n — это вектор с длиной, равной единице
Единичный вектор nA в направлении какого-то вектора а равен
Особую роль играют единичные векторы вдоль положительных направлений осей , , системы координат.
Единичные векторы вдоль положительных направлений осей , , системы координат
называются ортами.Совокупность ортов состовляет базис данной системы координат.
Иногда оси маркируются цифрами (1,2,3 ) или индексами соответствия осям (x,y,z) обозначают так
или
Любой вектор а можно представить в виде разложения по базису
На рис. 1.14 показано разложение вектора вдоль координатных осей
Рис. 1.14. Разложение вектора вдоль координатных осей
1.14. Разложение вектора вдоль координатных осей
Скалярное произведение двух векторов а и b — это число, равное сумме произведений одноименных проекций векторов — сомножителей
Отсюда следует, что скалярное произведение вектора на самого себя равно квадрату длины вектора
Второе следствие: скалярное произведение коммутативно, то есть
Справедливо также соотношение
Скалярное произведение не зависит от поворотов системы координат. Можно систему повернуть так, чтобы оба вектора лежали в плоскости и ось была направлена вдоль вектора а. В этой повернутой системе координат векторы-сомножители имеют следующие проекции:
Поэтому скалярное произведение может быть также представлено в виде
Здесь — угол между векторами а и b.
Если векторы ортогональны, то есть
то скалярное произведение равно нулю:
Обратно: если скалярное произведение равно нулю, то либо один из сомножителей — вектор нулевой длины, либо они ортогональны.
Рис. 1.15. Скалярное произведение
Приведем пример использования скалярного произведения (рис. 1.16). Пусть
Возведем в квадрат обе части равенства:
Это — так называемая теорема косинусов; в частном случае прямоугольного треугольника из нее следует теорема Пифагора.
Рис. 1.16. Теорема косинусов
Векторное произведение двух векторов а и b — это вектор с, чьи компоненты равны
Отсюда следует, что разложение векторного произведения по базису может быть представлено в виде определителя
(1.5.1)
Для обозначения векторного произведения используется либо косой крест между сомножителями, либо помещение разделенных запятой (запятая необязательна, если и без неё ясно, где кончается первый сомножитель и начинается второй) сомножителей в квадратные скобки.
Видно также, что в векторном произведении важен порядок сомножителей
Справедливо соотношение
Чтобы понять, куда направлено векторное произведение и чему равна его длина, снова повернем систему координат так, чтобы плоскость осей совпала с плоскостью векторов а и b и ось была направлена вдоль вектора а. Тогда
Тогда
Подставляя эти значения в определитель (1.5.1) для векторного произведения, получаем
Это значит, что длина векторного произведения равна
и оно ортогонально обоим сомножителям а и b, причем направление его определяется по правилу правого винта.
Если правый винт вращается от первого вектора — сомножителя ко второму по кратчайшему пути, то этот винт перемещается по направлению их векторного произведения.
Применение правила буравчика иллюстрируется на рис. 1.17.
Рис. 1.17. Правило буравчика для определения направления векторного произведения
Видео 1.2. Правое и левое вращение. Векторное произведение векторов
Если сомножители векторного произведения коллинеарны (, ; = 0), то векторное произведение равно нулю. Обратно, из равенства нулю векторного произведения вытекает, что либо векторы — сомножители коллинеарны, либо один из векторов равен нулю.
Операция деления на вектор не определена.
Производная вектора a — это вектор, чьи компоненты равны производным от соответствующих компонент вектора а.
Пусть, например, вектор а зависит от времени t. Тогда
Производные от скалярного и векторного произведений выглядят обычным образом:
Подчеркнем, что в выражении для производной векторного произведения необходимо сохранять исходный порядок сомножителей.
Дополнительная информация
http://www.plib.ru/library/book/14978.html — Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г.– стр. 54–59 (§ 7, п.п.9–11 и задачи 1–4): о векторных и скалярных величинах в физике.
http://www.plib.ru/library/book/14978.html — Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г.– стр. 44–48 (§ 6): о смысле производной и интеграла в физических приложениях.
Вектор а вектор б вектор с: Сложение и вычитание векторов — ЭкоДом: Дом своими руками
Содержание
Сложение и вычитание векторов [wiki.
 eduVdom.com]
eduVdom.com]Пусть $\overrightarrow{a}$ и $\overrightarrow{b}$ — два вектора (рис.1, а).
Сложение двух векторов
Рис.1
Возьмем произвольную точку О и построим вектор $\overrightarrow{ОА} = \overrightarrow{a}$ . Затем от точки А отложим вектор $\overrightarrow{AB} = \overrightarrow{b}$. Вектор $\overrightarrow{OB}$, соединяющий начало первого слагаемого вектора с концом второго (рис.1, б), называется суммой этих векторов и обозначается $\overrightarrow{a} + \overrightarrow{b}$$ (правило треугольника).
Ту же самую сумму векторов можно получить иным способом. Отложим от точки О векторы $\overrightarrow{ОА} = \overrightarrow{a} \,и\, \overrightarrow{ОС} = \overrightarrow{b} $ (рис.1, в). Построим на этих векторах как на сторонах параллелограмм ОABC. Вектор $\overrightarrow{ОВ}$, служащий диагональю этого параллелограмма, проведенной из вершины О, является, очевидно, суммой векторов $\overrightarrow{a} + \overrightarrow{b}$ { правило параллелограмма). Из рисунка 1, в непосредственно следует, что сумма двух векторов обладает переместительным свойством: $\overrightarrow{a} + \overrightarrow{b} = \overrightarrow{b} + \overrightarrow{a}$
Из рисунка 1, в непосредственно следует, что сумма двух векторов обладает переместительным свойством: $\overrightarrow{a} + \overrightarrow{b} = \overrightarrow{b} + \overrightarrow{a}$
Действительно, каждый из векторов $\overrightarrow{a} + \overrightarrow{b} \,и\, = \overrightarrow{b} + \overrightarrow{a}$ равен одному и тому же вектору $\overrightarrow{OB}$ .
Пример 1. В треугольнике ABC АВ = 3, ВС = 4, ∠ В = 90°. Найти: $а)\,\ \overrightarrow{|АВ|} + \overrightarrow{|ВС|};\,\,\ б)\,\ |\overrightarrow{АВ} + \overrightarrow{ВС}|$ .
Решение
а) Имеем: $|\overrightarrow{АВ}| = АВ,\,\,\ |\overrightarrow{ВС}| = ВС$ и, значит, $|\overrightarrow{АВ}| + |\overrightarrow{BC}| = 7$ .
б) Так как $\overrightarrow{AB} + \overrightarrow{ВС} = \overrightarrow{АС} \,\,,\,\, то\,\, |\overrightarrow{АВ} + \overrightarrow{ВС}| = |\overrightarrow{АС}| = АС$ . 2} = \sqrt{9 + 16} = 5
\\ т.е.\, |\overrightarrow{АВ} + \overrightarrow{ВС}| = 5.
$$
Понятие суммы векторов можно обобщить на случай любого конечного числа слагаемых векторов.
Пусть, например, даны три вектора $\overrightarrow{a}, \overrightarrow{b} \,и\, \overrightarrow{c}$ (рис.2).
Сложение трех векторов
Рис.2
Построив сначала сумму векторов $\overrightarrow{a} + \overrightarrow{b}$ , а затем прибавив к этой сумме вектор $\overrightarrow{c}$, получим вектор $(\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c}$ . На рисунке 2
\\ и
\\ \overrightarrow{ОС} = \overrightarrow{ОВ} + \overrightarrow{ВС} = (\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c}
$$
Из рисунка 2 видно, что тот же вектор $\overrightarrow{ОС}$ мы получим, если к вектору $\overrightarrow{ОА} = \overrightarrow{a}$ прибавим вектор
$\overrightarrow{АВ} = \overrightarrow{b} + \overrightarrow{c}$ .
 Таким образом, $(\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c} = \overrightarrow{a} + (\overrightarrow{b} + \overrightarrow{c})$ , т. е. сумма векторов обладает сочетательным свойством.
Таким образом, $(\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c} = \overrightarrow{a} + (\overrightarrow{b} + \overrightarrow{c})$ , т. е. сумма векторов обладает сочетательным свойством.Поэтому сумму трех векторов $\overrightarrow{a}\,,\,\overrightarrow{b}\,,\,\overrightarrow{c}$ записывают просто $\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c}$ .
Разностью двух векторов $\overrightarrow{a} \,и\, \overrightarrow{b}$ называется третий вектор $\overrightarrow{c} = \overrightarrow{a} — \overrightarrow{b}$ , сумма которого с вычитаемым вектором $\overrightarrow{b}$ дает вектор $\overrightarrow{a}$. Таким образом, если $\overrightarrow{c} = \overrightarrow{a} — \overrightarrow{b}\,,\, то\, \overrightarrow{c} + \overrightarrow{b} = \overrightarrow{a}$ .
Из определения суммы двух векторов вытекает правило построения вектора-разности (рис.3).
Вычитание векторов
Рис.3
Откладываем векторы $\overrightarrow{ОА} = \overrightarrow{a} \,и\, \overrightarrow{OB} = \overrightarrow{b}$ из общей точки О. Вектор $\overrightarrow{BA}$ , соединяющий концы уменьшаемого вектора $\overrightarrow{a}$ и вычитаемого вектора $\overrightarrow{b}$ и направленный от вычитаемого к уменьшаемому, является разностью $\overrightarrow{c} = \overrightarrow{a} — \overrightarrow{b}$ . Действительно, по правилу
Вектор $\overrightarrow{BA}$ , соединяющий концы уменьшаемого вектора $\overrightarrow{a}$ и вычитаемого вектора $\overrightarrow{b}$ и направленный от вычитаемого к уменьшаемому, является разностью $\overrightarrow{c} = \overrightarrow{a} — \overrightarrow{b}$ . Действительно, по правилу
Пример 2. Сторона равностороннего треугольника ABC равна а. Найти: $а) |\overrightarrow{ВА} — \overrightarrow{ВС}|\,;\,\ б)\,\,\ |\overrightarrow{АВ} — \overrightarrow{АС}|$ .
Решение
а) Так как $\overrightarrow{ВА} — \overrightarrow{ВС} = \overrightarrow{СА}\text{ , а }|\overrightarrow{СА}| = а\text{ , то }|\overrightarrow{ВА} — \overrightarrow{ВС}| = а$ .
б) Так как $\overrightarrow{АВ} — \overrightarrow{АС} = \overrightarrow{СВ}\text{ , а }|\overrightarrow{СВ}| = а\text{ , то }|\overrightarrow{АВ} — \overrightarrow{АС}| = а$ .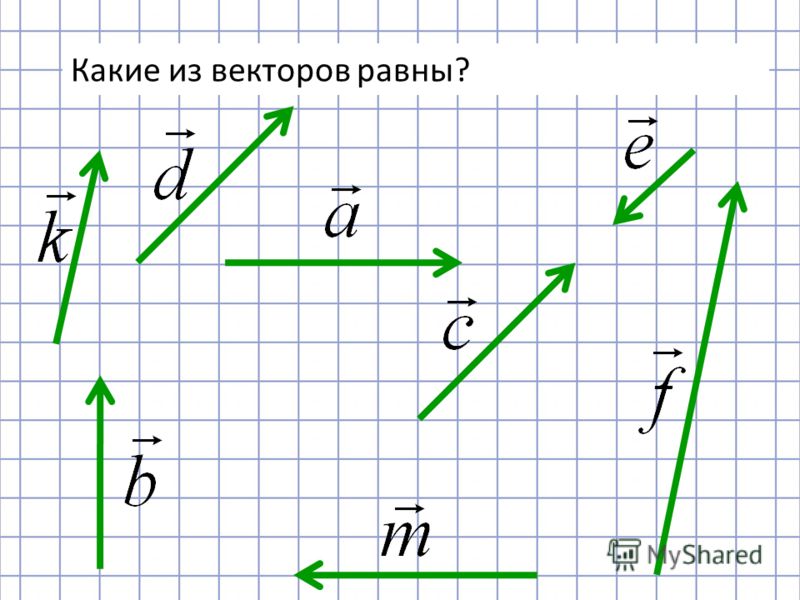
Произведением вектора $\overrightarrow{a}$(обозначается $=\lambda\overrightarrow{a}$ или $\overrightarrow{a}\lambda$) на действительное число $\lambda$ называется вектор $\overrightarrow{b}$, коллинеарный вектору $\overrightarrow{a}$, имеющий длину, равную $|\lambda||\overrightarrow{a}|$, и то же направление, что и вектор $\overrightarrow{a}$, если $\lambda > 0$ , и направление, противоположное направлению вектора $\overrightarrow{a}$, если $\lambda < 0$ . Так, например, $2\overrightarrow{a}$ есть вектор, имеющий то же направление, что и вектор $\overrightarrow{a}$ , а длину, вдвое большую, чем вектор $\overrightarrow{a}$ (рис.4).
Умножение вектора на число
Рис.4
В случае, когда $\lambda = 0$ или $\overrightarrow{a} = 0$ , произведение $\lambda\overrightarrow{a}$ представляет
собой нулевой вектор. Противоположный вектор $-\overrightarrow{a}$ можно рассматривать как результат умножения вектора $\overrightarrow{a}$ на $\lambda = -1$ (см. рис.4):
Очевидно, что $\overrightarrow{a} + (-\overrightarrow{a}) = \overrightarrow{0}$ .

Пример 3. Доказать, что если О, А, В и С — произвольные точки, то $\overrightarrow{ОА} + \overrightarrow{АВ} + \overrightarrow{ВС} + \overrightarrow{СО} = 0$ .
Решение. Сумма векторов $\overrightarrow{ОА} + \overrightarrow{АВ} + \overrightarrow{СВ} = \overrightarrow{ОС}$ , вектор $\overrightarrow{CO}$ — противоположный вектору $\overrightarrow{ОС}$ . Поэтому $\overrightarrow{ОС} + \overrightarrow{СО} = \overrightarrow{0}$ .
Пусть дан вектор $\overrightarrow{a}$. Рассмотрим единичный вектор $\overrightarrow{a_0}$ , коллинеарный вектору $\overrightarrow{a}$ и одинаково с ним направленный. Из определения умножения вектора на число следует, что
, т.е. каждый вектор равен произведению его модуля на единичный вектор того же направления. Далее из того же определения следует, что если $\overrightarrow{b} = \lambda\overrightarrow{a}$ , где $\overrightarrow{a}$ — ненулевой вектор, то векторы $\overrightarrow{a} \,и\, \overrightarrow{b}$ коллинеарны.
 Очевидно, что и обратно, из коллинеарности векторов $\overrightarrow{a} \,и\, \overrightarrow{b}$ следует, что $\overrightarrow{b} = \lambda\overrightarrow{a}$.
Очевидно, что и обратно, из коллинеарности векторов $\overrightarrow{a} \,и\, \overrightarrow{b}$ следует, что $\overrightarrow{b} = \lambda\overrightarrow{a}$.Таким образом, получаем следующую теорему.
Пример 4. Длина вектора AB равна 3, длина вектора AC равна 5.
Косинус угла между этими векторами равен 1/15. Найдите длину вектора AB + AC.
Видео-решение.
Векторы примеры решения задач, формулы и онлайн калькуляторы
Содержание:
Вектора применяются во многих науках, таких как: математика, физика, геометрия и многих других
прикладных науках. На практике, они позволяют не делать лишних операций и сократить время выполнения задач.
Поэтому, будущим специалистам очень важно понять теорию векторов и научиться решать задачи с ними.
Перед изучением примеров решения задач советуем изучить теоретический материал по векторам, прочитать
все определения и свойства. Список тем находится в правом меню.
Список тем находится в правом меню.
Координаты вектора
Теоретический материал по теме — координаты вектора.
Пример
Запись $\overline{a}=(5 ;-2)$ означает, что вектор $\overline{a}$
имеет следующие координаты: абсцисса равна 5, ордината равна -2.
Слишком сложно?
Примеры решения задач с векторами не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Заданы векторы $\overline{a}=(-3 ; 5)$
и $\overline{b}=(0 ;-1)$. Найти координаты вектора $\overline{c}=\overline{a}+\overline{b}$
Решение. $\overline{c}=\overline{a}+\overline{b}=(-3 ; 5)+(0 ;-1)=(-3+0 ; 5+(-1))=(-3 ; 4)$
Пример
Задание. {\circ}$$
Разложение вектора по ортам координатных осей
Теоретический материал по теме — разложение вектора по ортам.
Пример
Задание. Зная разложения вектора $\overline{a}$
по базисной системе векторов: $\overline{a}=3 \overline{i}-\overline{k}$, записать координаты этого вектора в пространстве.
Решение. Коэффициенты при ортах и есть координатами вектора, поэтому из того, что $\overline{a}=3 \overline{i}-0 \cdot \overline{j}-\overline{k}$,
получаем, что $\overline{a}=(3 ; 0 ;-1)$
Пример
Задание. Вектор $\overline{a}$ задан
своими координатами: $\overline{a}=(2 ;-1 ; 5)$. Записать разложение данного вектора по ортам осей координат.
Решение. Координаты вектора — это коэффициенты при ортах координатных осей в разложении вектора
по базисной системе векторов, поэтому искомое разложение:
$\overline{a}=2 \overline{i}-\overline{j}+5 \overline{k}$
Скалярное произведение векторов
Теоретический материал по теме — скалярное произведение векторов. {\circ}=6 \cdot \frac{1}{2}=3$
Пример
Задание. Найти скалярное произведение векторов $\overline{a}=(3 ;-1)$ и
$\overline{b}=(-2 ; 7)$
Решение. Скалярное произведение
$\overline{a} \overline{b}=3 \cdot(-2)+(-1) \cdot 7=-6-7=-13$
Векторное произведение векторов
Теоретический материал по теме — векторное произведение векторов.
Пример
Задание. Найти векторное произведение векторов $\overline{a}=(6 ; 7 ; 10)$ и
$\overline{b}=(8 ; 5 ; 9)$
Решение. Составляем определитель и вычисляем его:
$\overline{a} \times \overline{b}=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {6} & {7} & {10} \\ {8} & {5} & {9}\end{array}\right|=\overline{i} \left| \begin{array}{cc}{7} & {10} \\ {5} & {9}\end{array}\right|-\overline{j} \left| \begin{array}{cc}{6} & {10} \\ {8} & {9}\end{array}\right|+\overline{k} \left| \begin{array}{cc}{6} & {7} \\ {8} & {5}\end{array}\right|=$
$=\overline{i}(7 \cdot 9-5 \cdot 10)-\overline{j}(6 \cdot 9-8 \cdot 10)+\overline{k}(6 \cdot 5-8 \cdot 7)=$
$=13 \overline{i}+26 \overline{j}-26 \overline{k}=(13 ; 26 ;-26)$
Смешанное произведение векторов
Теоретический материал по теме — смешанное произведение векторов.
Пример
Задание. Вычислить объем пирамиды, построенной на векторах $\overline{a}=(2 ; 3 ; 5)$,
Вычислить объем пирамиды, построенной на векторах $\overline{a}=(2 ; 3 ; 5)$,
$\overline{b}=(1 ; 4 ; 4)$,
$\overline{c}=(3 ; 5 ; 7)$
Решение. Найдем смешанное произведение заданных векторов, для это составим определитель,
по строкам которого запишем координаты векторов $\overline{a}$,
$\overline{b}$ и $\overline{c}$:
$(\overline{a}, \overline{b}, \overline{c})=\left| \begin{array}{lll}{2} & {3} & {5} \\ {1} & {4} & {4} \\ {3} & {5} & {7}\end{array}\right|=2 \cdot 4 \cdot 7+1 \cdot 5 \cdot 5+3 \cdot 4 \cdot 3-$
$-3 \cdot 4 \cdot 5-5 \cdot 4 \cdot 2-1 \cdot 3 \cdot 7=-4$
$$V_{пир}=\frac{1}{6}|(\overline{a}, \overline{b}, \overline{c})|=\frac{1}{6} \cdot 4=\frac{2}{3}$$
Читать первую тему — операции над векторами,
раздела векторы.
Сложение и вычитание векторов | matematicus.ru
Сложение векторов по правилу параллелограмма
Правило параллелограмма
Если слагаемые a и b не коллинеарны, то
c=a+b
Сложение векторов по правилу треугольника
Правило треугольника
Суммой векторов a (на рисунке зелёный вектор) и b (на рисунке синий вектор) называется третий вектор c (на рисунке красный вектор) , получаемый следующее построение:
Примечание
Нельзя смешивать понятие «сумма отрезков» с понятием «сумма векторов».
Правило параллелепипеда
Если три вектора a, b, c после приведения к общему началу не лежат в одной плоскости , то их сумма равна диагонали параллелепипеда
d=a+b+c
Сложение противоположных векторов
Сумма противоположных векторов равна нуль-вектору, т.е.
a+(-a)=0
Свойство переместительности (переместительный закон)
От перестановки слагаемых сумма векторов не меняется.
с=a+b= b+a
Сочетательное свойство (сочетательный закон)
Слагаемые векторы можно группировать как угодно.
a+(b+c+d) = a+b+c+d
Вычесть вектор а (вычитаемое) из вектора b (уменьшаемое) значит найти новый вектор x (разность), который в сумме с вектором а даёт вектор b.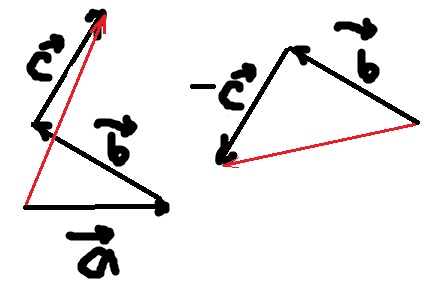
Разность векторов обозначается: a-b
Вычитание есть действие обратное сложению (сложение векторов).
Вычитание векторов показаны на рисунках ниже:
Примечание
Модуль разности может быть меньше модуля «уменьшаемого», но может быть и больше или равен ему. Эти случаи показаны на рисунке выше.
Сложение и вычитание векторов.
Определение.
Сложение векторов (сумма векторов) a + b есть операция вычисления вектора c, все элементы которого равны попарной сумме соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен:
сi = ai + bi
Определение.
Вычитание векторов (разность векторов) a — b есть операция вычисления вектора c, все элементы которого равны попарной разности соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен:
сi = ai — bi
Формулы сложения и вычитания векторов
Формулы сложения и вычитания векторов для плоских задач
В случае плоской задачи сумму и разность векторов a = {ax ; ay} и b = {bx ; by} можно найти воспользовавшись следующими формулами:
a + b = {ax + bx; ay + by}
a — b = {ax — bx; ay — by}
Формулы сложения и вычитания векторов для пространчтвенных задач
В случае пространственной задачи сумму и разность векторов a = {ax ; ay ; az} и b = {bx ; by ; bz} можно найти воспользовавшись следующими формулами:
a + b = {ax + bx; ay + by; az + bz}
a — b = {ax — bx; ay — by; az — bz}
Формулы сложения и вычитания n -мерных векторов
В случае n -мерного пространства сумму и разность векторов a = {a1 ; a2 ; .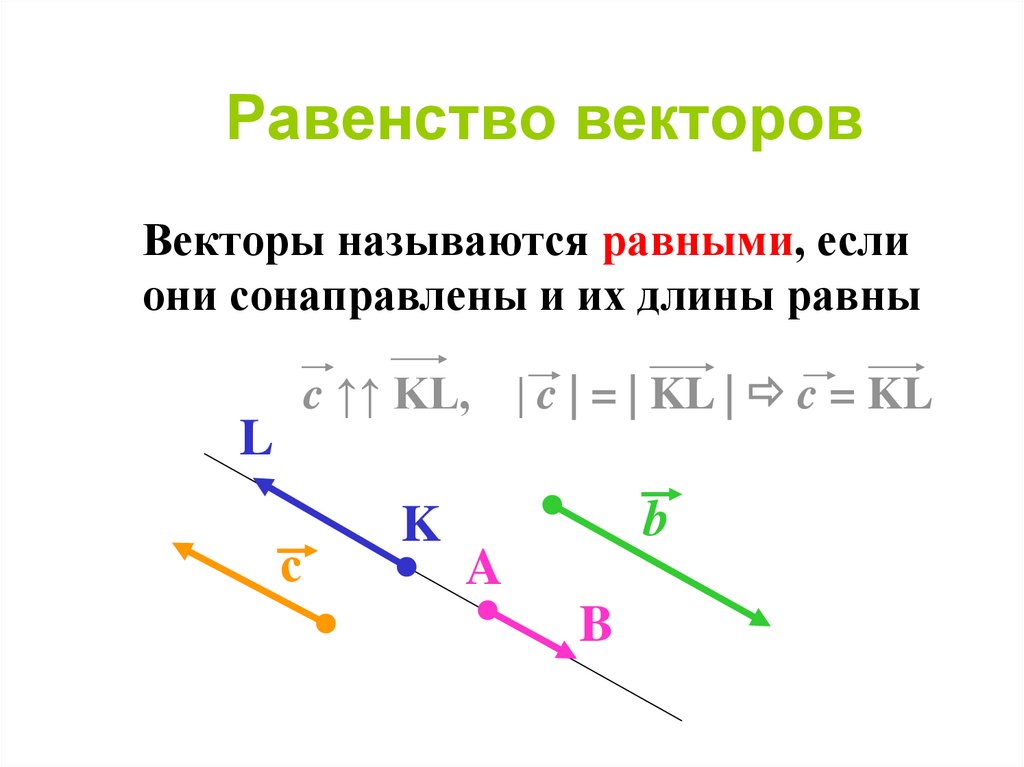 .. ; an} и b = {b1 ; b2 ; … ; bn} можно найти воспользовавшись следующими формулами:
.. ; an} и b = {b1 ; b2 ; … ; bn} можно найти воспользовавшись следующими формулами:
a + b = {a1 + b1; a2 + b2; … ; an + bn}
a — b = {a1 — b1; a2 — b2; … ; an — bn}
Действия над векторами /qualihelpy
Линейные действия над векторами
К линейным действиям с векторами относят сложение векторов, вычитание векторов и умножение вектора на число.
Сложение векторов с заданными координатами
Чтобы сложить (вычесть) векторы и необходимо сложить (вычесть) их соответствующие координаты: (3.8)
Умножение вектора на число
Чтобы умножить вектор на число , необходимо каждую координату вектора умножить на это число: (3.9)
Сочетая действия сложения и вычитания векторов, а также умножение вектора на число, получим линейную комбинацию векторов.
Аналогично выполняются линейные действия над -мерными векторами.
Скалярное произведение векторов
Скалярным произведением векторов и называется число, равное произведению длин этих векторов на косинус угла между ними: (3.10)Угол между векторами и находят по формуле:. (3.11)Векторы и перпендикулярны, если угол между ними равен . Поскольку то скалярное произведение перпендикулярных векторов равно нулю.
Проекцией вектора на вектор называют длину отрезка, концами которого являются основания перпендикуляров, опущенных из начала и конца вектора на вектор .
Записывают: пр. На рисунке 3.7 пр
Проекцию вектора на вектор находят по формуле:
пр (3.12)
где – угол между векторами и .
Свойства скалярного произведения:
1) 2) где 3) 4) Скалярное произведение векторов и можно найти и по формуле: (3.13)Аналогично в -мерном пространстве: (3.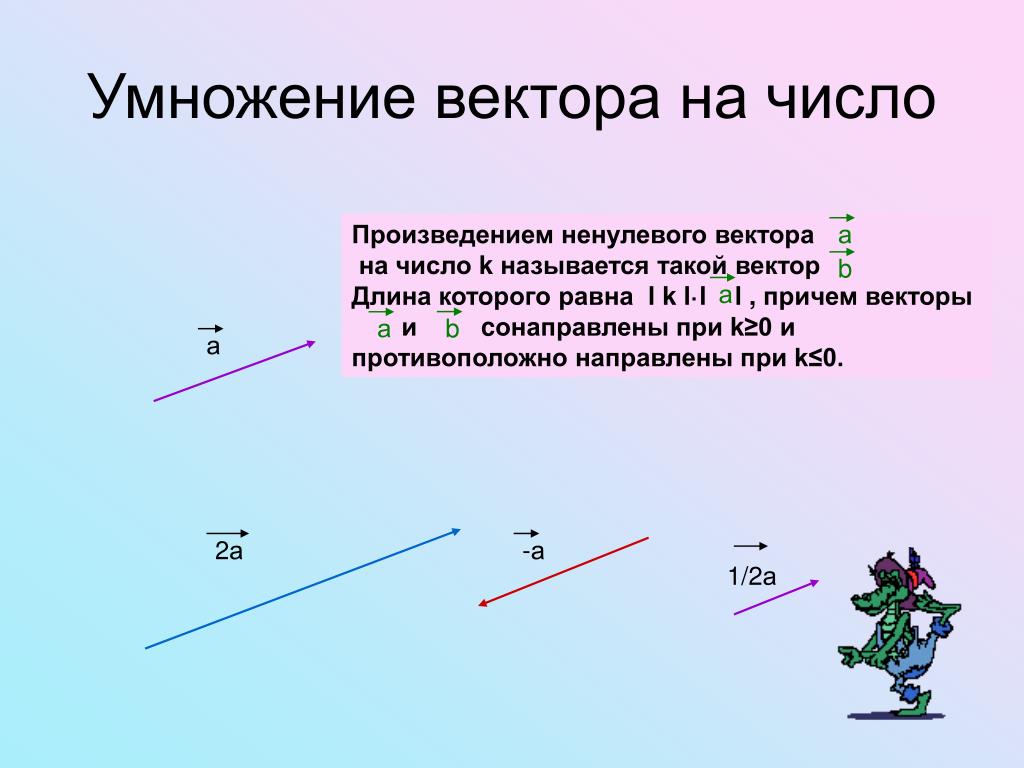 13.1)
13.1)
Векторное произведение векторов
Векторное произведение векторов и находят по формуле: , (3. 14)где векторы и – орты.Площадь параллелограмма, построенного на векторах и , находят по формуле: (3.15)
Площадь треугольника, построенного на этих же векторах, находят по формуле:
(3.16)
Смешанное произведение векторов
Рассмотрим векторы , и Смешанным произведением этих векторов называют число, которое получено в результате скалярного умножения вектора на векторное произведение векторов и Смешанное произведение векторов и и находят по формуле: . (3.17)Объем параллелепипеда, построенного на векторах , и , находят по формуле: (3.18)Объем пирамиды, построенной на векторах , и , находят по формуле: (3.19)
Скалярное произведение векторов. Он-лайн калькуляторы скалярного произведения и угла между векторами по координатам.
Скалярное произведение векторов.
Скалярное произведение векторов.
 Он-лайн калькуляторы скалярного произведения и угла между векторами по координатам.
Он-лайн калькуляторы скалярного произведения и угла между векторами по координатам.
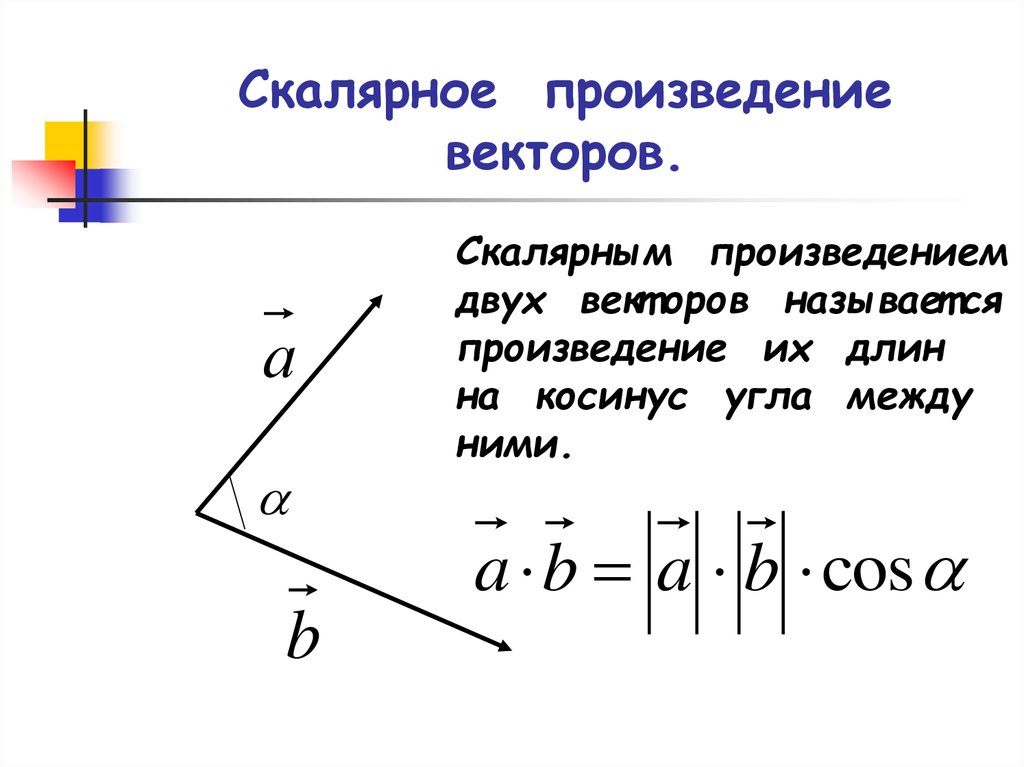
Скалярное произведение векторов — это операция над двумя векторами, результатом которой является число (не вектор).
Определяется скалярное произведение, как правило, следующим образом:
Иными словами, скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними . Необходимо заметить, что угол между двумя векторами — это угол, который они образуют, если отложить их от одной точки, то есть начала векторов должны совпадать.
Непосредственно из определения следуют следующие простейшие свойства:
1. Скалярное произведение произвольного вектора а на себя же (скалярный квадрат вектора а) всегда неотрицательно, и равно квадрату длины этого вектора. Причем скалярный квадрат вектора равен нулю тогда и только тогда, когда данный вектор — нулевой.
2.Скалярное произведение любых перпендикулярных векторов a и b равно нулю.
3.Скалярное произведение двух векторов равно нулю тогда и только тогда, когда они перепендикулярны или хотя бы один из них — нулевой.
4. Скалярное произведение двух векторов a и b положительно тогда и только тогда, когда между ними острый угол.
5.Скалярное произведение двух векторов a и b отрицательно тогда и только тогда, когда между ними тупой угол.
Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами.
(Вычислить координаты вектора, если заданы координаты его начала и его конца очень просто —
Пусть есть вектор AB, А — начало вектора, В — конец, и координаты этих точек
А=(a1,a2,a3), В=(b1,b2,b3)
Тогда координаты вектора АВ:
АВ={b1-a1, b2-a2, b3-a3}.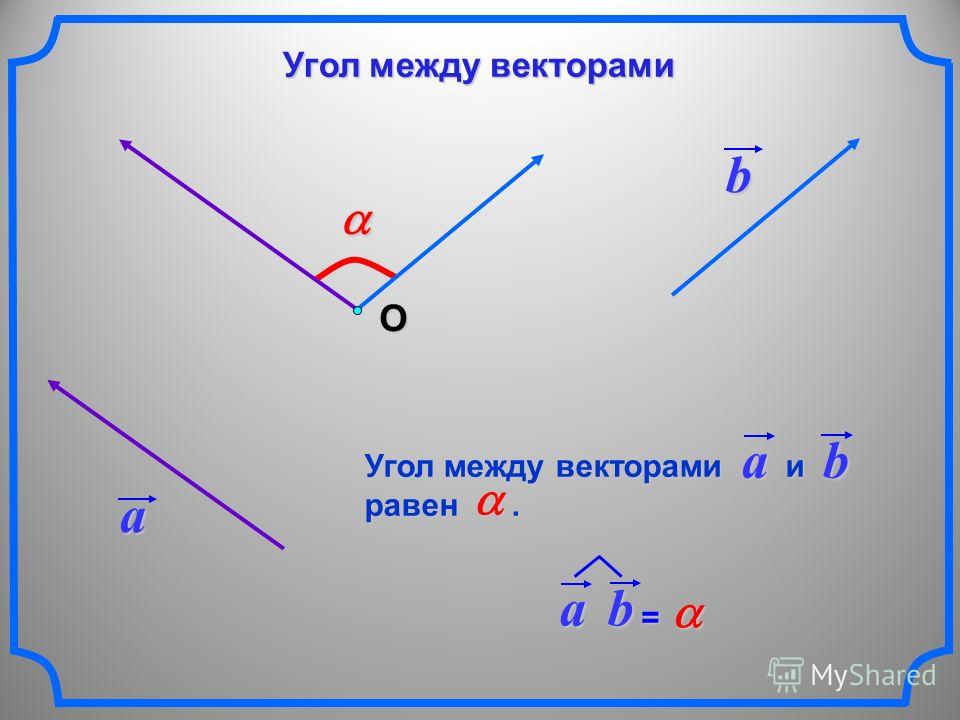
Аналогично в двухмерном пространстве — просто отсутствуют третьи координаты)
Итак, пусть даны два вектора, заданные набором своих координат:
а) В двухмерном пространстве(на плоскости).
Тогда их скалярное произведение можно вычислить по формуле:
б) В трехмерном пространстве
Аналогично двухмерному случаю, их скалярное произведение вычисляется по формуле:
Вычисление угла между векторами с помощью скалярного произведения.
Самое распространенное математическое приложение скалярного произведения двух векторов — это вычисление угла между векторами, заданными своими координатами. Для примера возьмем трехмерный случай. (Если вектора заданы на плоскости, то есть двумя координатами, во всех формулах просто отсутствуют третьи координаты.)
Итак, пусть у нас есть два вектора:
И нам нужно найти угол между ними. С помощью их координат найдем их длины, а затем просто приравняем две формулы для скалярного произведения. Таким образом мы получим косинус искомого угла.
Таким образом мы получим косинус искомого угла.
Длина вектора а вычисляется как корень из скалярного квадрата вектора а, который мы вычислим по формуле для скалярного произведения векторов, заданных координатами:
Аналогично вычисляется длина вектора b.
Итак,
Значит,
Искомый угол найден.
Он-лайн калькулятор скалярного произведения двух векторов.
Чтобы найти скалярное произведение двух векторов с помощью данного калькулятора, нужно ввести в первую строку по порядку координаты первого вектора, во вторую- второго. Координаты векторов могут быть вычислены по координатам их начала и конца (см. выше Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами. )
Если вектора заданы двумя координатами, то на месте третьей координаты каждого вектора нужно поставить ноль.
Он-лайн калькулятор угла между векторами.
Аналогично предыдущему калькулятору, необходимо ввести координаты обоих векторов по порядку, и если вектора заданы двумя координатами — на месте третьих координат следует поставить ноль.
умножение, сложение векторов по правилу многоугольника
Прежде чем приступить к тематике статьи, напомним основные понятия.
Определение 1
Вектор – отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху. При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.
Определение 2
Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху.
Определение 3
Длина вектора – величина, равная или большая нуля, определяющая длину отрезка, составляющего вектор.
Определение 4
Коллинеарные векторы – лежащие на одной прямой или на параллельных прямых.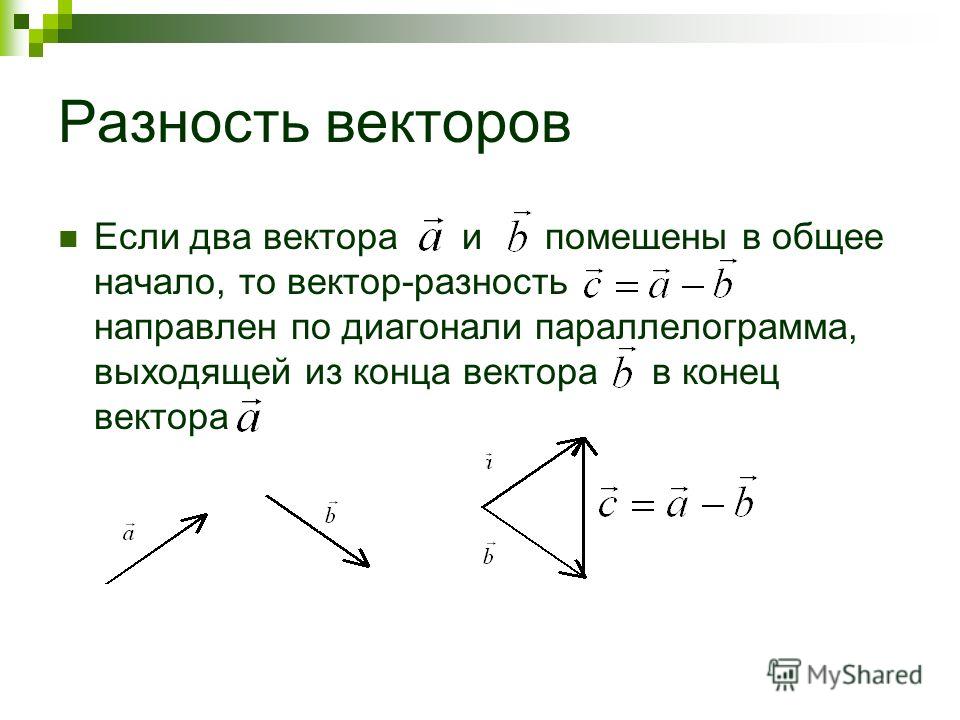 Не выполняющие это условие векторы называют неколлинеарными.
Не выполняющие это условие векторы называют неколлинеарными.
Сложение двух векторов
Определение 5
Исходные данные: векторы a→ и b→ . Для выполнения над ними операции сложения необходимо из произвольной точки отложить вектор AB→, равный вектору а→; из полученной точки undefined – вектор ВС→, равный вектору b→. Соединив точки undefined и C, получаем отрезок (вектор) АС→, который и будет являться суммой исходных данных. Иначе описанную схему сложения векторов называют правилом треугольника.
Геометрически сложение векторов выглядит так:
— для неколлинеарных векторов:
— для коллинеарных (сонаправленных или противоположнонаправленных) векторов:
Сложение нескольких векторов
Взяв за основу описанную выше схему, мы получаем возможность произвести операцию сложения векторов в количестве более 2: поочередно прибавляя каждый последующий вектор.
Определение 6
Исходные данные: векторы a→ , b→, c→,d→. Из произвольной точки А на плоскости необходимо отложить отрезок (вектор), равный вектору a→; затем от конца полученного вектора откладывается вектор, равный вектору b→; далее – по тому же принципу откладываются последующие векторы. Конечной точкой последнего отложенного вектора будет точка B, а полученный отрезок (вектор) AB→ – суммой всех исходных данных. Описанную схему сложения нескольких векторов называют также правилом многоугольника .
Из произвольной точки А на плоскости необходимо отложить отрезок (вектор), равный вектору a→; затем от конца полученного вектора откладывается вектор, равный вектору b→; далее – по тому же принципу откладываются последующие векторы. Конечной точкой последнего отложенного вектора будет точка B, а полученный отрезок (вектор) AB→ – суммой всех исходных данных. Описанную схему сложения нескольких векторов называют также правилом многоугольника .
Геометрически оно выглядит следующим образом:
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Определение 7
Отдельной схемы действия по вычитанию векторов нет, т.к. по сути разность векторов a→и b→есть сумма векторов a→ и — b→.
Умножение вектора на число
Определение 8
Чтобы произвести действие умножения вектора на некое число k, необходимо учитывать следующие правила:
— еслиk>1, то это число приведет к растяжению вектора в k раз;
— если 0<k<1, то это число приведет к сжатию вектора в 1k раз;
— если k<0, то это число приведет к смене направления вектора при одновременном выполнении одного из первых двух правил;
— если k=1, то вектор остается прежним;
— если одно из множителей – нулевой вектор или число, равное нулю, результатом умножения будет нулевой вектор.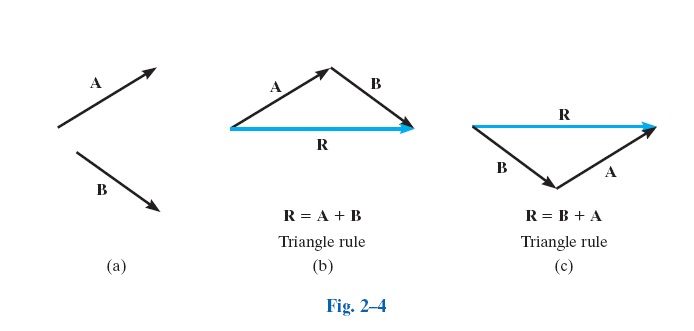
Исходные данные:
1) вектор a→и число k=2;
2) вектор b→и число k=-13.
Геометрически результат умножения в соответствии с указанными выше правилами будет выглядеть следующим образом:
Свойства операций над векторами
Описанным выше операциям над векторами присущи свойства, некоторые из которых очевидны, а прочие можно обосновать геометрически.
Исходные данные: векторы a→, b→, c→и произвольные действительные числа λ и μ.
- Свойство коммутативности: a⇀+b→=b→+a→ .
- Свойство ассоциативности: (a→+b→)+c→=a→+(b→+c→) .
- Свойство использования нейтрального элемента по сложению (нулевой вектор 0→ ⃗). Это очевидное свойство: a→+0→=a→
- Свойство использования нейтрального элемента по умножению (число, равное единице): 1·a→=a→. Это очевидное свойство, не предполагающее никаких геометрических преобразований.
- Любой ненулевой вектор a→ имеет противоположный вектор -a→ и верным является равенство: a→+(-a→)=0→.
 Указанное свойство — очевидное.
Указанное свойство — очевидное. - Сочетательное свойство операции умножения: ( λ · µ ) · a→ = λ · ( µ·a→ ). Например, растяжение вектора при умножении на число 10 можно произвести, сначала растянув вектор в 2 раза, а затем полученный результат еще в 5 раз. Также возможен вариант умножения на число 10 при сжатии вектора в 5 раз и последующего растяжения полученного результата в 50 раз.
- Первое распределительное свойство (очевидно): ( λ + µ ) · a→ = λ ·a→ + µ · a→.
- Второе распределительное свойство: λ · (a→ +b→) = λ ·a→ + λ · b→ .
Геометрически это свойство определяется подобием треугольников:
Свойства коммутативности и ассоциативности дают возможность складывать векторы в произвольном порядке.
Перечисленные свойства операций позволяют осуществлять необходимые преобразования векторно-числовых выражений аналогично привычным числовым. Рассмотрим это на примере.
Пример 1
Задача: упростить выражение a→-2·(b→+3·a→)
Решение
— используя второе распределительное свойство, получим: a→-2·(b→+3·a→)=a→-2·b→-2·(3·a→)
— задействуем сочетательное свойство умножения, выражение приобретет следующий вид: a→-2·b→-2·(3·a→)=a→-2·b→-(2·3)·a→=a→-2·b→-6·a→
— используя свойство коммутативности, меняем местами слагаемые:a→-2·b→-6·a→=a→-6·a→-2·b→
— затем по первому распределительному свойству получаем:a→-6·a→-2·b→=(1-6)·a→-2·b→=-5·a→-2·b→Краткая запись решения будет выглядеть так:a→-2·(b→+3·a→)=a→-2·b→-2·3·a→=5·a→-2·b→
Ответ: a→-2·(b→+3·a→)=-5·a→-2·b→
Умножение векторов — Гипертекст по физике
Обсуждение
скалярно-векторное умножение
Умножение вектора на скаляр изменяет величину вектора, но оставляет его направление неизменным. Скаляр изменяет размер вектора. Скаляр «масштабирует» вектор. Например, вектор полярной формы…
Скаляр изменяет размер вектора. Скаляр «масштабирует» вектор. Например, вектор полярной формы…
r = r r̂ + θ θ̂
, умноженное на скаляр , а получается…
.
a r = ar r̂ + θ θ̂
Умножение вектора на скаляр дистрибутивно.
a ( A + B ) = a A + a B
Следовательно, вектор прямоугольной формы…
r = x î + y ĵ
, умноженное на скаляр , а получается…
.
a r = ax î + ay ĵ
точечный продукт
Геометрически, скалярное произведение двух векторов является величиной, умноженной на проекцию второго на первый.
Символ, используемый для представления этой операции, представляет собой небольшую точку на средней высоте (·), отсюда и произошло название «скалярный продукт». Поскольку это произведение имеет только величину, оно также известно как скалярное произведение .
Поскольку это произведение имеет только величину, оно также известно как скалярное произведение .
A · B = AB cos θ
Скалярное произведение распределительное…
A · ( B + C ) = A · B + A · C
и коммутативный…
A · B = B · A
Поскольку проекция вектора на сам себя оставляет его величину неизменной, точечное произведение любого вектора на себя является квадратом величины этого вектора.
A · A = AA cos 0 ° = A 2
Применение этого следствия к единичным векторам означает, что скалярное произведение любого единичного вектора на себя равно единице. Кроме того, поскольку вектор не имеет проекции, перпендикулярной самому себе, скалярное произведение любого единичного вектора на любой другой равно нулю.
î · î = · = · ̂ = (1) (1) (cos 0 °) = 1
î · = ĵ · k̂ = k̂ · î = (1) (1) (cos 90 °) = 0
Используя эти знания, мы можем вывести формулу для скалярного произведения любых двух векторов в прямоугольной форме.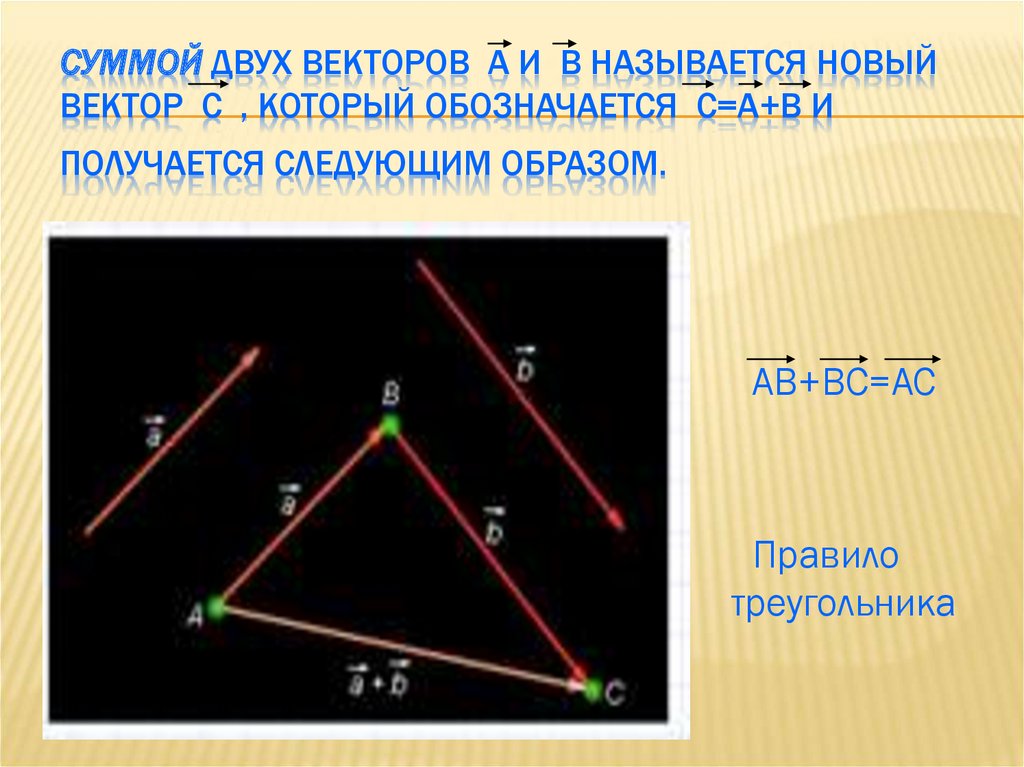 Полученный продукт выглядит так, как будто он будет ужасным беспорядком, но в основном состоит из нулевых членов.
Полученный продукт выглядит так, как будто он будет ужасным беспорядком, но в основном состоит из нулевых членов.
| A · B = | ( A x до + A y ĵ + A z k̂ ) · ( B x до + B 8 y ĵ + B z k̂ ) | |||||||||||
| A · B = | A x или | · | B x или | + | A x или | · | B y ĵ | + | A x или | · | B z k̂ | |
| + | A y ĵ | · | B x или | + | A y ĵ | · | B y ĵ | + | A y ĵ | · | B z k̂ | |
| + | A z k̂ | · | B x или | + | A z k̂ | · | B y ĵ | + | A z k̂ | · | B z k̂ | |
| A · B = | A x B x + A y B y + A z B z | |||||||||||
Скалярное произведение двух векторов, таким образом, является суммой произведений их параллельных компонентов.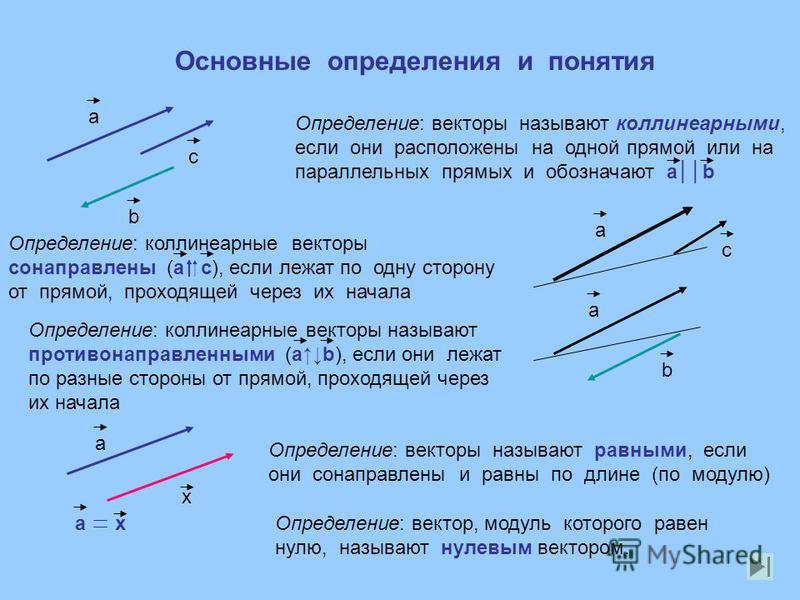 Отсюда мы можем вывести теорему Пифагора в трех измерениях.
Отсюда мы можем вывести теорему Пифагора в трех измерениях.
A · A = AA cos 0 ° = A x A x + A y A y + A z A z
A 2 = A x 2 + A y 2 + A z 2
перекрестное произведение
Геометрически, перекрестное произведение двух векторов — это площадь параллелограмма между ними.
Символ, используемый для представления этой операции, представляет собой большой диагональный крест (×), отсюда и произошло название «перекрестное произведение». Поскольку это произведение имеет величину и направление, оно также известно как векторное произведение .
A × B = AB sin θ n̂
Вектор n̂ (n hat) — это единичный вектор, перпендикулярный плоскости, образованной двумя векторами. Направление n̂ определяется правилом правой руки, которое мы вскоре обсудим.
Направление n̂ определяется правилом правой руки, которое мы вскоре обсудим.
Перекрестное произведение распределительное…
A × ( B + C ) = ( A × B ) + ( A × C )
, но не коммутативный…
A × B = — B × A
Изменение порядка перекрестного умножения меняет направление произведения на противоположное.
Поскольку два идентичных вектора образуют вырожденный параллелограмм без площади , векторное произведение любого вектора на себя равно нулю…
A × A = 0
Применение этого следствия к единичным векторам означает, что произведение любого единичного вектора на себя равно нулю.
î × î = ĵ × ĵ = k̂ × k̂ = (1) (1) (sin 0 °) = 0
Следует отметить, что произведение любого единичного вектора на любой другой будет иметь величину, равную единице.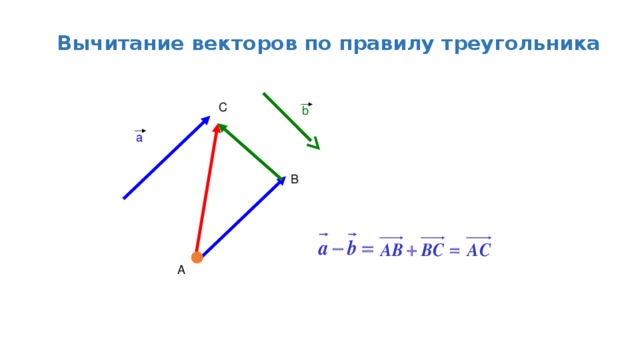 (В конце концов, синус 90 ° равен единице.) Однако направление не является интуитивно очевидным. Правило правой руки для перекрестного умножения связывает направление двух векторов с направлением их произведения. Поскольку перекрестное умножение является , а не коммутативным , порядок операций важен.
(В конце концов, синус 90 ° равен единице.) Однако направление не является интуитивно очевидным. Правило правой руки для перекрестного умножения связывает направление двух векторов с направлением их произведения. Поскольку перекрестное умножение является , а не коммутативным , порядок операций важен.
- Держите правую руку ровно так, чтобы большой палец был перпендикулярен пальцам. Никогда не сгибайте большой палец.
- Укажите пальцами в направлении первого вектора.
- Сориентируйте ладонь так, чтобы при сгибании пальцев они указывали в направлении второго вектора.
- Ваш большой палец теперь указывает в направлении перекрестного произведения.
Правая система координат , которая является обычной системой координат, используемой в физике и математике, — это система, в которой любое циклическое произведение трех осей координат положительно, а любое антициклическое произведение отрицательно.Представьте себе часы с тремя буквами x-y-z вместо обычных двенадцати цифр. Любое произведение этих трех букв, которое круглосуточно движется в том же направлении, что и последовательность x-y-z, равно циклическому и положительному. Любой продукт, который движется в обратном направлении, — это антициклический, и отрицательный.
Любое произведение этих трех букв, которое круглосуточно движется в том же направлении, что и последовательность x-y-z, равно циклическому и положительному. Любой продукт, который движется в обратном направлении, — это антициклический, и отрицательный.
| Перекрестное произведение циклической пары единичных векторов равно положительным . | Перекрестное произведение антициклической пары единичных векторов равно отрицательным . |
Используя эти знания, мы можем вывести формулу для векторного произведения любых двух векторов в прямоугольной форме. Полученный продукт выглядит так, как будто это будет ужасный беспорядок, и это так!
A × B = ( A x î + A y ĵ + A z k̂ ) × ( B x î + B y ĵ + B z k̂ )
Произведение двух трехчленов состоит из девяти членов.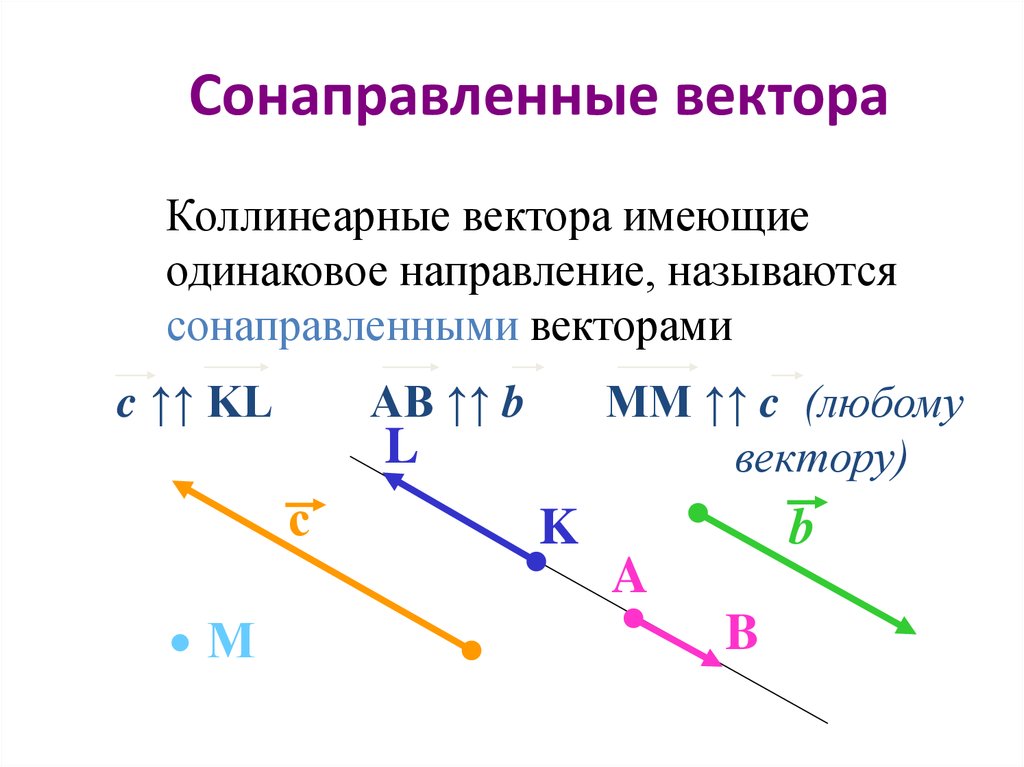
| A × B | = | A x или | × | B x или | + | A x или | × | B y ĵ | + | A x или | × | B z k̂ |
| + | A y ĵ | × | B x или | + | A y ĵ | × | B y ĵ | + | A y ĵ | × | B z k̂ | |
| + | A z k̂ | × | B x или | + | A z k̂ | × | B y ĵ | + | A z k̂ | × | B z k̂ |
Три из них равны нулю.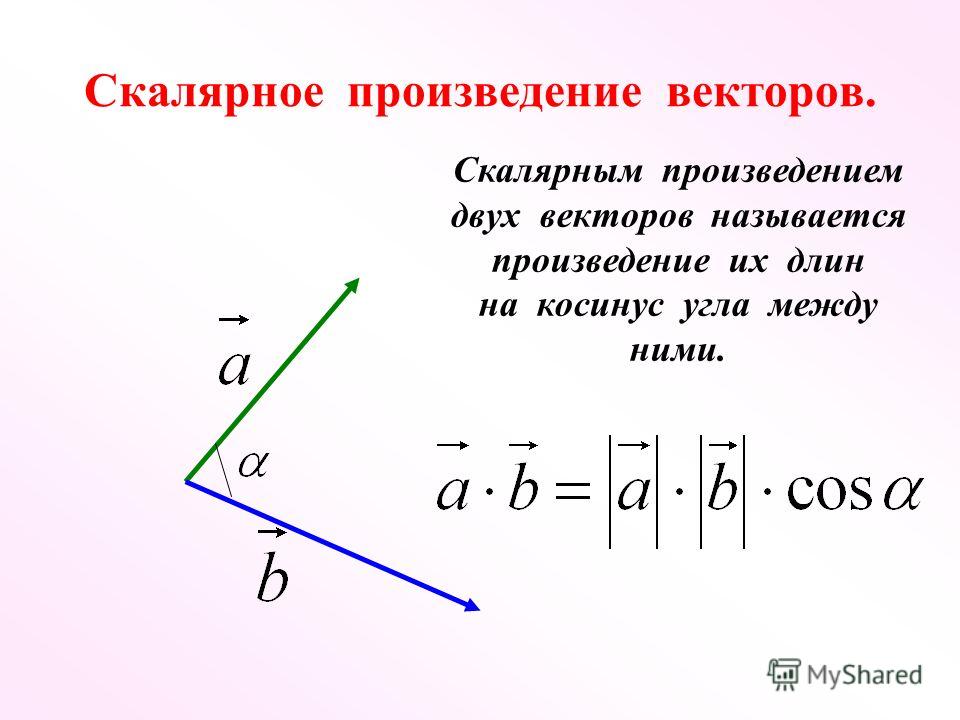 Устраните их.
Устраните их.
| A × B | = | A x B y k̂ | – | A x B z ĵ |
| – | A y B x k̂ | + | A y B z или | |
| + | A z B x ĵ | – | A z B y или |
Сгруппируйте термины по единичному вектору и коэффициенту.
A × B = ( A y B z — A z B y ) î
Есть более простой способ написать это.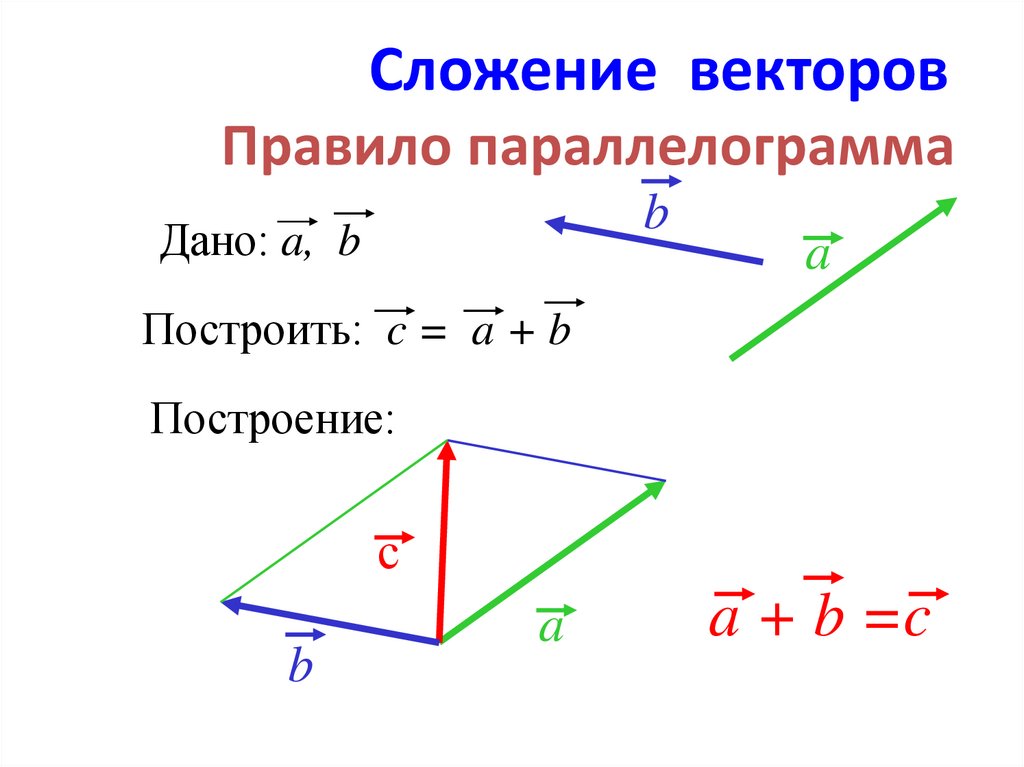 Для тех из вас, кто знаком с матрицами, перекрестное произведение двух векторов является определителем матрицы, первая строка которой является единичными векторами, вторая строка — первым вектором, а третья строка — вторым вектором.Условно…
Для тех из вас, кто знаком с матрицами, перекрестное произведение двух векторов является определителем матрицы, первая строка которой является единичными векторами, вторая строка — первым вектором, а третья строка — вторым вектором.Условно…
| A × B = | до | ĵ | k |
| A x | A y | A z | |
| B x | B y | B z |
Расширение определителя 3 × 3 его первой строкой является первым шагом.Это дает нам три определителя 2 × 2.
| A × B = | A y | A z | до — | A x | A z | ĵ + | A x | A y | k |
| B y | B z | B x | B z | B x | B y |
Эти детерминанты 2 × 2 можно найти быстро. Они также дают нам решение, предварительно отсортированное по единичному вектору, поэтому нет необходимости сортировать термины и множители.
Они также дают нам решение, предварительно отсортированное по единичному вектору, поэтому нет необходимости сортировать термины и множители.
A × B = ( A y B z — A z B y ) î
2.4 произведения векторов | University Physics Volume 1
Вектор можно умножить на другой вектор, но нельзя разделить на другой вектор. Есть два вида произведений векторов, широко используемых в физике и технике. Один из видов умножения — это скалярное умножение двух векторов . В результате скалярного произведения двух векторов получается число (скаляр), как указывает его название. Скалярные произведения используются для определения отношений между работой и энергией. Например, работа, которую сила (вектор) выполняет с объектом, вызывая его смещение (вектор), определяется как скалярное произведение вектора силы на вектор смещения.Совершенно другой вид умножения — это умножение векторов векторов . Получение векторного произведения двух векторов возвращает в результате вектор, как следует из его названия. Векторные произведения используются для определения других производных векторных величин. Например, при описании вращений векторная величина, называемая крутящим моментом , определяется как векторное произведение приложенной силы (вектора) и ее расстояния от точки поворота до силы (вектор). Важно различать эти два вида векторных умножений, потому что скалярное произведение — это скалярная величина, а векторное произведение — это векторная величина.
Например, работа, которую сила (вектор) выполняет с объектом, вызывая его смещение (вектор), определяется как скалярное произведение вектора силы на вектор смещения.Совершенно другой вид умножения — это умножение векторов векторов . Получение векторного произведения двух векторов возвращает в результате вектор, как следует из его названия. Векторные произведения используются для определения других производных векторных величин. Например, при описании вращений векторная величина, называемая крутящим моментом , определяется как векторное произведение приложенной силы (вектора) и ее расстояния от точки поворота до силы (вектор). Важно различать эти два вида векторных умножений, потому что скалярное произведение — это скалярная величина, а векторное произведение — это векторная величина.
Скалярное произведение двух векторов (точечное произведение)
Скалярное умножение двух векторов дает скалярное произведение.
Скалярное произведение (скалярное произведение)
Скалярное произведение [латекс] \ overset {\ to} {A} · \ overset {\ to} {B} [/ latex] двух векторов [латекс] \ overset {\ to} {A} [/ latex ] и [латекс] \ overset {\ to} {B} [/ latex] — это число, определяемое уравнением
[латекс] \ overset {\ to} {A} · \ overset {\ to} {B} = AB \, \ text {cos} \, \ phi, [/ latex]
где [latex] \ phi [/ latex] — угол между векторами (показан на (Рисунок)).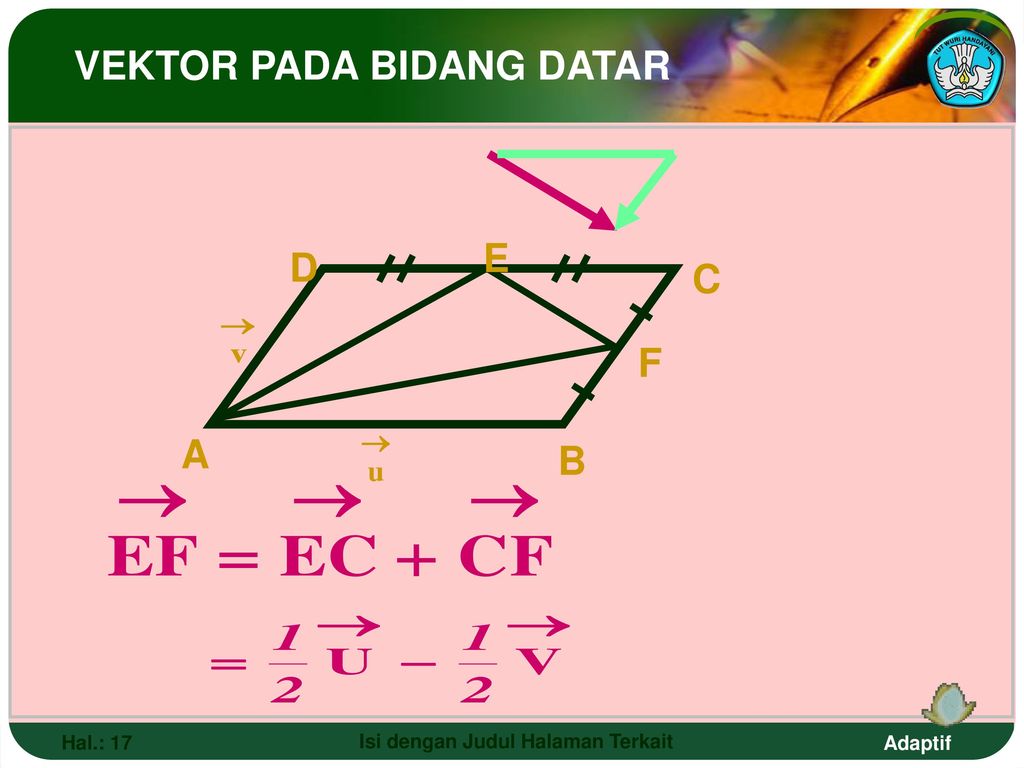 Скалярное произведение также называется скалярным произведением из-за точечной записи, которая его обозначает.
Скалярное произведение также называется скалярным произведением из-за точечной записи, которая его обозначает.
В определении скалярного произведения направление угла [латекс] \ phi [/ latex] не имеет значения, а [латекс] \ phi [/ latex] может быть измерен от одного из двух векторов к другому, потому что [ latex] \ text {cos} \, \ phi = \ text {cos} \, (\ text {-} \ phi) = \ text {cos} \, (2 \ pi — \ phi) [/ latex]. Точечное произведение — отрицательное число, когда [латекс] 90 \ text {°} {2}.[/ латекс]
Рисунок 2.27 Скалярное произведение двух векторов. (а) Угол между двумя векторами. (b) Ортогональная проекция [латекс] {A} _ {\ perp} [/ latex] вектора [латекс] \ overset {\ to} {A} [/ latex] на направление вектора [латекс] \ overset { \ to} {B} [/ латекс]. (c) Ортогональная проекция [латекс] {B} _ {\ perp} [/ latex] вектора [латекс] \ overset {\ to} {B} [/ latex] на направление вектора [латекс] \ overset { \ to} {A} [/ латекс].
Пример
Скалярное произведение
Для векторов, показанных на (Рисунок), найдите скалярное произведение [latex] \ overset {\ to} {A} · \ overset {\ to} {F} [/ latex].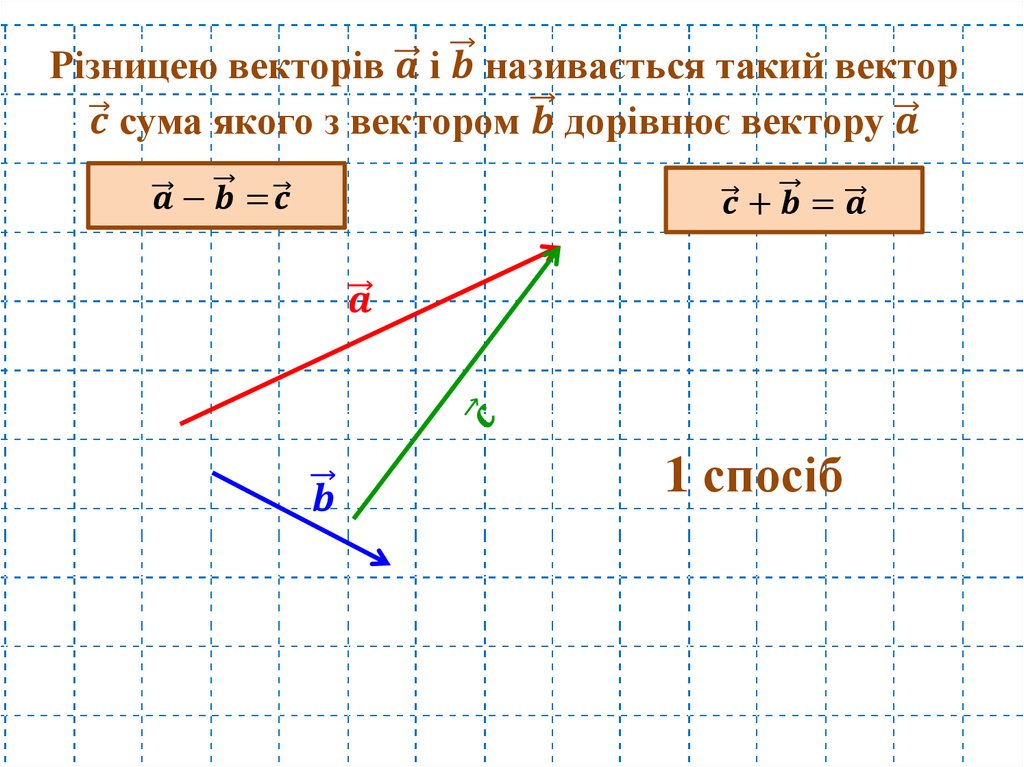
Стратегия
Из (Рисунок), величины векторов [latex] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {F} [/ latex] равны A = 10,0 и F = 20,0. Угол [латекс] \ theta [/ latex] между ними является разницей: [latex] \ theta = \ phi — \ alpha = 110 \ text {°} -35 \ text {°} = 75 \ text {°} [/латекс]. Подстановка этих значений в (рисунок) дает скалярное произведение.
Решение
Покажи ответ
Простой расчет дает нам
[латекс] \ overset {\ to} {A} · \ overset {\ to} {F} = AF \, \ text {cos} \, \ theta = (10.0) (20,0) \, \ text {cos} \, 75 \ text {°} = 51,76. [/ латекс]
Проверьте свое понимание
Для векторов, приведенных на (Рисунок), найдите скалярные произведения [latex] \ overset {\ to} {A} · \ overset {\ to} {B} [/ latex] и [latex] \ overset {\ to} {F} · \ overset {\ to} {C} [/ latex].
Показать решение
[латекс] \ overset {\ to} {A} · \ overset {\ to} {B} = — 57,3 [/ латекс], [латекс] \ overset {\ to} {F} · \ overset {\ to} {C} = 27,8 [/ латекс]
В декартовой системе координат скалярные произведения единичного вектора оси на другие единичные векторы осей всегда обращаются в нуль, потому что эти единичные векторы ортогональны:
[латекс] \ begin {array} {c} \ hat {i} · \ hat {j} = | \ hat {i} || \ hat {j} | \, \ text {cos} \, 90 \ text {°} = (1) (1) (0) = 0, \ hfill \\ \ hat {i} · \ hat {k} = | \ hat {i} || \ hat {k} | \, \ text {cos} \, 90 \ text {°} = (1) (1) (0) = 0, \ hfill \\ \ hat {k} · \ hat {j} = | \ hat {k} || \ hat {j} | \, \ text {cos} \, 90 \ text {°} = (1) (1) (0) = 0. {2} = 1. [/ латекс]
{2} = 1. [/ латекс]
Скалярное произведение [латекс] \ overset {\ to} {A} · \ overset {\ to} {B} [/ latex] также можно интерпретировать как произведение B с ортогональной проекцией [латекс] { A} _ {\ perp} [/ latex] вектора [latex] \ overset {\ to} {A} [/ latex] на направление вектора [latex] \ overset {\ to} {B} [/ latex] ((Рисунок) (b)) или произведение A с ортогональной проекцией [латекс] {B} _ {\ perp} [/ latex] вектора [латекс] \ overset {\ to} {B} [/ латекс] в направлении вектора [латекс] \ overset {\ to} {A} [/ latex] ((Рисунок) (c)):
[латекс] \ begin {array} {ll} \ hfill \ overset {\ to} {A} · \ overset {\ to} {B} & = AB \, \ text {cos} \, \ phi \ hfill \ \ & = B (A \, \ text {cos} \, \ phi) = B {A} _ {\ perp} \ hfill \\ & = A (B \, \ text {cos} \, \ phi) = A {B} _ {\ perp}.\ hfill \ end {array} [/ latex]
Например, в прямоугольной системе координат на плоскости скалярная компонента вектора размером x является его скалярным произведением на единичный вектор [latex] \ hat {i} [/ latex] и скаляр y -компонент вектора — это его скалярное произведение с единичным вектором [latex] \ hat {j} [/ latex]:
[латекс] \ {\ begin {array} {l} \ overset {\ to} {A} · \ hat {i} = | \ overset {\ to} {A} || \ hat {i} | \, \ text {cos} \, {\ theta} _ {A} = A \, \ text {cos} \, {\ theta} _ {A} = {A} _ {x} \\ \ overset {\ to} {A} · \ hat {j} = | \ overset {\ to} {A} || \ hat {j} | \, \ text {cos} \, (90 \ text {°} — {\ theta} _ {A}) = A \, \ text {sin} \, {\ theta} _ {A} = {A} _ {y} \ end {array}.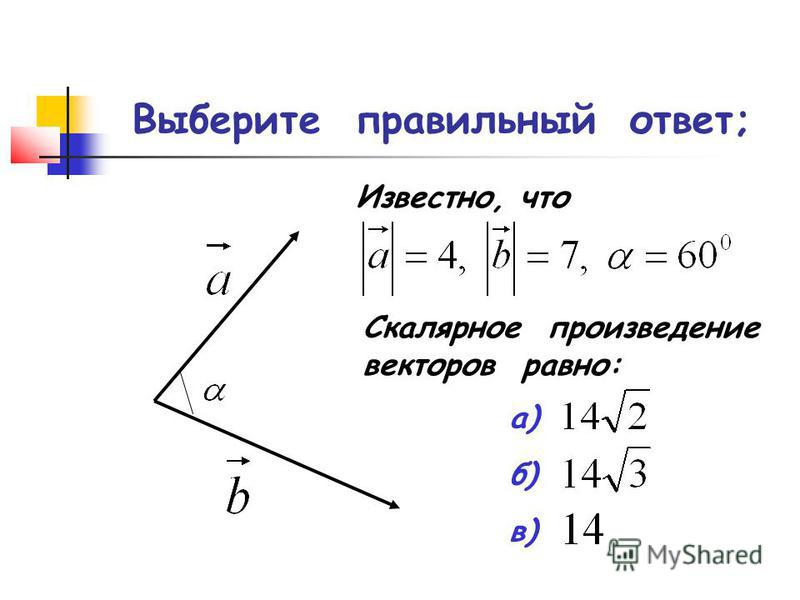 [/ латекс]
[/ латекс]
Скалярное умножение векторов коммутативно,
[латекс] \ overset {\ to} {A} · \ overset {\ to} {B} = \ overset {\ to} {B} · \ overset {\ to} {A}, [/ latex]
и подчиняется закону о распределении доходов:
[латекс] \ overset {\ to} {A} · (\ overset {\ to} {B} + \ overset {\ to} {C}) = \ overset {\ to} {A} · \ overset {\ to} {B} + \ overset {\ to} {A} · \ overset {\ to} {C}. [/ латекс]
Мы можем использовать законы коммутативности и распределения для вывода различных соотношений для векторов, таких как выражение скалярного произведения двух векторов через их скалярные компоненты.
Проверьте свое понимание
Для вектора [латекс] \ overset {\ to} {A} = {A} _ {x} \ hat {i} + {A} _ {y} \ hat {j} + {A} _ {z} \ hat {k} [/ latex] в прямоугольной системе координат, используйте (Рисунок) — (Рисунок), чтобы показать, что [latex] \ overset {\ to} {A} · \ hat {i} = {A} _ {x } [/ латекс] [латекс] \ overset {\ to} {A} · \ hat {j} = {A} _ {y} [/ latex] и [латекс] \ overset {\ to} {A} · \ шляпа {k} = {A} _ {z} [/ latex].
Если векторы на (Рисунок) даны в форме их векторных компонентов,
[латекс] \ overset {\ to} {A} = {A} _ {x} \ hat {i} + {A} _ {y} \ hat {j} + {A} _ {z} \ hat { k} \, \ text {и} \, \ overset {\ to} {B} = {B} _ {x} \ hat {i} + {B} _ {y} \ hat {j} + {B} _ {z} \ hat {k}, [/ latex]
, мы можем вычислить их скалярное произведение следующим образом:
[латекс] \ begin {array} {lll} \ hfill \ overset {\ to} {A} · \ overset {\ to} {B} & = \ hfill & ({A} _ {x} \ hat {i } + {A} _ {y} \ hat {j} + {A} _ {z} \ hat {k}) · ({B} _ {x} \ hat {i} + {B} _ {y} \ hat {j} + {B} _ {z} \ hat {k}) \ hfill \\ & = \ hfill & \ enspace {A} _ {x} {B} _ {x} \ hat {i} · \ hat {i} + {A} _ {x} {B} _ {y} \ hat {i} · \ hat {j} + {A} _ {x} {B} _ {z} \ hat {i } · \ Hat {k} \ hfill \\ & & + {A} _ {y} {B} _ {x} \ hat {j} · \ hat {i} + {A} _ {y} {B} _ {y} \ hat {j} · \ hat {j} + {A} _ {y} {B} _ {z} \ hat {j} · \ hat {k} \ hfill \\ & & + {A } _ {z} {B} _ {x} \, \ hat {k} · \ hat {i} + {A} _ {z} {B} _ {y} \ hat {k} · \ hat {j } + {A} _ {z} {B} _ {z} \, \ hat {k} · \ hat {k}. \ hfill \ end {array} [/ latex]
\ hfill \ end {array} [/ latex]
Поскольку скалярные произведения двух различных единичных векторов осей дают ноль, а скалярные произведения единичных векторов сами на себя дают единицу (см. (Рисунок) и (рисунок)), в этом выражении есть только три ненулевых члена. Таким образом, скалярное произведение упрощается до
.
[латекс] \ overset {\ to} {A} · \ overset {\ to} {B} = {A} _ {x} {B} _ {x} + {A} _ {y} {B} _ {y} + {A} _ {z} {B} _ {z}. [/ латекс]
Мы можем использовать (рисунок) для скалярного произведения в терминах скалярных компонентов векторов, чтобы найти угол между двумя векторами .Когда мы разделим (рисунок) на AB , мы получим уравнение для [latex] \ text {cos} \, \ phi [/ latex], в которое подставим (рисунок):
[латекс] \ text {cos} \, \ phi = \ frac {\ overset {\ to} {A} · \ overset {\ to} {B}} {AB} = \ frac {{A} _ {x } {B} _ {x} + {A} _ {y} {B} _ {y} + {A} _ {z} {B} _ {z}} {AB}. [/ латекс]
Угол [латекс] \ phi [/ latex] между векторами [latex] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {B} [/ latex] получается путем взятия обратный косинус выражения на (рисунок).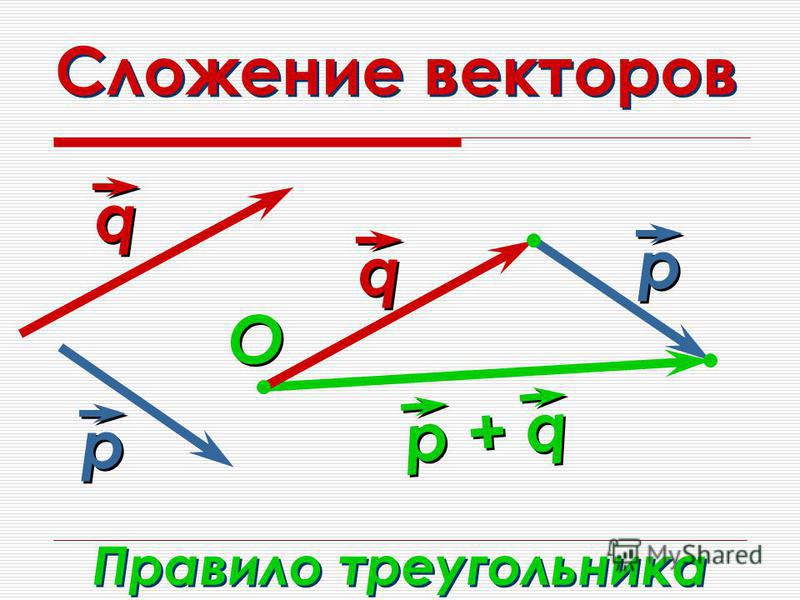
Пример
Угол между двумя силами
Три собаки тянут палку в разные стороны, как показано на (Рисунок). Первая собака тянет с силой [латекс] {\ overset {\ to} {F}} _ {1} = (10.0 \ hat {i} -20.4 \ hat {j} +2.0 \ hat {k}) \ text { N} [/ latex], вторая собака тянет с силой [latex] {\ overset {\ to} {F}} _ {2} = (- 15.0 \ hat {i} -6.2 \ hat {k}) \ text {N} [/ latex], а третья собака тянет с силой [латекс] {\ overset {\ to} {F}} _ {3} = (5.0 \ hat {i} +12.5 \ hat {j}) \ текст {N} [/ latex]. Каков угол между силами [латекс] {\ overset {\ to} {F}} _ {1} [/ latex] и [латекс] {\ overset {\ to} {F}} _ {2} [/ latex ]?
Рисунок 2.28 Три собаки играют с палкой.
Стратегия
Компоненты вектора силы [латекс] {\ overset {\ to} {F}} _ {1} [/ latex] равны [латекс] {F} _ {1x} = 10.0 \, \ text {N} [/ латекс], [латекс] {F} _ {1y} = — 20,4 \, \ text {N} [/ latex] и [латекс] {F} _ {1z} = 2,0 \, \ text {N} [/ латекс], а вектор силы [латекс] {\ overset {\ to} {F}} _ {2} [/ latex] — [латекс] {F} _ {2x} = — 15. 0 \, \ text {N } [/ latex], [latex] {F} _ {2y} = 0.0 \, \ text {N} [/ latex] и [latex] {F} _ {2z} = — 6.2 \, \ text {N } [/ латекс].{-1} (- 0,439) = 116,0 \ text {°}. [/ латекс]
0 \, \ text {N } [/ latex], [latex] {F} _ {2y} = 0.0 \, \ text {N} [/ latex] и [latex] {F} _ {2z} = — 6.2 \, \ text {N } [/ латекс].{-1} (- 0,439) = 116,0 \ text {°}. [/ латекс]
Значение
Обратите внимание, что когда векторы задаются в терминах единичных векторов осей, мы можем найти угол между ними, не зная специфики географических направлений, которые представляют единичные векторы. Здесь, например, направление + x может быть на восток, а направление + y — на север. Но угол между силами в задаче будет таким же, если направление + x направлено на запад, а направление + y — на юг.
Проверьте свое понимание
Найдите угол между силами [латекс] {\ overset {\ to} {F}} _ {1} [/ latex] и [латекс] {\ overset {\ to} {F}} _ {3} [/ latex ] в (рисунок).
Показать решение
[латекс] 131.9 \ text {°} [/ латекс]
Пример
Работа силы
Когда сила [латекс] \ overset {\ to} {F} [/ latex] тянет объект и вызывает его смещение [латекс] \ overset {\ to} {D} [/ latex], мы говорим, что сила выполняет работу. Количество работы, которое совершает сила, — это скалярное произведение [латекс] \ overset {\ to} {F} · \ overset {\ to} {D} [/ latex].Если палка на (рис.) На мгновение сдвинется и смещается вектором [латекс] \ overset {\ to} {D} = (- 7.9 \ hat {j} -4.2 \ hat {k}) \, \ text {cm} [/ latex], сколько работы проделывает третья собака на (Рисунок)?
Количество работы, которое совершает сила, — это скалярное произведение [латекс] \ overset {\ to} {F} · \ overset {\ to} {D} [/ latex].Если палка на (рис.) На мгновение сдвинется и смещается вектором [латекс] \ overset {\ to} {D} = (- 7.9 \ hat {j} -4.2 \ hat {k}) \, \ text {cm} [/ latex], сколько работы проделывает третья собака на (Рисунок)?
Стратегия
Мы вычисляем скалярное произведение вектора смещения [latex] \ overset {\ to} {D} [/ latex] на вектор силы [latex] {\ overset {\ to} {F}} _ {3} = (5.0 \ hat {i} +12.5 \ hat {j}) \ text {N} [/ latex], который является натяжением третьей собаки. Давайте использовать [latex] {W} _ {3} [/ latex] для обозначения работы, выполняемой силой [latex] {\ overset {\ to} {F}} _ {3} [/ latex] при перемещении [латекс] \ overset {\ to} {D} [/ латекс].
Решение
Покажи ответ
Расчет работы — это простое применение скалярного произведения:
[латекс] \ begin {array} {cc} \ hfill {W} _ {3} & = {\ overset {\ to} {F}} _ {3} · \ overset {\ to} {D} = { F} _ {3x} {D} _ {x} + {F} _ {3y} {D} _ {y} + {F} _ {3z} {D} _ {z} \ hfill \\ & = ( 5.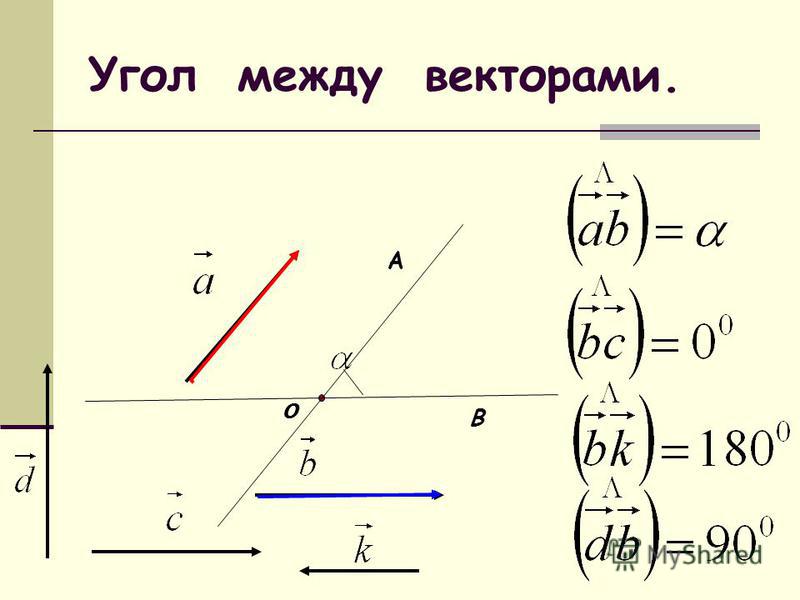 0 \, \ text {N}) (0.0 \, \ text {cm}) + (12.5 \, \ text {N}) (- 7.9 \, \ text {cm}) + (0.0 \, \ text {N }) (- 4.2 \, \ text {cm}) \ hfill \\ & = -98.7 \, \ text {N} · \ text {cm}. \ Hfill \ end {array} [/ latex]
0 \, \ text {N}) (0.0 \, \ text {cm}) + (12.5 \, \ text {N}) (- 7.9 \, \ text {cm}) + (0.0 \, \ text {N }) (- 4.2 \, \ text {cm}) \ hfill \\ & = -98.7 \, \ text {N} · \ text {cm}. \ Hfill \ end {array} [/ latex]
Значение
Единица работы в системе СИ называется джоуль [латекс] (\ text {J}) [/ latex], где 1 Дж = 1 [латекс] \ text {N} · \ text {m} [/ latex].{-2} \ text {J} [/ latex], поэтому ответ можно выразить как [latex] {W} _ {3} = — 0,9875 \, \ text {J} \ приблизительно -1,0 \, \ text { J} [/ латекс].
Проверьте свое понимание
Сколько работы выполняет первая собака и вторая собака на (Рис.) Над смещением на (Рис.)?
Показать решение
[латекс] {W} _ {1} = 1,5 \, \ text {J} [/ latex], [латекс] {W} _ {2} = 0,3 \, \ text {J} [/ latex]
Векторное произведение двух векторов (перекрестное произведение)
Векторное умножение двух векторов дает векторное произведение.
Векторное произведение (перекрестное произведение)
Векторное произведение двух векторов [латекс] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {B} [/ latex] обозначается [латекс] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} [/ latex] и часто упоминается как перекрестное произведение . Векторное произведение — это вектор, направление которого перпендикулярно обоим векторам [latex] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {B} [/ latex]. Другими словами, вектор [латекс] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} [/ latex] перпендикулярен плоскости, содержащей векторы [латекс] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {B} [/ latex], как показано на (Рисунок).Величина векторного произведения определяется как
Векторное произведение — это вектор, направление которого перпендикулярно обоим векторам [latex] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {B} [/ latex]. Другими словами, вектор [латекс] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} [/ latex] перпендикулярен плоскости, содержащей векторы [латекс] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {B} [/ latex], как показано на (Рисунок).Величина векторного произведения определяется как
.
[латекс] | \ overset {\ to} {A} \, × \, \ overset {\ to} {B} | = \, AB \, \ text {sin} \, \ phi, [/ latex]
, где угол [латекс] \ phi [/ latex] между двумя векторами измеряется от вектора [latex] \ overset {\ to} {A} [/ latex] (первый вектор в продукте) до вектора [латекс] \ overset {\ to} {B} [/ latex] (второй вектор в продукте), как показано на (Рисунок), и находится между [latex] 0 \ text {°} [/ latex] и [latex] 180 \ текст {°} [/ латекс].
Согласно (Рисунок), векторное произведение исчезает для пар векторов, которые либо параллельны [латекс] (\ phi = 0 \ text {°}) [/ latex], либо антипараллельны [латекс] (\ phi = 180 \ text { °}) [/ latex], потому что [латекс] \ text {sin} \, 0 \ text {°} = \ text {sin} \, 180 \ text {°} = 0 [/ latex].
Рисунок 2.29 Векторное произведение двух векторов нарисовано в трехмерном пространстве. (a) Векторное произведение [латекс] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} [/ latex] — это вектор, перпендикулярный плоскости, который содержит векторы [латекс] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {B} [/ latex]. Маленькие квадраты, нарисованные в перспективе, обозначают прямые углы между [латексом] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {C} [/ latex], а также между [latex] \ overset {\ to} {B} [/ latex] и [latex] \ overset {\ to} {C} [/ latex], так что если [latex] \ overset {\ to} {A} [/ latex] и [latex ] \ overset {\ to} {B} [/ latex] лежать на полу, вектор [latex] \ overset {\ to} {C} [/ latex] направлен вертикально вверх к потолку.(b) Векторное произведение [латекс] \ overset {\ to} {B} \, × \, \ overset {\ to} {A} [/ latex] является вектором, антипараллельным вектору [латекс] \ overset {\ to } {A} \, × \, \ overset {\ to} {B} [/ latex].
На линии, перпендикулярной плоскости, которая содержит векторы [латекс] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {B} [/ latex], есть два альтернативных направления — либо вверх, либо вниз, как показано на (Рисунок) — и направление векторного произведения может быть одним из них. В стандартной правой ориентации, когда угол между векторами измеряется против часовой стрелки от первого вектора, vector [latex] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} [/ латекс] указывает вверх на , как показано на (Рисунок) (а).Если мы изменим порядок умножения на обратный, так что теперь [latex] \ overset {\ to} {B} [/ latex] идет первым в продукте, затем vector [latex] \ overset {\ to} {B} \, × \, \ overset {\ to} {A} [/ latex] должен указывать вниз на , как показано на (Рисунок) (b). Это означает, что векторы [латекс] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} [/ latex] и [latex] \ overset {\ to} {B} \, × \, \ overset {\ to} {A} [/ latex] антипараллельны друг другу, а умножение вектора не коммутативно , а антикоммутативно . Антикоммутативное свойство означает, что векторное произведение меняет знак при обратном порядке умножения:
Антикоммутативное свойство означает, что векторное произведение меняет знак при обратном порядке умножения:
[латекс] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} = \ text {-} \ overset {\ to} {B} \, × \, \ overset { \ to} {A}. [/ латекс]
Штопор , правый Правило — это обычная мнемоника, используемая для определения направления векторного произведения. Как показано на (Рисунок), штопор помещается в направлении, перпендикулярном плоскости, которая содержит векторы [латекс] \ overset {\ to} {A} [/ latex] и [латекс] \ overset {\ to} {B} [/ latex], а его ручка повернута в направлении от первого вектора ко второму в изделии.Направление поперечного произведения задается движением штопора.
Рис. 2.30 Правило правой руки штопора можно использовать для определения направления перекрестного произведения [латекс] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} [/ латекс]. Поместите штопор в направлении, перпендикулярном плоскости, содержащей векторы [латекс] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {B} [/ latex], и поверните его в направлении от первого вектора ко второму в произведении. Направление поперечного произведения задается движением штопора. (а) Движение вверх означает, что вектор перекрестного произведения направлен вверх. (b) Движение вниз означает, что вектор перекрестного произведения направлен вниз.
Направление поперечного произведения задается движением штопора. (а) Движение вверх означает, что вектор перекрестного произведения направлен вверх. (b) Движение вниз означает, что вектор перекрестного произведения направлен вниз.
Пример
Крутящий момент силы
Механическое преимущество, которое дает знакомый инструмент под названием гаечный ключ ((Рисунок)), зависит от величины F приложенного усилия, его направления по отношению к рукоятке гаечного ключа и от того, насколько далеко от гайки это усилие. применяемый.Расстояние R от гайки до точки, где приложен вектор силы [latex] \ overset {\ to} {F} [/ latex], и представлено радиальным вектором [latex] \ overset {\ to} {R } [/ латекс]. Физическая векторная величина, которая заставляет гайку поворачиваться, называется крутящим моментом (обозначается [latex] \ overset {\ to} {\ tau}) [/ latex], и это векторное произведение расстояния между стержнем и силой с силой: [латекс] \ overset {\ to} {\ tau} = \ overset {\ to} {R} \, × \, \ overset {\ to} {F} [/ latex].
Чтобы ослабить ржавую гайку, к рукоятке гаечного ключа прикладывают усилие 20,00 Н под углом [латекс] \ phi = 40 \ text {°} [/ latex] и на расстоянии 0,25 м от гайки, как показано на (Рисунок) (а). Найдите величину и направление крутящего момента, прилагаемого к гайке. Каковы были бы величина и направление крутящего момента, если бы сила была приложена под углом [латекс] \ phi = 45 \ text {°} [/ latex], как показано на (Рисунок) (b)? Для какого значения угла [латекс] \ фи [/ латекс] крутящий момент имеет наибольшую величину?
Рисунок 2.31 Гаечный ключ обеспечивает сцепление и механическое преимущество при приложении крутящего момента для поворота гайки. (a) Поверните против часовой стрелки, чтобы ослабить гайку. (b) Поверните по часовой стрелке, чтобы затянуть гайку.
Стратегия
Мы принимаем систему отсчета, показанную на (Рисунок), где векторы [латекс] \ overset {\ to} {R} [/ latex] и [latex] \ overset {\ to} {F} [/ latex] лежат в плоскость xy , а исходная точка находится в положении гайки. Радиальное направление вдоль вектора [латекс] \ overset {\ to} {R} [/ latex] (указывающее от начала координат) является опорным направлением для измерения угла [латекс] \ phi [/ latex], потому что [латекс] \ overset {\ to} {R} [/ latex] — это первый вектор в векторном произведении [latex] \ overset {\ to} {\ tau} = \ overset {\ to} {R} \, × \, \ overset {\ to} {F} [/ латекс].Вектор [latex] \ overset {\ to} {\ tau} [/ latex] должен лежать вдоль оси z , потому что это ось, перпендикулярная плоскости xy , где оба [latex] \ overset {\ to} {R} [/ latex] и [latex] \ overset {\ to} {F} [/ latex] лгут. Чтобы вычислить величину [латекс] \ тау [/ латекс], мы используем (рисунок). Чтобы найти направление [latex] \ overset {\ to} {\ tau} [/ latex], мы используем правило правой руки со штопором ((Рисунок)).
Радиальное направление вдоль вектора [латекс] \ overset {\ to} {R} [/ latex] (указывающее от начала координат) является опорным направлением для измерения угла [латекс] \ phi [/ latex], потому что [латекс] \ overset {\ to} {R} [/ latex] — это первый вектор в векторном произведении [latex] \ overset {\ to} {\ tau} = \ overset {\ to} {R} \, × \, \ overset {\ to} {F} [/ латекс].Вектор [latex] \ overset {\ to} {\ tau} [/ latex] должен лежать вдоль оси z , потому что это ось, перпендикулярная плоскости xy , где оба [latex] \ overset {\ to} {R} [/ latex] и [latex] \ overset {\ to} {F} [/ latex] лгут. Чтобы вычислить величину [латекс] \ тау [/ латекс], мы используем (рисунок). Чтобы найти направление [latex] \ overset {\ to} {\ tau} [/ latex], мы используем правило правой руки со штопором ((Рисунок)).
Решение
Покажи ответ
Для ситуации в (а) правило штопора дает направление [латекс] \ overset {\ to} {R} \, × \, \ overset {\ to} {F} [/ latex] в положительном направлении ось z. Физически это означает, что вектор крутящего момента [latex] \ overset {\ to} {\ tau} [/ latex] направлен за пределы страницы перпендикулярно рукоятке гаечного ключа. Мы определяем F = 20,00 N и R = 0,25 м и вычисляем величину, используя (Рисунок):
Физически это означает, что вектор крутящего момента [latex] \ overset {\ to} {\ tau} [/ latex] направлен за пределы страницы перпендикулярно рукоятке гаечного ключа. Мы определяем F = 20,00 N и R = 0,25 м и вычисляем величину, используя (Рисунок):
[латекс] \ tau \, = | \ overset {\ to} {R} \, × \, \ overset {\ to} {F} | = \, RF \, \ text {sin} \, \ phi = (0,25 \, \ text {m}) (20,00 \, \ text {N}) \, \ text {sin} \, 40 \ text {°} = 3,21 \, \ text {N} · \ text {m} . [/ latex] Для ситуации в (b) правило штопора дает направление [latex] \ overset {\ to} {R} \, × \, \ overset {\ to} {F} [/ latex] в отрицательное направление оси z.Физически это означает, что вектор [латекс] \ overset {\ to} {\ tau} [/ latex] указывает на страницу перпендикулярно рукоятке гаечного ключа. Величина этого крутящего момента
[латекс] \ tau \, = | \ overset {\ to} {R} \, × \, \ overset {\ to} {F} | = \, RF \, \ text {sin} \, \ phi = (0,25 \, \ text {m}) (20,00 \, \ text {N}) \, \ text {sin} \, 45 \ text {°} = 3,53 \, \ text {N} · \ text {m} . [/ latex] Крутящий момент имеет наибольшее значение, когда [latex] \ text {sin} \, \ phi = 1 [/ latex], что происходит, когда [latex] \ phi = 90 \ text {°} [/ latex]. Физически это означает, что гаечный ключ наиболее эффективен — давая нам лучшее механическое преимущество — когда мы прикладываем силу перпендикулярно рукоятке гаечного ключа.Для ситуации в этом примере это значение наилучшего крутящего момента [latex] {\ tau} _ {\ text {best}} = RF = (0.25 \, \ text {m}) (20.00 \, \ text {N} ) = 5,00 \, \ text {N} · \ text {m} [/ latex].
[/ latex] Крутящий момент имеет наибольшее значение, когда [latex] \ text {sin} \, \ phi = 1 [/ latex], что происходит, когда [latex] \ phi = 90 \ text {°} [/ latex]. Физически это означает, что гаечный ключ наиболее эффективен — давая нам лучшее механическое преимущество — когда мы прикладываем силу перпендикулярно рукоятке гаечного ключа.Для ситуации в этом примере это значение наилучшего крутящего момента [latex] {\ tau} _ {\ text {best}} = RF = (0.25 \, \ text {m}) (20.00 \, \ text {N} ) = 5,00 \, \ text {N} · \ text {m} [/ latex].
Значение
При решении задач механики нам часто вообще не нужно использовать правило штопора, как мы сейчас увидим в следующем эквивалентном решении. Обратите внимание: как только мы определили, что вектор [латекс] \ overset {\ to} {R} \, × \, \ overset {\ to} {F} [/ latex] лежит вдоль оси z , мы можем написать этот вектор в терминах единичного вектора [latex] \ hat {k} [/ latex] оси z :
[латекс] \ overset {\ to} {R} \, × \, \ overset {\ to} {F} = RF \, \ text {sin} \, \ phi \ hat {k}. [/ латекс]
[/ латекс]
В этом уравнении число, умножающее [latex] \ hat {k} [/ latex], является скалярной z -компонентой вектора [latex] \ overset {\ to} {R} \, × \, \ overset {\ to} {F} [/ latex]. При вычислении этого компонента необходимо следить за тем, чтобы угол [латекс] \ phi [/ latex] измерялся против часовой стрелки от [latex] \ overset {\ to} {R} [/ latex] (первый вектор) до [латекс] \ overset {\ to} {F} [/ latex] (второй вектор). Следуя этому принципу для углов, мы получаем [latex] RF \, \ text {sin} \, (+ 40 \ text {°}) = + 3.2 \, \ text {N} · \ text {m} [/ latex] для ситуации в (a), и мы получаем [latex] RF \, \ text {sin} \, (- 45 \ text {°} ) = — 3.5 \, \ text {N} · \ text {m} [/ latex] для ситуации в (b). В последнем случае угол отрицательный, потому что график на (Рисунок) показывает, что угол измеряется по часовой стрелке; но тот же результат получается, когда этот угол измеряется против часовой стрелки, потому что [латекс] + (360 \ text {°} -45 \ text {°}) = + 315 \ text {°} [/ latex] и [latex] \ текст {грех} \, (+ 315 \ текст {°}) = \ текст {грех} \, (- 45 \ текст {°}) [/ латекс].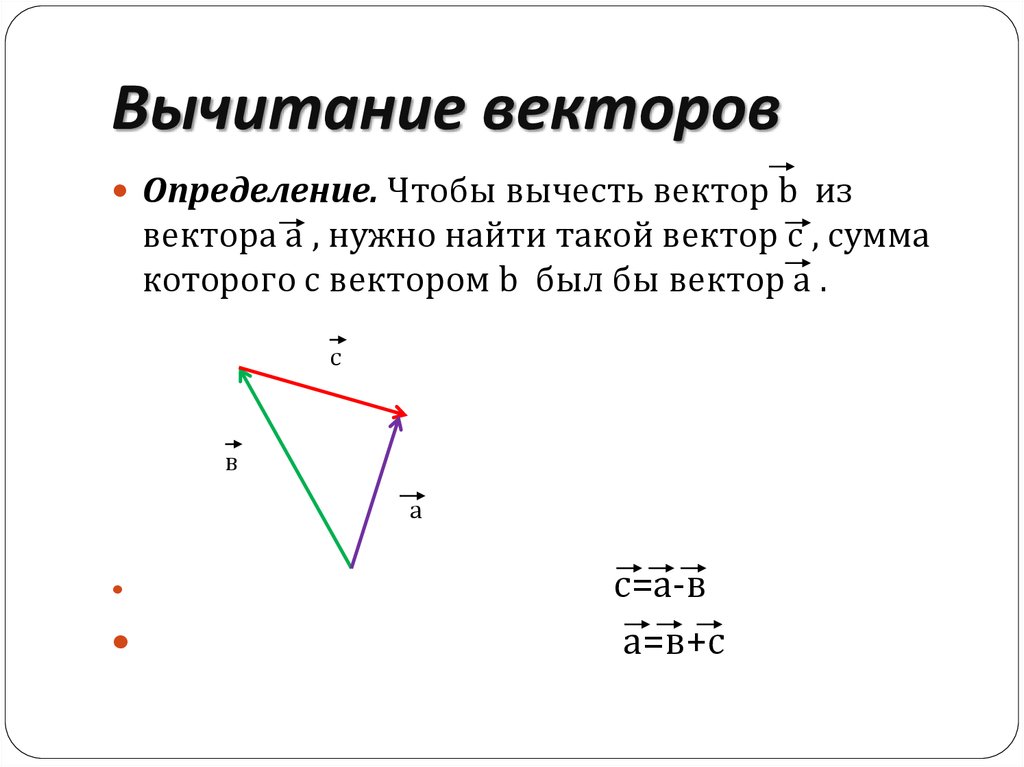 Таким образом, мы получаем решение без привязки к правилу штопора. Для ситуации в (a) решением является [latex] \ overset {\ to} {R} \, × \, \ overset {\ to} {F} = + 3.2 \, \ text {N} · \ text {м} \ шляпа {к} [/ латекс]; для ситуации в (b) решением является [latex] \ overset {\ to} {R} \, × \, \ overset {\ to} {F} = — 3.5 \, \ text {N} · \ text {m} \ hat {k} [/ латекс].
Таким образом, мы получаем решение без привязки к правилу штопора. Для ситуации в (a) решением является [latex] \ overset {\ to} {R} \, × \, \ overset {\ to} {F} = + 3.2 \, \ text {N} · \ text {м} \ шляпа {к} [/ латекс]; для ситуации в (b) решением является [latex] \ overset {\ to} {R} \, × \, \ overset {\ to} {F} = — 3.5 \, \ text {N} · \ text {m} \ hat {k} [/ латекс].
Проверьте свое понимание
Для векторов, указанных на (Рисунок), найдите векторные произведения [latex] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} [/ latex] и [latex] \ overset {\ to} {C} \, × \, \ overset {\ to} {F} [/ latex].
Показать решение
[латекс] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} = — 40.1 \ hat {k} [/ latex] или, что то же самое, [латекс] | \ overset { \ to} {A} \, × \, \ overset {\ to} {B} | = 40,1 [/ latex], направление — внутрь страницы; [латекс] \ overset {\ to} {C} \, × \, \ overset {\ to} {F} = + 157.6 \ hat {k} [/ latex] или, что то же самое, [латекс] | \ overset {\ to} {C} \, × \, \ overset {\ to} {F} | = 157,6 [/ latex], и направление — вне страницы.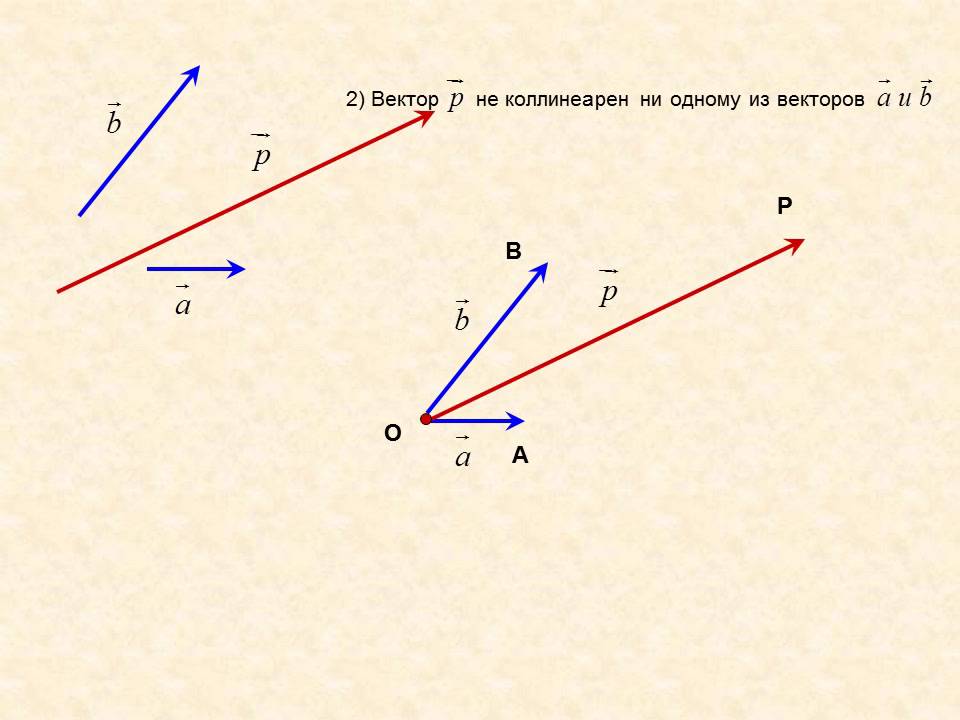
Подобно скалярному произведению ((Рисунок)), перекрестное произведение имеет следующее свойство распределения:
[латекс] \ overset {\ to} {A} \, × \, (\ overset {\ to} {B} + \ overset {\ to} {C}) = \ overset {\ to} {A} \ , × \, \ overset {\ to} {B} + \ overset {\ to} {A} \, × \, \ overset {\ to} {C}.[/ латекс]
Свойство распределения часто применяется, когда векторы выражаются в их составных формах в терминах единичных векторов декартовых осей.
Когда мы применяем определение перекрестного произведения (рисунок) к единичным векторам [latex] \ hat {i} [/ latex], [latex] \ hat {j} [/ latex] и [latex] \ hat {k} [/ latex], которые определяют положительные x -, y — и z — направления в пространстве, мы находим, что
[латекс] \ hat {i} \, × \, \ hat {i} = \ hat {j} \, × \, \ hat {j} = \ hat {k} \, × \, \ hat {k } = 0.[/ латекс]
Все другие перекрестные произведения этих трех единичных векторов должны быть векторами единичной величины, потому что [latex] \ hat {i} [/ latex], [latex] \ hat {j} [/ latex] и [latex] \ hat { k} [/ latex] ортогональны.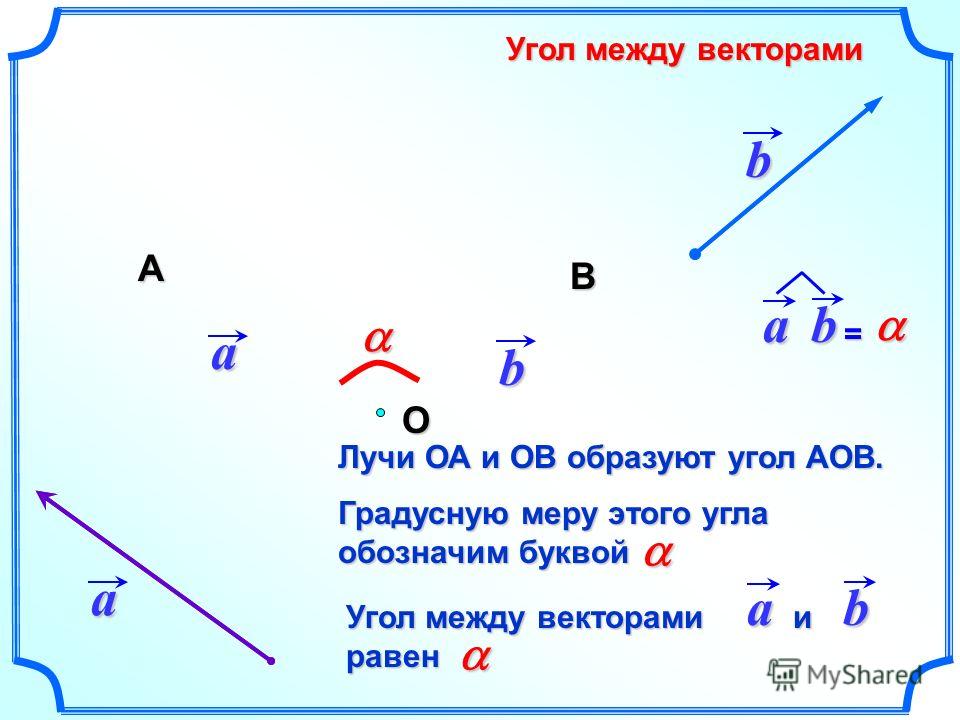 Например, для пары [латекс] \ hat {i} [/ latex] и [latex] \ hat {j} [/ latex] величина будет [latex] | \ hat {i} \, × \, \ шляпа {j} | = ij \, \ text {sin} \, 90 \ text {°} = (1) (1) (1) = 1 [/ latex]. Направление векторного произведения [латекс] \ hat {i} \, × \, \ hat {j} [/ latex] должно быть ортогонально плоскости xy , что означает, что оно должно быть вдоль z — ось.Единственные единичные векторы вдоль оси z — это [latex] \ text {-} \ hat {k} [/ latex] или [latex] + \ hat {k} [/ latex]. По правилу штопора направление вектора [латекс] \ hat {i} \, × \, \ hat {j} [/ latex] должно быть параллельно положительной оси z . Следовательно, результат умножения [latex] \ hat {i} \, × \, \ hat {j} [/ latex] идентичен [latex] + \ hat {k} [/ latex]. Мы можем повторить аналогичные рассуждения для остальных пар единичных векторов. Результатом умножения будет
Например, для пары [латекс] \ hat {i} [/ latex] и [latex] \ hat {j} [/ latex] величина будет [latex] | \ hat {i} \, × \, \ шляпа {j} | = ij \, \ text {sin} \, 90 \ text {°} = (1) (1) (1) = 1 [/ latex]. Направление векторного произведения [латекс] \ hat {i} \, × \, \ hat {j} [/ latex] должно быть ортогонально плоскости xy , что означает, что оно должно быть вдоль z — ось.Единственные единичные векторы вдоль оси z — это [latex] \ text {-} \ hat {k} [/ latex] или [latex] + \ hat {k} [/ latex]. По правилу штопора направление вектора [латекс] \ hat {i} \, × \, \ hat {j} [/ latex] должно быть параллельно положительной оси z . Следовательно, результат умножения [latex] \ hat {i} \, × \, \ hat {j} [/ latex] идентичен [latex] + \ hat {k} [/ latex]. Мы можем повторить аналогичные рассуждения для остальных пар единичных векторов. Результатом умножения будет
.
[латекс] \ {\ begin {array} {l} \ hat {i} \, × \, \ hat {j} = + \ hat {k}, \\ \ hat {j} \, × \, \ hat {k} = + \ hat {i}, \\ \ hat {k} \, × \, \ hat {i} = + \ hat {j}. \ end {array} [/ latex]
\ end {array} [/ latex]
Обратите внимание, что на (Рисунок) три единичных вектора [latex] \ hat {i} [/ latex], [latex] \ hat {j} [/ latex] и [latex] \ hat {k} [/ latex ] появляются в циклическом порядке , показанном на диаграмме (Рисунок) (a). Циклический порядок означает, что в формуле продукта [latex] \ hat {i} [/ latex] следует за [latex] \ hat {k} [/ latex] и предшествует [latex] \ hat {j} [/ latex] , или [латекс] \ hat {k} [/ latex] следует за [latex] \ hat {j} [/ latex] и предшествует [latex] \ hat {i} [/ latex] или [latex] \ hat { j} [/ latex] следует за [latex] \ hat {i} [/ latex] и предшествует [latex] \ hat {k} [/ latex].Перекрестное произведение двух разных единичных векторов всегда является третьим единичным вектором. Когда два единичных вектора в перекрестном произведении появляются в циклическом порядке, результатом такого умножения является оставшийся единичный вектор, как показано на (Рисунок) (b). Когда единичные векторы в перекрестном произведении появляются в другом порядке, результатом является единичный вектор, антипараллельный оставшемуся единичному вектору (т. Е. Результат со знаком минус, как показано в примерах на (Рисунок) (c) и (Рисунок) (d). На практике, когда задача состоит в том, чтобы найти перекрестные произведения векторов, которые даны в форме компонентов вектора, это правило перекрестного умножения единичных векторов очень полезно.
Е. Результат со знаком минус, как показано в примерах на (Рисунок) (c) и (Рисунок) (d). На практике, когда задача состоит в том, чтобы найти перекрестные произведения векторов, которые даны в форме компонентов вектора, это правило перекрестного умножения единичных векторов очень полезно.
Рисунок 2.32 (a) Диаграмма циклического порядка единичных векторов осей. (b) Единственные перекрестные произведения, в которых единичные векторы появляются в циклическом порядке. Эти продукты имеют положительный знак. (c, d) Два примера перекрестных произведений, где единичные векторы не появляются в циклическом порядке. Эти товары имеют отрицательный знак.
Предположим, мы хотим найти перекрестное произведение [латекс] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} [/ latex] для векторов [latex] \ overset {\ to} {A} = {A} _ {x} \ hat {i} + {A} _ {y} \ hat {j} + {A} _ {z} \ hat {k} [/ латекс] и [латекс] \ overset {\ to} {B} = {B} _ {x} \ hat {i} + {B} _ {y} \ hat {j} + {B} _ {z} \ hat {k} [/ латекс]. Мы можем использовать свойство распределения ((рисунок)), антикоммутативное свойство ((рисунок)) и результаты (рисунок) и (рисунок) для единичных векторов, чтобы выполнить следующую алгебру:
Мы можем использовать свойство распределения ((рисунок)), антикоммутативное свойство ((рисунок)) и результаты (рисунок) и (рисунок) для единичных векторов, чтобы выполнить следующую алгебру:
[латекс] \ begin {array} {ccc} \ hfill \ overset {\ to} {A} \, × \, \ overset {\ to} {B} & = \ hfill & ({A} _ {x} \ hat {i} + {A} _ {y} \ hat {j} + {A} _ {z} \ hat {k}) \, × \, ({B} _ {x} \ hat {i} + {B} _ {y} \ hat {j} + {B} _ {z} \ hat {k}) \ hfill \\ & = \ hfill & {A} _ {x} \ hat {i} \, × \, ({B} _ {x} \ hat {i} + {B} _ {y} \ hat {j} + {B} _ {z} \ hat {k}) + {A} _ {y } \ hat {j} \, × \, ({B} _ {x} \ hat {i} + {B} _ {y} \ hat {j} + {B} _ {z} \ hat {k} ) + {A} _ {z} \ hat {k} \, × \, ({B} _ {x} \ hat {i} + {B} _ {y} \ hat {j} + {B} _ {z} \ hat {k}) \ hfill \\ & = \ hfill & \ enspace {A} _ {x} {B} _ {x} \ hat {i} \, × \, \ hat {i} + {A} _ {x} {B} _ {y} \ hat {i} \, × \, \ hat {j} + {A} _ {x} {B} _ {z} \ hat {i} \ , × \, \ hat {k} \ hfill \\ & & + {A} _ {y} {B} _ {x} \ hat {j} \, × \, \ hat {i} + {A} _ {y} {B} _ {y} \ hat {j} \, × \, \ hat {j} + {A} _ {y} {B} _ {z} \ hat {j} \, × \, \ hat {k} \ hfill \\ & & + {A} _ {z} {B} _ {x} \ hat {k} \, × \, \ hat {i} + {A} _ {z} { B} _ {y} \ hat {k} \, × \, \ hat {j} + {A} _ {z} {B} _ {z} \ hat {k} \, × \, \ hat {k } \ hfill \\ & = \ hfill & \ enspace {A} _ {x} {B} _ {x} (0) + {A} _ {x} {B} _ {y} (+ \ hat {k }) + {A} _ {x} {B} _ {z} (\ text {-} \ hat {j}) \ hfill \\ & & + {A} _ {y} {B} _ {x} (\ text {-} \ hat {k}) + {A} _ {y} {B} _ {y} (0) + {A} _ {y} {B} _ {z} (+ \ hat { i}) \ hfill \\ & & + {A} _ {z} {B} _ {x} (+ \ hat {j} ) + {A} _ {z} {B} _ {y} (\ text {-} \ hat {i}) + {A} _ {z} {B} _ {z} (0).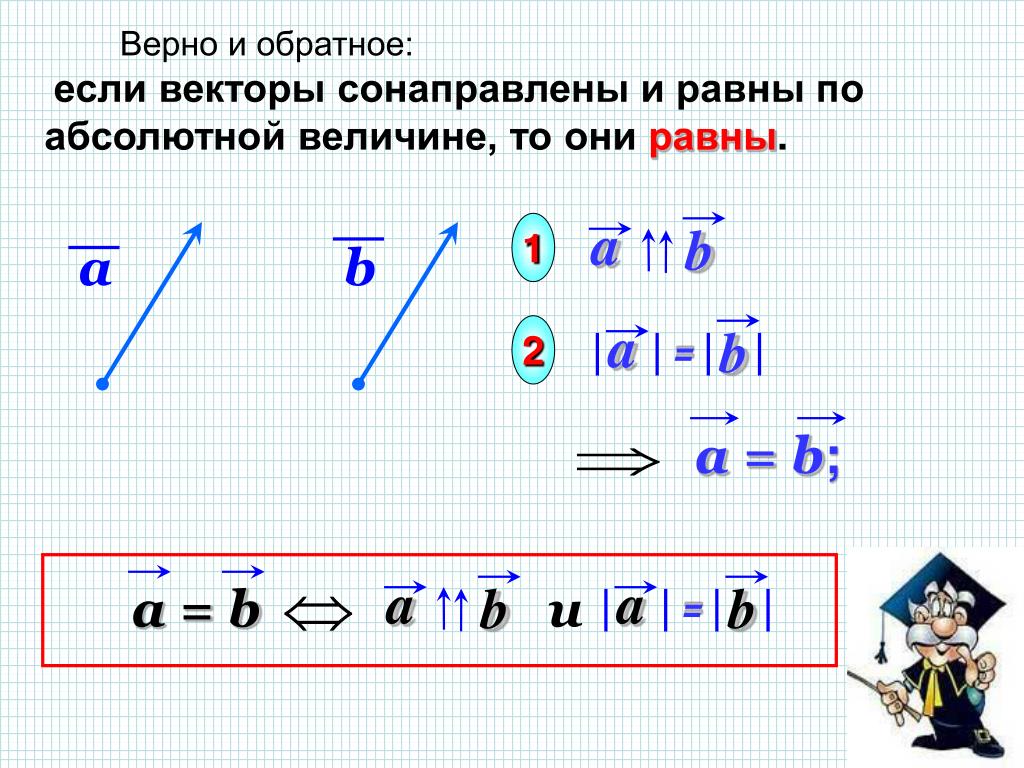 \ hfill \ end {array} [/ latex]
\ hfill \ end {array} [/ latex]
При выполнении алгебраических операций, связанных с перекрестным произведением, будьте очень осторожны с соблюдением правильного порядка умножения, потому что перекрестное произведение антикоммутативно. Последние два шага, которые нам еще предстоит сделать для выполнения нашей задачи, — это, во-первых, группировка терминов, содержащих общий единичный вектор, и, во-вторых, факторинг. Таким образом, мы получаем следующее очень полезное выражение для вычисления перекрестного произведения:
[латекс] \ overset {\ to} {C} = \ overset {\ to} {A} \, × \, \ overset {\ to} {B} = ({A} _ {y} {B} _ {z} — {A} _ {z} {B} _ {y}) \ hat {i} + ({A} _ {z} {B} _ {x} — {A} _ {x} {B } _ {z}) \ hat {j} + ({A} _ {x} {B} _ {y} — {A} _ {y} {B} _ {x}) \ hat {k}.[/ латекс]
В этом выражении скалярные компоненты вектора перекрестного произведения равны
.
[латекс] \ {\ begin {array} {c} {C} _ {x} = {A} _ {y} {B} _ {z} — {A} _ {z} {B} _ {y }, \\ {C} _ {y} = {A} _ {z} {B} _ {x} — {A} _ {x} {B} _ {z}, \\ {C} _ {z } = {A} _ {x} {B} _ {y} — {A} _ {y} {B} _ {x}.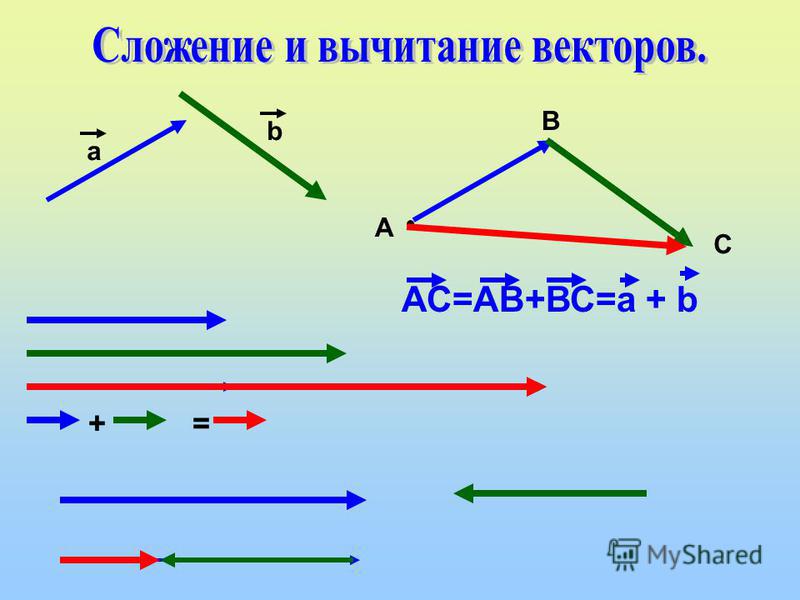 \ End {array} [/ latex]
\ End {array} [/ latex]
На практике при нахождении перекрестного произведения мы можем использовать либо (рисунок), либо (рисунок), в зависимости от того, какое из них кажется менее сложным в вычислительном отношении. Оба они приводят к одному и тому же конечному результату. Один из способов убедиться, что окончательный результат верен, — использовать их оба.
Пример
Частица в магнитном поле
При движении в магнитном поле некоторые частицы могут испытывать магнитную силу. Не вдаваясь в подробности — подробное изучение магнитных явлений будет в следующих главах — давайте признаем, что магнитное поле [латекс] \ overset {\ to} {B} [/ latex] является вектором, магнитная сила [латекс] \ overset {\ to} {F} [/ latex] — это вектор, а скорость [latex] \ overset {\ to} {u} [/ latex] частицы — это вектор. Вектор магнитной силы пропорционален векторному произведению вектора скорости на вектор магнитного поля, которое мы выражаем как [latex] \ overset {\ to} {F} = \ zeta \ overset {\ to} {u} \, × \, \ overset {\ to} {B} [/ латекс]. В этом уравнении константа [latex] \ zeta [/ latex] заботится о согласованности физических единиц, поэтому мы можем опускать физические единицы в векторах [latex] \ overset {\ to} {u} [/ latex] и [ латекс] \ overset {\ to} {B} [/ латекс]. В этом примере предположим, что константа [latex] \ zeta [/ latex] положительна.
В этом уравнении константа [latex] \ zeta [/ latex] заботится о согласованности физических единиц, поэтому мы можем опускать физические единицы в векторах [latex] \ overset {\ to} {u} [/ latex] и [ латекс] \ overset {\ to} {B} [/ латекс]. В этом примере предположим, что константа [latex] \ zeta [/ latex] положительна.
Частица, движущаяся в пространстве с вектором скорости [latex] \ overset {\ to} {u} = — 5.0 \ hat {i} -2.0 \ hat {j} +3.5 \ hat {k} [/ latex], входит в область с магнитным полем и испытывает магнитную силу.Найдите магнитную силу [латекс] \ overset {\ to} {F} [/ latex] на этой частице в точке входа в область, где вектор магнитного поля равен (a) [latex] \ overset {\ to} {B } = 7.2 \ hat {i} — \ hat {j} -2.4 \ hat {k} [/ latex] и (b) [latex] \ overset {\ to} {B} = 4.5 \ hat {k} [/ латекс]. В каждом случае найдите величину F магнитной силы и угол [latex] \ theta [/ latex], который вектор силы [latex] \ overset {\ to} {F} [/ latex] создает с заданным вектором магнитного поля. [латекс] \ overset {\ to} {B} [/ латекс].{2}} [/ latex], или вычислением величины [latex] | \ overset {\ to} {u} \, × \, \ overset {\ to} {B} | [/ latex] напрямую с помощью (рисунок). В последнем подходе нам нужно будет найти угол между векторами [latex] \ overset {\ to} {u} [/ latex] и [latex] \ overset {\ to} {B} [/ latex]. Когда у нас есть [latex] \ overset {\ to} {F} [/ latex], общий метод определения угла направления [latex] \ theta [/ latex] включает вычисление скалярного произведения [latex] \ overset { \ to} {F} · \ overset {\ to} {B} [/ latex] и подставляем в (рисунок).Для вычисления векторного произведения мы можем либо использовать (рисунок), либо вычислить произведение напрямую, в зависимости от того, что будет проще.
[латекс] \ overset {\ to} {B} [/ латекс].{2}} [/ latex], или вычислением величины [latex] | \ overset {\ to} {u} \, × \, \ overset {\ to} {B} | [/ latex] напрямую с помощью (рисунок). В последнем подходе нам нужно будет найти угол между векторами [latex] \ overset {\ to} {u} [/ latex] и [latex] \ overset {\ to} {B} [/ latex]. Когда у нас есть [latex] \ overset {\ to} {F} [/ latex], общий метод определения угла направления [latex] \ theta [/ latex] включает вычисление скалярного произведения [latex] \ overset { \ to} {F} · \ overset {\ to} {B} [/ latex] и подставляем в (рисунок).Для вычисления векторного произведения мы можем либо использовать (рисунок), либо вычислить произведение напрямую, в зависимости от того, что будет проще.
Решение
Покажи ответ
Компоненты вектора скорости: [латекс] {u} _ {x} = — 5.0 [/ latex], [latex] {u} _ {y} = — 2.0 [/ latex] и [latex] {u} _ {z} = 3,5 [/ латекс].
(a) Компонентами вектора магнитного поля являются [латекс] {B} _ {x} = 7,2 [/ латекс], [латекс] {B} _ {y} = — 1,0 [/ латекс] и [латекс ] {B} _ {z} = — 2,4 [/ латекс].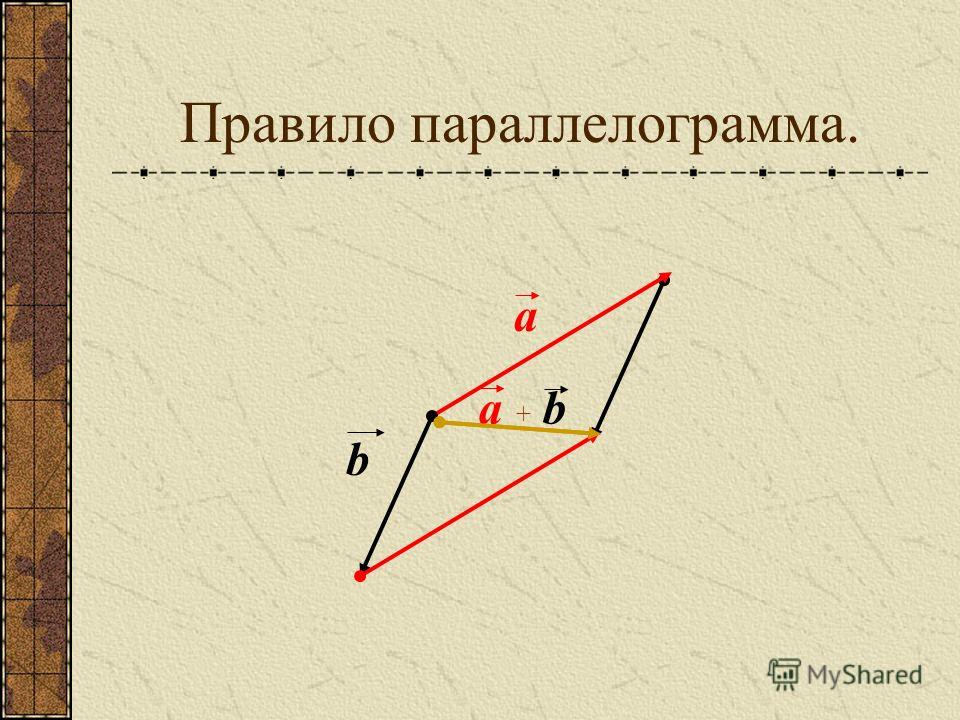 Подстановка их в (рисунок) дает скалярные компоненты вектора [latex] \ overset {\ to} {F} = \ zeta \ overset {\ to} {u} \, × \, \ overset {\ to} {B} [/ latex]:
Подстановка их в (рисунок) дает скалярные компоненты вектора [latex] \ overset {\ to} {F} = \ zeta \ overset {\ to} {u} \, × \, \ overset {\ to} {B} [/ latex]:
[латекс] \ {\ begin {array} {l} {F} _ {x} = \ zeta ({u} _ {y} {B} _ {z} — {u} _ {z} {B} _ {y}) = \ zeta [(-2.{2}} = 7.6, [/ latex] и скалярное произведение [latex] \ overset {\ to} {F} · \ overset {\ to} {B} [/ latex]:
[латекс] \ overset {\ to} {F} · \ overset {\ to} {B} = {F} _ {x} {B} _ {x} + {F} _ {y} {B} _ {y} + {F} _ {z} {B} _ {z} = (8.3 \ zeta) (7.2) + (13.2 \ zeta) (- 1.0) + (19.4 \ zeta) (- 2.4) = 0. [/ latex] Теперь замена в (Рисунок) дает угол [латекс] \ theta [/ latex]:
[латекс] \ text {cos} \, \ theta = \ frac {\ overset {\ to} {F} · \ overset {\ to} {B}} {FB} = \ frac {0} {(18.2 \ zeta) (7.6)} = 0 \, ⇒ \ enspace \ theta = 90 \ text {°}. [/ латекс]
Следовательно, вектор магнитной силы перпендикулярен вектору магнитного поля.(Мы могли бы сэкономить время, если бы вычислили скалярное произведение раньше. )
)
(b) Поскольку вектор [latex] \ overset {\ to} {B} = 4.5 \ hat {k} [/ latex] имеет только один компонент, мы можем быстро выполнить алгебру и найти векторное произведение напрямую:
[латекс] \ begin {array} {ll} \ hfill \ overset {\ to} {F} & = \ zeta \ overset {\ to} {u} \, × \, \ overset {\ to} {B} = \ zeta (-5.0 \ hat {i} -2.0 \ hat {j} +3.5 \ hat {k}) \, × \, (4.5 \ hat {k}) \ hfill \\ & = \ zeta [(- 5.0) (4.5) \ hat {i} \, × \, \ hat {k} + (- 2.0) (4.5) \ hat {j} \, × \, \ hat {k} + (3.{2}} = 24,2 \ дзета. [/ latex] Поскольку скалярное произведение равно
[латекс] \ overset {\ to} {F} · \ overset {\ to} {B} = {F} _ {x} {B} _ {x} + {F} _ {y} {B} _ {y} + {F} _ {z} {B} _ {z} = (- 9.0 \ zeta) (0) + (22.5 \ zeta) (0) + (0) (4.5) = 0, [/ латекс ] вектор магнитной силы [латекс] \ overset {\ to} {F} [/ latex] перпендикулярен вектору магнитного поля [latex] \ overset {\ to} {B} [/ latex].
Значение
Даже без фактического вычисления скалярного произведения мы можем предсказать, что вектор магнитной силы всегда должен быть перпендикулярен вектору магнитного поля из-за способа построения этого вектора. А именно, вектор магнитной силы — это векторное произведение [латекс] \ overset {\ to} {F} = \ zeta \ overset {\ to} {u} \, × \, \ overset {\ to} {B} [/ латекс] и, по определению векторного произведения (см. (рисунок)), вектор [латекс] \ overset {\ to} {F} [/ latex] должен быть перпендикулярен обоим векторам [латекс] \ overset {\ to} {u} [/ latex] и [latex] \ overset {\ to} {B} [/ latex].
А именно, вектор магнитной силы — это векторное произведение [латекс] \ overset {\ to} {F} = \ zeta \ overset {\ to} {u} \, × \, \ overset {\ to} {B} [/ латекс] и, по определению векторного произведения (см. (рисунок)), вектор [латекс] \ overset {\ to} {F} [/ latex] должен быть перпендикулярен обоим векторам [латекс] \ overset {\ to} {u} [/ latex] и [latex] \ overset {\ to} {B} [/ latex].
Проверьте свое понимание
Даны два вектора [латекс] \ overset {\ to} {A} = \ text {-} \ hat {i} + \ hat {j} [/ latex] и [latex] \ overset {\ to} {B} = 3 \ hat {i} — \ hat {j} [/ latex], найдите (a) [latex] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} [/ латекс], (b) [латекс] | \ overset {\ to} {A} \, × \, \ overset {\ to} {B} | [/ latex], (c) угол между [латексом] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {B} [/ latex], и (d) угол между [латексом] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} [/ latex] и вектором [латексом] \ overset {\ to} {C} = \ hat { i} + \ hat {k} [/ латекс].
Показать решение
а. [латекс] -2 \ шляпа {k} [/ латекс], б. 2, в. [латекс] 153.4 \ text {°} [/ латекс], d. [латекс] 135 \ text {°} [/ латекс]
В заключение этого раздела мы хотим подчеркнуть, что «скалярное произведение» и «перекрестное произведение» — это совершенно разные математические объекты, которые имеют разное значение. Скалярное произведение — это скаляр; перекрестное произведение — это вектор. В последующих главах термины скалярное произведение и скалярное произведение используются как взаимозаменяемые. Точно так же термины перекрестное произведение и векторное произведение используются взаимозаменяемо.
вектор | Определение, физика и факты
Вектор , в физике величина, имеющая как величину, так и направление. Обычно он представлен стрелкой, направление которой совпадает с направлением количества, а длина пропорциональна величине величины. Хотя вектор имеет величину и направление, у него нет позиции.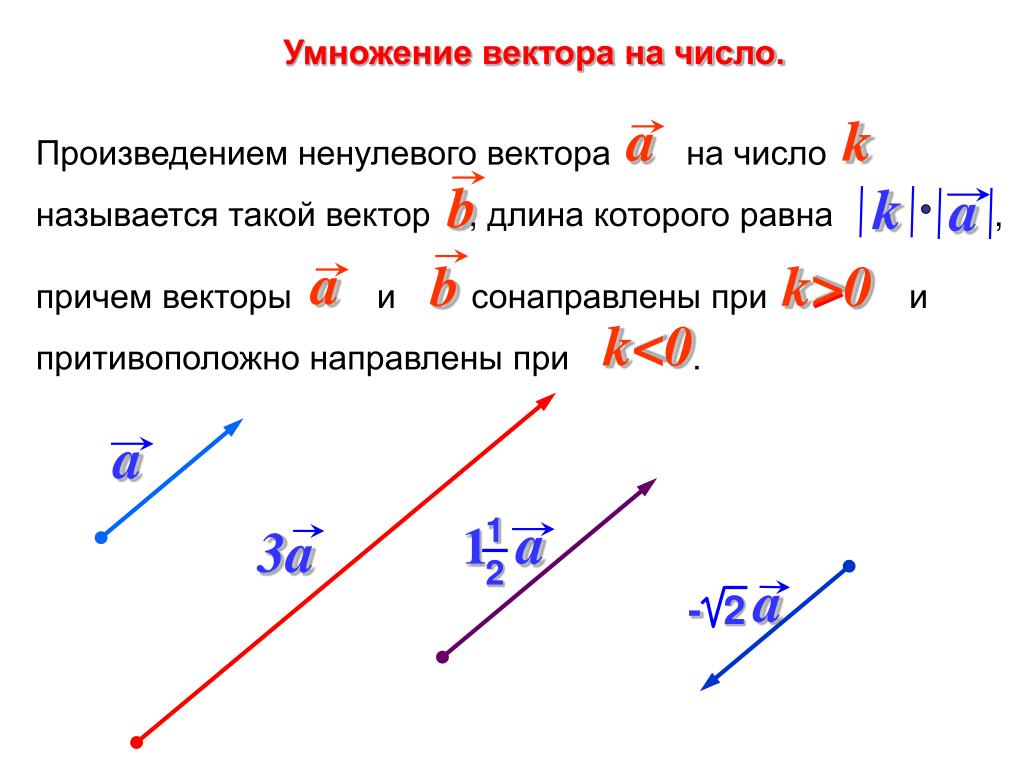 То есть, пока его длина не изменяется, вектор не изменяется, если он смещается параллельно самому себе.
То есть, пока его длина не изменяется, вектор не изменяется, если он смещается параллельно самому себе.
В отличие от векторов, обычные величины, которые имеют величину, но не направление, называются скалярами.Например, смещение, скорость и ускорение — векторные величины, а скорость (величина скорости), время и масса — скаляры.
Чтобы считаться вектором, величина, имеющая величину и направление, также должна подчиняться определенным правилам комбинирования. Одним из них является сложение векторов, символически записываемое как A + B = C (векторы обычно обозначаются жирным шрифтом). С геометрической точки зрения векторную сумму можно визуализировать, поместив хвост вектора B в начало вектора A и нарисовав вектор C, начиная с хвоста A и заканчивая в голове B, так, чтобы он завершал треугольник.Если A, B и C являются векторами, должна быть возможность выполнить ту же операцию и получить тот же результат (C) в обратном порядке, B + A = C. Величины, такие как смещение и скорость, обладают этим свойством (закон коммутативности).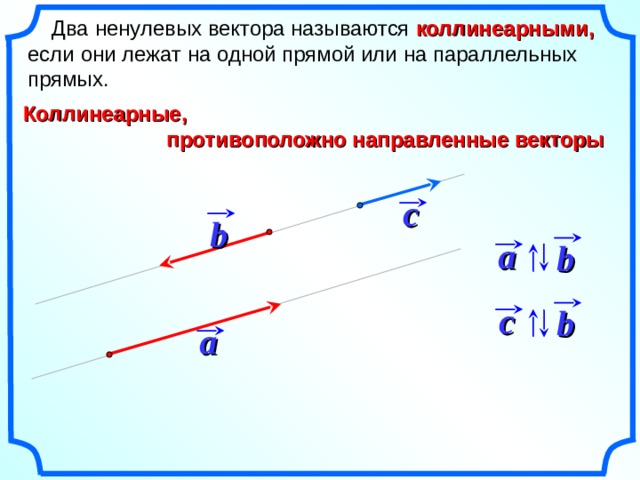 , но есть величины (например, конечные вращения в пространстве), которые не являются векторами и поэтому не являются векторами.
, но есть величины (например, конечные вращения в пространстве), которые не являются векторами и поэтому не являются векторами.
векторный параллелограмм для сложения и вычитания
Один из методов сложения и вычитания векторов состоит в том, чтобы соединить их хвосты вместе, а затем подвести еще две стороны, чтобы сформировать параллелограмм.Вектор от их хвостов к противоположному углу параллелограмма равен сумме исходных векторов. Вектор между их головами (начиная с вычитаемого вектора) равен их разности.
Encyclopædia Britannica, Inc.
Другими правилами обработки векторов являются вычитание, умножение на скаляр, скалярное умножение (также известное как скалярное произведение или внутреннее произведение), векторное умножение (также известное как перекрестное произведение) и дифференцирование. .Нет операции, соответствующей делению на вектор. Описание всех этих правил см. В векторном анализе .
Правило правой руки для векторного векторного произведения
Обычное, или точечное, произведение двух векторов — это просто одномерное число или скаляр. Напротив, перекрестное произведение двух векторов приводит к другому вектору, направление которого ортогонально обоим исходным векторам, как показано правилом правой руки. Величина или длина вектора векторного произведения задается следующим образом: v w sin θ , где θ — это угол между исходными векторами v и w .
Напротив, перекрестное произведение двух векторов приводит к другому вектору, направление которого ортогонально обоим исходным векторам, как показано правилом правой руки. Величина или длина вектора векторного произведения задается следующим образом: v w sin θ , где θ — это угол между исходными векторами v и w .
Encyclopædia Britannica, Inc.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
Хотя векторы математически просты и чрезвычайно полезны при обсуждении физики, они не были разработаны в их современной форме до конца XIX века, когда Джозайя Уиллард Гиббс и Оливер Хевисайд (из США и Англии соответственно) применили векторный анализ в своих исследованиях. чтобы помочь выразить новые законы электромагнетизма, предложенные Джеймсом Клерком Максвеллом.
Сложение векторов
Введение
Все измеримые величины могут быть классифицированы как векторные величины или как скалярные величины. Скалярные величины полностью описываются одним числом (с соответствующими единицами), представляющим величину величины; примерами являются масса, время, температура, энергия и объем. Для векторных величин, таких как скорость, сила и ускорение, величина сопровождается качеством направленности.(Векторы будут обозначены A , а единичные векторы — .)
Скалярные величины полностью описываются одним числом (с соответствующими единицами), представляющим величину величины; примерами являются масса, время, температура, энергия и объем. Для векторных величин, таких как скорость, сила и ускорение, величина сопровождается качеством направленности.(Векторы будут обозначены A , а единичные векторы — .)
Когда в вычислениях используются скалярные величины, применяются обычные правила арифметики; но когда задействованы векторные величины, процесс более сложен, поскольку необходимо учитывать направление вектора. В этом эксперименте будут рассмотрены три метода сложения векторов: графический, аналитический и экспериментальный.
Теория
Векторная величина может быть представлена графически прямой линией со стрелкой на конце.Направление, в котором указывает стрелка, дает смысл вектора, а длина линии указывает величину вектора. Например, сила 3 Н, действующая горизонтально, может быть описана линией длиной три единицы (каждая единица представляет 1 Н), как показано на рисунке 1.
Когда два или более вектора используются для описания процесса, они могут быть заменены одним результирующим вектором, который несет эквивалентную информацию. В качестве примера рассмотрим автомобиль, который движется из точки O в точку P , сначала двигаясь на 50 км на северо-запад, затем на 20 км на запад и, наконец, на 40 км на север.Теперь вместо того, чтобы двигаться к точке P в серии из трех шагов, представленных векторами A , B и C , автомобиль может следовать по более прямому пути, показанному вектором R . Этот вектор R , называемый результирующим, эквивалентен комбинации трех векторов A , B и C , поскольку автомобиль все еще начинается в точке O и заканчивается в точке P . Это можно символически записать как
Следует отметить, что в этом случае все пути, которые представляют движение от O до P , эквивалентны R и друг другу.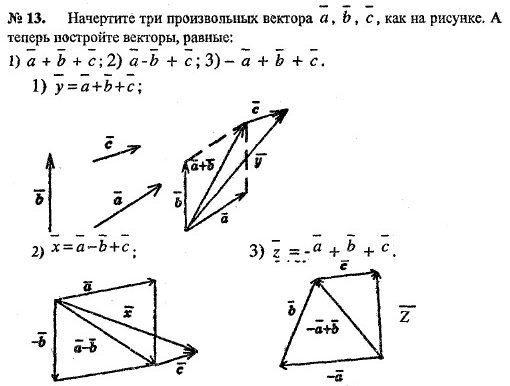 Итак, на рисунке 3
Итак, на рисунке 3
(2)
R = A + B + C = C + A + B = C + D .
Хотя этот графический метод, в котором последовательные векторы помещаются лицом к хвосту, полезен в качестве визуального описания, его точность ограничена тем, что может быть получено с помощью инструментов рисования. Когда требуются результаты более точные, чем те, которые предоставлены графическим анализом, применяются аналитические методы.Чтобы использовать аналитические методы для сложения векторов, все векторы описываются с помощью единичных векторов. Единичный вектор — это вектор, имеющий величину один (без каких-либо единиц) с заданной ориентацией. Его единственное использование — это описание определенного направления в космосе. В системе координат xy обычно назначают единичный вектор î в направлении положительной оси x и единичный вектор ĵ в направлении положительной оси y . Любой отдельный вектор может быть выражен как сумма двух (или более) компонентных векторов. На рисунке 4 вектор A имеет звездную величину A и ориентацию θ от оси x .
Любой отдельный вектор может быть выражен как сумма двух (или более) компонентных векторов. На рисунке 4 вектор A имеет звездную величину A и ориентацию θ от оси x .
Этот вектор можно рассматривать как результат двух компонентных векторов: A x = A x î , указывающих вдоль направления î и A y = A y ĵ в направлении ĵ ; или символически следующим образом.Компонент A x является положительным или отрицательным, так как A x находится в направлении + î или — î , а A y является положительным или отрицательным как A y находится в направлении + ĵ или — ĵ . Величину компонентов A можно вычислить из определений тригонометрических функций.
Величину компонентов A можно вычислить из определений тригонометрических функций.
или же
а также
или же
Кроме того,
и по теореме Пифагора величина A равна
(11)
| A | =
| A x 2 + A y 2 |
.Когда векторы добавляются аналитически, каждый вектор сначала записывается в его компонентной форме, затем компоненты x всех векторов складываются алгебраически (уделяя особое внимание знаку), чтобы получить результирующую компоненту x и y. -компоненты всех векторов складываются, чтобы получить результирующую -компоненту и .
Предположим, что добавлены два параллельных вектора. Для графического метода «голова к хвосту» вектор B помещается на острие стрелки вектора A (или наоборот), и результирующий, R , проводится от O к вершине . B , как показано на Рисунке 5.На рисунке 6 векторы C и D добавлены аналитически. Математически векторы можно записать
B , как показано на Рисунке 5.На рисунке 6 векторы C и D добавлены аналитически. Математически векторы можно записать
Поскольку результат R является суммой векторов C и D
(16)
R = C x î + C y ĵ + D x 918 5 918 5
(17)
R = ( C x + D x ) î + ( C y + D 29.
9.Сравнение с уравнением (14) R = R x î + R y ĵ . дает значения для компонентов x и y результирующего:
Из компонентов R величина и направление результирующего
(20)
| R | =
| R x 2 + R y 2 |
Если добавляется более двух векторов, уравнения (18)
R x = C x + D x
и (19)
R y = C y + D y .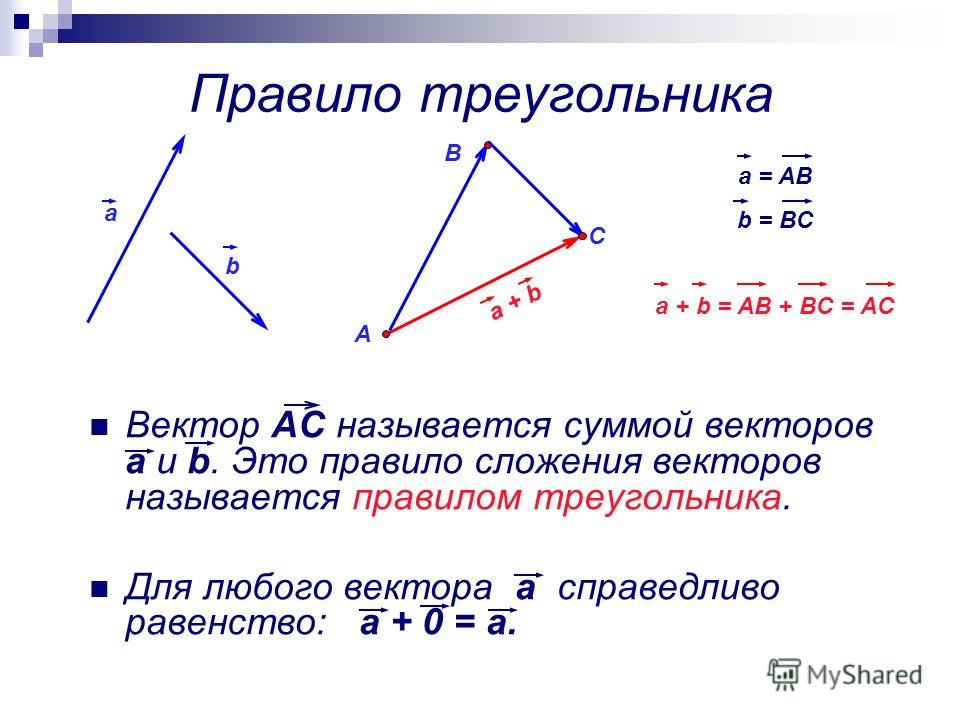
можно обобщить на
(22)
R x = A x + B x + C x + D x +
(23)
R y = A y + B y + C y + D y +
и соотношения уравнений (20) | R | =
| R x 2 + R y 2 |
и (21) могут применяться для получения величины и направления результирующего.Когда добавляемые векторы представляют силы, отрицательная величина равнодействующей называется уравновешивающей (или антирезультантной) сил. Равновесие — это единственная сила, которая в сочетании с другими силами приводит систему в равновесие. Обратите внимание, что равновесие равно по величине, но противоположно по направлению равнодействующей векторов.
Цель
Задача этой лаборатории — найти уравновешивающую силу для одной или нескольких известных сил с помощью таблицы сил и сравнить этот результат с результатами, полученными с использованием графических и аналитических методов.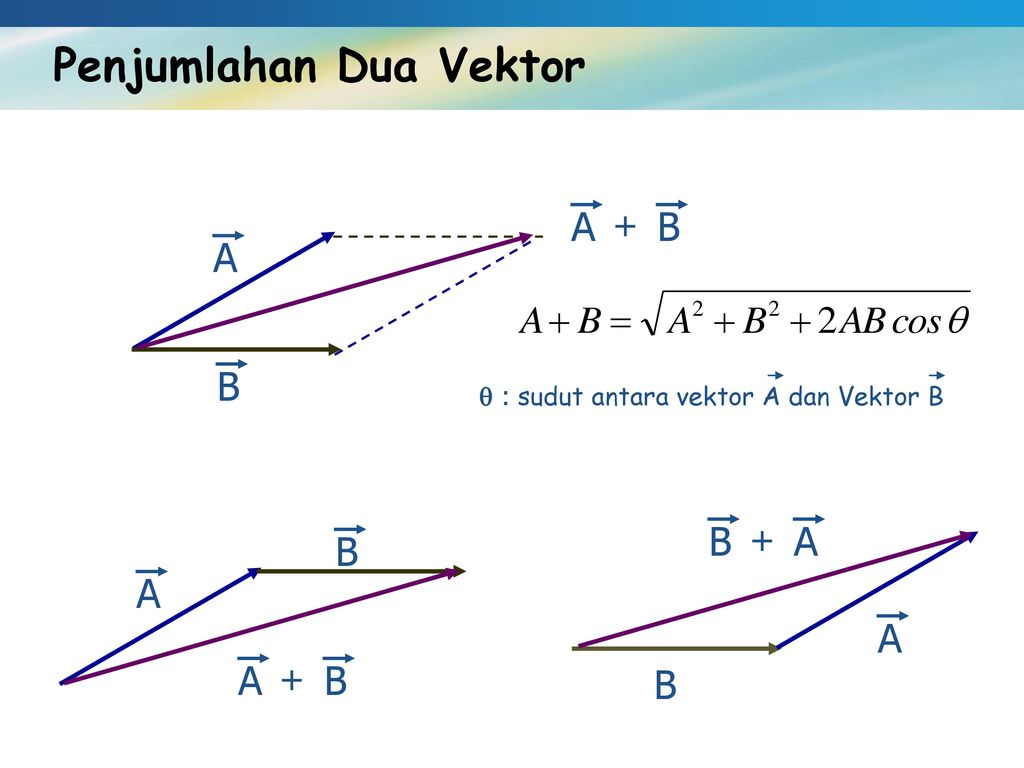
Аппарат
- Линейка транспортира
- Три шкива
- Набор шлицевых масс
- Три массовых вешалки
- Таблица сил с центральным штифтом и кольцом
- Пузырьковый уровень
Процедура
Распечатайте лист для этой лабораторной работы. Этот лист понадобится вам для записи ваших данных.
Таблица сил состоит из горизонтально установленной поверхности, градуированной по периметру в градусах.Штифт, вставленный в центр стола, удерживает кольцо на месте, когда система не сбалансирована. Кольцо — это объект, который будет находиться в равновесии, и натяжение трех прикрепленных к нему струн будет обеспечивать силы, которые необходимо уравновесить. При условии, что трением в шкивах можно пренебречь, натяжение каждой струны равно весу груза, помещенного на ее концах, вниз (это будет темой дальнейшего обсуждения в классе). Шкивы можно зажимать под любым желаемым углом, и направление каждой силы указывается положением индексной метки шкива на круговой шкале стола.
A: Экспериментальный метод определения результата двух векторов
Перед использованием таблицы сил важно, чтобы она была выровнена. Используйте пузырьковый уровень, чтобы проверить горизонтальность платформы силового стола. Если это не так, используйте регулировочные винты, чтобы отрегулировать поверхность до тех пор, пока поверхность не станет горизонтальной.
1
Используя значения, предоставленные WebAssign для случая 1, расположите шкивы в угловых положениях двух векторов, указанных на диаграмме.
Осторожно:
Обратите внимание, что очень легко перетянуть зажимы, удерживающие шкивы на поверхности стола, поэтому будьте осторожны, затягивайте эти зажимы только на долю оборота после того, как зажим коснется поверхности стола (затяните вручную) .
Подвесьте веса, указанные для каждого вектора, на соответствующий шкив. Обязательно учитывайте вес держателя при расчете массы струн.
Как только эти веса установлены, используйте третью систему шкивов и весов, чтобы найти вектор равновесия, связанный с двумя векторами, которые вам были даны. Отрегулируйте угол силы на столе, а также массу, пока не найдете равновесную конфигурацию.
Отрегулируйте угол силы на столе, а также массу, пока не найдете равновесную конфигурацию.
2
Осторожно постучите по кольцу, чтобы немного сместить его от центра; если кольцо возвращается в исходное положение, значит, оно находится в равновесии.Когда кажется, что кольцо находится в равновесии, осторожно снимите центральный штифт и еще раз постучите по кольцу, чтобы немного сместить его. Если кольцо не возвращается в центральное положение, замените центральный штифт и отрегулируйте массу и положение шкива для равновесия, пока не установится равновесие.
Для тела в равновесии результирующая сила, действующая на тело, равна нулю. Для трех векторов, представленных в таблице сил,
A + B + C = 0
или
A + B = -C,
, где C является равновесным.Результирующий, R , из двух векторов на карте назначений равен
R = A + B
, поэтому
R = -C
, и результат является отрицательным для равновесия.
3
Запишите положение равновесия с точностью до долей градуса и запишите его величину с точностью до наименьшей доступной массы. Нарисуйте расположение векторов, как оно изображено на карточке заданий, и включите равновесие, найденное из таблицы сил, на диаграмму. Сохраняйте угол равновесия фиксированным.
4
Сохраняйте угол равновесия фиксированным. Чтобы найти экспериментальную неопределенность для величины равновесия, добавьте к шкиву (или снимите с него) достаточно веса, чтобы кольцо на силовом столе значительно отклонилось от своего положения равновесия. Величина, на которую была изменена масса, является мерой экспериментальной неопределенности в величине вектора. Запишите эту погрешность для наименьшей доступной массы (обязательно укажите правильные единицы).
5
Снова приведите кольцо в состояние равновесия.Удерживая величину равновесия фиксированной, найдите экспериментальную неопределенность в направлении равновесия, слегка перемещая шкив, пока кольцо не перестанет находиться в равновесии.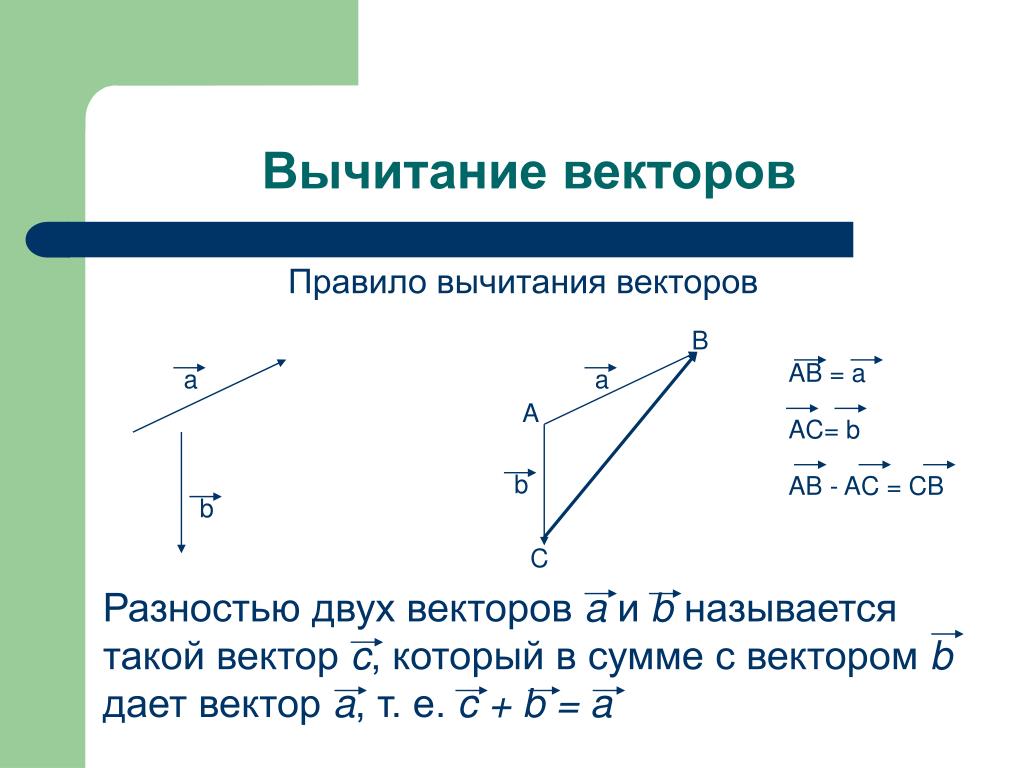 Изменение угла, необходимого для вывода кольца из положения равновесия, представляет собой экспериментальную неопределенность в направлении равновесия. Запишите эту неопределенность с точностью до долей градуса.
Изменение угла, необходимого для вывода кольца из положения равновесия, представляет собой экспериментальную неопределенность в направлении равновесия. Запишите эту неопределенность с точностью до долей градуса.
6
Повторите процедуры 1–5 для случая 2.
B: Графический метод определения результата двух векторов
1
На листе линейной миллиметровой бумаги сложите два вектора, показанные в случае, используя метод «голова к хвосту», описанный на рисунке 3.
2
Нарисуйте векторы в масштабе (используя как можно больший масштаб) и точно измерьте угол с помощью транспортира.
3
Изобразите результирующее и равновесное на диаграмме, измерьте и запишите величину и направление двух векторов. Сделайте это в обоих случаях.
C: Аналитический метод определения результата двух векторов
1
На наборе осей координат x-y нарисуйте приблизительно в масштабе и в любой удобной ориентации два вектора, перечисленные в этом случае. Разложите каждый вектор на его компоненты x и y и перечислите их в таблице над эскизом.
Разложите каждый вектор на его компоненты x и y и перечислите их в таблице над эскизом.
2
Из этих значений получите компоненты x и y для результирующего и, используя уравнения (20) | R | =
| R x 2 + R y 2 |
и (21), определите величину и направление результирующего и нарисуйте его на эскизе. Сделайте это в обоих случаях.
D: Расчеты
1
Определите% ошибки для величины результирующего, полученной экспериментальными и аналитическими методами.
2
Определите% разницы для величины результирующего, полученного экспериментальным и графическим методами.
E: Вопросы
1
Сопутствующие силы — это силы, действующие в одной точке. Карты назначений показывают параллельные силы, но силы в таблице сил действуют на кольцо, а не на точку.Тем не менее, силы по-прежнему совпадают. Объяснять.
2
Могут ли все три шкива на силовом столе быть размещены в одном квадранте и по-прежнему находиться в равновесии? Объяснять.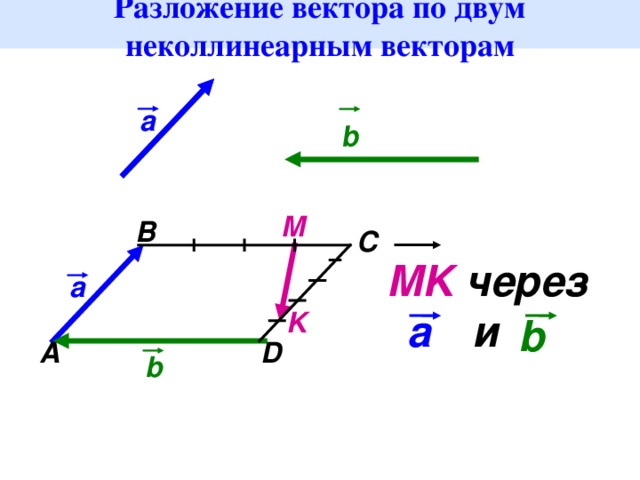
3
Предположим, что три силы с величинами 220 Н, 270 Н и 200 Н находятся в равновесии. Если сила 200 Н действует в направлении + y , какие две конфигурации в плоскости xy могут иметь оставшиеся силы? Приведите числовые значения углов и покажите результаты на эскизе.
4
Какое условие необходимо для равновесия (рассматривать только линейное движение)?
Авторские права © 2012-2013 Advanced Instructional Systems, Inc. и Техасский университет A&M. Части из Университета штата Северная Каролина. | Кредиты
Кросс-произведение векторов
— обзор
1.3 Основные концепции релятивистской квантовой механики
Третий вопрос, поставленный выше: «Как нужно модифицировать квантовую теорию, преподаваемую на курсах химии для студентов-бакалавров, чтобы учесть релятивистские эффекты?», Требует несколько более развернутый ответ. Рассмотрим нерелятивистский не зависящий от времени SE для электрона с потенциальной энергией V ,
(11) hˆnrelψnrel = V + Tˆψnrel = V + 12mepˆ⋅pˆψnrel = ψnrelEnrel
Как уже упоминалось, член кинетической энергии получается путем квантования нерелятивистская кинетическая энергия T = p 2 / (2 m e ), используя pˆ = −iℏ∇.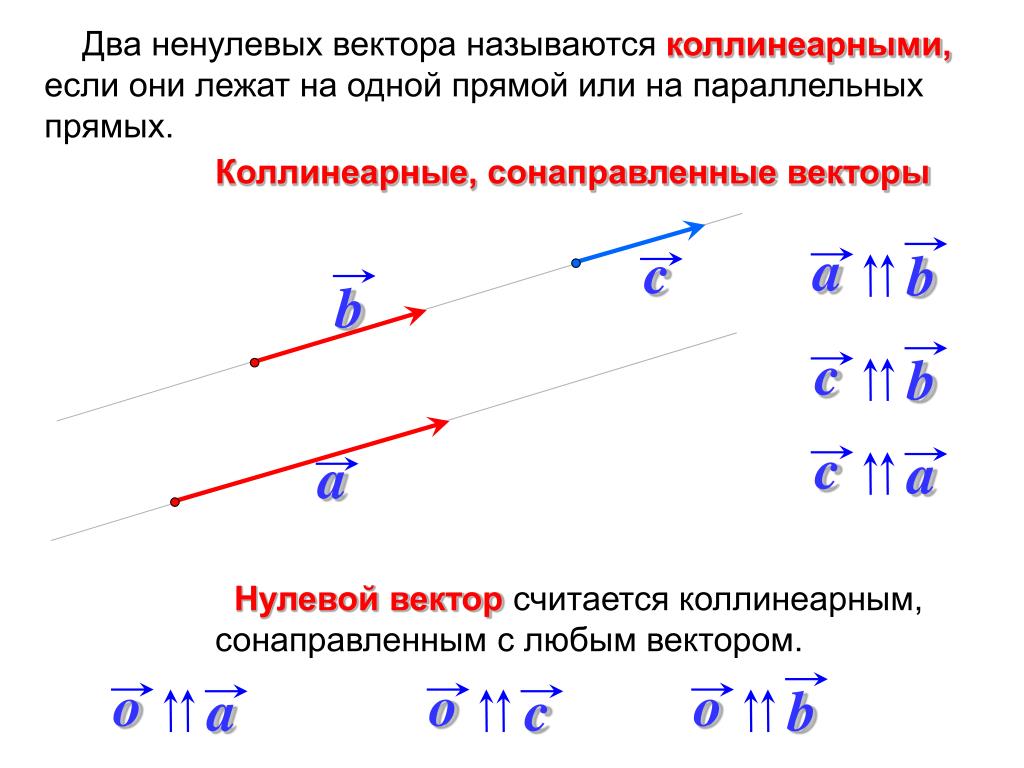 Проблема с релятивистским случаем заключается в следующем: как квантовать выражение квадратного корня (6) для релятивистской энергии? Одна из возможностей — использовать расширение корня в c — 2 , как в уравнении.(7), а затем квантовать импульс. Однако это приводит к сильно сингулярным операторам, и спин, естественно, не возникает из этого подхода. Другая возможность — квантовать W 2 уравнения. (5) и решим уравнение типа Hˆ2ψ = ψE2. Это действительно представляет собой релятивистское квантово-теоретическое уравнение (названное в честь Клейна и Гордона). Оказалось, что это неправильное уравнение для частиц со спином 1/2 (таких как электроны), и есть другие проблемы, связанные с уравнением, связанным с тем фактом, что в его зависящей от времени версии производные по времени имеют второй заказ [11].
Проблема с релятивистским случаем заключается в следующем: как квантовать выражение квадратного корня (6) для релятивистской энергии? Одна из возможностей — использовать расширение корня в c — 2 , как в уравнении.(7), а затем квантовать импульс. Однако это приводит к сильно сингулярным операторам, и спин, естественно, не возникает из этого подхода. Другая возможность — квантовать W 2 уравнения. (5) и решим уравнение типа Hˆ2ψ = ψE2. Это действительно представляет собой релятивистское квантово-теоретическое уравнение (названное в честь Клейна и Гордона). Оказалось, что это неправильное уравнение для частиц со спином 1/2 (таких как электроны), и есть другие проблемы, связанные с уравнением, связанным с тем фактом, что в его зависящей от времени версии производные по времени имеют второй заказ [11].
Дирак утверждал, что релятивистский квантовый гамильтониан должен быть линейным по импульсу, так что временные и пространственные производные появляются в первом порядке в зависящем от времени волновом уравнении. 9 Соответственно, он предложил линеаризацию квадратного корня выражения (6) в виде
9 Соответственно, он предложил линеаризацию квадратного корня выражения (6) в виде
(12) W = me2c4 + c2p2 = mec2β + cα · p
Это приводит к гамильтониану Дирака при квантовании
(13 ) hˆD = V + mec2β + cα⋅pˆ
Тогда возникает вопрос: что такое β и вектор 10 α = ( α x , α y , α z )? Взяв квадрат с обеих сторон уравнения.(12) и предполагая, что p коммутирует с β и α дает ( u , v ∈ { x , y , z })
(14 ) m2c4 + c2p2 = me2c4β4 + c2∑u, vpupvαuαv + mec3∑upuβαu + αuβ
Отсюда следует, что 11
(15) β2 = 1, αuαv + αvαu = 2δuv, βα6 9 + αuβ правая часть уравнения. (14) равна левой части. Эти условия не могут быть выполнены, если β и α u являются числами.Вместо этого можно удовлетворить условиям с набором матриц 4 × 4 (или с матрицами более высокой четной размерности), потому что матричные произведения, в отличие от чисел, обычно не коммутируют.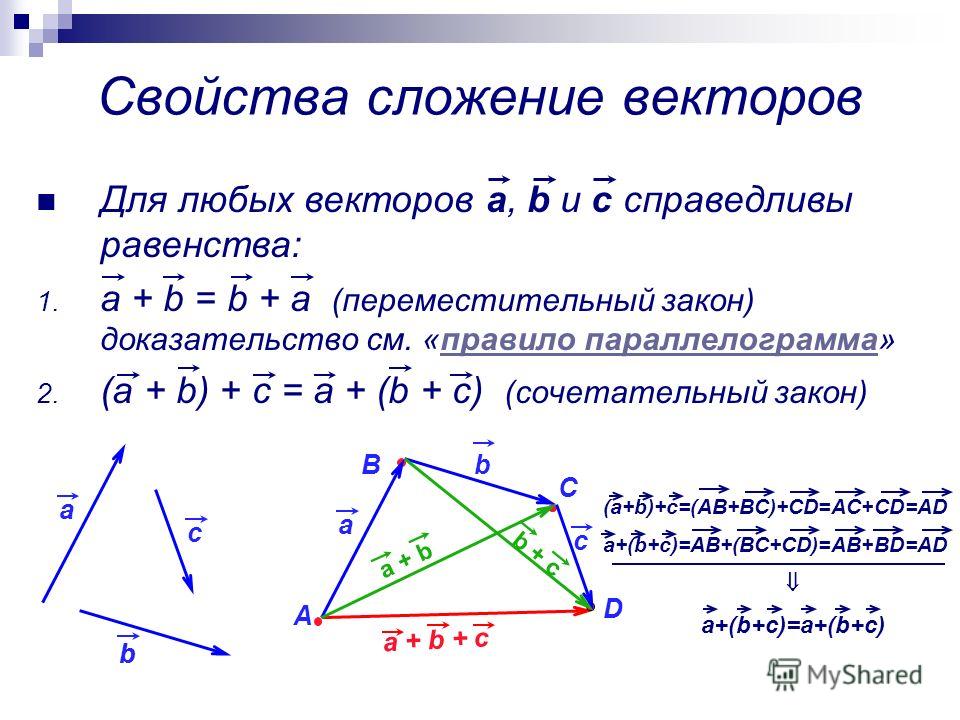 Стандартное представление матриц Дирака:
Стандартное представление матриц Дирака:
(16) β = 1000010000−10000−1, αx = 0001001001001000, αy = 000 − i00i00 − i00i000, αz = 0010000−110000−100
В уравнении. (15) «0» следует интерпретировать как матрицу, заполненную нулями, а «1» соответствует единичной матрице 4 × 4 (1 на диагонали, ноль в другом месте).См. Также упражнение 2.
Возможно, читатель заметил, что недиагональные блоки 2 × 2 из α -матриц являются спиновыми матрицами Паули
(17) σx = 0110, σy = 0 − ii0, σz = 100−1
, которые можно сгруппировать в векторный оператор σ = ( σ x , σ y , σ z ). Оператор электронного спина Sˆ = 1 / 2σℏ. Существует удобное обозначение матриц Дирака в виде блоков 2 × 2, в которых используются матрицы Паули:
(18) β = 100-1, α = 0σσ0
Каждый элемент матриц в уравнении.(18) представляет собой блок 2 × 2, где «0» представляет блок нулей, а «1» представляет единичную матрицу (а не блок 2 × 2, заполненный единицей). В этих разделенных обозначениях одноэлектронный гамильтониан Дирака уравнения (13) читается как
В этих разделенных обозначениях одноэлектронный гамильтониан Дирака уравнения (13) читается как
(19) hˆD = V + mec2β + cα · pˆ = V + mec2cσ · pˆcσ⋅pˆV − mec2
Этот вид сильно отличается от нерелятивистской SE. Более того, поскольку гамильтониан Дирака имеет матричную структуру 4 × 4, волновая функция должна быть четырехкомпонентным объектом
(20) ψD = ψ1ψ2ψ3ψ4 = ψUψL, ψU = ψ1ψ2, ψL = ψ3ψ4
Каждый из ψ i — это функция трехмерного пространства.Квадратные скобки указывают разделение обозначений, соответствующих формуле. (19), где U обозначает два верхних, а L обозначает два нижних из четырех компонентов волновой функции. Обозначения, обозначающие «большой» и «малый» компоненты, чаще используются в соответствующей литературе, при этом малым компонентом является ψ L для электронных состояний. Волновая функция нормирована,
(21) 1 = ∫ψ † ψdV = ∫ (ψ1, ψ2, ψ3, ψ4) ⁎ψ1ψ2ψ3ψ4dV = ∫ψU † ψU + ψL † ψLdV
ψ 60 i не являются независимыми. друг от друга, но взаимосвязаны пространственной и спиновой симметрией физической задачи и матричной структурой hˆD.Наличие оператора спина в hˆD указывает на то, что многокомпонентный характер оператора и волновой функции так или иначе связан со спиновыми степенями свободы электрона. Поэтому четырехкомпонентная волновая функция Дирака также называется четырехспинором. Верхняя и нижняя компоненты, ψ U , ψ L , являются двухспинорами.
друг от друга, но взаимосвязаны пространственной и спиновой симметрией физической задачи и матричной структурой hˆD.Наличие оператора спина в hˆD указывает на то, что многокомпонентный характер оператора и волновой функции так или иначе связан со спиновыми степенями свободы электрона. Поэтому четырехкомпонентная волновая функция Дирака также называется четырехспинором. Верхняя и нижняя компоненты, ψ U , ψ L , являются двухспинорами.
Прежде чем продолжить, мы установили нуль шкалы энергии на + mc 2 , как в уравнении.(8). Для согласованности нам нужно вычесть mc 2 из потенциальной энергии в уравнении. (19), что эквивалентно замене
(22) β = 100−1 → β ′ = 000−2
в уравнении. (19). ДЭ для электрона, наконец, имеет вид
(23) hˆDψD = Vcσ · pˆcσ · pˆV − 2mec2ψUψL = ψUψLE
Это уравнение может не иметь четко определенного нерелятивистского предела, c → ∞, потому что скорость света не фигурируют в знаменателях. Похоже, что весь оператор просто уходит в бесконечность при c → ∞.Однако нерелятивистский предел действительно содержится в формуле. (23). Сначала запишем два уравнения для ψ U и ψ L явно:
Похоже, что весь оператор просто уходит в бесконечность при c → ∞.Однако нерелятивистский предел действительно содержится в формуле. (23). Сначала запишем два уравнения для ψ U и ψ L явно:
(24a) VψU + cσ · pˆψL = ψUE
(24b) cσ · pˆψU + V − 2mec2ψL7 = ψL7
Из второго уравнения получаем
(25) ψL = XˆψU, ψU = Xˆ − 1ψL, где Xˆ = 12meckσ · pˆ
, где
(26) k = 1 − V − E2mec2−1 = 1 + ∑n = 1∞V − E2mec2n
Из-за множителя 1 / (2 c ) в уравнении. (25), ψ L традиционно называют «малым» компонентом.Это действительно обычно намного меньше, чем верхний компонент ψ U . Мы подставляем уравнение. (25) в уравнение. (24a) и получить релятивистское уравнение для верхних компонент
(27) hˆESCψU = V + 12meσ · pˆkcσ · pˆψU = ψUE
Исключаются нижние (малые) компоненты четырехкомпонентной волновой функции. Поэтому процедуру часто называют удалением мелких компонентов (ESC). Процедура показывает, что в принципе можно проводить релятивистские квантовые вычисления только с одной из двухспинорных компонент, ψ U или ψ L , поскольку другая компонента может быть создана с помощью оператора Xˆ или Xˆ − 1, как в уравнении.(25). Уравнение ESC не имеет большого практического значения, поскольку оператор зависит от энергии. Кроме того, нормализация волновой функции требует учета вкладов от обоих компонентов в уравнение. (21).
Процедура показывает, что в принципе можно проводить релятивистские квантовые вычисления только с одной из двухспинорных компонент, ψ U или ψ L , поскольку другая компонента может быть создана с помощью оператора Xˆ или Xˆ − 1, как в уравнении.(25). Уравнение ESC не имеет большого практического значения, поскольку оператор зависит от энергии. Кроме того, нормализация волновой функции требует учета вкладов от обоих компонентов в уравнение. (21).
В последние годы был достигнут огромный прогресс в разработке процедур, позволяющих строить не зависящие от энергии формально точные двухкомпонентные релятивистские одноэлектронные гамильтонианы, которые можно использовать для релятивистских вычислений. Этот маршрут может быть более эффективным при четырехкомпонентных вычислениях, потому что нужно оптимизировать и хранить только две компоненты волновой функции вместо четырех, хотя четырехкомпонентные методы также становятся очень быстрыми. 12 Кроме того, существует множество эффективных с вычислительной точки зрения приближенных («квазирелятивистских») двухкомпонентных гамильтонианов, доступных в пакетах программ для квантовой химии, которые позволяют исследователям проводить достаточно точные релятивистские вычисления для атомов и молекул. Как это часто бывает, эффективность достигается за счет введения приближений.
Как это часто бывает, эффективность достигается за счет введения приближений.
Для конечного потенциала V (конечные ядра) k стремится к 1, когда скорость света стремится к бесконечности.Позже мы можем взять предел точечного ядра, что оставляет k → 1 в качестве нерелятивистского предела. Из уравнения. (27), тогда получаем
(28) hˆnrelψ = V + 12meσ⋅pˆσ⋅pˆψ = ψE
Читателю предлагается (Упражнение 3) использовать определение матриц Паули, чтобы подтвердить, что
(29) σ ⋅pˆσ⋅pˆ = 1001pˆ⋅pˆ
Следовательно, уравнение. (28) во многом эквивалентно нерелятивистской СЭ. Волновые функции могут быть выбраны в качестве собственных функций σ z или любой другой линейной комбинации матриц Паули, и двухспинорная природа имеет отношение только к спинорным факторам.При σ z собственных функций,
ψr, «spin» = ψrtimes10or01
, где ψ ( r ) является решением уравнения.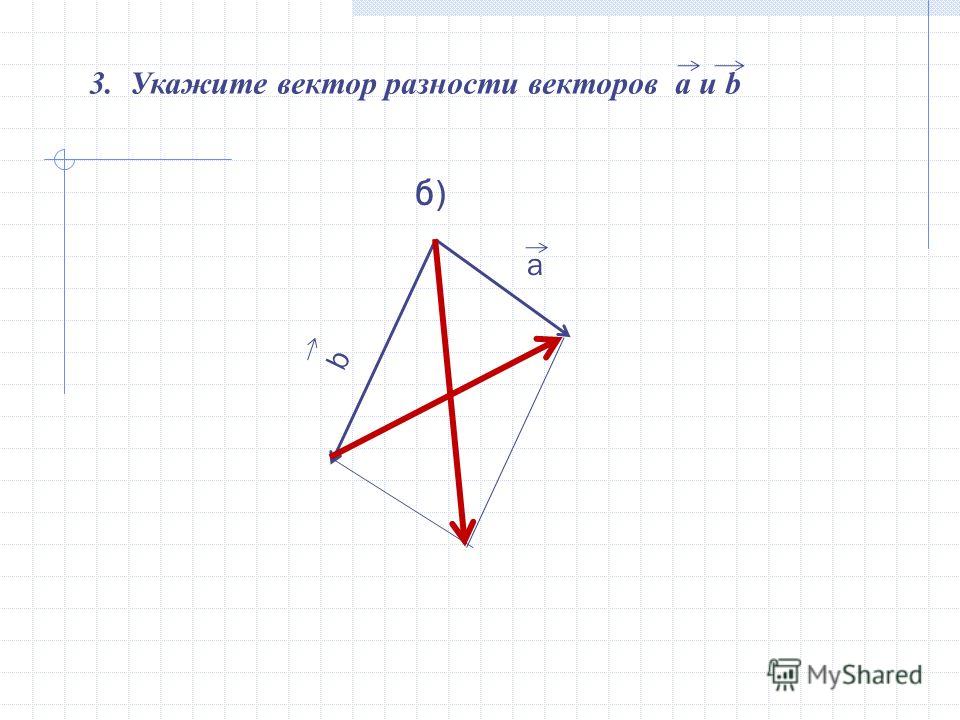 (11). Следовательно, ДЭ действительно включает нерелятивистский предел, хотя и не очевидным образом. Спин электрона естественным образом возникает из релятивистской теории электрона и входит в нерелятивистский предел по формуле. (28).
(11). Следовательно, ДЭ действительно включает нерелятивистский предел, хотя и не очевидным образом. Спин электрона естественным образом возникает из релятивистской теории электрона и входит в нерелятивистский предел по формуле. (28).
Вместо того, чтобы идти за нерелятивистским пределом, сохраняя некоторые члены в разложении k в уравнении.(26) дает приближенные двухкомпонентные релятивистские гамильтонианы. Например, в порядке c -2 получается (см. Упражнения 4 и 5) 13
(30) hˆrel = hˆnrel + 14me2c2pˆV − Epˆ + i4me2c2σ⋅pˆV × pˆ
. Порядок c — 2 представляет собой скалярные релятивистские поправки. Последний член, зависящий от спина, отвечает за спин-орбитальное взаимодействие. Приближенный гамильтониан зависит от энергии и поэтому не имеет большого практического применения.Однако можно подумать об использовании его для теории возмущений, где сначала вычисляется нормированная нерелятивистская волновая функция, а затем используется уравнение. (30) с нерелятивистской энергией E для вычисления младшего порядка c — 2 поправки к энергии. В порядке возмущения выше, чем самый низкий, необходимо учитывать как расширения c — 2 из ψ L и ψ U и члены более высокого порядка в операторе.
(30) с нерелятивистской энергией E для вычисления младшего порядка c — 2 поправки к энергии. В порядке возмущения выше, чем самый низкий, необходимо учитывать как расширения c — 2 из ψ L и ψ U и члены более высокого порядка в операторе.
С учетом перенормировки верхних компонент волновой функции (см. [12], глава 17) релятивистский двухкомпонентный гамильтониан порядка c — 2 превращается в оператор Паули
(31 ) hˆPauli = hˆnrel − pˆ48me3c2 + ℏ2∇2V8mec2 + i4me2c2σ⋅pˆV × pˆ
Энергия возмущения первого порядка, взятая с нерелятивистской волновой функцией, 〈ψnrel | hˆrel − hˆnrel | ψnrel | . (30) и (31) (операторы SO идентичны).Стоит выделить несколько особенностей оператора Pauli. Первый член, называемый членом массы-скорости, можно рассматривать как квантованную версию члена квадратного корня разложения в уравнении ( p 4 ). (7). Этот термин обычно интерпретируется как поправка к кинетической энергии, связанной с релятивистским увеличением массы электрона (член массы-скорости). Второй оператор в правой части уравнения. (31) можно рассматривать как поправку к потенциальной энергии, которая возникает из-за того факта, что электростатическое взаимодействие между электроном и ядром не является мгновенным (термин Дарвина).Последний член — это оператор связи SO. Оператор Паули содержит сильно сингулярные члены, которые приводят к вариационному коллапсу и вызывают проблемы также при расчетах по теории возмущений, за исключением низшего порядка. Поэтому его использование не рекомендуется. Однако у него есть характерные компоненты двухкомпонентных релятивистских гамильтонианов, которые часто используются: есть скалярные релятивистские (бессиновые) члены и есть SO-связь. Для многоэлектронных систем есть дополнительные члены, похожие на члены одноэлектронного гамильтониана, но с потенциалом отталкивания электронов, заменяющим V , и новые спин-зависимые члены, которые возникают из релятивистских поправок к электрон-электронному взаимодействию.
(7). Этот термин обычно интерпретируется как поправка к кинетической энергии, связанной с релятивистским увеличением массы электрона (член массы-скорости). Второй оператор в правой части уравнения. (31) можно рассматривать как поправку к потенциальной энергии, которая возникает из-за того факта, что электростатическое взаимодействие между электроном и ядром не является мгновенным (термин Дарвина).Последний член — это оператор связи SO. Оператор Паули содержит сильно сингулярные члены, которые приводят к вариационному коллапсу и вызывают проблемы также при расчетах по теории возмущений, за исключением низшего порядка. Поэтому его использование не рекомендуется. Однако у него есть характерные компоненты двухкомпонентных релятивистских гамильтонианов, которые часто используются: есть скалярные релятивистские (бессиновые) члены и есть SO-связь. Для многоэлектронных систем есть дополнительные члены, похожие на члены одноэлектронного гамильтониана, но с потенциалом отталкивания электронов, заменяющим V , и новые спин-зависимые члены, которые возникают из релятивистских поправок к электрон-электронному взаимодействию.
Пример для вариационно устойчивого приближенного двухкомпонентного оператора получается следующим образом: Переписывая безразмерный объект k уравнения. (26) как
(32) k = 1 − V − E2mec2−1 = 2mec22mec2 − V1 + E2mec2 − V − 1
и приблизительно k как
(33) K = 2mec22mec2 − V≈k
взяв только нулевой порядок разложения правой части уравнения. (32) дает гамильтониан, который часто используется для релятивистских расчетов ЯМР. Это называется регулярным приближением нулевого порядка (ZORA) или гамильтонианом Чанга – Пелисье – Дюрана [13,14].Его версия без полей 14 читает
(34a) hˆZORA = V + 12meσ⋅pˆKσ⋅pˆ
(34b) = V + 12mepˆ⋅Kpˆ + i2meσ⋅pˆK × pˆ
Как и другие двухкомпонентные релятивистские операторы, гамильтониан ZORA можно разделить на скалярную и SO-часть (переход от уравнений 34a к 34b, см. упражнение 4). Нерелятивистский предел дается K → 1. Из-за потенциала V в выражении K зависит от положения. На рис. 3 показан график Kr для атома Hg. Видно, что K сильно отличается от K в областях, близких к ядру, где потенциал достигает значений, сравнимых с mc 2 .Для точечного ядра K → 0 при r → 0. Для конечного ядра K остается конечным, но небольшим, вблизи и внутри ядра. Видно, что электронный потенциал, экранирующий ядерный заряд, имеет значение для значений r , соответствующих внутреннему и внешнему ядру, валентной оболочке и далее. 15
На рис. 3 показан график Kr для атома Hg. Видно, что K сильно отличается от K в областях, близких к ядру, где потенциал достигает значений, сравнимых с mc 2 .Для точечного ядра K → 0 при r → 0. Для конечного ядра K остается конечным, но небольшим, вблизи и внутри ядра. Видно, что электронный потенциал, экранирующий ядерный заряд, имеет значение для значений r , соответствующих внутреннему и внешнему ядру, валентной оболочке и далее. 15
Рис. 3. Кинематический фактор ZORA K для атома Hg как функция расстояния от ядра. Синий (сплошной): используется V ( r ) из численного расчета DFT с конечным ядром.Красный (пунктир): Использование V ( r ) = потенциал только ядра для точечного ядра с зарядом Z = 80 в выражении для K. Среднеквадратичный радиус ядра составляет 5,5 × 10 — 5 Å. [4].
ZORA, как известно, является хорошим приближением для валентных орбиталей в HAs, а также для связывания и орбиталей неподеленных пар в молекулах с HAs. Из уравнения. (32) обрезание правой части нулевого порядка оправдано, пока E мало. Это верно для валентных орбиталей, даже в HAs, но не верно для глубоких ядерных орбиталей в тяжелых элементах.Для расчетов молекулярных свойств, которые являются «химическими» в том смысле, что они определяются валентными орбиталями, ZORA является подходящим приближенным релятивистским методом. Существуют и другие вариационно устойчивые приближенные, а также формально точные двухкомпонентные подходы, которые используются для расчетов ЯМР (избранные ссылки см. В разделе 2.2). Эти операторы, как правило, не имеют компактных простых операторных представлений, в частности, для членов, зависящих от магнитного поля. Поэтому для целей этой главы структура ZORA, хотя и приблизительная, используется для иллюстрации различий между четырехкомпонентными, двухкомпонентными релятивистскими и нерелятивистскими операторами.
Из уравнения. (32) обрезание правой части нулевого порядка оправдано, пока E мало. Это верно для валентных орбиталей, даже в HAs, но не верно для глубоких ядерных орбиталей в тяжелых элементах.Для расчетов молекулярных свойств, которые являются «химическими» в том смысле, что они определяются валентными орбиталями, ZORA является подходящим приближенным релятивистским методом. Существуют и другие вариационно устойчивые приближенные, а также формально точные двухкомпонентные подходы, которые используются для расчетов ЯМР (избранные ссылки см. В разделе 2.2). Эти операторы, как правило, не имеют компактных простых операторных представлений, в частности, для членов, зависящих от магнитного поля. Поэтому для целей этой главы структура ZORA, хотя и приблизительная, используется для иллюстрации различий между четырехкомпонентными, двухкомпонентными релятивистскими и нерелятивистскими операторами.
Прежде чем перейти к обсуждению параметров ЯМР, мы кратко обсудим еще несколько аспектов одноэлектронного оператора SO. Для сферически-симметричного ядерного потенциала V ( r ) = — Ze 2 / (4 πε 0 r ) (т.е. для атомов 16 ) в операторе Паули SO
Для сферически-симметричного ядерного потенциала V ( r ) = — Ze 2 / (4 πε 0 r ) (т.е. для атомов 16 ) в операторе Паули SO
pˆV = −iℏ∇V = iℏZe24πε0rr3
(см. Упражнение 6). Напомним, что оператор углового момента имеет вид Lˆ = r × pˆ. Кроме того, σℏ = 2Sˆ.Таким образом, SO-оператор электрона для атома может быть записан как
(35) hˆSO = Ze28πε0me2c2Sˆ⋅Lˆr3 = Ze28πε0me2c2Lˆ⋅Sˆr3
В упражнениях 7 и 8 свойства этого оператора исследуются более подробно. В упражнении 9 читатель может рассчитать влияние взаимодействия SO на энергию атомизации молекулы TlH. Как уже упоминалось в разделе 1.2, оператор SO приводит к расщеплению вырожденных состояний в атомной оболочке с заданным угловым моментом ℓ . Собственные функции больше не являются проекциями спина в чистом виде, а смешивают α (↑) со спином β (↓).SO-взаимодействие в атомах также смешивает состояния с разными магнитными квантовыми числами m ℓ . Как будет показано ниже, сочетание SO может иметь сильное влияние на химические сдвиги ЯМР в системах с тяжелыми элементами.
Как будет показано ниже, сочетание SO может иметь сильное влияние на химические сдвиги ЯМР в системах с тяжелыми элементами.
Наконец, необходимо отметить, что рассмотрение электронной корреляции в релятивистской теории электронной структуры является очень активной областью исследований (см. [15] и обзоры, перечисленные в разделе 6), как и расчет спектроскопические свойства, такие как параметры ЯМР с помощью методов релятивистской квантовой химии.В тематических исследованиях, представленных в этой главе, использовалась некоторая форма приближения к проблеме электронной корреляции. Для выбранных примеров этому способствовало использование ДПФ, а приближенный двухкомпонентный гамильтониан использовался для учета релятивистских эффектов в расчетах. Относительно конкретных вопросов ДПФ в релятивистских вычислениях, в частности, общего использования нерелятивистских функционалов в сочетании с релятивистскими плотностями, см. [16].
Подводя итог этому разделу:
- •
Релятивистское квантовое уравнение для электрона, разработанное Дираком, является четырехкомпонентным уравнением.
 Электронный спин естественным образом возникает из релятивистской теории.
Электронный спин естественным образом возникает из релятивистской теории.- •
Уравнения можно преобразовать в двухкомпонентную форму. Для релятивистских квантово-химических расчетов доступны приближенные и (в принципе) точные двухкомпонентные гамильтонианы.
- •
Для c → ∞ решения DE и его двухкомпонентные версии становятся эквивалентными решениям SE (со спином).
- •
Для многоэлектронных систем необходимо также учитывать релятивистские эффекты для электрон-электронного взаимодействия.Это активный объект исследований, наряду с разработкой точных и эффективных четырех- и двухкомпонентных релятивистских методов для расчета спектроскопических свойств, таких как параметры ЯМР.
- •
Обычно существует различие между скалярными релятивистскими эффектами (от операторов без спина) и SO-связью. Часто для квантово-химических расчетов используются приближенные скалярно-релятивистские методы (без учета SO-связи).
 В этом случае вычислительная установка очень похожа на обычные нерелятивистские вычисления с реальными «однокомпонентными» спиновыми орбиталями.К этой категории также относятся расчеты со свободными от спина эффективными потенциалами ядра, которые имитируют скалярные релятивистские эффекты на валентных оболочках.
В этом случае вычислительная установка очень похожа на обычные нерелятивистские вычисления с реальными «однокомпонентными» спиновыми орбиталями.К этой категории также относятся расчеты со свободными от спина эффективными потенциалами ядра, которые имитируют скалярные релятивистские эффекты на валентных оболочках.
Данный вектор A: 10 см под углом 240 градусов, вектор B: 20 см под углом 135 градусов, вектор C: 15 см под углом 30 градусов. Как сложить и вычесть эти три вектора?
Быстрый набросок — это обычно хороший ход. На экзамене нет причин, по которым вы не можете сделать это на контрольной бумаге. Или на черновой бумаге, если она есть. Подчеркивая работу «быстро».Или как альтернатива; нарисуйте поле на правой стороне листа для ответов, четко обозначив это как черновую работу, и сделайте какие-либо наброски и т. д. в этой области.
Пусть вертикальный компонент будет # y #
Пусть горизонтальный компонент будет # x #
(традиционно вы использовали # i, j и k # в качестве векторной оси)
Пусть результирующий вектор будет # R #
#color (blue) («Рассмотрим вектор A») #
#x_A = -rsin (theta) = -10sin (30) = -10xx1 / 2 = -10 / 2 #
# y_A = -rcos (theta) = — 10cos (30) = — (10sqrt (3)) / 2 #
…………………………………………… …………………………………………. . ……………
. ……………
#color (blue) («Рассмотрим вектор B») #
# x_B = -rcos (theta) = — 20cos (45) = — 20xx1 / sqrt (2) = — (10sqrt (2)) / 2 #
# y_B = + rsin (theta) = + 20sin (45) = + 20xx1 / sqrt (2) = + (10sqrt (2)) / 2 #
…………………………………………. ………………………………………….. ……………..
#color (blue) («Рассмотрим вектор C») #
# x_C = + rcos (theta) = + 15cos (45) = + 15xx1 / sqrt (2) = + (15sqrt (2)) / 2 #
# y_c = + rsine (theta) = + 15sin (45) = + 15xx1 / sqrt (2) = + (15sqrt (2)) / 2 #
++++++++++++++++++++++++++++++++++++++++++++
++++ ++++++++++++++++++++++++++++++++++++++++++++
#color (blue) («Собираем все вместе») #
# x_R = x_A + x_B + x_C = -10 / 2- (10sqrt (2)) / 2+ (15sqrt (2)) / 2 #
# «» = -10 / 2 + (5sqrt (2)) / 2 #
# y_R = y_A + y_B + y_C = — (10sqrt (3)) / 2+ (10sqrt (2)) / 2+ (15sqrt (2)) / 2 #
# «» = (25sqrt (2)) / 2- (10sqrt (3)) / 2 #
~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~
Итак # R ^ 2 = (x_R) ^ 2 + (y_R) ^ 2 «» -> «» || R | | = sqrt (R ^ 2) #
Итак #tan (theta_R) = (y_R) / (x_R) «» -> «» theta_R = tan ^ (- 1) ((y_R) / (x_R)) #
Добавление компонентов (т.
 е., Аналитический метод добавления вектора)
е., Аналитический метод добавления вектора)Ранее в этом уроке мы узнали, что векторы, ориентированные под прямым углом друг к другу, можно сложить вместе с помощью теоремы Пифагора. Например, два вектора смещения с величиной и направлением 11 км, север и 11 км, восток, могут быть сложены вместе, чтобы получить результирующий вектор, направленный как на север, так и на восток. Когда два вектора складываются вместе, как показано ниже, в результате получается гипотенуза прямоугольного треугольника. Стороны прямоугольного треугольника имеют длину 11 км и 11 км.Результирующий можно определить с помощью теоремы Пифагора; его величина составляет 15,6 км. Решение показано под диаграммой.
Этот подход Пифагора является полезным подходом для добавления любых двух векторов, направленных под прямым углом друг к другу. Прямоугольный треугольник имеет две стороны плюс гипотенузу; так что теорема Пифагора идеально подходит для сложения двух векторов под прямым углом. Но есть пределы полезности теоремы Пифагора при решении задач сложения векторов.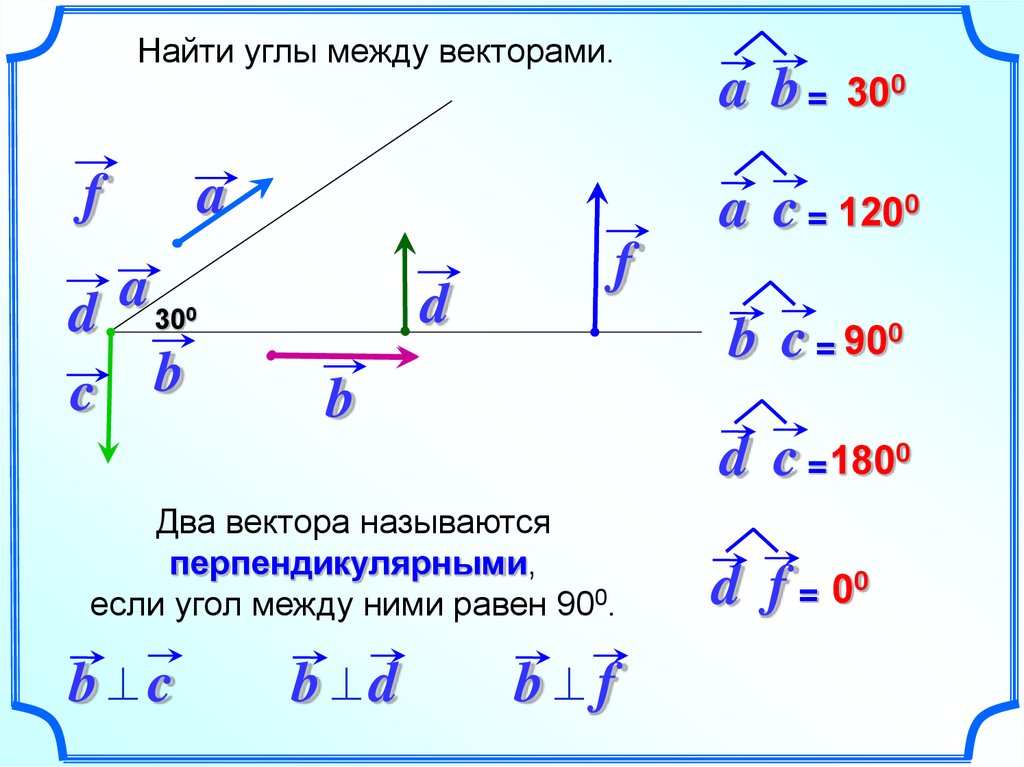 Например, сложение трех или четырех векторов не приводит к образованию прямоугольного треугольника с двумя сторонами и гипотенузой. Поэтому на первый взгляд может показаться, что невозможно использовать теорему Пифагора для определения результата сложения трех или четырех векторов. Кроме того, теорема Пифагора работает, когда два добавленных вектора находятся под прямым углом друг к другу — например, для добавления вектора севера и вектора востока. Но что делать, если два складываемых вектора не расположены под прямым углом друг к другу? Есть ли способ использования математики для надежного определения результирующей для таких ситуаций сложения векторов? Или студенту-физику остается определять такие результирующие с помощью масштабированной векторной диаграммы? Здесь, на этой странице, мы узнаем, как подходить к более сложным ситуациям сложения векторов, комбинируя концепцию векторных компонентов (обсуждавшихся ранее) и принципов векторного разрешения (обсужденных ранее) с использованием теоремы Пифагора (обсуждавшейся ранее).
Например, сложение трех или четырех векторов не приводит к образованию прямоугольного треугольника с двумя сторонами и гипотенузой. Поэтому на первый взгляд может показаться, что невозможно использовать теорему Пифагора для определения результата сложения трех или четырех векторов. Кроме того, теорема Пифагора работает, когда два добавленных вектора находятся под прямым углом друг к другу — например, для добавления вектора севера и вектора востока. Но что делать, если два складываемых вектора не расположены под прямым углом друг к другу? Есть ли способ использования математики для надежного определения результирующей для таких ситуаций сложения векторов? Или студенту-физику остается определять такие результирующие с помощью масштабированной векторной диаграммы? Здесь, на этой странице, мы узнаем, как подходить к более сложным ситуациям сложения векторов, комбинируя концепцию векторных компонентов (обсуждавшихся ранее) и принципов векторного разрешения (обсужденных ранее) с использованием теоремы Пифагора (обсуждавшейся ранее).
Сложение трех или более прямоугольных векторов
В качестве первого примера рассмотрим следующую задачу сложения векторов:
Пример 1:
Студент проезжает на своей машине 6,0 км на север, затем делает поворот направо и едет на 6,0 км на восток. Наконец, ученик поворачивает налево и едет еще 2,0 км на север. Какова величина общего перемещения студента?
Как и любая проблема в физике, успешное решение начинается с выработки мысленной картины ситуации.Построение диаграммы, подобной приведенной ниже, часто оказывается полезным в процессе визуализации.
Когда эти три вектора складываются вместе по принципу «голова к хвосту», результатом является вектор, который простирается от хвоста первого вектора (6,0 км, север, показан красным) до стрелки третьего вектора (2,0 км, Север, показан зеленым цветом). Схема сложения векторов «голова к хвосту» показана ниже.
Как видно на диаграмме, результирующий вектор (нарисованный черным цветом) не является гипотенузой какого-либо прямоугольного треугольника — по крайней мере, не любого сразу очевидного прямоугольного треугольника.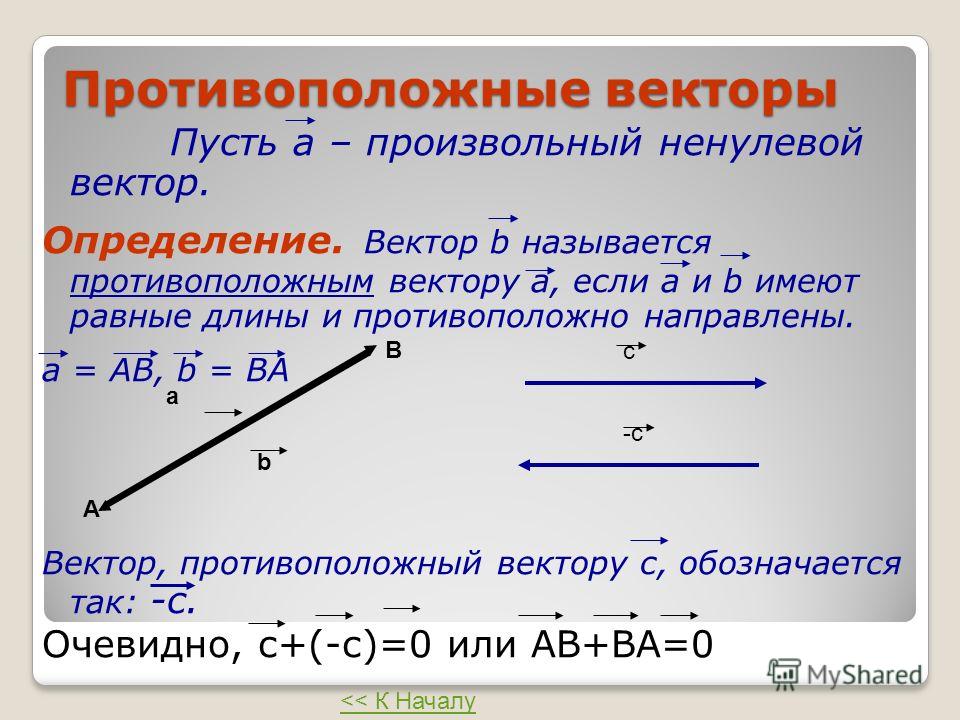 Но можно ли заставить этот результирующий вектор быть гипотенузой прямоугольного треугольника? Ответ — да! Для этого необходимо изменить порядок добавления трех векторов. Вышеупомянутые векторы были нарисованы в том порядке, в котором они были запущены. Студент поехал на север, затем на восток, а затем снова на север. Но если сложить три вектора в порядке 6.0 км, N + 2.0 км, N + 6.0 км, E, то диаграмма будет выглядеть так:
Но можно ли заставить этот результирующий вектор быть гипотенузой прямоугольного треугольника? Ответ — да! Для этого необходимо изменить порядок добавления трех векторов. Вышеупомянутые векторы были нарисованы в том порядке, в котором они были запущены. Студент поехал на север, затем на восток, а затем снова на север. Но если сложить три вектора в порядке 6.0 км, N + 2.0 км, N + 6.0 км, E, то диаграмма будет выглядеть так:
После изменения порядка добавления трех векторов результирующий вектор теперь является гипотенузой прямоугольного треугольника.Длина перпендикулярных сторон прямоугольного треугольника составляет 8,0 м, север (6,0 км + 2,0 км) и 6,0 км, восток. Величину результирующего вектора (R) можно определить с помощью теоремы Пифагора.
R 2 = (8,0 км) 2 + (6,0 км) 2
R 2 = 64,0 км 2 + 36,0 км 2
R 2 = 100,0 км 2
R = SQRT (100,0 км2)
R = 10,0 км
(SQRT означает квадратный корень)
На первой диаграмме сложения векторов выше три вектора были добавлены в том порядке, в котором они управляются.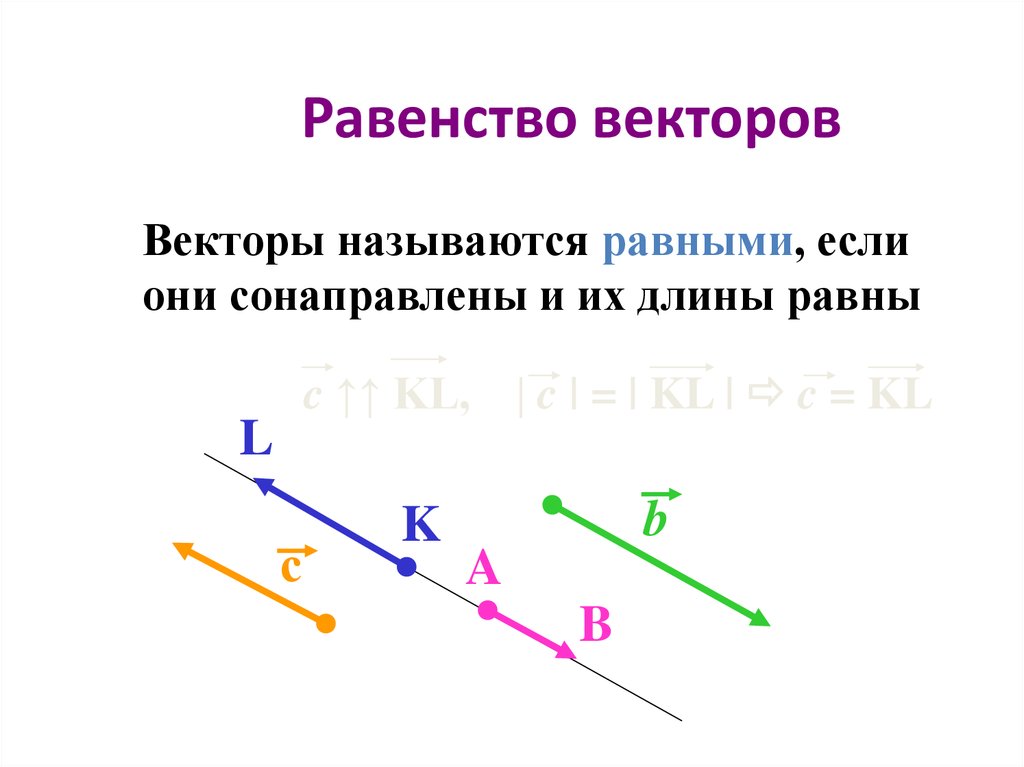 На второй диаграмме сложения векторов (непосредственно выше) порядок, в котором были добавлены векторы, был изменен. Это изменение порядка не повлияло на размер полученного результата. Это иллюстрирует важный момент о добавлении векторов: результат не зависит от порядка, в котором они добавляются. Сложение векторов A + B + C дает тот же результат, что и добавление векторов B + A + C или даже C + B + A . Пока все три вектора включены с указанными величиной и направлением, результат будет таким же.Это свойство векторов является ключом к стратегии, используемой при определении ответа на приведенный выше пример проблемы. Чтобы проиллюстрировать эту стратегию, давайте рассмотрим ситуацию сложения векторов, описанную в Примере 2 ниже.
На второй диаграмме сложения векторов (непосредственно выше) порядок, в котором были добавлены векторы, был изменен. Это изменение порядка не повлияло на размер полученного результата. Это иллюстрирует важный момент о добавлении векторов: результат не зависит от порядка, в котором они добавляются. Сложение векторов A + B + C дает тот же результат, что и добавление векторов B + A + C или даже C + B + A . Пока все три вектора включены с указанными величиной и направлением, результат будет таким же.Это свойство векторов является ключом к стратегии, используемой при определении ответа на приведенный выше пример проблемы. Чтобы проиллюстрировать эту стратегию, давайте рассмотрим ситуацию сложения векторов, описанную в Примере 2 ниже.
Пример 2:
Mac и Тош делают Vector Walk Lab . Начиная с дверей своего класса физики, они проходят 2 метра на юг. Они делают поворот направо и идут 16.0 метров, запад. Они снова поворачивают направо и проходят 24,0 метра на север.
Затем они поворачивают налево и проходят 36 метров на запад. Какова величина их общего смещения?
Графическое представление данной проблемы поможет визуализировать происходящее. На диаграмме ниже показано такое представление.
Когда эти четыре вектора складываются вместе по принципу « голова к хвосту », в результате получается вектор, идущий от хвоста первого вектора (2.0 м, юг, показан красным) до стрелки четвертого вектора (36,0 м, запад, показан зеленым). Схема сложения векторов «голова к хвосту» показана ниже.
Результирующий вектор (нарисованный черным цветом и обозначенный как R ) на приведенной выше диаграмме сложения векторов не является гипотенузой какого-либо сразу очевидного правого треугольника. Но, изменив порядок сложения этих четырех векторов, можно заставить этот результирующий вектор быть гипотенузой прямоугольного треугольника. Например, добавляя векторы в порядке 2.0 м, S + 24,0 м, N + 16,0 м, W + 36,0 м. W, результирующая становится гипотенузой прямоугольного треугольника.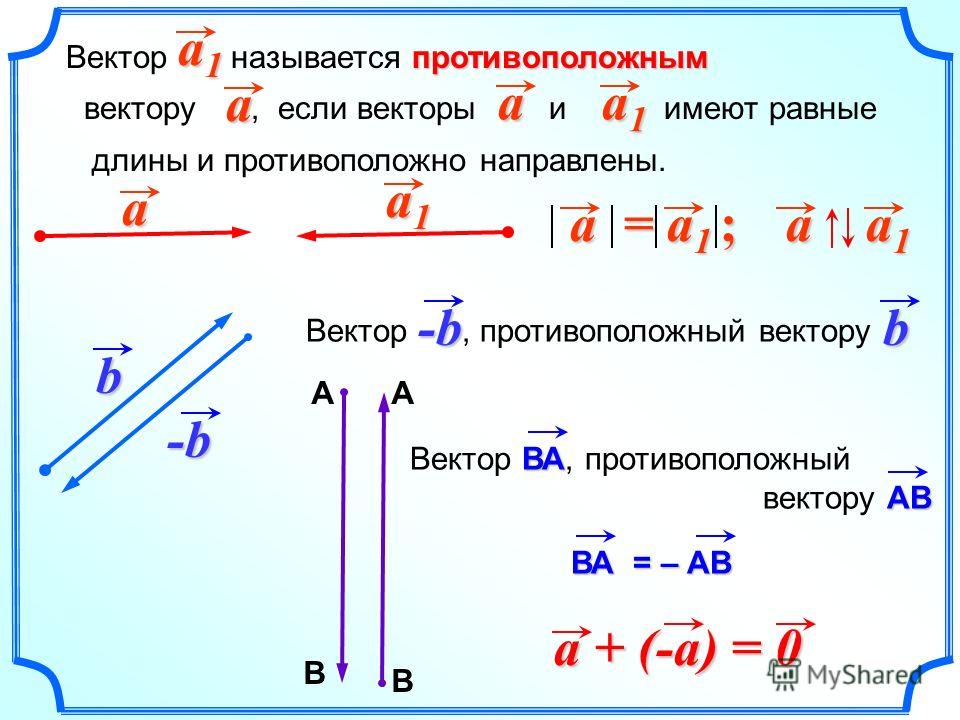 Это показано на диаграмме сложения векторов ниже.
Это показано на диаграмме сложения векторов ниже.
После перестановки векторов результирующая теперь гипотенуза прямоугольного треугольника, имеющего две перпендикулярные стороны длиной 22,0 м, север и 52,0 м, запад. 22,0 м, северная сторона — результат 2,0 м, юга и 24,0 м, сложенных вместе. 52,0 м, западная сторона — результат 16,0 м, запад и 36,0 м, сложенные вместе.Величину результирующего вектора (R) можно определить с помощью теоремы Пифагора.
R 2 = (22,0 м) 2 + (52,0 м) 2
R 2 = 484,0 м 2 + 2704,0 м 2
R 2 = 3188,0 м 2
R = SQRT (3188,0 м2 2 )
R = 56,5 м
(SQRT означает квадратный корень)
Как видно из этих двух примеров, результат сложения трех или более векторов под прямым углом может быть легко определен с помощью теоремы Пифагора.Это включает добавление векторов в другом порядке.
SOH CAH TOA и направление векторов
Вышеупомянутое обсуждение объясняет метод определения величины результирующего для трех или более перпендикулярных векторов.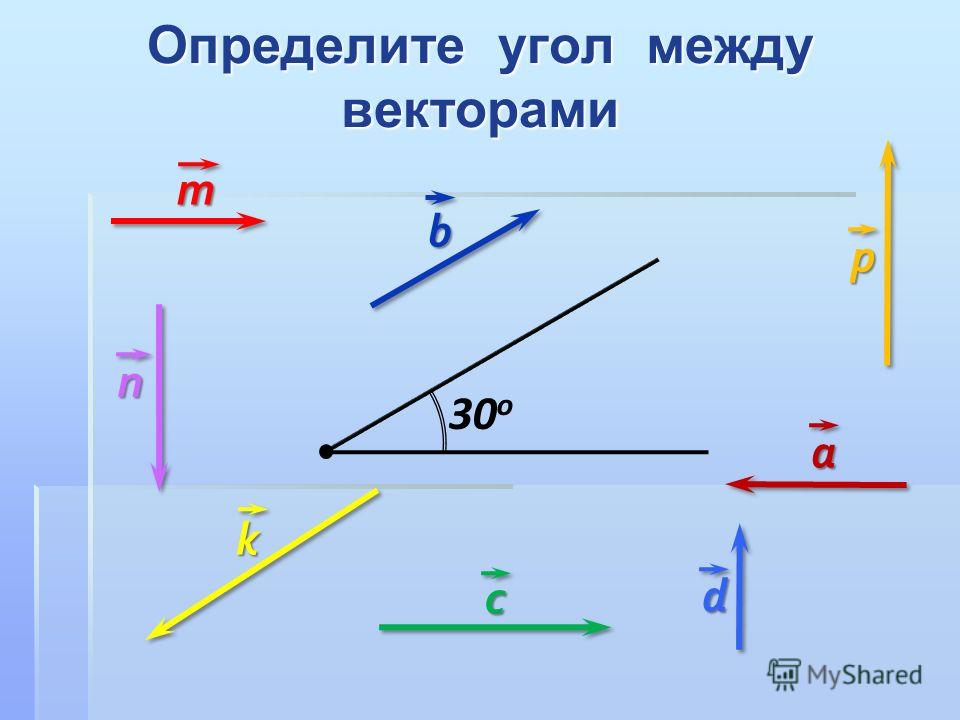 Тема направления в обсуждении проигнорирована. Теперь обратим внимание на способ определения направления результирующего вектора. В качестве беглого обзора напомним, что ранее в этом уроке было введено соглашение для выражения направления вектора.Соглашение известно как «против часовой стрелки от восточного соглашения», часто сокращенно CCW . Используя это соглашение, направление вектора часто выражается как угол поворота вектора против часовой стрелки вокруг его хвоста от восточного направления.
Тема направления в обсуждении проигнорирована. Теперь обратим внимание на способ определения направления результирующего вектора. В качестве беглого обзора напомним, что ранее в этом уроке было введено соглашение для выражения направления вектора.Соглашение известно как «против часовой стрелки от восточного соглашения», часто сокращенно CCW . Используя это соглашение, направление вектора часто выражается как угол поворота вектора против часовой стрелки вокруг его хвоста от восточного направления.
Чтобы начать обсуждение, вернемся к , Пример 1 выше, где мы попытались добавить три вектора: 6.0 км, N + 6.0 км, E + 2.0 км, N. В решении порядок сложения трех векторов был переставлен так, чтобы образовался прямоугольный треугольник, в результате чего получилась гипотенуза треугольника.Треугольник перерисовывается справа. Обратите внимание, что угол в нижнем левом углу треугольника обозначен как тета (Θ). Тета (Θ) представляет угол, который вектор образует с северной осью.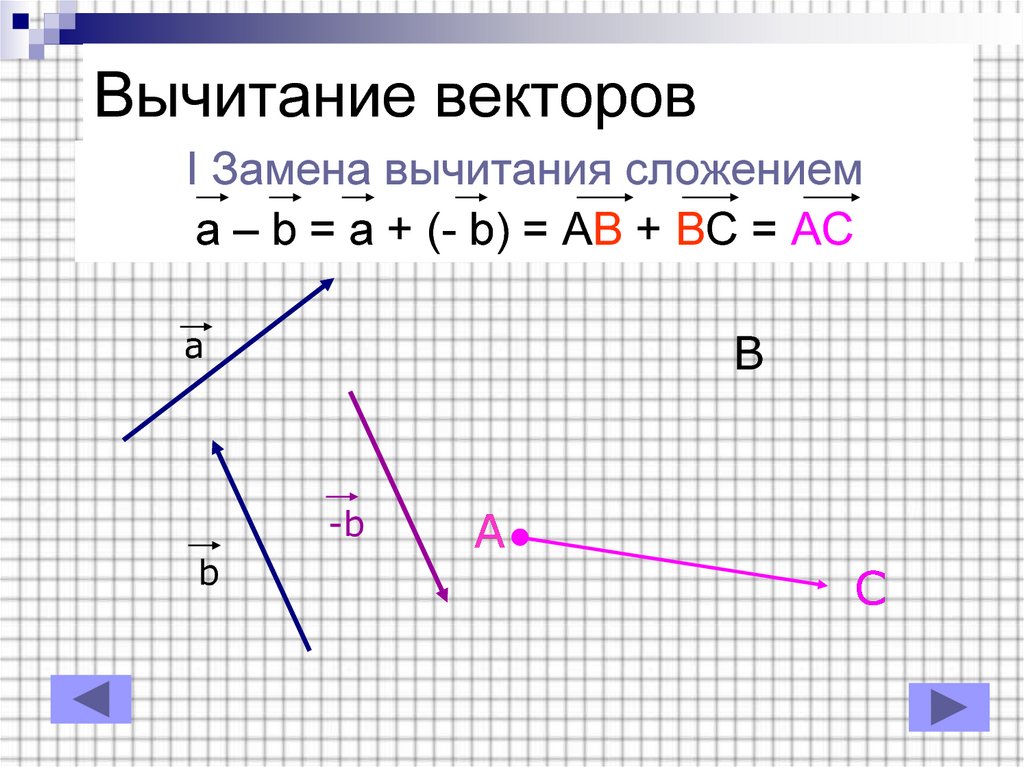 Тета (Θ) можно вычислить с помощью одной из трех тригонометрических функций, представленных ранее в этом уроке — синуса, косинуса или тангенса. Мнемоника SOH CAH TOA — полезный способ запомнить, какую функцию использовать. В этой задаче мы хотим определить угловую меру тэты (), и нам известна длина стороны, противоположной тэте () — 6.0 км — и длина стороны, прилегающей к углу тета (Θ) — 8,0 км. TOA SOH CAH TOA указывает, что тангенс любого угла — это отношение длин стороны, противоположной стороне, смежной с этим углом. Таким образом, тангенциальная функция будет использоваться для вычисления угловой меры теты (). Работа представлена ниже.
Тета (Θ) можно вычислить с помощью одной из трех тригонометрических функций, представленных ранее в этом уроке — синуса, косинуса или тангенса. Мнемоника SOH CAH TOA — полезный способ запомнить, какую функцию использовать. В этой задаче мы хотим определить угловую меру тэты (), и нам известна длина стороны, противоположной тэте () — 6.0 км — и длина стороны, прилегающей к углу тета (Θ) — 8,0 км. TOA SOH CAH TOA указывает, что тангенс любого угла — это отношение длин стороны, противоположной стороне, смежной с этим углом. Таким образом, тангенциальная функция будет использоваться для вычисления угловой меры теты (). Работа представлена ниже.
Касательная (Θ) = напротив / рядом
Касательная (Θ) = 6,0 / 8,0
Касательная (Θ) = 0,75
Θ = загар -1 (0,75)
Θ = 36.869… °
Θ = 37 °
Проблема не исчезнет после того, как будет вычислено значение тета (Θ). Теперь эту угловую меру необходимо использовать для определения направления. Один из способов сделать это — просто указать, что направление полученного результата — 37 ° к востоку от севера. В качестве альтернативы можно использовать условное обозначение против часовой стрелки. Поскольку угол, который получается в результате с востоком, является дополнением к углу, который получается с севером, мы могли бы выразить направление как 53 ° против часовой стрелки.
В качестве альтернативы можно использовать условное обозначение против часовой стрелки. Поскольку угол, который получается в результате с востоком, является дополнением к углу, который получается с севером, мы могли бы выразить направление как 53 ° против часовой стрелки.
Теперь мы рассмотрим Пример 2 как второй пример того, как использовать SOH CAH TOA для определения направления результирующего.В Примере 2 мы пытались определить величину 2,0 м. S + 16,0 м, W + 24,0 м, N + 36,0 м, W. Решение включало изменение порядка сложения так, чтобы в результате получилась гипотенуза прямоугольного треугольника с известными сторонами. Правый треугольник показан ниже. Результат отображается черным цветом. Еще раз обратите внимание, что угол в правом нижнем углу треугольника обозначен как тета (Θ). Тета (Θ) представляет угол, который вектор образует с северной осью.
Theta (Θ) можно вычислить с помощью касательной функции.В этой задаче мы хотим определить угловую меру тета (), и нам известна длина стороны, противоположной тета (Θ) — 52,0 м — и длина стороны, примыкающей к углу тета (Θ) — 22,0 м. TOA SOH CAH TOA указывает, что тангенс любого угла — это отношение длин стороны, противоположной стороне, смежной с этим углом. Таким образом, тангенциальная функция будет использоваться для вычисления угловой меры теты (). Работа представлена ниже.
TOA SOH CAH TOA указывает, что тангенс любого угла — это отношение длин стороны, противоположной стороне, смежной с этим углом. Таким образом, тангенциальная функция будет использоваться для вычисления угловой меры теты (). Работа представлена ниже.
Касательная (Θ) = напротив / рядом
Касательная (Θ) = 52.0 / 22,0
Касательная (Θ) = 2,3636…
Θ = загар -1 (2,3636…)
Θ = 67,067… °
Θ = 67,1 °
Проблема не исчезнет после того, как будет вычислено значение тета (Θ). Теперь эту угловую меру необходимо использовать для определения направления. Один из способов сделать это — просто указать, что направление полученного результата составляет 67,1 ° к западу от севера. В качестве альтернативы можно использовать условное обозначение против часовой стрелки. Ось севера повернута на 90 ° против часовой стрелки от востока, и этот вектор равен дополнительным 67.1 ° против часовой стрелки после севера. Таким образом, направление CCW составляет 157,1 ° CCW.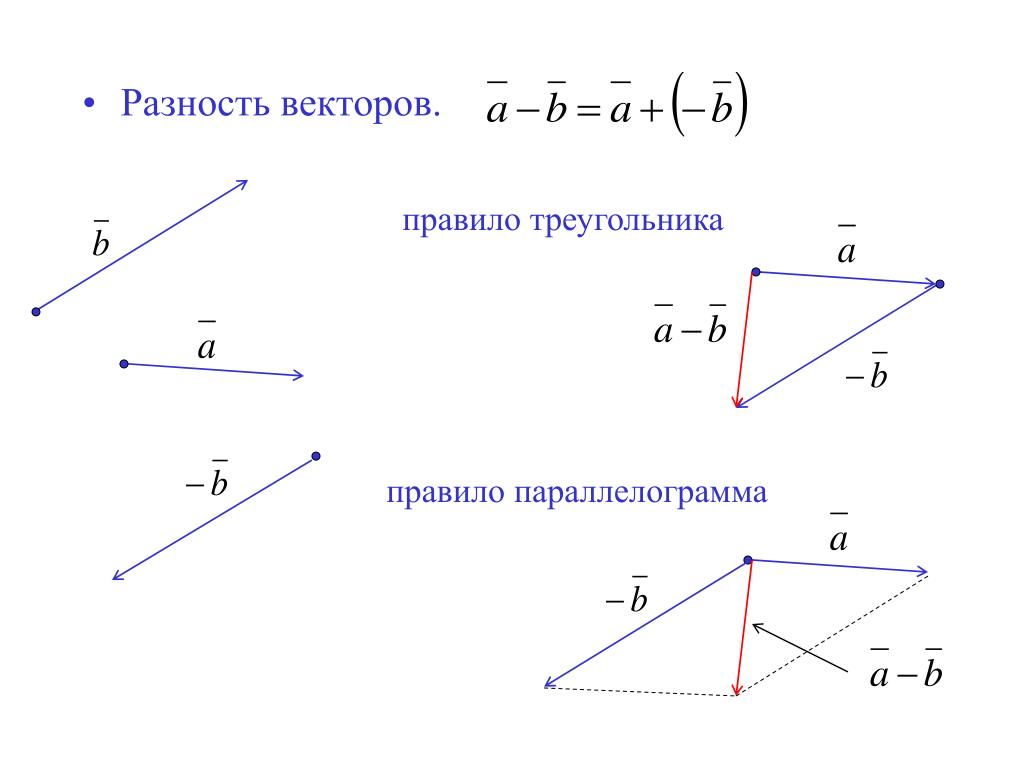
Таким образом, направление вектора может быть определено так же, как он всегда определяется — путем определения угла поворота против часовой стрелки с востока. Поскольку результат — гипотенуза прямоугольного треугольника, этого можно достичь, сначала найдя угол, который получается у одной из ближайших осей треугольника. После этого нужно немного подумать, чтобы связать угол с направлением.
Сложение неперпендикулярных векторов
Теперь мы рассмотрим ситуации, в которых два (или более) добавляемых вектора не расположены под прямым углом друг к другу. Теорема Пифагора неприменима к таким ситуациям, поскольку применима только к прямоугольным треугольникам. Два неперпендикулярных вектора не образуют прямоугольный треугольник. Тем не менее, можно заставить два (или более) неперпендикулярных вектора преобразовываться в другие векторы, которые образуют прямоугольный треугольник.Уловка включает в себя концепцию векторного компонента и процесс векторного разрешения.
Компонент вектора описывает влияние вектора в заданном направлении. Любой вектор , расположенный под углом , имеет две компоненты; один направлен горизонтально, а другой — вертикально. Например, северо-западный вектор имеет северную составляющую и западную составляющую. Вместе эффект этих двух компонентов равен общему эффекту вектора , расположенного под углом . В качестве примера рассмотрим самолет, который летит на северо-запад из аэропорта Чикаго О’Хара в сторону границы с Канадой.Вектор северо-западного смещения плоскости имеет две составляющие — северную и западную. При сложении эти две составляющие равны общему северо-западному смещению. Это показано на схеме ниже.
Любой вектор , расположенный под углом , имеет две компоненты; один направлен горизонтально, а другой — вертикально. Например, северо-западный вектор имеет северную составляющую и западную составляющую. Вместе эффект этих двух компонентов равен общему эффекту вектора , расположенного под углом . В качестве примера рассмотрим самолет, который летит на северо-запад из аэропорта Чикаго О’Хара в сторону границы с Канадой.Вектор северо-западного смещения плоскости имеет две составляющие — северную и западную. При сложении эти две составляющие равны общему северо-западному смещению. Это показано на схеме ниже.
Вектор северо-запад имеет северную и западную компоненты, которые представлены как A x и A y . Можно сказать что
A = A x + A y
Поэтому всякий раз, когда мы думаем о векторе северо-запад, мы можем думать вместо двух векторов — вектора севера и вектора запада.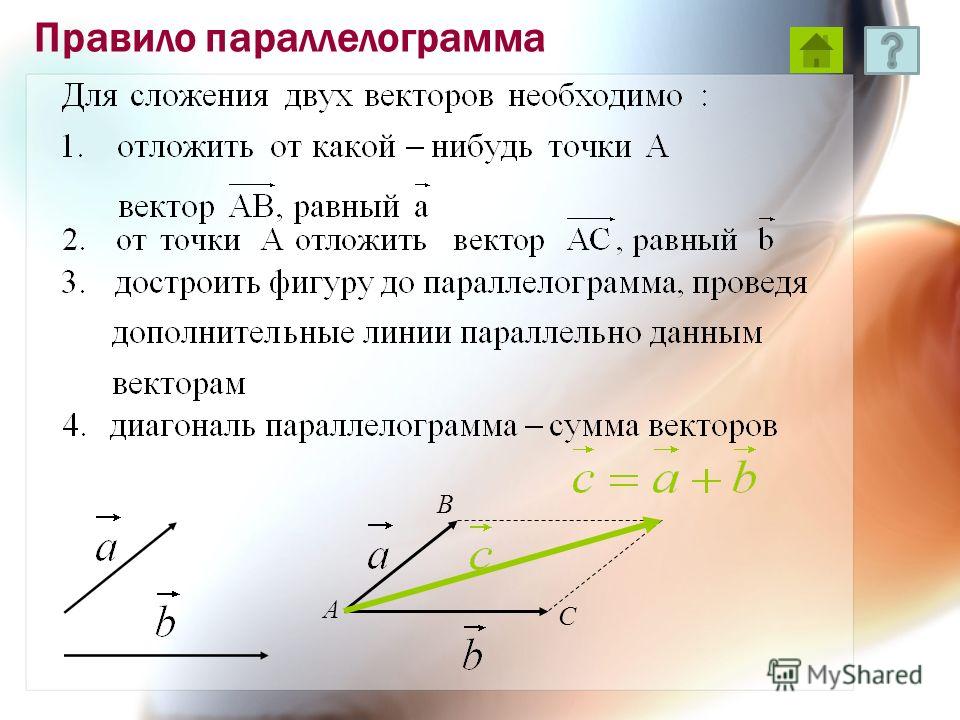 Два компонента A x + A y могут быть заменены на один вектор A в задаче.
Два компонента A x + A y могут быть заменены на один вектор A в задаче.
Теперь предположим, что ваша задача состоит в сложении двух неперпендикулярных векторов. Мы будем называть векторы A и B . Вектор — это угловатый вектор , который не является ни горизонтальным, ни вертикальным. А вектор B — красивый, вежливый вектор, направленный горизонтально. Ситуация показана ниже.
Конечно неприятный вектор A имеет два компонента — A x и A y . Эти две компоненты вместе равны вектору A . То есть A = A x + A y .
И поскольку это правда, то можно сказать, что A + B = A x + A y + B .
Таким образом, проблема A + B превратилась в проблему, в которой все векторы расположены под прямым углом друг к другу.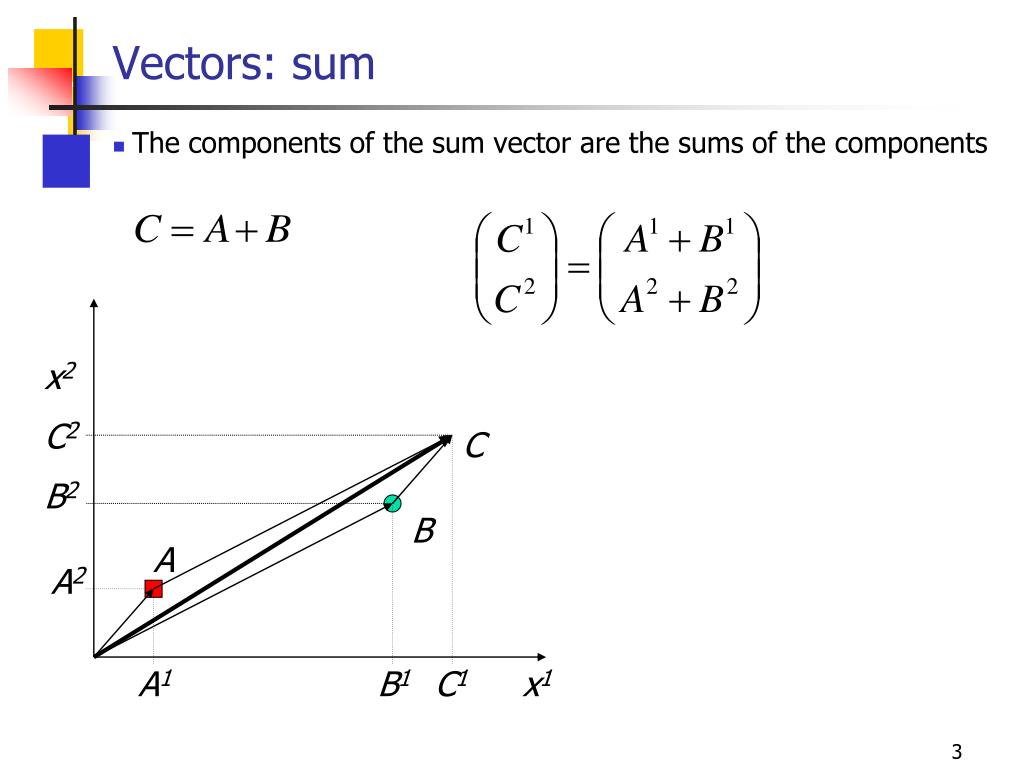 Nasty был заменен на nice , и это должно порадовать любого студента-физика. Поскольку все векторы расположены под прямым углом друг к другу, их сложение приводит к результату, который находится в гипотенузе прямоугольного треугольника. Затем теорему Пифагора можно использовать для определения величины результирующего.
Nasty был заменен на nice , и это должно порадовать любого студента-физика. Поскольку все векторы расположены под прямым углом друг к другу, их сложение приводит к результату, который находится в гипотенузе прямоугольного треугольника. Затем теорему Пифагора можно использовать для определения величины результирующего.
Чтобы увидеть, как этот процесс работает с реальной проблемой сложения векторов, рассмотрим пример 3, показанный ниже.
Пример 3:
Макс играет среднего полузащитника футбольной команды Юга.Во время одной игры в матче в прошлую пятницу против Академии Нью-Грир, он сделал следующие движения после того, как мяч был захвачен третьим падением. Сначала он дал задний ход в южном направлении на 2,6 метра. Затем он переместился влево (на запад) на расстояние 2,2 метра. Наконец, он сделал пол-оборота и побежал вниз на расстояние 4,8 метра в направлении 240 ° против часовой стрелки с востока (30 ° з.д.), прежде чем окончательно выбить ветер из широкого приемника New Greer.
Определите величину и направление общего смещения Макса.
Как обычно, решение начинается с диаграммы добавляемых векторов.
Для облегчения обсуждения три вектора были помечены как векторы A , B и C . Результат — векторная сумма этих трех векторов; диаграмма сложения векторов «голова к хвосту» показывает, что результат направлен на юго-запад. Из трех добавляемых векторов вектор C явно является неприятным вектором .Его направление не строго на юг и не на запад. Решение включает в себя разложение этого вектора на его составляющие.
Процесс векторного разрешения обсуждался ранее в этом уроке. Этот процесс включает использование модуля и функций синуса и косинуса для определения x- и y-компонентов вектора. Вектор C образует угол 30 ° с южным направлением. Изобразив прямоугольный треугольник с горизонтальным и вертикальным катетами и C в качестве гипотенузы, становится возможным определить компоненты вектора C.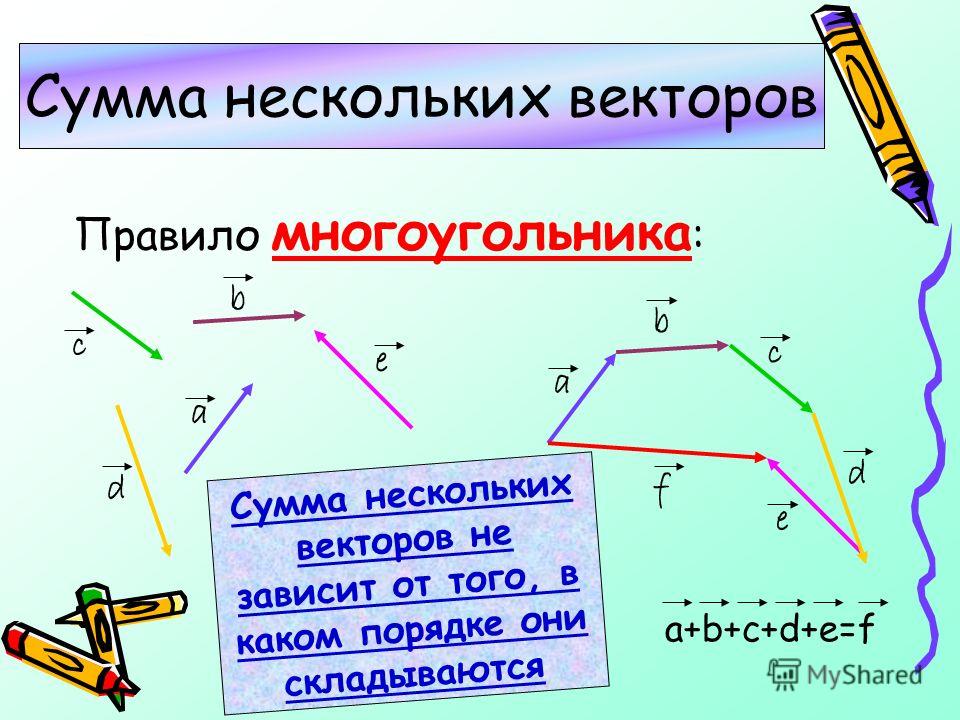 Это показано на схеме ниже. Сторона, примыкающая к этому углу в 30 ° в треугольнике, является вертикальной стороной; вертикальная сторона представляет собой вертикальную (южную) составляющую C — C y . Итак, чтобы определить C y , используется функция косинуса. Сторона, противоположная углу 30 °, является горизонтальной стороной; горизонтальная сторона представляет собой горизонтальную (западную) составляющую C — C x . Значения C x и C y можно определить с помощью SOH CAH TOA. Функция косинуса используется для определения компонента, направленного на юг, поскольку компонент, направленный на юг, примыкает к углу 30 °.Синусоидальная функция используется для определения западной составляющей, поскольку западная составляющая является стороной, противоположной углу 30 °. Работа представлена ниже.
Это показано на схеме ниже. Сторона, примыкающая к этому углу в 30 ° в треугольнике, является вертикальной стороной; вертикальная сторона представляет собой вертикальную (южную) составляющую C — C y . Итак, чтобы определить C y , используется функция косинуса. Сторона, противоположная углу 30 °, является горизонтальной стороной; горизонтальная сторона представляет собой горизонтальную (западную) составляющую C — C x . Значения C x и C y можно определить с помощью SOH CAH TOA. Функция косинуса используется для определения компонента, направленного на юг, поскольку компонент, направленный на юг, примыкает к углу 30 °.Синусоидальная функция используется для определения западной составляющей, поскольку западная составляющая является стороной, противоположной углу 30 °. Работа представлена ниже.
Теперь наша задача сложения векторов была преобразована из добавления двух хороших векторов и одного неприятного вектора в добавление четырех хороших векторов.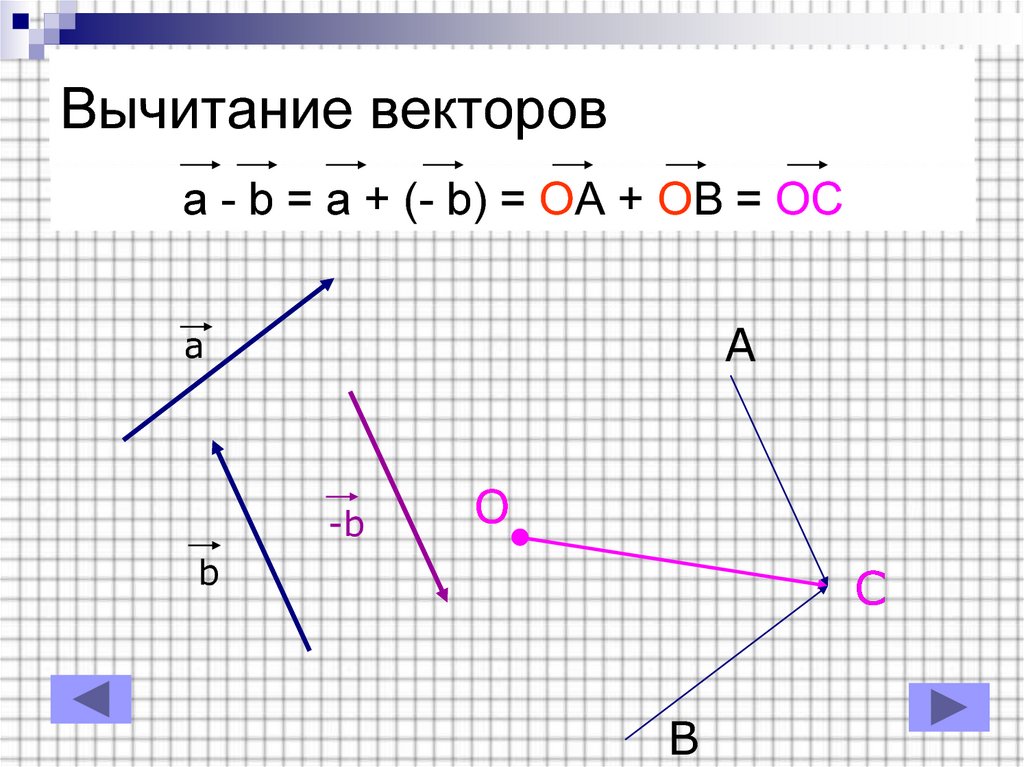
Поскольку все векторы ориентированы вдоль обычных осей север-юг и восток-запад, они могут быть добавлены в любом порядке, чтобы получить прямоугольный треугольник, гипотенуза которого является результирующей.Такая диаграмма представлена ниже.
Перпендикулярные стороны треугольника имеют длину 4,6 метра и 6,756 метра. Длина горизонтальной стороны (4,6 м) была определена путем сложения значений B (2,2 м) и C x (2,4 м). Длина вертикальной стороны (6,756… м) определялась сложением значений A (2,6 м) и C y (4,156… м). Результирующая величина (R) теперь может быть определена с помощью теоремы Пифагора.
R 2 = (6.756… м) 2 + (4,6 м) 2
R 2 = 45,655… м 2 + 21,16 м 2
R 2 = 66,815… м 2
R = SQRT (66,815… м 2 )
R = 8,174… м
R = ~ 8,2 м
Направление результирующей можно определить, найдя угол, который она составляет с вектором север-юг или восток-запад.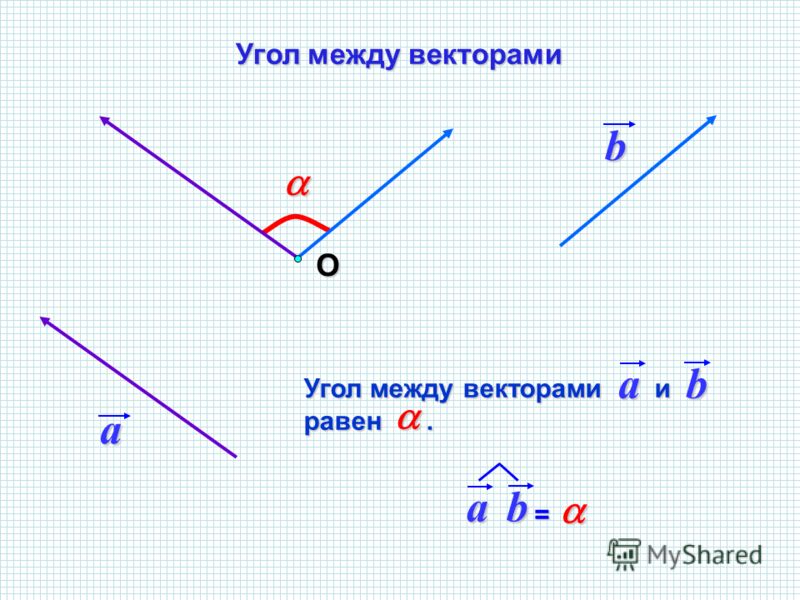 На диаграмме справа показан угол тета (Θ), отмеченный внутри треугольника сложения векторов.Этот угол тета — это угол, который получается в результате с западом. Его значение можно определить с помощью функции касательной. Функция касательной (как в TOA) связывает значение угла с отношением длин противоположной стороны к соседней стороне. Это,
На диаграмме справа показан угол тета (Θ), отмеченный внутри треугольника сложения векторов.Этот угол тета — это угол, который получается в результате с западом. Его значение можно определить с помощью функции касательной. Функция касательной (как в TOA) связывает значение угла с отношением длин противоположной стороны к соседней стороне. Это,
касательная (Θ) = (6,756… м) / (4,6 м) = 1,46889…
Используя функцию обратной тангенсации, можно определить угол тета (Θ). На большинстве калькуляторов для этого используются кнопки 2-го касания.
Θ = загар -1 (1.46889…) = 55,7536… °
Θ = ~ 56 °
Этот угол 56 ° представляет собой угол между результирующим вектором (нарисованным черным цветом выше) и направлением на запад. Это делает направление 56 ° к югу от запада. Направление результирующего, основанное на соглашении против часовой стрелки от восточного (CCW), можно определить, добавив 180 ° к 56 °. Таким образом, направление против часовой стрелки составляет 236 °.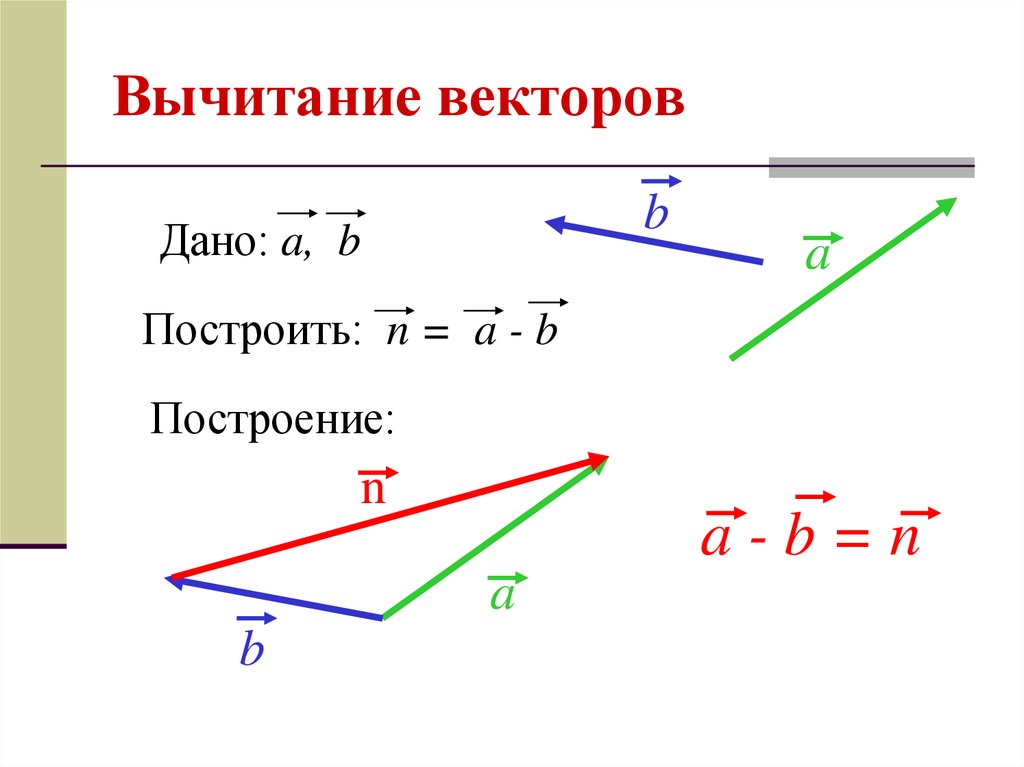
Пример 4 предоставляет последний пример того, как объединить разрешение вектора со сложением векторов, чтобы добавить три или более неперпендикулярных вектора.Поскольку этот пример включает в себя три особенно неприятных вектора , таблица будет использоваться для организации информации о величине и направлении компонентов. Использование таблицы — разумная идея, когда проблемы усложняются.
Пример 4:
Кэмерон Пер (его друзья зовут его Кэмом) и Бакстер Натур отправляются в поход. Начиная с домашней базы, они совершают следующие движения.
A: 2,65 км, 140 ° против часовой стрелки
А: 4.77 км, 252 ° против часовой стрелки
C: 3,18 км, 332 ° против часовой стрелкиОпределите величину и направление их общего смещения.
Наглядное представление ситуации показано ниже.
Чтобы определить результат, три отдельных вектора разделяются на горизонтальные и вертикальные компоненты. Информация об угле каждого вектора используется для формирования прямоугольного треугольника, в котором вектор является гипотенузой, а его перпендикулярные стороны ориентированы по осям восток-запад и север-юг.Это показано на схеме ниже.
Информация об угле каждого вектора используется для формирования прямоугольного треугольника, в котором вектор является гипотенузой, а его перпендикулярные стороны ориентированы по осям восток-запад и север-юг.Это показано на схеме ниже.
Затем тригонометрические функции — синус, косинус и тангенс — используются для определения величины горизонтальной и вертикальной составляющих каждого вектора. Работа показана и организована в таблице ниже.
Вектор | Компонент Восток-Запад | Компонент Север-Юг |
| A 2.65 км 140 ° против часовой стрелки | (2,65 км) • cos (40 °) = 2,030… км, запад | (2,65 км) • sin (40 °) = 1,703… км, север |
| B 4.77 км 252 ° против часовой стрелки | (4,77 км) • sin (18 °) = 1,474… км, запад | (4,77 км) • cos (18 °) = 4,536… км, юг |
| С 3.  18 км 18 км 332 ° против часовой стрелки | (3.18 км) • cos (28 °) = 2,808… км, восток | (3,18 км) • sin (28 °) = 1,493… км, юг |
| Сумма А + В + С | 0,696 км, Запад | 4.326 км, Юг |
Последняя строка вышеприведенной таблицы представляет собой сумму всех компонентов Восток-Запад и сумму всех компонентов Север-Юг. Результирующий состоит из этих двух компонентов.Результирующая определяется путем сложения этих двух компонентов, чтобы сформировать прямоугольный треугольник с гипотенузой, равной результирующей. Обычно это включает в себя добавление всех горизонтальных компонентов для определения общей длины горизонтальной стороны прямоугольного треугольника… и добавление всех вертикальных компонентов для определения общей длины вертикальной стороны прямоугольного треугольника. Это делается в таблице выше, просто добавляя еще одну строку в таблицу для векторной суммы всех компонентов. При сложении компонентов восток-запад всех отдельных векторов необходимо учитывать, что компонент, направленный на восток, и компонент, направленный на запад, суммируются как положительный и отрицательный . Некоторые студенты предпочитают думать об этом как о вычитании, а не как о сложении. На самом деле это действительно сложение — сложение векторов с противоположным направлением. Точно так же северная и южная составляющие также суммируются как положительный и отрицательный .Как только нижняя строка определена точно, величина результирующего может быть определена с помощью теоремы Пифагора.
При сложении компонентов восток-запад всех отдельных векторов необходимо учитывать, что компонент, направленный на восток, и компонент, направленный на запад, суммируются как положительный и отрицательный . Некоторые студенты предпочитают думать об этом как о вычитании, а не как о сложении. На самом деле это действительно сложение — сложение векторов с противоположным направлением. Точно так же северная и южная составляющие также суммируются как положительный и отрицательный .Как только нижняя строка определена точно, величина результирующего может быть определена с помощью теоремы Пифагора.
R 2 = (0,696 км) 2 + (4,326 км) 2
R 2 = 0,484 км 2 + 18,714 км 2
R 2 = 19,199 км 2
R = SQRT (19,199 км 2 )
R = ~ 4,38 км
Направление результирующего смещения можно определить, построив последний треугольник из составляющих результирующего.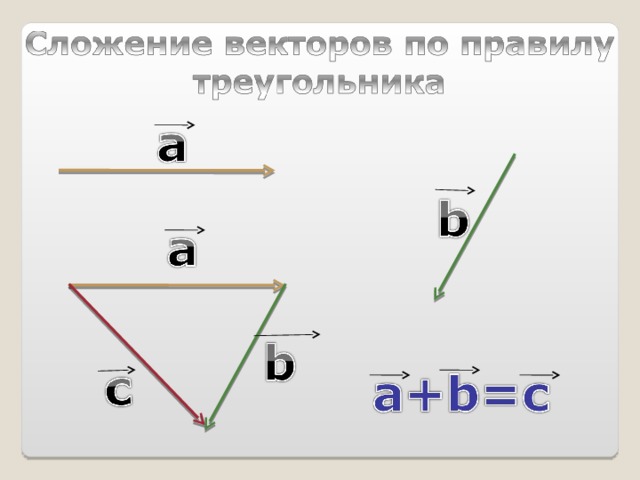 Компоненты результирующего — это просто сумма компонентов восток-запад и север-юг. После этого SOH CAH TOA используется для определения угла, который получается в результате с ближайшей осью. Схема показана справа. Угол, обозначенный как тета (Θ), представляет собой угол между результирующим вектором и западной осью. Этот угол можно рассчитать следующим образом:
Компоненты результирующего — это просто сумма компонентов восток-запад и север-юг. После этого SOH CAH TOA используется для определения угла, который получается в результате с ближайшей осью. Схема показана справа. Угол, обозначенный как тета (Θ), представляет собой угол между результирующим вектором и западной осью. Этот угол можно рассчитать следующим образом:
Касательная (Θ) = напротив / рядом
Касательная (Θ) = (4,326 км) / (0,696 км)
Касательная (Θ) = 6,216
Θ = загар -1 (6.216)
Θ = 80,9 °
Эта угловая мера представляет собой угол поворота вектора к югу от западного направления. Это будет выглядеть как 80,9 ° к югу от запада. Поскольку запад равен 180 ° против часовой стрелки от востока, направление также может быть выражено против часовой стрелки (CCW) от восточного соглашения как 260,9 °.
Итак, результатом нашего анализа является то, что общее смещение составляет 4,38 км при направлении 260,9 ° (против часовой стрелки).
На этой странице были рассмотрены следующие вопросы:
- Как можно сложить три или более перпендикулярных вектора, чтобы определить результат?
- Как можно сложить два или более неперпендикулярных вектора, чтобы определить результат?
По обоим вопросам мы обнаружили, что любые два, три или более вектора можно преобразовать или переставить так, чтобы они складывались вместе, образуя прямоугольный треугольник, в котором гипотенуза является результирующей.После того, как прямоугольный треугольник сформирован, можно использовать теорему Пифагора и SOH CAH TOA для вычисления результата.
Мы хотели бы предложить …
Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения «Назови этот вектор», нашего интерактивного элемента «Сложение векторов» или «Интерактивной игры по угадыванию векторов». Все три интерактивных элемента можно найти в разделе «Интерактивная физика» нашего веб-сайта и обеспечить интерактивный опыт с навыком добавления векторов.
Все три интерактивных элемента можно найти в разделе «Интерактивная физика» нашего веб-сайта и обеспечить интерактивный опыт с навыком добавления векторов.
Поэкспериментируйте с виджетом ниже, а затем попробуйте решить задачи в разделе «Проверьте свое понимание», чтобы проверить свои навыки добавления векторов с помощью компонентов.
Практика!
Виджет ниже вычисляет сумму трех векторов, если известны x- и y-компоненты.Используйте виджет, чтобы попрактиковаться и проверить проблему.
Проверьте свое понимание
Рассмотрим схему ниже. В сетке представлены девять уникальных помеченных мест. Каждый квадрат в сетке представляет собой площадь 20 х 20 метров. Справа по сетке — в восточном направлении, а вверх по сетке — в северном направлении. Используйте сетку, чтобы ответить на следующие несколько вопросов.
1.Предположим, что человек начинает с позиции A и идет в позицию E, а затем в позицию G.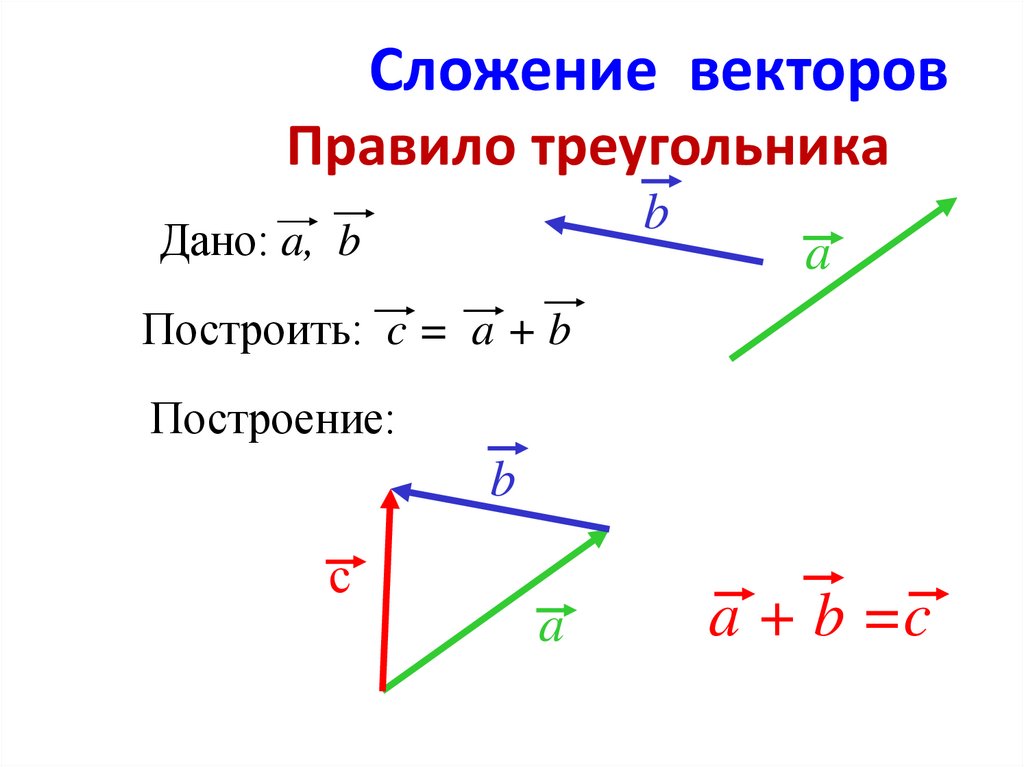 Заполните приведенную ниже таблицу, чтобы указать компоненты восток-запад и север-юг отдельных этапов прогулки и компоненты результирующего смещения. . Делайте измерения вне сетки. Наконец, используйте теорему Пифагора и SOH CAH TOA, чтобы определить величину и направление результирующего смещения.
Заполните приведенную ниже таблицу, чтобы указать компоненты восток-запад и север-юг отдельных этапов прогулки и компоненты результирующего смещения. . Делайте измерения вне сетки. Наконец, используйте теорему Пифагора и SOH CAH TOA, чтобы определить величину и направление результирующего смещения.
Вектор | Компонент Восток-Запад | Компонент Север-Юг |
| от A до E | ||
| От E до G | ||
| Результат От A до G |
Величина результата: _________________________
Направление результата: _________________________
2.Используя ту же сетку, повторите измерения для прогулки от точки C до точки B и до точки F. Выполните измерения вне сетки и используйте теорему Пифагора и SOH CAH TOA, чтобы определить величину и направление результирующего смещения.
Вектор | Компонент Восток-Запад | Компонент Север-Юг |
| C к B | ||
| От B до F | ||
| Результат C к F |
Величина результата: _________________________
Направление результата: _________________________
3.Наконец, используйте ту же сетку, чтобы повторить измерения для прогулки от точки I до точки B, от точки G до точки H. Сделайте измерения вне сетки и используйте теорему Пифагора и SOH CAH TOA, чтобы определить величину и направление движения. результирующее смещение.
Вектор | Компонент Восток-Запад | Компонент Север-Юг |
| от I до B | ||
| B к G | ||
| от G до H | ||
| Результат Я к H |
Величина результата: _________________________
Направление результата: _________________________
4. Во время своего недавнего похода в продуктовый магазин Клэр де Иль прошла 28 м до конца прохода. Затем она повернула направо и прошла 12 м до конца прохода. Наконец, она сделала еще один поворот направо и прошла 12 м в направлении, противоположном ее первоначальному направлению. Определите величину результирующего смещения Клэр. (Фактическое направление — восток, запад, север, юг — не в фокусе.)
Во время своего недавнего похода в продуктовый магазин Клэр де Иль прошла 28 м до конца прохода. Затем она повернула направо и прошла 12 м до конца прохода. Наконец, она сделала еще один поворот направо и прошла 12 м в направлении, противоположном ее первоначальному направлению. Определите величину результирующего смещения Клэр. (Фактическое направление — восток, запад, север, юг — не в фокусе.)
5. В заключительной игре прошлогоднего регулярного сезона Саут играл в Академии Нью-Грира за чемпионство Конференции.В последней игре игры звездный квотербек Эйвери отвлекся от схватки и ускользнул назад (на север) на 8,0 ярдов. Затем он пробежал боком (на запад) из кармана на 12,0 ярдов, прежде чем, наконец, бросил пас на 34,0 ярда прямо вниз по полю (на юг) Кендаллу для выигрышной игры. Определите величину и направление смещения мяча.
6. Миа Андер выходит через парадную дверь своего дома и идет по дорожке, показанной на схеме справа (не в масштабе).Прогулка состоит из четырех этапов и имеет следующие величины:
.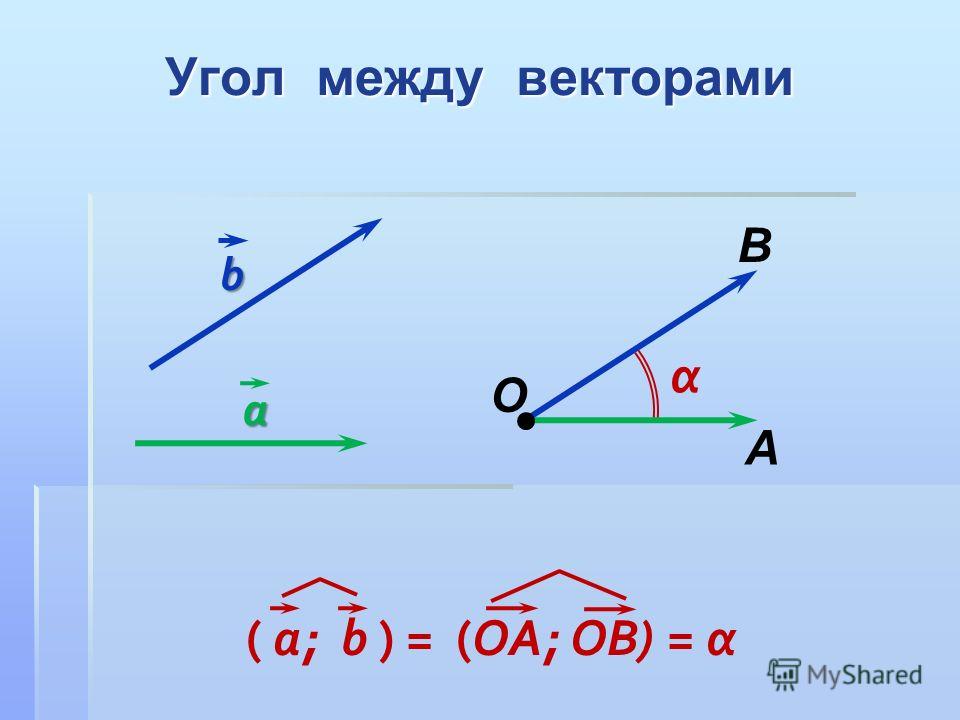
A = 46 м
B = 142 м
C = 78 м
D = 89 м
Определите величину и направление результирующего смещения Миа.
Свой AR. Основы векторной алгебры / Хабр
В настоящий момент появилось достаточно большое количество библиотек дополненной реальности с богатым функционалом (ARCore, ARKit, Vuforia). Тем не менее я решил начать свой открытый проект, попутно описывая как это работает изнутри. Если повезет, то позже получится добавить какой-то особый интересный функционал, которого нет в других библиотеках. В качестве целевых платформ пока возьмем Windows и Android. Библиотека пишется на C++, и сторонние библиотеки будут задействованы по минимуму, т.е. преимущественно не будет использовано ничего готового. Фокус в статьях будет направлен на алгоритмы и математику, которые постараюсь описать максимально доступно и подробно. В этой статье пойдет речь про основы векторной алгебры.
Дополненная реальность — это совмещение виртуального мира и реального. Для этого, нам нужно представить окружающее реальное пространство в виде математической модели, понимая закономерности которой, мы сможем получить данные для совмещения. Начнем с основ векторной алгебры.
Для этого, нам нужно представить окружающее реальное пространство в виде математической модели, понимая закономерности которой, мы сможем получить данные для совмещения. Начнем с основ векторной алгебры.
Вектора — это частный случай матриц, состоящие либо из одного столбца, либо из одной строки. Когда мы говорим о векторе, обычно имеется вектор-столбец . Но записывать вектор как столбец неудобно, поэтому будем его транспонировать — .
Длина вектора
Первое, что мы рассмотрим — получение длины вектора — , где — значение длины, — наш вектор. Для примера возьмем двумерный вектор:
, где и — компоненты вектора, значения проекций вектора на оси двумерных координат. И мы видим прямоугольный треугольник, где и — это длины катетов, а — длина его гипотенузы. По теореме Пифагора получается, что . Значит . Вид формулы сохраняется и для векторов большей размерности, например — .
Скалярное произведение
Скалярное произведение векторов — это сумма произведение их компонентов: .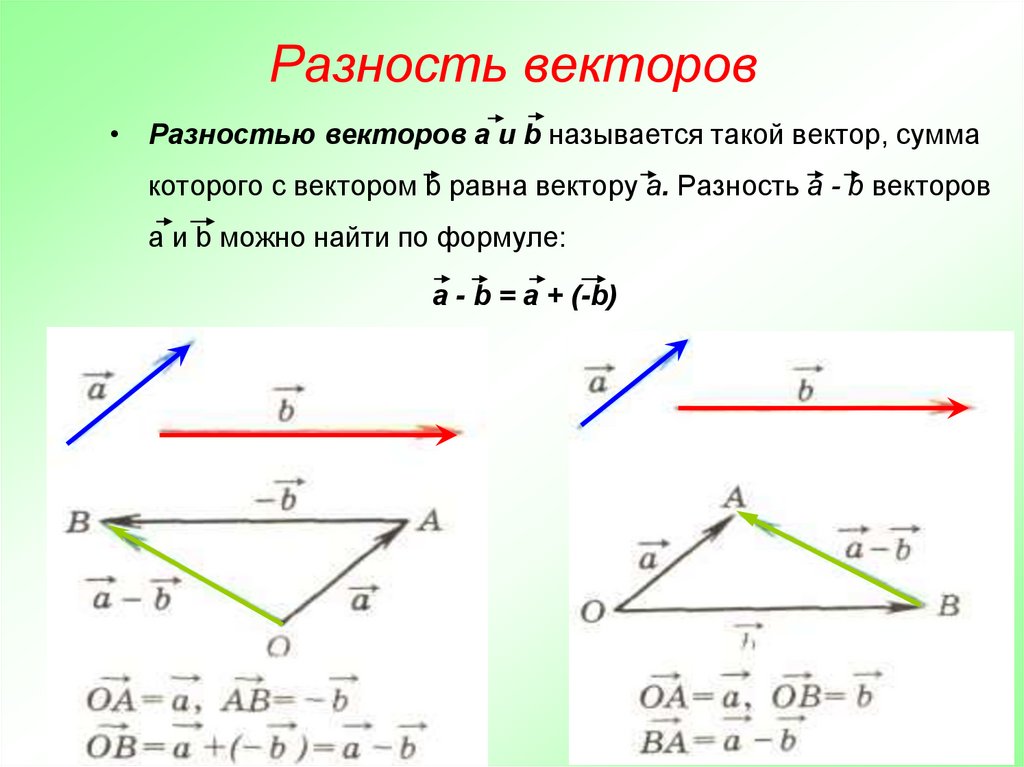 Но так как мы знаем, что вектора — это матрицы, то тогда удобнее записать это в таком виде: . Это же произведение можно записать в другой форме: , где — угол между векторами и (для двумерного случая эта формула доказывается через теорему косинусов). По этой формуле можно заключить, что скалярное произведение — это мера сонаправленности векторов. Ведь, если , то , и — это просто произведение длин векторов. Так как — не может быть больше 1, то это максимальное значение, которые мы можем получить, изменяя только угол . Минимальное значение будет равно -1, и получается при , т.е. когда вектора смотрят в противоположные направления. Также заметим, что при , а значит какие бы длины не имели вектора и , все равно . Можно в таком случае сказать, что вектора не имеют общего направления, и называются ортогональными.
Но так как мы знаем, что вектора — это матрицы, то тогда удобнее записать это в таком виде: . Это же произведение можно записать в другой форме: , где — угол между векторами и (для двумерного случая эта формула доказывается через теорему косинусов). По этой формуле можно заключить, что скалярное произведение — это мера сонаправленности векторов. Ведь, если , то , и — это просто произведение длин векторов. Так как — не может быть больше 1, то это максимальное значение, которые мы можем получить, изменяя только угол . Минимальное значение будет равно -1, и получается при , т.е. когда вектора смотрят в противоположные направления. Также заметим, что при , а значит какие бы длины не имели вектора и , все равно . Можно в таком случае сказать, что вектора не имеют общего направления, и называются ортогональными.
Также при помощи скалярного произведения, мы можем записать формулу длины вектора красивее: , .
Проекция вектора на другой вектор
Возьмем два вектора: и .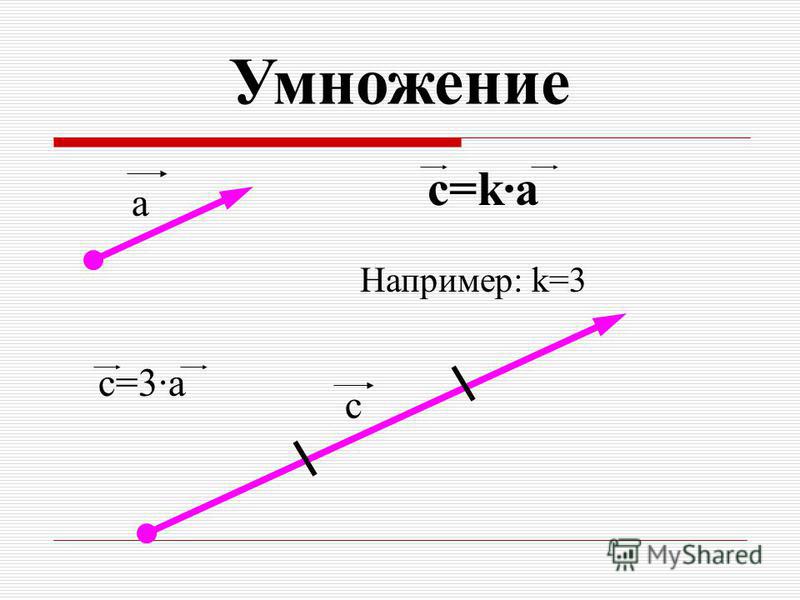
Проекцию вектора на другой вектор можно рассматривать в двух смыслах: геометрическом и алгебраическом. В геометрическом смысле проекция вектора на ось — это вектор, а в алгебраическом – число.
Вектора — это направления, поэтому их начало лежит в начале координат. Обозначим ключевые точки: — начало координат, — конечная точка вектора , — конечная точка вектора .
В геометрическом смысле мы ищем такой , чтобы конечная точка вектора (обозначим ее как — ) была ближайшей точкой к точке , лежащей на прямой .
Иначе говоря, мы хотим найти составляющую в , т.е. такое значение , чтобы и
Расстояние между точками и будет минимальным, если . Получаем прямоугольный треугольник — . Обозначим . Мы знаем, что по определению косинуса через соотношение сторон прямоугольного треугольника
( — гипотенуза, — прилежащий катет).
Также возьмем скалярное произведение . Отсюда следует, что . А значит .
Тут вспоминаем, что — это искомый вектор , а — , и получаем . Умножаем обе части на и получаем — . Теперь мы знаем длину . Вектор отличается от вектора длинной, но не направлением, а значит через соотношение длин можно получить: . И мы можем вывести финальные формулы:
Умножаем обе части на и получаем — . Теперь мы знаем длину . Вектор отличается от вектора длинной, но не направлением, а значит через соотношение длин можно получить: . И мы можем вывести финальные формулы:
и
Нормализованный вектор
Хороший способ упростить работу над векторами — использовать вектора единичной длины. Возьмем вектор и получим сонаправленный вектор единичной длины. Для этого вектор разделим на его длину: . Эта операция называется нормализацией, а вектор — нормализованным.
Зная нормализованный вектор и длину исходного вектора, можно получить исходный вектор: .
Зная нормализованный вектор и исходный вектор, можно получить его длину: .
Хорошим преимуществом нормализованных векторов является то, что сильно упрощается формула проекции (т.к. длина равна 1, то она сокращается). Проекция вектора на единичной длины:
Матрица поворота двумерного пространства
Предположим у нас есть некая фигура:
Чтобы ее нарисовать, заданы координаты ее вершин, от которых строятся линии.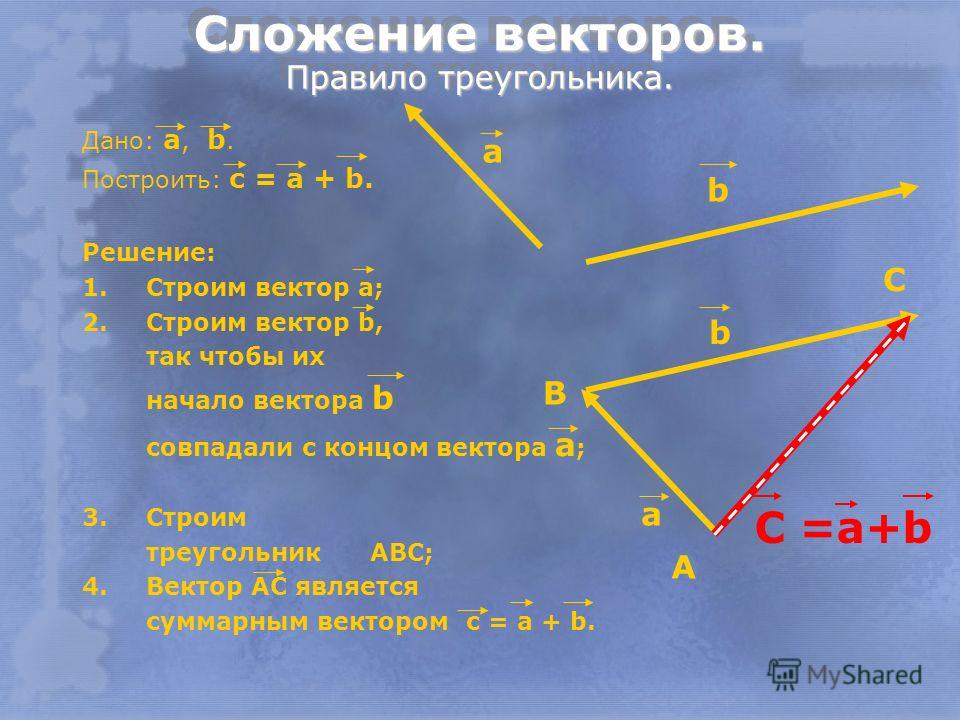 Координаты заданы в виде набора векторов следующим образом . Наша координатная сетка задана двумя осями — единичными ортогональными (перпендикулярными) векторами. В двумерном пространстве можно получить два перпендикулярных вектора к другому вектору такой же длины следующим образом: — левый и правый перпендикуляры. Берем вектор, задающим ось — и ось — левый к нему перпендикуляр — .
Координаты заданы в виде набора векторов следующим образом . Наша координатная сетка задана двумя осями — единичными ортогональными (перпендикулярными) векторами. В двумерном пространстве можно получить два перпендикулярных вектора к другому вектору такой же длины следующим образом: — левый и правый перпендикуляры. Берем вектор, задающим ось — и ось — левый к нему перпендикуляр — .
Выведем новый вектор, получаемый из наших базисный векторов:
Сюрприз — он совпадает с нашим исходным вектором.
Теперь попробуем как-то изменить нашу фигуру — повернем ее на угол . Для этого повернем векторы и , задающих оси координат. Поворот вектора задается косинусом и синусом угла — . А чтобы получить вектор оси , возьмем перпендикуляр к : . Выполнив эту трансформацию, получаем новую фигуру:
Вектора и являются ортонормированным базисом, потому как вектора ортогональны между собой (а значит базис ортогонален), и вектора имеют единичную длину, т.е. нормированы.
Теперь мы говорим о нескольких системах координат — базовой системы координат (назовем ее мировой), и локальной для нашего объекта (которую мы поворачивали). Удобно объединить наш набор векторов в матрицу —
Тогда .
В итоге — .
Матрица , составляющая ортонормированный базис и описывающая поворот, называется матрицей поворота.
Также матрица поворота имеет ряд полезных свойств, которые следует иметь ввиду:
- При , где — единичная матрица, матрица соответствует нулевому повороту (угол ), и в таком случае локальные оси совпадают с мировыми. Как рассматривали выше, матрица никак не меняет исходный вектор.
- — определитель матрицы равен 1, если у нас, как обычно бывает, правая тройка векторов. , если тройка векторов левая.
- .
- .
. - , поворот не меняет длины вектора.
- зная и , можем получить исходный вектор — . Т.е. умножая вектор на матрицу поворота мы выполняем преобразование координат вектора из локальной системы координат объекта в мировую, но также мы можем поступать и наоборот — преобразовывать мировые координаты в локальную систему координат объекта, умножая на обратную матрицу поворота.

Теперь попробуем повернуть наш объект два раза, первый раз на угол , второй раз на угол . Матрицу, полученную из угла , обозначим как , из угла — . Распишем наше итоговое преобразование:
.
Обозначим , тогда . И из двух операций мы получили одну. Так как поворот — это линейное преобразование (описали ее при помощи одной матрицы), множество преобразований можно описать одной матрицей, что сильно упрощает над ними работу.
Масштабирование в двумерном пространстве
Масштабировать объект достаточно просто, нужно только умножить координаты точек на коэффициент масштаба: . Если мы хотим масштабировать объект на разную величину по разным осям, то формула принимает вид: . Для удобства переведем операцию в матричный вид: .
Теперь предположим, что нам нужно повернуть и масштабировать наш объект. Нужно отметить, что если сначала масштабировать, а затем повернуть, то результат будет отличаться, от того результата, где мы сначала повернули, а затем масштабировали:
Сначала поворот, а затем масштабирование по осям:
Сначала масштабирование по осям, а затем поворот:
Как мы видим порядок операций играет большое значение, и его нужно обязательно учитывать.
Также здесь мы также можем объединять матрицы преобразования в одну:
Хотя в данном случае, если , то . Тем не менее, с порядком преобразований нужно быть очень аккуратным. Их нельзя просто так менять местами.
Векторное произведение векторов
Перейдем в трехмерное пространство и рассмотрим определенное на нем векторное произведение.
Векторное произведение двух векторов в трёхмерном пространстве — вектор, ортогональный к обоим исходным векторам, длина которого равна площади параллелограмма, образованного исходными векторами.
Для примера возьмем два трехмерных вектора — , . И в результате векторного произведения получим
Визуализируем данную операцию:
Здесь наши вектора , и . Вектора начинаются с начала координат, обозначенной точкой . Конечная точка вектора — точка . Конечная точка — точка . Параллелограмм из определения формируются точками , , , . Координаты точки находим как — . В итоге имеем следующие соотношения:
- , где — площадь,
- ,
- .

Два вектора образуют плоскость, а векторное произведение позволяет получить перпендикуляр к этой плоскости. Получившиеся вектора образуют образуют правую тройку векторов. Если берем обратный вектор, то получаем второй перпендикуляр к плоскости, и тройка векторов будет уже левой.
Для запоминания этой формулы удобно использовать мнемонический определитель. Пусть , и мы раскладываем определить по строке как сумму определителей миноров исходной матрицы :
Некоторые удобные свойства данного произведения:
- Если два вектора ортогональны и нормализованы, то вектор также будет иметь единичную длину. Параллелограмм, который образуется двумя исходными векторами, станет квадратом с длинной сторон равной единице. Т.е. площадь равна единице, отсюда длина выходного вектора — единица.
Матрица поворота трехмерного пространства.
С тем, как формировать матрицу в двумерном пространстве мы разобрались. В трехмерном она формируется уже не двумя, а тремя ортогональными векторами — . По свойствам, описанным выше, можно вывести следующие отношения между этими векторам:
По свойствам, описанным выше, можно вывести следующие отношения между этими векторам:
Вычислить вектора этих осей сложнее, чем в матрице поворота двумерного пространства. Для примера получения этих векторов рассмотрим алгоритм, который в трехмерных движках называется lookAt. Для этого нам понадобятся вектор направления взгляда — и опорный вектор для оси — . Сам алгоритм:
- Обычно направление камеры совпадает с осью . Поэтому нормализуем и получаем ось — .
- Получаем вектор оси — . В итоге у нас есть два нормализованных ортогональных вектора и , описывающих оси и , при этом ось сонаправлена с входным вектором , а ось перпендикулярна к входному опорному вектору .
- Получаем вектор оси из полученных и — .
- В итоге
В трехмерных редакторах и движках в интерфейсах часто используются углы Эйлера для задания поворота. Углы Эйлера более интуитивно понятны — это три числа, обозначающие три последовательных поворота вокруг трех основных осей .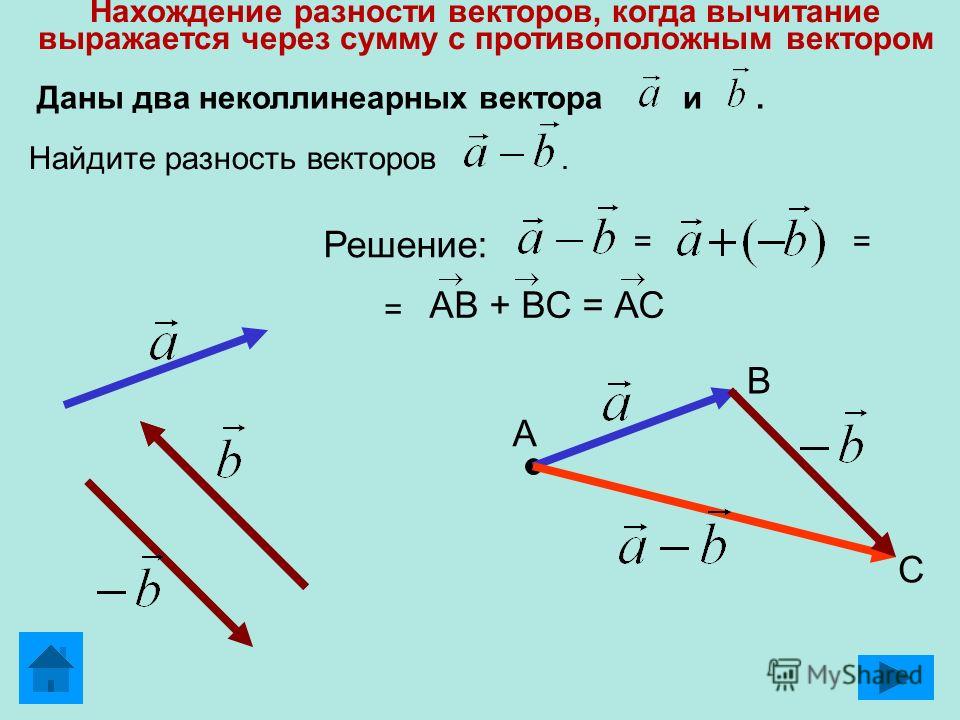 Однако, работать с ними не очень то просто. Если попробовать выразить итоговый вектор напрямую через эти повороты, то получим довольно объемную формулу, состоящую из синусов и косинусов наших углов. Есть еще пара проблем с этими углами. Первая проблема — это то, что сами по себе углы не задают однозначного поворота, так как результат зависит от того, в какой последовательности происходили повороты — или или как-то еще. Углы Эйлера — это последовательность поворотов, а как мы помним, смена порядка трансформаций меняет итоговый результат. Вторая проблема — это gimbal lock.
Однако, работать с ними не очень то просто. Если попробовать выразить итоговый вектор напрямую через эти повороты, то получим довольно объемную формулу, состоящую из синусов и косинусов наших углов. Есть еще пара проблем с этими углами. Первая проблема — это то, что сами по себе углы не задают однозначного поворота, так как результат зависит от того, в какой последовательности происходили повороты — или или как-то еще. Углы Эйлера — это последовательность поворотов, а как мы помним, смена порядка трансформаций меняет итоговый результат. Вторая проблема — это gimbal lock.
Внутри же трехмерные движки чаще всего используют кватернионы, которых мы касаться не будем.
Существуют разные способы задания поворота в трехмерном пространстве, и каждый имеет свои плюсы и минусы:
- Матрица поворота. С ней просто работать (т.к. это просто матрицы). Но есть логическая избыточность данных — все элементы матрицы связаны определенными условиями, так как количество элементов больше степеней свободы (12 элементов против трех степеней).
 Т.е. мы не можем взять матрицу и наполнить ее случайными числами, так при несоблюдении условий матрица просто не будет являться матрицей поворота.
Т.е. мы не можем взять матрицу и наполнить ее случайными числами, так при несоблюдении условий матрица просто не будет являться матрицей поворота. - Углы Эйлера. Они интуитивно понятны, но работать с ними сложно.
- Вектор оси вращения и угол порота вокруг нее. Любой возможный поворот можно описать таким образом. Поворота вектора вокруг заданной оси рассмотрим ниже.
- Вектор поворота Родрига. Это трехмерный вектор, где нормализованный вектор представляет собой ось вращения, а длина вектора угол поворота. Этот способ задания поворота похож на предыдущий способ, но количество элементов здесь равно числу степеней свободы, и элементы не связаны между собой жесткими ограничениями. И мы можем взять трехмерный вектор с абсолютно случайными числами, и любой полученный вектор будет задавать какое-то возможное вращение.
Поворот вектора вокруг заданной оси
Теперь рассмотрим операцию, позволяющую реализовать поворот вектора вокруг оси.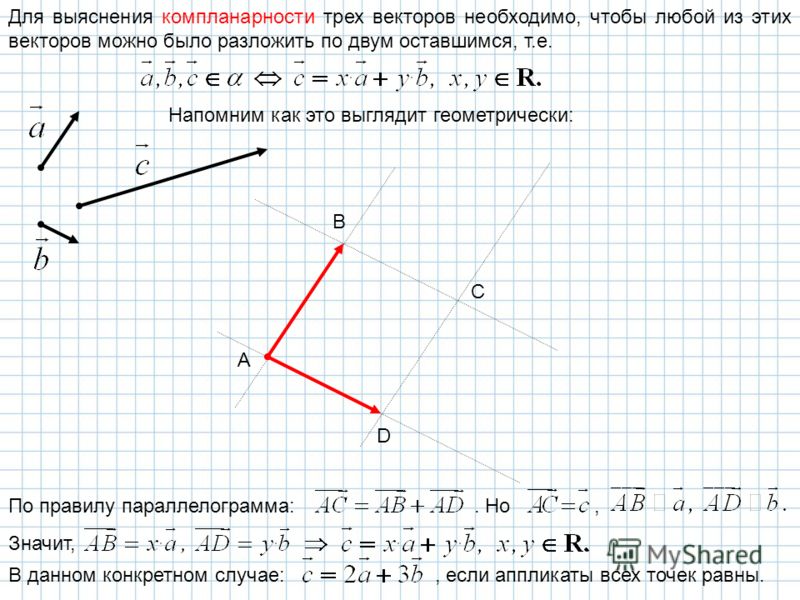
Возьмем вектор — описывающий ось, вокруг которой нужно повернуть вектор на угол . Результирующий вектор обозначим как . Иллюстрируем процесс:
Вектор мы можем разложить сумму векторов: вектора, параллельный к вектору — , и вектора, перпендикулярному к вектору к вектору — .
.
Вектор — это проекция вектора на вектор . Т.к. — нормализованный вектор, то:
Та часть , которая принадлежит оси вращения () не измениться во время вращения. Повернуть нам нужно только в плоскости перпендикулярной к на угол , Обозначим этот вектор как . Тогда наш искомый вектор — .
Вектор можем найти следующим образом:
Для того, чтобы повернуть , выведем оси и в плоскости, в которой будем выполнять поворот. Это должны быть два ортогональных нормализованных вектора, ортогональных к . Один ортогональный вектор у нас уже есть — , нормализуем его и обозначим как ось — .
Теперь получим вектор оси . Это должен быть вектор, ортогональный к и (т.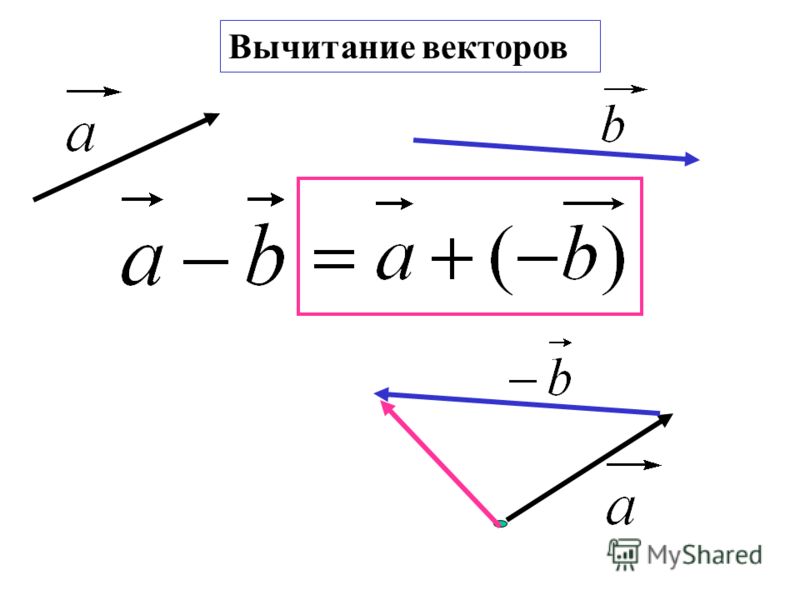 е. и к ). Получить его можно через векторное произведение: . Значит . По свойству векторного произведения будет равно площади параллелограмма, образуемого двумя исходными векторами ( и ). Так как вектора ортогональны, то у нас будет не параллелограмм, а прямоугольник, а значит . . Значит .
е. и к ). Получить его можно через векторное произведение: . Значит . По свойству векторного произведения будет равно площади параллелограмма, образуемого двумя исходными векторами ( и ). Так как вектора ортогональны, то у нас будет не параллелограмм, а прямоугольник, а значит . . Значит .
Поворот двумерного вектора на угол можно получить через синус и косинус — . Т.к. в координатах полученной плоскости сонаправлен с осью , то он будет равен . Этот вектор после поворота — . Отсюда можем вывести:
Теперь мы можем получить наш искомый вектор:
Мы разобрались с тем, как поворачивать вектор вокруг заданной оси на заданный угол, значит теперь мы умеем использовать поворот, заданный таким образом.
Получить вектор оси вращения и угол из вектора Родрига не составляет большого труда, а значит мы теперь умеем работать и с ним тоже.
Напоминаю, что матрица поворота представляет собой три базисных вектора , а углы Эйлера — три последовательных поворота вокруг осей , , . Значит мы можем взять единичную матрицу, как нулевой поворот , а затем последовательно поворачивать базисные вектора вокруг нужных нам осей. В результате получим матрицу поворота соответствующую углам Эйлера. Например:
Значит мы можем взять единичную матрицу, как нулевой поворот , а затем последовательно поворачивать базисные вектора вокруг нужных нам осей. В результате получим матрицу поворота соответствующую углам Эйлера. Например:
Также можно отдельно вывести матрицы вращения по каждой из осей , , (, , соответственно) и получить итоговую матрицу последовательным их умножением:
Таким же образом можно перевести вектор поворота Родрига в матрицу поворота: также поворачиваем оси матрицы поворота, полученные от единичной матрицы.
Итак, с вращением объекта разобрались. Переходим к остальным трансформациям.
Масштабирование в трехмерном пространстве
Все тоже самое что и двумерном пространстве, только матрица масштабирования принимает вид:
Перемещение объекта
До этого момента точка начала локальных координат не смещалась в мировом пространстве. Так как точка начала координат нашего объекта — это его центр, то центр объект никуда не смещался.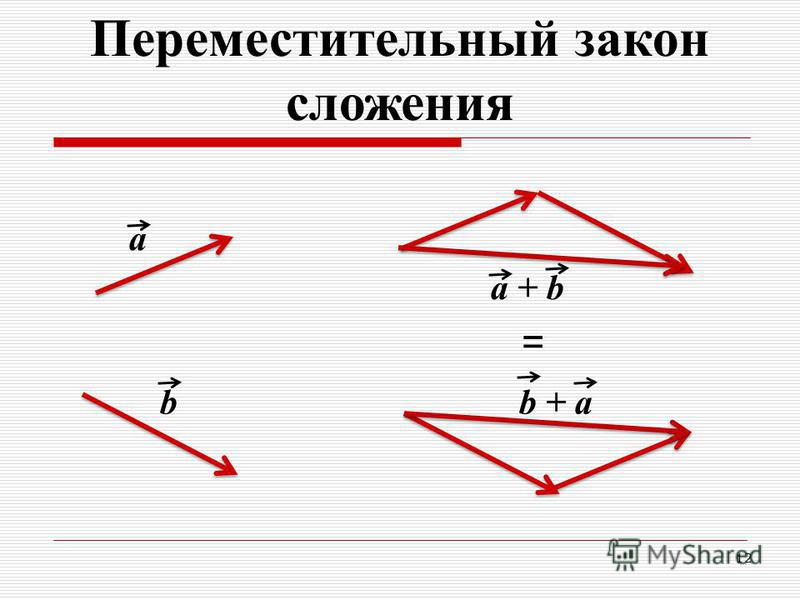 Реализовать это смещение просто: , где — вектор, задающий смещение.
Реализовать это смещение просто: , где — вектор, задающий смещение.
Теперь мы умеем масштабировать объект по осям, поворачивать его и перемещать.
Объединим все одной формулой: :
Чтобы упростить формулу, мы можем, как уже делали ранее, объединить матрицы . В итоге наше преобразование описывает матрица и вектор . Объединение вектора с матрицей еще более бы упростило формулу, однако сделать в данном случае не получится, потому как сложение здесь — это не линейная операция. Тем не менее сделать это возможно, и рассмотрим этот момент уже в следующей статье.
Для какого-то покажется, что статья описывает очевидные вещи, кому-то может показаться наоборот немного запутанной. Тем не менее это базовый фундамент, на котором будет строиться все остальное. Векторная алгебра — является фундаментом для многих областей, так что статья может вам оказаться полезной не только в дополненной реальности. Следующая статья будет уже более узконаправленной.
Сложение и вычитание векторов, умножение вектора на число
Используй поиск, чтобы найти научные материалы и собрать список литературы
База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны
Содержание статьи
1.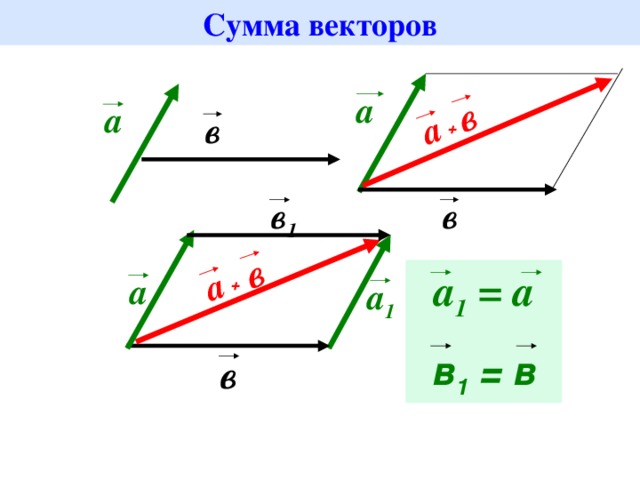 Откладывание вектора от данной точки
Откладывание вектора от данной точки
2. Сложение векторов. Правило треугольника
3. Вычитание векторов
4. Построение разности двух векторов рассмотрим с помощью задачи
5. Умножение вектора на число
6. Пример задачи
Откладывание вектора от данной точки
Перед тем как ввести понятие суммы, разности векторов и умножения вектора на число, вначале разберем такое понятие, как откладывание вектора от точки.
Определение 1
Если точка $A$ начала какого-либо вектора $\overrightarrow{a}$, то говорят, что вектор $\overrightarrow{a}$ отложен от точки $A$ (рис. 1).
Рисунок 1.
Теорема 1
От любой точки $K$ можно отложить вектор единственный $\overrightarrow{a}$.
Доказательство.
Существование: Имеем два следующих случая:
Вектор $\overrightarrow{a}$ — нулевой.
Здесь получаем, что искомый нами вектор совпадает с вектором $\overrightarrow{KK}$.
Вектор $\overrightarrow{a}$ не является нулевым.

Пусть точка $A$ является началом вектора $\overrightarrow{a}$, а точкой $B$ — конец вектора $\overrightarrow{a}$. Проведем через точку $K$ прямую $b$ параллельную вектору $\overrightarrow{a}$. Будем откладывать на прямой отрезки $\left|KL\right|=|AB|$ и $\left|KM\right|=|AB|$. Рассмотрим векторы $\overrightarrow{KL}$ и $\overrightarrow{KM}$. Из этих двух векторов нужный нам вектор — вектор, сонаправленный с вектором $\overrightarrow{a}$ (рис.2)
Рисунок 2.
Из данного выше построения сразу же будет следовать единственность данного вектора.
Сложение векторов. Правило треугольника
Рассмотрим векторы $\overrightarrow{a}$ и $\overrightarrow{b}$.
Определение 2
Вектор $\overrightarrow{c}=\overrightarrow{AC}$ называется суммой векторов $\overrightarrow{a}+\overrightarrow{b}$ который получается из векторов $\overrightarrow{a}$ и $\overrightarrow{b}$ следующим образом: От точки $A$ отложим $\overrightarrow{AB}=\overrightarrow{a}$, от точки $B$ отложим $\overrightarrow{BC}=\overrightarrow{b}$ и соединим точку $A$ c точкой $C$ (рис. 3).
3).
Рисунок 3.
Замечание 1
Также это определение называется правилом треугольника для сложения двух векторов.
Отметим несколько свойств сложения двух векторов:
Для произвольного вектора $\overrightarrow{a}$ выполняется равенство
\[\overrightarrow{a}+\overrightarrow{0}=\overrightarrow{a}\]Для произвольных точек $A,\ B\ и\ C$ справедливо следующее равенство
\[\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\]
Замечание 2
Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.
Вычитание векторов
Рассмотрим векторы $\overrightarrow{a}$ и $\overrightarrow{b}$.
Определение 3
Разностью двух векторов $\overrightarrow{a}$ и $\overrightarrow{b}$ называется такой вектор $\overrightarrow{c}$, который при сложении с вектором $\overrightarrow{b}$ дает вектор $\overrightarrow{a}$, то есть
\[\overrightarrow{b}+\overrightarrow{c}=\overrightarrow{a}\]
Обозначение: $\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{c}$.
Построение разности двух векторов рассмотрим с помощью задачи
Пример 1
Пусть даны векторы $\overrightarrow{a}$ и $\overrightarrow{b}$. Построить вектор $\overrightarrow{a}-\overrightarrow{b}$.
Решение.
Построим произвольную точку $O$ и отложим от нее векторы $\overrightarrow{OA}=\overrightarrow{a}$ и $\overrightarrow{OB}=\overrightarrow{b}$. Соединив точку $B$ с точкой $A$, получим вектор $\overrightarrow{BA}$ (рис. 4).
Рисунок 4.
По правилу треугольника для построения суммы двух векторов видим, что
\[\overrightarrow{OB}+\overrightarrow{BA}=\overrightarrow{OA}\]
То есть
\[\overrightarrow{b}+\overrightarrow{BA}=\overrightarrow{a}\]
Из определения 2, получаем, что
\[\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{BA}\]
Ответ: $\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{BA}$.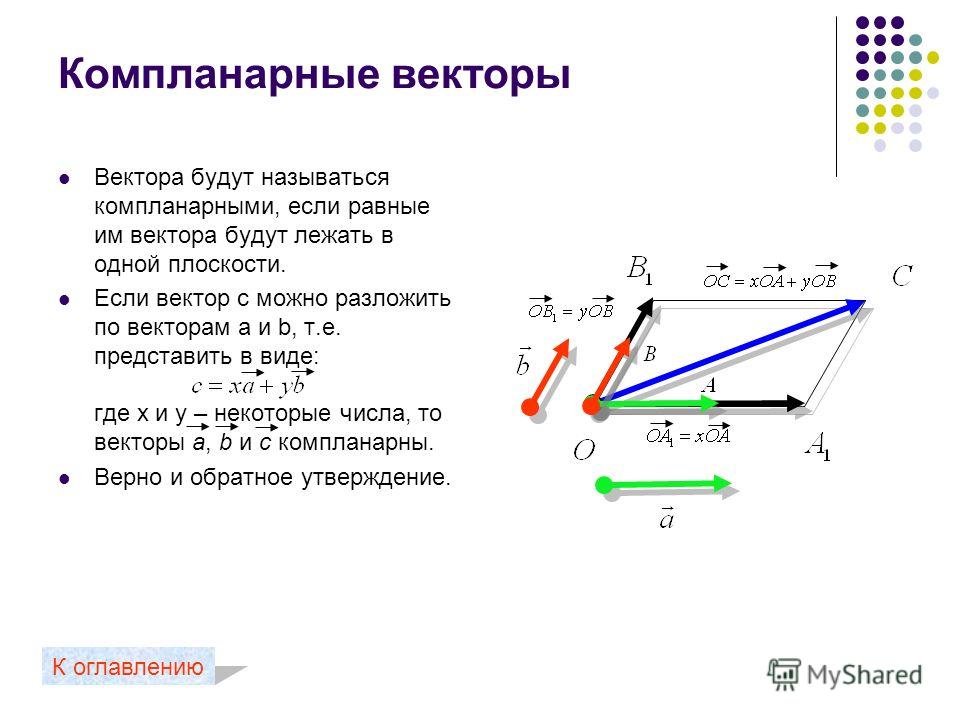
Из этой задачи получаем следующее правило для нахождения разности двух векторов. Чтобы найти разность $\overrightarrow{a}-\overrightarrow{b}$ нужно от произвольной точки $O$ отложить векторы $\overrightarrow{OA}=\overrightarrow{a}$ и $\overrightarrow{OB}=\overrightarrow{b}$ и соединить конец второго вектор с концом первого вектора.
Умножение вектора на число
Пусть нам дан вектор $\overrightarrow{a\ }$ и действительное число $k$.
Определение 4
Произведением вектора $\overrightarrow{a\ }$ на действительное число $k$ называется вектор $\overrightarrow{b\ }$ удовлетворяющий следующим условиям:
Длина вектора $\overrightarrow{b\ }$ равна $\left|\overrightarrow{b\ }\right|=\left|k\right||\overrightarrow{a\ }|$;
Векторы $\overrightarrow{a\ }$ и $\overrightarrow{b\ }$ сонаправлены, при $k\ge 0$ и противоположно направлены, если $k
Обозначение: $\ \overrightarrow{b\ }=k\overrightarrow{a\ }$.
Пример задачи
Пример 2
Дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Доказать, что $\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA_1}=\overrightarrow{AC_1}$
Доказать, что $\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA_1}=\overrightarrow{AC_1}$
Рисунок 5.
Доказательство.
Воспользуемся свойством правила треугольника $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$, получим:
\[\overrightarrow{AC_1}=\overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{CC_1}\]
Так как $\overrightarrow{DC}=\overrightarrow{AB},\ \ \overrightarrow{CC_1}=\overrightarrow{AA_1}$
То есть
\[\overrightarrow{AC_1}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA_1}\]
ч. т. д.
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 27.04.2022
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
Основные сведения о векторах
Основные сведения о векторах 1.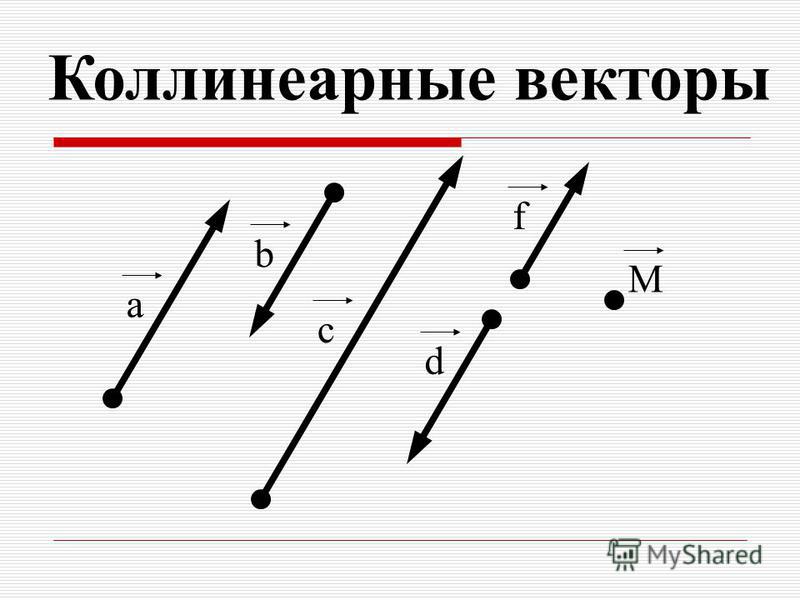 Векторы и векторные алгебраические операции
Векторы и векторные алгебраические операции
Векторы следуют алгебре, мотивированной их приложениями,
и мы будем использовать их часто. Эти алгебраические операции описаны в
вашу книгу, но они включают:
правило 2 — Вектор A умножить на скаляр m — вектор, неизменный по направлению, но изменена по длине в 9 раз0014 m .
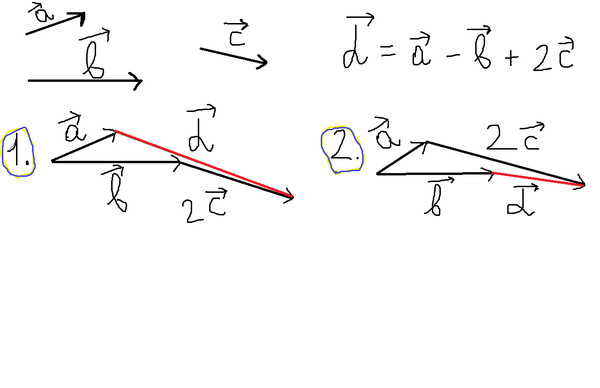 rule 3 — Отрицательный вектор является исходным вектором
перевернулся на 180 градусов;
rule 3 — Отрицательный вектор является исходным вектором
перевернулся на 180 градусов; правило 4 — добавлены два вектора, A и B . положив хвост одного на голову другой (в любом порядке) и определение суммы быть нарисованным вектором
из хвоста первого в голову второго. Правило 5 — Вектор B можно вычесть из вектора А путем добавления -B к A .
В дополнение к этим правилам два разных способа умножения
векторы полезны. Первый — это скаляр или скалярное произведение .
векторов A и B и определяется как результат скаляра, имеющего
Значение
где alpha это угол между А и В .
Почему эта операция определена именно так? Причина в том, что оказывается
быть полезным при описании некоторых физических величин, например работы.
Второй способ умножения векторов предназначен для получения вектора.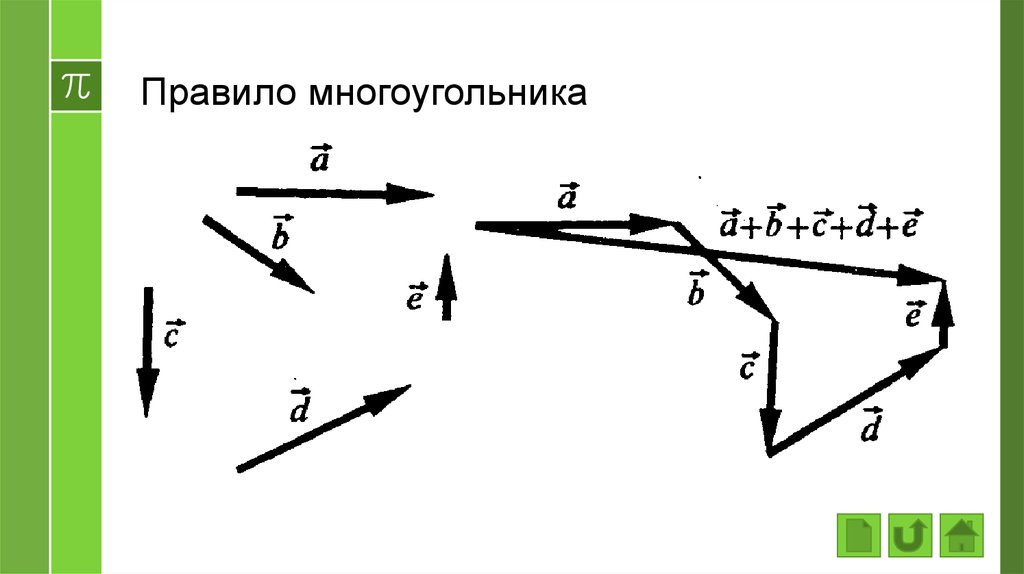 вектор или крест
продукт определен как имеющий величину
вектор или крест
продукт определен как имеющий величину
где alpha снова угол между двумя векторами
(меньший из двух возможных углов). Векторный продукт полезен
например, при описании вращательного движения. В отличие от скалярного произведения,
векторное произведение есть вектор. Направление вектора ( A крест B )
определяется так называемым правилом правой руки. Использование пальцев правой
рука указала на A , пальцы повернуты в
вектор B (помните — меньший из двух возможных углов).
Вектор ( A пересечение B ) перпендикулярен обоим A и B и указывает в направлении большого пальца. Пунктирный вектор
в себя дает квадрат длины вектора. Таким образом, А точка А = А 2 .
Мы также видим, что если A перпендикулярно B , то А точка B = 0. Напротив, вектор пересекается сам с собой ( A крест А )
равно 0. Согласно правилу правой руки, хотя скалярное произведение коммутирует,
векторный продукт не работает. То есть, хотя A точка B = Б точка A , ( A крест B ) не равно ( B крест А ). Вместо этого ( A пересечение B ) = — ( B пересечение A ). В этом обсуждении мы сосредоточимся на операциях
сложения и вычитания. Операция скалярного и векторного умножения
будут обсуждаться позже в курсе, но только в той мере, в какой они
необходимы.
Согласно правилу правой руки, хотя скалярное произведение коммутирует,
векторный продукт не работает. То есть, хотя A точка B = Б точка A , ( A крест B ) не равно ( B крест А ). Вместо этого ( A пересечение B ) = — ( B пересечение A ). В этом обсуждении мы сосредоточимся на операциях
сложения и вычитания. Операция скалярного и векторного умножения
будут обсуждаться позже в курсе, но только в той мере, в какой они
необходимы.
 Тогда вектор можно определить, если мы
знать его длину и угол по отношению к x ось. Альтернативно, вектор полностью определен, если мы знаем его компоненты вдоль обеих осей x и y соответственно. Для вектора A ,
который имеет длину A и составляет угол альфа по отношению к х ось, компоненты называются А х и А у .
Они определяются как проекция вектора вдоль каждой оси. Местоположение
вектора значения не имеет. Все векторы имеют одинаковую длину
и одинаковая ориентация в заданной системе координат x — y имеют
одни и те же компоненты и эквивалентны друг другу.
Тогда вектор можно определить, если мы
знать его длину и угол по отношению к x ось. Альтернативно, вектор полностью определен, если мы знаем его компоненты вдоль обеих осей x и y соответственно. Для вектора A ,
который имеет длину A и составляет угол альфа по отношению к х ось, компоненты называются А х и А у .
Они определяются как проекция вектора вдоль каждой оси. Местоположение
вектора значения не имеет. Все векторы имеют одинаковую длину
и одинаковая ориентация в заданной системе координат x — y имеют
одни и те же компоненты и эквивалентны друг другу. A x = A cos(alpha) ; A y = A sin(alpha)
Таким образом, мы полностью задаем вектор либо
написав A в терминах ( A , альфа ) или A в терминах
из ( А х , А у ).
Оглядываясь назад на рис. 1, мы можем нарисовать на рисунке любое
какой бы то ни было прямоугольной системы, затем вычислить компоненты векторов А и B отдельно в нарисованной нами системе. Затем, зная
компоненты A и B по отдельности, мы также автоматически знаем
компоненты суммы C = A + B в той же системе, потому что
Алгебра сложения и вычитания векторов становится
Чисто. Выбираем систему координат, вычисляем компоненты в ней
системы и добавлять и вычитать компоненты!
Задание 1: Векторы A и B определяются как A = (5,37°) и B = (10,53° ) в
конкретная x-y система координат. (Предположим, 37° , 90° и 53° определяет треугольник 3-4-5.)
а) Найдите каждый вектор в компонентной форме в той же системе x-y .
б) Найдите компоненты векторов С = А + В и D = А — В.
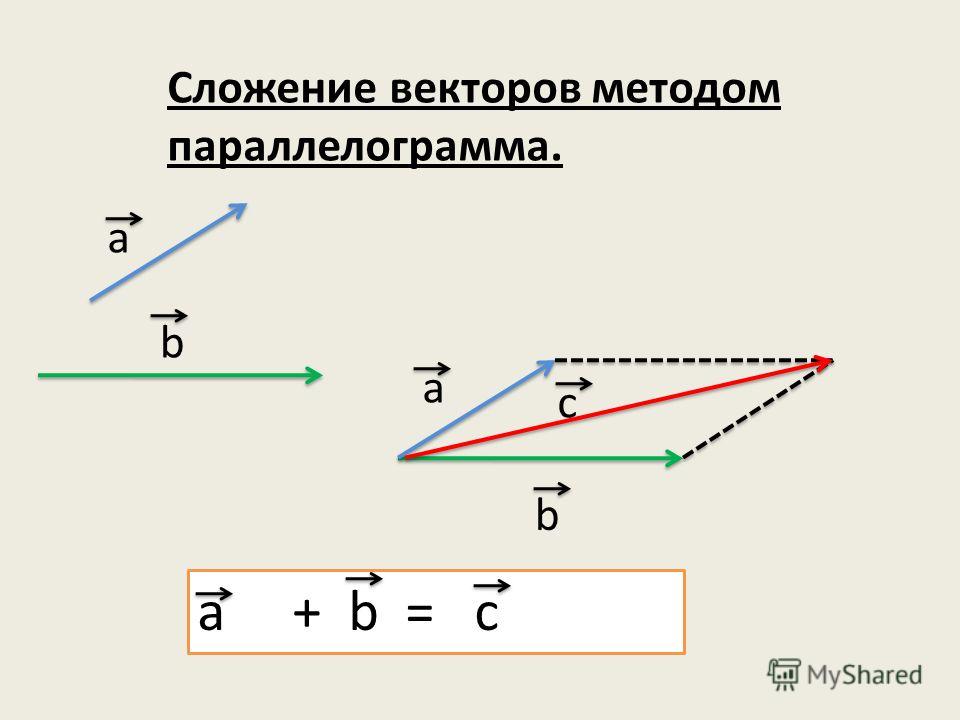
c) Используйте триггер, чтобы найти векторы C и D в (величина, угол) обозначение.
3. Расширение до трех измерений; Базовые векторы в декартовой системе координат Координаты При описании движения решения многих задач становятся просто, если выбрана правильная система координат. Иногда правильная координата система прямоугольная; иногда лучшим выбором может быть полярный или цилиндрический или даже сферическая полярная. В основном мы будем иметь дело с прямоугольным или декартовым система, в которой x-y-z все оси ортогональны (ортогональные означает перпендикулярно) друг к другу и в порядке, показанном на рис. 2. В этом системы рисуем в точке P ( x,y,z ) в пространстве вектор A с тремя компонентами A x A y и A z, относится к система координат.
Как и в двумерном случае, этот вектор полностью
определяется, как только мы знаем его компоненты по каждой из трех осей. В
чтобы выразить A в выбранной системе координат мы
нужно написать его так, чтобы была ясна его векторная природа.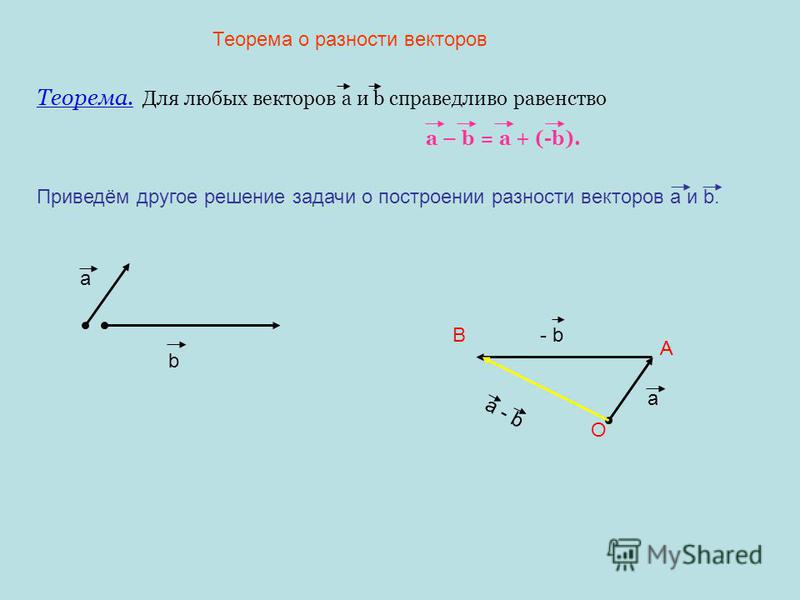 К
Для этой цели мы определяем три единичных вектора (векторы с величиной
1), каждая из которых параллельна одной из трех осей. В нашей системе x-y-z эти единичные векторы равны i, j и k и параллельны x , г и z соответственно. Теперь, если единичный вектор i умножить
скаляром Ax , затем Ax i — вектор длины Ax и направлен параллельно оси x . Как следствие, А можно написать
К
Для этой цели мы определяем три единичных вектора (векторы с величиной
1), каждая из которых параллельна одной из трех осей. В нашей системе x-y-z эти единичные векторы равны i, j и k и параллельны x , г и z соответственно. Теперь, если единичный вектор i умножить
скаляром Ax , затем Ax i — вектор длины Ax и направлен параллельно оси x . Как следствие, А можно написать
Это удобное обозначение, зная, что сложение и вычитание
векторов делается с использованием компонентов. Обозначение дает нам алгебраическую форму
в котором можно выразить множество векторных операций. Таким образом, например,
разница между двумя векторами, A и B могут быть выражены
как B — A = ( B x — A x ) i + ( B y — А у ) j + ( Б z — А z ) к . Для многих задач полные три измерения могут не понадобиться
потому что движение ограничивается плоскостью. В этом случае обычная практика
это использовать x и y , исключая z .
Для многих задач полные три измерения могут не понадобиться
потому что движение ограничивается плоскостью. В этом случае обычная практика
это использовать x и y , исключая z .
Как обсуждалось ранее, общий вектор описывает физическое
величина в точке пространства и не зависит ни от какой системы координат.
Оси координат можно размещать где угодно и с любой ориентацией. Когда описано
в терминах разных декартовых систем данный вектор может иметь разные
компоненты, но длина и ориентация вектора остаются
одинаковый.
Упражнение 2: Вернитесь к Упражнению 1 и выразите все результаты представлены в виде единичного вектора.
Упражнение 3: (небольшой вызов): Учитывая
вектор G = i + 2j + k, используйте тригонометрию до
найти длину вектора и угол, который он образует с
относительно оси x .
4. Вектор положения в декартовых координатах Предположим, что мы хотим описать положение объекта при его движении в пространстве по траектории, описываемой функцией Р ( х , у , з ).
 Мы используем прямоугольную систему, как и раньше, с ортогональными осями x-y-z .
В этой системе координат мы рисуем особый тип вектора, называемый позицией .
вектор с хвостом в начале координат и головой в позиции P ( x , y , z ).
Этот вектор, обозначенный R на рис. 3, полностью задается заданием
компоненты вдоль каждой оси. В
Чтобы выразить R через выбранную систему координат, мы
использовать три единичных вектора i, j и k . Как следствие, Р является
Мы используем прямоугольную систему, как и раньше, с ортогональными осями x-y-z .
В этой системе координат мы рисуем особый тип вектора, называемый позицией .
вектор с хвостом в начале координат и головой в позиции P ( x , y , z ).
Этот вектор, обозначенный R на рис. 3, полностью задается заданием
компоненты вдоль каждой оси. В
Чтобы выразить R через выбранную систему координат, мы
использовать три единичных вектора i, j и k . Как следствие, Р является R = R x i + R y j + R z k º x i + y j + z k ,
При движении объекта в пространстве вектор положения
прослеживает путь. Предположим, что значение R при двух разных
времена известны. Разница между этими двумя векторами положения равна

Это последнее выражение является вектором, который идет от ( x 1 , у 1 , з 1 )
до ( х 2 , у 2 , г 2 )
и точно такой же, как векторы A или B , рассмотренные в разделе .
4 . Важное различие между вектором положения R и
общий вектор, такой как дельта R , заключается в том, что компоненты R x , y и z , тогда как для дельта R компоненты
дельта x , дельта y и дельта z . Это важно
различать истинные векторы и векторы положения. Истинный вектор
не зависит от системы координат, а только от разницы между
один конец вектора и другой. Вектор положения, напротив,
зависит от системы координат, потому что она используется для определения положения
относительно заданной точки отсчета.
Часть предыдущего обсуждения может показаться вам абстрактной.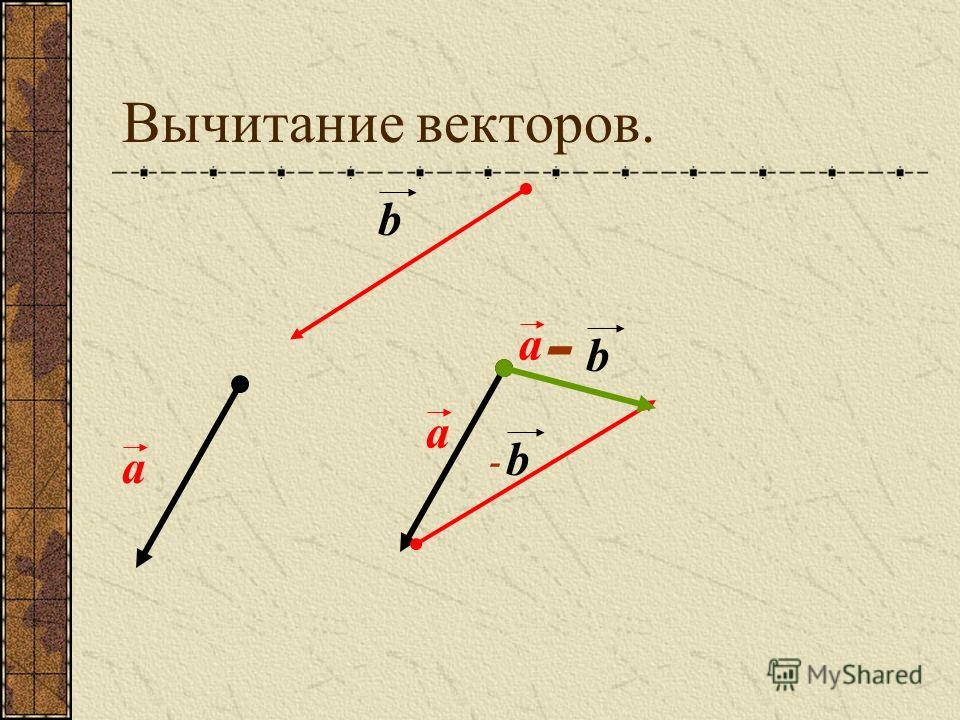 Не беспокойтесь об этом, потому что постепенно вы освоитесь с
идеи, как вы их используете и как вы видите, затем используются в лекциях. Вектор
нотация — это просто сокращенный способ представления информации в компактном виде.
но точный способ.
Не беспокойтесь об этом, потому что постепенно вы освоитесь с
идеи, как вы их используете и как вы видите, затем используются в лекциях. Вектор
нотация — это просто сокращенный способ представления информации в компактном виде.
но точный способ.
1. а) А х = 4, А у = 3, Б х = 6, В у = 8
б) С х = 10, С у = 11, Д х = -2, Д у = -5
в) С = (14,9,48°
), D = (5,4,-68° )
2. А = 4 i + 3 j , B = 6 я + 8 j , C = 10 i + 11 j , D = — 2 i — 5 и
3. Квадрат длины вектора равен G 2 = 1 2 + 2 2 + 1 2 . Таким образом, L = sqrt 6.
Угол между вектором и осью x составляет
угол, косинус которого равен G x /G.
Этот угол равен 66°.
Видео с вопросами: Найдите единичный вектор в направлении вектора, заданного двумя точками
Стенограмма видео
Найдите единичный вектор в направление вектора 𝐀𝐁, учитывая, что вектор 𝐀 равен нулю, единице, минус двум и вектор 𝐁 — это один, один, два.
В этом вопросе нам дано два
векторы: вектор 𝐀 и вектор 𝐁. Нам нужно определить единицу
вектор, который имеет то же направление, что и вектор 𝐀𝐁. И для этого начнем с
вспоминая, что мы подразумеваем под единичным вектором. Мы говорим, что любой вектор, имеющий
величина один является единичным вектором, и мы часто представляем это с помощью нотации шляпы. Например, шляпа 𝐀 будет
вектор в том же направлении, что и вектор 𝐀; однако его величина будет равна
один. Поэтому, когда вопрос просит нас
найдите единичный вектор в направлении 𝐀𝐁, мы могли бы также записать это как
𝐀𝐁 шляпа.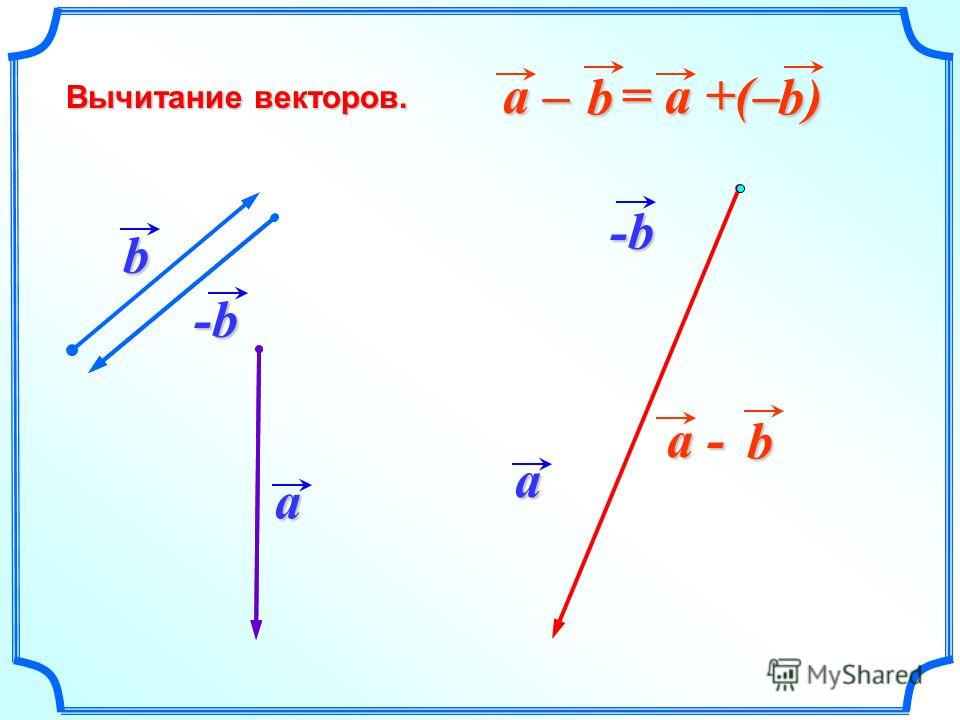 Это вектор в том же
направление как 𝐀𝐁. Однако его величина будет
равен единице.
Это вектор в том же
направление как 𝐀𝐁. Однако его величина будет
равен единице.
Мы также знаем формулу для нахождения единичный направленный вектор, указывающий в том же направлении, что и вектор 𝐯. 𝐯 шапка будет равна единице больше величина 𝐯, умноженная на вектор 𝐯. И в нашем случае мы собираемся хотите применить это к вектору 𝐀𝐁. Итак, сначала нам понадобится найти вектор 𝐀𝐁. Во-первых, вспомним вектор из 𝐀 в 𝐁 будет вектором 𝐁 минус вектор 𝐀. Это вектор один, один, два минус вектор ноль, один, минус два. И помните, чтобы вычесть два векторов с одинаковым количеством компонентов, нам нужно вычесть каждый из наших соответствующие компоненты отдельно. Это дает нам вектор один минус ноль, один минус один и два минус минус два.
Теперь мы можем просто вычислить каждый
этих компонентов по отдельности.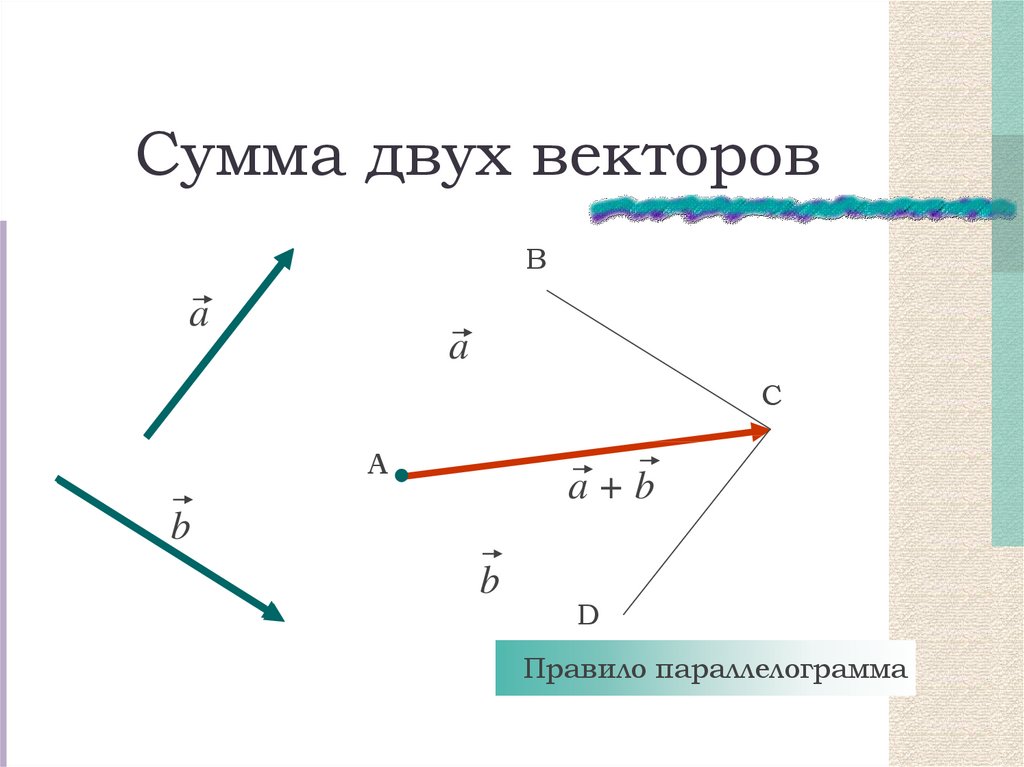 Мы получаем вектор 𝐀𝐁
вектор один, ноль, четыре. Теперь мы собираемся подать заявку
наша формула, чтобы найти единичный вектор направления, который указывает в том же направлении
как 𝐀𝐁. Мы понимаем, что шляпа 𝐀𝐁 будет
равно единице на величину 𝐀𝐁, умноженную на наш вектор 𝐀𝐁. Но мы пока не можем это оценить
потому что мы не знаем величину нашего вектора 𝐀𝐁. Итак, прежде чем мы это сделаем, мы собираемся
нужно найти величину вектора 𝐀𝐁. И для этого нам понадобится
чтобы вспомнить, как мы находим величину вектора. Величина вектора
квадратный корень из сумм квадратов его компонентов. Таким образом, величина вектора 𝐚,
𝐛, 𝐜 будет квадратным корнем из 𝐚 в квадрате плюс 𝐛 в квадрате плюс 𝐜 в квадрате.
Мы получаем вектор 𝐀𝐁
вектор один, ноль, четыре. Теперь мы собираемся подать заявку
наша формула, чтобы найти единичный вектор направления, который указывает в том же направлении
как 𝐀𝐁. Мы понимаем, что шляпа 𝐀𝐁 будет
равно единице на величину 𝐀𝐁, умноженную на наш вектор 𝐀𝐁. Но мы пока не можем это оценить
потому что мы не знаем величину нашего вектора 𝐀𝐁. Итак, прежде чем мы это сделаем, мы собираемся
нужно найти величину вектора 𝐀𝐁. И для этого нам понадобится
чтобы вспомнить, как мы находим величину вектора. Величина вектора
квадратный корень из сумм квадратов его компонентов. Таким образом, величина вектора 𝐚,
𝐛, 𝐜 будет квадратным корнем из 𝐚 в квадрате плюс 𝐛 в квадрате плюс 𝐜 в квадрате.
Затем мы можем использовать это, чтобы найти
величина нашего вектора 𝐀𝐁. Наша ценность 𝐚 одна, наша ценность
𝐛 равно нулю, а наше значение 𝐜 равно четырем.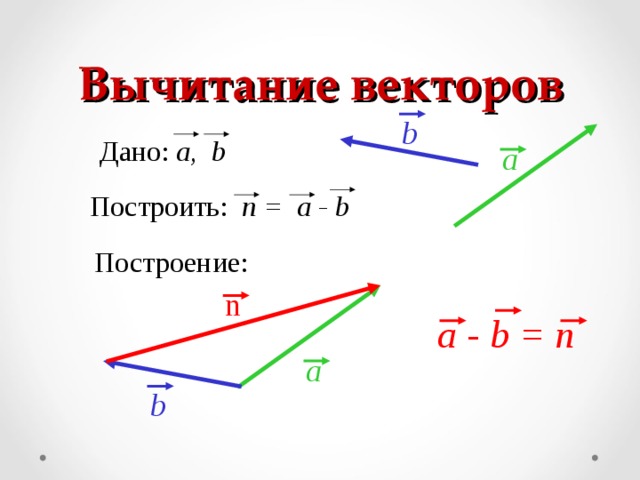 Нам нужно извлечь квадратный корень из
суммы квадратов этих компонент. Это дает нам квадратный корень из
один в квадрате плюс ноль в квадрате плюс четыре в квадрате. И если мы посчитаем это, мы увидим
он равен квадратному корню из 17. Теперь мы можем заменить оба
их в наше уравнение для шляпы 𝐀𝐁. Получаем, что шляпа 𝐀𝐁 равна
один над корнем 17, умноженный на вектор один, ноль, четыре. Теперь мы могли бы оставить наш ответ как
это. Однако мы можем упростить это
потому что мы можем заметить, что умножаем константу на вектор. Таким образом, мы можем упростить это, используя
скалярное умножение вектора.
Нам нужно извлечь квадратный корень из
суммы квадратов этих компонент. Это дает нам квадратный корень из
один в квадрате плюс ноль в квадрате плюс четыре в квадрате. И если мы посчитаем это, мы увидим
он равен квадратному корню из 17. Теперь мы можем заменить оба
их в наше уравнение для шляпы 𝐀𝐁. Получаем, что шляпа 𝐀𝐁 равна
один над корнем 17, умноженный на вектор один, ноль, четыре. Теперь мы могли бы оставить наш ответ как
это. Однако мы можем упростить это
потому что мы можем заметить, что умножаем константу на вектор. Таким образом, мы можем упростить это, используя
скалярное умножение вектора.
Вспомним, как умножить скаляр на
вектор, нам нужно умножить все наши компоненты на наш скаляр. Другими словами, 𝑘 умножить на
вектор 𝐚, 𝐛, 𝐜 равен вектору 𝑘𝐚, 𝑘𝐛, 𝑘𝐜. Итак, нам нужно умножить все
компоненты нашего вектора на наш скалярный над корнем 17. Это дает нам вектор один над
корень 17 раз один, один над корнем 17 раз ноль, один над корнем 17 раз четыре. И мы можем оценить каждый из них
составные части. Получаем единицу над корнем 17, ноль, четыре
над корнем 17. И мы могли бы просто оставить наш ответ
как это. Однако мы также можем упростить
компоненты нашего вектора путем рационализации их знаменателей.
Это дает нам вектор один над
корень 17 раз один, один над корнем 17 раз ноль, один над корнем 17 раз четыре. И мы можем оценить каждый из них
составные части. Получаем единицу над корнем 17, ноль, четыре
над корнем 17. И мы могли бы просто оставить наш ответ
как это. Однако мы также можем упростить
компоненты нашего вектора путем рационализации их знаменателей.
В нашем первом и третьем компонентах
мы хотим умножить на векторный корень 17, разделенный на корень 17. А затем вычислив это и
упрощая, мы получаем окончательный ответ, который представляет собой векторный корень 17 из 17, ноль, четыре
корень 17 на 17. Таким образом, мы смогли показать,
учитывая, что вектор 𝐀 равен нулю, единице, минус двум, а вектор 𝐁 равен единице, единице, двум,
мы смогли найти вектор 𝐀𝐁, вычитая вектор 𝐀 из нашего вектора
𝐁. Тогда мы смогли найти единицу
вектор в том же направлении, что и 𝐀𝐁, умножив 𝐀𝐁 на единицу над его
величина. Это дало нам 𝐀𝐁 шляпа равна
корень вектора 17 над 17, ноль, четыре корня 17 над 17.
Тогда мы смогли найти единицу
вектор в том же направлении, что и 𝐀𝐁, умножив 𝐀𝐁 на единицу над его
величина. Это дало нам 𝐀𝐁 шляпа равна
корень вектора 17 над 17, ноль, четыре корня 17 над 17.
Графические методы – College Physics: OpenStax
Глава 3 Двумерная кинематика
Резюме
- Понимание правил сложения, вычитания и умножения векторов.
- Применение графических методов сложения и вычитания векторов для определения смещения движущихся объектов.
Вектор — это величина, которая имеет величину и направление.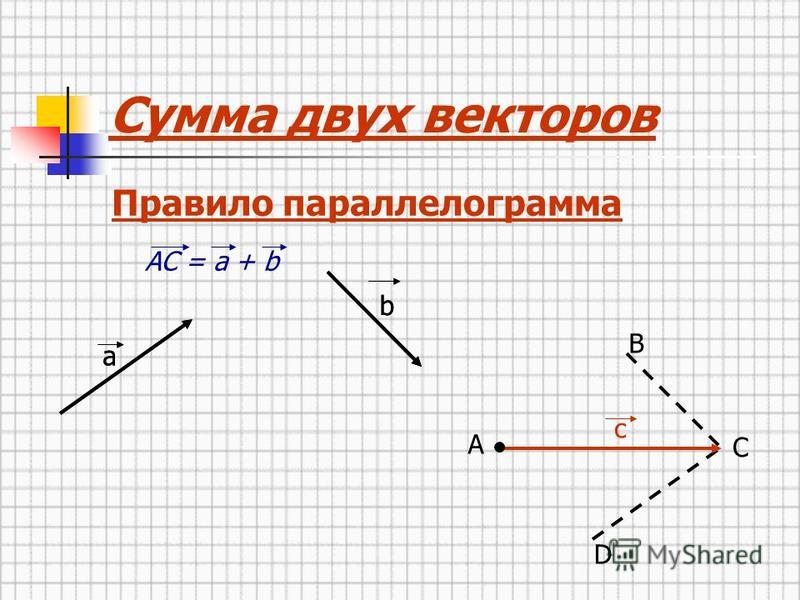 Например, перемещение, скорость, ускорение и сила — все это векторы. В одномерном или прямолинейном движении направление вектора может быть задано просто знаком плюс или минус. Однако в двух измерениях (2-d) мы указываем направление вектора относительно некоторой системы отсчета (т. е. системы координат), используя стрелку, длина которой пропорциональна величине вектора и указывает направление вектора.
Например, перемещение, скорость, ускорение и сила — все это векторы. В одномерном или прямолинейном движении направление вектора может быть задано просто знаком плюс или минус. Однако в двух измерениях (2-d) мы указываем направление вектора относительно некоторой системы отсчета (т. е. системы координат), используя стрелку, длина которой пропорциональна величине вектора и указывает направление вектора.
На рис. 2 показано такое графическое представление вектора на примере полного перемещения человека, идущего по городу, рассмотренного в главе 3.1 «Кинематика в двух измерениях: введение». Мы будем использовать обозначение, что жирный шрифт, такой как [latex]\textbf{D}[/latex], обозначает вектор. Его величина представлена символом, выделенным курсивом, [латекс]\жирныйсимвол{D},[/латекс], а его направление — [латекс]\жирныйсимвол{\тета}.[/латекс]
ВЕКТОРА В ЭТОМ ТЕКСТЕ
В этом тексте мы будем представлять вектор переменной, выделенной жирным шрифтом. Например, мы представим количественную силу вектором[latex]\textbf{F},[/latex], который имеет как величину, так и направление. Величина вектора будет представлена переменной, выделенной курсивом, например [латекс]\жирныйсимвол{F},[/латекс], а направление переменной будет задано углом[латекс]\жирныйсимвол{\тета} .[/латекс]
Например, мы представим количественную силу вектором[latex]\textbf{F},[/latex], который имеет как величину, так и направление. Величина вектора будет представлена переменной, выделенной курсивом, например [латекс]\жирныйсимвол{F},[/латекс], а направление переменной будет задано углом[латекс]\жирныйсимвол{\тета} .[/латекс]
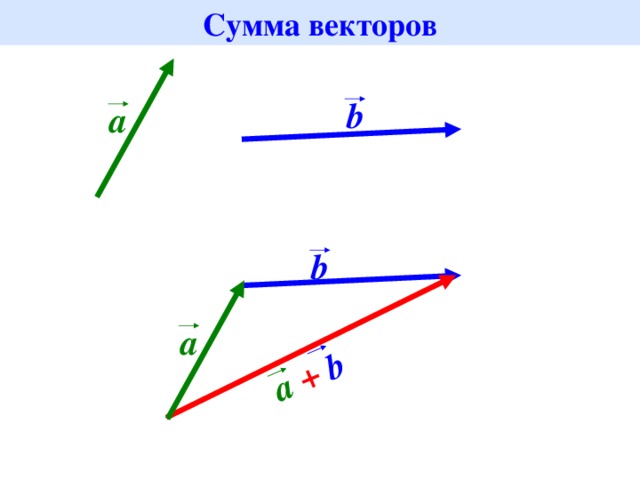
Метод «голова к хвосту» представляет собой графический способ добавления векторов, описанный на рис. 4 ниже и в следующих шагах. Конец вектора является начальной точкой вектора, а головка (или кончик) вектора является конечным заостренным концом стрелки.
Рисунок 4. Метод «голова к хвосту»: метод «голова к хвосту» графического сложения векторов проиллюстрирован для двух перемещений человека, идущего по городу, рассмотренного на рисунке 2. (a) Нарисуйте вектор, представляющий перемещение на восток. (b) Нарисуйте вектор, представляющий смещение на север. Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Проведите линию от хвоста вектора, указывающего на восток, до начала вектора, указывающего на север, чтобы получить сумму или результирующий вектор D . Длина стрелки D пропорциональна модулю вектора и составляет 10,3 единицы. Его направление, описываемое как угол относительно востока (или горизонтальной оси) θ , измеренное с помощью транспортира, равно 29,1 0 .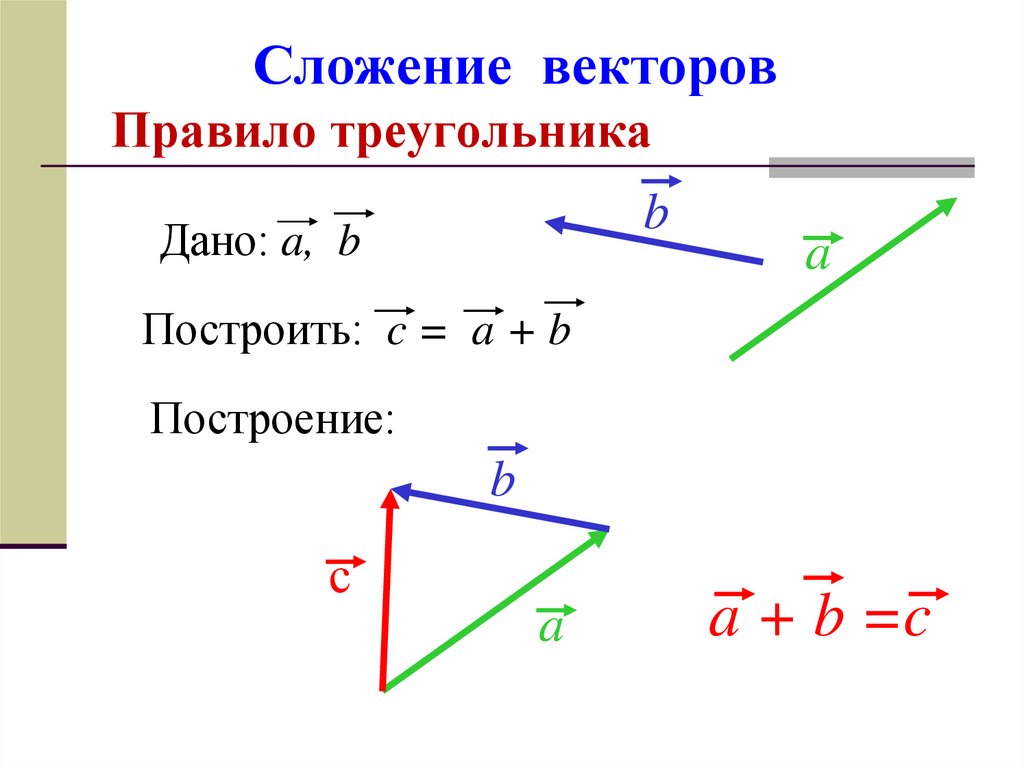
Шаг 1. Нарисуйте стрелку, представляющую первый вектор (9 блоков на восток), используя линейку и транспортир .
Рис. 5.Шаг 2. Теперь нарисуйте стрелку, представляющую второй вектор (5 кварталов на север). Поместите конец второго вектора в начало первого вектора .
Рисунок 6.Шаг 3. Если имеется более двух векторов, продолжайте этот процесс для каждого добавляемого вектора. Обратите внимание, что в нашем примере у нас есть только два вектора, поэтому мы закончили размещать стрелки от начала до конца .
Шаг 4. Проведите стрелку от конца первого вектора к началу последнего вектора . Это результирующее или сумма других векторов.
Рисунок 7. Шаг 5. Чтобы получить величину равнодействующей, измерьте ее длину линейкой. (Обратите внимание, что в большинстве расчетов мы будем использовать теорему Пифагора для определения этой длины.)
(Обратите внимание, что в большинстве расчетов мы будем использовать теорему Пифагора для определения этой длины.)
Шаг 6. Чтобы получить направление равнодействующей, измерьте угол, который она образует с системой отсчета, используя транспортир. (Обратите внимание, что в большинстве расчетов мы будем использовать тригонометрические соотношения для определения этого угла.)
Точность графического сложения векторов ограничена только точностью, с которой могут быть выполнены чертежи, и точностью измерительных инструментов. Это справедливо для любого количества векторов.
Пример 1. Графическое добавление векторов методом «голова к хвосту»: женщина на прогулке 9о}[/latex]северо-восток. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0° к югу от востока.
Стратегия
Представьте каждый вектор смещения графически стрелкой, обозначив первый[latex]\textbf{A},[/latex]второй[latex]\textbf{B},[/latex]и третий [latex]\textbf{C},[/latex] делая длины пропорциональными расстоянию и направлениям, указанным относительно линии восток-запад. Описанный выше метод «голова к хвосту» позволяет определить величину и направление результирующего смещения, обозначаемого[latex]\textbf{R}.[/latex]
Описанный выше метод «голова к хвосту» позволяет определить величину и направление результирующего смещения, обозначаемого[latex]\textbf{R}.[/latex]
Решение
(1) Нарисуйте три вектора смещения.
Рис. 8.(2) Разместите векторы от начала до конца, сохранив их первоначальную величину и направление.
Рисунок 9.(3) Нарисуйте результирующий вектор,[latex]\textbf{R}.[/latex]
Рисунок 10.(4) Используйте линейку для измерения величины[latex]\ textbf{R},[/latex]и транспортир для измерения направления[latex]\textbf{R}.[/latex]Хотя направление вектора можно задать разными способами, проще всего измерить угол между вектором и ближайшей горизонтальной или вертикальной осью. Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх ногами и измеряем угол между осью, направленной на восток, и вектором. 9о}[/latex]юго-восток.
Обсуждение
Графический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результирующая не зависит от порядка добавления векторов. Следовательно, мы можем добавлять векторы в любом порядке, как показано на рис. 12, и все равно получим то же решение.
Также важно отметить, что результирующая не зависит от порядка добавления векторов. Следовательно, мы можем добавлять векторы в любом порядке, как показано на рис. 12, и все равно получим то же решение.
Здесь мы видим, что при сложении одних и тех же векторов в другом порядке результат будет тот же. Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов равно коммутативный . Векторы можно добавлять в любом порядке.
[латекс]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{B}+\textbf{A}}.[/latex]
(Это верно для сложения обычных чисел как хорошо — вы получите тот же результат, если вы добавите, например, [латекс]\жирныйсимвол{2+3}[/латекс]или [латекс]\жирныйсимвол{3+2},[/латекс]).
Вычитание векторов — это прямое расширение сложения векторов. Чтобы определить вычитание (скажем, мы хотим вычесть [латекс]\textbf{B}[/латекс]из [латекс]\текстбф{А},[/латекс]написанного[латекс]\жирныйсимвол{\текстбф{А}-\текстбф {B}}[/latex], мы должны сначала определить, что мы подразумеваем под вычитанием.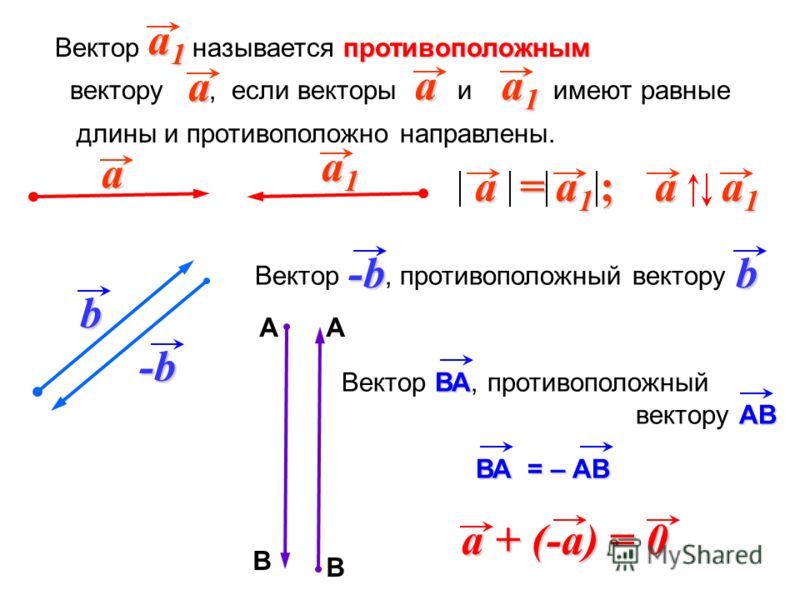 0700 отрицательный вектора[latex]\textbf{B}[/latex] определяется как [latex]\boldsymbol{-\textbf{B}};[/latex]то есть графически отрицательный для любого вектора имеет ту же величину, но в противоположном направлении , как показано на рисунке 13. Другими словами, [latex]\textbf{B}[/latex] имеет ту же длину, что и [latex]\boldsymbol{-\textbf{B}} ,[/latex], но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.
0700 отрицательный вектора[latex]\textbf{B}[/latex] определяется как [latex]\boldsymbol{-\textbf{B}};[/latex]то есть графически отрицательный для любого вектора имеет ту же величину, но в противоположном направлении , как показано на рисунке 13. Другими словами, [latex]\textbf{B}[/latex] имеет ту же длину, что и [latex]\boldsymbol{-\textbf{B}} ,[/latex], но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.
Затем вычитание вектора[latex]\textbf{B}[/latex]из vector[latex]\textbf{A}[/latex] просто определяется как сложение [latex]\boldsymbol{ -\textbf{B}}[/latex]to[latex]\textbf{A}.[/latex]Обратите внимание, что вычитание векторов — это добавление отрицательного вектора. o}[/latex]к западу от севера). Если женщина совершает ошибку и путешествует в 907:00 в противоположном направлении для второго этапа поездки, где она окажется? Сравните это место с расположением дока.
o}[/latex]к западу от севера). Если женщина совершает ошибку и путешествует в 907:00 в противоположном направлении для второго этапа поездки, где она окажется? Сравните это место с расположением дока.
Стратегия
Мы можем представить первый этап пути с помощью вектора[latex]\textbf{A},[/latex], а второй этап пути с помощью вектора[latex] \textbf{B}.[/latex]Док расположен в месте[latex]\boldsymbol{\textbf{A}\:+\:\textbf{B}}.[/latex]Если женщина по ошибке путешествует в напротив 9о}[/latex]юго-восток. Мы представляем это как[latex]\boldsymbol{-\textbf{B}},[/latex], как показано ниже. Вектор[latex]\boldsymbol{-\textbf{B}}[/latex] имеет ту же величину, что и [latex]\textbf{B}[/latex], но направлен в противоположном направлении. Таким образом, она окажется в месте [латекс]\boldsymbol{\textbf{A}+(-\textbf{B})},[/latex]или[латекс]\boldsymbol{\textbf{A}-\textbf {B}}.[/latex]
Рисунок 15. Выполним сложение векторов для сравнения расположения дока,[latex]\boldsymbol{\textbf{A}+\textbf{B}},[/ латекс]с местом, куда по ошибке прибыла женщина,[латекс]\boldsymbol{\textbf{A}+(-\textbf{B})}.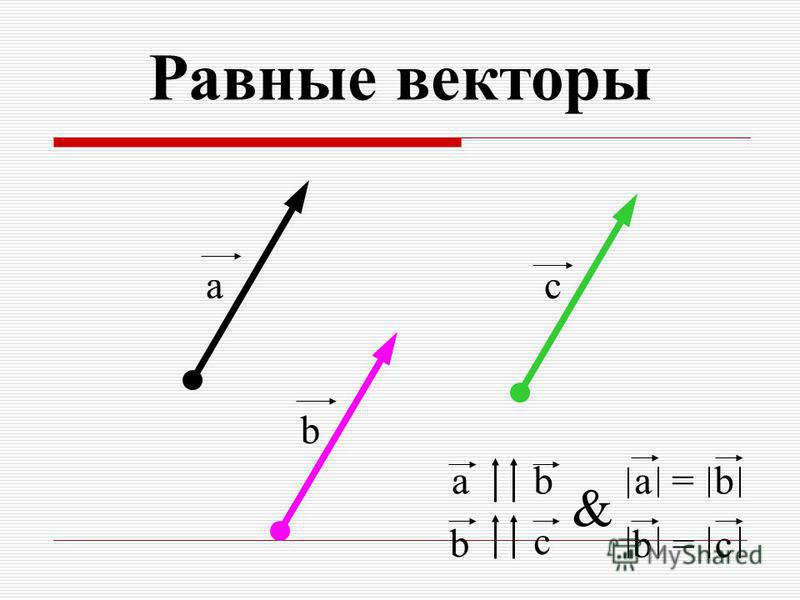 [/latex]
[/latex]
Решение
(1) Чтобы определить место, куда случайно попала женщина, нарисуйте векторы[latex]\textbf{A}[/latex]и[latex]\boldsymbol{-\textbf{B}} .[/latex]
(2) Разместите векторы от начала до конца.
(3) Нарисуйте результирующий вектор[latex]\textbf{R}.[/latex]
(4) Используйте линейку и транспортир для измерения величины и направления [latex]\textbf{R}.[/ латекс]
Рисунок 16.о}[/latex]юго-восток. 9о}[/latex]северо-восток.
Мы видим, что женщина окажется на значительном расстоянии от причала, если она отправится в противоположном направлении на второй этап поездки.
Обсуждение
Поскольку вычитание вектора аналогично сложению вектора с противоположным направлением, графический метод вычитания векторов работает так же, как и сложение.
Если бы мы решили пройти в три раза больше первого этапа пути, рассмотренного в предыдущем примере, то мы бы прошли[latex]\boldsymbol{3 \times 27,5\textbf{ м}},[/latex]или 82,5 м, в направлении[латекс]\boldsymbol{66. o}[/латекс]северо-восток. Это пример умножения вектора на положительное число 9.0693 скаляр . Обратите внимание, что величина меняется, но направление остается прежним.
o}[/латекс]северо-восток. Это пример умножения вектора на положительное число 9.0693 скаляр . Обратите внимание, что величина меняется, но направление остается прежним.
Если скаляр отрицательный, то умножение на него вектора изменяет величину вектора и дает новому вектору направление , противоположное . Например, если умножить на -2, величина удвоится, но изменится направление. Мы можем обобщить эти правила следующим образом: когда вектор[латекс]\текстбф{А}[/латекс] умножается на скаляр[латекс]\жирныйсимвол{с},[/латекс]
- модуль вектора становится абсолютным значением[latex]\boldsymbol{cA},[/latex]
- , если [latex]\boldsymbol{c}[/latex] положительный, направление вектора не меняется,
- , если [латекс]\boldsymbol{c}[/латекс]отрицательно, направление меняется на противоположное.
В нашем случае [латекс]\boldsymbol{c=3}[/latex]и [латекс]\boldsymbol{\textbf{A}=27,5\textbf{ m}}.[/latex]Вектора умножаются на скаляры во многих ситуациях. Обратите внимание, что деление является обратным умножению. Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр между 0 и 1.
Обратите внимание, что деление является обратным умножению. Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр между 0 и 1.
В приведенных выше примерах мы добавляли векторы для определения результирующего вектора. Однако во многих случаях нам нужно будет сделать обратное. Нам нужно будет взять один вектор и найти, какие другие векторы, сложенные вместе, дают его. В большинстве случаев это включает в себя определение перпендикулярных компонентов одного вектора, например, x – и y -компоненты или компоненты север-юг и восток-запад. 9o}[/latex]к северу от востока и хотите узнать, сколько кварталов нужно было пройти на восток и на север. Этот метод называется нахождением компонентов (или частей) смещения в восточном и северном направлениях, и он является обратным процессу, применяемому для нахождения полного смещения. Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в главе 3.4 «Движение снаряда» и многое другое, когда мы рассмотрим 9.0693 действует на в главе 4 «Динамика: законы движения Ньютона». Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в главе 3.3 Сложение и вычитание векторов: аналитические методы, идеально подходят для нахождения компонент вектора.
Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в главе 3.4 «Движение снаряда» и многое другое, когда мы рассмотрим 9.0693 действует на в главе 4 «Динамика: законы движения Ньютона». Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в главе 3.3 Сложение и вычитание векторов: аналитические методы, идеально подходят для нахождения компонент вектора.
PHET EXPLORATIONS: MAZE GAME
Узнайте о положении, скорости и ускорении на «Арене боли». Используйте зеленую стрелку, чтобы переместить мяч. Добавьте больше стен на арену, чтобы усложнить игру. Постарайтесь достичь цели как можно быстрее.
Рисунок 18. Игра «Лабиринт»- Графический метод сложения векторов [latex]\textbf{A}[/latex]и[latex]\textbf{B}[/latex] включает в себя рисование векторов на графике и их сложение с использованием прямого метод хвоста.
 Результирующий вектор[latex]\textbf{R}[/latex] определяется таким образом, что[latex]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex]Величина и направление[latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно.
Результирующий вектор[latex]\textbf{R}[/latex] определяется таким образом, что[latex]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex]Величина и направление[latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно. - графический метод вычитания вектора [latex]\textbf{B}[/latex]из [latex]\textbf{A}[/latex] включает добавление противоположного вектора[latex]\textbf{B},[/latex ] который определяется как [латекс]\boldsymbol{-\textbf{B}}.[/latex]В этом случае [латекс]\boldsymbol{\textbf{A}-\textbf{B}=\textbf{A} +(-\textbf{B})=\textbf{R}}.[/latex]Затем обычным методом сложения головы к хвосту получается результирующий вектор[latex]\textbf{R }.[/латекс]
- Сложение векторов коммутативно , так что [латекс]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{B}+\textbf{A}}.[/latex]
- Метод «голова к хвосту» сложения векторов включает рисование первого вектора на графике, а затем размещение хвоста каждого последующего вектора в начале предыдущего вектора.
 Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора.
Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора. - Если вектор[latex]\textbf{A}[/latex] умножается на скалярную величину[latex]\boldsymbol{c},[/latex]величина произведения определяется как[latex]\boldsymbol{cA }.[/latex]Если [латекс]\boldsymbol{c}[/латекс] положителен, направление произведения указывает на то же направление, что и [латекс]\текстбф{А};[/латекс]если[латекс] \boldsymbol{c}[/latex]отрицательно, направление произведения указывает на направление, противоположное [latex]\textbf{A}.[/latex]
- компонент (двумерного вектора)
- часть вектора, указывающего либо в вертикальном, либо в горизонтальном направлении; каждый двумерный вектор может быть выражен как сумма двух компонент вертикального и горизонтального векторов
- коммутативный
- относится к взаимозаменяемости порядка в функции; сложение векторов является коммутативным, потому что порядок сложения векторов не влияет на окончательную сумму
- направление (вектора)
- ориентация вектора в пространстве
- головка (вектора)
- конечная точка вектора; расположение кончика стрелки вектора; также называется «наконечник»
- метод «голова к хвосту»
- метод сложения векторов, при котором конец каждого вектора помещается в начало предыдущего вектора
- величина (вектора)
- длина или размер вектора; величина является скалярной величиной
- результирующая
- сумма двух или более векторов
- результирующий вектор
- векторная сумма двух или более векторов
- скаляр
- количество с величиной, но без направления
- хвост
- начальная точка вектора; напротив наконечника или наконечника стрелки
Алгебраическое сложение и вычитание векторов
Введение
В этой статье мы рассмотрим вектор. Векторы, в отличие от простых чисел (скаляров), которые имеют только величину, имеют как величину (длину), так и направление. Мы изучим, как представлять векторные величины, а также как их складывать и вычитать.
Векторы, в отличие от простых чисел (скаляров), которые имеют только величину, имеют как величину (длину), так и направление. Мы изучим, как представлять векторные величины, а также как их складывать и вычитать.
Ключевые члены
Отдельные числа, то есть значения, имеющие только (положительную или отрицательную) величину, называются скалярами . Числа 0, –3, π, i, 1.3, e, и т. д. – все это примеры скаляров. Другой тип значения, который часто используется в математике, — это вектор. А вектор — это величина, которая имеет как величину , так и направление . В этой статье мы рассмотрим некоторые математические характеристики векторов. Векторы имеют широкое применение, например, в физике.
В этой статье мы рассмотрим некоторые математические характеристики векторов. Векторы имеют широкое применение, например, в физике.
Введение в векторы
Чтобы понять разницу между скаляром и вектором, полезно подумать о физических примерах. Возьмем, к примеру, температуру. Вы можете использовать термометр для измерения температуры воздуха в разных местах. В каждом случае вы получаете некоторое число (и единицу измерения), скажем, 65°F. Это величина, но с ней не связано никакого направления; таким образом, это скалярная величина. Теперь рассмотрим измерения ветра в тех же местах. Когда вы измеряете ветер, вы, скорее всего, измеряете и скорость, и направление. Таким образом, ваши измерения ветра составляют вектор. Мы могли бы выразить этот вектор как стрелку, направленную в направлении ветра, причем длина стрелки пропорциональна скорости ветра. Ниже приведена иллюстрация двух измерений ветра, сделанных в разных точках; стрелки представляют векторы, связанные с этими измерениями.
Векторы имеют величину и направление, но не имеют назначенного местоположения как такового. То есть, пока сохраняется направление и длина «стрелки», мы можем перемещать ее куда угодно, не меняя ее. Это важная характеристика, которая позволит нам широко работать с векторами.
A Представление векторов
Наша первая задача — найти способ четкого и последовательного представления векторов. Графически это просто: поскольку мы можем перемещать вектор куда угодно, давайте всегда располагать «хвост» вектора в начале координат плоскости. (Обратите внимание, что «голова» и «хвост» вектора определяются, как показано ниже.)
Теперь, поместив хвост вектора в начало координат (помните, что мы можем перемещать вектор куда угодно, пока сохраняем его направление и длину), мы можем количественно определить его как координаты голова. Пример показан ниже для вектора v . (Обратите внимание, что для того, чтобы отличить символы, представляющие векторы, от символов, представляющих скаляры, мы используем жирный шрифт. Другой распространенный метод — использовать маленькую стрелку над символом: например, вектор.)
Пример показан ниже для вектора v . (Обратите внимание, что для того, чтобы отличить символы, представляющие векторы, от символов, представляющих скаляры, мы используем жирный шрифт. Другой распространенный метод — использовать маленькую стрелку над символом: например, вектор.)
Хотите узнать больше? Почему бы не пройти онлайн-курс Precalculus?
Таким образом, вектор v — это просто координаты точки (2, 3). Обратите внимание, что все векторы, показанные ниже, равны (2, 3) — наше соглашение состоит в том, что вектор описывается координатами точки в его начале только , когда его конец расположен в начале координат.
Хотя мы показали вектор только в двух измерениях, этот подход можно обобщить на любое количество измерений. Например, в трех измерениях вектор будет иметь вид ( x, y, z ). Все свойства двумерных векторов можно легко распространить на три измерения.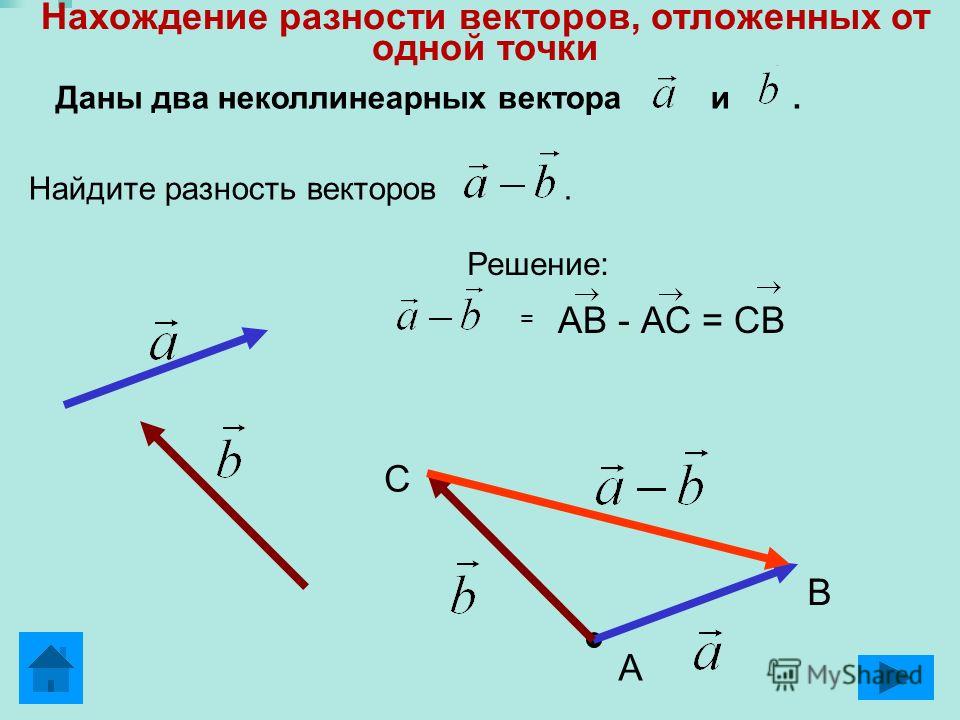
Но как нам «переместить» вектор с числовой точки зрения? Например, скажем, вектор v имеет голову в (3, 2) и хвост в (1, 4).
Ответ заключается в перемещении (или перемещении) головы и хвоста на одинаковое расстояние и в одном направлении. Этот перевод должен привести к перемещению хвоста вектора в начало координат — простой процесс, который включает вычитание каждой хвостовой координаты из самой себя. В приведенном выше примере результат равен (3 – 3, 2 – 2) = (0, 0). Чтобы переместить голову, аналогичным образом вычтите координаты хвоста из координат головы — это удовлетворяет нашему критерию, согласно которому перемещение имеет фиксированное расстояние и направление. Таким образом, голову следует двигать следующим образом: (1 – 3, 4 – 2) = (–2, 2). Таким образом, в общем случае, чтобы найти значение произвольно расположенного вектора, нужно вычесть координаты хвоста из координат головы. Этот процесс проиллюстрирован ниже.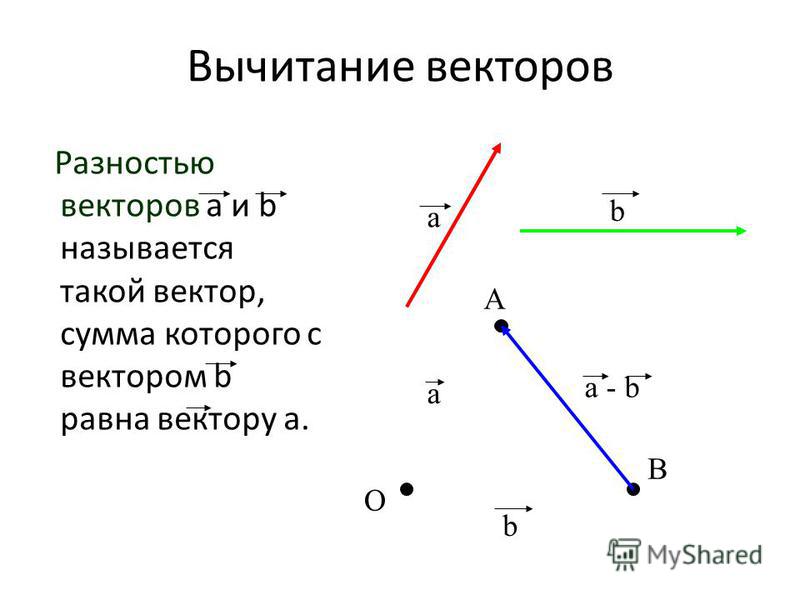
Обратите внимание, что вектор (0, 0), иногда называемый нулевым вектором , имеет длину 0, но не имеет определенного направления. (То есть независимо от того, какое направление вы выберете, нулевой вектор один и тот же.)
Практическая задача: Определите значение каждого вектора, показанного на графике ниже.
Решение: В каждом случае можно найти координатное выражение для вектора, вычитая хвостовые координаты из соответствующих головных координат. Это работает, даже если хвост находится в начале координат, который имеет координаты (0, 0). Но если хвост находится в начале координат, вектор также просто равен координатам головы. Если это вам поможет, перерисуйте векторы так, чтобы хвосты располагались в начале координат.
а = (–1, 4)
б = (–3, –3)
в = (2, – 0 3) = (3 – 0 3)
d = (3 – 2, –4 – [–1]) = (1, –3)
Сложение и вычитание векторов
6 и вычесть векторы.
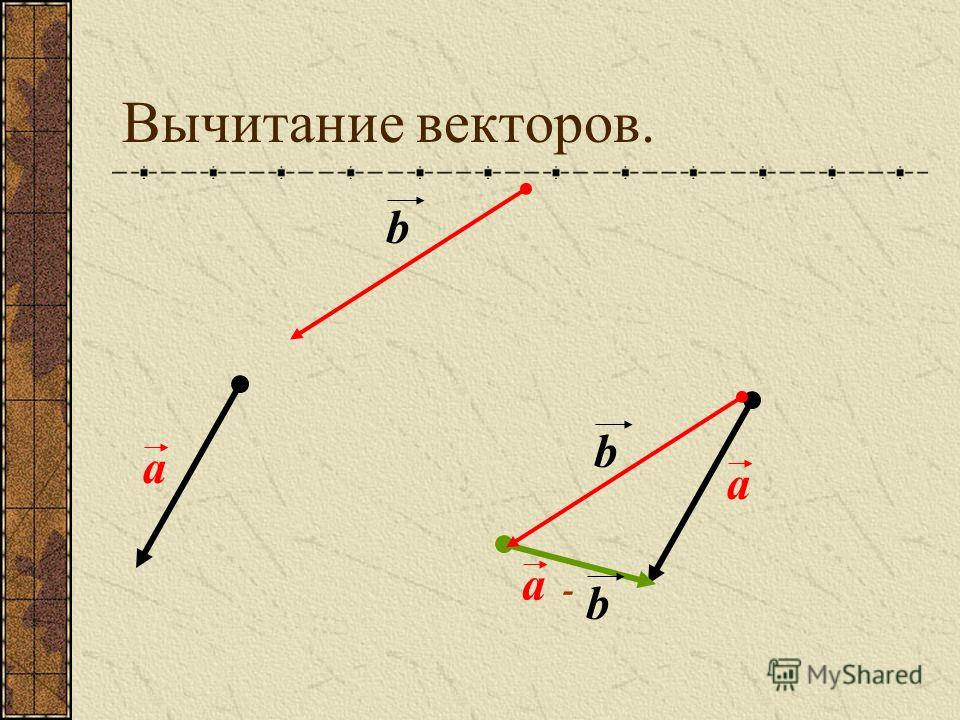 Процесс аналогичен, но с одной или двумя оговорками. Чтобы сложить или вычесть два вектора a и b добавить или вычесть соответствующие координаты вектора. То есть там, где a и b определяются следующим образом, здесь действуют правила сложения и вычитания.
Процесс аналогичен, но с одной или двумя оговорками. Чтобы сложить или вычесть два вектора a и b добавить или вычесть соответствующие координаты вектора. То есть там, где a и b определяются следующим образом, здесь действуют правила сложения и вычитания.
Обратите внимание, что, как и в случае со скалярами, сложение векторов не является коммутативным, но вычитание не является коммутативным. Графически мы добавляем два вектора a и b , позиционируя хвост b в начале a , а затем создание нового вектора, начинающегося с хвоста a и заканчивающегося в начале b . Координаты этого нового вектора определяются так же, как и раньше: размещением его хвоста в начале координат. Этот процесс проиллюстрирован ниже для векторов a = (4, 1) и b = (-1, 2).
Обратите внимание, что
Вычитание векторов происходит в основном по той же процедуре, что и сложение, за исключением того, что вычитаемый вектор «обратен» по направлению. Рассмотрим те же векторы a и b , что и выше, за исключением того, что мы будем вычислять a – b. (Обратите внимание, что это то же самое, что и , где – b имеет ту же длину, что и b , но имеет противоположное направление.)
Практическая задача: Выполните следующие векторные операции.
а. (3, 2) — (4, 5) б. (-1, 5) + (10, -6) в. (-1, 0) — (0, 0)
Решение: В каждом случае сложите или вычтите соответствующие координаты, чтобы найти результат. Один из полезных способов проверить свой ответ — нарисовать векторы на графике, показать сложение или вычитание и сравнить полученные результаты.
Один из полезных способов проверить свой ответ — нарисовать векторы на графике, показать сложение или вычитание и сравнить полученные результаты.
а. (-1, -3) б. (9, -1) в. (-1, 0)
Векторы
Если наша цель состоит в том, чтобы описать и понять движение, то просто движение вверх и вниз по линии не будет достаточно. Движение в реальном мире происходит в трех измерениях. Мы нужен способ описания движения такой сложный, как у пчелы или игрушечного вертолета. Мы делаем это с помощью векторов.Вначале я хочу, чтобы вы думали о векторах как о геометрических объектах. Модель для все векторы — смещение. Что-то начинается в одном месте, а заканчивается в другом. Один можно натянуть эластичный шнур между двумя точками в пространстве и отметить, какой конец был пункт назначения маленькой бумажной стрелкой. Вы можете видеть, что есть два аспекта этого смещение, которое мы называем вектором. Во-первых, у него есть длина или величина.
Во-вторых у него есть направление: что-то связанное с его углом. Первый пункт нашей повестки дня описание векторов состоит в том, чтобы выяснить, когда два вектора равны.
Давайте совершим еще одно маленькое путешествие той же длины, что и первое, но с другой стороны. направление. Если вы протянете шнур между начальным и конечным местоположениями, вы можете визуализировать два вектора. Они равны? Совершите еще одну поездку в том же направлении, что и первый, но теперь иду дальше. Это другой вектор. Он равен первому?
Когда векторы равны?
В обоих случаях, когда векторы имеют либо разные направления, либо разную длину, они не равны. Точно так же, если и направление, и длина различны, они не равны. Два вектора равны только тогда, когда оба направления и длины одинаковы. Два вектора могут быть равными, но в разных местах. Векторы, представленные параллельными прямыми, которые имеют одинаковые длины и направления равны.
Как добавлять векторы
Когда что-то совершает одно перемещение, затем другое, полное перемещение равно сумма двух индивидуальных.Пусть a представляют первую поездку, а b вторую поездку. общая поездка определяется путем выстраивания векторов, представляющих поездки, от кончика к хвосту. Положите хвост вторая поверх хвоста первой. Полное перемещение принимается за вектор от хвоста первого до кончика второго. Этот способ добавления векторов происходит естественно, когда мы говорим о перемещениях. Иногда другой вектор количества, такие как силы, должны быть добавлены. Тогда часто необходимо переместить один вектор чтобы его хвост совпадал с хвостом другого, потому что диаграммы сил обычно показывают силы всеми хвостами вместе на предмет, к которому приложена сила. Когда вектор не забудьте сохранить его длину и направление одинаковыми.
Коммутативность сложения
Сумма векторов может быть записана как c = a + b . Это означает, что хвост b находится на кончик a и хвост c находится на хвосте a , а кончик c находится на кончике b .Это также можно добавить a к b . Будет ли результат таким же, как при добавлении b к a ? Если смещение наше вектор модели, то результат будет одинаковым независимо от того, какое путешествие будет предпринято первым. Итак, мы потребует, чтобы векторы давали одинаковую сумму независимо от того, какой из них добавляется первым. а + б = б + а . Это свойство называется коммутативностью.
Не все величины, которым можно присвоить величину и направление, обладают этим свойством, и таким образом, эти некоммутативные величины не могут быть векторами. (Это клуб с высокие стандарты!) Например вращения вокруг оси имеют размер, угол поворота, и направление, направление оси вращения. Попробуйте сначала повернуть книгу на 90° примерно в вертикальная ось, а затем 90° относительно горизонтальной оси, идущей влево-вправо. Обратный порядок эти два поворота, и вы в конечном итоге с книгой в другом положении. В случае оборотов, a + b не равно b + a .На бумаге легко рисовать векторы, чтобы визуализировать процесс добавления векторов. Также следует попытаться представить векторы в трех измерениях. Все, что мы говорим о двумерные векторы, могут быть расширены до трех измерений без особых усилий. трудность. Представьте себе вертолет, выходящий из ангара. Рулит 100 м к северу, затем меняется направлении, рулит 200 м на восток и затем поднимается на 300 м. Общее водоизмещение Вертолет получается путем сложения всех трех векторов от кончика к хвосту, как мы делаем в двух измерениях.
Отрицательное значение вектора и вычитание
Всегда есть случай, когда человек начинает с поручения, а затем на полпути к цели. пункт назначения меняет свое мнение и возвращается домой. Два смещения, наружу и назад добавить к нулю. Второе смещение можно записать как отрицательное значение первая — имеет ту же величину, но противоположное направление. Первый этап поездки и , второй — a . Следовательно, a +(− и ) = 0,Определив отрицание вектора, происходит процесс вычитания естественно.
Чтобы вычесть b из a , просто найдите отрицательное число b , а затем прибавьте его к a .
Другой способ найти a b состоит в том, чтобы сложить хвосты a и b вместе и нарисовать вектор от наконечника b до наконечника a . Этот метод означает поиск вектора, который вы добавляете к b , чтобы получить a. (Это a = b + ( a − b ))
Попробуйте оба метода вычитания, и вы увидите, что они дают вектор с одинаковыми величину и направление. (Хотя они будут в разных местах после постройки, но это не имеет значения.) Вы можете выбрать любой метод вычитания, который кажется чтобы иметь больше смысла для вас.Умножение на скаляр
Иногда векторы умножаются или делятся на масштабный коэффициент. Например, если один растягивает эластичный шнур, представляющий вектор, в два раза больше его длины, сохраняя его направление то же самое, то исходный вектор умножается на два.Точно так же, если позволить ему сократиться до половина его длины делится на два или умножается на половину. что вам нравится. Обычные числа называются скалярами, чтобы отличать их от векторов. Вы были используя скаляры, так как вы научились считать.
Существуют также операции с двумя векторами, называемые умножением векторов. Эти мы постараюсь избегать в этом курсе, но вам, возможно, придется изучить их, если вы пойдете дальше курсы физики или математики. Такие величины, как перемещение, скорость, ускорение и сила, являются векторами. Масса и время являются скалярами, как и такие величины, как температура, влажность и энергия.
Векторы скорости и ускорения
Смещение — наш вектор-прототип. Скорость получается из смещения на разделив его на интервал времени. Результат деления вектора на скаляр является вектором. Аналогичным образом, деление вектора, представляющего разность скоростей, на временной интервал дает вектор — ускорение.Масса, скаляр, умножение ускорения, вектор, дает силу, другая векторная величина.
Чтобы увидеть, как скорости могут складываться, как векторы, я использую игрушечный трактор. Он сидит на длинном куске мясная бумага, покрывающая стол. Допустим, длина стола ориентирована с востока на запад. Ширина стола около 1 м. Если я направлю его через стол на север, он закроет 1 м дистанции за 10 секунд. Это скорость 0,1 м/с, на север. Второй раз я позволил трактор пересекает стол, я тяну разделочную бумагу со скоростью примерно 0,05 м/с, на восток, половина скорости трактора и под прямым углом к его курсу. На этот раз трактор пересекает бумаги прямо, а по отношению к столу пересекает под углом. Скорость трактора по отношению к таблице уже не 0,1 м/с, а векторная сумма 0,1 м/с, север и 0,5 м/с, вост. В сумме это, как показано на диаграмме, составляет 0,112 м/с на 27° к востоку от севера. Аналогичные навигационные задачи можно решать с ветром или течением под любым углом к горизонту.
курс судна, просто добавляя, если необходимо, графически векторы, представляющие скорость судна и скорость ветра. 9{-1}\left(\frac{v_{\rm trac}}{v_{\rm paper}}\right)$$
Навигация
Следующей проблемой было бы выяснить, как достичь желаемого направления, когда крест дует ветер. Например, предположим, что мы хотим лететь прямо на север на самолете, но дует встречный ветер с востока на запад. В каком направлении должен лететь самолет так что он в конечном итоге едет прямо на север? Допустим, боковой ветер дует со скоростью 40 км/ч и что самолет движется со скоростью 100 км/ч по отношению к воздуху. Решите задачу графически, как следует:
- Проведите прямую линию с севера на юг в нужном направлении.
- Нарисуйте вектор в масштабе, представляющий скорость ветра: 40 км/ч на запад с его вершиной на линии север-юг.
- Скорость самолета 100 км/ч, но мы не знаем, в каком направлении. Поместите вектор острием на хвост вектора скорости ветра и найти угол, при котором хвост вектор скорости самолета проходит по линии север-юг.
Теперь у вас есть вектор, 100 км/ч. длинной и указывающей в таком направлении, что при добавлении к скорости ветра получается полная скорость строго на север. 9{-1}\left(\frac{v_{\rm ветер}}{v_{\rm самолет}}\right)$$ В этом случае курс, который позволяет самолету лететь строго на север, составляет 23,6° к востоку от северной широты. а скорость самолета относительно земли 92 км/ч.
Ускорение
Ускорение также является вектором, поскольку представляет собой разность двух скоростей (вектор). разделить на интервал времени (скаляр). Результат — вектор. Закон Ньютона гласит, что сила равна массе, умноженной на ускорение. Масса скаляр, ускорение вектор; следовательно, сила также является вектором.Что удивительно в векторах ускорения и силы, так это то, что они не обязательно указать направление движения. Мы узнаем это, когда будем говорить о криволинейных движение и, в частности, движение по окружности.
Векторы
Векторы в R n
Определение и свойства
Мы предполагаем, что вы уже знакомы с векторами в R 2 и R 3 ,
так что вы увидите, что определение расширяется естественным образом.
А вектор в R N является n x 1 матрицей.
набор всех векторов в R n называется n-space .
Мы определяют сумму и разность двух векторов и произведение скаляра на вектор, просто поняв, что векторы — это матрицы.
Пример
Пусть
тогда
Недвижимость векторов
Векторов пользоваться следующими свойствами.
Если и , v и w являются векторами и c и д скаляры, затем
- у + v = v + u
- и + ( v + w ) = ( u + v ) + w
- Есть это 0 с х + 0 = 0 + х = х для всех векторов u .
- Для
любые и там
это -у с и + ( -и )
= 0 .

- с и является вектором в R n .
- с( и + v ) = c u + c v
- (с + d) u = c u + d u
- с(д и ) = (кд) u
- 1 и = у
доказательства всего этого исходят из свойств действительных чисел, поскольку дано определение сложения вычитания и скалярного умножения покомпонентно. Например, чтобы доказать число 6, у нас есть
[(c + d) u ] i = (c + d)[ u ] i = c[ u ] i + d[ u ] i = [c u ] i + [д и ] я
Скалярное произведение и длина
Так же, как мы определили скалярное произведение для векторов в R 2 и
Р 3 ,
аналогичным образом мы определяем скалярное произведение для двух векторов в более общем R n .
Определение
Пусть
тогда скалярное произведение (или скалярное произведение) u и против определяется
у . v = S и и в я
Определяем длину или звездной величины вектор как
А вектор представляет собой единичный вектор если он имеет длину один. Блок вектор в направлении u дается
и
|| и ||
и расстояние между и и против по
Расстояние = || и — v ||
угол q между двумя векторами определяется
у. v
потому что q
=
|| и || || v||
и и против ортогональны если
и . v = 0
Пример
Пусть
как в первом примере, то
у . v = (1)(-4) + (4)(2) + (3)(0) +
(2)(4) = 12
v = (1)(-4) + (4)(2) + (3)(0) +
(2)(4) = 12
и расстояние между u и v это
единичный вектор в направлении u равен
угол между u и v определяется
и
Недвижимость скалярного продукта
Далее мы даем некоторые основные свойства скалярного произведения.
Пусть и , против , и с быть векторами и c быть скаляром, тогда
- у . u > 0; у . и = 0 тогда и только тогда, когда и = 0,
- у . v = v . и .
- ( и + v ) . w = u . с + по сравнению с . с .

- (с и ) . v = u . (с по ) = c( u . v) .
Мы докажет свойство 2 и оставит остальные доказательства вам.
Доказательство из 2
у . v = S u i v i = S v i u i = v . у
Еще одно важное свойство под названием Коши-Шварца неравенство достаточно важно, чтобы стоять отдельно.
Неравенство Коши-Шварца
Если и и против являются векторами, тогда
| ты . в| < ||и|| ||в||
Если выполняется равенство, мы говорим, что u и против параллельны . Это произойдет, только если u кратно v .
Доказательство
Доказательство довольно сложное. Мы позволяем х
быть скаляром и отметить из свойства 1, что
Мы позволяем х
быть скаляром и отметить из свойства 1, что
0 < (x u + v ) . (х и + против )
= u . u x 2 + 2 u . v х + v . v
Поскольку скалярное произведение дает скаляр, приведенное выше уравнение является квадратным в Икс. Квадратичный всегда положительный имеет неположительный дискриминант. Отсюда
(2 u . v ) 2 — 4( u . u )( v . v ) < 0
деление на 4 дает
( и . v ) 2 — ( у . u )( v . v ) < 0
или
( u . v ) 2 < ( u . u )( v . против )
Получение квадратного корня из обеих сторон дает результат.
Последнее свойство скалярного произведения, которое мы обсудим, исходит из геометрия. Все мы знаем, что кратчайшее расстояние между двумя точками равно прямая линия. Если мы хотим отправиться из начала координат в точку P, быстрее идти по прямому пути, чем идти в точку Q сначала, а затем в P. Если мы выберем точку P быть вершиной вектора u + v, а Q — вершиной вектора ты, тогда мы иметь следующую схему.
Это приводит нас к неравенству треугольника.
Неравенство треугольника
Если и и против векторов, затем
|| и + против || < || и || + || против ||
Доказательство
Возьмем квадрат левой стороны
|| и + против || 2 = ( u + v ) . ( и + v ) = u .

 6 СТО
6 СТО
 Указанное свойство — очевидное.
Указанное свойство — очевидное. Электронный спин естественным образом возникает из релятивистской теории.
Электронный спин естественным образом возникает из релятивистской теории. В этом случае вычислительная установка очень похожа на обычные нерелятивистские вычисления с реальными «однокомпонентными» спиновыми орбиталями.К этой категории также относятся расчеты со свободными от спина эффективными потенциалами ядра, которые имитируют скалярные релятивистские эффекты на валентных оболочках.
В этом случае вычислительная установка очень похожа на обычные нерелятивистские вычисления с реальными «однокомпонентными» спиновыми орбиталями.К этой категории также относятся расчеты со свободными от спина эффективными потенциалами ядра, которые имитируют скалярные релятивистские эффекты на валентных оболочках.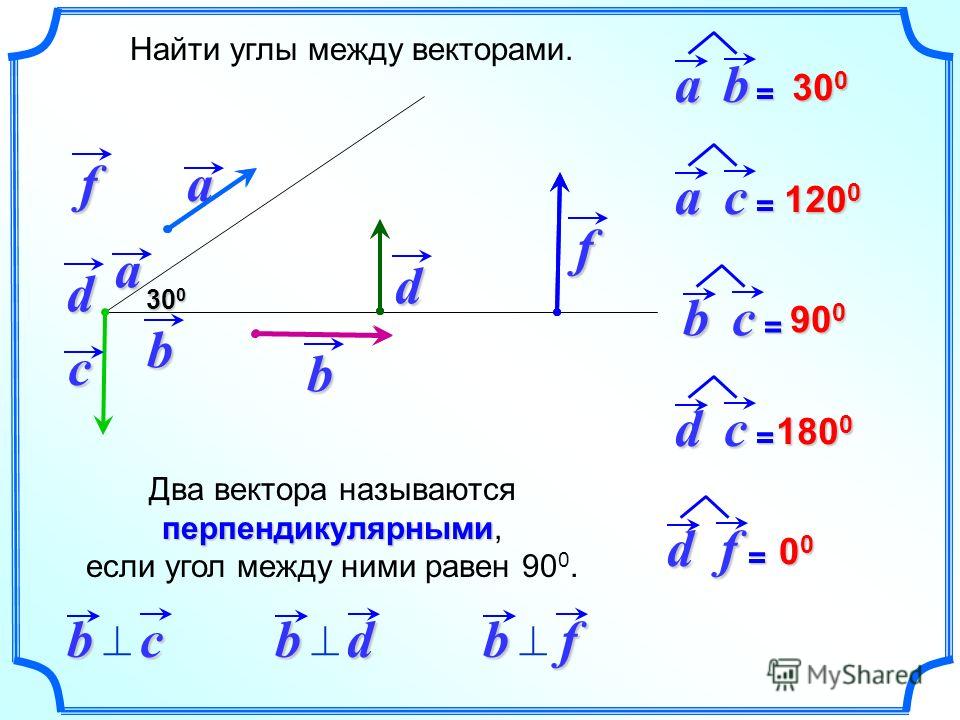 Затем они поворачивают налево и проходят 36 метров на запад. Какова величина их общего смещения?
Затем они поворачивают налево и проходят 36 метров на запад. Какова величина их общего смещения?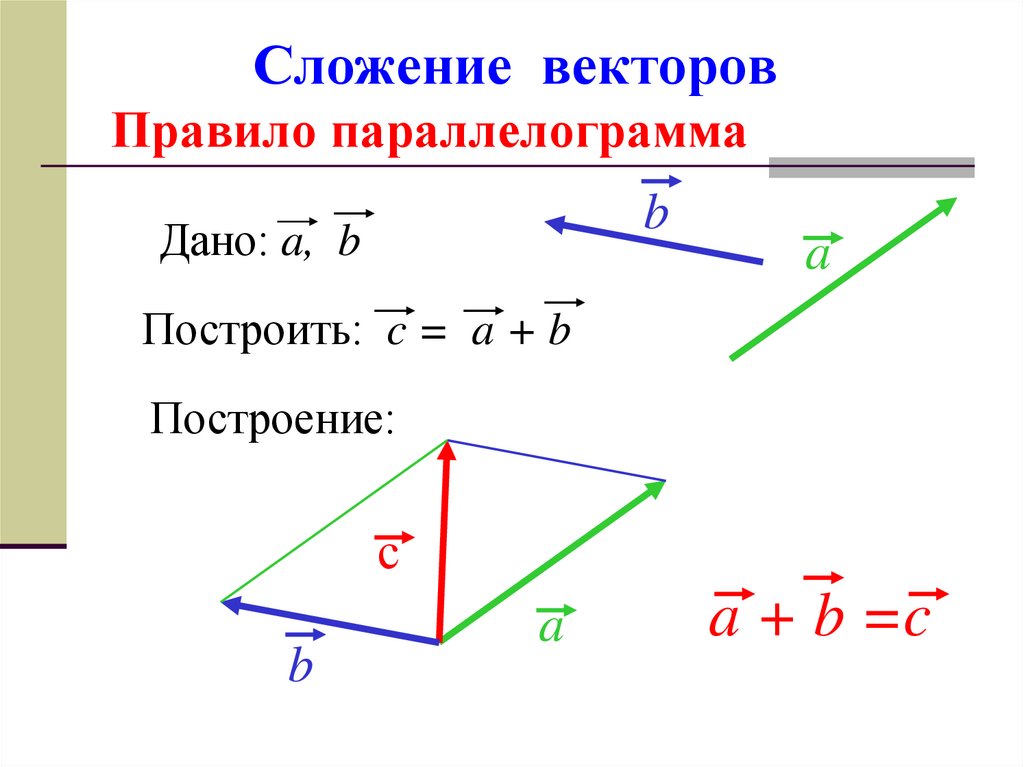 Определите величину и направление общего смещения Макса.
Определите величину и направление общего смещения Макса.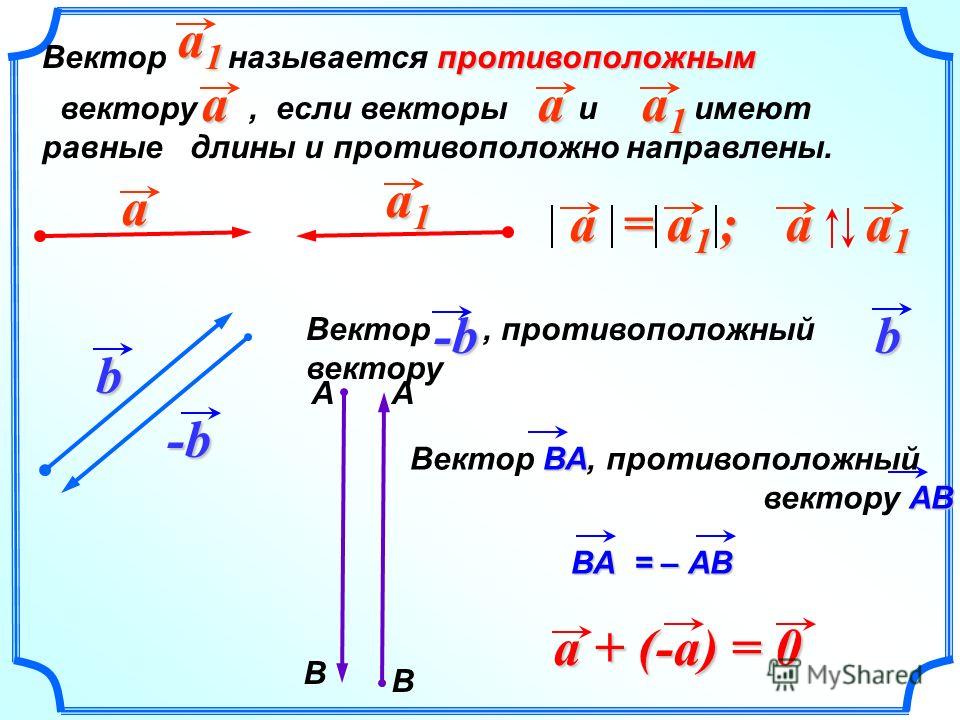
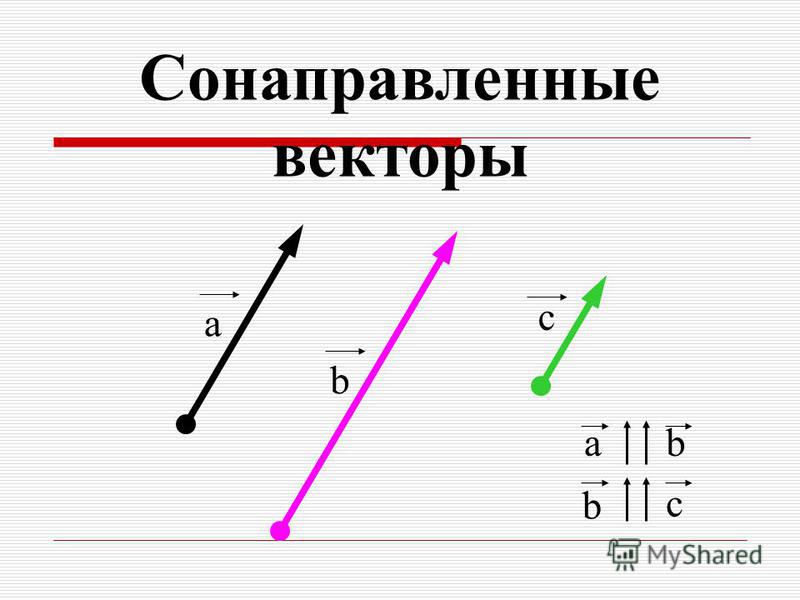
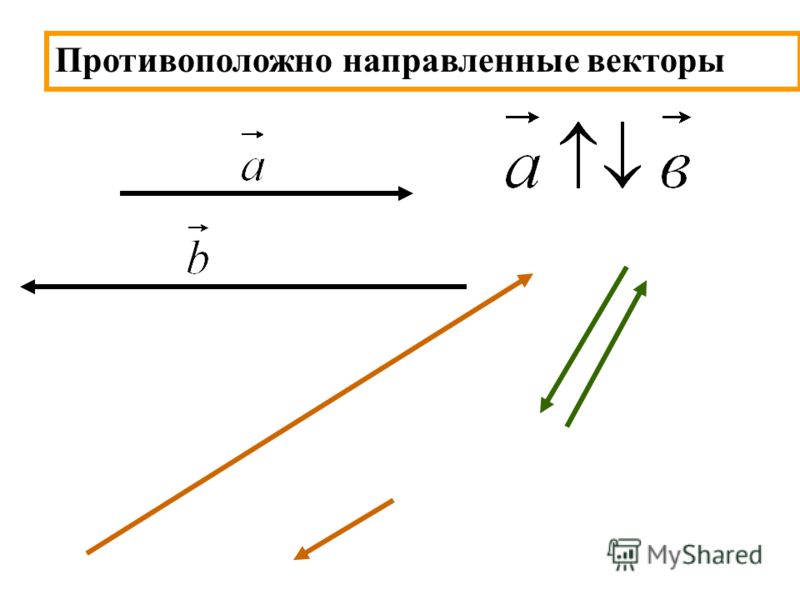 Т.е. мы не можем взять матрицу и наполнить ее случайными числами, так при несоблюдении условий матрица просто не будет являться матрицей поворота.
Т.е. мы не можем взять матрицу и наполнить ее случайными числами, так при несоблюдении условий матрица просто не будет являться матрицей поворота.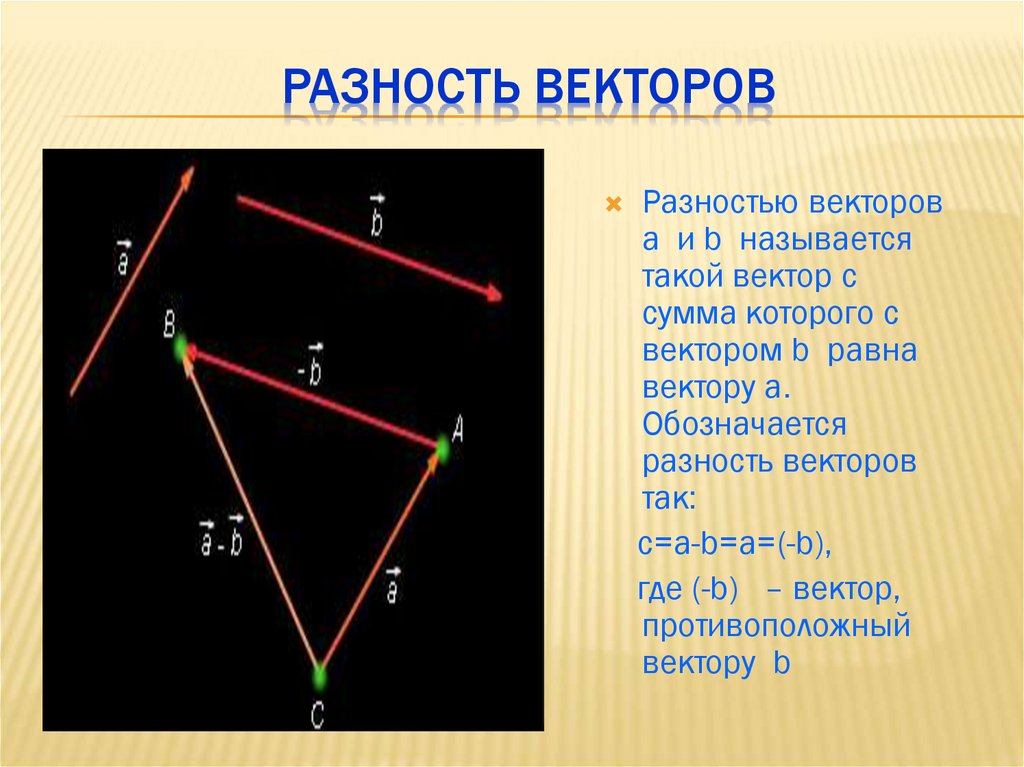
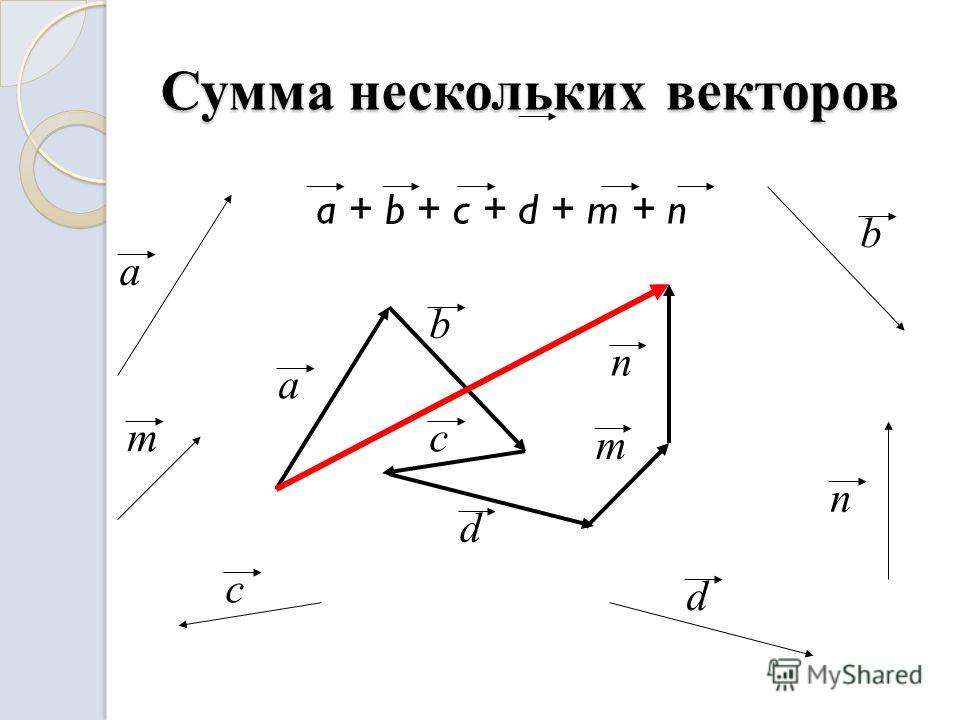 Результирующий вектор[latex]\textbf{R}[/latex] определяется таким образом, что[latex]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex]Величина и направление[latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно.
Результирующий вектор[latex]\textbf{R}[/latex] определяется таким образом, что[latex]\boldsymbol{\textbf{A}+\textbf{B}=\textbf{R}}.[/latex]Величина и направление[latex]\textbf{R}[/latex] затем определяются с помощью линейки и транспортира соответственно.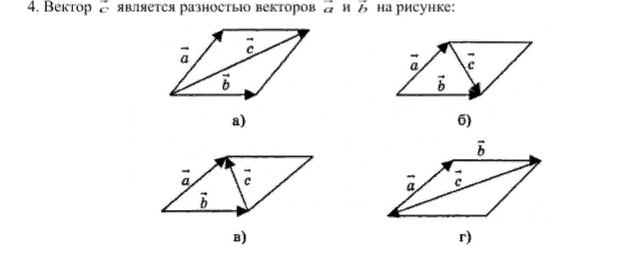 Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора.
Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора.